1 Introduction

One of the widely utilized vibration control techniques in engineering is passive vibration isolation. Nonlinear vibration isolation systems (VIS) have drawn a lot of interest from academics because they can provide superior vibration isolation properties than linear isolation systems [1,2,3,4,5,6,7]. Ibrahim [8] thoroughly evaluated the development and application of nonlinear vibration isolators under different external excitation. Lu and Chen [9] summarized the research and development of nonlinear vibration isolation theory and application recently and introduced in detail the VIS with high-static-low-dynamic stiffness and its coupling form with nonlinear damping. Ji et al. [10] reviewed the dynamics of mechanical metamaterials and origami structures along with some applications in vibration and sound control. Jing [11] reviewed the development of X-structure/mechanism, which can provide high-static ultra-low dynamic stiffness, geometric nonlinear damping, and low-static high-dynamic nonlinear inertia respectively or synchronously.

Many academics are interested in the nonlinear VIS with quasi-zero stiffness (QZS), which may accomplish broadband vibration isolation features in terms of vibration isolation with nonlinear stiffness. Scholars mainly study the different structural realization forms within nonlinear VIS with QZS and the improvement of vibration isolation performance. Among them, the implementation of negative stiffness structure mainly relies on pre-compressed mechanical springs, magnetic or electromagnetic springs, air springs, and so on. Scholars have conducted in-depth research on the VIS with QZS containing mechanical springs. Carrella et al. [12, 13] analyzed the statics characteristics of a nonlinear VIS with QZS, and derived the force transmissibility of its main resonance, where the QZS is composed of a vertical linear stiffness spring and dual oblique springs with linear stiffness. Zhou et al. [14] suggested a passive VIS with QZS by combining V-shaped lever, plate spring and cross-shaped structure vibration isolation platform, and discussed the static and dynamical mechanical properties of the VIS. Wen et al. [15] designed a nonlinear VIS with QZS by using a mechanism with six objective springs and a coil spring, and adopted the semi-active control strategy to expand the effective displacement range of the system. Shaw et al. [16] proposed a simple VIS with QZS, which consists of two adjusters with adjustable stiffness and static load. To achieve superior ultra-low frequency vibration isolation characteristics, Wang et al. [17] put two subordinate QZS mechanisms in parallel with a vertical connecting rod, and constructed a new ultra-low-frequency VIS with QZS. Suman et al. [18] used QZS to construct a nonlinear vehicle suspension, where the negative stiffness is constructed through the inclined spring. Chen et al. [19] utilize a positive stiffness configuration consisting of a pair of torsion springs, diagonal rods, and linear bearings, parallel to the negative stiffness provided by the diagonal rods connected to the linear spring in the direction perpendicular to motion, to expand the effective displacement range of QZS. Zhao et al. [20] presented a design of QZS isolator with three pairs of linear oblique springs. On the research of achieving QZS by magnetic springs [21,22,23] or electromagnetic springs [24,25,26], scholars have also made many attempts. Some scholars have also studied the use of air springs to construct quasi-zero stiffness [27, 28]. In addition, there are some hybrid springs to achieve negative stiffness for QZS [29, 30].

In order to achieve amplitude attenuation and reduce the force transmissibility of the VIS in the effective vibration isolation frequency band, the main methods currently used are dynamic vibration absorbers [31,32,33] and nonlinear damping for vibration reduction. In the research of nonlinear damping, Yan et al. [34] summarized the progress of nonlinear damping of electromagnetic mechanisms for QZS vibration isolators. Ma and Yan [35] performed theoretical modeling and parameter analyses on the mass and damping effects of the nonlinear electromagnetic shunt damping for the nonlinear VIS with permanent magnets. Huang et al. [36] investigated the transmissibility of a VIS with non-polynomial form restoring force and real-power exponent fractional damping under time-delayed cubic velocity feedback control. Ho et al. [37] designed of a single-degree-of-freedom nonlinear VIS with QZS and cubic damping, and explored its vibration isolation performance via the harmonic balance method. Dong et al. [38] designed a new QZS isolator coupled with geometric nonlinear damping, which is realized by semi-active electromagnetic shunt damping, and studied the low-frequency vibration isolation performance of the isolator subjected to base excitation. Gao and Teng [39] presented a hydropneumatic VIS with high-static low-dynamic stiffness to isolate the low-frequency disturbance vibration of heavy machinery. The designed VIS includes bellows structure, fluid damping and friction damping, and its vibration isolation transmissibility is studied via the harmonic balance method. According to Lv and Yao [40], damping coefficients have an impact on the PR's force and displacement transmissibility of the VIS. They also examined the vibration isolation performance of the VIS with nth power viscous damping under force excitation. Cheng et al. [41] analyzed the PR’s transmissibility of both the force and displacement of the QZS system with geometric nonlinear damping by applying the averaging method. Liu et al. [42] presented a QZS isolator with cam-roller structure and horizontal damping and discussed its vibration isolation performance for low-frequency excitation by using the harmonic balance method. Peng et al. [43] explored the impact of cubic nonlinear damping on the displacement transmissibility and force transmissibility of passive VIS by using the harmonic balance method. Lu et al. [44] assessed the vibration isolation performance of QZS isolators for single-stage and two-stage with nonlinear damping formed by horizontal linear damping with that of isolators with linear viscous damping only, and discovered that isolators with nonlinear damping have superior vibration isolation performance under high-frequency force excitation.

In a nonlinear VIS with QZS, the nonlinear stiffness introduced by the realization of the QZS may cause the secondary resonance of the system under single-frequency excitation. For example, Liu and Yu [45] studied the superharmonic resonance of the nonlinear VIS with QZS induced by force excitation. In addition, the engineering implementation of quadratic damping is relatively simple, and it can be realized by hydraulic damper under the assumption of ignoring the compressibility of the fluid [39, 46]. Moreover, the quadratic damping can effectively suppress resonance amplitude without deteriorating the absolute displacement transmissibility in the high-frequency region [39]. Therefore, this paper focuses on the transmission characteristics of displacement and force for the PR and 1/3 subharmonic resonance (SR) of nonlinear VIS with QZS caused by the base displacement excitation, and uses the quadratic damping to passively control the resonance of nonlinear VIS. In Sect. 2, the considered system model of nonlinear VIS with QZS and quadratic damping is exhibited. In Sect. 3, PR’s approximate analytical solution for the nonlinear VIS with QZS and quadratic damping is resolved through the averaging method. Moreover, this section includes a derivation of the stability conditions of the steady-state solution. The approximate analytical solution of SR of the nonlinear VIS with QZS and quadratic damping is obtained in Sect. 4, and the existence and stability conditions of the steady-state periodic solution of SR for the nonlinear VIS with QZS and quadratic damping are derived. In Sect. 5, the transmissibility of both force and relative displacement for PR and SR of the nonlinear VIS are deduced. In Sect. 6, the findings are compared with numerical solutions to validate the applicability of the approximate analytical solutions of the PR and SR. In Sect. 7, the amplitude attenuation and force isolation effect of QZS parameter and quadratic damping are analyzed.

2 System model

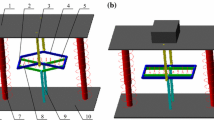
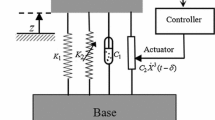
The considered nonlinear VIS with QZS and quadratic damping is displayed in Fig. 1. The quadratic damping is an important kind of damping caused by fluid or gas motion, which can be achieved through hydraulic dampers [47, 48]. In the system, m indicates the mass, c and c1 indicate the linear viscous damping coefficient and the quadratic damping coefficient, respectively, \(k\) and \(k_{1}\) represent the linear stiffness coefficients of the vertical spring and two horizontal springs, respectively. \(L_{{\text{h}}}\) represents the horizontal spring’s length when the mass is at the static balance position, and the original length of the horizontal spring is \(L_{0}\). \(x_{0} = A\cos \omega t\) is the displacement excitation from the base with amplitude A and angular frequency \(\omega\).

Fig. 1
figure 1

System model of nonlinear VIS

Full size image

Let \(y = x - x_{0}\), the elastic restoring force provided by two horizontal springs in the vertical direction can be represented as

$$f_{{\text{h}}} = 2k_{1} \left( {1 - \frac{{L_{0} }}{{\sqrt {L_{{\text{h}}}^{2} + y^{2} } }}} \right)y.$$
(1)

Accordingly, the motion equation of the nonlinear VIS with QZS and quadratic damping under base excitation is given by

$$m\ddot{x} = F_{{\text{r}}},$$
(2a)
$$F_{{\text{r}}} = - c\dot{y} - c_{1} \dot{y}^{2} {\text{sgn}} \left( {\dot{y}} \right) - ky - f_{{\text{h}}},$$
(2b)

where \(F_{{\text{r}}}\) is the resultant force transferred to the mass. And substitute \(x = y + x_{0}\) into Eq. (2a), which can be reformulated as

$$m\ddot{y} - F_{{\text{r}}} = mA\omega^{2} \cos \left( {\omega t} \right).$$
(3)

For \(L_{{\text{h}}} = 0.7L_{0}\) and \(y \le 0.2L_{0}\), Eq. (1) can be approximately expressed as [49]

$$f_{{\text{h}}} \approx 2k_{1} \left( {1 - \frac{{L_{0} }}{{L_{{\text{h}}} }}} \right)y + \frac{{L_{0} }}{{L_{{\text{h}}}^{3} }}k_{1} y^{3}.$$
(4)

Considering the following parameter transformation:\(\omega_{0}^{2} = {k \mathord{\left/ {\vphantom {k m}} \right. \kern-0pt} m}\), \(\varepsilon \kappa = {{2\left( {1 - {{L_{0} } \mathord{\left/ {\vphantom {{L_{0} } {L_{{\text{h}}} }}} \right. \kern-0pt} {L_{{\text{h}}} }}} \right)k_{1} } \mathord{\left/ {\vphantom {{2\left( {1 - {{L_{0} } \mathord{\left/ {\vphantom {{L_{0} } {L_{{\text{h}}} }}} \right. \kern-0pt} {L_{{\text{h}}} }}} \right)k_{1} } m}} \right. \kern-0pt} m}\), \(\varepsilon \mu = {c \mathord{\left/ {\vphantom {c m}} \right. \kern-0pt} m}\), \(\varepsilon \zeta = {{c_{{1}} } \mathord{\left/ {\vphantom {{c_{{1}} } m}} \right. \kern-0pt} m}\),\(\varepsilon \alpha = {{k_{1} L_{0} } \mathord{\left/ {\vphantom {{k_{1} L_{0} } {\left( {mL_{{\text{h}}}^{3} } \right)}}} \right. \kern-0pt} {\left( {mL_{{\text{h}}}^{3} } \right)}}\), \(\varepsilon g = A\omega^{2}\), and \(\varepsilon\)is small parameter, then Eq. (3) can be approximately expressed as.

$$\ddot{y} + \omega_{0}^{2} y = \varepsilon g\cos \left( {\omega t} \right) - \varepsilon \left[ {\kappa y + \mu \dot{y} + \zeta \dot{y}^{2} {\text{sgn}} \left( {\dot{y}} \right) + \alpha y^{3} } \right].$$
(5)

By introducing the small parameter for parameter transformation, Eq. (5) formally meets the solving requirements of the averaging method.

3 Primary resonance

Firstly, the PR’s approximate analytical solution of the nonlinear VIS under base excitation is solved through the averaging method, and the stability of the steady-state solution is judged.

3.1 Approximate analytical solution

Consider the PR of nonlinear VIS with QZS and quadratic damping. By introducing

$$\omega^{2} = \omega_{0}^{2} + \varepsilon \sigma_{1},$$
(6)

and Eq. (5) can be re-expressed as

$$\ddot{y} + \omega^{2} y = \varepsilon P_{11} + \varepsilon P_{12},$$
(7a)
$$P_{11} = g\cos \left( {\omega t} \right) + \left( {\sigma_{1} - \kappa } \right)y - \mu \dot{y} - \alpha y^{3},$$
(7b)
$$P_{12} = - \zeta \dot{y}^{2} {\text{sgn}} \left( {\dot{y}} \right).$$
(7c)

The approximate periodic solution of Eq. (7a) is assumed as

$$\left\{ \begin{gathered} y = a\cos \psi \hfill \\ \dot{y} = - a\omega \sin \psi \hfill \\ \end{gathered} \right..$$
(8)

In Eq. (8), \(\psi = \omega t + \theta\), \(a\) and \(\theta\) are slowly changing functions with respect to time.

By applying the averaging method, one could get

$$\dot{a} = - \frac{\varepsilon }{T\omega }\int_{0}^{T} {\left( {P_{11} + P_{12} } \right)\sin \psi {\text{d}}t},$$
(9a)
$$a\dot{\theta } = - \frac{\varepsilon }{T\omega }\int_{0}^{T} {\left( {P_{11} + P_{12} } \right)\cos \psi {\text{d}}t},$$
(9b)

where \(T = {{2{\uppi }} \mathord{\left/ {\vphantom {{2{\uppi }} \omega }} \right. \kern-0pt} \omega }\).

And the first part of Eq. (9) can be calculated as follows

$$\begin{aligned} \dot{a}_{1} = &\,- \frac{\varepsilon }{{2{\uppi }\omega }}\int_{0}^{{2{\uppi }}} {P_{11} \sin \psi {\text{d}}\psi } \hfill \\ =&\, - \frac{\varepsilon }{{2{\uppi }\omega }}\int_{0}^{{2{\uppi }}} {\left[ {g\cos \left( {\varphi - \theta } \right) + \left( {\sigma_{1} - \kappa } \right)a\cos \psi } \right.} \hfill \\ &\,\left. { + \,\mu a\omega \sin \psi - \alpha a^{3} \cos^{3} \psi } \right]\sin \psi {\text{d}}\psi \hfill \\ =&\, - \frac{\varepsilon \mu a}{2} - \frac{\varepsilon g}{{2\omega }}\sin \theta \hfill \\ \end{aligned},$$
(10a)
$$\begin{aligned} a\dot{\theta }_{1} = &\,- \frac{\varepsilon }{{2{\uppi }\omega }}\int_{0}^{{2{\uppi }}} {P_{11} \cos \psi {\text{d}}\psi } \hfill \\ =&\, \frac{{3\varepsilon \alpha a^{3} }}{8\omega } - \frac{{a\varepsilon \left( {\sigma_{1} - \kappa } \right)}}{2\omega } - \frac{\varepsilon g}{{2\omega }}\cos \theta \hfill \\ \end{aligned}.$$
(10b)

Assuming that \(a > 0\), the second part of Eq. (9) can be obtained as

$$\begin{aligned} \dot{a}_{2} = &\,- \frac{\varepsilon }{2\pi \omega }\int_{0}^{2\pi } {P_{12} \sin \psi d\psi } \hfill \\ =&\, - \frac{{\varepsilon \zeta a^{2} \omega }}{2\pi }\int_{0}^{\pi } {\left( {\sin^{2} \psi } \right)\sin \psi d\psi } \hfill \\ &\,- \frac{{\varepsilon \zeta a^{2} \omega }}{2\pi }\int_{\pi }^{2\pi } {\left( { - \sin^{2} \psi } \right)\sin \psi d\psi } \hfill \\ =&\, - \frac{{4\varepsilon \zeta a^{2} \omega }}{3\pi } \hfill \\ \end{aligned},$$
(11a)
$$a\dot{\theta }_{2} = - \frac{\varepsilon }{{2{\uppi }\omega }}\int_{0}^{{2{\uppi }}} {P_{12} \cos \psi {\text{d}}\psi } = 0.$$
(11b)

For \(a < 0\), a similar calculation can be carried out. Finally, the second part of Eq. (9) can be uniformly expressed as

$$\dot{a}_{2} = - \frac{{4\varepsilon \zeta a^{3} \omega }}{3\pi \left| a \right|},$$
(12a)
$$a\dot{\theta }_{2} = 0.$$
(12b)

Substituting the original variables of the nonlinear VIS into Eqs. (10) and (12) to replace the variables with \(\varepsilon\), and then substituting Eqs. (10) and (12) into Eq. (9), one could get

$$\dot{a} = - \frac{ca}{{2m}} - \frac{{4c_{1} a^{3} \omega }}{3\pi m\left| a \right|} - \frac{A\omega }{2}\sin \theta,$$
(13a)
$$a\dot{\theta } = - \frac{{a\left( {m\omega^{2} - k_{2} } \right)}}{2m\omega } + \frac{{3k_{3} a^{3} }}{8m\omega } - \frac{A\omega }{2}\cos \theta,$$
(13b)

where \(k_{2} = k + 2\left( {1 - {{L_{0} } \mathord{\left/ {\vphantom {{L_{0} } {L_{{\text{h}}} }}} \right. \kern-0pt} {L_{{\text{h}}} }}} \right)k_{1}\) and \(k_{3} = {{k_{1} L_{0} } \mathord{\left/ {\vphantom {{k_{1} L_{0} } {L_{{\text{h}}}^{3} }}} \right. \kern-0pt} {L_{{\text{h}}}^{3} }}\).

3.2 Steady-state solution and its stability

Let \(\dot{a} = 0\) and \(\dot{\theta } = 0\) in Eq. (13), the steady-state motion equation for the PR of the nonlinear VIS with QZS and quadratic damping can be acquired as

$$c\overline{a}\omega + \frac{{8c_{1} \overline{a}^{3} \omega^{2} }}{{3\pi \left| {\overline{a}} \right|}} = - mA\omega^{2} \sin \overline{\theta },$$
(14a)
$$\overline{a}Q_{1} = - mA\omega^{2} \cos \overline{\theta },$$
(14b)

where \(Q_{1} = \left[ {m\omega^{2} - k_{2} - \frac{{3k_{3} \overline{a}^{2} }}{4}} \right]\). And \(\overline{a}\) is the amplitude of steady-state solution, \(\overline{\theta }\) is the phase of steady-state solution of PR.

According to Eq. (14), the amplitude-frequency equation and phase-frequency equation of the PR for the nonlinear VIS with QZS and quadratic damping can be obtained as

$$\overline{a}^{2} Q_{1}^{2} + \overline{a}^{2} \omega^{2} \left( {c + \frac{{8c_{1} \overline{a}^{2} \omega }}{{3\pi \left| {\overline{a}} \right|}}} \right)^{2} = m^{2} A^{2} \omega^{4},$$
(15a)
$$\tan \overline{\theta } = \frac{{c\omega + \frac{{8c_{1} \overline{a}^{2} \omega^{2} }}{{3\pi \left| {\overline{a}} \right|}}}}{{Q_{1} }}.$$
(15b)

From Eq. (15a), the equivalent natural frequency of the system is 0, as a result of the QZS makes \(k_{2} { = }0\) by introducing negative linear stiffness. The quadratic damping affects the amplitude-frequency response of the PR of the system, which is related to the excitation frequency and amplitude, and the larger the amplitude, the larger the damping value.

Next, analyze the stability condition of the steady-state periodic solution of the nonlinear VIS with QZS and quadratic damping. Let \(a = \overline{a} + \Delta a\) and \(\theta = \overline{\theta } + \Delta \theta\), and substitute them into Eq. (13). And the linearized equations can be gained as

$$\frac{{{\text{d}}\Delta a}}{{{\text{d}}t}} = - \left( {\frac{c}{2m} + \frac{{8c_{1} \overline{a}^{2} \omega }}{3\pi m\left| \overline{a} \right|}} \right)\Delta a - \frac{{A\omega \cos \overline{\theta }}}{2}\Delta \theta,$$
(16a)
$$\frac{{{\text{d}}\Delta \theta }}{{{\text{d}}t}} = \left( {\frac{{3k_{3} \overline{a}}}{4m\omega } + \frac{A\omega }{{2\overline{a}^{2} }}\cos \overline{\theta }} \right)\Delta a + \frac{{A\omega \sin \overline{\theta }}}{{2\overline{a}}}\Delta \theta.$$
(16b)

By applying Eq. (14) to eliminate the trigonometric functions in Eq. (16), the characteristic equation of the PR of the nonlinear VIS is obtained as

$$\det \left[ \begin{gathered} - \frac{c}{2m} - 2S_{2} - \lambda \begin{array}{*{20}c} {} \\ \end{array} \begin{array}{*{20}c} {} \\ \end{array} \frac{{\overline{a}Q_{1} }}{2m\omega } \hfill \\ S_{1} - \frac{{Q_{1} }}{{2m\omega \overline{a}}}\begin{array}{*{20}c} {} \\ \end{array} \begin{array}{*{20}c} {} \\ \end{array} - \frac{c}{2m} - S_{2} - \lambda \hfill \\ \end{gathered} \right] = 0,$$
(17)

where \(S_{1} = \frac{{3k_{3} \overline{a}}}{4m\omega }\), \(S_{2} = \frac{{4c_{1} \overline{a}^{2} \omega }}{{3\pi m\left| {\overline{a}} \right|}}\).

Expanding the characteristic determinant in Eq. (17), it can be re-expressed as

$$\lambda^{2} + \left( {\frac{c}{m} + 3S_{2} } \right)\lambda + \frac{{c^{2} }}{{4m^{2} }} + 2S_{2}^{2} + \frac{{3cS_{2} }}{2m} - \frac{{S_{1} \overline{a}Q_{1} }}{2m\omega } + \frac{{Q_{1}^{2} }}{{4m^{2} \omega^{2} }} = 0.$$
(18)

Because of \({c \mathord{\left/ {\vphantom {c m}} \right. \kern-0pt} m} + 3S_{2} > 0\), the necessary and sufficient condition for asymptotic stability of PR of the nonlinear VIS with QZS and quadratic damping will yield to

$$\frac{{c^{2} }}{{4m^{2} }} + 2S_{2}^{2} + \frac{{3cS_{2} }}{2m} - \frac{{S_{1} \overline{a}Q_{1} }}{2m\omega } + \frac{{Q_{1}^{2} }}{{4m^{2} \omega^{2} }} > 0.$$
(19)

4 Subharmonic resonance

By taking the SR response of the nonlinear VIS with QZS and quadratic damping as an increment, the approximate analytical solution for the SR of the system is computed through the averaging method, and the existence and stability conditions of the SR steady-state solution are presented.

4.1 Approximate analytical solution

In order to calculate the SR response, the incremental equation of nonlinear VIS is obtained based on the PR response of the system under base excitation. Let

$$\left\{ \begin{gathered} y = a\cos \psi + u \hfill \\ \dot{y} = - a\omega_{1} \sin \psi + \dot{u} \hfill \\ \end{gathered} \right.,$$
(20)

and substitute Eq. (20) into Eq. (5). Simplifying it by using the approximate periodic solution of the PR for the nonlinear VIS under base excitation and eliminating its same order harmonic terms, it can be transformed into

$$\ddot{u} + \frac{1}{9}\omega^{2} u = \varepsilon \left[ {P_{21} + P_{22} } \right],$$
(21a)
$$P_{21} = \sigma_{2} u - \kappa u - \mu \dot{u} - \alpha \left( {a\cos \psi + u} \right)^{3} + \frac{3}{4}\alpha a^{3} \cos \psi,$$
(21b)
$$\begin{aligned} P_{22} = &\,- \zeta \left( { - a\omega \sin \psi + \dot{u}} \right)^{2} {\text{sgn}} \left( { - a\omega \sin \psi + \dot{u}} \right) \hfill \\ &\,+ \zeta \left( { - a\omega \sin \psi } \right)^{2} {\text{sgn}} \left( { - a\omega \sin \psi } \right) \hfill \\ \end{aligned},$$
(21c)

where \(\varepsilon \sigma_{2} = {{\omega^{2} } \mathord{\left/ {\vphantom {{\omega^{2} } 9}} \right. \kern-0pt} 9} - \omega_{0}^{2}\).

The periodic solution of Eq. (21a) is assumed as

$$u = b\cos \varphi,$$
(22a)
$$\dot{u} = - \frac{b\omega }{3}\sin \varphi,$$
(22b)

where \(\varphi = \frac{\omega }{3}t + \vartheta\).

On the basis of averaging method, one could get

$$\dot{b} = - \frac{3\varepsilon }{{T_{1} \omega }}\int_{0}^{{T_{1} }} {\left( {P_{21} + P_{22} } \right)\sin \varphi {\text{d}}t},$$
(23a)
$$b\dot{\vartheta } = - \frac{3\varepsilon }{{T_{1} \omega }}\int_{0}^{{T_{1} }} {\left( {P_{21} + P_{22} } \right)\cos \varphi {\text{d}}t},$$
(23b)

where \(T_{1} = {{6{\uppi }} \mathord{\left/ {\vphantom {{6{\uppi }} \omega }} \right. \kern-0pt} \omega }\).

For the first part of Eq. (23), one could have

$$\begin{aligned} \dot{b}_{1} =&\, - \frac{3\varepsilon }{{2{\uppi }\omega }}\int_{0}^{{2{\uppi }}} {P_{21} \sin \varphi {\text{d}}\varphi } \hfill \\ = &\,- \frac{3\varepsilon }{{2{\uppi }\omega }}\int_{0}^{{2{\uppi }}} {\left\{ {\left( {\sigma_{2} - \kappa } \right)b\cos \varphi + \frac{1}{3}\mu b\omega \sin \varphi } \right.} \hfill \\ &\,- \alpha \left[ {a\cos \left( {3\varphi - 3\vartheta + \theta } \right) + b\cos \varphi } \right]^{3} \hfill \\ &\,\left. { + \,\frac{3}{4}\alpha a^{3} \cos \left( {3\varphi - 3\vartheta + \theta } \right)} \right\}\sin \varphi {\text{d}}\varphi \hfill \\ = &\,- \frac{\varepsilon \mu b}{2} - \frac{{9\varepsilon \alpha ab^{2} }}{8\omega }\sin \left( {\theta - 3\vartheta } \right) \hfill \\ \end{aligned},$$
(24a)
$$\begin{aligned} b\dot{\vartheta }_{1} = &\,- \frac{3\varepsilon }{{2{\uppi }\omega }}\int_{0}^{{2{\uppi }}} {P_{21} \cos \varphi {\text{d}}\varphi } \hfill \\ =&\, \frac{9\varepsilon \alpha b}{{8\omega }}\left( {2a^{2} + b^{2} } \right) - \frac{{3b\varepsilon \left( {\sigma_{2} - \kappa } \right)}}{2\omega } \hfill \\ &\,+ \frac{{9\varepsilon \alpha ab^{2} }}{8\omega }\cos \left( {\theta - 3\vartheta } \right) \hfill \\ \end{aligned}.$$
(24b)

To solve the second part of Eq. (23), expand the sign function using the first-order Taylor formula [50]:

$${\text{sgn}} \left( {z + \Delta z} \right) = {\text{sgn}} \left( z \right) + 2\delta \left( z \right)\Delta z ,$$
(25)

where \(\delta (z)\) represents the Dirac delta function. It should be noted that only when \(\Delta z \to 0\), the error of the first-order Taylor formula expansion can tend to 0.

When \(\left| {\dot{u}} \right|\) is small relative to \(\left| {a\omega \sin \varphi } \right|\), according to Eq. (25), \(P_{22}\) can be approximated as

$$\begin{aligned} P_{22} =&\, - \zeta \left[ { - 2\dot{u}a\omega \sin \psi + \dot{u}^{2} } \right]{\text{sgn}} \left( { - a\omega \sin \psi } \right) \hfill \\ &\,- 2\zeta \left( { - a\omega \sin \psi + \dot{u}} \right)^{2} \delta \left( { - a\omega \sin \psi } \right)\dot{u} \hfill \\ \end{aligned}.$$
(26)

By using the Fourier series expansion, the Dirac function in Eq. (26) can be expanded as.

$$\delta \left( { - a\omega \sin \psi } \right) = v_{0} + \sum\limits_{n = 1}^{\infty } {(v_{n} \cos n\psi + w_{n} \sin n\psi )},$$
(27)

where \(v_{0}\), \(v_{n}\) and \(w_{n}\) are the Fourier coefficients. And the period of this function is \(T_{2} = {{\uppi } \mathord{\left/ {\vphantom {{\uppi } \omega }} \right. \kern-0pt} \omega }\).

The Fourier coefficients in Eq. (27) can be calculated as follows

$$\begin{aligned} v_{0} = &\,\frac{1}{{T_{2} }}\int_{{ - T_{2} /2}}^{{T_{2} /2}} {\delta ( - a\omega \sin \psi ){\text{d}}t} \hfill \\ = &\,\frac{1}{{{\uppi }\left| a \right|\omega }}\int_{{ - {{\uppi } \mathord{\left/ {\vphantom {{\uppi } 2}} \right. \kern-0pt} 2}}}^{{{{\uppi } \mathord{\left/ {\vphantom {{\uppi } 2}} \right. \kern-0pt} 2}}} {\delta (\sin \psi ){\text{d}}\psi } \hfill \\ =&\, \frac{1}{{{\uppi }\left| a \right|\omega }}\int_{ - 1}^{1} {\frac{\delta (\sin \psi )}{{\cos \psi }}{\text{dsin}}\psi } \hfill \\ =&\, \frac{1}{{{\uppi }\left| a \right|\omega }} \hfill \\ \end{aligned},$$
(28a)
$$\begin{aligned} v_{n} =&\, \frac{2}{{T_{2} }}\int_{{ - T_{2} /2}}^{{T_{2} /2}} {\delta ( - a\omega \sin \psi )\cos n\psi {\text{d}}t} \hfill \\ =&\, \frac{2}{{{\uppi }\left| a \right|\omega }}\int_{ - 1}^{1} {\frac{\delta (\sin \psi )}{{\cos \psi }}\cos n\psi {\text{d}}\sin \psi } \hfill \\ =&\,\frac{2}{{{\uppi }\left| a \right|\omega }} \hfill \\ \end{aligned},$$
(28b)
$$\begin{gathered} w_{n} = \frac{2}{{T_{2} }}\int_{{ - T_{2} /2}}^{{T_{2} /2}} {\delta ( - a\omega \sin \psi )\sin n\psi {\text{d}}t} = 0 \end{gathered}.$$
(28c)

Therefore, Eq. (27) can be re-expressed as

$$\delta \left( { - a\omega \sin \psi } \right) = \frac{1}{{{\uppi }\left| a \right|\omega }} + \frac{2}{{{\uppi }\left| a \right|\omega }}\sum\limits_{n = 1}^{\infty } {\cos \left( {n\psi } \right)}.$$
(29)

Similarly, the sign function in Eq. (26) can be expanded by Fourier series, which is

$${\text{sgn}} \left( { - a\omega \sin \psi } \right) = - \frac{4a}{{\left( {2n{ + }1} \right){\uppi }\left| a \right|}}\sum\limits_{n = 0}^{\infty } {\sin \left[ {\left( {2n{ + }1} \right)\psi } \right]}.$$
(30)

Substituting Eq. (29) and Eq. (30) into Eq. (26), and calculating the second part of Eq. (23), we can get

$$\begin{aligned} \dot{b}_{2} = &\,- \frac{3\varepsilon }{{2\pi \omega }}\int_{0}^{2\pi } {P_{22} \sin \varphi d\varphi } \hfill \\ =&\, - \frac{{2\varepsilon \zeta a^{2} b\omega }}{\pi \left| a \right|} - \frac{{\varepsilon \zeta b^{3} \omega }}{12\pi \left| a \right|} + \frac{{\varepsilon \zeta ab^{2} \omega }}{6\pi \left| a \right|}\cos \left( {\theta - 3\vartheta } \right) \hfill \\ \end{aligned},$$
(31a)
$$\begin{aligned} b\dot{\vartheta }_{2} = &\,- \frac{3\varepsilon }{{2\pi \omega }}\int_{0}^{2\pi } {P_{22} \cos \varphi d\varphi } \hfill \\ = &\,\frac{{\varepsilon \zeta ab^{2} \omega }}{6\pi \left| a \right|}\sin \left( {\theta - 3\vartheta } \right) \hfill \\ \end{aligned}.$$
(31b)

Combining Eqs. (24) and (31), and replacing the variables with \(\varepsilon\) by the original system parameters of the nonlinear VIS with QZS and quadratic damping, one could have

$$\begin{gathered} \dot{b} = - \frac{cb}{{2m}} - \frac{{9ab^{2} k_{3} }}{8m\omega }\sin \left( {\theta - 3\vartheta } \right) - \frac{{2c_{1} a^{2} b\omega }}{\pi m\left| a \right|} - \frac{{c_{1} b^{3} \omega }}{12\pi m\left| a \right|} + \frac{{c_{1} ab^{2} \omega }}{6\pi m\left| a \right|}\cos \left( {\theta - 3\vartheta } \right) \hfill \\ \end{gathered},$$
(32a)
$$\begin{gathered} b\dot{\vartheta } = \frac{{9bk_{3} \left( {2a^{2} + b^{2} } \right)}}{8m\omega } - \frac{{3b\left( {{{m\omega^{2} } \mathord{\left/ {\vphantom {{m\omega^{2} } 9}} \right. \kern-0pt} 9} - k_{2} } \right)}}{2m\omega } + \frac{{9ab^{2} k_{3} }}{8m\omega }\cos \left( {\theta - 3\vartheta } \right) + \frac{{c_{1} ab^{2} \omega }}{6\pi m\left| a \right|}\sin \left( {\theta - 3\vartheta } \right) \hfill \\ \end{gathered}.$$
(32b)

4.2 Steady-state solution of SR

The steady-state motion amplitude and phase of the SR of the nonlinear VIS with QZS and quadratic damping are denoted as \(\overline{b}\) and \(\overline{\vartheta }\), respectively. Let \(\dot{b} = 0\) and \(\dot{\vartheta } = 0\) in Eq. (32), the steady-state equations of motion of the nonlinear VIS are obtained as

$$Q_{2} = \overline{b}\sqrt {\left( {\frac{{9\overline{a}k_{3} }}{4}} \right)^{2} + \left( {\frac{{c_{1} \omega^{2} }}{3\pi }} \right)^{2} } \cos \left( {\overline{\theta } - 3\overline{\vartheta } + \beta } \right),$$
(33a)
$$Q_{3} = \overline{b}\sqrt {\left( {\frac{{9\overline{a}k_{3} }}{4}} \right)^{2} + \left( {\frac{{c_{1} \omega^{2} }}{3\pi }} \right)^{2} } \sin \left( {\overline{\theta } - 3\overline{\vartheta } + \beta } \right).$$
(33b)

where \(Q_{2} = c\omega + \frac{{4c_{1} \overline{a}^{2} \omega^{2} }}{{\pi \left| {\overline{a}} \right|}} + \frac{{c_{1} \overline{b}^{2} \omega^{2} }}{{6\pi \left| {\overline{a}} \right|}}\), \(Q_{3} = 3\left( {\frac{{m\omega^{2} }}{9} - k_{2} } \right) - \frac{{9k_{3} \left( {2\overline{a}^{2} + \overline{b}^{2} } \right)}}{4}\),

\(\beta = \arctan {{\left( {27k_{3} {\uppi }\left| {\overline{a}} \right|} \right)} \mathord{\left/ {\vphantom {{\left( {27k_{3} {\uppi }\left| {\overline{a}} \right|} \right)} {\left( {4c_{1} \omega^{2} } \right)}}} \right. \kern-0pt} {\left( {4c_{1} \omega^{2} } \right)}}\).

Accordingly, the amplitude-frequency and phase-frequency response equation for the SR of the nonlinear VIS can be expressed as

$$Q_{2}^{2} + Q_{3}^{2} = \overline{b}^{2} \left( {\frac{{81\overline{a}^{2} k_{3}^{2} }}{16} + \frac{{c_{1}^{2} \omega^{4} }}{{9{\uppi }^{2} }}} \right),$$
(34a)
$$\tan \left( {\overline{\theta } - 3\overline{\vartheta } + \beta } \right) = \frac{{Q_{3} }}{{Q_{2} }}.$$
(34b)

From Eq. (34a), the role of the quadratic damping on the SR amplitude-frequency response is related to the excitation frequency and the resonance amplitude.

Therefore, the approximate analytical solution of the SR of the nonlinear VIS with QZS and quadratic damping is rewritten as

$$y = \overline{a}\cos \left( {\omega t + \overline{\theta }} \right) + \overline{b}\cos \left( {{{\omega t} \mathord{\left/ {\vphantom {{\omega t} 3}} \right. \kern-0pt} 3} + \overline{\vartheta }} \right),$$
(35)

where, the values of \(\overline{a}\) and \(\overline{\theta }\) can be solved according to Eq. (15), while the values of \(\overline{b}\) and \(\overline{\vartheta }\) can be determined by Eq. (34).

4.3 Existence conditions and stability conditions

Firstly, the existence conditions of SR steady-state solution of nonlinear VIS are deduced. Let \(z = \overline{b}^{2}\), the amplitude-frequency equation of the nonlinear VIS is rearranged to

$$A_{1} z^{2} + B_{1} z + C_{1} = 0,$$
(36)

where \(A_{1} = \frac{{c_{1}^{2} \omega^{4} }}{{36\pi^{2} \overline{a}^{2} }} + \frac{{81k_{3}^{2} }}{16}\), \(B_{1} = \frac{{c_{1} c\omega^{3} }}{{3\pi \left| {\overline{a}} \right|}} + \frac{{11c_{1}^{2} \omega^{4} }}{{9\pi^{2} }} - \frac{{3k_{3} }}{2}\left( {m\omega^{2} - 9k_{2} } \right) + \frac{{243k_{3}^{2} \overline{a}^{2} }}{16}\), \(C_{1} = \left( {c\omega + \frac{{4c_{1} \overline{a}^{2} \omega^{2} }}{{\pi \left| {\overline{a}} \right|}}} \right)^{2} + 9\left( {\frac{{m\omega^{2} }}{9} - k_{2} - \frac{{3k_{3} \overline{a}^{2} }}{2}} \right)^{2}\).

According to the conditions for the existence of positive real roots of univariate quadratic algebraic equations, it can be obtained that the necessary conditions for the existence of SR of the nonlinear VIS with QZS and quadratic damping is

$$\frac{3}{2}\left( {m\omega^{2} - 9k_{2} } \right) > \frac{{c_{1} c\omega^{3} }}{{3\pi \left| {\overline{a}} \right|k_{3} }} + \frac{{11c_{1}^{2} \omega^{4} }}{{9\pi^{2} k_{3} }} + \frac{{243k_{3} \overline{a}^{2} }}{16},$$
(37a)
$$\begin{aligned} \left[ {\frac{{c_{1} \omega^{2} }}{{9\pi \overline{a}}}\left( {m\omega^{2} - 9k_{2} } \right) + \frac{{9\pi \overline{a}}}{{2c_{1} \omega^{2} }}Q_{4} } \right]^{2} < = &\,\frac{{81\pi^{2} \overline{a}^{2} Q_{4}^{2} }}{{4c_{1}^{2} \omega^{4} }} + \left( {\frac{{c_{1} c\omega^{3} }}{{3\pi \left| {\overline{a}} \right|}} + \frac{{11c_{1}^{2} \omega^{4} }}{{9\pi^{2} }} + \frac{{243k_{3}^{2} \overline{a}^{2} }}{16}} \right)^{2} \hfill \\ &\,- \left( {\frac{{c_{1}^{2} \omega^{4} }}{{9\pi^{2} \overline{a}^{2} }} + \frac{{81k_{3}^{2} }}{4}} \right)\left( {c\omega + \frac{{4c_{1} \overline{a}^{2} \omega^{2} }}{{\pi \left| {\overline{a}} \right|}}} \right)^{2} - \frac{{9k_{3}^{2} c_{1}^{2} \omega^{4} \overline{a}^{2} }}{{4\pi^{2} }} - \frac{{6561k_{3}^{4} \overline{a}^{4} }}{16} \hfill \\ \end{aligned},$$
(37b)

where \(Q_{4} = \frac{{8c_{1}^{2} \omega^{4} k_{3} }}{{3{\uppi }^{2} }} + \frac{{k_{3} c_{1} c\omega^{3} }}{{{\uppi }\left| {\overline{a}} \right|}} - \frac{{243k_{3}^{3} \overline{a}^{2} }}{16}\). It can be seen from Eq. (37) that when there is SR in the nonlinear VIS with QZS and quadratic damping, it only exists in a certain excitation frequency range.

Then, investigate the stability of the steady-state solution of SR for the nonlinear VIS. Substituting \(b = \overline{b} + \Delta b\) and \(\vartheta = \overline{\vartheta } + \Delta \vartheta\) into Eq. (32), the linearized equations can be attained as

$$\frac{{{\text{d}}\Delta b}}{{{\text{d}}t}} = U_{1} \Delta b + U_{2} \Delta \vartheta,$$
(38a)
$$\frac{{{\text{d}}\Delta \vartheta }}{{{\text{d}}t}} = U_{3} \Delta b + U_{4} \Delta \vartheta,$$
(39b)

where \(U_{1} = - \left( {\frac{c}{2m} + \frac{{2c_{1} \overline{a}^{2} \omega }}{{{\uppi }m\left| {\overline{a}} \right|}} + \frac{{c_{1} \overline{b}^{2} \omega }}{{4{\uppi }m\left| {\overline{a}} \right|}}} \right) - \frac{{9\overline{a}\overline{b}k_{3} }}{4m\omega }\sin \left( {\overline{\theta } - 3\overline{\vartheta }} \right) + \frac{{c_{1} \overline{a}\overline{b}\omega }}{{3{\uppi }m\left| {\overline{a}} \right|}}\cos \left( {\overline{\theta } - 3\overline{\vartheta }} \right)\),

\(U_{2} = \frac{{27\overline{a}\overline{b}^{2} k_{3} }}{8m\omega }\cos \left( {\overline{\theta } - 3\overline{\vartheta }} \right) + \frac{{c_{1} \overline{a}\overline{b}^{2} \omega }}{{2\pi m\left| {\overline{a}} \right|}}\sin \left( {\overline{\theta } - 3\overline{\vartheta }} \right)\),

\(U_{3} = \frac{{9k_{3} \overline{b}}}{4m\omega } + \frac{{9\overline{a}k_{3} }}{8m\omega }\cos \left( {\overline{\theta } - 3\overline{\vartheta }} \right) + \frac{{c_{1} \overline{a}\omega }}{{6\pi m\left| {\overline{a}} \right|}}\sin \left( {\overline{\theta } - 3\overline{\vartheta }} \right)\),

\(U_{4} = \frac{{27\overline{a}\overline{b}k_{3} }}{8m\omega }\sin \left( {\overline{\theta } - 3\overline{\vartheta }} \right) - \frac{{c_{1} \overline{a}\overline{b}\omega }}{{2\pi m\left| {\overline{a}} \right|}}\cos \left( {\overline{\theta } - 3\overline{\vartheta }} \right)\).

The characteristic equation of the SR of nonlinear VIS is further obtained as

$$\det \left[ \begin{array}{l@{\quad}l} U_{1} -\lambda_{2} & U_{2} \hfill \\ U_{3} & U_{4} - \lambda_{2} \hfill \\ \end{array} \right] = 0.$$
(39)

By expanding the characteristic determinant, the characteristic equation of SR of nonlinear VIS with QZS and quadratic damping can be rewritten as

$$\lambda_{2}^{2} - \left( {U_{1} + U_{4} } \right)\lambda_{2} + U_{1} U_{4} - U_{2} U_{3} = 0,$$
(40)

where \(U_{1} + U_{4} = - \frac{c}{m} - \frac{{4c_{1} \overline{a}^{2} \omega }}{{\pi m\left| {\overline{a}} \right|}} - \frac{{c_{1} \overline{b}^{2} \omega }}{{3\pi m\left| {\overline{a}} \right|}}\).

Since \(- \left( {U_{1} + U_{4} } \right) > 0\), it can be obtained that the asymptotic stability condition of the steady-state solution for the SR of the nonlinear VIS with QZS and quadratic damping is

$$U_{1} U_{4} - U_{2} U_{3} > 0.$$
(41)

5 Transmissibility of primary resonance and subharmonic resonance

On the basis of the dynamic motion equation of the nonlinear VIS displayed in Fig. 1, the resultant force transmitted from the foundation to the mass block is \(F_{{\text{r}}}\). Therefore, the force transmissibility and relative displacement transmissibility of the nonlinear VIS exposed to the base excitation can be obtained by

$$\eta_{f} = \frac{{\left\| {F_{r} } \right\|}}{{\left\| {mA\omega^{2} \cos \left( {\omega t} \right)} \right\|}},$$
(42a)
$$\eta_{r} = \frac{\left\| y \right\|}{{\left\| {A\cos \left( {\omega t} \right)} \right\|}},$$
(42b)

where \(\| {\,}\|\) represents modulus of vector.

According to the approximate periodic solution of the PR, the force transmissibility of the PR for the nonlinear VIS with QZS and quadratic damping exposed to the base excitation is represented as

$$\eta_{1} = \frac{{\left\| {F_{r1} } \right\|}}{{mA\omega^{2} }},$$
(43a)
$$\begin{aligned} F_{r1} = &\,- c\overline{a}\omega \sin \overline{\psi } + c_{1} \overline{a}^{2} \omega^{2} \sin^{2} \overline{\psi }{\text{sgn}} \left( { - \overline{a}\omega \sin \overline{\psi }} \right) \hfill \\ &\,+ \left[ {k + 2k_{1} \left( {1 - \frac{{L_{0} }}{{L_{h} }}} \right)} \right]\overline{a}\cos \overline{\psi } + \frac{{L_{0} }}{{L_{h}^{3} }}k_{1} \overline{a}^{3} \cos^{3} \overline{\psi } \hfill \\ \end{aligned},$$
(43b)

where \(\overline{\psi } = \omega t + \overline{\theta }\).

Correspondingly, PR’s relative displacement transmissibility for the nonlinear VIS subjected to the base excitation can be given as

$$\eta_{r1} = \frac{{\left| {\overline{a}} \right|}}{A}.$$
(44)

According to the approximate analytical solution of the SR, the force transmissibility of the SR for the nonlinear VIS with QZS and quadratic damping subjected to the base excitation can be obtained as

$$\eta_{2} = \frac{{\left\| {F_{r2} } \right\|}}{{mA\omega^{2} }},$$
(45a)
$$\begin{aligned} F_{r2} = &\,c\left[ { - \overline{a}\omega \sin \overline{\psi } - \frac{{\overline{b}\omega }}{3}\sin \overline{\varphi }} \right] + c_{1} \left( { - \overline{a}\omega \sin \overline{\psi } - \frac{{\overline{b}\omega }}{3}\sin \overline{\varphi }} \right)^{2} {\text{sgn}} \left[ { - \overline{a}\omega \sin \overline{\psi } - \frac{{\overline{b}\omega }}{3}\sin \overline{\varphi }} \right] \hfill \\ &\,+ \left[ {k + 2k_{1} \left( {1 - \frac{{L_{0} }}{{L_{h} }}} \right)} \right]\left( {\overline{a}\cos \overline{\psi } + \overline{b}\cos \overline{\varphi }} \right) + \frac{{L_{0} }}{{L_{h}^{3} }}k_{1} \left( {\overline{a}\cos \overline{\psi } + \overline{b}\cos \overline{\varphi }} \right)^{3} \hfill \\ \end{aligned},$$
(45b)

where \(\overline{\varphi } = {{\omega t} \mathord{\left/ {\vphantom {{\omega t} 3}} \right. \kern-0pt} 3} + \overline{\vartheta }\).

Correspondingly, the relative displacement transmissibility of the SR of the nonlinear VIS subjected to the base excitation is given as

$$\eta_{r2} = \frac{{\left\| {\overline{a}\cos \overline{\psi } + \overline{b}\cos \overline{\varphi }} \right\|}}{A}.$$
(46)

6 Verification by numerical solutions

A set of parameters of the nonlinear VIS are chosen as follows: m = 30 kg, c = 50 N•s/m, c1 = 50 N•(s/m)2, k1 = 500 kN/m, L0 = 0.2 m, \(k = 2\left( {{{L_{0} } \mathord{\left/ {\vphantom {{L_{0} } {L_{{\text{h}}} - 1}}} \right. \kern-0pt} {L_{{\text{h}}} - 1}}} \right)k_{1} = {42}{\text{.857}}\) kN/m, \({{L_{{\text{h}}} } \mathord{\left/ {\vphantom {{L_{{\text{h}}} } {L_{0} = 0.7}}} \right. \kern-0pt} {L_{0} = 0.7}}\), A = 0.005 m. According to Eq. (3), the amplitude-frequency response curve of the nonlinear VIS with QZS and quadratic damping is drawn by the Runge–Kutta method, which is displayed in Fig. 2. The abscissa in the figure represents the excitation to natural frequency ratio of the original linear system, namely \(\gamma = {\omega \mathord{\left/ {\vphantom {\omega {\omega_{0} }}} \right. \kern-0pt} {\omega_{0} }}\). According to Eq. (15) and Eq. (35), the amplitude-frequency curves of the nonlinear VIS can also be obtained by the approximate analytical solutions of the PR and SR, separately. And according to the stability conditions of PR and SR, the stable solutions and unstable solutions are obtained respectively. According to Fig. 2, the approximate analytical solution and the numerical solution yielded similar amplitude-frequency response curves for the PR and SR of the nonlinear VIS. However, when the amplitude is greater than \(0.2L_{0}\), the deviation of approximate analytical will gradually increase compared with the numerical solution. There is an obvious multi-solution phenomenon in the PR response region of the nonlinear VIS with QZS and quadratic damping. And the starting frequency of the SR is shifted to the PR region. The numerical solution also reveals that the system contains other lower order subharmonic resonance except for 1/3 subharmonic resonance. The SR of the nonlinear VIS with QZS and quadratic damping only exists in a certain excitation frequency range, which is consistent with the conclusion of Eq. (37).

Fig. 2
figure 2

Comparison of amplitude-frequency response curves

Full size image

According to Eq. (3), the force transmissibility curve and the relative displacement transmissibility curve of the nonlinear VIS transmitted from the foundation to the mass block are drawn by the numerical solution, which are shown in Figs. 3 and 4, individually. According to Eqs. (43) and (45), the approximate analytical solution is used to draw the force transmissibility curves of the PR and SR of the system, which are shown in Fig. 3. According to Eqs. (44) and (46), the relative displacement transmissibility curves of the PR and SR of the nonlinear VIS are plotted via the approximate analytical solution, which are displayed in Fig. 4. As demonstrated in Fig. 3, there is also a strong agreement between the approximative analytical and numerical solutions for the force transmissibility of the PR and SR of the nonlinear VIS with QZS and quadratic damping. The occurrence of SR will make the force isolation effect of the nonlinear VIS worse, and even cause the system to lose the force isolation effect. As shown in Fig. 4, it can be seen that the approximate analytical and numerical solutions of the relative displacement transmissibility of the nonlinear VIS are also well fitted. Moreover, the relative displacement transmissibility curve and amplitude-frequency response curve of the system have the same variation law, only the ordinate becomes the ratio of the amplitude response of steady state to the excitation displacement.

Fig. 3
figure 3

Comparison of force transmissibility

Full size image
Fig. 4
figure 4

Comparison of relative displacement transmissibility

Full size image

7 Analysis of vibration control effect

Based on the approximate analytical solutions, the impacts of the QZS parameter and quadratic damping on the force transmissibility and relative displacement transmissibility for the nonlinear VIS are analyzed.

7.1 Effect of QZS parameter

When the quadratic damping coefficient c1 = 50 N•(s/m)2, the PR force transmissibility curve and the relative displacement transmissibility curve of the original linear system (represented as L0 = 0 m) are drawn respectively according to the approximate analytical solutions, which are shown in Fig. 5. At the same time, the force transmissibility curves and relative displacement transmissibility curves of the PR and SR of the nonlinear VIS with QZS and quadratic damping are obtained analytically, for the original lengths of the QZS horizontal springs are L0 = 0.2 m, L0 = 0.4 m and L0 = 1 m respectively. As shown in Fig. 5a, the initial vibration isolation frequency of the system is significantly reduced due to the introduction of QZS. On the contrast with the original linear system, the nonlinear VIS with QZS and quadratic damping can obtain a smaller initial vibration isolation frequency even when the system has subharmonic resonance. As the original length of the QZS horizontal spring increases, the maximum force transmissibility decreases gradually. When the original length of the horizontal spring increases to a certain extent, the nonlinear VIS with QZS can effectively isolate the force caused by the given base excitation begin with a frequency close to 0. From Fig. 5b, it could be found that the introduction of QZS significantly reduces the relative displacement transmissibility of the VIS at high frequencies, but increases the relative displacement transmissibility at low frequencies. With the increase of the original length of the QZS horizontal spring, the PR peak gradually decreases, and the SR region also gradually decreases until it disappears. When the original length of the horizontal spring increases to a certain extent, the maximum relative displacement transmissibility of the nonlinear VIS with QZS subjected to the base excitation can be reduced to 1. At this time, it means that the nonlinear VIS does not produce resonance phenomena.

Fig. 5
figure 5

Effects of different QZS parameters (crosses for the unstable solutions)

Full size image

7.2 Effect of quadratic damping

Set the original length of the QZS horizontal spring to L0 = 0.4 m, the force transmissibility curves and relative displacement transmissibility curves of the PR and SR for the nonlinear VIS with QZS can be drawn according to the approximate analytical solution for the quadratic damping coefficients c1 = 0 N•(s/m)2, c1 = 50 N•(s/m)2 and c1 = 100 N•(s/m)2 respectively, as shown in Fig. 6. To make the comparison more clearer, only the stable solutions of the nonlinear VIS with QZS are shown in the figures. From Fig. 6a it can be found that, with the increase of the quadratic damping coefficient, the initial vibration isolation frequency of the nonlinear VIS with QZS gradually decreases, and the force transmissibility of the nonlinear VIS within the effective vibration isolation frequency range will increase slightly. As shown in Fig. 6b, with the increase of the quadratic damping coefficient, not only the SR of the nonlinear VIS with QZS can be eliminated, but also the maximum relative displacement transmissibility of the PR can be effectively reduced. Furthermore, the increase of quadratic damping will not worsen the relative displacement transmissibility in the high-frequency region.

Fig. 6
figure 6

Effects of different quadratic damping

Full size image

To better illustrate the elimination of 1/3 subharmonic resonance, the bifurcation diagram of the relative displacement transmissibility with quadratic damping is drawn for the frequency ratios \(\gamma = 0.12\) and \(\gamma = 0.22\), as shown in Fig. 7. It can be seen that as the quadratic damping increases, both the 1/3 subharmonic resonance branch in the middle and the upper branch of the primary resonance will gradually disappear.

Fig. 7
figure 7

Bifurcation of relative displacement transmissibility with quadratic damping (red circle denotes primary resonance, blue circle denotes subharmonic resonance, black solid line denotes the corresponding unstable solution)

Full size image

In order to compare the roles of linear damping and nonlinear damping, the original length of the QZS horizontal spring is set to L0 = 0.4 m and the base excitation amplitude is set to A = 0.005 m. When the system includes only linear damping for c = 150 N•s/m and c1 = 0 N•(s/m)2, and the system includes quadratic damping for c = 50 N•s/m and c1 = 100 N•(s/m)2, the force transmissibility curve and the relative displacement transmissibility curve of the nonlinear VIS with QZS can be obtained, as shown in Fig. 8. It can be found that, when the excitation amplitude is too small to cause resonance in the nonlinear VIS with QZS, only using linear damping can obtain lower initial vibration isolation frequency and better relative displacement transmissibility than quadratic damping. The quadratic damping can achieve lower force transmissibility at low frequencies in the effective isolation frequency range, but the force transmissibility of a nonlinear VIS with QZS and quadratic damping at high frequencies is slightly larger than that of only linear damping.

Fig. 8
figure 8

Comparison of linear damping and quadratic damping for A = 0.005 m (crosses for the unstable solutions)

Full size image

Increase the amplitude of the base excitation to A = 0.012 m, and keep other parameters unchanged. Again, the approximate analytical solutions are used to draw the transmissibility curves for the force and relative displacement of the nonlinear VIS with QZS and with or without quadratic damping, as shown in Fig. 9. Only the stable solutions of the nonlinear VIS are shown in Fig. 9. It can be found that, when the nonlinear VIS with QZS is subjected to a large amplitude base excitation sufficient to cause significant resonance response, utilizing quadratic damping can obtain a lower beginning vibration isolation frequency and better relative displacement transmissibility than linear damping. Moreover, compared with only linear damping with the same coefficient value, the nonlinear VIS with QZS and quadratic damping can obtain better amplitude suppression effect and smaller subharmonic resonance region when the system has significant resonance response. Therefore, considering the uncertainty of the foundation excitation amplitude, it is necessary to introduce quadratic damping in order to obtain a lower initial isolation frequency.

Fig. 9
figure 9

Comparison of linear damping and quadratic damping for A = 0.012 m

Full size image

8 Conclusions

The PR and SR of the nonlinear VIS with QZS and quadratic damping are investigated through the averaging method. It can be inferred from the amplitude-frequency response equation of the nonlinear VIS that the resonance amplitude and excitation frequency have a role in how the quadratic damping affects the amplitude-frequency response characteristics of PR or SR. Additionally, amplitude suppression caused by quadratic damping is also more pronounced the bigger the steady-state amplitude is. The approximate analytical solution's stability is assessed, and the SR of the nonlinear VIS with QZS and quadratic damping's existence conditions are deduced. It is proved that when the SR of the system exists, it only exists in a certain excitation frequency range. By comparing with the amplitude-frequency response curve, the transmissibility curves for force and relative displacement of the nonlinear VIS obtained by the numerical solution, the correctness of the approximate analytical solutions of the PR and SR is verified.

By comparing the transmissibility for the force and relative displacement of nonlinear VIS with different parameters, it can be found that for a given base excitation, the larger the QZS horizontal spring’s original length results in a smaller PR peak value and smaller force transmissibility. The SR can also be eliminated when the horizontal spring's initial length is increased to a certain level. At the same time, when the quadratic damping is increased to a certain extent, the SR of the nonlinear VIS with QZS can also be eliminated. When the quadratic damping coefficient has the same value as the linear damping coefficient, the nonlinear VIS with QZS and quadratic damping can achieve better amplitude suppression effect and smaller initial isolation frequency in the presence of significant resonance response. While the nonlinear VIS with QZS using linear damping alone can achieve good isolation effects without resonance response.