1 Introduction

A passive isolation system in general contains mass, spring, and damping elements. The mass and spring stiffness determine the natural frequency of the system. Damping causes energy dissipation and has a secondary effect on natural frequency [1–4]. It is known that traditional viscous damping cannot give satisfactory result over resonant region and non-resonant regions of frequencies simultaneously. To overcome this dilemma, novel damping mechanism has been developed, such as the nonlinear damping and the three-parameter isolator (also named as Zener isolation model, elastically coupled damping, elastically coupled damping) [5, 6]. For the former, research has been proposed for velocity-nth power damping \(c\left| {\dot{x}} \right| ^{n-1}\dot{x}\) [7–17]; nonlinear anti-symmetric damping [18, 19] (which is essentially still the velocity-nth power damping); velocity- and displacement-dependent damping \(c\left| x \right| ^{m}\left| {\dot{x}} \right| ^{n-1}\dot{x}\) [1, 20–24]; displacement-dependent damping [25]. Other types of nonlinear damping are dry friction damping [26–28] (for Coulomb friction, the velocity exponent \(n=0\)), hysteretic type nonlinearity [29], fast parametric nonlinear viscous damping and delayed nonlinear damping [30, 31]. In addition, nonlinearity in both stiffness and damping terms have been investigated when nonlinear stiffness is introduced in the isolator [32, 33]. Scholars, such as Ivana Kovacic, Lang and Peng etc., have made enormous contribution in this area and promote the understanding for different kinds of nonlinear damping.

For velocity-nth power damping, it is demonstrated that small velocity exponent \(n<1\) is desirable for base excitation to lower the resonant peak and meanwhile keeping the rise in the displacement transmissibility over the high-frequency range is relatively small. A power of the velocity greater than unity can be beneficial to force transmissibility but be detrimental for base motion transmissibility [12]. The damping can lead to better absolute displacement transmissibility than traditional linear damping if \(n<1\). Among velocity-nth power damping, the cubic nonlinearity has drawn particular attentions [10, 11, 13, 22], both pure cubic nonlinearity and combined viscous and cubic order nonlinear damping were investigated [22]. It has been discovered that pure cubic damping has a detrimental effect on absolute displacement transmissibility in the isolation region and the absolute displacement transmissibility is higher tending to unity (0 dB, i.e., base excitation and the isolated mass move almost together) as the excitation frequency increases [10]. The unexpected disadvantage becomes more pronounced for larger excitation amplitudes [34]. This detrimental effect is one of the undergoing difficulties to overcome. Furthermore, the influence of the pure cubic damping has been found to be dependent on the amplitude of the excitation input [13], which is an intrinsic feature of a nonlinear system. However, for engineering applications, it is desirable that the isolation performance is predictable and stable without being influenced by the amplitude of the excitation input.

On one hand, it is difficult to obtain a remarkable improvement for the isolation performance by changing velocity exponent n only. Furthermore, extremely low or high exponent n is hard to achieve by the hydraulic dampers whose velocity exponent usually ranges from 0.2 to 1.95. On the other hand, the influence of the actual excitation amplitude on the damping effect also deserves considerable attention. The frequency and amplitude characteristics of the actual excitation usually exhibit low-frequency-large-amplitude and high-frequency-small-amplitude; i.e., the amplitude is large at low frequencies, and small at high frequencies. To explain this, a counter example for velocity-nth damping is given to illustrate that a small value of velocity exponent n may not bring high isolation performance in actual applications. Coulomb friction damping, which was widely used in the suspension for earlier vehicles, could supply comfortable ride feeling on rough road, but it would lock the suspension on smooth surface road and give a poor ride feeling [35]. This is because the large-amplitude excitation on rough road leads to small damping effect at the isolation region, but the small amplitude excitation on the smooth road has large damping.

For the two reasons listed above, velocity- and displacement-dependent damping (VDD) has been advanced and it shows potential advantages in vibration isolation. To realize this kind of nonlinear damping, novel forms of dampers or absorbers have been proposed, such as hydraulic damper generated by valves [1], hydraulic shock membrane absorber [20, 36–40], clearance variable damper [41], horizontally installed linear damping [21–23] and so on. Among these forms, the engine mount with amplitude- and frequency-sensitive hydraulic shock membrane absorber has appealed many researchers’ attention for its high performance [20]. Golnaraghi and Jazar [4] employed a VDD damping force to describe the flow resistance of the decoupler. Deshpande et al. [36] considered the stiffness and damping coefficient of the mount as piecewise and introduced a numerical procedure to obtain the optimal stiffness and damping parameters. Jazar et al. [38, 39] and Christopherson et al. [40, 42] also contributed a lot to this mount. The horizontal installed linear damping was a newly developed damper with VDD damping [21], which shows better performance than that with traditional viscous linear damping. This kind of damping has received attention after it was creatively proposed. Sun et al. [23] studied a more generalized case where the isolator has horizontally installed velocity-nth power damper for a two DOF system with free boundary condition and suggested that the velocity exponent is chosen as \(0<n<2\). Xiao et al. [22] investigated a nonlinear damping, which includes a kind of VDD damping which has been investigated by Tang and Brennan, and it turns out that this kind of damping can make isolators produce better isolation performance under both force excitation and base displacement excitation.

For the theoretical aspect of nonlinear damping, a lot of methods have been developed, such as the multiple scale perturbation method [4], the Harmonic balance method (HBM) [13], the method of averaging [10, 11, 24, 29], the elliptic averaging method [8], the elliptic Krylov–Bogoliubov method [43], the Output Frequency Response Functions (OFRFs) [15, 33, 44], the Ritz–Galerkin method [12] and so on.

For the experimental aspect of nonlinear damping, there are emerging studies concerning this aspect. One method for realizing nonlinear damping is achieved by active actuators with a suitable control algorithm. For example, a cubic damping characteristic was implemented by using an electromagnetic shaker with a simple nonlinear velocity feedback control [34]. The nonlinear damping was reproduced using a simple velocity feedback for both harmonic and broadband base excitation. The theoretical results showing the detrimental effects of cubic damping were confirmed experimentally. An ideal nonlinear damping characteristic was realized by using a magnetorheological MR damper with feedback control [45, 46]. The cubic viscous nonlinear damping was also implemented by employing active vibration isolation test rig composed of electrodynamic shakers [47], in which the theoretical findings about cubic damping and the selection of the cubic damping characteristic parameters required to achieve a desired performance were experimentally verified. These solutions can be used to implement any desired damping characteristics and have a great potential to be applied in engineering practice.

In this article, a more generalized kind of VDD damping than that investigated in Ref. [21, 23] is proposed. Through this extension, new characteristics of proposed VDD damping are discovered. Firstly, displacement transmissibility of the proposed damping is analyzed by using the averaging method. Results show that for certain conditions this kind of damping has some advantages in improving the transmissibility both at resonance and in the high frequencies. Then, the case that the proposed damping is combined with a linear damping together is considered. The condition that the isolation performance is independent on the amplitude of the input excitation is obtained by different combinations of displacement and velocity exponents. An experiment is carried out by using active actuator with suitable velocity feedback control algorithm. Some theoretical findings have been validated. It is demonstrated that VDD nonlinear damping will give a possible solution to reduce the disadvantageous of cubic damping under base displacement excitation, of which one is the detrimental effect in the isolation region and the other is that the isolation performance is dependent on the excitation amplitude.

2 Dynamic modeling of SDOF isolation system with VDD damping

2.1 Proposed VDD damping model

For traditional velocity-nth power damping, the damping is assumed to be related to the relative velocity by a power law and the damping force is usually described by [9]

$$\begin{aligned} f(t)=c_n \left| {\dot{\delta }} \right| ^{n-1}\dot{\delta } \end{aligned}$$
(1)

where \(\delta \) is the relative displacement; ‘dot’ is the relative velocity across the damper; n is the exponent of the power law damping which ranges from 1 to 3; \(c_{n}\) is the dimensional damping coefficient assumed to be constant. When \(n=1\), the damping is linear viscous damping and other cases are considered as nonlinear. In most applications, the damping coefficient \(c_{n}\) and the velocity exponent n are constants. The VDD damping is expressed as follows [21, 23]

$$\begin{aligned} f(t)=c_n \left| {\delta ^{n+1}\dot{\delta }^{n-1}} \right| \dot{\delta } \end{aligned}$$
(2)

The damping in Eq. (2) shows better isolation performance, however, its displacement exponent is dependent on the velocity exponent. Hence, a more general kind of VDD damping force is proposed as follows

$$\begin{aligned} f(t)=c_n \left| {\delta ^{q}\dot{\delta }^{n-1}} \right| \dot{\delta },\quad (q\ge 0,n\ge 1) \end{aligned}$$
(3)

where q is an arbitrary positive number. The expression in Eq. (3) is general. Many more kinds of nonlinear damping can be described by changing power indexes q and n. When \(q=n+1\), Eq. (3) can be transformed into Eq. (2). When \(q=0\), it is velocity-nth power damping.

2.2 Solution of SDOF isolation system with VDD damping

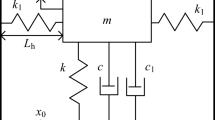
For the SDOF vibration isolation system subjected to base excitation as shown in Fig. 1, the mass to be protected is suspended on the combination of a spring k, a linear damper \(c_{l}\) and a nonlinear damper. The expression for VDD damping is shown in Eq. (3), in which, \(\delta =x(t)-y(t)\) is the relative displacement between the mass and the base. The base excitation is harmonic

$$\begin{aligned} y(t)=Y\sin (\omega t) \end{aligned}$$
(4)

where Y denotes the excitation magnitude and \(\omega \) is the excitation frequency.

Fig. 1
figure 1

SDOF vibration isolation system with a spring and a nonlinear damper subjected to base excitation

Full size image

System motion equation subject to the base excitation can be generally described by

$$\begin{aligned} m\ddot{\delta }+c_l \dot{\delta }+c_n \left| {\delta ^{q}\dot{\delta }^{n-1}} \right| \dot{\delta }+k\delta {=}-m\ddot{y}{=}mY\omega ^{2}\sin (\omega t)\nonumber \\ \end{aligned}$$
(5)

Introducing the following non-dimensional parameters

$$\begin{aligned} u= & {} \frac{\delta }{Y},\quad \omega _0 =\sqrt{\frac{k}{m}},\quad \varOmega =\frac{\omega }{\omega _0 },\quad \tau =\omega _0 t,\nonumber \\ \zeta _0= & {} \frac{c_l }{2\sqrt{km}},\quad \zeta _1 =\frac{c_n Y^{q+n-1}\omega _0^{n-2} }{2m} \end{aligned}$$
(6)

Equation (5) can be transformed to

$$\begin{aligned} {u}''+2\zeta _0 {u}'+2\zeta _1 \left| {u^{q}({u}')^{n-1}} \right| {u}'+u=\varOmega ^{2}\sin (\varOmega \tau ) \end{aligned}$$
(7)

To get the approximate solution of Eq. (7), some methods are applicable, such as HBM, OFRF [22]. However, considering the computing for \(\left| {u^{q}({u}')^{n-1}} \right| {u}'\), the averaging method is used [8, 9, 18]. It is worth pointing out that when the nonlinear system considered in this study is excited by a sinusoidal disturbance input, the output of the system not only contains the fundamental frequency of the input but also additional harmonic components. However, since there is only nonlinear damping in the system, additional harmonics are often negligible compared with the system response at the fundamental frequency. Therefore, only the response at the fundamental frequency is considered. The solution to Eq. (7) can be assumed to be

$$\begin{aligned}&u=U(\tau )\sin (\varphi (\tau )) \end{aligned}$$
(8)
$$\begin{aligned} \varphi&(\tau )=\varOmega \tau +\psi (\tau ) \end{aligned}$$
(9)

along with the assumption,

$$\begin{aligned} {u}'=U(\tau )\varOmega \cos (\varphi (\tau )) \end{aligned}$$
(10)

Equations (9) and (10) imply

$$\begin{aligned}&{U}'\sin \varphi +U{\psi }'\cos \varphi =0 \end{aligned}$$
(11)
$$\begin{aligned}&\quad {u}''=\varOmega {U}'\cos \varphi -\varOmega U(\varOmega +{\psi }')\sin \varphi \end{aligned}$$
(12)

Submitting Eqs. (8), (10) and (12) into (7), leads to

$$\begin{aligned}&\varOmega {U}'\cos \varphi -\varOmega U(\varOmega +{\psi }')\sin \varphi +2\zeta _0 U\varOmega \cos \varphi \nonumber \\&\qquad +\,2\zeta _1 U^{q+n}\varOmega ^{n} \left| {\sin ^{q}\varphi \cos ^{n-1}\varphi } \right| \cos \varphi +U\sin \varphi \nonumber \\&\quad =\varOmega ^{2}\sin (\varOmega \tau ) \end{aligned}$$
(13)

Solving Eq. (11) and (13), yields

$$\begin{aligned}&\varOmega {U}'=-\left[ U(1-\varOmega ^{2})\sin \varphi -\varOmega ^{2}\sin (\varOmega \tau )\right. \nonumber \\&\quad +\, 2\zeta _0 U\varOmega \cos \varphi +2\zeta _1 U^{q+n}\varOmega ^{n}\nonumber \\&\quad \left. \left| {\sin ^{q}\varphi \cos ^{n-1}\varphi } \right| \cos \varphi \right] \cos \varphi \end{aligned}$$
(14)
$$\begin{aligned}&\varOmega U{\psi }'=\left[ U(1-\varOmega ^{2})\sin \varphi -\varOmega ^{2}\sin (\varOmega \tau )\right. \nonumber \\&\quad +\,2\zeta _0 U\varOmega \cos \varphi +2\zeta _1 U^{q+n}\varOmega ^{n}\nonumber \\&\quad \left. \left| {\sin ^{q}\varphi \cos ^{n-1}\varphi } \right| \cos \varphi \right] \sin \varphi \end{aligned}$$
(15)

Averaging the right-hand sides of above Eqs. (14, 15) over a period of \(2\pi \)

$$\begin{aligned}&\varOmega {U}'=-\frac{1}{2\pi }\mathop {\int }\limits _0^{2\pi } \left[ U(1-\varOmega ^{2})\sin \varphi -\varOmega ^{2}\sin (\varOmega \tau )\right. \nonumber \\&\quad +\,2\zeta _0 U\varOmega \cos \varphi +2\zeta _1 U^{q+n}\varOmega ^{n}\nonumber \\&\quad \left. \left| {\sin ^{q}\varphi \cos ^{n-1}\varphi } \right| \cos \varphi \right] \cos \varphi \hbox {d}\varphi \end{aligned}$$
(16)
$$\begin{aligned}&\quad \varOmega U{\psi }'=\frac{1}{2\pi }\mathop {\int }\limits _0^{2\pi } \left[ U(1-\varOmega ^{2})\sin \varphi -\varOmega ^{2}\sin (\varOmega \tau )\right. \nonumber \\&\quad +\,2\zeta _0 U\varOmega \cos \varphi +2\zeta _1 U^{q+n}\varOmega ^{n}\nonumber \\&\quad \left. \left| {\sin ^{q}\varphi \cos ^{n-1}\varphi } \right| \cos \varphi \right] \sin \varphi \hbox {d}\varphi \end{aligned}$$
(17)

They can be simplified to by employing \(\varOmega \tau =\varphi -\psi \)

$$\begin{aligned}&2\pi \varOmega {U}'=-\pi \varOmega ^{2}\sin \psi -2\zeta _0 \pi U\varOmega \nonumber \\&\quad -\,8\zeta _1 U^{q+n}\varOmega ^{n}\mathop {\int }\limits _0^{\pi /2} {\left| {\sin ^{q}\varphi \cos ^{n+1}\varphi } \right| \hbox {d}\varphi } \nonumber \\&=-\pi \varOmega ^{2}\sin \psi -2\zeta _0 \pi U\varOmega \nonumber \\&\quad -\,4\zeta _1 U^{q+n}\varOmega ^{n}B\left( \frac{q+1}{2},\frac{n+2}{2}\right) \end{aligned}$$
(18)
$$\begin{aligned}&2\pi \varOmega U{\psi }'=\pi U(1-\varOmega ^{2})-\pi \varOmega ^{2}\cos \psi \end{aligned}$$
(19)

where \(B(\frac{q+1}{2},\frac{n+2}{2})=\mathop {\int }\limits _0^{\pi /2} {\left| {\sin ^{q}\varphi \cos ^{n+1}\varphi } \right| \hbox {d}\varphi } \) is the Beta function. This is valid for q and n as both integer power and fractional power.

$$\begin{aligned}&\pi \varOmega ^{2}\sin \psi =2\zeta _0 \pi U\varOmega +4 \zeta _1 U^{q+n}\varOmega ^{n}\nonumber \\&\quad B\left( \frac{q+1}{2},\frac{n+2}{2}\right) \end{aligned}$$
(20)
$$\begin{aligned}&\pi \varOmega ^{2}\cos \psi =\pi U(1-\varOmega ^{2}) \end{aligned}$$
(21)

Eliminating \(\psi \) in the above equations, the implicit amplitude–frequency equation can be obtained

$$\begin{aligned}&\left[ {2\zeta _0 \pi U\varOmega +4\zeta _1 U^{q+n}\varOmega ^{n}B \left( \frac{q+1}{2},\frac{n+2}{2}\right) } \right] ^{2}\nonumber \\&\quad +\,\left[ {\pi U(1-\varOmega ^{2})} \right] ^{2}=\pi ^{2}\varOmega ^{4} \end{aligned}$$
(22)

In the case of base excitation, displacement transmissibility is the most common index to estimate the isolation performance. In this study, the amplitude ratio between the input and response amplitude at the fundamental frequency is employed to represent the transmissibility. The amplitude ratio can be constructed using either the ratio of the root mean square (RMS) values or the ratio of the Fourier coefficients at the excitation frequency between the output and the input. This study employs the latter form. According to the definition of amplitude U, the relative displacement transmissibility \(T_{r}\) and the absolute displacement transmissibility \(T_{a }\) are

$$\begin{aligned} T_r= & {} U \end{aligned}$$
(23)
$$\begin{aligned} T_a= & {} \sqrt{U^{2}+2U\cos \psi +1}{=}\sqrt{\frac{2-\varOmega ^{2}}{\varOmega ^{2}}U^{2}{+}1} \end{aligned}$$
(24)

More details about \(T_{a}\) can be found in references [10, 39]. Displacement transmissibility characteristics are presented in dB as \(20\log _{10}T_{a}\) and \(20\log _{10}T_{r}\). Because the complexity of the implicit amplitude–frequency equation, it is impossible to find an exact analytical solution to express the relative displacement transmissibility \(T_{r}\), so the numerical method is resorted to tackle with the problem.

Fig. 2
figure 2

Validation of the averaging method by the Runge–Kutta method (\(n=1.5, q=0.5,\zeta _1 =0.1\))

Full size image

Moreover, to confirm the reasonability of the results by using the averaging method, Eq. (7) was numerically solved by using the four-order Runge–Kutta method. At each frequency of excitation, the response is calculated numerically and the steady-state response at the fundamental frequency is used to plot the displacement transmissibility. Comparisons between the analytical and the numerical results have been carried out. The validation results are shown in Fig. 2. It is found that the results by the averaging method have good agreement with those from the numerical method.

2.3 Stability analysis

Stability of stationary oscillations plays an important role in the vibration system. The stability of frequency response is discussed. A very small displacement \(e(\tau )\) is used to the steady-state solution. The form is

$$\begin{aligned} u(\tau )=u_0 (\tau )+e(\tau ) \end{aligned}$$
(25)

where \(u_{0}\) is the periodic solution of the system described in Eq. (7). Inserting Eq. (25) into (7) yields

$$\begin{aligned}&(u_0 +e)^{\prime \prime }+2\zeta _0 (u_0 +e)^{\prime }\nonumber \\&\quad +\,2\zeta _1 \left| {(u_0 +e)^{q}({u}'_0 +{e}')^{n-1}} \right| \nonumber \\&\quad ({u}'_0 +{e}')+(u_0 +e)=\varOmega ^{2}\sin (\varOmega \tau ) \end{aligned}$$
(26)

Since e and \({e}'\) are assumed to be small, the nonlinearity can be neglected. The simplified equation is as follows

$$\begin{aligned}&{e}''+2\zeta _0 {e}'+2\zeta _1 \left| {u_0^q {u}^{\prime {n-1}}_{0}} \right| {e}'\pm 2(n-1)\zeta _1 \nonumber \\&\quad \left| {u_0^q {u}^{\prime {n-1}}_{0} } \right| {e}'+e\pm 2q\zeta _1 \left| {u^{q-1}_{0} {u}^{\prime {n}}_{0} } \right| e=0 \end{aligned}$$
(27)

Time is shifted by \(\psi /\varOmega \), and the form of e can be assumed as follows

$$\begin{aligned} e=A\sin (\varOmega \tau )+B\cos (\varOmega \tau ) \end{aligned}$$
(28)

Substituting Eq. (29) in (27) and employing Eqs. (8) and (9) produces

$$\begin{aligned}&cA\sin (\varOmega \tau )+cB\cos (\varOmega \tau )+2\zeta _0 \varOmega A\cos (\varOmega \tau )\nonumber \\&\qquad -\,2\zeta _0 \varOmega B\sin (\varOmega \tau )\nonumber \\&\quad = \left[ -aA\left| {\sin (\varOmega \tau )} \right| \cos (\varOmega \tau ) -aB\left| {\sin (\varOmega \tau )} \right| \sin (\varOmega \tau )\right. \nonumber \\&\qquad \left. -\,bA\left| {\cos (\varOmega \tau )} \right| \sin (\varOmega \tau ) +bB\left| {\cos (\varOmega \tau )} \right| \cos (\varOmega \tau ) \right] \nonumber \\&\qquad \left| {\sin ^{q}(\varOmega \tau )\cos ^{n-1}(\varOmega \tau )} \right| \end{aligned}$$
(29)

where \(a=\left( {2\zeta _1 \varOmega \pm 2(n-1)\zeta _1 \varOmega } \right) \left| {U^{q+n-1}\varOmega ^{n-1}} \right| \), \(b=\pm 2q\zeta _1 \left| {U^{q+n-1}\varOmega ^{n}} \right| \), \(c=1-\varOmega ^{2}\).

For the integer power law damping \(n, q\in N\), the following expressions are employed.

$$\begin{aligned} \sin ^{2n}x= & {} \cos ^{2n}x=\frac{1}{2^{2n}} \frac{(2n)!}{(n!)^{2}}\nonumber \\&+\,\hbox {even}~\hbox {harmonic}~\hbox {terms},\quad \nonumber \\&\hbox {for }n=1,2,3,{\ldots }., \nonumber \\ \sin ^{2n+1}x= & {} \frac{1}{2^{2n}}\left( \begin{array}{c} {2n+1} \\ n \\ \end{array}\right) \sin x\nonumber \\&+\,\hbox {higher}~\hbox {order}~\hbox {harmonics}, \nonumber \\ \cos ^{2n+1}x= & {} \frac{1}{2^{2n}}\left( \begin{array}{c} {2n+1} \\ n \\ \end{array}\right) \cos x\nonumber \\&+\,\hbox {higher}~\hbox {order}~\hbox {harmonics} \end{aligned}$$
(30)

where for positive integers N and \(M<N, \left( \begin{array}{c} N \\ M \\ \end{array} \right) \equiv \frac{N!}{(N-M)!M!}\). Neglecting the coefficients of \(\sin (k \varOmega \tau )\) and \(\cos (k\varOmega \tau )\) when \(k\ge 2\), Eq. (29) is rewritten as follows for four different combinations of n and q.

  1. (i)

    \(q=2j\) and \(n=2k\)

    $$\begin{aligned}&\left[ {cA-2\zeta _0 \varOmega B} \right] \sin (\varOmega \tau )\nonumber \\&\quad +\,\left[ {2\zeta _0 \varOmega A+cB} \right] \cos (\varOmega \tau )\nonumber \\&\quad +\,A\left[ {c\frac{C_{2j}^j C_{2k-1}^k }{2^{2j+2k-2}}+b\frac{C_{2j-1}^j C_{2k}^k }{2^{2j+2k-2}}} \right] =0 \end{aligned}$$
    (31)
  2. (ii)

    \(q=2j\) and \(n=2k+1\)

    $$\begin{aligned}&\left\{ cA-B\left[ 2\xi _0 \varOmega +a\frac{C_{2j}^j C_{2k}^k }{2^{2j+2k}}\right. \right. \nonumber \\&\left. \left. +\left. b\frac{C_{2j-1}^j C_{2k+1}^{k+1} }{2^{2j+2k}}\right) \right] \right\} \sin (\varOmega \tau )\nonumber \\&+\, \left\{ A\left[ 2\xi _0 \varOmega +a\frac{C_{2j}^j C_{2k}^k }{2^{2j+2k}}\right. \right. \nonumber \\&\left. \left. +\left. b\frac{C_{2j-1}^j C_{2k+1}^{k+1} }{2^{2j+2k}}\right) \right] +cB \right\} \cos (\varOmega \tau )=0 \end{aligned}$$
    (32)
  3. (iii)

    \(q=2j+1\) and \(n=2k\)

    $$\begin{aligned}&\left\{ A\left[ c+a\frac{C_{2j+1}^{j+1} C_{2k-1}^k }{2^{2j+2k}}\right. \right. \nonumber \\&\left. \left. +\, b\frac{C_{2j}^j C_{2k}^k }{2^{2j+2k}} \right] -2\zeta _0 \varOmega B \right\} \sin (\varOmega \tau )\nonumber \\&+\,\left\{ 2\zeta _0 \varOmega A+B\left[ c+a\frac{C_{2j+1}^{j+1} C_{2k-1}^k }{2^{2j+2k}}\right. \right. \nonumber \\&\left. \left. +b\frac{C_{2j}^j C_{2k}^k }{2^{2j+2k}} \right] \right\} \cos (\varOmega \tau )=0 \end{aligned}$$
    (33)
  4. (iv)

    \(q=2j+1\) and \(n=2k+1\)

    $$\begin{aligned}&\left[ {cA-2\zeta _0 \varOmega B} \right] \sin (\varOmega \tau )\nonumber \\&+ \left[ {2\zeta _0 \varOmega A+cB} \right] \cos (\varOmega \tau )\nonumber \\&+\, A\left[ {a\frac{C_{2j}^j C_{2k-1}^k }{2^{2j+2k-2}}+ b\frac{C_{2j-1}^j C_{2k}^k }{2^{2j+2k-2}}} \right] =0 \end{aligned}$$
    (34)

For the fraction power law damping \( n, q\in N/M\ (N<M)\), the power is a fraction expressible as the ratio of (co-prime) odd integers with the form \(2m+1/2p+1\) (\(m\ne p\)) or co-prime positive integers, one of which is odd and the other even with the form as \(2m+1/2p\) and \(2m/2p+1\). For \(n=2m+1/2p+1\), \(q=2r+1/2s+1\), both sides of Eq. (34) are raised by (\(2p+1\))(\(2s+1\)) power, so that both sides contain odd powers

$$\begin{aligned}&\left[ cA\sin (\varOmega \tau )+cB\cos (\varOmega \tau )+2\zeta _0 \varOmega A\cos (\varOmega \tau )\right. \nonumber \\&\left. \qquad -2\zeta _0 \varOmega B \sin (\varOmega \tau ) \right] ^{(2p+1)(2\mathrm{s}+1)}\nonumber \\&\quad = \left[ -aA\left| {\sin (\varOmega \tau )} \right| \cos (\varOmega \tau )-aB\left| {\sin (\varOmega \tau )} \right| \right. \nonumber \\&\qquad \sin (\varOmega \tau ) -bA\left| {\cos (\varOmega \tau )}\right| \sin (\varOmega \tau )\nonumber \\&\left. \qquad +\, bB\left| {\cos (\varOmega \tau )} \right| \cos (\varOmega \tau ) \right] ^{(2p+1)(2\mathrm{s}+1)} \nonumber \\&\qquad \times \, \left[ \left| \sin ^{2(r-s)/(2s+1)}(\varOmega \tau )\right. \right. \nonumber \\&\qquad \left. \left. \cos ^{2(m-p)/(2p+1)}(\varOmega \tau ) \right| \right] ^{(2p+1)(2\mathrm{s}+1)} \end{aligned}$$
(35)

By using the expansion formula for a polynomial \((a+b+c\cdots +l)^{n}=\sum {\frac{n!}{p!q!r!\cdots s!}a^{p}b^{q}c^{r}\ldots l^{s}} \) (\(p+q+r+{\ldots }+s=n\)); the polynomial in both sides of Eq. (35) can be expressed as the integer powers of \(\sin ( \varOmega \tau )\) and \(\cos (\varOmega \tau )\). Then, using the terms for the integer powers of \(\sin (\varOmega \tau )\) and \(\cos ( \varOmega \tau )\) and neglecting the coefficients of \(\sin (k \varOmega \tau )\) and \(\cos (k\varOmega \tau )\) when \(k\ge 2\), Eq. (35) can also rewritten as follows a general form as

$$\begin{aligned} f(A,B)\sin (\varOmega \tau )+g(A,B)\cos (\varOmega \tau )+h(A,B)=0\nonumber \\ \end{aligned}$$
(36)

Since the equations with other form as \(2m+1/2p\) and \(2m/2p+1\) are tedious and these cases are omitted here. The above equations are identical to zero. On the other hand, \(\sin (\varOmega \tau )\) and \(\cos (\varOmega \tau )\) cannot be zero at the same time, therefore, the coefficients of \(\sin (\varOmega \tau )\) and \(\cos (\varOmega \tau )\) should be zero, which produces an equation set for A and B

$$\begin{aligned} f(A,B)=0; g(A,B)=0; h(A,B)=0 \end{aligned}$$
(37)

One can find that Eq. (37) holds only for \(A=B=0\) simultaneously. Through the above analysis, the conclusion can be drawn that the periodic solution of Eq. (7) is stable.

2.4 Influence of the base excitation amplitude Y

From Eq. (6), it is seen that the parameter \(\zeta _1 \) is variable with the external excitation for the fact that

$$\begin{aligned} \zeta _1 =\frac{c_n Y^{q+n-1}\omega _0^{n-2} }{2m} \end{aligned}$$
(38)

For typical base excitation is with low-frequency-large-amplitude and high-frequency-small-amplitude characteristics, the isolation performance of the VDD damping is influenced by the excitation amplitude. It is of significance to study the relationship between \(\zeta _1 \) and Y. The derivation of \(\zeta _1 \) by Y is

$$\begin{aligned} \frac{\hbox {d}\zeta _1 }{\hbox {d}Y}=(q+n-1)\frac{c_n Y^{q+n-2}\omega _0^{n-2} }{2m} \end{aligned}$$
(39)

The variation of \(\zeta _1 \) on Y is dependent on whether the expression in Eq. (39) is positive or negative. It is divided into four cases and discussed as following.

Fig. 3
figure 3

Absolute displacement transmissibility for nonlinear damping with \(\zeta _1 =0.1, \zeta _0 =0\). The displacement exponent a \(q=0\), b \(q=1,\) c \(q=2\) and d \(q=3\)

Full size image

For \(q+n>2\), \(\zeta _1 \) is a monotonic increasing function of Y, which means that the damping coefficient will increase as Y increases and decrease as Y decreases. Considering the nature of excitation, this kind damping will have strong damping effect in low frequency and light damping effect in high frequency, and it will exhibit large damping when a very large Y occurs at resonance. The isolator will have good performance at both resonance frequency and high frequency at the same time. For \(q+n=2, \frac{d\zeta _1 }{\hbox {d}Y}=\frac{c_n \omega _0^{n-2} }{2m}, \zeta _1 \) is the linear function of Y and increases as Y increases. For \(1<q+n<2\), \(\zeta _1 \) is a monotonic decreasing function of Y. Considering the nature of excitation, this condition is adverse for vibration isolation. For \(q+n=1, \zeta _1 \) is independent of Y. The traditional viscous linear damping with \(q=0\) and \(n=1\) can meet this requirement. This formula implies that for VDD damping with \(q+n=1\), the damping coefficient is constant. Considering the dry friction damping with \(q=1\) and \(n=0, \zeta _1 =\frac{c_n Y^{-1}\omega _0^{n-2} }{2m}\), it is shown that even if rather small friction exists, the damping coefficient should be enormous if Y is small. For \(q+n<1, \zeta _1 \) is an increasing function of Y.

For traditional velocity-nth power damping, \(q=0\) and \(n>1\) can meet the condition that \(q+n>1\). However, whether the condition \(q+n>2\) is fulfilled or not is crucial for the performance of this kind of damping. However, for the same damping coefficient \(\zeta _1, n>1\) will lead to worse absolute transmissibility than those with viscous linear damping. The larger the velocity exponent n is, the worse the transmissibility becomes. i.e., it cannot get remarkable improvement by way of changing the velocity exponent n merely. It is necessary to optimize parameter n to obtain good performance according to the characteristics of the excitation in practical applications. The proposed VDD damping will be a feasible way. For example, if \(q=2, n>0\) always meets the condition that \(q+n>2\), so the contradiction can be alleviated.

3 Parametric analysis of isolators with only VDD damping

In this section, effect of parameters in the VDD damping on the displacement transmissibility is discussed. If \(\zeta _0 =0\), Eq. (22) can be simplified to

$$\begin{aligned}&\left[ \zeta {4\zeta _1 U^{q+n}\varOmega ^{n}B \left( \frac{q+1}{2},\frac{n+2}{2}\right) } \right] ^{2}\nonumber \\&\quad +\,\left[ {\pi U(1-\varOmega ^{2})} \right] ^{2}=\pi ^{2}\varOmega ^{4} \end{aligned}$$
(40)

In the following subsection, the influence of parameters in the coefficient of VDD damping will be analyzed.

3.1 Influence of the parameter n

The absolute displacement transmissibility \(T_{a}\) and relative displacement transmissibility \(T_{r}\) of isolation systems with different values of exponent q and n are obtained, and shown in Figs. 3 and 4, respectively.

For \(T_{a}\), the low-frequency attenuation rate is independent of q and n, it is equal to 0 dB per decade. For a fixed displacement exponent q, if the velocity exponent n is increased, the resonant frequency and the corresponding absolute transmissibility value are decreased as seen from the enlarged view. Furthermore, the amount of decrease is more obvious for smaller q. It can also be seen that the maximum absolute transmissibility is decreased as q is increased. However, the absolute transmissibility is increased as n is increased at high frequencies.

Fig. 4
figure 4

Relative displacement transmissibility for nonlinear damping with \(\zeta _1 =0.1, \zeta _0 =0\), the displacement exponent a q=0, b \(q=1,\) c \(q=2\) and d \(q=3\)

Full size image

For \(T_{a}\), compared with the velocity n-th power shown in Fig. 3a, the VDD damping will not only further lower the amplification at resonance, but also increase the attenuation rate in the high-frequency isolation region, as shown by the curves with the same category in Fig. 3b–d. Compared with the previously studied nonlinear damping with the form of Eq. (2), i.e., \(q=n+1\), the more general VDD nonlinear damping also shows enhanced performance for \(T_{a}\). The previously studied cases are denoted by the thin solid line in Fig. 3b (\(q=1,n=0\)), the dotted line in Fig 3c (\(q=2,n=1\)), and the dash-dotted line in Fig 3d (\(q=3, n=2\)). Comparing these curves with the left curves in the same subfigure in Fig. 3b–d respectively, it is seen that merely increasing the velocity component will only produce good effect at resonance but has bad effect in the high frequency range. Comparing the solid line in Fig 3c (\(q=2, n=0\)) and Fig 3d (\(q=3,n=0\)) with the curve denoting (\(q=1,n=0\)), it is shown that varying q is beneficial for enhancing the isolation performance in the whole frequency range.

Fig. 5
figure 5

Maximums of absolute displacement transmissibility near the resonance, under different values of the parameters q and n, with \(\zeta _1 =0.1\), \(\zeta _0 =0\)

Full size image

If the displacement exponent \(q=0\), the damping degrades to be velocity-nth power damping, which are shown in Fig. 3a. A more detailed discussion will be carried out for this case. It turns out that the performance of isolation systems at high frequencies improves as the value of the exponent n decreases. For \(n=1\), it corresponds to a linear viscous damping. It can be seen that the performance of proposed damping is superior to the linear viscous damping only if \(n<1\). For \(n<2\), the absolute transmissibility tends to zero (\({-}\infty \) dB) as \(\varOmega \rightarrow \infty \), which agrees with the available conclusion that the high-frequency attenuation rate is about 20(2-n)dB per decade for \(n\le 2\) with velocity-nth power damping by using the equivalent damping method. Meanwhile, the widely accepted conclusion that \(n >1\) is detrimental for base excitation is verified. For \(n=2\), it corresponds to a quadratic damping. The absolute displacement transmissibility \( T_{a}\) is equal to a constant value \(\sqrt{{(1.7\zeta _1 +1)}/{1.7\zeta _1 }}\) approximately at high frequencies and the high frequency attenuation rate is 0 dB/decade. For \(n=3\), it corresponds to a pure cubic damping, the absolute displacement transmissibility tends to unity (0 dB), which is identical to a rigidly connected system. This result agrees well with the previous studies. In this case, the absolute transmissibility has a local minimum, the existence of which was also observed by Ruzicka and Derby [9]. More generally, for \(n>2\), the absolute transmissibility \( T_{a}\) tends to unity and the high-frequency attenuation rate is 0 dB/decade. Cubic damping is found to be a good example, showing the beneficial and detrimental effects of velocity-nth power law damping. The displacement response amplitude of the isolated mass at excitation frequencies well above the resonance frequency for \(n=2\) is constant, whereas the curves for \(n>2\) tend toward the amplitude of the base excitation. It is anticipated that the isolated mass will move almost together with the base excitation. At this stage the phase lag is close to zero. One might consider that the damping element locks the isolated mass and base together.

Obviously, \(n=2\) is a critical value in determining the value of \(\mathop {\lim }\limits _{\varOmega \rightarrow \infty } T_a \). When \(n>2, \mathop {\lim }\limits _{\varOmega \rightarrow \infty } T_a =1\); when \(n<2, \mathop {\lim }\limits _{\varOmega \rightarrow \infty } T_a =0\). This can be explained through the amplitude–frequency equation as shown in Eq. (40). Obviously

$$\begin{aligned} \left[ {\frac{4}{\pi }\zeta _1 U^{q+n}\varOmega ^{n-2} B\left( \frac{q+1}{2},\frac{n+2}{2}\right) } \right] ^{2}\le & {} 1 \end{aligned}$$
(41)
$$\begin{aligned} \left[ {U(1-\varOmega ^{-2})} \right] ^{2}\le & {} 1 \end{aligned}$$
(42)

If \(n>2\) and \(U\ne 0\), the left part of Eq. (41) tends to infinite as \(\varOmega \) increases. To meet Eq. (42), U must approach zero for \(n>2\), i.e., \(\mathop {\lim }\limits _{\varOmega \rightarrow \infty } T_r =0\) and \(\mathop {\lim }\limits _{\varOmega \rightarrow \infty } T_a =1\). Based on the analysis above, it can be concluded that n has a great influence on the displacement transmissibility for VDD damping.

Fig. 6
figure 6

Absolute displacement transmissibility for nonlinear damping with \(q=1\), the velocity exponent (a) \(n=0,\) b \(n=1,\) c \(n=2\) and d \(n=3\)

Full size image

For \(T_{r}\), the low-frequency attenuation rate is independent of the value of q and n, it is equal to 40 dB per decade. The high frequency relative transmissibility approaches to unity (i.e., 0 dB) except for the case with very large n, which will become less than unity (for example, the case \(n=3\)). For a fixed displacement exponent q, if velocity exponent n is increased, the resonant frequency and the corresponding relative transmissibility is decreased as seen from the enlarged view. Furthermore, the amount of decrease is more obvious for smaller q. It can also be seen that the maximum relative transmissibility is decreased as q is increased.

From Fig. 4a for velocity-nth power damping, it turns out that the performance of isolation systems improves both in the region of amplification and the region of isolation as the exponent n increases. This conclusion holds for other exponent vale of q. Therefore, with respect to the relative displacement transmissibility, the velocity component should be larger than 2 if better isolation performance is desired.

3.2 Influence of the parameter q

The parameter q affects the size of absolute transmissibility \(T_{a}\) over the whole frequency range, but does not change the overall trend. From Fig. 3, in the resonance region, the magnitude of the maximum \(T_{a}\) can be reduced to less than 10 dB by introducing q into isolators. In the high-frequency isolation, the isolation performance is also improved, which can be seen in Fig. 3. From Fig. 4, it is seen exponent q can improve the transmissibility both in the region of resonance and isolation.

At resonance frequency around \(\varOmega \approx 1\), the maximum \(T_{a}\) occurs and is dependent on both q and n. With \(\zeta _1 =0.1\), the maximum \(T_{a}\) at resonance under different values of q and n is shown in Fig. 5. It can be found that, when the damping is of velocity-nth power (\(q=0\)), the magnitude of maximum \(T_{a}\) is remarkably large and decreases quickly as n increases. In the cases of \(0<q<1\), the magnitude is very large for \(n=0\) and decreases quickly as n increases. In other case that \(q\ge 1\), the magnitude is relatively small and changes slowly with n.

3.3 Influence of the parameter \(\zeta _1 \)

Influence of nonlinear damping coefficient \(\zeta _1 \) on the absolute displacement transmissibility is investigated and the results are shown in Fig. 6. The main function of nonlinear damping coefficient \(\zeta _1 \) is to suppress response in resonance region; however, it will degrade the isolation performance in the high-frequency isolation region. This effect is more obvious as \(\zeta _1 \) increases. The low-frequency attenuation rate is independent of the value of \(\zeta _1 \) and it is equal to unity (0 dB). The high-frequency amplification rate is 40 dB per decade for \(n=0\) and \(n=1\). The increase in \(\zeta _1 \) does not influence the attenuation rate, but slightly postpones the corner frequency for \(n=1\) and \(n=2\), which implies that the frequency region of attenuation is narrowed. It can be seen that as \(\zeta _1 \) increases, the resonant frequency and the corresponding absolute transmissibility are decreased. For \(n>2\), given very large value of \(\zeta _1 \), the resonance peaks will disappear. However, the price is the high-frequency attenuation rate of the absolute transmissibility approaches unity (0 dB) as \(\varOmega \rightarrow \infty \), as well as no local minimum exists any more for the absolute transmissibility. The observations hold also for the systems with linear viscous damping. From this point, damping coefficient \(\zeta _1 \) has a similar function to the damping ratio \(\zeta \) in linear viscous damping, except that the former is variable and the latter is constant. However, from physical point of view, the damping coefficient \(\zeta _1 \) is different from the damping ratio \(\zeta \) in linear viscous damping. Only if \(q=0\) and \(n=1, \zeta _1 =\zeta \). At this time, the damping coefficient is a parameter to measure the level of damping in the isolation system. For other cases, the damping coefficient, together with the time-varying velocity and displacement response determines the amount of damping in the system. In addition, the value of \(\zeta _1\) does not influence the tendency of absolute transmissibility curves, which is determined by the velocity exponent n and the displacement exponent q collaboratively.

Figure. 7 shows the maximum of the absolute transmissibility \(T_{a}\) and relative transmissibility \(T_{r}\) under different values of q and \(\zeta _1 \), when \(n=1\). It is clear that the maximum transmissibility decreases as \(\zeta _1 \) increases. It is worth mentioning that for a special case \(q=0\), i.e., the velocity-nth damping, the magnitude of the maximum transmissibility is remarkably large, while it decreases very quickly as \(\zeta _1 \) increases. That is to say, increasing \(\zeta _1 \) is more effective for this case. However, the influence of \(\zeta _1 \) is weakened when \(\zeta _1 \) is larger than a certain value. The maximum transmissibility decreases slightly when \(q>0\) as seen from Fig. 7. Results also show that, enlarging q is helpful to reduce the maximum transmissibility for isolators with \(\zeta _1 <0.2\); while enlarging q will degrade the performance at resonance region if \(\zeta _1 >0.25\). Therefore, the condition that the displacement exponent \(q>0\) is helpful to suppress the response at resonance and to improve high-frequency isolation performance at the same time satisfies only when \(\zeta _1 \) is less than a certain value. The variation of the maximum relative transmissibility exhibits similar trend except for the results with very large damping ratio, where \(T_{r}\) for different values of q is equal to 0 dB.

Fig. 7
figure 7

Maximums of the absolute and relative displacement transmissibility near the resonance with \(n=1\), under different values of the parameters q and \(\zeta _1 \)

Full size image
Fig. 8
figure 8

Absolute and relative displacement transmissibility for nonlinear isolators with VDD damping (\(\zeta _0 =0)\), a \(\zeta _1 =0.1\), b \(\zeta _1 =0.5\), c \(\zeta _1 =1\)

Full size image
Fig. 9
figure 9

Absolute and relative displacement transmissibility for nonlinear isolators with both VDD damping and viscous linear damping with \(\zeta _0 =0.1\), a \(n=1\), b \(n=0.5\), c n\(=2\)

Full size image

3.4 Influence of different combinations of q and n

As discussed above, if \(q+n=1\), \(\zeta _1 \) is constant and independent of Y. An equivalent damping coefficient defined as \(\zeta _1 \left| {u^{q}({u}')^{n-1}} \right| \) is only dependent on q and n. Different combinations of n and q which satisfy \(q+n=1\) are performed to investigate their influence. The results are shown in Fig. 8. For all the three cases \(\zeta _1 =0.1\), \(\zeta _1 =0.5\) and \(\zeta _1 =1\), the variation trend is the same. The traditional viscous linear damping with \(q=0\) and \(n=1\) performs the best at resonance; however, it is the worst at high frequencies. The variation is monotonous about the increase of q, of which the absolute and relative transmissibility results are deteriorated at resonance and improved at high frequencies. By comparing the results for the three cases of \(\zeta _1 \), it is shown that the deterioration or the improvement is enhanced as \(\zeta _1 \) becomes larger. This can be explained by the fact that \(\zeta _1 \) is the coefficient of \(\left| {u^{q}({u}')^{n-1}} \right| \).

Fig. 10
figure 10

Block diagram of the control loop for an electromagnetic actuator as a passive VDD damper

Full size image

4 Isolators with both VDD damping and linear damping

From the above sections, it is shown that vibration system with only VDD damping has potential in improving isolation performance at resonance and high frequencies. In the following part, vibration system with both VDD damping and linear viscous damping will be discussed.

In Fig. 9, absolute and relative displacement transmissibility curves for isolators with different parameters with velocity exponent \(n=1\), 0.5, 2 are given. For \(n=1\), the solid line represents the linear viscous damping with \(\zeta _0 =0.1\). The dashed line is the case for the linear viscous damping with \(\zeta _0 =0.2\), because if \(q=0\) and \(n=1\), \(\zeta _0 =\zeta _1 \). Obviously, increasing viscous damping will suppress resonance but degrade isolation performance at high frequencies. However, if VDD damping is introduced, this dilemma will be relieved. The maximum transmissibility at resonance is the same level as the case \(\zeta _0 =0.2\), the attenuation rate at high frequencies gradually approaches to that as the case \(\zeta _0 =0.1\) as q increases from 0 to 3. The reason is that the VDD damping becomes stronger at resonance as the response becomes larger so that it can suppress resonance efficiently; the VDD damping becomes weaker or even can be ignored (if q is big enough) when the excitation frequency locates in isolation region since the relative displacement is small. Under this circumstance, the system can be approximately considered as working with only linear viscous damping. Hence, it is a useful way to suppress resonance by adopting VDD damping, which has tiny adverse effect on the performance at high frequencies.

For \(n=0.5\), the suppression of response at resonance is not so obvious if \(q<2\). This observation agrees with the conclusion that VDD damping is more effective for \(q+n>2\). The suppression in the isolation region is slightly enhanced since velocity-nth power damping shows better absolute displacement transmissibility if \(n<1\). For \(n=2\), the suppression of response at resonance is almost the same for all q since all of them satisfy the condition \(q+n>2\). The suppression in the isolation region for absolute displacement transmissibility is greatly deteriorated.

5 Experimental study of vibration isolation system with VDD nonlinear damping using electromagnetic actuator

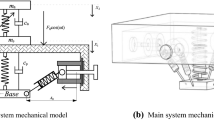
5.1 Experimental configuration

As shown in Fig. 10, principle diagram of an experimental configuration is constructed by using an electromagnetic actuator to implement the VDD nonlinear damping. The damper is connected to a shaker at one end and to a supported mass at the other end. A spring is installed in parallel to the damper. The shaker supplies an acceleration input at a given form with a given amplitude and frequency range to one end of the damper. The mass is allowed to move freely in the horizontal direction. The accelerations on the shake table and the loaded mass are measured by the acceleration sensors. The relative acceleration of the damper is given by the difference between the two measured acceleration at the two terminals. It is then integrated once and twice to respectively get the relative velocity and relative displacement. The experimental system includes a controller designed to regulate the current i that is fed into the electromagnetic actuator, which is capable to control the actuator to generate the desired output damping force.

Fig. 11
figure 11

Experimental rig for a SDOF base excited isolation system with VDD damping

Full size image
Fig. 12
figure 12

Electromagnetic actuator and the dynamic representation of the test rig

Full size image
Fig. 13
figure 13

Absolute transmissibility of velocity-nth damping and VDD damping \(C_{V}=20{,}000\)

Full size image

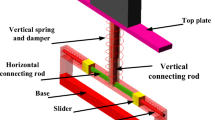
To avoid increasing the complexity of the experimental rig, a simple test rig with only the necessary instrument and equipment is designed, which behaves as a simple SDOF base excitation system, as shown in Fig. 11. The damping component is implemented using an electromagnetic actuator, which is shown in Fig. 12. By referring to Fig. 13, the diaphragm spring acts as the spring and the permanent magnet and the metal casing acts as the mass. The approximate stiffness values of the diaphragm spring are 27.93 kN/m. The mass of the permanent magnet and the metal casing is about 2.3 kg. Hence, the natural frequency of the bounce mode could be estimated as 17.5 Hz. The coil winding is fixed to the base and receives the base excitation from the shaker. The electromagnetic vibration shaker receives sweeping sine signals from a signal generator and generates the corresponding base excitation. The signal generator generates sweeping sine signals with frequency increasing rate as 0.5 Hz/s. The acceleration sensors on the base and the mass are used to acquire accelerations, which are then amplified by the charge amplifier and sent to the NI PCI-6259 DAQ Card (Data Acquisition Card). The DAQ Card processes the inputted real-time acceleration data by employing the control algorithms compiled by the virtual instrument software in the computer and sends out the required control voltage to the power amplifier. The electromagnetic actuator receives the control current by the power amplifier and produces the desired damping force. The damping force will be applied on the mass to control the vibration of the mass. After the algorithm works stable, the accelerations on the base and the mass are then sent to LMS for real-time acquisition and processing. For the experimental system, the active control force \(f_{d}(t)\) with the desired nonlinear damping characteristics is implemented by the NI PCI-6259 DAQ Card based controller to generate control voltage proportional to the control force. The algorithm is coded by employing the NI LabVIEW environment and implemented digitally at a sample rate of 2 kHz with a NI PCI-6259 DAQ Card. The NI PCI-6259 DAQ Card has 32D/A and 4A/D channels (all being of a 16 bit resolution) and the two acceleration measurements are amplified to be within the \(\pm \)5 V operating range of the A/D’s to avoid resolution errors. The process in the DAQ Card includes filtering of the acceleration signals by a Butterworth low-pass filter with a cut off frequency of 40 Hz to remove high-frequency components, integrating the signals once and twice to respectively get the relative velocity \(\dot{\delta }\) and relative displacement \(\delta \), calculating the voltage V(t) by employing the relative velocity \(\dot{\delta }\) and relative displacement \(\delta \), which is proportional to \(c_n \left| {\delta ^{q}\dot{\delta }^{n-1}} \right| \dot{\delta }\). The computer generates the control input, which is converted to analogue (voltage) signal and amplified before being fed to control the actuators. Then the actuator will response with a nonlinear force \(f_{d}(t)=C_{V}V (t)\) with \(C_{V}\) as the proportional damping amplification coefficient. The block diagram of the feedback loop is shown in Fig. 10. When there is no active control, the constructed system behaves as a SDOF vibration system with linear viscous damping.

5.2 Results and discussion

5.2.1 The effectiveness of the proposed VDD damping

Firstly, the effectiveness of using an electromagnetic actuator-based nonlinear damping is verified. The absolute transmissibility of velocity-nth damping and VDD damping with \(C_{V}=20{,}000\) is compared in Fig. 13. It is shown that the absolute transmissibility is decreased at resonance if n increases. However, the performance in the high-frequency range is deteriorated. Figure 13 clearly indicates that if VDD damping is adopted with displacement exponent \(q=1\), this not only reduces the absolute transmissibility over the resonant frequency region (15, 20 Hz), but also produces only a very small increase in the transmitted force over the isolation frequency range (20, 30 Hz), which is an ideal damping for vibration control. Therefore, the theoretically proved conclusions relating to the beneficial effect of VDD nonlinear damping on vibration control are experimentally verified.

5.2.2 The effects of damping coefficient \(C_{V}\)

The influence of the damping coefficient \(C_{V}\) on the output damping is investigated. One of the time history results is shown in Fig. 14 for velocity and displacement exponent \(n=0.5\), \(q=0.5\). Four different damping coefficients are used in the controller to generate the actuator control voltage, which are 1000, 2000, 4000 and 6000, respectively. The results for the four cases are given. The vibration amplitude at the isolation region is greatly attenuated for all the four cases. The vibration amplitude at the resonance region is gradually suppressed as \(C_{V}\) increases from 1000 to 2000, 4000, 6000, which indicates a gradual change for a stronger VDD damping, i.e., the attenuation effect improves as \(C_{V}\) increases. This observation validates the theoretical prediction. On the other hand, for this particular device, the peak and the valley at resonance is not symmetric, suggesting that there is inherent nonlinearity characteristic of this particular device when the response amplitude is large. Especially for a larger \(C_{V}\), the hardening characteristics are observed as the peaks deviate to the right, which is usually attributed to the nonlinearity in stiffness.

Fig. 14
figure 14

Time history of accelerations at the base and the mass under sweeping sine excitation (\(n=0.5, q=0.5\)) a \( C_{V} =1000\), b \( C_{V} =2000\), c \( C_{V} =4000\), d \( C_{V} =6000\)

Full size image

The transmissibility under sweeping sine excitation for different damping coefficients \(C_{V}\) is shown in Fig. 15 with three kinds of combinations of n and p. Damping coefficient \(C_{V}\) is respectively set to be 1000, 2000, 4000, 6000 for \(n=0.5\) and \(q=0.5\); 250, 500, 750, 1000 for \(n=0.8\) and \(q=0.2\); 10,000, 20,000, 30,000 for \(n=0\) and \(q=1.0\). The transmissibility is obtained by the ratio of the accelerations on the mass and the base after the acquired time-history acceleration is transformed to the frequency domain by the Fourier analysis. It can be seen that there is a second harmonic at 35 Hz, which is an indication of stiffness nonlinearity. The attenuation effect at fundamental resonance and the second harmonic improves as \(C_{V}\) inceases. The attenuation rate in the higher frequency range also increases slightly as \(C_{V}\) increases. The attenuation rate in the higher frequency range seems to be unchanged if \(C_{V}\) inceases to be larger than a certain value, as shown by the case for \(n=0.5\) and \(q=0.5\), \(n=0\) and \(q=1.0\). This correlates well with the theoretical conclusion that relating to the effect of nonlinear damping coefficient \(\zeta _1 \) on the absolute displacement transmissibility.

Fig. 15
figure 15

Absolute transmissibility of the vibration isolation system for different damping coefficients \(C_{V}\) under sweeping sine excitation a \(n=0.5\) and \(q=0.5\); b \(n=0.8\) and \(q=0.2\); c \(n=0\) and \(q=1.0\)

Full size image

5.2.3 The case for the transmissibility that is independent on the excitation amplitudes

It is shown theoretically that if \(q+n=1\), the displacement transmissibility is independent on the excitation amplitude. This theoretical prediction is validated by employing different input voltage of the shaker and defining \(q=0.5\) and \(n=0.5\). The controlled transmissibility under different driving voltages for the vibration shaker is shown in Fig. 16. It is seen that the transmissibility does not differ much from each other for the input voltage of 1 and 2 v before the second harmonic, especially over the region of the resonant frequency. Under these two circumstances, the nonlinearity is relatively small and the second harmonic is not obvious. This founding is consistent with the theoretical analysis. However, if the driving voltage increases further to be 4 and 5 v, the jumping phenomena will happen as a result of the inherent nonlinearity in stiffness is excited due to large displacement input.

Fig. 16
figure 16

Absolute transmissibility of the vibration isolation system under different driving voltages for the vibration shaker

Full size image

5.2.4 The effects of different combinations of q and n

The transmissibility results for different combinations of n and q under constraints of \(q+n=1\) are measured and the results are shown in Fig. 17. It is seen that as the displacement exponent q increases, the absolute transmissibility will be deteriorated at resonance and improved in the high-frequency range, which is consistent with the theoretical prediction.

Fig. 17
figure 17

Absolute transmissibility of the vibration isolation system for different combinations of n and q under sweeping sine excitation (\(C_{V} =4000\))

Full size image

As pointed out by the previous researchers, the controllers in Fig. 11 are tuned for each combinations of q and n and have the same gain values for the whole experimental frequency range, i.e., the damping coefficient \(C_{V}\) is kept the same over the whole frequency range (0\(\sim \)40 Hz). That is to say, the controller gains are dependent on the electromagnetic actuator and the designed damping characteristic, but not on other system parameters of the vibration isolation system. This is the most distinct difference between the electromagnetic actuator as nonlinear damper and the conventional approach in active vibration control, of which the controller is adjusted according to the real-time measured signals. For use as a nonlinear viscous damper, the electromagnetic actuator is a stand-alone self-contained two-terminal device with a specific damping constant by employing an embedded controller which only takes measurements from the damper itself. When applying it in a vibration isolation application, no further monitoring is required once the controller is tuned according to the predefined nonlinear damping constant and exponent.

6 Conclusions

Vibration isolation systems with a general VDD nonlinear damping which has arbitrary nonnegative velocity exponent and displacement exponent are investigated theoretically and experimentally. For the SDOF vibration isolation system with VDD nonlinear damping, this study has proved that

  1. (1)

    The introduction of the VDD nonlinear damping produces ideal vibration isolation. The absolute displacement transmissibility at resonance is suppressed, but the transmissibility in the high frequency region remains unaffected. The parameter analysis reveals that

    1. (i)

      The velocity exponent n has a crucial influence on the high frequency attenuation rate. Under the same value of the damping coefficient \(\zeta _1 \) and the displacement exponent q, decreasing the value of n will improve the high-frequency performance for the base excitation. If \(n>2\), the absolute displacement transmissibility will always tend to unity as excitation frequency increases, i.e., the isolated mass will move almost together with the base excitation, which would be bad for vibration isolation under base excitation;

    2. (ii)

      The displacement exponent \(q>0\) is helpful to suppress the response at resonance and to improve isolation performance in the high-frequency range at the same time, but this works only when \(\zeta _1 \) is less than a certain value;

    3. (iii)

      The damping coefficient \(\zeta _1 \) has a similar function as the viscous linear damping.

  2. (2)

    The velocity exponent n and the displacement exponent q collaboratively determine the tendency of damping coefficient with the excitation amplitude. A nonlinear damping that whose isolation performance is independent with the excitation amplitude is proposed and validated by using an electromagnetic actuator. For the practical application of velocity-nth power damping, it needs to optimize the value of n to get an optimal isolation performance according to the characteristics of the excitation, instead of minimizing the value of n merely.

  3. (3)

    The proposed VDD damping can be achieved by employing active control with an electromagnetic actuator. It seems to have some potential values in applications.

The results sufficiently demonstrate the significant benefits that can be introduced through the use of VDD nonlinear damping in SDOF vibration isolation systems, which will provide an important basis for the design and practical application of nonlinear damping for a vibration isolation system in engineering practice.