1 Introduction

Composite materials with a precisely defined profile are called functionally graded materials (FGMs) and are made by continuously varying volume fractions in the thickness direction. The benefits of these materials in lowering thermal stress and narrowing the gap between the characteristics of different materials have garnered much attention in recent years. The FGMs exhibit optimal behavior due to the continuous variation of their mechanical properties. So FGMs are mainly used in high-tech applications such as aeronautics, biomedical, aerospace, semiconductors, nuclear, and civil engineering. For a good design, to have strong structures, and to reduce the costs associated with their treatment and manufacture, it is crucial to study and understand the behavior of FG structures subjected to various mechanical loads. Through the analysis of the literature, many researchers have established different theories for studying vibrational behaviors [1,2,3,4,5,6,7,8,9,10] and buckling [11,12,13,14,15,16] of different types of FG structures. Using an HSDT, Atmane et al. [17] analyzed the free vibration of simply supported FG plates resting on elastic foundations (EFs). The hygro-thermal effects on the free vibration of laminated composite plates resting on EFs with random system parameters are examined by Kumar et al. [18] using a micromechanical model and the finite element method. Under various boundary conditions, Sobhy [19] examined the buckling and vibration behaviors of an FG sandwich plate resting on a Pasternak EFs. [20] investigated the free vibration of FG plates resting on EFs, considering the influence of transverse shear deformations. Han et al. [21] proposed a quasi-three-dimensional theory for the dynamic reactions of power law and sigmoid FG plates. Nebab et al. [22] investigated the vibration and wave propagation of FG plates resting on EFs. The effect of grading pattern and porosity on the eigen characteristics of the FG porous structure is studied by Ramteke et al. [23] using the isoparametric finite element technique. An analytical solution procedure for the natural frequency analysis of the FG beams has been presented by AlSaid-Alwan and Avcar [24] using different beam theories. Ramteke et al. [25] carried out the static analysis of a two-directional graded structure using a commercial FE method. A numerical model for the calculation of transient deviations of an FG structure taking into account various types of models (power law, sigmoid, and exponential) including a variable distribution of porosity is developed by Ramteke et al. [26]. Avcar et al. [27] studied the natural frequencies of FG sigmoid sandwich beams using HSDT. A three-dimensional (3D) nonlinear formulation based on surface elasticity was presented by Fan et al. [28] to explore the post-buckling thermal characteristics of porous composite nanoplates made of an FGM material having a central cutout with different shapes. Ramteke and Panda [29] obtained the solutions of the free vibration for a multidirectional FG structure by considering the variable gradation models (power law, sigmoid, and exponential), including the effect of the porosity distribution using a mathematical model. Besides, the bending behavior of a functionally graded structure with variable grading patterns as well as variable porosity was studied by Ramteke et al. [30] using the finite element method. Ramteke et al. [31] examined the effect of large-scale geometric nonlinearity on the natural frequencies of the porous graded curved panel structure. Rao et al. [32] investigated the nonlinear bending response of composite rectangular microplates having functionally graded porosity is predicted by incorporating a type of small-scale effect torque stress using isogeometric finite element methodology. In their research, Song et al. [33] used an isogeometric numerical technique incorporating non-uniform rational B-splines to study the nonlinear thermal post-buckling characteristics of a functionally gradient porous material microplate with a central cutout of different shapes. Hadji et al. [34] analyzed the natural frequencies of an imperfect FG sandwich plate resting on two-parameter elastic foundations. Choudhary et al. [35] proposed a numerical study of the deflection responses of a cracked porous FG structure under variable loading conditions. The vibration and buckling behavior of multidirectional P-FGM, S-FGM, and E-FGM porous structures fouled by damage taking into account the effect of porosity, is well discussed by Hissaria et al. [36]. Ramteke et al. [37] determined frequencies of double curvature FG panels considering the influence of multidirectional dimming, large geometric deformation, and porosity. Numerical modelling of the structures of the multidirectional porous panel using a single-layer higher-order polynomial model is proposed by Ramteke et al. [38], taking into account the cubic variation of the displacement in extension to maintaining the necessary stress/strain. Ramteke et al. [39, 40]analyzed the nonlinear dynamic response of FG shell panels in a thermal environment using the finite element method. Sahoo et al. [41] developed a finite element code to analyze the nonlinear free vibration of the FG sandwich shells based on the higher-order shear deformation theory (HSDT). Wang et al. [42] presented nonlinear buckling and post-buckling characteristics of porous composite microplates. The free vibration, modal, and stress state of honeycomb sandwich structures with different boundary conditions were studied by Safaei et al. [43] using the representative volume element method. Feng et al. [44] proposed a novel design of sandwich composites inspired by nature and prepared for vibration suppression, where conventional blended composites and pure epoxy resin samples are also prepared as a reference. The nonlinear static and dynamic behaviors of FG porous structures of varying geometric shapes exposed to mechanical/thermomechanical loadings are investigated by Ramteke and Panda [45,46,47] using HSDT. Ramteke and Panda [48] analyzed the stresses of the bidirectional FG shell panel under variable mechanical loadings, numerically and experimentally.

The first-order shear deformation theory (FSDT) is commonly used to predict the mechanical behaviors of homogeneous and FG structures resting on EFs [49, 50]. Besides, the HSDT is also used to examine the mechanical behaviors of FG structures resting on EFs [51,52,53,54,55,56].

Unlike plate structures, the literature on dynamic response and buckling analysis of FG beams resting on EFs is still limited. Atmane et al. [57] offered a numerical shear displacement model to analyze the free vibration of FG porous beams. Chaht et al. [58] investigated the bending and buckling behaviors of size-dependent FG nano-beams while considering the thickness stretching effect. The static response and free vibration of an FG beam are investigated by Hadji et al. [59] using an HSDT. Vo et al. [60, 61] developed a new quasi-three-dimensional theory to analyze the mechanical behaviors of FG sandwich beams. Akbaş [62] studied the temperature-dependent nonlinear static response of FG porous beams. Al-Shujairi and and Mollamahmutoğlu [63] established a nonlocal deformation theory to investigate the buckling and free vibration behaviors of FG sandwich micro-beams resting on an EF. Sayyad and Ghugal [64] investigated the mechanical behaviors of laminated composite and sandwich beams using trigonometric shear and normal deformation theories. Zenkour and Radwan [65] studied the bending reactions of FG plates resting on Winkler-Pasternak foundations under various boundary conditions using hyperbolic shear deformation theory. Bouiadjra et al. [66] developed an analytical model to investigate the thermodynamic behavior of an FG beam resting on EFs.

The effect of Winkler’s parameter varying in one direction on the behavior of an FG structure resting on an EF has recently been the subject of several recent works [67,68,69,70,71]. The influence of VEFs on the static behavior of FG plates is demonstrated using sinusoidal shear deformation in Nebab et al. [72], while the impact of VEFs on the free vibration of FG plates is presented in Nebab et al. [73]. Merzoug et al. [74] proposed 2D and quasi-3D theories to examine the effect of micromechanical models on the thermoelastic bending of FG beams resting on VEFs. Bouiadjra et al. [75] created an analytical model to investigate the thermodynamic response of FG sandwich plates supported by a VEF. Benaberrahmane et al. [76] analyze the free vibration of bidirectional functional gradient beams resting on a VEF. Atmane et al. [77] established a novel HSDT in the same context to explore the dynamic behavior of FG beams on different EFs. A shear deformation theory with four unknowns based on finite elements is proposed in Giang and Hong’s [78] work to explore the hygro-thermal–mechanical stability of FG porous sandwich plates sitting on VEFs.

As a result of the literature review above, it is seen that most of the research on the behavior of FG beams based on variable foundations is limited to the vibration response of non-porous, i.e., perfect beams. Hence, an attempt to address this issue is made in the present study. To do this, in the current research, an HSDT is proposed to analyze the impact of VEFs on the free vibration and the buckling of FG beams, including porosities. Unlike the other HSDTs, in this study, the number of unknown functions involved is only three, while the other HSDTs include four unknown functions. Besides, this theory meets the boundary requirements of zero tension on the beam surfaces and allows for hyperbolic distributions of transverse shear stresses without the need for shear correction factors. The elastic medium is supposed to have two parameters (i.e., Winkler-Pasternak foundations), with the Winkler parameter in the longitudinal direction being variable variations (linear, parabolic, sinusoidal, cosine, exponential, and uniform) and the Pasternak parameter being fixed, at first. Then, the effective material characteristics of the FG beam are assumed to follow a simple power-law distribution in the thickness direction, and the influence of porosity is investigated by considering four different porosity PDPs. Next, the equations of motion are derived using Hamilton’s principle, and then Navier’s method is used to solve the system of equations for the FG beam with simply supported ends analytically. Finally, parametric studies are done to explore the impacts of various parameters on the free vibration and buckling behaviors of FG beams, such as the power law index, the length-to-thickness ratio, the type of VEFs, and the PDPs.

2 The formulation of the problem

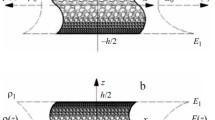
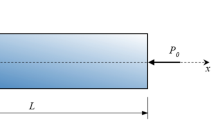
2.1 Geometrical configuration

Consider an FG beam resting on the VEFs of length L, width b, and thickness h, as illustrated in Fig. 1. When the x and y axes are located in the middle of the beam, the Cartesian coordinate system (x, y, and z) is taken as the basis for mathematical formulas. Note that both ends of the FG beam are considered to be simply supported. Namely, the following limit intervals are considered:

$$\frac{ - h}{2} \le z \le \frac{h}{2},\;\frac{ - b}{2} \le y \le \frac{b}{2},\quad 0 \le x \le L$$
(1)
Fig. 1
figure 1

Configuration of an FG beam resting on the VEFs

Full size image

2.2 Material properties

The imperfect FG beam with porosity volume fraction \(\alpha \left( {\alpha \ll 1} \right)\) is assumed to be composed of two materials, i.e., metal and ceramic, whose material characteristics vary through the thickness direction, and the volume fractions of these components are dispersed according to the modified rule of mixture [8]:

$$P\left( z \right) = \left( {P_{{\text{c}}} - P_{{\text{m}}} } \right)V_{{\text{c}}} + P_{{\text{m}}} - \left( {P_{{\text{c}}} + P_{{\text{m}}} } \right)\frac{\alpha }{2}$$
(2)

here \(P_{{\text{c}}}\) and \(P_{{\text{m}}}\), denote material characteristics of ceramic and metal, and \(V_{{\text{c}}}\) and \(V_{{\text{m}}}\), indicate volume fraction of ceramic and metal, respectively. Note that the material properties of a perfect beam can be obtained by setting the porosity volume fraction to zero (α = 0).

The following relationship exists between the total volume fraction of the metal and ceramic constituents:

$$V_{{\text{m}}} + V_{{\text{c}}} = 1$$
(3)

The power law function for the volume fraction of ceramic is defined as follows:

$$V_{{\text{c}}} = \left( {\frac{z}{h} + \frac{1}{2}} \right)^{p}$$
(4)

here \(z\) is the distance from the mid-plane and \(p\) is the power law index (\(0 \le p \le \infty\)), and the beam is entirely composed of ceramic as \(p = 0\), whereas when \(p = \infty\), the beam is wholly comprised of metal.

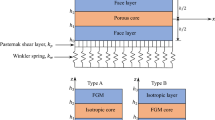
According to the modified rule of mixture, material characteristics, i.e., Young’s modulus and density, of the IP-FG beam may be written; Table 1 shows the expressions and illustrations for material characteristics of the IP-FG beam for different PDPs, i.e., Homogenous (H), X, O, and V PDPs [79,80,81].

Table 1 The expressions and illustrations for material characteristics of different PDPs
Full size table

In this study, the Poisson’s ratio is kept constant since its impact is very low compared to the effect of Young’s modulus on the mechanical behaviors of perfect FG beams [66, 82].

2.3 Variables of the EFs

The IP-FG beam is supposed to rest on an elastic foundation with multiple layers. The first layer consists of Winkler springs without including the coupling effect, whereas the second layer is connected to the first one by the shear layer of Pasternak. The following general formulation describes the Winkler-Pasternak EFs:

$$R_{{\text{e}}} (x) = K_{{\text{w}}} (x)w - K_{{\text{p}}} \left( {\frac{{\partial^{2} w}}{{\partial x^{2} }}} \right)$$
(5)

where Re(x) is the reaction of the EF, Kw(x) is Winkler’s variable parameter, Kp is the Pasternak parameter of the shear layer; note that if the shear layer is neglected, the Winkler–Pasternak EFs transform to the Winkler EF [83,84,85,86].

$$K_{{\text{w}}} (x) = \frac{{k_{{\text{w}}} D_{i} }}{{a^{4} }}\left\{ {\begin{array}{*{20}c} {1 + \psi \frac{x}{a}} & {{\text{Linear}}} \\ {1 + \psi \left( \frac{x}{a} \right)^{2} } & {{\text{Parabolic}}} \\ {1 + \psi \sin \left( {\pi \frac{x}{a}} \right)} & {{\text{Sinusoidal}}} \\ {1 + \psi \cos \left( {\pi \frac{x}{2a}} \right)} & {{\text{Cosine}}} \\ {1 + \psi \left( {\exp \left( \frac{x}{a} \right) - \exp \left( \frac{x}{a} \right)^{n} } \right)} & {{\text{Exponential}}} \\ \end{array} } \right.$$
(6)

where: Kw(x) is the variable Winkler foundation stiffness, \(k_{{\text{w}}}\) and \(\psi\) are constant and variable parameters. Note that if \(\psi\) is zero, the EF becomes uniform Winkler–Pasternak EFs.

2.4 Kinematics and strains

Based on HSDT, the current displacement field contains three unknowns [9, 77, 87] as follows:

$$\begin{aligned} & u(x,z,t) = u_{0} (x,t) - z\frac{{\partial w_{0} }}{\partial x} + kA^{{\prime }} f(z)\frac{\partial \theta }{{\partial x}} \\ & w(x,z,t) = w_{0} (x,t) \\ \end{aligned}$$
(7)

To minimize the number of unknown variables, indefinite integrals have been introduced in the displacement field. Note that, \(\varphi_{x} = \int {\theta (x,t)\,{\text{d}}x}\) is considered in the displacement mentioned above, where, \(u_{0}\) is the displacement of the mid-plane of the FG beam in the longitudinal direction, \(\theta\) and \(w_{0}\) represent the shear and bending components of transverse displacement, respectively, and \(f(z)\) is the shape function based on HSDT that governs the distribution of the transverse shear satisfying across the stress-free boundary conditions on the top and bottom surfaces of the FG beam. In this study, a sinusoidal type shape function proposed by Touratier [88] is expressed as follows:

$$f(z) = \frac{h}{\pi }\sin \left( {\frac{\pi z}{h}} \right)$$
(8a)
$$g(z) = \frac{{{\text{d}}f(z)}}{{{\text{d}}z}} \Rightarrow g(z) = - \left( {\frac{h}{\pi }} \right)^{2} \cos \left( {\frac{\pi z}{h}} \right)$$
(8b)

According to the theory of linear elasticity of small strains, the linear strain can be defined as follows:

$$\varepsilon_{x} = \varepsilon_{x}^{0} + zk_{x}^{b} + f(z)k_{x}^{s}$$
(9)

here

$$\begin{aligned} & \varepsilon_{x}^{0} = \frac{{\partial u_{0} }}{\partial x},\;\;k_{x}^{b} = - \frac{{\partial^{2} w_{0} }}{{\partial x^{2} }},\;\;k_{x}^{s} = k\theta ,\;\;\gamma_{xz}^{0} = k\int {\theta \;{\text{d}}x} \end{aligned}$$

and

$$\begin{aligned}& g(z) = \frac{{{\text{d}}f(z)}}{{{\text{d}}z}} \\ \end{aligned}$$
(10)

Using Navier’s approach, the format derivation of the undefined integral included in the strains relation may be simplified and rewritten as follows:

$$\int {\theta \;{\text{d}}x} = A^{{\prime }} \frac{\partial \theta }{{\partial x}}$$
(11)

here following definitions apply

$$A^{{\prime }} = - \frac{1}{{\lambda^{2} }},\;{\text{and}}\;k = \lambda^{2}$$
(12)

and

$$\lambda = \frac{m\pi }{L}$$
(13)

2.5 Constitutive equations

Transverse shear and normal deformations are considered in the stress and strain relationships as follows:

$$\sigma_{x} = C_{11} \varepsilon_{x} ,\quad \tau_{xz} = C_{55} \gamma_{xz}$$
(14)

where \(\left( {\sigma_{x} ,\tau_{xz} } \right)\), \(\left( {\varepsilon_{x} \gamma_{xz} } \right)\) and \(C_{ij}\) are the components of stress and strain and stiffness coefficients which can be defined as below, respectively:

$$C_{11} = \frac{E(z)}{{\left( {1 - \nu^{2} } \right)}},\;\;C_{55} = \frac{E(z)}{{2\left( {1 + \nu } \right)}}$$
(15)

2.6 Equations of motion

The equations of motion for FG beams resting on VEFs are derived using the Hamilton principle as below [17, 89,90,91,92]:

$$\int\limits_{0}^{t} {\left( {\delta U + \delta U_{{{\text{ef}}}} - \delta K + \delta V} \right){\text{d}}t = 0}$$
(16)

where \(\delta\) indicates the variation, U, Uef, K and V represent the strain energy, the strain energy of EFs, the kinetic energy of the FG beam, and the variation of the external work done by the applied external load.

The variation of the strain energy of the FG beam can be expressed as:

$$\begin{aligned} \delta U & = \int\limits_{V} {\left( {\sigma_{xx} \delta \varepsilon_{xx} + \tau_{xz} \delta \tau_{xz} } \right)} {\text{d}}V \\ & = \int\limits_{A} {\left( {N_{x} \delta \varepsilon_{x}^{0} + M_{x}^{b} \delta k_{x}^{b} + M_{x}^{s} \delta k_{x}^{s} + R_{xz}^{s} \delta \gamma_{xz}^{0} } \right)} {\text{d}}A \\ \end{aligned}$$
(17)

where

$$\left( {N_{x} ,M_{x}^{b} ,M_{x}^{s} } \right) = \int\limits_{ - h/2}^{h/2} {\left( {1,z,f} \right)\sigma_{i} {\text{d}}z} ,\;{\text{and}}\;R_{xz}^{s} = \int\limits_{ - h/2}^{h/2} {g.\tau_{xz} {\text{d}}z}$$
(18)

The variation of the strain energy of VEFs can be given as:

$$\delta U_{{{\text{ef}}}} = \int\limits_{A} {\left( {K_{w} (x)w_{0} \delta w_{0} - K_{s} \left( {\frac{{{\text{d}}^{2} w_{0} }}{{{\text{d}}x^{2} }}} \right)\delta w} \right){\text{d}}A}$$
(19)

The variation in kinetic energy may be expressed as follows:

$$\begin{aligned} \delta K & = \int\limits_{V} {\rho (z)\left( {\dot{u}\delta \dot{u} + \dot{w}\delta \dot{w}} \right){\text{d}}V} \\ & = \int\limits_{A} {\left\{ {I_{0} \left[ {\dot{u}_{0} \delta \dot{u}_{0} + \dot{w}_{0} \delta \dot{w}_{0} } \right]} - I_{1} \left( {\dot{u}_{0} \frac{{\partial \delta {\kern 1pt} \dot{w}_{0} }}{\partial x} + \frac{{\partial \dot{w}_{0} }}{\partial x}\delta \, \dot{u}_{0} } \right) + J_{1} \left( {\left( {k_{1} \,A^{{\prime }} } \right)\left( {\dot{u}_{0} \frac{{\partial \delta \,\dot{\theta }{\kern 1pt} }}{\partial x} + \frac{{\partial {\kern 1pt} \dot{\theta }}}{\partial x}\delta \, \dot{u}_{0} } \right)} \right) \right.}\\ & \quad + I_{2} \left( {\frac{{\partial \dot{w}_{0} }}{\partial x}\frac{{\partial \delta \, \dot{w}_{0} }}{\partial x}} \right) + K_{2} \left( {\left( {k_{1} \,A^{{\prime }} } \right)^{2} \left( {\frac{{\partial \dot{\theta }}}{\partial x}\frac{{\partial \delta \, \dot{\theta }}}{\partial x}} \right)} \right)\left. { - J_{2} \left( {\left( {k_{1} \,A^{{\prime }} } \right)\left( {\frac{{\partial \dot{w}_{0} }}{\partial x}\frac{{\partial \delta \, \dot{\theta }}}{\partial x} + \frac{{\partial \dot{\theta }}}{\partial x}\frac{{\partial \delta \, \dot{w}_{0} }}{\partial x}} \right)} \right)} \vphantom{\left( {\dot{u}_{0} \frac{{\partial \delta \,\dot{\theta }{\kern 1pt} }}{\partial x} + \frac{{\partial {\kern 1pt} \dot{\theta }}}{\partial x}\delta \, \dot{u}_{0} } \right)}\right\}{\text{d}}A \\ \end{aligned}$$
(20)

where the dot-exponent (\(^{ \cdot }\)) indicates the differentiation concerning the time variable t, and the mass moment of inertias may be defined as:

$$\begin{aligned} & \left( {I_{0} ,I_{1} ,I_{2} } \right) = \int\limits_{ - h/2}^{h/2} {\left( {1,z,z^{2} } \right)} p(z){\text{d}}z \\ & \left( {J_{1} ,J_{2} ,K_{2} } \right) = \int\limits_{ - h/2}^{ + h/2} {\left( {f,zf,f^{2} } \right)\rho (z){\text{d}}z} \\ \end{aligned}$$
(21)

The variation of the external work may be given as:

$$\delta V = - \int\limits_{A} {\left( {N_{x}^{0} \frac{{\partial w_{0} }}{\partial x}\frac{{\partial \delta w_{0} }}{\partial x}} \right){\text{d}}A}$$
(22)

where \(N_{x}^{0}\) is the applied axial load.

By inserting the expressions of δU, δUef, δK and δV from Eqs. (17), (19), (20) and (22) in Eq. (16) and integrating by parts and collecting the coefficients of (\(\delta u_{0}\), \(\delta w_{0}\) and \(\delta \theta\)), the equation of motion of FG beam resting on VEFs is found as follows:

$$\begin{aligned} & \delta u_{0} :\frac{{\partial N_{x} }}{\partial x} - I_{0} \ddot{u}_{0} + I_{1} \frac{{\partial \ddot{w}_{0} }}{\partial x} - kA^{{\prime }} \,J_{1} \frac{{\partial \ddot{\theta }}}{\partial x} = 0 \\ & \delta w_{0} :\frac{{\partial^{2} M_{x}^{b} }}{{\partial x^{2} }} + K_{{\text{w}}} w_{0} - K_{{\text{s}}} \left( {\frac{{\partial^{2} w_{0} }}{{\partial x^{2} }}} \right) + N_{x}^{0} \frac{{\partial^{2} w_{0} }}{{\partial x^{2} }} - I_{0} \ddot{w}_{0} - I_{1} \left( {\frac{{\partial \ddot{u}_{0} }}{\partial x}} \right) + I_{2} \left( {\frac{{\partial^{2} \ddot{w}_{0} }}{{\partial x^{2} }}} \right) - J_{2} \left( {k\,A^{{\prime }} \frac{{\partial^{2} \ddot{\theta }}}{{\partial x^{2} }}} \right) = 0 \\ & \delta \theta : - k_{1} \,M_{x}^{s} + k\,A^{{\prime }} \frac{{\partial S_{xz}^{s} }}{\partial x} + J_{1} \left( {kA^{{\prime }} \frac{{\partial \ddot{u}_{0} }}{\partial x}} \right) + K_{2} \left( {\left( {k\,A^{{\prime }} } \right)^{2} \frac{{\partial^{2} \ddot{\theta }}}{{\partial x^{2} }}} \right) - J_{2} \left( {kA^{{\prime }} \frac{{\partial^{2} \ddot{w}_{0} }}{{\partial x^{2} }}} \right) = 0 \\ \end{aligned}$$
(23)

Inserting Eq. (12) into Eq. (14) and the consequent outcomes in Eq. (18), the stress resultants are found concerning strains as:

$$\left\{ {\begin{array}{*{20}c} {N_{x} } \\ {M_{x}^{b} } \\ {M_{x}^{s} } \\ \end{array} } \right\} = \left[ {\begin{array}{*{20}c} {A_{11} } &\quad {B_{11} } &\quad {B_{11}^{s} } \\ {B_{11} } &\quad {D_{11} } &\quad {D_{11}^{s} } \\ {B_{11}^{s} } &\quad {D_{11}^{s} } &\quad {H_{11}^{s} } \\ \end{array} } \right]\left\{ {\begin{array}{*{20}c} {\varepsilon_{x}^{0} } \\ {k_{x}^{b} } \\ {k_{x}^{s} } \\ \end{array} } \right\},$$
(24)

and

$$S_{xz}^{s} = A_{55}^{s} \gamma_{xz}$$
(25)

where the stiffness components are:

$$\left\{ {\begin{array}{*{20}c} {A_{11} } & {B_{11} } & {D_{11} } & {B_{11}^{s} } & {D_{11}^{s} } & {H_{11}^{s} } \\ \end{array} } \right\} = \int\limits_{ - h/2}^{h/2} {C_{11} \left( {1,z,z^{2} ,f(z),z \, f(z),f^{2} (z)} \right)} \;{\text{d}}z$$
(26a)
$$A_{55}^{s} = \int\limits_{ - h/2}^{h/2} {C_{55} \left[ {g(z)} \right]^{2} \;{\text{d}}z} ,$$
(26b)

Substituting Eqs. (24)–(26) in Eq. (23), the equations of motion for FG beams resting on VEFs may be rewritten regarding the displacements (\(u_{0}\), \(w_{0}\) and \(\theta\)):

$$A_{11} \frac{{\partial^{2} u_{0} }}{{\partial x^{2} }} - B_{11} \frac{{\partial^{3} w_{0} }}{{\partial x^{3} }} + \left( {B_{11}^{s} k} \right)\,\frac{\partial \theta }{{\partial x}} - I_{0} \frac{{\partial^{2} u_{0} }}{{\partial t^{2} }} + I_{1} \,\frac{{\partial^{3} u_{0} }}{{\partial t^{2} \partial x}}w_{0} - J_{1} \,A^{{\prime }} k\frac{{\partial^{3} \theta }}{{\partial t^{2} \partial x}} = 0,$$
(27a)
$$\begin{aligned} & B_{11} \frac{{\partial^{3} u_{0} }}{{\partial x^{3} }} - D_{11} \frac{{\partial^{3} w_{0} }}{{\partial x^{3} }} + \left( {D_{11}^{s} k} \right)\frac{{\partial^{2} \theta }}{{\partial x^{2} }} + K_{{\text{w}}} w_{0} - K_{{\text{s}}} \left( {\frac{{\partial^{2} w_{0} }}{{\partial x^{2} }}} \right) + N_{x}^{0} \left( {\frac{{\partial^{2} w_{0} }}{{\partial x^{2} }}} \right) - \,I_{0} \frac{{\partial^{2} w_{0} }}{{\partial t^{2} }} - I_{1} \,\left( {\frac{{\partial^{3} u_{0} }}{{\partial t^{2} \partial x}}} \right)\, \\ & \quad + I_{2} \left( {\frac{{\partial^{4} w_{0} }}{{\partial t^{2} \partial x^{2} }}} \right) - J_{2} \left( {kA^{{\prime }} \frac{{\partial^{4} \theta }}{{\partial t^{2} \partial x^{2} }}} \right) = 0 \\ \end{aligned}$$
(27b)
$$\begin{aligned} & - \left( {B_{11}^{s} k} \right)\frac{{\partial u_{0} }}{\partial x} - \left( {D_{11}^{s} k} \right)\frac{{\partial^{2} w_{0} }}{{\partial x^{2} }} - H_{11}^{s} k^{2} \theta + A_{55}^{s} \left( {k\,A^{{\prime }} } \right)^{2} \frac{{\partial^{2} \theta }}{{\partial x^{2} }} + J_{1} \,\left( {k\,A^{{\prime }} \frac{{\partial^{3} u_{0} }}{{\partial t^{2} \partial x}}} \right) - J_{2} \,\left( {k\,A^{{\prime }} \frac{{\partial^{4} w_{0} }}{{\partial t^{2} \partial x^{2} }}} \right) \\ & \quad + K_{2} \left( {\left( {k\,A^{{\prime }} } \right)^{2} \frac{{\partial^{4} \theta }}{{\partial t^{2} \partial x^{2} }}} \right) = 0 \\ \end{aligned}$$
(27c)

3 Analytical solution

Navier’s method is employed to solve the governing differential equation of the current problem. For this aim, the following series of Fourier is utilized:

$$\left\{ {\left. {\begin{array}{*{20}c} {u_{0} } \\ {w_{0} } \\ \theta \\ \end{array} } \right\}} \right. = \sum\limits_{m = 1}^{\infty } {\left. {\left\{ {\begin{array}{*{20}c} {U_{m} e^{i\omega \,t} \cos \left( {\lambda x} \right)} \\ {W_{m} e^{i\omega \,t} \sin \left( {\lambda x} \right)} \\ {X_{m} e^{i\omega \,t} \sin \left( {\lambda x} \right)} \\ \end{array} } \right.} \right\}}$$
(28)

here U, W and X are random unknown parameters to be found and \(\omega\) is the natural frequency. Note that, \(\sqrt i = - 1\) is the imaginary unit.

For the free vibration of FG beams resting on VEFs, Eq. (28) is inserted in the equations of motion (27), and finally, the following eigenvalue equations are found for any fixed value of m:

$$\left[ {\begin{array}{*{20}c} {\Gamma_{11} } &\quad {\Gamma_{12} } &\quad {\Gamma_{13} } \\ {\Gamma_{21} } &\quad {\Gamma_{22} } &\quad {\Gamma_{23} } \\ {\Gamma_{31} } &\quad {\Gamma_{32} } &\quad {\Gamma_{33} } \\ \end{array} } \right] - \omega^{2} \left[ {\begin{array}{*{20}c} {M_{11} } &\quad {M_{12} } &\quad {M_{13} } \\ {M_{21} } &\quad {M_{22} } &\quad {M_{23} } \\ {M_{31} } &\quad {M_{32} } &\quad {M_{33} } \\ \end{array} } \right]\left\{ {\begin{array}{*{20}c} {U_{m} } \\ {V_{m} } \\ {W_{m} } \\ \end{array} } \right\} = \left\{ {\begin{array}{*{20}c} 0 \\ 0 \\ 0 \\ \end{array} } \right\}$$
(29)

Additionally, the following equation is found for the buckling of FG beams resting on VEFs:

$$\left( {\left[ {\begin{array}{*{20}c} {\Gamma {}_{11}} &\quad {\Gamma {}_{12}} &\quad {\Gamma {}_{13}} \\ {\Gamma {}_{12}} &\quad {\Gamma {}_{22}} &\quad {\Gamma_{23} } \\ {\Gamma {}_{13}} &\quad {\Gamma {}_{23}} &\quad {\Gamma {}_{33}} \\ \end{array} } \right] + \Lambda \left[ {\begin{array}{*{20}c} 0 &\quad 0 &\quad 0 \\ 0 &\quad \beta &\quad 0 \\ 0 &\quad 0 &\quad 0 \\ \end{array} } \right]} \right)\left\{ {\left. {\begin{array}{*{20}c} {U_{m} } \\ {W_{m} } \\ {X_{m} } \\ \end{array} } \right\}} \right. = \left\{ {\left. {\begin{array}{*{20}c} 0 \\ 0 \\ 0 \\ \end{array} } \right\}} \right.$$
(30)

where

$$\begin{aligned} M_{11} & = - I_{0} ,M_{12} = M_{21} = \lambda \,I_{1} ,M_{13} = M_{31} = - \,J_{1} k\,A^{{\prime }} \,\lambda \\ M_{22} & = - I_{0} - \left( {I_{2} \lambda^{2} } \right),M_{44} = - K_{2} \left( {\left( {k\,A^{{\prime }} } \right)^{2} \lambda^{2} } \right) \\ M_{32} & = M_{23} = J_{2} \left( {k\,A^{{\prime }} \lambda^{2} } \right) \\ \end{aligned}$$
(31a)

and

$$\begin{gathered} \Gamma_{11} = - \left( {A_{11} \lambda^{2} } \right),\;\Gamma_{12} = \left( {B_{11} \lambda^{3} } \right),\;\Gamma_{13} = \lambda \left( {kB_{11}^{s} } \right),\;\beta = N_{cr} \lambda^{2} \hfill \\ \Gamma_{21} = \alpha \left( {B_{11} \lambda^{2} } \right),\;\Gamma_{22} = - \left( {D_{11} \lambda^{4} } \right) - K_{W} - K_{P} \lambda^{2} ,\;\Gamma_{23} = - k\left( {D_{11}^{s} \lambda^{2} } \right) \hfill \\ \Gamma_{31} = \lambda \left( {kB_{11}^{s} } \right),\;\Gamma_{32} = - k\left( {D_{11}^{s} \lambda^{2} } \right),\;L_{33} = - k\left( {H_{11}^{s} k} \right) - \left( {k\,A^{{\prime }} } \right)^{2} \;A_{55}^{s} \lambda^{2} \hfill \\ \end{gathered}$$
(31b)

4 Numerical results

This section presents various examples, including validations for the free vibration and buckling of the FG beams resting on VEFs. The FG beam is supposed to be made of a mixture of metal (Aluminum, Al) and ceramic (Alumina, Al2O3):

Ceramic (Alumina, Al2O3): Ec = 380 GPa, ν = 0.3 and ρc = 3960 kg/m3.

Metal (Aluminium, Al): Em = 70 GPa, ν = 0.3 and ρm = 2702 kg/m3.

For the sake of simplicity and comparisons, the following dimensionless parameters are used for the natural frequency and critical buckling load:

$$\begin{aligned} & D_{{\text{c}}} = \frac{{E_{{\text{c}}} h^{3} }}{{12\left( {1 - 2\nu^{2} } \right)}},\;D_{m} = \frac{{E_{m} h^{3} }}{{12\left( {1 - 2\nu^{2} } \right)}},\;\overline{\omega }_{n} = \sqrt[4]{{\frac{{\rho_{{\text{c}}} AL^{4} \omega_{n}^{2} }}{EI}}}, \\ & \hat{\omega }_{n} = \frac{{\omega_{n} L^{2} }}{h}\sqrt {\frac{{\rho_{m} }}{{E_{m} }}} ,\;K_{{\text{p}}} = \frac{{k_{{\text{p}}} D_{i} }}{{L^{2} }},\;\;i = m,c \\ \end{aligned}$$
$$\overline{N} = N_{{{\text{cr}}}} \frac{{12L^{2} }}{{h^{3} E_{m} }},\;\overline{T}_{{{\text{cr}}}} = N_{{{\text{cr}}}} \frac{{L^{2} }}{{I_{{\text{s}}} E_{{\text{c}}} }},\;K_{{\text{p}}} = \frac{{k_{{\text{p}}} D_{i} }}{{L^{2} }},\;i = m,c$$

4.1 Validation studies

In this section, the accuracy of the proposed formulation is validated. Isotropic beams, FG beams, as well as different cases of geometry, foundation parameters, and thickness (thin or thick) are considered.

4.1.1 Comparison study 1: investigation of the free vibration of FG beams

Table 2 shows the comparisons of the values of dimensionless natural frequencies (DNFs) of the P-FG beams with the results of Nguyen et al. [93], Ibnorachid et al. [94] and Simsek [95].

Table 2 Comparisons of the DNFs of P-FG beams
Full size table

Besides, the present results are also validated for isotropic homogenous beams resting on Winkler–Pasternak EFs with the results of Chen et al. [96], Fahsi et al. [97], and Chikh [98] in Table 3.

Table 3 Comparisons of the DNFs of isotropic homogeneous beams resting on a Winkler–Pasternak EFs
Full size table

Consequently, the results obtained and given in Tables 2 and 3 are compatible with those available in the literature, so these results validate the validity of the current formulation for natural frequency analysis of FG beams with and without EFs.

4.1.2 Comparison study 2: investigation of the buckling of FG beams

Table 4 shows the comparisons of the values of dimensionless buckling loads (DBLs) P-FG beams with the results of Nguyen et al. [93] and Vo et al. [99].

Table 4 Comparison of the DBL of perfect simply-supported P-FG beams
Full size table

Table 5 compares the DBLs of the homogeneous slender beams (L/h = 20) resting on two-parameter EFs with the results of Atmane et al. [53], Fahsi et al. [97], and Chikh [98].

Table 5 The parameter Ncr of the buckling load of an isotropic homogeneous beam with L/h = 20 resting on an EF
Full size table

According to the two comparisons mentioned above, it is concluded that the present formulation using a new beam theory with three unknowns is in good agreement with the solutions given by the previously mentioned works.

4.2 Parametrical studies

4.2.1 Study 1: effects of VEFs on the DNFs of FG-beams

In this example, the effects of the variation of the Winkler parameter of the EFs on the DNFs of P-FG beams are examined. For this context, Figs. 2, 3 and 4 show the variation of dimensionless fundamental natural frequencies (DFNFs) FG beams resting on different types of EFs (linear, parabolic, sinusoidal, cosine, exponential, and uniform) versus power-law index (p) and length-to-thickness ratio (L/h), and coefficient ψ, respectively. Figure 2. shows that the DFNFs increase with the rise of p for the types of uniform and parabolic EFs, whereas the DFNFs decrease for the other kinds of EFs with the growth of p. Figure 3. illustrates that the DFNFs increase with the rise of L/h for all types of EFs. Figure 4 demonstrates that the DFNFs increase with the rise in the coefficient ψ, except in the case of a parabolic EF, where the relation between the DNF and coefficient ψ becomes an inverse. Furthermore, the sinusoidal variation of the Winkler EF results in the highest DFNFs, whereas the lowest DFNFs are observed for the parabolic variation of the Winkler EF in all cases.

Fig. 2
figure 2

The variation of DFNF of P-FG beams with different types of EFs versus p (L/h = 5, kw = 100, kp = 10 and \(\psi\) =20)

Full size image
Fig. 3
figure 3

The variation of DFNF of P-FG beams with different types of EFs versus L/h (p = 2, kw = 100, kp = 10 and \(\psi\) =20)

Full size image
Fig. 4
figure 4

The variation of DFNF of P-FG beams with different types of EFs versus coefficient \(\psi\) coefficient (p = 2, L/h = 10, kw = 100 and kp = 10)

Full size image

4.2.2 Study 2: effects of VEFs on the DBLs of FG-beams

In the second study, the effects of the variation of the Winkler parameter of the EFs on the DBLs of P-FG beams are investigated. For this framework, Figs. 5, 6 and 7 demonstrate the variation of DBLs FG beams resting on different types of EFs against the power-law index (p), length-to-thickness ratio (L/h), and coefficient ψ, respectively. According to Fig. 5, it is clear that DBLs decrease with the increment of p. Furthermore, the highest values of DBLs are observed in the sinusoidal variation of the Winkler EF. Interestingly, the DBLs decline rapidly for p < 2, i.e., for FG beams with high stiffness, and then it remains nearly constant as the FG beam becomes softer.

Fig. 5
figure 5

The variation of DBL of P-FG beams with different types of EFs versus p(L/h = 10, kw = 10, kp = 10 and \(\psi\) = 20)

Full size image
Fig. 6
figure 6

The variation of DBL of P-FG beams with different types of EFs versus L/h (p = 2, kw = 10, kp = 10 and \(\psi\) =20)

Full size image
Fig. 7
figure 7

The variation of DBL of P-FG beams with different types of EFs versus \(\psi\) (L/h = 10, kw = 10, ks = 10 and \(p\) =2)

Full size image

Figure 6 illustrates a beam FG with the different types of foundations whose power index is taken to be 2. We can notice from this figure that the values of DBL increase slightly with the increase of the value of the ratio (L/h), in particular for (L/h \(\in\)] 2, 10[), then the rate of variation of Ncr tends to stabilize. In addition, the same mechanical behavior is observed for the variation of DBL as a function of coefficient ψ (Fig. 7), except that the increase in the DBL is more significant than that observed in Fig. 6 for linear foundations, sinusoidal, cosine, and exponential. For the case of the FG beam resting on an elastic foundation of a form of parabolic variation, the parameter DBL decreases with the increase in the coefficient ψ. It can also be seen that the maximum and minimum values of the DBL are obtained for the cases of beams with sinusoidal and parabolic EFs, respectively.

After this analysis, it could be concluded that the sigmoidal variation of the Winkler foundation should be used to obtain a higher natural frequency and critical buckling load in the design of FG beams.

4.2.3 Study 3: investigation of the free vibration of imperfect FG beams

The curves of variation of the DNF of the first mode of the different beams FG according to the parameter of power index of the material “p” with four models of the distribution of porosity, namely type 1 (uniform), type 2 (X shape), type 3 (O shape) and type 4 (V shape) and different porosity coefficients (α = 0; 0.1 and 0.2) have been presented in Figs. 8, 9, 10 and 11 for different types of distribution of Winkler EFs: constant, linear, parabolic and sigmoid, respectively.

Fig. 8
figure 8

The variation of FNF of imperfect FG beams resting on constant type of VEFs according to p (kw = 10 and kp = 10)

Full size image
Fig. 9
figure 9

The variation of DFNF of imperfect FG beams resting on linear type of VEFs according to p (kw = 10, kp = 10 and \(\psi\) =20)

Full size image
Fig. 10
figure 10

The variation of DFNF of imperfect FG beams resting on parabolic type of VEFs according to p (kw = 10, kp = 10 and \(\psi\) =20)

Full size image
Fig. 11
figure 11

The variation of DFNF of imperfect FG beams resting on sigmoidal type of VEFs according to p (kw = 10, kp = 10 and \(\psi\) =20)

Full size image

It can be seen from the curves of Figs. 8, 9, 10 and 11 that the increase in the porosity parameter leads to the rise in the DFNF of the FG beams. It is also quite remarkable that the parameter of the DFNF of the FG beams also increases with the increase of the parameter of the material for the two cases of the thickness ratios L/h = 5 and 20, except that the case of the beams FG for L/h = 5. The increase in DFNF stops when the “p” equals 2, whereas it begins to decrease with the rise in “p”.

This can be explained by the decrease in the stiffness of the FG beam with the increase in the percentage of pores, which led to the weakening of the FG beam. In addition, it is observed that the maximum DFNF is obtained for the FG beams with a porosity factor equal to 0.2; this remark concerns all the cases studied regardless of the type of porosity distribution form or the type of VEFs. It can also be seen that the ratio (L/h) considerably affects the DFNF of the FG beam.

4.2.4 Study 4: investigation of the buckling of imperfect FG beams

The parametric study of this last example covers the effects of the porosity coefficient and the shape of the porosity distribution on the stability (dimensionless buckling loads DBLs) of the P-FGM porous beam resting on VEFs under an axial load.

The buckling analysis is performed on the FG beam resting on VEFs whose variation of the Winkler parameter is in linear, parabolic, and sinusoidal form, of L∕h = 5 and 20. The effect of porosity volume fraction and distribution pattern (H, X, O and V) on the buckling behavior is given in Table 6. The foundation parameters kw, kp and the coefficient ψ are taken to be 100, 2.5 and 5, respectively. It can be seen that the DBL increases monotonically when the power index “p” and the porosity parameter “α” decrease. It is also observed that DBL decreases as the L/h decreases. In addition, the lowest values of the DBL are obtained for the case of the H-PDP, whereas the highest values of the DBL are found for the case of the X-PDP. In perspective of this work, it is planned to apply a Quasi-3D theory for the analysis of the mechanical behavior of functionally graded porous beams resting on elastic foundations whose two parameters of Winkler and Pasternak are taken to be varied in the direction of the length of the beam under the combination of the different types of loading (thermal, mechanical, hygrothermal).

Table 6 The variation of DBL of the imperfect FG beam resting on the different types of VEFs versus various PDPs (kw = 100, ks = 2.5 and \(\psi\) =5)
Full size table

5 Conclusions

The vibration response and stability of perfect and imperfect FG beams resting on VEFs are investigated in this work using a novel high-order theory of successful SDT. The current HSDT has only three unknowns without needing a shear correction coefficient, which means it is better than other similar HSDTs found in the literature. The FG beams are assumed to rest on VEFs. Because the beam is supposed to be simply supported, and the analytical solution is obtained using the Navier solution method. The impacts of various parameters on the free vibration and buckling behaviors of FG beams, such as the power law index, the length-to-thickness ratio, the type of VEFs, and the porosity distribution patterns, are examined in detail. For the shear deformation theory used in this article, the results obtained were compared against those reported by various beam theories. Thus, the developed HSDT produces results with good precision compared to other HSDTs with a higher number of unknowns. Finally, it can be said that the proposed theory effectively predicts the effect of VEFs on the analysis of the dynamic and buckling behaviors of porous FG beams.

Based on the results obtained, the following conclusions can be drawn from this analysis:

  • The length-to-thickness ratio significantly impacts DNF and DBL.

  • The DBL increase as the length-to-thickness ratio increases.

  • The DFNF decreases when the volume fraction index increases.

  • The DBL decreases with the increment of the power law index.

  • The type of elastic Winkler foundation variable along the axial direction (linear, parabolic, sinusoidal, cosine, exponential and uniform) has a considerable effect on the variation of DFNF and DBL of FG beams.

  • In the presence of porosity, the DFNs of the FG beams increase, whereas the DBL decreases.

In the future, the present study will be extended to the several mechanical behaviors of FG beams under different thermal loads and other boundary conditions.