1. Introduction

Laminated composite plates are widely used in industry and new fields of technology. Due to the high degrees of anisotropy and the low rigidity in transverse shear of the plates, the Kirchhoff hypothesis as a classical theory is no longer adequate. The hypothesis states that the normal to the midplane of a plate remains straight and normal after deformation because of the negligible transverse shear effects. Refined theories without this assumption have been used recently. The free vibration frequencies calculated by using the classical theory of thin plates are higher than those obtained by the Mindlin theory of plates [1], in which the transverse shear and rotary inertia effects are included.

A number of shear deformation theories have been proposed to date. The first such theory for laminated isotropic plates was apparently [2]. This theory was generalized to laminated anisotropic plates in [3]. It was shown in [4–6] that the Yang–Norris–Stavski (YNS) theory [3] is adequate for predicting the flexural vibration response of laminated anisotropic plates in the first few modes. In [7], the YNS theory was employed to study the cylindrical bending of antisymmetric cross-ply and angle-ply plate-strips under sinusoidal loading and the free vibration of antisymmetric angle-ply plate-strips (see also [8, 9]. Using the YNS theory, a closed-form solution for the free vibration of simply supported rectangular plates of antisymmetric angle-ply laminates was obtained in [10]. In [11] were also presented exact three-dimensional elasticity solutions for the free vibration of isotropic and anisotropic composite laminated plates, which serve as benchmark solutions for comparison by many researchers. The free vibration of antisymmetric angle-ply laminated plates, with account of transverse shear deformations, was investigated in [12] by using the finite-element method The author also derived a set of variationally consistent equilibrium equations for the kinematic models originally proposed by Levinson and Murthy [13]. In [14], analytical and finite- element solutions for the vibration and buckling of laminated composite plates were found by using various theories of plates to prove the necessity for shear deformation theories to predict the behavior of composite laminates. Using a higher-order shear deformation theory, finite-element solutions for free vibration analysis of laminated composite plates were also obtained in [15]. The complete set of linear equations of a second-order theory was derived in [16] to analyze the free vibration behavior of cross-ply and antisymmetric angle-ply laminated plates. In [17], the natural frequencies of composite plates with random material properties were determined by using a higher-order shear deformation theory (including the rotatory inertia effect). The natural frequencies of laminated composite plates were also found in [18] by employing a third-order shear deformation theory. In [19], the dynamic deflections and the stresses of a functionally graded simply supported beam subjected to a moving mass were investigated by using the Euler–Bernoulli, Timoshenko, and the parabolic shear deformation theory of beams. In [20], the free vibration of functionally graded beams with different boundary conditions was examined by using the classical, first-order, and different higher-order shear deformation theories of beams. A stress analysis of a functionally graded plate subjected to thermal and mechanical loads was performed in [21] by using a two-dimensional higher-order theory. A new trigonometric shear deformation theory for isotropic and composite laminated and sandwich plates was developed recently in [22], where displacements of the middle surface were expanded in terms of tangential trigonometric functions of the thickness coordinate, and the transverse displacements were assumed to be constant across the thickness.

In this paper, a refined and simple theory of plates is presented and applied to the investigation of free vibration behavior of laminated composite plates on elastic foundations. This theory is based on the assumption that the in-plane and transverse displacements consist of bending and shear components where the bending components do not contribute to shear forces, and likewise, the shear components do not contribute to bending moments. The most interesting feature of this theory is that it allows for parabolic distributions of transverse shear stresses across the plate thickness and satisfies zero shear stress conditions at the top and bottom surfaces of the plate without using shear correction factors. In addition, it contains four independent variables, as against five in other shear deformation theories. The elastic foundation is modeled as a two-parameter Pasternak foundation. The equations of motion are derived using Hamilton’s principle. The fundamental frequencies are found by solving an eigenvalue equation. The results obtained by the present method are compared with solutions derived from other models known from the literature and are found to be in good agreement with them.

2. Theoretical Formulations

2.1. Basic assumptions

The assumptions of the present theory are as follows.

  1. (i)

    Displacements are small in comparison with plate thickness, and therefore the strains involved are infinitesimal.

  2. (ii)

    The transverse displacement w includes two components — the bending w b and shear w s ones, which are functions only of x and y coordinates,

    $$ w\left( {x,y,z} \right)={w_b}\left( {x,y} \right)+{w_s}\left( {x,y} \right). $$
    (1)
  3. (iii)

    The transverse normal stress σ z is negligible in comparison with the in-plane stresses σ x and σ y .

  4. (iv)

    The displacements u in the x-direction and v in the y-direction consist of extension, bending, and shear components,

    $$ \begin{array}{*{20}{c}} {u={u_0}+{u_b}+{u_s},} & {\nu ={\nu_0}+} \\ \end{array}{\nu_b}+{\nu_s}. $$
    (2)

The bending components u b and v b are assumed to be similar to the displacements given by the classical theory of plates, namely

$$ \begin{array}{*{20}{c}} {{u_b}=-z\frac{{\partial {w_b}}}{{\partial x}},} & {{\nu_b}=-z\frac{{\partial {w_b}}}{{\partial y}}.} \\ \end{array} $$
(3)

The shear components u s and v s , in conjunction with w s , give rise to parabolic variations in the shear strains γ xz and γ yz and hence in the shear stresses τ xz and τ yz across the thickness of the plate in such a way that the stresses τ xz and τ yz are zero at the top and bottom faces of the plate. Consequently, the expression for u s and v s can be given as

$$ \begin{array}{*{20}{c}} {{u_s}=-f(z)\frac{{\partial {w_s}}}{{\partial x}},} & {{\nu_s}=-f(z)\frac{{\partial {w_s}}}{{\partial y}}.} \\ \end{array} $$
(4)

2.2. Kinematics

Based on the assumptions made in the preceding section, the displacement field can be obtained using Eqs. (1)-(4):

$$ \begin{array}{*{20}{c}} {u\left( {x,y,z} \right)={u_0}\left( {x,y} \right)-z\frac{{\partial {w_b}}}{{\partial x}}-f(z)\frac{{\partial {w_s}}}{{\partial x}},} \\ {\nu \left( {x,y,z} \right)={\nu_0}\left( {x,y} \right)-z\frac{{\partial {w_b}}}{{\partial y}}-f(z)\frac{{\partial {w_s}}}{{\partial y}},} \\ {w\left( {x,y,z} \right)={w_b}\left( {x,y} \right)+{w_s}\left( {x,y} \right),} \\ \end{array} $$
(5)

where the shape function f (z) is given as

$$ f(z)=\frac{{\left( {{h \left/ {\pi } \right.}} \right)\sinh \left( {\frac{\pi }{h}z} \right)-z}}{{\cosh \left( {{\pi \left/ {2} \right.}} \right)-1}}. $$

This function ensures zero transverse shear stresses at the top and bottom surfaces of the plate. The parabolic distributions of transverse shear stresses across the plate thickness are taken into account in the analysis by means of a hyperbolic function of the displacement field assumed.

The strains associated with the displacements in Eq. (5) are

$$ \begin{array}{*{20}{c}} {\left\{ {\begin{array}{*{20}{c}} {{\varepsilon_x}} \\ {{\varepsilon_y}} \\ {{\gamma_{xy }}} \\ \end{array}} \right\}=\left\{ {\begin{array}{*{20}{c}} {\varepsilon_x^0} \\ {\varepsilon_y^0} \\ {\gamma_{xy}^0} \\ \end{array}} \right\}+z\left\{ {\begin{array}{*{20}{c}} {k_x^b} \\ {k_y^b} \\ {k_{xy}^b} \\ \end{array}} \right\}+f(z)\left\{ {\begin{array}{*{20}{c}} {k_x^s} \\ {k_y^s} \\ {k_{xy}^s} \\ \end{array}} \right\},} & {\left\{ {\begin{array}{*{20}{c}} {{\gamma_{yz }}} \\ {{\gamma_{xz }}} \\ \end{array}} \right\}=g(z)\left\{ {\begin{array}{*{20}{c}} {\gamma_{yz}^s} \\ {\gamma_{xz}^s} \\ \end{array}} \right\},} \\ \end{array} $$

where

$$ \begin{array}{*{20}{c}} {\left\{ {\begin{array}{*{20}{c}} {\varepsilon_x^0} \\ {\varepsilon_y^0} \\ {\gamma_{xy}^0} \\ \end{array}} \right\}=\left\{ {\begin{array}{*{20}{c}} {\frac{{\partial {u_0}}}{{\partial x}}} \\ {\frac{{\partial {\nu_0}}}{{\partial x}}} \\ {\frac{{\partial {u_0}}}{{\partial y}}+\frac{{\partial {\nu_0}}}{{\partial x}}} \\ \end{array}} \right\},} & {\left\{ {\begin{array}{*{20}{c}} {k_x^b} \\ {k_y^b} \\ {k_{xy}^b} \\ \end{array}} \right\}=\left\{ {\begin{array}{*{20}{c}} {-\frac{{{\partial^2}{w_b}}}{{\partial {x^2}}}} \\ {-\frac{{{\partial^2}{w_b}}}{{\partial {y^2}}}} \\ {-2\frac{{{\partial^2}{w_b}}}{{\partial x\partial y}}} \\ \end{array}} \right\},} & {\left\{ {\begin{array}{*{20}{c}} {k_x^s} \\ {k_y^s} \\ {k_{xy}^s} \\ \end{array}} \right\}=\left\{ {\begin{array}{*{20}{c}} {-\frac{{{\partial^2}{w_s}}}{{\partial {x^2}}}} \\ {-\frac{{{\partial^2}{w_s}}}{{\partial {y^2}}}} \\ {-2\frac{{{\partial^2}{w_s}}}{{\partial x\partial y}}} \\ \end{array}} \right\},} & {\left\{ {\begin{array}{*{20}{c}} {\gamma_{yz}^s} \\ {\gamma_{xz}^s} \\ \end{array}} \right\}=\left\{ {\begin{array}{*{20}{c}} {\frac{{\partial {w_s}}}{{\partial y}}} \\ {\frac{{\partial {w_s}}}{{\partial x}}} \\ \end{array}} \right\}} \\ \end{array} $$
(6)

and

$$ g(z)=1-{f}^{\prime}(z)\quad \mathrm{with}\quad {f}^{\prime}(z)=\frac{df(z) }{dz }. $$

2.3. Constitutive equations

The stress state in each layer is given by Hooke’s law

$$ \left\{ {\begin{array}{*{20}{c}} {{\sigma_x}} \hfill \\ {{\sigma_y}} \hfill \\ {{\tau_{xy }}} \hfill \\ {{\tau_{yz }}} \hfill \\ {{\tau_{xz }}} \hfill \\ \end{array}} \right\}=\left[ {\begin{array}{*{20}{c}} {{Q_{11 }}} \hfill & {{Q_{12 }}} \hfill & 0 \hfill & 0 \hfill & 0 \hfill \\ {{Q_{12 }}} \hfill & {{Q_{22 }}} \hfill & 0 \hfill & 0 \hfill & 0 \hfill \\ 0 \hfill & 0 \hfill & {{Q_{66 }}} \hfill & 0 \hfill & 0 \hfill \\ 0 \hfill & 0 \hfill & 0 \hfill & {{Q_{44 }}} \hfill & 0 \hfill \\ 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & {{Q_{55 }}} \hfill \\ \end{array}} \right]\left\{ {\begin{array}{*{20}{c}} {{\varepsilon_x}} \hfill \\ {{\varepsilon_y}} \hfill \\ {{\gamma_{xy }}} \hfill \\ {{\gamma_{yz }}} \hfill \\ {{\gamma_{xz }}} \hfill \\ \end{array}} \right\}, $$

where Q ij are the stiffnesses, which are defined in terms of engineering constants in the material axes of the layer:

$$ \begin{array}{*{20}{c}} {{Q_{11 }}=\frac{{{E_{11 }}}}{{1-{\nu_{12 }}{\nu_{21 }}}},} \hfill & {{Q_{12 }}=\frac{{{\nu_{12 }}{E_{22 }}}}{{1-{\nu_{12 }}{\nu_{21 }}}},} \hfill & {{Q_{22 }}=\frac{{{E_{22 }}}}{{1-{\nu_{12 }}{\nu_{21 }}}},} \hfill & {{Q_{66 }}={G_{12 }},} \hfill & {{Q_{44 }}={G_{23 }},} \hfill & {{Q_{55 }}={G_{13 }}.} \hfill \\ \end{array} $$

Since the laminate is made of several orthotropic layers with their material axes oriented arbitrarily with respect to laminate coordinates, the constitutive equations of each layer must be transformed to the laminate coordinates x, y, and z. The stress–strain relations in the laminate coordinates of a kth layer are

$$ {{\left\{ {\begin{array}{*{20}{c}} {{\sigma_x}} \hfill \\ {{\sigma_y}} \hfill \\ {{\tau_{xy }}} \hfill \\ {{\tau_{yz }}} \hfill \\ {{\tau_{xz }}} \hfill \\ \end{array}} \right\}}^{(k) }}={{\left[ {\begin{array}{*{20}{c}} {{{\bar{Q}}_{11 }}} \hfill & {{{\bar{Q}}_{12 }}} \hfill & {{{\bar{Q}}_{16 }}} \hfill & 0 \hfill & 0 \hfill \\ {{{\bar{Q}}_{12 }}} \hfill & {{{\bar{Q}}_{22 }}} \hfill & {{{\bar{Q}}_{26 }}} \hfill & 0 \hfill & 0 \hfill \\ {{{\bar{Q}}_{16 }}} \hfill & {{{\bar{Q}}_{26 }}} \hfill & {{{\bar{Q}}_{66 }}} \hfill & 0 \hfill & 0 \hfill \\ 0 \hfill & 0 \hfill & 0 \hfill & {{{\bar{Q}}_{44 }}} \hfill & {{{\bar{Q}}_{45 }}} \hfill \\ 0 \hfill & 0 \hfill & 0 \hfill & {{{\bar{Q}}_{45 }}} \hfill & {{{\bar{Q}}_{55 }}} \hfill \\ \end{array}} \right]}^{(k) }}{{\left\{ {\begin{array}{*{20}{c}} {{\varepsilon_x}} \hfill \\ {{\varepsilon_y}} \hfill \\ {{\gamma_{xy }}} \hfill \\ {{\gamma_{yz }}} \hfill \\ {{\gamma_{xz }}} \hfill \\ \end{array}} \right\}}^{(k) }}, $$
(7)

where \( {{\bar{Q}}_{ij }} \) are the transformed material constants, which an given in [23].

2.4. Governing equations

Using Hamilton’s energy principle, we derive the equation of motion of the laminated composite plate

$$ \delta \int\limits_{{{t_1}}}^{{{t_2}}} {\left( {U+{U_F}-V-T} \right)dt=0,} $$

where U is the strain energy, T is the kinetic energy of the plate, U F is the strain energy of foundation, and V is the work of external forces. Employing the principle of minimum total energy leads to the general equation of motion and boundary conditions. Taking the variation of the above equation and integrating by parts, we obtain

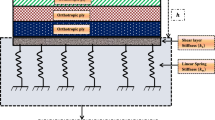
$$ \begin{array}{*{20}{c}} {\int\limits_{{{t_1}}}^{{{t_2}}} {\left[ {\int\limits_V {\left( {{\sigma_x}\delta {\varepsilon_x}+{\sigma_y}\delta {\varepsilon_y}+{\tau_{xy }}\delta {\gamma_{xy }}+{\tau_{yz }}\delta {\gamma_{yz }}+{\tau_{zx }}\delta {\gamma_{zx }}} \right)} } \right.} } \\ {\left. {-\rho \left( {{{\ddot{u}}_0}\delta {u_0}+{{\ddot{\nu}}_0}\delta {\nu_0}+\left( {{{\ddot{w}}_b}+{{\ddot{w}}_s}} \right)\delta \left( {{w_b}+{w_s}} \right)} \right)d\nu -\int\limits_A {{f_e}\delta \left( {{w_b}+{w_s}} \right)dA} } \right]dt=0,} \\ \end{array} $$
(8)

where two points above a variable means the second derivative with respect to time, and f e is the density of the reaction force of foundation. For the Pasternak foundation,

$$ {f_e}={k_0}w-{k_1}{\nabla^2}w. $$
(9)

If the foundation is modeled as a linear Winkler foundation, the coefficient k 1 in Eq. (9) is zero. With account of Eqs. (6), Eq. (8) takes the form

$$ \begin{array}{*{20}{c}} {\int\limits_{{{t_1}}}^{{{t_2}}} {\left[ {\int\limits_A {\left( {-\delta {u_0}{N_{x,x }}-\delta {\nu_0}{N_{y,y }}-\delta {u_0}{N_{xy,y }}-\delta {\nu_0}{N_{xy,x }}-\delta {w_b}M_{x,xx}^b-\delta {w_b}M_{y,yy}^b-2\delta {w_b}M_{xy,xy}^b} \right.} } \right.} } \\ {\left. {-\delta {w_s}M_{x,xx}^s-\delta {w_s}M_{y,yy}^s-2\delta {w_s}M_{xy,xy}^s-\delta {w_s}S_{xz,x}^s-\delta {w_s}S_{yz,y}^s} \right)dA} \\ {+\int\limits_A {{f_e}\left( {\delta {w_b}+\delta {w_s}} \right)dA-\int\limits_A {\left\{ {\delta {u_0}\left( {{I_1}{{\ddot{u}}_0}-{I_2}{{\ddot{w}}_{b,x }}-{I_4}{{\ddot{w}}_{s,x }}} \right)+\delta {\nu_0}\left( {{I_1}{{\ddot{\nu}}_0}-{I_2}{{\ddot{w}}_{b,y }}-{I_4}{{\ddot{w}}_{s,y }}} \right)} \right.} } } \\ {+\delta {w_b}\left[ {{I_1}\left( {{{\ddot{w}}_b}+{{\ddot{w}}_s}} \right)+{I_2}\left( {{{\ddot{u}}_{0x }}+{{\ddot{u}}_{0y }}} \right)-{I_3}\left( {{{\ddot{w}}_{b,xx }}+{{\ddot{w}}_{b,yy }}} \right)-{I_5}\left( {{{\ddot{w}}_{s,xx }}+{{\ddot{w}}_{s,yy }}} \right)} \right]} \\ {\left. {\left. {+\delta {w_s}\left[ {{I_1}\left( {{{\ddot{w}}_b}+{{\ddot{w}}_s}} \right)+{I_4}\left( {{{\ddot{u}}_{0x }}+{\nu_{0y }}} \right)-{I_5}\left( {{{\ddot{w}}_{b,xx }}+{{\ddot{w}}_{b,yy }}} \right)-{I_6}\left( {{{\ddot{w}}_{s,xx }}+{{\ddot{w}}_{s,yy }}} \right)} \right]} \right\}dA} \right]dt=0.} \\ \end{array} $$
(10)

The stress resultants N, M, and S are defined as

$$ \begin{array}{*{20}{c}} {\left\{ {\begin{array}{*{20}{c}} {{N_x},} & {{N_y},} & {{N_{xy }}} \\ {M_x^b,} & {M_y^b,} & {M_{xy}^b} \\ {M_x^s,} & {M_y^s,} & {M_{xy}^s} \\ \end{array}} \right\}=\int\limits_{{{-h \left/ {2} \right.}}}^{{{h \left/ {2} \right.}}} {\left( {{\sigma_x},{\sigma_y},{\tau_{xy }}} \right)\left\{ {\begin{array}{*{20}{c}} 1 \\ z \\ {f(z)} \\ \end{array}} \right\}dz,} } \\ {\left( {S_{xz}^s,S_{yz}^s} \right)=\int\limits_{{{-h \left/ {2} \right.}}}^{{{h \left/ {2} \right.}}} {\left( {{\tau_{xz }},{\tau_{yz }}} \right)g(z)dz.} } \\ \end{array} $$
(11)

Inserting Eq. (7) into Eqs. (11) and integrating across the thickness of the plate, the stress resultants are obtained

$$ \begin{array}{*{20}{c}} {\left\{ {\begin{array}{*{20}{c}} N \\ {{M^b}} \\ {{M^s}} \\ \end{array}} \right\}=\left[ {\begin{array}{*{20}{c}} A & B & {{B^s}} \\ A & D & {{D^s}} \\ {{B^s}} & {{D^s}} & {{H^s}} \\ \end{array}} \right]\left\{ {\begin{array}{*{20}{c}} \varepsilon \\ {{k^b}} \\ {{k^s}} \\ \end{array}} \right\},} & {S={A^2}\gamma, } \\ \end{array} $$

where

$$ \begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} {N={{{\left\{ {{N_x},{N_y},{N_{xy }}} \right\}}}^t},} & {{M^b}={{{\left\{ {M_x^b,M_y^b,M_{xy}^b} \right\}}}^t},} & {{M^s}=\left\{ {M_x^s,M_y^s,M_{xy}^s} \right\},} \\ \end{array}} \\ {\begin{array}{*{20}{c}} {\varepsilon =\left\{ {\varepsilon_x^0,\varepsilon_y^0,\gamma_{xy}^0} \right\},} & {{k^b}={{{\left\{ {k_x^b,k_y^b,k_{xy}^b} \right\}}}^t},} & {{k^s}={{{\left\{ {k_x^s,k_y^s,k_{xy}^s} \right\}}}^t},} \\ \end{array}} \\ {\begin{array}{*{20}{c}} {A=\left[ {\begin{array}{*{20}{c}} {{A_{11 }}} & {{A_{12 }}} & {{A_{16 }}} \\ {{A_{12 }}} & {{A_{22 }}} & {{A_{26 }}} \\ {{A_{16 }}} & {{A_{26 }}} & {{A_{66 }}} \\ \end{array}} \right],} & {B=\left[ {\begin{array}{*{20}{c}} {{B_{11 }}} & {{B_{12 }}} & {{B_{16 }}} \\ {{B_{12 }}} & {{B_{22 }}} & {{B_{26 }}} \\ {{B_{16 }}} & {{B_{26 }}} & {{B_{66 }}} \\ \end{array}} \right],} & {D=\left[ {\begin{array}{*{20}{c}} {{D_{11 }}} & {{D_{12 }}} & {{D_{16 }}} \\ {{D_{12 }}} & {{D_{22 }}} & {{D_{26 }}} \\ {{D_{16 }}} & {{D_{26 }}} & {{D_{66 }}} \\ \end{array}} \right],} \\ \end{array}} \\ {\begin{array}{*{20}{c}} {{B^s}=\left[ {\begin{array}{*{20}{c}} {B_{11}^s} & {B_{12}^s} & {B_{16}^s} \\ {B_{12}^s} & {B_{22}^s} & {B_{26}^s} \\ {B_{16}^s} & {B_{26}^s} & {B_{66}^s} \\ \end{array}} \right],} & {{D^s}=\left[ {\begin{array}{*{20}{c}} {D_{11}^s} & {D_{12}^s} & {D_{16}^s} \\ {D_{12}^s} & {D_{22}^s} & {D_{26}^s} \\ {D_{16}^s} & {D_{26}^s} & {D_{66}^s} \\ \end{array}} \right],} & {{H^s}=\left[ {\begin{array}{*{20}{c}} {H_{11}^s} & {H_{12}^s} & {H_{16}^s} \\ {H_{12}^s} & {H_{22}^s} & {H_{26}^s} \\ {H_{16}^s} & {H_{26}^s} & {H_{66}^s} \\ \end{array}} \right],} \\ \end{array}} \\ {\begin{array}{*{20}{c}} {S={{{\left\{ {S_{xz}^s,S_{yz}^s} \right\}}}^t},} & {\gamma ={{{\left\{ {{\gamma_{xz }},{\gamma_{yz }}} \right\}}}^t},} & {{A^s}=\left[ {\begin{array}{*{20}{c}} {A_{44}^s} & {A_{45}^s} \\ {A_{45}^s} & {A_{55}^s} \\ \end{array}} \right],} \\ \end{array}} \\ \end{array} $$
(12)

and the stiffness components and inertias are given as

$$ \begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} {\left( {{A_{ij }},{B_{ij }},{D_{ij }},B_{ij}^s,D_{ij}^s,H_{ij}^s} \right)=\int\limits_{{{-h \left/ {2} \right.}}}^{{{h \left/ {2} \right.}}} {{{\bar{Q}}_{ij }}\left( {1,z,{z^2},f(z),z\;f(z),{f^2}(z)} \right)dz,} } & {\left( {i,j} \right)=\left( {1,2,6} \right),} \\ \end{array}} \\ {\begin{array}{*{20}{c}} {A_{ij}^s=\int\limits_{{{-h \left/ {2} \right.}}}^{{{h \left/ {2} \right.}}} {{{\bar{Q}}_{ij }}{{{\left[ {g(z)} \right]}}^2}dz,} } & {\left( {i,j} \right)=\left( {4,5} \right),} \\ \end{array}} \\ {\left( {{I_1},{I_2},{I_3},{I_4},{I_5},{I_6}} \right)=\int\limits_{{{-h \left/ {2} \right.}}}^{{{h \left/ {2} \right.}}} {\rho \left( {1,z,{z^2},f(z),z\;f(z),{{{\left[ {f(z)} \right]}}^2}} \right)dz.} } \\ \end{array} $$
(13)

Collecting the coefficients of δu 0, δv 0, δw b , and δw s in Eq. (10), the equations of motion are obtained as

$$ \begin{array}{*{20}{c}} {\delta {u_0}:{N_{x,x }}+{N_{xy,y }}={I_1}{{\ddot{u}}_0}-{I_2}{{\ddot{w}}_{b,x }}-{I_4}{{\ddot{w}}_{s,s }},} \\ {\delta {\nu_0}:{N_{xy,x }}+{N_{y,y }}={I_1}{{\ddot{\nu}}_0}-{I_2}{{\ddot{w}}_{b,y }}-{I_4}{{\ddot{w}}_{s,y }},} \\ {\delta {w_b}:M_{x,xx}^b+2\,M_{xy,xy}^b+M_{y,yy}^b-{k_0}\left( {{w_b}+{w_s}} \right)+{k_1}{\nabla^2}\left( {{w_b}+{w_s}} \right)} \\ {={I_1}\left( {{{\ddot{w}}_b}+{{\ddot{w}}_s}} \right)+{I_2}\left( {{{\ddot{u}}_{0,x }}+{{\ddot{\nu}}_{0,y }}} \right)-{I_3}\left( {{{\ddot{w}}_{b,xx }}+{{\ddot{w}}_{b,yy }}} \right)-{I_5}\left( {{{\ddot{w}}_{s,xx }}+{{\ddot{w}}_{x,yy }}} \right),} \\ {\delta {w_s}:M_{x,xx}^s+2\;M_{xy,xy}^s+M_{y,yy}^s+S_{xz,x}^s+S_{yz,y}^s-{k_0}\left( {{w_b}+{w_s}} \right)+{k_1}{\nabla^2}\left( {{w_b}+{w_s}} \right)} \\ {={I_1}\left( {{{\ddot{w}}_b}+{{\ddot{w}}_s}} \right)+{I_4}\left( {{{\ddot{u}}_{0,x }}+{{\ddot{\nu}}_{0,y }}} \right)-{I_5}\left( {{{\ddot{w}}_{b,xx }}+{{\ddot{w}}_{b,yy }}} \right)-{I_6}\left( {{{\ddot{w}}_{s,xx }}+{{\ddot{w}}_{s,yy }}} \right).} \\ \end{array} $$
(14)

Clearly, when the effect of transverse shear deformation is neglected ( w s  = 0 ), Eqs. (14) yield the equations of motion of a composite plate based on the classical theory of plates.

2.5. Analytical solutions for simply supported rectangular laminates

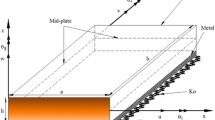
Rectangular laminated composites plates are generally classified in accordance with the type of support used. We are concerned here with analytical solutions of Eqs. (14) for simply supported composite plate. The following boundary conditions are imposed at the side edges:

$$ \begin{array}{*{20}{c}} {{\nu_0}\left( {0,y} \right)={w_b}\left( {0,y} \right)={w_s}\left( {0,y} \right)=\frac{{\partial {w_b}}}{{\partial y}}\left( {0,y} \right)=\frac{{\partial {w_s}}}{{\partial y}}\left( {0,y} \right)=0,} \\ {{\nu_0}\left( {a,y} \right)={w_b}\left( {a,y} \right)={w_s}\left( {a,y} \right)=\frac{{\partial {w_b}}}{{\partial y}}\left( {a,y} \right)=\frac{{\partial {w_s}}}{{\partial y}}\left( {a,y} \right)=0,} \\ {{N_x}\left( {0,y} \right)=M_x^b\left( {0,y} \right)=M_x^s\left( {0,y} \right)={N_x}\left( {a,y} \right)=M_x^b\left( {a,y} \right)=M_x^s\left( {a,y} \right)=0,} \\ {{u_0}\left( {x,0} \right)={w_b}\left( {x,0} \right)={w_s}\left( {x,0} \right)=\frac{{\partial {w_b}}}{{\partial x}}\left( {x,0} \right)=\frac{{\partial {w_s}}}{{\partial x}}\left( {x,0} \right)=0,} \\ {{u_0}\left( {x,b} \right)={w_b}\left( {x,b} \right)={w_s}\left( {x,b} \right)=\frac{{\partial {w_b}}}{{\partial x}}\left( {x,b} \right)=\frac{{\partial {w_s}}}{{\partial x}}\left( {x,b} \right)=0,} \\ {{N_y}\left( {x,0} \right)=M_y^b\left( {x,0} \right)=M_y^s\left( {x,0} \right)={N_y}\left( {x,b} \right)=M_y^b\left( {x,b} \right)=M_y^s\left( {x,b} \right)=0.} \\ \end{array} $$
(15)

The displacement functions that satisfy boundary conditions (15) are taken in the form Fourier series

$$ \left\{ {\begin{array}{*{20}{c}} {{u_0}} \\ {{\nu_0}} \\ {{w_b}} \\ {{w_s}} \\ \end{array}} \right\}=\sum\limits_{m=1}^{\infty } {\sum\limits_{n=1}^{\infty } {\left\{ {\begin{array}{*{20}{c}} {{U_{mn }}\cos \left( {\lambda x} \right)\sin \left( {\mu y} \right){e^{{i\omega t}}}} \\ {{V_{mn }}\sin \left( {\lambda x} \right)\cos \left( {\mu y} \right){e^{{i\omega t}}}} \\ {{W_{bmn }}\sin \left( {\lambda x} \right)\sin \left( {\mu y} \right){e^{{i\omega t}}}} \\ {{W_{smn }}\sin \left( {\lambda x} \right)\sin \left( {\mu y} \right){e^{{i\omega t}}}} \\ \end{array}} \right\},} } $$

where U mn , V mn , W bmn , and W smn are arbitrary parameters to be determined, ω is the eigenfrequency associated with an ( m, n )th eigenmode; λ = mπ/a and μ = nπ/b.

Inserting Eqs. (15), (12), and (13) into the equations of motion (14) we get the following eigenvalue equations for the free vibration problem at any fixed values of m and n :

$$ \left( {\left[ K \right]-{\omega^2}\left[ M \right]} \right)\left\{ \varDelta \right\}=\left\{ 0 \right\}, $$
(16)

where {Δ} denotes the column

$$ {{\left\{ \varDelta \right\}}^T}=\left\{ {{U_{mn }},{V_{mn }},{W_{bmn }},{W_{smn }}} \right\}, $$

and

$$ \begin{array}{*{20}{c}} {\left[ K \right]=\left[ {\begin{array}{*{20}{c}} {{a_{11 }}} & {{a_{12 }}} & {{a_{13 }}} & {{a_{14 }}} \\ {{a_{12 }}} & {{a_{22 }}} & {{a_{23 }}} & {{a_{24 }}} \\ {{a_{13 }}} & {{a_{23 }}} & {{a_{33 }}} & {{a_{34 }}} \\ {{a_{14 }}} & {{a_{24 }}} & {{a_{34 }}} & {{a_{44 }}} \\ \end{array}} \right],} & {\left[ M \right]=\left[ {\begin{array}{*{20}{c}} {{m_{11 }}} & 0 & 0 & 0 \\ 0 & {{m_{22 }}} & 0 & 0 \\ 0 & 0 & {{m_{33 }}} & {{m_{34 }}} \\ 0 & 0 & {{m_{34 }}} & {{m_{44 }}} \\ \end{array}} \right].} \\ \end{array} $$

Here,

$$ \begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} {{a_{11 }}={A_{11 }}{\lambda^2}+{A_{66 }}{\mu^2},} & {{a_{12 }}=\lambda \mu \left( {{A_{12 }}+{A_{66 }}} \right),} & {{a_{13 }}={B_{11 }}{\lambda^3},} & {{a_{14 }}=-B_{11}^s{\lambda^3},} \\ \end{array}} \\ {\begin{array}{*{20}{c}} {{a_{22 }}={A_{66 }}{\lambda^2}+{A_{22 }}{\mu^2},} & {{a_{23 }}={B_{11 }}{\mu^3},} & {{a_{24 }}=B_{11}^s{\mu^3},} \\ \end{array}} \\ {{a_{33 }}={D_{11 }}{\lambda^4}+2\left( {{D_{12 }}+2{D_{66 }}} \right){\lambda^2}{\mu^2}+{D_{22 }}{\mu^4}+{k_0}+{k_1}\left( {{\lambda^2}+{\mu^2}} \right),} \\ {{a_{34 }}=D_{11}^s{\lambda^4}+2\left( {D_{12}^s+2D_{66}^s} \right){\lambda^2}{\mu^2}+D_{22}^s{\mu^4}+{k_0}+{k_1}\left( {{\lambda^2}+{\mu^2}} \right),} \\ {{a_{44 }}=H_{11}^s{\lambda^4}+2\left( {H_{12}^s+2H_{66}^s} \right){\lambda^2}{\mu^2}+H_{22}^s{\mu^4}+A_{55}^s{\lambda^2}+A_{44}^s{\mu^2}+{k_0}+{k_1}\left( {{\lambda^2}+{\mu^2}} \right),} \\ {\begin{array}{*{20}{c}} {{m_{11 }}={m_{22 }}={I_1},} & {{m_{33 }}={I_1}+{I_3}\left( {{\lambda^2}+{\mu^2}} \right),} & {{m_{34 }}={I_1}+{I_5}\left( {{\lambda^2}+{\mu^2}} \right),} & {{m_{44 }}={I_1}+{I_{{6}}}\left( {{\lambda^2}+{\mu^2}} \right).} \\ \end{array}} \\ \end{array} $$

The natural frequencies of the laminates can be obtained by setting the determinant of the coefficient matrix in Eq. (16) to zero.

3. Numerical Results and Discussion

In this study, a free vibration analysis of symmetrically and antisymmetrically laminated composite plates resting on an elastic foundation by using the present shear deformation theory for laminated plates is suggested. The Navier solutions for free vibrations of laminated composite plates are found by solving eigenvalue equations. Comparisons are made with various theories of plates and with exact solutions of three-dimensional elasticity theory. The description of various displacement models is given in Table 1.

Table 1 Displacement Models
Full size table

In order to verify the accuracy of the present analysis, some numerical examples were solved. It was assumed that the thickness and the material properties for all laminas were the same. In the analysis, the elastic properties of a lamina were taken to be as follows:

$$ \begin{array}{*{20}{c}} {{G_{12 }}={G_{13 }}=0.6{E_2},} & {{G_{23 }}=0.5{E_2},} & {{\nu_{12 }}={\nu_{13 }}=0.25} \\ \end{array}. $$

The following nondimensional fundamental frequency, nondimensional linear Winkler foundation parameter, and nondimensional Pasternak foundation parameter were used:

$$ \begin{array}{*{20}{c}} {\bar{\omega}=\omega \frac{{{a^2}}}{h}\sqrt{{\frac{\rho }{{{E_2}}}}},} & {{K_0}=\frac{{{k_0}{L^4}}}{{{E_2}{h^3}}},} & {{K_1}=\frac{{{k_1}{L^4}}}{{{E_2}{h^3}}}.} \\ \end{array} $$

The fundamental frequencies of the systems were calculated by Eq. (16) as an eigenvalue problem.

In Tables 2 and 3, the nondimensional fundamental frequencies of antisymmetrically laminated cross-ply plates obtained by using different shear deformation theories are shown for various values of a/h and moduli ratios. It can be seen that, in general, the present theory gives more accurate results in predicting the natural frequencies than the PSDT and the three-dimensional elasticity solution given in [11]. It should be noted that unknown functions in present theory are four, while the unknown functions in the FSDT and higher-order shear deformation theories (PSDT, ESDT, and SSDT) are five. It can be concluded that the present theory is not only accurate, but also simple in predicting the natural frequencies of laminated plates.

Table 2 Nondimensional Fundamental Frequencies of Antisymmetric Square Plates at Various Values of Orthotropy Ratio with a / h = 5
Full size table
Table 3 Nondimensional Fundamental Frequencies of Antisymmetric Square Plates at Various Values of a / h with E 1 / E 2 = 40
Full size table

In order to validate the present theory in the case of plates resting on an elastic foundation, the results for the fundamental natural frequency parameter of an isotropic thick plate with three different values of thickness-to-length ratios and three different values of Winkler elastic coefficients are compared in Table 4 with those obtained in [26, 27]. A excellent agreement of the three methods can be seen. We should note here that, in Table 4, D = Eh 3 /12(1 − ν2), as defined in [26].

Table 4 Comparison of the Fundamental Frequency Parameter \( \Omega =\omega {a^2}\sqrt{{{{{\rho h}} \left/ {D} \right.}}} \) of Isotropic Square Plates
Full size table

In Fig. 1, variations in the nondimensional fundamental frequencies of symmetrically and antisymmetrically laminated orthotropic cross-ply plates on an elastic foundation are given. It is seen from the figures that an increase in the degree of orthotropy produces an increase in the fundamental frequency. The effect of foundation stiffness on the vibration of thick laminated plates is illustrated in Fig. 2. The figure shows that the frequencies of laminates increase when foundation parameters increase.

Fig. 1
figure 1

Effect of the orthotropy ratio E 1/E 2 on the nondimensional fundamental frequencies ω of laminated cross-ply plates with layups (0/90/90/0) (a) and (0/90/0/90) (b) on an elastic foundation. (K 0, K 1) = (0, 0) (––––) and (100, 10) (– – –); a/h = 5 (1), 10 (2), 20 (3), 50 (4), and 100 (5).

Full size image
Fig. 2
figure 2

Effect of the orthotropy ratio E 1/E 2 on the nondimensional fundamental frequency \( \bar{\omega} \) of antisymmetrically laminated (0/90/0/90) cross-ply plate on an the elastic foundation at (K 0, K 1) = (0, 10) (1), (20, 10) (2), (40, 10) (3), (60, 10) (4), (80, 10) (5), and (100, 10) (6) (a) and (K 0, K 1) = (100, 0) (1), (100, 2) (2), (100, 4) (3), (100, 6) (4), (100, 8) (5), and (100, 10) (6) (b).

Full size image

4. Conclusions

A refined hyperbolic shear deformation theory of plates has been successfully developed for the free vibration of simply supported laminated plates on an elastic foundation. The theory allows for a square-law variation in the transverse shear strains across the plate thickness and satisfies the zero-traction boundary conditions on the top and bottom surfaces of the plate without using shear correction factors. The equations of motion were derived from Hamilton’s principle. All comparison studies show that the natural frequencies obtained by the proposed theory with four unknowns are almost identical to those predicted by the shear deformation theories containing five unknowns. It can be concluded that the theory proposed is accurate and efficient in predicting the vibration responses of composite plates.