A New Higher-Order Finite Element Model for Free Vibration and Buckling of Functionally Graded Sandwich Beams with Porous Core Resting on a Two-Parameter Elastic Foundation Using Quasi-3D Theory

Abstract

In this paper, a new higher-order finite element model is proposed for free vibration and buckling analysis of functionally graded (FG) sandwich beams with porous core resting on a two-parameter Winkler-Pasternak elastic foundation based on quasi-3D deformation theory. The material properties of FG sandwich beams vary gradually through the thickness according to the power-law distribution. The governing equation of motion is derived from the Lagrange's equations. Three different porosity patterns including uniform, symmetric, and asymmetric are considered. The accuracy and convergence of the proposed model are verified with several numerical examples. A comprehensive parametric study is carried out to explore the effects of the boundary conditions, skin-to-core thickness ratio, power-law index, slenderness, porosity coefficient, porous distribution of the core, and elastic foundation parameters on the natural frequencies and critical buckling loads of FG sandwich beams.

1 Introduction

Functionally graded porous materials (FGPMs) are a new emerging class of functionally graded materials (FGMs) that have gained considerable interest due to their distinctive composition and properties. In addition to gradual variation in the material properties of conventional FGMs, these materials introduce porosity as an additional variable to the material gradient. Beyond sharing the common advantages of conventional FGMs, their lightweight nature, high strength, enhanced energy absorption capabilities, and improved thermal and acoustic insulation properties have driven the development of functionally graded sandwich structures with FG porous core (Bang and Cho 2015; Conde et al. 2006; Betts 2012). With their potential for improved performance and durability, these structures in various forms such as beams, plates, and shells have found potential applications in a variety of engineering fields (Magnucka-Blandzi and Magnucki 2007; Patel et al. 2018; Smith et al. 2012).

Numerous researchers have performed extensive studies to emphasize the mechanical behaviors of FGP sandwich beams using various theories and solution methods (Han et al. 2012; Wu et al. 2020; Lefebvre et al. 2008). A variety of theories available to analyze FGP sandwich beams can be classified mainly as classical beam theory (CBT), first-order shear deformation theory (FSDT), higher-order shear deformation theories (HSDT), and quasi-3D deformation theory. Tang et al. (2018) conducted linear and nonlinear buckling analysis of porous beams based on Euler Bernoulli beam theory. Wattanasakulpong and Ungbhakorn (2014) employed CBT to assess both the linear and nonlinear vibrations of FGP beams. Eltaher et al. (2018) used CBT to investigate the bending and vibration behavior of porous nanobeams. Turan et al. (2023) used the Ritz method, finite element method (FEM), and artificial neural networks (ANNs) based on FSDT to investigate the free vibration and buckling behavior of FG porous beams under various boundary conditions.

Using FSDT, Chen et al. (2016) investigated the nonlinear free vibration of sandwich beams with an FG porous core. Chen et al. (2015) explored the buckling and bending of FG porous Timoshenko beams. Bamdad et al. (2019) investigated the vibration and buckling behavior of a sandwich Timoshenko beam with a porous core. Grygorowicz et al. (2015) conducted the buckling analysis of a sandwich beam with an FG porous core using FSDT. Alambeigi et al. (2020) investigated the free and forced vibration characteristics of a sandwich beam with an FG porous core and composite face layers embedded with shape memory alloy via FSDT.

Derikvand et al. (2023) studied the buckling of FG sandwich beams with porous ceramic core using HSDT. Ramteke and Panda (2021) examined the free vibrations of a multi-directional FG structure considering the influences of variable grading and porosity distribution with HSDT. Hung and Truong (2018) investigated the free vibration response of sandwich beams with an FG porous core resting on a Winkler elastic foundation using various shear deformation theories. Nguyen et al. (2022a) proposed a two-variable shear deformation theory to investigate the buckling, bending, and vibration characteristics of FGP beams considering various porosity distribution patterns. Srikarun et al. (2021) used Reddy's third-order shear deformation theory to examine the linear and nonlinear bending analysis of sandwich beams with FG porous core under various types of distributed loads. Nguyen et al. (2023) developed a Legendre-Ritz approach to investigate the bending, buckling, and free vibration behavior of porous beams resting on elastic foundations using HSDT. Hamad et al. (2020) conducted static stability analysis on an FG sandwich beam with a porous core subjected to axial load functions to investigate and optimize critical buckling loads using HSDT. Chami et al. (2022) examined the influence of porosity on fundamental natural frequencies of the simple supported FG sandwich beam with HSDT. Bargozini et al. (2024) studied buckling of a sandwich beam with carbon nano rod reinforced composite and porous core under axially variable forces based on HSDT. Sayyad et al. (2022) investigated the static deformation and free vibration of simply supported porous FG circular beams using the Navier method based on HSDT. Masjedi et al. (2019) investigated the large deflection of FGP beams using a geometrically exact theory with a fully intrinsic formulation and the orthogonal Chebyshev collocation method. Su et al. (2019) investigated the surface effect on the static bending of FGP nanobeams using Reddy's higher-order beam theory. Chinh et al. (2021) applied a point interpolation mesh-free method based on a polynomial basic function to conduct static flexural analysis of an FG sandwich beam with a porous metal core using HSDT. Xin and Kiani (2023) studied the vibration behavior of a thick sandwich beam with an FG porous core resting on an elastic medium using quasi-3D theory and the Navier method.

Among computational methods, FEM has garnered significant attention as one of the prominent numerical techniques for the analysis of FG and sandwich structures over the last few decades (Kahya and Turan 2017; Belarbi et al. 2022; Koutoati et al. 2021a, 2021b; Arslan and Gunes 2018; Van 2022; Vinh et al. 2023; Gupta and Chalak 2023; Vo et al. 2015). Akbaş et.al. (2022) studied the vibration of FG porous, thick beam under the dynamic sine pulse load using FEM. Patil et al. (2023) investigated the static bending and vibration of FG porous sandwich beams with viscoelastic boundary conditions using FSDT and FEM. Zghal et al. (Zghal et al. 2022) explored the effect of porosity on the static bending behavior of FG porous beams using a refined mixed FEM. Malhari Ramteke et al. (2020) introduced an FE solution based on HSDT for the static analysis of FG structures, considering variable grading patterns, including the porosity effect. Vinh et al. (2022) developed a new enhanced finite element model based on the neutral surface position for bending analysis of the FG porous beams with the FSDT. Turan and Adiyaman (2023) used parabolic shear deformation theory to carry out static analysis on two-directional functionally graded (2D-FG) porous beams. Al-Itbi and Noori (2022) investigated the static response of sandwich beams with porous core under uniformly distributed loads along the beam span, using ANSYS finite element software. Grygorowicz et al. (2015) used ANSYS software to analyse the buckling characteristics of sandwich beams with metal foam core. Madenci and Özkılıç (2021) explored the influence of porosity on free vibrational behaviour of FG beam using analytical, ABAQUS FEM package and ANN technique. Using Carrera’s Unified Formulation and finite element approximation, Foroutan et al. (2021) investigated post-buckling and large-deflection analysis of a sandwich FG plate with FG porous. Nguyen et al. (2022b) introduced a novel finite element formulation for static bending analysis of functionally graded porous sandwich plates using Quasi-3D theory. Li et al. (2023) conducted nonlinear FE simulations to study nonlinear vibration behavior of FG sandwich beams with auxetic porous Copper core in thermal environments.

Several models have been developed to express the interaction between the beam and elastic foundations. Nguyen Thi (2022) examined the bending, buckling, and free vibration of FG sandwich curved beams resting on the Pasternak foundation using the analytical method and FSDT. Zenkour et al. (2019) used third-order shear deformation theory to carry out the buckling analysis of a size-dependent FG nanobeam resting on a two-parameter elastic foundation. Mohammed et al. (2021) conducted the bending and buckling analysis of the FG Euler–Bernoulli beam resting on the Winkler-Pasternak elastic foundation. Matinfar et al. (2019) conducted static bending aanalysis of 2D FG porous sandwich beam resting on Winkler-Pasternak Foundation in Hygrothermal environment, Based on the Layerwise Theory and Chebyshev Tau Method. Songsuwan et al. (2018) explored the free vibration and dynamic response of FG sandwich Timoshenko beams resting on an elastic foundation and subjected to a moving harmonic load. Fahsi et al. (2019) proposed a novel refined quasi-3D theory for the free vibration, bending, and buckling analysis of FG porous beams resting on an elastic foundation. Ait Atmane et al. (2017) introduced a novel refined quasi-3D theory for the analysis of free vibration, bending, and buckling of FG porous beams resting on an elastic foundation. Fazzolari (2018) conducted the free vibration and elastic stability analysis of 3D porous FG sandwich beams resting on Winkler-Pasternak elastic foundations using the method of series expansion of displacement components. Ghazwani et al. (2024) performed the high frequency analysis of the FG sandwich nanobeams resting on elastic foundations using nonlocal quasi-3D theory and Navier method.

Based on the above-given literature review, despite many works available on the analysis of single-layer FG porous beams, studies on the analysis of FG sandwich beams with porous core are rare. Shear deformation theories neglecting transverse normal deformations are found to be the most widely used theories for the analysis of FG sandwich beams. Additionally, there is a noticeable absence of studies in the literature addressing the free vibration and buckling analysis of FG sandwich beams with softcore (metal core) using higher order shear and normal deformation theory. Moreover, the application of a quasi-3D theory-based FEM to FG sandwich beams with the porous core is notably restricted due to difficulties in addressing complex problems, such as satisfying the C¹-continuity requirement of the quasi-3D beam theory. The literature on the free vibration and buckling behavior of FG sandwich beams resting on an elastic foundation is limited and fragmented as well. It appears that no study has yet investigated the combined effects of core porosity and elastic foundation on the free vibration and buckling characteristics of FG sandwich beams, considering both shear and normal deformations. In this regard, the present work aims to explore for the first time an investigation into the free vibration and buckling characteristics of FG sandwich beams with porous metal core and sandwich beams with FG porous core resting on a two-parameter Winkler-Pasternak elastic foundation using a new higher-order finite element model based on quasi-3D deformation theory, that account both the effects of transverse shear and normal deformations. The FG material property distribution obeys the power-law rule through the thickness. Three different porosity patterns including uniform, symmetric, and asymmetric are considered. A three-node 15-degrees-of-freedom (DOFs) FE is proposed for the numerical solution. The accuracy and convergence of the proposed model are verified with several numerical examples. A comprehensive parametric investigation is conducted to explore the effects of the skin-to-core thickness ratio, power-law index, boundary conditions, slenderness, porosity coefficient, and porous distribution of the core and elastic foundation parameters on the natural frequencies and critical buckling loads of FG sandwich beams. It is expected that the results of this work evaluate the effect of core porosity and Winkler-Pasternak elastic foundation on the free vibration and buckling behavior of FG sandwich beams with porous core. Additionally, it aims present some benchmark results for the fundamental natural frequencies and buckling loads of FG sandwich beams with porous core.

2 Problem

2.1 Geometrical Configuration

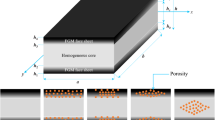
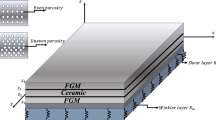
As shown in Fig. 1, a three-layered FG sandwich beam with uniform thickness $h$, width $b$, and length $L$ is considered. The top and bottom faces are at $z=\pm h/2$. The beam is supported by a two-parameter elastic foundation with spring constants ${k}_{w}$ and ${k}_{p}$, where the former represents the Winkler foundation while the latter is for the Pasternak shear layer. A sandwich beam with FG face layers and an isotropic porous metal core (Type A) and a sandwich beam with isotropic homogenous face layers and an FG porous core (Type B) are examined. The face layers of Type A are graduated from ceramic to metal, whereas the core is porous and entirely metal. The face layers of Type B are made of metal and ceramic layers, respectively, while the core layer is porous and FG from ceramic to metal.

Fig. 1

Configuration of FG sandwich beam resting on elastic foundation

2.2 FG Material Properties

The effective material properties of the FG sandwich beam vary gradually and continuously through the thickness direction according to the power law distribution as

$$\begin{aligned} E\left( z \right) & = E_{c} + \left( {E_{m} - E_{c} } \right)V_{c} \left( z \right) \\ \rho \left( z \right) & = \rho_{c} + \left( {\rho_{m} - \rho_{c} } \right)V_{c} \left( z \right) \\ \end{aligned}$$

(1)

for Type A and

$$\begin{aligned} E\left( z \right) & = E_{m} + \left( {E_{c} - E_{m} } \right)V_{c} \left( z \right) \\ \rho \left( z \right) &_{{}} = \rho_{m} + \left( {\rho_{c} - \rho_{m} } \right)V_{c} \left( z \right) \\ \end{aligned}$$

(2)

for Type B. Here, $E(z)$ is Young’s modulus, and $\rho (z)$ is the density of the material. Subscripts $m$ and $c$ denote metal and ceramic constituents of material, respectively.

The volume fraction of FG sandwich beams is assumed to obey a power-law function in the direction of thickness which can be stated as follows:

$$\begin{aligned} V_{c} \left( z \right) & = \left( {\frac{{z - h_{0} }}{{h_{1} - h_{0} }}} \right)^{p} {\text{for }}z \in \left[ {h_{0} ,h_{1} } \right] \\ V_{c} \left( z \right) & = 1{\text{ for }}z \in \left[ {h_{1} ,h_{2} } \right] \\ V_{c} \left( z \right) & = \left( {\frac{{z - h_{3} }}{{h_{2} - h_{3} }}} \right)^{p} {\text{for }}z \in \left[ {h_{2} ,h_{3} } \right] \\ \end{aligned}$$

(3)

for Type A and

$$\begin{aligned} V_{c} \left( z \right) & = 0{\text{ for }}z \in \left[ {h_{0} ,h_{1} } \right] \\ V_{c} \left( z \right) & = \left( {\frac{{z - h_{1} }}{{h_{2} - h_{1} }}} \right)^{p} {\text{ for }}z \in \left[ {h_{1} ,h_{2} } \right] \\ V_{c} \left( z \right) & = 1 \,{\text{for }}z \in \left[ {h_{2} ,h_{3} } \right] \\ \end{aligned}$$

(4)

for Type B, where ${V}_{c}\left(z\right)$ is the volume fraction $p$ is the power-law index.

2.3 Mechanical Properties of Porous Core

Uniform, symmetrical, and asymmetrical distribution of porosity are considered as indicated in Fig. 2. The Young’s modulus and the mass density of porous core vary through the thickness according to the following (Chen et al. 2016; Srikarun et al. 2021):

Fig. 2

Porosity distributions in porous core

(i) Uniform porosity distribution (UD)

$$E\left( z \right) = E_{{{\text{max}}}} \left[ {1 - e_{0} \alpha } \right], \quad \rho \left( z \right) = \rho_{{{\text{max}}}} \sqrt {1 - e_{0} \alpha } \,{\text{for}} \,z \in \left[ {h_{1} ,h_{2} } \right]$$

(5)

(ii) Symmetric porosity distribution (SD)

$$\begin{aligned} E\left( z \right) & = E_{{{\text{max}}}} \left[ {1 - e_{0} {\text{cos}}\left( {\frac{\pi z}{{h_{2} - h_{1} }}} \right)} \right], \\ \rho \left( z \right) & = \rho_{{{\text{max}}}} \left[ {1 - e_{m} {\text{cos}}\left( {\frac{\pi z}{{h_{2} - h_{1} }}} \right)} \right] {\text{for}} z \in \left[ {h_{1} ,h_{2} } \right] \\ \end{aligned}$$

(6)

(iii) Asymmetric porosity distribution (ASD)

$$\begin{aligned} E\left( z \right) & = E_{{{\text{max}}}} \left[ {1 - e_{0} {\text{cos}}\left( {\frac{\pi z}{{2(h_{2} - h_{1} )}} + \frac{\pi }{4}} \right)} \right], \\ \rho \left( z \right) & = \rho_{{{\text{max}}}} \left[ {1 - e_{m} {\text{cos}}\left( {\frac{\pi z}{{2(h_{2} - h_{1} )}} + \frac{\pi }{4}} \right)} \right]{\text{ for }} z \in \left[ {h_{1} ,h_{2} } \right] \\ \end{aligned}$$

(7)

where ${E}_{\text{max}}\left(z\right)$ and ${\rho }_{\text{max}}(z)$ are the maximum values of Young’s modulus and mass density, ${e}_{0}$ and ${e}_{m}$ represent the coefficients of porosity and mass density. Coefficient of $\alpha$ and ${e}_{m}$ are obtained as follows:

$$\alpha = \frac{1}{{e_{0} }} - \frac{1}{{e_{0} }}\left( {\frac{2}{\pi }\sqrt {1 - e_{0} } - \frac{2}{\pi } + 1} \right)^{2} e_{m } = 1 - \sqrt {1 - e_{0} }$$

(8)

3 Theoretical Formulation

3.1 Equation of Motion

The displacement field of the present quasi-3D theory is given as follows:

$$u\left( {x,z,t} \right) = u_{0} \left( x \right) - z\frac{{{\text{d}}w_{o} }}{{{\text{d}}x}} + f\left( z \right)\phi_{y} \left( x \right)\quad w\left( {x,z,t} \right) = w_{0} \left( x \right) + g\left( z \right)\phi_{z} \left( x \right)$$

(9)

where $u$ and $w$ are the displacements of an arbitrary point of FG sandwich beam in $x$- and $z$-directions. ${u}_{0}$ and ${w}_{0}$ are displacements at the mid-plane of the beam, ${\phi }_{y}$ and ${\phi }_{z}$ are the shear slope associated with the transverse shear and normal deformations $g\left(z\right)=f{\prime}\left(z\right)$, where the shear shape function $f\left(z\right)$ is chosen as follows (Reddy 1984):

$$f=z-\frac{4{z}^{3}}{3{h}^{2}}$$

(10)

The strain field of the present theory is obtained by using the strain–displacement relationship from the elasticity theory, and can be expressed as follows:

$${\varepsilon }_{x}={\varepsilon }_{x}^{0}-{zk}_{x}+{f\varepsilon }_{x}^{1}, {\varepsilon }_{z}={g}{\prime}\left(z\right){\phi }_{z}\left(x\right), {\gamma }_{xz}=g\left(z\right){\gamma }_{xz}^{0}$$

(11)

where

$${\varepsilon }_{x}^{0}=\frac{\partial {u}_{0}}{\partial x}, {k}_{x}=\frac{{\partial }^{2}{w}_{0}}{{\partial x}^{2}}, {\varepsilon }_{x}^{1}=\frac{\partial {\phi }_{y}}{\partial x} , {\gamma }_{xz}^{0}= {\phi }_{y}+ \frac{\partial {\phi }_{z}}{\partial x}$$

(12)

The stress–strain relationship of the FG sandwich beam is given as the following:

$$\left\{\begin{array}{l}{\sigma }_{x}\\ {\sigma }_{z}\\ {\tau }_{xz}\end{array}\right\}=\left[\begin{array}{ccc}{Q}_{11}(z)& {Q}_{13}(z)& 0\\ {Q}_{13}(z)& {Q}_{33}(z)& 0\\ 0& 0& {Q}_{55}(z)\end{array}\right]\left\{\begin{array}{l}{\varepsilon }_{x}\\ {\varepsilon }_{z}\\ {\gamma }_{xz}\end{array}\right\}$$

(13)

where

$${Q}_{11}\left(z\right)={Q}_{33}\left(z\right)=\frac{E\left(z\right)}{1-{\upsilon }^{2}}, {Q}_{13}\left(z\right)=\frac{\upsilon E\left(z\right)}{1-{\upsilon }^{2}}, {Q}_{55}(z)=\frac{E(z)}{2(1+\upsilon )}$$

(14)

where $\upsilon$ is Poisson’s ratio.

The strain energy of the beam can be expressed as follows:

$$\begin{aligned} U & = \frac{1}{2}\mathop \int \limits_{0}^{L} \mathop \int \limits_{{ - \frac{h}{2}}}^{\frac{h}{2}} \left( {\sigma_{x} \varepsilon_{x} + \sigma_{z} \varepsilon_{z} + \tau_{xz} \gamma_{xz} } \right){\text{d}}z{\text{d}}x \\ & = \frac{1}{2}\mathop \int \limits_{0}^{L} \left[ {A_{11} \left( {\frac{{\partial u_{0} }}{\partial x}} \right)^{2} } \right. + E_{11} \left( {\frac{{\partial^{2} w_{0} }}{{\partial x^{2} }}} \right)^{2} + F_{11} \left( {\frac{{\partial \phi_{y} }}{\partial x}} \right)^{2} - 2B_{11} \frac{{\partial u_{0} }}{\partial x}\frac{{\partial^{2} w_{0} }}{{\partial x^{2} }} \\ & \quad + 2C_{11} \frac{{\partial u_{0} }}{\partial x}\frac{{\partial \phi_{y} }}{\partial x} - 2D_{11} \frac{{\partial^{2} w_{0} }}{{\partial x^{2} }}\frac{{\partial \phi_{y} }}{\partial x} + 2B_{S13} \frac{{\partial u_{0} }}{\partial x}\phi_{z} - 2C_{S13} \frac{{\partial^{2} w_{0} }}{{\partial x^{2} }}\phi_{z} \\ & \quad + 2E_{S13} \frac{{\partial \phi_{y} }}{\partial x}\phi_{z} + D_{S33} \left( {\phi_{z} } \right)^{2} + A_{S55} \left( {\phi_{y} } \right)^{2} + A_{S55} \left( {\frac{{\partial \phi_{z} }}{\partial x}} \right)^{2} \left. { + 2A_{S55} \frac{{\partial \phi_{z} }}{\partial x}\phi_{y} } \right]{\text{d}}x \\ \end{aligned}$$

(15)

where

$$\begin{aligned} \left[ {A_{11} ,B_{11} ,C_{11} ,D_{11} ,E_{11} ,F_{11} ,D_{S33} } \right] & = \mathop \int \limits_{ - h/2}^{h/2} Q_{11} \left( z \right)\left[ {1,z,f\left( z \right),{\text{z}}f\left( z \right),z^{2} ,f^{2} \left( z \right),\left[ {g^{\prime}\left( z \right)} \right]^{2} } \right]{\text{d}}z \\ \left[ {B_{S13} ,C_{S13} ,E_{S13} } \right] & = \mathop \int \limits_{{ - \frac{h}{2}}}^{\frac{h}{2}} Q_{13} \left( z \right)g^{\prime}\left( z \right)\left[ {1,z,f\left( z \right)} \right]{\text{d}}z \\ A_{S55} & = \mathop \int \limits_{ - h/2}^{h/2} Q_{55} \left( z \right)\left[ {g\left( z \right)} \right]^{2} {\text{d}}z \\ \end{aligned}$$

(16)

The kinetic energy can be defined as

$$\begin{aligned} K & = \frac{1}{2}\mathop \int \limits_{0}^{L} \mathop \int \limits_{{ - \frac{h}{2}}}^{\frac{h}{2}} \rho \left( z \right)\left( {\dot{U}^{2} + \dot{W}^{2} } \right){\text{d}}z{\text{d}}x \\ & = \frac{1}{2}\mathop \int \limits_{0}^{L} \left[ {I_{1} \left( {\frac{{\partial u_{0} }}{\partial t}} \right)^{2} } \right. + I_{3} \left( {\frac{{\partial^{2} w_{0} }}{\partial t\partial x}} \right)^{2} + I_{6} \left( {\frac{{\partial \phi_{y} }}{\partial t}} \right)^{2} - 2I_{2} \frac{{\partial u_{0} }}{\partial t}\frac{{\partial^{2} w_{0} }}{\partial t\partial x} + 2I_{4} \frac{{\partial u_{0} }}{\partial t}\frac{{\partial \phi_{y} }}{\partial t} \\ & \quad - 2I_{5} \frac{{\partial^{2} w_{0} }}{\partial t\partial x}\frac{{\partial \phi_{y} }}{\partial t} + I_{1} \left( {\frac{{\partial w_{0} }}{\partial t}} \right)^{2} + \left. {I_{8} \left( {\frac{{\partial \phi_{z} }}{\partial t}} \right)^{2} + 2I_{7} \frac{{\partial w_{0} }}{\partial t}\frac{{\partial \phi_{z} }}{\partial t}} \right]{\text{d}}x \\ \end{aligned}$$

(17)

where

$$\left[{I}_{1},{I}_{2},{I}_{3},{I}_{4},{I}_{5},{I}_{6},{I}_{7},{I}_{8}\right]={\int }_{-h/2}^{h/2} \rho \left(z\right)\left[1,z,{z}^{2},f\left(z\right),\text{z}f\left(z\right),{f}^{2}\left(z\right),g\left(z\right),{\left[g\left(z\right)\right]}^{2}\right]\text{d}z$$

(18)

The potential energy due to external axial force can be written as

$$V=-\frac{1}{2}{\int }_{0}^{L} \left[{N}_{0}{\left(\frac{\partial {w}_{0}}{\partial x}\right)}^{2}\right]\text{d}x$$

(19)

where ${N}_{0}$ is the axial force.

The strain energy induced by the elastic foundation can be expressed as

$${U}_{F}=\frac{1}{2}{\int }_{0}^{L} \left[\left({k}_{\text{w}}{w}^{2}+{k}_{p}{\left(\frac{\text{d}w}{\partial x}\right)}^{2}\right)\right]\text{d}x$$

(20)

where ${k}_{\text{w}}$ and ${k}_{p}$ are the constants of Winkler and shear layer springs.

Total potential energy can then be obtained as follows:

$$\begin{aligned} \varPi & = U + U_{F} + V - K \\ & = \frac{1}{2}\mathop \int \limits_{0}^{L} \left[ {A_{11} \left( {\frac{{\partial u_{0} }}{\partial x}} \right)^{2} } \right. + E_{11} \left( {\frac{{\partial^{2} w_{0} }}{{\partial x^{2} }}} \right)^{2} + F_{11} \left( {\frac{{\partial \phi_{y} }}{\partial x}} \right)^{2} - 2B_{11} \frac{{\partial u_{0} }}{\partial x}\frac{{\partial^{2} w_{0} }}{{\partial x^{2} }} \\ & \quad + 2C_{11} \frac{{\partial u_{0} }}{\partial x}\frac{{\partial \phi_{y} }}{\partial x} - 2D_{11} \frac{{\partial^{2} w_{0} }}{{\partial x^{2} }}\frac{{\partial \phi_{y} }}{\partial x} + 2B_{S13} \frac{{\partial u_{0} }}{\partial x}\phi_{z} - 2C_{S13} \frac{{\partial^{2} w_{0} }}{{\partial x^{2} }}\phi_{z} \\ & \quad + 2E_{S13} \frac{{\partial \phi_{y} }}{\partial x}\phi_{z} + D_{S33} \left( {\phi_{z} } \right)^{2} + A_{S55} \left( {\phi_{y} } \right)^{2} \left. { + A_{S55} \left( {\frac{{\partial \phi_{z} }}{\partial x}} \right)^{2} + 2A_{S55} \frac{{\partial \phi_{z} }}{\partial x}\phi_{y} } \right]{\text{d}}x \\ & - \frac{1}{2}\mathop \int \limits_{0}^{L} \left[ {I_{1} \left( {\frac{{\partial u_{0} }}{\partial t}} \right)^{2} } \right. + I_{3} \left( {\frac{{\partial^{2} w_{0} }}{\partial t\partial x}} \right)^{2} + I_{6} \left( {\frac{{\partial \phi_{y} }}{\partial t}} \right)^{2} - 2I_{2} \frac{{\partial u_{0} }}{\partial t}\frac{{\partial^{2} w_{0} }}{\partial t\partial x} + 2I_{4} \frac{{\partial u_{0} }}{\partial t}\frac{{\partial \phi_{y} }}{\partial t} \\ & \quad - 2I_{5} \frac{{\partial^{2} w_{0} }}{\partial t\partial x}\frac{{\partial \phi_{y} }}{\partial t} + I_{1} \left( {\frac{{\partial w_{0} }}{\partial t}} \right)^{2} \left. { + I_{8} \left( {\frac{{\partial \phi_{z} }}{\partial t}} \right)^{2} + 2I_{7} \frac{{\partial w_{0} }}{\partial t}\frac{{\partial \phi_{z} }}{\partial t}} \right]{\text{d}}x \\ & - \frac{1}{2}\mathop \int \limits_{0}^{L} \left[ {N_{0} \left( {\frac{{\partial w_{0} }}{\partial x}} \right)^{2} } \right]{\text{d}}x + \frac{1}{2}\mathop \int \limits_{0}^{L} \left[ {\left( {k_{w} \left( {w_{0} + g\phi_{z} } \right)^{2} + k_{p} \left( {\frac{{{\text{d}}\left( {w_{0} + g\phi_{z} } \right)}}{\partial x}} \right)^{2} } \right)} \right]{\text{d}}x \\ \end{aligned}$$

(21)

Lagrange’s equation which gives the equation of motion can be written as follows:

$$\frac{\text{d}}{\text{d}t}\left(\frac{\partial \Pi }{\partial {\dot{q}}_{j}}\right)-\frac{\partial \Pi }{\partial {q}_{j}}=0$$

(22)

where ${q}_{j}$ represents the generalized coordinates, and over dot represents the time derivative.

3.2 Finite Element Formulation

To investigate the free vibration and buckling of FG sandwich beams with porous core resting on an elastic foundation, a three-node higher-order beam finite element having a total of 15 DOFs shown in Fig. 3 is proposed. This new element is formulated based on the present quasi-3D deformation theory. The displacement unknows ${u}_{0}$, ${\phi }_{y}$ and ${\phi }_{z}$ are approximated using a linear polynomial interpolation function ${\psi }_{i}\left(x\right)$, and ${w}_{0}$ is approximated by a Hermite-cubic polynomial interpolation function ${\varphi }_{i}\left(x\right)$. The generalized displacements within the element are expressed as:

$$\begin{aligned}{u}_{0}\left(x,t\right)&=\sum_{i=1}^{3}{\psi }_{i}\left(x\right){u}_{i}, {w}_{0}\left(x,t\right)=\sum_{i=1}^{6}{\varphi }_{i}\left(x\right){w}_{i}\\ {\phi }_{y}\left(x,t\right)&=\sum_{i=1}^{3}{\psi }_{i}\left(x\right){\phi }_{yi}, {\phi }_{z}\left(x,t\right)=\sum_{i=1}^{3}{\psi }_{i}\left(x\right){\phi }_{zi}\end{aligned}$$

(23)

where ${u}_{i}$, ${w}_{i}$, ${\phi }_{yi}$, and ${\phi }_{zi}$ are generalized nodal displacement variables and the suffix $i$ donates the corresponding nodal coordinates, ${\psi }_{i}\left(x\right)$ and ${\varphi }_{i}\left(x\right)$ are the shape functions which are given in the Appendix.

Fig. 3

Three-node higher-order beam element with corresponding DOFs

3.3 Analytical Solution: Ritz Method

Analytical solutions for free vibration and buckling analysis of FG sandwich beams can be obtained using the Ritz method with the present theory. For the Ritz method, the displacement functions ${u}_{0}$(x), ${w}_{0}(x),{\phi }_{y}$(x) and ${\phi }_{z}$(x) are presented by the following polynomial series which are satisfy the kinematic boundary conditions,

$$\begin{aligned} u_{0} \left( {x,t} \right) & = \mathop \sum \limits_{j = 1}^{m} a_{j} \psi_{j, x} \left( x \right)e^{i\omega t} , \quad w_{0} \left( {x,t} \right) = \mathop \sum \limits_{j = 1}^{m} b_{j} \psi_{j} \left( x \right)e^{i\omega t} \\ \phi_{y} \left( {x,t} \right) & = \mathop \sum \limits_{j = 1}^{m} c_{j} \psi_{j,x} \left( x \right)e^{i\omega t} , \quad \phi_{z} \left( {x,t} \right) = \mathop \sum \limits_{j = 1}^{m} d_{j} \psi_{j} \left( x \right)e^{i\omega t} \\ \end{aligned}$$

(24)

where ω is the natural frequency of free vibration of the beam, $\sqrt{i}=1$ the imaginary unit, (${a}_{j}$,${b}_{j}$, ${c}_{j}$ and ${d}_{j}$) denotes the values to be determine and ${\psi }_{j}\left(x\right)$ is the admissible shape function. To derive analytical solutions, polynomial and exponential form (Nguyen et al. 2022a) admissible shape functions for various boundary conditions (SS: Simple Supported, CC: Clamped – Clamped, and CF: Clamped – Free beams) are given in the Table 1.

Table 1 The admissible shape function and kinematics BCs of the beams

Substituting Eqs. (23) and (24) into Eq. (21), and using the result in Eq. (22) yields the following matrix equations for free vibration and buckling, respectively:

$$[\mathbf{K}-{\omega }^{2}\mathbf{M}]{\varvec{\Delta}}=0$$

(25)

$$\left[\mathbf{K}-{N}_{0}\mathbf{G}\right]{\varvec{\Delta}}=0$$

(26)

where $\mathbf{K}$ represents the stiffness matrix, $\mathbf{M}$ is the mass matrix, $\mathbf{G}$ is the geometric stiffness matrix, and ${\varvec{\Delta}}$ is the vector of unknown coefficients. ω and ${N}_{0}$ are the natural frequency and buckling load, respectively. The components of these matrices are given in the Appendix.

4 Numerical Results and Discussion

This section presents various numerical examples to validate the accuracy of the proposed FE model. FG layers of sandwich beams are assumed to be made from a mixture of Alumina (Al₂O₃) and Aluminum (Al). A parametric study is performed to evaluate the effects of the power-law index, span-to-height ratio, skin–core-skin thickness ratio, boundary conditions, elastic foundation parameters, and porosity on the free vibration and buckling behavior of FG sandwich beams. The material properties adopted here are: ${E}_{c}=380 \text{GPa}$, ${\rho }_{c}=3960 \text{kg}/{\text{m}}^{3}$, ${\nu }_{c}=0.3$ for ceramic material (Alumina) and ${E}_{m}=70 \text{GPa}$, ${\rho }_{m}=2702 \text{kg}/{\text{m}}^{3}$, ${\nu }_{m}=0.3$ for metal material (Aluminum). Table 1 shows the kinematic relations for various boundary conditions. As seen, three different boundary conditions namely simple-simple (SS), clamped–clamped (CC), and clamped-free (CF) are considered. For simplicity, the natural frequency, critical buckling load, and elastic foundation parameters are, respectively, defined in the following nondimensional forms:

$$\overline{\omega }=\frac{\omega {L}^{2}}{h}\sqrt{\frac{{\rho }_{m}}{{E}_{m}}}, {\overline{N} }_{cr}=\frac{12{N}_{cr}{L}^{2}}{{E}_{m}{h}^{3}}, {K}_{w}=\frac{12{k}_{w}{L}^{4}}{{E}_{m}{h}^{3}}, {K}_{p}=\frac{{12k}_{p}{L}^{2}}{{E}_{m}{h}^{3}}$$

(27)

4.1 Convergency and Validation

To demonstrate the accuracy of the present quasi-3D theory and the proposed FE model, free vibration and buckling analyses of FG sandwich beams without the elastic foundation and porosity are performed. To the best of the authors’ knowledge, natural frequencies, and critical buckling loads of FG sandwich beams with porous metal core and sandwich beams with FG porous core resting on a Winkler-Pasternak foundation, have not been documented in available literature.

Tables 2 and 3 show the convergency of the proposed FE for simple-simple (SS), clamped–clamped (CC), and clamped-free (CF) beams with length-to-thickness ratios of $L/h=5$ and $20$. As seen, the proposed FE yields highly accurate results, showing excellent agreement with those of previous studies as well as that of Ritz method. It is noticed that the nondimensional fundamental natural frequencies and critical buckling loads of simply supported (SS) beams converge rapidly with four elements for both beam types. Conversely, in the case of clamped–clamped (CC) and clamped-free (CF) boundary conditions, consistent outcomes are achieved after twenty elements. To ensure accuracy, 24 beam elements are, therefore, used for further analyses.

Table 2 Convergence study of nondimensional fundamental natural frequencies of the beams with various boundary conditions and length-to-thickness ratios

Table 3 Convergence study of nondimensional critical buckling loads of the beams with various boundary conditions and length-to-thickness ratios

Tables 4, 5, 6, 7 show a comparison of the nondimensional fundamental natural frequencies and critical buckling loads of FG sandwich beams. Length-to-thickness ratios of $L/h=5$ and $20$, skin–core-skin thickness ratios of 1–2–1, and three boundary conditions are considered. The results are compared to those of the references, which are based on HSDT (Vo et al. 2014; Nguyen et al. 2015) and Quasi-3D theory (Nguyen et al. 2016) as well as the Ritz solution obtained with the present theory by the authors. The study, based on quasi-3D theory (Nguyen et al. 2016) investigated only the free vibration and buckling characteristics of sandwich beams with FG core (Type B). Fundamental natural frequencies and critical buckling loads of FG sandwich beams with metal core (Type A) obtained with a quasi-3D theory are not available in the literature. Therefore, the results of Type A are only compared to HSDT (Vo et al. 2014) and the Ritz solution in order to validate the accuracy of the results and present some benchmark results for the fundamental natural frequencies and buckling loads of FG sandwich beams with softcore. It is observed that the solutions derived from the proposed FE model are in excellent agreement with the studies that consider transverse normal deformations. The slight difference with the current reference studies using HSDT is since they neglected the effect of the transverse normal strain. Furthermore, the tables illustrate that as the power-law index increases, the fundamental natural frequencies and critical buckling loads increase in FG sandwich beams with porous metal core, whereas they decrease for sandwich beams with FG porous core. This is explained by the fact that a higher value of $p$ indicates a higher proportion of the ceramic phase, leading to an increase in Young’s modulus and consequently in the bending stiffness. The observed correlation between the power-law index and the beam’s responses underlines the significance of material composition in determining the overall free vibration and buckling responses of FG sandwich beams. Consequently, the choice of the power-law index is crucial for predicting and adopting the mechanical performance of the FG sandwich beams for specific applications.

Table 4 Comparison of nondimensional fundamental natural frequencies of FG sandwich beams (Type A)

Table 5 Comparison of nondimensional fundamental natural frequencies of FG sandwich beams (Type B)

Table 6 Comparison of nondimensional critical buckling loads of FG sandwich beams (Type A)

Table 7 Comparison of nondimensional critical buckling loads of FG sandwich beams (Type B)

For the sake of completeness, the first three natural frequencies of 1–2–1 FG sandwich beams are presented for $L/h=5$ in Tables 8 and 9. Noticeably, accounting for normal strain effects yields higher outcomes, emphasizing the significance of considering such an effect.

Table 8 The first three nondimensional natural frequencies of FG sandwich beams (Type A)

Table 9 The first three nondimensional natural frequencies of FG sandwich beams (Type B)

4.2 Effect of Porosity

In Tables 10 and 11, the nondimensional fundamental natural frequencies are computed for the FG sandwich beam with configuration 1–2–1 considering three core porosity patterns with different values of porosity coefficient (${e}_{0}=0.4, 0.6, 0.8$) under three different foundation conditions: no elastic foundation, a Winkler foundation, and a Pasternak foundation. The power-law index is set to $p=2$, and length-to-thickness ratios $L/h=5$ and $20$ are considered. The results indicate a consistent trend across all boundary conditions in both types. For all three types of porosity patterns and length-to-thickness ratios, the nondimensional fundamental natural frequencies increase with the porosity coefficient. This is because increasing the porosity reduces both the bending stiffness and the mass density of the beam. The combination of these two effects increases the natural frequency of the beam overall. However, a notable exception is observed for CC beams when $L/h =5$, where the nondimensional fundamental natural frequencies decrease as the porosity coefficient increases. This phenomenon can be explained by the fact that when the length-to-thickness ratio is relatively small $L/h =5$, the reduction in bending stiffness becomes more significant than the reduction in mass density for CC beams. As a result, the natural frequency of the beam decreases overall. The nondimensional fundamental natural frequencies of sandwich beams are arranged in descending order of porosity as follows: symmetrical, asymmetrical, and uniform patterns. It is evident that the nondimensional fundamental natural frequencies of FG sandwich porous beams of Type A (with FG face layers and an isotropic porous metal core) are significantly higher than those of Type B (with isotropic homogeneous face layers and an FG porous core) for all boundary conditions, porosity distributions, and elastic foundation cases considered. This can be attributed to the presence of FG face layers, which provide superior bending stiffness compared to the isotropic homogeneous face layers in Type B beams, outweighing the effect of porosity on the mass density of the beam.

Table 10 Variation of nondimensional fundamental natural frequencies of Type A beam under different BCs, porosity distribution, and elastic foundation (1–2–1, $p=2$)

Table 11 Variation of nondimensional fundamental natural frequencies of Type B beam under different BCs, porosity distribution, and elastic foundation (1–2–1, $p=2$)

Similarly, Tables 12 and 13 show the variation of the nondimensional critical buckling load of the beams for the core porosity coefficient of three different porosity patterns and the $L/h$ ratio for various BCs. Regardless of the porosity patterns or and $L/h$ ratio, the nondimensional critical buckling loads decrease as the parameter ${e}_{0}$ increases. This behavior is attributed to an increase in core porosity that reduces the beam's bending stiffness, resulting in a reduction in critical buckling loads. It is noticed that for all conditions, the presence of elastic foundation yields an increment in nondimensional fundamental natural frequencies and critical buckling loads of FG sandwich beams. The inclusion of a shear layer further enhances this effect by increasing the shear stiffness of the beams.

Table 12 Variation of nondimensional critical buckling loads of Type A beam under different BCs, porosity distribution, and elastic foundation (1–2–1, $p=2$)

Table 13 Variation of nondimensional critical buckling loads of type B beam under different BCs, porosity distribution, and elastic foundation (1–2–1, $p=2$)

Figures 4 and 5 visualize the variation of nondimensional fundamental natural frequencies and critical buckling loads of the SS beams with respect to porosity coefficients for three different cases: Case 1 with ${K}_{w}=0$ and ${K}_{p}=0$, Case 2 with ${K}_{w}=10$ and ${K}_{p}=0$, and Case 3 with ${K}_{w}=10$ and ${K}_{p}=10$. The skin–core-skin thickness ratio of 1–2–1, $L/h=10$, $p=5,$ and symmetric porosity distribution are considered. It is revealed that for all cases, nondimensional fundamental natural frequencies increase as the porosity coefficient increases. In terms of critical buckling loads, there is a decrease observed for all cases as the porosity coefficient increases. In Case 2 introduction of the Winkler parameter (${K}_{w}$) results in a slight increase in the fundamental natural frequencies and critical buckling loads of the beams. This phenomenon can be attributed to the stiffness of the Winkler foundation, which provides additional support and stability to the beams. Conversely, in case 3 the inclusion of the Pasternak parameter (${K}_{p})$ leads to a significant enhancement in the fundamental natural frequencies and critical buckling loads effect by increasing the shear stiffness of the beams, resulting in a significant improvement in its free vibration and buckling behaviors. This observation suggests that the effect of the Pasternak parameter on both the natural frequency and critical buckling load is considerably more significant than the Winkler parameter.

Fig. 4

The effect of porosity coefficient on fundamental natural frequencies of simple supported FG sandwich beams for symmetric porosity distribution and different elastic foundation constants (1–2–1, $L/h=10$, $p=5$)

Fig. 5

The effect of porosity coefficient critical buckling loads of simply supported FG sandwich beams for symmetric porosity distribution and different elastic foundation constants (1–2–1, $L/h=10$, $p=5$)

4.3 Effect of Skin–Core-Skin Thickness Ratio

Tables 14 and 15 illustrate the effect of the skin–core-skin thickness ratio on the nondimensional fundamental natural frequencies and critical buckling loads for $L/h =5$ and $p=5$ with respect to the variation of the porosity coefficient of the three porosity patterns. It is, generally, noticeable that the nondimensional fundamental natural frequencies experience a decrease as the skin–core-skin thickness ratio decreases for Type A whereas an increase for Type B. This behavior can be attributed to the decrease in the beam's bending stiffness for Type A and the enhancement of the bending stiffness of the beam for Type B as the porous core thickness increases. The results indicate that the skin–core-skin thickness ratios 2–1–2 and 1–2–1 exhibit the lowest and highest values of the fundamental natural frequencies for Type A and reversely for Type B. However, for clamped Type B beams, the fundamental natural frequencies decrease as the skin–core-skin thickness ratio decreases for all types of porosity. Due to a relatively small length-to-thickness ratio $L/h=5$ and an FG core, the reduction rate in bending stiffness is more significant than the mass density for a CC beam. As a result, there is a decrease in the natural frequency as the thickness of the FG porous core increases. Similarly, the nondimensional critical buckling loads show a consistent decrease as the skin–core-skin thickness ratio decreases for both types. The results showcased in the tables emphasize the critical importance of carefully considering the geometric configurations, when designing FG sandwich beams with porous core to align with the desired performance criteria.

Table 14 Variation of nondimensional fundamental natural frequencies of FG sandwich beams with different skin–core-skin thickness ratio, BCs, and porosity distribution ($L/h=5$, $p=5$, ${K}_{w}=25$, ${K}_{p}=10$)

Table 15 Variation of nondimensional critical buckling loads of FG sandwich beams with different skin–core skin thickness ratio, BCs, and porosity distribution ($L/h=5$, $p=5$, ${K}_{w}=25$, ${K}_{p}=10$)

4.4 Effect of Power Index and Length-to-Thickness Ratio

Figures 6 and 7 illustrate the effect of the power index on the fundamental natural frequencies and critical buckling loads of FG sandwich beams with the three different porosity distribution patterns. A CC beam (1–2–1, $L/h=15$, ${e}_{0}=0.8$, ${K}_{w}=50$, ${K}_{p}=10$) is considered. As expected, the nondimensional fundamental natural frequencies and critical buckling loads of FG sandwich beams increase with the power index for Type A, while for Type B, they decrease inversely for all porosity distributions. It is seen that the effect of porosity distributions on nondimensional fundamental natural frequencies and critical buckling loads of Type A is relatively small compared to that observed for Type B beams. This smaller variation in natural frequencies and buckling loads for Type A beam with different porosity distributions can be attributed to the presence of FG face layers, which contribute significantly to the overall stiffness and dynamic properties of the beam, thereby reducing the relative impact of porosity distribution in the isotropic metal core. Conversely, in Type B the porosity distribution in the FG porous core has a more pronounced influence on the overall stiffness and natural frequencies than isotropic homogeneous face layers. However, the symmetric porosity distribution generally yields higher natural frequencies in both types. This is because a symmetric porosity distribution leads to a more uniform stiffness distribution along the beam's length, resulting in higher overall stiffness and natural frequencies. This highlights the importance of carefully considering the porosity distribution during the manufacturing process. Optimization of porosity distribution can lead to achieve desired mechanical performance of the beams while ensuring cost-effectiveness and feasibility during the design and manufacturing process.

Fig. 6

Variation of nondimensional fundamental natural frequencies of clamped FG sandwich beams with the power index for different porosity distribution types (1–2–1, $L/h=15$, ${e}_{0}=0.8$, ${K}_{w}=50$, ${K}_{p}=10$)

Fig. 7

Variation of nondimensional critical buckling loads of clamped FG sandwich beams with the power index for different porosity distribution types (1–2–1, $L/h=15$, ${e}_{0}=0.8$, ${K}_{w}=50$, ${K}_{p}=10$)

Figures 8 and 9 demonstrate the effect of length-to-thickness ratio $L/h$ on the fundamental natural frequencies and critical buckling loads of FG sandwich beams with the three porosity distribution patterns. A CC beam (1–2–1, ${e}_{0}=0.8$, ${K}_{w}={K}_{p}=10$, $p=1$) is considered. It is seen that the nondimensional fundamental natural frequencies and critical buckling loads of FG sandwich beam increase as the increase of length-to-thickness ratio $L/h$ for all porosity distributions. Moreover, the difference in nondimensional fundamental natural frequencies and critical buckling loads for porosity distribution patterns becomes significant as the length-to-thickness ratio increases. This is because, with higher length-to-thickness ratios, porosity has a more significant impact on the overall stiffness and mechanical behavior of the beam. The findings illustrated that incorporating porosity can effectively lead to a reduction in overall material density while still maintaining adequate stiffness and buckling resistance, particularly evident in beams with higher $L/h$ ratios. This implies that for applications where weight reduction is a priority, the use of porous core materials in FG sandwich beams with higher $L/h$ ratios can be advantageous.

Fig. 8

Variation of nondimensional fundamental natural frequencies of clamped FG sandwich beams with the length-to-thickness ratio for different porosity distribution types (1–2–1, ${e}_{0}=0.8$, ${K}_{w}={K}_{p}=10$, $p=1$)

Fig. 9

Variation of nondimensional critical buckling loads of clamped–clamped FG sandwich beams with the length-to-thickness ratio for different porosity distribution types (1–2–1, ${e}_{0}=0.8$, ${K}_{w}={K}_{p}=10$, $p=1$)

4.5 Effect of Elastic Foundation

To study the effects of foundation parameters with different porosity patterns and BCs on free vibration and buckling behavior of 1–2–1 sandwich beam with $L/h=5$, ${e}_{0}=0.5$, $p=5$ are considered. The variation of nondimensional fundamental natural frequencies and critical buckling loads with different foundation parameters, porosity patterns, and BCs are summarized in Tables 16 and 17. It is seen that the nondimensional fundamental frequencies and critical buckling loads increase with the enhancement of foundation parameters for all porosity distributions and BCs. This behavior is attributed to the fact that increasing the elastic foundation parameter amplifies the bending stiffness of the beam, thereby improving its vibrational and buckling resistance.

Table 16 Variation of nondimensional fundamental natural frequencies of FG sandwich beams with various foundation parameters, BCs, and porosity distribution types (1–2–1, $L/h=5$, ${e}_{0}=0.5$, $p=5$)

Table 17 Variation of nondimensional critical buckling loads of FG sandwich beams with various foundation parameters, BCs, and porosity distribution types (1–2–1, $L/h=5$, ${e}_{0}=0.5$, $p=5$)

Figures 10 and 11 show the variations of nondimensional fundamental natural frequencies and critical buckling loads as a function of elastic foundation parameters to evaluate separately the effects of Winkler and Pasternak elastic foundation parameters. It should be noted that the nondimensional fundamental natural frequencies and critical buckling loads increase considerably with the increase of the Pasternak parameter. From this, it can be inferred that changes in ${K}_{p}$ have a more pronounced impact on fundamental frequencies and critical buckling loads compared to changes in ${K}_{w}$. Besides, the effect of porosity distribution patterns is found to be negligible, especially for the CF beam. This is primarily attributed to the fact that the elastic foundation has a more significant effect on the bending stiffness than the porosity effect.

Fig. 10

Variation of nondimensional fundamental natural frequencies of Type B for various BCs and porosity distributions (1–2–1, $L/h=5$, ${e}_{0}=0.8$, $p=5$) under ${K}_{w}$ and ${K}_{p}$

Fig. 11

Variation of nondimensional critical buckling loads of Type B for various BCs and porosity distributions (1–2–1, $L/h=5$, ${e}_{0}=0.8$, $p=5$) under ${K}_{w}$ and ${K}_{p}$

5 Conclusion

This paper presented a new finite element model based on quasi-3D deformation theory for free vibration and buckling analysis of FG sandwich beams with porous core resting on a two-parameter Winkler-Pasternak elastic foundation. Three different porosity patterns including uniform, symmetric, and asymmetric are considered. A three-nodded finite element having 15-DOFs is proposed for the numerical solution. The accuracy and convergence of the proposed model is verified with several examples. A comprehensive parametric study is carried out to explore the effects of the boundary conditions, skin-to-core thickness ratio, power-law index, slenderness, porosity, and elastic foundation parameters on the natural frequencies and critical buckling loads of FG sandwich beams. The main findings from the study can be summarized as follows:

• 1. For FG sandwich beams with a porous metal core, the fundamental natural frequencies and critical buckling loads increase with the increase of the power-law index and inversely they decrease with the power-law index for sandwich beams with FG core.

• 2. As the porosity coefficient increases, the fundamental natural frequencies increase, while the critical buckling loads decrease due to the concurrent reduction in the bending stiffness and mass density.

• 3. Symmetric porosity distribution yields the most favorable fundamental natural frequencies and critical buckling loads.

• 4. As the skin–core-skin thickness ratio decreases, the fundamental natural frequencies decrease for Type A and increase for Type B. Critical buckling loads decrease for both types.

• 5. An increase in the length-to-thickness ratio results in higher fundamental natural frequencies and critical buckling loads for FG sandwich beams and the porosity distribution effect becomes more significant.

• 6. The fundamental natural frequencies and critical buckling loads of the FG sandwich beam increase significantly as the spring and shear constants of the elastic foundation increase, particularly when the shear layer constant increases.

Appendix

The shape functions ${\psi }_{i}\left(x\right)$ and ${\varphi }_{i}\left(x\right)$ are given are given as follows:

$$\begin{aligned} \psi_{1} & = 1 - \frac{3x}{L} + 2\left( \frac{x}{L} \right)^{2} ,\quad \psi_{2} = \frac{4x}{L} - \frac{{4x^{2} }}{{L^{2} }},\quad \psi_{3} = - \frac{x}{L} + 2\left( \frac{x}{L} \right)^{2} , \\ \varphi_{1} { } & = 1 - \frac{{23x^{2} }}{{L^{2} }} + \frac{{66x^{3} }}{{L^{3} }} - \frac{{68x^{4} }}{{L^{4} }} + \frac{{24x^{5} }}{{L^{5} }},\quad \varphi_{2} { } = x - \frac{{6x^{2} }}{L} + \frac{{13x^{3} }}{{L^{2} }} - \frac{{12x^{4} }}{{L^{3} }} + \frac{{4x^{5} }}{{L^{4} }}, \\ \varphi_{3} { } & = \frac{{16x^{2} }}{{L^{2} }} - \frac{{32x^{3} }}{{L^{3} }} + \frac{{16x^{4} }}{{L^{4} }},\quad \varphi_{4} { } = - \frac{{8x^{2} }}{L} + \frac{{32x^{3} }}{{L^{2} }} - \frac{{40x^{4} }}{{L^{3} }} + \frac{{16x^{5} }}{{L^{4} }}, \\ \varphi_{5} { } & = \frac{{7x^{2} }}{{L^{2} }} - \frac{{34x^{3} }}{{L^{3} }} + \frac{{52x^{4} }}{{L^{4} }} - \frac{{24x^{5} }}{{L^{5} }},\quad \varphi_{6} { } = - \frac{{x^{2} }}{L} + \frac{{5x^{3} }}{{L^{2} }} - \frac{{8x^{4} }}{{L^{3} }} + \frac{{4x^{5} }}{{L^{4} }} \\ \end{aligned}$$

(A1)

The components of the stiffness matrix K and the mass matrix M are given as follows:

$$\begin{aligned}\mathbf{K}&=\left[\begin{array}{c} {K}_{11} { K}_{12} {K}_{13} {K}_{14}\\ \\ {K}_{12} { K}_{22} {K}_{23} {K}_{24}\\ \\ {K}_{13} { K}_{23} {K}_{33} {K}_{34}\\ \\ {K}_{14} { K}_{24} {K}_{34} {K}_{44} \\ \end{array}\right],\mathbf{M}=\left[\begin{array}{c} {M}_{11} { M}_{12} {M}_{13} {M}_{14}\\ \\ {M}_{12} { M}_{22} {M}_{23} {M}_{24}\\ \\ {M}_{13} { M}_{23} {M}_{33} {M}_{34}\\ \\ {M}_{14} { M}_{24} {M}_{34} {M}_{44} \\ \end{array}\right],\\ {\varvec{G}} &= \left[ {\begin{array}{*{20}c} 0 & 0 & 0 & 0 \\ & & & \\ {0 } & { N_{22} } & 0 & { 0} \\ & & & \\ { 0} & 0 & { 0} & 0 \\ & & & \\ 0 & { 0} & 0 & 0 \\ \end{array} } \right],\quad {{\varvec{\Delta}}} = \left\{ {\begin{array}{*{20}c} {u_{i} } \\ \\ {w_{i} } \\ \\ {\phi_{yi} } \\ \\ {\phi_{zi} } \\ \end{array} } \right\}\end{aligned}$$

(A2)

where

$$\begin{aligned} K_{11} \left( {i,j} \right) & = A_{11} \mathop \int \limits_{0}^{L} \psi_{i,x} \psi_{j,x} {\text{d}}x,K_{12} \left( {i,j} \right) = - B_{11} \mathop \int \limits_{0}^{L} \psi_{i,x} \varphi_{j,xx} {\text{d}}x, \\ K_{13} \left( {i,j} \right) & = C_{11} \mathop \int \limits_{0}^{L} \psi_{i,x} \psi_{j,x} {\text{d}}x,K_{14} \left( {i,j} \right) = B_{S13} \mathop \int \limits_{0}^{L} \psi_{i,x} \psi_{j} {\text{d}}x, \\ K_{22} \left( {i,j} \right) & = E_{11} \mathop \int \limits_{0}^{L} \varphi_{i,xx} \varphi_{j,xx} {\text{d}}x - N_{0} \mathop \int \limits_{0}^{L} \varphi_{i,x} \varphi_{j,x} {\text{d}}x + k_{w} \mathop \int \limits_{0}^{L} \varphi_{i} \varphi_{j} dx + k_{p} \mathop \int \limits_{0}^{L} \varphi_{i,x} \varphi_{j,x} {\text{d}}x, \\ K_{23} \left( {i,j} \right) & = - D_{11} \mathop \int \limits_{0}^{L} \varphi_{i,xx} \psi_{j,x} {\text{d}}x, \\ K_{24} \left( {i,j} \right) & = - C_{S13} \mathop \int \limits_{0}^{L} \varphi_{i,xx} \psi_{j} {\text{d}}x + gk_{w} \mathop \int \limits_{0}^{L} \varphi_{i} \psi_{j} {\text{d}}x + gk_{p} \mathop \int \limits_{0}^{L} \varphi_{i,x} \psi_{j,x} {\text{d}}x, \\ K_{33} \left( {i,j} \right) & = F_{11} \mathop \int \limits_{0}^{L} \psi_{i,x} \psi_{j,x} {\text{d}}x + A_{s55} \mathop \int \limits_{0}^{L} \psi_{i} \psi_{j} {\text{d}}x, \\ K_{34} \left( {i,j} \right) & = E_{S13} \mathop \int \limits_{0}^{L} \psi_{i,x} \psi_{j} {\text{d}}x + A_{s55} \mathop \int \limits_{0}^{L} \psi_{i} \psi_{j,x} {\text{d}}x, \\ K_{44} \left( {i,j} \right) & = D_{S33} \mathop \int \limits_{0}^{L} \psi_{i} \psi_{j} {\text{d}}x + A_{s55} \mathop \int \limits_{0}^{L} \psi_{i,x} \psi_{j,x} {\text{d}}x + g^{2} k_{w} \mathop \int \limits_{0}^{L} \psi_{i} \psi_{j} {\text{d}}x + g^{2} k_{p} \mathop \int \limits_{0}^{L} \psi_{i,x} \psi_{j,x} {\text{d}}x, \\ M_{11} \left( {i,j} \right) & = I_{1} \mathop \int \limits_{0}^{L} \psi_{i} \psi_{j} {\text{d}}x,M_{12} \left( {i,j} \right) = - I_{2} \mathop \int \limits_{0}^{L} \psi_{i} \varphi_{j,x} {\text{d}}x,M_{13} \left( {i,j} \right) = I_{4} \mathop \int \limits_{0}^{L} \psi_{i} \psi_{j} {\text{d}}x,M_{14} \left( {i,j} \right) = 0, \\ M_{22} \left( {i,j} \right) & = I_{1} \mathop \int \limits_{0}^{L} \varphi_{i} \varphi_{j} {\text{d}}x + I_{3} \mathop \int \limits_{0}^{L} \varphi_{i,x} \varphi_{j,x} {\text{d}}x,M_{23} \left( {i,j} \right) = - I_{5} \mathop \int \limits_{0}^{L} \varphi_{i,x} \psi_{j} {\text{d}}x,M_{24} \left( {i,j} \right) = I_{7} \mathop \int \limits_{0}^{L} \varphi_{i} \psi_{j} {\text{d}}x, \\ M_{33} \left( {i,j} \right) & = I_{6} \mathop \int \limits_{0}^{L} \psi_{i} \psi_{j} {\text{d}}x,M_{34} \left( {i,j} \right) = 0,M_{44} \left( {i,j} \right) = I_{8} \mathop \int \limits_{0}^{L} \psi_{i} \psi_{j} {\text{d}}x,N_{22} \left( {i,j} \right) = N_{0} \mathop \int \limits_{0}^{L} \varphi_{i,x} \varphi_{j,x} {\text{d}}x \\ \end{aligned}$$

(A3)