1 Introduction

User interest in very large, space deployable antennas has emerged in recent years. These applications are pertinent in several scientific fields, such as mobile communication, military reconnaissance, and Earth resource sensing. A deployable structure is folded when carried by vehicles during transportation and deployed to its full scale in its final state when working in orbit [1,2,3,4]. Deployable antennas have presented effective solutions to address the volume restrictions when building antennas with large apertures [5,6,7]. Therefore, according to the low weight demand, deployable antennas must be designed to meet the restrictions of the launcher’s capability. The annular tensegrity structure has shown many advantages in deployability, control design, structural integrity and minimum mass. Therefore, the structure is an ideal structural scheme for creating a large aperture for deployable antennas.

Many studies have presented several concepts for large deployable antennas, such as modular [8, 9], radial [10, 11], umbrella [12, 13] and tetrahedron truss [14] antennas. By supporting the mesh reflector, deployable structures are employed to offer enough rigidity to resist deformation and vibration. However, because of their size requirements, ultralarge microwave-transmitting antennas, are designed to reach hundreds of meters in scale. Their designed weight, volume and rigidity must satisfy the demands of the mission [15].

To meet the increasing requirements of high stiffness and large aperture of deployable antennas, many academic institutions have performed considerable work on structural design. Astro Aerospace Corporation has developed four types of AM satellites and put three of them into use [16]. Datashvili [17] developed a double-scissor ring truss structure and analyzed its rigidity. Yuan et al. [18] proposed cable-network structures of deployable satellite antennas. Moshtaghzadeh [19] proposed a reconfigurable antenna structure, which is simulated using Hodges’s fully intrinsic, nonlinear composite beam theory with strict geometry. Medzmariashvili [1] presented a conical ring structure composed of several V-folding bars and implemented it in a demonstrator model. The designs according to the recent European Space Agency (ESA) patents are successfully manufactured and tested. Tserodze [20] presented a deployable structure with unique features, a differential lever mechanism. Compared to similar structures, the synchronous devices no longer need to be installed in the upper and lower kinematic chains within the connecting members. Zheng [21] established a new simplified large deployable reflector that has a better folding ratio in both the radial direction and height direction. A prototype with an aperture of 3 m is fabricated and tested to show the deployment test of the backbone. The Japan Aerospace Exploration Agency (JAXA) developed a 30 m class of large deployable reflectors with a lower overall mass and high folding ratio. The structure consists of several deployable truss modules of tri-folding bars. The feasibility of the design of tri-fold deployable trusses has been validated via structural analyses [22]. Liu [23] proposed a new large deployable antenna structure with radial ribs and tensioned cables and analyzed the deployment process of the antenna. The structure has been designed with a series of advantages, such as a high stiffness and low mass. An experimental prototype of 1.8 m is fabricated and its dynamic characteristics are tested to demonstrate the feasibility of the design. Kan [24,25,26] presented a symplectic instantaneous optimal control (IOC) method for solving the problems of cable slacking. The solutions of static and dynamic analysis for deployable tensegrity antennas illustrate the advantages of robustness and effectiveness of the proposed approach.

The total weight of the deployed antenna increases with an increase in the antenna’s aperture due to additional bars and hinges. Thus, when the antenna aperture has reached 100 m, the number of truss bars should be limited to reduce the weight of the antenna. However, the structural stiffness should also be guaranteed to be large enough to meet the requirement. Prestressed structures are built for the conditions of low mass and large scale. Highly coupled structures often experience large displacements. Moreover, the geometrical nonlinearity of the structure should not be disregarded to achieve a more accurate model. Several studies have investigated design of the large antenna structures (for which the aperture exceed 30 m) and have paid less attention to the influence of the number of truss bars and the geometrical nonlinearity on the overall structural stiffness.

This paper proposes our work on a spatial annular tensegrity structure that can be utilized as a deployable antenna based on the analysis of dynamic characteristics of parameterized truss structures. First the parameterized hoop unit is equivalent to an anisotropic beam element to simplify the calculations. The explicit formulations of its strain energy are obtained when taking the directional derivative of the displacement components at the center of the hoop unit. Second, the column, which is considered a variable section beam, is also equivalent to a beam element based on the principle of strain energy equivalence in the energy method. Additionally, the equivalent mechanical model has considered the geometric nonlinearity caused by cables. Third, the equivalent dynamic model comprises multiple deployable hoop, column and tensioned cables. The behaviors of the natural frequencies and vibration mode shapes of the antenna are obtained using the dynamic model, which employs different hoop geometrical configurations. Last, priority approaches to improve the structural stiffness when employing different geometrical configurations of the hoop are given based on an analysis of the sensitivity of the structural parameters.

This paper is organized as follows. In Sect. 2, a large spatial annular tensegrity structure is introduced based on the Hoop-Column antenna. Section 3 presents the corresponding equivalent mechanical modeling methods for the parameterized components of the tensegrity structure. Section 4 shows the results of the dynamic analysis of the antenna structure when various typical schemes of the deployable hoop unit are employed. The effect of the structural parameter variation on the dynamic characteristics is investigated. Moreover, the sensitivity to the dynamic behaviors leads to a method to improve the structural stiffness when different hoop units are employed. A design approach to improve the structural stiffness, which provides a guidance for engineering applications, is proposed. In Sect. 5, the conclusion is summarized, and suggestions for future work are provided.

2 Large annular tensegrity structure

A large annular tensegrity structure is a spatial structure consisting of compressive and tension members. The self-stable structure is a system of struts and cables. As shown in Fig. 1, the conventional Hoop-Column antenna is constructed in an annular tensegrity to achieve a large structural scale. The Hoop-Column antenna mainly consists of a telescoping column that deploys from the central pedestal supported hub and the cables that connect the hoop and column [27]. The column is sequentially deployed and is symmetrical about the center, which simultaneously extends in both directions. The cables emanate from the upper and lower extremities of the column and are connected with hinge platforms of the hoop.

Fig. 1
figure 1

Annular tensegrity structure

Full size image

The hoop, which supports the periphery of the reflective surface, consists of several jointed segments. The deployable hoop structure can become a rigid ring structure around the column after fully deploying. Several joint platforms and segments are precisely supported by the cables and form a rigid boundary. To date, several ring structures and associated technologies have been thoroughly developed. A majority of the ring mechanisms are described in Fig. 2, in both the spatial case and planar case, and exhibit a single degree of freedom. Generally, this is the case for the single ring, double ring, scissor ring and pyramidal ring, because coaligned hinge axes are employed in 3D space. However, the stiffness of the annular tensegrity structure will vary since different hoop forms are employed, which will affect the stability of the structure. The influences of the geometric properties such as the cross-sectional area of the truss or the aperture of the ring truss on the dynamic characteristics of the tensegrity are also worth exploring.

Fig. 2
figure 2

The hoop of the antenna structure

Full size image

The dynamic performance is related to the folding schemes and, the height and length of the hoop unit. It is much more complicated to evaluate the dynamic performance when different hoop units are considered. Therefore, it is convenient that the parameterized dynamic model of the annular tensegrity structure is obtained based on an equivalent method. The dynamic characteristics of the continuum beam and cable model can be written in terms of the geometrical properties of the components. In this paper, the antenna is modeled as follows:

  1. (1)

    The column is rigid and its bottom is fixed;

  2. (2)

    The central hoop consists of 36 repeating truss units through which the column passes;

  3. (3)

    The support cables at the top and bottom of the tensegrity structure are modeled as two sets of mass identical cables arranged 10 degrees apart.

3 Equivalent mechanics modeling of the annular tensegrity structure

3.1 The equivalent principle of the hoop structure

The annular hoop, which is an articulated truss, comprises bars and hinges, and consists of periodic units connected end to end in the clockwise direction. Equivalent modeling is a homogenization method that is widely employed for dynamic analysis of lattice structures. The derivation of kinetic and strain energy at the center of the truss unit can help establish the equivalent homogenized model. Based on the principle that the stiffness and mass matrices of the hoop structure are similar to those of the anisotropic Euler‒Bernoulli beam element, the dynamic equivalent model can be obtained in terms of the structural and material properties. This method proposes a simple approach for comparing the dynamic behaviors of hoops with different structural configurations.

3.1.1 The equivalent stiffness

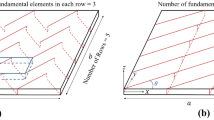
The hoop structure consists of several plane truss units that are inter linked. Based on an analytical approach of the continuum modeling method, the kinetic and potential energies of the truss unit must be derived with respect to the strain and velocity components of the node [28]. As the hoop units are constructed of bars with connected joints, linear variations are assumed for the displacement of the components (u, v, and w) within the midcross section of the hoop unit, as shown in Fig. 3. As outlined in Fig. 3, the cross section of hoop unit is perpendicular to x coordinate, and has dimensions only in the z coordinate when its orthography can be approximate to a straight line along the z axis. The displacement components of hoop unit can be calculated by rotation around both x and y directions, as well as tensile strain in the z direction. Therefore, the displacement components are obtained as [29, 30]:

$$ \left\{ {\begin{array}{*{20}l} {u\left( {x,y,z} \right) = u^{0} \left( x \right) + z\phi_{y}^{0} \left( x \right)} \\ {v\left( {x,y,z} \right) = v^{0} \left( x \right) - z\phi_{x}^{0} \left( x \right)} \\ {w\left( {x,y,z} \right) = w^{0} \left( x \right) + z_{z}^{0} \left( x \right)} \\ \end{array} } \right. $$
(1)

where \(u^{0} \left( x \right)\), \(v^{0} \left( x \right)\), and \(w^{0} \left( x \right)\) denote the displacement components obtained at the center of the cross section; \(\phi_{x}^{0} \left( x \right)\) and \(\phi_{y}^{0} \left( x \right)\) are the rotations at the center of the mid-cross-section. \(\epsilon_{z}^{0}\) denotes the strain component in the z direction. The variations in displacements are linear along the z-axis and depend on the x coordinate. The strain components depend on the derivatives of the displacement field along the coordinates x, y, and z can be written as:

$$ \left\{ {\begin{array}{*{20}l} {\epsilon_{x} = \frac{\partial u}{{\partial x}} = \frac{{\partial u^{0} }}{\partial x} + z\frac{{\partial \phi_{y}^{0} }}{\partial x} = \epsilon_{x}^{0} + z\kappa_{z}^{0} \, } \hfill \\ {\epsilon_{y} = \frac{\partial v}{{\partial y}} = \frac{{\partial v^{0} }}{\partial y} - z\frac{{\partial \phi_{x}^{0} }}{\partial y} = \epsilon_{y}^{0} - z\kappa_{t}^{0} \, } \hfill \\ {\epsilon_{z} = \frac{\partial w}{{\partial z}} = \epsilon_{z}^{0} \, } \hfill \\ {\gamma_{xz} = \frac{1}{2}\left( {\frac{\partial u}{{\partial z}} + \frac{\partial w}{{\partial x}}} \right) = \frac{1}{2}\left( {\phi_{y}^{0} + z\frac{{\partial \epsilon_{z}^{0} }}{\partial x}} \right)} \hfill \\ \end{array} } \right. $$
(2)

where \(\epsilon_{x}^{0}\), \(\epsilon_{y}^{0}\), and \(\epsilon_{z}^{0}\) denote the tensile strains along the three directions of the coordinate system in the hoop unit center; \(\gamma_{xz}^{0}\) denotes the tensile strain; \(\kappa_{z}^{0}\) and \(\kappa_{t}^{0}\) are the curvatures of the hoop unit center. Then, the strain components can be expanded in a Taylor series around the origin of the coordinates. According to the strain values at locations where x ≠ 0, the relations are written as follows:

$$ \left\{ {\begin{array}{*{20}l} {\epsilon_{x}^{(k)} = \epsilon_{x}^{0} + z^{(k)} \kappa_{z}^{0} + x^{(k)} \left( {\frac{{\partial \epsilon_{x}^{0} }}{\partial x} + z^{(k)} \frac{{\partial \kappa_{z}^{0} }}{\partial x}} \right)} \hfill \\ {\epsilon_{z}^{(k)} = \epsilon_{z}^{0} } \hfill \\ {\epsilon_{xz}^{(k)} = \epsilon_{xz}^{0} + x^{(k)} \left( {\frac{{\partial \epsilon_{x} }}{\partial x}} \right)} \hfill \\ {\frac{{\partial^{2} v}}{{\partial x^{2} }} = \kappa_{y}^{0} - z^{(k)} \frac{{\partial \kappa_{t}^{0} }}{\partial x} + x^{(k)} \left( {\frac{{\partial \kappa_{y}^{0} }}{\partial x} + z^{(k)} \frac{{\partial \kappa_{z}^{0} }}{\partial x}} \right)} \hfill \\ {\frac{{\partial^{2} w}}{{\partial x^{2} }} = 2\frac{{\partial \gamma_{xz}^{0} }}{\partial x} - \kappa_{z}^{0} - z^{(k)} \frac{{\partial \kappa_{t}^{0} }}{\partial x} + x^{(k)} \left( {2\frac{{\partial^{2} \gamma_{xz}^{0} }}{{\partial x^{2} }} - \frac{{\partial \kappa_{z}^{0} }}{\partial x} - z^{(k)} \frac{{\partial^{2} \kappa_{t}^{0} }}{{\partial x^{2} }}} \right)} \hfill \\ {\frac{{\partial \phi_{x} }}{\partial x} = \kappa_{t}^{0} + x^{(k)} \frac{{\partial \kappa_{t}^{0} }}{\partial x}} \hfill \\ {\frac{{\partial \phi_{z} }}{\partial x} = \kappa_{y}^{0} + x^{(k)} \frac{{\partial \kappa_{y}^{0} }}{\partial x}} \hfill \\ {\kappa_{y}^{0} = \left. {\frac{{d\phi_{z0} }}{dx}} \right|_{x = 0} } \hfill \\ \end{array} } \right. $$
(3)

where k is the kth rod in the unit.

Fig. 3
figure 3

Displacement components of the hoop unit

Full size image

Note that the displacement of the rotation must be transferred to the local coordinate when calculating the strain energy and kinetic energy. As shown in Fig. 4, the local coordinate system is set up along the length of the beam element. α is the angle between the x-axis of the coordinate system and the \(\overline{x}\)-axis of the local coordinate system of the kth bar. Then, the tensile strain of the kth beam element in the plane is obtained by using direction cosines:

$$ \epsilon^{(k)} = \epsilon_{x}^{(k)} \cos^{2} \alpha + 2\epsilon_{xz}^{(k)} \cos \alpha \sin \alpha + \epsilon_{z}^{(k)} \sin^{2} \alpha $$
(4)
Fig. 4
figure 4

Local coordinate frame of a member

Full size image

The parametric hoop unit can be regarded as the repeating unit which consists of a continuum model, as shown in Fig. 5.

Fig. 5
figure 5

Parameterized model of the hoop unit

Full size image

The kinetic energy of the unit can be described by that of beam element members as follows:

$$ U_{A} = \sum\limits_{m = 1}^{i} {U^{(m)} } + \frac{1}{2}\sum\limits_{n = 1}^{j} {U^{(n)} } + \sum\limits_{k = 1}^{p} {U^{(k)} } $$
(5)

where i, j, and p are the number of the horizontal bars, longitudinal bars and diagonal bars, respectively, of the unit. Using each rod of the unit as the space beam unit, its deformation includes the tensile direction, bending direction and torsional direction. For the strain energy including bending and rotational deformations of the kth beam element, we obtain:

$$ U^{(k)} = \frac{1}{2}\int_{L} {\left[ {EA\left( {\frac{{\partial \overline{u}}}{{\partial \overline{x}}}} \right)^{2} + EI_{z} \left( {\frac{{\partial^{2} \overline{v}}}{{\partial \overline{x}^{2} }}} \right)^{2} + EI_{y} \left( {\frac{{\partial^{2} \overline{w}}}{{\partial \overline{x}^{2} }}} \right)^{2} + GJ\left( {\frac{{\partial \overline{\phi }_{x} }}{{\partial \overline{x}}}} \right)^{2} } \right]} {\text{d}}\overline{x} $$
(6)

Using Eqs. (4), (5), (6), and Eqs. (2), the strain energy of the hoop unit can be calculated by:

$$ U_{A} = \frac{j}{2}E_{l} A_{l} L_{l} \left( {\epsilon_{x} } \right)^{2} + \frac{v}{2}E_{v} A_{v} L_{v} \left( {\epsilon_{z} } \right)^{2} + \frac{p}{2}E_{d} A_{d} L_{d} \left( {\epsilon_{x} \cos^{2} \alpha + 2\epsilon_{x} \epsilon_{z} \cos^{2} \alpha + \epsilon_{z} \sin^{2} \alpha } \right)^{2} $$
(7)

According to the position of each beam of the unit, the strain energy of the unit can be written as follows:

$$ U_{A} = \frac{1}{2}\left\{ \begin{array}{l} \left[ \begin{array}{l} E_{d} A_{d} L_{d} \sum\limits_{k = 1}^{p} {\left( {\epsilon_{x} \cos^{2} \alpha_{k} + \epsilon_{z} \sin^{2} \alpha_{k} + 2\gamma_{xz} \sin \alpha_{k} \cos \alpha_{k} - \frac{{h_{k} \kappa_{z}^{0} }}{2}\cos^{2} \alpha_{k} } \right)^{2} } \hfill \\ + 2iE_{l} A_{l} L_{l} \left( {\epsilon_{x}^{2} + \frac{{L_{v}^{2} \left( {\kappa_{z}^{0} } \right)^{2} }}{4} + i^{ + } \epsilon_{x} L_{v} \kappa_{z}^{0} - i^{ - } \epsilon_{x} L_{v} \kappa_{z}^{0} } \right) + jE_{v} A_{v} L_{v} \left( {\epsilon_{z}^{2} } \right) \hfill \\ \end{array} \right] \hfill \\ + \left[ {pE_{d} I_{z}^{d} \left( {\kappa_{y}^{0} } \right)^{2} + \sum\limits_{k = 1}^{p} {\left[ {E_{d} I_{y}^{d} \left( {\kappa_{z}^{0} } \right)^{2} \cos^{2} \alpha_{k} + G_{d} J_{d} \left( {\left( {\kappa_{t}^{0} \cos \alpha_{k} + \kappa_{y}^{0} \sin \alpha_{k} } \right)^{2} } \right)} \right]} } \right] \hfill \\ + \left[ {i\left( {E_{l} I_{z}^{l} \left( {\kappa_{y}^{0} } \right)^{2} + E_{l} I_{y}^{l} \left( {\kappa_{z}^{0} } \right)^{2} + G_{l} J_{l} \left( {\kappa_{t}^{0} } \right)^{2} } \right)} \right] \hfill \\ + \left[ {j\left( {E_{v} I_{z}^{v} \left( {\kappa_{y}^{0} } \right)^{2} + G_{v} J_{v} \left( {\kappa_{y}^{0} } \right)^{2} } \right)} \right] \hfill \\ \end{array} \right\} $$
(8)

where i+ is the number of upper horizontal bars, i− is the number of lower horizontal bars; A, L, E denote the cross-sectional area, length, and modulus, respectively, of the bars. Their subscripts v, d, l refer to the longitudinal bars, diagonal bars, and horizontal bars, respectively, and h is the displacement component of the diagonal along the z axis. Similar to the approach used in Ref. [31], the strain gradient of the derivatives of the strain energy should be zero. Therefore, we obtain:

$$ \frac{{\partial U_{A} }}{{\partial_{z} }} = 0 $$
(9)

Using Eqs. (8) and (9), we derive the following:

$$ \left\{ {\begin{array}{*{20}l} {E_{d} A_{d} L_{d} \sum\limits_{k = 1}^{p} {\left[ {\left( {\epsilon_{x} \cos^{2} \alpha_{k} - \frac{{h_{k} \kappa_{z}^{0} }}{2}\cos^{2} \alpha_{k} + \epsilon_{z} \sin^{2} \alpha_{k} + 2\gamma_{xz} \cos \alpha_{k} \sin \alpha_{k} } \right)\sin^{2} \alpha_{k} } \right]} + jE_{v} A_{v} L_{v} \epsilon_{z} = 0} \\ {\alpha_{k} = \arccos \left( {L_{l} /L_{d} } \right)} \\ \end{array} } \right. $$
(10)

Thus,

$$ \epsilon_{z} = - \frac{{E_{d} A_{d} L_{d} \sum\nolimits_{k = 1}^{p} {\left[ {\sin^{2} \alpha_{k} \left( {\epsilon_{x} \cos^{2} \alpha_{k} - \frac{{h_{k} \kappa_{z}^{0} }}{2}\cos^{2} \alpha_{k} + 2\gamma_{x} \cos \alpha_{k} \sin \alpha_{k} } \right)} \right]} }}{{\sum\nolimits_{k = 1}^{p} {E_{d} } A_{d} L_{d} \sin^{2} \alpha_{k} + jE_{v} A_{v} L_{v} }} $$
(11)

Finally, the equivalent continuum model of the hoop unit can be calculated as:

$$ \begin{aligned} U_{A} & = \frac{1}{2}C_{11} \left( {\epsilon_{x}^{0} } \right)^{2} + \frac{1}{2}C_{22} \left( {\gamma_{xz}^{0} } \right)^{2} + \frac{1}{2}C_{33} \left( {\kappa_{t}^{0} } \right)^{2} + \frac{1}{2}C_{44} \left( {\kappa_{y}^{0} } \right)^{2} \\ & \quad + \frac{1}{2}C_{55} \left( {\kappa_{z}^{0} } \right)^{2} + \frac{1}{2}C_{12} \epsilon_{x}^{0} \gamma_{xz}^{0} + \frac{1}{2}C_{34} \kappa_{t}^{0} \kappa_{y}^{0} + \frac{1}{2}C_{15} \epsilon_{x}^{0} \kappa_{z}^{0} + \frac{1}{2}C_{25} \gamma_{x}^{0} \kappa_{z}^{0} \\ \end{aligned} $$
(12)

where

$$ C_{11} = 2iE_{l} A_{l} L_{l} + \sum\limits_{k = 1}^{p} {\left[ {\begin{array}{*{20}c} {\frac{{\left( {E_{d} A_{d} L_{d} \sin^{4} \alpha_{k} + jE_{v} A_{v} L_{v} } \right)E_{d} A_{d} L_{d} \cos^{4} \alpha_{k} \sin^{8} \alpha_{k} }}{{\left( {E_{d} A_{d} L_{d} \sin^{2} \alpha_{k} + E_{v} A_{v} L_{v} } \right)^{2} }}} \\ { + E_{d} A_{d} L_{d} \cos^{4} \alpha_{k} - \frac{{2\left( {E_{d} A_{d} L_{d} } \right)^{2} \cos^{4} \alpha_{k} \sin^{4} \alpha_{k} }}{{E_{d} A_{d} L_{d} \sin^{2} \alpha_{k} + E_{v} A_{v} L_{v} }}} \\ \end{array} } \right]} ; $$
$$ C_{22} = \sum\limits_{k = 1}^{p} {\left[ {\frac{{4\cos^{2} \alpha_{k} \sin^{2} \alpha_{k} \left( {jE_{v} A_{v} L_{v} + E_{d} A_{d} L_{d} \sin^{4} \alpha_{k} } \right)}}{{\left( {E_{d} A_{d} L_{d} \sin^{2} \alpha_{k} + E_{v} A_{v} L_{v} } \right)^{2} }} + 4E_{d} A_{d} L_{d} \cos^{2} \alpha_{k} \sin^{2} \alpha_{k} - \frac{{2E_{d} A_{d} L_{d} \cos^{2} \alpha_{k} \sin^{6} \alpha_{k} }}{{E_{d} A_{d} L_{d} \sin^{2} \alpha_{k} + E_{v} A_{v} L_{v} }}} \right]} $$
$$ C_{33} = \sum\limits_{k = 1}^{p} {\left[ {G_{d} J_{d} \cos^{2} \alpha_{k} } \right]} + iG_{l} J_{l} ; $$
$$ C_{44} = pE_{d} I_{z}^{d} + \sum\limits_{k = 1}^{p} {\left[ {G_{d} J_{d} \sin^{2} \alpha_{k} } \right]} + iE_{l} I_{z}^{l} + j\left( {E_{v} I_{z}^{v} + G_{v} J_{v} } \right); $$

\(C_{55} = \frac{i}{2}\left( {E_{l} A_{l} L_{l} \left( {L_{v} } \right)^{2} + E_{l} I_{y}^{l} } \right) + \sum\limits_{k = 1}^{p} {\left( {E_{d} I_{y}^{d} \cos^{2} \alpha_{k} } \right)} ;\);

$$ C_{12} = \sum\limits_{k = 1}^{p} {\left( {\frac{{4E_{d} A_{d} L_{d} \cos^{3} \alpha_{k} \sin^{5} \alpha_{k} \left( {E_{d} A_{d} L_{d} \sin^{4} \alpha_{k} + jE_{v} A_{v} L_{v} } \right)}}{{\left( {E_{d} A_{d} L_{d} \sin^{2} \alpha_{k} + E_{v} A_{v} L_{v} } \right)^{2} }}} \right)} - \sum\limits_{k = 1}^{p} {\left( {\frac{{4\left( {E_{d} A_{d} L_{d} + \left( {E_{d} A_{d} L_{d} } \right)^{2} } \right)\cos^{3} \alpha_{k} \sin^{5} \alpha_{k} }}{{E_{d} A_{d} L_{d} \sin^{2} \alpha_{k} + E_{v} A_{v} L_{v} }}} \right)} $$
$$ C_{34} = 2G_{d} J_{d} \sum\limits_{k = 1}^{p} {\left( {\cos \alpha_{k} \sin \alpha_{k} } \right)} ; $$
$$ C_{15} = - \sum\limits_{k = 1}^{p} {\left[ {E_{d} A_{d} L_{d} h_{k} \cos^{4} \alpha_{k} - E_{d} A_{d} L_{d} \frac{{E_{d} A_{d} L_{d} h_{k} \cos^{4} \alpha_{k} \sin^{4} \alpha_{k} }}{{E_{d} A_{d} L_{d} \sin^{2} \alpha_{k} + E_{v} A_{l} L_{v} }}} \right]} + 2iE_{l} A_{l} L_{l} \left( {i^{ + } L_{v} - i^{ - } L_{v} } \right); $$
$$ C_{25} = - 2\sum\limits_{k = 1}^{p} {\left[ {E_{d} A_{d} L_{d} h_{k} \sin \alpha_{k} \cos^{3} \alpha_{k} - E_{d} A_{d} L_{d} \frac{{h_{k} \cos^{3} \alpha_{k} \sin^{5} \alpha_{k} }}{{E_{d} A_{d} L_{d} \sin^{2} \alpha_{k} + E_{v} A_{v} L_{v} }}} \right]} . $$

The strain energy contains the coupling terms of the tensile, shear, and torsional deformation energy. The anisotropic beam element is used for the equivalence of the hoop unit. Also for the strain energy of the anisotropic beam element we can get the equations as follows:

$$ U_{C} = \frac{1}{2}\int_{L} {{\varvec{\varGamma}}^{T} {\varvec{D}}}{\varvec{\varGamma}}{\text{d}}x $$
(13)
$$ {\varvec{D}} = \left[ {\begin{array}{*{20}c} {EA^{\prime } } &\quad {\eta_{12} } &\quad {\eta_{13} } &\quad {\eta_{14} } &\quad {\eta_{15} } \\ {} &\quad {GA_{z}^{\prime } } &\quad {\eta_{23} } &\quad {\eta_{24} } &\quad {\eta_{25} } \\ {} &\quad {} &\quad {GJ^{\prime } } &\quad {\eta_{34} } &\quad {\eta_{35} } \\ {} &\quad {} &\quad {} &\quad {EI_{z}^{\prime } } &\quad {\eta_{45} } \\ {} &\quad {} &\quad {} &\quad {} &\quad {EI_{y}^{\prime } } \\ \end{array} } \right] $$
(14)

where \(\Gamma = \left( {\epsilon_{1}^{0} ,\gamma_{xz}^{0} ,\kappa_{2}^{0} ,\kappa_{3}^{0} ,\kappa_{t}^{0} } \right)^{T}\) is the strain vector along the central axis of the beam, and D is the elastic matrix, which contains the coupling terms for the stiffness. The length of the horizontal rod is set to the length of the equivalent beam model. According to the equal strain energy of the hoop unit and the anisotropic beam, the elastic matrix of the equivalent beam model can be obtained as:

$$ \begin{gathered} EA^{\prime } = \frac{{C_{11} }}{{L_{l} }},\;\;\;{\kern 1pt} GA_{z}^{\prime } = \frac{{C_{22} }}{{L_{l} }},\;\;\;{\kern 1pt} GJ^{\prime } = \frac{{C_{33} }}{{L_{l} }}, \hfill \\ EI_{z}^{\prime } = \frac{{C_{44} }}{{L_{l} }}, EI_{y}^{\prime } = \frac{{C_{55} }}{{L_{l} }},\;\;\;{\kern 1pt} \eta_{12(34)(15)(25)} = \frac{{C_{12(34)(15)(25)} }}{{2L_{l} }} \hfill \\ \end{gathered} $$
(15)

When the hoop unit is equivalent to an anisotropic beam, the beam element is used to establish a finite element model (FEM) of the structure. When external force is considered, the method of geometric nonlinearity is also applied to the geometrical stiffness matrix of beam element. Thus, we obtained the following the stiffness matrix Kb that can be decomposed into two parts:

$$ {\varvec{K}}_{b} = {\varvec{K}}_{E,b} + {\varvec{K}}_{G,b} $$
(16)

where KE,b and KG,b denote the elastic stiffness matrix affected by material properties, and the geometrical stiffness matrix affected by self-stresses, respectively; the elastic stiffness matrix KE,b and geometric matrix KG,b are given by:

$$ {\varvec{K}}_{E,b} = \left[ {\begin{array}{*{20}l} {{\varvec{K}}_{11}^{E,b} } \hfill &\quad {{\varvec{K}}_{12}^{E,b} } \hfill \\ {{\varvec{K}}_{21}^{E,b} } \hfill &\quad {{\varvec{K}}_{22}^{E,b} } \hfill \\ \end{array} } \right]_{12 \times 12} $$
(17)
$$ {\varvec{K}}_{{{\text{G}},b}} = \frac{P}{{L_{b} }}\left[ {\begin{array}{*{20}l} {{\varvec{K}}_{11}^{G,b} } \hfill &\quad {{\varvec{K}}_{12}^{G,b} } \hfill \\ {{\varvec{K}}_{21}^{G,b} } \hfill &\quad {{\varvec{K}}_{22}^{G,b} } \hfill \\ \end{array} } \right]_{12 \times 12} $$
(18)

where Lb is the length of the beam element, and P is the vector of the beam internal forces at nodes. The sub-matrices are expressed in Ref. (33).

3.1.2 Equivalent mass

When considering the tensile, bending, and torsional deformation, it is easily proved that the kinetic energy of the kth beam is written in the following form:

$$ T^{(k)} = \frac{1}{2}\rho A\int_{L} {\left[ {\left( {\frac{{\partial \overline{u}}}{\partial t}} \right) + \left( {\frac{{\partial \overline{v}}}{\partial t}} \right) + \left( {\frac{{\partial \overline{w}}}{\partial t}} \right)} \right]} {\text{d}}x + \frac{1}{2}\int_{L} {J_{x} } \left( {\frac{{\partial \overline{\theta }_{x} }}{\partial t}} \right){\text{d}}x $$
(19)

where ρA and Jx are the mass and torsional moment of inertia per unit length, respectively.

The Taylor series expansion of coordinates of Eq. (1), with respect to the origin can be found to have the following form:

$$ \left\{ {\begin{array}{*{20}l} {u \approx u_{0} + z\phi_{y0} + x\varepsilon_{x0} + xz\kappa_{z0} } \hfill \\ {v \approx v_{0} - z\phi_{x0} + x\phi_{z0} - xz\kappa_{t0} + \frac{1}{2}x^{2} \kappa_{y0} } \hfill \\ {w \approx w_{0} + z\varepsilon_{x0} + x\left( {\gamma_{xz0} - \phi_{y0} } \right) - \frac{1}{2}x^{2} \kappa_{z0} } \hfill \\ {\phi_{x} \approx \phi_{x0} + x\kappa_{t0} } \hfill \\ \end{array} } \right. $$
(20)

Using Eqs. (19) and (20), we obtain the following equation:

$$ \begin{aligned} T^{(k)} & = \frac{1}{2}\rho A\left[ {\begin{array}{*{20}l} {L\left[ {\left( {\frac{{\partial u^{0} }}{\partial t}} \right)^{2} + \left( {\frac{{\partial v^{0} }}{\partial t}} \right)^{2} + \left( {\frac{{\partial w^{0} }}{\partial t}} \right)^{2} } \right] + z^{2} L\left( {\frac{{\partial \phi_{x} }}{\partial t}} \right)^{2} + \left( {z^{2} L^{2} + \frac{1}{3}L^{3} } \right)\left( {\frac{{\partial \phi_{y} }}{\partial t}} \right)^{2} } \hfill \\ { + \frac{1}{3}L^{3} \left( {\frac{{\partial \phi_{z} }}{\partial t}} \right)^{2} + 2zL\frac{{\partial \phi_{y} }}{\partial t}\frac{{\partial u^{0} }}{\partial t} - L^{2} \frac{{\partial \phi_{y} }}{\partial t}\frac{{\partial w^{0} }}{\partial t} - 2zL\frac{{\partial \phi_{x} }}{\partial t}\frac{{\partial v^{0} }}{\partial t} + L^{2} \frac{{\partial \phi_{z} }}{\partial t}\frac{{\partial v^{0} }}{\partial t} - L^{2} z\frac{{\partial \phi_{x} }}{\partial t}\frac{{\partial \phi_{z}^{0} }}{\partial t}} \hfill \\ \end{array} } \right] \\ & \quad + \frac{1}{2}J_{x} \left( {\frac{{\partial \phi_{x} }}{\partial t}} \right)^{2} \\ \end{aligned} $$
(21)

where L is the length of the beam element, and z is the distance between the center of the beam and the origin of coordinates along the z direction. Additionally, the kinetic energy of a hoop unit of the structure by assembling each beam elements involved can be written as:

$$ T_{A} = \sum\limits_{m = 1}^{i} {T^{\left( m \right)} } + \frac{1}{2}\sum\limits_{n = 1}^{j} {T^{\left( n \right)} } + \sum\limits_{k = 1}^{p} {T^{\left( k \right)} } $$
(22)

The solution for Eqs. (21) and (22) can be expressed as follows:

$$ \begin{aligned} T_{A} & = \frac{1}{2}\rho A_{l} L_{l} \left[ \begin{gathered} i\left[ {\left( {\frac{{\partial u^{0} }}{\partial t}} \right)^{2} + \left( {\frac{{\partial v^{0} }}{\partial t}} \right)^{2} + \left( {\frac{{\partial w^{0} }}{\partial t}} \right)^{2} } \right] + \left[ {\sum\limits_{i = 1}^{i + } {\left( {L_{v + }^{i} } \right)^{2} + \sum\limits_{i = 1}^{i - } {\left( {L_{v - }^{i} } \right)^{2} + \frac{i}{3}L_{l}^{2} } } } \right]\left( {\frac{{\partial \phi_{y} }}{\partial t}} \right)^{2}\\ \quad + \left( {\sum\limits_{i = 1}^{i + } {\left( {L_{v + }^{i} } \right)^{2} + \sum\limits_{i = 1}^{i - } {\left( {L_{v - }^{i} } \right)^{2} } } } \right)\left( {\frac{{\partial \phi_{x} }}{\partial t}} \right)^{2} \hfill \\ + \frac{i}{3}L_{l}^{2} \left( {\frac{{\partial \phi_{z} }}{\partial t}} \right)^{2} + 2\left( {\sum\limits_{i = 1}^{i + } {\left( {L_{v + }^{i} } \right)^{2} + \sum\limits_{i = 1}^{i - } {\left( {L_{v - } } \right)^{2} } } } \right)\frac{{\partial u^{0} }}{\partial t}\frac{{\partial \phi_{y} }}{\partial t} - iL_{l} \frac{{\partial w^{0} }}{\partial t}\frac{{\partial \phi_{y} }}{\partial t} \\ \quad - 2\left( {\sum\limits_{i = 1}^{i + } {\left( {L_{v + }^{i} } \right)^{2} + \sum\limits_{i = 1}^{i - } {\left( {L_{v - } } \right)^{2} } } } \right)\frac{{\partial v^{0} }}{\partial t}\frac{{\partial \phi_{x} }}{\partial t} + \left( {iL_{l} \frac{{\partial v^{0} }}{\partial t}\frac{{\partial \phi_{z} }}{\partial t}} \right) \hfill \\ - \left( {\sum\limits_{i = 1}^{i + } {\left( {L_{v + }^{i} } \right)^{2} + \sum\limits_{i = 1}^{i - } {\left( {L_{v - } } \right)^{2} } } } \right)L_{l} \frac{{\partial \phi_{z} }}{\partial t}\frac{{\partial \phi_{x} }}{\partial t} \hfill \\ \end{gathered} \right] \\ & \quad + \frac{j}{4}\rho A_{v} L_{v} \left[ {\left( {\frac{{\partial u^{0} }}{\partial t}} \right)^{2} + \left( {\frac{{\partial v^{0} }}{\partial t}} \right)^{2} + \left( {\frac{{\partial w^{0} }}{\partial t}} \right)^{2} + \frac{1}{3}L_{v} \left[ {\left( {\frac{{\partial \phi_{y} }}{\partial t}} \right)^{2} + \left( {\frac{{\partial \phi_{z} }}{\partial t}} \right)^{2} + \frac{{\partial v^{0} }}{\partial t}\frac{{\partial \phi_{z} }}{\partial t} - \frac{{\partial w^{0} }}{\partial t}\frac{{\partial \phi_{y} }}{\partial t}} \right]} \right] \\ & \quad + \frac{1}{2}\rho A_{d} L_{d} \left[ \begin{gathered} p\left[ {\left( {\frac{{\partial u^{0} }}{\partial t}} \right)^{2} + \left( {\frac{{\partial v^{0} }}{\partial t}} \right)^{2} + \left( {\frac{{\partial w^{0} }}{\partial t}} \right)^{2} } \right] + \left[ {\sum\limits_{i = 1}^{p + } {\left( {h_{p + }^{i} } \right)^{2} + \sum\limits_{i = 1}^{p - } {\left( {h_{p - }^{i} } \right)^{2} + \frac{p}{3}L_{d}^{2} } } } \right]\left( {\frac{{\partial \phi_{y} }}{\partial t}} \right)^{2}\\ \quad + \left( {\sum\limits_{i = 1}^{i + } {\left( {h_{p + }^{i} } \right)^{2} + \sum\limits_{i = 1}^{p - } {\left( {h_{p - }^{i} } \right)^{2} } } } \right)\left( {\frac{{\partial \phi_{x} }}{\partial t}} \right)^{2} \hfill \\ + \frac{p}{3}L_{d}^{2} \left( {\frac{{\partial \phi_{z} }}{\partial t}} \right)^{2} + 2\left( {\sum\limits_{i = 1}^{p + } {\left( {h_{p + }^{i} } \right) + \sum\limits_{i = 1}^{p - } {\left( {h_{p - }^{i} } \right)} } } \right)\frac{{\partial u^{0} }}{\partial t}\frac{{\partial \phi_{y} }}{\partial t} - pL_{d} \frac{{\partial w^{0} }}{\partial t}\frac{{\partial \phi_{y} }}{\partial t} \\ \quad - 2\left( {\sum\limits_{i = 1}^{p + } {\left( {h_{p + }^{i} } \right) + \sum\limits_{i = 1}^{p - } {\left( {h_{p - }^{i} } \right)} } } \right)\frac{{\partial v^{0} }}{\partial t}\frac{{\partial \phi_{x} }}{\partial t} + \left( {pL_{d} \frac{{\partial v^{0} }}{\partial t}\frac{{\partial \phi_{z} }}{\partial t}} \right) \hfill \\ - \left( {\sum\limits_{i = 1}^{p + } {\left( {h_{p + }^{i} } \right) + \sum\limits_{i = 1}^{p - } {\left( {h_{p - }^{i} } \right)} } } \right)L_{d} \frac{{\partial \phi_{z} }}{\partial t}\frac{{\partial \phi_{x} }}{\partial t} \hfill \\ \end{gathered} \right] \\ \end{aligned} $$
(23)

Finally, the equivalent continuum model of the hoop unit can be calculated as:

$$ \begin{aligned} T_{A} & = \frac{1}{2}D_{1} \left[ {\left( {\frac{{\partial u^{0} }}{\partial t}} \right)^{2} + \left( {\frac{{\partial v^{0} }}{\partial t}} \right)^{2} + \left( {\frac{{\partial w^{0} }}{\partial t}} \right)^{2} } \right] + \frac{1}{2}D_{2} \left( {\frac{{\partial \phi_{x} }}{\partial t}} \right)^{2} + \frac{1}{2}D_{3} \left( {\frac{{\partial \phi_{y} }}{\partial t}} \right)^{2} \\ & \quad + \frac{1}{2}D_{4} \left( {\frac{{\partial \phi_{z} }}{\partial t}} \right)^{2} + \frac{1}{2}D_{4} \left( {\frac{{\partial \phi_{x} }}{\partial t}} \right)\left( {\frac{{\partial \phi_{z} }}{\partial t}} \right) + \frac{1}{2}D_{5} \left( {\frac{{\partial \phi_{y} }}{\partial t}} \right)\left( {\frac{{\partial u^{0} }}{\partial t}} \right) + \frac{1}{2}D_{6} \left( {\frac{{\partial \phi_{y} }}{\partial t}} \right)\left( {\frac{{\partial u^{0} }}{\partial t}} \right) \\ & \quad + \frac{1}{2}D_{7} \left( {\frac{{\partial \phi_{y} }}{\partial t}} \right)\left( {\frac{{\partial w^{0} }}{\partial t}} \right) + \frac{1}{2}D_{8} \left( {\frac{{\partial \phi_{x} }}{\partial t}} \right)\left( {\frac{{\partial v^{0} }}{\partial t}} \right) + \frac{1}{2}D_{9} \left( {\frac{{\partial \phi_{z} }}{\partial t}} \right)\left( {\frac{{\partial v^{0} }}{\partial t}} \right) \\ \end{aligned} $$
(24)

where \(h_{p - }^{i}\) and \(h_{p + }^{i}\) are the displacement components of the center of the ith left diagonal and right diagonal, respectively, along the z axis.

$$ \begin{aligned} D_{1} & = i\rho A_{l} L_{l} + \frac{j}{2}\rho A_{l} L_{l} + p\rho A_{d} L_{d} ; \\ D_{2} & = \frac{1}{2}\rho A_{l} L_{l} \left( {\sum\limits_{i = 1}^{i + } {\left( {L_{v + }^{i} } \right)^{2} } + \sum\limits_{i = 1}^{i - } {\left( {L_{v - }^{i} } \right)^{2} } } \right) + \frac{1}{2}\rho A_{d} L_{d} \left( {\sum\limits_{i = 1}^{p + } {\left( {h_{p + }^{i} } \right)^{2} } + \sum\limits_{i = 1}^{p - } {\left( {h_{p - }^{i} } \right)^{2} } } \right); \\ D_{3} & = \frac{1}{2}\rho A_{i} L_{l} \left( {\sum\limits_{i = 1}^{i + } {\left( {L_{v + }^{i} } \right)^{2} } + \sum\limits_{i = 1}^{i - } {\left( {L_{v - }^{i} } \right)^{2} } + \frac{i}{3}L_{l}^{2} } \right) + \frac{1}{6}\rho A_{i} L_{l}^{2} + \frac{1}{2}\rho A_{d} L_{d} \left( {\sum\limits_{i = 1}^{p + } {\left( {h_{p + }^{i} } \right)^{2} } + \sum\limits_{i = 1}^{p - } {\left( {h_{p - }^{i} } \right)^{2} } + \frac{p}{3}L_{d}^{2} } \right); \\ D_{4} & = \frac{i}{3}\rho A_{l} L_{l}^{3} + \frac{j}{6}\rho A_{v} L_{v}^{2} + \frac{p}{3}\rho A_{d} L_{d}^{3} D_{5} ; \\ D_{5} & = 2\rho A_{l} L_{l} \left( {\sum\limits_{i = 1}^{i + } {L_{v + }^{i} } + \sum\limits_{i = 1}^{i - } {L_{v - }^{i} } } \right) - 2\rho A_{d} L_{d} \left( {\sum\limits_{i = 1}^{p + } {h_{p + }^{i} } + \sum\limits_{i = 1}^{p - } {h_{p - }^{i} } } \right); \\ D_{6} & = - 2\rho A_{l} L_{l} \left( {\sum\limits_{i = 1}^{i + } {L_{v + }^{i} } + \sum\limits_{i = 1}^{i - } {L_{v - }^{i} } } \right) - 2\rho A_{d} L_{d} \left( {\sum\limits_{i = 1}^{p + } {h_{p + }^{i} } + \sum\limits_{i = 1}^{p - } {h_{p - }^{i} } } \right); \\ D_{7} & = - 2i\rho A_{l} L_{l}^{2} - \frac{j}{2}\rho A_{l} L_{l}^{2} - p\rho A_{d} L_{d}^{2} D_{8} ; \\ D_{8} & = - 2\rho A_{l} L_{l} \left( {\sum\limits_{i = 1}^{i + } {L_{v + }^{i} } + \sum\limits_{i = 1}^{i - } {L_{v - }^{i} } } \right) - 2\rho A_{d} L_{d} \left( {\sum\limits_{i = 1}^{p + } {h_{p + }^{i} } + \sum\limits_{i = 1}^{p - } {h_{p - }^{i} } } \right); \\ D_{9} & = i\rho A_{i} L_{l}^{2} + \frac{j}{2}\rho A_{l} L_{l}^{2} + p\rho A_{d} L_{d}^{2} ; \\ \end{aligned} $$

The anisotropic beam element is used for the equivalence of the hoop unit, for which the kinetic energy is calculated by:

$$ T_{c} = \frac{1}{2}\int_{L} {\dot{\delta }^{T} } {\varvec{M}}\dot{\delta }{\text{d}}x $$
(25)

where \(\dot{\delta } = \left( {\frac{{\partial u^{0} }}{\partial t},\frac{{\partial v^{0} }}{\partial t},\frac{{\partial w^{0} }}{\partial t},\frac{{\partial \phi_{x}^{0} }}{\partial t},\frac{{\partial \phi_{y}^{0} }}{\partial t},\frac{{\partial \phi_{z}^{0} }}{\partial t}} \right)\) is the velocity vector along the centerline of the beam; M is the mass matrix, which is defined:

$$ {\varvec{M}} = \left[ {\begin{array}{*{20}c} {m_{11} } &\quad {m_{12} } &\quad {m_{13} } &\quad {m_{14} } &\quad {m_{15} } &\quad {m_{16} } \\ {} &\quad {m_{22} } &\quad {m_{23} } &\quad {m_{24} } &\quad {m_{25} } &\quad {m_{26} } \\ {} &\quad {} &\quad {m_{33} } &\quad {m_{34} } &\quad {m_{35} } &\quad {m_{36} } \\ {} &\quad {} &\quad {} &\quad {m_{44} } &\quad {m_{45} } &\quad {m_{46} } \\ {} &\quad {} &\quad {} &\quad {} &\quad {m_{55} } &\quad {m_{56} } \\ {} &\quad {} &\quad {} &\quad {} &\quad {} &\quad {m_{66} } \\ \end{array} } \right] $$

Since the strain term has been disregarded when calculating the kinetic energy of the hoop unit, the velocity within the truss element is constant. Therefore, the velocity of the equivalent beam model is also constant along its length, which is equal to that of the hoop unit at its centerline. m11, m22 and m33 are the mass of the beam per unit length; according to the equality principle of kinetic energy, m44, m55 and m66 denote the torsional and bending moment of inertia of the beam per unit length, respectively, and mij (i ≠ j) are the inertial coupling terms. The results can be written as m11 = m12 = m13 = D1/L; m44 = D2/L; m55 = D3/L; m15 = D4/L; m24 = D5/L, and the remaining values are 0.

3.2 Equivalent principle of the column structure

The column is considered a variable cross-section beam, and the cross-section of each microsegment is changed. During the derivation process, the cross section of the beam is assumed to change in a linear fashion, as shown in Fig. 6. The value of the radius R(z) of the cross section at height z can be obtained by a numerical interpolation method.

Fig. 6
figure 6

Variable cross-section beam

Full size image

The relation between R(z) and z must satisfy the following equation:

$$ R\left( z \right) = R_{0} - \frac{{R_{0} - R_{1} }}{h}z $$
(26)

where h is the height of the beam element of the column, and R0 and R1 are the radii of the cross sections of the lower extremity and upper extremity, respectively, of beam element. The moment of inertia of a beam with a circular section is calculated by:

$$ I(z) = \int_{0}^{h} {\left( {R(z)^{2} - (R(z) - s)^{2} } \right)} {\text{d}}A $$
(27)

where s is the thickness of the beam. Then, we obtain:

$$ \left\{ {\begin{array}{*{20}l} {{\text{d}}A(z) = \pi \left( {R(z)^{2} - (R(z) - s)^{2} } \right){\text{d}}z = \pi \left[ {2\left( {R_{0} - \frac{{R_{0} - R_{1} }}{h}z} \right)s - s^{2} } \right]{\text{d}}z} \hfill \\ {A = \pi hs\left( {R_{0} - s + R_{1} } \right)} \hfill \\ \end{array} } \right. $$
(28)

According to the strain energy equivalence principle, the bending moment and the tension stress of the equivalent beam and variable section beam are equal. Then, we obtain:

$$ \left\{ {\begin{array}{*{20}l} {\displaystyle\int\limits_{0}^{h} {\frac{{M^{2} (z)}}{2EI(z)}} {\text{d}}z = \displaystyle\int_{0}^{h} {\frac{{M^{2} (z)}}{{2EI_{0} }}} {\text{d}}z} \hfill \\ {\displaystyle\int\limits_{0}^{h} {\frac{{F^{2} (z)}}{2EA(z)}} {\text{d}}z = \displaystyle\int_{0}^{h} {\frac{{F^{2} (z)}}{{2EA_{0} }}} {\text{d}}z} \hfill \\ {M(z) = - P(h - z)} \hfill \\ {I_{0} = \pi \displaystyle\int\limits_{0}^{l} {\left( {2R(z)s - s^{2} } \right)^{2} } {\text{d}}z} \hfill \\ \end{array} } \right. $$
(29)

where I0 is the moment of inertia of the equivalent beam, and P and F are the external axial load of the beam and external horizontal load of the beam, respectively. Using Eqs. (27) and (29), we obtain:

$$ I_{0} = \pi /\left[ {\left( {2R_{0} s - s^{2} } \right)^{2} h + \frac{{4s^{2} h}}{3}\left( {R_{0} - R_{1} } \right)^{2} - 2s^{2} h\left( {2R_{0} - s} \right)\left( {R_{0} - R_{1} } \right)} \right] $$
(30)

Knowing that the variable section beam changes linearly along the z direction, the inertia moment in the y direction Iy is equal to that in the x direction Ix. Thus, the moments of inertia and torsional inertia satisfy the following relations: Iy = I0, Iy = I0, J = 2I0. By substituting Eqs. (30) into the classic Euler‒Bernoulli beam element in terms of the corresponding items, the equivalent stiffness and equivalent mass matrices of a variable section beam is obtained.

3.3 The equivalent principle of the cables

When an annular tensegrity that can serve as a deployable antenna structure is deployed, the effect of gravity should not be considered. Therefore, the tensioned cable can be simulated by a beam element with two nodes and each node has three degrees of freedom. In this paper, both the linearly elastic constitutive law and the geometrical nonlinearity caused by large displacement of the structure are considered. The stiffness matrix Ks of the tensioned cables that can be decomposed into the elastic stiffness matrix KE,s and the geometrical stiffness matrix KG,s are obtained as follows:

$$ {\varvec{K}}_{s} = {\varvec{K}}_{E,s} + {\varvec{K}}_{G,s} $$
(32)

where KE,s reflects an external property of the ability to resist axial deformation of the cable element, and KG,s reflects the intrinsic property of the ability to resist changes caused by pretension of the cable element. Both KE,s and KG,s of the cable element are characterized by the following matrices:

$$ {\varvec{K}}_{E,s} = \frac{{EA_{s} }}{{L_{s} }}\left[ {\begin{array}{*{20}l} 1 \hfill &\quad 0 \hfill &\quad 0 \hfill &\quad { - 1} \hfill &\quad 0 \hfill &\quad 0 \hfill \\ 0 \hfill &\quad 0 \hfill &\quad 0 \hfill &\quad 0 \hfill &\quad 0 \hfill &\quad 0 \hfill \\ 0 \hfill &\quad 0 \hfill &\quad 0 \hfill &\quad 0 \hfill &\quad 0 \hfill &\quad 0 \hfill \\ { - 1} \hfill &\quad 0 \hfill &\quad 0 \hfill &\quad 1 \hfill &\quad 0 \hfill &\quad 0 \hfill \\ 0 \hfill &\quad 0 \hfill &\quad 0 \hfill &\quad 0 \hfill &\quad 0 \hfill &\quad 0 \hfill \\ 0 \hfill &\quad 0 \hfill &\quad 0 \hfill &\quad 0 \hfill &\quad 0 \hfill &\quad 0 \hfill \\ \end{array} } \right],{\varvec{K}}_{G,s} = \frac{T}{{L_{s} }}\left[ {\begin{array}{*{20}l} 1 \hfill &\quad 0 \hfill &\quad 0 \hfill &\quad { - 1} \hfill &\quad 0 \hfill &\quad 0 \hfill \\ 0 \hfill &\quad 0 \hfill &\quad 0 \hfill &\quad 0 \hfill &\quad { - 1} \hfill &\quad 0 \hfill \\ 0 \hfill &\quad 0 \hfill &\quad 0 \hfill &\quad 0 \hfill &\quad 0 \hfill &\quad { - 1} \hfill \\ { - 1} \hfill &\quad 0 \hfill &\quad 0 \hfill &\quad 1 \hfill &\quad 0 \hfill &\quad 0 \hfill \\ 0 \hfill &\quad { - 1} \hfill &\quad 0 \hfill &\quad 0 \hfill &\quad 0 \hfill &\quad 0 \hfill \\ 0 \hfill &\quad 0 \hfill &\quad { - 1} \hfill &\quad 0 \hfill &\quad 0 \hfill &\quad 0 \hfill \\ \end{array} } \right] $$
(32)

where E, As, Ls and T denote the elastic modulus, member area, length and prestress, respectively, of cable element. Additionally, the mass matrix of the cable element is given by:

$$ {\varvec{M}}_{s} = \frac{{\rho A_{s} L_{s} }}{6}\left[ {\begin{array}{*{20}l} 2 \hfill &\quad 0 \hfill &\quad 0 \hfill &\quad 1 \hfill &\quad 0 \hfill &\quad 0 \hfill \\ 0 \hfill &\quad 2 \hfill &\quad 0 \hfill &\quad 0 \hfill &\quad 1 \hfill &\quad 0 \hfill \\ 0 \hfill &\quad 0 \hfill &\quad 2 \hfill &\quad 0 \hfill &\quad 0 \hfill &\quad 1 \hfill \\ 1 \hfill &\quad 0 \hfill &\quad 0 \hfill &\quad 2 \hfill &\quad 0 \hfill &\quad 0 \hfill \\ 0 \hfill &\quad 1 \hfill &\quad 0 \hfill &\quad 0 \hfill &\quad 2 \hfill &\quad 0 \hfill \\ 0 \hfill &\quad 0 \hfill &\quad 1 \hfill &\quad 0 \hfill &\quad 0 \hfill &\quad 2 \hfill \\ \end{array} } \right] $$
(33)

where ρ refers to the density of the cable element.

4 Dynamic modeling of the annular tensegrity structure

To meet the total weight requirements, the hoop structure of the tensegrity is designed as full carbon-composite articulated truss when working on orbit. When its aperture is greater than 30 m, its total mass can exceed several hundred kilos which makes it difficult to maintain the limits on the total weight. Therefore, the number of unit bars connected by revolute and translational joints is below 5. Currently, several hoop units of linkages with 5 bars or less connected by revolute joints have been successfully employed. Table 1 presents five types of the typical schemes of hoop configurations with single mobility. The five representative hoop units represent different quantities of horizontal, vertical, diagonal beams. Among them, the horizontal beams, that are AB and CD, are located at the plane xy; the vertical beam, that are AC and BD, are perpendicular to the vertical beam; the diagonal beams, that are BC and AD, are located at an angle with the horizontal/vertical beams. The quantities of these three types of beam elements are defined as nh-nv-nd that are indicated in Table 1. According to the Gr\(\ddot{\mathrm{u}}\)bler‒Kutzbach criterion, all annular tensegrities that employ different hoop units are overconstrained, exhibiting a single degree of freedom. These tensegrities can be employed in the hoop structure of the annular tensegrity. Based on the equivalent dynamics principle, the dynamic characteristics of the annular tensegrity structure which employs a variety of hoop geometrical configurations are analyzed.

4.1 Cable-beam structure

Based on the substitute continuum approach, the annular tensegrity structure is equivalent to a simple truss structure by homogenization. Additionally, the developed three-dimensional structure unit is considered an Euler‒Bernoulli beam element in view of the equivalent stiffness and mass. In the previous study, both Ks and Ms of each element are established in the local coordinate system where its x-axis extends along the length direction of horizontal beam element. However, the tensegrity consists of several beam and cable elements in different orientations. Thus, when the stiffness matrix and mass matrix are assembled, the coordinate systems of the beams must be transformed to the global system. The transformation matrix T is employed to illustrate the relationship between the global coordinate system and local coordinate system.

$$ {\varvec{T}} = \left[ {\begin{array}{*{20}l} {\varvec{\lambda}} &\quad {0_{3 \times 3} } &\quad {0_{3 \times 3} } &\quad {0_{3 \times 3} } \\ {0_{3 \times 3} } &\quad {\varvec{\lambda}} &\quad {0_{3 \times 3} } &\quad {0_{3 \times 3} } \\ {0_{3 \times 3} } &\quad {0_{3 \times 3} } &\quad {\varvec{\lambda}} &\quad {0_{3 \times 3} } \\ {0_{3 \times 3} } &\quad {0_{3 \times 3} } &\quad {0_{3 \times 3} } &\quad {\varvec{\lambda}} \\ \end{array} } \right] $$
(34)
$$ {\varvec{\lambda}} = \left[ {\begin{array}{*{20}l} {\cos \left( {x,x^{e} } \right)} \hfill & {\cos \left( {x,y^{e} } \right)} \hfill & {\cos \left( {x,z^{e} } \right)} \hfill \\ {\cos \left( {y,x^{e} } \right)} \hfill & {\cos \left( {y,y^{e} } \right)} \hfill & {\cos \left( {y,z^{e} } \right)} \hfill \\ {\cos \left( {z,x^{e} } \right)} \hfill & {\cos \left( {z,y^{e} } \right)} \hfill & {\cos \left( {z,z^{e} } \right)} \hfill \\ \end{array} } \right] $$
(35)

where λ is the direction cosine matrix, and \(\left( {x,x^{e} } \right)\), \(\left( {y,x^{e} } \right)\) and \(\left( {z,x^{e} } \right)\) denote the angles of the xe position vector described in the global coordinates with respect to the x-axis, y-axis, and z-axis, respectively, described in the local coordinate.

The relationship between the \({\varvec{K}}_{b}^{\prime }\) described in the local coordinate system and the \({\varvec{K}}_{b}\) described in the global coordinate system is compatible with this condition, which is calculated by:

$$ {\varvec{K}}_{b} = {\varvec{TK}}_{b}^{^{\prime}} {\varvec{T}}^{T} $$
(36)

The entire stiffness and mass matrices of the cables and beams in the global coordinates are obtained based on the expansion and transformation of the element. By assembling the equivalent beam elements of the hoop, column and cables, the entire stiffness and mass matrices are obtained. By using the transformation matrix T, the entire stiffness matrix K and mass matrix M can be assembled by the element stiffness mass matrices and mass matrices, respectively, that is:

$$ \left\{ {\begin{array}{*{20}l} {{\varvec{K}} = \sum\limits_{i = 1}^{{n_{b} }} {{\varvec{T}}^{T} } \left( {{\varvec{K}}_{E,b} + {\varvec{K}}_{G,b} } \right){\varvec{T}} + \sum\limits_{i = 1}^{{n_{s} }} {{\varvec{T}}^{T} } \left( {{\varvec{K}}_{E,s} + {\varvec{K}}_{G,s} } \right){\varvec{T}}} \hfill \\ {{\varvec{M}} = \sum\limits_{i = 1}^{{n_{b} }} {{\varvec{T}}^{T} } {\varvec{M}}_{b} {\varvec{T}} + \sum\limits_{i = 1}^{{n_{s} }} {{\varvec{T}}^{T} } {\varvec{M}}_{s} {\varvec{T}}} \hfill \\ \end{array} } \right. $$
(37)

4.2 Vibration analysis of the annular tensegrity structure

4.2.1 Eigenvalue equation

When the effect of the damping term is disregarded, the vibration equation of the tensegrity structure is written as follows [33]:

$$ {\varvec{M}}\ddot{u} + {\varvec{K}}u = {\varvec{F}} $$
(38)

where M, and K are the mass matrix, and stiffness matrix, respectively; F is the applied external force; u and \(\ddot{u}\) are the vectors of the displacement and acceleration, respectively, of the node. When the external forces are disregarded, the dynamic problem of the tensegrity structure is addressed by Eqs. (38). The standard eigenproblem [34] is obtained by

$$ {\varvec{K}}\overline{u} - \omega^{2} {\varvec{M}}\overline{u} = {\mathbf{0}} $$
(39)

where ω is the natural fundamental frequency; \(\overline{u}\) is the corresponding amplitude vector. The ith natural fundamental frequencies ωi and its corresponding vibration modes can be solved by spectral decomposition [35].

To reduce the total mass, the tensegrity structure is fabricated from lightweight composite materials, and the support structures, hoop and column, are considered rigid. A model of the tensegrity structure is built by using the finite element method after equivalence and the material properties of the corresponding element utilized in the study are shown in Table 2. The components of the tensegrity structure are classified by the elements of 38 beams, 72 cables, and 39 nodes, as shown in Fig. 7. Each beam element of the hoop is numbered in counterclockwise order. The shape of the column is symmetric from top to bottom, and the fixed support is set at node 39.

Table 1 Several typical schemes of the deployable hoop unit within 5 bars
Full size table
Fig. 7
figure 7

Nodes and elements distributions

Full size image

4.2.2 Influence of the structural parameters on the dynamic characteristics of the parameterized structures

When the aperture of the structure is 100 m, and the height of the column is also 100 m, modal analysis of the tensegrity structure is performed according to the dynamic equation. Experience with Harris antenna structure has shown that the model with cables has double stiffness [36]. The components of the mode results have 3 orders of magnitude of the vibration modal within the former 3 natural fundamental frequencies. The comparison of the natural frequencies of the numerical and FEM simulated results based on ANSYS are listed in Table 3. Additionally, the corresponding vibration modes of the first 3 orders are distributed.

Table 2 Material properties of the cables and beams
Full size table
Table 3 Natural frequencies of the numerical and FEM simulated results
Full size table

The results show that each vibration mode is composed of the bending mode and hoop surface mode. The frequency of each mode between the numerical results and the simulated results is quite similar, which proves the validity of the dynamic modeling of non-damping free vibration equations. The results of each vibration mode can help explain the dynamic characteristics of structures with five representative hoop units when their geometrical structure parameters vary.

In order to reveal the high efficiency and correctness of equivalent mechanical modeling method, the comparison of dynamic characteristic between the original structure and equivalent model is made. Each hoop structural configuration shown in Table 1 has been taken into consideration. Additionally, the simulation results calculated by ANSYS software are obtained. The quantities of nodes and elements of each original model is calculated. The numerical and simulation results based on Eq. (40) and ANSYS, respectively, are obtained in Table 4.

Table 4 Calculating results of 1st order natural frequencies using equivalent and original methods
Full size table
Table 5 Sensitivity of each structural parameter to the dynamic behaviors
Full size table

The calculating results of the former 3 natural fundamental frequencies show that the equivalent models for each original structure has a high accuracy. The FEM results also verify the feasibility of both the calculating results of equivalent models and original structures. It is interesting to find that the 1st order natural frequency of equivalent model when employing configuration (a) is closer to that of original structure. It is noticeable for the models which have less bars. Because the equivalent method is assumed to neglect the last few components of strain energy of each beam element when expanded in a Taylor series. Therefore, the errors of natural frequency results of the structural configurations with five bars are found to be more than those with those with four. According to the running time of MATLAB, it is indicated that the equivalent model shows high computational efficiency for over 10 times more than processing that for original model. The equivalent mechanical method allows insight into the kinetic and strain energies to propose a simpler analysis tool with high efficiency.

To better comprehend the effect of structural parameters on the eigenfrequencies and corresponding model shapes, we present a modal analysis of tensegrity structures that employ different hoop structural configurations. The effect of different structural parameters, including the self-tress levels of the tensioned cables fs, the height of the hoop Lv, the aperture of the structure Ra and the diameters of R0 are fully considered. The modal contrast analysis is focused on the structural configurations when different schemes of the hoop units listed in Table 1 are employed. The results are compared in Figs. 8, 9, 10, 11.

Fig. 8
figure 8

The 1st natural frequency varies with cables pretension fs

Full size image
Fig. 9
figure 9

1st natural frequency varies with both Ra and Lv

Full size image
Fig. 10
figure 10

Special vibration mode of configuration (b)

Full size image
Fig. 11
figure 11

Variation in natural frequencies with respect to R0

Full size image

Figure 8 indicates that the increase in the self-stress levels will increase the overall stiffness of the structure because the key component of the stiffness matrix KT is the geometrical stiffness matrix KG, which is related to the pretension of the cables. The plotted results illustrate that the 1st natural fundamental frequency is almost scaled up by 20% when the pretension of the cables varies from 100 to 1000 N. The numerical results of configurations (a) and (b) are quite similar because KG depends on the cable pretension. Likewise, the results of configurations (c), (d) and (e) are similar. It can be concluded that the number of beams of hoop unit n is mainly related to the 1st-order natural frequency and that an increase in the number of diagonal beams will make it more sensitive to its overall stiffness.

Figure 9 shows that 1st-order natural frequencies will decrease when the aperture of the structure varies from 30 to 100 m and that the hoop height changes from 0.3 to 8.4 m. Mainly because the reduction in the pretension of the tensioned cables will decrease the stiffness of both the hoop and column. Note that the 1st-order natural frequency of configuration (b) greatly varies, while configuration (c) only slightly changes. It is also particularly noticeable that the 1st-order natural frequency of configuration (b) becomes approximately zero when their apertures exceed 80 m. Because there is no horizontal beam within the hoop unit, the special vibration mode of configuration (b) will present the new characteristic that the hoop has collapsed, as shown in Fig. 10. The number of beams of hoop unit n is also mainly concerned with the 1st-order natural frequencies when the length of the longitudinal beam changes. Moreover, if n is constant within the hoop unit, the horizontal beams between the longitudinal beams will have a more important role in the overall stiffness than the diagonal beams.

Figure 11 shows that the 1st-order natural frequencies will increase when the diameter of the column increases. The vibration mode corresponds to the first mast bending modes of a simple column. Notably, the frequency values of configurations (a) and (b) are considerably higher than those of other configurations. The stiffness of the hoop is not much different among the several configurations when the longitudinal beam of the hoop unit is 0.3 m even smaller than the horizontal beam of 8.3 m, whereas configurations (a) and (b) have the lowest total mass of the hoop.

4.2.3 Sensitivity of the dynamic characteristics

In our previous study, the influences of the structural parameters on the natural frequencies of tensegrity structures that employ different hoop configurations were analyzed. To further investigate the dynamic characteristics, the sensitivity of the structural parameters to the natural frequencies of Modes 1–3 will be described in this section. According to Spearman rank correlation coefficients [31], the sensitivity of the dynamic characteristics can be evaluated by:

$$ r_{s} = \frac{{\sum\nolimits_{i = 1}^{n} {\left( {R_{i} - \overline{R}} \right)} \left( {P_{i} - \overline{P}} \right)}}{{\sqrt {\sum\nolimits_{i = 1}^{n} {\left( {R_{i} - \overline{R}} \right)^{2} } } \sqrt {\sum\nolimits_{i = 1}^{n} {\left( {P_{i} - \overline{P}} \right)^{2} } } }} $$
(40)

where \(\overline{R} = \sum\nolimits_{i = 1}^{n} {R_{i} } /n\), \(\overline{P} = \sum\nolimits_{i = 1}^{n} {P_{i} } /n\), n is the capacity of the samples, Ri is the ith structural parameter, and Pi is the ith structural response. The sensitivities of dynamic behaviors of different hoop configurations are calculated by Eq. (39), as shown in Fig. 12.

Fig. 12
figure 12

Sensibility of the dynamic characteristics

Full size image

The sensitivity of the structural parameters of each configuration to the natural frequencies of modes 1–3 of the annular tensegrity structure is calculated by Eq. (40). As shown in Fig. 12, a positive or negative value in the figure indicates that the frequency increases or decreases with an increase in the structural parameters. For Mode 1, R0 is the most sensitive to the modal shapes of the structure. For Mode 2, R0 is also the most sensitive to the modal shapes of the structure, with the exception of configuration (b), for which Lv is the most sensitive because there are no horizontal beams in the truss unit. For Mode 3, Lv has the highest sensitivity to its modal shapes. The percentage of the sensitivity of each structural parameter to the fundamental frequency of the hoop-column structure is shown in Table 5.

Different hoop geometrical configurations (Con. (a)–(e))are employed in the 100 m hoop column antenna structure based on the annular tensegrity, and four main structural parameters are considered as design variables:

  • Tension of the cables, fs;

  • Aperture of the antenna structure, Ra;

  • Height of the hoop structure, Lv;

  • Envelop radius of the cross-section of column, R0.

Consider that the parameter ranges of each design variable are given as: fs ∈ [fs1, fs2]; Ra ∈ [Ra1, Ra2]; Lv ∈ [Lv1, Lv2]; and R0 ∈ [R1, R2]. The flow chart of the design approach to improve the overall stiffness of the structure is shown in Fig. 13. Following the proposed method, it is convenient and highly efficient to obtain the most appropriate solutions to develop a required annular structure with different hoop configurations.

Fig. 13
figure 13

Flow chart of the proposed approach to improve the stiffness of the tensegrity structure

Full size image

5 Conclusion

This paper presents an equivalent mechanical modeling approach for an annular tensegrity structure based on deriving the governing partial differential equations for the vibration of the repeating hoop units. A nonlinear mechanical model of the annular tensegrity structure based on the geometric nonlinearity of cables and parametric trusses is proposed. Moreover, modal analysis is conducted, and the stiffness of the entire structure, which employs 5 schemes of the hoop structure, considering different structural parameters is determined. The results show that the column stiffness is the key factor to the overall stiffness of the tensegrity structure. The horizontal beams between the longitudinal beams will have a more important role in the overall stiffness than the diagonal beams. The presence or absence of the horizontal beams within a hoop unit will have an effect on the local modal shapes of the hoop based on the analysis of the hoop configuration (b). The sensitivity of the structural parameters is demonstrated by comparing the dynamic characteristics of structures with different hoop configurations. When four structural variables are selected as the design parameters, their design ranges are certain. A set of priority approaches to improve the overall stiffness of the structure with different hoop units is demonstrated based on equivalent mechanical modeling and dynamic analysis. This work will provide a method to guide the design of different large-scale deployable antenna structures when employing different hoop structural configurations.