Dynamic Behavior and Vibration Suppression of a Generally Restrained Pre-pressure Beam Structure Attached with Multiple Nonlinear Energy Sinks

Abstract

Beam structures are extensively used in many engineering branches. For marine engineering, the ship shafting system is generally simplified as a vibration model with single or multiple beam structures connected by the coupling stiffness. In engineering, multiple nonlinear energy sinks (NESs) can be arranged on the premise of sufficient installation space to ensure their vibration suppression effect. Considering engineering practice, this study investigates the dynamic behavior and vibration suppression of a generally restrained pre-pressure beam structure with multiple uniformly distributed NESs, where the pre-pressure is typically caused by thrust bearings, installation ways, and others. System governing equations are derived through the generalized Hamiltonian principle and the variational procedure. Dynamic responses of the pre-pressure beam structure are predicted by the Galerkin truncation method. The effect of NESs on dynamic responses and vibration suppression of the pre-pressure beam structure is studied and discussed. Suitable parameters of NESs have a beneficial effect on the vibration suppression at both ends of the pre-pressure beam structure. NESs can modify the vibration frequency and energy transmission characteristics of the vibration system. For different boundary conditions, the optimized parameters of NESs significantly suppress the vibration energy of the pre-pressure beam structure.

1 Introduction

Beam structures are extensively used in many engineering branches, including aerospace engineering, mechanical engineering, civil engineering, marine engineering, and so on. In marine engineering, some complex structures such as the ship shafting system, fluid-conveying pipes, and others are typically regarded as a combination of beam structures. Taking the ship shafting system as an example, such a vibration system is generally simplified as a vibration model with single or multiple beam structures connected through the coupling stiffness. In engineering, the ship shafting system is subjected to external excitations caused by power equipment. Such external excitations motivate the vibration of the shafting system, which may cause serious accidents. To effectively suppress the vibration response level of complex structures, a deep understanding of the dynamic behavior of beam structures seems extremely significant.

Vibration characteristics of beam structures were widely studied in the early stage [1,2,3,4,5]. To accurately and effectively study the vibration characteristics of beam structures under various boundary conditions, Li [6] proposed an improved Fourier series, in which four additional terms were introduced into the traditional Fourier series to improve its boundary differentiability. Such an improved Fourier series was also regarded as the boundary-smoothed Fourier series. Then, numerous scholars studied the vibration characteristics of various beam structures by using the boundary-smoothed Fourier series, including laminated beams [7], double-beam structures [8], rotating beams [9], and ship shafting systems [10]. The corresponding studies verified the correctness and stability of the boundary-smoothed Fourier series in predicting the vibration characteristics of various beam structures under general boundary conditions. However, the above research was limited to linear cases.

With the development of nonlinear vibration theory, some attempts have been made to utilize nonlinear stiffness to suppress structural vibration. Vakakis [11] firstly proposed a special type of nonlinear passive vibration oscillator, with the positive stiffness being zero. The corresponding oscillator was regarded as the nonlinear energy sink (NES). Then, numerous studies extensively investigated the energy pumping behavior of NESs [12,13,14,15,16,17]. The relevant studies suggested that the targeted energy transfer occurred under certain parameters of NESs. Then, Vakakis [18] deeply studied the relaxation oscillations, subharmonic orbits, and chaos of the linear lattice with cubic nonlinearity. Sapsis et al. [19] investigated the stiffening and damping effects of NESs. Zhang et al. [20] proposed a new type of nonlinear energy sink which was enhanced by an inerter. Zhang et al. [21] established the evaluation system of NESs according to their transmissibility. Chen et al. [22] investigated the dynamic effect of weight on the vibration of a structure coupled with an NES. Lee et al. [23], Gatti et al. [24], and Ding and Chen [25] summarized the above research related to NESs and suggested that NESs had good application prospects in vibration suppression and vibration energy harvesting.

For beam structures with NESs, Georgiades and Vakakis [26] established a vibration model of a linear beam structure with an attached local NES. Samani and Pellicano [27, 28] investigated the influence of linear and nonlinear dynamic absorbers on vibration suppression of beam structures subjected to moving loads. Ahmadabadi and Khadem [29, 30] studied the nonlinear vibration control and energy harvesting of beam structures under different boundary conditions by employing NESs. Parseh et al. [31] investigated the stability of beam structures under different boundary conditions attached to NESs. Kani et al. [32, 33] studied the vibration suppression of NESs on beam structures under different boundary conditions. Bab et al. [34] employed an NES to suppress the vibration level of a rotating beam structure. Parseh et al. [35] studied the stable steady-state dynamic responses of a nonlinear beam attached to an NES. Zhang et al. [36] studied a highly efficient and promising control of an axially moving beam structure under forced responses, where the beam structure was subjected to an NES. Chen et al. [37] established the vibration model of a beam structure with parallel NESs. Fang et al. [38] investigated the vibration control of a beam structure with an NES, which was composed of a cantilever beam with partially constrained layer damping. Li et al. [39] established the vibration model of the acoustic black hole beam structure attached to an NES. Zhang et al. [40] proposed a novel approach to suppress the bending vibration of flexible structures via boundary NESs, where the vibration reduction effect is significant and feasible to implement. The above research mainly focused on the dynamic responses of beam structure with single or double NESs. Few studies investigated the dynamic responses and vibration suppression of beam structure with multiple NESs. For complex structures, the optimal position of NESs cannot be determined easily. Therefore, multiple NESs can be arranged on the premise of sufficient installation space to ensure their vibration suppression effect in engineering.

Considering engineering practice and potential applications of NESs in marine engineering, this study investigates the dynamic behavior and vibration suppression of a generally restrained pre-pressure beam structure with multiple uniformly distributed NESs, in which the pre-pressure is typically caused by thrust bearings, installation ways, and others. System governing equations are derived through the generalized Hamiltonian principle and the variational procedure. Dynamic responses of the pre-pressure beam structure are predicted by the Galerkin truncation method (GTM), where the harmonic balance method (HBM) is also employed to verify the correctness of the GTM. On this basis, the effect of NESs on dynamic responses and vibration suppression of the pre-pressure beam structure is studied and discussed.

2 Theoretical Formulations

2.1 Model Description

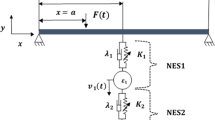
The physical model of a generally restrained pre-pressure beam structure with multiple uniformly distributed NESs is illustrated in Fig. 1. The vibration system is composed of three parts: the pre-pressure beam structure, boundary conditions, and uniformly distributed NESs.

Fig. 1

A generally restrained pre-pressure beam structure with multiple uniformly distributed NESs

For the pre-pressure beam structure, E, ρ, S, I, C_B, and P are its elastic modulus, mass density, sectional area, moment of inertia, external viscous damping, and pre-pressure, respectively. Such a beam structure is modeled as the Euler–Bernoulli model. The transverse vibration displacement of the pre-pressure beam structure is u(x,t). F(x_F,t) is the external excitation force, namely

$$ F\left( {x_{\rm{F}} ,t} \right) = {\text{Dirca}} \left( {x - x_{\rm{F}} } \right)F_{0} \sin \left( {\omega t} \right) $$

(1)

where x_F is the position of the excitation force, Dirca(.) is the Dirca function, and ω is the circular frequency.

Boundary restraining springs are introduced to simulate boundary conditions, where k_L, k_R, K_L, and K_R are the corresponding stiffness coefficients. Multiple NESs are uniformly installed on the beam structure. k_NES, m_NES, and C_NES are the nonlinear stiffness, inertial mass, and viscous damping of each NES. In this study, the structural parameters of NESs located at different positions are set the same. For the zth NES, its position is derived as

$$ x_{z} = \frac{zL}{{\left( {{\text{Z}} + 1} \right)}} $$

(2)

Additionally, u_z(t) is the vibration displacement of the zth NES, where z = 1, 2, …, Z.

According to the energy principle, the kinetic and potential energies of the vibration system are, respectively, derived as

$$ T = T_{\text{B}} + T_{\text{NES}} $$

(3a)

and

$$ V = V_{\text{B}} + V_{\text{Boundary}} + V_{\text{P}} + V_{\text{NES}} $$

(3b)

where T_B and V_B are, respectively, the kinetic energy and potential energy of the pre-pressure beam structure; V_P is the potential energy of the pre-pressure beam structure introduced by the per-pressure; T_NES and V_NES are, respectively, the kinetic and potential energies associated with NESs; and V_Boundary is the potential energy stored in boundary restraining springs.

The virtual work done by the external excitation force and the viscous damping is derived as

$$ \delta W = \delta W_{\text{F}} + \delta W_{\text{C}} + \delta W_{\text{CNES}} $$

(4)

where δW_F is the virtual work done by the external force, δW_C is the virtual work done by the viscous damping of the pre-pressure beam structure, and δW_CNES is the virtual work done by the viscous damping of NESs. The corresponding terms are given in “Appendix A”.

After applying the generalized Hamiltonian principle and the variational procedure, the governing equation of the pre-pressure beam structure is derived as

$$ \begin{aligned} & \rho S\frac{{\partial^{2} u}}{{\partial t^{2} }} + C_{\text{B}} \frac{\partial u}{{\partial t}} + EI\frac{{\partial^{4} u}}{{\partial x^{4} }} + P\frac{{\partial^{2} u}}{{\partial x^{2} }} + \delta \left( {x - x_{\text{F}} } \right)F_{0} \sin \left( {\omega t} \right) \\ & \quad + \sum\limits_{z = 1}^{Z} {\left\{ {\delta \left( {x - x_{z} } \right)\left[ {C_{{\text{NES}}} \left( {\frac{\partial u}{{\partial t}} - \frac{{{\text{d}} u_{z} }}{{{\text{d}} t}}} \right) + k_{\text{NES}} \left( {u - u_{z} } \right)^{3} } \right]} \right\}} = 0 \\ \end{aligned} $$

(5)

The governing equation of the zth NES is derived as

$$ m_{\text{NES}} \frac{{{\text{d}}^{2} u_{z} }}{{{\text{d}} t^{2} }} + C_{{\text{NES}}} \left[ {\frac{{{\text{d}} u_{z} }}{{{\text{d}} t}} - \frac{{\partial u\left( {x_{z} ,t} \right)}}{\partial t}} \right] + k_{\text{NES}} \left[ {u_{z} - u\left( {x_{z} ,t} \right)} \right]^{3} = 0 $$

(6)

Boundary conditions of the pre-pressure beam structure are derived as

$$ x = 0:k_{\text{L}} u + EI\frac{{\partial^{3} u}}{{\partial x^{3} }} + P\frac{\partial u}{{\partial x}} = 0,K_{\text{L}} \frac{\partial u}{{\partial x}} - EI\frac{{\partial^{2} u}}{{\partial x^{2} }} = 0 $$

(7a)

and

$$ x = L:k_{\text{R}} u - EI\frac{{\partial^{3} u}}{{\partial x^{3} }} - P\frac{\partial u}{{\partial x}} = 0,K_{\text{R}} \frac{\partial u}{{\partial x}} + EI\frac{{\partial^{2} u}}{{\partial x^{2} }} = 0 $$

(7b)

The corresponding terms of the generalized Hamiltonian principle are listed in “Appendix B”.

2.2 Solution Procedure

The governing equation of the vibration system is solved by applying the GTM. The transverse vibration displacement of the pre-pressure beam structure is expanded as

$$ u\left( {x,t} \right) = \sum\limits_{i = 1}^{N} {\varphi_{i} \left( x \right)q_{i} \left( t \right)} $$

(8)

where φ_i(x) is the ith trial function, q_i(t) is the ith unknown time term, and N is the truncation number.

Substituting Eq. (8) into Eq. (5) and utilizing the Galerkin discretization condition, the mth residual equation of the vibration system is derived as

$$ {\displaystyle\int}_{0}^{L} {\left\{ \begin{gathered} \rho S\frac{{\partial^{2} u}}{{\partial t^{2} }} + C_{\text{B}} \frac{\partial u}{{\partial t}} + EI\frac{{\partial^{4} u}}{{\partial x^{4} }} + P\frac{{\partial^{2} u}}{{\partial x^{2} }} + \delta \left( {x - x_{\text{F}} } \right)F_{0} \sin \left( {\omega t} \right) \hfill \\ \quad + \sum\limits_{z = 1}^{\text{Z}} {\left\{ {C_{{\text{NES}}} \left[ {\frac{{\partial u\left( {x_{z} ,t} \right)}}{\partial t} - \frac{{{\text{d}} u_{z} }}{{{\text{d}} t}}} \right] + k_{\text{NES}} \left[ {u\left( {x_{z} ,t} \right) - u_{z} } \right]^{3} } \right\}} \hfill \\ \end{gathered} \right\}\psi_{m} \left( x \right)} {\text{d}} x = 0 $$

(9)

where ψ_m(x) is the mth weight function (m = 1, 2, … M). According to Eqs. (7a) and (7b), the mode functions of a generally restrained pre-pressure beam structure are selected as the trail and weight functions of the GTM, which can be accurately predicted by applying the boundary-smoothed Fourier series [6,7,8,9,10].

To simplify the mth residual equation, Eq. (9) is rewritten as

$$ R_{m1} + R_{m2} + R_{m3} + R_{m4} + R_{m5} + R_{m6} + R_{m7} = 0 $$

(10)

where the corresponding residual terms are listed in “Appendix C”. According to the definition of R_m1, its specific expression is written as

$$ R_{m1} = C_{m1} \frac{{{\text{d}}^{2} q_{1} }}{{{\text{d}} t^{2} }} + \ldots + C_{mi} \frac{{{\text{d}}^{2} q_{i} }}{{{\text{d}} t^{2} }} + \ldots + C_{mN} \frac{{{\text{d}}^{2} q_{{N}} }}{{{\text{d}} t^{2} }} $$

(11)

Substituting Eq. (11) into Eq. (10), Eq. (10) is rewritten as

$$ C_{m1} \frac{{{\text{d}}^{2} q_{1} }}{{{\text{d}} t^{2} }} + \cdots + C_{mi} \frac{{{\text{d}}^{2} q_{i} }}{{{\text{d}} t^{2} }} + \cdots + C_{mN} \frac{{{\text{d}}^{2} q_{{N}} }}{{{\text{d}} t^{2} }} = - \sum\limits_{{{{i}} = 2}}^{7} {R_{mi} } $$

(12)

Then, the matrix form of residual equations is derived as

$$ \left\{ {\begin{array}{*{20}c} {\frac{{{\text{d}}^{2} q_{1} }}{{{\text{d}} t}}} \\ \ldots \\ {\frac{{{\text{d}}^{2} q_{i} }}{{{\text{d}} t^{2} }}} \\ \ldots \\ {\frac{{{\text{d}}^{2} q_{{N}} }}{{{\text{d}} t^{2} }}} \\ \end{array} } \right\} = - \left[ {\begin{array}{*{20}c} {C_{11} } \ldots {C_{1i} } \ldots {C_{{1{{N}} }} } \\ \ldots \ldots \ldots \ldots \ldots \\ {C_{m1} } \ldots {C_{mi} } \ldots {C_{{m{{N}} }} } \\ \ldots \ldots \ldots \ldots \ldots \\ {C_{{{{M}} 1}} } \ldots {C_{{{{M}} i}} }\ldots {C_{{{{M}} {{N}} }} } \\ \end{array} } \right]^{ - 1} \left\{ {\begin{array}{*{20}c} {\sum\limits_{{{{i}} = 2}}^{7} {R_{1i} } } \\ \ldots \\ {\sum\limits_{{{{i}} = 2}}^{7} {R_{mi} } } \\ \ldots \\ {\sum\limits_{{{{i}} = 2}}^{7} {R_{{{{M}} i}} } } \\ \end{array} } \right\} $$

(13)

Substituting Eq. (8) into Eq. (6), the governing equation of the zth NES is derived as

$$\begin{aligned} \frac{{{\text{d}}^{2} u_{z} }}{{{\text{d}} t^{2} }} &= - \frac{1}{{m_{\text{NES}} }}\left\{C_{\text{NES}} \left[ {\frac{{{\text{d}} u_{z} }}{{{\text{d}} t}} - \sum\limits_{i = 1}^{{N}} {\varphi_{i} \left( {x_{z} } \right)\frac{{{\text{d}} q_{i} \left( t \right)}}{{{\text{d}} t}}} } \right] \right.\\ &\quad + \left. k_{\text{NES}} \left[ {u_{z} - \sum\limits_{i = 1}^{{N}} {\varphi_{i} \left( {x_{z} } \right)q_{i} \left( t \right)} } \right]^{3} \right\}\end{aligned} $$

(14)

The Runge–Kutta method is employed to solve Eqs. (13) and (14). Dynamic responses of the vibration system can be obtained by substituting the numerical results into Eq. (8).

3 Numerical Results and Discussion

3.1 Model Effectiveness

With the continuous development of material and manufacture, some materials with lightweight and high-strength properties are applied in the shipbuilding industry as an alternative to the traditional materials, including aluminum alloy, carbon fiber, and others. In this context, this section investigates the potential application of multiple uniformly distributed NESs on vibration suppression of the beam structure manufactured by aluminum alloy. Parameters of the single NES, pre-pressure beam structure, external excitation, and boundary conditions are listed in Table 1. In this study, the nonlinear stiffness of the NES is the positive cubic nonlinear stiffness (k_NES > 0 N/m³).

Table 1 Parameters of the single NES, pre-pressure beam structure, external excitation, and boundary conditions

In this study, the calculation time domain is 0–500 T_e, where T_e is the external excitation period. The dynamic responses in 401–500 T_e are selected as stable responses. Additionally, N = M is employed as the relation of different truncation numbers. Under such a relation, the coefficient matrix of Eq. (13) is squared.

Firstly, the correctness of the GTM is investigated. The HBM is employed to verify the dynamic responses predicted by the GTM. Solution forms of the HBM are set as the fundamental harmonic. The truncation number is selected as 4-term. In the GTM, initial values are set as

$$ q_{1} \left( 0 \right) = 0.001 $$

(15a)

$$ q_{2} \left( 0 \right) = q_{3} \left( 0 \right) = q_{4} \left( 0 \right) = 0 $$

(15b)

and

$$ \frac{{{\text{d}} q_{1} \left( 0 \right)}}{{{\text{d}} t}} = \frac{{{\text{d}} q_{2} \left( 0 \right)}}{{{\text{d}} t}} = \frac{{{\text{d}} q_{3} \left( 0 \right)}}{{{\text{d}} t}} = \frac{{{\text{d}} q_{4} \left( 0 \right)}}{{{\text{d}} t}} = 0 $$

(15c)

Dynamic responses of the vibration system predicted by the GTM and HBM are shown in Fig. 2, where the external excitation frequency varies from 1 to 250 Hz. In Fig. 2, the relative errors of dynamic responses predicted by the GTM and HBM are less than 1%, which verifies the correctness of the GTM.

Fig. 2

Dynamic responses of the pre-pressure beam structure predicted by the GTM and HBM

Secondly, the stability of the GTM is investigated. The truncation numbers are selected as 2-term, 4-term, 6-term, and 8-term. Initial values of the GTM are set as

$$ q_{1} \left( 0 \right) = 0.001 $$

(16a)

$$ q_{2} \left( 0 \right) = \cdots = q_{i} \left( 0 \right) = \cdots = q_{N} \left( 0 \right) = 0 $$

(16b)

and

$$ \frac{{{\text{d}} q_{1} \left( 0 \right)}}{{{\text{d}} t}} = \cdots = \frac{{{\text{d}} q_{i} \left( 0 \right)}}{{{\text{d}} t}} = \cdots = \frac{{{\text{d}} q_{N} \left( 0 \right)}}{{{\text{d}} t}} = 0 $$

(16c)

Dynamic responses of the pre-pressure beam structure with different truncation numbers are plotted in Fig. 3. In this figure, the number of primary resonance regions corresponds to the truncation number. After the truncation number exceeds 6-term, dynamic responses of the vibration system keep stable, which indicates that the 6-term truncation number guarantees the stability of the GTM. In the subsequent study, the truncation number of the GTM is set as 6-term.

Fig. 3

Dynamic responses of the pre-pressure beam structure with different truncation numbers

Thirdly, the initial value sensitivity of the vibration system is investigated. For this part, the viscous damping of a single NES is set as C_NES = 4 Ns/m and the number of NESs is set as Z = 4. Dynamic responses of the pre-pressure beam structure under the forward and reverse sweeping ways are plotted in Fig. 4. In the forward sweeping way, the external excitation frequency ranges from 1 to 250 Hz. In the reverse sweeping way, the external excitation frequency ranges from 250 to 1 Hz. In Fig. 4, the amplitude–jumping phenomenon occurs in dynamic responses, where the amplitude–jumping frequency is different under different sweeping ways. In the amplitude–frequency response curves, there exist two unstable regions under the forward sweeping way and one unstable region under the reverse sweeping way. Phase diagrams and the Poincare points are also plotted in Fig. 4 to judge the vibration state of such unstable regions. From the corresponding figures, the Poincare points tend to form a closed curve and each phase path keeps stable, which indicates that the unstable regions are in a quasi-periodic state. The NESs change the vibration state of the pre-pressure beam structure, resulting in the quasi-periodic vibration state of the vibration system.

Fig. 4

Dynamic responses of the pre-pressure beam under the forward and reverse sweeping ways

3.2 The Influence of NESs on Dynamic Responses

On many engineering occasions, once NESs are manufactured, their certain parameters including inertial mass, viscous damping, and others are determined or can only be changed in a limited range of variation. However, the nonlinear stiffness of NESs can be effectively changed by replacing their nonlinear structural elements. Additionally, the number of NESs can be adjusted according to the installation space of practical structures. Considering the above engineering practice, this section mainly studies the dynamic responses influenced by the number of NESs as well as their nonlinear stiffness.

Firstly, the influence of the NES number on dynamic responses is studied, where the NES number is set as 2, 4, 6, 8, and 10. Viscous damping of the single NES is set as 8 Ns/m. Dynamic responses of the pre-pressure beam under different numbers of NESs are plotted in Fig. 5. In this figure, an unstable region appears in dynamic responses of the pre-pressure beam structure as the number of NESs is 2. Phase diagrams and time waveforms of the unstable region are also plotted in Fig. 5 to further study its vibration state. From the phase diagrams, it can be seen that the Poincare points form a closed curve. The corresponding phase path and vibration waveform keep stable. According to the above phenomenon, the unstable region is in a quasi-periodic state. Such an unstable region vanishes with the increase in the number of NESs. Additionally, the increase in the number of NESs beneficially affects the vibration suppression at both ends of the pre-pressure beam structure. The vibration suppression is obvious in the 2nd, 3rd, and 4th primary resonance regions.

Fig. 5

Dynamic responses of the pre-pressure beam under different numbers of NESs

The fast Fourier transformation of dynamic responses under the unstable region is plotted in Fig. 6, where the excitation frequency is 46 Hz. In Fig. 6, two main-frequency regions appear in the frequency domain. The 1st main-frequency region is close to 46 Hz, while the 2nd main-frequency region is close to 138 Hz, where 46 Hz and 138 Hz correspond, respectively, to the one-time and three-times of excitation frequency. The above phenomenon suggests that NESs can convert low-frequency vibration into high-frequency vibration.

Fig. 6

The fast Fourier transformation of dynamic responses of the pre-pressure beam under 46 Hz (Z = 2)

Then, the time-domain variation of the vibration system kinetic energy in the unstable region is shown in Fig. 7, where the excitation frequency is 46 Hz. In Fig. 7, T_B and T_NES of the unstable region oscillate periodically. The oscillation period of the kinetic energy is consistent with that of dynamic responses of the pre-pressure beam structure. The phenomenon of the targeted energy transfer of the vibration system appears when the vibration is in the quasi-periodic state. From Fig. 7c, the kinetic energy of the beam structure is targeted to transport to NESs within the time interval of T_s. Such a phenomenon suggests that appropriate parameters of NESs can motivate the targeted energy transfer of the vibration system, which is beneficial to the vibration suppression of the beam structure. Furthermore, according to the forced responses studied in this work, the above time interval presents a periodic character.

Fig. 7

The time-domain variation of kinetic energy of the vibration system under 46 Hz (Z = 2)

Secondly, the influence of the nonlinear stiffness of NESs on dynamic responses is studied, where the nonlinear stiffness of NESs is set as 10¹⁰ N/m³, 2 × 10¹⁰ N/m³, 3 × 10¹⁰ N/m³, 4 × 10¹⁰ N/m³, and 5 × 10¹⁰ N/m³. The number of NESs is set as 4. Dynamic responses under different k_NES are plotted in Fig. 8. In this figure, the unstable regions of amplitude appear with the increase of k_NES. The unstable regions appear in the dynamic responses for k_NES being 4 × 10¹⁰ N/m³ and 5 × 10¹⁰ N/m³. Phase diagrams of the unstable regions are plotted to further study their vibration state, where the Poincare points form a closed curve and the corresponding phase path keeps stable, which indicates that the vibration state of such unstable regions is quasi-periodic. With the increase of k_NES, the unstable regions and primary resonance regions shift to higher-frequency regions. Furthermore, in primary resonance regions without complex dynamic responses, the increase of k_NES beneficially influences the vibration suppression at both ends of the pre-pressure beam structure. Especially, the vibration suppression effect is obvious in the 3rd primary resonance region.

Fig. 8

Dynamic responses of the pre-pressure beam under different k_NES

The fast Fourier transformation of dynamic responses in the unstable regions is plotted in Fig. 9. In this figure, three main-frequency regions appear in the frequency domain. Such main-frequency regions correspond to the one, three, and five times of the excitation frequency, which indicates that NESs can convert the vibration frequency, where the increase of nonlinear stiffness of NESs strengthens such an ability of NESs.

Fig. 9

The fast Fourier transform of dynamic responses at both ends of the pre-pressure beam under unstable regions

Then, the time-domain variation of vibration system kinetic energy in the unstable regions is shown in Fig. 10. In this figure, the vibration system kinetic energy of unstable region periodically oscillates, where the oscillation state of kinetic energy is the same as that of dynamic responses of the pre-pressure beam structure. Furthermore, the kinetic energy of the vibration system can be converted between the pre-pressure beam structure and NESs. The kinetic energy of the beam structure is targeted to transport to NESs within the time interval of T_s, which suggests that appropriate parameters of NESs can motivate the targeted energy transfer of the vibration system. According to the forced responses studied in this work, the above time interval presents a periodic character.

Fig. 10

The time-domain variation of the vibration system kinetic energy under unstable regions

Eventually, the influence of the excitation amplitude on the dynamic behavior of the vibration system is investigated. Dynamic responses under different amplitudes of the excitation are plotted in Fig. 11. In Fig. 11, the increase in the excitation amplitude motivates the complex dynamic behavior of the vibration system. According to the previous analysis, when the vibration state of the vibration system is in the quasi-periodic state, the phenomenon of the targeted energy transfer of the vibration system appears. Therefore, the threshold of the excitation amplitude for the occurrence of targeted energy transfer can be obtained by judging the vibration state of the vibration system. For parameters of the vibration system employed in Fig. 11a, the corresponding threshold is 9.1 N. For parameters of the vibration system employed in Fig. 11b, the corresponding threshold is 8.1 N. Furthermore, for different parameters of the vibration system, the threshold of the excitation amplitude for the occurrence of targeted energy transfer is different.

Fig. 11

Dynamic responses of the pre-pressure beam under different amplitudes of the excitation

3.3 Optimization of the NESs

According to the analysis in Sect. 3.2, suitable parameters of NESs have a beneficial influence on the vibration suppression of the pre-pressure beam structure. For obtaining a suitable combination of the number of NESs and their nonlinear stiffness, it is of great significance to investigate the optimization of NESs. Therefore, this section investigates the optimization of NESs on the pre-pressure beam structure with symmetric and unsymmetrical boundary conditions. Parameters of the pre-pressure beam structure and external excitation are the same as those given in Table 1.

Before the optimization of NESs, it is crucial to select the appropriate objective function. From the perspective of energy, the kinetic energy of the beam structure corresponds to its vibration level. Figures 12 and 13 show the maximum kinetic energy of the pre-pressure beam structure with different parameters of NESs under symmetric and unsymmetrical boundary conditions, where the energy reference is selected as 10^–6 J. From Figs. 12 and 13, the maximum kinetic energy of the pre-pressure beam structure ranges with the variation of the number of NESs and their nonlinear stiffness, especially in the 2nd and 3rd primary resonance regions. Therefore, the maximum kinetic energy of the pre-pressure beam structure in the 2nd and 3rd primary resonance regions is selected as the corresponding objective function.

Fig. 12

Maximum kinetic energy of the pre-pressure beam structure with different parameters of NESs under the symmetric boundary condition

Fig. 13

Maximum kinetic energy of the pre-pressure beam structure with different parameters of NESs under the unsymmetrical boundary condition

Then, the optimization of the pre-pressure beam structure with different parameters of NESs under symmetric and unsymmetrical boundary conditions is shown in Figs. 14 and 15. For the symmetric boundary condition, the increase in the number of NESs and their nonlinear stiffness beneficially influences the vibration suppression of the pre-pressure beam structure. As k_NES = 10¹¹ N/m³ and Z = 10, the maximum kinetic energy of the pre-pressure beam structure is at its minimum. Therefore, k_NES = 10¹¹ N/m³ and Z = 10 are regarded as the suitable parameters of NESs for vibration suppression of the pre-pressure beam structure under the symmetric boundary condition. For the unsymmetrical boundary condition, the increase in the number of NESs monotonically strengthens the vibration suppression of the pre-pressure beam structure. With the increase of nonlinear stiffness of NESs, the maximum kinetic energy of the pre-pressure beam structure monotonically changes in the 3rd primary resonance region. In the above process, the maximum kinetic energy of the pre-pressure beam structure changes nonmonotonically in the 2nd primary resonance region. As k_NES = 4.898 × 10¹⁰ N/m³ and Z = 10, the maximum kinetic energy of the pre-pressure beam structure in the 2nd primary resonance region is at its minimum. In the 3rd primary resonance region, the maximum kinetic energy of the beam structure under such parameters of NESs is close to its minimum. Therefore, k_NES = 4.898 × 10¹⁰ N/m³ and Z = 10 are regarded as the suitable parameters of NESs for vibration suppression of the pre-pressure beam structure under the unsymmetrical boundary condition.

Fig. 14

Optimization of the pre-pressure beam structure with different parameters of NESs under the symmetric boundary condition

Fig. 15

Optimization of the pre-pressure beam structure with different parameters of NESs under the unsymmetrical boundary condition

The responses of maximum kinetic energy frequency of the pre-pressure beam structure with optimized NESs under symmetric and unsymmetrical boundary conditions are shown in Fig. 16. For the symmetric boundary condition, k_NES = 10¹¹ N/m³ and Z  =  10. For the unsymmetrical boundary condition, k_NES = 4.898 × 10¹⁰ N/m³ and Z = 10. In Fig. 16, the vibration energy of the pre-pressure beam structure is effectively suppressed by choosing the suitable number of NESs and their nonlinear stiffness for symmetric and unsymmetrical boundary conditions. Additionally, such suitable parameters of NESs have a significant effect on the vibration suppression of multiple primary resonance regions of the responses of maximum kinetic energy frequency.

Fig. 16

Responses of maximum kinetic energy frequency of the pre-pressure beam structure with optimized NESs under symmetric and unsymmetrical boundary conditions

4 Conclusions

In this study, the system governing equations of the pre-pressure beam structure is formulated through the generalized Hamiltonian principle and the variational procedure. Dynamic responses of a generally restrained pre-pressure beam structure with multiple uniformly distributed NESs are predicted by the GTM. The effectiveness of the vibration model established is studied firstly. On this basis, the effect of NESs on dynamic responses and vibration suppression of the pre-pressure beam structure is studied. For the structural parameters and vibration analysis model studied in this work, some conclusions are obtained.

• 1. The GTM has good stability and correctness in predicting the dynamic responses of the pre-pressure beam structure with multiple uniformly distributed NESs. In this study, a 6-term truncation number can keep the stability of the GTM. Dynamic responses of such a vibration analysis model are sensitive to the initial values for calculation.

• 2. Parameters of NESs significantly influence dynamic responses of the pre-pressure beam structure with multiple uniformly distributed NESs. For the vibration analysis model established, suitable parameters of NESs have a beneficial effect on the vibration suppression at both ends of the pre-pressure beam structure.

• 3. Complex dynamic responses occur in the primary resonance regions as the parameters of NESs reach certain values. NESs can convert the vibration frequency and energy transfer characteristics of the vibration system.

• 4. For different boundary conditions, optimized parameters of NESs significantly suppress the vibration energy of the pre-pressure beam structure. Such suitable parameters of NESs have a beneficial effect on the vibration suppression of multiple primary resonance regions.

Appendices

Appendix A

$$ T_{\text{B}} = \int_{0}^{L} {\frac{1}{2}\rho S} \left( {\frac{\partial u}{{\partial t}}} \right)^{2} {\text{d}} t $$

(A-1)

$$ T_{\text{NES}} = \sum\limits_{z = 1}^{\text{Z}} {\left( {\frac{1}{2}m_{\text{NES}} \frac{{{\text{d}} u_{z} }}{{{\text{d}} t}}} \right)^{2} } $$

(A-2)

$$ V_{{\text{B}}} = \int_{0}^{L} {\frac{1}{2}EI} \left( {\frac{{\partial^{2} u}}{{\partial x^{2} }}} \right)^{2} {\text{d}} x $$

(A-3)

$$ V_{{\text{P}}} = \int_{0}^{L} {\frac{1}{2}P} \left( {\frac{\partial u}{{\partial x}}} \right)^{2} {\text{d}} x $$

(A-4)

$$ \begin{aligned} V_{\text{Boundary}} & = \frac{1}{2}k_{\text{L}} \left[ {u\left( {0,t} \right)} \right]^{2} + \frac{1}{2}k_{\text{R}} \left[ {u\left( {L,t} \right)} \right]^{2} \\ & \quad + \frac{1}{2}K_{\text{L}} \left[ {\frac{{\partial u\left( {0,t} \right)}}{\partial x}} \right]^{2} + \frac{1}{2}K_{\text{R}} \left[ {\frac{{\partial u\left( {L,t} \right)}}{\partial x}} \right]^{2} \\ \end{aligned} $$

(A-5)

$$ V_{\text{NES}} = \frac{1}{4}k_{\text{NES}} \sum\limits_{\text{z} = 1}^{Z} {\left[ {u_{z} - u\left( {x_{z} ,t} \right)} \right]^{4} } $$

(A-6)

$$ \delta W_{\text{B}} = - \int_{0}^{L} {C_{\text{B}} } \frac{\partial u}{{\partial t}}\delta u{\text{d}} x $$

(A-7)

$$ \delta W_{\text{NES}} = - C_{{\text{NES}}} \sum\limits_{z = 1}^{Z} {\left\{ {\left[ {\frac{{{\text{d}} u_{z} }}{{{\text{d}} t}} - \frac{{\partial u\left( {x_{z} ,t} \right)}}{\partial t}} \right]\delta \left[ {u_{z} - u\left( {x_{z} ,t} \right)} \right]} \right\}} $$

(A-8)

$$ \delta W_{\text{F}} = - \int_{0}^{L} {{\text{Dirca}} \left( {x - x_{\text{F}} } \right)F_{0} \sin \left( {\omega t} \right)} \delta u{\text{d}} x $$

(A-9)

Appendix B

$$ \int_{{t_{1} }}^{{t_{2} }} {\delta T_{\text{B}} {\text{d}} t = } - \int_{{t_{1} }}^{{t_{2} }} {\int_{0}^{L} {\rho S\frac{{\partial^{2} u}}{\partial t}} } \delta u{\text{d}} x{\text{d}} t $$

(B-1)

$$ \int_{{t_{1} }}^{{t_{2} }} {\delta T_{\text{NES}} {\text{d}} t} = - \sum\limits_{z = 1}^{Z} {\left( {\int_{{t_{1} }}^{{t_{2} }} {m_{\text{NES}} \frac{{{\text{d}}^{2} u_{z} }}{{{\text{d}} t^{2} }}\delta u_{z} } {\text{d}} t} \right)} $$

(B-2)

$$ \begin{aligned} \int_{{t_{1} }}^{{t_{2} }} {\delta V_{{\text{B}}} {\text{d}} t} & = \int_{{t_{1} }}^{{t_{2} }} {\int_{0}^{L} {EI\frac{{\partial^{4} u}}{{\partial x^{4} }}} \delta u{\text{d}} x{\text{d}} t} \\ & \quad + \int_{{t_{1} }}^{{t_{2} }} {\left[ \begin{gathered} - EI\frac{{\partial^{2} u\left( {0,t} \right)}}{{\partial x^{2} }}\delta \left( {\frac{\partial u}{{\partial x}}} \right) + EI\frac{{\partial^{3} u\left( {0,t} \right)}}{{\partial x^{3} }}\delta u \hfill \\ + EI\frac{{\partial^{2} u\left( {L,t} \right)}}{{\partial x^{2} }}\delta \left( {\frac{\partial u}{{\partial x}}} \right) - EI\frac{{\partial^{3} u\left( {L,t} \right)}}{{\partial x^{3} }}\delta u \hfill \\ \end{gathered} \right]} {\text{d}} t \\ \end{aligned} $$

(B-3)

$$ \int_{{t_{1} }}^{{t_{2} }} {\delta V_{\text{P}} {\text{d}} t} = P\frac{{\partial u\left( {0,t} \right)}}{\partial x}\delta u - P\frac{{\partial u\left( {L,t} \right)}}{\partial x}\delta u + \int_{{t_{1} }}^{{t_{2} }} {\int_{0}^{L} {P\frac{{\partial^{2} u}}{{\partial x^{2} }}\delta u{\text{d}} x{\text{d}} } t} $$

(B-4)

$$ \int_{{t_{1} }}^{{t_{2} }} {\delta V_{\text{Boundary}} {\text{d}} t} = \int_{{t_{1} }}^{{t_{2} }} {\left[ \begin{gathered} k_{\text{L}} u\left( {0,t} \right)\delta u + K_{\text{L}} \frac{{\partial u\left( {0,t} \right)}}{\partial x}\delta \left( {\frac{\partial u}{{\partial x}}} \right) \hfill \\ \quad + k_{\text{R}} u\left( {L,t} \right)\delta u + K_{\text{R}} \frac{{\partial u\left( {L,t} \right)}}{\partial x}\delta \left( {\frac{\partial u}{{\partial x}}} \right) \hfill \\ \end{gathered} \right]{\text{d}} t} $$

(B-5)

$$ \int_{{t_{1} }}^{{t_{2} }} {\delta V_{\text{NES}} {\text{d}} t} = \sum\limits_{z = 1}^{Z} {\left\{ {\int_{{t_{1} }}^{{t_{2} }} {k_{\text{NES}} \left[ {u_{z} - u\left( {x_{z} ,t} \right)} \right]^{3} \delta \left[ {u_{z} - u\left( {x_{z} ,t} \right)} \right]{\text{d}} t} } \right\}} $$

(B-6)

$$ \int_{{t_{1} }}^{{t_{2} }} {\delta W_{\text{B}} {\text{d}} t} = - \int_{{t_{1} }}^{{t_{2} }} {\int_{0}^{L} {C_{\text{B}} } \frac{\partial u}{{\partial t}}\delta u{\text{d}} x{\text{d}} t} $$

(B-7)

$$ \int_{{t_{1} }}^{{t_{2} }} {\delta W_{\text{NES}} {\text{d}} t} = - \sum\limits_{z = 1}^{{Z}} {\int_{{t_{1} }}^{{t_{2} }} {C_{\text{NES}} \left[ {\frac{{{\text{d}} u_{z} }}{{{\text{d}} t}} - \frac{{\partial u\left( {x_{z} ,t} \right)}}{\partial t}} \right]\delta \left[ {u_{z} - u\left( {x_{z} ,t} \right)} \right]{\text{d}} t} } $$

(B-8)

$$ \int_{{t_{1} }}^{{t_{2} }} {\delta W_{\text{F}} {\text{d}} t} = - \int_{{t_{1} }}^{{t_{2} }} {\int_{0}^{L} {\delta \left( {x - x_{\text{F}} } \right)F_{0} \sin \left( {\omega t} \right)} \delta u{\text{d}} x{\text{d}} t} $$

(B-9)

Appendix C

$$ R_{m1} = \int_{0}^{L} {\rho S\left[ {\sum\limits_{i = 1}^{{N}} {\varphi_{i} \left( x \right)\frac{{{\text{d}}^{2} q_{i} \left( t \right)}}{{{\text{d}} t^{2} }}} } \right]\psi_{m} \left( x \right){\text{d}} x} $$

(C-1)

$$ R_{m2} = \int_{0}^{L} {C_{\text{B}} \left[ {\sum\limits_{i = 1}^{{N}} {\varphi_{i} \left( x \right)\frac{{{\text{d}} q_{i} \left( t \right)}}{{{\text{d}} t}}} } \right]\psi_{m} \left( x \right){\text{d}} x} $$

(C-2)

$$ R_{m3} = \int_{0}^{L} {EI\left[ {\sum\limits_{i = 1}^{{N}} {\frac{{{\text{d}}^{4} \varphi_{i} \left( x \right)}}{{{\text{d}} x^{4} }}q_{i} \left( t \right)} } \right]\psi_{m} \left( x \right){\text{d}} x} $$

(C-3)

$$ R_{m4} = \int_{0}^{L} {P\left[ {\sum\limits_{i = 1}^{{N}} {\frac{{{\text{d}}^{2} \varphi_{i} \left( x \right)}}{{{\text{d}} x^{2} }}q_{i} \left( t \right)} } \right]\psi_{m} \left( x \right){\text{d}} x} $$

(C-4)

$$ R_{m5} = \psi_{m} \left( {x_{F} } \right)F_{0} \sin \left( {\omega t} \right) $$

(C-5)

$$ R_{m6} = \sum\limits_{z = 1}^{Z} {\left\{ {C_{\text{NES}} \left[ {\sum\limits_{{{\text{i}} = 1}}^{{N}} {\varphi_{i} \left( {x_{z} } \right)\frac{{{\text{d}} q_{i} \left( t \right)}}{{{\text{d}} t}}} - u_{z} \left( t \right)} \right]\psi_{m} \left( {x_{z} } \right)} \right\}} $$

(C-6)

$$ R_{{m{7}}} = \sum\limits_{z = 1}^{{Z}} {\left\{ {k_{\text{NES}} \left[ {\sum\limits_{i = 1}^{{N}} {\varphi_{i} \left( {x_{z} } \right)q_{i} \left( t \right)} - u_{z} \left( t \right)} \right]^{3} \psi_{m} \left( {x_{z} } \right)} \right\}} $$

(C-7)