Equivalent continuum modeling method for transient response analysis of large space truss structures with nonlinear elastic joints

Abstract

This study presented an equivalent continuum modeling method for analysis of the transient response of the large space truss structures with nonlinear elastic joints. Firstly, a two-node hybrid joint-beam element model was established for a truss member with two nonlinear joints at its both ends based on the geometrical relationship and equilibrium condition between the truss member and the nonlinear joints. Subsequently, an equivalent 8-DOFs nonlinear beam element including the warping and distortional deformations was derived for approximating the repeating element of the beam-like truss structure with rectangular cross-sections based on the energy equivalence method, the external force vector and nonlinear restoring force vector of the truss structure were transferred to the external force vector and nonlinear restoring force vector of the equivalent beam element. The equation of motion of the equivalent nonlinear beam model was solved by the combination of the Newmark-β method and the Newton–Raphson iteration method. In the numerical studies, a cantilevered truss structure and a spacecraft with a truss support structure were simulated by considering the joint have piece-wise linear stiffness. The correctness and high efficiency of the presented modeling method was verified by comparison of the results of the equivalent models with the original nonlinear finite element models established by ANSYS.

1 Introduction

Large space truss structures (LSTS) are ideal support platforms in various space applications such as satellite communication, earth observation and deep space exploration [1,2,3]. The high precision and high stability of space missions put forward very high requirements on the dynamic performance of the LSTS. In order to realize on-orbit deployment or assembly, a large number of mechanical joints are used in LSTS [4, 5]. These joints inevitably have nonlinear factors such as clearance, contact, friction, and slip [6,7,8], which make the overall structure possess the characteristics of high dimensionality, strong nonlinear and non-smooth [9,10,11], and bring great challenges to the dynamic modeling, analysis, and control of the LSTS.

The finite element modeling (FEM) method can be used to establish the dynamic model of LSTS [12], however, for LSTS with thousands of nonlinear joints, the models established directly using the FEM method will be very high-dimensional, and needs a huge computational cost for nonlinear dynamic analysis. The LSTS with nonlinear joints belong to the dynamical systems with local nonlinearities; in order to obtain low-dimensional dynamic models for such systems, various model order reduction techniques have been proposed, such as the dynamic condensation technique [13], the component mode synthesis method [14], the hybrid reduced order method [15], etc. However, these methods have not been applied in a complex system having more than thousands of local nonlinearities such as the LSTS.

The LSTS are usually repetitive structures composed of repeating elements (or named “unit cells”). From the point view of equivalence of dynamics, if the repetitive structure consists of a considerable number of repeating elements, it may be convenient to approximate the dynamic behavior of the repetitive structure by a continuum model via a suitable equivalent modeling method [16]. In the past decades, the use of equivalent continuum modeling (ECM) method to establish low-dimensional equivalent model for the truss-like structures was favored by many researchers [17,18,19,20,21,22]. In the early stage, these studies were carried out on truss-like structures with ideal pin joints or rigid joints. For examples, Noor et al. [23] proposed an ECM method based on the equivalence of energy. Sun and Liebbe [24] proposed an ECM method based on the equivalence of static displacement. Stephen and Zhang [25] adopted the transfer matrix method to carry out the ECM for ideal pin-jointed truss structures. Later, in order to consider the mechanical properties of the truss joints more accurately, the stiffness and damping characteristics of the joints are considered in the process of ECM [26,27,28,29,30]. For example, Salehian and Inman [26] established an equivalent beam model for the planar repetitive truss structure considering the torsional stiffness of the joint. Liu et al. [27, 28] presented an ECM method for the truss structures considering the joint have both stiffness and damping characteristics in the directions of all six degrees-of-freedom, and compared the accuracies of the equivalent classical beam model and the equivalent micropolar beam model. All the above studies modelled the truss joints as linear spring/damping elements without considering the complex nonlinear characteristics in the joints.

The modeling and identification of the nonlinear joints in structures have been well studied [31, 32], and different simplified models are used to characterize the nonlinear stiffness and damping of the joints such as the piecewise linear stiffness model [6, 33], the cubic stiffness model [34], the hysteresis model [10, 35], etc. However, the studies on ECM methods for repetitive truss structures with nonlinear joints are very limited. Webster [33] first proposed a modeling method that considered joint nonlinearity in the equivalent continuum model of space truss structures. He used the describing function method to equivalently linearize the joint nonlinearity and established an equivalent nonlinear beam model for analyzing the harmonic motion of the truss structure. Zhang et al. [34] considered the cubic stiffness characteristic of truss joint, obtained the equivalent linearized stiffness coefficient of joint using the description function method, and established the equivalent beam model of the truss structure based on the energy equivalence method. Liu et al. [35] established the equivalent beam model of beam-like space truss structure considering the friction-slip nonlinearity of the truss joint, and analyzed the amplitude-frequency characteristics of the truss structure. Li et al. [36] proposed a multi-harmonic ECM method for steady-state response analysis of space truss structures by considering higher-order harmonic components caused by the joint nonlinearity. However, all the above studies on ECM of LSTS with nonlinear joints obtained equivalent continuum models in the frequency domain and can’t be used for transient response analysis directly. Till now, an ECM method for transient dynamic analysis of LSTS with nonlinear joints has not been established.

This study presented an ECM method for the transient dynamic analysis of repetitive truss structures with nonlinear elastic joints. The organization of the paper is as follows: In Sect. 2, the equivalent continuum modeling method for repetitive truss structure with nonlinear elastic joints is introduced. Section 3 gives the solution method for the equivalent nonlinear beam model. Numerical examples including a cantilevered truss structure and a spacecraft structure with piece-wise linear stiffness joints are given in Sect. 4 to verify the correctness and high efficiency of the presented equivalent modeling method.

2 Equivalent continuum modeling of the space truss structure

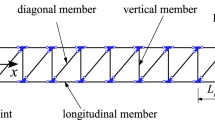
Taking the repetitive truss structure shown in Fig. 1 as an example. Considering the nonlinearities of the joints, the equation of motion of the truss structure can be established by using the FEM method as

$${\mathbf{M}\ddot{\mathbf{u}}} + {{\mathbf{C}\dot{\mathbf{u}}}} + {\mathbf{Ku}} + {\mathbf{f}}_{NL} ({\mathbf{u}},{\dot{\mathbf{u}}}) = {\mathbf{F}}$$

(1)

where M, C and K are the mass, damping and linear stiffness matrices of the truss structure, respectively, ${\mathbf{f}}_{NL}$ is the nonlinear restoring force vector caused by the nonlinear joints, F is the external load vector, ${\mathbf{u}}$, ${\dot{\mathbf{u}}}$ and ${\ddot{{\mathbf{u}}}}$ are the displacement, velocity and acceleration vectors of the truss structure, respectively. The nonlinear dynamic model established in Eq. (1) is extremely high-dimensional. Alternatively, an ECM method will be proposed for this kind of truss structure in order to obtain a low-dimensional equivalent dynamic model.

Fig. 1

Beam-like repetitive truss structure

2.1 Model condensation

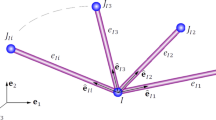
Firstly, the truss member with nonlinear joints at its two ends was modelled using the FEM method as a hybrid joint-beam element model, as shown in Fig. 2, where the truss member is modelled as a spatial beam element, the joint is modelled as a six degrees-of-freedom (DOFs) nonlinear spring-damper element connected with a rigid link element. The length of the rigid link element equals to the real length of the joint, and the length of the spring-damper element is zero.

Fig. 2

Hybrid joint-beam element model of the truss member with two end nonlinear joints

The equation of motion of this hybrid joint-beam element is

$${\mathbf{M}}_{H} {\ddot{{\mathbf{u}}}}_{H} + {\mathbf{C}}_{H} {\dot{\mathbf{u}}}_{H} + {\mathbf{K}}_{H} {\mathbf{u}}_{H} + {\mathbf{f}}_{NLH} ({\mathbf{u}}_{H} , {\dot{\mathbf{u}}}_{H} ) = {\mathbf{F}}_{H}$$

(2)

where M_H, C_H, K_H are the mass, damping and linear stiffness matrices of the hybrid joint-beam element model, respectively, f_NLH is the nonlinear restoring force vector, and F_H is the vector of nodal internal forces at the ends of the hybrid joint-beam element,

$${\mathbf{u}}_{H} = \left\{ {{\mathbf{u}}_{i}^{{\text{T}}} ,{\mathbf{u}}_{k}^{{\text{T}}} ,{\mathbf{u}}_{m}^{{\text{T}}} ,{\mathbf{u}}_{n}^{{\text{T}}} ,{\mathbf{u}}_{l}^{{\text{T}}} ,{\mathbf{u}}_{j}^{{\text{T}}} } \right\}^{{\text{T}}}$$

(3a)

$${\mathbf{F}}_{H} = \left\{ {{\mathbf{F}}_{i}^{{\text{T}}} ,{\mathbf{0}} ,{\mathbf{0}} ,{\mathbf{0}} ,{\mathbf{0}} ,{\mathbf{F}}_{j}^{{\text{T}}} } \right\}^{{\text{T}}}$$

(3b)

$${\mathbf{f}}_{NLH} = \left\{ {{\mathbf{0}} , - {\mathbf{f}}_{s1}^{{\text{T}}} ,{\mathbf{f}}_{s1}^{{\text{T}}} , - {\mathbf{f}}_{s2}^{{\text{T}}} ,{\mathbf{f}}_{s2}^{{\text{T}}} ,{\mathbf{0}}} \right\}^{{\text{T}}}$$

(3c)

where u_p (p = i, j, k, l, m, n) is the nodal displacement vector of node p, ${\mathbf{f}}_{s1}$ and ${\mathbf{f}}_{s2}$ are the nonlinear restoring force vectors caused by the left and right nonlinear joints, respectively.

Denoting ${\mathbf{q = }}\left\{ {{\mathbf{u}}_{i}^{{\text{T}}} ,{\mathbf{u}}_{j}^{{\text{T}}} } \right\}^{{\text{T}}}$, ${\mathbf{q}}_{a} {\mathbf{ = }}\left\{ {{\mathbf{u}}_{k}^{{\text{T}}} ,{\mathbf{u}}_{l}^{{\text{T}}} } \right\}^{{\text{T}}}$, ${\mathbf{q}}_{b} {\mathbf{ = }}\left\{ {{\mathbf{u}}_{m}^{{\text{T}}} ,{\mathbf{u}}_{n}^{{\text{T}}} } \right\}^{{\text{T}}}$, according to the geometric relationship, it be obtained that

$${\mathbf{q}}_{a} {\mathbf{ = }}({\mathbf{I + E}}){\mathbf{q}}$$

(4)

where I is a 12 × 12 identity matrix, and

$${\mathbf{E}} = \left[ {\begin{array}{*{20}c} {{\mathbf{E}}_{1} } & \quad {\mathbf{0}} \\ {\mathbf{0}} & \quad {{\mathbf{E}}_{2} } \\ \end{array} } \right],\quad {\mathbf{E}}_{1} = \left[ {\begin{array}{*{20}c} 0 & \quad 0 & \quad 0 & \quad 0 & \quad 0 & \quad 0 \\ 0 & \quad 0 & \quad 0 & \quad 0 & \quad 0 & \quad {e_{1}^{m} } \\ 0 & \quad 0 & \quad 0 & \quad 0 & \quad { - e_{1}^{m} } & \quad 0 \\ 0 & \quad 0 & \quad 0 & \quad 0 & \quad 0 & \quad 0 \\ 0 & \quad 0 & \quad 0 & \quad 0 & \quad 0 & \quad 0 \\ 0 & \quad 0 & \quad 0 & \quad 0 & \quad 0 & \quad 0 \\ \end{array} } \right],\quad {\mathbf{E}}_{2} = \left[ {\begin{array}{*{20}c} 0 & \quad 0 & \quad 0 & \quad 0 & \quad 0 & \quad 0 \\ 0 & \quad 0 & \quad 0 & \quad 0 & \quad 0 & \quad { - e_{2}^{m} } \\ 0 & \quad 0 & \quad 0 & \quad 0 & \quad {e_{2}^{m} } & \quad 0 \\ 0 & \quad 0 & \quad 0 & \quad 0 & \quad 0 & \quad 0 \\ 0 & \quad 0 & \quad 0 & \quad 0 & \quad 0 & \quad 0 \\ 0 & \quad 0 & \quad 0 & \quad 0 & \quad 0 & \quad 0 \\ \end{array} } \right]$$

(5)

where $e_{1}^{m}$ and $e_{2}^{m}$ (m = l, v, t, and d) are the eccentricities of the two joints connected with the member (the superscripts l, v, t, and d represent the longitudinal, vertical, transverse, and diagonal members, respectively).

Denoting

$${\mathbf{x}}_{1} {\mathbf{ = u}}_{k} - {\mathbf{u}}_{m} ,\quad {\mathbf{x}}_{2} {\mathbf{ = u}}_{l} - {\mathbf{u}}_{n} ,\quad {\mathbf{x = }}\left\{ {{\mathbf{x}}_{1}^{{\text{T}}} , \, {\mathbf{x}}_{2}^{{\text{T}}} } \right\}^{{\text{T}}}$$

(6)

where ${\mathbf{x}}_{1}$ and ${\mathbf{x}}_{2}$ represent the deformation vectors of the two nonlinear joints, then it can be obtained that

$${\mathbf{x = q}}_{a} - {\mathbf{q}}_{b}$$

(7)

The member and the two end joints satisfy the following dynamic equilibrium relationship

$${\mathbf{K}}_{s} {\mathbf{x}}+{\mathbf{C}}_{s} {\dot{\mathbf{x}}} + {\mathbf{f}}_{s} {(}{\mathbf{x}}, {\dot{\mathbf{x}}}{) = }{\mathbf{M}}_{b} {{\ddot{\mathbf{q}}}}_{b} + {\mathbf{C}}_{b} {\dot{\mathbf{q}}}_{b} + {\mathbf{K}}_{b} {\mathbf{q}}_{b}$$

(8)

where

$${\mathbf{K}}_{s} = {\text{diag}}\left( {\left[ {k_{uxi} ,k_{uyi} ,k_{uzi} ,k_{\theta xi} ,k_{\theta yi} ,k_{\theta zi} ,k_{uxj} ,k_{uyj} ,k_{uzj} ,k_{\theta xj} ,k_{\theta yj} ,k_{\theta zj} } \right]} \right)$$

(9a)

$${\mathbf{C}}_{s} = {\text{diag}}\left( {\left[ {c_{uxi} ,c_{uyi} ,c_{uzi} ,c_{\theta xi} ,c_{\theta yi} ,c_{\theta zi} ,c_{uxj} ,c_{uyj} ,c_{uzj} ,c_{\theta xj} ,c_{\theta yj} ,c_{\theta zj} } \right]} \right)$$

(9b)

$${\mathbf{f}}_{s} =\left\{ { - {\mathbf{f}}_{s1}^{{\text{T}}} ,{\mathbf{f}}_{s2}^{{\text{T}}} } \right\}^{{\text{T}}}$$

(9c)

M_b, K_b and C_b are the mass, stiffness and the damping matrices of the member, respectively, the coefficients in Eqs. (9a) and (9b) are the linear stiffness and damping coefficients in six directions of the two joints.

Considering the nonlinearity of the joint is elastic, the nonlinear restoring force vector of the two end joints can be approximated by using the tangent stiffness of the nonlinear joint as [37, 38]

$${\mathbf{f}}_{s} {(}{\mathbf{x}}{)} \approx {\mathbf{K}}_{sT} {(}{\mathbf{x}}{) }{\mathbf{x}}$$

(10)

where

$${\mathbf{K}}_{sT} = {\text{diag}}\left( {\left[ {\tilde{k}_{uxi} ,\tilde{k}_{uyi} ,\tilde{k}_{uzi} ,\tilde{k}_{\theta xi} ,\tilde{k}_{\theta yi} ,\tilde{k}_{\theta zi} ,\tilde{k}_{uxj} ,\tilde{k}_{uyj} ,\tilde{k}_{uzj} ,\tilde{k}_{\theta xj} ,\tilde{k}_{\theta yj} ,\tilde{k}_{\theta zj} } \right]} \right)$$

(11)

The coefficients in Eq. (11) are the tangent stiffness coefficients in six directions of the two joints.

Considering that the fundamental frequencies of large space truss structures are usually very low, the inertial force and damping force in Eq. (8) will be neglected when the low frequency vibration of the truss structure is considered, which yields

$$\left[ {{\mathbf{K}}_{s} + {\mathbf{K}}_{sT} {(}{\mathbf{x}}{)}} \right]{\mathbf{x}} = {\mathbf{K}}_{b} {\mathbf{q}}_{b}$$

(12)

Combining Eqs. (4), (7) and (12) yields

$${\mathbf{q}}_{b} = {(}{\mathbf{I}} + {\mathbf{G}}_{b} {)}{\mathbf{q,}}\quad {\mathbf{x}} = {\mathbf{Sq}}_{a} ={\mathbf{G}}_{s} {\mathbf{q}}$$

(13)

where

$${\mathbf{S}} = \left[ {{\mathbf{K}}_{s} + {\mathbf{K}}_{sT} {(}{\mathbf{x}}{)} + {\mathbf{K}}_{b} } \right]^{ - 1} {\mathbf{K}}_{b} ,\quad {\mathbf{G}}_{b} = - {\mathbf{S}} + {\mathbf{E}} - {\mathbf{SE}},\quad {\mathbf{G}}_{s} = {\mathbf{S}}({\mathbf{I}} + {\mathbf{E}})$$

(14)

Utilizing Eq. (13), the nodal displacement vector q_b of the member and the deformation vector x of the joints can be expressed with the displacement vector q. Afterwards, a new two-node condensed hybrid joint-beam element can be derived by using the condensation method in [27, 37], with the mass, stiffness, and damping matrices of

$${\mathbf{K}}_{HC} = {\mathbf{K}}_{b} + ({\mathbf{G}}_{b}^{{\text{T}}} {\mathbf{K}}_{b} + {\mathbf{K}}_{b} {\mathbf{G}}_{b} + {\mathbf{G}}_{b}^{{\text{T}}} {\mathbf{K}}_{b} {\mathbf{G}}_{b} {)} + {\mathbf{G}}_{s}^{{\text{T}}} {\mathbf{K}}_{s} {\mathbf{G}}_{s}$$

(15a)

$${\mathbf{K}}_{HCT} = {\mathbf{K}}_{b} + ({\mathbf{G}}_{b}^{{\text{T}}} {\mathbf{K}}_{b} + {\mathbf{K}}_{b} {\mathbf{G}}_{b} + {\mathbf{G}}_{b}^{{\text{T}}} {\mathbf{K}}_{b} {\mathbf{G}}_{b} {)} + {\mathbf{G}}_{s}^{{\text{T}}} \left[ {{\mathbf{K}}_{s} + {\mathbf{K}}_{sT} {(}{\mathbf{x}}{)}} \right]{\mathbf{G}}_{s}$$

(15b)

$${\mathbf{M}}_{HC} = {\mathbf{M}}_{b} + ({\mathbf{G}}_{b}^{{\text{T}}} {\mathbf{M}}_{b} + {\mathbf{M}}_{b} {\mathbf{G}}_{b} + {\mathbf{G}}_{b}^{{\text{T}}} {\mathbf{M}}_{b} {\mathbf{G}}_{b} {)}$$

(15c)

$${\mathbf{C}}_{HC} = {\mathbf{C}}_{b} + ({\mathbf{G}}_{b}^{{\text{T}}} {\mathbf{C}}_{b} + {\mathbf{C}}_{b} {\mathbf{G}}_{b} + {\mathbf{G}}_{b}^{{\text{T}}} {\mathbf{C}}_{b} {\mathbf{G}}_{b} {)} + {\mathbf{G}}_{s}^{{\text{T}}} {\mathbf{C}}_{s} {\mathbf{G}}_{s}$$

(15d)

where ${\mathbf{K}}_{HC}$ is the linear stiffness matrix of the condensed hybrid joint-beam element, ${\mathbf{K}}_{HCT}$ is the tangent stiffness matrix of the condensed hybrid joint-beam element including both linear and nonlinear stiffnesses of the joints.

The equation of the motion of the condensed hybrid joint-beam element is

$${\mathbf{M}}_{HC} {\ddot{{\mathbf{u}}}}_{HC} + {\mathbf{C}}_{HC} {\dot{\mathbf{u}}}_{HC} + {\mathbf{K}}_{HC} {\mathbf{u}}_{HC} + {\mathbf{f}}_{NLHC} ({\mathbf{u}}_{HC} ,{\dot{\mathbf{u}}}_{HC} ) = {\mathbf{F}}_{HC}$$

(16)

where

$${\mathbf{u}}_{HC} = \left\{ {{\mathbf{u}}_{i}^{{\text{T}}} ,{\mathbf{u}}_{j}^{{\text{T}}} } \right\}^{{\text{T}}} ,\quad {\mathbf{f}}_{NLHC} = \left\{ { - \, {\mathbf{f}}_{s1}^{{\text{T}}} ,{\mathbf{f}}_{s2}^{{\text{T}}} } \right\}^{{\text{T}}} ,\quad {\mathbf{F}}_{HC} = \left\{ {{\mathbf{F}}_{i}^{{\text{T}}} ,{\mathbf{F}}_{j}^{{\text{T}}} } \right\}^{{\text{T}}}$$

(17)

Utilizing the above condensed hybrid joint-beam element, the condensed model of the repeating element can be assembled, as shown in Fig. 3, with the mass matrix ${\mathbf{M}}_{BC}$, the damping matrix ${\mathbf{C}}_{BC}$, the linear stiffness matrix ${\mathbf{K}}_{BC}$, and the nonlinear restoring force vector ${\mathbf{f}}_{NLBC}$. The tangent stiffness matrix ${\mathbf{K}}_{BCT}$ of the condensed repeating element can be obtained by assembling the tangent stiffness matrix ${\mathbf{K}}_{HCT}$ of the condensed hybrid joint-beam element.

Fig. 3

Condensed model of the repeating element of the truss structure

The displacement vector of the condensed repeating element is

$${\mathbf{u}}_{BC} = \left\{ {{\mathbf{u}}_{C1}^{{\text{T}}} ,{\mathbf{u}}_{C2}^{{\text{T}}} ,{\mathbf{u}}_{C3}^{{\text{T}}} ,{\mathbf{u}}_{C4}^{{\text{T}}} ,{\mathbf{u}}_{C5}^{{\text{T}}} ,{\mathbf{u}}_{C6}^{{\text{T}}} ,{\mathbf{u}}_{C7}^{{\text{T}}} ,{\mathbf{u}}_{C8}^{{\text{T}}} } \right\}^{{\text{T}}}$$

(18)

where

$${\mathbf{u}}_{Ck} = \left\{ {u_{Cxk} ,u_{Cyk} ,u_{Czk} ,\theta_{Cxk} ,\theta_{Cyk} ,\theta_{Czk} } \right\}^{{\text{T}}} , \, (k = 1,2, \ldots ,8)$$

(19)

2.2 Equivalent continuum modeling of the truss structure

Considering the geometrical feature of the truss structure in Fig. 1, it can be equivalently modelled as a thin-walled box beam. So, the displacement functions of an arbitrary point on the cross section of the truss structure can be written using the deformation assumption of the thin-walled box beam [35, 39]. Making a Taylor series expansion for the displacement functions, the nodal displacement vector of the condensed repeating element can be expressed with the displacement and strain components at the center of the repeating element [35]

$${\mathbf{u}}_{BC} \approx {\mathbf{T}}_{BC} {\mathbf{s}}_{0}$$

(20)

where

$$\begin{aligned} {\mathbf{s}}_{0} & = \left\{ {u_{x0} ,u_{y0} ,u_{z0} ,\phi_{x0} ,\phi_{y0} ,\phi_{z0} ,\varepsilon_{x0} ,\gamma_{xy0} ,\gamma_{xz0} ,\kappa_{x0} ,\kappa_{y0} ,\kappa_{z0} ,} \right.\varpi_{x0} ,\partial_{x} \varpi_{x0} ,\gamma_{yz0} ,\partial_{x} \gamma_{yz0} , \\ & \quad \left. {\varepsilon_{y0} ,\varepsilon_{z0} ,\varpi_{y0} ,\varpi_{z0} } \right\}^{{\text{T}}} \\ \end{aligned}$$

(21)

in which $u_{x0}$, $u_{y0}$, $u_{z0}$, $\phi_{x0}$, $\phi_{y0}$ and $\phi_{z0}$ are the displacements and rotations of the cross section at the center of the repeating element, $\varepsilon_{x0}$, $\varepsilon_{y0}$, $\varepsilon_{z0}$, $\gamma_{xy0}$, $\gamma_{xz0}$ and $\gamma_{yz0}$ are the extensional strain and shear strains at the center of the repeating element, $\varpi_{x0}$ is the warping of the cross section, $\varpi_{y0}$ and $\varpi_{z0}$ denote the in-plane bending of the cross section, $\partial_{x} ( \cdot ) = {{\partial ( \cdot )} \mathord{\left/ {\vphantom {{\partial ( \cdot )} {\partial x}}} \right. \kern-0pt} {\partial x}}$, T_BC is a 48 × 20 transformation matrix.

As a result, the kinetic energy, strain energy and Rayleigh dissipation function of the repeating element can be evaluated as

$$T_{BC} = \frac{1}{2}{\dot{\mathbf{u}}}_{BC}^{{\text{T}}} {\mathbf{M}}_{BC} {\dot{\mathbf{u}}}_{BC} = \frac{1}{2}{\dot{\mathbf{s}}}_{0}^{{\text{T}}} {\mathbf{M}}_{0} {\dot{\mathbf{s}}}_{0}$$

(22a)

$$U_{BCL} = \frac{1}{2}{\mathbf{u}}_{BC}^{{\text{T}}} {\mathbf{K}}_{BC} {\mathbf{u}}_{BC} = \frac{1}{2}{\mathbf{s}}_{0}^{{\text{T}}} {\mathbf{K}}_{0} {\mathbf{s}}_{0}$$

(22b)

$$U_{BC} \approx \frac{1}{2}{\mathbf{u}}_{BC}^{{\text{T}}} {\mathbf{K}}_{BCT} {\mathbf{u}}_{BC} = \frac{1}{2}{\mathbf{s}}_{0}^{{\text{T}}} {\mathbf{K}}_{0T} {\mathbf{s}}_{0}$$

(22c)

$$R_{BC} = \frac{1}{2}{\dot{\mathbf{u}}}_{BC}^{{\text{T}}} {\mathbf{C}}_{BC} {\dot{\mathbf{u}}}_{BC} = \frac{1}{2}{\dot{\mathbf{s}}}_{0}^{{\text{T}}} {\mathbf{C}}_{0} {\dot{\mathbf{s}}}_{0}$$

(22d)

where

$${\mathbf{M}}_{0} = {\mathbf{T}}_{BC}^{{\text{T}}} {\mathbf{M}}_{BC} {\mathbf{T}}_{BC} ,\quad {\mathbf{K}}_{0} = {\mathbf{T}}_{BC}^{{\text{T}}} {\mathbf{K}}_{BC} {\mathbf{T}}_{BC}$$

(23a)

$${\mathbf{K}}_{0T} = {\mathbf{T}}_{BC}^{{\text{T}}} {\mathbf{K}}_{BCT} {\mathbf{T}}_{BC} ,\quad {\mathbf{C}}_{0} = {\mathbf{T}}_{BC}^{{\text{T}}} {\mathbf{C}}_{BC} {\mathbf{T}}_{BC}$$

(23b)

$U_{BCL}$ and $U_{BC}$ are the strain energies of the linear part and the whole of the repeating element, respectively.

Since the classical beam theory does not consider the in-plane extension and bending of the cross section, so the strain components $\varepsilon_{y0}$, $\varepsilon_{z0}$, $\varpi_{y0}$ and $\varpi_{z0}$ in s₀ should be eliminated to obtain an equivalent beam model. The static condensation method [40, 41] can be used for this purpose, after condensation, Eq. (22) becomes

$$T_{BC} \approx \frac{1}{2}{\dot{\mathbf{s}}}_{1}^{{\text{T}}} {\mathbf{M}}_{1} {\dot{\mathbf{s}}}_{1} ,\quad U_{BCL} \approx \frac{1}{2}{\mathbf{s}}_{1}^{{\text{T}}} {\mathbf{K}}_{1} {\mathbf{s}}_{1} ,\quad U_{BC} \approx \frac{1}{2}{\mathbf{s}}_{1}^{{\text{T}}} {\mathbf{K}}_{1T} {\mathbf{s}}_{1} ,\quad R_{BC} \approx \frac{1}{2}{\dot{\mathbf{s}}}_{1}^{{\text{T}}} {\mathbf{C}}_{1} {\dot{\mathbf{s}}}_{1}$$

(24)

where M₁, K₁, K_1T and C₁ are the condensed matrices of M₀, K₀, K_0T and C₀, respectively, s₁ is the vector contains the first 16 variables in s₀.

Considering the generalized warping displacement (ϖ_x0) and the generalized distortional displacement (γ_yz0) of the cross section of the truss structure, an equivalent 8-DOFs spatial beam element is proposed for the repeating element, whose nodal displacement vector is

$${\mathbf{u}}_{BE} = \left\{ {{\mathbf{u}}_{E1}^{{\text{T}}} ,{\mathbf{u}}_{E2}^{{\text{T}}} } \right\}^{{\text{T}}}$$

(25)

where

$${\mathbf{u}}_{Ei} = \left\{ {u_{Exi} {,}u_{Eyi} {,}u_{Ezi} {,}\phi_{Exi} {,}\phi_{Eyi} {,}\phi_{Ezi} {,}\varpi_{Exi} {,}\gamma_{Eyzi} } \right\}^{{\text{T}}} , \, (i = 1,2)$$

(26)

Using the Taylor series expansion method, the nodal displacement vector of the equivalent beam element can also be expressed with the vector s₁ as [35]

$${\mathbf{u}}_{BE} \approx {\mathbf{T}}_{BE} {\mathbf{s}}_{1}$$

(27)

where T_BE is a 16 × 16 transformation matrix.

Then, the kinetic energy, strain energy and Rayleigh dissipation function of the equivalent beam element can be evaluated as

$$T_{BE} = \frac{1}{2}{\dot{\mathbf{u}}}_{BE}^{{\text{T}}} {\mathbf{M}}_{BE} {\dot{\mathbf{u}}}_{BE} = \frac{1}{2}{\dot{\mathbf{s}}}_{1}^{{\text{T}}} {\mathbf{T}}_{BE}^{{\text{T}}} {\mathbf{M}}_{BE} {\mathbf{T}}_{BE} {\dot{\mathbf{s}}}_{1}$$

(28a)

$$U_{BEL} = \frac{1}{2}{\mathbf{u}}_{BE}^{{\text{T}}} {\mathbf{K}}_{BE} {\mathbf{u}}_{BE} = \frac{1}{2}{\mathbf{s}}_{1}^{{\text{T}}} {\mathbf{T}}_{BE}^{{\text{T}}} {\mathbf{K}}_{BE} {\mathbf{T}}_{BE} {\mathbf{s}}_{1}$$

(28b)

$$U_{BE} \approx \frac{1}{2}{\mathbf{u}}_{BE}^{{\text{T}}} {\mathbf{K}}_{BET} {\mathbf{u}}_{BE} = \frac{1}{2}{\mathbf{s}}_{1}^{{\text{T}}} {\mathbf{T}}_{BE}^{{\text{T}}} {\mathbf{K}}_{BET} {\mathbf{T}}_{BE} {\mathbf{s}}_{1}$$

(28c)

$$R_{BE} = \frac{1}{2}{\dot{\mathbf{u}}}_{BE}^{{\text{T}}} {\mathbf{C}}_{BE} {\dot{\mathbf{u}}}_{BE} = \frac{1}{2}{\dot{\mathbf{s}}}_{1}^{{\text{T}}} {\mathbf{T}}_{BE}^{{\text{T}}} {\mathbf{C}}_{BE} {\mathbf{T}}_{BE} {\dot{\mathbf{s}}}_{1}$$

(28d)

where ${\mathbf{M}}_{BE}$, ${\mathbf{C}}_{BE}$, ${\mathbf{K}}_{BE}$ and ${\varvec{K}}_{BET}$ are the mass, damping, linear stiffness and tangent stiffness matrices of the equivalent beam element, respectively.

According to the energy equivalence between the repeating element and the equivalent beam element, it can be obtained that

$${\mathbf{M}}_{BE} = ({\mathbf{T}}_{BE}^{{\text{T}}} )^{ - 1} {\mathbf{M}}_{1} {\mathbf{T}}_{BE}^{ - 1}$$

(29a)

$${\mathbf{K}}_{BE} = ({\mathbf{T}}_{BE}^{{\text{T}}} )^{ - 1} {\mathbf{K}}_{1} {\mathbf{T}}_{BE}^{ - 1}$$

(29b)

$${\mathbf{K}}_{BET} = ({\mathbf{T}}_{BE}^{{\text{T}}} )^{ - 1} {\mathbf{K}}_{1T} {\mathbf{T}}_{BE}^{ - 1}$$

(29c)

$${\mathbf{C}}_{BE} = ({\mathbf{T}}_{BE}^{{\text{T}}} )^{ - 1} {\mathbf{C}}_{1} {\mathbf{T}}_{BE}^{ - 1}$$

(29d)

2.3 Equivalence of the external loads and the nonlinear restoring forces

Considering that the external loads are applied on the joints of the truss structures, the nodal load vector of the condensed repeating element will be transferred to the nodal load vector of the equivalent beam element here.

Taking the case that three concentrate loads F_x1, F_y1 and F_z1 acting on node 1 of the condensed repeating element as an example, as shown in Fig. 4.

Fig. 4

Equivalence of the external loads on the truss structure

The equivalent nodal loads on the equivalent beam element produced by the load F_x1 are

$$F_{Ex1} = F_{x1} ,\quad M_{Ey1} = F_{x1} z_{1} ,\quad M_{Ez1} = - F_{x1} y_{1} ,\quad B_{Ex1} = F_{x1} y_{1} z_{1}$$

(30)

the equivalent nodal loads produced by the loads F_y1 and F_z1 are

$$F_{Ey1} = F_{y1} ,\quad M_{Ex1} = - F_{y1} z_{1} ,\quad B_{Eyz1} = F_{y1} \frac{{z_{1} }}{2}$$

(31)

and

$$F_{Ez1} = F_{z1} ,\quad M_{Ex1} = F_{z1} y_{1} ,\quad B_{Eyz1} = F_{z1} \frac{{y_{1} }}{2}$$

(32)

where F_Ex1, F_Ey1 and F_Ez1 are the equivalent nodal forces, M_Ex1, M_Ey1 and M_Ez1 are the equivalent nodal moments, B_Ex1 and B_Eyz1 are the equivalent warping bimoment and distortional bimoment.

Denoting the external load vector of the condensed repeating element as

$${\mathbf{F}}_{BC} = \left\{ {{\mathbf{F}}_{C1}^{\text{T}} ,{\mathbf{F}}_{C2}^{\text{T}} ,{\mathbf{F}}_{C3}^{\text{T}} ,{\mathbf{F}}_{C4}^{\text{T}} ,{\mathbf{F}}_{C5}^{\text{T}} ,{\mathbf{F}}_{C6}^{\text{T}} ,{\mathbf{F}}_{C7}^{\text{T}} ,{\mathbf{F}}_{C8}^{\text{T}} } \right\}^{\text{T}}$$

(33)

where

$${\mathbf{F}}_{Ck} = \left\{ {F_{xk} ,F_{yk} ,F_{zk} ,0,0,0} \right\}^{{\text{T}}} , \, (k = 1,2, \ldots ,8)$$

(34)

According to Eqs. (30), (31) and (32), the external load vector of the equivalent beam element can be written as

$${\mathbf{F}}_{BE} = \left\{ {{\mathbf{F}}_{E1}^{{\text{T}}} ,{\mathbf{F}}_{E2}^{{\text{T}}} } \right\}^{\text{T}} = {\mathbf{T}}_{F} {\mathbf{F}}_{BC}$$

(35)

where

$${\mathbf{F}}_{Ei} = \left\{ {F_{Exi} ,F_{Eyi} ,F_{Ezi} ,M_{Exi} ,M_{Eyi} ,M_{Ezi} ,B_{Exi} ,B_{Eyzi} } \right\}^{\text{T}} {, }(i = 1,2)$$

(36)

$${\mathbf{T}}_{F} = \left[ {\begin{array}{*{20}l} {{\mathbf{T}}_{F1} } &\quad {{\mathbf{T}}_{F2} } &\quad {{\mathbf{T}}_{F3} } &\quad {{\mathbf{T}}_{F4} } &\quad {\mathbf{0}} &\quad {\mathbf{0}} &\quad {\mathbf{0}} &\quad {\mathbf{0}} \\ {\mathbf{0}} &\quad {\mathbf{0}} &\quad {\mathbf{0}} &\quad {\mathbf{0}} &\quad {{\mathbf{T}}_{F5} } &\quad {{\mathbf{T}}_{F6} } &\quad {{\mathbf{T}}_{F7} } &\quad {{\mathbf{T}}_{F8} } \\ \end{array} } \right]$$

(37)

$${\mathbf{T}}_{Fk} = \left[ {\begin{array}{*{20}c} 1 & \quad 0 & \quad 0 & \quad 0 & \quad 0 & \quad 0 \\ 0 & \quad 1 & \quad 0 & \quad 0 & \quad 0 & \quad 0 \\ 0 & \quad 0 & \quad 1 & \quad 0 & \quad 0 & \quad 0 \\ 0 & \quad { - z_{k} } & \quad {y_{k} } & \quad 0 & \quad 0 & \quad 0 \\ {z_{k} } & \quad 0 & \quad 0 & \quad 0 & \quad 0 & \quad 0 \\ { - y_{k} } & \quad 0 & \quad 0 & \quad 0 & \quad 0 & \quad 0 \\ {y_{k} z_{k} } & \quad 0 & \quad 0 & \quad 0 & \quad 0 & \quad 0 \\ 0 & \quad {{{z_{k} } \mathord{\left/ {\vphantom {{z_{k} } 2}} \right. \kern-0pt} 2}} & \quad {{{y_{k} } \mathord{\left/ {\vphantom {{y_{k} } 2}} \right. \kern-0pt} 2}} & \quad 0 & \quad 0 & \quad 0 \\ \end{array} } \right], \, (k = 1,2, \ldots 8)$$

(38)

Similar to the equivalence of the external loads, the nonlinear restoring force vector of the repeating element can be transfer to the nonlinear restoring force vector of the equivalent beam element

$${\mathbf{f}}_{NLBE} = {\mathbf{T}}_{F} {\mathbf{f}}_{NLBC}$$

(39)

At last, the equation of motion of the equivalent nonlinear beam model of the truss structure can be obtained as

$${\mathbf{M}}_{E} {\ddot{{\mathbf{u}}}}_{E} + {\mathbf{C}}_{E} {\dot{\mathbf{u}}}_{E} + {\mathbf{K}}_{E} {\mathbf{u}}_{E} + {\mathbf{f}}_{NLE} = {\mathbf{F}}_{E}$$

(40)

and the global tangent stiffness matrix K_ET of the equivalent beam model can be assembled by the tangent stiffness matrix K_BET of the equivalent beam element.

3 Solution of the equivalent nonlinear beam model

The equation of motion (40) of the equivalent beam model can be solved by the combination of the Newmark-β method and the Newton–Raphson iteration method [42]. Assuming the result at time t_i is known, in order to solve the result at time t_i+1, rewrite Eq. (40) in the quasi-static form

$${\hat{\mathbf{f}}}_{E(i + 1)} = {\mathbf{F}}_{{E}{(i + 1)}}$$

(41)

where

$${\hat{\mathbf{f}}}_{E(i + 1)} = {\mathbf{M}}_{E} {\ddot{{\mathbf{u}}}}_{E(i + 1)} + {\mathbf{C}}_{E} {\dot{\mathbf{u}}}_{E(i + 1)} + {\mathbf{K}}_{E} {\mathbf{u}}_{E(i + 1)} + {\mathbf{f}}_{NLE(i + 1)}$$

(42)

Using the Newton–Raphson iteration method to solve Eq. (41), in the (j + 1)th iteration step

$${\hat{\mathbf{f}}}_{E(i + 1)}^{(j + 1)} \approx {\hat{\mathbf{f}}}_{E(i + 1)}^{(j)} + \left( {\frac{{\partial {\hat{\mathbf{f}}}_{E} }}{{\partial {\mathbf{u}}_{E} }}} \right)_{(i + 1)}^{(j)} \Delta {\mathbf{u}}_{E(i + 1)}^{(j)} = {\mathbf{F}}_{E(i + 1)}$$

(43)

where

$$\left( {\frac{{\partial {\hat{\mathbf{f}}}_{E} }}{{\partial {\mathbf{u}}_{E} }}} \right)_{(i + 1)}^{(j)} = {\mathbf{M}}_{E} \left( {\frac{{\partial {\ddot{{\mathbf{u}}}}_{E} }}{{\partial {\mathbf{u}}_{E} }}} \right)_{(i + 1)}^{(j)} + {\mathbf{C}}_{E} \left( {\frac{{\partial {\dot{\mathbf{u}}}_{E} }}{{\partial {\mathbf{u}}_{E} }}} \right)_{(i + 1)}^{(j)} + {\mathbf{K}}_{E} + \left( {\frac{{\partial {\mathbf{f}}_{NLE} }}{{\partial {\mathbf{u}}_{E} }}} \right)_{(i + 1)}^{(j)}$$

(44)

$$\Delta {\mathbf{u}}_{E(i + 1)}^{(j)} = {\mathbf{u}}_{E(i + 1)}^{(j + 1)} - {\mathbf{u}}_{E(i + 1)}^{(j)}$$

(45)

Making use of the Newmark-β method

$$\left( {\frac{{\partial {\ddot{{\mathbf{u}}}}_{E} }}{{\partial {\mathbf{u}}_{E} }}} \right)_{(i + 1)}^{(j)} = \frac{1}{{\beta (\Delta t)^{2} }} \equiv c_{0} ,\quad \left( {\frac{{\partial {\dot{\mathbf{u}}}_{C} }}{{\partial {\mathbf{u}}_{C} }}} \right)_{(i + 1)}^{(j)} = \frac{\gamma }{\beta \Delta t} \equiv c_{1}$$

(46)

where β and γ are parameters of the Newmark-β method, $\Delta t$ is the time step. Then, Eq. (44) can be rewritten as

$$\left( {\frac{{\partial {\hat{\mathbf{f}}}_{E} }}{{\partial {\mathbf{u}}_{E} }}} \right)_{(i + 1)}^{(j)} = {\mathbf{K}}_{ET(i + 1)}^{(j)} + c_{0} {\mathbf{M}}_{E} + c_{1} {\mathbf{C}}_{E} + {\mathbf{K}}_{E} \equiv {\hat{\mathbf{K}}}_{ET(i + 1)}^{(j)}$$

(47)

where ${\mathbf{K}}_{ET(i + 1)}^{(j)} = \left( {\frac{{\partial {\mathbf{f}}_{NLE} }}{{\partial {\mathbf{u}}_{E} }}} \right)_{(i + 1)}^{(j)}$ is the global tangent stiffness matrix of the equivalent beam model in the jth iteration step at time t_i.

Substituting Eq. (47) into (43) yields

$${\hat{\mathbf{K}}}_{ET(i + 1)}^{(j)} \Delta {\mathbf{u}}_{E(i + 1)}^{(j)} = {\mathbf{F}}_{E(i + 1)} - {\hat{\mathbf{f}}}_{E(i + 1)}^{(j)} \equiv {\hat{\mathbf{R}}}_{(i + 1)}^{(j)}$$

(48)

where ${\hat{\mathbf{R}}}_{(i + 1)}^{(j)}$ is the residual force vector. Substituting Eq. (42) into (48) yields

$${\hat{\mathbf{R}}}_{(i + 1)}^{(j)} = {\mathbf{F}}_{E(i + 1)} - {\mathbf{f}}_{NLE(i + 1)}^{(j)} - {\mathbf{M}}_{E} {\ddot{{\mathbf{u}}}}_{E(i + 1)}^{(j)} - {\mathbf{C}}_{E} {\dot{\mathbf{u}}}_{E(i + 1)}^{(j)} - {\mathbf{K}}_{E} {\mathbf{u}}_{E(i + 1)}^{(j)}$$

(49)

According to the Newmark-β method

$${\ddot{{\mathbf{u}}}}_{E(i + 1)}^{(j)} = c_{0} \left( {{\mathbf{u}}_{E(i + 1)}^{(j)} - {\mathbf{u}}_{E(i)} } \right) - c_{2} {\dot{\mathbf{u}}}_{E(i)} - c_{3} {\ddot{{\mathbf{u}}}}_{E(i)}$$

(50)

$${\dot{\mathbf{u}}}_{E(i + 1)}^{(j)} = c_{1} \left( {{\mathbf{u}}_{E(i + 1)}^{(j)} - {\mathbf{u}}_{E(i)} } \right) - c_{4} {\dot{\mathbf{u}}}_{E(i)} - c_{5} {\ddot{{\mathbf{u}}}}_{E(i)}$$

(51)

where

$$c_{2} = \frac{1}{\beta \Delta t},\quad c_{3} = \frac{1}{2\beta } - 1,\quad c_{4} = \frac{\gamma }{\beta } - 1,\quad c_{5} = \left( {\frac{\gamma }{2\beta } - 1} \right)\Delta t$$

(52)

Substituting Eqs. (50) and (51) into (49) yields

$${\hat{\mathbf{R}}}_{(i + 1)}^{(j)} = {\hat{\mathbf{F}}}_{E(i + 1)} - {\mathbf{f}}_{NLE(i + 1)}^{(j)} - \left( {c_{0} {\mathbf{M}}_{E} + c_{1} {\mathbf{C}}_{E} } \right){\mathbf{u}}_{E(i + 1)}^{(j)}$$

(53)

where

$${\hat{\mathbf{F}}}_{E(i + 1)} ={\mathbf{F}}_{E(i + 1)} + {\mathbf{M}}_{E} (c_{0} {\mathbf{u}}_{E(i)} + c_{2} {\dot{\mathbf{u}}}_{E(i)} + c_{3} {\ddot{{\mathbf{u}}}}_{E(i)} ) + {\mathbf{C}}_{E} (c_{1} {\mathbf{u}}_{E(i)} + c_{4} {\dot{\mathbf{u}}}_{E(i)} + c_{5} {\ddot{{\mathbf{u}}}}_{E(i)} )$$

(54)

From Eq. (48), it can be solve that

$$\Delta {\mathbf{u}}_{E(i + 1)}^{(j)} ={(}{\hat{\mathbf{K}}}_{ET(i + 1)}^{(j)} {)}^{ - 1} {\hat{\mathbf{R}}}_{i + 1}^{(j)}$$

(55)

At last, the solution of the j + 1 iteration step can be obtained as

$${\mathbf{u}}_{E(i + 1)}^{(j + 1)} = {\mathbf{u}}_{E(i + 1)}^{(j)} + \Delta {\mathbf{u}}_{E(i + 1)}^{(j)}$$

(56)

After each iteration the solution is checked and the iterative process is terminated when the convergency criteria is satisfied. The convergency criteria can be chosen as

$$\frac{{\left| {\Delta {\mathbf{u}}_{E(i + 1)}^{(j)} } \right|}}{{\left| {{\mathbf{u}}_{E(i + 1)}^{(j + 1)} - {\mathbf{u}}_{E(i)} } \right|}} \le \varepsilon$$

(57)

where ε is a specified tolerance.

The flowchart of the above solving process of the equivalent beam model is shown in Fig. 5.

Fig. 5

Flowchart of the solution process of the nonlinear equivalent beam model

In each iteration step the nonlinear restoring force and the tangent stiffness of each nonlinear joint need to be updated, which can be evaluated by the following procedures: Firstly, evaluate the displacement vector of the condensed repeating element from the displacement vector of the equivalent beam element,

$${\mathbf{u}}_{BC} = {\mathbf{T}}_{BC1} {\mathbf{T}}_{BE}^{ - 1} {\mathbf{u}}_{BE}$$

(58)

where T_BC1 is a 48 × 16 matrix that obtained by dropping the last 4 columns of matrix T_BC. Then, extract the nodal displacement vector q of each condensed hybrid joint-beam element from the displacement vector u_BC of the condensed repeating element, and evaluate the deformation vector x of the two joints in the condensed hybrid joint-beam element using Eq. (13). At last, the nonlinear restoring force and the tangent stiffness of the nonlinear joint can be obtained.

4 Numerical examples

4.1 Example 1: A cantilevered truss structure

A cantilevered truss structure as shown in Fig. 6a is firstly used as a numerical example to verify the presented modeling method. This truss structure consists of 20 repeating elements, the size of the repeating element is L_l = L_v = L_b = 1.5 m. The truss members are made of carbon fiber tubes with the outer diameter d_o = 40 mm and the inner diameter d_i = 34 mm. The material properties of the carbon fiber cube are: Young’s modulus E = 205 GPa, density ρ = 1720 kg/m³, and Poison ratio ν = 0.3. Considering the vertical and transverse members are rigid connected, and the longitudinal and diagonal members are connected with them by nonlinear joints. The eccentricities of the joints connected with the longitudinal and the diagonal members are $e_{1}^{l} = e_{2}^{l} = 20\;{\text{mm}}$ and $e_{1}^{d} = e_{2}^{d} = 30\;{\text{mm}}$, respectively. The linear stiffness and damping coefficients of the joints are listed in Table 1.

Fig. 6

The cantilevered truss structure and its equivalent model

Table 1 Linear stiffness and damping coefficients of the joint in six directions

Furthermore, considering the joint has additional piece-wise linear stiffness in axial direction, as shown Fig. 7, the restoring force of this nonlinearity can be written as

$$f_{NL} (x) = k_{1} x + k_{1} (\alpha - 1)(|x| - x_{y} ){\text{sign}}(x)\frac{{{\text{sign}}(|x| - x_{y} ) + 1}}{2}$$

(59)

where k₁ is the initial stiffness coefficient, α is the stiffness ratio between the branches, α > 1 represents the stiffness-hardening nonlinearity and α < 1 represents the stiffness-hardening nonlinearity, x is the deformation of the joint, x_y is the critical deformation for which a change of stiffness occurs, ${\text{sign}}( \cdot )$ is the signum function. In this example, the parameters of the nonlinear model are set as k₁ = 5 × 10⁶ N/m, x_y = 10 μm, and different values of α from 0.4 to 4 are used for consideration of the joints with stiffness-hardening or stiffness-softening nonlinearity.

Fig. 7

Piece-wise linear stiffness model

The equivalent beam model of the cantilever truss structure is shown in Fig. 6b, which consists of 20 equivalent beam elements and 21 nodes. In order to verify the accuracy of the equivalent beam model, the commercial FEM software ANSYS is used to established a full finite element model for the original truss structure, in which, the truss member is modeled by spatial beam element (Beam4 element), the joint is modelled by spring elements (Combin14 element for linear stiffness and damping and Combin39 element for nonlinear stiffness) and rigid constraint element (MPC184 element). The full finite element model of the truss structure consists of 2804 elements.

At first, a sweep-sine excitation is used to excite the first resonance mode of the structure, the excitation is applied at node A at the free end of the truss in the Z-axis direction with the magnitude of

$$F_{Z} = F_{Z0} \sin \left( {\omega_{l} t + \frac{{\omega_{u} - \omega_{l} }}{2T}t^{2} } \right)$$

(60)

where $F_{Z0}$ is the excitation amplitude, $\omega_{l}$ and $\omega_{u}$ are the lower and upper limits of the excitation frequency, T is the duration of the excitation. The equivalent loads on node 21 of the equivalent beam model are

$$F_{EZ} = F_{Z} ,\quad M_{EX} = - \frac{{F_{Z} L_{b} }}{2},\quad B_{EYZ} = - \frac{{F_{Z} L_{b} }}{4}$$

(61)

The displacements in the Z-axis direction of node A evaluated by the equivalent beam model and the ANSYS FEM model under the sweep-sine excitation with F_Z0 = 50 N and T = 500 s are compared in Fig. 8. It can be found that for the truss structure with stiffness-softening nonlinear joints (α = 0.2 and 0.4) the results of the two models are almost the same, for the truss structure with stiffness-hardening nonlinear joint (α = 1.6 and 4.0), the resonant frequency obtained by the equivalent beam model is a little bigger than that of the ANSYS model, but the error doesn’t increase with the increasement of the stiffness ratio α. This error maybe caused by the approximation used in the derivation of the condensed hybrid joint-beam element, which uses the static equilibrium relationship [Eq. (12)] instead of the real dynamic equilibrium relationship [Eq. (8)]. This phenomenon is also observed in the Guyan reduction method, which is also a static reduction method, the natural frequencies obtained by the Guyan reduced model are also a little bigger than those of the original structures [43]. From Fig. 8, it also can be found that the resonant frequency of the truss structure increases with the increasement of the stiffness ratio α, the equivalent beam model can also accurately predict the resonant frequency for the for the truss structure.

Fig. 8

Displacement response of the cantilevered truss model under the sweep-sine excitation

Next, a triangular impulse load as shown in Fig. 9 is applied at node A in the Z-axis direction to excite multiple modes of vibration of the truss structure. The peak value and duration of the excitation are F_Z0 = 1000 N and T = 0.1 s, respectively. The displacements of node A in the Z-axis direction evaluated by the equivalent beam model and the ANSYS model for this excitation are shown in Fig. 10. It can be found that joint nonlinearity has an obvious influence on the displacement response of the truss structure, and the equivalent beam model predicts the response accurately for truss structure with both stiffness-softening nonlinear joints and stiffness-hardening nonlinear joints under the impulse load.

Fig. 9

Triangular impulse excitation

Fig. 10

Displacement response of the cantilevered truss model under the triangular impulse excitation

It is worth to remark that the proposed method requires only 20 elements for modeling this truss structure instead of 2804 elements in the original FEM model, which brings a very high promotion on the computational efficiency.

4.2 Example 2: a spacecraft structure

The second example is a spacecraft structure as shown in Fig. 11a, which consists of a satellite, a payload and a supported truss structure. The truss structure is assumed the same as in the first example, one end of the truss is attached to the satellite, and the other end is connected with the payload. For simplicity, the satellite and the payload are all assumed to be a cube with side length of 1.5 m, the equivalent densities of the satellite and the payload are assumed as ρ₁ = 50 kg/m³ and ρ₂ = 10 kg/m³, respectively. The mass centers of the satellite and the payload are all assumed on the central axis of the truss structure.

Fig. 11

The spacecraft structure and its equivalent dynamic model

The equivalent dynamic model of the spacecraft is shown in Fig. 11b, where the satellite and the payload are modelled as mass elements on the end nodes of the equivalent beam model of the truss structure. Since the mass elements are not on the mass centers of the satellite and the payload, the effect of eccentricity should be considered, which yields the mass matrices of the satellite and the payload as

$${\mathbf{M}}_{1} = \left[ {\begin{array}{*{20}c} {m_{1} } & \quad 0 &\quad 0 &\quad 0 &\quad 0 &\quad 0 \\ 0 &\quad {m_{1} } &\quad 0 &\quad 0 &\quad 0 &\quad { - m_{1} e_{m1} } \\ 0 &\quad 0 &\quad {m_{1} } &\quad 0 &\quad {m_{1} e_{m1} } &\quad 0 \\ 0 &\quad 0 &\quad 0 &\quad {I_{x1} } &\quad 0 &\quad 0 \\ 0 &\quad 0 &\quad {m_{1} e_{m1} } &\quad 0 &\quad {I_{y1} } &\quad 0 \\ 0 &\quad { - m_{1} e_{m1} } &\quad 0 &\quad 0 &\quad 0 &\quad {I_{z1} } \\ \end{array} } \right]$$

(62)

and

$${\mathbf{M}}_{2} = \left[ {\begin{array}{*{20}c} {m_{2} } & \quad 0 & \quad 0 & \quad 0 & \quad 0 & \quad 0 \\ 0 & \quad {m_{2} } & \quad 0 & \quad 0 & \quad 0 & \quad {m_{2} e_{m2} } \\ 0 & \quad 0 & \quad {m_{2} } & \quad 0 & \quad { - m_{2} e_{m2} } & \quad 0 \\ 0 & \quad 0 & \quad 0 & \quad {I_{x2} } & \quad 0 & \quad 0 \\ 0 & \quad 0 & \quad { - m_{2} e_{m2} } & \quad 0 & \quad {I_{y2} } & \quad 0 \\ 0 & \quad {m_{2} e_{m2} } & \quad 0 & \quad 0 & \quad 0 & \quad {I_{z2} } \\ \end{array} } \right]$$

(63)

where m₁ and m₂ are the masses of the satellite and the payload, respectively, e_m1 and e_m2 are the distances from the truss ends to the mass centers of the satellite and the payload, respectively,

$$I_{xi} = \frac{1}{6}m_{i} a_{i}^{2} ,\quad I_{yi} = \frac{5}{12}m_{i} a_{i}^{2} ,\quad I_{zi} = \frac{5}{12}m_{i} a_{i}^{2} ,\quad (i = 1,2)$$

(64)

a₁ and a₂ are the side lengths of the satellite and the payload, respectively.

A triangular impulse moment M_Z is applied on the satellite for simulating the attitude maneuvering of the spacecraft. The peak value and duration of the impulse moment are M_Z0 = 5000 N m and T = 0.1 s, respectively. The displacement and acceleration in the Y-axis direction of node A on the truss structure evaluated by the ANSYS model and the equivalent dynamic model are shown in Figs. 12 and 13, respectively. It can be found that the presented ECM method can also produce accurate transient dynamic response when used in modeling of the spacecraft structure with repetitive truss structure.

Fig. 12

Displacement response of the spacecraft model under the triangular impulse excitation

Fig. 13

Acceleration response of the spacecraft model under the triangular impulse excitation

5 Conclusions

In this study, an equivalent continuum modeling method for analysis of the transient response of the large space truss structures with nonlinear elastic joints was presented. A two-node condensed hybrid joint-beam element model for a truss member with nonlinear joints at its two ends was obtained, and an equivalent 8-DOFs nonlinear beam element was derived for the repeating element of the truss structure with rectangular cross-sections based on the energy equivalence method. The equation of motion of the nonlinear equivalent beam model of the whole truss structure was solved by the combination of the Newmark-β method and the Newton–Raphson iteration method. The numerical example of a cantilevered truss structure with joints having piece-wise linear extensional stiffnesses under sweep-sine excitation and impulse excitation demonstrated that the presented modeling method could accurately predict the transient response of the truss structure with a very high computational efficiency. The applicability of the presented equivalent modeling method on spacecraft with repetitive truss structure was also validated.