1 Introduction

Truss structures are ideal structural foundations for large spacecrafts, such as the deployable trusses used in solar panels, space antennas and telescopes [1,2,3], the on-orbit assembled trusses used in space station [4]. Unlike the truss structures used in civil engineering, which are connected by the welded or bolted joints, the large space truss structures (LSTS) are usually connected by deployable joints or erectable joints. Because of the inevitable clearances in these joints, they exhibit more significant nonlinear mechanical properties [5, 6]. Accurate modeling and analyzing the nonlinear characteristics of LSTS considering joint nonlinearity is very important to the design and vibration control of these structures [7, 8].

The modeling and analysis methods of nonlinear dynamics of large structures can be divided into two categories: the time domain methods and the frequency domain methods. The time domain methods mainly use the nonlinear finite element method to establish the model, and then solve the dynamic responses by time integration methods [9,10,11]. The frequency domain methods mainly use the harmonic balance method (HBM) or the describing function method in the modeling, and then solve the nonlinear algebraic equation systems (NAES) to obtain the frequency responses of the structures [12,13,14,15,16]. Due to the large number of flexible members and nonlinear joint connections in LSTS, the dimensions of the nonlinear dynamic model of these structures are usually very high, which makes the nonlinear dynamic analysis extremely difficult. Therefore, it is very necessary to establish reduced order nonlinear dynamics models for LSTS. In the past decades, by using the periodicity of LSTS, the equivalent continuum modeling (ECM) method has been widely used to establish analytic PDE models or low-dimensional discrete models for LSTS [14,15,16,17,18,19,20,21,22,23,24]. In the early studies, the space truss structures were modelled as ideal pin-jointed or rigid-jointed in order to obtain the equivalent continuum models [17,18,19], which ignore the actual mechanical characteristics of the joints. Recently, researchers began to consider the stiffness and damping properties of the joints in the equivalent continuum modeling methods. For examples, Salehian and Inman [20] presented an ECM method of beam-like truss structures with linear torsional joints by using the micropolar continuum theory. Webster [8] presented an ECM method for truss structures with axial nonlinear joints by considering the fundamental harmonic response and using the describing function method. Liu et al. [21,22,23] presented an ECM method for truss structures with nonlinear joints having six degree-of-freedoms characteristics based on the energy equivalence method and analyzed the fundamental harmonic response of spatial truss structure with hysteretic joints. Li et al. [24] presented a multi-harmonic ECM method for planar truss structures with polynomial-type nonlinear joints based on the displacement equivalence method. Although the modeling method of LSTS has achieved a great progress, a comprehensive reduced-order modeling method which can consider the complex nonlinear characteristics of the joints and fits any form of LSTS is needed.

Another crucial issue in nonlinear dynamic analysis of LSTS is the solution method of the high-dimensional nonlinear dynamic models. In the frequency domain, the models are large-scale NAES. Although the traditional iterative method such as the Newton–Raphson method can be used for solving NAES, it will fail at turning points and branch points because the Jacobian matrix is singular at such points [25]. Alternatively, the arc-length continuation method is a powerful technique for solving NAES which can pass through the singularity points and trace the entire solution path. The arc-length method originally presented by Riks has been developed and improved for decades, and various forms of ‘arc-length-type method’ have been proposed, such as the pseudo arc-length method [26, 27], the adaptive arc-length method [28], and the curvature-controlled arc-length method [29], etc. Nowadays, these methods have been widely used in nonlinear static finite element analysis (FEA) of structures [30,31,32]. However, compared with the mature application in static structural analysis, the application of the arc-length method in nonlinear vibration or frequency response analysis of structures is still under development, and in most cases the researchers need to develop their own algorithms and programs [33,34,35,36,37,38,39,40,41,42,43]. Lewandowski [33] used the Newton-type algorithm with arc-length procedure to solve the nonlinear steady-state response of structures with geometrically nonlinearity. Groll and Ewins [34] applied the arc-length continuation method on analysis of the rotor/stator interaction dynamic problem which was modelled as a two degree-of-freedoms (DOFs) model with contact and gap nonlinearity. Ferreira and Serpa [35] wrote a special paper to introduce and discuss the application of the arc-length method in nonlinear frequency response analysis, and employed the arc-length method on three DOFs systems with cubic stiffness nonlinearity and gap nonlinearity. Li et al. [24] used the arc-length method to solve the frequency response of a planar repetitive truss structure with polynomial-type nonlinear joints. Comparing the arc-length methods used in the previous studies, it is found that the methods they used have some differences in the procedures, such as the definitions of the constraint equation [35, 43], the ways of evaluating the predict solution and determining the tracking direction [36,37,38], which means that the algorithm suitable for one certain problem may encounter difficulties in other problems. In addition, the solution tracking of high-dimensional nonlinear systems, such as the LSTS, using the arc-length method is rather more difficult than that of low-dimensional nonlinear systems [39]. Thus, a suitable arc-length continuation algorithm is in demand for the nonlinear frequency response analysis of LSTS.

This paper presents a comprehensive reduced-order modeling and solution method for multi-harmonic frequency response analysis of large space truss structures with nonlinear joints, which considers six DOFs mechanical characteristics of the joints and is suitable for any form of truss structures. In Sect. 2, the reduced-order modeling method for the space truss structures with nonlinear joints are introduced. In Sect. 3, a detailed procedure of the arc-length continuation method for solving the reduced frequency-domain model of the LSTS are elaborated. In Sect. 4, two numerical examples including a planar truss structure with nonlinear rotational stiffness joints and a spatial truss structure with nonlinear axial stiffness joints are given to verity the correctness of the presented method and show the influence of joint nonlinearity on the frequency response of the truss structures. In Sect. 5, the conclusions are given.

2 Reduced-order modeling method of the large space truss structures

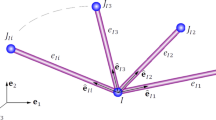
Taking the planar truss structure shown in Fig. 1 as an example, the truss members are connected by mechanical joints such as the deployable joints and erectable joints. Nonlinear stiffness and damping are usually existed in these joints since there are contacts and deformations between the joint parts. Different types of joints exhibit different nonlinear behaviors, which can be described approximately by different nonlinear models, such as the clearance model [44, 45], the cubic stiffness model [14, 46, 47], the piecewise linear stiffness model [8, 23], and the hysteresis model [13, 22], etc. In order to incorporate the stiffness and damping of the joints in the dynamic model of the truss structure, the connection between the truss member and the joint is modelled by a spring-damper system which has stiffness and damping properties in six directions, corresponding to the six degrees-of-freedom at each end of the truss member, as shown in Fig. 2. The stiffness and damping of the joints are represented by kux, kuy, kuz, kθx, kθy, kθz and cux, cuy, cuz, cθx, cθy, cθz, respectively, which can be linear or nonlinear.

Fig. 1
figure 1

Planar truss structure with nonlinear joints

Full size image
Fig. 2
figure 2

Truss member connected with two nonlinear joints at its ends (kθx and the damping models are not depicted here)

Full size image

2.1 Equivalent linearized model of the nonlinear joint

Considering that the steady-state response of the truss structure under harmonic excitation contains N harmonics, i.e., harmonic h1, h2, …, and hN, the relative displacement of the nonlinear joint in a certain direction s can be expressed as

$$ \delta_{s} \approx \tilde{\delta }_{s}^{{h_{N} }} = {\text{Im}} \left( {\sum\limits_{{n = h_{1} }}^{{h_{N} }} {\Delta_{sn} e^{{{\rm i}n\omega t}} } } \right) = {\text{Im}} \left( {\sum\limits_{{n = h_{1} }}^{{h_{N} }} {\Delta_{sn} e^{{{\rm i}n\psi }} } } \right) $$
(1)

where \(\psi = \omega t\),\({\rm i} = \sqrt { - 1}\),\(\Delta_{sn}\) is the displacement amplitude of the nth harmonic, \({\text{Im} (} \cdot {)}\) denotes taking the imaginary part.

The nonlinear restoring force of the joint in the direction s can be approximated by the Fourier series as

$$ f_{s} (\delta_{s} ,\dot{\delta }_{s} ) \approx f_{s} (\tilde{\delta }_{s}^{{h_{N} }} ,\dot{\tilde{\delta }}_{s}^{{h_{N} }} ) \approx {\text{Im}} \left( {\sum\limits_{{n = h_{1} }}^{{h_{N} }} {F_{sn} e^{{{\rm i}n\psi }} } } \right) $$
(2)

with the coefficients

$$ F_{sn} {(}\tilde{\delta }_{s}^{{h_{N} }} {) = }\frac{{\text{i}}}{\pi }\int_{0}^{{{2}\pi }} {f_{s} (\tilde{\delta }_{s}^{{h_{N} }} ,\dot{\tilde{\delta }}_{s}^{{h_{N} }} )e^{{ - {\rm i}n\psi }} {\rm d}\psi } ,\;\;\left( {n = h_{1} ,h_{2} \ldots ,h_{N} } \right) $$
(3)

Utilizing the multi-harmonic describing function method [48], the coefficients Fsn can be expressed by functions of the displacement amplitudes of the harmonics

$$ F_{sn} {(}\tilde{\delta }_{s}^{{h_{N} }} {) = }\sum\limits_{{m = h_{1} }}^{{h_{N} }} {g_{snm} \Delta_{sm} } , \, \left( {n = h_{1} ,h_{2} \ldots ,h_{N} } \right) $$
(4)

where the coefficients \(g_{snm}\) are called multi-harmonic describing functions, which can be obtained by

$$ g_{snm} = \left\{ \begin{array}{l} \frac{{F_{sn} {(}\tilde{\delta }_{s}^{m} {)}}}{{\Delta_{sm} }}, \, m = h_{1} \hfill \\ \frac{{F_{sn} {(}\tilde{\delta }_{s}^{m} {)} - F_{sn} {(}\tilde{\delta }_{s}^{m - 1} {)}}}{{\Delta_{sm} }}, \, m = h_{2} , \ldots ,h_{N} \hfill \\ \end{array} \right. $$
(5)

For smooth nonlinear joint model, the analytical expressions of the multi-harmonic describing functions can be obtained from Eq. (5) directly. For example, for the cubic stiffness model

$$ f_{s} (\delta_{s} ) = k_{1} \delta_{s} + k_{3} \delta_{s}^{3} $$
(6)

When only the first harmonic is considered, the describing function is

$$ g_{s11} = k_{1} + \frac{3}{4}k_{3} \Delta_{s1}^{2} $$
(7)

When the first and the third harmonics are considered, the describing functions are

$$ \left\{ \begin{array}{l} g_{s11} = k_{1} + \frac{3}{4}k_{3} \Delta_{s1}^{2} \hfill \\ g_{s13} = \frac{3}{2}k_{3} \Delta_{s1} \Delta_{s3} - \frac{3}{4}k_{3} \Delta_{s1}^{2} \hfill \\ g_{s31} = - \frac{1}{4}k_{3} \Delta_{s1}^{2} \hfill \\ g_{s33} = k_{1} + \frac{3}{2}k_{3} \Delta_{s1}^{2} + \frac{3}{4}k_{3} \Delta_{s3}^{2} \hfill \\ \end{array} \right. $$
(8)

For non-smooth nonlinear joint model, the analytical expressions of the multi-harmonic describing functions can’t be obtained since the integral in Eq. (3) can’t be analytically evaluated, but if only the first harmonic is considered, the analytical expression of the describing function can also be derived. For example, for the piece-wise linear stiffness model as shown in Fig. 3, the nonlinear restoring force is

$$ f_{s} (\delta_{s} ) = \left\{ \begin{array}{l} k_{1} \delta_{s} , \, \left| {\delta_{s} } \right| \le \delta_{sy} \hfill \\ k_{2} \delta_{s} + \text{sign}(\delta_{s} )(k_{1} - k_{2} )\delta_{sy} , \, \left| {\delta_{s} } \right| > \delta_{sy} \hfill \\ \end{array} \right. $$
(9)

the first-harmonic describing function can be obtained as

$$ g_{s11} = \left\{ \begin{array}{l} k_{1} , \, \left| {\delta_{s} } \right| \le \delta_{sy} \hfill \\ \frac{2}{\pi }\left[ {\arcsin \frac{{\delta_{sy} }}{{\Delta_{s1} }} + \frac{{\delta_{sy} }}{{\Delta_{s1} }}\sqrt {1 - \left( {\frac{{\delta_{sy} }}{{\Delta_{s1} }}} \right)^{2} } } \right](k_{1} - k_{2} ) + k_{2} , \, \left| {\delta_{s} } \right| > \delta_{sy} \hfill \\ \end{array} \right. $$
(10)
Fig. 3
figure 3

Piece-wise linear stiffness model

Full size image

2.2 Reduced order modeling of the truss structure with nonlinear joints

Denoting the displacement vectors \({\mathbf{u}}_{H} = \left\{ {{\mathbf{u}}_{i}^{{\text{T}}} ,{\mathbf{u}}_{j}^{{\text{T}}} } \right\}^{{\text{T}}}\), \({\tilde{\mathbf{u}}} = \left\{ {{\mathbf{u}}_{k}^{{\text{T}}} ,{\mathbf{u}}_{l}^{{\text{T}}} } \right\}^{{\text{T}}}\), and \({\mathbf{u}}_{B} = \left\{ {{\mathbf{u}}_{m}^{{\text{T}}} ,{\mathbf{u}}_{n}^{{\text{T}}} } \right\}^{{\text{T}}}\), where \({\mathbf{u}}_{p} \, (p = i,j,k,l,m,n)\) is the nodal displacement vector of node p, and the deformation vector of the two joints \({{\varvec{\updelta}}}_{J} = \left\{ {{{\varvec{\updelta}}}_{1} ,{{\varvec{\updelta}}}_{2} } \right\}^{{\text{T}}}\), where \(\left\{ {{\varvec{\updelta}}}_{1} \right\}^{\text{T}} \) and \(\left\{ {{\varvec{\updelta}}}_{2} \right\}^{\text{T}} \) are deformation vectors of the joints at the left and the right end of the member, respectively, the superscript “T” denotes the transpose of a matrix or a vector.

Considering the higher order harmonics in the response of the truss structure, the nodal displacement vector and the joint deformation vector can be written as

$$ {\mathbf{u}}_{p} = \sum\limits_{{n = h_{1} }}^{{h_{N} }} {{\mathbf{U}}_{pn} e^{{\text{i}n\psi }} } , \, (p = i,j,k,l,m,n),\;{{\varvec{\updelta}}}_{q} = \sum\limits_{{n = h_{1} }}^{{h_{N} }} {{{\varvec{\Delta}}}_{qn} e^{{\text{i}n\psi }} } , \, (q = 1,2) $$
(11)

then

$$ {\mathbf{u}}_{H} = \sum\limits_{{n = h_{1} }}^{{h_{N} }} {{\mathbf{U}}_{Hn} e^{{\text{i}n\psi }} } ,\;{\tilde{\mathbf{u}}} = \sum\limits_{{n = h_{1} }}^{{h_{N} }} {{\tilde{\mathbf{U}}}_{n} e^{{\text{i}n\psi }} } ,\;{\mathbf{u}}_{B} = \sum\limits_{{n = h_{1} }}^{{h_{N} }} {{\mathbf{U}}_{Bn} e^{{\text{i}n\psi }} } ,\;{{\varvec{\updelta}}}_{J} = \sum\limits_{{n = h_{1} }}^{{h_{N} }} {{{\varvec{\Delta}}}_{Jn} e^{{\text{i}n\psi }} } $$
(12)

where

$$ {\mathbf{U}}_{Hn} = \left\{ \begin{array}{c} {\mathbf{U}}_{in} \hfill \\ {\mathbf{U}}_{jn} \hfill \\ \end{array} \right\},\;{\tilde{\mathbf{U}}}_{n} = \left\{ \begin{array}{c} {\mathbf{U}}_{kn} \hfill \\ {\mathbf{U}}_{ln} \hfill \\ \end{array} \right\},\;{\mathbf{U}}_{Bn} = \left\{ \begin{array}{c} {\mathbf{U}}_{mn} \hfill \\ {\mathbf{U}}_{nn} \hfill \\ \end{array} \right\},\;{{\varvec{\Delta}}}_{Jn} = \left\{ \begin{array}{c} {{\varvec{\Delta}}}_{1n} \hfill \\ {{\varvec{\Delta}}}_{2n} \hfill \\ \end{array} \right\} $$
(13)

According to the kinematic relationship between the joints and the member, it can be obtained that

$$ {\mathbf{u}}_{B} = {\tilde{\mathbf{u}}} - {{\varvec{\updelta}}},\;{\tilde{\mathbf{u}}} = ({\mathbf{I + E}}){\mathbf{u}}_{H} $$
(14)

where I is a 12 × 12 identity matrix, and

$$ {\mathbf{E}} = \left[ {\begin{array}{*{20}c} {{\mathbf{E}}_{1} } & {\mathbf{0}} \\ {\mathbf{0}} & {{\mathbf{E}}_{2} } \\ \end{array} } \right] $$
(15)

with

$$ {\mathbf{E}}_{1} = \left[ {\begin{array}{*{20}c} 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & {e_{1} } \\ 0 & 0 & 0 & 0 & { - e_{1} } & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 \\ \end{array} } \right],\;{\mathbf{E}}_{2} = \left[ {\begin{array}{*{20}c} 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & { - e_{2} } \\ 0 & 0 & 0 & 0 & {e_{2} } & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 \\ \end{array} } \right] $$
(16)

Substituting Eq. (12) into (14) yields

$$ \sum\limits_{{n = h_{1} }}^{{h_{N} }} {{\mathbf{U}}_{Bn} e^{{\text{i}n\psi }} } = \sum\limits_{{n = h_{1} }}^{{h_{N} }} {{\tilde{\mathbf{U}}}_{n} e^{{\text{i}n\psi }} } - \sum\limits_{{n = h_{1} }}^{{h_{N} }} {{{\varvec{\Delta}}}_{Jn} e^{{\text{i}n\psi }} } ,\;\sum\limits_{{n = h_{1} }}^{{h_{N} }} {{\tilde{\mathbf{U}}}_{n} e^{{\text{i}n\psi }} } = ({\mathbf{I + E}})\sum\limits_{{n = h_{1} }}^{{h_{N} }} {{\mathbf{U}}_{Hn} e^{{\text{i}n\psi }} } $$
(17)

According to the harmonic balance condition, it can be obtained that

$$ {\mathbf{U}}_{BN} = {\tilde{\mathbf{U}}}_{N} - {{\varvec{\Delta}}}_{JN} ,\;{\tilde{\mathbf{U}}}_{N} = ({\mathbf{I}}_{N} {\mathbf{ + E}}_{N} ){\mathbf{U}}_{HN} $$
(18)

where

$$ {\mathbf{U}}_{HN} = \left\{ {\begin{array}{*{20}c} {{\varvec{U}}_{{Hh_{1} }} } \\ {{\varvec{U}}_{{Hh_{2} }} } \\ \vdots \\ {{\varvec{U}}_{{Hh_{N} }} } \\ \end{array} } \right\},\;{\tilde{\mathbf{U}}}_{N} = \left\{ {\begin{array}{*{20}c} {{\tilde{\mathbf{U}}}_{{h_{1} }} } \\ {{\tilde{\mathbf{U}}}_{{h_{2} }} } \\ \vdots \\ {{\tilde{\mathbf{U}}}_{{h_{N} }} } \\ \end{array} } \right\},\;{\mathbf{U}}_{BN} = \left\{ {\begin{array}{*{20}c} {{\mathbf{U}}_{{Bh_{1} }} } \\ {{\mathbf{U}}_{{Bh_{2} }} } \\ \vdots \\ {{\mathbf{U}}_{{Bh_{N} }} } \\ \end{array} } \right\},\;{{\varvec{\Delta}}}_{JN} = \left\{ {\begin{array}{*{20}c} {{{\varvec{\Delta}}}_{{Jh_{1} }} } \\ {{{\varvec{\Delta}}}_{{Jh_{2} }} } \\ \vdots \\ {{{\varvec{\Delta}}}_{{Jh_{N} }} } \\ \end{array} } \right\} $$
(19)

\({\mathbf{I}}_{N}\) is a 12N × 12N identity matrix, \({\mathbf{E}}_{N}\) is a block diagonal matrix composed of N matrices of E.

According to the dynamic equilibrium between the joints and the member, it can be obtained that

$$ \sum\limits_{{n = h_{1} }}^{{h_{N} }} {{\mathbf{D}}_{Bn} {\mathbf{U}}_{Bn} e^{{\text{i}n\psi }} } = \sum\limits_{{n = h_{1} }}^{{h_{N} }} {{\mathbf{D}}_{Jn} {{\varvec{\Delta}}}_{Jn} e^{{\text{i}n\psi }} } {\mathbf{ + f}}_{J} $$
(20)

where

$$ {\mathbf{D}}_{Bn} = {\mathbf{K}}_{B} - n^{2} \omega^{2} {\mathbf{M}}_{B} + \text{i}n\omega {\mathbf{C}}_{B} $$
(21)
$$ {\mathbf{D}}_{Jn} = {\mathbf{K}}_{J} + \text{i}n\omega {\mathbf{C}}_{J} $$
(22)
$$ {\mathbf{f}}_{J} = \left\{ {f_{ux1} ,f_{uy1} ,f_{uz1} ,f_{\theta x1} ,f_{\theta y1} ,f_{\theta z1} ,f_{ux2} ,f_{uy2} ,f_{uz2} ,f_{\theta x2} ,f_{\theta y2} ,f_{\theta z2} } \right\}^{{\text{T}}} $$
(23)

with

$$ {\mathbf{K}}_{J} = \text{diag}\left( {\left[ {k_{ux1} ,k_{uy1} ,k_{uz1} ,k_{\theta x1} ,k_{\theta y1} ,k_{\theta z1} ,k_{ux2} ,k_{uy2} ,k_{uz2} ,k_{\theta x2} ,k_{\theta y2} ,k_{\theta z2} } \right]} \right) $$
(24)
$$ {\mathbf{C}}_{J} = \text{diag}\left( {\left[ {c_{ux1} ,c_{uy1} ,c_{uz1} ,c_{\theta x1} ,c_{\theta y1} ,c_{\theta z1} ,c_{ux2} ,c_{uy2} ,c_{uz2} ,c_{\theta x2} ,c_{\theta y2} ,c_{\theta z2} } \right]} \right) $$
(25)

Corresponding to the six degrees of freedom at the end of the member, the nonlinear characteristics of the six degrees of freedom direction of the joint are considered, thus the nonlinear restoring force vector of the joint can be written as

$$ {\mathbf{f}}_{J} ({{\varvec{\updelta}}}_{J} ,{\dot{\varvec{\delta }}}_{J} ) \approx {\mathbf{f}}_{J} ({\tilde{\varvec{\delta }}}_{J}^{{h_{N} }} ,{\tilde{\dot{\varvec{\delta }}}}_{J}^{{h_{N} }} ) \approx \sum\limits_{{n = h_{1} }}^{{h_{N} }} {{\mathbf{F}}_{Jn} e^{{\text{i}n\psi }} } $$
(26)

where

$$ {{\varvec{\updelta}}}_{J} = \left\{ {\delta_{ux1} ,\delta_{uy1} ,\delta_{uz1} ,\delta_{\theta x1} ,\delta_{\theta y1} ,\delta_{\theta z1} ,\delta_{ux2} ,\delta_{uy2} ,\delta_{uz2} ,\delta_{\theta x2} ,\delta_{\theta y2} ,\delta_{\theta z2} } \right\}^{{\rm T}} $$
(27)
$$ {\mathbf{F}}_{Jn} = \left\{ {F_{ux1n} ,F_{uy1n} ,F_{uz1n} ,F_{\theta x1n} ,F_{\theta y1n} ,F_{\theta z1n} ,F_{ux2n} ,F_{uy2n} ,F_{uz2n} ,F_{\theta x2n} ,F_{\theta y2n} ,F_{\theta z2n} } \right\}^{{\rm T}} $$
(28)

According to Eq. (4), the coefficient vector \({\mathbf{F}}_{Jn}\) in Eq. (26) can be written as

$$ {\mathbf{F}}_{Jn} {(}{\tilde{\mathbf{\delta }}}^{{h_{N} }} {) = }\sum\limits_{{m = h_{1} }}^{{h_{N} }} {{\mathbf{g}}_{Jnm} {{\varvec{\Delta}}}_{Jm} } , \, \left( {n = h_{1} ,h_{2} \ldots ,h_{N} } \right) $$
(29)

where

$$ \begin{gathered} {\mathbf{g}}_{Jnm} = {\text{diag}}\left( {\left[ {g_{ux1nm} ,g_{uy1nm} ,g_{uz1nm} ,g_{\theta x1nm} ,g_{\theta y1nm} ,g_{\theta z1nm} ,} \right.} \right. \hfill \\ \left. { \, \left. { \, g_{ux2nm} ,g_{uy2nm} ,g_{uz2nm} ,g_{\theta x2nm} ,g_{\theta y2nm} ,g_{\theta z2nm} } \right]} \right) \hfill \\ \end{gathered} $$
(30)

Substituting Eqs. (26) and (29) into (20) yields

$$ \sum\limits_{{n = h_{1} }}^{{h_{N} }} {{\mathbf{D}}_{Bn} {\mathbf{U}}_{Bn} e^{{\text{i}n\psi }} } = \sum\limits_{{n = h_{1} }}^{{h_{N} }} {{\mathbf{D}}_{Jn} {{\varvec{\Delta}}}_{Jn} e^{{\text{i}n\psi }} } + \sum\limits_{{n = h_{1} }}^{{h_{N} }} {\sum\limits_{{m = h_{1} }}^{{h_{N} }} {{\mathbf{g}}_{Jnm} {{\varvec{\Delta}}}_{Jm} e^{{\text{i}n\psi }} } } $$
(31)

According to the harmonic balance condition, Eq. (31) can be expressed in the following matrix form

$$ {\mathbf{D}}_{BN} {\mathbf{U}}_{BN} = \left( {{\mathbf{D}}_{JN} {\mathbf{ + g}}_{JN} } \right){{\varvec{\Delta}}}_{JN} $$
(32)

where

$$ {\mathbf{D}}_{BN} = \left[ {\begin{array}{*{20}c} {{\mathbf{D}}_{{Bh_{1} }} } & {\mathbf{0}} & \cdots & {\mathbf{0}} \\ {\mathbf{0}} & {{\mathbf{D}}_{{Bh_{2} }} } & \cdots & {\mathbf{0}} \\ \vdots & \vdots & \ddots & \vdots \\ {\mathbf{0}} & {\mathbf{0}} & \cdots & {{\mathbf{D}}_{{Bh_{N} }} } \\ \end{array} } \right],\;{\mathbf{D}}_{JN} = \left[ {\begin{array}{*{20}c} {{\mathbf{D}}_{{Jh_{1} }} } & {\mathbf{0}} & \cdots & {\mathbf{0}} \\ {\mathbf{0}} & {{\mathbf{D}}_{{Jh_{2} }} } & \cdots & {\mathbf{0}} \\ \vdots & \vdots & \ddots & \vdots \\ {\mathbf{0}} & {\mathbf{0}} & \cdots & {{\mathbf{D}}_{{Jh_{N} }} } \\ \end{array} } \right] $$
(33)
$$ {\mathbf{g}}_{JN} = \left[ {\begin{array}{*{20}c} {{\mathbf{g}}_{{Jh_{1} h_{1} }} } & {{\mathbf{g}}_{{Jh_{1} h_{2} }} } & \cdots & {{\mathbf{g}}_{{Jh_{1} h_{N} }} } \\ {{\mathbf{g}}_{{Jh_{2} h_{1} }} } & {{\mathbf{g}}_{{Jh_{2} h_{2} }} } & \cdots & {{\mathbf{g}}_{{Jh_{2} h_{N} }} } \\ \vdots & \vdots & \ddots & \vdots \\ {{\mathbf{g}}_{{Jh_{N} h_{1} }} } & {{\mathbf{g}}_{{Jh_{N} h_{2} }} } & \cdots & {{\mathbf{g}}_{{Jh_{N} h_{N} }} } \\ \end{array} } \right] $$
(34)

From Eqs. (18) and (32), it can be solved that

$$ {\mathbf{U}}_{BN} = {\mathbf{G}}_{BN} {\mathbf{U}}_{HN} ,\;{{\varvec{\Delta}}}_{JN} = {\mathbf{G}}_{JN} {\mathbf{U}}_{HN} $$
(35)

where

$$ {\mathbf{S}}_{N} = \left( {{\mathbf{D}}_{JN} {\mathbf{ + g}}_{JN} + {\mathbf{D}}_{BN} } \right)^{ - 1} {\mathbf{D}}_{BN} $$
(36)
$$ {\mathbf{G}}_{BN} = \left( {{\mathbf{I}}_{N} - {\mathbf{S}}_{N} } \right)\left( {{\mathbf{I}}_{N} + {\mathbf{E}}_{N} } \right),\;{\mathbf{G}}_{JN} {\mathbf{ = S}}_{N} ({\mathbf{I}}_{N} + {\mathbf{E}}_{N} ) $$
(37)

In order to obtain a condensed two-node hybrid joint-beam element for the truss member with two nonlinear joints at its ends, the energy method in [21] can be used. However, for the multi-harmonic response, the analytical evaluation of the total energy of the member with two nonlinear joints is very complicated due to the product terms between different harmonics. Based on the energy equivalence of each harmonic, an approximated energy equivalence relationship can be written as

$$ \frac{1}{2}{\mathbf{U}}_{HN}^{{\text{T}}} {\mathbf{D}}_{HN} {\mathbf{U}}_{HN} = \frac{1}{2}{\mathbf{U}}_{BN}^{{\text{T}}} {\mathbf{D}}_{BN} {\mathbf{U}}_{BN} + \frac{1}{2}{{\varvec{\Delta}}}_{JN}^{{\text{T}}} \left( {{\mathbf{D}}_{JN} {\mathbf{ + g}}_{JN} } \right){{\varvec{\Delta}}}_{JN} $$
(38)

where \({\mathbf{D}}_{HN}\) is the multi-harmonic dynamic stiffness matrix of the condensed hybrid element.

Substituting Eq. (35) into (38) yields

$$ {\mathbf{D}}_{HN} = {\mathbf{G}}_{BN}^{{\text{T}}} {\mathbf{D}}_{BN} {\mathbf{G}}_{BN} + {\mathbf{G}}_{JN}^{{\text{T}}} \left( {{\mathbf{D}}_{JN} {\mathbf{ + g}}_{JN} } \right){\mathbf{G}}_{JN} $$
(39)

Using this hybrid joint-beam element, a condensed truss model can be obtained for the original truss structure, as shown in Fig. 4.

Fig. 4
figure 4

Condensed model of the planar truss structure with nonlinear joints

Full size image

Utilizing the multi-harmonic dynamic stiffness matrix \({\mathbf{D}}_{HN}\) of the hybrid joint-beam element to assemble the global dynamic stiffness matrix of the condensed truss structure, then the equation of motion of the condensed truss model in the frequency domain can be written as

$$ {\mathbf{D}}_{CTN} \left( {{\mathbf{U}}_{CTN} ,\omega } \right) \cdot { }{\mathbf{U}}_{CTN} (\omega ) = {\mathbf{F}}_{CTN} (\omega ) $$
(40)

where \({\mathbf{D}}_{CTN}\),\({\mathbf{U}}_{CTN}\) and \({\mathbf{F}}_{CTN}\) are the global dynamic stiffness matrix, the global nodal displacement amplitude vector, and the global nodal force amplitude vector of the condensed model of the truss structure considering N harmonics, respectively.

Furtherly, utilizing the equivalent continuum modeling method presented in [22], an equivalent beam model can be established for the truss structure as shown in Fig. 5.

Fig. 5
figure 5

Equivalent beam model of the planar truss structure with nonlinear joints

Full size image

Denoting the multi-harmonic displacement amplitude vectors of the repeating element and the equivalent beam element as.

$$ {\mathbf{U}}_{CRN} = \left\{ {{\mathbf{U}}_{{CRh_{1} }}^{{\text{T}}} {\mathbf{ U}}_{{CRh_{2} }}^{{\text{T}}} \cdots {\mathbf{U}}_{{CRh_{N} }}^{{\text{T}}} } \right\}^{{\text{T}}} ,\;{\mathbf{U}}_{ERN} = \left\{ {{\mathbf{U}}_{{ERh_{1} }}^{{\text{T}}} {\mathbf{ U}}_{{ERh_{2} }}^{{\text{T}}} \cdots {\mathbf{U}}_{{ERh_{N} }}^{{\text{T}}} } \right\}^{{\text{T}}} $$
(41)

Based on the hypothesis of the displacement and rotation fields for the repeating element [22], they can be transformed to.

$$ {\mathbf{U}}_{CRN} = {\mathbf{T}}_{CRN} {\mathbf{S}}_{0RN} ,\;{\mathbf{U}}_{ERN} = {\mathbf{T}}_{ERN} {\mathbf{S}}_{1RN} $$
(42)

where \({\mathbf{S}}_{0RN}\) is the multi-harmonic amplitude vector of the displacement and strain components at the center of the repeating element, \({\mathbf{S}}_{1RN}\) is a subvector of \({\mathbf{S}}_{0RN}\) by discarding some strain components which are not included in the classical beam theory, \({\mathbf{T}}_{CRN}\) and \({\mathbf{T}}_{ERN}\) are the transformation matrices determined by the hypothesis of the displacement and rotation fields.

Utilizing the following approximated energy equivalence relationship

$$ \frac{1}{2}{\mathbf{U}}_{CRN}^{{\text{T}}} {\mathbf{D}}_{CRN} {\mathbf{U}}_{CRN} = \frac{1}{2}{\mathbf{U}}_{ERN}^{{\text{T}}} {\mathbf{D}}_{ERN} {\mathbf{U}}_{ERN} $$
(43)

the multi-harmonic dynamic stiffness matrix \({\mathbf{D}}_{ERN}\) of the equivalent beam element can be derived from the multi-harmonic dynamic stiffness matrix \({\mathbf{D}}_{CRN}\) of the repeating element of the condensed truss model. Then by assembling the global dynamic stiffness matrix of the equivalent beam model, the equation of motion of the equivalent beam model in the frequency domain can be written as

$$ {\mathbf{D}}_{ETN} \left( {{\mathbf{U}}_{ETN} ,\omega } \right) \cdot {\mathbf{U}}_{ETN} (\omega ) = {\mathbf{F}}_{ETN} (\omega ) $$
(44)

where \({\mathbf{D}}_{ETN}\),\({\mathbf{U}}_{ETN}\) and \({\mathbf{F}}_{ETN}\) are the global dynamic stiffness matrix, the global nodal displacement amplitude vector, and the global nodal force amplitude vector of the equivalent beam model of the truss structure considering N harmonics, respectively.

3 Solution method of the nonlinear frequency response

The equation of motion of the condensed truss model or the equivalent beam model of the original truss structure can be written in the following form

$$ {\varvec{\mathcal{F}}}({\mathbf{U}},\omega ) = {\mathbf{0}} $$
(45)

where \({\mathbf{\mathcal{F}}}\) denotes a vector function, U represents UCTN or UETN corresponding to the condensed truss model or the equivalent beam model. In order to solve Eq. (45) by the arc-length continuation method, the parameter of arc length s is introduced in Eq. (45), then one obtains

$$ {\varvec{\mathcal{F}}}({\mathbf{U}}(s),\omega \, (s)) = {\mathbf{0}} $$
(46)

Since the unknown variable s is added in the system equation, an additional constraint equation is needed to solve the system equation. When the displacement amplitude vector U is real-valued, the constraint equation can be defined as

$$ g({\mathbf{U}},\omega ) = \Delta {\mathbf{U}}^{{\text{T}}} \Delta {\mathbf{U}} + \psi^{2} \Delta \omega^{2} - \Delta s^{2} = 0 $$
(47)

where \(\Delta {\mathbf{U}} = {\mathbf{U}} - {\mathbf{U}}_{i}\), \(\Delta \omega = \omega - \omega_{i}\), \(\left( {{\mathbf{U}}_{i} ,\omega_{i} } \right)\) is the known solution at the last frequency, ψ is a scaling parameter that governs the relative contributions of the displacement and frequency increments.

The implementation of the arc-length method usually consists two phases, i.e., the prediction phase and the correction phase.

3.1 Prediction phase of the arc-length continuation method

In the prediction phase, an initial predict solution will be obtained for the nonlinear equation system. Several different approaches are available to obtain the initial predict solution, such as the tangent predictor method [26], the secant predictor method [36], the extrapolated predictor method [32], etc. The tangent predictor is used in this study.

Differentiating Eq. (46) with respect to the arc length s yields

$$ \frac{{\partial {\varvec{\mathcal{F}}}}}{{\partial {\mathbf{U}}}}\frac{{\text{d}{\mathbf{U}}}}{{\text{d}s}} + \frac{{\partial {\varvec{\mathcal{F}}}}}{\partial \omega }\frac{{\text{d}\omega }}{{\text{d}s}}{\mathbf{ = K}}_{T} {\mathbf{U^{\prime} + q}}\omega^{\prime} = {\mathbf{0}} $$
(48)

where \({\mathbf{K}}_{T} \equiv \frac{{\partial {\varvec{\mathcal{F}}}}}{{\partial {\mathbf{U}}}}\), \({\mathbf{q}} \equiv \frac{{\partial {\varvec{\mathcal{F}}}}}{\partial \omega }\), \({\mathbf{U^{\prime}}} \equiv \frac{{{\text{d}}{\mathbf{U}}}}{{{\text{d}}s}}\), \(\omega^{\prime} \equiv \frac{{{\text{d}}\omega }}{{{\text{d}}s}}\), in structural dynamics \({\mathbf{K}}_{T}\) represents the tangent stiffness matrix of the structure at frequency \(\omega\).

Rewriting Eq. (48) as

$$ \left[ {\begin{array}{*{20}c} {{\mathbf{K}}_{T} } & {\mathbf{q}} \\ \end{array} } \right]\left\{ \begin{gathered} {{\mathbf{U^{\prime}}}} \hfill \\ {\omega^{\prime}} \hfill \\ \end{gathered} \right\}{\mathbf{ = At}} = {\mathbf{0}} $$
(49)

where t is the tangent vector at the point \(\left( {{\mathbf{U}},\omega } \right)\) on the solution path. Since the number of unknown variables in t is one more than the number of rows in the matrix A, the solution of Eq. (49) is nonunique. In order to determine the tangent vector t uniquely, an additional equation needs to be supplemented. A convenient additional equation is specified by the Euclidean arclength normalization [26]

$$ \left\| {\mathbf{t}} \right\| = {\mathbf{U^{\prime}}}^{{\text{T}}} {\mathbf{U^{\prime}}} + \omega^{{\prime}{2}} = 1 $$
(50)

One solution method for Eqs.(49) and (50) is given in [26] as follows: Firstly solving the following equation

$$ {\mathbf{K}}_{T} {\mathbf{z}} = - {\mathbf{q}} $$
(51)

for the vector z, then owing to the linearity of Eq. (49) in \({\mathbf{U^{\prime}}}\) and \(\omega^{\prime}\), it can be obtained that

$$ {\mathbf{U^{\prime}}} = {\mathbf{z}}\omega^{\prime} $$
(52)

Substituting Eq. (52) into Eq. (50) yields

$$ \omega^{\prime} = \pm (1 + {\mathbf{z}}^{{\text{T}}} {\mathbf{z}})^{ - 1/2} $$
(53)

where the plus and minus signs determine the direction of the continuation. If the sign is not chosen appropriately, the direction for searching the next point is incorrect and the corrector phase may travel back to the previously computed solution [33].

The above method requires the evaluation of the inverse of the tangent stiffness matrix \({\mathbf{K}}_{T}\), so it may fail at turning points and other bifurcation points where \({\mathbf{K}}_{T}\) is singular. In order to avoid this problem, the idea used in the scheme presented by Kubíček [26, 49] was adopted here, namely, although \({\mathbf{K}}_{T}\) is singular at a turning point, one can find a nonsingular submatrix by deleting one certain column (for example the kth column, the value of k can be found by using a Gaussian elimination scheme with pivoting). Here, the tangent vector t was solved as follows:

Firstly, assuming the kth element \(t_{k}\) in the tangent vector t equals to 1, and then transferring Eq. (49) to

$$ {\tilde{\mathbf{A}}} {\tilde {\mathbf{t}}} = - {\mathbf{a}}_{k} $$
(54)

where \({\tilde{\mathbf{A}}} = \left[ {{\mathbf{a}}_{1}, \ldots {\mathbf{a}}_{k - 1} ,{\mathbf{a}}_{k + 1} , \cdots ,{\mathbf{a}}_{n + 1} } \right]\), \({\tilde{\mathbf{t}}} = \left\{ {t_{1} , \ldots ,t_{k - 1} ,t_{k + 1} , \cdots ,t_{n} } \right\}^{{\text{T}}}\), \({\mathbf{a}}_{k}\) is the vector of the kth column of the matrix A. Since \({\tilde{\mathbf{A}}}\) is nonsingular, \({\tilde{\mathbf{t}}}\) can be solved from Eq. (54), then a special solution of t can be obtained as \({\mathbf{t}}_{s} = \left\{ {t_{1} , \ldots ,t_{k - 1} ,1,t_{k + 1} , \ldots t_{n} } \right\}^{{\text{T}}}\), then the normalized vector t is

$$ {\mathbf{t}} = \pm \frac{{{\mathbf{t}}_{s} }}{{\left\| {{\mathbf{t}}_{s} } \right\|}} $$
(55)

Following the method used in [35], the sign of t is determined by the sign of the determinant of the matrix \({\tilde{\mathbf{A}}}\). At last, the tangent vector t is obtained as

$$ {\mathbf{t}} = {\text{sign}}\left( {\det ({\tilde{\mathbf{A}}})} \right)\frac{{{\mathbf{t}}_{s} }}{{\left\| {{\mathbf{t}}_{s} } \right\|}} $$
(56)

After obtaining the tangent vector t, the predict solution at the arc length \(s + \Delta s\) can be obtained as

$$ {\mathbf{U}}^{(0)} = {\mathbf{U}}_{i} + {\mathbf{U^{\prime}}}\Delta s,\;\omega^{(0)} = \omega_{i} + \omega^{\prime}\Delta s $$
(57)

3.2 Correction phase of the arc-length continuation method

In the correction phase, the predict solution obtained above will be corrected iteratively until the final convergent solution is obtained. In order to obtain the iterative scheme of the corrected solution, the first order Taylor expansion is performed on Eqs. (46) and (47), which yields

$$ {\varvec{\mathcal{F}}}({\mathbf{U}},\omega ) \approx {\varvec{\mathcal{F}}}_{0} + \frac{{\partial {\varvec{\mathcal{F}}}}}{{\partial {\mathbf{U}}}}\delta {\mathbf{U}}{ + }\frac{{\partial {\varvec{\mathcal{F}}}}}{\partial \omega }\delta \omega { = }{\varvec{\mathcal{F}}}_{0} + {\mathbf{K}}_{T} \delta {\mathbf{U}}{ + }{\mathbf{q}}\delta \omega = {\mathbf {0}} $$
(58a)
$$ g({\mathbf{U}},\omega ) \approx g_{0} + 2\Delta {\mathbf{U}}^{{\text{T}}} \delta {\mathbf{U}} + 2\psi^{2} \Delta \omega \delta \omega = 0 $$
(58b)

Equation (58) can be rewritten as

$$ \left[ {\begin{array}{*{20}c} {{\mathbf{K}}_{T} } & {\mathbf{q}} \\ {2\Delta {\mathbf{U}}^{{\text{T}}} } & {2\psi^{2} \Delta \omega } \\ \end{array} } \right]\left\{ \begin{gathered} \delta {\mathbf{U}} \hfill \\ \delta \lambda \hfill \\ \end{gathered} \right\} = - \left\{ \begin{gathered} {\varvec{\mathcal{F}}}_{0} \hfill \\ g_{0} \hfill \\ \end{gathered} \right\} $$
(59)

Equation (59) can be solved by the Newton–Raphson iterative method, which yields

$$ \left\{ \begin{gathered} {\mathbf{U}}^{(k + 1)} { = }{\mathbf{U}}^{(k)} { + }r\delta {\mathbf{U}}^{(k + 1)} \hfill \\ \omega^{(k + 1)} { = }\omega^{(k)} { + }r\delta \omega^{(k + 1)} \hfill \\ \end{gathered} \right. $$
(60)

where r (0 < r ≤ 1) is the relaxation parameter [26], which is helpful to improve the convergence of the algorithm, \(\delta {\mathbf{U}}^{(k + 1)}\) and \(\delta \omega^{(k + 1)}\) are the increments from the kth step to the (k + 1) th step, which satisfy the following equation

$$ \left[ {\begin{array}{*{20}c} {{\mathbf{K}}_{T}^{(k)} } & {{\mathbf{q}}^{(k)} } \\ {2\Delta {\mathbf{U}}^{{{(}k{)\text{T}}}} } & {2\psi^{2} \Delta \omega^{(k)} } \\ \end{array} } \right]\left\{ \begin{gathered} \delta {\mathbf{U}}^{(k + 1)} \hfill \\ \delta \omega^{(k + 1)} \hfill \\ \end{gathered} \right\} = - \left\{ \begin{gathered} {\varvec{\mathcal{F}}}^{(k)} \hfill \\ g^{(k)} \hfill \\ \end{gathered} \right\} $$
(61)

where \(\Delta {\mathbf{U}}^{(k)} = {\mathbf{U}}^{(k)} - {\mathbf{U}}_{i}\), \(\Delta \omega^{(k)} = \omega^{(k)} - \omega_{i}\). This equation can be solved by evaluating the inversion of the coefficient matrix. However, this coefficient matrix is neither symmetric nor banded. In order to utilize the banded symmetric property of the tangent stiffness matrix \({\mathbf{K}}_{T}^{(k)}\), some other methods have been proposed in the past studies.

When the matrix \({\mathbf{K}}_{T}^{(k)}\) is nonsingular, Eq. (61) can be solved by using the bordering algorithm [43], which gives

$$ \delta {\mathbf{U}}^{(k + 1)} { = }{\mathbf{Z}}_{1} + \delta \omega^{(k + 1)} {\mathbf{Z}}_{2} $$
(62)

where

$$ {\mathbf{Z}}_{1} { = } - \left[ {{\mathbf{K}}_{T}^{(k)} } \right]^{ - 1} {\varvec{\mathcal{F}}}^{(k)} ,\;{\mathbf{Z}}_{2} { = } - \left[ {{\mathbf{K}}_{T}^{(k)} } \right]^{ - 1} {\mathbf{q}}^{(k)} $$
(63)

Substituting Eq. (62) into the second equation of Eq. (61), the frequency increment can be solved as

$$ \delta \omega^{(k + 1)} = - \frac{{2\Delta {\mathbf{U}}^{{{(}k{)\text{T}}}} {\mathbf{Z}}_{1} { + }g^{(k)} }}{{{2}\Delta {\mathbf{U}}^{{{(}k{)\text{T}}}} {\mathbf{Z}}_{2} + 2\psi^{2} \Delta \omega^{(k)} }} $$
(64)

3.3 The algorithm modification for evaluating complex-valued frequency response

A problem needs to be mentioned is that when damping is considered in the structure the frequency response is complex-valued, but the above arc-length method can’t be directly used to solve the complex-variable nonlinear equation system. This is because the first-order Taylor expansion used in Eq. 58(b) is only suitable for real-variable function, consequently, the iterative formula (61) based on the Taylor expansion is also only suitable for real-variable nonlinear equation system. In order to solve this problem, the usual approach is to separate the real part and the imaginary part of the complex-variable equation system to obtain a new augmented real-variable equation system before the arc-length method was applied [50, 51]. Here, a direct solution method is presented by modifying the iterative formula in the arc-length method.

When the solution vector U is complex-valued, the additional restraint Eq. (47) needs to be modified as

$$ g({\mathbf{U}},\omega ) = \Delta {\mathbf{U}}^{{\text{H}}} \Delta {\mathbf{U}} + \psi^{2} \Delta \omega^{2} - \Delta s^{2} = 0 $$
(65)

where the superscript ‘H’ denotes the conjugate transpose of a matrix or vector.

Equation (65) is a real-valued scalar function with the complex variable U, its first-order Taylor expansion is [52]

$$ \begin{gathered} g({\mathbf{U}},{\mathbf{U}}^{*} ,\omega ) \approx \, g_{o} + \left[ {\frac{{\partial {(}\Delta {\mathbf{U}}^{{\text{H}}} \Delta {\mathbf{U}})}}{{\partial {\mathbf{U}}}}\delta {\mathbf{U}} + \frac{{\partial {(}\Delta {\mathbf{U}}^{{\text{H}}} \Delta {\mathbf{U}})}}{{\partial {\mathbf{U}}^{*} }}\delta {\mathbf{U}}^{*} } \right] + 2\psi^{2} \Delta \omega \delta \omega \hfill \\ { = }g_{o} + \left[ {\frac{{\partial {(}\Delta {\mathbf{U}}^{{\text{H}}} \Delta {\mathbf{U}})}}{{\partial {\mathbf{U}}}}\delta {\mathbf{U}} + \frac{{\partial {(}\Delta {\mathbf{U}}^{{\text{T}}} \Delta {\mathbf{U}}^{*} )}}{{\partial {\mathbf{U}}^{*} }}\delta {\mathbf{U}}^{*} } \right] + 2\psi^{2} \Delta \omega \delta \omega \hfill \\ { = }g_{o} + \left( {\Delta {\mathbf{U}}^{{\text{H}}} \delta {\mathbf{U}} + \Delta {\mathbf{U}}^{{\text{T}}} \delta {\mathbf{U}}^{*} } \right) + 2\psi^{2} \Delta \omega \delta \omega = 0 \hfill \\ \end{gathered} $$
(66)

where the superscript ‘*’ denotes the conjugate operation. Note that the derivation of Eq. (66) utilizes the equality \(\Delta {\mathbf{U}}^{{\text{H}}} \Delta {\mathbf{U}}{ = }\left( {\Delta {\mathbf{U}}^{{\text{H}}} \Delta {\mathbf{U}}} \right)^{{\text{T}}} { = }\Delta {\mathbf{U}}^{{\text{T}}} \Delta {\mathbf{U}}^{*}\) considering that \(\Delta {\mathbf{U}}^{{\text{H}}} \Delta {\mathbf{U}}\) is a real number.

The iterative scheme of Eq. (66) is

$$ \Delta {\mathbf{U}}^{(k){\rm H}} \delta {\mathbf{U}}^{(k + 1)} + \Delta {\mathbf{U}}^{(k){\rm T}} \delta {\mathbf{U}}^{(k + 1)*} + 2\psi^{2} \Delta \omega^{(k)} \delta \omega^{(k + 1)} =- g^{(k)} $$
(67a)

or

$$ 2{\text{Re}} \left( {\Delta {\mathbf{U}}^{{{(}k{)\text{H}}}} \delta {\mathbf{U}}^{(k + 1)} } \right) + 2\psi^{2} \Delta \omega^{(k)} \delta \omega^{(k + 1)} = - g^{(k)} $$
(67b)

As a result, the iterative scheme for the increments \(\delta {\mathbf{U}}^{(k + 1)}\) and \(\delta \omega^{(k + 1)}\) becomes

$$ \left[ {\begin{array}{*{20}c} {{\mathbf{K}}_{T}^{(k)} } & {\mathbf{0}} & {{\mathbf{q}}^{(k)} } \\ {\mathbf{0}} & {{\mathbf{K}}_{T}^{{(k){*}}} } & {{\mathbf{q}}^{{(k){*}}} } \\ {\Delta {\mathbf{U}}^{{{(}k{)\text{H}}}} } & {\Delta {\mathbf{U}}^{{{(}k{)\text{T}}}} } & {2\psi^{2} \Delta \omega^{(k)} } \\ \end{array} } \right]\left\{ {\begin{array}{*{20}c} {\delta {\mathbf{U}}^{(k + 1)} } \\ {\delta {\mathbf{U}}^{(k + 1)*} } \\ {\delta \omega^{(k + 1)} } \\ \end{array} } \right\} = - \left\{ {\begin{array}{*{20}c} {{\varvec{\mathcal{F}}}^{(k)} } \\ {{\varvec{\mathcal{F}}}^{{(k){*}}} } \\ {g^{(k)} } \\ \end{array} } \right\} $$
(68a)

or

$$ \left[ {\begin{array}{*{20}c} {{\text{Re}} ({\mathbf{K}}_{T}^{(k)} )} & { - {\text{Im}} ({\mathbf{K}}_{T}^{(k)} )} & {{\text{Re}} ({\mathbf{q}}^{(k)} )} \\ {{\text{Im}} ({\mathbf{K}}_{T}^{(k)} )} & {{\text{Re}} ({\mathbf{K}}_{T}^{(k)} )} & {{\text{Im}} ({\mathbf{q}}^{(k)} )} \\ {2{\text{Re}} (\Delta {\mathbf{U}}^{{{(}k{)\text{H}}}} )} & { - 2{\text{Im}} (\Delta {\mathbf{U}}^{{{(}k{)\text{H}}}} )} & {2\psi^{2} \Delta \omega^{(k)} } \\ \end{array} } \right]\left\{ {\begin{array}{*{20}c} {{\text{Re}} (\delta {\mathbf{U}}^{(k + 1)} )} \\ {{\text{Im}} (\delta {\mathbf{U}}^{(k + 1)} )} \\ {\delta \omega^{(k + 1)} } \\ \end{array} } \right\}{ = } - \left\{ {\begin{array}{*{20}c} {{\text{Re}} ({\varvec{\mathcal{F}}}^{(k)} )} \\ {{\text{Im}} ({\varvec{\mathcal{F}}}^{(k)} )} \\ {g^{(k)} } \\ \end{array} } \right\} $$
(68b)

Correspondingly, the bordering algorithm for solving the frequency increment is modified as

$$ \delta \omega^{(k + 1)} = - \frac{{\Delta {\mathbf{U}}^{{{(}k{)\text{H}}}} {\mathbf{Z}}_{1} { + }\Delta {\mathbf{U}}^{{{(}k{)\text{T}}}} {\mathbf{Z}}_{1}^{*} { + }g^{(k)} }}{{\Delta {\mathbf{U}}^{{{(}k{)\text{H}}}} {\mathbf{Z}}_{2} + \Delta {\mathbf{U}}^{{{(}k{)\text{T}}}} {\mathbf{Z}}_{2}^{*} + 2\psi^{2} \Delta \omega^{(k)} }} $$
(69)

4 Numerical examples

4.1 Example 1: A planar truss structure with rotational nonlinear joints

The planar truss structure, as shown in Fig. 1, is made up of 10 repeating elements and 60 nonlinear joints. The lengths of the horizontal and vertical members are Ll = 1.5 m (including the lengths of two end joints) and Lv = 1.5 m. The eccentricities of the joints connected with longitudinal members are assumed as \(e_{1}^{l} = e_{2}^{l} = 0.02\;{\text{m}}\), and those with diagonal member are \(e_{1}^{d} = e_{2}^{d} = 0.03\;{\text{m}}\). All members are made of carbon fiber tubes with Young’s modulus E = 205 GPa and density ρ = 1720 kg/m3. The outer and inner diameters of the members are do = 40 mm and di = 34 mm, respectively. The damping of the truss members is considered by using the Rayleigh damping model and the mass-proportional and stiffness-proportional damping coefficients are assumed as α = 0.05 and β = 0.005, respectively. The truss structure is assumed clamped at its left end. Considering that the planar truss structure is prone to take place of out-of-plane bending and twisting vibrations, the influence of nonlinear rotational stiffness of all joints on the out-of-plane vibration characteristics of the planar truss structure is studied here. For the sake of simplicity, all joints are assumed to have the same properties, and the stiffness and damping coefficients of the joint in six directions are assumed as in Table 1.

Table 1 Stiffness and damping coefficients of the joints in the planar truss structure
Full size table

For this planar truss structure, a condensed truss model can be established by the presented modeling method, which contains 22 nodes and 132 DOFs. In order to verify the accuracy of the presented method, the commercial finite element package ANSYS is used to established a full finite element model for the original truss structure, in which, each truss member is modeled by a spatial beam element (Beam4 element), the connection between the joint and the member is modelled by six spring-damper elements (using Combin14 element for modeling linear stiffness and damping of the joint and Combin39 element for modeling nonlinear stiffness of the joint), the rigid body of the joint is modelled by a rigid constraint element (MPC184 element). The total FEM model contains 82 nodes and 492 DOFs.

The first two linear modes obtained by the ANSYS model (The rotational stiffness kθz of the joint is assumed as 1 × 104 N m/rad in the linear model) are shown in Fig. 6. It can be found that the first two linear modes of this planar truss structure are all out-of-plane vibration modes, and the frequencies of these two modes are well separated.

Fig. 6
figure 6

First two linear modes of the planar truss structure

Full size image

4.1.1 The joint has cubic rotational stiffness

Firstly, considering the joint has cubic rotational stiffness as in Eq. (6) around the z-axis direction. A sinusoidal excitation with amplitude F = 1N is applied at point A along the y-axis direction to excite the out-of-plane vibration of the planar truss structure.

Letting the stiffness coefficient k1 = 1 × 104 N m/rad and k2 = 5 × 108 N m/rad, the displacement amplitudes of the first harmonic and the third harmonic of point A along the y-axis direction evaluated by the presented condensed truss model are shown in Fig. 7. It can be found that under the influence of cubic rotational stiffnesses of all the joints the amplitude-frequency curve of the first harmonic bends to right and shows obvious stiffness hardening characteristics. From the amplitude-frequency curve of the third harmonic it can be seen that the amplitude of the third harmonic is much smaller than that of the first harmonic, and the 3 super-harmonic resonance phenomena can be observed in the third harmonic. Furthermore, it can be found that whether the third harmonic is considered in the model has little influence on the calculation result of the first harmonic.

Fig. 7
figure 7

The first and the third harmonic responses of the planar truss structure with joints having cubic rotational stiffness

Full size image

Letting the stiffness coefficient k1 = 1 × 104 N m/rad and varying the stiffness coefficient k2, the displacement amplitudes of point A along the y-axis direction near the first resonant frequency of the truss are shown in Fig. 8. It shows that under the influence of cubic rotational stiffnesses of all the joints the amplitude-frequency curve for the first primary resonance of the planar truss structure bends to the right and shows obvious stiffness hardening characteristics, the first resonant frequency of the planar truss structure increases with the increase of the stiffness coefficient k2. Furthermore, it can be found that the range of unstable region of the amplitude-frequency curve also increases with the increase of k2.

Fig. 8
figure 8

Influence of joint parameter on the frequency response of the planar truss structure with joints having cubic rotational stiffness

Full size image

In order to investigate the effect of excitation amplitude on the nonlinear frequency response of the planar truss structure, assume the joint parameters are k1 = 1 × 104 N m/rad and k2 = 5 × 108 N m/rad, and vary the excitation amplitude that applied on point A. The displacement amplitude of point A along the y-axis direction for the first and second resonances of the planar truss structure under different excitation amplitudes are shown in Fig. 9. The result shows that the first two resonant frequencies of the planar truss structure all increase with the excitation amplitude gradually. Moreover, it can be found that the amplitude-frequency curve of the planar truss structure in the vicinity of a certain resonant frequency is resemble to that of a single-degree-of-freedom Duffing system since the vibration modes of this planar truss are well separated.

Fig. 9
figure 9

Influence of excitation amplitude on the frequency response of the planar truss structure with joints having cubic rotational stiffness

Full size image

4.1.2 The joint has piece-wise linear rotational stiffness

Next, considering the joint in the planar truss structure has piece-wise linear rotational stiffness as in Eq. (9) around the z-axis direction.

Letting the joint parameters k1 = 1 × 104 N m/rad, δy = 1 × 10−3 rad, and the excitation amplitude F = 1N, the displacement amplitude of point A of the planar truss structure with different joint stiffness parameter k2 are shown in Fig. 8, which gives similar conclusions as Fig. 10, but there is a little difference in the shapes of the amplitude-frequency curves of these two nonlinear joint models.

Fig. 10
figure 10

Influence of joint parameter on the frequency response of the planar truss structure with joints having piece-wise linear rotational stiffness

Full size image

Assuming the nonlinear joint parameters are k1 = 1 × 104 N m/rad, k2 = 5 × 104 N m/rad and δy = 1 × 10−3 rad, the frequency responses of the planar truss structure under different excitation amplitudes are shown in Fig. 11. It can be found that the first two resonant frequencies of the truss structure also increase with the excitation amplitude like the cubic stiffness nonlinearity, but it gradually tends to a constant value which is different from the cubic stiffness nonlinearity.

Fig. 11
figure 11

Influence of excitation amplitude on the frequency response of the planar truss structure with joints having piece-wise linear rotational stiffness

Full size image

Since the ANSYS package we used cannot obtain the nonlinear frequency response directly in the frequency domain, the time domain response analysis using the forward and backward linear swept-sine excitations are carried out on the ANSYS model. The excitation force of the swept-sine excitation is

$$ F_{Z} = F\sin (at + bt^{2} ) $$
(70)

where

$$ \left\{ \begin{gathered} a = \omega_{s} , \, b = \frac{{\omega_{e} - \omega_{s} }}{2T}{\text{ for forward swept - sine excitaion}} \hfill \\ a = \omega_{e} , \, b = \frac{{\omega_{s} - \omega_{e} }}{2T}{\text{ for backward swept - sine excition}} \hfill \\ \end{gathered} \right. $$
(71)

where F is the excitation amplitude, \(\omega_{s}\) and \(\omega_{e}\) are the starting and ending values of the excitation frequency, T is the time duration of the excitation.

A nonlinear transient response analysis is carried out in ANSYS to obtain the time response of the truss structure under the swept-sine excitation (In order to obtain accurate resonant frequency and resonant amplitude, the swept-sine excitation should be applied very slowly). The comparison of the results obtained by the presented method and ANSYS is shown in Fig. 12. It can be found that the amplitude-frequency curve obtained by the presented method coincides with the envelopes of the time responses obtained by ANSYS very well, and the jump-up and jump-down frequencies obtained by these two methods also match very well.

Fig. 12
figure 12

Comparison of the results obtained by the presented method and the ANSYS time response analysis method for planar truss structure with joints having piece-wise linear rotational stiffness

Full size image

4.2 Example 2: A spatial truss structure with axial nonlinear joints

Next, a more complex truss structure will be considered. This truss structure, as shown in Fig. 13, is made up of 20 repeating elements. The size of the repeating element is Ll = Lv = Lb = 1.5 m. The geometric and material parameters of the truss members are the same as those in the previous planar truss example. Considering that the low frequency vibration of this truss structure mainly causes the axial deformations of the truss members, the influence of the axial nonlinear stiffness of the joints on the dynamic characteristics of the truss structure is studied. Furthermore, considering that the deformations of the longitudinal and diagonal members are dominant for this structure, only the longitudinal and diagonal members are assumed to be connected with nonlinear joints, while the transverse and vertical members are assumed to be rigid connected. There are a total of 320 nonlinear joints in this structure, the stiffness and damping coefficients of the joints are listed in Table 2.

Fig. 13
figure 13

Spatial truss structure with nonlinear joints

Full size image
Table 2 Stiffness and damping coefficients of the joints in the spatial truss structure
Full size table

For this spatial truss structure, an equivalent beam model is established using the presented modeling method, which contains 21 nodes and 168 DOFs. Besides, in order to verify the accuracy of the presented method, a full FEM model is also established by ANSYS, which contains 884 nodes and 5304 DOFs.

The first four linear modes obtained by the ANSYS model (The axial stiffness kux of the joint is assumed as 3 × 106 N/m in the linear model) are shown in Fig. 14, which shows that the first and second natural frequencies are very close, and the same is true of the third and fourth natural frequencies. Moreover, it can be found that the flexural vibrations around the y-axis and the z-axis are coupling in each mode since the asymmetric arrangement of the diagonal members.

Fig. 14
figure 14

First four linear modes of the spatial truss structure

Full size image

Assume the joint has piece-wise linear stiffness in the axial direction with the parameters k1 = 3 × 106 N/m, k2 = 5 × 106 N/m and δy = 1 × 10−5 m, and apply a sinusoidal excitation along the z-axis direction at point A on the truss structure, the displacement amplitudes of point A along the z-axis direction under different excitation amplitudes evaluated by the equivalent beam model are shown in Fig. 15. It can be found that the frequency responses of this spatial truss structure are more complex than the previous planar truss structure, under some excitation amplitudes the frequency response of the spatial truss structure has 5 steady-state solutions in some frequency ranges, including 3 stable solutions and 2 unstable solutions, and there is an additional small peak in addition to the main peak in the amplitude-frequency curve. For the first resonance region, the above phenomenon appears when the excitation amplitude is small, while for the second resonance region the above phenomenon appears when the excitation amplitude is large. The reason for the above phenomenon is that there are two closely spaced modes in each resonance region in the corresponding linear model of this truss structure, as shown in Fig. 14, since the spatial truss structure is asymmetric caused by the arrangement of the diagonal members, the sinusoidal excitation acting on point A will arouse the vibrations of the two closely spaced modes simultaneously which makes the amplitude-frequency curves of these two modes overlap in certain frequency ranges.

Fig. 15
figure 15

Frequency responses of the spatial truss structure with piece-wise linear axial stiffness in the joints under different excitation amplitudes

Full size image

In order to verify the correctness of the presented method for the spatial truss structure, the frequency responses obtained by the equivalent beam model are compared with the time responses obtained by the ANSYS model. Figure 16 shows the comparison result in the first resonance region under the excitation amplitude F = 2N, and Fig. 17 shows the comparison result in the second resonance region under the excitation amplitude F = 8N. It can be found that the amplitude-frequency curve obtained by the presented method coincides with the envelopes of the time responses obtained by ANSYS very well, and the jump-up and jump-down frequencies obtained by these two methods also match very well.

Fig. 16
figure 16

Comparison of the results obtained by the presented method and the ANSYS time response analysis method (excitation amplitude F = 2N)

Full size image
Fig. 17
figure 17

Comparison of the results obtained by the presented method and the ANSYS time response analysis method (excitation amplitude F = 8N)

Full size image

At last, the influence of joint damping on the nonlinear frequency response of the spatial truss structure will be investigated. A high joint damping is considered by magnifying the joint damping coefficients in Table 1 by 5 times. The comparison of the models with low joint damping and high joint damping is shown in Fig. 18. It can be found that for high joint damping both the resonant frequency and the resonant amplitude of the truss structure decrease. Furthermore, the shape of the amplitude-frequency curve can change greatly, such as the two peaks in the second resonance region reduce to one. This result indicates that complex nonlinear dynamics phenomena are easy to occur in large space truss structures with low damping.

Fig. 18
figure 18

Influence of joint damping on the frequency response of the spatial truss structure with joints having piece-wise linear axial stiffness

Full size image

5 Conclusions

In this study, the nonlinear frequency response analysis of large space truss structures with nonlinear joints was studied using the presented reduced-order modeling method and the arc-length continuation method. Some critical issues encountered in the implementation of the arc-length continuation algorithm in solving high-dimensional nonlinear algebraic equation system were emphatically described such as the evaluation of the tangent vector at singular points, the selection of the prediction direction, and the algorithm modification for evaluation of complex response. The numerical studies were carried out on a planar truss structure with rotational nonlinear joints and a spatial truss structure with axial nonlinear joints. The results indicated that for the planar truss structure whose vibration modes are well separated its amplitude-frequency curve in the vicinity of a certain resonant frequency is resemble to the amplitude-frequency curve of a single-degree-of-freedom nonlinear system. The 3 super-harmonic resonance was found from the amplitude-frequency curve of the third harmonic in the planar truss structure with cubic rotational joints. The frequency response of the spatial truss structure is more complex than the planar truss structure since the exist of closely spaced modes and coupling vibration, which has 5 steady-state solutions in certain frequency ranges. Furthermore, the result shows that the damping has important influence on the nonlinear dynamic response of the space truss structure, complex nonlinear dynamics phenomena are easy to occur in large space truss structures with low damping. The comparison of the results obtained by the presented method and the ANSYS time-domain analysis verify the correctness of the presented modeling and solution method.