1 Introduction

The piezoelectric semiconductor (PS) has attracted much attention in recent years. In PS, the charge carrier is driven by piezoelectric potential, and the electric potential is produced by external load. This kind of coupled characteristic between piezoelectricity and semiconduction in PS belongs to the field of piezotronics [1, 2]. With the development of manufacture technology, various PS structures have been synthesized, such as nanowires, nanobelts or nanodiskettes. [3]. Based on these structures, PS has been successfully used to fabricate many kinds of electric devices, such as nanogenerators [4, 5], sensors [6,7,8], transistors [9, 10], logic devices [11, 12] and so on.

To reveal the underlying mechanisms of electro-elastic coupling properties, many research works on PS are carried out. Zhang et al. [13, 14] demonstrated the carrier redistribution in ZnO nanofiber systematically and concluded how external load adjusts the electro-elastic fields thoroughly. Based on the mechanism of the interaction between stress and the electrical field quantities in PS, Fan et al. [15] proposed the potential barrier and well in semiconductor can be realized by applying piecewise stresses. Dai [16] and Zhang [17] et al. studied the carrier redistribution when the PS fiber undergoes bending deformation. By applying harmonic loads, Li [18] and Wang [19] et al. studied the forced vibration and revealed the charge carriers tend to reduce the efficiency of energy conversion in PS. When the acoustic waves propagate in PS, Yang [20, 21] and Gu [22] et al. found that the acoustic waves are amplified. Besides, Yang [23], Hu [24], Sladek [25] and Zhao [26] et al. analyzed the cracks in PS. As the element of integrated circuit, PN junction between p-type semiconductor and n-type semiconductor is also studied. Luo [27] and Guo [28] et al. studied the potential barrier and the carrier redistribution, as well as concluded the mechanism of interaction between load and electrical properties in a PS fiber with PN junction. Considering the thermoelasticity and pyroelectricity of ZnO, Cheng et al. [29, 30] studied the thermal induced carrier redistribution in single PS fiber and revealed the electrical and mechanical properties in a fiber with PN junction.

Notably, the functions in PS can also be realized in composite piezoelectric semiconductor structures, such as acoustoelectric effect [31] or acoustoelectric amplification [32]. Significantly, some new conclusions are obtained in composite piezoelectric semiconductor structures. By manipulating the thickness ratio between piezoelectric and semiconductor materials, the carrier distribution is sensitively altered [33, 34]. These studies explored a new approach to adjust the transportation of carriers. Besides, the composite structure which is composed by multiferroic magneto-electric materials and semiconductor is also studied [35, 36]. With magneto-electric coupling effect, the carrier in semiconductor can be driven by external magnetic field. This discovery enriches the method adjusting the carrier transportation. All of the discussions above show that the composite structure has great potential in semiconductor-based devices.

Apart from piezoelectric potential, flexoelectric potential could also be an alternative internal field driving the charge carrier. Zhao [37, 38] et al. analyzed the effects of flexoelectricity and strain gradient on the electrical or mechanical characteristics in PS nanowires. Sun [39] et al. studied the effect of flexoelectricity on piezotronic responses in PS bilayer structure. However, these studies treated the flexoelectricity as a kind of higher-order effect. Recently, the study on silicon [40] proved the existence of flexoelectric coupling in centrosymmetric semiconductors experimentally. And the concept of flexotronics, which concerns the flexoelectric potential-driven carrier transportation [41,42,43,44] mainly, is proposed.

However, the small flexoelectric coefficient limits the development of flexoelectric semiconductor (FS). To obtain considerable flexoelectric coupling, a beam with non-uniform cross section can be designed [45, 46]. Ren et al. [47] illustrated the variation of cross section can provide strain gradient. Inspired by this, the electro-elastic coupling properties in a FS fiber with non-uniform cross section are studied in this paper. And the mechanism of the interaction among load, electric potential and carrier will be explored.

Beginning with the basic theory of FS in Sect. 2.1, the theoretical model for a FS fiber with arbitrary cross section is established in Sect. 2.2. To solve the differential equations with variable coefficients, differential quadrature method is adopted to approximate the exact solutons in Sect. 3. In Sect. 4, the influences of cross section parameter, flexoelectric coefficient and initial carrier density on the field quantities are investigated. At the same time, the charge production is discussed. In Sect. 5, the potential barrier and well, which are induced by axial load or piecewise loads in symmetric non-uniform fiber, are studied. Furthermore, the distribution of perturbation carrier density in PN junction is also focused in Sect. 6. As a summary, some conclusions are drawn in Sect. 7.

2 Fundamental equations for flexoelectric semiconductor nanofiber

2.1 Basic theory of flexoelectric semiconductor

In this subsection, the basic theory for FS is reviewed briefly. To depict the electro-elastic coupling behaviors, the coupled field theory was developed. It consists of the equation of motion (Newton’s law), the charge equation of electro-static (Gauss’s law), and the conservations of charge for holes and electrons (continuity equations). Mathematically, the governing equations are expressed as [41,42,43]

$$\begin{gathered} T_{{{\it\text{ij}},j}} - \tau_{{{\it\text{ijk}},jk}} = \rho \ddot{u}_{i},\, D_{i,i} = q(p - n + N_{D}^{ + } - N_{A}^{ - } ), \hfill \\ J_{i,i}^{p} = - q\dot{p}, J_{i,i}^{n} = q\dot{n}, \hfill \\ \end{gathered}$$
(1)

where \(T_{ij}\) is the stress tensor, \(\tau_{ijk}\) represents the higher-order stress tensor, and \(\rho\) is mass density. \(u_{i}\) and \(D_{i}\), respectively, stand for the mechanical displacement tensor and electric displacement tensor, and q is the electronic charge. p and n are concentrations of holes and electrons, \(N_{D}^{ + }\) and \(N_{A}^{ - }\) denote the impurity concentrations of donors and accepters. \(J_{i}^{p}\) and \(J_{i}^{n}\) are hole and electron current densities, respectively. The superscript of dot means a time derivative, and repeated subscripts indicate summation operation. Besides, the corresponding constitutive relations describing material behaviors are given as

$$\begin{gathered} T_{{{\it\text{ij}}}} = c_{{{\it\text{ijkl}}}} S_{{{\it\text{kl}}}},\,\;\tau_{{{\it\text{ijk}}}} = g_{{{\it\text{ijklmn}}}} \eta_{{{\it\text{lmn}}}} - f_{{{\it\text{lijk}}}} E_{\it l},\;\,D_{i} = \varepsilon_{{{\it\text{ij}}}} E_{\it j} + f_{{{\it\text{ijkl}}}} \eta_{{{\it\text{jkl}}}} , \hfill \\ J_{i}^{p} = qp\mu_{{{\it\text{ij}}}}^{p} E_{j} - qd_{{{\it\text{ij}}}}^{p} p_{,j},\,\; J_{i}^{n} = qn\mu_{{{\it\text{ij}}}}^{n} E_{j} + qd_{{{\it\text{ij}}}}^{n} n_{,j} , \hfill \\ \end{gathered}$$
(2)

where \(c_{{{\it\text{ijkl}}}}\), \(g_{{{\it\text{ijklmn}}}}\), \(f_{{{\it\text{lijk}}}}\) and \(\varepsilon_{{{\it\text{ij}}}}\) are the elastic constants, higher material constants, flexoelectric constants and dielectric constants, respectively. Referencing to MarkusLazar [48], in order to simplify the higher gradient elasticity and to connect it with the nonlocal isotropic elasticity, the higher-order stress tensors are just simple gradients of the Cauchy-like stress tensor multiplied by two gradient coefficients. Thereby, higher material constants can be approximated by \(l_{0}^{2} c_{{{\it\text{ijlm}}}} \delta_{{{\it\text{kn}}}}\) based on strain gradient theory. Here, \(l_{0}\) is scale coefficient and \(\delta_{{{\it\text{kn}}}}\) is Kronecker delta. \(\mu_{{{\it\text{ij}}}}^{p}\) \(\left( {\mu_{{{\it\text{ij}}}}^{n} } \right)\) and \(d_{{{\it\text{ij}}}}^{p}\) \(\left( {d_{{{\it\text{ij}}}}^{n} } \right)\) represent the carrier mobility and carrier diffusion constants of holes (electrons). And the strain \(S_{{{\it\text{ij}}}}\), electric field \(E_{\it k}\) and strain gradient \(\eta_{{{\it\text{jkl}}}}\) can be expressed by the mechanical displacement \(u_{i}\) and electric potential \(\varphi\) via

$$S_{{{\it\text{ij}}}} = \frac{1}{2}(u_{i,j} + u_{j,i} ),\,\eta_{{{\it\text{jkl}}}} = S_{{{\it\text{jk}},l}},\,E_{k} = - \varphi_{,k} .$$
(3)

It should be noted that the nonlinear terms are contained in current densities, which cause the difficulty in deriving analytical solutions. For the purpose of simplifying derivation, linearization approach is introduced here, i.e.,

$$p = p_{0} + \Delta p,\,n = n_{0} + \Delta n,\,p_{0} = N_{A}^{ - } ,\,n_{0} = N_{D}^{ + } ,$$
(4)

where \(N_{A}^{ - }\) and \(N_{D}^{ + }\) are constants for the uniform impurities, and \(\Delta p\) and \(\Delta n\) are assumed as small perturbation for carrier concentration. With the help of linearization process, (1)2–4 and (2)4–5 can be rewritten as

$$D_{i,i} = q(\Delta p - \Delta n),\,\,J_{i,i}^{p} = - q\Delta \dot{p},\,\,J_{i,i}^{n} = q\Delta \dot{n},$$
(5)
$$J_{i}^{p} \cong qp_{0} \mu_{ij}^{p} E_{j} - qd_{ij}^{p} \Delta p_{,j},\,J_{i}^{n} \cong qn_{0} \mu_{ij}^{n} E_{j} + qd_{ij}^{n} \Delta n_{,j} .$$
(6)

The linear and homogeneous equations above can be utilized conveniently to analyze the electro-elastic coupling behaviors in FS within the small deformation assumption. After the geometric model and boundary conditions are given, the multi-field coupling problem can be solved mathematically.

2.2 One-dimensional model for flexoelectric semiconductor nanofiber

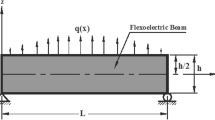
A fiber with arbitrary cross section is considered, and the sketch is given in Fig. 1. The fiber has fixed length L along x3 direction and height 2h along x1 direction. Herein, the width of the fiber is changed symmetrically in the form of \(b\left( {x_{3} } \right)\), where certain function describes corresponding profile. Besides, the material of semiconductor belongs to the class of crystal that is a centrosymmetric cubic (m3m) without the piezoelectric coupling.

Fig. 1
figure 1

Sketch of a FS fiber with non-uniform cross section

Full size image

Referencing to Fang [49], when a non-uniform fiber is stretched by external load along x3 direction, the variation of electrical properties in cross section is small and then its influences on the axial results are tiny. Therefore, the mechanical displacement, electric potential, and carrier concentration perturbation can be approximated by

$$\begin{gathered} u_{3} (x_{1} ,x_{2} ,x_{3} ,t) \cong u_{3} (x_{3} ,t),\,\,\varphi (x_{1} ,x_{2} ,x_{3} ,t) \cong \varphi (x_{3} ,t),\,\,\Delta p(x_{1} ,x_{2} ,x_{3} ,t) \cong \Delta p(x_{3} ,t), \hfill \\ \Delta n(x_{1} ,x_{3} ,t) \cong \Delta n(x_{3} ,t). \hfill \\ \end{gathered}$$
(7)

Correspondingly, the relevant strain S33, strain gradient \(\eta_{333}\) and electric field E3 can be expressed by

$$S_{33} = u_{3,3} , \eta_{333} = u_{3,33} , E_{3} = - \varphi_{,3} .$$
(8)

And the relevant stress \(T_{33}\), higher-order stress \(\tau_{333}\), electric displacement \(D_{3}\), and current densities \(J_{3}^{p}\) and \(J_{3}^{n}\) are given by

$$\begin{gathered} T_{33} = c_{33} u_{3,3},\,\tau_{333} = l_{0}^{2} c_{33} u_{3,33} + f_{3333} \varphi_{,3},\,D_{3} = - \varepsilon_{33} \varphi_{,3} + f_{3333} u_{3,33}, \hfill \\ J_{3}^{p} = - qp_{0} \mu_{33}^{p} \varphi_{,3} - qd_{33}^{p}\Delta p_{,3},\,J_{3}^{n} = - qn_{0} \mu_{33}^{n} \varphi_{,3} + qd_{33}^{n}\Delta n_{,3} . \hfill \\ \end{gathered}$$
(9)

Considering static problem, where the external load is constant, the time derivatives should be vanished. And the one-dimensional governing equations for axial deformation can be obtained, i.e.,

$$\begin{gathered} {}[c_{33} A(x_{3} )u_{3,3} - c_{33} l_{0}^{2} A(x_{3} )u_{3,333} - f_{3333} A(x_{3} )\varphi_{,33} ]_{,3} = 0, \hfill \\ [ - \varepsilon_{33} A(x_{3} )\varphi_{,3} + f_{3333} A(x_{3} )u_{3,33} ]_{,3} = qA(x_{3} )(\Delta p - \Delta n), \hfill \\ \left[ { - p_{0} \mu_{33}^{p} A(x_{3} )\varphi_{,3} - d_{33}^{p} A(x_{3} )\Delta p_{,3} } \right]_{,3} = 0, \hfill \\ \left[ { - n_{0} \mu_{33}^{n} A(x_{3} )\varphi_{,3} + d_{33}^{n} A(x_{3} )\Delta n_{,3} } \right]_{,3} = 0, \hfill \\ \end{gathered}$$
(10)

where \(A(x_{3} ) = 4b(x_{3} )h\) is the area of cross section. The governing equations can be used to explain the electro-elastic behaviors in FS fiber along axial direction. It can be found that Eq. (10) will degenerate to the governing equation investigating the pure flexoelectric fiber when semiconduction terms are dropped. In this paper, the FS fiber with extension deformation is one-dimensional problem, according to the research works on strain gradient [50], electric field gradient [51] and semiconductor [37], the general boundary conditions can be simplified and described as

$$\begin{gathered} u_{3} = \overline{u}_{3} \;{\text{or}}\;N = T_{33} + \tau_{333,3} = \overline{F},\,u_{3,3} = \overline{u}_{3,3} \;{\text{or}}\;\tau_{333} = \overline{\tau },\,\varphi = \overline{\varphi }\;{\text{or}}\;D_{3} = \overline{D}, \hfill \\ \Delta p = \Delta \overline{p}\;{\text{or}}\;J_{3}^{p} = \overline{J}_{3}^{p} ,\,\Delta n = \Delta \overline{n}\;{\text{or}}\;J_{3}^{n} = \overline{J}_{3}^{n} , \hfill \\ \end{gathered}$$

where \(\overline{u}_{3}\), \(\overline{F}\), \(\overline{u}_{3,3}\), \(\overline{\tau }\), \(\overline{\varphi }\), \(\overline{D}\), \(\Delta \overline{p}(\Delta \overline{n})\) and \(\overline{J}_{3}^{p} (\overline{J}_{3}^{n} )\) are the certain displacement, axial force, displacement gradient, higher-order stress, electric potential, electric displacement, perturbation carrier density and electric current, respectively. For a specific problem, these quantities will be determined to make the solutions of governing equations unique.

3 Extension of a flexoelectric semiconductor nanofiber

3.1 Description of the problem

In this paper, a non-uniform fiber which is stretched by constant load F at two free ends is taken into account, as shown in Fig. 2. Here, considering the boundaries are electrically isolated, i.e., there are no concentrated charges at both ends and no currents flow in or out at the ends. Therefore, the relevant boundary conditions are [37]

$$\begin{gathered} N_{3} (0) = N_{3} (L) = F,\,\tau_{333} (0) = \tau_{333} (L) = 0,\,D_{3} (0) = D_{3} (L) = 0, \hfill \\ J_{3}^{p} (0) = J_{3}^{p} (L) = 0,\,J_{3}^{n} (0) = J_{3}^{n} (L) = 0. \hfill \\ \end{gathered}$$
(11)
Fig. 2
figure 2

Sketch for a stretched non-uniform fiber

Full size image

It can be found that the electrically isolated conditions at both ends indicate \(J_{3}^{p} = J_{3}^{n} = 0\). In this situation, the subtraction between Eq. (10)3 and Eq. (10)4 yields

$$- \left( {p_{0} \frac{{\mu_{33}^{p} }}{{d_{33}^{p} }} + n_{0} \frac{{\mu_{33}^{n} }}{{d_{33}^{p} }}} \right)\varphi_{,3} = \left( {\Delta p - \Delta n} \right)_{,3}$$
(12)

Significantly, according to the Einstein relation, carrier mobility \(\mu_{33}^{p} (\mu_{33}^{n} )\) and the carrier diffusion constants \(d_{33}^{p} (d_{33}^{n} )\) satisfy

$$\frac{{\mu_{33}^{p} }}{{d_{33}^{p} }} = \frac{{\mu_{33}^{n} }}{{d_{33}^{n} }} = \frac{q}{{k_{B} T}},$$
(13)

where kB is the Boltzmann constant and T is the absolute temperature. Substituting Eq. (13) into Eq. (12) and integrating the resultant equation leads to

$$\Delta p - \Delta n = - \left( {p_{0} + n_{0} } \right)\frac{q}{{k_{B} T}}\varphi + C,$$
(14)

where \(C\) can be treated as reference value for any point in entire fiber, which does not influence the distribution of electric potential. Here, \(C = 0\) is acceptable.

Besides, according to the discussions in Cheng’s studies [30], a reference value for displacement should be given for unique solution. Generally, the reference value is assumed as the displacement at the middle point in a symmetric fiber. Referencing to Zhang [52], the reference value can also be predetermined at one of the ends in the fiber, which does not influence the distributions of displacement, electric potential or the other field quantities. In this paper, we select the left end (i.e., \(x_{3} = 0\)) as reference point. In this condition, \(u_{3} (0) = 0\) replaces \(N_{3} (0) = F\) as a new boundary condition.

Eliminating \(\Delta p - \Delta n\), the governing equations are simplified to

$$\begin{gathered} \left[ {c_{33} A(x_{3} )u_{3,3} - c_{33} l_{0}^{2} A(x_{3} )u_{3,333} - f_{3333} A(x_{3} )\varphi_{,33} } \right]_{,3} = 0, \hfill \\ [ - \varepsilon_{33} A(x_{3} )\varphi_{,3} + f_{3333} A(x_{3} )u_{3,33} ]_{,3} + A(x_{3} )\frac{{q^{2} \left( {p_{0} + n_{0} } \right)}}{{k_{B} T}}\varphi = 0. \hfill \\ \end{gathered}$$
(15)

Solving Eq. (15), the electro-elastic fields in FS can be analyzed under the boundary conditions. Furthermore, the influences of all parameters on the electro-elastic coupling properties can be revealed.

3.2 Solutions

Obviously, the governing equations are the differential equations with variable coefficients, which are hard to look for analytical solutions. To study the problem that is described in Sect. 3.1, differential quadrature method (DQM) is adopted in this paper [53]. In DQM, a continuous function can be approximated by a linear sum of weighted coefficients and function values at all discrete points. According to the discrete rule of DQM, the unknown displacement \(u_{3}\), electric potential \(\varphi\) and the values at j-th point for their k-th derivatives can be expressed by

$$\left\{ {u_{3} (\xi ),\varphi (\xi )} \right\} = \sum\limits_{j = 1}^{N} {L_{j} (\xi )} \left\{ {U_{j} ,\Phi_{j} } \right\},\, \left\{ {u_{3}^{(k)} (\xi_{i} ),\varphi^{(k)} (\xi_{i} )} \right\} = \sum\limits_{j = 1}^{N} {C_{ij}^{(k)} } \left\{ {U_{j} ,\Phi_{j} } \right\},$$
(16)

where \(U_{j}\) and \(\Phi_{j}\) are the values of \(u_{3}\) and \(\varphi\) at jth discrete point, \(\xi = x_{3} /L\) is non-dimensional coordinate, \(L_{j} (\xi )\) is Lagrange interpolation polynomials, \(C_{ij}^{(k)}\) is k-th weighting coefficient, which is calculated by using recurrence relationship, the subscriptions i and j index the number of discrete points. Notably, the discrete points are selected in the pattern of

$$\xi_{j} = \frac{1}{2}\left[ {1 - \cos \frac{{(j - 1){\uppi }}}{N - 1}} \right],\,\,j = 1,2,3,...,N.$$
(17)

Applying the DQM to Eq. (15) yields algebraic equations respecting \(u_{j}\)and \(\varphi_{j}\),i.e.,

$$\begin{aligned}& \frac{{c_{33} }}{L}A_{,3} (\xi_{i} )\sum\limits_{j = 1}^{N} {C_{ij}^{(1)} } U_{j} - \frac{{c_{33} }}{{L^{3} }}l_{0}^{2} A_{,3} (\xi_{i} )\sum\limits_{j = 1}^{N} {C_{ij}^{(3)} } U_{j} - \frac{{f_{3333} }}{{L^{2} }}A_{,3} (\xi_{i} )\sum\limits_{j = 1}^{N} {C_{ij}^{(2)} } \Phi_{j} \hfill \\ &\quad +\frac{{c_{33} }}{{L^{2} }}A(\xi_{i} )\sum\limits_{j = 1}^{N} {C_{ij}^{(2)} } U_{j} - \frac{{c_{33} }}{{L^{4} }}l_{0}^{2} A(\xi_{i} )\sum\limits_{j = 1}^{N} {C_{ij}^{(4)} } U_{j} - \frac{{f_{3333} }}{{L^{3} }}A(\xi_{i} )\sum\limits_{j = 1}^{N} {C_{ij}^{(3)} } \Phi_{j} = 0, \hfill \\ &\quad i = 3,4,...,N - 2;j = 1,2,...,N, \hfill \\ &\quad - \frac{{\varepsilon_{33} }}{L}A_{,3} (\xi_{i} )\sum\limits_{j = 1}^{N} {C_{ij}^{(1)} } \Phi_{j} + \frac{{f_{3333} }}{{L^{2} }}A_{,3} (\xi_{i} )\sum\limits_{j = 1}^{N} {C_{ij}^{(2)} } U_{j} - \frac{{\varepsilon_{33} }}{{L^{2} }}A(\xi_{i} )\sum\limits_{j = 1}^{N} {C_{ij}^{(2)} } \Phi_{j} + \hfill \\ &\quad \frac{{f_{3333} }}{{L^{3} }}A(\xi_{i} )\sum\limits_{j = 1}^{N} {C_{ij}^{(3)} } U_{j}+ A(\xi_{i} )\frac{{q^{2} (p_{0} + n_{0} )}}{{k_{B} T}}\Phi_{i} = 0, \hfill \\ &\quad i = 2,3,...,N - 1;j = 1,2,...,N. \hfill \\ \end{aligned}$$
(18)

In the derivations before, the boundary conditions \(J_{3}^{p} (0) = J_{3}^{p} (L) = J_{3}^{n} (0) = J_{3}^{n} (L) = 0\) have been considered, which are not discussed later. It should be emphasized that the fiber is treated as electrically neutral for the reference state, the perturbation carrier density must satisfy the global charge neutrality conditions \(\int_{0}^{L} {A\Delta p} dx_{3} = 0\) and \(\int_{0}^{L} {A\Delta n} dx_{3} = 0\). Only one of them is independent. For pure p-type or n-type semiconductor, the global charge neutrality condition is satisfied automatically by integrating the Eq. (10)2 along the length under the electrically isolated boundary conditions. Now, the unsatisfied boundary conditions can be rewritten as

$$\begin{gathered} u_{3} (0) = 0, \, U_{1} = 0, \hfill \\ N_{3} (L) = F, \, \,\frac{{c_{33} }}{L}A(\xi_{N} )\sum\limits_{j = 1}^{N} {C_{Nj}^{(1)} } U_{j} - \frac{{c_{33} }}{{L^{3} }}l_{0}^{2} A(\xi_{N} )\sum\limits_{j = 1}^{N} {C_{Nj}^{(3)} } U_{j} - \frac{{f_{3333} }}{{L^{2} }}A(\xi_{N} )\sum\limits_{j = 1}^{N} {C_{Nj}^{(2)} } \Phi_{j} = F,\,\, \hfill \\ \tau_{333} (0) = 0, \, \,\frac{{c_{33} }}{{L^{2} }}l_{0}^{2} \sum\limits_{j = 1}^{N} {C_{1j}^{(2)} } U_{j} + \frac{{f_{3333} }}{L}\sum\limits_{j = 1}^{N} {C_{1j}^{(1)} } \Phi_{j} = 0, \,\,\hfill \\ \tau_{333} (L\,) = 0, \, \frac{{c_{33} }}{{L^{2} }}l_{0}^{2} \sum\limits_{j = 1}^{N} {C_{Nj}^{(2)} } U_{j} + \frac{{f_{3333} }}{L}\sum\limits_{j = 1}^{N} {C_{Nj}^{(1)} } \Phi_{j} = 0, \,\,\hfill \\ D_{3} (0) = 0, \, - \frac{{\varepsilon_{33} }}{L}\sum\limits_{j = 1}^{N} {C_{1j}^{(1)} } \Phi_{j} + \frac{{f_{3333} }}{{L^{2} }}\sum\limits_{j = 1}^{N} {C_{1j}^{(2)} } U_{j} = 0, \,\,\hfill \\ D_{3} (L) = 0, \, - \frac{{\varepsilon_{33} }}{L}\sum\limits_{j = 1}^{N} {C_{Nj}^{(1)} } \Phi_{j} + \frac{{f_{3333} }}{{L^{2} }}\sum\limits_{j = 1}^{N} {C_{Nj}^{(2)} } U_{j} = 0, \,\, \hfill \\ j = 1,2,...,N. \hfill \\ \end{gathered}$$
(19)

Equation (18) and Eq. (19) give a linear algebraic equation system, which can be used to solve the unknown values for displacement and electric potential at discrete points. With the help of derivations above, the differential equations with variable coefficients can be solved conveniently.

4 Electro-elastic fields in non-uniform FS nanofiber

In this section, we consider a p-type semiconductor for numerical analysis. Correspondingly, the initial carrier concentration n0 and perturbation carrier density \(\Delta n\) are eliminated from the derivations in Sect. 3. Here, a common used FS material Si is selected for numerical calculation. The relevant parameters are [42]

$$\begin{gathered} c_{{33}} = 165.7\;{\text{GPa}},\;\varepsilon _{{33}} = 0.1035 \times 10^{{ - 9}} {\text{F/m}},\;f_{{3333}} = 1 \times 10^{{ - 9}} {\text{C/m}},\;l_{0} = 1 \times 10^{{ - 9}} {\text{m}}, \hfill \\ p_{0} = 1 \times 10^{{20}} /{\text{m}}^{3} ,\;k_{B} T/q = 0.026{\text{V}},\;L = 1200\;{\text{nm}},\;h = 100\;{\text{nm}},\;F = 1\;{\text{nN}}. \hfill \\ \end{gathered}$$

In this paper, the variation of the cross section is focused, correspondingly, the variation pattern of the fiber should be given firstly. Reviewing the studies of Ren [47] and Fang [49], the linear profile and quadratic profile could lead to similar results. Consequently, only linear profile is selected as example, i.e., the width of the fiber varies in the form of

$$b(x_{3} ) = B\left( {1 - \lambda \frac{{x_{3} }}{L}} \right),$$
(20)

where B = 100 nm is the width at left end (\(x_{3} = 0\)) and the parameter \(\lambda\) varies in the range (0,1), which manipulates the shape of the fiber.

4.1 Convergence and validation

Before analysis, a proper number of grid point should be determined, which needs to satisfy the convergence requirement and ensure enough accuracy. After investigating different numbers of grid point, N = 150 for DQM provides enough convergence. Besides, to prove the correctness of the results from DQM in this paper, finite element method (FEM) is performed based on COMSOL Multiphysics software. The comparisons between the results from DQM and FEM are given in Fig. 3, where \(\lambda = 0.1,0.2,0.3,0.4,0.5\) are investigated, respectively. It can be observed that the DQM’s results coincide well with FEM’s results, as a result, the correctness of DQM is proved. In Fig. 4. the comparisons for the displacement and electric potential between linear and nonlinear theories [54] are carried, in which, the description on nonlinear theory can be found in Appendix 1. From the calculated results, it can be found the results from this paper are very close to the nonlinear results. It indicates the derivations in this paper are suitable to explain the underlying mechanisms of flexoelectric semiconductor accurately.

Fig. 3
figure 3

The comparisons between FEM and DQM. a Displacement \(u_{3}\); b Electric potential \(\varphi\)

Full size image
Fig. 4
figure 4

The comparisons between linear and nonlinear results. a Displacement \(u_{3}\); b Electric potential \(\varphi\)

Full size image

4.2 Effects of \(\lambda\) on the electro-elastic field quantities

To illustrate how the variation of cross section changes the electro-elastic field quantities, Fig. 5 gives the strain gradient \(\eta_{333}\), electric field \(E_{3}\), polarization \(P_{3}\) and perturbation carrier density \(\Delta p\). The polarization vector can be calculated through \(P_{3} = D_{3} - \varepsilon_{0} E_{3}\). The perturbation carrier can be obtained based on Eq. (14) by ignoring \(n_{0}\) and \(\Delta n\).

In Fig. 5a, it can be seen that the increment of \(\lambda\) increases the strain gradient for entire fiber. At the same time, the strain gradient increases along the axial direction for each given \(\lambda\). This phenomenon comes from the variation of stiffness. When \(\lambda\) is set in the range (0,1), the stiffness of entire fiber is cut down along axial direction continuously. Especially for right end, the stiffness reaches the minimum value. Therefore, it can be concluded that a large \(\lambda\) induces large strain gradient. Because of the increased strain gradient, the electric potential difference between two ends in the fiber is also increasing as shown in Fig. 3b. In Fig.5b and c, electric field and polarization are given, where the absolute values of these two quantities have similar tendency with strain gradient. It indicates the electric field and polarization are closely related to the strain gradient in FS. Driven by internal electric potential, more perturbation carriers are produced and reach the maximum values at the right end. From the calculated results, it can be concluded that the rapid variation of cross section produces large fields and the maximum values of field quantities appear in the zone whose stiffness is minimum in entire fiber. Furthermore, comparing the results for different \(\lambda\), it can also be concluded that the flexoelectric effect is enhanced by the variation of the cross section.

Fig. 5
figure 5

The effects of \(\lambda\) on the electro-elastic field quantities. a Strain gradient; b electric field; c Polarization; d Perturbation carrier density

Full size image

4.3 Effects of \(f_{3333}\) on the electrical field quantities

The flexoelectric coefficient \(f_{3333}\) is an electrical parameter, which mainly influences the electrical properties. In this section, the effects of \(f_{3333}\) on the electric potential, electric field, polarization and perturbation carrier density are focused, as shown in Fig. 6. Cooperating with the non-uniform cross section, all electrical field quantities exhibit the tendency of increment when the flexoelectric coefficient is set from \(0.5 \times 10^{ - 9} {\text{C/m}}\) to \(2.5 \times 10^{ - 9} {\text{C/m}}\). Especially, at the narrow end, the increments of field quantities are much faster than them at the broad end. Although a distinct flexoelectric effect can be observed with the help of non-uniform cross section, the values of all field quantities are still relative small in Si. For the purpose of obtaining considerable values of field quantities, another way to further enhance the flexoelectric effect should be explored on the basis of this paper. Or, a new FS material with large flexoelectric coefficient should be found to replace Si. For the purpose of this paper, we can conclude the general tendencies of flexoelectric effect from the calculated results, which provide useful reference data to study similar FS material in the future. In view of this, the study in this paper is still meaningful.

Fig. 6
figure 6

The effects of \(f_{3333}\) on the electro-elastic fields. a Electric potential; b Electric field; c Polarization; d Perturbation carrier density

Full size image

4.4 Effects of \(p_{0}\) on the electrical field quantities

As a parameter which can be adjusted artificially in experiment or engineering application, the effect of initial carrier density \(p_{0}\) on the electrical field quantity is not negligible. Figure 7 gives the electrical field quantities for different given initial carrier densities. Because the carrier screening effect, the electric potential and electric field are decreasing, however, the polarization and perturbation carrier density are increasing. It can also be found that the variation is relatively small when the initial carrier density is smaller than \(1 \times 10^{19} /{\text{m}}^{{3}}\). On the contrary, the variations in all results become much faster once the initial carrier density is larger than \(1 \times 10^{19} /{\text{m}}^{{3}}\). The reason for this phenomenon is because the low concentration doping cannot produce more carriers, while there are not enough free carrier screening the electric potential. For high concentration doping, more carriers are produced and the screening effect becomes stronger.

Fig. 7
figure 7

The effects of \(p_{0}\) on the electrical field quantities. a Electric potential; b Electric field; c Polarization; d Perturbation carrier density

Full size image

4.5 Charges in the non-uniform FS fiber

As a material which can realize the conversion between mechanical load and electrical properties, we prefer to concern the charge production in the fiber. Based on the results above, the expression of carrier charges is \(q\Delta p\) and total charge can be calculated through \(\rho^{t} = q\Delta p + \rho^{P} .\) Here, \(\rho^{P} = - P_{3,3}\) is polarization charge. Figure 8 gives the carrier charges and total charges at narrow end for different initial carrier densities when parameter \(\lambda\) varies in the range from 0.1 to 0.9. No matter for carrier charge or for total charge, the values are increasing in the form of approximate exponential rule. It illustrated that the adjustment method manipulating the cross section is feasible. It can be observed that the influence of initial carrier density on carrier charge is distinct. However, there are few influence of initial carrier density on total charge. Besides, the magnitude of total charge is much larger than carrier charge. It indicates that the total charge is dominated by polarization charge.

Fig. 8
figure 8

The charge at the narrow end. a Carrier charge; b Total charge

Full size image

5 Potential barriers and wells in non-uniform FS nanofiber

5.1 The non-uniform fiber under axial load

To further illustrate how non-uniform cross section adjusts electrical properties in FS fiber, two symmetric non-uniform FS fibers are considered in this subsection, as shown in Fig. 9. These two fibers are stretched by a pair of external load at the two ends. Differently, the profile is concave in Fig. 9a and is convex in Fig. 9b. Dividing each fiber into two parts, and setting the local coordinates beginning from the left of each part. The local coordinates are denoted as \(x^{\prime}_{3}\) and \(x^{\prime\prime}_{3}\), respectively. The length for each part is \(L_{1}\). In the given local coordinates, the widths vary in the form of

$$b = \left\{ {\begin{array}{*{20}c} {B\left( {1 - \lambda \frac{{x^{\prime}_{3} }}{{L_{1} }}} \right)} & \,\,{0 \le x^{\prime}_{3} < L_{1} } \\ {B\left[ {1 - \lambda \left( {1 - \frac{{x^{\prime\prime}_{3} }}{{L_{1} }}} \right)} \right]} & \,\,{0 \le x^{\prime\prime}_{3} \le L_{1} } \\ \end{array} } \right.$$
(21)

for the fiber with concave profile and

$$b = \left\{ {\begin{array}{*{20}c} {B\left[ {1 - \lambda \left( {1 - \frac{{x^{\prime}_{3} }}{{L_{1} }}} \right)} \right]} & \,\,{0 \le x^{\prime}_{3} < L_{1} } \\ {B\left( {1 - \lambda \frac{{x^{\prime\prime}_{3} }}{{L_{1} }}} \right)} & \,\,{0 \le x^{\prime\prime}_{3} \le L_{1} } \\ \end{array} } \right.$$
(22)

for the fiber with convex profile.

Fig. 9
figure 9

The sketch of the fiber with axial load

Full size image

To describe the electrical properties in the given fibers, the governing equation (i.e., Equation (15)) is still valid for each part. However, the boundary conditions should be reconsidered. For part I, the boundary conditions at left end are

$$N^{\prime}_{3} (x^{\prime}_{3} = 0) = F,\,\tau^{\prime}_{333} (x^{\prime}_{3} = 0) = 0,\,D^{\prime}_{3} (x^{\prime}_{3} = 0) = 0.$$
(23)

For part II, the boundary conditions at right end are

$$N^{\prime\prime}_{3} (x^{\prime\prime}_{3} = L_{1} ) = F,\,\tau^{\prime\prime}_{333} (x^{\prime\prime}_{3} = L_{1} ) = 0,\,D^{\prime\prime}_{3} (x^{\prime\prime}_{3} = L_{1} ) = 0.$$
(24)

At the interface between two parts, the continue conditions should be set, i.e.,

$$\begin{gathered} u^{\prime}_{3} (x^{\prime}_{3} = L_{1} ) = u^{\prime\prime}_{3} (x^{\prime\prime}_{3} = 0), \,N^{\prime}_{3} (x^{\prime}_{3} = L_{1} ) = N^{\prime\prime}_{3} (x^{\prime\prime}_{3} = 0), \hfill \\ u^{\prime}_{3,3} (x^{\prime}_{3} = L_{1} ) = u^{\prime\prime}_{3,3} (x^{\prime\prime}_{3} = 0), \,\tau^{\prime}_{333} (x^{\prime}_{3} = L_{1} ) = \tau^{\prime\prime}_{333} (x^{\prime\prime}_{3} = 0), \hfill \\ \varphi^{\prime} (x^{\prime}_{3} = L_{1} ) = \varphi^{\prime\prime} (x^{\prime\prime}_{3} = 0),\, D^{\prime}_{3} (x^{\prime}_{3} = L_{1} ) = D^{\prime\prime}_{3} (x^{\prime\prime}_{3} = 0). \hfill \\ \end{gathered}$$
(25)

Here, in order to fix the reference point for displacement, \(N^{\prime}_{3} (x^{\prime}_{3} = 0) = F\) is replaced by \(u^{\prime}_{3} (x^{\prime}_{3} = 0) = 0\) again. Applying the DQM to solve the governing equations under the given boundary conditions and continuity conditions for two parts, the solutions can be obtained. In the following studies, \(L_{1} = 600\,{\text{nm}}\) is assumed. In this subsection, we prefer to concern the distribution of electric potential. Figure 10a and b give the electric potentials for the fiber with concave profile and convex profile in global coordinate, respectively. It can be observed that the electric potential is symmetric respects to \(x_{3} = 0.6{\upmu} \text{m}\), which is quite different from the pattern in piezoelectric semiconductor [49]. There are potential barriers and potential wells in the non-uniform fibers. They prevent the mobile charge, whose initial velocity or kinetic energy is not large enough, traveling through the fiber. This phenomenon can be explained from the view of mathematics. The different distributions between FS fiber and PS fiber in symmetric structure are because the derivative of electric potential for FS is one order higher than it for PS fiber in the established model. It can also be explained that the electric potential is induced by the strain gradient, therefore, a symmetric strain gradient produces symmetric electric potential. In addition, it can be found that the potential barrier and well can be adjusted by manipulating the shape of cross section. With the increasing of parameter \(\lambda\), the higher potential barrier and deeper potential well can be set as shown in Fig. 10.

Fig. 10
figure 10

The distributions of electric potential in non-uniform fiber. a In the fiber with concave profile; b In the fiber with convex profile

Full size image

5.2 The non-uniform fiber with piecewise loads

Referencing to Fan et al. [15], the potential barrier or well can be induced by piecewise stresses. Inspired by this, we consider two fibers with piecewise loads, as shown in Fig. 11, where the part I is compressed and the part II is stretched. Comparing to Fig. 10, the electric potential exhibits quite different distribution rule along the axial direction, as shown in Fig. 12. In the same fiber, the potential barrier and well appear at the two sides of middle point because of the asymmetric strain gradient. With the increasing of parameter \(\lambda\), the electric potential difference is getting larger at the middle position in the fiber with concave profile. However, for the fiber with convex profile, the electric potential difference is changed distinctly at both ends. These phenomena confirm the conclusion that the maximum values of field quantities appear at the zone whose stiffness is minimum in entire fiber again.

Fig. 11
figure 11

The sketch of a fiber with piecewise loads

Full size image
Fig. 12
figure 12

The distributions of electric potential under piecewise loads. a In the fiber with concave profile; b In the fiber with convex profile

Full size image

6 Carrier redistribution in non-uniform PN junction

In the studies above, only p-type semiconductor is investigated. In this section, a PN junction which subjects to axial load is considered, as shown in Fig. 13. For part I, the initial carrier density for hole (electron) is denoted as \(p^{\prime}_{0}\) (\(n^{\prime}_{0}\)). In part II, the initial carrier density for hole (electron) is denoted as \(p^{\prime\prime}_{0}\) (\(n^{\prime\prime}_{0}\)). Here, \(p^{\prime}_{0} = n^{\prime\prime}_{0} = 0.8 \times 10^{20} {\text{/m}}^{3}\) and \(n^{\prime}_{0} = p^{\prime\prime}_{0} = 0.2 \times 10^{20} {\text{/m}}^{{3}}\) are assumed. When Eq. (15) is adopted, it can be found the distribution of electric potential in this section is same to it in Fig. 10, therefore, only the distribution of perturbation carrier density is focused here. Figure 14 gives the distributions of perturbation carrier density for the fibers with concave profile and convex profile, respectively. Because of the different initial carrier densities in two parts, no matter for holes or electrons, there are jumps at the interface for perturbation carrier density.

Fig. 13
figure 13

The sketch of PN junction between two non-uniform FS fibers

Full size image
Fig. 14
figure 14

The distributions of perturbation carrier densities. a \(\Delta p\) in the fiber with concave profile; b \(\Delta n\) in the fiber with concave profile; c \(\Delta p\) in the fiber with convex profile; d \(\Delta n\) in the fiber with convex profile

Full size image

For the same fiber, the distribution pattern for \(\Delta p\) is opposite to \(\Delta n\). For holes, the majority perturbation carriers exist in the part I. On the contrary, the majority perturbation carriers exist in the part II for electrons. Comparing two kinds of fibers, the majority perturbation carriers appear in the zone near the middle position for a fiber with concave profile. Differently, in the fiber with convex profile, the majority perturbation carriers appear in the zone near the narrow sides. The calculated results indicate that the perturbation carrier density near the interface can be conveniently adjusted by manipulating the shape of cross section to satisfy the requirements in experiment or engineering application.

7 Conclusions

Based on the flexoelectric semiconductor theory, the theoretical model for non-uniform fiber is established. The DQM is introduced to solve the governing equations with variable coefficients and reveal the mechanism how non-uniform cross section adjusts the electro-elastic properties in the FS fibers. Before analysis, the 150 grid points are determined for DQM to ensure enough accuracy. Comparing with the results which are calculated by FEM, the correctness of DQM is proved.

In p-type non-uniform FS fiber, the large electro-elastic field quantities can be produced by a quick variation of cross section along the axial direction. Especially, near the narrow ends, all quantities reach the maximum values. To reveal the underlying mechanisms of FS fiber, the influences of cross section parameter, flexoelectric coefficient and initial carrier density on the electrical properties are investigated. It is found that the electrical properties are sensitive to these parameters. Besides, the investigation about charge production indicates the total charge in the narrow end is dominated by polarization charge. To further illustrate the generality of the theoretical model and DQM, two kinds of fibers with concave and convex profiles are investigated, respectively. Stretched by axial load, there are potential barrier and potential well in the fibers with concave profile and convex profiles, respectively. From the view of mathematics and physics, the reason for this phenomenon is explained in detail. In addition, when the fibers subject to piecewise loads, it is found that the distributions of electric potential are asymmetric. In the end, we investigated the carrier redistribution in non-uniform fibers with PN junction. The calculated results indicate that the distribution of perturbation carrier density can be conveniently adjusted by manipulating the shape of cross section according to the requirements of applications.

In this paper, only the approach manipulating the cross section is adopted to adjust the electro-elastic properties. In the future, the functionally graded fiber or non-uniform composite fiber can also be the objects to study. In these studies, the DQM is still valid to deal with the relevant mathematical models. After surveying the performances which are adjusted by different approaches, the mechanisms of the interaction between mechanical and electrical properties in FS can be revealed thoroughly. These studies might be the guidance for the applications of FS material or the manufacture of smart devices.