Exact solutions for flexoelectric response in elastic dielectric nanobeams considering generalized constitutive gradient theories

Abstract

This paper deals with the derivation of the exact solutions for the static flexoelectric response of a simply supported dielectric nano-beam subjected to distributed mechanical and electrical loads. The governing differential equations and the boundary conditions are obtained based on the Gibbs free energy for linear dielectrics considering the strain and the electrical field gradients, and their conjugates in the form of the higher order stresses and higher order polarization fields. The trends and observations from the current study are compared with the literature. The electro-mechanical coupling observed from the current model is compared for different electrical boundary conditions. The polarization and the electric field profiles across the thickness, developed due to the direct effect are also presented. Due to the use of gradient field energies, and a subsequent evaluation of their conjugates, the size effects are better exhibited by the current model than the models in the literature derived without considering strain and electric field gradients. The present study suggests that upon considering strain gradient elasticity the sensitive nature of flexoelectric nanosensors, nano energy harvesters and nanoactuators is realized. The exact solutions developed in this paper may be used as benchmark solutions for further research on flexoelectric solids.

1 Introduction

Extensive research is carried out on the investigation of electro-mechanical coupling in dielectric materials. There exist numerous models based on continuum modelling of the system to study the elastic response of a dielectric body. The early continuum models have been postulated by Toupin (1956) and Mindlin (1968) for an elastic dielectric body. One of the popular dielectric materials exhibiting the electro-mechanical coupling is the piezoelectric material. Such materials generate an electric charge upon application of a strain, and are deformed due to the applied electric field. The structures usually studied for piezoelectric effects have dimensions large enough to ignore the effects of the strain gradient and electric field gradient proposed in the model by Mindlin (1968). The improvements in computational technology and micro and nano-fabrication techniques have led to the development of micro and nano electromechanical systems. The gradient effects at the micro- and nano-scale on the system response are compelling (Fleck et al. 1994; Fleck and Hutchinson 1993, 1997, 2001). The phenomenon by virtue of which a dielectric material develops electric polarization because of the presence of strain gradient is called the direct flexoelectric effect. On the other hand due to the converse flexoelectric effect, a dielectric material undergoes deformation upon application of electric field gradient. Such flexoelectric effect is significant in the low-dimensional dielectric structures (Maranganti et al. 2006).

Initially, the flexoelectric effects were theorized in crystals by Mashkevich (1957). Further understanding of the effect was provided by Kogan (1964) and Harris (1965). With the continuum models by Mindlin in place, the computation of the coupling coefficients were accomplished based on experiments on various dielectrics by Cross (2006) and Ma and Cross (2001). Theoretically, these coefficients were estimated by Sharma et al. (2007, 2010) and Yudin and Tagantsev (2013). The huge disparity in theoretical and experimental results opened a very attractive field of research on material modelling.

Continuum models postulated for the electromechanical coupled systems were further advanced for flexoelectric systems, taking the surface and size effects into consideration (Hu and Shen 2010; Shen and Hu 2010). Using such models, the flexoelectric response in different nanostructures have been investigated by Yan and Jiang (2013a, 2015), Ray (2014, 2016), Liang et al. (2014, 2017), Zhang et al. (2016) and Yang et al. (2015). For any continuum body, the mechanical response to an applied load is obtained as a solution of its governing differential equations. This is also called the solution of the strong form of the governing equations of the system, or the exact solution of the system. Such exact solutions, obtained without any a priori assumptions should be the benchmark solutions for comparing the results from approximate analytical and numerical methods, which are based on simplified assumptions. Given the infancy of the field, such benchmarks are essential for flexoelectric structures. Analytical solutions for flexoelectric systems are available for the Euler–Bernoulli cantilever beam (Liang et al. 2014; Yan and Jiang 2013b), Timoshenko dielectric beam (Zhang et al. 2016), simply supported beam (Ray 2014), dielectric nano-rings (Yan 2017) and plates based on classical plate theory (Yang et al. 2015). However, most of these works have assumed a displacement field (Liang et al. 2014; Zhang et al. 2016; Yang et al. 2015; Yan and Jiang 2013b), or taken a uniform electric field across the volume (Liang et al. 2014; Zhang et al. 2016; Yang et al. 2015; Yan and Jiang 2013b), or have not considered the complete effects of the presence of gradients (Ray 2014). Numerical solutions to these models following the above mentioned assumptions are also available using Finite Element Methods (FEM) (Choi and Kim 2017), Meshfree methods (Ray 2017; Abdollahi et al. 2014), Mixed-Finite Element formulation (Mao et al. 2016). Moreover, with the flexoelectric effect being linearly proportional to the gradient effects, the full scope of the flexoelectric effect cannot be realized in such formulations. Considering the gradient effects, partially, an exact solution has been proposed for a simply supported beam by Ray (2014). This paper presented the exact solutions for the dielectric nano-beam under applied mechanical and electrical loads. However, unlike the piezoelectric behavior, which exhibits coupling between the strain and electric field, thereby being energy conjugates of one other, the flexoelectric behavior does not exhibit such symmetry. Since, the strain gradients develop an electric field and electric field gradient causes mechanical strain in a flexoelectric body, the field gradients are not mutually conjugate to each other. The model presented by Ray (2014) did not consider the energy conjugates of strain gradient and electric field gradients for formulating the constitutive relations. For micro- and nano-structures, where the gradients can be very high, consideration of these gradients and gradient conjugates in the energy functional is expected to exhibit a stronger electromechanical coupling. The current paper is a step towards the complete energy formulation of the flexoelectric domains. The current model takes the higher order stresses and higher order electric fields into consideration while accounting the energy functional of the system . The objective of this investigation is to derive the exact solutions for the flexoelectric response of a simply supported dielectric beam activated by the combined mechanical and electric loads have been derived.

2 Flexoelectric constitutive modelling

The Gibbs free energy density U for a centro-symmetric dielectric solid, as a function of the strain, the electric field and their gradients, can be written for the dielectrics (Hu and Shen 2009, 2010; Abdollahi et al. 2014, Yan and Jiang 2011) as:

$$\begin{aligned} U=-\frac{1}{2}{\varvec{E}}\cdot {\varvec{a}}\cdot {\varvec{E}}-\frac{1}{2}{\varvec{V}}:{\varvec{b}}:{\varvec{V}}+\frac{1}{2}{\varvec{\epsilon }}:{\varvec{C}}:{\varvec{\epsilon }}-{\varvec{\epsilon }}:{\varvec{e}}:{\varvec{V}}-{\varvec{E}}\cdot {\varvec{\mu }}\vdots {\varvec{\eta }}+\frac{1}{2}{\varvec{\eta }}\vdots {\varvec{g}}\vdots {\varvec{\eta }} \end{aligned}$$

(1)

where $a_{ij}$ and $C_{ijkl}$ are the second order dielectric permittivity tensor and the fourth order elastic coefficient tensor, respectively, $e_{ijkl}$ and $\mu _{ijkl}$ are the direct and the converse flexoelectric tensors, respectively, while they are related as $e_{ijkl}=- \mu _{ijkl}$. Here, ${\varvec{\epsilon }}$ and ${\varvec{\eta }}$ are the strain and the strain gradient tensors, respectively, given by

$$\begin{aligned} {\varvec{\epsilon }}=\frac{1}{2}\left( {\varvec{\nabla }} \otimes {\varvec{u}}+{\varvec{u}}\otimes {\varvec{\nabla }}\right) ,\quad {\text {and}}\quad {\varvec{\eta }}={\varvec{\epsilon }}\otimes {\varvec{\nabla }} \end{aligned}$$

(2)

where ${\varvec{u}}$ denotes the displacement vector. The electric field vector ${\varvec{E}}$ and the second-order electric field gradient tensor ${\varvec{V}}$ are given by

$$\begin{aligned} {\varvec{E}}=-{\varvec{\nabla }}\phi ,\quad {\text {and}}\quad {\varvec{V}}=-{\varvec{\nabla }}\otimes {\varvec{\nabla }}\phi \end{aligned}$$

(3)

where $\phi$ is the scalar electric potential field within the volume. The linear constitutive equations expressed in terms of the free energy density U can be written as (Hu and Shen 2009, 2010; Yan and Jiang 2011; Abdollahi et al. 2014):

$$\begin{aligned} {\varvec{\sigma }}&=\frac{\partial U}{\partial {\varvec{\epsilon }}}={\varvec{C}}:{\varvec{\epsilon }}-{\varvec{e}}:{\varvec{V}} , \end{aligned}$$

(4a)

$$\begin{aligned} {\varvec{\tau }}&=\frac{\partial U}{\partial {\varvec{\eta }}}={\varvec{g}} \vdots {\varvec{\eta }}-{\varvec{E}}\cdot {\varvec{\mu }}, \end{aligned}$$

(4b)

$$\begin{aligned} {\varvec{D}}&=-\frac{\partial U}{\partial {\varvec{E}}}={\varvec{a}}\cdot {\varvec{E}}+{\varvec{\mu }}\vdots {\varvec{\eta }}, \end{aligned}$$

(4c)

$$\begin{aligned} {\varvec{Q}}&=-\frac{\partial U}{\partial {\varvec{V}}}={\varvec{b}}:{\varvec{V}}+{\varvec{\epsilon }}:{\varvec{e}} \end{aligned}$$

(4d)

Here $\sigma _{ij}$ and $D_{i}$ are the conventional stress and the electric displacement field tensors, respectively, and $\tau _{ijk}$ and $Q_{ij}$ are the higher-order stress (moment stress) and the electric quadrupoles, respectively. The sixth-order material elastic tensor ${\varvec{g}}$ is given by Zhou et al. (2016):

$$\begin{aligned} g_{ijklmn}&=\frac{a_{1}}{4}(\delta _{ij}\delta _{kl}\delta _{mn} +\delta _{im}\delta _{jk}\delta _{ln}+\delta _{ik}\delta _{jl}\delta _{mn} +\delta _{in}\delta _{jk}\delta _{lm})\\&+\frac{a_2}{4}(\delta _{ij}\delta _{km}\delta _{lm}+\delta _{ij}\delta _{kn} \delta _{lm}+\delta _{ik}\delta _{jm}\delta _{ln}+\delta _{ik}\delta _{jn} \delta _{lm})+a_{3}\delta _{il}\delta _{jk}\delta _{nm}\\&+\frac{a_{4}}{2}(\delta _{il}\delta _{jm}\delta _{kn}+\delta _{il}\delta _{jn} \delta _{km})+\frac{a_{5}}{4}(\delta _{im}\delta _{jl}\delta _{kn}+\delta _{im} \delta _{jn}\delta _{kl}+\delta _{in}\delta _{jl}\delta _{kn}+\delta _{in} \delta _{jn}\delta _{kl}) \end{aligned}$$

(5)

where

$$\begin{aligned} a_{2}&=\frac{2}{15}(27\mu l_0^2-4\mu l_1^2-15 \mu l_2^2),\quad a_{4}=\frac{2}{3}(\mu l_1^2+6 \mu l_2^2),\\ a_{5}&=\frac{4}{3}(\mu l_1^2-3 \mu l_2^2),\quad a_{1}=-\frac{2}{3}(a_2+a_5),\quad a_{3}=\frac{2}{3}a_2+\frac{1}{6}a_5 \end{aligned}$$

(6)

in which $l_0$, $l_1$ and $l_2$ are the three micro-structure-dependent material length parameters. It may be noted that the sixth order tensor $g_{ijklmn}$ defined above has been proposed for isotropic materials. The simplified models for the sixth order tensor, based on one micro-structure-dependent material length parameter, have been proved to be ineffective to capture the size effects (Fleck and Hutchinson 1993, 2001). Hence, the more general model of the sixth order tensor as presented above has been used in the current formulation. However, for an intuitive study and due to the dearth of the higher order tensor components for any known flexoelectric material, the authors have used the tensors proposed for an elastic isotropic material as described above for the current study. The material tensors for the mechanical and electrical properties of a centro-symmetric dielectric are given by Mindlin (1968), Hu and Shen (2010) and Shen and Hu (2010):

$$\begin{aligned} a_{ij}=a\delta _{ij},\quad b_{ijkl}=b_{c}\delta _{ijkl}+b_{12}\delta _{ij}\delta _{kl}+b_{44} (\delta _{ik}\delta _{jl}+\delta _{il}\delta _{jk}),\\ C_{ijkl}=C_{c}\delta _{ijkl}+C_{12}\delta _{ij}\delta _{kl}+C_{44} (\delta _{ik}\delta _{jl}+\delta _{il}\delta _{jk}),\quad \mu _{ijkl}=\mu _{c}\delta _{ijkl}+\mu _{12}\delta _{ij}\delta _{kl}+\mu _{44} (\delta _{ik}\delta _{jl}+\delta _{il}\delta _{jk}),\\ {\text {where,}}\quad b_{c}=b_{11}-b_{12}-2b_{44},\quad C_{c}=C_{11}-C_{12}-2C_{44},\quad \mu _{c}=\mu _{11}-\mu _{12}-2\mu _{44} \end{aligned}$$

(7)

In Eq. (7), $\delta _{ijkl}$ is equal to unity only if all the indices are identical, and otherwise equals zero, and a is the permittivity constant. Using Eqs. (4a)–(4d) in Eq. (1), the Gibbs free energy density can be expressed as:

$$\begin{aligned} U=\frac{1}{2}{\varvec{\sigma }}:{\varvec{\epsilon }}+\frac{1}{2}{\varvec{\tau }} \vdots {\varvec{\eta }}-\frac{1}{2}{\varvec{D}}\cdot {\varvec{E}}-\frac{1}{2}{\varvec{Q}}:{\varvec{V}} \end{aligned}$$

(8)

3 Governing differential equations of equilibrium

The total Gibbs free energy W, defined for a system occupying the domain with volume $\Omega$, and bounded by $\partial \Omega$ can be calculated from the free energy density of an elastic dielectric derived in the previous section. The governing equations and the associated boundary conditions for this system are derived by applying the variational principle over the total Gibbs free energy for the above system. The first variation of the Gibbs free energy can be expressed as:

$$\begin{aligned} \delta W=\int _{\Omega } \left( {\varvec{\sigma }} :(\delta {\varvec{ u}} \otimes {\varvec{\nabla }})+{\varvec{\tau }}\vdots (\delta {\varvec{ \epsilon }}\otimes {\varvec{\nabla }})+{\varvec{D}}\cdot ( {\varvec{\nabla }}\delta \phi )+{\varvec{Q}}:({\varvec{\nabla }} \otimes {\varvec{\nabla }})\delta \phi \right) d\Omega \end{aligned}$$

(9)

Upon applying the divergence theorem, Eq. (9) can be written as:

$$\begin{aligned} \begin{aligned} \delta W=&-\int _{\Omega } {\varvec{\nabla }}\cdot \left( {\varvec{\sigma }}-{\varvec{\nabla }}\cdot {\varvec{\tau }}\right) \cdot \delta {\varvec{u}} d\Omega + \int _{\Omega } {\varvec{\nabla }}\cdot \left( {\varvec{D}}-{\varvec{\nabla }}\cdot {\varvec{Q}}\right) \delta \phi d\Omega \\&+\int _{\partial \Omega } {\varvec{n}}\cdot \left( {\varvec{\sigma }}-{\varvec{\nabla }}\cdot {\varvec{\tau }}\right) \cdot \delta {\varvec{u}} dA+\int _{\partial \Omega } {\varvec{n}}\cdot {\varvec{\tau }}:\delta {\varvec{\epsilon }} dA\\&+\int _{\partial \Omega } {\varvec{n}}\cdot \left( {\varvec{D}}-{\varvec{\nabla }}\cdot {\varvec{Q}}\right) \delta \phi dA+\int _{\partial \Omega } {\varvec{n}}\cdot {\varvec{Q}} \cdot {\varvec{\nabla }}\delta \phi dA \end{aligned} \end{aligned}$$

(10)

As the variations of the gradients ${\varvec{\epsilon }}$ and ${\varvec{\nabla }}\phi$ are not independent of the variation of ${\varvec{u}}$ and $\phi$ over the surface $\partial \Omega$ these derivatives are split into surface and normal components as follows:

$$\begin{aligned} \delta {\varvec{u}}\otimes {\varvec{\nabla }}= {\varvec{R}}\cdot \left( \delta {\varvec{u}}\otimes {\varvec{\nabla }}\right) +\left( {\varvec{n}}\otimes {\varvec{n}}\right) \cdot \left( \delta {\varvec{u}}\otimes {\varvec{\nabla }}\right) ,\quad {\varvec{\nabla }}\delta \phi = {\varvec{R}}\cdot \left( {\varvec{\nabla }}\delta \phi \right) +\left( {\varvec{n}}\otimes {\varvec{n}}\right) \cdot \left( {\varvec{\nabla }}\delta \phi \right) \end{aligned}$$

(11)

where $\left( {\varvec{n}}\otimes {\varvec{n}}\right)$ gives the normal gradient, and ${\varvec{R}}$ denotes the surface projector defined as ${\varvec{R}}=1-\left( {\varvec{n}}\otimes {\varvec{n}}\right)$. Using the above definitions, it can be shown that:

$$\begin{aligned} \int _{\partial \Omega } {\varvec{n}}\cdot {\varvec{\tau }}:\delta {\varvec{\epsilon }} dA&=\int _{\partial \Omega } {\varvec{n}}\cdot {\varvec{\tau }}:({\varvec{R}}\cdot \left( \delta {\varvec{u}}\otimes {\varvec{\nabla }}\right) )+({\varvec{n}}\otimes {\varvec{n}}):{\varvec{\tau }}\cdot ({\varvec{n}}\cdot (\delta {\varvec{u}}\otimes {\varvec{\nabla }})) dA,\\ \int _{\partial \Omega } {\varvec{n}}\cdot {\varvec{Q}} \cdot \left( {\varvec{\nabla }}\delta \phi \right) dA&=\int _{\partial \Omega } {\varvec{n}}\cdot {\varvec{Q}} \cdot ({\varvec{R}}\cdot \left( {\varvec{\nabla }}\delta \phi \right) )+\left( ({\varvec{n}} \otimes {\varvec{n}}):{\varvec{Q}}\right) ({\varvec{n}}\cdot \left( {\varvec{\nabla }}\delta \phi \right) dA\\ \end{aligned}$$

(12)

where

$$\begin{aligned} ({\varvec{n}}\cdot {\varvec{\tau }}):({\varvec{R}}\cdot \left( \delta {\varvec{u}}\otimes {\varvec{\nabla }}\right) )&={\varvec{R}}:\left( {\varvec{\nabla }}\otimes \left[ ({\varvec{n}} \cdot {\varvec{\tau }})\cdot \delta {\varvec{u}}\right] \right) -\left[ {\varvec{R}}:\left( {\varvec{n}} \cdot {\varvec{\tau }}\right) \otimes {\varvec{\nabla }}\right] \cdot \delta {\varvec{u}},\\ ({\varvec{n}}\cdot {\varvec{Q}})\cdot ({\varvec{R}}\cdot \left( {\varvec{\nabla }}\delta \phi \right)&={\varvec{R}}:\left( {\varvec{\nabla }}\otimes \left[ ({\varvec{n}}\cdot {\varvec{Q}}) \delta \phi \right] \right) -\left[ {\varvec{R}}:\left( {\varvec{n}}\cdot {\varvec{Q}}\right) \otimes {\varvec{\nabla }}\right] \delta \phi \end{aligned}$$

(13)

In the above derivation, symmetry of the second-order strain tensor ${\varvec{\epsilon }}$ and the corresponding indices in third-order moment stress tensor ${\varvec{\tau }}$ have been utilized. Following (Gao and Park 2007), the surface gradient terms in Eqs. (12) and (13) can further be written in terms of the independent variations of ${\varvec{u}}$ and $\phi$ as:

$$\begin{aligned} {\varvec{R}}:\left( \left[ \left( {\varvec{n}}\cdot {\varvec{\tau }}\right) \otimes {\varvec{\nabla }}\right] \cdot \delta {\varvec{u}}\right)&=\left[ {\varvec{R}}:({\varvec{\nabla }}\otimes {\varvec{n}})\right] \left[ ({\varvec{n}}\otimes {\varvec{n}}):{\varvec{\tau }}\right] \cdot \delta {\varvec{u}} +{\varvec{n}}\cdot ({\varvec{\nabla }} \wedge ({\varvec{n}}\wedge (({\varvec{n}}\cdot {\varvec{\tau }})\cdot \delta {\varvec{u}})))\\ {\varvec{R}}:\left( {\varvec{\nabla }}\otimes \left[ ({\varvec{n}}\cdot {\varvec{Q}})\delta \phi \right] \right)&=\left[ {\varvec{R}}:({\varvec{\nabla }}\otimes {\varvec{n}})\right] \left[ ({\varvec{n}}\otimes {\varvec{n}}):{\varvec{Q}}\right] \delta \phi +{\varvec{n}}\cdot ({\varvec{\nabla }}\wedge ({\varvec{n}}\wedge (({\varvec{n}}\cdot {\varvec{Q}})\delta \phi )))\\ \end{aligned}$$

(14)

where $\wedge$ denotes the conventional vector-cross product. For bodies without any sharp edges or discontinuities, the second terms of the LHS of both the equations in Eq. (14) do not contribute to the $\delta W$ when integrated over the smooth surface (Yurkov 2011). However, due to the presence of sharp edges for the beam system, if these edges are represented using $\Gamma$, it can be shown using the Stoke’s theorem (Gao and Park 2007) that:

$$\begin{aligned} \int _{\partial \Omega } {\varvec{n}}\cdot ({\varvec{\nabla }}\wedge ({\varvec{n}}\wedge (({\varvec{n}}\cdot {\varvec{\tau }})\cdot \delta {\varvec{u}}))) dA&=\oint _{\Gamma }[[({\varvec{n}} \otimes {\varvec{m}}):{\varvec{\tau }}]]\cdot \delta {\varvec{u}} dL\\ \int _{\partial \Omega } {\varvec{n}}\cdot ({\varvec{\nabla }}\wedge ({\varvec{n}}\wedge (({\varvec{n}}\cdot {\varvec{Q}})\delta \phi ))) dA&=\oint _{\Gamma }[[({\varvec{n}}\otimes {\varvec{m}}):{\varvec{Q}}]]\delta \phi dL\\ \end{aligned}$$

(15)

where ${\varvec{m}}$ is the co-normal vector given by ${\varvec{m}}={\varvec{s}}\wedge {\varvec{n}}$ and ${\varvec{s}}$ is the unit vector tangent to the edge $\Gamma$, and $[[\cdot ]]$ denotes the jump across the $\Gamma$. Finally after simplification, the Eq. (9) can be written in terms of the independent variations of displacement vector, electrical potential and their respective normal gradients as follows:

$$\begin{aligned} \delta W&=-\int _{\Omega } {\varvec{\nabla }}\cdot \left( {\varvec{\sigma }}-{\varvec{\nabla }}\cdot {\varvec{\tau }}\right) \cdot \delta {\varvec{u}} d\Omega + \int _{\Omega } {\varvec{\nabla }}\cdot \left( {\varvec{D}}-{\varvec{\nabla }}\cdot {\varvec{Q}}\right) \delta \phi d\Omega \\&+\int _{\partial \Omega } \left[ {\varvec{n}}\cdot \left( {\varvec{\sigma }}-{\varvec{\nabla }}\cdot {\varvec{\tau }}\right) -\left[ {\varvec{R}}:\left( {\varvec{n}}\cdot {\varvec{\tau }}\right) \otimes {\varvec{\nabla }}\right] +\left[ {\varvec{R}}:({\varvec{\nabla }}\otimes {\varvec{n}})\right] \left[ ({\varvec{n}}\otimes {\varvec{n}}):{\varvec{\tau }}\right] \right] \cdot \delta {\varvec{u}} dA\\&+\int _{\partial \Omega } \left[ {\varvec{n}}\cdot \left( {\varvec{D}}-{\varvec{\nabla }}\cdot {\varvec{Q}}\right) -\left[ {\varvec{R}}:\left( {\varvec{n}}\cdot {\varvec{Q}}\right) \otimes {\varvec{\nabla }}\right] +\left[ {\varvec{R}}:({\varvec{\nabla }}\otimes {\varvec{n}})\right] \left[ ({\varvec{n}}\otimes {\varvec{n}}):{\varvec{Q}}\right] \right] \delta \phi dA\\&+\int _{\partial \Omega }({\varvec{n}}\otimes {\varvec{n}}):{\varvec{\tau }}\cdot ({\varvec{n}}\cdot (\delta {\varvec{u}}\otimes {\varvec{\nabla }})) dA+\int _{\partial \Omega }\left( ({\varvec{n}}\otimes {\varvec{n}}):{\varvec{Q}}\right) ({\varvec{n}}\cdot \left( {\varvec{\nabla }}\delta \phi \right) dA\\&+\oint _{\Gamma }[[({\varvec{n}}\otimes {\varvec{m}}):{\varvec{\tau }}]]\cdot \delta {\varvec{u}}+[[({\varvec{n}}\otimes {\varvec{m}}):{\varvec{Q}}]]\delta \phi \quad dl\\ \end{aligned}$$

(16)

Considering the total potential energy $\Pi$ in terms of the internal energy W and the external work done $V^{\text {ext}}$ as $\Pi =W-V^{\text {ext}}$, the variational principle $\delta \Pi =0$ yields:

$$\begin{aligned} \delta W&=\delta V^{ext}=\int _{\Omega }({\varvec{\overline{b}}}\cdot \delta {\varvec{u}} +\overline{h}\delta \phi ) d\Omega +\int _{\partial \Omega }({\varvec{\overline{t}}}\cdot \delta {\varvec{u}}+\overline{p}\delta \phi )dA\\&+\int _{\partial \Omega }({\varvec{\overline{d}}}\cdot ({\varvec{n}}\cdot (\delta {\varvec{u}}\otimes {\varvec{\nabla }}))+\overline{v}({\varvec{n}}\cdot \left( {\varvec{\nabla }}\delta \phi \right) )) dA+\oint _{\Gamma }({\varvec{\overline{r}}}\cdot \delta {\varvec{u}}+\overline{q}\delta \phi )dl \end{aligned}$$

(17)

where the mechanical loads ${\varvec{\overline{b}}}$, ${\varvec{\overline{t}}}$, ${\varvec{\overline{d}}}$ and ${\varvec{\overline{r}}}$ are the applied body force per unit volume, surface traction per unit area, double stress traction per unit surface area and the line load along the sharp edge, respectively, and the distributed electrical loads applied per unit volume and per unit area are given by $\overline{h}$, $\overline{p}$, respectively, $\overline{q}$ is the electrical line load applied along the sharp edge, and $\overline{v}$ is the quadrupole-associated electrical load applied per unit surface area. Substitution of Eq. (16) in Eq.(17), yields the following governing differential equations of motion:

$$\begin{aligned} - {\varvec{\nabla }}\cdot \left( {\varvec{\sigma }}-{\varvec{\nabla }}\cdot {\varvec{\tau }}\right) ={\varvec{\overline{b}}};\quad {\varvec{\nabla }}\cdot \left( {\varvec{D}}-{\varvec{\nabla }}\cdot {\varvec{Q}}\right) =\overline{h} \end{aligned}$$

(18)

while the boundary conditions are obtained as follows:

$$\begin{aligned}&{\varvec{n}}\cdot \left( {\varvec{\sigma }}-{\varvec{\nabla }}\cdot {\varvec{\tau }}\right) -\left[ {\varvec{R}}:\left( {\varvec{n}}\cdot {\varvec{\tau }}\right) \otimes {\varvec{\nabla }}\right] +\left[ {\varvec{R}}:({\varvec{\nabla }}\otimes {\varvec{n}})\right] \left[ ({\varvec{n}}\otimes {\varvec{n}}):{\varvec{\tau }}\right] ={\varvec{\overline{t}}} \; {{\text {or}}} \; {\varvec{u}}={\varvec{\overline{u}}} \; {{\text {on}}} \;\partial \Omega \end{aligned}$$

(19a)

$$\begin{aligned}&({\varvec{n}}\otimes {\varvec{n}}):{\varvec{\tau }}={\varvec{\overline{d}}} \; {\text {or}} \; ({\varvec{n}}\cdot (\delta {\varvec{u}}\otimes {\varvec{\nabla }}))=({\varvec{n}}\cdot (\delta {\varvec{\overline{u}}}\otimes {\varvec{\nabla }})) \;{{\text {on}}} \;\partial \Omega \end{aligned}$$

(19b)

$$\begin{aligned}&[[({\varvec{n}}\otimes {\varvec{m}}):{\varvec{\tau }}]]={\varvec{\overline{r}}}\; {\text {or}} \; {\varvec{u}}={\varvec{\overline{u}}} \; {{\text {on}}} \;\Gamma \end{aligned}$$

(19c)

$$\begin{aligned}&{\varvec{n}}\cdot \left( {\varvec{D}}-{\varvec{\nabla }}\cdot {\varvec{Q}}\right) -\left[ {\varvec{R}}:\left( {\varvec{n}}\cdot {\varvec{Q}}\right) \otimes {\varvec{\nabla }}\right] +\left[ {\varvec{R}}:({\varvec{\nabla }}\otimes {\varvec{n}})\right] \left[ ({\varvec{n}}\otimes {\varvec{n}}):{\varvec{Q}}\right] =\overline{p} \; {\text {or}} \; \phi =\overline{\phi } \; {{\text {on}}} \;\partial \Omega \end{aligned}$$

(19d)

$$\begin{aligned}&\left( ({\varvec{n}}\otimes {\varvec{n}}):{\varvec{Q}}\right) =\overline{v} \; {\text {or}} \; ({\varvec{n}}\cdot \left( {\varvec{\nabla }}\delta \phi \right) =({\varvec{n}}\cdot \left( {\varvec{\nabla }}\delta \overline{\phi }\right) \; {{\text {on}}}\; \partial \Omega \end{aligned}$$

(19e)

$$\begin{aligned}&[[({\varvec{n}}\otimes {\varvec{m}}):{\varvec{Q}}]]=\overline{q}\; {\text {or}} \; \phi =\overline{\phi } \; {\text {on}} \;\Gamma \end{aligned}$$

(19f)

where  ${\varvec{\overline{u}}}, \, {\varvec{n}}\cdot (\delta {\varvec{\overline{u}}}\otimes {\varvec{\nabla }}), \,\overline{\phi } \,{\text {and}} \,{\varvec{n}}\cdot \left( {\varvec{\nabla }}\delta \overline{\phi }\right)$ are specified values of the corresponding variables. These derived conditions agree very well with the results of Hu and Shen (2009) and Iesan (2018). In what follows, the exact solutions for the mechanical displacement and the electrical potential, satisfying the governing equations given by Eq. (18) and the boundary conditions given in Eq. (19) will be obtained in the next section.

The importance of including the strain gradient energy in the Gibbs energy can be asserted from the resulting singularity in strain gradient at the surface when ${\varvec{g}}\rightarrow {\varvec{0}}$ for a non-zero electrical field, as previously reported by Yurkov (2011). Despite this observation, a majority of the literature in this field has ignored the contribution of the strain gradient energy to the Gibbs free energy in Eq. (1). To re-emphasize the above observation from the variational approach used here, it may be noted that when ${\varvec{d}}=0$ in Eq. (19b), the natural boundary condition for ${\varvec{\tau }}\rightarrow {\varvec{0}}$ on $\partial \Omega$ can be written from Eq. (4b) as:

$$\begin{aligned} ({\varvec{n}}\otimes {\varvec{n}}):{\varvec{\tau }}=({\varvec{n}}\otimes {\varvec{n}}):\left( {\varvec{g}} \vdots {\varvec{\eta }}-{\varvec{E}}\cdot {\varvec{\mu }}\right) =0 \end{aligned}$$

(20)

So, when ${\varvec{g}}\rightarrow {\varvec{0}}$, either the strain gradient ${\varvec{\eta }}$ must tend to $\infty$ or the constraint ${\varvec{E}}={\varvec{0}}$ would be enforced on the surface. Keeping aside the singularity, the constraint over electric field is an entirely different essential constraint, and it overlaps Eq. (19e) involving normal gradient of electrical potential. Moreover, it would result in very different results and physical phenomena. Hence, given the significance of the strain gradient energy towards avoiding mathematical inconsistencies or arbitrary physical constraints, the authors have felt the need to include the strain gradient energy in the current study.

Fig. 1

Schematic of the simply supported flexoelectric nanobeam system with the applied mechanical load

Fig. 2

Variation of the center deflection $u_3$ along the length of the thin nanobeam compared with results from Ray (2014) ($h=L/100$, $q_0=10^{-6}\, {\text{N/m}}$, $V_2=0$)

Further, it must be noted that for literature involving constant electric field across the thickness or a specified electric field at the surfaces the essential boundary conditions for the normal gradients given in Eq. (19e) must be enforced. These result in a different study, which is not undertaken here as the authors feel such a constraint results in a behaviour which does not realize the full scope of gradient-dependent flexoelectric effect. Thus, only the natural boundary condition corresponding to the normal gradients of electric potential given in Eq. (19e) is enforced throughout.

4 Exact solutions

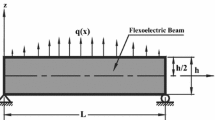
The governing equations and the associated boundary conditions derived in the previous section for a flexoelectric dielectric body possessing strain and electric field gradients are now solved for a specific case of a dielectric beam, schematically illustrated in Fig. 1. The length, width and the thickness of the beam are taken to be L, b and h, respectively. The origin of the coordinate system is chosen at one end of the beam such that $x_1=0$ and $x_1=L$ represent two ends of the beam and $x_3=0$ represents the mid-plane of the beam. The top surface of the beam is subjected to distributed mechanical load $q(x_1)$. The beam may also be actuated by an electrical load, and two separate cases of the circuit connections are studied. In the case of open circuit, the surfaces of the beam are left free without any constraint over the electrical potential developed. In the other case-study, the top surface is subjected to a distributed electrical potential given by $\phi _1(x_1)$ and the bottom surface of the beam is subjected to a distributed electrical loading given by $\phi _2(x_1)$. From the general flexoelectric constitutive relations given in Eqs. (4a–d) and the material constants given in Eqs. (5) and (7), the specific constitutive relations for use in the current system can be derived by varying the indices $i,j,k,l=1,3$. Similarly, the governing differential equations for the system under consideration can be obtained from Eq. (18) using $i,j,k=1,3$. These are given as follows:

$$\begin{aligned} \frac{\partial \sigma _{\text {11}}}{\partial x_{1}}+\frac{\partial \sigma _{\text {31}}}{\partial x_{3}}-\frac{\partial }{\partial x_{1}}\frac{\partial \tau _{\text {111}}}{\partial x_{1}}-\frac{\partial }{\partial x_{3}}\frac{\partial \tau _{\text {131}}}{\partial x_{1}}-\frac{\partial }{\partial x_{1}}\frac{\partial \tau _{\text {311}}}{\partial x_{3}}-\frac{\partial }{\partial x_{3}}\frac{\partial \tau _{\text {331}}}{\partial x_{3}}&=0,\\ \frac{\partial \sigma _{\text {33}}}{\partial x_{3}}+\frac{\partial \sigma _{\text {13}}}{\partial x_{1}}-\frac{\partial }{\partial x_{1}}\frac{\partial \tau _{\text {113}}}{\partial x_{1}}-\frac{\partial }{\partial x_{3}}\frac{\partial \tau _{\text {133}}}{\partial x_{1}}-\frac{\partial }{\partial x_{1}}\frac{\partial \tau _{\text {313}}}{\partial x_{3}}-\frac{\partial }{\partial x_{3}}\frac{\partial \tau _{\text {333}}}{\partial x_{3}}&=0,\\ \frac{\partial \text {D}_{1}}{\partial x_{1}}+\frac{\partial \text {D}_{3}}{\partial x_{3}}-\frac{\partial }{\partial x_{1}}\frac{\partial Q_{\text {11}}}{\partial x_{1}}-\frac{\partial }{\partial x_{3}}\frac{\partial Q_{\text {13}}}{\partial x_{1}}-\frac{\partial }{\partial x_{1}}\frac{\partial Q_{\text {31}}}{\partial x_{3}}-\frac{\partial }{\partial x_{3}}\frac{\partial Q_{\text {33}}}{\partial x_{3}}&=0 \end{aligned}$$

(21)

Subsequently, the boundary conditions expressed tensorially in Eq. (19) are also simplified for the model chosen by using $i,j,k=1,3$. The resulting mechanical boundary conditions from Eqs. (19a–b) are obtained as follows:

$$\begin{aligned} u_{3}\vert _{x_1=0,L}&=0, \end{aligned}$$

(22a)

$$\begin{aligned} (\sigma _{11}-\tau _{111,1}-\tau _{131,3}-\tau _{311,3})\vert _{x_1=0,L}&=0, \end{aligned}$$

(22b)

$$\begin{aligned} b (\sigma _{33}-\tau _{313,1}-\tau _{133,1}-\tau _{333,3})\vert _{x_3=h/2}&=q(x_1), \end{aligned}$$

(22c)

$$\begin{aligned} (\sigma _{33}-\tau _{313,1}-\tau _{133,1}-\tau _{333,3})\vert _{x_3=-h/2}&=0, \end{aligned}$$

(22d)

$$\begin{aligned} (\sigma _{31}-\tau _{311,1}-\tau _{131,1}-\tau _{331,3})\vert _{x_3=\pm h/2}&=0, \end{aligned}$$

(22e)

$$\begin{aligned} \tau _{331}\vert _{x_3=\pm h/2}&=0, \end{aligned}$$

(22f)

$$\begin{aligned} \tau _{333}\vert _{x_3=\pm h/2}&=0 \end{aligned}$$

(22g)

These boundary conditions have been previously used, and validated in the study of the size-dependent behaviour of elastic micro- and nano-beams (Sidhardh and Ray 2018). Additionally, the electrical boundary conditions for the current system can be written from Eqs. (19d–f) as:

$$\begin{aligned} \phi \vert _{x_1=0,L}&=0, \end{aligned}$$

(23a)

$$\begin{aligned} \phi \vert _{x_3=h/2}&=\phi _{1}(x_1)\quad {\text {or}}, \end{aligned}$$

(23b)

$$\begin{aligned} {D}_{3}-Q_{31,1}-Q_{13,1}-Q_{33,3}\vert _{x_3=h/2}&=0, \end{aligned}$$

(23c)

$$\begin{aligned} \phi \vert _{x_3=-h/2}&=\phi _{2}(x_1)\quad {\text {or}}, \end{aligned}$$

(23d)

$$\begin{aligned} {D}_{3}-Q_{31,1}-Q_{13,1}-Q_{33,3}\vert _{x_3=-h/2}&=0, \end{aligned}$$

(23e)

$$\begin{aligned} Q_{11}\vert _{x_1=0,L}&=0, \end{aligned}$$

(23f)

$$\begin{aligned} Q_{33}\vert _{x_3=\pm h/2}&=0 \end{aligned}$$

(23g)

The mechanical and electrical boundary conditions match excellently with those presented by Abdollahi et al. (2014). As discussed previously, two separate studies of the electrical loading will be carried out. For the open circuit connection where the potential over the top and bottom surfaces should not be enforced, the natural boundary conditions with respect to the electrical displacements and electrical quadrupole gradients given in Eqs. (23c) and (23e) will be utilized. Further, for the case-study where potential is applied over the beam, the essential boundary conditions involving electrical potentials at top and bottom surfaces given by Eqs. (23b) and (23d) will be employed. The displacement fields explicitly satisfying the essential mechanical boundary condition in Eq. (22a) and natural boundary condition given by Eq. (22b) are considered as follows:

$$\begin{aligned} u_1(x_1,x_3)=U_1(x_3)\cos (px_1),\quad u_3(x_1,x_3)=U_3(x_3)\sin (px_1) \end{aligned}$$

(24)

and the electrical potential field satisfying the essential electrical boundary condition given by Eq. (23a) and the natural boundary condition given by Eq. (23f), is assumed as:

$$\begin{aligned} \phi (x_1,x_3)=\Phi (x_3)\sin (px_1) \end{aligned}$$

(25)

where $U_i(x_3)$ and $\Phi (x_3)$ are unknown functions of $x_3$ and $p=n\pi /L$ (n is the mode number). With this choice of displacement and electric potential functions, the edge conditions in Eqs. (19c) and (19f) are automatically fulfilled. Further, it may be assumed that

$$\begin{aligned} \left[ U_1(x_3)\;U_3(x_3)\;\Phi (x_3)\right] =\left[ U_1^0\quad U_3^0\quad \Phi ^0\right] e^{sx_3} \end{aligned}$$

(26)

wheres s is a characteristic parameter and $U_1^0$, $U_3^0$ and $\Phi ^0$ are corresponding unknown constants. Substituting Eqs. (24–26) into the governing differential equations, a set of homogeneous algebraic equations are obtained as follows:

$$\begin{aligned} \begin{bmatrix} A_{11}&A_{12}&A_{13}\\ A_{21}&A_{22}&A_{23}\\ A_{31}&A_{32}&A_{33} \end{bmatrix} \begin{Bmatrix} U_1^0\\ U_3^0\\ \Phi ^0 \end{Bmatrix}= \begin{Bmatrix} 0\\ 0\\ 0 \end{Bmatrix} \end{aligned}$$

(27)

in which,

$$\begin{aligned} A_{11}&=4 p^4 \zeta _{2}-p^2 s^2 \zeta _{3}+s^4 \zeta _{1}+4 C_{11} p^2-4 C_{44} s^2,\quad -A_{12}=A_{21}=p s \left( (p-s) (p+s) \zeta _{5}+4 C_{12}+4 C_{44}\right) ,\\ A_{13}&=8 p \left( \zeta _{9} s^2-\mu _{11} p^2\right) ,\quad A_{33}=a_{11} (p-s) (p+s)+b_{11} \left( p^4+s^4\right) -2 \left( b_{13}+2 b_{44}\right) p^2 s^2,\\ A_{22}&=-p^2 s^2 \zeta _{3}+4 s^4 \zeta _{2}+p^4 \zeta _{1}+4 C_{44} p^2-4 C_{33} s^2,\\ A_{23}&=8 s \left( \mu _{11} s^2-\zeta _{9} p^2\right) ,\quad A_{31}=2 p \left( \mu _{11} p^2-\zeta _{9} s^2\right) ,\quad A_{32}=2 s \left( \mu _{11} s^2-\zeta _{9} p^2\right) , \end{aligned}$$

The expressions for $\zeta _{i}'s$, used for simplifying above expressions, are provided in the Appendix 1. From Eq. (27), the expressions for $U_1^0$, $U_3^0$ and $\Phi ^0$ can be related as:

$$\begin{aligned} U_3^0&=f(s)U_1^0,\quad \Phi ^0=g(s)U_1^0,\\ \text {where}&\quad f(s)=\frac{A_{23}A_{31}-A_{21}A_{33}}{A_{22}A_{33}-A_{23}A_{32}},\quad {\text {and}}\quad g(s)=\frac{A_{21}A_{32}-A_{22}A_{31}}{A_{22}A_{33}-A_{23}A_{32}} \end{aligned}$$

(28)

To eliminate the case of trivial solutions for $U_1^0$, $U_3^0$ and $\Phi ^0$, the determinant of the coefficient matrix from Eq. (27) must be equated to zero. This yields the characteristic equation for the governing differential equations as

$$\begin{aligned} A_{6}s^{12}+A_{5}s^{10}+A_{4}s^{8}+A_{3}s^6+A_{2}s^4+A_{1}s^2+A_{0}=0 \end{aligned}$$

(29)

where the expressions for $A_{i}(i=1\ldots 6)$ are expressed in the Appendix 1. The form of the roots of the polynomial vary for different material and geometric parameters. For the material properties of BaTiO₃, given in the next section, the following roots are obtained:

$$\begin{aligned} s_1,s_2&=\pm \alpha ,\quad s_3,s_4=\pm \beta ,\quad s_5,s_6=\pm \gamma ,\quad \\ s_7,s_8&=\pm \lambda ,\quad s_{9},s_{10}=\pm \kappa ,\quad s_{11},s_{12}=\pm \omega \quad \end{aligned}$$

(30)

Expanding Eq. (26), considering the solutions provided in Eq. (30), and utilizing the relations in Eq. (28), the exact solutions for the displacement and the electric potential functions are derived as follows:

$$\begin{aligned} u_1(x_1,x_3)&=(U_{1} e^{\alpha x_{3}}+U_{2} e^{-\alpha x_{3}}+U_{3} e^{\beta x_{3}}+U_{4} e^{-\beta x_{3}}+U_{5} e^{\gamma x_{3}}+U_{6} e^{-\gamma x_{3}}\\&+U_{7} e^{\lambda x_{3}}+U_{8} e^{-\lambda x_{3}}+U_{9} e^{\kappa x_{3}}+U_{10} e^{-\kappa x_{3}}+U_{11} e^{\omega x_{3}}+U_{12} e^{-\omega x_{3}})\cos (p x_{1}) \end{aligned}$$

(31)

$$\begin{aligned} u_3(x_1,x_3)&=(R_{1} U_{1} e^{\alpha x_{3}}+R_{2} U_{2} e^{-\alpha x_{3}}+R_{3} U_{3} e^{\beta x_{3}}+R_{4} U_{4} e^{-\beta x_{3}}+R_{5} U_{5} e^{\gamma x_{3}}+R_{6} U_{6} e^{-\gamma x_{3}}\\&+R_{7} U_{7} e^{\lambda x_{3}}+R_{8} U_{8} e^{-\lambda x_{3}}+R_{9} U_{9} e^{\kappa x_{3}}+R_{10} U_{10} e^{-\kappa x_{3}}+R_{11} U_{11} e^{\omega x_{3}}+R_{12} U_{12} e^{-\omega x_{3}})\sin (p x_{1}) \end{aligned}$$

(32)

$$\begin{aligned} \phi (x_1,x_3)&=(Q_{1} U_{1}e^{\alpha x_{3}}+Q_{2} U_{2}e^{-\alpha x_{3}}+Q_{3} U_{3}e^{\beta x_{3}}+Q_{4} U_{4}e^{-\beta x_{3}}+Q_{5} U_{5}e^{\gamma x_{3}}+Q_{6} U_{6}e^{-\gamma x_{3}}\\&+Q_{7} U_{7}e^{\lambda x_{3}}+Q_{8} U_{8}e^{-\lambda x_{3}}+Q_{9} U_{9}e^{\kappa x_{3}}+Q_{10} U_{10}e^{-\kappa x_{3}}+Q_{11} U_{11}e^{\omega x_{3}}+Q_{12} U_{12}e^{-\omega x_{3}})\sin (p x_{1}) \end{aligned}$$

(33)

Similarly the exact solutions for the Cauchy stresses can be derived from the constitutive relations as follows:

$$\begin{aligned} \sigma _{11}&=\left( T_1 U_1^1 e^{\alpha x_3}+T_2 U_1^2 e^{-\alpha x_3}+T_3 U_1^3 e^{\beta x_3}+T_4 U_1^4 e^{-\beta x_3}+T_5 U_1^5 e^{\gamma x_3}+T_6 U_1^6 e^{-\gamma x_3}\right. \\&\left. +T_7 U_1^7 e^{\kappa x_3}+T_8 U_1^8 e^{-\kappa x_3}+T_9 U_1^9 e^{\lambda x_3}+T_{10} U_1^{10} e^{-\lambda x_3}+T_{11} U_1^{11} e^{\omega x_3}+T_{12} U_1^{12} e^{-\omega x_3}\right) \sin (p x_1) \end{aligned}$$

(34)

$$\begin{aligned} \sigma _{33}&=\left( T_{13} U_1^1 e^{\alpha x_3}+T_{14} U_1^2 e^{-\alpha x_3}+T_{15} U_1^3 e^{\beta x_3}+T_{16} U_1^4 e^{-\beta x_3}+T_{17} U_1^5 e^{\gamma x_3}+T_{18} U_1^6 e^{-\gamma x_3}\right. \\&\left. +T_{19} U_1^7 e^{\kappa x_3}+T_{20} U_1^8 e^{-\kappa x_3}+T_{21} U_1^9 e^{\lambda x_3}+T_{22} U_1^{10} e^{-\lambda x_3}+T_{23} U_1^{11} e^{\omega x_3}+T_{24} U_1^{12} e^{-\omega x_3}\right) \sin (p x_1) \end{aligned}$$

(35)

$$\begin{aligned} \sigma _{13}&=\sigma _{31}=\left( T_{25} U_1^1 e^{\alpha x_3}+T_{26} U_1^2 e^{-\alpha x_3}+T_{27} U_1^3 e^{\beta x_3}+T_{28} U_1^4 e^{-\beta x_3}+T_{29} U_1^5 e^{\gamma x_3}+T_{30} U_1^6 e^{-\gamma x_3}\right. \\&\left. +T_{31} U_1^7 e^{\kappa x_3}+T_{32} U_1^8 e^{-\kappa x_3}+T_{33} U_1^9 e^{\lambda x_3}+T_{34} U_1^{10} e^{-\lambda x_3}+T_{35} U_1^{11} e^{\omega x_3}+T_{36} U_1^{12} e^{-\omega x_3}\right) \cos (p x_1) \end{aligned}$$

(36)

The unknown constants $U_1^i(i=1,2,3\ldots , 12)$ can be determined from the prescribed mechanical boundary conditions given by Eqs. (22) and the electrical boundary conditions from Eqs. (23). Also, the constants $R_i, Q_i$ in Eqs. (32) and (33) are obtained as follows:

$$\begin{aligned} R_i=f(s_i)\quad (i=1,2,\ldots 12)\quad Q_i=g(s_i)\quad (i=1,2,\ldots 12) \end{aligned}$$

(37)

The expressions for $T_i\;(i=1,2,\ldots 36 )$ are provided in Appendix 2. The expressions for the higher order stresses, electrical field displacements and the electrical quadrupole are derived from Eqs. (2–4) and (31–33), and for the sake of brevity only the expression for the $\tau _{311}$ is presented in Appendix 3. For all the electrical conditions, the mechanical load will be given by:

$$\begin{aligned} q(x_1)=q_0 \sin {p x_1} \end{aligned}$$

(38)

here $q_0$ is the amplitude of the applied sinusoidal mechanical load. For the open circuit condition, the electrical boundary conditions involving electrical displacements and electrical quadrupoles have been given in Eqs. (23c) and (23e). For the closed circuit condition, where a prescribed voltage is applied at the top and bottom surfaces, the following distributions are assumed:

$$\begin{aligned} \phi (x_1,x_3) \vert _{{x_3=h/2}}&=\phi _1\left( x_1\right) =V_1 \sin {p x_1},\quad {\text {and}}\quad \phi (x_1,x_3) \vert _{{x_3=-h/2}} =\phi _2\left( x_1\right) =V_2 \sin {p x_1} \end{aligned}$$

(39)

with $V_1$ and $V_2$ being the amplitudes of the sinusoidal electric potentials prescribed at the top and the bottom surfaces of the beam,respectively. With the above assumed loading conditions along with the conditions in Eqs. (22) and (23), the 12 unknown $U_1^{i}$’s are solved to evaluate the numerical values of the exact solutions. This results in a set of algebraic equations:

$$\begin{aligned}{}[K]\{X\}=\{F\} \end{aligned}$$

(40)

in which the elements of the matrix [K] are the coefficients of the unknown $U_{i}$’s. The vectors $\{X\}$ and $\{F\}$ are given by

$$\begin{aligned} \{X\}=[U_1^1\;\; U_1^2\;\; U_1^3\;\; \ldots \;\; U_1^{11}\;\; U_1^{12}]^{T},\quad \{F\}=[0\;\; 0\;\; q_0\;\; 0\;\; 0\;\; 0\;\; 0\;\; 0\;\; V_1\;\; V_2\;\; 0\;\; 0]^{T} \end{aligned}$$

Fig. 3

Variation of the center deflection $u_3$ along the length of the thick nanobeam compared with results from Ray (2014) ($h=L/10$, $q_0=10^{-2}\, {\text{N/m}}$, $V_2=0$)

Fig. 4

Variation of the axial stress $\sigma _{11}$ at mid-length across the thickness of the thick nanobeam compared with results from Ray (2014) ($h=L/10$, $q_0=10^{-2}\, {\text{N/m}}$, $V_2=0$)

Fig. 5

Variation of the axial stress $\sigma _{11}$ at mid-length across the thickness of the thin nanobeam compared with results from Ray (2014) ($h=L/100$, $q_0=10^{-6}\, {\text{N/m}}$, $V_2=0$)

Fig. 6

Variation of the center deflection $u_3$ along the length of the thick nanobeam ($h=L/10$, $q_0=10^{-1}\, {\text{N/m}}$, $V_2=0$)

5 Results and discussion

To investigate the flexoelectric responses in the dielectric beam using the model derived here, numerical results are evaluated for simply supported nanobeams made of barium titanate (BaTiO₃) which belongs to the centro-symmetric point group with cubic symmetry. The length of the beams considered here is fixed at 1 μm. The height of the beam is varied for each study and is mentioned for different cases. The elastic coefficients for BaTiO₃ are taken as $C_{11}=166 \text { GPa},C_{33}= 162 \text { GPa},C_{13}= 78 \text { GPa}$ and $C_{55}=42.9 \text { GPa}$ (Giannakopoulos and Suresh 1999). The material length scales deciding the elastic size-effects of the system response have been proposed to be of the order of lattice parameter for ferroelectrics, by Maranganti and Sharma (2007). Experimental results have identified the lattice parameter to be phase-dependent and varying with temperature from 3.963 to 5.704 Å (Giannakopoulos and Suresh 1999). Hence, for the current study the material length scales are all taken equal to a constant value of 5 Å, i.e. $l_0=l_1=l_2=l=5$ Å. As mentioned in the text, since the Lamé parameter cannot be defined for a non-isotropic material the value of $\mu$ necessary for evaluation of constants $a_{i}$’s in Eq. (6) has been considered to be equal to $C_{44}$. Moreover, given the elastic constants mentioned above, it may be noted that they are not significantly different from an isotropic material with the Lamé parameters $\lambda =78$ GPa and $\mu =42.9$ GPa. The dielectric properties for the BaTiO₃ at room temperature are taken as $\epsilon _{0}=8.85 \times 10^{-12}\, {\text{F}}\,{\text{m}}^{-1}$ and the value of $\chi /\epsilon _0$ is assumed as 1000 (Cross 2006). The flexoelectric coupling coefficients for the BaTiO₃, as used by Yudin and Tagantsev (2013), are taken as $f_{11}=5.1\, {\text {V}}, f_{13}=3.3 \, {\text {V}}$ and $f_{44}=0.045 \, {\text {V}}$. It may be mentioned that such values of the flexoelectric coupling tensors have been used for similar studies available in the literature (Yan and Jiang 2013b; Zhang et al. 2014). The flexoelectric coefficients, $\mu _{11}, \mu _{13}$ and $\mu _{44}$ for the dielectric can be calculated from the flexoelectric coupling coefficients by multiplying with the dielectric susceptibility $\chi$ (Yudin and Tagantsev 2013). Further, the values for the components of the tensor ${\varvec{b}}$ available in the literature for a similar dielectric material (Maranganti et al. 2006; Qi et al. 2016) have been scaled using $\chi$ for BaTiO₃. They have been taken as $b_{12}=0.87 \times 10^{-8}\, {\text{N}}\, {\text{m}}^4/{\text {C}}^2, b_{44}=0.5255 \times 10^{-8}\, {\text{N}}\, {\text{m}}^4/{\text {C}}^2$ and $b_{11}=1.921 \times 10^{-8}\, {\text{N}}\, {\text{m}}^4/{\text {C}}^2$ (Yudin and Tagantsev 2013).

Fig. 7

Variation of the center deflection $u_3$ along the length of the thin nanobeam. ($h=L/100$, $q_0=10^{-4}\, {\text{N/m}}$, $V_2=0$)

Fig. 8

Distribution of axial normal stress $\sigma _{11}$ across the thickness of the thick nanobeam ($h=L/10$, $\sigma =10^{-1}\,{\text{N/m}}$, $V_2=0$)

Fig. 9

Distribution of axial normal stress $\sigma _{11}$ across the thickness of the thin nanobeam ($h=L/100$, $\sigma =10^{-4}\,{\text{N/m}}$, $V_2=0$)

Table 1 Comparison of flexoelectric response for different aspect ratios for different electrical and mechanical conditions

To begin-with, results for the current model actuated by a mechanical load only are compared with the results from the purely elastic model by the authors (Sidhardh and Ray 2018). The above comparison is considered for both the open circuit and closed circuit connections. The results for this example are presented in Table 1. Owing to the very low flexoelectric coefficients, the mid-plane transverse displacements of the beam under open circuit condition and closed circuit connection with $\Delta V=V_1-V_2=0.0$ do not vary appreciably in comparison to the purely elastic size-dependent response of the beam. However, a marginal decrease of the transverse center deflection $(u_{3}(x_1,0))$ is noted for the coupled dielectric response over that of the purely elastic response, with or without strain gradient elasticity. This difference increases for aspect ratios $L/h=20$ and $L/h=100$, as expected. This reduction of the displacement for the coupled response from the purely elastic response in the above findings can be attributed to the direct flexoelectric effect. This is realized from the non-zero electric field induced due to mechanical load, which in turn causes further mechanical actuation due to converse flexoelectric effect. Thus, an increase in the difference between the coupled response and purely elastic response with increase in aspect ratio indicates an increase in the flexoelectric effect with increase in aspect ratio, while the length of the beam is maintained a constant. This observation is in agreement with a similar finding by Zhang et al. (2014), that the flexoelectric effect reduces as the thickness increases. Further, the higher electromechanical coupling for an open circuit configuration over closed circuit at smaller scales reported by Abdollahi et al. (2014), is also noted from the lower values of transverse displacement in open circuit against closed circuit configuration for higher aspect ratios in Table 1.

Fig. 10

Distribution of transverse shear stress $\sigma _{13}$ across the thickness of the thick nanobeam ($h=L/10$, $\sigma =10^{-1}\,{\text{N/m}}$, $V_2=0$)

Fig. 11

Distribution of transverse shear stress $\sigma _{13}$ across the thickness of the thin nanobeam ($h=L/100$, $\sigma =10^{-4}\,{\text{N/m}}$, $V_2=0$)

Fig. 12

Distribution of higher order stress $\tau _{311}$ across the thickness of the thin nanobeam ($h=L/100$, $\sigma =10^{-4}\,{\text{N/m}}$, $V_2=0$)

To analyze the converse flexoelectric effect, non-zero distributed potentials are applied at the top and bottom surfaces, under the closed circuit configuration. As seen from the Table 1, the beam can be mechanically actuated as a result of the converse flexoelectric effect, with an application of the non-zero electrical potential at the surfaces. The beam activated with a positive potential applied at the top surface counteracts the upward mechanical load causing decrease in the transverse displacement, while it aids the mechanical load when activated with a positive potential applied at the bottom surface. This is contrary to the previous finding reported in literature (Yan and Jiang 2013a). This can be attributed to the presence of $\mu _{11}$ in the constitutive relations of the current analysis, unlike in literature where $\mu _{11}$ is eliminated from the constitutive relations. The contrary behaviour can also be explained from the parametric study indicating opposing actuation of the structure to a purely electrical load upon consideration of flexoelectric coefficients $\mu _{11}$ and $\mu _{13}$ independently (Yan and Jiang 2015). Thus, the direction of final actuation is dependent on the net effect of counteracting flexoelectric responses. Finally, from Table 1, the proportionate increase of the gradients with reduction in the height of the beam, thereby resulting in a size-dependent flexoelectric behaviour is identified by comparison of the strain gradients and electrical potential gradients induced by an identical voltage applied for beams with aspect ratios (L/h) 10 and 20.

Further comparison with the previous work by Ray (2014) is carried out to elucidate the differences of the current work from one of the author’s previous work. The mid-plane deflections for a thin beam, with ${\text{L/h}}=100$, and a thick beam, with ${\text{L/h}}=10$, actuated under closed circuit configurations by $\Delta V=0.0$ and $\Delta V \ne 0$, are presented in Figs. 2 and 3, respectively. From the figures it may be noted that the transverse actuations experienced by the thick and thin beams without considering strain gradient elasticity (Ray 2014) are very low in comparison to the corresponding actuations obtained by the current model. Further, the stress profiles across the thickness obtained by considering the gradient-enhanced model are compared with the stress profiles, available in the literature, without considering them in Figs. 4 and 5. These comparisons confirm that an enhanced electro-mechanical coupling is exhibited if the gradient-enhanced model is used for flexoelectric actuation. Also, the strain gradient elasticity marginally influences the passive response ($\Delta V =0$) of the thin beam when compared with the results without considering the strain gradient elasticity (Ray 2014). The above findings emphasize the importance of considering the entire energy functional, without ignoring either the gradients or their corresponding conjugates, for a study involving flexoelectric response in structures.

Fig. 13

Distribution of electric potential $\phi$ induced across the thickness of the thick nanobeam ($h=L/10$, $\sigma _1=10^{-1}\,{\text{N/m}}$, and $\sigma _2=3\times 10^{-1}\,{\text{N/m}}$)

A comparison of the converse flexoelectric effect for closed circuit configuration for different voltages is illustrated in Fig. 6. For this study, the aspect ratio of the beam (L/h) is taken to be 10. The voltage at the bottom surface is kept at zero. As claimed previously in Table 1, it may be observed from Fig. 6 that with an applied positive voltage at the top surface, the activated beam due to flexoelectric effect counteracts the upward mechanical load and the actuation increases with the increase in the magnitude of the voltage. If the polarity of the applied electrical field is changed, the beam gets deflected in the opposite direction, as realized from the figure for a negative V₁. Similar study is conducted for a thin beam $({\text{L/h}}=100)$, under a distributed mechanical load of amplitude $q_0=10^{-4}$ N/m² and zero V₂ and the results are presented in Fig. 7. The trends noted for a thick beam are also exhibited by the thin beam.

Fig. 14

Distribution of electric potential $\phi$ induced across the thickness of the thin nanobeam ($h=L/100$, $\sigma _1=10^{-4}\,{\text{N/m}}$, and $\sigma _2=3\times 10^{-4}\,{\text{N/m}}$)

Next, the axial stress profiles across the thickness for different aspect ratios are presented for closed circuit condition and different amplitudes of applied voltages. The effect of the flexoelectric coupling cannot be solely determined from the values of the axial stresses at the top surface provided in Table 1. Even though, the values of the axial stress at the surfaces differ greatly from the axial stress due to mechanical load only, it may be observed from Figs. 8 and 9 that purely electrical load generates much lower values of this axial stress in the bulk, away from surfaces. This is true, in particular, for a thick beam $({\text{L/h}}=10)$ as seen in Fig. 8. The axial stress developed across the thickness is very low, in comparison to that developed at the surfaces. As noted from Table 1, the influence of the flexoelectric effect is expected to be higher for a thinner beam. This is also supported by the observations from Fig. 9, where it can be seen that the axial stress developed by the electrical load is considerably higher across major part of the thickness, and varies in a much more smooth fashion for a thin beam as compared to the thick beam in Fig. 8. These observations are in-line with the effects at the surface observed in Zhang et al. (2014) and Qi et al. (2016). As seen from Fig. 8, the axial stress generated when $\Delta V > 0$ and $q_0=0$ counteracts the axial stress generated by the upward mechanical load, thereby supporting previous observations.

Similar trends are followed in case of other Cauchy stresses, as well. The variation of transverse shear stress $\sigma _{13}$ across the thickness for a thick $({\text{L/h}}=10)$ and a thin $({\text{L/h}}=100)$ beam, under a combined mechanical and electrical loads, is illustrated in Figs. 10 and 11, respectively. Similar to the axial stresses, the shear stresses caused by the electrical load only are low across the bulk of the thickness, but show a sharp variation at the surface. This jump is sharp for a thick beam and smooth for a thinner beam. The zero values for the shear-stress at the surfaces expected in macro-structures is not observed in Figs. 10 and 11, because of the modification in the corresponding natural boundary conditions in Eq. (22e) by the higher order stresses. This was also noted for the purely-elastic size-dependent response studied by the authors (Sidhardh and Ray 2018). The higher order stresses $\tau _{311}$, developed across the thickness of a thin $({\text{L/h}}=100)$ beam under both the electrical and mechanical loads are presented in Fig. 12.

Fig. 15

Distribution of electric potential $\phi$ induced along the length of the thin nanobeam ($h=L/100$, $\sigma _1=10^{-4}\,{\text{N/m}}$, and $\sigma _2=3\times 10^{-4}\,{\text{N/m}}$)

The above studies involved converse flexoelectric effects and the study of it under different electrical loads. Now, the study is extended to analyze the direct flexoelectric effect, where the electric field and polarization generated by the applied mechanical load $q_0$ will be studied for open circuit and closed circuit with $\Delta V=0.0$ V. It may be mentioned that the direct flexoelectric effect is exploited to make the dielectric beam behave as a nano flexoelectric energy harvester. For a thick beam $({\text{L/h}}=10)$ under a distributed mechanical load a non-zero potential is induced across the domain. The distribution of this potential across the thickness for open and closed circuit conditions under varying mechanical loads have been compared in Fig. 13. A similar comparison for a thin beam is presented in Fig. 14. It can be clearly observed that under open circuit conditions a much larger electrical potential is induced across the thickness as compared to that under closed circuit condition, for a given mechanical load. Thereby, indicating a stronger electro-mechanical coupling exhibited by the open circuit boundary condition. Further, the electrical potential induced corresponding to an applied mechanical loading is remarkably lower for the thick nanobeam, further re-emphasizing the stronger flexoelectric effect demonstrated by the thin structures. Additionally, with an increase in the applied mechanical load, a proportionate increase in the induced potential is observed. The distribution of the induced electrical potential along the length of the thin beam has been illustrated in Fig. 15. This figure may serve as the representative exact solution for the flexoelectric energy harvested by the dielectric beam. As expected the polarity of the induced voltage at the top surface is opposite to that of the bottom surface. The variation of transverse electric field E₃ induced across the thickness is depicted in Fig. 16. Similar study conducted for a thin beam $({\text{L/h}}=100)$ is shown in Fig. 17. The difference between the electric field profiles for the open and the closed circuit conditions is not very significant for a thick beam, as seen in Fig. 16. However, from Fig. 17 for a thin beam, a much larger electrical field is induced in open circuit condition as compared to that under the closed circuit condition, for a given mechanical load. This induced electrical field proportionately increases with an increase in the applied load. In the closed circuit condition, enforcing ${\text{V}}_1={\text{V}}_2=0$ restricts the electrical field generated such that the potential induced across the thickness is very low when compared with the open circuit. This is the reason for the marginally lower values of the displacement observed in Table 1 for the open circuit as compared to purely elastic and closed circuit condition responses. Also, as evident in Fig. 16, there being no significant difference between the potentials developed for a thick beam, the differences in transverse displacements is not observed in thick beams. Finally, the profiles of polarization across the thickness of a thin beam with ${\text{L/h}}=100$ for the open circuit and closed circuit with $\Delta V=0.0$ V, due to different mechanical loads is given in Fig. 18. With variations found at the surfaces, and a constant value across the bulk away from the free surfaces, the results follow the expected trend for a gradient theory (Zhang et al. 2014; Qi et al. 2016). Further, the polarity of the polarization is reversed for both the conditions, as previously noted in Table 1.

Fig. 16

Distribution of transverse electrical field $E_{3}$ across the thickness of the thick nanobeam ($h=L/10$, $\sigma _1=10^{-1}\,{\text{N/m}}$, and $\sigma _2=3\times 10^{-1}\,{\text{N/m}}$)

Fig. 17

Distribution of transverse electrical field $E_{3}$ across the thickness of the thin nanobeam ($h=L/100$, $\sigma _1=10^{-4}\,{\text{N/m}}$, and $\sigma _2=3\times 10^{-4}\,{\text{N/m}}$)

Fig. 18

Distribution of transverse polarization $P_{3}$ developed across the thickness of the thin nanobeam ($h=L/100$, $\sigma _1=10^{-4}\,{\text{N/m}}$, and $\sigma _2=3\times 10^{-4}\,{\text{N/m}}$)

6 Conclusions

In this paper, exact solutions for the static flexoelectric response of a simply supported dielectric nanobeam have been developed. The beams under consideration are actuated by a distributed mechanical loading applied at the top surface, and/or distributed voltages applied at the top or the bottom surface. The constitutive relations for the flexoelectric material are derived from the energy functional for an elastic dielectric available in the literature. The strain gradient elasticity and polarization gradient which were neglected in the open literature on such studies have been considered in the current formulation. The governing differential equations and the associated boundary conditions for the beam are attained from the energy functional by using a variational principle. The governing differential equations are solved for axial, transverse displacements and electric potential by simultaneously satisfying the derived mechanical and electrical boundary conditions. The electrical boundary conditions for the open and closed circuit configurations are separately investigated and compared, with the mechanical conditions remaining the same throughout. Upon solving a numerical problem for BaTiO₃, it is ascertained that the converse flexoelectric effect in an active beam can be used to actuate a nanobeam using an electrical load. The actuation authority of the active beam is significantly found to increase if moment stresses and electric quadrupoles in the paradigm of strain gradient elasticity is incorporated for modelling the flexoelectric structures. Also, the direct flexoelectric effect induces an electric potential across the dielectric subjected to an applied mechanical load, which can be the basis for development of flexoelectric sensors and energy harvesters. For a particular length, the flexoelectric effects exhibit significant increase in their influence with an increase in the aspect ratio. This observation established the size dependence of the flexoelectric effect due to the strain and the electric field gradients. The behaviour of converse effect resulting in the development of mechanical stresses due to an applied electrical field is examined for different aspect ratios. A stronger coupling of the electromechanical behaviour is observed in an open circuit condition as compared to the closed circuit configuration. The thin beam is much more sensitive to exhibit converse flexoelectric responses than the thick beam implying the size dependence of the converse flexoelectric behaviour. The results presented here can be used as the benchmark results for verification of other analytical and numerical models based on simplified assumptions. The present study also reveals that the strain gradient elasticity based on moment stresses and electric quadrupoles must be considered for developing the models of highly sensitive flexoelectric nanosensors and nanoactuators.

Appendices

Appendix 1

The following constants are defined for ease in presentation of Eq. (27):

$$\begin{aligned} \zeta _{1}&=({a_{2}}+2 {a_{4}}+{a_{5}}),\quad \zeta _{2}=({a_{1}}+{a_{2}}+{a_{3}}+{a_{4}}+{a_{5}}),\\ \zeta _{3}&=(4 {a_{1}}+5 {a_{2}}+4 {a_{3}}+6 {a_{4}}+5 {a_{5}}),\quad \zeta _{4}=({a_{1}}+{a_{3}}-{a_{4}}),\\ \zeta _{5}&=(4 {a_{1}}+3 {a_{2}}+4 {a_{3}}+2 {a_{4}}+3 {a_{5}}),\quad \zeta _{6}=(2 {a_{1}}+{a_{2}}+2 {a_{3}}+{a_{5}}),\\ \zeta _{7}&=(2 {a_{1}}+3 {a_{2}}+2 {a_{3}}+4 {a_{4}}+3 {a_{5}}),\quad \zeta _{8}=(8 {a_{1}}+9 {a_{2}}+8 {a_{3}}+10 {a_{4}}+9 {a_{5}}),\quad \zeta _{9}=\left( \mu _{13}+2 \mu _{44}\right) \end{aligned}$$

The expressions for $A_{6}\ldots A_{0}$ in Eq. (29), simplified using the constants defined above, can be written as:

$$\begin{aligned} A_{6}&=4 b_{11} \zeta _{1} \zeta _{2},\\ A_{5}&=-4 \left( a_{11} \zeta _{1} \zeta _{2}+b_{11} \left( 4 \zeta _{2} \left( p^2 \zeta _{1}+C_{44}\right) +C_{33} \zeta _{1}\right) +2 \zeta _{1} \left( \left( b_{13}+2 b_{44}\right) p^2 \zeta _{2}+2 \mu _{11}^2\right) \right) \\ A_{4}&=4 \left( a_{11} \left( \zeta _{1} \left( 5 p^2 \zeta _{2}+C_{33}\right) +4 C_{44} \zeta _{2}\right) \right. \\&\left.\quad +2 \left( 2 \left( b_{44} p^2 \left( 4 \zeta _{2} \left( p^2 \zeta _{1}+C_{44}\right) +C_{33} \zeta _{1}\right) +\mu _{11}^2 \left( p^2 \zeta _{3}+4 C_{44}\right) +4 \zeta _{9}{}^2 p^2 \zeta _{2}-4 \mu _{11} \zeta _{9} p^2 \zeta _{6}\right) \right. \right. \\&\left. \left.\quad +b_{13} p^2 \left( 4 \zeta _{2} \left( p^2 \zeta _{1}+C_{44}\right) +C_{33} \zeta _{1}\right) \right) +b_{11} \left( p^2 \left( 4 C_{11} \zeta _{2}-2 C_{12} \zeta _{5}+C_{33} \zeta _{3}\right) +7 p^4 \zeta _{1} \zeta _{2}+4 C_{44} \left( C_{33}-p^2 \zeta _{4}\right) \right) \right) ,\\ A_{3}&=-4 \left( 2 a_{11} \left( p^2 \left( 2 C_{11} \zeta _{2}-C_{12} \zeta _{5}+C_{33} \zeta _{7}\right) +5 p^4 \zeta _{1} \zeta _{2}+2 C_{44} \left( p^2 \zeta _{1}+C_{33}\right) \right) \right. \\&\left.\quad +p^2 \left( b_{11} \left( p^2 \left( 4 \zeta _{1} \left( 2 p^2 \zeta _{2}+C_{44}\right) +C_{33} \zeta _{3}\right) +C_{11} \left( p^2 \zeta _{3}+4 C_{33}\right) -2 C_{12} \left( p^2 \zeta _{5}+4 C_{44}\right) -4 C_{12}^2\right) \right. \right. \\&\left. \left.\quad +2 \left( 2 \left( b_{44} \left( p^2 \left( 4 C_{11} \zeta _{2}-2 C_{12} \zeta _{5}+C_{33} \zeta _{3}\right) +6 p^4 \zeta _{1} \zeta _{2}+4 C_{44} \left( C_{33}-p^2 \zeta _{4}\right) \right) \right. \right. \right. \right. \\&\left. \left. \left. \left.\quad -2 \left( -2 \zeta _{9} \mu _{11} \left( p^2 \zeta _{7}-2 C_{12}\right) +\mu _{11}^2 \left( p^2 \zeta _{6}-2 C_{11}\right) +2 \zeta _{9}{}^2 \left( p^2 \zeta _{4}-C_{33}\right) \right) \right) \right. \right. \right. \\&\left. \left. \left.\quad +b_{13} \left( p^2 \left( 4 C_{11} \zeta _{2}-2 C_{12} \zeta _{5}+C_{33} \zeta _{3}\right) +6 p^4 \zeta _{1} \zeta _{2}+4 C_{44} \left( C_{33}-p^2 \zeta _{4}\right) \right) \right) \right) \right) ,\\ A_{2}&=4 p^2 \left( a_{11} \left( C_{33} p^2 \zeta _{8}+C_{11} \left( p^2 \zeta _{8}+4 C_{33}\right) +4 C_{12} \left( p^2 (-\zeta _{5})-2 C_{44}\right) +10 p^4 \zeta _{1} \zeta _{2}+4 C_{44} \left( C_{33}-2 p^2 \zeta _{4}\right) -4 C_{12}^2\right) \right. \\&\left.\quad +p^2 \left( 2 \left( 2 \left( b_{44} \left( C_{11} \left( p^2 \zeta _{3}+4 C_{33}\right) +2 \left( 2 p^2 \left( \zeta _{2} \left( p^2 \zeta _{1}+C_{33}\right) -C_{44} \zeta _{4}\right) +C_{12} \left( p^2 (-\zeta _{5})-4 C_{44}\right) -2 C_{12}^2\right) \right) \right. \right. \right. \right. \\&\left. \left. \left. \left.\quad +4 \zeta _{9} \mu _{11} \left( p^2 \zeta _{7}+2 C_{11}+2 C_{33}\right) -2 \mu _{11}^2 \left( p^2 \zeta _{6}+4 C_{12}+4 C_{44}\right) -4 \zeta _{9}{}^2 \left( p^2 \zeta _{4}+2 C_{12}\right) \right) \right. \right. \right. \\&\left. \left. \left.\quad +b_{13} \left( C_{11} \left( p^2 \zeta _{3}+4 C_{33}\right) +2 \left( 2 p^2 \left( \zeta _{2} \left( p^2 \zeta _{1}+C_{33}\right) -C_{44} \zeta _{4}\right) +C_{12} \left( p^2 (-\zeta _{5})-4 C_{44}\right) -2 C_{12}^2\right) \right) \right) \right. \right. \\&\left. \left.\quad +b_{11} \left( p^2 \left( C_{11} \zeta _{3}-2 C_{12} \zeta _{5}+C_{33} \zeta _{3}+7 p^2 \zeta _{1} \zeta _{2}\right) +4 C_{44} \left( p^2 \zeta _{1}+C_{11}+C_{33}\right) \right) \right) \right) ,\\ A_{1}&=-4 p^4 \left( a_{11} \left( p^2 \left( \zeta _{1} \left( 5 p^2 \zeta _{2}+4 C_{44}\right) +4 C_{33} \zeta _{2}\right) -2 C_{12} \left( p^2 \zeta _{5}+4 C_{44}\right) +C_{11} \left( 2 p^2 \zeta _{7}+4 C_{33}+4 C_{44}\right) -4 C_{12}^2\right) \right. \\&\left.\quad +p^2 \left( 2 \left( 2 \left( b_{44} \left( p^2 \zeta _{1}+4 C_{44}\right) \left( p^2 \zeta _{2}+C_{11}\right) +\mu _{11}^2 \left( p^2 \zeta _{3}+4 C_{33}\right) +4 \zeta _{9}{}^2 \left( p^2 \zeta _{2}+C_{11}\right) -4 \zeta _{9} \mu _{11} \left( p^2 \zeta _{6}+2 C_{12}\right) \right) \right. \right. \right. \\&\left. \left. \left.\quad +b_{13} \left( p^2 \zeta _{1}+4 C_{44}\right) \left( p^2 \zeta _{2}+C_{11}\right) \right) \right. \right. \\&\left. \left.\quad +b_{11} \left( C_{11} \left( p^2 \zeta _{3}+4 C_{33}\right) +2 \left( 2 p^2 \left( \zeta _{2} \left( p^2 \zeta _{1}+C_{33}\right) -C_{44} \zeta _{4}\right) +C_{12} \left( p^2 (-\zeta _{5})-4 C_{44}\right) -2 C_{12}^2\right) \right) \right) \right) ,\\ A_{0}&=\left( p^4 \zeta _{1}+4 C_{44} p^2\right) \left( 4 p^4 \left( a_{11}+b_{11} p^2\right) \left( p^2 \zeta _{2}+C_{11}\right) +16 \mu _{11}^2 p^6\right) \end{aligned}$$

Appendix 2

The terms $T_{i}(i=1,2,\ldots 36)$ used in Eqs. (34), (35) and (36) are:

$$\begin{aligned} T_1&=-C_{11} p+\alpha C_{12} R_{1}+\mu _{11} p^2 Q_{1}-\alpha ^2 \mu _{13} Q_{1},\quad T_2=-C_{11} p-\alpha C_{12} R_{2}+\mu _{11} p^2 Q_{2}-\alpha ^2 \mu _{13} Q_{2},\\ T_3&=-C_{11} p+\beta C_{12} R_{3}+\mu _{11} p^2 Q_{3}-\beta ^2 \mu _{13} Q_{3},\quad T_4=-C_{11} p-\beta C_{12} R_{4}+\mu _{11} p^2 Q_{4}-\beta ^2 \mu _{13} Q_{4},\\ T_5&=-C_{11} p+\gamma C_{12} R_{5}+\mu _{11} p^2 Q_{5}-\gamma ^2 \mu _{13} Q_{5},\quad T_6=-C_{11} p-\gamma C_{12} R_{6}+\mu _{11} p^2 Q_{6}-\gamma ^2 \mu _{13} Q_{6},\\ T_7&=-C_{11} p+C_{12} \lambda R_{7}+\mu _{11} p^2 Q_{7}-\lambda ^2 \mu _{13} Q_{7},\quad T_8=-C_{11} p-C_{12} \lambda R_{8}+\mu _{11} p^2 Q_{8}-\lambda ^2 \mu _{13} Q_{8},\\ T_9&=-C_{11} p+C_{12} \kappa R_{9}+\mu _{11} p^2 Q_{9}-\kappa ^2 \mu _{13} Q_{9},\quad T_{10}=-C_{11} p-C_{12} \kappa R_{10}+\mu _{11} p^2 Q_{10}-\kappa ^2 \mu _{13} Q_{10},\\ T_{11}&=-C_{11} p+C_{12} R_{11} \omega +\mu _{11} p^2 Q_{11}-\mu _{13} Q_{11} \omega ^2,\;T_{12}=-C_{11} p-C_{12} R_{12} \omega +\mu _{11} p^2 Q_{12}-\mu _{13} Q_{12} \omega ^2,\\ T_{13}&=-C_{12} p+\alpha C_{33} R_{1}+\mu _{13} p^2 Q_{1}-\alpha ^2 \mu _{11} Q_{1},\quad T_{14}=-C_{12} p-\alpha C_{33} R_{2}+\mu _{13} p^2 Q_{2}-\alpha ^2 \mu _{11} Q_{2},\\ T_{15}&=-C_{12} p+\beta C_{33} R_{3}+\mu _{13} p^2 Q_{3}-\beta ^2 \mu _{11} Q_{3},\quad T_{16}=-C_{12} p-\beta C_{33} R_{4}+\mu _{13} p^2 Q_{4}-\beta ^2 \mu _{11} Q_{4},\\ T_{17}&=-C_{12} p+\gamma C_{33} R_{5}+\mu _{13} p^2 Q_{5}-\gamma ^2 \mu _{11} Q_{5},\quad T_{18}=-C_{12} p-\gamma C_{33} R_{6}+\mu _{13} p^2 Q_{6}-\gamma ^2 \mu _{11} Q_{6},\\ T_{19}&=-C_{12} p+C_{33} \lambda R_{7}+\mu _{13} p^2 Q_{7}-\lambda ^2 \mu _{11} Q_{7},\quad T_{20}=-C_{12} p-C_{33} \lambda R_{8}+\mu _{13} p^2 Q_{8}-\lambda ^2 \mu _{11} Q_{8},\\ T_{21}&=-C_{12} p+C_{33} \kappa R_{9}+\mu _{13} p^2 Q_{9}-\kappa ^2 \mu _{11} Q_{9},\quad T_{22}=-C_{12} p-C_{33} \kappa R_{10}+\mu _{13} p^2 Q_{10}-\kappa ^2 \mu _{11} Q_{10},\\ T_{23}&=-C_{12} p+C_{33} R_{11} \omega +\mu _{13} p^2 Q_{11}-\mu _{11} Q_{11} \omega ^2,\;T_{24}=-C_{12} p-C_{33} R_{12} \omega +\mu _{13} p^2 Q_{12}-\mu _{11} Q_{12} \omega ^2,\\ T_{25}&=\alpha C_{44}+C_{44} p R_{1}-2 \alpha \mu _{44} p Q_{1},\quad T_{26}=-\alpha C_{44}+C_{44} p R_{2}+2 \alpha \mu _{44} p Q_{2},\\ T_{27}&=\beta C_{44}+C_{44} p R_{3}-2 \beta \mu _{44} p Q_{3},\quad T_{28}=-\beta C_{44}+C_{44} p R_{4}+2 \beta \mu _{44} p Q_{4},\\ T_{29}&=\gamma C_{44}+C_{44} p R_{5}-2 \gamma \mu _{44} p Q_{5},\quad T_{30}=-\gamma C_{44}+C_{44} p R_{6}+2 \gamma \mu _{44} p Q_{6},\\ T_{31}&=C_{44} \lambda +C_{44} p R_{7}-2 \lambda \mu _{44} p Q_{7},\quad T_{32}=-C_{44} \lambda +C_{44} p R_{8}+2 \lambda \mu _{44} p Q_{8},\\ T_{33}&=C_{44} \kappa +C_{44} p R_{9}-2 \kappa \mu _{44} p Q_{9},\quad T_{34}=-C_{44} \kappa +C_{44} p R_{10}+2 \kappa \mu _{44} p Q_{10},\\ T_{35}&=C_{44} p R_{11}+C_{44} \omega -2 \mu _{44} p Q_{11} \omega ,\quad T_{36}=C_{44} p R_{12}-C_{44} \omega +2 \mu _{44} p Q_{12} \omega \end{aligned}$$

Appendix 3

The expression for higher order stress $\tau _{311}$ derived using the constitutive relations and the assumed form of the exact solutions may be written as follows:

$$\begin{aligned} \tau _{311}&=\left( V_1 U_1^1 e^{\alpha x_3}+V_2 U_1^2 e^{-\alpha x_3}+V_3 U_1^3 e^{\beta x_3}+V_4 U_1^4 e^{-\beta x_3}+V_5 U_1^5 e^{\gamma x_3}+V_6 U_1^6 e^{-\gamma x_3}\right. \\&\left. +V_7 U_1^7 e^{\kappa x_3}+V_8 U_1^8 e^{-\kappa x_3}+V_9 U_1^9 e^{\lambda x_3}+V_{10} U_1^{10} e^{-\lambda x_3}+V_{11} U_1^{11} e^{\omega x_3}+V_{12} U_1^{12} e^{-\omega x_3}\right) \sin (p x_1) \end{aligned}$$

(44)

where, the expressions for $V_{i}$$(i=1,2,\ldots 12)$ are as follows:

$$\begin{aligned} V_1&=\frac{1}{4} \left( -\alpha p (a_{1}+4 (a_{3}+a_{4})+2 a_{5})+2 \alpha ^2 R_{1} (a_{1}+2 a_{3})+p^2 R_{1} (-(a_{1}+2 a_{5}))+4 \alpha \mu _{13} Q_{1}\right) \\ V_2&=\frac{1}{4} \left( \alpha p (a_{1}+4 (a_{3}+a_{4})+2 a_{5})+2 \alpha ^2 R_{2} (a_{1}+2 a_{3})+p^2 R_{2} (-(a_{1}+2 a_{5}))-4 \alpha \mu _{13} Q_{2}\right) \\ V_3&=\frac{1}{4} \left( -\beta p (a_{1}+4 (a_{3}+a_{4})+2 a_{5})+2 \beta ^2 R_{3} (a_{1}+2 a_{3})+p^2 R_{3} (-(a_{1}+2 a_{5}))+4 \beta \mu _{13} Q_{3}\right) \\ V_4&=\frac{1}{4} \left( \beta p (a_{1}+4 (a_{3}+a_{4})+2 a_{5})+2 \beta ^2 R_{4} (a_{1}+2 a_{3})+p^2 R_{4} (-(a_{1}+2 a_{5}))-4 \beta \mu _{13} Q_{4}\right) \\ V_5&=\frac{1}{4} \left( -\gamma p (a_{1}+4 (a_{3}+a_{4})+2 a_{5})+2 \gamma ^2 R_{5} (a_{1}+2 a_{3})+p^2 R_{5} (-(a_{1}+2 a_{5}))+4 \gamma \mu _{13} Q_{5}\right) \\ V_6&=\frac{1}{4} \left( \gamma p (a_{1}+4 (a_{3}+a_{4})+2 a_{5})+2 \gamma ^2 R_{6} (a_{1}+2 a_{3})+p^2 R_{6} (-(a_{1}+2 a_{5}))-4 \gamma \mu _{13} Q_{6}\right) \\ V_7&=\frac{1}{4} \left( -\lambda p (a_{1}+4 (a_{3}+a_{4})+2 a_{5})+2 \lambda ^2 R_{7} (a_{1}+2 a_{3})+p^2 R_{7} (-(a_{1}+2 a_{5}))+4 \lambda \mu _{13} Q_{7}\right) \\ V_8&=\frac{1}{4} \left( \lambda p (a_{1}+4 (a_{3}+a_{4})+2 a_{5})+2 \lambda ^2 R_{8} (a_{1}+2 a_{3})+p^2 R_{8} (-(a_{1}+2 a_{5}))-4 \lambda \mu _{13} Q_{8}\right) \\ V_9&=\frac{1}{4} \left( -\kappa p (a_{1}+4 (a_{3}+a_{4})+2 a_{5})+2 \kappa ^2 R_{9} (a_{1}+2 a_{3})+p^2 R_{9} (-(a_{1}+2 a_{5}))+4 \kappa \mu _{13} Q_{9}\right) \\ V_{10}&=\frac{1}{4} \left( \kappa p (a_{1}+4 (a_{3}+a_{4})+2 a_{5})+2 \kappa ^2 R_{10} (a_{1}+2 a_{3})+p^2 R_{10} (-(a_{1}+2 a_{5}))-4 \kappa \mu _{13} Q_{10}\right) \\ V_{11}&=\frac{1}{4} \left( -p \omega (a_{1}+4 (a_{3}+a_{4})+2 a_{5})+2 R_{11} \omega ^2 (a_{1}+2 a_{3})+p^2 R_{11} (-(a_{1}+2 a_{5}))+4 \mu _{13} Q_{11} \omega \right) \\ V_{12}&=\frac{1}{4} \left( p \omega (a_{1}+4 (a_{3}+a_{4})+2 a_{5})+2 R_{12} \omega ^2 (a_{1}+2 a_{3})+p^2 R_{12} (-(a_{1}+2 a_{5}))-4 \mu _{13} Q_{12} \omega \right) \end{aligned}$$

(45)