Propagation of SH-waves in inhomogeneous piezoelectric/piezomagnetic half-space with circular inclusion

Abstract

In this article, the dynamic characteristics of a circular inclusion in an inhomogeneous piezoelectric/piezomagnetic half-space with propagating anti-plane shear waves are studied. The exponential distribution of material parameters along the coordinate axis is considered. The Helmholtz equation includes variable coefficients due to inhomogeneity. First, the Helmholtz equation is transformed into standard form by introducing new variables. Next, integral equations with respective boundary conditions are composed and solved by orthogonal function expansion and effective truncation techniques. Obtained results enable to understand the influence on the dynamic stress concentration factor as well as the electric and magnetic field intensities under proper conditions. The conclusions of this article are verified by comparing the analytical solutions to the ones obtained by finite element method.

1 Introduction

Functionally graded materials play an important role in the design of sensors in aerospace and marine engineering. The mechanical–electric–magnetic coupling effects in piezoelectric/piezomagnetic materials enable to realize the exchange of mechanical vibration and alternating current. This makes piezoelectric materials widely used in residents’ life and industry. Piezoelectric/piezomagnetic composite structures such as beams, plates, shells, and columns can contain all kinds of defects caused by processing technology and polling. These defects lead to the concentration of dynamic stress around them, which aggravates the defect problem for functionally graded materials as compared to that for common materials. Moreover, concentration of the intensities of electric and magnetic fields near the defects takes place, which not only leads to the failure of the structure and fracturing in the linking sections of different materials, but also to electric leakage and magnetic breakdown. However, despite a large number of studies of the statics properties of homogeneous piezoelectric/piezomagnetic materials, there are only limited studies devoted to the dynamic properties of inhomogeneous materials because the corresponding governing equations are very complex, and the Helmholtz equation includes variable coefficients. The innovation of this article is that this complex problem is addressed by using separation of variables, and the effects of different parameters are analyzed and discussed.

A large number of studies [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21] is devoted to the problems of defects, among which the elastic wave problem is a hot research topic. Since Pao and Mow [1] analyzed an elastic wave in the whole space by separating the time variable, elastic wave theory was gradually improved and widely used in engineering. Wang [2] examined the dynamic electromechanical behavior of interacting interfacial cracks between two piezoelectric media under anti-plane mechanical loading. Guo et al. [3,4,5] studied the dynamic characteristics of on initially stressed piezoelectric/piezomagnetic plate under elastic wave. By means of stiffness matrix method, Hamdi Ezzin et al. [6,7,8] calculated the phase velocity in piezoelectric/piezomagnetic materials subjected to different elastic waves under magnetoelectric open circuit and short circuit conditions. Shi [9] used the transfer matrix method to study the coupling of elastic shear waves and electromagnetic waves in one-dimensional piezoelectric/piezomagnetic composites. With the aid of the integral equation method, Singh et al. [10, 11] investigated the characteristics of Love-type waves scattered through on irregular surface in piezoelectric composite structures. They also focused on the reflection of plane waves at the surface of a piezothermoelastic fiber-reinforced composite (PTFRC) half-space by classical dynamical coupled theory, Lord–Shulman theory, and Green–Lindsay theory. Song et al. [12, 13] investigated the dynamic problem of a cavity located near the horizontal boundary. Hui et al. [14,15,16] studied the dynamic stress around a cavity in piezoelectric bi-material media.

In recent years, the dynamic properties of inhomogeneous media including the piezoelectric/piezomagnetic half-space were studied. Manolis et al. [17] analyzed the amplitude of seismic displacement induced by anti-plane strain wave motion in an inhomogeneous geological region containing tunnels by BEM computation. Mahanty et al. [18] explored the effect of initial-stress, heterogeneity, and anisotropy on the propagation of SH-type, Rayleigh-type, and Love-type waves in a semi-infinite medium with a distinct initially stressed heterogeneous anisotropic layer by separate variable method. Nazarov [19] investigated the interaction of powerful and weak longitudinal acoustic waves in microscopically inhomogeneous media both experimentally and theoretically. With the help of “directional-ellipse” method, StanChiriţă et al. [20] obtained inhomogeneous plane wave solutions in the framework of the linear theory of poroelastic materials. Yang et al. [21] addressed the problems of dynamic stress induced by wave propagation in an inhomogeneous right-angle plane with a circular cavity by applying the theory of complex functions and the image principle.

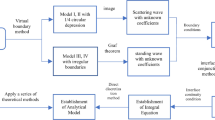
In this article, scattering of SH-waves by a circular inclusion in an inhomogeneous piezoelectric/piezomagnetic half-space is investigated. The inhomogeneity of materials leads to the first-order partial derivatives of variables x and y in the Helmholtz equation. Therefore, the variable separation method is applied to transform the Helmholtz equation into the standard form. Moreover, the series expansion and the image methods are used to perform the calculation. Finally, the dynamic stress concentration factor (DSCF), the electric field intensity concentration factor (EFICF), and the magnetic field intensity concentration factor (MFICF) around the circular inclusion are obtained and discussed.

At present, Mori–Tanaka model is widely used. However, this model is applicable only in micromechanics. In this paper, however, the wave problem is studied in the framework of macromechanics, so that the scope of research is different. Since most of the distribution functions that represent non-uniformity can be expanded into trigonometric series and trigonometric functions can be converted into exponential ones by the Euler formula, the exponential function distribution model has a high engineering significance. This paper provides a theoretical method for obtaining the non-uniform distributions in the form of exponential functions. This method establishes a theoretical basis for the analysis of distribution functions composed by addition of multiple exponential functions with the aid of superposition method.

The derivation of the formulas in Ref. [18] is based on the integral transformation method, while the formulas in this paper is constructed by Green’s function method, which is the difference between the research methods in the two articles. This paper studies piezoelectric/piezomagnetic materials, while Ref. [21] investigates ordinary materials, which is the difference between the research objects in the two articles. In particular, due to the effect of mechanical–electric–magnetic coupling, the derivation of the formulas in this paper is more complex than that in Ref. [21], and the model in this paper contains inclusions, which is lack of Ref. [18]. In summary, the research in this article has a certain significance.

2 Theoretical model

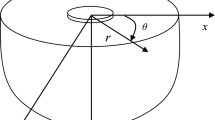
We consider two piezoelectric/piezomagnetic right-angle spaces are joined together to form a half-space and subjected to the impact of SH wave. The two-dimensional model is located in xoy-plane, and the polarized direction is along the z-axis, as shown in Fig. 1. All media in the model are transverse isotropic materials.

Fig. 1

Model of a piezoelectric/piezomagnetic half space with a circular inclusion

The Medium I is a homogeneous and isotropic piezoelectric right-angle space containing a circular cavity.

The Medium II is a right-angle space composed of piezomagnetic material with an inhomogeneity.

The horizontal boundaries of the Medium I and II are $B_{H}$, and the common vertical interface between them is $B_{V}$.

The Medium III is an inhomogeneous piezoelectric circular inclusion with the boundary $B_{{in}}$.

The geometric parameters of this model are as follows:

The radius of boundary $B_{{in}}$:$a$.

The distance between the center of the circular inclusion and the horizontal boundary $B_{H}$:$h$.

The distance between the center of the circular inclusion and the vertical interface $B_{V}$:$d$.

The material parameters of this model are shown in Table 1.

Table 1 Material parameters

The material parameters of a piezoelectric/piezomagnetic medium are assumed to have an exponential distribution along the x- and y-axis. Note that the superscripts I, II, and III are ignored:

$$ \begin{gathered} c_{{44}} (x,y) = c_{{440}} e^{{2(px + qy)}} ,e_{{15}} (x,y) = e_{{150}} e^{{2(px + qy)}} ,h_{{15}} (x,y) = h_{{150}} e^{{2(px + qy)}} , \hfill \\ \kappa _{{11}} (x,y) = \kappa _{{110}} e^{{2(px + qy)}} ,t_{{11}} (x,y) = t_{{110}} e^{{2(px + qy)}} ,\mu _{{11}} (x,y) = \mu _{{110}} e^{{2(px + qy)}} , \hfill \\ \rho (x,y) = \rho _{0} e^{{2(px + qy)}} , \hfill \\ \end{gathered} $$

(1)

where the parameters $c_{{440}}$, $e_{{150}}$, $h_{{150}}$, $\kappa _{{110}}$, $\mu _{{110}}$, $t_{{110}}$, and $\rho _{0}$ are material constants, $e^{{2(px + qy)}}$ is an inhomogeneous factor, and $p \le 0$ and $q \ge 0$ represent the powers of the exponential function, respectively. The physical meaning of the latter are the gradients of material parameters along the x- and y-axis, respectively.

The following assumptions were made to simplify calculations:

• 1. For the Medium I,$p_{1} = 0$ and $q_{1} = 0$, so that the inhomogeneous factor is $e^{{2(p_{1} x + q_{1} y)}} = 1$, meaning that the Medium I is homogeneous.

• 2. For the Medium II,$p_{2} < 0$, $q_{2} = 0$ and the inhomogeneous factor is $e^{{2p_{2} x}}$. This assumption is consistent with reality. In particular, when $x \to + \infty$ in the right-angle space, $e^{{2p_{2} x}} \to 0$, the piezomagnetic material becomes a homogeneous medium at this, and the material parameters do not become infinite.

• 3. For Medium III,$p_{3} < 0$ and $q_{3} > 0$ in the inhomogeneous factor $e^{{2(p_{3} x + q_{3} y)}}$. Because the values of coordinates x and y for the circular inclusion (i.e., the Medium III) are finite, the material parameters do not tend to infinity.

A special case is defined below.

Subcase: when $\rho ^{{{\text{III}}}} = 0$, the Medium III degenerates into a circular cavity. In this case, $p_{3} = 0$ and $q_{3} = 0$. If the center of the circular cavity is chosen on the horizontal boundary, the cavity is simplified into a semicircular hollow.

The expressions corresponding to the special case of the Medium III are presented in detail in Sect. 4.4.

3 Governing equations and boundary conditions

3.1 Governing equations

The derivation of the governing equation requires decoupling of the equilibrium and constitutive equations, which is a lengthy process. At this, the variables $f$ and $\zeta$ are introduced. The detailed derivation is shown in Part I of the Appendix,

$$ \begin{gathered} f = e_{{150}} u - \kappa _{{110}} \phi - t_{{110}} \varphi , \hfill \\ \zeta = h_{{150}} u - t_{{110}} \phi - \mu _{{110}} \varphi . \hfill \\ \end{gathered} $$

(2)

Equations (3) are obtained as a result of complex derivation, However, they still contain the powers of the exponential function $p$ and $q$:

$$ \begin{gathered} \nabla ^{2} u + 2\left(p\frac{{\partial u}}{{\partial x}} + q\frac{{\partial u}}{{\partial y}}\right) = \frac{1}{{c_{{SH}}^{2} }}\frac{{\partial ^{2} u}}{{\partial t^{2} }}, \hfill \\ \nabla ^{2} f + 2\left(p\frac{{\partial f}}{{\partial x}} + q\frac{{\partial f}}{{\partial y}}\right) = 0, \hfill \\ \nabla ^{2} \zeta + 2\left(p\frac{{\partial \zeta }}{{\partial x}} + q\frac{{\partial \zeta }}{{\partial y}}\right) = 0. \hfill \\ \end{gathered} $$

(3)

Here, $c_{{SH}} = \sqrt {{{c_{m} } \mathord{\left/ {\vphantom {{c_{m} } {\rho _{0} }}} \right. \kern-\nulldelimiterspace} {\rho _{0} }}}$ is the wave velocity, and $c_{m} = c_{{440}} + \frac{{e_{{150}}^{2} \mu _{{110}} + h_{{150}}^{2} \kappa _{{110}} - 2h_{{150}} e_{{150}} t_{{110}} }}{{\kappa _{{110}} \mu _{{110}} - t_{{110}}^{2} }}$ is the equivalent elastic constant, respectively.

Obviously, the first Eq. (3) contains the second derivative of time. However, only the steady-state problem of elastic wave is analyzed in this article. Therefore, a variable substitution method is applied to eliminate the influence of time factor $e^{{ - i\omega t}}$.

By introducing the variable $u = we^{{ - i\omega t}}$, the first Eq. (3) can be simplified as follows:

$$ \nabla ^{2} w + 2\left(p\frac{{\partial w}}{{\partial x}} + q\frac{{\partial w}}{{\partial y}}\right) + k^{2} w = 0 $$

(4)

where $k = {\omega \mathord{\left/ {\vphantom {\omega {c_{{SH}} }}} \right. \kern-\nulldelimiterspace} {c_{{SH}} }}$ represents wave numbers and $\omega$ is the frequency of the plane shear wave, respectively.

In order to eliminate the powers of the exponential function $p$ and $q$, the solutions of Eq. (3) can be assumed in the following form by using the separation of variables method:

$$ w = W(x,y)e^{{ - (px + qy)}} ,f = f_{0} (x,y)e^{{ - (px + qy)}} ,\zeta = \zeta _{0} (x,y)e^{{ - (px + qy)}} $$

(5)

,

By substituting Eq. (5) into Eqs. (3) and (4), the following equations are obtained:

$$ \nabla ^{2} W + k_{0}^{2} W = 0,\nabla ^{2} f_{0} + (ik^{\prime})^{2} f_{0} = 0,\nabla ^{2} \zeta _{0} + (ik^{\prime})^{2} \zeta _{0} = 0 $$

(6)

,

Here, $k_{0} = \sqrt {k^{2} - p^{2} - q^{2} }$, $k^{2} - p^{2} - q^{2} > 0$, $k^{\prime} = \sqrt {p^{2} + q^{2} }$, and$f_{0}$ and $\zeta _{0}$ represent electric and magnetic field parameters, respectively. The variable $W$ satisfies the Helmholtz equation.

Since the Laplace operator satisfies the relation $\nabla ^{2} ( \bullet ) = \nabla \cdot (\nabla ( \bullet ))$, the physical meaning of the first Eq. (6) is that it describes the spread of the elastic wave in time and space.

For the Medium I, $k^{\prime} = 0$,$p_{1} = 0$, and $q_{1} = 0$. Therefore, the second and third Eq. (6) degenerate into Laplace equation as follows:

$$\nabla ^{2} f_{0} = 0,\nabla ^{2} \zeta _{0} = 0$$

(7)

Equations (7) mean that the gradient fields of the variables $f_{0}$ and $\zeta _{0}$ are non-source and the vibration frequency is zero.

By means of Cramer’s Rule, variables $\phi$ and $\varphi$ in Eq. (2) can be expressed as follows:

$$ \begin{gathered} \phi = a_{1} w + b_{1} f + c_{1} \zeta , \hfill \\ \varphi = a_{2} w + b_{2} f + c_{2} \zeta . \hfill \\ \end{gathered} $$

(8)

where:

$a_{1} = \frac{{\mu _{{110}} e_{{150}} - t_{{110}} h_{{150}} }}{{\mu _{{110}} \kappa _{{110}} - t_{{110}}^{2} }}$, $b_{1} = \frac{{ - \mu _{{110}} }}{{\mu _{{110}} \kappa _{{110}} - t_{{110}}^{2} }}$, $c_{1} = \frac{{t_{{110}} }}{{\mu _{{110}} \kappa _{{110}} - t_{{110}}^{2} }}$,

$a_{2} = \frac{{\kappa _{{110}} h_{{150}} - t_{{110}} e_{{150}} }}{{\mu _{{110}} \kappa _{{110}} - t_{{110}}^{2} }}$, $b_{2} = \frac{{t_{{110}} }}{{\mu _{{110}} \kappa _{{110}} - t_{{110}}^{2} }}$, $c_{2} = \frac{{ - \kappa _{{110}} }}{{\mu _{{110}} \kappa _{{110}} - t_{{110}}^{2} }}$.

Each field contains the time factor $e^{{ - i\omega t}}$, which is omitted to simplify the calculation. Therefore, $u$ in Eqs. (8) and (9) may be replaced by $w$.

In the complex plane, the inhomogeneous factor is $e^{{2(px + qy)}} = e^{{p(\eta + \bar{\eta }) - q(\eta - \bar{\eta })i}}$, and the constitutive equation can be expressed as follows:

$$ \begin{aligned} \tau _{{rz}} & = e^{{p(\eta + \bar{\eta }) - q(\eta - \bar{\eta })i}} \left[ {M_{1} \left( {\frac{{\partial w}}{{\partial \eta }}e^{{i\theta }} + \frac{{\partial w}}{{\partial \bar{\eta }}}e^{{ - i\theta }} } \right) + M_{2} \left( {\frac{{\partial f}}{{\partial \eta }}e^{{i\theta }} + \frac{{\partial f}}{{\partial \bar{\eta }}}e^{{ - i\theta }} } \right) + M_{3} \left( {\frac{{\partial \zeta }}{{\partial \eta }}e^{{i\theta }} + \frac{{\partial \zeta }}{{\partial \bar{\eta }}}e^{{ - i\theta }} } \right)} \right], \\ \tau _{{\theta z}} & = e^{{p(\eta + \bar{\eta }) - q(\eta - \bar{\eta })i}} i\left[ {M_{1} \left( {\frac{{\partial w}}{{\partial \eta }}e^{{i\theta }} - \frac{{\partial w}}{{\partial \bar{\eta }}}e^{{ - i\theta }} } \right) + M_{2} \left( {\frac{{\partial f}}{{\partial \eta }}e^{{i\theta }} - \frac{{\partial f}}{{\partial \bar{\eta }}}e^{{ - i\theta }} } \right) + M_{3} \left( {\frac{{\partial \zeta }}{{\partial \eta }}e^{{i\theta }} - \frac{{\partial \zeta }}{{\partial \bar{\eta }}}e^{{ - i\theta }} } \right)} \right], \\ D_{r} & = e^{{p(\eta + \bar{\eta }) - q(\eta - \bar{\eta })i}} \left( {\frac{{\partial f}}{{\partial \eta }}e^{{i\theta }} + \frac{{\partial f}}{{\partial \bar{\eta }}}e^{{ - i\theta }} } \right),D_{\theta } = e^{{p(\eta + \bar{\eta }) - q(\eta - \bar{\eta })i}} i\left( {\frac{{\partial f}}{{\partial \eta }}e^{{i\theta }} - \frac{{\partial f}}{{\partial \bar{\eta }}}e^{{ - i\theta }} } \right), \\ B_{r} & = e^{{p(\eta + \bar{\eta }) - q(\eta - \bar{\eta })i}} \left( {\frac{{\partial \zeta }}{{\partial \eta }}e^{{i\theta }} + \frac{{\partial \zeta }}{{\partial \bar{\eta }}}e^{{ - i\theta }} } \right),B_{\theta } = e^{{p(\eta + \bar{\eta }) - q(\eta - \bar{\eta })i}} i\left( {\frac{{\partial \zeta }}{{\partial \eta }}e^{{i\theta }} - \frac{{\partial \zeta }}{{\partial \bar{\eta }}}e^{{ - i\theta }} } \right) \\ \end{aligned} $$

(9)

where $M_{1} = c_{{440}} + a_{1} e_{{150}} + a_{2} h_{{150}}$, $M_{2} = b_{1} e_{{150}} + b_{2} h_{{150}}$, and $M_{3} = c_{1} e_{{150}} + c_{2} h_{{150}}$, respectively.

3.2 Boundary conditions

To study the dynamic behavior of piezoelectric/piezomagnetic materials considered in this paper, the boundary conditions on the horizontal boundary $B_{H}$, vertical boundary $B_{V}$, and boundary $B_{{in}}$ should be formulated.

• 1. The boundary conditions on the horizontal boundary $B_{H}$ imply mechanical stress-free, electrical open circuit and magnetic short circuit state:

  $$ \left\{ \begin{gathered} \left. {\tau _{{yz}}^{{\text{I}}} } \right|_{{y = h}} = 0,\left. {D_{y}^{{\text{I}}} } \right|_{{y = h}} = 0{\kern 1pt} {\kern 1pt} ,\left. {B_{y}^{{\text{I}}} } \right|_{{y = h}} = 0 \hfill \\ \left. {\tau _{{yz}}^{{{\text{II}}}} } \right|_{{y = h}} = 0,\left. {D_{y}^{{{\text{II}}}} } \right|_{{y = h}} = 0{\kern 1pt} {\kern 1pt} ,\left. {B_{y}^{{{\text{II}}}} } \right|_{{y = h}} = 0 \hfill \\ \end{gathered} \right.{\kern 1pt} {\kern 1pt} $$

  (10)

  .

• 2. The conditions on the boundary $B_{{in}}$ describe the continuous stress, electric, and magnetic fields:

  $$ \left\{ \begin{gathered} \left. {w^{{\text{I}}} } \right|_{{r = a}} = \left. {w^{{{\text{III}}}} } \right|_{{r = a}} ,\left. {\tau _{{rz}}^{{\text{I}}} } \right|_{{r = a}} = \left. {\tau _{{rz}}^{{{\text{III}}}} } \right|_{{r = a}} \hfill \\ \left. {\phi ^{{\text{I}}} } \right|_{{r = a}} = \left. {\phi ^{{{\text{III}}}} } \right|_{{r = a}} ,\left. {D_{r}^{{\text{I}}} } \right|_{{r = a}} = \left. {D_{r}^{{{\text{III}}}} } \right|_{{r = a}} , \hfill \\ \left. {\varphi ^{{\text{I}}} } \right|_{{r = a}} = \left. {\varphi ^{{{\text{III}}}} } \right|_{{r = a}} ,\left. {B_{r}^{{\text{I}}} } \right|_{{r = a}} = \left. {B_{r}^{{{\text{III}}}} } \right|_{{r = a}} . \hfill \\ \end{gathered} \right.{\kern 1pt} {\kern 1pt} $$

  (11)

• 3. At the vertical interface $B_{V}$ the stress, electric, and magnetic fields are continuous as well.

4 Physical fields caused by SH-wave

4.1 SH-wave

SH-waves are the simplest plane shear waves, which are widely used for nondestructive testing and underwater detection. In this paper, the characteristics of propagation of SH waves in piezoelectric/piezomagnetic materials are studied. The incident wave is considered as a vibration source. This wave is reflected and refracted at the vertical interface resulting in induction of elastic, electric, and magnetic fields.

We consider the steady-state time-harmonic displacement, electric, and magnetic waves incident in the piezoelectric/piezomagnetic half-space at an angle $\alpha _{0}$ to the horizontal plane as shown in Fig. 2.

Fig. 2

SH-wave in a piezoelectric/piezomagnetic half space

According to [2], the incident wave $w^{i}$ satisfying the boundary conditions Eq. (10) on the horizontal boundary $B_{H}$ generates the electric potential $\phi ^{i}$ and magnetic potential $\varphi ^{i}$ expressed as follows:

$$ \begin{aligned} w^{r} & = w_{1} \left\{ {\exp \left\{ {\frac{{ik_{1} }}{2}\left[ {(\eta - hi)e^{{ - i\beta }} + (\bar{\eta } + hi)e^{{i\beta }} } \right]} \right\} + } \right.\left. {\exp \left\{ {\frac{{ik_{1} }}{2}\left[ {(\eta - hi)e^{{i\beta }} + (\bar{\eta } + hi)e^{{ - i\beta }} } \right]} \right\}} \right\}, \\ \phi ^{r} & = \phi _{1} \left\{ {\exp \left\{ {\frac{{ik_{1} }}{2}\left[ {(\eta - hi)e^{{ - i\beta }} + (\bar{\eta } + hi)e^{{i\beta }} } \right]} \right\} + } \right.\left. {\exp \left\{ {\frac{{ik_{1} }}{2}\left[ {(\eta - hi)e^{{i\beta }} + (\bar{\eta } + hi)e^{{ - i\beta }} } \right]} \right\}} \right\}, \\ \varphi ^{r} & = \varphi _{1} \left\{ {\exp \left\{ {\frac{{ik_{1} }}{2}\left[ {(\eta - hi)e^{{ - i\beta }} + (\bar{\eta } + hi)e^{{i\beta }} } \right]} \right\} + } \right.\left. {\exp \left\{ {\frac{{ik_{1} }}{2}\left[ {(\eta - hi)e^{{i\beta }} + (\bar{\eta } + hi)e^{{ - i\beta }} } \right]} \right\}} \right\} ,\\ \end{aligned} $$

(12)

Note that the superscript i refers to the incident wave.

Similarly, the electric potential $\phi ^{r}$ and magnetic potential $\varphi ^{r}$ caused by the reflected wave $w^{r}$ are obtained as follows:

$$ \begin{aligned} w^{r} & = w_{1} \left\{ {\exp \left\{ {\frac{{ik_{1} }}{2}\left[ {(\eta - hi)e^{{ - i\beta }} + (\bar{\eta } + hi)e^{{i\beta }} } \right]} \right\} + } \right.\left. {\exp \left\{ {\frac{{ik_{1} }}{2}\left[ {(\eta - hi)e^{{i\beta }} + (\bar{\eta } + hi)e^{{ - i\beta }} } \right]} \right\}} \right\}, \\ \phi ^{r} & = \phi _{1} \left\{ {\exp \left\{ {\frac{{ik_{1} }}{2}\left[ {(\eta - hi)e^{{ - i\beta }} + (\bar{\eta } + hi)e^{{i\beta }} } \right]} \right\} + } \right.\left. {\exp \left\{ {\frac{{ik_{1} }}{2}\left[ {(\eta - hi)e^{{i\beta }} + (\bar{\eta } + hi)e^{{ - i\beta }} } \right]} \right\}} \right\}, \\ \varphi ^{r} & = \varphi _{1} \left\{ {\exp \left\{ {\frac{{ik_{1} }}{2}\left[ {(\eta - hi)e^{{ - i\beta }} + (\bar{\eta } + hi)e^{{i\beta }} } \right]} \right\} + } \right.\left. {\exp \left\{ {\frac{{ik_{1} }}{2}\left[ {(\eta - hi)e^{{i\beta }} + (\bar{\eta } + hi)e^{{ - i\beta }} } \right]} \right\}} \right\} ,\\ \end{aligned} $$

(13)

where the reflection angle $\beta = \pi - \alpha _{0}$. Here, the superscript r refers to the reflected wave.

Since the refracted wave $w^{f}$ propagates in Medium II composed of inhomogeneous piezomagnetic materials, in order to make it satisfy the governing Eq. (6), it is necessary to introduce the complex variable $e^{{ - p_{2} x}} = e^{{ - \frac{{p_{2} (\eta + \bar{\eta })}}{2}}}$ as the product factor which describes the inhomogeneity. Therefore, the physical meaning of Eq. (14) of this paper is different from that of Eqs. (12)–(13) in [2]

$$ \begin{aligned} w^{f} & = e^{{ - \frac{{p_{2} (\eta + \bar{\eta })}}{2}}} w_{2} \left\{ {\exp \left\{ {\frac{{ik_{{02}} }}{2}\left[ {(\eta - hi)e^{{ - i\alpha _{2} }} + (\bar{\eta } + hi)e^{{i\alpha _{2} }} } \right]} \right\} + } \right.\left. {\exp \left\{ {\frac{{ik_{{02}} }}{2}\left[ {(\eta - hi)e^{{i\alpha _{2} }} + (\bar{\eta } + hi)e^{{ - i\alpha _{2} }} } \right]} \right\}} \right\} ,\\ \phi ^{f} & = e^{{ - \frac{{p_{2} (\eta + \bar{\eta })}}{2}}} \phi _{2} \left\{ {\exp \left\{ {\frac{{ik_{{02}} }}{2}\left[ {(\eta - hi)e^{{ - i\alpha _{2} }} + (\bar{\eta } + hi)e^{{i\alpha _{2} }} } \right]} \right\} + } \right.\left. {\exp \left\{ {\frac{{ik_{{02}} }}{2}\left[ {(\eta - hi)e^{{i\alpha _{2} }} + (\bar{\eta } + hi)e^{{ - i\alpha _{2} }} } \right]} \right\}} \right\} ,\\ \varphi ^{f} & = e^{{ - \frac{{p_{2} (\eta + \bar{\eta })}}{2}}} \varphi _{2} \left\{ {\exp \left\{ {\frac{{ik_{02} }}{2}\left[ {(\eta - hi)e^{{ - i\alpha _{2} }} + (\bar{\eta } + hi)e^{{i\alpha _{2} }} } \right]} \right\} + } \right.\left. {\exp \left\{ {\frac{{ik_{{02}} }}{2}\left[ {(\eta - hi)e^{{i\alpha _{2} }} + (\bar{\eta } + hi)e^{{ - i\alpha _{2} }} } \right]} \right\}} \right\} ,\\ \end{aligned} $$

(14)

Here, $k_{{02}} = \sqrt {k_{2}^{2} - p_{2}^{2} }$, $k_{2}^{2} - p_{2}^{2} > 0$, and $\alpha _{2}$ represents angle of refraction, respectively. Note that the superscript f refers to the refracted wave.

The variables introduced above should satisfy the continuity conditions on the vertical boundary $B_{{\text{V}}} (x = 0)$:

$$ \left\{ \begin{gathered} w^{i} + w^{r} = w^{f} ,\tau _{{xz}}^{i} + \tau _{{xz}}^{r} = \tau _{{xz}}^{f} , \hfill \\ \phi ^{i} + \phi ^{r} = \phi ^{f} ,D_{x}^{i} + D_{x}^{r} = D_{x}^{f} , \hfill \\ \varphi ^{i} + \varphi ^{r} = \varphi ^{f} ,B_{x}^{i} + B_{x}^{r} = B_{x}^{f} . \hfill \\ \end{gathered} \right. $$

(15)

With the help of Cramer’s Rule, Eq. (15) can be solved, and the relationships between all parameters can be obtained:

$$ \begin{aligned} w_{1} & = w_{1} (w_{0} ,\phi _{0} ,\varphi _{0} ),w_{2} = w_{2} (w_{0} ,\phi _{0} ,\varphi _{0} ),\phi _{1} = \phi _{1} (w_{0} ,\phi _{0} ,\varphi _{0} ) ,\\ \phi _{2} & = \phi _{2} (w_{0} ,\phi _{0} ,\varphi _{0} ),\varphi _{1} = \varphi _{1} (w_{0} ,\phi _{0} ,\varphi _{0} ),\varphi _{2} = \varphi _{2} (w_{0} ,\phi _{0} ,\varphi _{0} ) ,\\ \end{aligned} $$

(16)

The detailed expressions are shown in the Part III of the Appendix.

4.2 Scattering wave

When the incident wave $w^{i}$ propagates to the circular inclusion (i.e., the Medium III) that can be regarded as an obstacle, the diffraction and scattering of the wave occurs, and the scattered wave $w^{s}$ propagates from the center of the Medium III as the emission origin. Therefore, the variable $\eta ^{\prime} = \eta + d$ is introduced to create a new coordinate system $x^{\prime}o^{\prime}y^{\prime}$ with the center of Medium III as the origin, as shown in Fig. 1.

The transformations of coordinates between the two coordinate systems look as follows:

$$ \left\{ \begin{gathered} x^{\prime} = x + d, \hfill \\ y^{\prime} = y. \hfill \\ \end{gathered} \right. $$

(17)

As shown in Fig. 3, the scattered wave $w^{s}$ is reflected and refracted at the vertical interface $B_{V} (x^{\prime} = d)$. However, the expressions for the reflected and refracted waves caused by $w^{s}$ are very complicated, so that only the approximate formulas can be obtained.

Fig. 3

Reflection of the scattering wave at a vertical interface

The image method is applied for mathematical simplicity and to eliminate the influence of $w^{s}$ on the vertical interface, as shown in Fig. 4. At this time, the shear stress caused by $w^{s}$ is zero at the vertical boundary. Moreover, the scattered wave $w^{s}$ also satisfies the boundary conditions (10) on the horizontal boundary $B_{H}$. Since the Medium I is homogeneous piezoelectric material, the factor $e^{{2(px + qy)}}$ can be omitted.

Fig. 4

The image of the scattering wave

Based on the above analysis, the expression for the scattered wave $w^{s}$ can be constructed as follows:

$$ w^{s} = \sum\limits_{{n = - \infty }}^{{ + \infty }} {A_{n} } \sum\limits_{{j = 1}}^{4} {S_{n}^{{(j)}} } $$

(18)

where $S_{n}^{{(1)}} = H_{n}^{{(1)}} (k_{1} \left| {\eta ^{\prime}} \right|)\left[ {{{\eta ^{\prime}} \mathord{\left/ {\vphantom {{\eta ^{\prime}} {\left| {\eta ^{\prime}} \right|}}} \right. \kern-\nulldelimiterspace} {\left| {\eta ^{\prime}} \right|}}} \right]^{n}$, $S_{n}^{{(2)}} = H_{n}^{{(1)}} (k_{1} \left| {\eta ^{\prime}_{1} } \right|)\left[ {{{\eta ^{\prime}_{1} } \mathord{\left/ {\vphantom {{\eta ^{\prime}_{1} } {\left| {\eta ^{\prime}_{1} } \right|}}} \right. \kern-\nulldelimiterspace} {\left| {\eta ^{\prime}_{1} } \right|}}} \right]^{{ - n}}$, $S_{n}^{{(3)}} = ( - 1)^{n} H_{n}^{{(1)}} (k_{1} \left| {\eta ^{\prime}_{2} } \right|)\left[ {{{\eta ^{\prime}_{2} } \mathord{\left/ {\vphantom {{\eta ^{\prime}_{2} } {\left| {\eta ^{\prime}_{2} } \right|}}} \right. \kern-\nulldelimiterspace} {\left| {\eta ^{\prime}_{2} } \right|}}} \right]^{n}$, $S_{n}^{{(4)}} = ( - 1)^{n} H_{n}^{{(1)}} (k_{1} \left| {\eta ^{\prime}_{3} } \right|)\left[ {{{\eta ^{\prime}_{3} } \mathord{\left/ {\vphantom {{\eta ^{\prime}_{3} } {\left| {\eta ^{\prime}_{3} } \right|}}} \right. \kern-\nulldelimiterspace} {\left| {\eta ^{\prime}_{3} } \right|}}} \right]^{{ - n}}$, $\eta ^{\prime}_{1} = \eta ^{\prime} - 2hi$,$\eta ^{\prime}_{2} = \eta ^{\prime}_{1} - 2d$,$\eta ^{\prime}_{3} = \eta ^{\prime} - 2d$.

Note that the superscript s refers to the scattered wave.

The electric potential $\phi ^{s}$ and magnetic potential $\varphi ^{s}$ induced by the scattered wave $w^{s}$ are obtained as follows:

$$ \begin{aligned} \phi ^{s} & = a_{1}^{I} w^{s} + b_{1}^{I} f^{s} + c_{1}^{I} \zeta ^{s} ,\varphi ^{s} = a_{2}^{I} w^{s} + b_{2}^{I} f^{s} + c_{2}^{I} \zeta ^{s} , \\ f^{s} & = \sum\limits_{{n = 1}}^{\infty } {\left[ {B_{n} \sum\limits_{{j = 1}}^{4} {\varphi _{{1n}}^{{(j)}} } + C_{n} \sum\limits_{{j = 1}}^{4} {\varphi _{{2n}}^{{(j)}} } } \right]} ,\zeta ^{s} = \sum\limits_{{n = 1}}^{\infty } {\left[ {D_{n} \sum\limits_{{j = 1}}^{4} {\varphi _{{1n}}^{{(j)}} } + E_{n} \sum\limits_{{j = 1}}^{4} {\varphi _{{2n}}^{{(j)}} } } \right]} \\ \end{aligned} $$

(19)

where $\varphi _{{1n}}^{{(1)}} = \eta ^{{\prime - n}}$,$\varphi _{{1n}}^{{(2)}} = (\bar{\eta }^{\prime} + 2hi)^{{ - n}}$, $\varphi _{{1n}}^{{(3)}} = ( - 1)^{n} (\bar{\eta }^{\prime} - 2d)^{{ - n}}$,$\varphi _{{1n}}^{{(4)}} = ( - 1)^{n} (\eta ^{\prime} - 2d - 2hi)^{{ - n}}$, $\varphi _{{2n}}^{{(1)}} = \bar{\eta }^{{\prime - n}}$,$\varphi _{{2n}}^{{(2)}} = (\eta ^{\prime} - 2hi)^{{ - n}}$, $\varphi _{{2n}}^{{(3)}} = ( - 1)^{n} (\eta ^{\prime} - 2d)^{{ - n}}$,$\varphi _{{2n}}^{{(4)}} = ( - 1)^{n} (\bar{\eta }^{\prime } - 2d + 2hi)^{{ - n}}$, $a_{{\text{1}}}^{{\text{I}}} = \frac{{\mu _{{{\text{110}}}}^{{\text{I}}} e_{{{\text{150}}}}^{{\text{I}}} }}{{\mu _{{{\text{110}}}}^{{\text{I}}} \kappa _{{{\text{110}}}}^{{\text{I}}} - t_{{110}}^{2} }}$, $b_{{\text{1}}}^{{\text{I}}} = \frac{{ - \mu _{{{\text{110}}}}^{{\text{I}}} }}{{\mu _{{{\text{110}}}}^{{\text{I}}} \kappa _{{{\text{110}}}}^{{\text{I}}} - t_{{110}}^{2} }}$,$c_{{\text{1}}}^{{\text{I}}} = \frac{{t_{{110}} }}{{\mu _{{{\text{110}}}}^{{\text{I}}} \kappa _{{{\text{110}}}}^{{\text{I}}} - t_{{110}}^{2} }}$, $a_{{\text{2}}}^{{\text{I}}} = \frac{{ - t_{{110}} e_{{{\text{150}}}}^{{\text{I}}} }}{{\mu _{{{\text{110}}}}^{{\text{I}}} \kappa _{{{\text{110}}}}^{{\text{I}}} - t_{{110}}^{2} }}$, $b_{{\text{2}}}^{{\text{I}}} = \frac{{t_{{110}} }}{{\mu _{{{\text{110}}}}^{{\text{I}}} \kappa _{{{\text{110}}}}^{{\text{I}}} - t_{{110}}^{2} }}$, $c_{{\text{2}}}^{{\text{I}}} = \frac{{ - \kappa _{{{\text{110}}}}^{{\text{I}}} }}{{\mu _{{{\text{110}}}}^{{\text{I}}} \kappa _{{{\text{110}}}}^{{\text{I}}} - t_{{110}}^{2} }}$.

This assumption of Eq. (19) is plausible because the physical variables $f^{s}$ and $\zeta ^{s}$ do not tend to infinity at $\eta ^{\prime} \to + \infty$ and $\bar{\eta ^{\prime}} \to + \infty$.

Thus, the total displacement field $w^{{\text{I}}}$, total electric field $\phi ^{{\text{I}}}$, and total magnetic field $\varphi ^{{\text{I}}}$ in the Medium I are obtained by the superposition method:

$$ w^{{\text{I}}} = w^{i} + w^{r} + w^{s} ,\phi ^{{\text{I}}} = \phi ^{i} + \phi ^{r} + \phi ^{s} ,\varphi ^{{\text{I}}} = \varphi ^{i} + \varphi ^{r} + \varphi ^{s} $$

(20)

,

Similarly, the total displacement field $w^{{{\text{II}}}}$, total electric field $\phi ^{{{\text{II}}}}$, and total magnetic field $\varphi ^{{{\text{II}}}}$ of the Medium II are obtained as follows:

$$ w^{{II}} = w^{f},\,\phi ^{{II}} = \phi ^{f},\,\varphi ^{{II}} = \varphi ^{f} $$

(21)

,

4.3 Standing wave

When the piezoelectric material is subjected to the shear wave, the standing wave is formed in the circular inclusion (i.e., the Medium III). Due to the inhomogeneity of the Medium III, the factor $e^{{ - (p_{3} x^{\prime} + q_{3} y^{\prime})}} = e^{{ - p_{3} (\frac{{\eta ^{\prime} + \bar{\eta }^{\prime}}}{2}) - q_{3} (\frac{{\eta ^{\prime} - \bar{\eta }^{\prime}}}{{2i}})}}$ should be introduced.

The expression of the standing wave in Medium III can be established as follows:

$$ w^{{st}} = W^{{st}} e^{{ - p_{3} \left( {\frac{{\eta ^{\prime} + \bar{\eta }^{\prime}}}{2}} \right) - q_{3} \left( {\frac{{\eta ^{\prime} - \bar{\eta }^{\prime}}}{{2i}}} \right)}} ,W^{{st}} = \sum\limits_{{n = - \infty }}^{{ + \infty }} {R_{n} J_{n} (k_{{03}} \left| {\eta ^{\prime}} \right|)\left[ {{{\eta ^{\prime}} \mathord{\left/ {\vphantom {{\eta ^{\prime}} {\left| {\eta ^{\prime}} \right|}}} \right. \kern-\nulldelimiterspace} {\left| {\eta ^{\prime}} \right|}}} \right]^{n} } $$

(22)

where $k_{{03}} = \sqrt {k_{3}^{2} - p_{3}^{2} - q_{3}^{2} }$ and $k_{3}^{2} - p_{3}^{2} - q_{3}^{2} > 0$.

Equations (22) are based on the assumption that the standing wave consists of two types of waves:

• 1. The wave propagating outward the center of the Medium III, and

• 2. The wave converging toward the center of the Medium III.

The two scenarios mentioned above are described by the terms $J_{n} (k_{{03}} \left| {\eta ^{\prime}} \right|)\left[ {{{\eta ^{\prime}} \mathord{\left/ {\vphantom {{\eta ^{\prime}} {\left| {\eta ^{\prime}} \right|}}} \right. \kern-\nulldelimiterspace} {\left| {\eta ^{\prime}} \right|}}} \right]^{n}$ in Eqs. (22).

Therefore, Eqs. (22) describe the distribution of waves in Medium III. Since both waves mentioned above are related to the center of Medium III, the coordinate system $x^{\prime}o^{\prime}y^{\prime}$ is adopted. Note that the superscript st refers to the standing wave.

The complex variable $ik^{\prime}$ is equivalent to $k$ in the first Eq. (6). Therefore, the expressions for electric potential $\phi ^{{st}}$ and magnetic potential $\varphi ^{{st}}$ induced by the standing wave $w^{{st}}$ can be written as follows:

$$ \begin{gathered} \phi ^{{st}} = a_{{\text{1}}}^{{{\text{III}}}} w^{{st}} + b_{{\text{1}}}^{{{\text{III}}}} f^{{st}} + c_{{\text{1}}}^{{{\text{III}}}} \zeta ^{{st}} , \hfill \\ \varphi ^{{st}} = a_{2}^{{{\text{III}}}} w^{{st}} + b_{2}^{{{\text{III}}}} f^{{st}} + c_{2}^{{{\text{III}}}} \zeta ^{{st}} , \hfill \\ \end{gathered} $$

$$ f^{{st}} = f_{0}^{{st}} e^{{ - p_{3} \left( {\frac{{\eta ^{\prime} + \bar{\eta }^{\prime}}}{2}} \right) - q_{3} \left( {\frac{{\eta ^{\prime} - \bar{\eta }^{\prime}}}{{2i}}} \right)}} ,\zeta ^{{st}} = \zeta _{0}^{{st}} e^{{ - p_{3} \left( {\frac{{\eta ^{\prime} + \bar{\eta }^{\prime}}}{2}} \right) - q_{3} \left( {\frac{{\eta ^{\prime} - \bar{\eta }^{\prime}}}{{2i}}} \right)}}, $$

$$ \begin{aligned} f_{0}^{{st}} & = \sum\limits_{{n = - \infty }}^{{ + \infty }} {\left[ {L_{n} H_{n}^{{(1)}} (ik^{\prime}_{3} \left| {\eta ^{\prime}} \right|) + T_{n} H_{n}^{{(2)}} (ik^{\prime}_{3} \left| {\eta ^{\prime}} \right|)} \right]\left[ {{{\eta ^{\prime}} \mathord{\left/ {\vphantom {{\eta ^{\prime}} {\left| {\eta ^{\prime}} \right|}}} \right. \kern-\nulldelimiterspace} {\left| {\eta ^{\prime}} \right|}}} \right]^{n} } , \\ \zeta _{0}^{{st}} & = \sum\limits_{{n = - \infty }}^{{ + \infty }} {\left[ {U_{n} H_{n}^{{(1)}} (ik^{\prime}_{3} \left| {\eta ^{\prime}} \right|) + V_{n} H_{n}^{{(2)}} (ik^{\prime}_{3} \left| {\eta ^{\prime}} \right|)} \right]\left[ {{{\eta ^{\prime}} \mathord{\left/ {\vphantom {{\eta ^{\prime}} {\left| {\eta ^{\prime}} \right|}}} \right. \kern-\nulldelimiterspace} {\left| {\eta ^{\prime}} \right|}}} \right]^{n} } . \\ \end{aligned} $$

(23)

Here: $k^{\prime}_{3} = \sqrt {p_{3}^{2} + q_{3}^{2} }$,

$a_{{\text{1}}}^{{{\text{III}}}} = \frac{{\mu _{{{\text{110}}}}^{{{\text{III}}}} e_{{{\text{150}}}}^{{{\text{III}}}} }}{{\mu _{{{\text{110}}}}^{{{\text{III}}}} \kappa _{{{\text{110}}}}^{{{\text{III}}}} - t_{{110}}^{2} }}$,$b_{{\text{1}}}^{{{\text{III}}}} = \frac{{ - \mu _{{{\text{110}}}}^{{{\text{III}}}} }}{{\mu _{{{\text{110}}}}^{{{\text{III}}}} \kappa _{{{\text{110}}}}^{{{\text{III}}}} - t_{{110}}^{2} }}$,$c_{{\text{1}}}^{{{\text{III}}}} = \frac{{t_{{110}} }}{{\mu _{{{\text{110}}}}^{{{\text{III}}}} \kappa _{{{\text{110}}}}^{{{\text{III}}}} - t_{{110}}^{2} }}$,

$a_{{\text{2}}}^{{{\text{III}}}} = \frac{{ - t_{{110}} e_{{{\text{150}}}}^{{{\text{III}}}} }}{{\mu _{{{\text{110}}}}^{{{\text{III}}}} \kappa _{{{\text{110}}}}^{{{\text{III}}}} - t_{{110}}^{2} }}$,$b_{{\text{2}}}^{{{\text{III}}}} = \frac{{t_{{110}} }}{{\mu _{{{\text{110}}}}^{{{\text{III}}}} \kappa _{{{\text{110}}}}^{{{\text{III}}}} - t_{{110}}^{2} }}$,$c_{{\text{2}}}^{{{\text{III}}}} = \frac{{ - \kappa _{{{\text{110}}}}^{{{\text{III}}}} }}{{\mu _{{{\text{110}}}}^{{{\text{III}}}} \kappa _{{{\text{110}}}}^{{{\text{III}}}} - t_{{110}}^{2} }}$.

Since the complex variables $\eta ^{\prime}$ and $\bar{\eta ^{\prime}}$ for the Medium III are finite, the variables $f^{{st}}$ and $\zeta ^{{st}}$ cannot be infinite, and all the terms $H_{n}^{{(1)}} ( \bullet )$ and $H_{n}^{{(2)}} ( \bullet )$ are the solutions for $\phi ^{{st}}$ and $\varphi ^{{st}}$.

The total displacement field $w^{{{\text{III}}}}$, total electric field $\phi ^{{{\text{III}}}}$, and total magnetic field $\varphi ^{{{\text{III}}}}$ in the Medium III are obtained by the superposition method:

$$ w^{{{\text{III}}}} = w^{{st}} ,\phi ^{{{\text{III}}}} = \phi ^{{st}} ,\varphi ^{{{\text{III}}}} = \varphi ^{{st}} $$

(24)

According to the boundary condition (11) on the boundary $B_{{in}}$, the equations to find the unknown coefficients $A_{n}$,$B_{n}$,$C_{n}$,$D_{n}$,$E_{n}$,$R_{n}$,$L_{n}$,$T_{n}$,$U_{n}$, and $V_{n}$ are obtained. The details of the calculations are presented in Part I of the Appendix.

4.4 Special case related to medium III

At $\rho ^{{{\text{III}}}} = 0$, Medium III degenerates into a circular cavity. In this case, $p_{3} = 0$ and $q_{3} = 0$.

Because no elastic field can be formed in the air in the cavity, the electric potential $\phi ^{c}$ and magnetic potential $\varphi ^{c}$ of the air can be obtained as follows:

$$ \begin{aligned} \phi ^{c} & = - \frac{1}{{\kappa _{0}^{c} }}f^{c} ,\varphi ^{c} = - \frac{1}{{\mu _{0}^{c} }}\zeta ^{c} , \\ f^{c} & = F_{0} + \sum\limits_{{n = 1}}^{{ + \infty }} {(F_{n} \eta ^{\prime\,n} + X_{n} \bar{\eta }^{\prime\,n} )} ,\zeta ^{c} = Y_{0} + \sum\limits_{{n = 1}}^{{ + \infty }} {(Y_{n} \eta ^{\prime\,n} + Z_{n} \bar{\eta }^{\prime\,n} )} . \\ \end{aligned} $$

(25)

Here, $\kappa _{0}^{c} = 8.85 \times 10^{{ - 12}} F/m$ is the dielectric constant of air, and $\mu _{0}^{c} = 12.566 \times 10^{{ - 7}} H/m$ is the permeability of air, respectively.

At $\eta ^{\prime} \to 0$ and $\bar{\eta ^{\prime}} \to 0$, $f^{c}$ and $\zeta ^{c}$ have finite values, so that the terms $( \bullet )^{{ - n}}$ in Eq. (25) should be omitted.

5 Green’s function method and calculation index

5.1 Brief introduction of Green’s function

In Sect. 4.2, we use the image method to simplify the calculation of the scattered wave. However, this assumption does not correspond to reality. In order to obtain the real distribution of elastic, electric, and magnetic fields, the Green’s function method is used.

The total displacement field $w^{t}$, total electric field $\phi ^{t}$ and total magnetic field $\varphi ^{t}$ in the Medium I are the superpositions of Green’s functions and SH-wave:

$$ \begin{gathered} w^{t} = w^{I} + \int_{0}^{{ + \infty }} {f_{1} (r^{\prime\prime}_{0} ,\theta ^{\prime\prime}_{0} )G_{w}^{I} (r^{\prime\prime}_{0} ,\theta ^{\prime\prime}_{0} ,r^{\prime\prime},\theta ^{\prime\prime})} {\text{d}}r^{\prime\prime}_{0} ,\quad \theta ^{\prime\prime}_{0} = {{ - \pi } \mathord{\left/ {\vphantom {{ - \pi } 2}} \right. \kern-\nulldelimiterspace} 2} \hfill\,, \\ \phi ^{t} = \phi ^{I} + \int_{0}^{{ + \infty }} {f_{3} (r^{\prime\prime}_{0} ,\theta ^{\prime\prime}_{0} )G_{\phi }^{I} (r^{\prime\prime}_{0} ,\theta ^{\prime\prime}_{0} ,r^{\prime\prime},\theta ^{\prime\prime})} {\text{d}}r^{\prime\prime}_{0} ,\quad \theta ^{\prime\prime}_{0} = {{ - \pi } \mathord{\left/ {\vphantom {{ - \pi } 2}} \right. \kern-\nulldelimiterspace} 2} \hfill, \\ \varphi ^{t} = \varphi ^{I} + \int_{0}^{{ + \infty }} {f_{5} (r^{\prime\prime}_{0} ,\theta ^{\prime\prime}_{0} )G_{\varphi }^{I} (r^{\prime\prime}_{0} ,\theta ^{\prime\prime}_{0} ,r^{\prime\prime},\theta ^{\prime\prime})} {\text{d}}r^{\prime\prime}_{0} ,\quad \theta ^{\prime\prime}_{0} = {{ - \pi } \mathord{\left/ {\vphantom {{ - \pi } 2}} \right. \kern-\nulldelimiterspace} 2} \hfill. \\ \end{gathered} $$

(26)

Here, $G_{w}^{{\text{I}}}$,$G_{\phi }^{{\text{I}}}$, and $G_{\varphi }^{{\text{I}}}$ are obtained by Green’s function method and represent displacement, electric potential and magnetic potential in the Medium I, respectively. The variable $(r^{\prime\prime},\theta ^{\prime\prime})$ is the polar coordinate in the system having the top of the right-angle region as the origin; the variable $(r^{\prime\prime}_{0} ,\theta ^{\prime\prime}_{0} )$ represents the coordinates of the point source.

The details of the calculations are provided in Part II of the Appendix.

5.2 Dynamic stress concentration factor

DSCF is a dimensionless coefficient, which characterizes variation of dynamic stress at each position of the boundary $B_{{in}}$. After the position is defined by variables $(r^{\prime\prime},\theta ^{\prime\prime})$, the DSCF in the points above can be calculated by introducing the complex variables $\eta = r^{\prime\prime}e^{{i\theta ^{\prime\prime}}}$, $\bar{\eta } = r^{\prime\prime}e^{{ - i\theta ^{\prime\prime}}}$. When DSCF of a certain location of the boundary $B_{{in}}$ is relatively large, this location is prone to damage and fracture. Therefore, DSCF indicates the structural strength to a certain extent. The tangential shear stress around the Medium III can be expressed as follows:

$$ \begin{aligned} \tau _{{\theta z}} & = \tau _{{\theta z}}^{{\text{I}}} + \int_{0}^{{ + \infty }} {f_{1} (r^{\prime\prime}_{0} ,\beta _{1} )} \frac{{c_{{440}}^{{\text{I}}} }}{{r^{\prime\prime}_{0} }}\frac{{\partial G_{w}^{{\text{I}}} (r^{\prime\prime}_{0} ,\beta _{1} ;r^{\prime\prime},\theta ^{\prime\prime})}}{{\partial \theta ^{\prime\prime}}}{\text{d}}r^{\prime\prime}_{0} \\ & \quad + \int_{0}^{{ + \infty }} {f_{3} (r^{\prime\prime}_{0} ,\beta _{1} )} \frac{{e_{{150}}^{{\text{I}}} }}{{r^{\prime\prime}_{0} }}\frac{{\partial G_{\phi }^{{\text{I}}} (r^{\prime\prime}_{0} ,\beta _{1} ;r^{\prime\prime},\theta ^{\prime\prime})}}{{\partial \theta ^{\prime\prime}}}{\text{d}}r^{\prime\prime}_{0} \,\,,\\ \end{aligned} $$

(27)

The DSCF can be expressed as follows:

$$ \tau _{{\theta z}}^{*} = \left| {{{\tau _{{\theta z}} } \mathord{\left/ {\vphantom {{\tau _{{\theta z}} } {\tau _{0} }}} \right. \kern-\nulldelimiterspace} {\tau _{0} }}} \right| $$

(28)

where $\beta _{1} = - {\pi \mathord{\left/ {\vphantom {\pi 2}} \right. \kern-\nulldelimiterspace} 2}$, and $\tau _{0} = ik_{1} (c_{{{\text{440}}}}^{{\text{I}}} w_{0} + e_{{{\text{150}}}}^{{\text{I}}} \phi _{0} )$ is the amplitude of the shear stress induced by incident waves, respectively.

The expression for DSCF contains three contributions:

• 1. dynamic stress induced by SH-wave,

• 2. dynamic stress caused by the external forces, and

• 3. dynamic stress produced by the external electric potential.

5.3 Electric field intensity concentration factor

The dimensionless EFICF characterizes the change of electric potential at each position of the boundary $B_{{in}}$. The EFICF can be obtained by a combination of the integral equation and complex function methods. When EFICF of a certain position of boundary $B_{{in}}$ is relatively large, the boundary is prone to leakage. Therefore, EFICF reflects the safety of piezoelectric/piezomagnetic material. The electric field intensity can be expressed as follows:

$$ E_{\theta } = i\left( {\frac{{\partial \phi ^{{\text{I}}} }}{{\partial \eta ^{\prime\prime}}}e^{{i\theta ^{\prime\prime}}} - \frac{{\partial \phi ^{{\text{I}}} }}{{\partial \bar{\eta }^{\prime\prime}}}e^{{ - i\theta ^{\prime\prime}}} } \right) + i\int_{0}^{{ + \infty }} {f_{3} (\eta ^{\prime\prime}_{0} )} \left( {\frac{{\partial G_{\phi }^{{\text{I}}} }}{{\partial \eta ^{\prime\prime}}}e^{{i\theta ^{\prime\prime}}} - \frac{{\partial G_{\phi }^{{\text{I}}} }}{{\partial \bar{\eta }^{\prime\prime}}}e^{{ - i\theta ^{\prime\prime}}} } \right){\text{d}}\left| {\eta ^{\prime\prime}_{0} } \right| ,$$

(29)

The EFICF is expressed as follows:

$$ E_{\theta }^{*} = \left| {{{E_{\theta } } \mathord{\left/ {\vphantom {{E_{\theta } } {E_{0} }}} \right. \kern-\nulldelimiterspace} {E_{0} }}} \right| $$

(30)

where $E_{0} = ik_{1} \phi _{0}$ is the amplitude of the electric potential of the incident wave.

The expression of EFICF contains two parts:

• 1. electric potential induced by SH-wave, and

• 2. external electric potential.

5.4 Magnetic field intensity concentration factor

The dimensionless MFICF characterizes the magnetic induction intensity at each position of the boundary $B_{{in}}$. The MFICF can be calculated by the superposition of different physical fields. If MFICF is too large, magnetic breakdown damaging the material structure will occur at the boundary $B_{{in}}$ due to too strong magnetic field. Therefore, MFICF is an important index of piezoelectric/piezomagnetic material. The MFICF can be expressed as follows:

$$ \begin{aligned} H_{\theta } = i\left( {\frac{{\partial \varphi ^{{\text{I}}} }}{{\partial \eta ^{\prime\prime}}}e^{{i\theta ^{\prime\prime}}} - \frac{{\partial \varphi ^{{\text{I}}} }}{{\partial \bar{\eta }^{\prime\prime}}}e^{{ - i\theta ^{\prime\prime}}} } \right) + i\int_{0}^{{ + \infty }} {f_{3} (\eta ^{\prime\prime}_{0} )} \left( {\frac{{\partial G_{\varphi }^{{\text{I}}} }}{{\partial \eta ^{\prime\prime}}}e^{{i\theta ^{\prime\prime}}} - \frac{{\partial G_{\varphi }^{{\text{I}}} }}{{\partial \bar{\eta }^{\prime\prime}}}e^{{ - i\theta ^{\prime\prime}}} } \right){\text{d}}\left| {\eta ^{\prime\prime}_{0} } \right| \\ \end{aligned}\,, $$

(31)

The MFICF is expressed as follows:

$$ H_{\theta }^{*} = \left| {{{H_{\theta } } \mathord{\left/ {\vphantom {{H_{\theta } } {H_{0} }}} \right. \kern-\nulldelimiterspace} {H_{0} }}} \right| $$

(32)

where $H_{0} = ik_{1} \varphi _{0}$ is the amplitude of the magnetic potential caused by incident waves.

The expression of MFICF contains two contributions:

• 1. magnetic potential caused by SH-wave, and

• 2. external magnetic potential.

6 Numerical examples and analysis

6.1 Verification of the method

Figure 5 presents the distribution of DSCF around as circular inclusion influenced by SH-wave under the extreme condition of $e_{{{\text{150}}}}^{{\text{I}}} = 0$, $\kappa _{{{\text{110}}}}^{{\text{I}}} = 0$, $\mu _{{{\text{110}}}}^{{\text{I}}} = 0$, $t_{{{\text{110}}}}^{{\text{I}}} = 0$;$h_{{{\text{150}}}}^{{{\text{II}}}} = 0$, $\kappa _{{{\text{110}}}}^{{{\text{II}}}} = 0$, $\mu _{{{\text{110}}}}^{{{\text{II}}}} = 0$, $t_{{{\text{110}}}}^{{{\text{II}}}} = 0$, and $\rho _{{\text{0}}}^{{{\text{III}}}} = 0$.The numerical examples in this article can be degenerated into a circular cavity in an elastic bi-material half-space, which is revealed in the case reported in [14]. At the parameters of media identical to those in [14], our results have a good agreement with those from the references above.

Fig. 5

Verification of the method in this article

As can be seen from Fig. 6, in which the Medium I is shown in green color and the Medium II in red color, respectively, the contact points of these media merge to make the stress transfer between them effective. We constructed a model for finite element calculations with hexahedral mesh elements for calculation accuracy. When the parameters of this model are set in accordance with the numerical example considered above, the results provided by both methods are almost identical. This means that the methods applied in this article are correct and valid.

Fig. 6

Comparison of finite element method

Fourier series expansion was applied to the wave functions presented in this article. The number of terms in the series expansion was increased by one until the difference between two consecutive calculation results was less than $10^{{ - 12}}$. Such approach ensures the accuracy of the expression for the wave function and convergence of calculation results. In the finite element calculations, the quality of the mesh was verified first. The irregular mesh was preprocessed to normalize its size and shape. In this way, the influence of the irregular mesh on the computational convergence was eliminated. Second, a smaller substep was set in the iterative calculations, leading to the decrease of the increment caused by inhomogeneity at each calculation step. This procedure enabled to guarantee the convergence of the iterative calculations.

In this Section, the value of DSCF, EFICF, and MFICF is provided as well as the effects of free boundary, and frequency of SH-wave, and different combinations of material parameters are discussed. The values of the dimensionless parameters obtained in numerical examples in this article are as follows:$h^{*} = {h \mathord{\left/ {\vphantom {h a}} \right. \kern-\nulldelimiterspace} a}$, $d^{*} = {d \mathord{\left/ {\vphantom {d a}} \right. \kern-\nulldelimiterspace} a}$, and $b^{*} = {b \mathord{\left/ {\vphantom {b a}} \right. \kern-\nulldelimiterspace} a}$.The parameters of common piezoelectric/piezomagnetic materials are shown in Tables 2 and 3.

Table 2 Parameters of piezoelectric material

Table 3 Parameters of piezomagnetic material

Among these parameters, the position $h^{*}$, $d^{*}$ and $b^{*}$ of the circular inclusion are geometry parameters, and the frequency $k_{1} a$ of the incident wave is a loading parameter. In this article, the Medium I is PZT-7 material by default. When the power of the exponential function $p_{2} = 0$, the Medium II becomes a homogeneous CoFe₂O₄ material by default. When the power of the exponential function $p_{3} = 0$ and $q_{3} = 0$, the Medium III becomes a homogeneous PZT-5A material by default. In the calculations, the value of the magnetoelectric coefficient $t_{{110}}$ is set to $5 \times 10^{{ - 12}} (NS/VC)$ by default.

The power coefficients of the exponential functions are shown in Table 4.

Table 4 Powers of exponential functions

As was noticed above, piezoelectric/piezomagnetic materials are widely used in engineering [1]. At this, various kinds of defects are formed in these materials during manufacture and exploitation. The numerical examples described in this article have engineering implications. For example, the model presented here is a simplified model of inhomogeneous piezoelectric/piezomagnetic composite plates with irregular defects, which may be caused by the production process or dislocation of piezoelectric/piezomagnetic laminates during pressing. When such a plate is subjected to dynamic load, its behavior and properties can be approximately described by the model presented in this article.

6.2 Case1: Propagation of SH-wave in an inhomogeneous piezoelectric/piezomagnetic half-space

Figure 7 shows the distribution of DSCF ($\tau _{{\theta z}}^{*}$) around a circular inclusion at different values of $k_{1} a$ under incident SH-wave. At $h^{*} = 40$, the value of $\tau _{{\theta z}}^{*}$ decreases with the value of $k_{1} a$ because of higher probability of resonance at low frequencies.$\tau _{{\theta z}}^{*}$ reaches the maximum value of 2.63 ($\theta = - 90^{ \circ }$) at $k_{1} a = 1$ and $h^{*} = 20$. When the incident wave frequency is $k_{1} a = 0.1$ and $h^{*} = 40$, $\tau _{{\theta z}}^{*}$ reaches the maximum value of 3.87 ($\theta = - 90^{ \circ }$), which exceeds the respective value at $k_{1} a = 1$ and $h^{*} = 20$ by more than 30%.The maximum value of $\tau _{{\theta z}}^{*}$ in both examples($h^{*} = 20$ and $h^{*} = 40$) is obtained at $\theta = - 90^{ \circ }$. So, the damage of high frequency is significant, and this angle value $\theta = - 90^{ \circ }$ should be given especial attention.

Fig. 7

Distribution of DSCF around a circular inclusion versus $k_{1} a$ under incident SH-wave

In order to further analyze the influence of $k_{1} a$ on DSCF ($\tau _{{\theta z}}^{*}$), Fig. 8 presents the variation curve of DSCF with $k_{1} a$.

Fig. 8

Distribution of maximum value of DSCF around a circular inclusion versus $k_{1} a$ under incident SH-wave

Figure 8 shows the distribution of the maximum value of DSCF ($\tau _{{\theta z}}^{*}$) around a circular inclusion varying as $k_{1} a$ under incident SH-wave. Apparent oscillations in the curves can be seen from this Figure. These oscillations are particularly strong in the range of $k_{1} a$ from 0.1 to 5. The upper limit of the maximum value of $\tau _{{\theta z}}^{*}$ is about 4.

Figure 9 presents the distribution of DSCF ($\tau _{{\theta z}}^{*}$) around a circular inclusion versus different incident angles of SH-wave. It can be seen from Fig. 9a that the curves are symmetrical and $\tau _{{\theta z}}^{*}$ is the largest at $\alpha _{0} = 0^{ \circ }$. When the incident angle $\alpha _{0} = 90^{ \circ }$,$\tau _{{\theta z}}^{*}$ is the smallest, so that this angle is optimum. Figure 9b shows the stress distribution curve at $\alpha _{0} = 0^{ \circ }$, and $\tau _{{\theta z}}^{*}$ reaches the maximum value of 5.45($\theta = - 102^{ \circ }$).

Fig. 9

Distribution of DSCF around a circular inclusion versus incident angles of SH-wave

Figure 10 shows the distribution of EFICF ($E_{\theta }^{*}$) around a circular inclusion varying as $k_{1} a$ under incident SH-wave. Compared with DSCF, $E_{\theta }^{*}$ has a smaller value. The curve is almost symmetrical at $h^{*} = 20$, and $E_{\theta }^{*}$ reaches the maximum value of $0.19 \times 10^{{ - 3}}$ ($\theta = - 93^{ \circ }$). At $h^{*} = 40$, $E_{\theta }^{*}$ reaches the maximum value of $0.29 \times 10^{{ - 3}}$ ($\theta = 112^{ \circ }$). Therefore, the influence of $h$ should not be ignored.

Fig. 10

Distribution of EFICF around a circular inclusion at different values of $k_{1} a$ under incident SH-wave

Figure 11 presents the distribution of EFICF ($H_{\theta }^{*}$) around a circular inclusion varying as $k_{1} a$ under incident SH-wave.$H_{\theta }^{*}$ is smaller as compared to DSCF. At $h^{*} = 40$ and $k_{1} a = 0.1$, $H_{\theta }^{*}$ reaches the maximum value of $0.11 \times 10^{{ - 4}}$ ($\theta = - 86^{ \circ }$). Low frequencies are more likely to induce resonance. Obviously, $H_{\theta }^{*}$ in the two examples has the maximum values at low frequency. Therefore, low frequency has a great influence on the magnetic field.

Fig. 11

Distribution of MFICF around a circular inclusion versus $k_{1} a$ under incident SH-wave

In Fig. 12, the distributions of DSCF ($\tau _{{\theta z}}^{*}$) around a circular inclusion varying as different material parameters under incident SH-wave are shown. When Medium is are composed of PZT-5H, $\tau _{{\theta z}}^{*}$ reaches the maximum value of 3.39 ($\theta = - 180^{ \circ }$), which is larger than the maximum value of 2.63 ($\theta = - 90^{ \circ }$) in the case of $k_{1} a = 1$ and $h^{*} = 20$ by more than 22%.Therefore, different piezoelectric materials have different corresponding values of $\tau _{{\theta z}}^{*}$, and attention should be paid to the dangerous angle of $\theta = - 180^{ \circ }$, at which $\tau _{{\theta z}}^{*}$ can reach the maximum.

Fig. 12

Distribution of DSCF ($\tau _{{\theta z}}^{*}$) around a circular inclusion at different material parameters under incident SH-wave

6.3 Special cases: the DSCF around a circular cavity

Figure 13 shows the distributions of the maximum value of DSCF ($\tau _{{\theta z}}^{*}$) around a circular cavity versus $k_{1} a$ under incidence of SH-wave. In Fig. 13a, the range of frequency $k_{1} a$ is from 1 to 20, Fig. 13b is the local amplification of Fig. 13a in the frequency range $k_{1} a$ from 0.2 to 7.4. Obviously, the curves show a stable trend as a whole, and DSCF has the maximum values at $k_{1} a = 0.1$ and $k_{1} a = 7.5$, and these values are close to 5.5 and 4.5, respectively. In the range of $k_{1} a$ from 0.2 to 7.4, the maximum value of DSCF is less than 1.

Fig. 13

Distribution of the maximum value of DSCF ($\tau _{{\theta z}}^{*}$) around a circular cavity versus $k_{1} a$ under incidence of SH-wave

Figure 14 presents the distribution of DSCF ($\tau _{{\theta z}}^{*}$) around a circular cavity varying as $k_{1} a$ under incident SH-wave. It can be seen from this Figure that the value of $\tau _{{\theta z}}^{*}$ decreases with increases of $k_{1} a$ due to higher probability of having resonance at low frequencies. At $k_{1} a = 0.1$ and $h^{*} = 40$, $\tau _{{\theta z}}^{*}$ reaches the maximum value of 5.53. The stress on the boundary of the circular cavity is uniform this pointing to significant damage of low frequency.

Fig. 14

Distribution of DSCF around a circular cavity versus $k_{1} a$ under incident SH-wave

7 Conclusions

In this paper, the theory of elastic wave, variable separation method, and series expansion method are applied to investigate the problem of scattering SH-wave by a circular inclusion in an inhomogeneous piezoelectric/piezomagnetic half-space. Numerous valuable statistics are obtained, which can provide references for the engineering applications. Numerical calculations show that DSCF, EFICF, and MFICF are somewhat influenced by the frequency of incident wave, position of circular inclusion, and characteristics of the materials.

• 1. Load parameter $k_{1} a$ has an obvious effect on DSCF. High frequency has a great impact on $\tau _{{\theta z}}^{*}$;

• 2. EFICF and MFICF have smaller values as compared to DSCF;

• 3. The low frequency has a great influence on the magnetic field, and electric field is greatly affected by the middle frequency.

• 4. For DSCF ($\tau _{{\theta z}}^{*}$), $\theta = - 90^{ \circ }$ is a dangerous angle;

• 5. The upper limit of maximum $\tau _{{\theta z}}^{*}$ is about 4;

• 6. In a special case, the maximum value of DSCF is less than 1 in the frequency range $k_{1} a$ from 0.2 to 7.4.

Specific combinations of physical parameters of a piezoelectric/piezomagnetic half-space can lead to a decrease of DSCF value. Therefore, optimum choice of parameters can reduce the possibility of fracture of the structure.

Appendix

1.1 Part I: Decoupling of governing equations

The constitutive equations for a piezoelectric/piezomagnetic material look as follows:

$$ \begin{aligned} \tau _{{xz}} & = c_{{44}} (x,y)\frac{{\partial u}}{{\partial x}} + e_{{15}} (x,y)\frac{{\partial \phi }}{{\partial x}} + h_{{15}} (x,y)\frac{{\partial \varphi }}{{\partial x}}, \\ \tau _{{yz}} & = c_{{44}} (x,y)\frac{{\partial u}}{{\partial y}} + e_{{15}} (x,y)\frac{{\partial \phi }}{{\partial y}} + h_{{15}} (x,y)\frac{{\partial \varphi }}{{\partial y}}, \\ D_{x} & = e_{{15}} (x,y)\frac{{\partial u}}{{\partial x}} - \kappa _{{11}} (x,y)\frac{{\partial \phi }}{{\partial x}} - t_{{11}} (x,y)\frac{{\partial \varphi }}{{\partial x}}, \\ D_{y} & = e_{{15}} (x,y)\frac{{\partial u}}{{\partial y}} - \kappa _{{11}} (x,y)\frac{{\partial \phi }}{{\partial y}} - t_{{11}} (x,y)\frac{{\partial \varphi }}{{\partial y}}, \\ B_{x} & = h_{{15}} (x,y)\frac{{\partial u}}{{\partial x}} - t_{{11}} (x,y)\frac{{\partial \phi }}{{\partial x}} - \mu _{{11}} (x,y)\frac{{\partial \varphi }}{{\partial x}}, \\ B_{y} & = h_{{15}} (x,y)\frac{{\partial u}}{{\partial y}} - t_{{11}} (x,y)\frac{{\partial \phi }}{{\partial y}} - \mu _{{11}} (x,y)\frac{{\partial \varphi }}{{\partial y}}. \\ \end{aligned} $$

(33)

Here, $\sigma _{{xz}}$ and $\sigma _{{yz}}$ are stress tensor components;$D_{x}$ and $D_{y}$ are electric displacement tensor components;$B_{x}$ and $B_{y}$ are magnetic induction components;$w$, $\phi$, and $\varphi$ are displacement, electric potential, and magnetic potential, respectively.

Taking into account the absence of body forces and free charges for the dynamic problem, the equilibrium equations of the piezoelectric/piezomagnetic medium are written as follows:

$$ \begin{aligned} \frac{{\partial \tau _{{xz}} }}{{\partial x}} + \frac{{\partial \tau _{{yz}} }}{{\partial y}} & = \rho \frac{{\partial ^{2} u}}{{\partial t^{2} }}, \\ \frac{{\partial D_{x} }}{{\partial x}} + \frac{{\partial D_{y} }}{{\partial y}} & = 0, \\ \frac{{\partial B_{x} }}{{\partial x}} + \frac{{\partial B_{y} }}{{\partial y}} & = 0. \\ \end{aligned} $$

(34)

Employing Eqs. (34) into (33), the following governing equations are obtained:

$$ \begin{aligned} \frac{{\partial c_{{44}} (x,y)}}{{\partial x}}\frac{{\partial u}}{{\partial x}} + c_{{44}} (x,y)\frac{{\partial ^{2} u}}{{\partial x^{2} }} + \frac{{\partial e_{{15}} (x,y)}}{{\partial x}}\frac{{\partial \phi }}{{\partial x}} + e_{{15}} (x,y)\frac{{\partial ^{2} \phi }}{{\partial x^{2} }} + \frac{{\partial h_{{15}} (x,y)}}{{\partial x}}\frac{{\partial \varphi }}{{\partial x}} + h_{{15}} (x,y)\frac{{\partial ^{2} \varphi }}{{\partial x^{2} }} + \frac{{\partial c_{{44}} (x,y)}}{{\partial y}}\frac{{\partial u}}{{\partial y}} + c_{{44}} (x,y)\frac{{\partial ^{2} u}}{{\partial y^{2} }} + \frac{{\partial e_{{15}} (x,y)}}{{\partial y}}\frac{{\partial \phi }}{{\partial y}} + e_{{15}} (x,y)\frac{{\partial ^{2} \phi }}{{\partial y^{2} }} + \frac{{\partial h_{{15}} (x,y)}}{{\partial y}}\frac{{\partial \varphi }}{{\partial y}} + h_{{15}} (x,y)\frac{{\partial ^{2} \varphi }}{{\partial y^{2} }} = \rho (x,y)\frac{{\partial ^{2} u}}{{\partial t^{2} }} \\ \,,\end{aligned} $$

$$ \begin{aligned} & \frac{{\partial e_{{15}} (x,y)}}{{\partial x}}\frac{{\partial u}}{{\partial x}} + e_{{15}} (x,y)\frac{{\partial ^{2} u}}{{\partial x^{2} }} - \frac{{\partial \kappa _{{11}} (x,y)}}{{\partial x}}\frac{{\partial \phi }}{{\partial x}} \\ & \quad - \kappa _{{11}} (x,y)\frac{{\partial ^{2} \phi }}{{\partial x^{2} }} - \frac{{\partial t_{{11}} (x,y)}}{{\partial x}}\frac{{\partial \varphi }}{{\partial x}} - t_{{11}} (x,y)\frac{{\partial ^{2} \varphi }}{{\partial x^{2} }} \\ & \quad + \frac{{\partial e_{{15}} (x,y)}}{{\partial y}}\frac{{\partial u}}{{\partial y}} + e_{{15}} (x,y)\frac{{\partial ^{2} u}}{{\partial y^{2} }} - \frac{{\partial \kappa _{{11}} (x,y)}}{{\partial y}}\frac{{\partial \phi }}{{\partial y}} \\ & \quad - \kappa _{{11}} (x,y)\frac{{\partial ^{2} \phi }}{{\partial y^{2} }} - \frac{{\partial t_{{11}} (x,y)}}{{\partial y}}\frac{{\partial \varphi }}{{\partial y}} - t_{{11}} (x,y)\frac{{\partial ^{2} \varphi }}{{\partial y^{2} }} = 0 \\ \,,\end{aligned} $$

$$ \begin{aligned} \frac{{\partial h_{{15}} (x,y)}}{{\partial x}}\frac{{\partial u}}{{\partial x}} + h_{{15}} (x,y)\frac{{\partial ^{2} u}}{{\partial x^{2} }} - \frac{{\partial t_{{11}} (x,y)}}{{\partial x}}\frac{{\partial \phi }}{{\partial x}} \\ & \quad - t_{{11}} (x,y)\frac{{\partial ^{2} \phi }}{{\partial x^{2} }} - \frac{{\partial \mu _{{11}} (x,y)}}{{\partial x}}\frac{{\partial \varphi }}{{\partial x}} - \mu _{{11}} (x,y)\frac{{\partial ^{2} \varphi }}{{\partial x^{2} }} \\ & \quad + \frac{{\partial h_{{15}} (x,y)}}{{\partial y}}\frac{{\partial u}}{{\partial y}} + h_{{15}} (x,y)\frac{{\partial ^{2} u}}{{\partial y^{2} }} - \frac{{\partial t_{{11}} (x,y)}}{{\partial y}}\frac{{\partial \phi }}{{\partial y}} \\ & \quad - t_{{11}} (x,y)\frac{{\partial ^{2} \phi }}{{\partial y^{2} }} - \frac{{\partial \mu _{{11}} (x,y)}}{{\partial y}}\frac{{\partial \varphi }}{{\partial y}} - \mu _{{11}} (x,y)\frac{{\partial ^{2} \varphi }}{{\partial y^{2} }} = 0 \,.\\ \end{aligned} $$

(35)

By substituting Eqs. (1) into (35), the governing equations can be described as follows:

$$ \begin{aligned} c_{{440}} \nabla ^{2} u + 2c_{{440}} \left( {p\frac{{\partial u}}{{\partial x}} + q\frac{{\partial u}}{{\partial y}}} \right) + e_{{150}} \nabla ^{2} \phi + 2e_{{150}} \left( {p\frac{{\partial \phi }}{{\partial x}} + q\frac{{\partial \phi }}{{\partial y}}} \right) + h_{{150}} \nabla ^{2} \varphi + 2h_{{150}} \left( {p\frac{{\partial \varphi }}{{\partial x}} + q\frac{{\partial \varphi }}{{\partial y}}} \right) = \rho _{0} \frac{{\partial ^{2} u}}{{\partial t^{2} }} \\ \,,\end{aligned} $$

$$ \begin{aligned} e_{{150}} \nabla ^{2} u + 2e_{{150}} \left( {p\frac{{\partial u}}{{\partial x}} + q\frac{{\partial u}}{{\partial y}}} \right) - \kappa _{{110}} \nabla ^{2} \phi - 2\kappa _{{110}} \left( {p\frac{{\partial \phi }}{{\partial x}} + q\frac{{\partial \phi }}{{\partial y}}} \right) - t_{{110}} \nabla ^{2} \varphi - 2t_{{110}} \left( {p\frac{{\partial \varphi }}{{\partial x}} + q\frac{{\partial \varphi }}{{\partial y}}} \right) = 0 h_{{150}} \nabla ^{2} u + 2h_{{150}} \left( {p\frac{{\partial u}}{{\partial x}} + q\frac{{\partial u}}{{\partial y}}} \right) - t_{{110}} \nabla ^{2} \phi - 2t_{{110}} \left( {p\frac{{\partial \phi }}{{\partial x}} + q\frac{{\partial \phi }}{{\partial y}}} \right) - \mu _{{110}} \nabla ^{2} \varphi - 2\mu _{{110}} \left( {p\frac{{\partial \varphi }}{{\partial x}} + q\frac{{\partial \varphi }}{{\partial y}}} \right) = 0 \\ \,,\end{aligned} $$

(36)

where $\nabla ^{2}$ represents the two-dimensional Laplace operator.

1.2 Part I: Calculation of unknown coefficients

According to the boundary conditions (11) on the boundary $B_{{in}}$, the integral equations with unknown coefficients $A_{n}$,$B_{n}$,$C_{n}$,$D_{n}$,$E_{n}$,$R_{n}$,$L_{n}$,$T_{n}$,$U_{n}$ and $V_{n}$ are established as follows:

$$ \sum\limits_{{n = - \infty }}^{{ + \infty }} {A_{n} \xi _{n}^{{(11)}} + } \sum\limits_{{n = - \infty }}^{{ + \infty }} {R_{n} \xi _{n}^{{(16)}} } = \xi ^{{(1)}} \,,$$

$$ \begin{gathered} \sum\limits_{{n = - \infty }}^{{ + \infty }} {A_{n} \xi _{n}^{{(21)}} + } \sum\limits_{{n = 1}}^{{ + \infty }} {B_{n} \xi _{n}^{{(22)}} + \sum\limits_{{n = 1}}^{{ + \infty }} {C_{n} \xi _{n}^{{(23)}} + } \sum\limits_{{n = 1}}^{{ + \infty }} {D_{n} \xi _{n}^{{(24)}} + } } \sum\limits_{{n = 1}}^{{ + \infty }} {E_{n} \xi _{n}^{{(25)}} } + \sum\limits_{{n = - \infty }}^{{ + \infty }} {R_{n} \xi _{n}^{{(26)}} } \hfill \\ + \sum\limits_{{n = - \infty }}^{{ + \infty }} {L_{n} \xi _{n}^{{(27)}} + } \sum\limits_{{n = - \infty }}^{{ + \infty }} {T_{n} \xi _{n}^{{(28)}} } + \sum\limits_{{n = - \infty }}^{{ + \infty }} {U_{n} \xi _{n}^{{(29)}} + } \sum\limits_{{n = - \infty }}^{{ + \infty }} {V_{n} \xi _{n}^{{(210)}} } = \xi ^{{(2)}} \,,\hfill \\ \end{gathered} $$

$$ \begin{gathered} \sum\limits_{{n = - \infty }}^{{ + \infty }} {A_{n} \xi _{n}^{{(31)}} + } \sum\limits_{{n = 1}}^{{ + \infty }} {B_{n} \xi _{n}^{{(32)}} + \sum\limits_{{n = 1}}^{{ + \infty }} {C_{n} \xi _{n}^{{(33)}} + } \sum\limits_{{n = 1}}^{{ + \infty }} {D_{n} \xi _{n}^{{(34)}} + } } \sum\limits_{{n = 1}}^{{ + \infty }} {E_{n} \xi _{n}^{{(35)}} } + \sum\limits_{{n = - \infty }}^{{ + \infty }} {R_{n} \xi _{n}^{{(36)}} } \hfill \\ + \sum\limits_{{n = - \infty }}^{{ + \infty }} {L_{n} \xi _{n}^{{(37)}} + } \sum\limits_{{n = - \infty }}^{{ + \infty }} {T_{n} \xi _{n}^{{(38)}} } + \sum\limits_{{n = - \infty }}^{{ + \infty }} {U_{n} \xi _{n}^{{(39)}} + } \sum\limits_{{n = - \infty }}^{{ + \infty }} {V_{n} \xi _{n}^{{(310)}} } = \xi ^{{(3)}} \hfill \,,\\ \end{gathered} $$

$$\sum\limits_{{n = 1}}^{{ + \infty }} {B_{n} \xi _{n}^{{(42)}} + \sum\limits_{{n = 1}}^{{ + \infty }} {C_{n} \xi _{n}^{{(43)}} + } } \sum\limits_{{n = - \infty }}^{{ + \infty }} {L_{n} \xi _{n}^{{(47)}} + } \sum\limits_{{n = - \infty }}^{{ + \infty }} {T_{n} \xi _{n}^{{(48)}} } = \xi ^{{(4)}}\,, $$

$$ \begin{gathered} \sum\limits_{{n = - \infty }}^{{ + \infty }} {A_{n} \xi _{n}^{{(51)}} + } \sum\limits_{{n = 1}}^{{ + \infty }} {B_{n} \xi _{n}^{{(52)}} + \sum\limits_{{n = 1}}^{{ + \infty }} {C_{n} \xi _{n}^{{(53)}} + } \sum\limits_{{n = 1}}^{{ + \infty }} {D_{n} \xi _{n}^{{(54)}} + } } \sum\limits_{{n = 1}}^{{ + \infty }} {E_{n} \xi _{n}^{{(55)}} } + \sum\limits_{{n = - \infty }}^{{ + \infty }} {R_{n} \xi _{n}^{{(56)}} } \hfill \\ + \sum\limits_{{n = - \infty }}^{{ + \infty }} {L_{n} \xi _{n}^{{(57)}} + } \sum\limits_{{n = - \infty }}^{{ + \infty }} {T_{n} \xi _{n}^{{(58)}} } + \sum\limits_{{n = - \infty }}^{{ + \infty }} {U_{n} \xi _{n}^{{(59)}} + } \sum\limits_{{n = - \infty }}^{{ + \infty }} {V_{n} \xi _{n}^{{(510)}} } = \xi ^{{(5)}} \hfill \,,\\ \end{gathered} $$

$$ \sum\limits_{{n = 1}}^{{ + \infty }} {D_{n} \xi _{n}^{{(64)}} + } \sum\limits_{{n = 1}}^{{ + \infty }} {E_{n} \xi _{n}^{{(65)}} } + \sum\limits_{{n = - \infty }}^{{ + \infty }} {U_{n} \xi _{n}^{{(69)}} + } \sum\limits_{{n = - \infty }}^{{ + \infty }} {V_{n} \xi _{n}^{{(610)}} } = \xi ^{{(6)}} $$

(37)

where: $\xi _{n}^{{(11)}} = \sum\limits_{{j = 1}}^{4} {S_{n}^{{(j)}} }$,$\xi _{n}^{{(16)}} = - J_{n} (k_{{03}} \left| {\eta ^{\prime}} \right|)\left[ {{{\eta ^{\prime}} \mathord{\left/ {\vphantom {{\eta ^{\prime}} {\left| {\eta ^{\prime}} \right|}}} \right. \kern-\nulldelimiterspace} {\left| {\eta ^{\prime}} \right|}}} \right]^{n} e^{{ - p_{3} (\frac{{\eta ^{\prime} + \bar{\eta }^{\prime}}}{2}) - q_{3} (\frac{{\eta ^{\prime} - \bar{\eta }^{\prime}}}{{2i}})}}$,

$\xi _{n}^{{(21)}} = \frac{{k_{1} M_{{\text{1}}}^{{\text{I}}} }}{2}\left[ {\sum\limits_{{j = 1}}^{4} {\chi _{n}^{{(j)}} } \exp (i\theta ) + \sum\limits_{{j = 1}}^{4} {\gamma _{n}^{{(j)}} } \exp ( - i\theta )} \right]$,$\xi _{n}^{{(22)}} = M_{2}^{{\text{I}}} \left[ {\sum\limits_{{j = 1}}^{2} {\varsigma _{n}^{{(j)}} \exp (i\theta )} + \sum\limits_{{j = 1}}^{2} {\vartheta _{n}^{{(j)}} \exp ( - i\theta )} } \right]$,

$\xi _{n}^{{(23)}} = M_{2}^{{\text{I}}} \left[ {\sum\limits_{{j = 1}}^{2} {\upsilon _{n}^{{(j)}} \exp (i\theta )} + \sum\limits_{{j = 1}}^{2} {\psi _{n}^{{(j)}} \exp ( - i\theta )} } \right]$,$\xi _{n}^{{(24)}} = {{(M_{3}^{{\text{I}}} } \mathord{\left/ {\vphantom {{(M_{3}^{{\text{I}}} } {M_{2}^{{\text{I}}} }}} \right. \kern-\nulldelimiterspace} {M_{2}^{{\text{I}}} }})\xi _{n}^{{(22)}}$,$\xi _{n}^{{(25)}} = {{(M_{3}^{{\text{I}}} } \mathord{\left/ {\vphantom {{(M_{3}^{{\text{I}}} } {M_{2}^{{\text{I}}} }}} \right. \kern-\nulldelimiterspace} {M_{2}^{{\text{I}}} }})\xi _{n}^{{(23)}}$,

$\xi _{n}^{{(26)}} = - \frac{{k_{{03}} M_{{\text{1}}}^{{{\text{III}}}} }}{2}\left[ {\iota _{1} \exp (i\theta ) + \nu _{1} \exp ( - i\theta )} \right]$,$\xi _{n}^{{(27)}} = - M_{2}^{{{\text{III}}}} \left[ {\iota _{2} \exp (i\theta ) + \nu _{2} \exp ( - i\theta )} \right]$,

$\xi _{n}^{{(28)}} = - M_{2}^{{{\text{III}}}} \left[ {\iota _{3} \exp (i\theta ) + \nu _{3} \exp ( - i\theta )} \right]$,$\xi _{n}^{{(29)}} = {{(M_{3}^{{{\text{III}}}} } \mathord{\left/ {\vphantom {{(M_{3}^{{{\text{III}}}} } {M_{2}^{{{\text{III}}}} }}} \right. \kern-\nulldelimiterspace} {M_{2}^{{{\text{III}}}} }})\xi _{n}^{{(27)}}$,$\xi _{n}^{{(210)}} = {{(M_{3}^{{{\text{III}}}} } \mathord{\left/ {\vphantom {{(M_{3}^{{{\text{III}}}} } {M_{2}^{{{\text{III}}}} }}} \right. \kern-\nulldelimiterspace} {M_{2}^{{{\text{III}}}} }})\xi _{n}^{{(28)}}$,

$\xi _{n}^{{(31)}} = a_{{\text{1}}}^{{\text{I}}} \xi _{n}^{{(11)}}$, $\xi _{n}^{{(32)}} = b_{{\text{1}}}^{{\text{I}}} \sum\limits_{{j = 1}}^{4} {\varphi _{{1n}}^{{(j)}} }$,$\xi _{n}^{{(33)}} = b_{{\text{1}}}^{{\text{I}}} \sum\limits_{{j = 1}}^{4} {\varphi _{{2n}}^{{(j)}} }$,$\xi _{n}^{{(34)}} = {\text{ }}(c_{1}^{I} /b_{1}^{I} )\xi _{n}^{{(32)}}$,$\xi _{n}^{{(35)}} = ({{c_{{\text{1}}}^{{\text{I}}} } \mathord{\left/ {\vphantom {{c_{{\text{1}}}^{{\text{I}}} } {b_{{\text{1}}}^{{\text{I}}} }}} \right. \kern-\nulldelimiterspace} {b_{{\text{1}}}^{{\text{I}}} }})\xi _{n}^{{(33)}}$,

$\xi _{n}^{{(36)}} = a_{{\text{1}}}^{{{\text{III}}}} \xi _{n}^{{(16)}}$,$\xi _{n}^{{(37)}} = - b_{{\text{1}}}^{{{\text{III}}}} e^{{ - p_{3} (\frac{{\eta ^{\prime} + \bar{\eta }^{\prime}}}{2}) - q_{3} (\frac{{\eta ^{\prime} - \bar{\eta }^{\prime}}}{{2i}})}} H_{n}^{{(1)}} (ik^{\prime}_{3} \left| {\eta ^{\prime}} \right|)\left[ {{{\eta ^{\prime}} \mathord{\left/ {\vphantom {{\eta ^{\prime}} {\left| {\eta ^{\prime}} \right|}}} \right. \kern-\nulldelimiterspace} {\left| {\eta ^{\prime}} \right|}}} \right]^{n}$,

$\xi _{n}^{{(38)}} = - b_{{\text{1}}}^{{{\text{III}}}} e^{{ - p_{3} (\frac{{\eta ^{\prime} + \bar{\eta }^{\prime}}}{2}) - q_{3} (\frac{{\eta ^{\prime} - \bar{\eta }^{\prime}}}{{2i}})}} H_{n}^{{(2)}} (ik^{\prime}_{3} \left| {\eta ^{\prime}} \right|)\left[ {{{\eta ^{\prime}} \mathord{\left/ {\vphantom {{\eta ^{\prime}} {\left| {\eta ^{\prime}} \right|}}} \right. \kern-\nulldelimiterspace} {\left| {\eta ^{\prime}} \right|}}} \right]^{n}$,$\xi _{n}^{{(39)}} = ({{c_{{\text{1}}}^{{{\text{III}}}} } \mathord{\left/ {\vphantom {{c_{{\text{1}}}^{{{\text{III}}}} } {b_{{\text{1}}}^{{{\text{III}}}} }}} \right. \kern-\nulldelimiterspace} {b_{{\text{1}}}^{{{\text{III}}}} }})\xi _{n}^{{(37)}}$,$\xi _{n}^{{(310)}} = ({{c_{{\text{1}}}^{{{\text{III}}}} } \mathord{\left/ {\vphantom {{c_{{\text{1}}}^{{{\text{III}}}} } {b_{{\text{1}}}^{{{\text{III}}}} }}} \right. \kern-\nulldelimiterspace} {b_{{\text{1}}}^{{{\text{III}}}} }})\xi _{n}^{{(38)}}$,

$\xi _{n}^{{(42)}} = {{(1} \mathord{\left/ {\vphantom {{(1} {M_{2}^{{\text{I}}} }}} \right. \kern-\nulldelimiterspace} {M_{2}^{{\text{I}}} }})\xi _{n}^{{(22)}}$,$\xi _{n}^{{(43)}} = {{(1} \mathord{\left/ {\vphantom {{(1} {M_{2}^{{\text{I}}} }}} \right. \kern-\nulldelimiterspace} {M_{2}^{{\text{I}}} }})\xi _{n}^{{(23)}}$, $\xi _{n}^{{(47)}} = {{(1} \mathord{\left/ {\vphantom {{(1} {M_{2}^{{{\text{III}}}} }}} \right. \kern-\nulldelimiterspace} {M_{2}^{{{\text{III}}}} }})\xi _{n}^{{(27)}}$,$\xi _{n}^{{(48)}} = {{(1} \mathord{\left/ {\vphantom {{(1} {M_{2}^{{{\text{III}}}} }}} \right. \kern-\nulldelimiterspace} {M_{2}^{{{\text{III}}}} }})\xi _{n}^{{(28)}}$,

$\xi _{n}^{{(51)}} = ({{a_{2}^{{\text{I}}} } \mathord{\left/ {\vphantom {{a_{2}^{{\text{I}}} } {a_{{\text{1}}}^{{\text{I}}} }}} \right. \kern-\nulldelimiterspace} {a_{{\text{1}}}^{{\text{I}}} }})\xi _{n}^{{(31)}}$, $\xi _{n}^{{(52)}} = ({{b_{2}^{{\text{I}}} } \mathord{\left/ {\vphantom {{b_{2}^{{\text{I}}} } {b_{{\text{1}}}^{{\text{I}}} }}} \right. \kern-\nulldelimiterspace} {b_{{\text{1}}}^{{\text{I}}} }})\xi _{n}^{{(32)}}$,$\xi _{n}^{{(53)}} = ({{b_{2}^{{\text{I}}} } \mathord{\left/ {\vphantom {{b_{2}^{{\text{I}}} } {b_{{\text{1}}}^{{\text{I}}} }}} \right. \kern-\nulldelimiterspace} {b_{{\text{1}}}^{{\text{I}}} }})\xi _{n}^{{(33)}}$,$\xi _{n}^{{(54)}} = ({{c_{2}^{{\text{I}}} } \mathord{\left/ {\vphantom {{c_{2}^{{\text{I}}} } {b_{2}^{{\text{I}}} }}} \right. \kern-\nulldelimiterspace} {b_{2}^{{\text{I}}} }})\xi _{n}^{{(52)}}$,$\xi _{n}^{{(55)}} = ({{c_{2}^{{\text{I}}} } \mathord{\left/ {\vphantom {{c_{2}^{{\text{I}}} } {b_{2}^{{\text{I}}} }}} \right. \kern-\nulldelimiterspace} {b_{2}^{{\text{I}}} }})\xi _{n}^{{(53)}}$,$\xi _{n}^{{(56)}} = ({{a_{2}^{{{\text{III}}}} } \mathord{\left/ {\vphantom {{a_{2}^{{{\text{III}}}} } {a_{{\text{1}}}^{{{\text{III}}}} }}} \right. \kern-\nulldelimiterspace} {a_{{\text{1}}}^{{{\text{III}}}} }})\xi _{n}^{{(36)}}$,$\xi _{n}^{{(57)}} = ({{b_{2}^{{{\text{III}}}} } \mathord{\left/ {\vphantom {{b_{2}^{{{\text{III}}}} } {b_{{\text{1}}}^{{{\text{III}}}} }}} \right. \kern-\nulldelimiterspace} {b_{{\text{1}}}^{{{\text{III}}}} }})\xi _{n}^{{(37)}}$, $\xi _{n}^{{(58)}} = ({{b_{2}^{{{\text{III}}}} } \mathord{\left/ {\vphantom {{b_{2}^{{{\text{III}}}} } {b_{{\text{1}}}^{{{\text{III}}}} }}} \right. \kern-\nulldelimiterspace} {b_{{\text{1}}}^{{{\text{III}}}} }})\xi _{n}^{{(38)}}$,$\xi _{n}^{{(59)}} = ({{c_{2}^{{{\text{III}}}} } \mathord{\left/ {\vphantom {{c_{2}^{{{\text{III}}}} } {b_{2}^{{{\text{III}}}} }}} \right. \kern-\nulldelimiterspace} {b_{2}^{{{\text{III}}}} }})\xi _{n}^{{(57)}}$, $\xi _{n}^{{(510)}} = ({{c_{2}^{{{\text{III}}}} } \mathord{\left/ {\vphantom {{c_{2}^{{{\text{III}}}} } {b_{2}^{{{\text{III}}}} }}} \right. \kern-\nulldelimiterspace} {b_{2}^{{{\text{III}}}} }})\xi _{n}^{{(58)}}$, $\xi _{n}^{{(64)}} = \xi _{n}^{{(42)}}$,$\xi _{n}^{{(65)}} = \xi _{n}^{{(43)}}$,$\xi _{n}^{{(69)}} = \xi _{n}^{{(64)}}$,$\xi _{n}^{{(610)}} = \xi _{n}^{{(65)}}\,,$.

$\chi _{n}^{{(1)}} = H_{{n - 1}}^{{(1)}} (k_{1} \left| {\eta ^{\prime}} \right|)\left[ {{{\eta ^{\prime}} \mathord{\left/ {\vphantom {{\eta ^{\prime}} {\left| {\eta ^{\prime}} \right|}}} \right. \kern-\nulldelimiterspace} {\left| {\eta ^{\prime}} \right|}}} \right]^{{n - 1}}$, $\chi _{n}^{{(2)}} = - H_{{n + 1}}^{{(1)}} (k_{1} \left| {\eta ^{\prime}_{1} } \right|)\left[ {{{\eta ^{\prime}_{1} } \mathord{\left/ {\vphantom {{\eta ^{\prime}_{1} } {\left| {\eta ^{\prime}_{1} } \right|}}} \right. \kern-\nulldelimiterspace} {\left| {\eta ^{\prime}_{1} } \right|}}} \right]^{{ - n - 1}}$, $\chi _{n}^{{(3)}} = ( - 1)^{n} H_{{n - 1}}^{{(1)}} (k_{1} \left| {\eta ^{\prime}_{2} } \right|)\left[ {{{\eta ^{\prime}_{2} } \mathord{\left/ {\vphantom {{\eta ^{\prime}_{2} } {\left| {\eta ^{\prime}_{2} } \right|}}} \right. \kern-\nulldelimiterspace} {\left| {\eta ^{\prime}_{2} } \right|}}} \right]^{{n - 1}}$,$\chi _{n}^{{(4)}} = - ( - 1)^{n} H_{{n + 1}}^{{(1)}} (k_{1} \left| {\eta ^{\prime}_{3} } \right|)\left[ {{{\eta ^{\prime}_{3} } \mathord{\left/ {\vphantom {{\eta ^{\prime}_{3} } {\left| {\eta ^{\prime}_{3} } \right|}}} \right. \kern-\nulldelimiterspace} {\left| {\eta ^{\prime}_{3} } \right|}}} \right]^{{ - n - 1}}$,

$\gamma _{n}^{{(1)}} = - H_{{n + 1}}^{{(1)}} (k_{1} \left| {\eta ^{\prime}} \right|)\left[ {{{\eta ^{\prime}} \mathord{\left/ {\vphantom {{\eta ^{\prime}} {\left| {\eta ^{\prime}} \right|}}} \right. \kern-\nulldelimiterspace} {\left| {\eta ^{\prime}} \right|}}} \right]^{{n + 1}}$, $\gamma _{n}^{{(2)}} = H_{{n - 1}}^{{(1)}} (k_{1} \left| {\eta ^{\prime}_{1} } \right|)\left[ {{{\eta ^{\prime}_{1} } \mathord{\left/ {\vphantom {{\eta ^{\prime}_{1} } {\left| {\eta ^{\prime}_{1} } \right|}}} \right. \kern-\nulldelimiterspace} {\left| {\eta ^{\prime}_{1} } \right|}}} \right]^{{ - n + 1}}$.

$\gamma _{n}^{{(3)}} = - ( - 1)^{n} H_{{n + 1}}^{{(1)}} (k_{1} \left| {\eta ^{\prime}_{2} } \right|)\left[ {{{\eta ^{\prime}_{2} } \mathord{\left/ {\vphantom {{\eta ^{\prime}_{2} } {\left| {\eta ^{\prime}_{2} } \right|}}} \right. \kern-\nulldelimiterspace} {\left| {\eta ^{\prime}_{2} } \right|}}} \right]^{{n + 1}}$,$\gamma _{n}^{{(4)}} = ( - 1)^{n} H_{{n - 1}}^{{(1)}} (k_{1} \left| {\eta ^{\prime}_{3} } \right|)\left[ {{{\eta ^{\prime}_{3} } \mathord{\left/ {\vphantom {{\eta ^{\prime}_{3} } {\left| {\eta ^{\prime}_{3} } \right|}}} \right. \kern-\nulldelimiterspace} {\left| {\eta ^{\prime}_{3} } \right|}}} \right]^{{ - n + 1}}$,

$\varsigma _{n}^{{(1)}} = - n\eta ^{{\prime - n - 1}}$,$\varsigma _{n}^{{(2)}} = - ( - 1)^{n} n(\eta ^{\prime} - 2d - 2hi)^{{ - n - 1}}$, $\vartheta _{n}^{{(1)}} = - n(\bar{\eta }^{\prime} + 2hi)^{{ - n - 1}}$,$\vartheta _{n}^{{(2)}} = - ( - 1)^{n} n(\bar{\eta }^{\prime} - 2d)^{{ - n - 1}}$,

$\upsilon _{n}^{{(1)}} = - n(\eta ^{\prime} - 2hi)^{{ - n - 1}}$,$\upsilon _{n}^{{(2)}} = - n( - 1)^{n} (\eta ^{\prime} - 2d)^{{ - n - 1}}$,$\psi _{n}^{{(1)}} = - n\bar{\eta }^{{\prime - n - 1}}$,$\psi _{n}^{{(2)}} = - ( - 1)^{n} n(\bar{\eta }^{\prime} - 2d + 2hi)^{{ - n - 1}}$,

$$ \iota _{1} = e^{{p_{3} \left( {\frac{{\eta ^{\prime} + \bar{\eta }^{\prime}}}{2}} \right) + q_{3} \left( {\frac{{\eta ^{\prime} - \bar{\eta }^{\prime}}}{{2i}}} \right)}} \left[ {\frac{{k_{{03}} }}{2}J_{{n - 1}}^{{(1)}} (k_{{03}} \left| {\eta ^{\prime}} \right|)\left[ {{{\eta ^{\prime}} \mathord{\left/ {\vphantom {{\eta ^{\prime}} {\left| {\eta ^{\prime}} \right|}}} \right. \kern-\nulldelimiterspace} {\left| {\eta ^{\prime}} \right|}}} \right]^{{n - 1}} - \frac{1}{2}(p_{3} - q_{3} i)J_{n}^{{(1)}} (k_{{03}} \left| {\eta ^{\prime}} \right|)\left[ {{{\eta ^{\prime}} \mathord{\left/ {\vphantom {{\eta ^{\prime}} {\left| {\eta ^{\prime}} \right|}}} \right. \kern-\nulldelimiterspace} {\left| {\eta ^{\prime}} \right|}}} \right]^{n} } \right], $$

$$ \nu _{1} = e^{{p_{3} \left( {\frac{{\eta ^{\prime} + \bar{\eta }^{\prime}}}{2}} \right) + q_{3} \left( {\frac{{\eta ^{\prime} - \bar{\eta }^{\prime}}}{{2i}}} \right)}} \left[ { - \frac{{k_{{03}} }}{2}J_{{n + 1}}^{{(1)}} (k_{{03}} \left| {\eta ^{\prime}} \right|)\left[ {{{\eta ^{\prime}} \mathord{\left/ {\vphantom {{\eta ^{\prime}} {\left| {\eta ^{\prime}} \right|}}} \right. \kern-\nulldelimiterspace} {\left| {\eta ^{\prime}} \right|}}} \right]^{{n + 1}} - \frac{1}{2}(p_{3} + q_{3} i)J_{n}^{{(1)}} (k_{{03}} \left| {\eta ^{\prime}} \right|)\left[ {{{\eta ^{\prime}} \mathord{\left/ {\vphantom {{\eta ^{\prime}} {\left| {\eta ^{\prime}} \right|}}} \right. \kern-\nulldelimiterspace} {\left| {\eta ^{\prime}} \right|}}} \right]^{n} } \right], $$

$$ \iota _{3} = e^{{p_{3} \left( {\frac{{\eta ^{\prime} + \bar{\eta }^{\prime}}}{2}} \right) + q_{3} \left( {\frac{{\eta ^{\prime} - \bar{\eta }^{\prime}}}{{2i}}} \right)}} \left[ {\frac{{ik^{\prime}_{3} }}{2}H_{{n - 1}}^{{(1)}} (ik^{\prime}_{3} \left| {\eta ^{\prime}} \right|)\left[ {{{\eta ^{\prime}} \mathord{\left/ {\vphantom {{\eta ^{\prime}} {\left| {\eta ^{\prime}} \right|}}} \right. \kern-\nulldelimiterspace} {\left| {\eta ^{\prime}} \right|}}} \right]^{{n - 1}} - \frac{1}{2}(p_{3} - q_{3} i)H_{n}^{{(1)}} (ik^{\prime}_{3} \left| {\eta ^{\prime}} \right|)\left[ {{{\eta ^{\prime}} \mathord{\left/ {\vphantom {{\eta ^{\prime}} {\left| {\eta ^{\prime}} \right|}}} \right. \kern-\nulldelimiterspace} {\left| {\eta ^{\prime}} \right|}}} \right]^{n} } \right], $$

$$ \nu _{3} = e^{{p_{3} \left( {\frac{{\eta ^{\prime} + \bar{\eta }^{\prime}}}{2}} \right) + q_{3} \left( {\frac{{\eta ^{\prime} - \bar{\eta }^{\prime}}}{{2i}}} \right)}} \left[ { - \frac{{ik^{\prime}_{3} }}{2}H_{{n + 1}}^{{(1)}} (ik^{\prime}_{3} \left| {\eta ^{\prime}} \right|)\left[ {{{\eta ^{\prime}} \mathord{\left/ {\vphantom {{\eta ^{\prime}} {\left| {\eta ^{\prime}} \right|}}} \right. \kern-\nulldelimiterspace} {\left| {\eta ^{\prime}} \right|}}} \right]^{{n + 1}} - \frac{1}{2}(p_{3} + q_{3} i)H_{n}^{{(1)}} (ik^{\prime}_{3} \left| {\eta ^{\prime}} \right|)\left[ {{{\eta ^{\prime}} \mathord{\left/ {\vphantom {{\eta ^{\prime}} {\left| {\eta ^{\prime}} \right|}}} \right. \kern-\nulldelimiterspace} {\left| {\eta ^{\prime}} \right|}}} \right]^{n} } \right], $$

$$ \iota _{2} = e^{{p_{3} \left( {\frac{{\eta ^{\prime} + \bar{\eta }^{\prime}}}{2}} \right) + q_{3} \left( {\frac{{\eta ^{\prime} - \bar{\eta }^{\prime}}}{{2i}}} \right)}} \left[ {\frac{{ik^{\prime}_{3} }}{2}H_{{n - 1}}^{{(2)}} (ik^{\prime}_{3} \left| {\eta ^{\prime}} \right|)\left[ {{{\eta ^{\prime}} \mathord{\left/ {\vphantom {{\eta ^{\prime}} {\left| {\eta ^{\prime}} \right|}}} \right. \kern-\nulldelimiterspace} {\left| {\eta ^{\prime}} \right|}}} \right]^{{n - 1}} - \frac{1}{2}(p_{3} - q_{3} i)H_{n}^{{(2)}} (ik^{\prime}_{3} \left| {\eta ^{\prime}} \right|)\left[ {{{\eta ^{\prime}} \mathord{\left/ {\vphantom {{\eta ^{\prime}} {\left| {\eta ^{\prime}} \right|}}} \right. \kern-\nulldelimiterspace} {\left| {\eta ^{\prime}} \right|}}} \right]^{n} } \right], $$

$$ \nu _{2} = e^{{p_{3} \left( {\frac{{\eta ^{\prime} + \bar{\eta }^{\prime}}}{2}} \right) + q_{3} \left( {\frac{{\eta ^{\prime} - \bar{\eta }^{\prime}}}{{2i}}} \right)}} \left[ { - \frac{{ik^{\prime}_{3} }}{2}H_{{n + 1}}^{{(2)}} (ik^{\prime}_{3} \left| {\eta ^{\prime}} \right|)\left[ {{{\eta ^{\prime}} \mathord{\left/ {\vphantom {{\eta ^{\prime}} {\left| {\eta ^{\prime}} \right|}}} \right. \kern-\nulldelimiterspace} {\left| {\eta ^{\prime}} \right|}}} \right]^{{n + 1}} - \frac{1}{2}(p_{3} + q_{3} i)H_{n}^{{(2)}} (ik^{\prime}_{3} \left| {\eta ^{\prime}} \right|)\left[ {{{\eta ^{\prime}} \mathord{\left/ {\vphantom {{\eta ^{\prime}} {\left| {\eta ^{\prime}} \right|}}} \right. \kern-\nulldelimiterspace} {\left| {\eta ^{\prime}} \right|}}} \right]^{n} } \right], $$

$$ \begin{aligned} \xi ^{{(1)}} & = - (w^{i} + w^{r} ),\xi ^{{(2)}} = - (\tau _{{\theta z}}^{i} + \tau _{{\theta z}}^{r} ),\xi ^{{(3)}} = - (\phi ^{i} + \phi ^{r} ), \\ \xi ^{{(4)}} & = - (D_{\theta }^{i} + D_{\theta }^{r} ),\xi ^{{(5)}} = - (\varphi ^{i} + \varphi ^{r} ),\xi ^{{(6)}} = - (B_{\theta }^{i} + B_{\theta }^{r} ). \\ \end{aligned} $$

In order to solve Eq. (37), we multiply both sides of these equations by the coefficient $\exp ( - im\theta ^{\prime})$ and integrate the variable $\theta ^{\prime}$ in the known coefficient of Eq. (37) in the range of $( - \pi ,\pi )$. Such operation enables to simplify Eq. (37) into linear algebraic equations.

1.3 Part II: Green’s function

Green’s function method is also called point source method.

Firstly, the piezoelectric/piezomagnetic half-space is divided into two right angle regions along the vertical interface $B_{V}$, and the unit point source load $\delta (\eta - \eta _{0} ){\kern 1pt}$,$\eta _{0} = yi(y \le h)$ is applied on the boundary $B_{V}$ as the incident wave source, as shown in Fig. 

Fig. 15

Point source load

15.

The displacement function also satisfies the governing Eq. (6) and the boundary conditions (10), (11) on the boundaries $B_{H}$ and $B_{{in}}$. Unlike the boundary conditions on the vertical boundary $B_{H} {\kern 1pt}$ in Sect. 4.1, here it becomes:

$$ {\kern 1pt} {\kern 1pt} \left. {\tau _{{xz}}^{{\text{I}}} } \right|_{{x = 0}} = \delta (\eta - \eta _{0} ) \,,$$

(38)

Since Medium I is homogeneous, the displacement function $G_{{w1}}^{i}$ can be expressed as follows according to [15]:

$$ G_{{w1}}^{i} = H_{0}^{{(1)}} (k_{1} \left| {\eta - \eta _{0} } \right|) + H_{0}^{{(1)}} (k_{1} \left| {\eta - \bar{\eta }_{0} - 2hi} \right|)\,, $$

(39)

Taking into account that Medium II is inhomogeneous, the displacement function $G_{{w2}}^{i}$ can be expressed in the following form:

$$ G_{{w2}}^{i} = e^{{ - \frac{{p_{2} (\eta + \bar{\eta })}}{2}}} \left[ {H_{0}^{{(1)}} (k_{{02}} \left| {\eta - \eta _{0} } \right|) + H_{0}^{{(1)}} (k_{{02}} \left| {\eta - \bar{\eta }_{0} - 2hi} \right|)} \right]\,, $$

(40)

The displacement field $G_{{w1}}^{{( \bullet )}}$,$G_{{w2}}^{{( \bullet )}}$, electric field $G_{{\phi 1}}^{{( \bullet )}}$,$G_{{\phi 2}}^{{( \bullet )}}$, and magnetic field $G_{{\varphi 1}}^{{( \bullet )}}$,$G_{{\varphi 2}}^{{( \bullet )}}$ are obtained by means of the same procedure as used for calculating SH-wave (Note that the superscript $( \bullet )$ refers to I, II, III).

To make the calculations more convenient, the polar coordinate system $(r^{\prime\prime},\theta ^{\prime\prime})$ is set at the origin of the right-angle plane, and the respective complex variables are $\eta ^{\prime\prime} = r^{\prime\prime}e^{{i\theta ^{\prime\prime}}}$ and $\bar{\eta ^{\prime\prime}} = r^{\prime\prime}e^{{ - i\theta ^{\prime\prime}}}$.

Then pairs of unknown external force $f_{1} (r^{\prime\prime},\theta ^{\prime\prime})$,$f_{2} (r^{\prime\prime},\theta ^{\prime\prime})$, external electric field $f_{3} (r^{\prime\prime},\theta ^{\prime\prime})$,$f_{4} (r^{\prime\prime},\theta ^{\prime\prime})$, and external magnetic field $f_{5} (r^{\prime\prime},\theta ^{\prime\prime})$,$f_{6} (r^{\prime\prime},\theta ^{\prime\prime})$ are applied on the boundary $B_{V}$ as the amplitude function of $\delta (\eta - \eta _{0} ){\kern 1pt}$, as shown in Fig. 

Fig. 16

Systems of external force

16. Note that unknown parameters in each pair introduced above have equal values and opposite directions.

Finally, these unknown coefficients above are obtained with the aid of the continuous conditions (15) on the boundary $B_{V}$:

$$ \begin{aligned} & w^{{\text{I}}} + w^{{f1}} = w^{{{\text{II}}}} + w^{{f2}} ,\phi ^{{\text{I}}} + \phi ^{{f3}} = \phi ^{{{\text{II}}}} + \phi ^{{f4}} , \\ & \varphi ^{{\text{I}}} + \varphi ^{{f5}} = \varphi ^{{{\text{II}}}} + \varphi ^{{f6}} \,,\\ \end{aligned} $$

(41)

where:

$w^{{f1}} = \int_{0}^{{ + \infty }} {f_{1} (r^{\prime\prime}_{0} ,\beta _{1} )G_{w}^{{\text{I}}} (r^{\prime\prime}_{0} ,\beta _{1} ;r^{\prime\prime},\theta ^{\prime\prime})} dr^{\prime\prime}_{0}$,$w^{{f2}} = - \int_{0}^{{ + \infty }} {f_{2} (r^{\prime\prime}_{0} ,\beta _{1} )G_{w}^{{{\text{II}}}} (r^{\prime\prime}_{0} ,\beta _{1} ;r^{\prime\prime},\theta ^{\prime\prime})} dr^{\prime\prime}_{0}$,

$\phi ^{{f1}} = \int_{0}^{{ + \infty }} {f_{3} (r^{\prime\prime}_{0} ,\beta _{1} )G_{\phi }^{{\text{I}}} (r^{\prime\prime}_{0} ,\beta _{1} ;r^{\prime\prime},\theta ^{\prime\prime})} dr^{\prime\prime}_{0}$,$\phi ^{{f2}} = - \int_{0}^{{ + \infty }} {f_{4} (r^{\prime\prime}_{0} ,\beta _{1} )G_{\phi }^{{{\text{II}}}} (r^{\prime\prime}_{0} ,\beta _{1} ;r^{\prime\prime},\theta ^{\prime\prime})} dr^{\prime\prime}_{0}$,

$\varphi ^{{f1}} = \int_{0}^{{ + \infty }} {f_{5} (r^{\prime\prime}_{0} ,\beta _{1} )G_{\varphi }^{{\text{I}}} (r^{\prime\prime}_{0} ,\beta _{1} ;r^{\prime\prime},\theta ^{\prime\prime})} dr^{\prime\prime}_{0}$,$\varphi ^{{f2}} = - \int_{0}^{{ + \infty }} {f_{6} (r^{\prime\prime}_{0} ,\beta _{1} )G_{\varphi }^{{{\text{II}}}} (r^{\prime\prime}_{0} ,\beta _{1} ;r^{\prime\prime},\theta ^{\prime\prime})} dr^{\prime\prime}_{0}$,

$\beta _{1} = - {\pi \mathord{\left/ {\vphantom {\pi 2}} \right. \kern-\nulldelimiterspace} 2}$ and physical variable $( \bullet )^{{fi}}$ is produced by $f_{i} (r^{\prime\prime},\theta ^{\prime\prime})$, $(i = 1,2,3,4)$.

The scattering wave has no effect on the boundary $B_{V}$. According to Eq. (15), the continuity conditions for stress, electric displacement, and magnetic induction must be satisfied as follows:

$f_{1} (r^{\prime\prime}_{0} ,\beta _{1} ) = f_{2} (r^{\prime\prime}_{0} ,\beta _{1} )$, $f_{3} (r^{\prime\prime}_{0} ,\beta _{1} ) = f_{4} (r^{\prime\prime}_{0} ,\beta _{1} )$,$f_{5} (r^{\prime\prime}_{0} ,\beta _{1} ) = f_{6} (r^{\prime\prime}_{0} ,\beta _{1} )$,

$$ \begin{aligned} & \int_{0}^{{ + \infty }} {f_{1} (r^{\prime\prime}_{0} ,\beta _{1} )\left[ {G_{w}^{{\text{I}}} (r^{\prime\prime}_{0} ,\beta _{1} ;r^{\prime\prime},\theta ^{\prime\prime}) + } \right.} \left. {G_{w}^{{{\text{II}}}} (r^{\prime\prime}_{0} ,\beta _{1} ;r^{\prime\prime},\theta ^{\prime\prime})} \right]{\text{d}}r^{\prime\prime}_{0} = - w^{s} , \\ & \int_{0}^{{ + \infty }} {f_{3} (r^{\prime\prime}_{0} ,\beta _{1} )\left[ {G_{\phi }^{{\text{I}}} (r^{\prime\prime}_{0} ,\beta _{1} ;r^{\prime\prime},\theta ^{\prime\prime}) + } \right.} \left. {G_{\phi }^{{{\text{II}}}} (r^{\prime\prime}_{0} ,\beta _{1} ;r^{\prime\prime},\theta ^{\prime\prime})} \right]{\text{d}}r^{\prime\prime}_{0} = - \phi ^{s} , \\ & \int_{0}^{{ + \infty }} {f_{5} (r^{\prime\prime}_{0} ,\beta _{1} )\left[ {G_{\varphi }^{{\text{I}}} (r^{\prime\prime}_{0} ,\beta _{1} ;r^{\prime\prime},\theta ^{\prime\prime}) + } \right.} \left. {G_{\varphi }^{{{\text{II}}}} (r^{\prime\prime}_{0} ,\beta _{1} ;r^{\prime\prime},\theta ^{\prime\prime})} \right]{\text{d}}r^{\prime\prime}_{0} = - \varphi ^{s} . \\ \end{aligned} $$

(42)

Equations (42) are Fredholm equations of the first kind. By selecting different coordinate points, they can be solved by the interpolation method.

1.4 Part III: Relationship between different parameters of SH-waves

Based on the continuity of displacement as well as electric potential and magnetic potential on the vertical boundary in Eq. (15), the following relationship can be known:

$$ k_{1} \sin \alpha _{0} = k_{2} \sin \alpha _{2} \,,$$

(43)

For mathematical simplicity, the following parameters are introduced:

$\lambda _{1} = \cos \alpha _{0}$,$\lambda _{2} = \cos \alpha _{2}$,$c_{1} = c_{{{\text{440}}}}^{{\text{I}}}$,$c_{2} = c_{{{\text{440}}}}^{{{\text{II}}}}$,$e_{1} = e_{{{\text{150}}}}^{{\text{I}}}$,$e_{2} = e_{{{\text{150}}}}^{{{\text{II}}}}$,$h_{1} = h_{{{\text{150}}}}^{{\text{I}}}$,$h_{2} = h_{{{\text{150}}}}^{{{\text{II}}}}$,$d_{1} = \kappa _{{{\text{110}}}}^{{\text{I}}}$,$d_{2} = \kappa _{{{\text{110}}}}^{{{\text{II}}}}$,$t_{1} = t_{{{\text{110}}}}^{{\text{I}}}$,$t_{2} = t_{{{\text{110}}}}^{{{\text{II}}}}$,$\mu _{1} = \mu _{{{\text{110}}}}^{{\text{I}}}$,$\mu _{2} = \mu _{{{\text{110}}}}^{{{\text{II}}}}$.

Combining with Eq. (15), the following equations are obtained:

$$ \left\{ \begin{gathered} w_{0} c_{1} (ik_{1} \lambda _{1} ) - w_{1} c_{1} (ik_{1} \lambda _{1} ) + \phi _{0} e_{1} (ik_{1} \lambda _{1} ) - \phi _{1} e_{1} (ik_{1} \lambda _{1} ) + \varphi _{0} h_{1} (ik_{1} \lambda _{1} )_{1} - \varphi _{1} h_{1} (ik_{1} \lambda _{1} ) \hfill \\ = w_{2} c_{2} (ik_{{02}} \lambda _{2} - p_{2} ) + \phi _{2} e_{2} (ik_{{02}} \lambda _{2} - p_{2} ) + \varphi _{2} h_{2} (ik_{{02}} \lambda _{2} - p_{2} ) \hfill \\ w_{0} e_{1} (ik_{1} \lambda _{1} ) - w_{1} e_{1} (ik_{1} \lambda _{1} )_{1} - \left[ {\phi _{0} d_{1} (ik_{1} \lambda _{1} ) - \phi _{1} d_{1} (ik_{1} \lambda _{1} )} \right] - \left[ {\varphi _{0} t_{1} (ik_{1} \lambda _{1} ) - \varphi _{1} t_{1} (ik_{1} \lambda _{1} )} \right] \hfill \\ = w_{2} e_{2} (ik_{{02}} \lambda _{2} - p_{2} ) - \phi _{2} d_{2} (ik_{{02}} \lambda _{2} - p_{2} ) - \varphi _{2} t_{2} (ik_{{02}} \lambda _{2} - p_{2} ) \hfill \\ w_{0} h_{1} (ik_{1} \lambda _{1} ) - w_{1} h_{1} (ik_{1} \lambda _{1} ) - \left[ {\phi _{0} t_{1} (ik_{1} \lambda _{1} ) - \phi _{1} t_{1} (ik_{1} \lambda _{1} )} \right] - \left[ {\varphi _{0} \mu _{1} (ik_{1} \lambda _{1} ) - \varphi _{1} \mu _{1} (ik_{1} \lambda _{1} )} \right] \hfill \\ = w_{2} h_{2} (ik_{{02}} \lambda _{2} - p_{2} ) - \phi _{2} t_{2} (ik_{{02}} \lambda _{2} - p_{2} ) - \varphi _{2} \mu _{2} (ik_{{02}} \lambda _{2} - p_{2} ). \hfill \\ \end{gathered} \right. $$

(44)

Note that $w_{0}$, $\phi _{0}$, and $\varphi _{0}$ in Eq. (44) are known quantities, so Eq. (44) can be transformed into the following form:

$$ \left\{ \begin{gathered} w_{1} c_{1} (ik_{1} \lambda _{1} ) + w_{2} c_{2} (ik_{{02}} \lambda _{2} - p_{2} ) + \phi _{1} e_{1} (ik_{1} \lambda _{1} ) + \phi _{2} e_{2} (ik_{{02}} \lambda _{2} - p_{2} ) + \varphi _{1} h_{1} (ik_{1} \lambda _{1} ) + \varphi _{2} h_{2} (ik_{{02}} \lambda _{2} - p_{2} ) \hfill \\ = w_{0} c_{1} (ik_{1} \lambda _{1} ) + \phi _{0} e_{1} (ik_{1} \lambda _{1} ) + \varphi _{0} h_{1} (ik_{1} \lambda _{1} ) \hfill \\ w_{1} e_{1} (ik_{1} \lambda _{1} ) + w_{2} e_{2} (ik_{{02}} \lambda _{2} - p_{2} ) - \phi _{1} d_{1} (ik_{1} \lambda _{1} ) - \phi _{2} d_{2} (ik_{{02}} \lambda _{2} - p_{2} ) - \varphi _{1} t_{1} (ik_{1} \lambda _{1} ) - \varphi _{2} t_{2} (ik_{{02}} \lambda _{2} - p_{2} ) \hfill \\ = w_{0} e_{1} (ik_{1} \lambda _{1} ) - \phi _{0} d_{1} (ik_{1} \lambda _{1} ) - \varphi _{0} t_{1} (ik_{1} \lambda _{1} ) \hfill \\ w_{1} h_{1} (ik_{1} \lambda _{1} ) + w_{2} h_{2} (ik_{{02}} \lambda _{2} - p_{2} ) - \phi _{1} t_{1} (ik_{1} \lambda _{1} ) - \phi _{2} t_{2} (ik_{{02}} \lambda _{2} - p_{2} ) - \varphi _{1} \mu _{1} (ik_{1} \lambda _{1} ) - \varphi _{2} \mu _{2} (ik_{{02}} \lambda _{2} - p_{2} ) \hfill \\ = w_{0} h_{1} (ik_{1} \lambda _{1} ) - \phi _{0} t_{1} (ik_{1} \lambda _{1} ) - \varphi _{0} \mu _{1} (ik_{1} \lambda _{1} ). \hfill \\ \end{gathered} \right. $$

(45)

For mathematical simplicity, the parameters $\gamma _{1} = ik_{1} \lambda _{1}$ and $\gamma _{2} = ik_{{02}} \lambda _{2} - p_{2}$ are introduced. In Eq. (45),$w_{0}$, $\phi _{0}$, and $\varphi _{0}$ are regarded as known coefficients. Cramer’s Rule can be used to find the unknown coefficients $w_{1}$,$w_{2}$,$\phi _{1}$,$\phi _{2}$,$\varphi _{1}$, and $\varphi _{2}$.