Analytical Solution for the Reissner–Sagoci Problem of a Piezoelectric Half-Space

Abstract

In this paper, a transversely isotropic piezoelectric half-space with the isotropy axis parallel to the z-axis is considered under rotation on a rigid circular disk bonded to the surface of the piezoelectric medium. This is a type of Reissner–Sagoci mixed boundary value problem. By utilizing the Hankel transform, the mixed boundary value problem is simplified into solving a pair of dual integral equations. Full-field analytical expressions for displacement, stresses, and electric displacement inside the half-space are obtained. The shear stresses and electric displacement on the surface are found to be singular at the edge of the rigid circular disk, and the stress intensity factors and electric displacement intensity factor are defined. Numerical results show that material properties and geometric size have significant effects on displacement, shear stresses, and electric displacement.

1 Introduction

The static Reissner–Sagoci problem has been studied in isotropic elasticity to determine the displacement and stress fields in the interior of a semi-infinite elastic body when a rigid circular disk of radius a completely bonded to the surface of the half-space is forced to rotate about an axis normal to the undeformed surface [1]. Reissner and Sagoci [1] firstly studied the problem by employing a system of oblate spherical coordinates and obtained an explicit solution of the tangential displacement and stress on the half-space surface. Sneddon [2] provided the complete solution for the elastic field inside the half-space by using Hankel transforms and dual integral equations. Hanson and Puja [3] solved the Reissner–Sagoci problem for a transversely isotropic half-space by applying the potential theory of Fabrikant [4].

Piezoelectric materials have been widely used in transducers, sensors, and actuators because of their intrinsic electro-mechanical coupling effect. Due to the brittleness and low fracture toughness of piezoelectric materials, the stress concentration caused by inharmonious contact, such as contact between the piezoelectric components and other components, could lead to structural failure [5]. Some theoretical investigations have been conduced to obtain the solution of the elastic and electric fields around the contact region of piezoelectric ceramics [6,7,8].

While many studies have focused on the Reissner-Sagoci problems for either isotropic or transversely isotropic materials, few have offered an analytical solution for the fullfield both on the surface and inside the half-spaces. In this work, by employing an approach similar to Sneddon’s [9], the mixed boundary value problem is solved analytically, and full-field solutions for displacement, shear stresses, and electric displacement are obtained. The shear stresses and electric displacement are found to be singular at the edge of the circular disk, and the stress intensity factors (SIFs) and electric displacement intensity factor (EDIF) are determined. Although Xiong et al. [5] has studied the problem by integrating the point force potential functions and expressing the electro-elastic fields by elementary functions, the singularity properties of the torsional contact problem has not been analyzed due to the complicated expression of the solution. The simpler-form analytical solution obtained in this work seems to be easier and more convenient for singularity analysis at the edge of the circular disk, and the present work provides basic benchmarking and fundamental understanding of torsional contact phenomena.

2 Problem Statement and Method of Solution

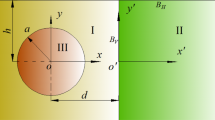
Consider a transversely isotropic piezoelectric half-space in the cylindrical coordinate system ($r,\theta ,z$), as shown in Fig. 1. The piezoelectric half-space is subjected to a constant torsion on a rigid circular disk of radius $a$ bonded to the surface of the medium at $z = 0$.

Fig. 1

A piezoelectric half-space subjected to a constant torsion on a rigid circular disk bonded to the surface of the medium

In this problem, the axis of symmetry is parallel to the $z{ - }$ axis, and the displacement vector only contains the non-vanishing component, i.e., $u_{\theta } = u_{\theta } (r,z)$, as presented by Ding and Chen [7]. We have

$$ \begin{gathered} u_{r} = u_{z} = 0,\,\Phi = 0 \hfill \\ \sigma_{rr} = \sigma_{\theta \theta } = \sigma_{zz} = \sigma_{zr} = 0, D_{r} = D_{z} = 0 \hfill \\ u_{\theta } = u_{\theta } (r,z) \hfill \\ \end{gathered} $$

(1)

where $u_{r}, u_{z}$ and $u_{\theta }$ are displacements, $\Phi$ is electric potential, $\sigma_{rr} , \sigma_{\theta \theta } , \sigma_{zz}$ and $\sigma_{zr}$ are stresses, and $D_{r}$ and $D_{z}$ are electric displacements. It is noted that the solution of the electric potential is zero, i.e.,$\Phi = 0$, as given in Eq. (1), and the proof is given in Appendix A.

The non-vanishing components of stresses $\sigma_{\theta z}$, $\sigma_{\theta r}$ and electric displacement $D_{\theta }$ are:

$$ \begin{gathered} \sigma_{\theta z} (r,z) = C_{44} \frac{{\partial u_{\theta } (r,z)}}{\partial z} \hfill \\ \sigma_{\theta r} (r,z) = C_{66} r\frac{\partial }{\partial r}\left[ {\frac{{u_{\theta } (r,z)}}{r}} \right] \hfill \\ D_{\theta } (r,z) = e_{15} \frac{{\partial u_{\theta } (r,z)}}{\partial z} \hfill \\ \end{gathered} $$

(2)

where $C_{44}$ and $C_{66}$ are elastic constants, and $e_{15}$ is piezoelectric constant.

The equations of elastic equilibrium and Gauss’s law of electrostatics in three dimensions and in the absence of body forces and free electric volume charge are given by

$$ \frac{{\partial \sigma_{\theta r} }}{\partial r} + \frac{{\partial \sigma_{\theta z} }}{\partial z} + 2\frac{{\sigma_{\theta r} }}{r} = 0 $$

(3-1)

$$ \frac{{\partial D_{r} }}{\partial r} + \frac{{\partial D_{z} }}{\partial z} + \frac{{D_{r} }}{r} = 0 $$

(3-2)

It is noted that Eq. (3-2) is automatically satisfied given that $D_{r} = D_{z} = 0$, as shown in Eq. (1).

Substituting Eq. (2) into Eq. (3-1) leads to the equilibrium equation in the following form

$$ C_{66} \left( {\frac{{\partial^{2} u_{\theta } }}{{\partial r^{2} }} + \frac{1}{r}\frac{{\partial u_{\theta } }}{\partial r} - \frac{{u_{\theta } }}{{r^{2} }}} \right) + C_{44} \frac{{\partial^{2} u_{\theta } }}{{\partial z^{2} }} = 0 $$

(4)

The boundary conditions of the mixed boundary value problem are:

$$ u_{\theta } (r,0) = f(r) = \theta_{0} \cdot r,\mathop {}\nolimits \Phi = 0\quad (0 \le r \le a) $$

(5-1)

$$ \sigma_{\theta z} (r,0) = 0,\mathop {}\nolimits D_{z} = 0\quad (r > a) $$

(5-2)

where $\theta_{0}$ is the angle of rotation of the circular rigid disk.

Applying the Hankel integral transform of the first order of $u_{\theta } (r,z)$ in the radial direction, one has

$$ U_{\theta } (s,z) = \int_{0}^{\infty } {u_{\theta } (r,z)J_{1} (rs)r{\text{d}}r} $$

(6-1)

$$ u_{\theta } (r,z) = \int_{0}^{\infty } {U_{\theta } (s,z)J_{1} (rs)s{\text{d}}s} $$

(6-2)

where $J_{1} ()$ is the Bessel function of the first kind and of order one. The partial differential Eq. (4) is reduced to

$$ C_{44} \frac{{\partial^{2} U_{\theta } (s,z)}}{{\partial z^{2} }} - s^{2} C_{66} U_{\theta } = 0 $$

(7)

and the solution satisfying the regularity condition at infinity can be obtained as

$$ U_{\theta } (s,z) = A(s){\text{e}}^{{{ - }s\lambda z}} $$

(8)

The displacement can be obtained as

$$ u_{\theta } (r,z) = \int_{0}^{\infty } {A(s){\text{e}}^{ - s\lambda z} J_{1} (rs){\text{d}}s} $$

(9)

where $\lambda = \sqrt {{{C_{66} } \mathord{\left/ {\vphantom {{C_{66} } {C_{44} }}} \right. \kern-0pt} {C_{44} }}}$, and $A(s)$ is the unknown function to be determined by the mixed boundary conditions.

The non-vanishing stresses $\sigma_{\theta z}$,$\sigma_{\theta r}$ and electric displacement $D_{\theta }$ are:

$$ \sigma_{\theta z} (r,z) = - \lambda C_{44} \int_{0}^{\infty } {sA(s){\text{e}}^{ - s\lambda z} J_{1} (rs){\text{d}}s} $$

(10)

$$ D_{\theta } (r,z) = \frac{{e_{15} }}{{C_{44} }}\sigma_{\theta z} (r,z) = - \lambda e_{15} \int_{0}^{\infty } {sA(s){\text{e}}^{ - s\lambda z} J_{1} (rs){\text{d}}s} $$

(11)

$$ \sigma_{\theta r} (r,z) = - C_{66} \int_{0}^{\infty } {sA(s){\text{e}}^{ - s\lambda z} J_{2} (rs){\text{d}}s} $$

(12)

where $J_{2} ()$ is the Bessel function of the first kind and of order two.

The satisfaction of the mixed boundary conditions leads to the following dual integral equations

$$ \int_{0}^{\infty } {A(s)J_{1} (rs){\text{d}}s} = f(r) = \theta_{0} \cdot r\quad (0 \le r \le a) $$

(13-1)

$$ \int_{0}^{\infty } {sA(s)J_{1} (rs){\text{d}}s} = 0\quad (r > a) $$

(13-2)

from which the unknown function $A(s)$ can be determined.

Following the procedure of Sneddon [9], it is assumed that

$$ A(s) = \int_{0}^{a} {g(t)\sin (ts){\text{d}}t} ,\mathop {}\nolimits g(0) = 0 $$

(14)

and the solution of $g(t)$ can be obtained as

$$ g(t) = \frac{2}{\pi }\int_{0}^{t} {\frac{{\text{d}}}{{{\text{d}}r}}\left[ {rf(r)} \right]\frac{{{\text{d}}r}}{{\sqrt {t^{2} - r^{2} } }}} = \frac{{4\theta_{0} }}{\pi }t\quad (0 \le t \le a) $$

(15)

from which it can be seen that the assumption $g(0) = 0$ is satisfied automatically.

The torque $T$ which must be applied to produce prescribed boundary conditions can be expressed as

$$ T = - \int_{0}^{2\pi } {\int_{0}^{a} {\sigma_{\theta z} (r,0)r \cdot r{\text{d}}r} } {\text{d}}\theta $$

(16)

The substitution of $\sigma_{\theta z} (r,0)$ into the above equation leads to

$$ T = 2\pi \mu_{0} \int_{0}^{a} {r^{2} \int_{0}^{\infty } {sA(s)J_{1} (rs){\text{d}}s} {\text{d}}r} $$

(17)

where $\mu_{0} = \sqrt {C_{44} C_{66} }$.

By using the relation

$$ \int_{0}^{a} {r^{2} J_{1} (rs){\text{d}}r} = \frac{{a^{2} }}{s}J_{2} (sa) $$

(18)

we have the expression for the torque $T$ as

$$ T = 2\pi \mu_{0} a^{2} \int_{0}^{\infty } {A(s)J_{2} (sa){\text{d}}s} $$

(19)

The substitution of Eq. (14) into Eq. (19) leads to the expression

$$ T = 4\pi \mu_{0} \int_{0}^{a} {g(t)t{\text{d}}t} $$

(20)

in which the following integral identity is used:

$$ \int_{0}^{\infty } {\sin (ts)J_{2} (sa){\text{d}}s} = \frac{2t}{{a^{2} }} $$

(21)

From Eqs. (14) and (15), we can get the expression of $A(s)$ as

$$ A(s) = \frac{{4\theta_{0} }}{\pi }\int_{0}^{a} {t\sin (ts){\text{d}}t} = \frac{{4\theta_{0} }}{{\pi s^{2} }}\left[ {\sin (sa) - sa\cos (sa)} \right] $$

(22)

and the torque $T$ as

$$ T = 4\pi \mu_{0} \int_{0}^{a} {g(t)t{\text{d}}t} = 16\mu_{0} \theta_{0} \int_{0}^{a} {t^{2} {\text{d}}t} = \frac{{16\mu_{0} \theta_{0} a^{3} }}{3} $$

(23)

The displacement on the surface $(z = 0)$ can be determined as

$$ \begin{aligned} u_{\theta } (r,0) & = \frac{{4\theta_{0} }}{r\pi }\int_{0}^{a} {\frac{{t^{2} }}{{\sqrt {r^{2} - t^{2} } }}{\text{d}}t} = \frac{{4\theta_{0} }}{r\pi }\\ & \quad\times\left[ {\int_{0}^{a} {\sqrt {r^{2} - t^{2} } {\text{d}}t} - a\sqrt {r^{2} - a^{2} } } \right] \\ & = \frac{{2\theta_{0} }}{\pi }\left[ {r\arcsin \left( \frac{a}{r} \right) - \frac{a}{r}\sqrt {r^{2} - a^{2} } } \right]\quad (r > a) \\ \end{aligned} $$

(24)

The shear stress $\sigma_{\theta z}$ on the surface ($z = 0$) is

$$ \sigma_{\theta z} (r,0) = - \frac{{4\mu_{0} \theta_{0} r}}{{\pi \sqrt {a^{2} - r^{2} } }}\quad (0 \le r < a) $$

(25)

It is noted that for the special case when $C_{44} = C_{66}$, i.e., for a homogeneous isotropic elastic problem, we have $\mu_{0} = C_{44}$, and the result in Eq. (25) agrees with the classical results for the Reissner–Sagoci problem of isotropic elasticity [1, 2].

The shear stress $\sigma_{\theta r}$ on the surface is

$$ \begin{aligned}\sigma_{\theta r} (r,0) &= - \frac{{C_{66} }}{{r^{2} }}\frac{{4\theta_{0} }}{\pi }\\&\times\left[ {m\sqrt {r^{2} - m^{2} } - a\frac{{r^{2} - 2a^{2} }}{{\sqrt {r^{2} - a^{2} } }}H(r - a)} \right]\end{aligned} $$

(26)

where $m = \min (r,a)$ and H( ) is the Heavyside step function. When $0 \le r < a$, $\sigma_{\theta r} (r,0) = 0$; and when $r > a$, we have

$$ \sigma_{\theta r} (r,0) = - \frac{{4\theta_{0} C_{66} }}{\pi }\frac{a}{{\sqrt {r^{2} - a^{2} } }}\left( \frac{a}{r} \right)^{2} \quad (r > a) $$

(27)

The electric displacement $D_{\theta }$ on the surface ($z = 0$) is

$$ D_{\theta } (r,0) = - \frac{{4e_{15} \mu_{0} \theta_{0} r}}{{\pi C_{44} \sqrt {a^{2} - r^{2} } }}\quad (0 \le r < a) $$

(28)

It is evident that the shear stresses $\sigma_{\theta z} (r,0)$ and $\sigma_{\theta r} (r,0)$ are singular near the inside and outside edges of the rigid disk, respectively. This square-root singularity at the edge of the circular disk is similar to the singularity observed in crack problems in a piezoelectric medium [10, 11].

The shear stress intensity factors $K_{\theta z}$ and $K_{\theta r}$ can be defined as

$$ K_{\theta z} = \mathop {\lim }\limits_{{r \to a^{ - } }} \sqrt {2(a - r)} \sigma_{\theta z} (r,0) = - \frac{{4\mu_{0} \theta_{0} }}{\pi }\sqrt a $$

(29)

$$ K_{\theta r} = \mathop {\lim }\limits_{{r \to a^{ + } }} \sqrt {2(r - a)} \sigma_{\theta r} (r,0) = - \frac{{4C_{66} \theta_{0} }}{\pi }\sqrt a $$

(30)

Similarly, the electric displacement is singular near the inside edge of the rigid disk, and the electric displacement intensity factor can be defined as

$$ K_{D\theta } = \mathop {\lim }\limits_{{r \to a^{ - } }} \sqrt {2(a - r)} D_{\theta } (r,0) = - \frac{{4\theta_{0} e_{15} \lambda }}{\pi }\sqrt a $$

(31)

It is shown from Eqs. (29–31) that the stress intensity factors and electric displacement intensity factor are dependent on material properties of the piezoelectric medium, the radius of the circular rigid disk, and the rotation angle.

3 Full-Field Solutions in the Half-Space

Once the expression of $A(s)$ has been obtained as in Eq. (22), the full-field solutions for the displacement $u_{\theta }$, the shear stresses $\sigma_{\theta z} , \sigma_{\theta r}$ and the electric displacement $D_{\theta }$ can be obtained as

$$\begin{aligned} u_{\theta } (r,z) &= \frac{{4\theta_{0} }}{\pi }\left[ {\int_{0}^{\infty } {\frac{1}{{s^{2} }}\sin (sa){\text{e}}^{ - s\lambda z} J_{1} (rs){\text{d}}s}}\right. \\ &\quad\left.{- a\int_{0}^{\infty } {\frac{1}{s}\cos (sa){\text{e}}^{ - s\lambda z} J_{1} (rs){\text{d}}s} } \right] \end{aligned}$$

(32)

$$\begin{aligned} \sigma_{\theta z} (r,z) &= - \frac{{4\mu_{0} \theta_{0} }}{\pi }\left[ {\int_{0}^{\infty } {\frac{1}{s}\sin (sa){\text{e}}^{ - s\lambda z} J_{1} (rs){\text{d}}s} }\right. \\ & \left.{- a\int_{0}^{\infty } {\cos (sa){\text{e}}^{ - s\lambda z} J_{1} (rs){\text{d}}s} } \right] \end{aligned}$$

(33)

$$\begin{aligned} \sigma_{\theta r} (r,z) &= - \frac{{4\theta_{0} C_{66} }}{\pi }\left[ {\int_{0}^{\infty } {\frac{1}{s}\sin (sa){\text{e}}^{ - s\lambda z} J_{2} (rs){\text{d}}s} }\right. \\ & \left.{- a\int_{0}^{\infty } {\cos (sa){\text{e}}^{ - s\lambda z} J_{2} (rs){\text{d}}s} } \right] \end{aligned}$$

(34)

$$ D_{\theta } (r,z) = {{e_{15} \sigma_{\theta z} (r,z)} \mathord{\left/ {\vphantom {{e_{15} \sigma_{\theta z} (r,z)} {C_{44} }}} \right. \kern-0pt} {C_{44} }} $$

(35)

By using the following integral identity [2]:

$$ \begin{aligned} I_{1} &= \int_{0}^{\infty } {\frac{1}{{s^{2} }}\sin (sa){\text{e}}^{ - s\lambda z} J_{1} (rs){\text{d}}s} \hfill \\ &\mathop {}\nolimits = a\left[ {\frac{{\lambda_{0} R\sin (\theta + \phi ) - \lambda_{0}^{2} \sin (2\theta )}}{2\rho }}\right. \\& \quad \left.{ + \frac{\rho }{2}\tan^{ - 1} \left( {\frac{{R\sin \phi + \lambda_{0} \sin \theta }}{{R\cos \phi + \lambda_{0} \cos \theta }}} \right)} \right] \hfill \\ \end{aligned} $$

(36-1)

where the quantities $\lambda_{0} , R, \theta$, and $\phi$ are defined by the relations

$$ \begin{gathered} \lambda_{0}^{2} = 1 + \xi^{2} , \xi = {{\lambda z} \mathord{\left/ {\vphantom {{\lambda z} a}} \right. \kern-0pt} a}, \xi \tan \theta = 1, \rho = {r \mathord{\left/ {\vphantom {r a}} \right. \kern-0pt} a} \hfill \\ R^{4} = (\rho^{2} + \xi^{2} - 1)^{2} + 4\xi^{2} , 2\xi \cot 2\phi = \rho^{2} + \xi^{2} - 1 \hfill \\ \end{gathered} $$

(36-2)

and

$$ I_{2} = \int_{0}^{\infty } {\frac{1}{s}\cos (sa){\text{e}}^{ - s\lambda z} J_{1} (rs){\text{d}}s} = \frac{1}{r}{\text{Re}} \left[ {\sqrt {r^{2} + z^{*2} } - z^{*} } \right] $$

(37)

where $z^{*} = \lambda z - {\text{i}}a$, and “Re” denotes the real part of a complex number.

The exact solution for the displacement $u_{\theta } (r,z)$ can be given as

$$ u_{\theta } (r,z) = \frac{{4\theta_{0} }}{\pi }\left[ {I_{1} - aI_{2} } \right] $$

(38)

Similarly, the shear stresses $\sigma_{\theta z} (r,z), \sigma_{\theta r} (r,z)$ and the electric displacement $D_{\theta } (r,z)$ can be obtained as

$$\begin{aligned} \sigma_{\theta z} (r,z)& = - \frac{{4\theta_{0} \mu_{0} }}{\pi r}\left[ {{\text{Im}} \left[ {\sqrt {r^{2} + z^{*2} } - z^{*} } \right]}\right. \\ & \left.{ - a + a{\text{Re}} \left( {\frac{{z^{*} }}{{\sqrt {r^{2} + z^{*2} } }}} \right)} \right] \end{aligned}$$

(39)

$$\begin{aligned} \sigma_{\theta r} (r,z) &= - \frac{{2\theta_{0} C_{66} }}{{\pi r^{2} }}\left\{ {{\text{Im}} \left( {\sqrt {r^{2} + z^{*2} } - z^{*} } \right)^{2} }\right. \\ & \left.{- 2a{\text{Re}} \left[ {\frac{{\left( {\sqrt {r^{2} + z^{*2} } - z^{*} } \right)^{2} }}{{\sqrt {r^{2} + z^{*2} } }}} \right]} \right\} \end{aligned}$$

(40)

$$\begin{aligned} D_{\theta } (r,z) &= - \frac{{4\theta_{0} }}{\pi r}e_{15} \sqrt {\frac{{C_{66} }}{{C_{44} }}} \left[ {{\text{Im}} \left[ {\sqrt {r^{2} + z^{*2} } - z^{*} } \right]}\right. \\ & \left.{ - a + a{\text{Re}} \left( {\frac{{z^{*} }}{{\sqrt {r^{2} + z^{*2} } }}} \right)} \right] \end{aligned}$$

(41)

Equations (38–41) give the full-field solutions for the displacement, shear stresses, and electric displacement in analytical form. Some integral identities are used during the derivation of Eqs. (38–41), and are provided in Appendix B.

It is noted that the explicit analytical solutions for full-field displacement, stresses, and electric displacement, as shown in Eqs. (38–41), are given in quite different form from those provided by Xiong et al. [5], who solved the problem by integrating point force potential functions. Despite the methodological differences, a numerical analysis shows that the analytical solution presented in this paper is equivalent to the expressions given in [5]. The shear stress intensity factors and electric displacement intensity factor are defined for the first time to characterize the singular fields near the edge of the rigid circular disk, and the solution appears to be new. The method of the current work allows a much simpler form of the solution, and the result obtained is easy to be used for numerical calculation and engineering design.

4 Numerical Results and Discussions

In this section, some numerical examples are given to show the influences of material properties and torsional load on displacement and shear stresses. The normalized displacements ${{u_{\theta } (r,z)} \mathord{\left/ {\vphantom {{u_{\theta } (r,z)} {(\theta_{0} a}}} \right. \kern-0pt} {(\theta_{0} a}})$ at the surface and inside the half-space are displayed in Fig. 2 for the case $\lambda^{2} = {{C_{66} } \mathord{\left/ {\vphantom {{C_{66} } {C_{44} }}} \right. \kern-0pt} {C_{44} }} = 2$. It is clear that the displacement on the surface (${z \mathord{\left/ {\vphantom {z a}} \right. \kern-0pt} a} = 0$) is proportional to the rotation angle $\theta_{0}$ from the center to the edge of the circular rigid disk, as shown in Eq. (5–1). The displacement ${{u_{\theta } } \mathord{\left/ {\vphantom {{u_{\theta } } {(\theta_{0} a}}} \right. \kern-0pt} {(\theta_{0} a}})$ decreases as the normalized depth ${z \mathord{\left/ {\vphantom {z a}} \right. \kern-0pt} a}$ increases. When the depth ratio ${z \mathord{\left/ {\vphantom {z a}} \right. \kern-0pt} a} = {\text{Inf}}{.}$, the displacement vanishes, i.e., when the depth is sufficiently large, the displacement disappears. In the figure, “Inf.” denotes a very large number. The variation of ${{u_{\theta } (r,z)} \mathord{\left/ {\vphantom {{u_{\theta } (r,z)} {a\theta_{0} }}} \right. \kern-0pt} {a\theta_{0} }}$ versus ${r \mathord{\left/ {\vphantom {r a}} \right. \kern-0pt} a}$ for different values of $\lambda^{2}$ when ${z \mathord{\left/ {\vphantom {z a}} \right. \kern-0pt} a} = 0.3$ is displayed in Fig. 3. The displacement ${{u_{\theta } (r,z)} \mathord{\left/ {\vphantom {{u_{\theta } (r,z)} {a\theta_{0} }}} \right. \kern-0pt} {a\theta_{0} }}$ increases from zero to a maximum value and then decreases to zero as the radial distance from the center of the disk increases.

Fig. 2

Variation of ${{u_{\theta } (r,z)} \mathord{\left/ {\vphantom {{u_{\theta } (r,z)} {a\theta_{0} }}} \right. \kern-0pt} {a\theta_{0} }}$ versus ${r \mathord{\left/ {\vphantom {r a}} \right. \kern-0pt} a}$ for different values of ${z \mathord{\left/ {\vphantom {z a}} \right. \kern-0pt} a}$ when $\lambda^{2} = {{C_{66} } \mathord{\left/ {\vphantom {{C_{66} } {C_{44} }}} \right. \kern-0pt} {C_{44} }} = 2$

Fig. 3

Variation of ${{u_{\theta } (r,z)} \mathord{\left/ {\vphantom {{u_{\theta } (r,z)} {a\theta_{0} }}} \right. \kern-0pt} {a\theta_{0} }}$ versus ${r \mathord{\left/ {\vphantom {r a}} \right. \kern-0pt} a}$ for different values of $\lambda^{2}$ when ${z \mathord{\left/ {\vphantom {z a}} \right. \kern-0pt} a} = 0.3$

Figures 4 and 5 respectively show the variations of the normalized shear stresses ${{ - \sigma_{\theta z} (r,z)} \mathord{\left/ {\vphantom {{ - \sigma_{\theta z} (r,z)} {\mu_{0} }}} \right. \kern-0pt} {\mu_{0} }}$ and $- {{\sigma_{\theta r} (r,z)} \mathord{\left/ {\vphantom {{\sigma_{\theta r} (r,z)} {\mu_{0} }}} \right. \kern-0pt} {\mu_{0} }}$ versus ${r \mathord{\left/ {\vphantom {r a}} \right. \kern-0pt} a}$ for different values of ${z \mathord{\left/ {\vphantom {z a}} \right. \kern-0pt} a}$ when $\lambda^{2} = 2$. The normalized shear stress on the surface ${{ - \sigma_{\theta z} (r,0)} \mathord{\left/ {\vphantom {{ - \sigma_{\theta z} (r,0)} {\mu_{0} }}} \right. \kern-0pt} {\mu_{0} }}$ under the circular disk increases from zero at the center and approaches to infinity at the inside edge of the disk, and the normalized shear stress $- {{\sigma_{\theta z} (r,0)} \mathord{\left/ {\vphantom {{\sigma_{\theta z} (r,0)} {\mu_{0} }}} \right. \kern-0pt} {\mu_{0} }}$ vanishes on the surface outside of the disk (${r \mathord{\left/ {\vphantom {r a}} \right. \kern-0pt} a} > 0$), as shown in Fig. 4.

Fig. 4

Variation of ${{ - \sigma_{\theta z} (r,z)} \mathord{\left/ {\vphantom {{ - \sigma_{\theta z} (r,z)} {\mu_{0} }}} \right. \kern-0pt} {\mu_{0} }}$ versus ${r \mathord{\left/ {\vphantom {r a}} \right. \kern-0pt} a}$ for different values of ${z \mathord{\left/ {\vphantom {z a}} \right. \kern-0pt} a}$ when $\lambda^{2} = {{C_{66} } \mathord{\left/ {\vphantom {{C_{66} } {C_{44} }}} \right. \kern-0pt} {C_{44} }} = 2$

Fig. 5

Variation of ${{ - \sigma_{\theta r} (r,z)} \mathord{\left/ {\vphantom {{ - \sigma_{\theta r} (r,z)} {\mu_{0} }}} \right. \kern-0pt} {\mu_{0} }}$ versus ${r \mathord{\left/ {\vphantom {r a}} \right. \kern-0pt} a}$ for different values of ${z \mathord{\left/ {\vphantom {z a}} \right. \kern-0pt} a}$ when $\lambda^{2} = {{C_{66} } \mathord{\left/ {\vphantom {{C_{66} } {C_{44} }}} \right. \kern-0pt} {C_{44} }} = 2$

It can be observed in Fig. 5 that the shear stress on the surface ${{\sigma_{\theta r} (r,0)} \mathord{\left/ {\vphantom {{\sigma_{\theta r} (r,0)} {\mu_{0} }}} \right. \kern-0pt} {\mu_{0} }}$ under the circular disk ${r \mathord{\left/ {\vphantom {r a}} \right. \kern-0pt} a} < 1$ is zero, the shear stress is singular at the outside edge of the circular disk, and the magnitude of ${{ - \sigma_{\theta r} (r,0)} \mathord{\left/ {\vphantom {{ - \sigma_{\theta r} (r,0)} {\mu_{0} }}} \right. \kern-0pt} {\mu_{0} }}$ decreases from infinity to zero as the distance from the center of the disk increases. It is noted that the shear stresses $\sigma_{\theta z} (r,z)$ and $\sigma_{\theta r} (r,z)$ are of negative values. Inside the half-space, the values of $- {{\sigma_{\theta z} (r,z)} \mathord{\left/ {\vphantom {{\sigma_{\theta z} (r,z)} {\mu_{0} }}} \right. \kern-0pt} {\mu_{0} }}$ and ${{ - \sigma_{\theta r} (r,z)} \mathord{\left/ {\vphantom {{ - \sigma_{\theta r} (r,z)} {\mu_{0} }}} \right. \kern-0pt} {\mu_{0} }}$ increase from zero to a maximum value then decrease as ${r \mathord{\left/ {\vphantom {r a}} \right. \kern-0pt} a}$ increases. The magnitude of the shear stresses decreases as the depth ${z \mathord{\left/ {\vphantom {z a}} \right. \kern-0pt} a}$ increases, and the shear stresses are very small when the normalized depth ${z \mathord{\left/ {\vphantom {z a}} \right. \kern-0pt} a} > 2.0$.

The variations of ${{ - \sigma_{\theta z} (r,z)} \mathord{\left/ {\vphantom {{ - \sigma_{\theta z} (r,z)} {\mu_{0} \theta_{0} }}} \right. \kern-0pt} {\mu_{0} \theta_{0} }}$ and ${{ - \sigma_{\theta r} (r,z)} \mathord{\left/ {\vphantom {{ - \sigma_{\theta r} (r,z)} {\mu_{0} \theta_{0} }}} \right. \kern-0pt} {\mu_{0} \theta_{0} }}$ versus ${r \mathord{\left/ {\vphantom {r a}} \right. \kern-0pt} a}$ for different values of $\lambda^{2}$ when ${z \mathord{\left/ {\vphantom {z a}} \right. \kern-0pt} a} = 0.3$ are shown in Fig. 6 and Fig. 7, respectively. It is illustrated that the normalized shear stresses ${{ - \sigma_{\theta z} (r,z)} \mathord{\left/ {\vphantom {{ - \sigma_{\theta z} (r,z)} {\mu_{0} \theta_{0} }}} \right. \kern-0pt} {\mu_{0} \theta_{0} }}$ and $- {{\sigma_{\theta r} (r,z)} \mathord{\left/ {\vphantom {{\sigma_{\theta r} (r,z)} {\mu_{0} \theta_{0} }}} \right. \kern-0pt} {\mu_{0} \theta_{0} }}$ increase from zero to a maximum value and decrease as the distance from the center of the disk ${r \mathord{\left/ {\vphantom {r a}} \right. \kern-0pt} a}$ increases. The magnitude of the shear stress ${{ - \sigma_{\theta z} (r,z)} \mathord{\left/ {\vphantom {{ - \sigma_{\theta z} (r,z)} {\mu_{0} \theta_{0} }}} \right. \kern-0pt} {\mu_{0} \theta_{0} }}$ decreases as the value of $\lambda^{2}$ increases, while the magnitude of ${{ - \sigma_{\theta r} (r,z)} \mathord{\left/ {\vphantom {{ - \sigma_{\theta r} (r,z)} {\mu_{0} \theta_{0} }}} \right. \kern-0pt} {\mu_{0} \theta_{0} }}$ increases as $\lambda^{2}$ increases from 0.25 to 1.0, and then decreases as $\lambda^{2}$ increases from 1.0 to 4.0.

Fig. 6

Variation of ${{ - \sigma_{\theta z} (r,z)} \mathord{\left/ {\vphantom {{ - \sigma_{\theta z} (r,z)} {\mu_{0} \theta_{0} }}} \right. \kern-0pt} {\mu_{0} \theta_{0} }}$ versus ${r \mathord{\left/ {\vphantom {r a}} \right. \kern-0pt} a}$ for different values of $\lambda^{2}$ when ${z \mathord{\left/ {\vphantom {z a}} \right. \kern-0pt} a} = 0.3$

Fig. 7

Variation of ${{ - \sigma_{\theta r} (r,z)} \mathord{\left/ {\vphantom {{ - \sigma_{\theta r} (r,z)} {\mu_{0} \theta_{0} }}} \right. \kern-0pt} {\mu_{0} \theta_{0} }}$ versus ${r \mathord{\left/ {\vphantom {r a}} \right. \kern-0pt} a}$ for different values of $\lambda^{2}$ when ${z \mathord{\left/ {\vphantom {z a}} \right. \kern-0pt} a} = 0.3$

5 Conclusions

Utilizing Hankel transforms and dual integral equations, an analytical solution for the static Reissner-Sagoci problem in a transversely isotropic piezoelectric half-space is provided. The Full-field displacement, stresses and electric displacement are obtained in analytical form. It is found that the shear stresses on the surface, $\sigma_{\theta z} (r,0)$ and $\sigma_{\theta r} (r,0)$, are singular near the inside and outside edges of the rigid disk, respectively. The shear stress intensity factors and electric displacement intensity factor are dependent on material properties, the radius of the circular disk, and the rotation angle.

Appendices

Appendix A

This section is to prove that the electric potential for this torsional problem is zero.

Assuming that the electric potential is $\Phi (r,z)$, and the electric displacement $D_{r} = - \varepsilon_{11} \Phi_{,r} , D_{z} = - \varepsilon_{33} \Phi_{,z}$, then the satisfaction of Gauss’s law of electrostatics

$$ \frac{{\partial D_{r} }}{\partial r} + \frac{{\partial D_{z} }}{\partial z} + \frac{{D_{r} }}{r} = 0 $$

(A1)

leads to the following partial differential equation

$$ \varepsilon_{11} \left( {\frac{{\partial^{2} \Phi }}{{\partial r^{2} }} + \frac{1}{r}\frac{\partial \Phi }{{\partial r}}} \right) + \varepsilon_{33} \frac{{\partial^{2} \Phi }}{{\partial z^{2} }} = 0 $$

(A2)

The solution of this equation is in the form

$$ \Phi (r,z) = \int_{0}^{\infty } {\xi B(\xi ){\text e}^{ - \gamma \xi z} J_{0} (\xi r){\text{d}}\xi } $$

(A3)

where $\gamma = \sqrt {{{\varepsilon_{11} } \mathord{\left/ {\vphantom {{\varepsilon_{11} } {\varepsilon_{33} }}} \right. \kern-0pt} {\varepsilon_{33} }}}$, $\varepsilon_{11} , \varepsilon_{33}$ are dielectric constants, and $B(\xi )$ is unknown functions to be determined.

Under the boundary conditions

$$ \begin{gathered} \Phi = 0\,\mathop {}\nolimits (0 \le r \le a) \hfill \\ D_{z} = 0\,\mathop {}\nolimits (r > a) \hfill \\ \end{gathered} $$

(A4)

the following dual integral equations

$$ \int_{0}^{\infty } {\xi B(\xi )J_{0} (\xi r){\text{d}}s} = 0\quad (0 \le r \le a) $$

(A5-1)

$$ \int_{0}^{\infty } {\xi^{2} B(\xi )J_{0} (\xi r){\text{d}}s} = 0\quad (r > a) $$

(A5-2)

lead to the solution $B(\xi ) = 0$, and then we have $\Phi = 0$.

Appendix B

Some useful identities [12] are used in the derivation of analytical solutions for displacement, stresses and electric displacement:

$$ \int_{0}^{\infty } {\cos (ts)J_{1} (rs){\text{d}}s} = \frac{1}{r}\left[ {1 - \frac{t \cdot H(t - r)}{{\sqrt {t^{2} - r^{2} } }}} \right] = \left\{ {\begin{array}{*{20}c} {\frac{1}{r}\mathop {}\nolimits \mathop {}\nolimits (r > t)} \\ {\frac{1}{r}\left[ {1 - \frac{t}{{\sqrt {t^{2} - r^{2} } }}} \right]\mathop {}\nolimits \mathop {}\nolimits (r < t)} \\ \end{array} } \right. $$

(B1)

$$ \int_{0}^{\infty } {\sin (ts)J_{1} (rs){\text{d}}s} = \frac{t}{r}\left[ {\frac{H(r - t)}{{\sqrt {r^{2} - t^{2} } }}} \right] = \left\{ {\begin{array}{*{20}c} {0\mathop {}\nolimits \mathop {}\nolimits (r < t)} \\ {\frac{t}{{r\sqrt {r^{2} - t^{2} } }}\mathop {}\nolimits \mathop {}\nolimits (r > t)} \\ \end{array} } \right. $$

(B2)

For the following Abel-type integral equation

$$ \int_{0}^{r} {\frac{tg(t)}{{\sqrt {r^{2} - t^{2} } }}{\text{d}}t} = rf(r)\quad (0 \le r \le a) $$

(B3)

The solution is

$$ g(t) = \frac{2}{\pi }\int_{0}^{t} {\frac{{\text{d}}}{{{\text{d}}r}}\left[ {rf(r)} \right]\frac{{{\text{d}}r}}{{\sqrt {t^{2} - r^{2} } }}} \quad (0 \le t \le a) $$

(B4)

$$ \int_{0}^{a} {r^{2} J_{1} (rs){\text{d}}r} = \frac{{a^{2} }}{s}J_{2} (sa) $$

(B5)

$$ \int_{0}^{\infty } {\sin (ts)J_{2} (sa){\text{d}}s} = \frac{2t}{{a^{2} }} $$

(B6)

$$ \int_{0}^{\infty } {J_{2} (rs)\cos (ts){\text{d}}s} = \frac{{(r^{2} - 2t^{2} )H(r - t)}}{{r^{2} \sqrt {r^{2} - t^{2} } }} $$

(B7)

$$ \int_{0}^{\infty } {{\text{e}}^{ - sp} J_{1} (rs){\text{d}}s} = \frac{1}{r}\left[ {1 - \frac{p}{{\sqrt {r^{2} + p^{2} } }}} \right] $$

(B8)

$$ \int_{0}^{\infty } {\sin (ts){\text{e}}^{ - s\lambda z} J_{1} (rs){\text{d}}s} = - {\text{Im}} \left[ {\int_{0}^{\infty } {{\text{e}}^{ - sp} J_{1} (rs){\text{d}}s} } \right] $$

(B9)

where $p = \lambda z + {\text{i}}t$, and “Im” denotes the imaginary part of a complex number.

$$ \frac{{\text{d}}}{{{\text{d}}t}}\left[ {r^{2} \arcsin \left( \frac{t}{r} \right)} \right] = \sqrt {r^{2} - t^{2} } + \frac{{t^{2} }}{{\sqrt {r^{2} - t^{2} } }} $$

(B10)

$$ \int_{0}^{a} {\left[ {\sqrt {r^{2} - t^{2} } + \frac{{t^{2} }}{{\sqrt {r^{2} - t^{2} } }}} \right]{\text{d}}t} = r^{2} \arcsin \left( \frac{a}{r} \right) $$

(B11)

$$ \int_{0}^{a} {\frac{{t^{2} }}{{\sqrt {r^{2} - t^{2} } }}{\text{d}}t} = \int_{0}^{a} {( - t){\text{d}}\sqrt {r^{2} - t^{2} } } = \int_{0}^{a} {\sqrt {r^{2} - t^{2} } {\text{d}}t} - a\sqrt {r^{2} - a^{2} } $$

(B12)

From Eqs. (B11) and (B12), one has

$$ \int_{0}^{a} {\sqrt {r^{2} - t^{2} } {\text{d}}t} = \frac{1}{2}\left[ {a\sqrt {r^{2} - a^{2} } + r^{2} \arcsin \left( \frac{a}{r} \right)} \right] $$

(B13)

$$ \int_{0}^{\infty } {\frac{1}{x}{\text{e}}^{ - \alpha x} J_{v} (\beta x){\text{d}}x} = \frac{{\left( {\sqrt {\alpha^{2} + \beta^{2} } - \alpha } \right)^{v} }}{{v\beta^{v} }} $$

(B14)

$$ \int_{0}^{\infty } {{\text{e}}^{ - \alpha x} J_{v} (\beta x){\text{d}}x} = \frac{{\beta^{ - v} \left( {\sqrt {\alpha^{2} + \beta^{2} } - \alpha } \right)^{v} }}{{\sqrt {\alpha^{2} + \beta^{2} } }} $$

(B15)

$$ \int_{0}^{\infty } {{\text{e}}^{{ - sz^{*} }} J_{1} (rs){\text{d}}s} = \frac{1}{r}\frac{{\sqrt {r^{2} + z^{*2} } - z^{*} }}{{\sqrt {r^{2} + z^{*2} } }} $$

(B16)

$$ \int_{0}^{\infty } {\frac{1}{s}{\text{e}}^{{ - sz^{*} }} J_{2} (rs){\text{d}}s} = \frac{1}{{2r^{2} }}\left[ {\sqrt {r^{2} + z^{*2} } - z^{*} } \right]^{2} $$

(B17)

$$ \int_{0}^{\infty } {{\text{e}}^{{ - sz^{*} }} J_{2} (rs){\text{d}}s} = \frac{{\left[ {\sqrt {r^{2} + z^{*2} } - z^{*} } \right]^{2} }}{{r^{2} \sqrt {r^{2} + z^{*2} } }} $$

(B18)

where $z^{*} = \lambda z - {\text{i}}a$.

$$ I_{2} = \int_{0}^{\infty } {\frac{1}{s}\cos (sa){\text{e}}^{ - s\lambda z} J_{1} (rs){\text{d}}s} = \frac{1}{r}{\text{Re}} \left[ {\sqrt {r^{2} + z^{*2} } - z^{*} } \right] $$

(B19)

$$ I_{3} = \int_{0}^{\infty } {\frac{1}{s}\sin (sa){\text{e}}^{ - s\lambda z} J_{1} (rs){\text{d}}s} = \frac{1}{r}{\text{Im}} \left[ {\sqrt {r^{2} + z^{*2} } - z^{*} } \right] $$

(B20)

$$ I_{4} = \int_{0}^{\infty } {\cos (sa){\text{e}}^{ - s\lambda z} J_{1} (rs){\text{d}}s} = \frac{1}{r}\left\{ {1 - {\text{Re}} \left( {\frac{{z^{*} }}{{\sqrt {r^{2} + z^{*2} } }}} \right)} \right\} $$

(B21)

$$ I_{5} = \int_{0}^{\infty } {\frac{1}{s}\sin (sa){\text{e}}^{ - s\lambda z} J_{2} (rs){\text{d}}s} = \frac{1}{{2r^{2} }}{\text{Im}} \left[ {\sqrt {r^{2} + z^{*2} } - z^{*} } \right]^{2} $$

(B22)

$$ I_{6} = \int_{0}^{\infty } {\cos (sa){\text{e}}^{ - s\lambda z} J_{2} (rs){\text{d}}s} = \frac{1}{{r^{2} }}{\text{Re}} \left[ {\frac{{\left( {\sqrt {r^{2} + z^{*2} } - z^{*} } \right)^{2} }}{{\sqrt {r^{2} + z^{*2} } }}} \right] $$

(B23)