Indentation of a nanolayer on a substrate by a rigid cylinder in adhesive contact

Abstract

Nanoindentation is employed to characterize the mechanical properties at the nanoscale. This paper considers the mechanical response of a nanoscale elastic layer on an elastic substrate that is indented by an adhesively bonded flat-ended rigid cylindrical punch. The complete Gurtin–Murdoch continuum model is employed to capture the size effects. The contact problem is analyzed by relating displacements of the contact region to contact stresses by a flexibility equation system, which is developed by discretizing the contact region into annular elements. The flexibility equation involves displacement influence functions corresponding to axisymmetric normal and radial surface ring loads applied on the layer-substrate system. The displacement influence functions are derived by using the Hankel integral transforms. Convergence and accuracy of the proposed solution scheme are verified by comparing with limiting cases such as the classical elasticity solution. Selected numerical results indicate that the substrate becomes stiffer and the elastic field is size-dependent due to the surface energy effects.

1 Introduction

An interesting class of problems in continuum mechanics is concerned with stress analysis of an elastic medium subjected to a rigid punch on its surface due to its close relevance to indentation techniques that have been performed to obtain mechanical properties such as elastic modulus and hardness. For example, mechanical properties of thin films were obtained by Doerner and Nix [1] and Oliver and Pharr [2] from depth-sensing indentation experiments, in which the elastic modulus is obtained from the unloading curve and hardness is obtained from the load-deformation data. Several researchers obtained analytical solutions for indentation problems based on continuum mechanics models in the past. A classical solution was presented by Boussinesq [3] who studied axisymmetric indentation on a semi-infinite medium. Sneddon [4] then adopted Boussinesq’s solution to obtain analytical solutions for an indenter of arbitrary profile with the aid of Hankel integral transform techniques. Numerous solutions of smooth and adhesive contact problems based on the classical elasticity have appeared in the literature over the past five decades. It is not the intention of the present paper to review these solutions. Interested readers are referred to review articles by Galin and Gladwell [5] and Borodich [6].

Nowadays, nanoindentation is employed to examine mechanical properties of various material systems and devices such as nanocoatings, nanograined materials, and nanobeam resonators. For nanoscale systems, the effects from the excess energy associated with the surface/interface atoms become important due to their high ratio of surface-to-volume, and the mechanical behavior is then size-dependent [7]. Thus, the surface energy effects, which are normally disregarded in classical problems, must be taken into account in the analysis of nanoscale problems. Several continuum-based models have been proposed to incorporate the surface energy and the size-dependent material behavior such as the couple stress theory [8, 9], the strain gradient elasticity theory [10, 11], and the surface elasticity theory [12, 13]. The theory of surface elasticity by Gurtin and Murdoch [12, 13] has been widely adopted by many researchers to study various continuum mechanics problems where the effects of surface energy are important. These include elastic media under surface loading [14,15,16,17]; contact problems [18,19,20]; ultra-thin films [21,22,23]; and nano-sized cracks [24, 25]. The extensive uses of G-M surface elasticity theory in simulating the surface energy effects of nanoscale/nanostructured objects stem directly from its simplicity and efficiency in the modeling while still yielding sufficient accuracy and similar trend of predicted response in comparison with those from comprehensive discrete-based simulations such as molecular dynamics [26,27,28,29]. Results obtained from these simplified models should at least shed some light or offer preliminary insight on nanoscale-related phenomena when the dimensions of the systems considered are larger than several layers of atoms.

In the context of nanoindentation problems, Zhao [30] presented analytical solutions for a homogeneous elastic half-space under frictionless rigid indentation of various profiles, i.e., conical, cylindrical, and spherical. The numerical results presented in his work show size-dependent behavior, i.e., when the contact area is smaller, the medium becomes stiffer, even though an incomplete Gurtin–Murdoch model was employed in his formulation (no out-of-plane term). Pinyochotiwong et al. [31] then generalized Zhao’s work [30] and included the out-of-plane term to present the axisymmetric response of an elastic half-space under rigid smooth indentation. Recently, Intarit et al. [32] extended the work of Pinyochotiwong et al. [31] for the analysis of an elastic layer bonded to a rigid base under axisymmetric smooth indentation. To the best of the authors’ knowledge, the analysis of indentation problems with the existence of surface energy effects and adhesive contact has not been reported in the literature. Consideration of adhesive contact is important at the nanoscale as the contact is generally not smooth due to inter-atomic interactions and associated surface forces.

The objective of this paper is therefore to investigate the practically useful problem of a nanoscale elastic layer on an elastic substrate that is indented by a cylindrical flat-ended punch under adhesive contact condition. A complete version of the Gurtin–Murdoch’s theory of surface elasticity is used in the analysis of the adhesive indentation problem. In this paper, a mixed boundary-value problem is formulated for the problem under consideration with the displacement boundary conditions in the vertical and radial directions being enforced at the contact region by discretizing it into a series of annular rings. The unknown contact tractions under the punch are then obtained by solving a flexibility equation system constituted from the displacement boundary conditions and a set of displacement influence functions that are derived analytically by applying the Hankel integral transforms. The accuracy of the present solution is confirmed by verifying with simplified cases available in the literature. Numerical results for the elastic field are presented to illustrate the size-dependent response of the nanolayer-substrate system, effects of adhesive contact, and elastic properties of the system.

2 Basic equations

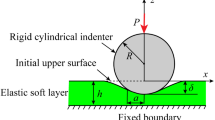
A nanoscale elastic layer h is fully bonded to a semi-infinite elastic substrate of different properties with a cylindrical coordinate system ($r, \theta , z)$ defined as shown in Fig. 1. The layer thickness is denoted by h, and it is indented by a rigid cylindrical flat-ended punch in full adhesive contact. In the absence of body forces, the field equations of the elastic substrate are the same as those in the classical theory of elasticity for axisymmetric deformations [33]. The thickness of the layer is assumed to be less than 100 nm such that the influence of surface/interface energy is important but more than several layers of atoms such that a continuum model is feasible. On the top surface of the nanolayer and the layer-substrate interface, the Young–Laplace equation [34], the stress–strain and the strain–displacement relationships should be considered to account for the surface/interface energies and resulting size-dependent behavior, and they are expressed respectively under axisymmetric response as [12, 13]

$$\begin{aligned}&\frac{\partial \sigma _{rr}^{s} }{\partial r}+\frac{\sigma _{rr}^{s} -\sigma _{\theta \theta }^{s} }{r}+\sigma _{zr} +t_{r}^{0} =0,\,\,\,\,\,\frac{\partial \sigma _{rz}^{s} }{\partial r}+\frac{\sigma _{rz}^{s} }{r}+\sigma _{zz} +t_{z}^{0} =0, \end{aligned}$$

(1)

$$\begin{aligned}&\sigma _{rr}^{s} =\tau ^{s}+\left( {2\mu ^{s}+\lambda ^{s}} \right) \varepsilon _{rr}^{s} +\left( {\lambda ^{s}+\tau ^{s}} \right) \varepsilon _{\theta \theta }^{s} ,\nonumber \\&\sigma _{\theta \theta }^{s} =\tau ^{s}+\left( {2\mu ^{s}+\lambda ^{s}} \right) \varepsilon _{\theta \theta }^{s} +\left( {\lambda ^{s}+\tau ^{s}} \right) \varepsilon _{rr}^{s} ,\,\,\sigma _{rz}^{s} =\tau ^{s}\frac{\text{ d }u_{z}^{s} }{\text{ d }r},\, \end{aligned}$$

(2)

$$\begin{aligned}&\varepsilon _{rr}^{s} =\frac{\text {d}u_{r}^{s}}{\text {d}r},\,\,\,\,\,\varepsilon _{\theta \theta }^{s} =\frac{u_{r}^{s} }{r}. \end{aligned}$$

(3)

In the above equations, the superscript “s” represents the parameters associated with the surface (or interface); $\tau ^{s}$ is the residual surface stress, which is assumed to be constant; $\lambda ^{s}$ and $\mu ^{s}$ are the Lamé constants of the surface; and $t_{r}^{0}$ and $t_{z}^{0}$, respectively, denote the prescribed vertical and radial tractions on the surface. Note that according to Gurtin-Murdoch [12, 13], the surface (or interface) is a zero-thickness layer fully bonded to the corresponding bulk material(s) such that displacement continuity exists at the surface (or interface).

Fig. 1

Indentation of a nanolayer bonded to an elastic substrate by a rigid flat-ended punch of radius a

3 Indentation on a nanolayer-substrate system with adhesive contact

Consider the axisymmetric indentation problem shown in Fig. 1 where the indenter is subjected to a vertical force P. At the nanoscale, the inter-atomic interactions and surface forces make the contact area under the indenter adhesive. On the top surface, normal and shear stresses on the domain outside the contact region (r > a) are zero. The surface inside the contact region ($r \le a)$ has prescribed displacements with the normal displacement equal to the indentation depth, which is represented by $\Delta$ and the radial displacement equal to zero. The quantities with the subscript “1” are associated with the nanolayer and the top surface, whereas those with the subscript “2” correspond to the substrate and the layer-substrate interface. The mixed boundary conditions can be expressed at the top surface as

$$\begin{aligned}&u_{z1} \left( {r,0} \right) =\Delta ;\,\, r\le a, \end{aligned}$$

(4)

$$\begin{aligned}&\sigma _{zz1} \left( {r,0} \right) +\tau _{1}^{s} \left( {\frac{\text {d}^{2}u_{z1} \left( {r,0} \right) }{\text {d}r^{2}}+\frac{1}{r}\frac{{\text {d}}u_{z1} \left( {r,0} \right) }{\text {d}r}} \right) =0; \,\, r>a, \end{aligned}$$

(5)

$$\begin{aligned}&u_{r1} \left( {r,0} \right) =0; \,\, r\le a, \end{aligned}$$

(6)

$$\begin{aligned}&\sigma _{zr1} \left( {r,0} \right) +\kappa _{1}^{s} \left( {\frac{\text {d}^{2}u_{r1} \left( {r,0} \right) }{\text {d}r^{2}}+\frac{1}{r}\frac{\text {d}u_{r1} \left( {r,0} \right) }{\text {d}r}-\frac{u_{r1} \left( {r,0} \right) }{r^{2}}} \right) =0;\,\,\,\,\,\,r>a. \end{aligned}$$

(7)

The continuity conditions at the layer-substrate interface can be expressed as

$$\begin{aligned}&u_{z1} \left( {r,h} \right) -u_{z2} \left( {r,h} \right) =0;\,\, r>0, \end{aligned}$$

(8)

$$\begin{aligned}&u_{r1} \left( {r,h} \right) -u_{r2} \left( {r,h} \right) =0;\,\, r>0, \end{aligned}$$

(9)

$$\begin{aligned}&\sigma _{zz1} \left( {r,h} \right) -\sigma _{zz2} \left( {r,h} \right) +\tau _{2}^{s} \left( {\frac{\text {d}^{2}u_{z2} \left( {r,h} \right) }{\text {d}r^{2}}+\frac{1}{r}\frac{\text {d}u_{z2} \left( {r,h} \right) }{\text {d}r}} \right) =0;\,\, r>0, \end{aligned}$$

(10)

$$\begin{aligned}&\sigma _{zr1} \left( {r,h} \right) -\sigma _{zr2} \left( {r,h} \right) +\kappa _{2}^{s} \left( {\frac{\text {d}^{2}u_{r2} \left( {r,h} \right) }{\text {d}r^{2}}+\frac{1}{r}\frac{\text {d}u_{r2} \left( {r,h} \right) }{\text {d}r}-\frac{u_{r2} \left( {r,h} \right) }{r^{2}}} \right) =0;\,\, r>0 \end{aligned}$$

(11)

where {$\sigma _{zz}, \sigma _{zr}$} and {$u_{r}, u_{z}$} represent the stress and displacement components of the bulk; and $\kappa _{i}^{s} =2\mu _{i}^{s} +\lambda _{i}^{s}$ ($i = 1,2$).

From the superposition method, the vertical and radial surface displacements under the punch can be expressed in terms of the normal contact traction $T_{z}$ and the shear contact traction $T_{r}$ by an integral equation system as shown below,

$$\begin{aligned}&\int _0^a {G_{z}^{Z} \left( {r;{r}'} \right) } \cdot T_{z} \left( {{r}'} \right) \text {d}{r}'+\int _0^a {G_{z}^{R} \left( {r;{r}'} \right) \cdot } \,T_{r} \left( {{r}'} \right) {\text {d}}{r}'=\Delta ; \quad r\le a, \end{aligned}$$

(12)

$$\begin{aligned}&\int _0^a {G_{r}^{Z} \left( {r;{r}'} \right) } \cdot T_{z} \left( {{r}'} \right) {\text {d}}{r}'+\int _0^a {G_{r}^{R} \left( {r;{r}'} \right) } \cdot T_{r} \left( {{r}'} \right) \text {d}{r}'=0; \quad r\le a, \end{aligned}$$

(13)

in which $G_{i}^{j} (r;{r}')$ is defined as Green’s functions, which are radial ($i = r)$ or vertical ($i = z)$ displacement at a distance r due to a unit ring load applied vertically ($j = Z)$ or radially ($j = R)$ with a radius ${r}'$ on the top surface of the nanolayer.

The above Green’s functions are determined from the general solutions to the governing equations derived by applying the Hankel integral transforms and solving the corresponding two-domain boundary value problems. The details are omitted here for brevity, and the final solutions are given below:

$$\begin{aligned}&G_{z}^{k} \left( {\bar{{r}};{\bar{{r}}}'} \right) =-\int _0^\infty {\Lambda _{1} \left( {\bar{{\lambda }}_{1} +1} \right) \left\{ {\zeta A_{k} +\left( {\frac{2}{\bar{{\lambda }}_{1} +1}} \right) B_{k} +\zeta C_{k} -\left( {\frac{2}{\bar{{\lambda }}_{1} +1}} \right) D_{k} } \right\} J_{0} \left( {\zeta \bar{{r}}} \right) \zeta ^{2}\text {d}\zeta } \end{aligned}$$

(14)

$$\begin{aligned}&G_{r}^{k} \left( {\bar{{r}};{\bar{{r}}}'} \right) =\int _0^\infty {\Lambda _{1} \left( {\bar{{\lambda }}_{1} +1} \right) \left\{ {-\zeta A_{k} +B_{k} +\zeta C_{k} +D_{k} } \right\} J_{1} \left( {\zeta \bar{{r}}} \right) \zeta ^{2}{\text {d}}\zeta } \end{aligned}$$

(15)

where $\bar{{r}}=r\text{/ }\Lambda _{1}$; ${\bar{{r}}}'={r}'\text{/ }\Lambda _{1}$; $\bar{{\lambda }}_{1} =\lambda _{1} \text{/ }\mu _{1}$; $\Lambda _{1} =(\kappa _{1}^{s} \text{/ }2\mu _{1} )\left[ {(\lambda _{1} +2\mu _{1} )/(\lambda _{1} +\mu _{1} )} \right]$ is a characteristic length of the nanolayer-substrate system; $\zeta$ is the Hankel transform parameter; and $A_{k}$, $B_{k}$, $C_{k}$, and $D_{k}$ are a set of arbitrary functions corresponding to the surface ring loading with the subscript “k” being used to identify a vertical ($k = Z)$ or radial ($k = R)$ ring load. The expressions of the arbitrary functions $A_{k}$, $B_{k}$, $C_{k}$, and $D_{k}$, for this particular case, are presented explicitly in the “Appendix”.

Equations (12) and (13) are a set of singular integral equations, and their analytical solution does not even exist for the classical elastic case due to the complexity of the associated Green’s functions. Their solution can be tackled by dividing the contact surface in to $N_{e}$ ring elements of equal or varying thickness, and the normalized normal traction $\bar{{T}}_{z} =T_{z} \text{/ }\mu _{1}$ and the normalized shear traction $\bar{{T}}_{r} =T_{r} \text{/ }\mu _{1}$ on the ith annular element occupying the region $r_{i} +\Delta r_{i} /2\le r\le r_{i} -\Delta r_{i} /2$ ($i=1,2,\ldots ,N_{e} )$ are approximated by

$$\begin{aligned} \bar{{T}}_{z} (r)=\bar{{T}}_{z(i)} , \bar{{T}}_{r} (r)=(\bar{{r}}/\bar{{r}}_{i} )\bar{{T}}_{r(i)} \end{aligned}$$

(16)

where $\bar{{r}}_{i} =r_{i} \text{/ }\Lambda _{1}$ and $\Delta \bar{{r}}_{i} =\Delta r_{i} \text{/ }\Lambda _{1}$ are the normalized radial coordinate at the center and the normalized thickness of the ith annular element, respectively, and $\bar{{T}}_{z(i)}$ and $\bar{{T}}_{r(i)}$ represent the values of the unknown normalized normal and shear tractions at the center of the element, respectively. In addition, the existence of the residual surface stress and the jump in the displacement gradient can also induce the concentrated vertical ring load $T_{za}$ and radial ring load $T_{ra}$ along the edge of a flat-ended punch ($r = a)$. To establish a set of conditions sufficient for determining the unknowns $\bar{{T}}_{z(i)}$, $\bar{{T}}_{r(i)}$ for $i=1,2,\ldots ,N_{e}$, $\bar{{T}}_{za} =T_{za} \text{/ }\mu _{1}$, and $\bar{{T}}_{ra} =T_{ra} \text{/ }\mu _{1}$, the approximations given by Eq. (16) are utilized together with collocating the pair of integral Eqs. (12)–(13) at the center of all annular elements and the edge of the punch. The final system of linear algebraic equations takes the following form:

$$\begin{aligned} \left[ {{\begin{array}{*{20}c} {{\mathbf{G}}_{z}^{Z} } &{} \quad {{\mathbf{G}}_{z}^{R} } \\ {{\mathbf{G}}_{r}^{Z} } &{}\quad {{\mathbf{G}}_{r}^{R} } \\ \end{array} }} \right] \left\{ {{\begin{array}{*{20}c} {{\mathbf{T}}_{z} } \\ {{\mathbf{T}}_{r} } \\ \end{array} }} \right\} =\left\{ {{\begin{array}{*{20}c} {{\mathbf{\Delta }}} \\ {{\mathbf{0}}} \\ \end{array} }} \right\} \end{aligned}$$

(17)

where ${\mathbf{T}}_{z} =\{{\begin{array}{*{20}c} {\bar{{T}}_{z(1)} } &{}\quad {\bar{{T}}_{z(2)} } &{}\quad \cdots &{}\quad {\bar{{T}}_{z(N_{e} )} } &{} \quad {\bar{{T}}_{za} } \\ \end{array} }\}^{T}$, ${\mathbf{T}}_{r} =\{{\begin{array}{*{20}c} {\bar{{T}}_{r(1)} } &{}\quad {\bar{{T}}_{r(2)} } &{}\quad \cdots &{}\quad {\bar{{T}}_{r(N_{e} )} } &{}\quad {\bar{{T}}_{ra} } \\ \end{array} }\}^{T}$, ${\mathbf{0}}$ is a null vector, ${{{\varvec{\Delta }} }}=\{{\begin{array}{*{20}c} {\bar{{\Delta }}} &{}\quad {\bar{{\Delta }}} &{}\quad \cdots &{}\quad {\bar{{\Delta }}} &{}\quad {\bar{{\Delta }}} \\ \end{array} }\}^{T}$ with $\bar{{\Delta }}=\Delta \text{/ }\Lambda _{1}$, and the sub-matrices ${\mathbf{G}}_{m}^{k}$, with $k=R,Z$, $m=r,z$ are given by

$$\begin{aligned} {\mathbf{G}}_{m}^{k} =\left[ {{\begin{array}{*{20}c} {\bar{{G}}_{m}^{k} (\bar{{r}}_{1} ;\bar{{r}}_{1} )} &{}\quad \cdots &{}\quad {\bar{{G}}_{m}^{k} (\bar{{r}}_{1} ;\bar{{r}}_{N_{e} } )} &{}\quad {G_{m}^{k} (\bar{{r}}_{1} ;\bar{{a}})} \\ \vdots &{}\quad \ddots &{}\quad \vdots &{}\quad \vdots \\ {\bar{{G}}_{m}^{k} (\bar{{r}}_{N_{e} } ;\bar{{r}}_{1} )} &{}\quad \cdots &{}\quad {\bar{{G}}_{m}^{k} (\bar{{r}}_{N_{e} } ;\bar{{r}}_{N_{e} } )} &{}\quad {G_{m}^{k} (\bar{{r}}_{N_{e} } ;\bar{{a}})} \\ {\bar{{G}}_{m}^{k} (\bar{{a}};\bar{{r}}_{1} )} &{}\quad \cdots &{}\quad {\bar{{G}}_{m}^{k} (\bar{{a}};\bar{{r}}_{N_{e} } )} &{}\quad {G_{m}^{k} (\bar{{a}};\bar{{a}})} \\ \end{array} }} \right] \end{aligned}$$

(18)

with $\bar{{G}}_{m}^{k} (\hat{{r}};\bar{{r}}_{i} )$ for $\hat{{r}}\in \{\bar{{r}}_{1} ,\bar{{r}}_{2} ,\ldots ,\bar{{r}}_{N_{e} } ,\bar{{a}}\}$ being defined by

(19)

It is worth noting that $\bar{{G}}_{m}^{Z} (\hat{{r}};\bar{{r}}_{i} )$ represents the radial ($m = r)$ or vertical ($m = z)$ displacement at a distance $\hat{{r}}$ due to a unit uniformly distributed normal load on the ith annular element, whereas $\bar{{G}}_{m}^{R} (\hat{{r}};\bar{{r}}_{i} )$ represents the radial ($m = r)$ or vertical ($m = z)$ displacement at a distance $\hat{{r}}$ due to a linearly distributed radial load $\bar{{r}}\text{/ }\bar{{r}}_{i}$ on the ith annular element. This physical meaning allows $\bar{{G}}_{m}^{k} (\hat{{r}};\bar{{r}}_{i} )$ to be evaluated without the direct integration of (19). In addition, $\bar{{G}}_{m}^{k} (\hat{{r}};\bar{{r}}_{i} )$ can be computed using the formulas given by Eqs. (14)–(15) with a different set of arbitrary functions $A_{k}$, $B_{k}$, $C_{k}$, and $D_{k}$ shown in the Appendix. When a frictionless contact between the nanolayer and the indenter is considered, the shear traction becomes zero, and the following reduced form of Eq. (16) is then obtained:

$$\begin{aligned} {\mathbf{G}}_{z}^{Z} \cdot {\mathbf{T}}_{z} ={{{\varvec{\Delta }} }}. \end{aligned}$$

(20)

Once the solution for traction vectors is obtained by solving Eq. (17) or (20), the elastic field of the layered system is obtained from the following relationship:

$$\begin{aligned} E(\bar{{r}},\bar{{z}})=\sum \limits _{i=1}^{N_{e} } {\bar{{E}}^{Z}(\bar{{r}};\bar{{r}}_{i} ,\bar{{z}})\cdot \bar{{T}}_{z(i)} } +\sum \limits _{i=1}^{N_{e} } {\bar{{E}}^{R}(\bar{{r}};\bar{{r}}_{i} ,\bar{{z}})\cdot \bar{{T}}_{r(i)} } +E^{Z}(\bar{{r}};\bar{{a}},\bar{{z}})\cdot \bar{{T}}_{za} +E^{R}(\bar{{r}};\bar{{a}},\bar{{z}})\cdot \bar{{T}}_{ra} \end{aligned}$$

(21)

where $E(\bar{{r}},\bar{{z}})$ denotes a component of the elastic field (displacement or stress) at an arbitrary point $(\bar{{r}},\bar{{z}})$ in the nanolayer-substrate system; $\bar{{E}}^{k}(\bar{{r}};\bar{{r}}_{i} ,\bar{{z}})$ for $k=Z,R$ are the influence functions of the chosen components of the elastic field at $(\bar{{r}},\bar{{z}})$ due to the unit uniformly distributed normal load ($k=Z)$ and the linearly distributed radial load $\bar{{r}}\text{/ }\bar{{r}}_{i}$ ($k=R)$ on the ith annular element; $E^{k}(\bar{{r}};\bar{{a}},\bar{{z}})$ for $k=Z,R$ are the influence functions of the chosen components of the elastic field at $(\bar{{r}},\bar{{z}})$ due to the unit normal ring load ($k=Z)$ and the unit radial ring load ($k=R)$ acting at the edge of the indenter. The required influence functions $\bar{{E}}^{k}(\bar{{r}};\bar{{r}}_{i} ,\bar{{z}})$ and $E^{k}(\bar{{r}};\bar{{a}},\bar{{z}})$ for $k=Z,R$ can be directly derived from the same set of constants $A_{k}$, $B_{k}$, $C_{k}$, and $D_{k}$ used for $\bar{{G}}_{m}^{k} (\hat{{r}};\bar{{r}}_{i} )$ and $G_{m}^{k} (\bar{{r}};\bar{{a}})$ following the basic relationships in elasticity [33].

4 Numerical results and discussion

A solution procedure based on the proposed discretization technique is implemented into a computer program to study the adhesive nanoindentation problem shown in Fig. 1. The required influence function, $\bar{{G}}_{m}^{k} (\hat{{r}};\bar{{r}}_{i} )$, is defined as a semi-infinite integral with respect to $\zeta$, and the integrand contains products of Bessel functions. To accurately evaluate these integrals, an adaptive numerical quadrature scheme is employed. This scheme adopts a 21-point Gauss–Kronrod rule to estimate the integral over each subdivided region. The convergence and accuracy of current results are then validated against existing solutions. Consider a classical problem of a homogeneous elastic half-space subjected to a flat-ended punch of radius a with an adhesive contact. Figure 2 shows comparisons between the current solutions with different numbers of annular elements ($N_{e})$ and no surface energy influence and the classical solution provided by Spence [35]. The Lamé constants are equal in both layer and substrate, and they are given as follows: $\lambda = 58.17\,\hbox {GPa}$; $\mu = 26.13\hbox { GPa}$. Note that the material properties of the surface are set to very small values to obtain the classical solution ($\tau _{1}^{s} =\tau _{2}^{s} \approx 0$ and $\kappa _{1}^{s} =\kappa _{2}^{s} \approx 0)$. It is found that radial profiles for both contact tractions and displacements from the present solution agree very closely with the existing solutions [35]. The number of discretized elements of the contact surface affects the accuracy of current solution, and converged results are obtained for $N_{e} \ge$ 50. All numerical results presented hereafter correspond to the case where $N_{e} = 50.$

The comparison of a homogeneous half-space under axisymmetric frictionless flat-ended punch in the presence of surface stresses with the solution obtained by Pinyochotiwong et al. [31] is shown in Fig. 3. In the present solution, the material parameters at the top surface are: $\tau _{1}^{s} = 1\hbox { N/m}$ and $\kappa _{1}^{s} = 6.0991\hbox { N/m}$; and $\tau _{2}^{s} = \kappa _{2}^{s} \approx 0$ at the interface between the layer and the substrate, and the bulk properties of the nanolayer and the substrate are also the same to simulate the case of an elastic half-space considered by Pinyochotiwong et al. [31]. Comparisons of radial variations of contact pressure and vertical displacement at the top surface shown in Fig. 3 indicate very good agreement between the two solutions.

Fig. 2

Comparison of the elastic field of a half-space subjected to an adhesively bonded indenter without the surface energy effects: a normalized contact pressure, and b normalized surface displacements

Fig. 3

Comparison of the elastic field of a half-space under smooth indentation with surface energy effects: a normalized contact pressure, and b normalized surface displacements

Fig. 4

Radial variation of the elastic field for the nanolayers of Al [1 1 1] and Si [1 0 0] with $\bar{h}=\bar{a} = 5$: a normalized contact pressure, and b normalized surface displacements

The indentation of the nanolayer-substrate system is investigated next. The dimensionless quantities employed in the numerical study are given as follows: $\bar{{z}} = z/\Lambda _{\mathrm {1}},\ \bar{{h}} = h/\Lambda _{\mathrm {1}}$ and $\bar{{a}} = a/\Lambda _{\mathrm {1}}$ together with $\textit{Ne} = 50$. Two types of materials, namely aluminum (Al [1 1 1]) and silicon (Si [1 0 0]), are selected for the top layer, whereas iron is chosen for the substrate. The material properties of the surface and the bulk of the layer-substrate system under consideration are obtained from Miller and Shenoy [26] and Shenoy [27], and they are defined as: $\lambda = 58.17\hbox { GPa}$, $\mu = 26.13\hbox { GPa}$, $\tau ^{s} = 1\hbox { N/m}$, $\kappa ^{s} = 6.0991\hbox { N/m}$ for Al [1 1 1]; and $\lambda = 78.08\hbox { GPa}$, $\mu = 40.23\hbox { GPa}$, $\tau ^{s} = 0.6056\hbox { N/m}$, $\kappa ^{s} = 10.0497\hbox { N/m}$ for Si [1 0 0]. In addition, $\lambda = 80\hbox { GPa}$, $\mu = 70\hbox { GPa}$ for iron [13].

Radial profiles of normalized contact pressure are presented in Fig. 4a with $\bar{{a}} = 5,\ \bar{{h}} = 5$, and $\Lambda _{1} = 0.15288\hbox { nm}$ (i.e. Al [1 1 1]). In addition, Fig. 4b shows radial variations of normalized surface displacements. In Figs. 4, 5, and 6, the dash lines correspond to the classical elasticity solutions without surface energy influence and size effects (i.e. $\tau ^{\mathrm {s}} = \kappa ^{\mathrm {s}} \approx$ 0). Numerical results presented in Fig. 4 show similar trends in radial profiles of both contact tractions and displacements from the current and the classical solutions, and the tractions (both normal and shear) from both solutions show singular behavior in the vicinity of the punch edge. As shown in the previous Section, the vertical and radial ring loads are applied along the indenter edge at $r = a$ in the present solution due to the existence of the residual surface stress. The applied load P is actually supported by both normal traction under the punch and the vertical ring loading As a result, normalized vertical displacements beyond the contact zone from the current scheme are larger than their classical counterparts as larger vertical load is needed to reach the same level of penetration as shown in Fig. 4b.

Fig. 5

Radial variation of the elastic field at various depths of the layer-substrate system with $\bar{h} = \bar{a} = 5$: a normalized displacements, and b normalized stresses

Fig. 6

Variation of the normalized indentation forces with layer thickness $\bar{h}$ for different radii of punch $\bar{a}$

Figure 5a displays radial profiles of normalized displacements of the layer-substrate system, while variations of normalized stresses in the radial direction are shown in Fig. 5b. Numerical results in both figures are shown at various depths for a cylindrical punch with normalized radius $\bar{{a}} = 5$ and a nanolayer with normalized thickness $\bar{{h}} = 5$. Note that Al [1 1 1] is chosen as the nanolayer material for the numerical solutions in Fig. 5. The solutions for elastic fields obtained from the current study and the classical elasticity shown in Fig. 5 display similar trends. Figure 5a reveals that larger normalized displacements (both vertical and radial) at various depths in the layer-substrate system are observed in the current study when compared to those obtained from the classical elasticity solutions. Numerical solutions shown in Fig. 5b for normalized shear and vertical stresses at various depths indicate a reduction in stresses within the contact zone due to the existence of surface stresses, whereas an increase in stresses is noted outside the contact area. It is also observed that the surface energy has a stronger influence on the elastic field at locations closer to the indenter, and its influence becomes trivial for r/a > 2.5.

Normalized indentation force, denoted by $P/P_{\mathrm {c}}$, applied on the layer-substrate system is plotted against the normalized layer thickness $\bar{{h}}$ of Al [1 1 1] in Fig. 6 for different normalized contact radii $\bar{{a}}$ to illustrate the size-dependent behavior of the nanolayer-substrate system due to the existence of surface energy effects. Note that $P_{\mathrm {c}}$ denotes the classical solution for a rigid punch under adhesive contact on a homogeneous half-space with the properties of Al [1 1 1] (i.e., $\lambda = 58.17\hbox { GPa}$, $\mu = 26.13\hbox { GPa}$, and $\tau ^{s} = \kappa ^{s}\approx$ 0). In Fig. 6, the dash lines once again represent the corresponding classical elasticity solutions with adhesive contact ($\tau ^{s} = \kappa ^{s}\approx 0$), whereas the dash double-dotted lines denote normalized indentation forces under smooth (frictionless) contact with surface energy. Numerical results shown in Fig. 6 reveal that under both frictionless and adhesive contacts normalized indentation forces with the presence of surface energy significantly depend on the nanolayer thickness and the radius of the punch. For the same radius of the cylindrical punch, the indentation force under the adhesive interface is higher than the frictionless indentation force. It is also noted from Fig. 6 that the force increases when the nanolayer thickness ($\bar{{h}})$ is reduced. This is due to the fact that the nanolayer (aluminum) is softer than the substrate (iron), and the layer-substrate system then becomes stiffer with a reduction in $\bar{{h}}$. It is clearly seen that the contribution from the surface energy decreases when the normalized contact radius $\bar{{a}}$ increases, and the current solution approaches the classical counterpart. Thus, the size-dependent behavior of the nanolayer-substrate system is clearly demonstrated in Fig. 6.

5 Conclusions

Axisymmetric indentation of a nanolayer fully bonded to an elastic substrate by a flat-ended rigid cylindrical indenter under adhesive contact is examined based on the Gurtin-Murdoch continuum theory and establishing a flexibility equation for the unknown contact tractions. It is shown that the current solution algorithm is numerically efficient and accurate. Numerical results indicate that the surface energy effects associated with the nanolayer make the layered system stiffer, and the elastic field is size-dependent. The size-dependent behavior under the surface stress effects diminishes with an increase in the radius of the cylindrical punch, and the current result ultimately approaches the classical one.

Appendix

The arbitrary functions $A_{k}$, $B_{k}$, $C_{k}$, and $D_{k}$ (with $k=Z,R)$ for arbitrarily distributed, normal load $p=p(r)$ and radial load $q=q(r)$ on the top surface are given by

$$\begin{aligned}&\left\{ {{\begin{array}{*{20}c} {\zeta A_{Z} } \\ {B_{Z} } \\ {\zeta C_{Z} } \\ {D_{Z} } \\ \end{array} }} \right\} =-\frac{\bar{{P}}(\zeta )}{2\zeta ^{2}\vert c_{ij} \vert }\left\{ {{\begin{array}{*{20}c} {c_{22} \left( {c_{33} c_{44} -c_{34} c_{43} } \right) +c_{23} \left( {c_{34} c_{42} -c_{32} c_{44} } \right) +c_{24} \left( {c_{32} c_{43} -c_{33} c_{42} } \right) } \\ {c_{21} \left( {c_{34} c_{43} -c_{33} c_{44} } \right) +c_{23} \left( {c_{31} c_{44} -c_{34} c_{41} } \right) +c_{24} \left( {c_{33} c_{41} -c_{31} c_{43} } \right) } \\ {c_{21} \left( {c_{32} c_{44} -c_{34} c_{42} } \right) +c_{22} \left( {c_{34} c_{41} -c_{31} c_{44} } \right) +c_{24} \left( {c_{31} c_{42} -c_{32} c_{41} } \right) } \\ {c_{21} \left( {c_{33} c_{42} -c_{32} c_{43} } \right) +c_{22} \left( {c_{31} c_{43} -c_{33} c_{41} } \right) +c_{23} \left( {c_{32} c_{41} -c_{31} c_{42} } \right) } \\ \end{array} }} \right\} , \qquad \quad \end{aligned}$$

(A.1)

$$\begin{aligned}&\left\{ {{\begin{array}{*{20}c} {\zeta A_{R} } \\ {B_{R} } \\ {\zeta C_{R} } \\ {D_{R} } \\ \end{array} }} \right\} =-\frac{\bar{{Q}}(\zeta )}{2\zeta ^{2}\vert c_{ij} \vert }\left\{ {{\begin{array}{*{20}c} {c_{12} \left( {c_{34} c_{43} -c_{33} c_{44} } \right) +c_{13} \left( {c_{32} c_{44} -c_{34} c_{42} } \right) +c_{14} \left( {c_{33} c_{42} -c_{32} c_{43} } \right) } \\ {c_{11} \left( {c_{33} c_{44} -c_{34} c_{43} } \right) +c_{13} \left( {c_{34} c_{41} -c_{31} c_{44} } \right) +c_{14} \left( {c_{31} c_{43} -c_{33} c_{41} } \right) } \\ {c_{11} \left( {c_{34} c_{42} -c_{32} c_{44} } \right) +c_{12} \left( {c_{31} c_{44} -c_{34} c_{41} } \right) +c_{14} \left( {c_{32} c_{41} -c_{31} c_{42} } \right) } \\ {c_{11} \left( {c_{32} c_{43} -c_{33} c_{42} } \right) +c_{12} \left( {c_{33} c_{41} -c_{31} c_{43} } \right) +c_{13} \left( {c_{31} c_{42} -c_{32} c_{41} } \right) } \\ \end{array} }} \right\} \qquad \quad \end{aligned}$$

(A.2)

where $\bar{{P}}(\zeta )$, $\bar{{Q}}(\zeta )$, $\vert c_{ij} \vert$, and $c_{ij} ,i,j\in \{1,2,3,4\}$ are defined by

$$\begin{aligned} \bar{{P}}(\zeta )= & {} \int \limits _0^\infty {\bar{{p}}(\bar{{r}})J_{0} (\zeta \bar{{r}})\bar{{r}}\text {d}\bar{{r}}}, \end{aligned}$$

(A.3)

$$\begin{aligned} \bar{{Q}}(\zeta )= & {} \int \limits _0^\infty {\bar{{q}}(\bar{{r}})J_{1} (\zeta \bar{{r}})\bar{{r}}{\text {d}}\bar{{r}}}, \end{aligned}$$

(A.4)

$$\begin{aligned} \left| {c_{ij} } \right|= & {} \left| {{\begin{array}{c@{\quad }c@{\quad }c@{\quad }c} {c_{11} } &{} {c_{12} } &{} {c_{13} } &{} {c_{14} } \\ {c_{21} } &{} {c_{22} } &{} {c_{23} } &{} {c_{24} } \\ {c_{31} } &{} {c_{32} } &{} {c_{33} } &{} {c_{34} } \\ {c_{41} } &{} {c_{42} } &{} {c_{43} } &{} {c_{44} } \\ \end{array} }} \right| , \end{aligned}$$

(A.5)

$$\begin{aligned} c_{11}= & {} \frac{\lambda _{1}^{\prime }}{2}\left( {2+\bar{{\zeta }}\bar{{\tau }}_{1}^{s} } \right) ;\,\,c_{12} =1+\bar{{\zeta }}\bar{{\tau }}_{1}^{s} ;\,\,c_{13} =\frac{\lambda _{1}^{\prime }}{2}\left( {\bar{{\zeta }}\bar{{\tau }}_{1}^{s} -2} \right) ;\,\,c_{14} =1-\bar{{\zeta }}\bar{{\tau }}_{1}^{s}, \end{aligned}$$

(A.6)

$$\begin{aligned} c_{21}= & {} \frac{\lambda _{1}^{\prime }}{2}\left( {2+\bar{{\zeta }}\bar{{\kappa }}_{1}^{s} } \right) ;\,\,c_{22} =1-c_{21} ;\,\,c_{23} =\frac{\lambda _{1}^{\prime }}{2}\left( {2-\bar{{\zeta }}\bar{{\kappa }}_{1}^{s} } \right) ;\,\,c_{24} =c_{23} -1, \end{aligned}$$

(A.7)

$$\begin{aligned} c_{31}= & {} \frac{e^{-2\bar{{\zeta }}\bar{{h}}}\lambda _{1}^{\prime }}{2}\left( {2-2\bar{{\mu }}_{2} +\bar{{\zeta }}\bar{{\tau }}_{2}^{s} } \right) , \end{aligned}$$

(A.8)

$$\begin{aligned} c_{32}= & {} {} \frac{e^{-2\bar{{\zeta }}\bar{{h}}}}{2}\left\{ {\bar{{\mu }}_{2} ^{2}\left( {\frac{2\lambda _{1}^{\prime }+4}{\lambda _{2}^{\prime }+2\bar{{\mu }}_{2} }} \right) +\left[ {\left( {\lambda _{1}^{\prime }\bar{{\zeta }}\bar{{h}}+2} \right) \left( {\bar{{\zeta }}\bar{{\tau }}_{2}^{s} -2\bar{{\mu }}_{2} } \right) +\left( {2\lambda _{1}^{\prime }\bar{{\zeta }}\bar{{h}}+2} \right) } \right] } \right\} , \end{aligned}$$

(A.9)

$$\begin{aligned} c_{33}= & {} -\frac{\lambda _{1}^{\prime }}{2}\left( {2+\frac{2\lambda _{2} ^{\prime }\bar{{\mu }}_{2} }{\lambda _{2}^{\prime }+2\bar{{\mu }}_{2} }-\bar{{\zeta }}\bar{{\tau }}_{2}^{s} } \right) , \end{aligned}$$

(A.10)

$$\begin{aligned} c_{34}= & {} {} \left( {1-\lambda _{1}^{\prime }\bar{{\zeta }}\bar{{h}}} \right) +\frac{\bar{{\zeta }}\bar{{\tau }}_{2}^{s} }{2}\left( {\lambda _{1} ^{\prime }\bar{{\zeta }}\bar{{h}}-2} \right) +\bar{{\mu }}_{2} \left[ {\left( {2-\lambda _{1}^{\prime }\bar{{\zeta }}\bar{{h}}} \right) +\bar{{\mu }}_{2} \left( {\frac{\lambda _{1}^{\prime }\left( {1+2\bar{{\zeta }}\bar{{h}}} \right) -2}{\lambda _{2}^{\prime }+2\bar{{\mu }}_{2} }} \right) } \right] , \end{aligned}$$

(A.11)

$$\begin{aligned} c_{41}= & {} \frac{e^{-2\bar{{h}}\bar{{\zeta }}}\lambda _{1}^{\prime }}{2}\left( {2-2\bar{{\mu }}_{2} +\bar{{\zeta }}\bar{{\kappa }}_{2}^{s} } \right) , \end{aligned}$$

(A.12)

$$\begin{aligned} c_{42}= & {} {} \frac{e^{-2\bar{{h}}\bar{{\xi }}}}{2}\left\{ {\left[ {2+\lambda _{1} ^{\prime }\left( {2-2\bar{{\mu }}_{2} +\bar{{\zeta }}\bar{{\kappa }}_{2}^{s} } \right) \left( {\bar{{\zeta }}\bar{{h}}-1} \right) } \right] -\bar{{\mu }}_{2}^{2}\frac{2\lambda _{1}^{\prime }+4}{\lambda _{2}^{\prime }+2\bar{{\mu }}_{2} }} \right\} , \end{aligned}$$

(A.13)

$$\begin{aligned} c_{43}= & {} \frac{\lambda _{1}^{\prime }}{2}\left( {2-\bar{{\zeta }}\bar{{\kappa }}_{2}^{s} +\frac{2\lambda _{2}^{\prime }\bar{{\mu }}_{2} }{\lambda _{2}^{\prime }+2\bar{{\mu }}_{2} }} \right) , \end{aligned}$$

(A.14)

$$\begin{aligned} c_{44}= & {} \frac{\lambda _{1}^{\prime }}{2}\left( {2+2\bar{{\mu }}_{2} -\bar{{\zeta }}\bar{{\kappa }}_{2}^{s} } \right) \left( {1+\bar{{\zeta }}\bar{{h}}} \right) +\bar{{\mu }}_{2}^{2}\left( {\frac{2-\lambda _{1} ^{\prime }\left( {1+2\bar{{\zeta }}\bar{{h}}} \right) }{\lambda _{2}^{\prime }+2\bar{{\mu }}_{2} }} \right) -1 \end{aligned}$$

(A.15)

with $\bar{{p}}=p\text{/ }\mu _{1}$; $\bar{{q}}=q\text{/ }\mu _{1}$; $\lambda _{1}^{\prime }=\bar{{\lambda }}_{1} +1$; $\lambda _{2}^{\prime }=\bar{{\lambda }}_{2} +\bar{{\mu }}_{2}$; $\bar{{\lambda }}_{2} ={\lambda _{2} } / {\mu _{1} }$; $\bar{{\mu }}_{2} ={\mu _{2} } / {\mu _{1} }$; $\bar{{\tau }}_{i}^{s} ={\tau _{i}^{s} } / {\mu _{1} \Lambda _{1} }$; and $\bar{{\kappa }}_{i}^{s} ={\kappa _{i}^{s} } / {\mu _{1} \Lambda _{1} }$ (for $i=1,2)$.

For a unit normalized normal ring load $\bar{{p}}(\bar{{r}})=\delta (\bar{{r}}-{\bar{{r}}}')$ and a unit normalized radial ring load $\bar{{q}}(\bar{{r}})=\delta (\bar{{r}}-{\bar{{r}}}')$, $\bar{{P}}(\zeta )$, $\bar{{Q}}(\zeta )$ become

$$\begin{aligned} \bar{{P}}(\zeta )={\bar{{r}}}'J_{0} (\zeta {\bar{{r}}}'), \end{aligned}$$

(A.16)

$$\begin{aligned} \bar{{Q}}(\zeta )={\bar{{r}}}'J_{1} (\zeta {\bar{{r}}}'). \end{aligned}$$

(A.17)

For a unit uniformly distributed, normalized normal load $\bar{{p}}(\bar{{r}})=1$ acting on the $i^{th}$ annular element $\bar{{r}}\in [\bar{{r}}_{i} -\Delta \bar{{r}}_{i} /2,\bar{{r}}_{i} +\Delta \bar{{r}}_{i} /2]$, $\bar{{P}}(\zeta )$ becomes

$$\begin{aligned} \bar{{P}}\left( \zeta \right) =\left. {\frac{\bar{{r}}J_{1} \left( {\zeta \bar{{r}}} \right) }{\zeta }} \right| _{\bar{{r}}=\bar{{r}}_{i} +{\Delta \bar{{r}}_{i} } / 2} -\left. {\frac{\bar{{r}}J_{1} \left( {\zeta \bar{{r}}} \right) }{\zeta }} \right| _{\bar{{r}}=\bar{{r}}_{i} -{\Delta \bar{{r}}_{i} } / 2} \end{aligned}$$

(A.18)

where $\bar{{r}}_{i} =r_{i} \text{/ }\Lambda _{1}$ and $\Delta \bar{{r}}_{i}$ are the normalized radial coordinate at the center and normalized thickness of the annular element, respectively. For a linearly distributed, normalized radial load $q(\bar{{r}})=\bar{{r}}/\bar{{r}}_{i}$ on the $i^{th}$ annular element $\bar{{r}}\in [\bar{{r}}_{i} -\Delta \bar{{r}}_{i} /2,\bar{{r}}_{i} +\Delta \bar{{r}}_{i} /2]$, $\bar{{Q}}(\zeta )$ then becomes

$$\begin{aligned} \bar{{Q}}\left( \zeta \right) =\left. {\left( {\frac{2\bar{{r}}}{\zeta ^{2}\bar{{r}}_{i} }J_{1} \left( {\zeta \bar{{r}}} \right) -\frac{\bar{{r}}^{2}}{\zeta \bar{{r}}_{i} }J_{0} \left( {\zeta \bar{{r}}} \right) } \right) } \right| _{\bar{{r}}=\bar{{r}}_{i} +{\Delta \bar{{r}}_{i} } / 2} -\left. {\left( {\frac{2\bar{{r}}}{\zeta ^{2}\bar{{r}}_{i} }J_{1} \left( {\zeta \bar{{r}}} \right) -\frac{\bar{{r}}^{2}}{\zeta \bar{{r}}_{i} }J_{0} \left( {\zeta \bar{{r}}} \right) } \right) } \right| _{\bar{{r}}=\bar{{r}}_{i} -{\Delta \bar{{r}}_{i} } / 2}. \end{aligned}$$

(A.19)