On the sliding frictional nanocontact of an exponentially graded layer/substrate structure

Abstract

This paper analyzes the sliding frictional nanocontact of an exponentially graded layer perfectly bonded to a homogeneous half-plane substrate under the nanoindentation of a rigid cylinder. The punch is subjected to both normal and tangential loads, satisfying Coulomb’s friction law. The contact interface is modeled by the full version of Steigmann–Ogden surface mechanical theory, in which surface tension, surface membrane stiffness and surface flexural rigidity are all taken into account. The method of Fourier integral transforms was applied to convert the governing equations and nonclassical boundary conditions into a Fredholm integral equation. By separating a nonsingular term from the integrand of the kernel function of the integral equation, numerical integration of the kernel function can be significantly improved. After that, Gauss–Chebyshev numerical quadratures are further employed to discretize and collocate the integral equation and the indentation force equilibrium condition. An iterative algorithm is subsequently developed to solve the resultant nonlinear algebraic system regarding discretized contact pressures and the two asymmetric contact boundaries. Stresses and displacements in the layer/substrate structure are also determined for completeness. Extensive parametric studies clarify the relative importance among three surface parameters, all helping to partially carry on the indentation loading in addition to the conventional bulk portion of the layer/substrate system. The sliding frictional condition significantly affects the symmetry of the contact pressure distribution and contact zone. The property gradation of the layer is another important factor affecting contact properties. The results reported in the current work show a concrete means of tailoring nanocontact responses of graded layers in nanosized materials and devices.

1 Introduction

Graded materials are a class of composites that contain two or more constituent phases. The mechanical properties of a graded material may vary continuously along one or more dimensions, in order to achieve desired functionalities. Graded materials have found their applications in metals, ceramics and organic composites, for the purpose of improving the thermal, wear and corrosion prevention capabilities (Schulz et al. 2003; Zhou et al. 2021; Argatov and Chai 2022). Suresh (2001) reported that, with a suitable spatial variation of elastic modulus, a graded layer can provide effective resistance to deformations and damages under the condition of spherical or conical indentations.

Benefitting from their continuous gradation of mechanical properties, numerous studies have been conducted to study the contact properties of graded materials. We start the literature review from the frictional contact of graded half-planes and half-spaces. Elloumi et al. (2010) explored the partial slip contact of a graded half-plane under the indentation of a rigid stamp. Dag et al. (2013) investigated the sliding frictional contact of a laterally graded substrate indented by a rigid punch with an arbitrary profile. Both semianalytical and finite element solutions were provided for the contact pressure and contact boundaries. For a graded orthotropic half-plane, Kucuksucu et al. (2015) and Guler et al. (2017) solved the frictional contact problem under the indentation of a rigid flat-ended and cylindric punch, respectively. Chen et al. (2015) further analyzed the contact problem between a rigid roller and a graded half-plane with an arbitrary gradient direction. In addition to single-direction gradation, Arslan (2020) examined the sliding frictional contact of a bidirectionally graded half-plane.

The above literature papers treat the whole half-plane or half-space as a graded medium. Engineering practice prefers to applying graded materials as a layer or a transitional medium. Guler and Erdogan (2007) investigated the sliding frictional contact of a graded layer bonded to a homogeneous half-plane. The effects of layer property gradation, frictional coefficient and geometry were analyzed in detail. Yang and Ke (2008) studied the contact properties of a graded transitional layer that is sandwiched between a homogeneous layer and a homogeneous substrate. The contact pressure and contact size were solved for the case of a rigid cylinder. Taking the frictional heat into account, Choi and Paulino (2008) reanalyzed the same contact problem by the use of the steady-state plane thermoelasticity theory. Jobin et al. (2017) developed a semianalytical solution for an inhomogeneously coated half-plane under the indentation of rigid stamps. The graded layer was discretized into multiple homogeneous sublayers. Such a multilayered discretization strategy works particularly well for graded layers with an arbitrary property gradation. Attia and El-Shafei (2019) developed finite element solutions to the nonlinear contact problem of graded layered materials. Arslan and Dag (2018) investigated the sliding frictional contact of an orthotropic layer/substrate structure. The dynamic frictional contact problems of a graded layer subjected to a moving cylinder (Balci and Dag 2019) or an angular-ended indenter (Balci and Dag 2020) have also been solved. In addition to the sliding frictional condition, the rolling contact between a graded layer and a rolling cylinder under the simultaneous applications of normal and tangential forces has also been considered (Alinia et al. 2014).

The frictional contact problems reviewed above were all studied with the classical theory of elasticity. The solutions are valid for regular scale contact models. However, as the indenter size in those contact models approaches to microscale, the contact zone will fall into the nanoscale. Under such a small length scale, surface effects enter into the mechanics and physics of contact problems. Numerous theoretical and experimental results have shown that surface effects have an evident impact on the mechanical properties of nanosized materials and structures (Cammarata 1994; Zhang et al. 2008; Rahman et al. 2016; Wang 2019). The very high surface-to-volume ratio in these materials and structures is responsible for surface effects. Gurtin and Murdoch (1975, 1978) proposed the first surface mechanical theory for solid materials. In this theory, a solid surface is treated as an elastic membrane possessing zero thickness and perfectly bonded to its abutting bulk solid. In addition to surface tension, the resistibility of a solid surface to in-plane stretching and shear deformations is also accommodated. For this reason, Gurtin–Murdoch surface mechanical theory is able to reflect the size-dependent feature of nanoscale materials and structures to a certain extent (Shenoy 2002; Mi et al. 2008).

In contact mechanics, Gurtin–Murdoch surface theory and its variants were first employed to analyze the nanocontact properties of homogeneous layers, half-planes and half-spaces subjected to traction loads. Zhao and Rajapakse (2009) determined the displacements and stresses in a two-dimensional homogeneous elastic layer bonded to a rigid substrate under the application of localized normal and tangential traction forces. Zhao and Rajapakse (2013) further considered a three-dimensional homogeneous layer subjected to localized tangential traction loads. The asymmetric displacements and stresses were determined. Zhou and Gao (2013) developed analytical solutions for homogeneous half-planes and half-spaces subjected to a distributive normal pressure. Mi (2017) investigated the asymmetric problem of a homogeneous half-space under the application of localized tangential tractions. Different from the conventional isotropic assumption, Shen (2019) restudied Boussinesq problem for a transversely isotropic half-space incorporating surface effects. Moradweysi et al. (2019) solved the contact problem of a homogeneous half-space by the coupling of strain gradient and surface theories. Le et al. (2021) analyzed the elastic response of a homogeneous half-plane under the application of normal, shear and couple tractions. The coupling effects of couple stress and Gurtin–Murdoch surface elasticity were studied.

The nanocontact properties of elastic layers, half-planes and half-spaces under the indentation of rigid stamps have also been studied with the account of surface effects. Due to the additional complexity introduced by mixed boundary conditions, this line of research is primarily concerned with frictionless contact problems. Argatov and Sabina (2012) addressed the spherical indentation of a transversely isotropic half-space reinforced by an extensible membrane. Pinyochotiwong et al. (2013) solved the nanocontact problem between an elastic half-space and a rigid indenter. Besides the conventional semianalytical approach, Gad et al. (2014) developed a finite element formulation to numerically analyze the nanocontact properties of a two-dimensional elastic strip. Tirapat et al. (2020) solved the nanoscale adhesive contact problem of a homogeneous elastic layer possessing a Gurtin–Murdoch type boundary that is indented by a flat-ended cylinder. Assuming an inner adhesion zone and an outer finite friction zone, Intarit et al. (2020) reconsidered the nanocontact model.

The nanocontact problems reviewed above neglected the resistibility of a solid surface to flexural deformations, since the solid surface is modeled as an elastic membrane without any bending rigidities (Ban and Mi 2021). By the use of molecular dynamics simulations, Chhapadia et al. (2011) clarified the bending deformation of the lateral surfaces of a cantilevered nanowire. They quantitatively evaluated its surface thickness. Their results explained the appreciably larger elastic modulus of a nanowire under bending than under extension. In fact, longer than two decades ago, Steigmann and Ogden (1997, 1999) have extended the Gurtin–Murdoch surface theory, in order to additionally take the surface bending rigidity into consideration. However, until the recent five years, the improved Steigmann–Ogden surface mechanical has received sufficient attentions (Walton and Zemlyanova 2016; Zemlyanova and Mogilevskaya 2018; Zemlyanova 2018, 2019; Mi 2018; Li and Mi 2019a, b, 2021).

As to the nanocontact mechanics of graded materials, much fewer works can be found in the open literature. Attia and Mahmoud (2015) proposed a finite element scheme for the frictionless nanoindentation of an elastic substrate reinforced with a power-law graded layer due to rigid or deformable indenters. The complete version of Gurtin–Murdoch surface theory was employed to address the surface effects. Vasu and Bhandakkar (2018) solved the nanocontact problem of an exponentially graded half-plane, reinforced with a Gurtin–Murdoch type boundary. Zhang et al. (2018) explored the frictionless nanocontact responses of a graded layer, by using the surface model proposed by Chen and Yao (2014). Zhu et al. (2019) considered a linearly graded half-plane subjected to uniform surface tractions. Surface tension was incorporated, in order to account for the graded half-plane boundary effects. Ban and Mi (2022) analyzed the competing mechanism between adhesive and surface effects on the determination of the nanocontact behavior of a graded layer/substrate structure.

This work aims at exploring the sliding frictional nanocontact properties of an exponentially graded layer/substrate structure. The exponential variation of the graded coating’s shear modulus is not just a mathematical assumption. Existing technology can already synthesize such graded coatings for structural components in order to guard against contact deformation and damage (Giannakopoulos and Suresh 1997). The major originality lies in two aspects. First, the full Steigmann–Ogden surface theory including surface tension, membrane stiffness and flexural rigidity is accounted for. Second, the effects of sliding friction are first considered in the nanocontact mechanics of graded materials. The proposed two-dimensional nanocontact model may be viewed as a plane-strain approximation to the sliding nanoindentation between a rigid microsized cylinder and a three-dimensional coating-substrate structure. The model may also be used as the plane-stress approximation for the engagement between two microsized gears. The remainder of this paper is structured as follows. Section 2 presents the theoretical formulation of the proposed nanocontact problem, leading to a governing Fredholm integral equation. In Sect. 3, the convergence of the infinite integrals inherent to the Fredholm integral equation is analyzed in detail. Along with the indentation force equilibrium equation, a numerical solution algorithm to the governing integral equation is outlined in Sect. 4. Section 5 first validates our method and algorithm against available literature data, followed by extensive parametric studies about surface parameters, frictional coefficient and layer property gradation. Finally, in Sect. 6, a few major conclusions of this work are drawn.

2 Formulation of dual integral equations

2.1 Problem statement

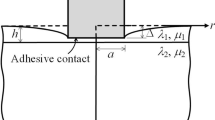
We consider the sliding frictional contact between a rigid cylinder and an exponentially graded layer perfectly bonded to a homogeneous half-place plane, as shown in Fig. 1. The graded layer has the finite thickness of h. The rigid cylinder has the radius R and is under the application of both normal (P) and tangential (Q) forces. They satisfy Coulomb’s law of friction, i.e., $Q = \eta P$. As a result, the sliding frictional condition is assumed in this work. Due to the presence of friction, the left ($x=-a$) and the right ($x=b$) contact boundaries are not symmetric about the symmetry axis (z) of the rigid cylinder. This is in contrast with frictionless contact.

Fig. 1

Geometry and loading configuration of the sliding frictional nanoindentation between a rigid cylinder and an exponentially graded layer perfectly bonded to a homogeneous half-plane substrate

The shear modulus of the graded layer is assumed to vary as an exponential function of the thickness coordinate

$$\begin{aligned} \mu \left( z \right) ={{\mu }_{1}}{{e}^{\beta z}}, \quad 0\le z\le h, \end{aligned}$$

(1)

where $\beta$ is a parameter that characterizes the property gradation along the layer thickness and $\mu _1$ represents the shear modulus of the graded layer at its upper surface ($z=0$). Since the half-plane substrate is homogeneous, its shear modulus is taken as the constant $\mu _2$. For simplicity, Poisson’s ratios of the layer and the substrate are taken as equal, denoted by Kolosov’s constant $\kappa$ in the subsequent formulation and solution procedure. Under plane strain condition, $\kappa =3-4\nu$. Across the layer/substrate interface, the shear modulus is treated as continuous

$$\begin{aligned} {{\mu }_{2}}={{\mu }_{1}}{{e}^{\beta h}}. \end{aligned}$$

(2)

The gradient index of the layer can therefore be given by

$$\begin{aligned} \beta h = \ln \Gamma , \end{aligned}$$

(3)

where $\Gamma =\mu _2/\mu _1$ denotes the shear moduli ratio between the substrate and the upper surface of the graded layer. Given the geometric model and loading conditions of the nanocontact problem, the fundamental unknowns are identified as the contact pressure and both contact boundaries. Only after they are determined, the elastic fields in the graded layer and the half-plane may be further evaluated.

2.2 Dual integral equations

Under nanoindentation, the contact interface is modeled by the Steigmann–Ogden surface theory (Steigmann and Ogden 1997, 1999; Zemlyanova and Mogilevskaya 2018). Different material properties than those of the abutting layer bulk need to be allocated. They are composed of the surface tension ($\tau _0$), membrane (tensile) stiffness ($k_0$) and flexural rigidity ($d_0$). Steigmann–Ogden surface theory treats a solid surface or interface as a thin plate, possessing surface tension, membrane stiffness and flexural rigidity. This theory functions through the modified boundary condition

$$\begin{aligned} \mathbf{{n}} \cdot {\varvec{\sigma }} = {\nabla _\mathrm{{S}}} \cdot {\varvec{\Sigma }} + ({\nabla _\mathrm{{S}}} \cdot \mathbf{{M}})\mathbf{{n}} - ({\nabla _\mathrm{{S}}} \cdot \mathbf{{n}})\mathbf{{n}} \cdot ({\nabla _\mathrm{{S}}} \cdot \mathbf{{M}})\mathbf{{n}} + {\mathbf{{T}}^{(\mathbf{{n}})}}, \end{aligned}$$

(4)

where $\mathbf{{n}}$ is the surface normal vector, ${\varvec{\sigma }}$ the Cauchy stress, ${\nabla }_\mathrm{{S}}$ the surface gradient operator, $\mathbf {\Sigma }$ the surface stress, $\textbf{M}$ the surface bending moment, and ${\mathbf{{T}}^{(\mathbf{{n}})}}$ the traction load.

For the contact interface ($z=0$) shown in Fig. 1, the nonclassical boundary condition (4) can be materialized (Li and Mi 2019b)

$$\begin{aligned}{} & {} {\sigma _{zx}} + q(x) + {k_0}\frac{{{\partial ^2}{u_1(x,0)}}}{{\partial {x^2}}} = 0, \end{aligned}$$

(5a)

$$\begin{aligned}{} & {} {\sigma _{zz}} + p(x) + {\tau _0}\frac{{{\partial ^2}{w_1(x,0)}}}{{\partial {x^2}}} - {d_0}\frac{{{\partial ^4}{w_1(x,0)}}}{{\partial {x^4}}} = 0, \end{aligned}$$

(5b)

where $q_x=\eta p(x)$ and p(x) are the tangential and normal contact pressures, and $u_1(x,0)$ and $w_1(x,0)$ denote the tangential and normal displacements on the layer upper surface.

Along the graded layer/substrate interface, perfect bonding condition leads to continuous tractions and displacements

$$\begin{aligned}{} & {} {\sigma _{zz2}}(x,h) = {\sigma _{zz1}}(x,h), \end{aligned}$$

(6a)

$$\begin{aligned}{} & {} {\sigma _{xz2}}(x,h) = {\sigma _{xz1}}(x,h), \end{aligned}$$

(6b)

$$\begin{aligned}{} & {} {u_2}(x,h) = {u_1}(x,h), \end{aligned}$$

(6c)

$$\begin{aligned}{} & {} {w_2}(x,h) = {w_1}(x,h). \end{aligned}$$

(6d)

In Fourier space, the general solution of displacements and stresses in an exponentially graded layer has been derived by Yan and Mi (2017), in terms of four unknown functions ($B_1$–$B_4$) of Fourier transform variable ($\xi$). The elastic fields in a positive half-plane was also given in terms of two unknown function ($A_5$ and $A_6$). The boundary conditions (5a, 5b) and (6a–d) provide six equations for determining these six unknown functions. Application of the standard linear algebra algorithm results in

$$\begin{aligned}{} & {} {B_j}(\xi ) = {( - 1)^j}\left( {\frac{{{M_{1j}}}}{M}{{{\tilde{q}}}(\xi )} - \frac{{{M_{2j}}}}{M}{{{\tilde{p}}}(\xi )}} \right) , \quad j = 1,...,4, \end{aligned}$$

(7a)

$$\begin{aligned}{} & {} {A_j}(\xi ) = {( - 1)^j}\left( {\frac{{{M_{1j}}}}{M}{{{\tilde{q}}}(\xi )} - \frac{{{M_{2j}}}}{M}{{{\tilde{p}}}(\xi )}} \right) , \quad j = 5,6, \end{aligned}$$

(7b)

where ${{\tilde{q}}}(\xi )$ and ${{\tilde{p}}}(\xi )$ stand for the Fourier transforms of the tangential and normal contact pressures exerted on the layer upper surface due to the nanoindentation of the rigid cylinder. In addition, $M_{ij}$ ($i = 1,2$; $j = 1-6$) denotes the elements of the cofactor matrix to the $6 \times 6$ coefficient matrix of the linear algebraic system with the determinant M. They are documented in Appendix A for brevity and easy reference.

Up to this point, the normal contact pressure p(x) is still an unknown. It can be solved by applying the displacement constraint along the contact interface ($z=h$)

$$\begin{aligned} \frac{{\partial {w_1}}}{{\partial x}} = - \frac{x}{R}, \quad - a \le x \le b. \end{aligned}$$

(8)

The substitution of the displacement along the contact interface into the above equation leads to the integral equation

$$\begin{aligned} \int _{ - a}^b {\eta p(t)} {\varphi _1}(x,t)dt + \int _{ - a}^b {p(t)} {\varphi _2}(x,t)dt = \frac{x}{R}, \quad -a\le x \le b, \end{aligned}$$

(9)

where

$$\begin{aligned}{} & {} {\varphi _1}(x,t) = \frac{1}{\pi }\int _0^{ + \infty } {I{E_1}} (\xi ,0)\cos (\xi (t - x))d\xi ,\end{aligned}$$

(10a)

$$\begin{aligned}{} & {} {\varphi _2}(x,t) = \frac{1}{\pi }\int _0^{ + \infty } {{E_2}} (\xi ,0)\sin (\xi (t - x))d\xi . \end{aligned}$$

(10b)

In the above equations, ${E_1}$ and ${E_2}$ are given by

$$\begin{aligned}{} & {} {E_1}(\xi ,0) = I\xi \sum \limits _{j = 1}^4 {{{( - 1)}^j}{s_j}\frac{{{M_{1j}}}}{M}}, \end{aligned}$$

(11a)

$$\begin{aligned}{} & {} {E_2}(\xi ,0) = \xi \sum \limits _{j = 1}^4 {{{( - 1)}^j}{s_j}\frac{{{M_{2j}}}}{M}}. \end{aligned}$$

(11b)

Note that, for frictionless nanocontact problems incorporating only surface tension, an explicit expression may be obtained for Eq. (11b) (Long et al. 2012; Le et al. 2021). In the presence of a graded layer possessing Steigmann–Ogden surface effects, it becomes not possible to develop such an analytical expression. Moreover, due to the sliding friction, Eq. (11a) was additionally introduced. This equation does not exist in any frictionless nanocontact problems. The complexity of Eqs. (11a, 11b) makes it impractical to derive an analytical solution for the infinite integrals (10a, 10b). In the literature (Pinyochotiwong et al. 2013; Li and Mi 2019b; Le et al. 2022), numerical quadratures of Gauss-type were employed instead to numerically evaluate these infinite integrals. Because of the critical importance of truncation scheme on integration accuracy and cost, next section makes detailed investigations on the numerical calculations of the infinite integrals (10a, 10b).

The integral Eq. (9) stands for one of the two governing equations that need to be numerically tackled for the proposed nanocontact problem. The other one is represented by the force equilibrium condition between the externally applied indentation force and the resultant of the contact pressure

$$\begin{aligned} \int _{ - a}^b {p(x)dx = P}. \end{aligned}$$

(12)

Under the condition of sliding friction, it is not necessary to consider the force equilibrium along the horizontal direction and the moment equilibrium.

3 Numerical evaluation of infinite integrals

The goal of this section is to develop an accurate algorithm to calculate the dual infinite integral Eqs. (10a, 10b). For this purpose, the asymptotic behavior of their integrands (11a, 11b) were first analyzed, as shown in Tables 1 and  2, respectively. For the graded layer/substrate structure shown in Fig. 1, both the classical and nonclassical cases are analyzed. In addition, following Vasu and Bhandakkar (2016, 2018), the reduced results for the degenerated case of a completely homogeneous half-plane ($\Gamma = 1$) can be employed to speed up the convergence of the dual infinite integrals. For this reason, the asymptotic behavior for this degenerated case and a few others are simultaneously tabulated in the tables. They were evaluated in MAPLE software package and are consistent with those available in the literature. The agreements help to validate the correctness of the asymptotic analysis.

Table 1 Asymptotic behavior of the infinite integral (10a)

In Tables 1 and  2, Asymptot.$\left( \cdot \right)$ denotes the leading term in the asymptotic expansion of its argument, as Fourier transform variable ($\xi$) approaches to infinity, sgn$\left( \cdot \right)$ is the sign function and $\delta$ $\left( \cdot \right)$ stands for the Dirac delta function. Based on literature results regarding the effects of surface material parameters on contact properties and the numerical tests of the present study, the surface tensile stiffness ($k_0$) alone shows negligible influence. As a result, the separated effects of $k_0$ on the asymptotic behavior of the infinite integrals (10a, 10b) does not need to be considered.

Table 2 Asymptotic behavior of the infinite integral (10b)

3.1 Classical case without surface effects

Let us first consider the classical case without any surface effects ($\tau _0=0$, $k_0=0$, $d_0=0$). From Tables 1 and  2, both integrands (11a, 11b) possess singular terms as $\xi$ approaches to infinity. Without separating the singular terms, the asymptotic behavior is shown in Fig. 2a and b. It can be observed that both integrants oscillate almost regularly with the increase of $\xi$.

Fig. 2

Asymptotic behavior of the integrands in the infinite integrals (10a, 10b), without separating the singular terms ($\tau _0=0, k_0=0, d_0=0$)

For reliable calculations of the infinite integrals, singular terms must be extracted from the integrands (Guler and Erdogan 2004, 2007). By using integral identities involving trigonometric functions and the singular terms, Eqs. (10a, 10b) can be recast into

$$\begin{aligned}{} & {} {\varphi _1}\left( {x,t} \right) = \int _0^{ + \infty } {\left[ {I{E_1} - {d_1}} \right] } \cos \left( {\xi \left( {t - x} \right) } \right) d\xi + {d_1}\pi \delta \left( {t - x} \right) , \end{aligned}$$

(13a)

$$\begin{aligned}{} & {} {\varphi _2}\left( {x,t} \right) = \int _0^{ + \infty } {\left[ {{E_2} - {d_2}} \right] } \sin \left( {\xi \left( {t - x} \right) } \right) d\xi + \frac{{{d_2}}}{{t - x}}, \end{aligned}$$

(13b)

where $d_1$ and $d_2$ denote the strength of singularity

$$\begin{aligned}{} & {} {d_1} = \frac{{ - \left( {\kappa - 1} \right) }}{{4{\mu _1}}}, \end{aligned}$$

(14a)

$$\begin{aligned}{} & {} {d_2} = \frac{{ - \left( {\kappa + 1} \right) }}{{4{\mu _1}}}. \end{aligned}$$

(14b)

Fig. 3

Asymptotic behavior of the integrands in the infinite integrals (10a, 10b), after separating the singular terms ($\tau _0=0, k_0=0, d_0=0$)

Figure 3a and b show the asymptotic behavior of the integrands after extracting the singular terms. Both integrands decay rapidly with $\xi$. Under such a condition, the infinite upper bound in (13a, 13b) may be safely truncated by a small number. After that, an accurate numerical solution can be obtained with the aid of Gauss–Legendre quadrature. Based on extensive tests, the upper bound is chosen as 500. The further substitution of (13a, 13b) back into the governing integral Eq. (9) leads to

$$\begin{aligned} \omega p\left( x \right) + \frac{1}{\pi }\int _{ - a}^b {\frac{p\left( t \right) }{{t - x}}dt} + \frac{1}{\pi }\int _{ - a}^b {\psi \left( {x,t} \right) p\left( t \right) dt} = \frac{x}{{R{d_2}}}, \end{aligned}$$

(15)

where

$$\begin{aligned} \psi \left( {x,t} \right) &= \eta \int _0^{ + \infty } {\left[ {\frac{{I{E_1} - {d_1}}}{{{d_2}}}} \right] } \cos \left( {\xi \left( {t - x} \right) } \right) d\xi \nonumber \\{} & {} \quad + \int _0^{ + \infty } {\left[ {\frac{{{E_2} - {d_2}}}{{{d_2}}}} \right] } \sin \left( {\xi \left( {t - x} \right) } \right) d\xi , \end{aligned}$$

(16a)

$$\begin{aligned} \omega &= \frac{\eta {{d_1}}}{{{d_2}}}. \end{aligned}$$

(16b)

It is noted that Eq. (15) belongs to the Fredholm integral equation of the second kind. Moreover, it is a singular integral equation of the Cauchy type, as indicated by the second term of its left-hand side.

3.2 Nonclassical case with surface tension only

Next, we aim at investigating the asymptotic behavior of the infinite integrals in the presence of surface effects. As can be observed from Tables 1 and  2, both integrands (11a, 11b) tend to zero as $\xi$ approaches to infinity for all four nonclassical cases. Therefore, there are no singular terms. However, the integrands of infinite integrals (10a, 10b) continuously oscillate from zero to a very large upper bound. The rate of convergence is thus very slow. Some mathematical manipulations may be conducted to optimize the convergence properties. When only surface tension ($\tau _0$) is taken into account, the asymptotic behavior of the integrands in Eqs. (10a, 10b) are presented in Fig. 4a and b. It can be observed that, although the integrands behave oscillatory decaying with $\xi$, the convergence is very slow.

Fig. 4

Asymptotic behavior of the integrands in the infinite integrals (10a, 10b), without separation ($\tau _0 \ne 0, k_0=0, d_0=0$)

To speed up the convergence rate, the asymptotic values of $IE_1$ and $E_2$ corresponding to a completely homogeneous half-plane ($\Gamma =1$) may be extracted from the original integrands. For such a particular condition, the infinite integral of the product between Asymptot.$(E_2)$ and sine function has a closed-form solution: $-\int _0^{ + \infty } { \left( {{1 / {\left( {{\tau _0}\xi } \right) }}} \right) } \sin \left[ {\xi \left( {x - t} \right) } \right] = - {{ \pi } / {\left( {2{\tau _0}\xi } \right) }}\mathrm{{sgn}}\left( {t - x} \right)$. As a result, the asymptotic value ($-1/(\tau _0{\xi })$) of $E_2$ may be set as the separation term. Although no corresponding analytical solution can be found for $IE_1$, the same algorithm may be employed. Following such a reasoning, the infinite integrals (10a, 10b) may be rewritten in the following forms that are ready for numerical evaluation

$$\begin{aligned} {\varphi _1}\left( {x,t} \right) &= \frac{1}{\pi }\int _0^{ + \infty } {\left[ {I{E_1} - {{\left. {I{E_1}} \right| }_{homo}}} \right] \cos } \left( {\xi \left( {t - x} \right) } \right) d\xi \nonumber \\{} & {} \quad + \frac{1}{\pi }\int _0^{ + \infty } {{{\left. {I{E_1}} \right| }_{homo}}\cos \left( {\xi \left( {t - x} \right) } \right) d\xi }, \end{aligned}$$

(17a)

$$\begin{aligned} {\varphi _2}\left( {x,t} \right) &= \frac{1}{\pi }\int _0^{ + \infty } {\left[ {{E_2}\left( {\xi ,0} \right) + \frac{1}{{{\tau _0}{\xi }}}} \right] } \sin \left( {\xi \left( {t - x} \right) } \right) d\xi - \frac{{\mathop {\textrm{sgn}}} \left( {t - x} \right) }{{2{\tau _0}\xi }}, \end{aligned}$$

(17b)

where the subscript “homo” denotes the reduced solution of $IE_1$ corresponding to a completely homogeneous half-plane ($\Gamma =1$). In Fig. 5a and b, we present the asymptotic behavior of the integrands in the first infinite integrals in the right-hand side of Eqs. (17a, 17b). As before, the infinite upper bound was set as 500 and Gauss–Legendre quadrature was employed for the numerical integration. In contrast to Fig. 4a and b, both integrands decay rapidly after the separation. In particular, Fig. 5b shows a more rapid convergence.

Fig. 5

Asymptotic behavior of the integrands in the infinite integrals (10a, 10b), after separating the solutions corresponding to a completely homogeneous half-plane ($\tau _0 \ne 0, k_0=0, d_0=0$)

In addition, the second infinite integral on the right-hand side of Eq. (17a) can also be analytically integrated

$$\begin{aligned} \frac{{1 - \kappa }}{{\pi {\tau _0}\left( {1 + \kappa } \right) }}\left[ { - \sin \left( {\left| {t - x} \right| \varpi } \right) \mathrm{{si}}\left( {\left| {t - x} \right| \varpi } \right) - \cos \left( {\left| {t - x} \right| \varpi } \right) \mathrm{{ci}}\left( {\left| {t - x} \right| \varpi } \right) } \right] , \end{aligned}$$

(18)

where

$$\begin{aligned} \varpi = \frac{{4{\mu _2}}}{{{\tau _0}\left( {\kappa + 1} \right) }}, \end{aligned}$$

(19)

and si$\left( \cdot \right)$ and ci$\left( \cdot \right)$ are sine and cosine integrals.

3.3 Nonclassical case with surface flexural rigidity only

In this subsection, we analyze the asymptotic behavior of the integrants in Eqs. (10a, 10b) when only surface flexural rigidity ($d_0$) is considered. Fig. 6a and b show the asymptotic behavior as Fourier transform variable ($\xi$) grows from zero to 300. The declining rate of the oscillatory integrands is quite slow. This behavior makes it nearly impossible to truncate the infinite upper bound of the improper integrals with a reasonably large number.

Fig. 6

Asymptotic behavior of the integrands in the infinite integrals (10a, 10b), without separation ($\tau _0 = 0, k_0=0, d_0 \ne 0$)

To accelerate the convergence rate, the infinite integrals (10a, 10b) can be recast in the form of

$$\begin{aligned} {\varphi _1}\left( {x,t} \right) & = \frac{1}{\pi }\int _0^{ + \infty } {\left[ {I{E_1} - {{\left. {I{E_1}} \right| }_{homo}}} \right] \cos \left( {\xi \left( {t - x} \right) } \right) d\xi } \nonumber \\{} & {} \quad + \frac{1}{\pi }\int _0^{ + \infty } {{{\left. {I{E_1}} \right| }_{homo}}\cos \left( {\xi \left( {t - x} \right) } \right) d\xi } , \end{aligned}$$

(20a)

$$\begin{aligned} {\varphi _2}\left( {x,t} \right) & = \frac{1}{\pi }\int _0^{ + \infty } {\left[ {{E_2} - {{\left. {{E_2}} \right| }_{homo}}} \right] \sin \left( {\xi \left( {t - x} \right) } \right) d\xi } \nonumber \\{} & {} \quad + \frac{1}{\pi }\int _0^{ + \infty } {{{\left. {{E_2}} \right| }_{homo}}\sin \left( {\xi \left( {t - x} \right) } \right) d\xi } . \end{aligned}$$

(20b)

This is equivalent to separate the values of $IE_1$ and $E_2$ corresponding to a completely homogeneous half-plane ($\Gamma =1$). When only the surface flexural rigidity is considered, the second term on the right-hand side of Eqs. (20a, 20b) can be analytically evaluated

$$\begin{aligned}{} & {} \begin{array}{l} - \frac{{\sqrt{3} \left( {\kappa - 1} \right) }}{{4 {\pi }^{3/2} {\mu _2} \left( {t - x} \right) }}\textrm{MeijeiG}\left( {\frac{1}{2},\mathrm{{ }}\left[ {} \right] ,\mathrm{{ }}\left[ {\frac{1}{6},\mathrm{{ }}\frac{1}{2},\mathrm{{ }}\frac{1}{2},\mathrm{{ }}\frac{5}{6},\mathrm{{ }}1} \right] ,\mathrm{{ }}\left[ {\frac{1}{3},\mathrm{{ }}\frac{2}{3}} \right] ,\mathrm{{ }}\frac{{{{\left( {t - x} \right) }^6}{\mu _2^2}}}{{2916{d_0^2}{{\left( {\kappa + 1} \right) }^2}}}} \right) \end{array}, \end{aligned}$$

(21a)

$$\begin{aligned}{} & {} \begin{array}{l} - \frac{{\sqrt{3} \left( {\kappa + 1} \right) }}{{4{\pi }^{3/2}{\mu _{20}} \left( {t - x} \right) }}\textrm{MeijeiG}\left( {1,\mathrm{{ }}\left[ {} \right] ,\mathrm{{ }}\left[ {\frac{1}{3},\mathrm{{ }}\frac{1}{2},\mathrm{{ }}\frac{2}{3},\mathrm{{ }}1,\mathrm{{ }}1} \right] ,\mathrm{{ }}\left[ {\frac{1}{6},\mathrm{{ }}\frac{5}{6}} \right] ,\mathrm{{ }}\frac{{{{\left( {t - x} \right) }^6}{\mu _{20}^2}}}{{2916{d_0^2}{{\left( {\kappa + 1} \right) }^2}}}} \right) \end{array}, \end{aligned}$$

(21b)

where MeijerG$\left( \cdot \right)$ stands for the Meijer’s G-function whose definition and main properties can be found in Gradshteyn and Ryzhik (2015).

Fig. 7

Asymptotic behavior of the integrands in the infinite integrals (10a, 10b), after separating the solutions corresponding to a completely homogeneous half-plane ($\tau _0 = 0, k_0=0, d_0 \ne 0$)

In Fig. 7a and b, we show the asymptotic behavior of the integrands belonging to the first infinite integrals on the right-hand side of Eqs. (20a, 20b). After the separation of the corresponding completely homogeneous half-plane solutions, both integrands decay very rapidly with the increase of $\xi$. Based on this observation, it has become possible to truncate the infinite upper bound with a reasonably large number (500). After that, Gauss–Legendre quadrature is employed to evaluate the finite integral.

3.4 Nonclassical case with full Steigmann–Ogden surface effects

When the full Steigmann–Ogden surface theory is accommodated, the same separation scheme can still be used. As a result, Eqs. (20a, 20b) remain effective. Similar to previous three cases studied in the present section, the integrands of the infinite integrals (10a, 10b) oscillates and decay slowly with the integration variable $\xi$ (Fig. 8a and b).

Fig. 8

Asymptotic behavior of the integrands in the infinite integrals (10a, 10b), without separation ($\tau _0 \ne 0, k_0 \ne 0, d_0 \ne 0$)

Fig. 9

Asymptotic behavior of the integrands in the infinite integrals (10a, 10b), after separating the solutions corresponding to a completely homogeneous half-plane ($\tau _0 \ne 0, k_0 \ne 0, d_0 \ne 0$)

After separating the corresponding homogeneous half-plane solutions of the integrands, much faster rate of decay can be identified (Fig. 9a and b). When compared with the nonclassical cases considering only surface tension or surface flexural rigidity, both integrands decay faster and nearly converge to zero as $\xi \rightarrow 300$. As before, Gauss–Legendre quadrature can be used to evaluate the infinite integrals after the proper separation of integrands. The upper bound of the infinite integrals are truncated as 500. It is sufficient to accurately evaluate the first infinite integrals in Eqs. (20a, 20b). However, analytical solutions cannot be found for the second infinite integrals anymore. Numerical integration must also be used. They are numerically evaluated by using the built-in “integral” function available in MATLAB. The upper bound of the integration interval was directly set as positive infinity.

4 Numerical solution algorithm

In this section, we develop an efficient solution algorithm to the integral Eqs. (9), (12) and (15). To proceed, let us first make the following replacements of variables

$$\begin{aligned} t = \frac{{b + a}}{2}r + \frac{{b - a}}{2}, \quad x = \frac{{b + a}}{2}s + \frac{{b - a}}{2}, \end{aligned}$$

(22a,b)

$$\begin{aligned} \phi \left( r \right) = \frac{{p\left( r \right) }}{{P/h}}. \end{aligned}$$

(22c)

Since both x and t are defined within the contact zone $[-a,b]$, the transformed variables r and s have the closed interval $[-1,1]$. Function $\phi (r)$ is the dimensionless form of the contact pressure.

4.1 Numerical scheme for the classical case

For the classical case without any surface effects, Eqs. (15) and (12) can be converted into the following expressions with the help of the dimensionless quantities defined in (22a–c)

$$\begin{aligned}{} & {} \frac{\eta \phi (s) d_1}{d_2} + \frac{1}{\pi }\int _{ - 1}^1 {\frac{\phi (r)}{{r - s}}} dr + \frac{1}{\pi }\int _{ - 1}^1 {{\psi ^*}(s,r)\phi (r)} dr = \frac{(b+a)s+(b-a)}{{2R{d_2}P/h}}, \quad \nonumber \\{} & {} \quad -1\le s \le 1, \end{aligned}$$

(23a)

$$\begin{aligned}{} & {} \frac{{b+a}}{{2h}}\int _{ - 1}^1 {\phi \left( r \right) } dr = 1, \end{aligned}$$

(23b)

where

$$\begin{aligned} {\psi ^*}(s,r) = \frac{{(b+a)}}{2}\psi (s,r). \end{aligned}$$

(24)

The singularity index of the integral Eq. (23a) is $-1$, since the contact pressure is zero and therefore bounded at both contact boundaries (Erdogan and Gupta 1972). As a result, the dimensionless contact pressure $\phi (r)$ may be expressed as

$$\begin{aligned} \phi \left( r \right) = g(r)\delta (r), \end{aligned}$$

(25)

where $\delta (r)$ is the weight function given by

$$\begin{aligned} \delta (r) = {(1 - r)^\alpha }{(1 + r)^\beta }. \end{aligned}$$

(26)

In the above equation, the powers $\alpha$ and $\beta$ are given by

$$\begin{aligned} \alpha &= \frac{1}{{2\pi I}}\ln \left(\frac{{\omega - I}}{{\omega + I}}\right) + N, \end{aligned}$$

(27a)

$$\begin{aligned}\beta &= - \frac{1}{{2\pi I}}\ln \left(\frac{{\omega - I}}{{\omega + I}}\right) + M, \end{aligned}$$

(27b)

where N and M can be arbitrary integers. In addition, the following relation should also be satisfied

$$\begin{aligned} \chi = - (\alpha + \beta ) = - (N + M) = - 1. \end{aligned}$$

(28)

Following Erdogan et al. (1973), Gauss–Jacobi quadratures are now employed to discretize and collocate the integral Eqs. (23a, 23b)

$$\begin{aligned}{} & {} \sum \limits _{m = 1}^N {W_m^N} g({r_m})\left[ {\frac{1}{{{r_m} - {s_k}}} + \psi ({r_m},{s_k})} \right] = \frac{(b+a)s_k+(b-a)}{{2R{d_2}P/h}}, \quad \nonumber \\{} & {} \quad k = 1,2,......,N + 1, \end{aligned}$$

(29a)

$$\begin{aligned}{} & {} \frac{{b+a}}{{2h}}\sum \limits _{m = 1}^N {W_m^Ng({r_m})} = \frac{1}{\pi }, \end{aligned}$$

(29b)

where $r_m$ and $s_k$ are the roots of the associated Jacobi polynomials and $W_m^N$ are the weights of quadratures

$$\begin{aligned}{} & {} P_N^{(\alpha ,\beta )}({r_m}) = 0, \quad m = 1,2,......,N, \end{aligned}$$

(30a)

$$\begin{aligned}{} & {} P_{N + 1}^{( - \alpha , - \beta )}({s_k}) = 0, \quad k = 1,2,......,N + 1, \end{aligned}$$

(30b)

$$\begin{aligned}{} & {} W_m^N = - {2^{ - \chi }}\frac{{\Gamma (\alpha )\Gamma (1 - \alpha )}}{\pi }\frac{{P_{N - \chi }^{( - \alpha , - \beta )}({r_m})}}{{P{{_N^{(\alpha ,\beta )}}^\prime }({r_m})}}. \end{aligned}$$

(30c)

Equations (29a, 29b) contain $N+2$ equations for the total number of $N+2$ unknowns, including the N discretized contact pressures $g(r_m)$ $(m=1,2, \cdots ,N)$ and the two contact boundaries a and b. Although this algebraic system is linear to the contact pressures $g(r_m)$, it is nonlinear about the contact boundaries a and b. Therefore, an iterative scheme needs to be implemented. An effective iterative algorithm for determining these unknowns has been developed by Comez and Erdol (2013) and is also adopted in the present work to solve the classical contact pressures and contact boundaries without surface effects.

4.2 Numerical scheme for the nonclassical case

By the use of equations (22a–c), the integral Eqs. (9) and (12) can be expressed as

$$\begin{aligned}{} & {} \frac{1}{\pi }\int _{ - 1}^1 {{\psi ^*}(s,r)\phi (r)} dr = \frac{(b+a)s+(b-a)}{{2R P/h}}, \quad -1\le s \le 1, \end{aligned}$$

(31a)

$$\begin{aligned}{} & {} \frac{{b+a}}{{2h}}\int _{ - 1}^1 {\phi \left( r \right) } dr = 1, \end{aligned}$$

(31b)

where

$$\begin{aligned}{} & {} {\psi ^*}(s,r) = \frac{{b+a}}{2}\psi (s,r), \end{aligned}$$

(32a)

$$\begin{aligned}{} & {} \psi \left( {s,r} \right) = \eta {\varphi _1}\left( {s,r} \right) + {\varphi _2}\left( {s,r} \right) . \end{aligned}$$

(32b)

In the presence of surface effects, the contact pressures at both contact boundaries are not zero anymore. However, they are still bounded. As a result, the singularity index of the integral Eq. (31a) is still $-1$ (Erdogan and Gupta 1972). Following Erdogan and Gupta (1972), we may employ Gauss–Chebyshev quadrature of the second kind to discretize the definite integral in (31a). In the meantime, we use Gauss–Chebyshev quadrature of the first kind to collocate this integral equation

$$\begin{aligned}{} & {} \sum \limits _{m = 1}^N {\frac{{(1 - r_m^2)}}{{N + 1}}} g({r_m}) {\psi ({r_m},{s_k})} = \frac{(b+a)s_k+(b-a)}{{2R P/h}}, \quad k = 1,2, \cdots ,N + 1, \end{aligned}$$

(33a)

$$\begin{aligned}{} & {} \frac{{b + a}}{{2h}}\sum \limits _{m = 1}^n {\frac{{(1 - r_m^2)}}{{N + 1}}g({r_m})} = \frac{1}{\pi }, \end{aligned}$$

(33b)

where

$$\begin{aligned}{} & {} g({r_m}) = \frac{{\phi \left( {{r_m}} \right) }}{{\sqrt{(1 - {{r_m}^2})} }}, \end{aligned}$$

(34a)

$$\begin{aligned}{} & {} {r_m} = \cos \left( {\frac{{m\pi }}{{N + 1}}} \right) , \quad m = 1,2, \cdots ,N, \end{aligned}$$

(34b)

$$\begin{aligned}{} & {} {s_k} = \cos \left( {\frac{{\pi (2k - 1)}}{{2(N + 1)}}} \right) , \quad k = 1,2, \cdots ,N + 1. \end{aligned}$$

(34c)

Similar to Eqs. (29a, 29b), the algebraic system (33a, 33b) also contains $N+2$ equations for the determination of the $N+2$ unknowns. They are composed of the discretized contact pressures $g(r_m)$ $(m=1,2, \ldots ,N)$ and both contact boundaries a and b. Again, the algebraic system is linear about the contact pressures, but nonlinear to the contact boundaries. To determine these unknowns, an iterative algorithm is needed. Note that (33a) has $N+1$ equations. When using them to determine the N contact pressures $g(r_m)$, anyone of them can be extracted and combined with (33b). As the first step, initial values of both contact boundaries (a and b) are proposed. Second, the N discretized contact pressures $g(r_m)$ are evaluated from Eq. (33a), by excluding anyone from the $N+1$ collocated equations. The standard algorithm is sufficient for this linear algebraic system. Third, the just solved contact pressures $g(r_m)$ are substituted into Eq. (33b) and the equation that was previously excluded from (33a). The residual errors of both equations are then calculated. Provided that both errors are less than or equal to $10^{-6}$, solutions deem to be found. Otherwise, both contact boundaries a and b need to be updated, by following the method of steepest descent, and the loop needs to be recycled again from the second step.

5 Results and discussion

We have presented the formulation and method of solution for the sliding frictional nanocontact problem between a rigid cylinder and an exponentially graded layer/substrate structure. The governing integral equations were converted into an algebraic system of equations for determining the asymmetric nanocontact pressures and boundaries. In this section, we conduct parametric studies with respect to surface properties, sliding frictional coefficient, and the gradient index of the layer modulus.

5.1 Validation of the solution algorithm

Since the classical case without surface effects has been studied in the literature (Guler and Erdogan 2007), it is beneficial to first verify and validate the accuracy of the developed method of solution and numerical algorithm (Sect. 4.1). Figs. 10a and b show the contact pressure distributions for the frictionless ($\eta =0$) and sliding frictional ($\eta =0.7$) conditions, respectively. Three shear moduli ratios are considered, standing for a hard ($\Gamma =1/7$), a homogeneous ($\Gamma =1$) and a soft ($\Gamma =7$) layer. From Eq. (2), defining $\Gamma$ is equivalent to assigning the gradient index $\beta h$ of the layer modulus. For all six cases, the agreement between our results and the literature data is perfect. This indicates the reliability of our method of solution (Sect. 4.1). In general, the maximum contact pressure corresponding to the soft layer ($\Gamma =7$) is much larger than that of the hard one ($\Gamma =1/7$). As expected, under the frictionless condition, the maximum pressure occurs at the center of the contact zone. For the frictional cases ($\eta =0.7$), the maximum contact pressure deviates appreciably from the center.

Fig. 10

Validation of the contact pressures with respect to Guler and Erdogan (2007) for the classical case without any surface effects. Two sliding frictional coefficients and three shear moduli ratios are considered ($R/h=100$, $(b+a)/R=0.01$, $\Gamma =\mu _2/\mu _1$)

Fig. 11

Validation of the contact pressure between a completely homogeneous half-plane and a rigid cylindrical indenter under the sole influence of surface tension (Long et al. 2012). Four indenter radii are considered ($\Gamma = 1$, $\mu _{1} =\mu _{2} = 1$ MPa, $\nu =0.4$, $\eta = 0$, $\tau _0=0.1$ nN/nm, $P=10$ nN/$\mu$m, $p_m=P/(b+a)$)

Next, let us verify and validate the method of solution and numerical algorithm for the nonclassical case (Sect. 4.2). For the nanocontact between a completely homogeneous half-plane and a rigid cylinder, Long et al. (2012) studied the sole influence of surface tension ($\tau _0$). In Fig. 11, we compared our results with the contact pressures extracted from Long et al. (2012), by considering the surface tension only. The classical solutions without surface tension are also presented. Note that, in the dimensionless form, the classical contact pressure has nothing to do with the radius of the rigid cylinder. For all six cases, our results agree perfectly with the literature data, indicating the reliability of our solution algorithm for the nonclassical scenario (Sect. 4.2).

5.2 Contact pressure and contact boundaries

Now, let us investigate the contact pressure distribution and contact boundaries under the influence of surface properties, shear moduli ratio and sliding frictional coefficient. In particular, the effects of three Steigmann–Ogden surface parameters are emphasized. The shear modulus of the substrate and Poisson’s ratio of both deformable media are fixed as $\mu _2=1$ MPa and $\nu =0.4$ (Long et al. 2012; Long and Wang 2013). The other parameters are taken as $h=1$ $\mu$m, $R=100$ $\mu$m and $P=10$nN.

Fig. 12

Distribution of contact pressure between the graded layer and the rigid cylindrical indenter for three levels of surface tension or surface flexural rigidity ($\eta = 0.4$, $\Gamma = 1/3$)

Figure 12 shows the effects of separate surface parameters on contact pressure and contact boundaries. As aforementioned, since the effects of surface tensile stiffness is very marginal, only surface tension and surface flexural rigidity are considered, when investigating the effects of individual surface parameters. Therefore, only $\tau _0$ and $d_0$ are considered separately in the current example. Three different magnitudes of either parameter are considered. The classical solutions are also presented for easy comparisons. The other variables are given in the captions of the figures.

From Fig. 12, both surface tension and surface flexural rigidity significantly affect the distribution pattern of the contact pressure. For either parameter, the maximum contact pressure occurs near the midpoint of the contact zone and decays monotonically toward the contact boundaries. In the presence of surface effects, the minimum contact pressure taking place at both contact boundaries becomes nonzero. Furthermore, with the inclusion of sliding friction, the contact pressure is not symmetric about the symmetry axis (z) of the rigid cylinder anymore. The contact pressure at the left boundary is always larger than that of the right boundary. The effects of surface tension are more significant than those of surface flexural rigidity with the equal magnitude. When only considering surface flexural rigidity, the maximum contact pressure slightly decreases with its increased magnitude. In contrast, with the increased surface tension, the maximum contact pressure increases obviously and the contact interval shrinks continuously.

Table 3 Definition of the dimensionless parameter $\alpha$ representing the equal magnitude of three Steigmann–Ogden surface parameters ($\tau _0$, $k_0$ and $d_0$)

Having explored the individual effects of surface tension and surface flexural rigidity, let us now consider the complete Steigmann–Ogden surface theory. We define a dimensionless parameter $\alpha$ to represent the equal magnitude of three independent Steigmann-Ogden surface parameters ($\tau _0$, $k_0$, $d_0$). In the subsequent parametric analysis, three levels of $\alpha$ will be considered (Table 3).

Fig. 13

Distribution of contact pressure between the graded layer and the rigid cylindrical indenter for three levels of the dimensionless parameter $\alpha$ ($\eta = 0.4$, $\Gamma = 1/3$)

Figure 13 shows the dimensionless contact pressure for three levels of the dimensionless parameter $\alpha$ denoting the equal magnitude of $\tau _0$, $k_0$ and $d_0$. The classical solution is also presented for comparison purpose. The common effects of the three surface parameters on contact pressure are similar to that of only considering surface tension (Fig. 12). This indicates that surface tension plays a leading role. For all four cases, the maximum pressures are near the center of the contact zone. The loss of symmetry about the $z-$axis is apparently due to the presence of sliding friction. Furthermore, the maximum contact pressure increases with the dimensionless parameter $\alpha$. Governed by the conservation of the external indentation force, an opposite trend can be observed for the contact size. Except the classical case, the contact pressure at both contact boundaries becomes nonzero. For all nonclassical curves, the contact pressure at the right boundary is slightly lower than that at the left boundary.

Fig. 14

Distribution of contact pressure between the graded layer and the rigid cylindrical indenter for three frictional coefficients ($\alpha =0.2$, $\Gamma = 1/3$)

Next, let us investigate the effects of sliding frictional coefficient $\eta$. Figure 14 shows the contact pressure for three frictional coefficients. The sliding frictional coefficient significantly affects the distribution symmetry of the contact pressure. With the increased frictional coefficient, the contact pressure at the left contact boundary increases apparently. An opposite trend can be found for the right contact boundary. As a result, for a nonzero frictional coefficient, the minimum pressure always takes place at the right boundary of the contact zone. In addition, the contact zone continuously deviates toward the sliding frictional direction with the increased $\eta$. While the sliding frictional coefficient greatly affects the distribution pattern of the contact pressure, the maximum contact pressure is much less influenced (Fathabadi and Alinia 2020).

Fig. 15

Distribution of normalized contact pressure between the graded layer and the rigid cylinder for five shear moduli ratios ($\alpha =0.2$, $\eta = 0.4$)

Figure 15 shows the effects of the shear moduli ratio or equivalently the gradient index on contact pressure and contact boundaries. Five shear moduli ratios are considered. They represent two hard graded layers ($\Gamma =1/6,1/3$), two soft graded layers ($\Gamma =3,6$) and one completely homogeneous layer ($\Gamma =1$). For the sliding frictional coefficient $\eta =0.4$, the maximum contact pressures still take place near the center of the contact zone and the minimum contact pressure always occurs at the right contact boundary. With the increased shear moduli ratio, the maximum contact pressure decays monotonically and the contact zone expands appreciably.

5.3 Stresses and displacements along the contact interface

The previous subsection examined the effects of Steigmann–Ogden surface parameters, shear moduli ratio and sliding frictional coefficient on contact pressures and contact boundaries. Nevertheless, their effects on displacements and stresses along the contact interface have not been studied. This is the objective of the current subsection. Following Eqs. (29b) and (33b), the tangential and normal contact pressures in Fourier space can be expressed by

$$\begin{aligned} {{\tilde{q}}}(\xi ) = \eta {{\tilde{p}}}(\xi ), \quad {{\tilde{p}}}(\xi ) = \frac{{\left( {a + b} \right) P}}{{2h}}\sum \limits _{m = 1}^N {T_m^N} g\left( {{r_m}} \right) {e^{{{I\xi {r_m}\left( {a + b} \right) } /2}}}. \end{aligned}$$

(35a,b)

For the classical case without surface elasticity

$$\begin{aligned} T_m^N = - \frac{{\Gamma \left( \alpha \right) \Gamma \left( {1 - \alpha } \right) }}{2\pi }\frac{{P_{N - \chi }^{\left( { - \alpha , - \beta } \right) }\left( {{r_m}} \right) }}{{P{{_N^{\left( {\alpha ,\beta } \right) }}^\prime }\left( {{r_m}} \right) }}. \end{aligned}$$

(36)

For the nonclassical case

$$\begin{aligned} T_m^N = \frac{{\mathrm{{1}} - {r_m^2}}}{{N + 1}}. \end{aligned}$$

(37)

Fig. 16

The effects of the dimensionless parameter $\alpha$ on (a) normal stress $\sigma _{zz}$, (b) shear stress $\sigma _{xz}$, (c) tangential stress $\sigma _{xx}$, and (d) subsidence displacement $u_{z}$ ($\eta = 0.4$, $\Gamma = 1/3$)

To proceed, we need to first substitute the contact pressures in Eqs. (35a,b) back into the expressions (7a, 7b). After that, the displacements and stresses in the transformed space can be evaluated. Finally, their inverse Fourier transforms lead to the displacements and stresses in the physical space. Once the contact pressures along the contact surface are obtained, the subsequent calculation process is not different from the analysis of a nanocontact problem loaded by surface tractions.

Figure 16a–d show the distribution of normal stress, shear stress, tangential stress and subsidence displacement along the contact interface ($z = 0$). Three levels of the dimensionless parameter $\alpha$ are considered. The classical solutions are also presented. For contact stresses shown in Fig. 16a–c, the peak values of the normalized stresses decay with the inclusion of surface effects. Furthermore, the very sharp transitions of the classical stress curves are significantly relaxed, due to the presence of surface effects. This phenomenon means that Steigmann–Ogden surface theory helps to reduce the impractical stress singularities that are inherent to the classical theory of elasticity.

With the increased $\alpha$, the maximum normal and tangential stresses continuously decrease. The position of peak shear stress deviates toward the opposite direction of the sliding friction. Resulting from the semiinfinity of the layer/substrate structure, the subsidence displacement shown in Fig. 16d can only be presented with respect to a reference position $x_0/h = 3$ (Li and Mi 2021). From Fig. 16d, the extreme value of the subsidence displacement decreases with the increased $\alpha$. Also, due to the presence of sliding friction, the displacement at $x/h = -3$ becomes nonzero.

Figure 17a-d show the effects of sliding frictional coefficient ($\eta$) on the contact stresses and the subsidence displacement. Based on these figures, the inclusion of sliding friction results in asymmetric distribution of all contact fields. With the increased $\eta$, the contact zone deviates toward the direction of the applied tangential force. For the normal stress shown in Fig. 17a, the extreme value decreases with the increased $\eta$. An opposite trend can be observed for the shear stress (Fig. 17b) and the tangential stress (Fig. 17c). In Fig. 17b, the shear stress appears at the contact interface for $\eta =0$, due to the presence of surface effects. For the subsidence displacement shown in Fig. 17d, the peak value near the midpoint of the contact zone continuously decreases with the increased sliding frictional coefficient.

Fig. 17

The effects of sliding frictional coefficient $\eta$ on a normal stress $\sigma _{zz}$, b shear stress $\sigma _{xz}$, c tangential stress $\sigma _{xx}$, and d subsidence displacement $u_{z}$ ($\alpha = 0.2$, $\Gamma = 1/3$)

Fig. 18

The effects of shear moduli ratio $\Gamma$ on a normal stress $\sigma _{zz}$, b shear stress $\sigma _{xz}$, c tangential stress $\sigma _{xx}$, and d subsidence displacement $u_{z}$ ($\alpha = 0.2$, $\eta = 0.4$)

Figure 18a–d show the contact stresses and subsidence displacement along the contact interface for five shear moduli ratios. The maximum stresses appearing in Fig. 18a–c decrease with the shear moduli ratio. However, the increase of shear moduli ratio leads to appreciably larger subsidence displacement (Fig. 18d). Due to the presence of sliding friction, the relative displacement at $x/h=-3$ becomes nonzero.

The classical normal and shear stress curves possess sharp corners at both contact boundaries (Fig. 16a and b). In the presence of surface effects, the sharp corners disappear. Smooth transitions of normal and shear stresses are found for all five shear moduli ratios. Furthermore, the softer the graded layer is, the more smooth the normal and shear stresses at the contact boundaries become (Fig. 18a and b).

5.4 Stresses and displacements inside the graded layer

In this subsection, let us investigate the distribution of vertical stress and subsidence displacement inside a hard graded layer ($\Gamma =1/3$). Figure 19a and b show the contour plots of the vertical stress for the classical ($\alpha =0$) and the nonclassical ($\alpha =0.5$) cases, respectively. In the presence of sliding friction ($\eta =0.4$), the distribution of the vertical stress becomes obviously asymmetric. By comparing the two subfigures, it is clear that the maximum vertical stress near the midpoint of the contact zone decreases apparently with the inclusion of surface effects. Moreover, an obviously smaller stress concentration can be found below the rigid cylinder. These phenomena indicate that surface effects help the graded layer/substrate structure to alleviate the stress concentrations and thus to elevate the loading capacity.

Fig. 19

Contour plots of the vertical stress $\sigma _{zz}$ for (a) the classical and (b) the nonclassical cases inside a hard graded layer ($\eta = 0.4$, $\Gamma = 1/3$)

Fig. 20

Contour plots of the subsidence displacement $u_{z}$ for (a) the classical and (b) the nonclassical cases inside a hard graded layer ($\eta = 0.4$, $\Gamma = 1/3$)

Figure 20a and b present the contour plots of the subsidence displacement inside a hard graded layer with the shear modulus $\Gamma =1/3$. Two magnitudes of the dimensionless surface parameter ($\alpha$) are considered ($\alpha =0$ and 0.5). A simple comparison between the two subfigures shows that the peak value of the subsidence displacement takes place under the rigid cylinder and decreases apparently with the inclusion of surface effects. For both cases, the subsidence displacement decays monotonically along the depth dimension of the graded layer.

6 Conclusions

We have successfully analyzed the sliding frictional nanocontact problem between a rigid cylinder and a graded layer perfectly bonded to a homogeneous half-plane. The sliding contact interface of the layer/substrate structure is modeled by Steigmann–Ogden surface mechanical theory. The asymmetric contact pressure, contact boundaries, stresses and displacements are semianalytically evaluated. For the plane-strain nanocontact problem, Fourier integral transforms were employed to convert the governing equations and nonclassical mixed boundary conditions into a Fredholm integral equation. Together with the static force equilibrium equation, the integral equation was discretized and collocated with Gaussian quadratures, leading to an algebraic system with respect to discretized contact pressures and two asymmetric contact boundaries. Since the algebraic system is nonlinear about contact boundaries, an iterative algorithm was further developed. Compared with literature results, we additionally evaluated the full elastic fields along both the contact interface and the depth dimension of the graded layer. A few important conclusions can be summarized from the extensive parametric studies about surface properties, sliding frictional coefficient and shear modulus gradation.

• Among the three Steigmann–Ogden surface parameters, the effects of surface tension are more significant than those of surface flexural rigidity. While both of them are important, the impact of surface membrane stiffness is marginal.

• When compared with classical solutions, higher contact pressures and smaller contact zones are found in nonclassical solutions with surface effects. Moreover, the pressures at both contact boundaries become nonzero. The sharp transitions of stresses across contact boundaries become more smooth.

• With increased sliding frictional coefficient, the contact zone deviates toward the frictional direction. The contact pressure on the sliding advancing side becomes appreciably larger than that of the receding side. While shear and tangential stresses increase with the frictional coefficients, an opposite trend is found for the normal stress and the subsidence displacement.

• Softer graded layers lead to higher subsidence displacements, lower peak contact pressures, and larger contact zones. The same argument remains valid for displacements and stresses.

Although the full surface effects were considered in the sliding nanoindentation of a graded coating-substrate structure, the nanocontact behavior is characterized by the simple Column’s law of friction. In rolling and fretting contact problems, the whole contact zone is typically composed of a stick and a slip zone. This could be a natural extension of the current work. In the meanwhile, more efforts are also worth being made toward the coupling of microstructure and surface energy induced scale-dependency of small-scale graded materials and structures (Fathabadi and Alinia 2020).

Appendix A

The determinant M appearing in (7a, 7b) is defined by the coefficient matrix of the linear system

$$\begin{aligned}{} & {} \left( {\begin{array}{*{20}{c}} {{\Delta _1}}&{}{{\Delta _2}}&{}{{\Delta _3}}&{}{{\Delta _4}}&{}0&{}0\\ {{\Pi _1}}&{}{{\Pi _2}}&{}{{\Pi _3}}&{}{{\Pi _4}}&{}0&{}0\\ {{{ K}_1}}&{}{{{ K}_2}}&{}{{{ K}_3}}&{}{{{ K}_4}}&{}{ - 2{\mu _2}I\xi \cdot {e^{ - \left| \xi \right| h}}}&{}{ - 2{\mu _2}I\left( {\frac{{\left( {1 + \kappa } \right) \xi }}{{2\left| \xi \right| }} + \xi h} \right) \cdot {e^{ - \left| \xi \right| h}}}\\ {{\Lambda _1}}&{}{{\Lambda _2}}&{}{{\Lambda _3}}&{}{{\Lambda _4}}&{}{2{\mu _2}\left| \xi \right| \cdot {e^{ - \left| \xi \right| h}}}&{}{ - 2{\mu _2}\left( {\frac{{1 - \kappa }}{2} - \left| \xi \right| h} \right) \cdot {e^{ - \left| \xi \right| h}}}\\ {{e^{{m_1}h}}}&{}{{e^{{m_2}h}}}&{}{{e^{{m_3}h}}}&{}{{e^{{m_4}h}}}&{}{ - {e^{ - \left| \xi \right| h}}}&{}{ - h{e^{ - \left| \xi \right| h}}}\\ {{s_1}{e^{{m_1}h}}}&{}{{s_2}{e^{{m_2}h}}}&{}{{s_3}{e^{{m_3}h}}}&{}{{s_4}{e^{{m_4}h}}}&{}{I\frac{\xi }{{\left| \xi \right| }} \cdot {e^{ - \left| \xi \right| h}}}&{}{I\left( {\frac{\xi }{{\left| \xi \right| }}h + \frac{\kappa }{\xi }} \right) \cdot {e^{ - \left| \xi \right| h}}} \end{array}} \right) \left( {\begin{array}{*{20}{c}} {{B_1}}\\ {{B_2}}\\ {{B_3}}\\ {{B_4}}\\ {{A_5}}\\ {{A_6}} \end{array}} \right) \nonumber \\{} & {} \quad = \left( {\begin{array}{*{20}{c}} { - {{{\tilde{q}}}}}\\ { - {{{\tilde{p}}}}}\\ 0\\ 0\\ 0\\ 0 \end{array}} \right) , \end{aligned}$$

(38)

where

$$\begin{aligned}{} & {} {\Delta _j} = {\mu _1}{q_j} - {k_0}{\xi ^2}, \end{aligned}$$

(39)

$$\begin{aligned}{} & {} {\Pi _j} = \frac{{{\mu _1}}}{{\kappa - 1}}{p_j} - \left( {{\tau _0}{\xi ^2} + {d_0}{\xi ^4}} \right) {s_j}, \end{aligned}$$

(40)

$$\begin{aligned}{} & {} {{ K}_j} = {\mu _1}\frac{{{e^{(\beta + {m_j})h}}}}{{\kappa - 1}}{p_j}, \end{aligned}$$

(41)

$$\begin{aligned}{} & {} {\Lambda _j} = {\mu _1}{e^{(\beta + {m_j})h}}{q_j}, \end{aligned}$$

(42)

with $j = 1-4$ and

$$\begin{aligned}{} & {} {q_j} = {m_j} - I\xi {s_j}, \end{aligned}$$

(43)

$$\begin{aligned}{} & {} {p_j} = - I\xi \left( {3 - \kappa } \right) + \left( {1 + \kappa } \right) {m_j}{s_j}. \end{aligned}$$

(44)