Nonlinear forced vibration of functionally graded carbon nanotube reinforced composite circular cylindrical shells

Abstract

The nonlinear forced vibration characteristics of functionally graded carbon nanotube reinforced composite (FG-CNTRC) circular cylindrical shells are investigated. On the basis of Reddy’s first-order shear deformation theory, von Kármán geometric nonlinearity and Hamilton’s principle, the equations of motion are derived. The Galerkin technique is applied to discretize the partial differential equations into nonlinear ordinary differential equations, which are reduced by using Volmir’s assumption and the static condensation method. The incremental harmonic balance method is applied to analyze the dynamic response of FG-CNTRC cylindrical shells. A convergence study on the mode expansions is conducted by considering both axisymmetric and asymmetric modes. The natural frequencies and the resonance responses are compared with existing studies to examine the validity of this study. The effects of distribution and volume fraction of carbon nanotube, thickness-to-radius ratio, length-to-radius ratio, dimensionless radial excitation amplitude and damping ratio on the resonance responses of FG-CNTRC cylindrical shells are discussed. The results show that the reduced model of the system is reasonable. The frequency responses of FG-CNTRC cylindrical shells show both hardening and softening types of nonlinearities, and they are greatly influenced by the change of the fundamental vibrational mode.

1 Introduction

Carbon nanotubes (CNTs) possess outstanding mechanical, electrical and thermodynamic performance, and they have become an ideal reinforcing material for advanced composites [1,2,3]. Many investigations related to carbon nanotube reinforced composites (CNTRCs) implied that the percentage and alignment of CNTs can remarkably affect the mechanical behavior of CNTRCs [4,5,6]. Adopting the notion of functionally graded materials and using CNTs as reinforcements in the matrix produce new emerging advanced composites, namely functionally graded carbon nanotube reinforced composites (FG-CNTRCs). It was reported that Kwon et al. [7] successfully implemented the fabrication of FG-CNTRCs in the laboratory. A variety of studies on the mechanical characteristic of FG-CNTRC structures have been conducted recently.

Shen et al. [8, 9] explored the large and small amplitude vibrations, thermal postbuckling and bending of thermally postbuckled CNTRC beams in the conditions of elastic foundations and thermal environments, considering the foundation-beam interaction and initial deformation resulting from thermal postbuckling. Their studies illustrated that the thermal postbuckling path of beams with asymmetric CNT distributions is no longer bifurcated. Lin and Xiang [10] and Ke et al. [11] researched the free vibration of FG-CNTRC beams in a linear and nonlinear field, respectively. Both their studies imply that beams with symmetric CNT distribution possess greater frequencies than those with uniform or asymmetric CNT distribution. Using several shear deformation theories, Wattanasakulpong and Ungbhakorn [12] studied the vibration and bending behavior of CNTRC beams under uniform and sinusoidal loads. Ansari et al. [13, 14] investigated the nonlinear primary resonance responses of perfect and geometrically imperfect FG-CNTRC beams. Wu et al. [15, 16] also reported the important influences of the initial geometric imperfections on the vibrational properties of FG-CNTRC beams. Mirzaei and Kiani [17] researched the large amplitude nonlinear free vibrations of sandwich beams with FG-CNTRC face sheets and stiff cores. Recently, Wu et al. [18] investigated the nonlinear primary and superharmonic resonances of FG-CNTRC beams utilizing the incremental harmonic balance (IHB) method. They found that only in FG-CNTRC beams possessing asymmetric CNT distribution can the 2 superharmonic resonance occur.

Several investigations on FG-CNTRC plates can be found in published works. Among those, Shen et al. [19,20,21] carried out a number of studies on the nonlinear bending characteristics, dynamic response, buckling and postbuckling behavior of FG-CNTRC plates. By using the element-free method, Zhang et al. [22,23,24] explored the free vibrations of FG-CNTRC triangular, quadrilateral and rectangular plates. Considering four different loadings, including uniform, linear, sinusoidal and exponential distributions, Sobhy [25] researched the bending characteristics and stresses of FG-CNTRC plates. Kiani et al. [26, 27] examined the free vibration and shear buckling of FG-CNTRC skew plates by using the FSDT and Ritz method. Kiani [28] also obtained the buckling loads and buckling mode shape of FG-CNTRC rectangular plates subjected to uniaxial compressive parabolic loading.

Some reports about FG-CNTRC shell structures are available in the literature. Shen and Xiang [29] investigated the free vibrations of FG-CNTRC cylindrical shells under thermal loading. Shen [30, 31] analyzed the postbuckling of FG-CNTRC cylindrical shells in different conditions, including uniform temperature rise, axial compression and external pressure. These two studies illustrated the remarkable influences of volume fraction and distribution of CNTs on the postbuckling behavior of FG-CNTRC cylindrical shells, such as the buckling load, buckling temperature, postbuckling strength postbuckling equilibrium path. Thang et al. [32] proposed an exact solution to explore the influences of imperfection parameters and material properties on the buckling characteristics of FG-CNTRC cylindrical shells under axial compressive force. Qin et al. [33] established a general model via artificial spring approach and Ritz method to examine the vibrations of FG-CNTRC cylindrical shells under arbitrary boundary conditions. Using the linear model, Song et al. [34, 35] studied the vibrational characteristics and impact response and active vibration control of FG-CNTRC cylindrical shells via the assumed mode method. Thomas and Roy [36] presented the finite element modeling and vibration analysis of FG-CNTRC shell structures, including spherical, ellipsoidal, doubly curved and cylindrical shells. Ansari et al. [37, 38] also studied the free vibration of FG-CNTRC cylindrical, conical and spherical shells. By means of the Galerkin technique combined with the Runge–Kutta method, Due et al. [39, 40] gave the vibration responses of shear deformable FG-CNTRC cylindrical and double curved shallow shells. Shojaee et al. [41] studied the free vibration behavior of FG-CNTRC skewed cylindrical shell panels based on FSDT. Considering various boundary and loading conditions, the vibrational and postbuckling properties of FG-CNTRC cylindrical shell panels were studied by Chakraborty et al. [42] using a semi-analytical approach. Pouresmaeeli and Fazelzadeh [43] investigated the vibrational characteristics of moderately thick doubly curved FG-CNTRC cylindrical, spherical and hyperbolic paraboloid shell panels.

As mentioned above, numerous researches have been presented about the vibration analysis of FG-CNTRC structures. The aforementioned studies related to FG-CNTRC cylindrical shells mainly focus on the linear or nonlinear free vibrations and postbuckling behaviors. At present, there are few studies on the nonlinear forced vibrations of FG-CNTRC cylindrical shells under resonance conditions, which prompts us to carry out this work. The nonlinear resonance of engineering structures should be avoided, which is worth studying through forced vibration analysis. The equations of motion are derived from FSDT and von Kármán geometric nonlinearity and discretized by the Galerkin technique. By using Volmir’s assumption and the static condensation method, two reduced models are established and compared with the full-order system. A convergence study on the mode expansions is conducted considering both asymmetric and axisymmetric modes. The incremental harmonic balance method [44] is utilized to calculate the nonlinear dynamic response of FG-CNTRC cylindrical shells under radial harmonic excitation. The effects of some key factors such as the distributions and volume fraction of CNTs, geometric and excitation parameters on the resonance responses of the system are revealed with numerical examples.

2 Functionally graded carbon nanotube reinforced composite cylindrical shells

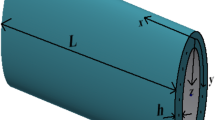
As shown in Fig. 1a, a simply supported FG-CNTRC cylindrical shell with length L, mean radius L and thickness h is considered. The origin of cylindrical coordinate system is at the center of the left end of the shell. x, $\theta$ and z axes are along the axial, circumferential and radial directions, respectively. In the present study, the FG-CNTRC cylindrical shell is under an external excitation $F(x,\theta )\cos (\varOmega t)$ in the radial direction. The FG-CNTRC cylindrical shell is composed of an isotropic matrix and CNTs. The CNTs are used as reinforcement and are dispersed in the form of uniform distribution (UD) or functionally graded distributions (FGA, FGV, FGO, FGX) along the shell’s thickness direction, as plotted in Fig. 1b. The inner surface of the FGA-CNTRC shell and the outer surface of the FGV-CNTRC shell are CNT-rich. Besides, both the outer and inner surfaces of the FGX-CNTRC shell are CNT-rich, and the mid-plane is CNT-rich for the FGO-CNTRC shell.

Fig. 1

Sketch of the FG-CNTRC cylindrical shell with different CNT distribution patterns: a geometry and cylindrical coordinate system of shell and b CNT distribution patterns in the thickness direction of shell

The material properties of FG-CNTRCs can be computed by the extended rule of mixture [19]

$$\begin{aligned} E_{11}= & {} \eta _{1} V_{\mathrm{cnt}} E_{11}^{\mathrm{cnt}} +V_{\mathrm{m}} E^{\mathrm{m}}, \end{aligned}$$

(1a)

$$\begin{aligned} \frac{\eta _{2} }{E_{22} }= & {} \frac{V_{\mathrm{cnt}} }{E_{22}^{\mathrm{cnt}} }+\frac{V_{\mathrm{m}} }{E^{\mathrm{m}}}, \end{aligned}$$

(1b)

$$\begin{aligned} \frac{\eta _{3} }{G_{12} }= & {} \frac{V_{\mathrm{cnt}} }{G_{12}^{\mathrm{cnt}} }+\frac{V_{\mathrm{m}} }{G^{\mathrm{m}}}, \end{aligned}$$

(1c)

where $E_{11}^{\mathrm{cnt}}$, $E_{22}^{\mathrm{cnt}}$ and $G_{12}^{\mathrm{cnt}}$ signify the Young’s and shear modulus of the CNTs, $E^{\mathrm{m}}$ and $G^{\mathrm{m}}$ are the properties of the matrix, and $\eta _{j}\,(j=1, 2, 3)$ denote the CNT efficiency parameters. $V_{\mathrm{m}}$ and $V_{\mathrm{cnt}}$ signify the volume fractions of matrix and CNTs, which are linear functions of z for each type of CNT distribution:

$$\begin{aligned} V_{\mathrm{cnt}} =\left\{ {{\begin{array}{ll} V_{\mathrm{cnt}}^{{*}} &{}\quad \text{(UD) } \\ \left( {1-\frac{2z}{h}} \right) V_{\mathrm{cnt}}^{{*}} &{}\quad \text{(FGA) } \\ \left( {1+\frac{2z}{h}} \right) V_{\mathrm{cnt}}^{{*}} &{}\quad \text{(FGV) } \\ 2\left( {1-\frac{2\left| z \right| }{h}} \right) V_{\mathrm{cnt}}^{{*}} &{}\quad \text{(FGO) } \\ 4\frac{\left| z \right| }{h}V_{\mathrm{cnt}}^{{*}} &{}\quad \text{(FGX) } \\ \end{array} }} \right. \quad V_{\mathrm{m}} =1-V_{\mathrm{cnt}} , \end{aligned}$$

(2)

where

$$\begin{aligned} V_{\mathrm{cnt}}^{{*}} =\frac{\varLambda _{\mathrm{cnt}} }{\varLambda _{\mathrm{cnt}} +\left( {{\rho ^{\mathrm{cnt}}} / {\rho ^{\mathrm{m}}}} \right) -\left( {{\rho ^{\mathrm{cnt}}} / {\rho ^{\mathrm{m}}}} \right) \varLambda _{\mathrm{cnt}}}, \end{aligned}$$

(3)

where $\varLambda _{\mathrm{cnt}}$ is the CNT mass fraction, and $\rho ^{\mathrm{cnt}}$ and $\rho ^{\mathrm{m}}$ signify the densities of CNT and matrix.

Besides, the Poisson’s ratio and density are obtained as

$$\begin{aligned} \begin{aligned} \nu _{12} =V_{\mathrm {cnt}} \nu _{12} ^{\mathrm {cnt}}+V_{\mathrm {m}} \nu ^{\mathrm {m}}, \quad \rho =V_{\mathrm {cnt}} \rho ^{\mathrm {cnt}}+V_{\mathrm {m}} \rho ^{\mathrm {m}} , \end{aligned} \end{aligned}$$

(4)

where $\nu _{12}^{\mathrm {cnt}}$ and $\nu ^{\mathrm{m}}$ signify the Poisson’s ratios of CNT and matrix.

3 Equations of motion

On basis of the FSDT, the displacement at an any position of the cylindrical shell is defined by

$$\begin{aligned} u_{1} (x,\theta ,z,t)= & {} u(x,\theta ,t)+z\phi _{x} (x,\theta ,t), \end{aligned}$$

(5a)

$$\begin{aligned} v_{1} (x,\theta ,z,t)= & {} v(x,\theta ,t)+z\phi _{\theta } (x,\theta ,t), \end{aligned}$$

(5b)

$$\begin{aligned} w_{1} (x,\theta ,z,t)= & {} w(x,\theta ,t), \end{aligned}$$

(5c)

where $u(x,\theta ,t)$, $v(x,\theta ,t)$ and $w(x,\theta ,t)$ signify the axial, circumferential and radial displacements in the mid-plane; $\phi _{x} (x,\theta ,t)$ and $\phi _{\theta } (x,\theta ,t)$ signify the rotations of transverse normal around x and $\theta$ axes.

In accordance with von Kármán geometric nonlinearity with Donnell’s shell theory, the strain–displacement relations are

$$\begin{aligned} \left\{ {{\begin{array}{*{20}c} {\varepsilon _{x} } \\ {\varepsilon _{\theta } } \\ {\varepsilon _{x\theta } } \\ \end{array} }} \right\} =\left\{ {{\begin{array}{*{20}c} {\varepsilon _{x}^{0} } \\ {\varepsilon _{\theta }^{0} } \\ {\varepsilon _{x\theta }^{0} } \\ \end{array} }} \right\} +z\left\{ {{\begin{array}{*{20}c} {\kappa _{x} } \\ {\kappa _{\theta } } \\ {\kappa _{x\theta } } \\ \end{array} }} \right\} , \quad \left\{ {{\begin{array}{*{20}c} {\varepsilon _{xz} } \\ {\varepsilon _{\theta z} } \\ \end{array} }} \right\} =\left\{ {{\begin{array}{*{20}c} {\varepsilon _{xz}^{0} } \\ {\varepsilon _{\theta z}^{0} } \\ \end{array} }} \right\} , \end{aligned}$$

(6)

in which the normal strains and shear strains in the mid-plane are

$$\begin{aligned} \left\{ {{\begin{array}{*{20}c} {\varepsilon _{x}^{0} } \\ {\varepsilon _{\theta }^{0} } \\ {\varepsilon _{x\theta }^{0} } \\ \end{array} }} \right\} =\left\{ {{\begin{array}{*{20}c} {\frac{\partial u}{\partial x}+\frac{1}{2}\left( {\frac{\partial w}{\partial x}} \right) ^{2}} \\ {\frac{1}{R}\frac{\partial v}{\partial \theta }+\frac{w}{R}+\frac{1}{2}\left( {\frac{1}{R}\frac{\partial w}{\partial \theta }} \right) ^{2}} \\ {\frac{1}{R}\frac{\partial u}{\partial \theta }+\frac{\partial v}{\partial x}+\frac{1}{R}\frac{\partial w}{\partial x}\frac{\partial w}{\partial \theta }} \\ \end{array} }} \right\} , \quad \left\{ {{\begin{array}{*{20}c} {\varepsilon _{xz}^{0} } \\ {\varepsilon _{\theta z}^{0} } \\ \end{array} }} \right\} =\left\{ {{\begin{array}{*{20}c} {\phi _{x} +\frac{\partial w}{\partial x}} \\ {\phi _{\theta } +\frac{\partial w}{R\partial \theta }} \\ \end{array} }} \right\} , \end{aligned}$$

(7)

and the changes of curvature and torsion are

$$\begin{aligned} \left\{ {{\begin{array}{*{20}c} {\kappa _{x} } \\ {\kappa _{\theta } } \\ {\kappa _{x\theta } } \\ \end{array} }} \right\} =\left\{ {{\begin{array}{*{20}c} {\frac{\partial \phi _{x} }{\partial x}} \\ {\frac{\partial \phi _{\theta } }{R\partial \theta }} \\ {\frac{1}{R}\frac{\partial \phi _{x} }{\partial \theta }+\frac{\partial \phi _{\theta } }{\partial x}} \\ \end{array} }} \right\} . \end{aligned}$$

(8)

The normal stress and shear stress can be expressed from Hooke’s law as

$$\begin{aligned} \left\{ {{\begin{array}{*{20}c} {\sigma _{x} } \\ {\sigma _{\theta } } \\ {\sigma _{\theta z} } \\ {\sigma _{xz} } \\ {\sigma _{x\theta } } \\ \end{array} }} \right\} =\left[ {{\begin{array}{*{20}c} {Q_{11} } &{} {Q_{12} } &{} 0 &{} 0 &{} 0 \\ {Q_{12} } &{} {Q_{22} } &{} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} {Q_{44} } &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{} {Q_{55} } &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 &{} {Q_{66} } \\ \end{array} }} \right] \left\{ {{\begin{array}{*{20}c} {\varepsilon _{x} } \\ {\varepsilon _{\theta } } \\ {\varepsilon _{\theta z} } \\ {\varepsilon _{xz} } \\ {\varepsilon _{x\theta } } \\ \end{array} }} \right\} , \end{aligned}$$

(9)

where the effective elasticity coefficients are

$$\begin{aligned} Q_{11} =\frac{E_{11} }{1-\nu _{12} \nu _{21}}, \quad Q_{22} =\frac{E_{22} }{1-\nu _{12} \nu _{21}}, \quad Q_{12} =\frac{\nu _{21} E_{11} }{1-\nu _{12} \nu _{21}}, \quad Q_{44} =G_{23}, \quad Q_{55} =G_{13}, \quad Q_{66} =G_{12}.\nonumber \\ \end{aligned}$$

(10)

The force and moment expressions could be acquired by integrating the stress components and their moments over the thickness of the shell

$$\begin{aligned} \left\{ {{\begin{array}{*{20}c} {N_{x} } \\ {N_{\theta } } \\ {N_{x\theta } } \\ \end{array} }} \right\} =\int _{-h/2}^{h/2} {\left\{ {{\begin{array}{*{20}c} {\sigma _{x} } \\ {\sigma _{\theta } } \\ {\sigma _{x\theta } } \\ \end{array} }} \right\} } \mathrm{d}z, \quad \left\{ {{\begin{array}{*{20}c} {M_{x} } \\ {M_{\theta } } \\ {M_{x\theta } } \\ \end{array} }} \right\} =\int _{-h/2}^{h/2} {\left\{ {{\begin{array}{*{20}c} {\sigma _{x} z} \\ {\sigma _{\theta } z} \\ {\sigma _{x\theta } z} \\ \end{array} }} \right\} } \mathrm{d}z, \quad \left\{ {{\begin{array}{*{20}c} {Q_{x} } \\ {Q_{\theta } } \\ \end{array} }} \right\} =\int _{-h/2}^{h/2} {\left\{ {{\begin{array}{*{20}c} {\sigma _{xz} } \\ {\sigma _{\theta z} } \\ \end{array} }} \right\} } \mathrm{d}z, \end{aligned}$$

(11)

Substituting Eqs. (6–8, 10) into Eq. (9) and then substituting the results into Eq. (11) gives rise to the constitutive relations as

$$\begin{aligned} \left\{ {{\begin{array}{*{20}c} {N_{x} } \\ {N_{\theta } } \\ {N_{x\theta } } \\ {M_{x} } \\ {M_{\theta } } \\ {M_{x\theta } } \\ \end{array} }} \right\} =\left[ {{\begin{array}{*{20}c} {A_{11} } &{} {A_{12} } &{} 0 &{} {B_{11} } &{} {B_{12} } &{} 0 \\ {A_{12} } &{} {A_{22} } &{} 0 &{} {B_{12} } &{} {B_{22} } &{} 0 \\ 0 &{} 0 &{} {A_{66} } &{} 0 &{} 0 &{} {B_{66} } \\ {B_{11} } &{} {B_{12} } &{} 0 &{} {D_{11} } &{} {D_{12} } &{} 0 \\ {B_{12} } &{} {B_{22} } &{} 0 &{} {D_{12} } &{} {D_{22} } &{} 0 \\ 0 &{} 0 &{} {B_{66} } &{} 0 &{} 0 &{} {D_{66} } \\ \end{array} }} \right] \left\{ {{\begin{array}{*{20}c} {\varepsilon _{x}^{0} } \\ {\varepsilon _{\theta }^{0} } \\ {\varepsilon _{x\theta }^{0} } \\ {\kappa _{x} } \\ {\kappa _{\theta } } \\ {\kappa _{x\theta } } \\ \end{array} }} \right\} , \quad \left\{ {{\begin{array}{*{20}c} {Q_{\theta } } \\ {Q_{x} } \\ \end{array} }} \right\} =\left[ {{\begin{array}{*{20}c} {A_{44} } &{} 0 \\ 0 &{} {A_{55} } \\ \end{array} }} \right] \left\{ {{\begin{array}{*{20}c} {\varepsilon _{\theta z}^{0} } \\ {\varepsilon _{xz}^{0} } \\ \end{array} }} \right\} , \end{aligned}$$

(12)

where the stiffness coefficients are defined by

$$\begin{aligned} (A_{ij} ,B_{ij} ,D_{ij} )= & {} \int _{-h/2}^{h/2} {Q_{ij} } (1,z,z^{2})\mathrm{d}z\quad \left( {i,j=1,\;2,\;6} \right) , \end{aligned}$$

(13a)

$$\begin{aligned} A_{44}= & {} k_{\mathrm{s}} \int _{-h/2}^{h/2} {Q_{44} } \mathrm{d}z, \quad A_{55} =k_{\mathrm{s}} \int _{-h/2}^{h/2} {Q_{55} } \hbox {d }z, \end{aligned}$$

(13b)

in which $k_{\mathrm{s}} =5/6$ is the shear correction factor.

The potential energy V and kinetic energy T of the shell are

$$\begin{aligned} T= & {} \frac{1}{2}\int _0^L {\int _0^{2\pi } {\int _{-h/2}^{h/2} {\rho (z)\left[ {\left( {\frac{\partial u}{\partial t}+z\frac{\partial \phi _{x} }{\partial t}} \right) ^{2}+\left( {\frac{\partial v}{\partial t}+z\frac{\partial \phi _{\theta } }{\partial t}} \right) ^{2}+\left( {\frac{\partial w}{\partial t}} \right) ^{2}} \right] } } } R\,\hbox {d}\,z\,\hbox {d}\,\theta \,\hbox {d}\,x, \end{aligned}$$

(14)

$$\begin{aligned} V= & {} \frac{1}{2}\int _0^L {\int _0^{2\pi } {\int _{-h/2}^{h/2} {\left( {\sigma _{x} \varepsilon _{x} +\sigma _{\theta } \varepsilon _{\theta } +\sigma _{x\theta } \varepsilon _{x\theta } +\sigma _{xz} \varepsilon _{xz} +\sigma _{\theta z} \varepsilon _{\theta z} } \right) } } } R\,\hbox {d}\,z\,\hbox {d}\,\theta \,\hbox {d}\,x. \end{aligned}$$

(15)

The virtual work done by the radial excitation can be expressed as

$$\begin{aligned} \delta W_{T} =\int _0^L {\int _0^{2\pi } {F(x,\theta )\cos (\varOmega t)\delta w} } R\mathrm{d}\theta \mathrm{d}x. \end{aligned}$$

(16)

Substituting Eqs. (14)–(16) into Hamilton’s principle

$$\begin{aligned} \int _{t_{1} }^{t_{2} } {(\updelta T-\updelta V)} \mathrm{d}t+\int _{t_{1} }^{t_{2} } {\updelta W_{\mathrm{T}} \mathrm{d}t} =0, \end{aligned}$$

(17)

the equations of motion in terms of the force and moment can be obtained:

$$\begin{aligned}&{\delta u:} \quad {\frac{\partial N_{x} }{\partial x}+\frac{1}{R}\frac{\partial N_{x\theta } }{\partial \theta }=I_{0} \frac{\partial ^{2}u}{\partial t^{2}}+I_{1} \frac{\partial ^{2}\phi _{x} }{\partial t^{2}}}, \end{aligned}$$

(18a)

$$\begin{aligned}&{\delta v:} \quad {\frac{\partial N_{x\theta } }{\partial x}+\frac{1}{R}\frac{\partial N_{\theta } }{\partial \theta }=I_{0} \frac{\partial ^{2}v}{\partial t^{2}}+I_{1} \frac{\partial ^{2}\phi _{\theta } }{\partial t^{2}}}, \end{aligned}$$

(18b)

$$\begin{aligned}&{\delta w:}\quad \frac{\partial Q_{x} }{\partial x}+\frac{1}{R}\frac{\partial Q_{\theta } }{\partial \theta }-\frac{N_{\theta } }{R}+\frac{\partial }{\partial x}\left( {N_{x} \frac{\partial w}{\partial x}+\frac{N_{x\theta } }{R}\frac{\partial w}{\partial \theta }} \right) \nonumber \\&\qquad +\frac{\partial }{\partial \theta }\left( {\frac{N_{\theta } }{R^{2}}\frac{\partial w}{\partial \theta }+\frac{N_{x\theta } }{R}\frac{\partial w}{\partial x}} \right) +F(x,\theta )\cos (\varOmega t)=I_{0} \frac{\partial ^{2}w}{\partial t^{2}}, \end{aligned}$$

(18c)

$$\begin{aligned}&{\delta \phi _{x} :\;} \quad {\frac{\partial M_{x} }{\partial x}+\frac{1}{R}\frac{\partial M_{x\theta } }{\partial \theta }-Q_{x} =I_{1} \frac{\partial ^{2}u}{\partial t^{2}}+I_{2} \frac{\partial ^{2}\phi _{x} }{\partial t^{2}}}, \end{aligned}$$

(18d)

$$\begin{aligned}&{\delta \phi _{\theta } :} \quad {\frac{1}{R}\frac{\partial M_{\theta } }{\partial \theta }+\frac{\partial M_{x\theta } }{\partial x}-Q_{\theta } =I_{1} \frac{\partial ^{2}v}{\partial t^{2}}+I_{2} \frac{\partial ^{2}\phi _{\theta }}{\partial t^{2}}} , \end{aligned}$$

(18e)

in which the inertia terms are

$$\begin{aligned} \left\{ {I_{1} ,I_{2} ,I_{3} } \right\} =\int _{{-h} / 2}^{h/2} {\rho (z)\left\{ {\;1,z,z^{2}} \right\} } \mathrm{d}z. \end{aligned}$$

(19)

Substituting the results obtained from Eq. (12) into Eq. (18), the nonlinear equations of motion in terms of displacements and rotations can be obtained. The dimensionless parameters are introduced as follows:

$$\begin{aligned}&\left( {x^{*},\theta ^{*},z^{*}} \right) =\left( {\frac{x}{L},\theta ,\frac{z}{h}} \right) , \quad \lambda _{1} =\frac{L}{R}, \quad \lambda _{2} =\frac{h}{R}, \quad \lambda _{3} =\frac{h}{L}, \quad \left( {u^{*},v^{*},w^{*}} \right) =\frac{(u,v,w)}{h}, \end{aligned}$$

(20a)

$$\begin{aligned}&t^{*}=\frac{t}{L}\sqrt{\frac{A_{110} }{I_{10} }},\quad \varOmega ^{*}=\varOmega L\sqrt{\frac{I_{10} }{A_{110} }},\quad \quad F^{*}=\frac{FL^{2}}{hA_{110}}, \end{aligned}$$

(20b)

$$\begin{aligned}&(a_{11} ,a_{12} ,a_{22} ,a_{44} ,a_{55} ,a_{66} )=\left( {\frac{A_{11} }{A_{110} },\frac{A_{12} }{A_{110} },\frac{A_{22} }{A_{110} },\frac{A_{44} }{A_{110} },\frac{A_{55} }{A_{110} },\frac{A_{66} }{A_{110} }} \right) , \end{aligned}$$

(20c)

$$\begin{aligned}&(b_{11} ,b_{12} ,b_{22} ,b_{66} )=\left( {\frac{B_{11} }{A_{110} h},\frac{B_{12} }{A_{110} h},\frac{B_{22} }{A_{110} h},\frac{B_{66} }{A_{110} h}} \right) , \end{aligned}$$

(20d)

$$\begin{aligned}&(d_{11} ,d_{12} ,d_{22} ,d_{66} )=\left( {\frac{D_{11} }{A_{110} h^{2}},\frac{D_{12} }{A_{110} h^{2}},\frac{D_{22} }{A_{110} h^{2}},\frac{D_{66} }{A_{110} h^{2}}} \right) , \end{aligned}$$

(20e)

$$\begin{aligned}&\left( {I_{1}^{*} ,I_{2}^{*} ,I_{3}^{*} } \right) =\left( {\frac{I_{1} }{I_{10} },\frac{I_{2} }{I_{10} h},\frac{I_{3} }{I_{10} h^{2}}} \right) , \end{aligned}$$

(20f)

where ${A}_{{110}}$ and ${I}_{10}$ the values of ${A}_{\mathrm {11}}$ and ${I}_{\mathrm {1}}$ for a homogeneous cylindrical shell made of polymer matrix material.

Omitting the asterisk for brevity, the resulting dimensionless partial differential equations (PDEs) of motion are given as

$$\begin{aligned}&{\delta u:} \quad a_{11} \frac{\partial ^{2}u}{\partial x^{2}}+a_{66} \lambda _{1}^{2} \frac{\partial ^{2}u}{\partial \theta ^{2}}+\left( {a_{12} +a_{66} } \right) \lambda _{1} \frac{\partial ^{2}v}{\partial x\partial \theta }+a_{12} \lambda _{1} \frac{\partial w}{\partial x}\nonumber \\&\qquad \quad +\,b_{11} \frac{\partial ^{2}\phi _{x} }{\partial x^{2}}+b_{66} \lambda _{1}^{2} \frac{\partial ^{2}\phi _{x} }{\partial \theta ^{2}}+\left( {b_{12} +b_{66} } \right) \lambda _{1} \frac{\partial ^{2}\phi _{\theta } }{\partial x\partial \theta } \nonumber \\&\qquad \quad +\,\frac{\partial w}{\partial x}\left( {a_{11} \lambda _{3} \frac{\partial ^{2}w}{\partial x^{2}}+a_{66} \lambda _{1} \lambda _{2} \frac{\partial ^{2}w}{\partial \theta ^{2}}} \right) +\left( {a_{12} +a_{66} } \right) \lambda _{1} \lambda _{2} \frac{\partial w}{\partial \theta }\frac{\partial ^{2}w}{\partial x\partial \theta }=I_{1} \frac{\partial ^{2}u}{\partial t^{2}}+I_{2} \frac{\partial ^{2}\phi _{x} }{\partial t^{2}}, \end{aligned}$$

(21a)

$$\begin{aligned}&{\delta v:} \quad \left( {a_{12} +a_{66} } \right) \lambda _{1} \frac{\partial ^{2}u}{\partial x\partial \theta }+a_{66} \frac{\partial ^{2}v}{\partial x^{2}}+a_{22} \lambda _{1}^{2} \frac{\partial ^{2}v}{\partial \theta ^{2}}+a_{22} \lambda _{1}^{2} \frac{\partial w}{\partial x}\nonumber \\&\qquad \quad +\,\left( {b_{12} +b_{66} } \right) \lambda _{1} \frac{\partial ^{2}\phi _{x} }{\partial x\partial \theta }+b_{66} \frac{\partial ^{2}\phi _{\theta } }{\partial x^{2}}+b_{22} \lambda _{1}^{2} \frac{\partial ^{2}\phi _{\theta } }{\partial \theta ^{2}} \nonumber \\&\qquad \quad +\,\left( {a_{12} +a_{66} } \right) \lambda _{2} \frac{\partial w}{\partial x}\frac{\partial ^{2}w}{\partial x\partial \theta }+\frac{\partial w}{\partial \theta }\left( {a_{66} \lambda _{2} \frac{\partial ^{2}w}{\partial x^{2}}+a_{22} \lambda _{1}^{2} \lambda _{2} \frac{\partial ^{2}w}{\partial \theta ^{2}}} \right) =I_{1} \frac{\partial ^{2}v}{\partial t^{2}}+I_{2} \frac{\partial ^{2}\phi _{\theta } }{\partial t^{2}}, \end{aligned}$$

(21b)

$$\begin{aligned}&{\delta w:} \quad -a_{12} \lambda _{1} \frac{\partial u}{\partial x}-a_{22} \lambda _{1}^{2} \frac{\partial v}{\partial \theta }+a_{55} \frac{\partial ^{2}w}{\partial x^{2}}+a_{44} \lambda _{1}^{2} \frac{\partial ^{2}w}{\partial \theta ^{2}}-a_{22} \lambda _{1}^{2} w\nonumber \\&\qquad \quad +\,\left( {\frac{a_{55} }{\lambda _{3} }-b_{12} \lambda _{1} } \right) \frac{\partial \phi _{x} }{\partial x}+\left( {a_{44} \frac{\lambda _{1} }{\lambda _{3} }-b_{22} \lambda _{1}^{2} } \right) \frac{\partial \phi _{\theta } }{\partial \theta } \nonumber \\&\qquad \quad +\,\frac{\partial w}{\partial x}\left( {a_{11} \lambda _{3} \frac{\partial ^{2}u}{\partial x^{2}}+a_{66} \lambda _{1} \lambda _{2} \frac{\partial ^{2}u}{\partial \theta ^{2}}} \right) +\left( {a_{12} +a_{66} } \right) \lambda _{1} \lambda _{2} \frac{\partial w}{\partial \theta }\frac{\partial ^{2}u}{\partial x\partial \theta }\nonumber \\&\qquad \quad +\frac{\partial u}{\partial x}\left( {a_{11} \lambda _{3} \frac{\partial ^{2}w}{\partial x^{2}}+a_{12} \lambda _{1} \lambda _{2} \frac{\partial ^{2}w}{\partial \theta ^{2}}} \right) \nonumber \\&\qquad \quad +\,2a_{66} \lambda _{1} \lambda _{2} \frac{\partial u}{\partial \theta }\frac{\partial ^{2}w}{\partial x\partial \theta }+\left( {a_{12} +a_{66} } \right) \lambda _{2} \frac{\partial w}{\partial x}\frac{\partial ^{2}v}{\partial x\partial \theta }+\frac{\partial w}{\partial \theta }\left( {a_{66} \lambda _{2} \frac{\partial ^{2}v}{\partial x^{2}}+a_{22} \lambda _{1}^{2} \lambda _{2} \frac{\partial ^{2}v}{\partial \theta ^{2}}} \right) \nonumber \\&\qquad \quad +2a_{66} \lambda _{2} \frac{\partial v}{\partial x}\frac{\partial ^{2}w}{\partial x\partial \theta } \nonumber \\&\qquad \quad +\,\frac{\partial v}{\partial \theta }\left( {a_{12} \lambda _{2} \frac{\partial ^{2}w}{\partial x^{2}}+a_{22} \lambda _{1}^{2} \lambda _{2} \frac{\partial ^{2}w}{\partial \theta ^{2}}} \right) +\frac{a_{12} }{2}\lambda _{2} \left( {\frac{\partial w}{\partial x}} \right) ^{2}+\frac{a_{22} }{2}\lambda _{1}^{2} \lambda _{2} \left( {\frac{\partial w}{\partial \theta }} \right) ^{2}\nonumber \\&\qquad \quad +\,\left( {a_{12} \lambda _{2} \frac{\partial ^{2}w}{\partial x^{2}}+a_{22} \lambda _{1}^{2} \lambda _{2} \frac{\partial ^{2}w}{\partial \theta ^{2}}} \right) w \nonumber \\&\qquad \quad +\,\frac{\partial w}{\partial x}\left( {b_{11} \lambda _{3} \frac{\partial ^{2}\phi _{x} }{\partial x^{2}}+b_{66} \lambda _{1} \lambda _{2} \frac{\partial ^{2}\phi _{x} }{\partial \theta ^{2}}} \right) +\left( {b_{12} +b_{66} } \right) \lambda _{1} \lambda _{2} \frac{\partial w}{\partial \theta }\frac{\partial ^{2}\phi _{x} }{\partial x\partial \theta }\nonumber \\&\qquad \quad +\frac{\partial \phi _{x} }{\partial x}\left( {b_{11} \lambda _{3} \frac{\partial ^{2}w}{\partial x^{2}}+b_{12} \lambda _{1} \lambda _{2} \frac{\partial ^{2}w}{\partial \theta ^{2}}} \right) \nonumber \\&\qquad \quad +\,2b_{66} \lambda _{1} \lambda _{2} \frac{\partial \phi _{x} }{\partial \theta }\frac{\partial ^{2}w}{\partial x\partial \theta }+\left( {b_{12} +b_{66} } \right) \lambda _{2} \frac{\partial w}{\partial x}\frac{\partial ^{2}\phi _{\theta } }{\partial x\partial \theta }+\frac{\partial w}{\partial \theta }\left( {b_{66} \lambda _{2} \frac{\partial ^{2}\phi _{\theta } }{\partial x^{2}}+b_{22} \lambda _{1}^{2} \lambda _{2} \frac{\partial ^{2}\phi _{\theta } }{\partial \theta ^{2}}} \right) \nonumber \\&\qquad \quad +\,2b_{66} \lambda _{2} \frac{\partial \phi _{\theta } }{\partial x}\frac{\partial ^{2}w}{\partial x\partial \theta } \nonumber \\&\qquad \quad +\,\frac{\partial \phi _{\theta } }{\partial \theta }\left( {b_{12} \lambda _{2} \frac{\partial ^{2}w}{\partial x^{2}}+b_{22} \lambda _{1}^{2} \lambda _{2} \frac{\partial ^{2}w}{\partial \theta ^{2}}} \right) +\left( {\frac{3a_{11} }{2}\lambda _{3}^{2} \frac{\partial ^{2}w}{\partial x^{2}}+\frac{a_{12} +2a_{66} }{2}\lambda _{2}^{2} \frac{\partial ^{2}w}{\partial \theta ^{2}}} \right) \left( {\frac{\partial w}{\partial x}} \right) ^{2} \nonumber \\&\qquad \quad +\,\left( {\frac{a_{12} +2a_{66} }{2}\lambda _{2}^{2} \frac{\partial ^{2}w}{\partial x^{2}}+\frac{3a_{22} }{2}\lambda _{1}^{2} \lambda _{2}^{2} \frac{\partial ^{2}w}{\partial \theta ^{2}}} \right) \left( {\frac{\partial w}{\partial \theta }} \right) ^{2}+\left( {2a_{12} +4a_{66} } \right) \lambda _{2}^{2} \frac{\partial w}{\partial x}\frac{\partial w}{\partial \theta }\frac{\partial ^{2}w}{\partial x\partial \theta } \nonumber \\&\qquad \quad +\,F\left( {x,\theta } \right) \cos (\varOmega t)=I_{1} \frac{\partial ^{2}w}{\partial t^{2}} , \end{aligned}$$

(21c)

$$\begin{aligned}&{\delta \phi _{x} :\;} \quad b_{11} \frac{\partial ^{2}u}{\partial x^{2}}+b_{66} \lambda _{1}^{2} \frac{\partial ^{2}u}{\partial \theta ^{2}}+\left( {b_{12} +b_{66} } \right) \lambda _{1} \frac{\partial ^{2}v}{\partial x\partial \theta }+\left( {b_{12} \lambda _{1} -\frac{a_{55} }{\lambda _{3} }} \right) \frac{\partial w}{\partial x}\nonumber \\&\qquad \quad +\,d_{11} \frac{\partial ^{2}\phi _{x} }{\partial x^{2}}+d_{66} \lambda _{1}^{2} \frac{\partial ^{2}\phi _{x} }{\partial \theta ^{2}}-\frac{a_{55} }{\lambda _{3}^{2} }\phi _{x} \nonumber \\&\qquad \quad +\,\left( {d_{12} +d_{66} } \right) \lambda _{1} \frac{\partial ^{2}\phi _{\theta } }{\partial x\partial \theta }+\frac{\partial w}{\partial x}\left( {b_{11} \lambda _{3} \frac{\partial ^{2}w}{\partial x^{2}}+b_{66} \lambda _{1} \lambda _{2} \frac{\partial ^{2}w}{\partial \theta ^{2}}} \right) \nonumber \\&\qquad \quad +\,\left( {b_{12} +b_{66} } \right) \lambda _{1} \lambda _{2} \frac{\partial w}{\partial \theta }\frac{\partial ^{2}w}{\partial x\partial \theta }=I_{2} \frac{\partial ^{2}u}{\partial t^{2}}+I_{3} \frac{\partial ^{2}\phi _{x} }{\partial t^{2}} , \end{aligned}$$

(21d)

$$\begin{aligned}&{\delta \phi _{\theta } :\;} \quad \left( {b_{12} +b_{66} } \right) \lambda _{1} \frac{\partial ^{2}u}{\partial x\partial \theta }+b_{66} \frac{\partial ^{2}v}{\partial x^{2}}+b_{22} \lambda _{1}^{2} \frac{\partial ^{2}v}{\partial \theta ^{2}}+\left( {b_{22} \lambda _{1}^{2} -a_{44} \frac{\lambda _{1} }{\lambda _{3} }} \right) \frac{\partial w}{\partial \theta }\nonumber \\&\qquad \quad +\,\left( {d_{12} +d_{66} } \right) \lambda _{1} \frac{\partial ^{2}\phi _{x} }{\partial x\partial \theta }+d_{66} \frac{\partial ^{2}\phi _{\theta } }{\partial x^{2}} \nonumber \\&\qquad \quad +\,d_{22} \lambda _{1}^{2} \frac{\partial ^{2}\phi _{\theta } }{\partial \theta ^{2}}-\frac{a_{44} }{\lambda _{3}^{2} }\phi _{\theta } +\left( {b_{12} +b_{66} } \right) \lambda _{2} \frac{\partial w}{\partial x}\frac{\partial ^{2}w}{\partial x\partial \theta }\nonumber \\&\qquad \quad +\,\frac{\partial w}{\partial \theta }\left( {b_{66} \lambda _{2} \frac{\partial ^{2}w}{\partial x^{2}}+b_{22} \lambda _{1}^{2} \lambda _{2} \frac{\partial ^{2}w}{\partial \theta ^{2}}} \right) =I_{2} \frac{\partial ^{2}v}{\partial t^{2}}+I_{3} \frac{\partial ^{2}\phi _{\theta } }{\partial t^{2}}. \end{aligned}$$

(21e)

4 Solution procedure

4.1 Model reduction

The mathematical expressions of simply supported boundary conditions are [45]

$$\begin{aligned} v=w=\phi _{\theta } =N_{x} =M_{x} =0\quad (x=0\quad \text{ and }\quad L). \end{aligned}$$

(22)

The Galerkin procedure is utilized to discretize PDEs. Considering both the asymmetric and axisymmetric modes, the approximate displacement functions to satisfy the boundary conditions can be written as [45, 46]

$$\begin{aligned} u(x,\theta ,t)= & {} \sum \limits _{m=1}^{M_{1} } {\sum \limits _{j=1}^J {u_{m,jn} (t)\cos (m\pi x)\cos (jn\theta )+\sum \limits _{m=1}^{M_{2} } {u_{(2m-1),0} (t)\cos ((2m-1)\pi x)} } }, \end{aligned}$$

(23a)

$$\begin{aligned} v(x,\theta ,t)= & {} \sum \limits _{m=1}^{M_{1} } {\sum \limits _{j=1}^J {v_{m,jn} (t)\sin (m\pi x)\sin (jn\theta )}}, \end{aligned}$$

(23b)

$$\begin{aligned} w(x,\theta ,t)= & {} \sum \limits _{m=1}^{M_{1} } {\sum \limits _{j=1}^J {w_{m,jn} (t)\sin (m\pi x)\cos (jn\theta )} } +\sum \limits _{m=1}^{M_{2} } {w_{(2m-1),0} (t)\sin ((2m-1)\pi x)}, \end{aligned}$$

(23c)

$$\begin{aligned} \phi _{x} (x,\theta ,t)= & {} \sum \limits _{m=1}^{M_{1} } {\sum \limits _{j=1}^J {\phi _{xm,jn} (t)\cos (m\pi x)\cos (jn\theta )+\sum \limits _{m=1}^{M_{2} } {\phi _{x(2m-1),0} (t)\cos ((2m-1)\pi x)} }}, \end{aligned}$$

(23d)

$$\begin{aligned} \phi _{\theta } (x,\theta ,t)= & {} \sum \limits _{m=1}^{M_{1} } {\sum \limits _{j=1}^J {\phi _{\theta m,jn} (t)\sin (m\pi x)\sin (jn\theta )} }, \end{aligned}$$

(23e)

where m and n, respectively, denotes the axial half wave number and circumferential wave number, $u_{m,jn} (t)$, $v_{m,jn} (t)$, $w_{m,jn} (t)$, $\phi _{xm,jn} (t)$ and $\phi _{\theta m,jn} (t)$ are generalized coordinates of asymmetric modes $({n}>0)$, $u_{(2m-1),0}$, $w_{(2m-1),0}$ and $\phi _{x(2m-1),0} (t)$ are generalized coordinates of axisymmetric modes $(n=0)$.

The external radial modal excitation is defined as $F\left( x,\theta ,t \right) =f\sin (m\pi x)\cos (n\theta )\cos (\varOmega t)$. Introducing Eq. (23) into Eq. (21) and executing the Galerkin integration yields the nonlinear ordinary differential equations (ODEs) in matrix-vector form as

$$\begin{aligned} {\mathbf{M}}\ddot{{\mathbf{q}}}+({\mathbf{K}}+{\mathbf{K}}^{(2)}+{\mathbf{K}}^{(3)}){\mathbf{q}}={\mathbf{F}}\cos (\varOmega t), \end{aligned}$$

(24)

where ${\mathbf{q}}=[{\mathbf{q}}_{u}^{\mathrm{T}} ,{\mathbf{q}}_{v}^{\mathrm{T}} ,{\mathbf{q}}_{w}^{\mathrm{T}} ,{\mathbf{q}}_{\phi _{x}}^{\mathrm{T}} ,{\mathbf{q}}_{\phi _{\theta } }^{\mathrm{T}} ]^{\mathrm{T}}$ and ${\mathbf{F}}=[{\mathbf{0}},\;{\mathbf{0}},{\mathbf{F}}_{w} ,\;{\mathbf{0}},\;{\mathbf{0}}]^{\mathrm{T}}$, respectively, represent the generalized coordinate and force vectors, ${\varOmega }$ is the frequency of radial harmonic excitation, and ${\mathrm {\mathbf {M}}}$, ${\mathrm {\mathbf {K}}}$, ${\mathrm {\mathbf {K}}}^{(2)}$ and ${\mathrm {\mathbf {K}}}^{(3)}$ are the mass, linear stiffness, quadratic and cubic nonlinear stiffness matrices, which, respectively, take the form

$$\begin{aligned} {\mathbf{M}}= & {} \left[ {{\begin{array}{*{20}c} {{\mathbf{M}}_{\mathrm{11}} } &{} {{\mathbf{0}}} &{} {{\mathbf{0}}} &{} {{\mathbf{M}}_{\mathrm{14}} } &{} {{\mathbf{0}}} \\ {{\mathbf{0}}} &{} {{\mathbf{M}}_{\mathrm{22}} } &{} {{\mathbf{0}}} &{} {{\mathbf{0}}} &{} {{\mathbf{M}}_{\mathrm{25}} } \\ {{\mathbf{0}}} &{} {{\mathbf{0}}} &{} {{\mathbf{M}}_{\mathrm{33}} } &{} {{\mathbf{0}}} &{} {{\mathbf{0}}} \\ {{\mathbf{M}}_{\mathrm{41}} } &{} {{\mathbf{0}}} &{} {{\mathbf{0}}} &{} {{\mathbf{M}}_{\mathrm{44}} } &{} {{\mathbf{0}}} \\ {{\mathbf{0}}} &{} {{\mathbf{M}}_{\mathrm{52}} } &{} {{\mathbf{0}}} &{} {{\mathbf{0}}} &{} {{\mathbf{M}}_{\mathrm{55}} } \\ \end{array} }} \right] , \quad {\mathbf{K}}=\left[ {{\begin{array}{*{20}c} {{\mathbf{K}}_{11} } &{} {{\mathbf{K}}_{12} } &{} {{\mathbf{K}}_{13} } &{} {{\mathbf{K}}_{14} } &{} {{\mathbf{K}}_{15} } \\ {{\mathbf{K}}_{21} } &{} {{\mathbf{K}}_{\mathrm{22}} } &{} {{\mathbf{K}}_{\mathrm{23}} } &{} {{\mathbf{K}}_{\mathrm{24}} } &{} {{\mathbf{K}}_{\mathrm{25}} } \\ {{\mathbf{K}}_{\mathrm{31}} } &{} {{\mathbf{K}}_{\mathrm{32}} } &{} {{\mathbf{K}}_{\mathrm{33}} } &{} {{\mathbf{K}}_{\mathrm{34}} } &{} {{\mathbf{K}}_{\mathrm{35}} } \\ {{\mathbf{K}}_{\mathrm{41}} } &{} {{\mathbf{K}}_{\mathrm{42}} } &{} {{\mathbf{K}}_{\mathrm{43}} } &{} {{\mathbf{K}}_{\mathrm{44}} } &{} {{\mathbf{K}}_{\mathrm{45}} } \\ {{\mathbf{K}}_{\mathrm{51}} } &{} {{\mathbf{K}}_{\mathrm{52}} } &{} {{\mathbf{K}}_{\mathrm{53}} } &{} {{\mathbf{K}}_{\mathrm{54}} } &{} {{\mathbf{K}}_{\mathrm{55}} } \\ \end{array} }} \right] , \end{aligned}$$

(25a)

$$\begin{aligned} {\mathbf{K}}^{(2)}= & {} \left[ {{\begin{array}{*{20}c} {{\mathbf{0}}} &{} {{\mathbf{0}}} &{} {{\mathbf{K}}_{13}^{(2)} } &{} {{\mathbf{0}}} &{} {{\mathbf{0}}} \\ {{\mathbf{0}}} &{} {{\mathbf{0}}} &{} {{\mathbf{K}}_{23}^{(2)} } &{} {{\mathbf{0}}} &{} {{\mathbf{0}}} \\ {{\mathbf{K}}_{31}^{(2)} } &{} {{\mathbf{K}}_{32}^{(2)} } &{} {{\mathbf{K}}_{33}^{(2)} } &{} {{\mathbf{K}}_{34}^{(2)} } &{} {{\mathbf{K}}_{35}^{(2)} } \\ {{\mathbf{0}}} &{} {{\mathbf{0}}} &{} {{\mathbf{K}}_{43}^{(2)} } &{} {{\mathbf{0}}} &{} {{\mathbf{0}}} \\ {{\mathbf{0}}} &{} {{\mathbf{0}}} &{} {{\mathbf{K}}_{53}^{(2)} } &{} {{\mathbf{0}}} &{} {{\mathbf{0}}} \\ \end{array} }} \right] , \quad {\mathbf{K}}^{(3)}=\left[ {{\begin{array}{*{20}c} {{\mathbf{0}}} &{} {{\mathbf{0}}} &{} {{\mathbf{0}}} &{} {{\mathbf{0}}} &{} {{\mathbf{0}}} \\ {{\mathbf{0}}} &{} {{\mathbf{0}}} &{} {{\mathbf{0}}} &{} {{\mathbf{0}}} &{} {{\mathbf{0}}} \\ {{\mathbf{0}}} &{} {{\mathbf{0}}} &{} {{\mathbf{K}}_{33}^{(3)} } &{} {{\mathbf{0}}} &{} {{\mathbf{0}}} \\ {{\mathbf{0}}} &{} {{\mathbf{0}}} &{} {{\mathbf{0}}} &{} {{\mathbf{0}}} &{} {{\mathbf{0}}} \\ {{\mathbf{0}}} &{} {{\mathbf{0}}} &{} {{\mathbf{0}}} &{} {{\mathbf{0}}} &{} {{\mathbf{0}}} \\ \end{array} }} \right] . \end{aligned}$$

(25b)

The elements of the above matrices are defined in Appendix A.

To reduce the degrees of freedom, the nonlinear dynamic model is simplified by using Volmir’s assumption and the static condensation method, respectively. First, the equations of motion can be rewritten as

$$\begin{aligned}&{\mathbf{K}}_{11} {\mathbf{q}}_{u} +{\mathbf{K}}_{12} {\mathbf{q}}_{v} +{\mathbf{K}}_{13} {\mathbf{q}}_{w} +{\mathbf{K}}_{14} {\mathbf{q}}_{\phi _{x} } +{\mathbf{K}}_{15} {\mathbf{q}}_{\phi _{\theta } } +{\mathbf{K}}_{13}^{(2)} {\mathbf{q}}_{w} =-{\mathbf{M}}_{\mathrm{11}} {{\ddot{\mathbf{q}}}}_{u} -{\mathbf{M}}_{\mathrm{14}} {{\ddot{\varvec{\upvarphi }}}}_{x}, \end{aligned}$$

(26a)

$$\begin{aligned}&{\mathbf{K}}_{21} {\mathbf{q}}_{u} +{\mathbf{K}}_{22} {\mathbf{q}}_{v} +{\mathbf{K}}_{23} {\mathbf{q}}_{w} +{\mathbf{K}}_{24} {\mathbf{q}}_{\phi _{x} } +{\mathbf{K}}_{25} {\mathbf{q}}_{\phi _{\theta } } +{\mathbf{K}}_{23}^{(2)} {\mathbf{q}}_{w} =-{\mathbf{M}}_{\mathrm{22}} {{\ddot{\mathbf{q}}}}_{v} -{\mathbf{M}}_{\mathrm{25}} {{\ddot{\mathbf{q}}}}_{\phi _{\theta } }, \end{aligned}$$

(26b)

$$\begin{aligned}&{\mathbf{M}}_{\mathrm{33}} {{\ddot{\mathbf{q}}}}_{w} +{\mathbf{K}}_{31} {\mathbf{q}}_{u} +{\mathbf{K}}_{32} {\mathbf{q}}_{v} +{\mathbf{K}}_{33} {\mathbf{q}}_{w} +{\mathbf{K}}_{34} {\mathbf{q}}_{\phi _{x} } +{\mathbf{K}}_{35} {\mathbf{q}}_{\phi _{\theta } } \nonumber \\&\quad {\mathbf{K}}_{31}^{(2)} {\mathbf{q}}_{u} +{\mathbf{K}}_{32}^{(2)} {\mathbf{q}}_{v} +{\mathbf{K}}_{33}^{(2)} {\mathbf{q}}_{w} +{\mathbf{K}}_{34}^{(2)} {\mathbf{q}}_{\phi _{x} } +{\mathbf{K}}_{35}^{(2)} {\mathbf{q}}_{\phi _{\theta } } +{\mathbf{K}}_{33}^{(3)} {\mathbf{q}}_{w} ={\mathbf{F}}_{w} , \end{aligned}$$

(26c)

$$\begin{aligned}&{\mathbf{K}}_{41} {\mathbf{q}}_{u} +{\mathbf{K}}_{42} {\mathbf{q}}_{v} +{\mathbf{K}}_{43} {\mathbf{q}}_{w} +{\mathbf{K}}_{44} {{{\varvec{\upvarphi }}}}_{x} +{\mathbf{K}}_{45} {\mathbf{q}}_{\phi _{\theta } } +{\mathbf{K}}_{43}^{(2)} {\mathbf{q}}_{w} =-{\mathbf{M}}_{\mathrm{41}} {{\ddot{\mathbf{q}}}}_{u} -{\mathbf{M}}_{\mathrm{44}} {{\ddot{\mathbf{q}}}}_{\phi _{x}}, \end{aligned}$$

(26d)

$$\begin{aligned}&{\mathbf{K}}_{51} {\mathbf{q}}_{u} +{\mathbf{K}}_{52} {\mathbf{q}}_{v} +{\mathbf{K}}_{53} {\mathbf{q}}_{w} +{\mathbf{K}}_{54} {\mathbf{q}}_{\phi _{x} } +{\mathbf{K}}_{55} {\mathbf{q}}_{\phi _{\theta } } +{\mathbf{K}}_{53}^{(2)} {\mathbf{q}}_{w} ={\mathbf{M}}_{\mathrm{52}} {{\ddot{\mathbf{q}}}}_{v} +{\mathbf{M}}_{\mathrm{55}} {{\ddot{\mathbf{q}}}}_{\phi _{\theta }}. \end{aligned}$$

(26e)

According to Volmir’s assumption [47], the in-plane displacements $(u_{m,n},v_{m,n})$ and the rotations $(\phi _{xm,n}, \phi _{\theta m,n})$ are much smaller than the radial displacement $w_{m,n}$. Neglecting the in-plane inertias and rotational inertias in Eqs. (26a–b) and (26d–e), one can write

$$\begin{aligned} \left[ {{\begin{array}{*{20}c} {{\mathbf{K}}_{11} } &{} {{\mathbf{K}}_{12} } &{} {{\mathbf{K}}_{14} } &{} {{\mathbf{K}}_{15} } \\ {{\mathbf{K}}_{21} } &{} {{\mathbf{K}}_{22} } &{} {{\mathbf{K}}_{24} } &{} {{\mathbf{K}}_{25} } \\ {{\mathbf{K}}_{41} } &{} {{\mathbf{K}}_{42} } &{} {{\mathbf{K}}_{44} } &{} {{\mathbf{K}}_{45} } \\ {{\mathbf{K}}_{51} } &{} {{\mathbf{K}}_{52} } &{} {{\mathbf{K}}_{54} } &{} {{\mathbf{K}}_{55} } \\ \end{array} }} \right] \left[ {{\begin{array}{*{20}c} {{\mathbf{q}}_{u} } \\ {{\mathbf{q}}_{v} } \\ {{\mathbf{q}}_{\phi _{x} } } \\ {{\mathbf{q}}_{\phi _{\theta } } } \\ \end{array} }} \right] =-\left[ {{\begin{array}{*{20}c} {{\mathbf{K}}_{13} } \\ {{\mathbf{K}}_{23} } \\ {{\mathbf{K}}_{43} } \\ {{\mathbf{K}}_{53} } \\ \end{array} }} \right] {\mathbf{q}}_{w} -\left[ {{\begin{array}{*{20}c} {{\mathbf{K}}_{13}^{(2)} } \\ {{\mathbf{K}}_{23}^{(2)} } \\ {{\mathbf{K}}_{43}^{(2)} } \\ {{\mathbf{K}}_{53}^{(2)} } \\ \end{array} }} \right] {\mathbf{q}}_{w}. \end{aligned}$$

(27)

Solving Eq. (27) with regard to the generalized coordinates of in-plane displacements and rotations (${\mathbf{q}}_{u}$, ${\mathbf{q}}_{v}$, ${\mathbf{q}}_{\phi _{x}}$ and ${\mathbf{q}}_{\phi _{\theta }}$), and then introducing the results into Eq. (26c), the equations of motion are converted into a reduced equation with regard to the generalized coordinates of radial displacement $({\mathbf{q}}_{w})$

$$\begin{aligned} {\mathbf{M}}_{\mathrm{33}} {{\ddot{\mathbf{q}}}}_{w} +({\mathbf{K}}_{\mathrm{s}} +{\mathbf{K}}_{\mathrm{s}}^{(2)} +{\mathbf{K}}_{\mathrm{s}}^{(3)} ){\mathbf{q}}_{w} ={\mathbf{F}}_{w}, \end{aligned}$$

(28)

where ${\mathbf{K}}_{\mathrm{s}}$, ${\mathbf{K}}_{\mathrm{s}}^{(2)}$ and ${\mathbf{K}}_{\mathrm{s}}^{(3)}$ are the generalized linear, quadratic and cubic nonlinear stiffness matrices.

In addition, the static condensation method [48] is also a technique to simplify the model. Solving Eq. (27) with respect to ${\mathbf{q}}_{u}$, ${\mathbf{q}}_{v}$, ${\mathbf{q}}_{\phi _{x}}$ and ${\mathbf{q}}_{\phi _{\theta }}$, and then introducing the results into the right hand side of Eqs. (26a–b) and (26d–e) yields

$$\begin{aligned} \left[ {{\begin{array}{*{20}c} {{\mathbf{K}}_{11} } &{} {{\mathbf{K}}_{12} } &{} {{\mathbf{K}}_{14} } &{} {{\mathbf{K}}_{15} } \\ {{\mathbf{K}}_{21} } &{} {{\mathbf{K}}_{22} } &{} {{\mathbf{K}}_{24} } &{} {{\mathbf{K}}_{25} } \\ {{\mathbf{K}}_{41} } &{} {{\mathbf{K}}_{42} } &{} {{\mathbf{K}}_{44} } &{} {{\mathbf{K}}_{45} } \\ {{\mathbf{K}}_{51} } &{} {{\mathbf{K}}_{52} } &{} {{\mathbf{K}}_{54} } &{} {{\mathbf{K}}_{55} } \\ \end{array} }} \right] \left[ {{\begin{array}{*{20}c} {{\mathbf{q}}_{u} } \\ {{\mathbf{q}}_{v} } \\ {{\mathbf{q}}_{\phi _{x} } } \\ {{\mathbf{q}}_{\phi _{\theta } } } \\ \end{array} }} \right] =-\left[ {{\begin{array}{*{20}c} {{\mathbf{K}}_{13} } \\ {{\mathbf{K}}_{23} } \\ {{\mathbf{K}}_{43} } \\ {{\mathbf{K}}_{53} } \\ \end{array} }} \right] {\mathbf{q}}_{w} -\left[ {{\begin{array}{*{20}c} {{\mathbf{K}}_{13}^{(2)} } \\ {{\mathbf{K}}_{23}^{(2)} } \\ {{\mathbf{K}}_{43}^{(2)} } \\ {{\mathbf{K}}_{53}^{(2)} } \\ \end{array} }} \right] {\mathbf{q}}_{w} +\left[ {{\begin{array}{*{20}c} {{\mathbf{M}}_{1} } \\ {{\mathbf{M}}_{2} } \\ {{\mathbf{M}}_{3} } \\ {{\mathbf{M}}_{4} } \\ \end{array} }} \right] {{\ddot{\mathbf{q}}}}_{w}, \end{aligned}$$

(29)

where ${\mathbf{M}}_{i} (i=1,\;2,\;3,\;4)$ are matrices obtained from Eq. (27).

Repeating the procedure to calculate ${\mathbf{q}}_{u}$, ${\mathbf{q}}_{v}$, ${\mathbf{q}}_{\phi _{x}}$ and ${\mathbf{q}}_{\phi _{\theta }}$ by solving Eq. (29) and then introducing the results into Eq. (26c), the equation of motion is converted into another reduced equation with regard to ${\mathbf{q}}_{w}$:

$$\begin{aligned} {\mathbf{M}}_{\mathrm{s}} {{\ddot{\mathbf{q}}}}_{w} +{\mathbf{C}{\dot{\mathbf{q}}}}_{w} +({\mathbf{K}}_{\mathrm{s}} +{\mathbf{K}}_{\mathrm{s}}^{(2)} +{\mathbf{K}}_{\mathrm{s}}^{(3)} ){\mathbf{q}}_{w} ={\mathbf{F}}_{w}, \end{aligned}$$

(30)

where the generalized mass matrix ${\mathbf{M}}_{\mathrm{s}}$ is a complicated function of the in-plane, radial direction and rotary inertias. Besides, the damping matrix is introduced as ${\mathbf{C}}=2c\omega _{m,\;n}{\mathbf{M}}_{\mathrm{s}}$, where $\omega _{m,n}$ and c represent the natural frequency and the damping ratio, respectively. In Sect. 5.1, the results of vibration analysis for FG-CNTRC cylindrical shells from these two reduced models are compared with those from the full-order system.

4.2 Incremental harmonic balance method

The process of calculating the dynamic response of nonlinear vibrational system by IHB method is briefly introduced. Introducing a new dimensionless time scale $\tau =\varOmega t$ and omitting the subscripts for brevity, Eq. (28) or Eq. (30) can be rewritten as

$$\begin{aligned} \varOmega ^{2}{\mathbf{M}}\ddot{{\mathbf{q}}}+\varOmega {\mathbf{C}}{\dot{\mathbf{q}}}+({\mathbf{K}}+{\mathbf{K}}^{(2)}+{\mathbf{K}}^{(3)}){\mathbf{q}}={\mathbf{F}}\cos (\tau ). \end{aligned}$$

(31)

The incremental process is performed firstly. A certain vibration state is denoted in terms of $q_{j0}$ and $\omega _{\mathrm {0}}$, and adding the corresponding small increments to them gives the adjacent state

$$\begin{aligned} q_{j} =q_{j0} +\Delta q_{j} , \quad (j=1,2,...,N), \quad \varOmega =\omega _{0} +\Delta \omega . \end{aligned}$$

(32)

Substituting Eq. (32) into Eq. (31) and omitting the higher-order terms of increments, the linearized incremental equation can be obtained:

$$\begin{aligned}&\omega _{0}^{2} {\mathbf{M}}\Delta {{\ddot{\mathbf{q}}}}+\omega _{0} {\mathbf{C}}\Delta {{\dot{\mathbf{q}}}}+({\mathbf{K}}+2{\mathbf{K}}^{(2)}+3{\mathbf{K}}^{(3)})\Delta {\mathbf{q}}={\mathbf{Re}}-(2\omega _{0} {\mathbf{M}\ddot{\mathbf{q}}}_{0} +{\mathbf{C}}{\dot{\mathbf{q}}}_{0} )\Delta \omega , \end{aligned}$$

(33a)

$$\begin{aligned}&{\mathbf{Re}}={\mathbf{F}}_{0} \cos (\tau )-\left[ \omega _{0}^{2} {\mathbf{M}}{\ddot{\mathbf{q}}}_{0} +\omega _{0} {\mathbf{C}}{\dot{\mathbf{q}}}_{0} +({\mathbf{K}}+{\mathbf{K}}^{(2)}+{\mathbf{K}}^{(3)}){\mathbf{q}}_{0} \right] , \end{aligned}$$

(33b)

where ${\mathbf{q}}_{0} =\left[ {q_{10} ,q_{20} ,...,q_{N0} } \right] ^{\mathrm{T}}$ and $\Delta {\mathbf{q}}=\left[ {\Delta q_{1} ,\Delta q_{2} ,...,\Delta q_{N} } \right] ^{\mathrm{T}}$, Re is the residual error and will become zero when ${\mathbf{q}}_{0}$ approaches the exact solution.

Secondly, the harmonic balance process is executed. The periodic solution and increment are assumed to be truncated Fourier series

$$\begin{aligned}&q_{j0} =\frac{1}{2}a_{j0} +\sum \limits _{k=1}^{N_{\mathrm{h}} } {a_{jk} \cos k\tau } +\sum \limits _{k=1}^{N_{\mathrm{h}} } {b_{jk} \sin k\tau } ={\mathbf{C}}_{\mathrm{s}} {\mathbf{A}}_{j} , \end{aligned}$$

(34a)

$$\begin{aligned}&\Delta q_{j0} =\frac{1}{2}\Delta a_{j0} +\sum \limits _{k=1}^{N_{\mathrm{h}} } {\Delta a_{jk} \cos k\tau } +\sum \limits _{k=1}^{N_{\mathrm{h}} } {\Delta b_{jk} \sin k\tau } ={\mathbf{C}}_{\mathrm{s}} \Delta {\mathbf{A}}_{j} , \end{aligned}$$

(34b)

where

$$\begin{aligned}&\begin{aligned}&{\mathbf {C}}_{\mathrm {s}} =\left[ {1,\cos \tau ,\cos 2\tau ,...,\cos N_{\mathrm {h}} \tau ,\sin \tau ,\sin 2\tau ,...,\sin N_{\mathrm {h}} \tau } \right] , \end{aligned} \end{aligned}$$

(34c)

$$\begin{aligned}&\begin{aligned}&{\mathbf {A}}_{j} =\left[ {\frac{1}{2}a_{j0} ,a_{j1} ,a_{j2} ,...,a_{jN_{\mathrm {h}} } ,b_{j1} ,b_{j2} ,...,b_{jN_{\mathrm {h}} } } \right] ^{\mathrm {T}}, \end{aligned} \end{aligned}$$

(34d)

$$\begin{aligned}&\begin{aligned}&\Delta {\mathbf {A}}_{j} =\left[ {\frac{1}{2}\Delta a_{j0} ,\Delta a_{j1} ,\Delta a_{j2} ,...,\Delta a_{jN_{\mathrm {h}} } ,\Delta b_{j1} ,\Delta b_{j2} ,...,\Delta b_{jN_{\mathrm {h}} } } \right] ^{\mathrm {T}}. \end{aligned} \end{aligned}$$

(34e)

$N_{\mathrm {h}}$ is the number of harmonic terms, which is determined by the required computational accuracy. The solution is a periodic function of $\tau$ with a period $T=2\pi$.

The unknown periodic solution ${\mathbf{q}}_{0}$ and increment $\Delta {\mathbf{q}}$ can be written as

$$\begin{aligned} {\mathbf{q}}_{0} ={\mathbf{SA}},\quad \Delta {\mathbf{q}}={\mathbf{S}}\Delta {\mathbf{A}}, \end{aligned}$$

(35)

where ${\mathbf{A}}=[{\mathbf{A}}_{1} ,{\mathbf{A}}_{2} ,...,{\mathbf{A}}_{m} ]^{\mathrm{T}}$, $\Delta {\mathbf{A}}=[\Delta {\mathbf{A}}_{1} ,\Delta {\mathbf{A}}_{2} ,...,\Delta {\mathbf{A}}_{m} ]^{\mathrm{T}}$ and ${\mathbf {S}}=\text { diag }.\,[{\mathbf {C}}_{\mathrm {s}} ,{\mathbf {C}}_{\mathrm {s}} ,...,{\mathbf {C}}_{\mathrm {s}} ]$.

Substituting Eq. (33) into Eq. (31) and executing the Galerkin averaging process yields

$$\begin{aligned}&\int _0^{2\pi } {\delta (\Delta {\mathbf {q}})^{\mathrm {T}}\left[ {\omega _{0}^{2} {\mathbf {M}}\Delta {{\ddot{\mathbf {q}}}}+\omega _{0} {\mathbf {C}}\Delta {{\dot{\mathbf {q}}}}+({\mathbf {K}}+2{\mathbf {K}}^{(2)}+3{\mathbf {K}}^{(3)})\Delta {\mathbf {q}}} \right] } \text{ d } \tau \nonumber \\&\quad =\int _0^{2\pi } {\delta (\Delta {\mathbf {q}})^{\mathrm {T}}\left[ {{\mathbf {Re}}-(2\omega _{0} {\mathbf {M}}\ddot{{\mathbf {q}}}_{0} +{\mathbf {C}}\dot{{\mathbf {q}}}_{0} )\Delta \omega } \right] } \text{ d } \tau . \end{aligned}$$

(36)

Then, the linear equations with respect to increments $\Delta {\mathbf{A}}$ and $\Delta \omega$ are obtained as

$$\begin{aligned} {\mathbf{K}}_{mc} \Delta {\mathbf{A}}={\mathbf{R}}-{\mathbf{R}}_{mc} \Delta \omega , \end{aligned}$$

(37)

where

$$\begin{aligned}&\begin{aligned}&{\mathbf {K}}_{mc} =\int _0^{2\pi } {{\mathbf {S}}^{\mathrm {T}}\left[ {\omega _{0}^{2} {\mathbf {M}}{\ddot{\mathbf {S}}}}+\omega _{0} {\mathbf {C}}{\dot{\mathbf {S}}}+({\mathbf {K}}+2{\mathbf {K}}^{(2)}+3{\mathbf {K}}^{(3)}){\mathbf {S}} \right] } \text{ d } \tau , \end{aligned} \end{aligned}$$

(38a)

$$\begin{aligned}&{\mathbf{R}}=\int _0^{2\pi } {{\mathbf{S}}^{\mathrm{T}}\left\{ {\mathbf{F}}_{0} \cos (\tau )-\left[ \omega _{0}^{2} {\mathbf{M}}{\ddot{\mathbf{S}}}+\omega _{0} {\mathbf{C}}{\dot{\mathbf{S}}}+({\mathbf{K}}+{\mathbf{K}}^{(2)}+{\mathbf{K}}^{(3)}){\mathbf{S}} \right] {\mathbf{A}} \right\} } \hbox {d }\tau , \end{aligned}$$

(38b)

$$\begin{aligned}&{\mathbf{R}}_{mc} =\int _0^{2\pi } {\mathbf{S}}^{\mathrm{T}}(2\omega _{0} {\mathbf{M}}{\ddot{\mathbf{S}}}+{\mathbf{C}}{\dot{\mathbf{S}}}){\mathbf{A}} \hbox {d }\tau . \end{aligned}$$

(38c)

The initial value used in solving Eq. (37) is assumed to be a guess solution or a known linear solution. Combined with the incremental arc-length method [44], the complicated frequency response curve for FG-CNTRC cylindrical shells can be automatically constructed.

5 Results and discussion

The nonlinear resonant responses of FG-CNTRC cylindrical shells are numerically simulated, and parameter studies are carried out in this section. Poly methyl methacrylate (PMMA) is chosen as the matrix with $E^{\mathrm {m}}=2.5\,\hbox {Gpa}$, $\rho ^{\mathrm {m}}=1190\,\hbox {kg/m}^{\mathrm {3}}$ and $\nu ^{\mathrm {m}}=0.3$. The (10, 10) single-walled carbon nanotubes are chosen as reinforcements with [29] $E_{\mathrm{11}}^{\mathrm{cnt}} =5.6466\,\text{ Tpa }$, $E_{\mathrm{22}}^{\mathrm{cnt}} =7.0800\,\text{ Tpa }$, $G_{\mathrm{12}}^{\mathrm{cnt}} =1.9445\,\text{ Tpa }$, $\rho ^{\mathrm {cnt}}=1400\,\hbox {kg/m}^{{3}}$ and $\nu _{12} ^{\mathrm {cnt}}=0.175$. The CNT efficiency parameters are: $\eta _{{1}}=0.137$, $\eta _{{2}}=1.022$ and $\eta _{{3}}= 0.715$ for $V_{\mathrm{cnt}}^{{*}} =0.12$, $\eta _{{1}}=0.142$, $\eta _{{2}}= 1.626$ and $\eta _{{3}}= 1.138$ for $V_{\mathrm{cnt}}^{{*}} =0.17$, and $\eta _{{1}}= 0.141$, $\eta _{{2}}=1.585$ and $\eta _{{3}}=1.109$ for $V_{\mathrm{cnt}}^{{*}} =0.28$.

5.1 Validation and convergence studies

To examine the validity of the structural dynamic model and solution method, comparison studies with results in the literature are conducted. Firstly, the natural frequencies of an isotropic cylindrical shell are computed by using the full-order system Eq. (24), reduced model Eq. (28) and reduced model Eq. (30), and they are compared with those of Shen and Xiang [29] and Song et al. [34] in Table 1. It is obvious that the present natural frequencies are consistent with those in the literature. The natural frequencies from the reduced model Eq. (30) (static condensation method) are very close to those from the full-order system, while the results from the reduced model Eq. (28) (Volmir’s assumption) are slightly larger than those from the full-order system.

Table 1 Comparisons of natural frequency (Hz) for an isotropic cylindrical shell ($L=410\,\hbox {mm}$, $R=301.5\,\hbox {mm}$, $h=1\,\hbox {mm}$, ${E}=210\,\hbox {GPa}$, $\nu =0.3$, $\rho =7850\,\hbox {kg/m}^{{3}})$

Secondly, the dimensionless natural frequencies $\varOmega =\omega ({R^{2}} / h)\sqrt{{\rho _{\mathrm{m}} } / {E_{\mathrm{m}} }}$ of FG-CNTRC cylindrical shells are computed in Table 2. As can be seen, the results from the reduced model equation (28) (Volmir’s assumption) are in accordance with those of Shen and Xiang [29] and Ansari et al. [37]. The natural frequencies from the reduced model equation (28) (Volmir’s assumption) are much larger than those from the full-order system. Ignoring the in-plane and rotational inertias will reduce the generalized mass and make the natural frequency larger. Therefore, the reduced model equation (30) using the static condensation method can describe the natural characteristics of FG-CNTRC cylindrical shells with more reasonable accuracy.

Table 2 Comparisons of the dimensionless natural frequency $\varOmega =\omega ({R^{2}} / h)\sqrt{{\rho _{\mathrm{m}} } / {E_{\mathrm{m}}}}$ for a FG-CNTRC circular cylindrical shell ($h=0.005\,\hbox {m}$, $R/h=10,L=\sqrt{500Rh}$)

The convergence on the mode expansions of Eq. (23) is tested for the frequency responses of FG-CNTRC cylindrical shells. Due to quadratic and cubic nonlinearities, the resonant mode (m, n) directly driven by modal harmonic excitation is coupled with asymmetric modes $(k\times m, j\times n)(k=1,\,3,\, j=1,\,2,\,3)$ and axisymmetric modes ($m,\,0$) ($m=1,\,3,\,5,\,7$) [45, 46]. Because of the symmetry of system and external excitation distribution, only modes having odd m axial half waves are considered. Therefore, the convergence is examined though introducing these additional modes to the mode expansions, and the following models with different degrees of freedom are established:

• (a) 2 dofs, modes $({m},\,{n})$ and (m, 0) for axial and radial displacements u, w and rotation ${\phi _{x}}$; modes $({m},\, {n})$ and (${m},\,2n$) for circumferential v and rotation ${\phi _\theta }$;

• (b) 3 dofs, modes $({m},\,{n})$, $({m},\,0)$ and $(3m,\,0)$ for u, w and ${\phi _x}$; modes (m, n), (m, 2n) and (3m, 2n) for v and ${\phi _\theta }$;

• (c) 4 dofs, modes (${m},\,{n}$), ($3{m},\,{n}$), (${m},\,0$) and ($3{m},\,0$) for u, w and ${\phi _x}$; modes (m, 2n), (${m}, 2_{n}$), ($3{m},\,{n}$) and ($3{m},\,2{n}$) for v and ${\phi _\theta }$;

• (d) 5 dofs, modes (${m},\,{n}$), ($3{m},\,{n}$), (${m},\, 0$), ($3{m},\,0$) and ($5m,\,0$) for u, w and ${\phi _x}$; modes (${m},\,{n}$), (${m},\,2n$), (${m},\,3n$), ($3{m},\,{n}$) and ($3m,\,2{n}$) for v and ${\phi _\theta }$;

• (e) 6 dofs, modes (${m},\, {n}$), ($3{m},\,{n}$), (${m},\,0$), ($3{m},\,0$), ($5{m},\,0$) and ($7{m},\, 0$) for u, w and ${\phi _x}$; modes (${m},\,{n}$), (${m},\,2{n}$), (${m},\,3{n}$), ($3{m},\,{n}$), ($3{m},\,2{n}$) and ($3{m},\,3{n}$) for v and ${\phi _\theta }$.

Fig. 2

Convergence analysis of frequency response curve of FGA-CNTRC cylindrical shells: a hardening behavior with $V_{\mathrm{cnt}}^{*}=0.17$, $L/R=2$, $h/R=0.005$, $c=0.001$, $f=0.00025$; b softening behavior with $V_{\mathrm{cnt}}^{*}=0.17$, $L/R=20$, $h/R=0.01$, $c=0.001$, $f=0015$

Figure 2 presents the frequency responses of FGA-CNTRC cylindrical shells under primary resonance (at $\varOmega$ near $\omega _{m,n}$) by using different mode expansions. The mode ($m=1$, $n=6$) is considered. From Fig. 2a, the hardening nonlinear behavior is expected for a short and very thin shell ($V_{\mathrm{cnt}}^{{*}} =0.17$, $L/R=2$, $h/R=0.005$), and the 2 dof model shows a more strongly but inaccurate hardening behavior. For a long and moderately thin shell ($V_{\mathrm{cnt}}^{{*}} =0.17$, $L/R=20$, $h/R=0.01$) in Fig. 2b, the 2 dof model with only the first axisymmetric mode used in the expansion gives a strongly hardening behavior. However, the 3 dof model gives a softening behavior and the higher-order expansions (5 dof and 6 dof models) converge to a more strongly softening behavior. False hardening behavior is obtained when the number of mode expansions is insufficient, which indicates that the axisymmetric modes play a key role in predicting the actual nonlinear behaviors of the shell. The above convergence study illustrates that the 5 dof model can gives accurate results and the corresponding computational time is reasonable. Consequently, the 5 dof model will be used in the subsequent numerical analysis.

Fig. 3

Comparison of frequency responses of isotropic cylindrical shells

As an example of verifying the nonlinear dynamic model and the accuracy of the solution procedure, the frequency responses of an isotropic cylindrical shell under the external modal excitation are calculated from the reduced model, and compared with those of Pellicano et al. [46] in Fig. 3. The material and geometric properties of the considered isotropic cylindrical shell are: $E^{\mathrm{m}}=71.02\,\hbox {Gpa}$, $\rho ^{\mathrm{m}}=2796\,\text{ kg }/\text{ m }^{\mathrm{3}}$ and $\nu ^{\mathrm{m}}=0.31$; $L=0.2\,\hbox {m}$, $R=0.1\,\hbox {m}$, $h=0.000247\,\hbox {m}$. The amplitude of external modal excitation is $f_{m,n} =0.0012h^{2}\rho ^{\mathrm{m}}\omega _{m,n}^{2}$ and the damping ratio is $\zeta _{m,n}=0.0005$. The mode studied is ($m=1$, $n=6$). Good consistency with the results in the literature can be seen from Fig. 3, which verifies the correctness of present nonlinear reduced model and solution procedure.

Fig. 4

Frequency response curve of different modes of FGA-CNTRC cylindrical shells ($V_{\mathrm{cnt}}^{*} =0.17$, $L/R=20$, $h/R=0.01$, $c=0.001$, $f=0.0015$). Solid and dashed lines represent the stable and unstable solutions, respectively

In this subsequent numerical simulation, the nonlinear primary resonance responses of the fundamental mode (with the lowest natural frequency $\omega _{m,n}$) of FG-CNTRC cylindrical shells are analyzed. Figure 4 plots the frequency responses of different asymmetric and axisymmetric modes for FGA-CNTRC cylindrical shells in the softening case ($V_{\mathrm{cnt}}^{{*}} =0.17,L/R=20,\,h/R=0.01$). The amplitudes of those additional modes are much smaller than that of the first asymmetric mode $w_{{1,\,6}}$ (driven mode). Besides, the first and fifth axisymmetric modes ($w_{{1,0}}$ and $w_{{5,0}})$ show negative amplitude. This is because the displacements of $w_{{1,0}}$ and $w_{{5,0}}$ are always negative and the minimum amplitudes are used in the frequency response curves. The first and fifth axisymmetric modes contribute to the axisymmetric shell contraction, and they are important in predicting the softening or weakly hardening behaviors of cylindrical shells.

5.2 Effect of CNT distributions on the system response

Figure 5 depicts the frequency responses of the fundamental mode of CNTRC cylindrical shells with the five distributions of CNTs. It be seen from Fig. 5a, for the long and thick shells ($V_{\mathrm{cnt}}^{{*}} =0.17$, $L/R=16$, $h/R=0.1$) with the five considered CNT distributions, the fundamental modes of the shells are all ($m=1$, $n=1$) and the their nonlinearities are hardening. The FGA-CNTRC shell has the lowest dimensionless fundamental natural frequency and highest peak amplitude. On the contrary, the FGV-CNTRC shell possesses the highest dimensionless fundamental natural frequency and lowest peak amplitude.

Fig. 5

Frequency response curves of the fundamental mode of CNTRC cylindrical shells with different CNT distributions: a hardening behavior with $V_{\mathrm{cnt}}^{*}=0.17$, $L/R=16$, $h/R=0.1$, $c=0.001$, $f=0.01$; b softening behavior with $V_{\mathrm{cnt}}^{*}=0.17$, $L/R=4$, $h/R=0.005$, $c=0.001$, $f=0.0004$

In Fig. 5b, a thin shell ($V_{\mathrm{cnt}}^{{*}} =0.17$, $L/R=4$, $h/R=0.005$) with softening behavior is studied. Similarly, the CNT distributions do not change the fundamental mode shape ($m=1$, $n=6$) and its nonlinearity. The highest fundamental natural frequency and lowest peak amplitude correspond to FGX-CNTRC shell. The lowest fundamental natural frequency and the largest peak amplitude belong to FGO-CNTRC shells.

Fig. 6

Frequency response curves of the fundamental mode of FGA-CNTRC cylindrical shells with different CNT volume fractions: a hardening behavior with $L/R=16$, $h/R=0.1$, $c=0.001$, $f=0.008$; b softening behavior with $L/R=4$, $h/R=0.005$, $c=0.001$, $f=0.0004$

5.3 Effect of CNT volume fraction on the system response

The influence of CNT volume fraction on the dynamic resonance responses of FGA-CNTRC cylindrical shells is analyzed in Fig. 6. With the increase in CNT volume fraction, the fundamental natural frequency increases and the peak amplitude decreases, whether the nonlinearity is hardening or softening. For both the thick and thin shells, the variations of CNT volume fraction do not change the fundamental mode shape and the nonlinearity (hardening or softening). The lower the CNT volume fraction, the stronger the hardening or softening nonlinear behavior becomes, and the wider the resonant region. For the thin shell with softening behavior, the unstable solution branch disappears when $V_{\mathrm{cnt}}^{{*}} =0.28$. Consequently, the FGA-CNTRC cylindrical shell having higher CNT volume fraction are more stable and safer.

Fig. 7

Variation of natural frequencies of FGA-CNTRC cylindrical shells with the circumferential wave number n under different h/R ratios ($V_{\mathrm{cnt}}^{*}=0.17$, $L/R=8$, $m=1$)

5.4 Effect of thickness-to-radius ratio on the system response

The linear natural frequencies of FGA-CNTRC cylindrical shells with various thickness-to-radius h/R ratios for $m=1$ are given in Fig. 7. As the ratio h/R is increasing, the circumferential wave number n corresponding to the fundamental mode decreases, $n=6$ for $h/R=0.002$; $n=5$ for $h/R=0.004$; $n=4$ for $h/R=0.006$ and 0.008; $n=3$ for $h/R=0.01$ and 0.02; and $n=2$ for $h/R=0.04$, 0.06, 0.08 and 0.1.

Fig. 8

Frequency response curves of the fundamental mode of FGA-CNTRC cylindrical shells with different h/R ratios: a thin shell with $f=0.001$; b thick shell with $f=0.003$ ($V_{\mathrm{cnt}}^{*}=0.17$, $L/R=8$, $c=0.001$)

Figure 8 illustrates the influence of the ratio h/R on the frequency responses of the fundamental mode of FGA-CNTRC cylindrical shells. Increasing the ratio h/R will enlarge the stiffness and fundamental natural frequency of the shell. For thin shells with smaller h/R in Fig. 8a, the resonance response curves show softening nonlinear behavior. The peak amplitude decreases markedly with increasing h/R ratio. It is noteworthy that for the case $h/R=0.004$ which has the highest peak amplitude, the resonance response curve displays a softening behavior initially and then tends to a hardening behavior at the higher vibration amplitudes.

With the h/R ratio increasing further, the thickness of shell is moderate and the nonlinearity tends from softening to hardening, as depicted in Fig. 8b. The fundamental mode of the shell with softening behavior is obtained for $n=3$ in the case of $h/R=0.02$, while the fundamental modes ($n=2$) for $h/R=0.04$, 0.06 and 0.08 have hardening behavior.

Fig. 9

Variation of natural frequencies of FGA-CNTRC cylindrical shells with the circumferential wave number n under different L/R ratios ($V_{\mathrm{cnt}}^{*}=0.17$, $h/R=0.01$, $m=1$)

5.5 Effect of length-to-radius ratio on the system response

Figure 9 shows the natural frequencies of FGA-CNTRC cylindrical thin shells with various length-to-radius ratios L/R for $m=1$. The circumferential wave number n of the fundamental mode decreases as the L/R ratio increases $n=7$ for $L/R=1$; $n=6$ for $L/R=2$; $n=5$ for $L/R=3$; $n=4$ for $L/R=4$, 5 and 6; $n=3$ for $L/R=8$, 12 and 16; and $n=2$ for $L/R=20$.

Fig. 10

Frequency response curves of the fundamental mode of FGA-CNTRC cylindrical shells with different L/R ratios: a moderately long shell and b long shell ($V_{\mathrm{cnt}}^{*}=0.17$, $h/R=0.01$, $c=0.001$, $f=0.0015$)

Figure 10 demonstrates the effect of L/R on the resonance responses of the fundamental mode of FGA-CNTRC cylindrical shells. With increasing L/R ratio for moderately long shells ($L/R=4{-}7$), the fundamental natural frequency $\omega _{{1,4}}$ increases, while for long shells ($L/R=8{-}16$), the fundamental natural frequency $\omega _{{1,3}}$ first decreases slightly and then increases. Accordingly, the peak amplitude $w_{{1,4}}$ of the shell is reduced by increasing the length-to-radius ratio, while $w_{{1,3}}$ is enlarged first and then reduced. Hardening behavior only shows in the short shells ($L/R=3{-}5$) and generally softening behavior is shown in long shells ($L/R=6{-}20$).

Fig. 11

Frequency response curves of the fundamental mode of FGA-CNTRC cylindrical shells with different excitation amplitudes: a hardening behavior with $V_{\mathrm{cnt}}^{*}=0.17$, $L/R=16$, $h/R=0.1$, $c=0.001$; b softening behavior with $V_{\mathrm{cnt}}^{*}=0.17$, $L/R=4$, $h/R=0.005$, $c=0.001$

5.6 Effects of excitation amplitude and damping ratio on the system response

The influences of excitation amplitude and damping ratio on the dynamic responses of the fundamental mode of a FGA-CNTRC cylindrical shell are, respectively, analyzed in Figs. 11 and 12.

Fig. 12

Frequency response curves of the fundamental mode of FGA-CNTRC cylindrical shells with different damping ratios: a hardening behavior with $V_{\mathrm{cnt}}^{*}=0.17$, $L/R=16$, $h/R=0.1$, $f=0.01$; b softening behavior with $V_{\mathrm{cnt}}^{*}=0.17$, $L/R=4$, $h/R=0.005$, $f=0.0004$

Figure 11 indicates that the increase in radial excitation amplitude can enlarge the resonant responses of the shell. The unstable solution branches appear and become broader with increasing the radial excitation amplitude. As the resonance response can be suppressed effectively by the damping, increasing the damping ratio can reduce the peak amplitudes. As shown in Fig. 12, with the damping ratio increasing, the unstable solution branches in both the hardening and softening frequency response curves are narrowed, and vanish when $c=0.0015$.

6 Conclusion

The nonlinear forced vibration characteristics of FG-CNTRC cylindrical shells under radial harmonic excitation are analyzed in view of FSDT and von Kármán geometric nonlinearity. Two reduced models are established by Volmir’s assumption and the static condensation method, and compared with the full-order system and previous studies in the literature. A convergence study on the mode expansions is conducted by introducing different asymmetric and axisymmetric modes. The dynamic responses of the fundamental mode of FG-CNTRC shells are calculated using the IHB method. The effects of distribution and volume fraction of CNT, geometric and excitation parameters on the nonlinear dynamic behaviors are discussed. The following conclusions can be drawn:

• 1. The variations of distribution and volume fraction of CNTs do not transform the fundamental mode shape of FG-CNTRC shells and its nonlinearity. The FGA-CNTRC shell has the lowest fundamental natural frequency and the highest peak amplitude for thick shell with hardening behavior, whereas these characteristics belong to the FGO type for thin shell with softening behavior.

• 2. The increase in CNT volume fraction results in enlarging the fundamental natural frequency and a decrease in the peak amplitude. The hardening or softening nonlinear behavior of the FGA-CNTRC shell becomes stronger and the unstable solution region is broader with the CNT volume fraction decreasing. The FG-CNTRC cylindrical shells having higher CNT volume fraction are more stable and safer.

• 3. The circumferential wave number n corresponding to the fundamental mode with increasing thickness-to-radius ratio and length-to-radius ratio. The increase in thickness-to-radius ratio causes the enhancements of stiffness and fundamental natural frequency of FG-CNTRC shells, and enables the nonlinearity of fundamental mode tend from softening to hardening.

• 4. As the length-to-radius ratio increases, the fundamental natural frequency increases and the peak amplitude of the fundamental mode of the shell decreases. Hardening nonlinear behavior only shows in short or thick shells and softening behavior is generally displayed in long shells. Increasing the excitation amplitude and decreasing the damping ratio will amplify the resonance response and broaden the unstable solution region.

The present study can be instructive for the nonlinear forced vibration analysis of FG-CNTRC cylindrical shells.

Appendix A

Rewrite Eq. (23) in vector form as

$$\begin{aligned} \begin{aligned}&u(x,\theta ,t)={\mathbf {U}}^{{\mathrm {T}}}(x,\theta ){\mathbf {q}}_{u} (t), \quad v(x,\theta ,t)={\mathbf {V}}^{{\mathrm {T}}}(x,\theta ){\mathbf {q}}_{v} (t), \quad w(x,\theta ,t)={\mathbf {W}}^{{\mathrm {T}}}(x,\theta ){\mathbf {q}}_{w} (t),\\ {}&\phi _{x} (x,\theta ,t)={{{\varvec{\Phi }} }}_{x}^{\mathrm {T}} (x,\theta ){\mathbf {q}}_{\phi _{x} } (t), \quad \phi _{\theta } (x,\theta ,t)={{{\varvec{\Phi }} }}_{\theta }^{\mathrm {T}} (x,\theta ){\mathbf {q}}_{\phi _{\theta } } (t), \end{aligned} \end{aligned}$$

where $U_{m,jn} (x,\theta )=\varPhi _{xm,jn} (x,\theta )=\cos (m\pi x)\cos (jn\theta )$, $V_{m,jn} (x,\theta )=\varPhi _{\theta m,jn} (x,\theta )=\sin (m\pi x)\sin (jn\theta )$ and $W_{m,jn} (x,\theta )=\sin (m\pi x)\cos (jn\theta )$.

The elements of the matrix ${\mathbf{M}}$ are

$$\begin{aligned} \begin{aligned} {\mathbf {M}}_{\mathrm {11}}=&{} \int _0^L {\int _0^{2\pi } {I_{0} {\mathbf {UU}}^{\mathrm {T}}} } \text{ d } \theta \, \text{ d } x, \quad {\mathbf {M}}_{\mathrm {14}} =\int _0^L {\int _0^{2\pi } {I_{1} {\mathbf {U}}{\varvec{\Phi }} _{x}^{\mathrm {T}} } } \text{ d } \theta \,\text{ d } x;\\ {\mathbf {M}}_{\mathrm {22}}=&{} \int _0^L {\int _0^{2\pi } {I_{0} {\mathbf {VV}}^{\mathrm {T}}} } \text{ d } \theta \,\text{ d } x, \quad {\mathbf {M}}_{\mathrm {25}} =\int _0^L \int _0^{2\pi } {I_{1} \mathbf {V}{\varvec{\Phi }}_{\theta }^{\mathrm {T}}} \text{ d } \theta \,\text{ d }\,x,\\ {\mathbf {M}}_{\mathrm {33}}=&{} \int _0^L {\int _0^{2\pi } {I_{0} {\mathbf {WW}}^{\mathrm {T}}} } \text{ d } \theta \,\text{ d }\,x;\\ {\mathbf {M}}_{\mathrm {41}}=&{} \int _0^L {\int _0^{2\pi } {I_{1} {{{\varvec{\Phi }}}}_{x} {\mathbf {U}}^{{\mathrm {T}}}} } \text{ d } \theta \,\text{ d }\,x, \quad {\mathbf {M}}_{\mathrm {44}} =\int _0^L {\int _0^{2\pi } {I_{2} {{{\varvec{\Phi }} }}_{x} {{{\varvec{\Phi }} }}_{x}^{\mathrm {T}} } } \text{ d }\,\theta \,\text{ d }\,x;\\ {\mathbf {M}}_{\mathrm {52}}=&{} \int _0^L {\int _0^{2\pi } {I_{1} {{{\varvec{\Phi }} }}_{\theta } {\mathbf {V}}^{\mathrm {T}}} } \text{ d }\,\theta \, \text{ d }\,x, \quad {\mathbf {M}}_{\mathrm {55}} =\int _0^L {\int _0^{2\pi } {I_{2} {{{\varvec{\Phi }} }}_{\theta } {{{\varvec{\Phi }} }}_{\theta }^{\mathrm {T}} } } \text{ d }\,\theta \,\text{ d }\,x. \end{aligned} \end{aligned}$$

The elements of the matrix ${\mathbf{K}}$ are

$$\begin{aligned} {\mathbf{K}}_{\mathrm{11}}= & {} -\int _0^1 {\int _0^{2\pi } {\left( {a_{11} {\mathbf{U}}\frac{\partial ^{2}{\mathbf{U}}^{\mathrm{T}}}{\partial x^{2}}+a_{66} \lambda _{1}^{2} {\mathbf{U}}\frac{\partial ^{2}{\mathbf{U}}^{\mathrm{T}}}{\partial \theta ^{2}}} \right) } } \hbox {d}\,\theta \,\hbox {d}\,x, \quad {\mathbf{K}}_{\mathrm{12}} =-\left( {a_{12} +a_{66} } \right) \lambda _{1} \int _0^1 {\int _0^{2\pi } {{\mathbf{U}}\frac{\partial ^{2}{\mathbf{V}}^{\mathrm{T}}}{\partial x\partial \theta }} } \hbox {d}\,\theta \,\hbox {d}\,x,\\ {\mathbf{K}}_{\mathrm{13}}= & {} -a_{12} \lambda _{1} \int _0^1 {\int _0^{2\pi } {{\mathbf{U}}\frac{\partial {\mathbf{W}}^{\mathrm{T}}}{\partial x}} } \hbox {d}\,\theta \,\hbox {d}\,x, \quad {\mathbf{K}}_{\mathrm{14}} =-\int _0^1 {\int _0^{2\pi } {\left( {b_{11} {\mathbf{U}}\frac{\partial ^{2}{{{\varvec{\Phi }} }}_{x}^{\mathrm{T}} }{\partial x^{2}}+b_{66} \lambda _{1}^{2} {\mathbf{U}}\frac{\partial ^{2}{{{\varvec{\Phi }} }}_{x}^{\mathrm{T}} }{\partial \theta ^{2}}} \right) } } \hbox {d}\,\theta \,\hbox {d}\,x,\\ {\mathbf{K}}_{\mathrm{15}}= & {} -\left( {b_{12} +b_{66} } \right) \lambda _{1} \int _0^1 {\int _0^{2\pi } {{\mathbf{U}}\frac{\partial ^{2}{{{\varvec{\Phi }} }}_{\theta }^{\mathrm{T}} }{\partial x\partial \theta }} } \hbox {d}\,\theta \,\hbox {d}\,x;\\ {\mathbf{K}}_{\mathrm{21}}= & {} -\left( {a_{12} +a_{66} } \right) \lambda _{1} \int _0^1 {\int _0^{2\pi } {{\mathbf{V}}\frac{\partial ^{2}{\mathbf{U}}^{\mathrm{T}}}{\partial x\partial \theta }} } \hbox {d}\,\theta \,\hbox {d}\,x, \quad {\mathbf{K}}_{\mathrm{22}} =-\int _0^1 {\int _0^{2\pi } {\left( {a_{66} {\mathbf{V}}\frac{\partial ^{2}{\mathbf{V}}^{\mathrm{T}}}{\partial x^{2}}+a_{22} \lambda _{1}^{2} {\mathbf{V}}\frac{\partial ^{2}{\mathbf{V}}^{\mathrm{T}}}{\partial \theta ^{2}}} \right) } } \hbox {d}\,\theta \,\hbox {d}\,x,\\ {\mathbf{K}}_{\mathrm{23}}= & {} -a_{22} \lambda _{1}^{2} \int _0^1 {\int _0^{2\pi } {{\mathbf{V}}\frac{\partial {\mathbf{W}}^{\mathrm{T}}}{\partial \theta }} } \hbox {d}\,\theta \,\hbox {d}\,x, \quad {\mathbf{K}}_{\mathrm{24}} =-\left( {b_{12} +b_{66} } \right) \lambda _{1} \int _0^1 {\int _0^{2\pi } {{\mathbf{V}}\frac{\partial ^{2}{{{\varvec{\Phi }} }}_{x}^{\mathrm{T}} }{\partial x\partial \theta }} } \hbox {d}\,\theta \,\hbox {d}\,x,\\ {\mathbf{K}}_{\mathrm{25}}= & {} -\int _0^1 {\int _0^{2\pi } {\left( {b_{66} {\mathbf{V}}\frac{\partial ^{2}{{{\varvec{\Phi }} }}_{\theta }^{\mathrm{T}} }{\partial x^{2}}+b_{22} \lambda _{1}^{2} {\mathbf{V}}\frac{\partial ^{2}{{{\varvec{\Phi }} }}_{\theta }^{\mathrm{T}} }{\partial \theta ^{2}}} \right) } } \hbox {d}\,\theta \,\hbox {d}\,x;\\ {\mathbf{K}}_{\mathrm{31}}= & {} a_{12} \lambda _{1} \int _0^1 {\int _0^{2\pi } {{\mathbf{W}}\frac{\partial {\mathbf{U}}^{\mathrm{T}}}{\partial x}} } \hbox {d}\,\theta \,\hbox {d}\,x, \quad {\mathbf{K}}_{\mathrm{32}} =a_{22} \lambda _{1}^{2} \int _0^1 {\int _0^{2\pi } {{\mathbf{W}}\frac{\partial {\mathbf{V}}^{\mathrm{T}}}{\partial \theta }} } \hbox {d}\,\theta \,\hbox {d}\,x,\\ {\mathbf{K}}_{\mathrm{33}}= & {} -\int _0^1 {\int _0^{2\pi } {\left( {a_{55} {\mathbf{W}}\frac{\partial ^{2}{\mathbf{W}}^{\mathrm{T}}}{\partial x^{2}}+a_{44} \lambda _{1}^{2} {\mathbf{W}}\frac{\partial ^{2}{\mathbf{W}}^{\mathrm{T}}}{\partial \theta ^{2}}-a_{22} \lambda _{1}^{2} {\mathbf{WW}}^{\mathrm{T}}} \right) } } \hbox {d}\,\theta \,\hbox {d}\,x,\\ {\mathbf{K}}_{\mathrm{34}}= & {} -\left( {\frac{a_{55} }{\lambda _{3} }-b_{12} \lambda _{1} } \right) \int _0^1 {\int _0^{2\pi } {{\mathbf{W}}\frac{\partial {{{\varvec{\Phi }} }}_{x}^{\mathrm{T}} }{\partial x}} } \hbox {d}\,\theta \,\hbox {d}\,x,\\ {\mathbf{K}}_{\mathrm{35}}= & {} -\left( {a_{44} \frac{\lambda _{1} }{\lambda _{3} }-b_{22} \lambda _{1}^{2} } \right) \int _0^1 \int _0^{2\pi } {{\mathbf{W}}{\varvec{\Phi }}_{\theta } \frac{\partial {{{\varvec{\Phi }} }}_{\theta }^{\mathrm{T}} }{\partial \theta }} \hbox {d}\,\theta \,\hbox {d}\,x;\\ {\mathbf{K}}_{\mathrm{41}}= & {} -\int _0^1 {\int _0^{2\pi } {\left( {b_{11} {{{\varvec{\Phi }} }}_{x} \frac{\partial ^{2}{\mathbf{U}}^{\mathrm{T}}}{\partial x^{2}}+b_{66} \lambda _{1}^{2} {{{\varvec{\Phi }} }}_{x} \frac{\partial ^{2}{\mathbf{U}}^{\mathrm{T}}}{\partial \theta ^{2}}} \right) } } \hbox {d}\,\theta \,\hbox {d}\,x, \\ {\mathbf{K}}_{\mathrm{42}}= & {} -\left( {b_{12} +b_{66} } \right) \lambda _{1} \int _0^1 {\int _0^{2\pi } {{{{\varvec{\Phi }} }}_{x} \frac{\partial ^{2}{\mathbf{V}}^{\mathrm{T}}}{\partial x\partial \theta }} } \hbox {d}\,\theta \,\hbox {d}\,x, \\ {\mathbf{K}}_{\mathrm{43}}= & {} -\left( {b_{12} \lambda _{1} -\frac{a_{55} }{\lambda _{3} }} \right) \int _0^1 {\int _0^{2\pi } {{{{\varvec{\Phi }} }}_{x} \frac{\partial {\mathbf{W}}^{\mathrm{T}}}{\partial x}} } \hbox {d}\,\theta \,\hbox {d}\,x,\\ {\mathbf{K}}_{\mathrm{44}}= & {} -\int _0^1 {\int _0^{2\pi } {\left( {d_{11} {{{\varvec{\Phi }} }}_{x} \frac{\partial ^{2}{{{\varvec{\Phi }} }}_{x}^{\mathrm{T}} }{\partial x^{2}}+d_{66} \lambda _{1}^{2} {{{\varvec{\Phi }} }}_{x} \frac{\partial ^{2}{{{\varvec{\Phi }} }}_{x}^{\mathrm{T}} }{\partial \theta ^{2}}-\frac{a_{55} }{\lambda _{3}^{2} }{{{\varvec{\Phi }} }}_{x} {{{\varvec{\Phi }} }}_{x}^{\mathrm{T}} } \right) } } \hbox {d}\,\theta \,\hbox {d}\,x,\\ {\mathbf{K}}_{\mathrm{45}}= & {} -\left( {d_{12} +d_{66} } \right) \lambda _{1} \int _0^1 {\int _0^{2\pi } {{{{\varvec{\Phi }} }}_{x} \frac{\partial ^{2}{{{\varvec{\Phi }} }}_{\theta }^{\mathrm{T}} }{\partial x\partial \theta }} } \hbox {d}\,\theta \,\hbox {d}\,x;\\ {\mathbf{K}}_{\mathrm{51}}= & {} -\left( {b_{12} +b_{66} } \right) \lambda _{1} \int _0^1 {\int _0^{2\pi } {{{{\varvec{\Phi }} }}_{\theta } \frac{\partial ^{2}{\mathbf{U}}^{\mathrm{T}}}{\partial x\partial \theta }} } \hbox {d}\,\theta \,\hbox {d}\,x, \\ {\mathbf{K}}_{\mathrm{52}}= & {} -\int _0^1 {\int _0^{2\pi } {\left( {b_{66} {{{\varvec{\Phi }} }}_{\theta } \frac{\partial ^{2}{\mathbf{V}}^{\mathrm{T}}}{\partial x^{2}}+b_{22} \lambda _{1}^{2} {{{\varvec{\Phi }}}}_{\theta } \frac{\partial ^{2}{\mathbf{V}}^{\mathrm{T}}}{\partial \theta ^{2}}} \right) } } \hbox {d}\,\theta \,\hbox {d}\,x, \\ {\mathbf{K}}_{\mathrm{53}}= & {} -\left( {b_{22} \lambda _{1}^{2} -a_{44} \frac{\lambda _{1} }{\lambda _{3} }} \right) \int _0^1 {\int _0^{2\pi } {{{{\varvec{\Phi }} }}_{\theta } \frac{\partial {\mathbf{W}}^{\mathrm{T}}}{\partial \theta }} } \hbox {d}\,\theta \,\hbox {d}\,x, \\ {\mathbf{K}}_{\mathrm{54}}= & {} -\left( {d_{12} +d_{66} } \right) \lambda _{1} \int _0^1 {\int _0^{2\pi } {{{{\varvec{\Phi }} }}_{\theta } \frac{\partial ^{2}{{{\varvec{\Phi }} }}_{x}^{\mathrm{T}} }{\partial x\partial \theta }} } \hbox {d}\,\theta \,\hbox {d}\,x, \\ {\mathbf{K}}_{\mathrm{55}}= & {} -\int _0^1 {\int _0^{2\pi } {\left( {d_{66} {{{\varvec{\Phi }} }}_{\theta } \frac{\partial ^{2}{{{\varvec{\Phi }} }}_{\theta }^{\mathrm{T}} }{\partial x^{2}}+d_{22} \lambda _{1}^{2} {{{\varvec{\Phi }} }}_{\theta } \frac{\partial ^{2}{{{\varvec{\Phi }} }}_{\theta }^{\mathrm{T}} }{\partial \theta ^{2}}-\frac{a_{44} }{\lambda _{3}^{2} }{{{\varvec{\Phi }} }}_{\theta } {{{\varvec{\Phi }} }}_{\theta }^{\mathrm{T}} } \right) } } \hbox {d}\,\theta \,\hbox {d}\,x. \end{aligned}$$

The elements of the matrix ${\mathbf{K}}^{(2)}$ are

$$\begin{aligned} {\mathbf{K}}_{13}^{(2)}&=-\int _0^1 {\int _0^{2\pi } {{\mathbf{U}}\frac{\partial {\mathbf{W}}^{\mathrm{T}}}{\partial x}{\mathbf{q}}_{w} \left( {a_{11} \lambda _{3} \frac{\partial ^{2}{\mathbf{W}}^{\mathrm{T}}}{\partial x^{2}}+a_{66} \lambda _{1} \lambda _{2} \frac{\partial ^{2}{\mathbf{W}}^{\mathrm{T}}}{\partial \theta ^{2}}} \right) } } \hbox {d}\,\theta \,\hbox {d}\,x \\&\quad -\left( {a_{12} +a_{66} } \right) \lambda _{1} \lambda _{2} \int _0^1 {\int _0^{2\pi } {{\mathbf{U}}\frac{\partial {\mathbf{W}}^{\mathrm{T}}}{\partial \theta }{\mathbf{q}}_{w} \frac{\partial ^{2}{\mathbf{W}}^{\mathrm{T}}}{\partial x\partial \theta }} } \hbox {d}\,\theta \,\hbox {d}\,x ;\\ {\mathbf{K}}_{23}^{(2)}&=-\left( {a_{12} +a_{66} } \right) \lambda _{2} \int _0^1 {\int _0^{2\pi } {{\mathbf{V}}\frac{\partial {\mathbf{W}}^{\mathrm{T}}}{\partial x}{\mathbf{q}}_{w} \frac{\partial ^{2}{\mathbf{W}}^{\mathrm{T}}}{\partial x\partial \theta }} } \hbox {d}\,\theta \,\hbox {d}\,x \\&\quad -\int _0^1 {\int _0^{2\pi } {{\mathbf{V}}\frac{\partial {\mathbf{W}}^{\mathrm{T}}}{\partial \theta }{\mathbf{q}}_{w} \left( {a_{66} \lambda _{2} \frac{\partial ^{2}{\mathbf{W}}^{\mathrm{T}}}{\partial x^{2}}+a_{22} \lambda _{1}^{2} \lambda _{2} \frac{\partial ^{2}{\mathbf{W}}^{\mathrm{T}}}{\partial \theta ^{2}}} \right) } } \hbox {d}\,\theta \,\hbox {d}\,x ;\\ {\mathbf{K}}_{31}^{(2)}&=-\int _0^1 {\int _0^{2\pi } {{\mathbf{W}}\frac{\partial {\mathbf{W}}^{\mathrm{T}}}{\partial x}{\mathbf{q}}_{w} \left( {a_{11} \lambda _{3} \frac{\partial ^{2}{\mathbf{U}}^{\mathrm{T}}}{\partial x^{2}}+a_{66} \lambda _{1} \lambda _{2} \frac{\partial ^{2}{\mathbf{U}}^{\mathrm{T}}}{\partial \theta ^{2}}} \right) } } \hbox {d}\,\theta \,\hbox {d}\,x \\&\quad -\left( {a_{12} +a_{66} } \right) \lambda _{1} \lambda _{2} \int _0^1 {\int _0^{2\pi } {{\mathbf{W}}\frac{\partial {\mathbf{W}}^{\mathrm{T}}}{\partial \theta }{\mathbf{q}}_{w} \frac{\partial ^{2}{\mathbf{U}}^{\mathrm{T}}}{\partial x\partial \theta }} } \hbox {d}\,\theta \,\hbox {d}\,x \\&\quad -\int _0^1 {\int _0^{2\pi } {{\mathbf{W}}\left( {a_{11} \lambda _{3} \frac{\partial ^{2}{\mathbf{W}}^{\mathrm{T}}}{\partial x^{2}}+a_{12} \lambda _{1} \lambda _{2} \frac{\partial ^{2}{\mathbf{W}}^{\mathrm{T}}}{\partial \theta ^{2}}} \right) } } {\mathbf{q}}_{w} \frac{\partial {\mathbf{U}}^{\mathrm{T}}}{\partial x}\hbox {d}\,\theta \,\hbox {d}\,x \\&\quad -2a_{66} \lambda _{1} \lambda _{2} \int _0^1 {\int _0^{2\pi } {{\mathbf{W}}\frac{\partial ^{2}{\mathbf{W}}^{\mathrm{T}}}{\partial x\partial \theta }} } {\mathbf{q}}_{w} \frac{\partial {\mathbf{U}}^{\mathrm{T}}}{\partial \theta }\hbox {d}\,\theta \,\hbox {d}\,x ,\\ {\mathbf{K}}_{32}^{(2)}&=-\left( {a_{12} +a_{66} } \right) \lambda _{2} \int _0^1 {\int _0^{2\pi } {{\mathbf{W}}\frac{\partial {\mathbf{W}}^{\mathrm{T}}}{\partial x}{\mathbf{q}}_{w} \frac{\partial ^{2}{\mathbf{V}}^{\mathrm{T}}}{\partial x\partial \theta }} } \hbox {d}\,\theta \,\hbox {d}\,x \\&\quad -\int _0^1 {\int _0^{2\pi } {{\mathbf{W}}\frac{\partial {\mathbf{W}}^{\mathrm{T}}}{\partial \theta }{\mathbf{q}}_{w} \left( {a_{66} \lambda _{2} \frac{\partial ^{2}{\mathbf{V}}^{\mathrm{T}}}{\partial x^{2}}+a_{22} \lambda _{1}^{2} \lambda _{2} \frac{\partial ^{2}{\mathbf{V}}^{\mathrm{T}}}{\partial \theta ^{2}}} \right) } } \hbox {d}\,\theta \,\hbox {d}\,x \\&\quad -2a_{66} \lambda _{2} \int _0^1 {\int _0^{2\pi } {{\mathbf{W}}\frac{\partial ^{2}{\mathbf{W}}^{\mathrm{T}}}{\partial x\partial \theta }} } {\mathbf{q}}_{w} \frac{\partial {\mathbf{V}}^{\mathrm{T}}}{\partial x}\hbox {d}\,\theta \,\hbox {d}\,x\\&\quad -\int _0^1 {\int _0^{2\pi } {{\mathbf{W}}\left( {a_{12} \lambda _{2} \frac{\partial ^{2}{\mathbf{W}}^{\mathrm{T}}}{\partial x^{2}}+a_{22} \lambda _{1}^{2} \lambda _{2} \frac{\partial ^{2}{\mathbf{W}}^{\mathrm{T}}}{\partial \theta ^{2}}} \right) } } {\mathbf{q}}_{w} \frac{\partial {\mathbf{V}}^{\mathrm{T}}}{\partial \theta }\hbox {d}\,\theta \,\hbox {d}\,x,\\ {\mathbf{K}}_{33}^{(2)}&=-\frac{a_{12} }{2}\lambda _{2} \int _0^1 {\int _0^{2\pi } {{\mathbf{W}}\frac{\partial {\mathbf{W}}^{\mathrm{T}}}{\partial x}{\mathbf{q}}_{w} \frac{\partial {\mathbf{W}}^{\mathrm{T}}}{\partial x}} } \hbox {d}\,\theta \,\hbox {d}\,x-\frac{a_{22} }{2}\lambda _{1}^{2} \lambda _{2} \int _0^1 {\int _0^{2\pi } {{\mathbf{W}}\frac{\partial {\mathbf{W}}^{\mathrm{T}}}{\partial \theta }{\mathbf{q}}_{w} \frac{\partial {\mathbf{W}}^{\mathrm{T}}}{\partial \theta }} } \hbox {d}\,\theta \,\hbox {d}\,x \\&\quad -\int _0^1 {\int _0^{2\pi } {{\mathbf{W}}\left( {a_{12} \lambda _{2} \frac{\partial ^{2}{\mathbf{W}}^{\mathrm{T}}}{\partial x^{2}}+a_{22} \lambda _{1}^{2} \lambda _{2} \frac{\partial ^{2}{\mathbf{W}}^{\mathrm{T}}}{\partial \theta ^{2}}} \right) } } {\mathbf{q}}_{w} {\mathbf{W}}^{\mathrm{T}}\hbox {d}\,\theta \,\hbox {d}\,x ,\\ {\mathbf{K}}_{34}^{(2)}&=-\int _0^1 {\int _0^{2\pi } {{\mathbf{W}}\frac{\partial {\mathbf{W}}^{\mathrm{T}}}{\partial x}{\mathbf{q}}_{w} \left( {b_{11} \lambda _{3} \frac{\partial ^{2}{{{\varvec{\Phi }} }}_{x}^{\mathrm{T}} }{\partial x^{2}}+b_{66} \lambda _{1} \lambda _{2} \frac{\partial ^{2}{{{\varvec{\Phi }} }}_{x}^{\mathrm{T}} }{\partial \theta ^{2}}} \right) } } \hbox {d}\,\theta \,\hbox {d}\,x \\&\quad -\left( {b_{12} +b_{66} } \right) \lambda _{1} \lambda _{2} \int _0^1 {\int _0^{2\pi } {{\mathbf{W}}\frac{\partial {\mathbf{W}}^{\mathrm{T}}}{\partial \theta }{\mathbf{q}}_{w} \frac{\partial ^{2}{{{\varvec{\Phi }} }}_{x}^{\mathrm{T}} }{\partial x\partial \theta }} } \hbox {d}\,\theta \,\hbox {d}\,x \\&\quad -\int _0^1 {\int _0^{2\pi } {{\mathbf{W}}\left( {b_{11} \lambda _{3} \frac{\partial ^{2}{\mathbf{W}}^{\mathrm{T}}}{\partial x^{2}}+b_{12} \lambda _{1} \lambda _{2} \frac{\partial ^{2}{\mathbf{W}}^{\mathrm{T}}}{\partial \theta ^{2}}} \right) } } {\mathbf{q}}_{w} \frac{\partial {{{\varvec{\Phi }} }}_{x}^{\mathrm{T}} }{\partial x}\hbox {d}\,\theta \,\hbox {d}\,x\\&\quad -2b_{66} \lambda _{1} \lambda _{2} \int _0^1 {\int _0^{2\pi } {{\mathbf{W}}\frac{\partial ^{2}{\mathbf{W}}^{\mathrm{T}}}{\partial x\partial \theta }{\mathbf{q}}_{w} } } \frac{\partial {{{\varvec{\Phi }} }}_{x}^{\mathrm{T}} }{\partial \theta }\hbox {d}\,\theta \,\hbox {d}\,x ,\\ {\mathbf{K}}_{35}^{(2)}&=-\left( {b_{12} +b_{66} } \right) \lambda _{2} \int _0^1 {\int _0^{2\pi } {{\mathbf{W}}\frac{\partial {\mathbf{W}}^{\mathrm{T}}}{\partial x}{\mathbf{q}}_{w} \frac{\partial ^{2}{{{\varvec{\Phi }} }}_{\theta }^{\mathrm{T}} }{\partial x\partial \theta }} } \hbox {d}\,\theta \,\hbox {d}\,x \\&\quad -\int _0^1 {\int _0^{2\pi } {{\mathbf{W}}\frac{\partial {\mathbf{W}}^{\mathrm{T}}}{\partial \theta }{\mathbf{q}}_{w} \left( {b_{66} \lambda _{2} \frac{\partial ^{2}{{{\varvec{\Phi }} }}_{\theta }^{\mathrm{T}} }{\partial x^{2}}+b_{22} \lambda _{1}^{2} \lambda _{2} \frac{\partial ^{2}{{{\varvec{\Phi }} }}_{\theta }^{\mathrm{T}} }{\partial \theta ^{2}}} \right) } } \hbox {d}\,\theta \,\hbox {d}\,x \\&\quad -2b_{66} \lambda _{2} \int _0^1 {\int _0^{2\pi } {{\mathbf{W}}\frac{\partial ^{2}{\mathbf{W}}^{\mathrm{T}}}{\partial x\partial \theta }{\mathbf{q}}_{w} } } \frac{\partial {{{\varvec{\Phi }} }}_{\theta }^{\mathrm{T}} }{\partial x}\hbox {d}\,\theta \,\hbox {d}\,x\\&\quad -\int _0^1 {\int _0^{2\pi } {{\mathbf{W}}\left( {b_{12} \lambda _{2} \frac{\partial ^{2}{\mathbf{W}}^{\mathrm{T}}}{\partial x^{2}}+b_{22} \lambda _{1}^{2} \lambda _{2} \frac{\partial ^{2}{\mathbf{W}}^{\mathrm{T}}}{\partial \theta ^{2}}} \right) } } {\mathbf{q}}_{w} \frac{\partial {{{\varvec{\Phi }} }}_{\theta }^{\mathrm{T}} }{\partial \theta }\hbox {d}\,\theta \,\hbox {d}\,x ;\\ {\mathbf{K}}_{43}^{(2)}&=-\int _0^1 {\int _0^{2\pi } {{{{\varvec{\Phi }} }}_{x} \frac{\partial {\mathbf{W}}^{\mathrm{T}}}{\partial x}{\mathbf{q}}_{w} \left( {b_{11} \lambda _{3} \frac{\partial ^{2}{\mathbf{W}}^{\mathrm{T}}}{\partial x^{2}}+b_{66} \lambda _{1} \lambda _{2} \frac{\partial ^{2}{\mathbf{W}}^{\mathrm{T}}}{\partial \theta ^{2}}} \right) } } \hbox {d}\,\theta \,\hbox {d}\,x \\&\quad -\left( {b_{12} +b_{66} } \right) \lambda _{1} \lambda _{2} \int _0^1 {\int _0^{2\pi } {{{{\varvec{\Phi }} }}_{x} \frac{\partial {\mathbf{W}}^{\mathrm{T}}}{\partial \theta }{\mathbf{q}}_{w} \frac{\partial ^{2}\mathrm{\mathbf{W}}^{\mathrm{T}}}{\partial x\partial \theta }} } \hbox {d}\,\theta \,\hbox {d}\,x ;\\ {\mathbf{K}}_{53}^{(2)}&=-\left( {b_{12} +b_{66} } \right) \lambda _{2} \int _0^1 {\int _0^{2\pi } {{{{\varvec{\Phi }} }}_{\theta } \frac{\partial {\mathbf{W}}^{\mathrm{T}}}{\partial x}{\mathbf{q}}_{w} \frac{\partial ^{2}{\mathbf{W}}^{\mathrm{T}}}{\partial x\partial \theta }} } \hbox {d}\,\theta \,\hbox {d}\,x \\&\quad -\int _0^1 {\int _0^{2\pi } {{{{\varvec{\Phi }} }}_{\theta } \frac{\partial {\mathbf{W}}^{\mathrm{T}}}{\partial \theta }{\mathbf{q}}_{w} \left( {b_{66} \lambda _{2} \frac{\partial ^{2}{\mathbf{W}}^{\mathrm{T}}}{\partial x^{2}}+b_{22} \lambda _{1}^{2} \lambda _{2} \frac{\partial ^{2}{\mathbf{W}}^{\mathrm{T}}}{\partial \theta ^{2}}} \right) } } \hbox {d}\,\theta \,\hbox {d}\,x . \end{aligned}$$

The elements of the matrix ${\mathbf{K}}^{(3)}$ are

$$\begin{aligned} \begin{aligned} {\mathbf{K}}_{33}^{(3)}&=-\int _0^1 {\int _0^{2\pi } {{\mathbf{W}}\left( {\frac{3a_{11} }{2}\lambda _{3}^{2} \frac{\partial ^{2}{\mathbf{W}}^{\mathrm{T}}}{\partial x^{2}}+\frac{a_{12} +2a_{66} }{2}\lambda _{2}^{2} \frac{\partial ^{2}{\mathbf{W}}^{\mathrm{T}}}{\partial \theta ^{2}}} \right) {\mathbf{q}}_{w} \frac{\partial {\mathbf{W}}^{\mathrm{T}}}{\partial x}{\mathbf{q}}_{w} \frac{\partial {\mathbf{W}}^{\mathrm{T}}}{\partial x}} } \hbox {d}\,\theta \,\hbox {d}\,x \\&\quad -\int _0^1 {\int _0^{2\pi } {{\mathbf{W}}\left( {\frac{a_{12} +2a_{66} }{2}\lambda _{2}^{2} \frac{\partial ^{2}{\mathbf{W}}^{\mathrm{T}}}{\partial x^{2}}+\frac{3a_{22} }{2}\lambda _{1}^{2} \lambda _{2}^{2} \frac{\partial ^{2}{\mathbf{W}}^{\mathrm{T}}}{\partial \theta ^{2}}} \right) } } {\mathbf{q}}_{w} \frac{\partial {\mathbf{W}}^{\mathrm{T}}}{\partial \theta }{\mathbf{q}}_{w} \frac{\partial {\mathbf{W}}^{\mathrm{T}}}{\partial \theta }\hbox {d}\,\theta \,\hbox {d}\,x \\&\quad -\left( {2a_{12} +4a_{66} } \right) \lambda _{2}^{2} \int _0^1 {\int _0^{2\pi } {{\mathbf{W}}\frac{\partial {\mathbf{W}}^{\mathrm{T}}}{\partial x}{\mathbf{q}}_{w} \frac{\partial {\mathbf{W}}^{\mathrm{T}}}{\partial \theta }{\mathbf{q}}_{w} \frac{\partial ^{2}{\mathbf{W}}^{\mathrm{T}}}{\partial x\partial \theta }} } \hbox {d}\,\theta \,\hbox {d}\,x. \end{aligned} \end{aligned}$$