Nonlinear thermal vibration of carbon nanotube polymer composite elliptical cylindrical shells

Abstract

This paper investigated the nonlinear vibration and dynamic response of the carbon nanotube polymer composite elliptical cylindrical shells on elastic foundations in thermal environment. The material properties of the nanocomposite elliptical cylindrical shells are assumed to depend on temperature and graded in the thickness direction according to various linear functions. The shell is subjected to the combination of the uniformly distributed transverse load in harmonic form and the uniform temperature rise. The motion and geometrical compatibility equations are derived based on the Reddy’s higher order shear deformation shell theory. The natural frequencies and the deflection amplitude–time curves of the shell are determined by using the Galerkin method and fourth-order Runge–Kutta method. The numerical results show not only the positive influences of carbon nanotube volume fraction and elastic foundations but also the negative influences of initial imperfection and temperature increment on the nonlinear vibration and dynamic response of the carbon nanotube polymer composite elliptical cylindrical shells. The reliability of the present results is verified by comparing with other publications.

1 Introduction

Nowadays, nanotechnology plays an important role in numerous industrial, commercial and engineering applications such as health, transportation, energy, environment, and many others. Because of unique features of mechanical strength, electrical and thermal conductivity, carbon nanotubes are chosen to be reinforcement in composite structures. Recently, carbon nanotube reinforced composites have been properly noticed. Arani et al. (2014) conducted the static stress analysis of carbon nanotube reinforced composite cylinder subjected to non-axisymmetric thermo-mechanical loads and uniform electro-magnetic fields. Shen (2009) presented an research on the nonlinear thermal bending of functionally graded single-walled carbon nanotube reinforced nanocomposite plates under a transverse uniform or sinusoidal load with simply supported edges. Based on the first order shear deformation theory, Lei et al. (2016) studied stability of functionally graded composites laminated plate reinforced by carbon nanotubes. Mirzaei and Kiani (2016) dealt with thermal buckling of functionally graded carbon nanotube reinforced conical shell. Zarei et al. (2017) evaluated multiple impact response of composite plates reinforced by carbon nanotube with general boundary conditions in case of temperature dependent properties. Kundalwal and Meguid (2015) studied the effect of carbon nanotube waviness on the active constrained layer damping of the laminated hybrid composite shells; Kundalwal and Ray (2016) also introduced the investigation of active constrained layer damping of smart laminated fuzzy fiber reinforced composite plates. Shen and Xiang (2012) investigated the nonlinear vibration of nanotube composite cylindrical shells reinforced by single-walled carbon nanotubes under a uniform temperature rise; Alibeigloo (2014) carried out the free vibration analysis of composite cylindrical panel with a polymeric matrix and carbon nanotube fibers embedded in piezoelectric layers based on theory of elasticity. A new approach—using analytical solution to investigate nonlinear dynamic response and vibration of imperfect functionally graded carbon nanotube reinforced composite double curved shallow shells was introduced in (Duc et al. 2017). Baloch et al. (2018) presented residual mechanical properties of lightweight concrete and normal strength concrete containing multi-walled carbon nanotubes after exposure to high temperatures. Kumar et al. (2017) concerned with the analysis of active constrained layer damping of geometrically nonlinear vibrations of doubly curved sandwich shells with facings composed of fuzzy fiber reinforced composite. Based on generalized differential quadrature method, Keleshteri et al. (2017) investigated stability of smart functionally graded carbon nanotube reinforced composites annular sector plates with surface-bonded piezoelectric layers. Further, Asadi and Wang (2017) examined dynamic stability of a pressurized functionally graded carbon nanotube reinforced composites cylindrical shell interacting with supersonic airflow.

In order to investigate the mechanical properties of thick structures, the higher order shear deformation plate and shell theories must be used because the Kirchoff hypothesis is not true in this case. Although the calculations of the higher order shear deformation plate and shell theories are much more complex than ones of the classical or the first order shear deformation plate and shell theories, there are still many publications on static and dynamic stability of structures using these theories. The dynamic instability behavior of laminated hypar and conoid shells using a higher order shear deformation theory were researched in (Pradyumna and Bandyopadhyay 2011). Dastjerdi et al. (2017) studied and solved the nonlinear local and nonlocal analysis of an annular sector plate based on a new modified higher-order shear deformation theory. Phung-Van et al. (2015) presented a simple and effective formulation based on isogeometric analysis and higher order shear deformation theory to investigate static, free vibration and dynamic control of piezoelectric composite plates integrated with sensors and actuators. Xie et al. (2019) proposed a general higher-order shear deformation zig-zag theory for predicting the nonlinear aerothermoelastic characteristics of composite laminated panels subjected to supersonic airflow. Chen et al. (2018) considered thermal vibration of beams made of FGM with general boundary conditions using third order shear deformation beam theory. Mantari et al. (2012) focused on bending and free vibration analysis of isotropic and multilayered plates and shells. Further, Tu et al. (2010) developed a nine-nodded rectangular element with nine degrees of freedom at each node for the bending and vibration analysis of laminated and sandwich composite plates. Duc et al. (2015) investigated the nonlinear vibration and dynamic analysis of imperfect thick functionally graded double curved shallow shells with piezoelectric actuators on elastic foundations subjected to the combination of electrical, thermal, mechanical and damping loading. Jadhav and Bajoria (2015) presented the buckling of functionally graded plate integrated with piezoelectric actuator and sensor at the top and bottom faces subjected to the combination of electrical and mechanical loading.

The elliptical cylindrical shell is one of the special shapes of the cylindrical shell. Because these structures are used extensively in various fields such as aerospace, marine, pipelines, missiles and automobiles engineering; they attracted great attention of the scientist around the world. Free and forced vibration characteristics of submerged finite elliptic cylindrical shell were conducted in (Zhang et al. 2017). Ganapathi et al. (2004) considered the free flexural vibration behavior of laminated angle-ply elliptical cylindrical shells. Kazemi et al. (2012) focused on the stability analysis of piezoelectric elliptical cylindrical shell using finite element method based on the shear deformation theory. Khalifa (2015) evaluated effects of non-uniform Winkler foundation and non-homogeneity on the free vibration of an orthotropic elliptical cylindrical shell. Li et al. (2014) investigated the elastic critical load of submerged elliptical cylindrical shell based on the vibro-acoustics model. Up to date, there are very few publications about elliptical cylindrical shells using higher order shear deformation theory. Duc et al. (2016) analyzed nonlinear thermal stability of FGM elliptical cylindrical shells reinforced by eccentrically stiffened. Ahmed (2016) considered the effects of the crease parameters and the elastic foundation on the buckling behavior of isotropic and orthotropic elliptic cylindrical shells with cosine-shaped meridian under radial loads. Recently, Xu et al. (2017) introduced a recent computational study to obtain the nonlinear buckling resistance of perfect elastic circular cylindrical shells subjected to uniform bending.

This paper introduces an analytical approach on the nonlinear dynamic response and vibration of carbon nanotube polymer composite elliptical cylindrical shells on elastic foundations in the thermal environment using the Reddy’s higher order shear deformation shell theory. The material properties of the shell are supposed to depend on temperature. The natural frequencies and deflection–time relationship are obtained by Galerkin method and fourth-order Runge–Kutta method. The numerical results show the effects of geometrical properties, temperature increment, initial imperfection, elastic foundations, volume fraction of carbon nanotube of the nonlinear dynamic response and vibration of the carbon nanotube polymer composite elliptical cylindrical shells.

2 Problem formulation

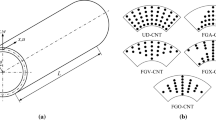
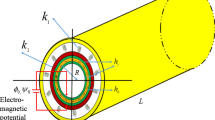
Consider a carbon nanotube polymer composite elliptical cylindrical shells as Fig. 1. The length, mean radius and total thickness of the shell are $L$,$R$ and $h$, respectively. A coordinate system $\left( {x,\,\theta ,\,z} \right)$ is defined in which $\theta$ and $x$ are in the circumferential and axial directions of the shell, respectively, and $z$ is perpendicular to the surface and points outwards $\left( { - h/2 \le z \le h/2} \right).$

Fig. 1

Geometry and the coordinate system of the carbon nanotube polymer composite elliptical cylindrical shells

The carbon nanotube polymer composite elliptical cylindrical shells are assumed to surround on elastic foundations as Fig. 2. The interaction between the elastic foundations and the shells is described by Pasternalk model as (Duc et al. 2015, 2016)

$$ q_{e} = k_{1} w - k_{2} \left( {\frac{{\partial^{2} w}}{{\partial x^{2} }} + \frac{{\partial^{2} w}}{{\partial y^{2} }}} \right), $$

(1)

where $w$ is the deflection of the carbon nanotube polymer composite elliptical cylindrical shells; $k_{1}$ and $k_{2}$ are stiffness of Winkler and Pasternak foundation, respectively.

Fig. 2

Model of the carbon nanotube polymer composite elliptical cylindrical shells on elastic foundations

The principal radii of curvature in the circumferential direction $R$ can be determined to the minor radius $b$ and the major radius $a$ of elliptical cross-section as (Duc et al. 2016; Xu et al. 2017)

$$ R = \left( {b^{2} /R_{0} } \right)\left( {1 + \mu_{0} \cos 2\theta } \right)^{ - 3/2} , $$

(2)

with

$$ R_{0} = \sqrt {\left( {a^{2} + b^{2} } \right)/2} ,\,\,\,\mu_{0} = a^{2} - b^{2} /\left( {a^{2} + b^{2} } \right), $$

(3)

3 The elastic moduli and the thermal expansion coefficients of the carbon nanotube polymer composite

3.1 Elastic moduli

It is assumed that the carbon nanotube polymer composite material is made from Poly (methyl methacrylate), referred to as PMMA, reinforced by (10,10) single-walled carbon nanotubes. The effective Young’s and shear modulus of the carbon nanotube polymer composite material are determined as (Shen 2009; Mirzaei and Kiani 2016)

$$ \begin{aligned} E_{11} & = \eta_{1} V_{CNT} E_{11}^{CNT} + V_{m} E_{m} , \\ \frac{{\eta_{2} }}{{E_{22} }} & = \frac{{V_{CNT} }}{{E_{22}^{CNT} }} + \frac{{V_{m} }}{{E_{m} }}, \\ \frac{{\eta_{3} }}{{G_{12} }} & = \frac{{V_{CNT} }}{{G_{12}^{CNT} }} + \frac{{V_{m} }}{{G_{m} }}, \\ \end{aligned} $$

(4)

where $V_{CNT}$ and $V_{m}$ are the volume fractions of the carbon nanotubes and the polymer matrix, respectively; $E_{11}^{CNT} ,\,\,E_{22}^{CNT} ,\,\,G_{12}^{CNT}$ are the mechanical properties of the carbon nanotubes; $E_{m,\,} \,G_{m}$ are Young’s and shear moduli of the polymer matrix and $\eta_{i} \,(i = \overline{1,3} )$ are the carbon nanotubes efficiency parameters.

The volume fractions of the carbon nanotubes and the polymer matrix are assumed to grade in the thickness direction according to linear functions. Three types of carbon nanotubes reinforcement, i.e. UD, V and X are considered with the volume fractions of the three distribution types are expressed as follows (Shen 2009; Mirzaei and Kiani 2016)

$$ \begin{aligned} V_{CNT} (z) & = \left\{ {\begin{array}{*{20}l} {V_{VCT}^{*} } \hfill & {\left( {UD} \right)} \hfill \\ {V_{VCT}^{*} \left( {1 + 2\frac{z}{h}} \right)} \hfill & {\left( V \right)} \hfill \\ {4V_{VCT}^{*} \frac{\left| z \right|}{h}} \hfill & {\left( X \right)} \hfill \\ \end{array} } \right., \\ V_{m} (z) & = 1 - V_{CNT} (z), \\ \end{aligned} $$

(5)

where

$$ V_{CNT}^{*} = \frac{{w_{CNT} }}{{w_{CNT} + \left( {\rho_{CNT} /\rho_{m} } \right) - \left( {\rho_{CNT} /\rho_{m} } \right)w_{CNT} }}, $$

(6)

in which $w_{CNT}$ is the mass fraction of carbon nanotubes, and $\rho_{CNT}$ and $\rho_{m}$ are the densities of carbon nanotubes and polymer matrix, respectively.

The elastic moduli (except the Poisson’s ratio) of the polymer matrix are dependent to temperature as (Shen 2009; Shen and Xiang 2012)

$$ \begin{aligned} E_{m} & = (3.52 - 0.0034T)\,{\text{GPa}}, \\ \nu_{m} & = 0.34, \\ \alpha_{m} & = 45\left( {1 + 0.0005\Delta T} \right) \times 10^{ - 6} \, / {\text{K}}, \\ \end{aligned} $$

(7)

where $T = 300 + \Delta T$, $\Delta T$ is the change of temperature in the environment.

The value of Young’s modulus, shear modulus and thermal expansion coefficient of of (10,10) single-walled carbon nanotubes are assumed to depend on temperature and they are calculated at five values of temperature by molecular dynamics simulations in Table 1 (Mirzaei and Kiani 2016). The Poisson’s ratio of single-walled carbon nanotubes is chosen to be constant $\nu_{12}^{CNT} = 0.175.$

Table 1 The material properties of (10, 10) single-walled carbon nanotubes at five values of temperature

Table 2 shows the values of the carbon nanotubes efficiency parameters $\eta_{i} \,(i = \overline{1,3} )$ at three values of nanotube volume fractions (Shen 2009; Mirzaei and Kiani 2016; Shen and Xiang 2012).

Table 2 The values of the carbon nanotubes efficiency parameters at three values of nanotube volume fractions

The effective Poisson’s ratio of the carbon nanotube polymer composite material depends on the temperature and the thickness direction as (Shen 2009; Shen and Xiang 2012)

$$ \nu_{12} = V_{CNT}^{*} v_{12}^{CNT} + V_{m} \nu_{m} , $$

(8)

where $\nu_{12}^{CNT}$ and $\,\nu_{m}$ are Poisson’s ratio of the carbon nanotubes and the polymer matrix, respectively.

3.2 Thermal expansion coefficients

The thermal expansion coefficients of the carbon nanotube polymer composite material in the longitudinal and transverse directions are expressed by (Shen 2009)

$$ \begin{aligned} \alpha_{11} & = \frac{{V_{CNT} E_{11}^{CNT} \alpha_{11}^{CNT} + V_{m} E_{m} \alpha_{m} }}{{V_{CNT} E_{11}^{CNT} + V_{m} E_{m} }}, \\ \alpha_{22} & = (1 + \nu_{12}^{CNT} )V_{CNT} \alpha_{22}^{CNT} + (1 + \nu_{m} )V_{m} \alpha_{m} - \nu_{12} \alpha_{11} , \\ \end{aligned} $$

(9)

with $\,\alpha_{m}$ and $\alpha_{11}^{CNT} ,\,\alpha_{22}^{CNT}$ are the thermal expansion coefficients of the polymer matrix and the carbon nanotubes, respectively.

4 Nonlinear strain–displacement relations

The nonlinear relations between strain and displacement of the carbon nanotube polymer composite elliptical cylindrical shells are (Brush and Almroth 1975; Reddy 2004)

$$\begin{aligned} & \left( {\begin{array}{*{20}c} {\varepsilon _{x} } \\ {\varepsilon _{y} } \\ {\gamma _{{xy}} } \\ \end{array} } \right) = \left( {\begin{array}{*{20}c} {\varepsilon _{x}^{0} } \\ {\varepsilon _{y}^{0} } \\ {\gamma _{{xy}}^{0} } \\ \end{array} } \right) + z\left( {\begin{array}{*{20}c} {k_{x}^{1} } \\ {k_{y}^{1} } \\ {k_{{xy}}^{1} } \\ \end{array} } \right) + z^{3} \left( {\begin{array}{*{20}c} {k_{x}^{3} } \\ {k_{y}^{3} } \\ {k_{{xy}}^{3} } \\ \end{array} } \right), \\ & \left( {\begin{array}{*{20}c} {\gamma _{{xz}} } \\ {\gamma _{{yz}} } \\ \end{array} } \right) = \left( {\begin{array}{*{20}c} {\gamma _{{xz}}^{0} } \\ {\gamma _{{yz}}^{0} } \\ \end{array} } \right) + z^{2} \left( {\begin{array}{*{20}c} {k_{{xz}}^{2} } \\ {k_{{yz}}^{2} } \\ \end{array} } \right), \\ \end{aligned}$$

(10)

where

$$ \begin{aligned} & \left( {\begin{array}{*{20}c} {\varepsilon_{x}^{0} } \\ {\varepsilon_{y}^{0} } \\ {\gamma_{xy}^{0} } \\ \end{array} } \right) = \left( {\begin{array}{*{20}c} {\frac{\partial u}{\partial x} + \frac{1}{2}\left( {\frac{\partial w}{\partial x}} \right)^{2} } \\ {\frac{\partial v}{\partial y} - \frac{w}{R} + \frac{1}{2}\left( {\frac{\partial w}{\partial y}} \right)^{2} } \\ {\frac{\partial u}{\partial y} + \frac{\partial v}{\partial x} + \frac{\partial w}{\partial x}\frac{\partial w}{\partial y}} \\ \end{array} } \right),\;\left( {\begin{array}{*{20}c} {k_{x}^{1} } \\ {k_{y}^{1} } \\ {k_{xy}^{1} } \\ \end{array} } \right) = \left( {\begin{array}{*{20}c} {\frac{{\partial \phi_{x} }}{\partial x}} \\ {\frac{{\partial \phi_{y} }}{\partial y}} \\ {\frac{{\partial \phi_{x} }}{\partial y} + \frac{{\partial \phi_{y} }}{\partial x}} \\ \end{array} } \right),\;\left( {\begin{array}{*{20}c} {\gamma_{xz}^{0} } \\ {\gamma_{yz}^{0} } \\ \end{array} } \right) = \left( {\begin{array}{*{20}c} {\phi_{x} + \frac{\partial w}{\partial x}} \\ {\phi_{y} + \frac{\partial w}{\partial y}} \\ \end{array} } \right), \\ & \left( {\begin{array}{*{20}c} {k_{x}^{3} } \\ {k_{y}^{3} } \\ {k_{xy}^{3} } \\ \end{array} } \right) = - c_{1} \left( {\begin{array}{*{20}c} {\frac{{\partial \phi_{x} }}{\partial x} + \frac{{\partial^{2} w}}{{\partial x^{2} }}} \\ {\frac{{\partial \phi_{y} }}{\partial y} + \frac{{\partial^{2} w}}{{\partial y^{2} }}} \\ {\frac{{\partial \phi_{x} }}{\partial y} + \frac{{\partial \phi_{y} }}{\partial x} + 2\frac{{\partial^{2} w}}{\partial x\partial y}} \\ \end{array} } \right),\;\left( {\begin{array}{*{20}c} {k_{xz}^{2} } \\ {k_{yz}^{2} } \\ \end{array} } \right) = - 3c_{1} \left( {\begin{array}{*{20}c} {\phi_{x} + \frac{\partial w}{\partial x}} \\ {\phi_{y} + \frac{\partial w}{\partial y}} \\ \end{array} } \right), \\ \end{aligned} $$

(11)

in which $c_{1} = 4/3h^{2}$; $\phi_{x} ,\,\phi_{y}$ are the rotations of normals to the midsurface with respect to the $y$ and $x$ axes, respectively.

5 Hooke’s law

Hooke’s law for a carbon nanotube polymer composite elliptical cylindrical shells with temperature-dependent properties is defined as (Alibeigloo 2014)

$$ \left[ {\begin{array}{*{20}c} {\sigma_{xx} } \\ {\sigma_{yy} } \\ {\sigma_{xy} } \\ {\sigma_{xz} } \\ {\sigma_{yz} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {Q_{11} } & {Q_{12} } & 0 & 0 & 0 \\ {Q_{12} } & {Q_{22} } & 0 & 0 & 0 \\ 0 & 0 & {Q_{66} } & 0 & 0 \\ 0 & 0 & 0 & {Q_{44} } & 0 \\ 0 & 0 & 0 & 0 & {Q_{55} } \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {\varepsilon_{xx} - \alpha_{11} \Delta T} \\ {\varepsilon_{yy} - \alpha_{22} \Delta T} \\ {\varepsilon_{xy} } \\ {\varepsilon_{xz} } \\ {\varepsilon_{yz} } \\ \end{array} } \right], $$

(12)

where

$$ Q_{11} = \frac{{E_{11} }}{{1 - \nu_{12} \nu_{21} }},\,\,Q_{22} = \frac{{E_{22} }}{{1 - \nu_{12} \nu_{21} }},\,\,Q_{12} = \frac{{\nu_{21} E_{11} }}{{1 - \nu_{12} \nu_{21} }},\,\,Q_{44} = G_{23} ,\,\,Q_{55} = G_{13} ,\,\,Q_{66} = G_{12} , $$

(13)

and we assume that $G_{13} = G_{12}$ and $G_{23} = 1.2G_{12}$ (Shen and Xiang 2012).

6 Forces and moments

The force and moment resultants of the carbon nanotube polymer composite elliptical cylindrical shells are expressed by

$$ \begin{aligned} \left( {N_{i} ,M_{i} ,P_{i} } \right) & = \int\limits_{ - h/2}^{h/2} {\sigma_{i} (1,z,z^{3} )} dz,\quad i = x,y,xy \\ \left( {Q_{i} ,R_{i} } \right) & = \int\limits_{ - h/2}^{h/2} {\sigma_{iz} (1,z^{2} )} dz,\quad i = x,y. \\ \end{aligned} $$

(14)

Substitution Eqs. (10) and (11) into Eqs. (12) then results into Eqs. (14) yields the constitutive relations as

$$ \left\{ {\begin{array}{*{20}c} {N_{x} } \\ {N_{y} } \\ {N_{xy} } \\ {M_{x} } \\ {M_{y} } \\ {M_{xy} } \\ {P_{x} } \\ {P_{y} } \\ {P_{xy} } \\ {Q_{x} } \\ {Q_{y} } \\ {R_{x} } \\ {R_{y} } \\ \end{array} } \right\} = \left[ {\begin{array}{*{20}c} {A_{11} } & {A_{12} } & 0 & {B_{11} } & {B_{12} } & 0 & {E_{11} } & {E_{12} } \\ {A_{12} } & {A_{22} } & 0 & {B_{12} } & {B_{22} } & 0 & {E_{12} } & {E_{22} } \\ 0 & 0 & {A_{66} } & 0 & 0 & {B_{66} } & 0 & 0 \\ {B_{11} } & {B_{12} } & 0 & {D_{11} } & {D_{12} } & 0 & {F_{11} } & {F_{12} } \\ {B_{12} } & {B_{22} } & 0 & {D_{12} } & {D_{22} } & 0 & {F_{12} } & {F_{22} } \\ 0 & 0 & {B_{66} } & 0 & 0 & {D_{66} } & 0 & 0 \\ {E_{11} } & {E_{12} } & 0 & {F_{11} } & {F_{12} } & 0 & {H_{11} } & {H_{12} } \\ {E_{12} } & {E_{22} } & 0 & {F_{12} } & {F_{22} } & 0 & {H_{12} } & {H_{22} } \\ 0 & 0 & {E_{66} } & 0 & 0 & {F_{66} } & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ \end{array} \begin{array}{*{20}c} 0 \\ 0 \\ {E_{66} } \\ 0 \\ 0 \\ {F_{66} } \\ 0 \\ 0 \\ {H_{66} } \\ 0 \\ 0 \\ 0 \\ 0 \\ \end{array} \begin{array}{*{20}c} 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \\ {A_{44} } & 0 & {D_{44} } & 0 \\ 0 & {A_{55} } & 0 & {D_{55} } \\ {D_{44} } & 0 & {F_{44} } & 0 \\ 0 & {D_{55} } & 0 & {F_{55} } \\ \end{array} } \right]\left\{ {\begin{array}{*{20}c} {\varepsilon_{x}^{0} } \\ {\varepsilon_{y}^{0} } \\ {\gamma_{xy}^{0} } \\ {k_{x}^{1} } \\ {k_{y}^{1} } \\ {k_{xy}^{1} } \\ {k_{x}^{3} } \\ {k_{y}^{3} } \\ {k_{xy}^{3} } \\ {\gamma_{xz}^{0} } \\ {\gamma_{yz}^{0} } \\ {k_{xz}^{2} } \\ {k_{yz}^{2} } \\ \end{array} } \right\} - \left\{ {\begin{array}{*{20}c} {\varPhi_{1} } \\ {\varPhi_{2} } \\ 0 \\ {\varPhi_{3} } \\ {\varPhi_{4} } \\ 0 \\ {\varPhi_{5} } \\ {\varPhi_{6} } \\ 0 \\ 0 \\ 0 \\ 0 \\ 0 \\ \end{array} } \right\} $$

(15)

in which

$$ \begin{aligned} & \left( {A_{ij} ,\,\,B_{ij} ,\,\,D_{ij} ,\,\,E_{ij} ,\,\,F_{ij} ,\,\,H_{ij} } \right) = \int\limits_{ - h/2}^{h/2} {Q_{ij} (1,\,\,z,\,\,z^{2} ,\,\,z^{3} ,\,\,z^{4} ,\,\,z^{6} )\,dz,\,\,ij = 11,12,22,66,} \\ & (A_{kl} ,\,\,D_{kl} ,\,\,F_{kl} ) = \int\limits_{ - h/2}^{h/2} {Q_{ij} (1,\,\,z^{2} ,\,\,z^{4} )\,dz,\,\,kl = 44,55,} \\ & \varPhi_{1} = \int\limits_{ - h/2}^{h/2} {Q_{11} \alpha_{11} \Delta T\,dz} + \int\limits_{ - h/2}^{h/2} {Q_{12} \alpha_{22} \Delta T\,dz} ,\,\, \\ & \varPhi_{2} = \int\limits_{ - h/2}^{h/2} {Q_{12} \alpha_{11} \Delta T\,dz} + \int\limits_{ - h/2}^{h/2} {Q_{22} \alpha_{22} \Delta T\,dz} , \\ & \varPhi_{3} = \int\limits_{ - h/2}^{h/2} {Q_{11} \alpha_{11} \Delta T\,zdz} + \int\limits_{ - h/2}^{h/2} {Q_{12} \alpha_{22} \Delta Tz\,dz} ,\,\, \\ & \varPhi_{4} = \int\limits_{ - h/2}^{h/2} {Q_{12} \alpha_{11} \Delta T\,zdz} + \int\limits_{ - h/2}^{h/2} {Q_{22} \alpha_{22} \Delta Tz\,dz} , \\ & \varPhi_{5} = \int\limits_{ - h/2}^{h/2} {Q_{11} \alpha_{11} \Delta T\,z^{3} dz} + \int\limits_{ - h/2}^{h/2} {Q_{12} \alpha_{22} \Delta T\,z^{3} dz} ,\,\, \\ & \varPhi_{6} = \int\limits_{ - h/2}^{h/2} {Q_{12} \alpha_{11} z^{3} \Delta T\,dz} + \int\limits_{ - h/2}^{h/2} {Q_{22} \alpha_{22} z^{3} \Delta T\,dz} , \\ \end{aligned} $$

(16)

From the constitutive relations (15), we have

$$ \begin{aligned} \varepsilon_{x}^{0} & = I_{11}^{{}} \frac{{\partial^{2} f}}{{\partial y^{2} }} - I_{12}^{{}} \frac{{\partial^{2} f}}{{\partial x^{2} }} + I_{13}^{{}} \frac{{\partial \phi_{x} }}{\partial x} + I_{14}^{{}} \frac{{\partial \phi_{y} }}{\partial y} - c_{1} I_{15}^{{}} \left( {\frac{{\partial^{2} w}}{{\partial x^{2} }} + \frac{{\partial \phi_{x} }}{\partial x}} \right) \\ & \quad - \,c_{1} I_{16}^{{}} \left( {\frac{{\partial^{2} w}}{{\partial y^{2} }} + \frac{{\partial \phi_{y} }}{\partial y}} \right) + I_{17}^{{}} \varPhi_{1} + I_{18}^{{}} \varPhi_{2}^{{}} , \\ \varepsilon_{y}^{0} & = I_{21}^{{}} \frac{{\partial^{2} f}}{{\partial x^{2} }} - I_{12}^{{}} \frac{{\partial^{2} f}}{{\partial y^{2} }} + I_{23}^{{}} \frac{{\partial \phi_{x} }}{\partial x} + I_{24}^{{}} \frac{{\partial \phi_{y} }}{\partial y} - c_{1} I_{25}^{{}} \left( {\frac{{\partial^{2} w}}{{\partial x^{2} }} + \frac{{\partial \phi_{x} }}{\partial x}} \right) \\ & \quad - \,c_{1} I_{26}^{{}} \left( {\frac{{\partial^{2} w}}{{\partial y^{2} }} + \frac{{\partial \phi_{y} }}{\partial y}} \right) + I_{27}^{{}} \varPhi_{1} + I_{28}^{{}} \varPhi_{2}^{{}} , \\ \gamma_{xy}^{0} & = - I_{31}^{{}} \frac{{\partial^{2} f}}{\partial x\partial y} + I_{32}^{{}} \left( {\frac{{\partial \phi_{x} }}{\partial y} + \frac{{\partial \phi_{y} }}{\partial x}} \right) - c_{1} I_{33}^{{}} \left( {2\frac{{\partial^{2} w}}{\partial x\partial y} + \frac{{\partial \phi_{x} }}{\partial y} + \frac{{\partial \phi_{y} }}{\partial x}} \right), \\ \end{aligned} $$

(17)

with the detail of coefficients $I_{ij} (i = \overline{1,2} ,j = \overline{1,8} ),\,\,I_{3k} (k = \overline{1,3} )$ are given in “Appendix A”.

The Airy’s stress function $f\left( {x,y,t} \right)$ is introduced as

$$ N_{x} = \frac{{\partial^{2} f}}{{\partial y^{2} }},N_{y} = \frac{{\partial^{2} f}}{{\partial x^{2} }},N_{xy} = - \frac{{\partial^{2} f}}{\partial x\partial y}. $$

(18)

7 The nonlinear motion equations and the geometrical compatibility equation

7.1 The nonlinear motion equations

The nonlinear motion equations the carbon nanotube polymer composite elliptical cylindrical shells are (Brush and Almroth 1975; Reddy 2004)

$$ \frac{{\partial N_{x} }}{\partial x} + \frac{{\partial N_{xy} }}{\partial y} = \bar{I}_{1} \frac{{\partial^{2} u}}{{\partial t^{2} }} + \bar{I}_{2} \frac{{\partial^{2} \phi_{x} }}{{\partial t^{2} }} - \bar{I}_{3} \frac{{\partial^{3} w}}{{\partial t^{2} \partial x}}, $$

(19a)

$$ \frac{{\partial N_{xy} }}{\partial x} + \frac{{\partial N_{y} }}{\partial y} = \overline{{I_{1}^{*} }} \frac{{\partial^{2} v}}{{\partial t^{2} }} + \overline{{I_{2}^{*} }} \frac{{\partial^{2} \phi_{y} }}{{\partial t^{2} }} - \overline{{I_{3}^{*} }} \frac{{\partial^{3} w}}{{\partial t^{2} \partial y}}, $$

(19b)

$$ \begin{aligned} & \frac{{\partial Q_{x} }}{\partial x} + \frac{{\partial Q_{y} }}{\partial y} - 3c_{1} \left( {\frac{{\partial R_{x} }}{\partial x} + \frac{{\partial R_{y} }}{\partial y}} \right) + c_{1} \left( {\frac{{\partial^{2} P_{x} }}{{\partial x^{2} }} + 2\frac{{\partial^{2} P_{xy} }}{\partial x\partial y} + \frac{{\partial^{2} P_{y} }}{{\partial y^{2} }}} \right) + \frac{{N_{y} }}{R} + q + N_{x} \frac{{\partial^{2} w}}{{\partial x^{2} }} \\ & \quad + \,2N_{xy} \frac{{\partial^{2} w}}{\partial x\partial y} + N_{y} \frac{{\partial^{2} w}}{{\partial y^{2} }} - k_{1} w + k_{2} \nabla^{2} w = I_{1} \frac{{\partial^{2} w}}{{\partial t^{2} }} + 2\varepsilon I_{1} \frac{\partial w}{\partial t} + \bar{I}_{3} \frac{{\partial^{3} u}}{{\partial t^{2} \partial x}} + \bar{I}_{5} \frac{{\partial^{3} \phi_{x} }}{{\partial t^{2} \partial x}} \\ & \quad + \,\overline{{I_{3}^{*} }} \frac{{\partial^{3} v}}{{\partial t^{2} \partial y}} + \overline{{I_{5}^{*} }} \frac{{\partial^{3} \phi_{y} }}{{\partial t^{2} \partial y}} - c_{1}^{2} I_{7} \left( {\frac{{\partial^{4} w}}{{\partial t^{2} \partial x^{2} }} + \frac{{\partial^{4} w}}{{\partial t^{2} \partial y^{2} }}} \right), \\ \end{aligned} $$

(19c)

$$ \frac{{\partial M_{x} }}{\partial x} + \frac{{\partial M_{xy} }}{\partial y} - Q_{x} + 3c_{1} R_{x} - c_{1} \left( {\frac{{\partial P_{x} }}{\partial x} + \frac{{\partial P_{xy} }}{\partial y}} \right) = \bar{I}_{2} \frac{{\partial^{2} u}}{{\partial t^{2} }} + \bar{I}_{4} \frac{{\partial^{2} \phi_{x} }}{{\partial t^{2} }} - \bar{I}_{5} \frac{{\partial^{3} w}}{{\partial t^{2} \partial x}}, $$

(19d)

$$ \frac{{\partial M_{xy} }}{\partial x} + \frac{{\partial M_{y} }}{\partial y} - Q_{y} + 3c_{1} R_{y} - c_{1} \left( {\frac{{\partial P_{xy} }}{\partial x} + \frac{{\partial P_{y} }}{\partial y}} \right) = \overline{{I_{2}^{*} }} \frac{{\partial^{2} v}}{{\partial t^{2} }} + \overline{{I_{4}^{*} }} \frac{{\partial^{2} \phi_{y} }}{{\partial t^{2} }} - \overline{{I_{5}^{*} }} \frac{{\partial^{3} w}}{{\partial t^{2} \partial y}}, $$

(19e)

with $q$ is an uniformly distributed pressure,$\varepsilon$ is the viscous damping coefficient and the detail of coefficients $\overline{{I_{i} }} (i = \overline{1,5} ),\,\,\overline{{I_{j}^{*} }} (j = \overline{1,5} )$ may be found in “Appendix B”.

Substituting Eq. (18) into Eqs. (19a) and (19b) gives

$$ \frac{{\partial^{2} u}}{{\partial t^{2} }} = - \frac{{\bar{I}_{2} }}{{\bar{I}_{1} }}\frac{{\partial^{2} \phi_{x} }}{{\partial t^{2} }} + \frac{{\bar{I}_{3} }}{{\bar{I}_{1} }}\frac{{\partial^{3} w}}{{\partial t^{2} \partial x}}, $$

(20a)

$$ \frac{{\partial^{2} v}}{{\partial t^{2} }} = - \frac{{\overline{{I_{2}^{*} }} }}{{\overline{{I_{1}^{*} }} }}\frac{{\partial^{2} \phi_{y} }}{{\partial t^{2} }} + \frac{{\overline{{I_{3}^{*} }} }}{{\overline{{I_{1}^{*} }} }}\frac{{\partial^{3} w}}{{\partial t^{2} \partial y}}. $$

(20b)

Replacing Eqs. (20a), (20b) into Eqs. (19c)–(19e) leads to

$$ \begin{aligned} & \frac{{\partial Q_{x} }}{\partial x} + \frac{{\partial Q_{y} }}{\partial y} - 3c_{1} \left( {\frac{{\partial R_{x} }}{\partial x} + \frac{{\partial R_{y} }}{\partial y}} \right) + c_{1} \left( {\frac{{\partial^{2} P_{x} }}{{\partial x^{2} }} + 2\frac{{\partial^{2} P_{xy} }}{\partial x\partial y} + \frac{{\partial^{2} P_{y} }}{{\partial y^{2} }}} \right) + \frac{1}{R}\frac{{\partial^{2} f}}{{\partial x^{2} }} + p + \frac{{\partial^{2} f}}{{\partial y^{2} }}\frac{{\partial^{2} w}}{{\partial x^{2} }} \\ & \quad - \,2\frac{{\partial^{2} f}}{\partial x\partial y}\frac{{\partial^{2} w}}{\partial x\partial y} + \frac{{\partial^{2} f}}{{\partial x^{2} }}\frac{{\partial^{2} w}}{{\partial y^{2} }} - k_{1} w + k_{2} \nabla^{2} w = I_{1} \frac{{\partial^{2} w}}{{\partial t^{2} }} + 2\varepsilon I_{1} \frac{\partial w}{\partial t} + \overline{\overline{{I_{5} }}} \frac{{\partial^{3} \phi_{x} }}{{\partial t^{2} \partial x}} + \overline{\overline{{I_{5}^{*} }}} \frac{{\partial^{3} \phi_{y} }}{{\partial t^{2} \partial y}} \\ & \quad + \,\overline{\overline{{I_{7} }}} \frac{{\partial^{4} w}}{{\partial t^{2} \partial x^{2} }} + \overline{\overline{{I_{7}^{*} }}} \frac{{\partial^{4} w}}{{\partial t^{2} \partial y^{2} }}, \\ & \frac{{\partial M_{x} }}{\partial x} + \frac{{\partial M_{xy} }}{\partial y} - Q_{x} + 3c_{1} R_{x} - c_{1} \left( {\frac{{\partial P_{x} }}{\partial x} + \frac{{\partial P_{xy} }}{\partial y}} \right) = \overline{\overline{{I_{3} }}} \frac{{\partial^{2} \phi_{x} }}{{\partial t^{2} }} - \overline{\overline{{I_{5} }}} \frac{{\partial^{3} w}}{{\partial t^{2} \partial x}}, \\ & \frac{{\partial M_{xy} }}{\partial x} + \frac{{\partial M_{y} }}{\partial y} - Q_{y} + 3c_{1} R_{y} - c_{1} \left( {\frac{{\partial P_{xy} }}{\partial x} + \frac{{\partial P_{y} }}{\partial y}} \right) = \overline{\overline{{I_{3}^{*} }}} \frac{{\partial^{2} \phi_{y} }}{{\partial t^{2} }} - \overline{\overline{{I_{5}^{*} }}} \frac{{\partial^{3} w}}{{\partial t^{2} \partial y}}, \\ \end{aligned} $$

(21)

with

$$ \begin{aligned} \overline{\overline{{I_{3} }}} & = \left( {\bar{I}_{4} - \bar{I}_{2} \frac{{\bar{I}_{2} }}{{\bar{I}_{1} }}} \right),\,\overline{\overline{{I_{3}^{*} }}} = \left( {\overline{{I_{4}^{*} }} - \overline{{I_{2}^{*} }} \frac{{\overline{{I_{2}^{*} }} }}{{\overline{{I_{1}^{*} }} }}} \right),\,\overline{\overline{{I_{5} }}} = \left( {\bar{I}_{5} - \bar{I}_{2} \frac{{\bar{I}_{3} }}{{\bar{I}_{1} }}} \right),\,\overline{\overline{{I_{5}^{*} }}} = \left( {\overline{{I_{5}^{*} }} - \overline{{I_{2}^{*} }} \frac{{\overline{{I_{3}^{*} }} }}{{\overline{{I_{1}^{*} }} }}} \right) \\ \overline{\overline{{I_{7} }}} & = \left( {\bar{I}_{3} \frac{{\bar{I}_{3} }}{{\bar{I}_{1} }} - c_{1}^{2} I_{7} } \right),\overline{\overline{{I_{7}^{*} }}} = \left( {\overline{{I_{3}^{*} }} \frac{{\overline{{I_{3}^{*} }} }}{{\overline{{I_{1}^{*} }} }} - c_{1}^{2} I_{7} } \right) \\ \end{aligned} $$

(22)

7.2 The geometrical compatibility equation

The geometrical compatibility equation for an imperfect carbon nanotube polymer composite elliptical cylindrical shell is written as (Duc et al. 2015, 2016)

$$ \begin{aligned} \frac{{\partial^{2} \varepsilon_{x}^{0} }}{{\partial y^{2} }} + \frac{{\partial^{2} \varepsilon_{y}^{0} }}{{\partial x^{2} }} - \frac{{\partial^{2} \gamma_{xy}^{0} }}{\partial x\partial y} = & \left( {\frac{{\partial^{2} w}}{\partial x\partial y}} \right)^{2} - \frac{{\partial^{2} w}}{{\partial x^{2} }}\frac{{\partial^{2} w}}{{\partial y^{2} }} + 2\frac{{\partial^{2} w}}{\partial x\partial y}\frac{{\partial^{2} w_{{}}^{*} }}{\partial x\partial y} - \frac{{\partial^{2} w}}{{\partial x^{2} }}\frac{{\partial^{2} w_{{}}^{*} }}{{\partial y^{2} }} \\ & \quad - \,\frac{{\partial^{2} w}}{{\partial y^{2} }}\frac{{\partial^{2} w_{{}}^{*} }}{{\partial x^{2} }} - \frac{1}{R}\frac{{\partial^{2} w}}{{\partial x^{2} }}, \\ \end{aligned} $$

(23)

with function $w^{*} (x,y)$ denotes initial small imperfection of the shell.

Substitution of Eqs. (11) into Eqs. (15) and introducing the results into Eqs. (21) yields

$$ \begin{aligned} & L_{11} \left( w \right) + L_{12} \left( {\phi_{x} } \right) + L_{13} \left( {\phi_{y} } \right) + L_{14} (f) + S\left( {w,f} \right) + q = I_{1} \frac{{\partial^{2} w}}{{\partial t^{2} }} + 2\varepsilon I_{1} \frac{\partial w}{\partial t} \\ & \quad + \,\overline{\overline{{I_{5} }}} \frac{{\partial^{3} \phi_{x} }}{{\partial t^{2} \partial x}} + \overline{\overline{{I_{5}^{*} }}} \frac{{\partial^{3} \phi_{y} }}{{\partial t^{2} \partial y}} + \overline{\overline{{I_{7} }}} \frac{{\partial^{4} w}}{{\partial t^{2} \partial x^{2} }} + \overline{\overline{{I_{7}^{*} }}} \frac{{\partial^{4} w}}{{\partial t^{2} \partial y^{2} }}, \\ & L_{21} \left( w \right) + L_{22} \left( {\phi_{x} } \right) + L_{23} \left( {\phi_{y} } \right) + L_{24} \left( f \right) = \overline{\overline{{I_{3} }}} \frac{{\partial^{2} \phi_{x} }}{{\partial t^{2} }} - \overline{\overline{{I_{5} }}} \frac{{\partial^{3} w}}{{\partial t^{2} \partial x}}, \\ & L_{31} \left( w \right) + L_{32} \left( {\phi_{x} } \right) + L_{33} \left( {\phi_{y} } \right) + L_{34} \left( f \right) = \overline{\overline{{I_{3}^{*} }}} \frac{{\partial^{2} \phi_{y} }}{{\partial t^{2} }} - \overline{\overline{{I_{5}^{*} }}} \frac{{\partial^{3} w}}{{\partial t^{2} \partial y}}, \\ \end{aligned} $$

(24)

in which

$$ \begin{aligned} L_{11} \left( w \right) & = X_{11} \frac{{\partial^{2} w}}{{\partial x^{2} }} + X_{12} \frac{{\partial^{2} w}}{{\partial y^{2} }} + X_{13} \frac{{\partial^{4} w}}{{\partial x^{4} }} + X_{14} \frac{{\partial^{4} w}}{{\partial x^{2} \partial y^{2} }} + X_{15} \frac{{\partial^{4} w}}{{\partial y^{4} }} - k_{1} w + k_{2} \left( {\frac{{\partial^{2} w}}{{\partial x^{2} }} + \frac{{\partial^{2} w}}{{\partial y^{2} }}} \right), \\ L_{12} \left( {\phi_{x} } \right) & = X_{11} \frac{{\partial \phi_{x} }}{\partial x} + X_{16} \frac{{\partial^{3} \phi_{x} }}{{\partial x^{3} }} + X_{17} \frac{{\partial^{3} \phi_{x} }}{{\partial x\partial y^{2} }},\,\,L_{13} \left( {\phi_{y} } \right) = X_{12} \frac{{\partial \phi_{y} }}{\partial y} + X_{18} \frac{{\partial^{3} \phi_{y} }}{{\partial y^{3} }} + X_{19} \frac{{\partial^{3} \phi_{y} }}{{\partial x^{2} \partial y}}, \\ L_{14} (f) & = X_{110} \frac{{\partial^{4} f}}{{\partial x^{4} }} + X_{111} \frac{{\partial^{4} f}}{{\partial x^{2} \partial y^{2} }} + X_{112} \frac{{\partial^{4} f}}{{\partial y^{4} }}, \\ \end{aligned} $$

$$ \begin{aligned} S\left( {w,f} \right) & = \frac{{\partial^{2} f}}{{\partial y^{2} }}\frac{{\partial^{2} w}}{{\partial x^{2} }} - 2\frac{{\partial^{2} f}}{\partial x\partial y}\frac{{\partial^{2} w}}{{\partial y^{2} }} + \frac{{\partial^{2} f}}{{\partial x^{2} }}\frac{{\partial^{2} w}}{{\partial y^{2} }} + \frac{1}{R}\frac{{\partial^{2} f}}{{\partial x^{2} }}, \\ L_{21} \left( w \right) & = X_{21} \frac{\partial w}{\partial x} + X_{22} \frac{{\partial^{3} w}}{{\partial x^{3} }} + X_{23} \frac{{\partial^{3} w}}{{\partial x\partial y^{2} }},\,\,L_{22} \left( {\phi_{x} } \right) = X_{21} \phi_{x} + X_{24} \frac{{\partial^{2} \phi_{x} }}{{\partial x^{2} }} + X_{25} \frac{{\partial^{2} \phi_{x} }}{{\partial y^{2} }}, \\ L_{23} \left( {\phi_{y} } \right) & = X_{26} \frac{{\partial^{2} \phi_{y} }}{\partial x\partial y},\,\,L_{24} (f) = X_{27} \frac{{\partial^{3} f}}{{\partial x^{3} }} + X_{28} \frac{{\partial^{3} f}}{{\partial x\partial y^{2} }}, \\ L_{31} \left( w \right) & = X_{31} \frac{\partial w}{\partial y} + X_{32} \frac{{\partial^{3} w}}{{\partial x^{2} \partial y}} + X_{33} \frac{{\partial^{3} w}}{{\partial y^{3} }},\,\,\,L_{32} \left( {\phi_{x} } \right) = X_{34} \frac{{\partial^{2} \phi_{x} }}{\partial x\partial y}, \\ L_{33} \left( {\phi_{y} } \right) & = X_{31} \phi_{y} + X_{35} \frac{{\partial^{2} \phi_{y} }}{{\partial x^{2} }} + X_{36} \frac{{\partial^{2} \phi_{y} }}{{\partial y^{2} }},\,\,L_{34} (f) = X_{37} \frac{{\partial^{3} f}}{{\partial x^{2} \partial y}} + X_{38} \frac{{\partial^{3} f}}{{\partial y^{3} }}, \\ \end{aligned} $$

(25)

and the detail of coefficients $X_{1i} (i = \overline{1,12} ),\,\,X_{2j} (j = \overline{1,8} ),\,\,X_{3k} (k = \overline{1,8} )$ may be found in “Appendix C”.

For an imperfect the carbon nanotube polymer composite elliptical cylindrical shell, Eqs. (24) may be transformed to the form as

$$ \begin{aligned} & L_{11} \left( w \right) + L_{12} \left( {\phi_{x} } \right) + L_{13} \left( {\phi_{y} } \right) + L_{14} (f) + S\left( {w,f} \right) + S_{{}}^{ * } (w^{*} ,f) + q = I_{1} \frac{{\partial^{2} w}}{{\partial t^{2} }} + 2\varepsilon I_{1} \frac{\partial w}{\partial t} \\ & \quad + \,\overline{\overline{{I_{5} }}} \frac{{\partial^{3} \phi_{x} }}{{\partial t^{2} \partial x}} + \overline{\overline{{I_{5}^{*} }}} \frac{{\partial^{3} \phi_{y} }}{{\partial t^{2} \partial y}} + \overline{\overline{{I_{7} }}} \frac{{\partial^{4} w}}{{\partial t^{2} \partial x^{2} }} + \overline{\overline{{I_{7}^{*} }}} \frac{{\partial^{4} w}}{{\partial t^{2} \partial y^{2} }}, \\ & L_{21} \left( w \right) + L_{22} \left( {\phi_{x} } \right) + L_{23} \left( {\phi_{y} } \right) + L_{24} \left( f \right) + L_{21}^{ * } (w^{*} ) = \overline{\overline{{I_{3} }}} \frac{{\partial^{2} \phi_{x} }}{{\partial t^{2} }} - \overline{\overline{{I_{5} }}} \frac{{\partial^{3} w}}{{\partial t^{2} \partial x}}, \\ & L_{31} \left( w \right) + L_{32} \left( {\phi_{x} } \right) + L_{33} \left( {\phi_{y} } \right) + L_{34} \left( f \right) + L_{31}^{ * } (w^{*} ) = \overline{\overline{{I_{3}^{*} }}} \frac{{\partial^{2} \phi_{y} }}{{\partial t^{2} }} - \overline{\overline{{I_{5}^{*} }}} \frac{{\partial^{3} w}}{{\partial t^{2} \partial y}}, \\ \end{aligned} $$

(26)

in which

$$ \begin{aligned} L_{11}^{*} (w^{*} ) & = X_{11} \frac{{\partial^{2} w^{*} }}{{\partial x^{2} }}{ + }X_{12} \frac{{\partial^{2} w^{*} }}{{\partial y^{2} }},\,S_{{}}^{ * } \left( {w^{*} ,f} \right) = \frac{{\partial^{2} f}}{{\partial y^{2} }}\frac{{\partial^{2} w^{*} }}{{\partial x^{2} }} - 2\frac{{\partial^{2} f}}{\partial x\partial y}\frac{{\partial^{2} w^{*} }}{\partial x\partial y} + \frac{{\partial^{2} f}}{{\partial x^{2} }}\frac{{\partial^{2} w^{*} }}{{\partial y^{2} }}, \\ L_{21}^{*} (w^{*} ) & = X_{21} \frac{{\partial w^{*} }}{\partial x},\,\,L_{31}^{*} (w^{*} ) = X_{31} \frac{{\partial w^{*} }}{\partial y}, \\ \end{aligned} $$

(27)

Introduction of Eqs. (17) into Eq. (23) gives the compatibility equation of the imperfect the carbon nanotube polymer composite elliptical cylindrical shell as

$$ \begin{aligned} & I_{21}^{{}} \frac{{\partial^{4} f}}{{\partial x^{4} }} + I_{11}^{{}} \frac{{\partial^{4} f}}{{\partial y^{4} }} + J_{1} \frac{{\partial^{4} f}}{{\partial x^{2} \partial y^{2} }} + J_{2} \frac{{\partial^{3} \phi_{x} }}{{\partial x^{3} }} + J_{3} \frac{{\partial^{3} \phi_{x} }}{{\partial x\partial y^{2} }} + J_{4} \frac{{\partial^{3} \phi_{y} }}{{\partial y^{3} }} \\ & \quad + \,J_{5} \frac{{\partial^{3} \phi_{y} }}{{\partial y\partial x^{2} }} - c_{1} I_{25}^{{}} \frac{{\partial^{4} w}}{{\partial x^{4} }} - c_{1} I_{16}^{{}} \frac{{\partial^{4} w}}{{\partial y^{4} }} + J_{6} \frac{{\partial^{4} w}}{{\partial x^{2} \partial y^{2} }} \\ & \quad - \,\left( {\frac{{\partial^{2} w}}{\partial x\partial y}^{2} - \frac{{\partial^{2} w}}{{\partial x^{2} }}\frac{{\partial^{2} w}}{{\partial y^{2} }} + 2\frac{{\partial^{2} w}}{\partial x\partial y}\frac{{\partial^{2} w^{*} }}{\partial x\partial y} - \frac{{\partial^{2} w}}{{\partial x^{2} }}\frac{{\partial^{2} w^{*} }}{{\partial y^{2} }} - \frac{{\partial^{2} w}}{{\partial y^{2} }}\frac{{\partial^{2} w^{*} }}{{\partial x^{2} }} - \frac{1}{R}\frac{{\partial^{2} w}}{{\partial x^{2} }}} \right) = 0 \\ \end{aligned} $$

(28)

where the detail of coefficients $J_{i} (i = \overline{1,6} )$ are represented in “Appendix D”.

Equations (26) and (28) are nonlinear governing equations in terms of four variables $w,\phi_{x} ,\phi_{y}$ and $f$ and they are used to study the nonlinear dynamic response and vibration of the imperfect carbon nanotube polymer composite elliptical cylindrical shells. Specifically, the natural frequency and the deflection–time curves could be determined from this equations system.

8 Boundary conditions and approximate solutions

8.1 Boundary conditions

In the present study, the edges of the carbon nanotube polymer composite elliptical cylindrical shells are assumed to be simply supported and immovable. The boundary conditions in this case are

$$ {\text{w}} = u = M_{x} = 0,\,N_{x} = N_{x0} \;{\text{at}}\;x = 0\;{\text{and}}\;x = L, $$

(29)

where $N_{x0}$ is pre-buckling compressive force effect on edges $x = 0,\,L$.

8.2 Approximate solutions

Based on the boundary condition (29), the approximate solutions are assumed to be the forms as (Duc et al. 2015)

$$ \begin{aligned} w\left( {x,y,t} \right) & = W\left( t \right)\sin \lambda_{m} x\sin \delta_{n} y, \\ \phi_{x} \left( {x,y,t} \right) & = \varPhi_{x} \left( t \right)\cos \lambda_{m} x\sin \delta_{n} y, \\ \phi_{y} \left( {x,y,t} \right) & = \varPhi_{y} \left( t \right)\sin \lambda_{m} x\cos \delta_{n} y, \\ \end{aligned} $$

(30)

in which $\lambda_{m} = m\pi /L,\delta_{n} = n/R$; $m,n$ are odd natural numbers and $W,\,\varPhi_{x} ,\,\varPhi_{y}$ are amplitude of the deflection and rotation angle, respectively.

In this study, we assume that the initial imperfection $w^{*}$ has the same form with the shell deflection, i.e.

$$ w^{*} \left( {x,y,t} \right) = W_{0} \sin \lambda_{m} x\sin \delta_{n} y, $$

(31)

where $W_{0}$ is amplitude of the imperfect function.

Composing Eqs. (30) and (31) into Eq. (28) then solving obtained equation for unknown variable $f$ leads to

$$ f\left( {x,y,t} \right) = P_{1} \left( t \right)\cos 2\lambda_{m} x + P_{2} \left( t \right)\cos 2\delta_{n} y + P_{3} (t)\sin \lambda_{m} x\sin \delta_{n} y + \frac{1}{2}N_{x0} y^{2} , $$

(32)

with

$$ \begin{aligned} P_{1} & = \frac{{\delta_{n}^{2} }}{{32I_{21}^{{}} \lambda_{m}^{2} }}W(W + 2\mu h),P_{2} = \frac{{\lambda_{m}^{2} }}{{32I_{11}^{{}} \delta_{n}^{2} }}W(W + 2\mu h),\, \\ P_{3} & = Q_{1} W + Q_{2} \varPhi_{x} + Q_{3} \varPhi_{y} , \\ \end{aligned} $$

(33)

and

$$ \begin{aligned} Q_{1} & = \frac{{\frac{{\lambda_{m}^{2} }}{R} + c_{1} I_{25}^{{}} \lambda_{m}^{4} + c_{1} I_{16}^{{}} \delta_{n}^{4} - J_{6} \lambda_{m}^{2} \delta_{n}^{2} }}{{I_{21}^{{}} \lambda_{m}^{4} + J_{1} \lambda_{m}^{2} \delta_{n}^{2} + I_{11}^{{}} \delta_{n}^{4} }}\,, \\ Q_{2} & = \frac{{ - (J_{2} \lambda_{m}^{3} + J_{3} \lambda_{m}^{{}} \delta_{n}^{2} )}}{{I_{21}^{{}} \lambda_{m}^{4} + J_{1} \lambda_{m}^{2} \delta_{n}^{2} + I_{11}^{{}} \delta_{n}^{4} }}, \\Q_{3} &= \frac{{ - (J_{4} \delta_{n}^{3} + J_{5} \lambda_{m}^{2} \delta_{n}^{{}} )}}{{I_{21}^{{}} \lambda_{m}^{4} + J_{1} \lambda_{m}^{2} \delta_{n}^{2} + I_{11}^{{}} \delta_{n}^{4} }}. \\ \end{aligned} $$

(34)

9 Vibration analysis

Substituting Eqs. (30)–(32) into Eqs. (26) and using the Galerkin method to the resulting equations gives

$$ \begin{aligned} & r_{11} W + r_{12} \varPhi_{x} + r_{13} \varPhi_{y} + r_{14}^{{}} (W + \mu h)\varPhi_{x} + r_{15}^{{}} (W + \mu h)\varPhi_{y} + \left[ {n_{1} - N_{x0} \lambda_{m}^{2} } \right](W + \mu h) \\ & \quad + \,n_{2} W(W + \mu h) + n_{3} W(W + 2\mu h) + n_{4} W(W + \mu h)(W + 2\mu h) \\ & \quad + \,n_{5} q = I_{0} \frac{{\partial^{2} W}}{{\partial t^{2} }} + 2\varepsilon I_{1} \frac{\partial W}{\partial t} - \lambda_{m} \overline{\overline{{I_{5} }}} \frac{{\partial^{2} \varPhi_{x} }}{{\partial t^{2} }} - \delta_{n} \overline{\overline{{I_{5}^{*} }}} \frac{{\partial^{2} \varPhi_{y} }}{{\partial t^{2} }}, \\ & r_{21} W + r_{22} \varPhi_{x} + r_{23} \varPhi_{y} + n_{6} (W + \mu h) + n_{7} W(W + 2\mu h) = \overline{\overline{{I_{3} }}} \frac{{\partial^{2} \varPhi_{x} }}{{\partial t^{2} }} - \lambda_{m} \overline{\overline{{I_{5} }}} \frac{{\partial^{2} W}}{{\partial t^{2} }}, \\ & r_{31} W + r_{32} \varPhi_{x} + r_{33} \varPhi_{y} + n_{8} (W + \mu h) + n_{9} W(W + 2\mu h) = \overline{\overline{{I_{3}^{*} }}} \frac{{\partial^{2} \varPhi_{y} }}{{\partial t^{2} }} - \delta_{n} \overline{\overline{{I_{5}^{*} }}} \frac{{\partial^{2} W}}{{\partial t^{2} }}, \\ \end{aligned} $$

(35)

in which the coefficients $r_{1i} (i = \overline{1,3} ),r_{jk} (j = \overline{2,3} ,k = \overline{1,2} ),n_{m} (m = \overline{1,9} )$ are given in “Appendix E”.

9.1 Temperature field

The condition showing the immovability of the edges of the carbon nanotube polymer composite elliptical cylindrical shells is satisfied in an average sense as (Duc et al. 2015)

$$ \int\limits_{0}^{2\pi R} {\int\limits_{0}^{L} {\frac{\partial u}{\partial x}dxdy = 0} } . $$

(36)

Form Eqs. (11) and (17) we have

$$ \begin{aligned} \frac{\partial u}{\partial x} & = I_{11}^{{}} f_{,yy} - I_{12}^{{}} f_{,xx} - I_{13}^{{}} \phi_{x,x} + I_{14}^{{}} \phi_{y,y} + c_{1} I_{15}^{{}} \left( {\phi_{x,x} + w_{,xx} } \right) \\ & \quad - \,c_{1} I_{16}^{{}} \left( {\phi_{y,y} + w_{,yy} } \right) + I_{17}^{{}} \varPhi_{1} + I_{18}^{{}} \varPhi_{2}^{{}} - \frac{1}{2}\left( {\frac{\partial w}{\partial x}} \right)^{2} - \frac{\partial w}{\partial x}\frac{{\partial w^{*} }}{\partial x}. \\ \end{aligned} $$

(37)

Replacing Eqs. (30)–(32) into Eq. (37) and substituting the results into Eq. (36) gives

$$ N_{x0} = \frac{{\lambda_{m}^{2} }}{{8I_{11} }}W\left( {W + 2W_{0} } \right) - \frac{{I_{17}^{{}} }}{{I_{11} }}\varPhi_{1} - \frac{{I_{18}^{{}} }}{{I_{11} }}\varPhi_{2}^{{}} . $$

(38)

9.2 Nonlinear deflection amplitude–time curves

Assume that the carbon nanotube polymer composite elliptical cylindrical shells subjected to uniformly distributed transverse load $q = Q\sin \varOmega t$ ($Q$ is the amplitude of uniformly excited load, $\varOmega$ is the frequency of the load). Introduction of Eqs. (38) into Eq. (35) gives

$$ \begin{aligned} & r_{11} W + r_{12} \varPhi_{x} + r_{13} \varPhi_{y} + r_{14} \left( {W + W_{0} } \right)\varPhi_{x} + r_{15} \left( {W + W_{0} } \right)\varPhi_{y} \\ & \quad + \,n_{1}^{*} \left( {W + W_{0} } \right) + n_{2} W\left( {W + W_{0} } \right) \\ & \quad + \,n_{3} W\left( {W + 2W_{0} } \right) + n_{4}^{*} W\left( {W + W_{0} } \right)\left( {W + 2W_{0} } \right) + n_{5} Q\sin \varOmega t \\ & = I_{0} \frac{{\partial^{2} W}}{{\partial t^{2} }} + 2\varepsilon I_{1} \frac{\partial W}{\partial t} - \lambda_{m} \overline{\overline{{I_{5} }}} \frac{{\partial^{2} \varPhi_{x} }}{{\partial t^{2} }} - \delta_{n} \overline{\overline{{I_{5}^{*} }}} \frac{{\partial^{2} \varPhi_{y} }}{{\partial t^{2} }}, \\ & r_{21} W + r_{22} \varPhi_{x} + r_{23} \varPhi_{y} + n_{6} \left( {W + W_{0} } \right) + n_{7} W\left( {W + 2W_{0} } \right) = \overline{\overline{{I_{3} }}} \frac{{\partial^{2} \varPhi_{x} }}{{\partial t^{2} }} - \lambda_{m} \overline{\overline{{I_{5} }}} \frac{{\partial^{2} W}}{{\partial t^{2} }}, \\ & r_{31} W + r_{32} \varPhi_{x} + r_{33} \varPhi_{y} + n_{8} \left( {W + W_{0} } \right) + n_{9} W\left( {W + 2W_{0} } \right) = \overline{\overline{{I_{3}^{*} }}} \frac{{\partial^{2} \varPhi_{y} }}{{\partial t^{2} }} - \delta_{n} \overline{\overline{{I_{5}^{*} }}} \frac{{\partial^{2} W}}{{\partial t^{2} }}, \\ \end{aligned} $$

(39)

where

$$ n_{1}^{*} = n_{1} + \lambda_{m}^{2} \left( {\frac{{I_{17} }}{{I_{11} }}\varPhi_{1} + \frac{{I_{18} }}{{I_{11} }}\varPhi_{2} } \right),n_{4}^{*} = n_{4} - \frac{{\lambda_{m}^{4} }}{{8I_{11} }}. $$

(40)

Equation (39) is the nonlinear governing equation which is used to study the nonlinear vibration for the imperfect carbon nanotube polymer composite elliptical cylindrical shells with immovable edges. The fourth-order Runge–Kutta method is applied to solve Eq. (39). The initial conditions are given as

$$ \begin{aligned}&W(0) = 0,\,\,\frac{dW}{dt}(0) = 0,\,\,\varPhi_{x} (0) = 0,\\ &\frac{{d\varPhi_{x} }}{dt}(0) = 0,\,\,\varPhi_{y} (0) = 0,\,\,\frac{{d\varPhi_{y} }}{dt}(0) = 0. \end{aligned}$$

(41)

9.3 Natural frequencies

In the absence of external forces and viscous damping, the natural frequencies of the perfect shell can be determined by solving the following equation

$$ \left| {\begin{array}{*{20}c} {l_{11} + n_{{_{1} }}^{*} + I_{0} \omega^{2} } & {l_{12} - \lambda_{m}^{{}} \overline{\overline{{I_{5}^{{}} }}} \omega^{2} } & {l_{13} - \delta_{n} \overline{\overline{{I_{5}^{*} }}} \omega^{2} } \\ {l_{21} + n_{6} - \lambda_{m}^{{}} \overline{\overline{{I_{5}^{{}} }}} \omega^{2} } & {l_{22} + \overline{\overline{{I_{3}^{{}} }}} \omega^{2} } & {l_{23} } \\ {l_{31} + n_{8} - \delta_{n} \overline{\overline{{I_{5}^{*} }}} \omega^{2} } & {l_{32} } & {l_{33} + \overline{\overline{{I_{3}^{*} }}} \omega^{2} } \\ \end{array} } \right| = 0. $$

(42)

Three values of natural frequencies are obtained from Eq. (42) and the lowest value of them is considered.

10 Numerical results and discussion

10.1 Comparison studies

To verify the accuracy of the present method, the dimensionless frequencies of isotropic cylindrical shell are calculated and compared in Table 3 with the results presented by Lam and Loy (1995) based on Love’s first approximation theory, Xuebin (2008) using the Flugge classical thin shell theory and Shen (2012) based on the higher order shear deformation shell theory with the material properties and the geometrical parameters are chosen as $E = 210\,{\text{GPa}},\,\,v = 0.3,\,\,\rho = 7850\,{\text{kg/m}}^{3} ,$$R/L = 2,\,h/R = 0.06$. The results from the Table 3 show that a good agreement is obtained in this comparison.

Table 3 Comparison of dimensionless frequencies $\varpi = \varOmega \left( {h/\pi } \right)\sqrt {2\left( {1 + v} \right)\rho /E}$ for an isotropic cylindrical shell

Next, Table 4 shows the comparison of fundamental frequencies of the carbon nanotube polymer composite elliptical cylindrical shells using the higher order shear deformation theory in this paper with the results of Shen and Xiang (2012) in cases of two values of ratio $\bar{Z} = L^{2} /Rh$. The geometric parameters of the shell are chosen as $R/h = 10,\,\left( {m,n} \right) = \left( {1,1} \right),\,h = 5\,{\text{mm}}.$ Again, the results from this approach are so close with the existing results.

Table 4 Comparison of fundamental frequencies $\overline{\varOmega } = \varOmega \left( {R^{2} /h} \right)\sqrt {\rho_{0} /E_{0} }$ for the carbon nanotube polymer composite elliptical cylindrical shells $(T = 300\,{\text{K}},\,R/h = 10,$$\left( {m,n} \right) = \left( {1,1} \right),\,h = 5\,{\text{mm}})$

10.2 Natural frequency

The effects of temperature increment $\Delta T,$ geometrical parameter $L/R$ and modes $\left( {m,n} \right)$ on the natural frequency of the carbon nanotube polymer composite elliptical cylindrical shells are considered in Table 5. It is clear that the value of the natural frequency of the shell increases when the values temperature increment $\Delta T,$ ratio $L/R$ and modes $\left( {m,n} \right)$ increase. Moreover, the lowest natural frequency corresponds to the modes of vibration of shells $\left( {m,n} \right) = \left( {1,1} \right)$. Note that, this mode will be used as a representative mode to investigate the natural frequencies and nonlinear dynamic responses of the carbon nanotube polymer composite elliptical cylindrical shells.

Table 5 Effects of temperature increment, $L/R$ ratio and mode $\left( {m,n} \right)$ on natural frequencies (s⁻¹) of the carbon nanotube polymer composite elliptical cylindrical shells

Table 6 shows influences of volume fraction of carbon nanotube $V_{CNT}^{*}$, geometrical parameter $b/h$, type of carbon nanotube reinforcement and elastic foundations on the natural frequencies $\left( {s^{ - 1} } \right)$ of the carbon nanotube polymer composite elliptical cylindrical shells. Clearly, the natural frequency of the nanocomposite elliptical cylindrical shell increases when the carbon nanotube volume fraction and the modulus $k_{1} \,({\text{GPa/m}}),\,\,k_{2} \,({\text{GPa}}\,{\text{m}})$ of elastic foundations increase and the ratio $b/h$ decreases. Moreover, the carbon nanotube polymer composite elliptical cylindrical shells with type carbon nanotube reinforcement X has the highest value of the natural frequency and the carbon nanotube polymer composite elliptical cylindrical shells with type carbon nanotube reinforcement V has the lowest value of the natural frequency of all.

Table 6 Effects of carbon nanotube volume fraction, ratio $b/h$, type of carbon nanotube reinforcemnt and elastic foundations on natural frequencies (s⁻¹) of the carbon nanotube polymer composite elliptical cylindrical shells

10.3 Nonlinear deflection amplitude–time curves

Figure 3 describes the effect of carbon nanotube volume fraction $V_{CNT}^{*}$ on the nonlinear deflection amplitude–time curves of the carbon nanotube polymer composite elliptical cylindrical shells with $b/h = 20,\,\,a/b = 1.5,\,\,L/R = 2$. We can see that the deflection amplitude of the carbon nanotube polymer composite elliptical cylindrical shells decreases when the factor $V_{CNT}^{*}$ increases. In other words, the carbon nanotube enhances the stiffness of the carbon nanotube polymer composite elliptical cylindrical shells.

Fig. 3

Influences of carbon nanotube volume fraction on the nonlinear deflection amplitude–time curves of the carbon nanotube polymer composite elliptical cylindrical shells

Figures 4 and 5 show the effects of elastic foundations with two coefficients $k_{1}$ and $k_{2}$ on the nonlinear deflection amplitude–time curves of the carbon nanotube polymer composite elliptical cylindrical shells. From the figures, it is clear that the deflection amplitude of the nanocomposite elliptical cylindrical shell decreases significantly when the shell is rested on the elastic foundations. Furthermore, the beneficial effect of the Pasternak foundation with the shear layer stiffness $k_{2}$ on the nonlinear deflection amplitude–time curves of the carbon nanotube polymer composite elliptical cylindrical shells is stronger than the Winkler one with the modulus $k_{1}$.

Fig. 4

Influences of the Winkler foundation on the nonlinear deflection amplitude–time curves of the carbon nanotube polymer composite elliptical cylindrical shells

Fig. 5

Influences of the Pasternak foundation on the nonlinear deflection amplitude–time curves of the carbon nanotube polymer composite elliptical cylindrical shells

Figure 6 illustrates the effect of temperature change $\Delta T$ on the nonlinear deflection amplitude–time curves of the carbon nanotube polymer composite elliptical cylindrical shells. Three values of $\Delta T:0,\,\,200\,{\text{K}}$ and 400 K are considered. Obviously, an increase of the temperature increment $\Delta T$ leads to an increase of the deflection amplitude of the carbon nanotube polymer composite elliptical cylindrical shells.

Fig. 6

Influences of temperature change $\Delta T$ on the nonlinear deflection amplitude–time curves of the carbon nanotube polymer composite elliptical cylindrical shells

Figure 7 indicates the nonlinear deflection amplitude–time curves of the carbon nanotube polymer composite elliptical cylindrical shells with various values of the imperfection amplitude $W_{0}$. As can be observed, the imperfection amplitude has a strong effect on the nonlinear deflection amplitude–time curves of the carbon nanotube polymer composite elliptical cylindrical shells; the amplitude of the shell increases when the initial imperfection amplitude increases.

Fig. 7

Influences of imperfection amplitude ${\text{W}}_{0}$ on the nonlinear deflection amplitude–time curves of the carbon nanotube polymer composite elliptical cylindrical shells

Figures 8, 9 and 10 give the influences of the geometrical factors $L/R,\,\,a/b$ and $b/h$ on the nonlinear deflection amplitude–time curves of the carbon nanotube polymer composite elliptical cylindrical shells, respectively. It can be seen that the fluctuation amplitude of the carbon nanotube polymer composite elliptical cylindrical shells increases when increasing the ratio $L/R,\,\,a/b$ and $b/h$.

Fig. 8

Influences of factor $L/R$ on the nonlinear deflection amplitude–time curves of the carbon nanotube polymer composite elliptical cylindrical shells

Fig. 9

Influences of factor $a/b$ on the nonlinear deflection amplitude–time curves of the carbon nanotube polymer composite elliptical cylindrical shells

Fig. 10

Influences of factor $b/h$ on the nonlinear deflection amplitude–time curves of the carbon nanotube polymer composite elliptical cylindrical shells

The effect of excitation force amplitude $Q_{0}$ on the nonlinear deflection amplitude–time curves of the carbon nanotube polymer composite elliptical cylindrical shells is shown in Fig. 11. As can be seen, the higher excitation force amplitude is, the higher vibration amplitude of the carbon nanotube polymer composite elliptical cylindrical shells is.

Fig. 11

Influences of excitation force amplitude ${\text{Q}}_{0}$ on the nonlinear deflection amplitude–time curves of the carbon nanotube polymer composite elliptical cylindrical shells

11 Concluding remarks

The nonlinear dynamic response and vibration of the carbon nanotube polymer composite elliptical cylindrical shells on elastic foundations subjected to the combination of the mechanical and thermal loads are presented in this paper. The material properties of the shells are supposed to depend on temperature and the shell thickness direction. The basic equations are derived based on the Reddy’s higher order shear deformation shell theory. The Galerkin method and fourth-order Runge–Kutta method are used to determine the natural frequencies and nonlinear deflection amplitude–time curves of the shells. The accuracy of present approach is also verified by comparing with the ones of other authors. From the obtained results in the study, there are some conclusions:

• The initial imperfection and temperature increment significant negative effect on the nonlinear vibration and dynamic response of the carbon nanotube polymer composite elliptical cylindrical shells. The deflection amplitude increases and the natural frequency decreases according to the increase of the initial imperfection amplitude and temperature increment.

• The elastic foundations dramatically enhance the natural frequencies and reduce the deflection amplitude of the carbon nanotube polymer composite elliptical cylindrical shells. Moreover, the influence of linear Winkler foundation is weaker than one of Pasternak foundation.

• The carbon nanotubes could be used to strengthen the mechanical properties of the carbon nanotube polymer composite elliptical cylindrical shells because they increase the natural frequencies and decrease the fluctuation amplitude of the shells.

• The geometrical parameters ratios have strongly effects on the nonlinear vibration and dynamic response of the carbon nanotube polymer composite elliptical cylindrical shells.

Appendices

Appendix A

$$ \begin{aligned} \Delta & = A_{11} A_{22} - A_{12}^{2} ,\,\,I_{11}^{{}} = \frac{{A_{22} }}{\Delta },\,\,I_{12}^{{}} = \frac{{A_{12} }}{\Delta },\,\,I_{13}^{{}} = \frac{{B_{12} A_{12} - B_{11} A_{22} }}{\Delta },\,\,\,I_{14}^{{}} = \frac{{B_{22} A_{12} - B_{12} A_{22} }}{\Delta }, \\ I_{15}^{{}} & = \frac{{E_{12} A_{12} - E_{11} A_{22} }}{\Delta },\,\,I_{16}^{{}} = \frac{{E_{22} A_{12} - E_{12} A_{22} }}{\Delta },\,\,I_{17}^{{}} = \frac{{A_{22} }}{\Delta },\,I_{18}^{{}} = - \frac{{A_{12} }}{\Delta }, \\ I_{21}^{{}} & = \frac{{A_{11} }}{\Delta },\,\,I_{23}^{{}} = \frac{{B_{11} A_{12} - B_{12} A_{11} }}{\Delta },\,I_{24}^{{}} = \frac{{B_{12} A_{12} - B_{22} A_{11} }}{\Delta },\,\,I_{25}^{{}} = \frac{{E_{11} A_{12} - E_{12} A_{11} }}{\Delta }\,, \\ I_{26}^{{}} & = \frac{{E_{12} A_{12} - E_{22} A_{11} }}{\Delta },\,I_{27}^{{}} = - \frac{{A_{12} }}{\Delta },\,\,I_{28}^{{}} = \frac{{A_{11} }}{\Delta },\,\,\,I_{31}^{{}} = \frac{1}{{A_{66} }},\,\,I_{32}^{{}} = - \frac{{B_{66} }}{{A_{66} }},\,\,I_{33}^{{}} = - \frac{{E_{66} }}{{A_{66} }}. \\ \end{aligned} $$

Appendix B

$$ \begin{aligned} \overline{{I_{1} }} & = I_{1} ,\overline{{I_{1}^{*} }} = I_{1} + \frac{{2I_{2} }}{R},\;\overline{{I_{2} }} = I_{2} - c_{1} I_{4} ,\;\overline{{I_{2}^{*} }} = I_{2} + \frac{{I_{3} }}{R} - c_{1} I_{4} - \frac{{c_{1} I_{5} }}{R}, \\ \overline{{I_{3} }} & = c_{1} I_{4} ,\overline{{I_{3}^{*} }} = c_{1} I_{4} + \frac{{c_{1} I_{5} }}{R},\;\overline{{I_{4} }} = \overline{{I_{4}^{*} }} = I_{3} - 2c_{1} I_{5} + c_{1}^{2} I_{7} ,\;\overline{{I_{5} }} = \overline{{I_{5}^{*} }} = c_{1} I_{5} - c_{1}^{2} I_{7} . \\ \end{aligned} $$

Appendix C

$$ \begin{aligned} X_{11} & = A_{44} - 6c_{1} D_{44} + 9c_{1}^{2} F_{44} ,\,\,X_{12} = A_{55} - 6c_{1} D_{55} + 9c_{1}^{2} F_{55} ,\,\,X_{13} = - c_{1}^{2} (E_{11} I_{15}^{{}} + E_{12} I_{25}^{{}} + H_{11} ),\,\, \\ X_{14} & = - c_{1}^{2} (4E_{66} I_{33}^{{}} + 4H_{66} + E_{11} I_{16} + E_{12} I_{26} + 2H_{12} + E_{12} I_{15} + E_{22} I_{25} ),\,\, \\ X_{15} & = - c_{1}^{2} (E_{12} I_{16} + E_{22} I_{26} + H_{22} ),\,\,X_{16} = c_{1} (E_{11} I_{13} - c_{1} E_{11} I_{15} + F_{11} - c_{1} H_{11} + E_{12} I_{23} - c_{1} E_{12} I_{25} ), \\ X_{17} & = c_{1} (2E_{66} I_{32} - 2c_{1} E_{66} I_{33} + 2F_{66} - 2c_{1} H_{66} + c_{1} E_{12} I_{13} - c_{1} E_{12} I_{15} + F_{12} - c_{1} H_{12} + E_{22} I_{23} - c_{1} E_{22} I_{25} ), \\ X_{18} & = c_{1} \left( {E_{12} I_{14} - c_{1} E_{12} I_{16} + E_{22} I_{24} - c_{1} E_{22} I_{26} + F_{22} - c_{1} H_{22} } \right),\,\, \\ X_{19} & = c_{1} (2E_{66} I_{32} - 2c_{1} E_{66} I_{33} + 2F_{66} - 2c_{1} H_{66} + E_{11} I_{14} - c_{1} E_{11} I_{16} + E_{12} I_{24} - c_{1} E_{12} I_{26} + F_{12} - c_{1} H_{12} ), \\ X_{110} & = - c_{1} (E_{11} I_{12} - E_{12} I_{21} ),\,\,X_{111} = - c_{1} (2E_{66} I_{31} - E_{11} I_{11} + 2E_{12} I_{12} - E_{22} I_{21} ),\,\,X_{112} = c_{1} (E_{12} I_{11} - E_{22} I_{12} ), \\ X_{21} & = - A_{44} + 6c_{1} D_{44} - 9c_{1}^{2} F_{44} ,\,\,X_{22} = - c_{1} (B_{11} I_{15} + F_{11} + B_{12} I_{25} - c_{1} E_{11} I_{15} - c_{1} H_{11} - c_{1} E_{12} I_{25} ), \\ X_{23} & = - c_{1} (B{}_{11}I_{16} + B_{12} I_{26} + F_{12} + 2B_{66} I_{33} + 2F_{66} - 2c_{1} E_{66} I_{33} - 2c_{1} H_{66} - c_{1} E_{11} I_{16} - c_{1} E_{12} I_{26} - c_{1} H_{12} ), \\ X_{24} & = B_{11} I_{13} - c_{1} B_{11} I_{15} + D_{11} - c_{1} F_{11} + B_{12} I_{23} - c_{1} B_{12} I_{25} - c_{1} E_{11} I_{13} + c_{1}^{2} E_{11} I_{15} - c_{1} F_{11} + c_{1}^{2} H_{11} \\ & \quad - \,c_{1} E_{12} I_{23} + c_{1}^{2} E_{12} I_{25} ,\,\,X_{25} = B_{66} I_{32} - c_{1} B_{66} I_{33} + D_{66} - c_{1} F_{66} - c_{1} E_{66} I_{32} + c_{1}^{2} E_{66} I_{33} - c_{1} F_{66} + c_{1}^{2} H_{66} , \\ X_{26} & = B_{11} I_{14} - c_{1} B_{11} I_{16} + B_{12} I_{24} - c_{1} B_{12} I_{26} + D_{12} - c_{1} F_{12} + B_{66} I_{32} - c_{1} B_{66} I_{33} + D_{66} - c_{1} F_{66} - c_{1} E_{66} I_{32} \\ & \quad + \,c_{1}^{2} E_{66} I_{33} - c_{1} F_{66} + c_{1}^{2} H_{66} - c_{1} E_{11} I_{14} + c_{1}^{2} E_{11} I_{16} - c_{1} E_{12} I_{24} + c_{1}^{2} E_{12} I_{26} - c_{1} F_{12} + c_{1}^{2} H_{12} , \\ X_{27} & = - B_{11} I_{12} + B_{12} I_{21} + c_{1} E_{11} I_{12} - c_{1} E_{12} I_{21} , \\ X_{28} & = B_{11} I_{11} - B_{12} I_{12} - B_{66} I_{31} - c_{1} E_{11} I_{11} + c_{1} E_{12} I_{12} + c_{1} E_{66} I_{31} ,\,\,X_{31} = - A_{55} + 6c_{1} D_{55} - 9c_{1}^{2} F_{55} , \\ X_{32} & = - c_{1} (2B_{66} I_{33} + 2F_{66} + B_{12} I_{15} + F_{12} + B_{22} I_{25} - 2c_{1} E_{66} I_{33} - 2c_{1} H_{66} - c_{1} E_{12} I_{15} - c_{1} H_{12} - c_{1} E_{22} I_{25} ), \\ X_{33} & = - c_{1} (B_{12} I_{16} + B_{22} I_{26} + F_{22} - c_{1} E_{12} I_{16} - \,c_{1} E_{22} I_{26} - c_{1} H_{22} ), \\ X_{34} & = B_{66} I_{32} - c_{1} B_{66} I_{33} + D_{66} - c_{1} F_{66} + B_{12} I_{13} - c_{1} B_{12} I_{15} + D_{12} - c_{1} F_{12} + B_{22} I_{23} - \,c_{1} B_{22} I_{25} - c_{1} E_{66} I_{32} \\ & \quad + \,c_{1}^{2} E_{66} I_{33} - c_{1} F_{66} + c_{1}^{2} H_{66} - c_{1} E_{12} I_{13} + c_{1}^{2} E_{12} I_{15} - c_{1} F_{12} + c_{1}^{2} H_{12} - c_{1} E_{22} I_{23} + \,c_{1}^{2} E_{22} I_{25} , \\ X_{35} & = B_{66} I_{32} - c_{1} B_{66} I_{33} + D_{66} - c_{1} F_{66} - c_{1} E_{66} I_{32} + c_{1}^{2} E_{66} I_{33} - c_{1} F_{66} + c_{1}^{2} H_{66} , \\ \end{aligned} $$

$$ \begin{aligned} X_{36} & = B_{12} I_{14} - c_{1} B_{12} I_{16} + B_{22} I_{24} - c_{1} B_{22} I_{26} + D_{22} - c_{1} F_{22} - c_{1} E_{12} I_{14} + c_{1}^{2} E_{12} I_{16} - c_{1} E_{22} I_{24} \\ & \quad + \,c_{1}^{2} E_{22} I_{26} - c_{1} F_{22} + c_{1}^{2} H_{22} ,\,\,X_{37} = - B_{66} I_{31} - B_{12} I_{12} + B_{22} I_{21} + c_{1} E_{66} I_{31} + c_{1} E_{12} I_{12} - c_{1} E_{22} I_{21} , \\ X_{38} & = B_{12} I_{11} - B_{22} I_{12} - c_{1} E_{12} I_{11} + c_{1} E_{22} I_{12} . \\ \end{aligned} $$

Appendix D

$$ \begin{aligned} J_{1} & = I_{31}^{{}} - 2I_{12}^{{}} ,\,\,J_{2} = I_{23}^{{}} - c_{1} I_{25}^{{}} ,\,\,J_{3} = I_{13}^{{}} - c_{1} I_{15}^{{}} - I_{32}^{{}} + c_{1} I_{33}^{{}} , \\ J_{4} & = I_{14}^{{}} - c_{1} I_{16}^{{}} ,\,J_{5} = I_{24}^{{}} - c_{1} I_{26}^{{}} - I_{32}^{{}} + c_{1} I_{33}^{{}} ,\,\,J_{6} = - c_{1} I_{15}^{{}} - c_{1} I_{26}^{{}} + 2c_{1} I_{33}^{{}} . \\ \end{aligned} $$

Appendix E

$$ \begin{aligned} & r_{11} = - k_{1} - k_{2} \left( {\lambda_{m}^{2} + \delta_{n}^{2} } \right) + X_{13} \lambda_{m}^{4} + X_{14} \lambda_{m}^{2} \delta_{n}^{2} + X_{15} \delta_{n}^{4} + X_{110} Q_{1} \lambda_{m}^{4} + X_{111} Q_{1} \lambda_{m}^{2} \delta_{n}^{2} + X_{112} Q_{1} \delta_{n}^{4} \\ & - \,Q_{1} \frac{{\lambda_{m}^{2} }}{R},\,\,r_{12} = - X_{11} \lambda_{m} + X_{16} \lambda_{m}^{3} + X_{17} \lambda_{m} \delta_{n}^{2} + X_{110} Q_{2} \lambda_{m}^{4} + X_{111} Q_{2} \lambda_{m}^{2} \delta_{n}^{2} + X_{112} Q_{2} \delta_{n}^{4} \\ & - \,Q_{2} \frac{{\lambda_{m}^{2} }}{R},\,\,r_{13} = - X_{12} \delta_{n} + X_{18} \delta_{n}^{3} + X_{19} \lambda_{m}^{2} \delta_{n}^{{}} + X_{110} Q_{3} \lambda_{m}^{4} + X_{111} Q_{3} \lambda_{m}^{2} \delta_{n}^{2} + X_{112} Q_{3} \delta_{n}^{4} \\ & - \,Q_{3} \frac{{\lambda_{m}^{2} }}{R},\,\,r_{14} = \frac{{32Q_{2} \lambda_{m} \delta_{n} }}{3LR\pi },\,\,r_{15} = \frac{{32Q_{3} \lambda_{m} \delta_{n} }}{3LR\pi },\,\,n_{1} = - X_{11} \lambda_{m}^{2} - X_{12} \delta_{n}^{2} ,\,\,n_{2} = \frac{{32Q_{1} \lambda_{m} \delta_{n} }}{3LR\pi }, \\ \end{aligned} $$

$$ \begin{aligned} n_{3} & = \frac{{2\delta_{n} }}{{3LR\pi I_{21}^{{}} \lambda_{m} R}} - \frac{{8X_{110} \lambda_{m} \delta_{n} }}{{3LR\pi I_{21}^{{}} }} - \frac{{8X_{112} \lambda_{m} \delta_{n} }}{{3LR\pi I_{11}^{{}} }},\,\,n_{4} = - \frac{{\lambda_{m}^{4} }}{{16I_{11}^{{}} }} - \frac{{\delta_{n}^{4} }}{{16I_{21}^{{}} }},\,\,n_{5} = \frac{16}{{mn\pi^{2} }}, \\ r_{21} & = - \lambda_{m}^{3} (X_{22} + Q_{1} X_{27} ) - \lambda_{m} \delta_{n}^{2} (X_{23} + Q_{1} X_{28} ),\,\,r_{22} = X_{21} - X_{24} \lambda_{m}^{2} - X_{25} \delta_{n}^{2} - X_{27} Q_{2} \lambda_{m}^{3} - X_{28} Q_{2} \lambda_{m} \delta_{n}^{2} , \\ r_{23} & = - X_{26} \lambda_{m} \delta_{n} - X_{27} Q_{3} \lambda_{m}^{3} - X_{28} Q_{3} \lambda_{m} \delta_{n}^{2} ,\,\,n_{6} = X_{21} \lambda_{m} ,\,\,n_{7} = \frac{{8X_{27} \delta_{n} }}{{3LR\pi I_{21}^{{}} }}, \\ r_{31} & = - \delta_{n}^{3} (X_{33} + Q_{1} X_{38} ) - \lambda_{m}^{2} \delta_{n}^{{}} (X_{32} + Q_{1} X_{37} ),\,\,r_{32} = - X_{34} \lambda_{m} \delta_{n} - X_{38} Q_{2} \delta_{n}^{3} - D_{37} Q_{2} \lambda_{m}^{2} \delta_{n}^{{}} , \\ r_{33} & = X_{31} - X_{35} \lambda_{m}^{2} - X_{36} \delta_{n}^{2} - \,X_{38} Q_{3} \delta_{n}^{3} - X_{37} Q_{3} \lambda_{m}^{2} \delta_{n}^{{}} ,\,\,n_{8} = X_{31} \delta_{n} ,\,\,n_{9} = \frac{{8X_{38} \lambda_{m} }}{{3LR\pi I_{11}^{{}} }}. \\ \end{aligned} $$