Mapping the mean monthly precipitation of a small island using kriging with external drifts

Abstract

This study focuses on the spatial distribution of mean annual and monthly precipitation in a small island (1128 km²) named Martinique, located in the Lesser Antilles. Only 35 meteorological stations are available on the territory, which has a complex topography. With a digital elevation model (DEM), 17 covariates that are likely to explain precipitation were built. Several interpolation methods, such as regression-kriging (𝖬𝖫𝖱𝖪, 𝖯𝖢𝖱𝖪, and 𝖯𝖫𝖲𝖪) and external drift kriging (𝖤𝖣𝖪) were tested using a cross-validation procedure. For the regression methods, predictors were chosen by established techniques whereas a new approach is proposed to select external drifts in a kriging which is based on a stepwise model selection by the Akaike Information Criterion (AIC). The prediction accuracy was assessed at validation sites with three different skill scores. Results show that using methods with no predictors such as inverse distance weighting (𝖨𝖣𝖶) or universal kriging (𝖴𝖪) is inappropriate in such a territory. 𝖤𝖣𝖪 appears to outperform regression methods for any criteria, and selecting predictors by our approach improves the prediction of mean annual precipitation compared to kriging with only elevation as drift. Finally, the predicting performance was also studied by varying the size of the training set leading to less conclusive results for 𝖤𝖣𝖪 and its performance. Nevertheless, the proposed method seems to be a good way to improve the mapping of climatic variables in a small island.

1 Introduction

Spatial climatic information is essential for many scientific studies of hydrology, agriculture, ecology, and environmental sciences. However, the weather network is often sparse and not deployed on a regular grid and so cannot provide good spatial information to capture environmental variability. Spatial interpolation techniques are therefore an essential tool in order to estimate precipitation over a domain, as they make it possible to predict the values at unmeasured locations from observed points.

Various methods (geometric, statistical, and geostatistical) can be used to map precipitation at high resolution. For example, Xu et al. (2014) used inverse distance weighting (𝖨𝖣𝖶) or ordinary kriging (𝖮𝖪) to estimate the spatial distribution of daily rainfall. Like universal kriging (Bostan et al. 2012) or the Thiessen polygon (Goovaerts 2000), these methods use only the observation locations, not covariates. It is well known however that precipitation is correlated with environmental information, such as longitude, latitude, elevation, or other geographical variables. Some spatial methods can take this relation into account to achieve more accurate estimates (Castro et al. 2014; Borges et al. 2015). Multiple linear regression (𝖬𝖫𝖱) is usually performed to relate precipitation to physical predictor variables (Goovaerts 2000; Hwang et al. 2012; Kurtzman et al. 2009). Bessafi et al. (2013) showed that principal component regression (𝖯𝖢𝖱) or partial least squares (𝖯𝖫𝖲) is also a good way to map climatic variables with predictors. In most cases, kriging residuals derived from regressions significantly improves the results of the method (Nalder and Wein 1998; Branislav et al. 2013) and is usually called regression-kriging (𝖱𝖪). Kriging with external drift is also a promising approach for predicting precipitation (Haberlandt 2007). According to these studies, the best method to predict precipitation depends both on the variables to be mapped (daily or monthly precipitation) and on the complexity of the land (mountainous, flat land, etc). Thus, in order to determine the most accurate prediction, a comparison between these methods is needed and is usually performed by cross-validation.

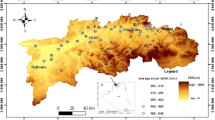
The present study focuses on the performance of spatial techniques to map the annual and monthly mean precipitation in a small island (1128 km²) named Martinique, located in the Lesser Antilles (see Fig. 1a). It is well known that, in this region, precipitation is strongly influenced by orography and the proximity of land (Smith et al. 2012) leading to great spatial variation. Using predictors for mapping precipitation therefore seems to be appropriate. With a digital elevation model (DEM), 17 covariates which are likely to explain precipitation were built. Most of the above-mentioned methods were tested via a cross-validation procedure on 35 meteorological stations. For the regression methods, predictors were chosen by established techniques whereas a new approach is proposed here to select external drifts in kriging based on a stepwise model selection by the Akaike Information Criterion (AIC). Because of the limited number of stations, local techniques presented in Sun et al. (2015) and Xie et al. (2011) were not tested.

Fig. 1

Location of Martinique in the West Indies (a). Location of the 37 stations in Martinique (b). Topography of Martinique provided by SRTM data (c)

The paper is sectioned as follows. A description of the data used (observation and predictors) is provided in Section 2. This is followed in Sections 3.1 and 3.2 by the interpolation techniques used in the study. The procedures to evaluate the performance of these methods are mentioned in Section 3.3. Then, selection the predictors is described in Section 3.4. Section 4 presents the performance of the different spatial methods in which two cross validation procedures were performed. Finally, results are discussed in Section 5, followed by a summary in Section 6.

2 Data

Generally, a mapping method requires two types of data. The first one, which is essential, corresponds to observation of the phenomenon we want to map. The second, which may or may not essential depending on the method used, is some variables, such as elevation, that are known over the whole territory and which can explain the phenomenon; these variables are called predictors in the following.

2.1 Observation

The precipitation data used in this study were provided by the French meteorological Institute (Météo-France). This dataset contains monthly precipitation amounts from 1991 to 2010. The rain gauge network consists of 37 rain gauges that are distributed across the whole island (see Fig. 1b) for a surface of 1128 km². Note that for January and December, two stations recorded no data during several days and were therefore removed from the database of mean monthly precipitation. Only weather stations with complete records were included.

The main statistical values of precipitation are shown in Table 1 to summarize the spatial and temporal variability of mean precipitation. The annual cycle comprises two seasons: the dry period between February and April and the wet season between June and November in which monthly precipitations are at least twice as high as in the dry season. The monthly precipitation can also vary considerably spatially (e.g., ratio > 6 in January). This variability can be explained by the complex topography of the island of Martinique (see Fig. 1c). It should be mentioned that the locations of the stations are not ideal: they are lacking in the mountainous area and are unevenly distributed on some coasts.

Table 1 Descriptive statistics of the monthly and annual precipitation (mm)

2.2 Building candidate predictors: physiographic variables

Building candidate predictors depends on the phenomenon to be mapped and is a fundamental step.

It is well known that the amount of rain that falls in the West Indies varies immensely from beach to mountain top, so the distance to the coast seems to be a good predictor for precipitation. Three distances were taken into account and are illustrated in Fig. 2g:

• 𝖽𝗂𝗌𝗍_𝖼𝗈𝖺𝗌𝗍: Minimum Distance to a coast,

• 𝖽𝗂𝗌𝗍_𝖼𝖺𝗋𝗂𝖻: Minimum Distance to the Caribbean Sea,

• 𝖽𝗂𝗌𝗍_𝖺𝗍𝗅𝖺𝗇: Minimum Distance to the Atlantic Ocean.

Besides, Martinique, like most of the islands of the Lesser Antilles, is characterized by a complex topography which tends to enhance the rainfall due to synoptic disturbances by orographic effects (Smith et al. 2012). This means that variables representing the topography should be a good way to predict precipitation.

Fig. 2

Candidate predictors used in this study

A high resolution Digital Elevation Model (DEM) is needed to capture the complex topography of the island, since with a too coarse DEM (for example, a 1×1 km² resolution), mountains named locally pitons are smoothed, and, hence the elevation of stations provided by the DEM and by metadata can differ significantly. That is why the SRTM data (resolution ∼90 m) which is available at http://www2.jpl.nasa.gov/srtm/ was used.

In Daly et al. (2002), smoothed altitude was also tested in the precipitation model selection process. Three predictors are introduced and illustrated in Fig. 2a:

• 𝗓90𝗆: elevation at 90 m resolution (SRTM data),

• 𝗓𝗌𝗆𝗈𝗈𝗍𝗁1: Average elevation in a 1 km neighborhood,

• 𝗓𝗌𝗆𝗈𝗈𝗍𝗁5: Average elevation in a 5 km neighborhood.

Agnew and Palutikof (2000) emphasized that the maximum elevation in a wedge is very useful in areas with dominant wind directions, because the leeward slopes are drier and warmer than windward slopes. In the present study, the north and south directions were not used since the main perturbations occurring in Martinique come from the Atlantic Ocean (East of the island). Six other predictors were added:

• 𝗓𝗑𝗐1, 𝗓𝗑𝗐5, 𝗓𝗑𝗐10: Maximum elevation in the West direction in a 1, 5, 10 km neighborhood (see Fig. 2e),

• 𝗓𝗑𝖾1, 𝗓𝗑𝖾5, 𝗓𝗑𝖾10: Maximum elevation in the East direction in a 1, 5, 10 km neighborhood (see Fig. 2c),

Daly et al. (2002) also suggested using some characteristics of the terrain since the relationship between precipitation and elevation can vary from one slope to another, depending on the location and orientation:

• 𝗌𝗅𝗈𝗉𝖾: slope evaluated with four neighbors (see Fig. 2b),

• 𝖼𝗎𝗋𝗏: curvature evaluated with four neighbors (see Fig. 2d),

• 𝖺𝗌𝗉𝖾𝖼𝗍: aspect evaluated with four neighbors (see Fig. 2f),

This set of 15 physiographic variables was generated from the DEM coming from the SRTM data and explains, a priori, spatial variability in the climate data. These variables can be easily generated with a geographical information system. In our case, the R functions focal and terrain of the ”raster” package (Hijmans 2014) were used.

Geographical positions (coordinates 𝖷 and 𝖸 in the UTM 20N spatial reference) were also considered as predictors.

3 Interpolation techniques used in this study

First, the interpolation techniques used in this study are briefly presented and are separated into two groups: techniques for which predictors (see Section 2.2) were used or not. In the following, the notations used are (here, the variable is the mean monthly precipitation):

• n the number of sites where the variable is known (observed),

• s _i : a site with observation, i=1..n,

• z(s _i ): the amount of the variable at site s _i ,

• s ₀: the location where we want to predict the amount of the variable,

• $\hat {z}(s_{0})$: the value predicted by the tested interpolation method at site s ₀,

• |s _i −s _j | the Euclidean distance between s _i and s _j ,

• X _j (s): the amount of the predictor j at location s.

3.1 Without predictors

To apply the following methods, only observation and location of the variable are needed.

• 1. Inverse distance weighting of order d:

  $$ \hat{z}(s_{0})=\sum\limits_{i=1}^{n}{\lambda_{i}.z(s_{i})} \text{ with } \lambda_{i} = \frac{1 / \vert s_{i} - s_{0} \vert^{d}}{{\sum}_{i=1}^{n}{1 / \vert s_{i} - s_{0} \vert^{d}}} $$

  (1)

  In our case, d=2 and this method is noted IDW

• 2. Kriging (simple, ordinary, and universal):Let Z ^∗(.) be the linear regression estimator ($Z^{\ast }(s_{0})=\hat {z}(s_{0})$) and Z(.) a random function where Z(s _i )=z(s _i ). Then, the value, $\hat {z}(s_{0})$, can be written:

  $$ \hat{z}(s_{0})=\mu(s_{0}) + \sum\limits_{i=1}^{n}{\omega_{i}(s_{0}).\left(z(s_{i})-\mu(s_{i})\right)} $$

  (2)

  where μ(s ₀) and μ(s _i ) are the expected values of Z ^∗(s ₀) and Z(s _i ), respectively. The kriging weights, ω _i (.) must be determined to minimize the estimation variance, Var[Z ^∗(s ₀)−Z(s ₀)], while ensuring the unbiasedness of the estimator, E[Z ^∗(s ₀)−Z(s ₀)]=0. Under some assumptions, kriging is regarded as the best linear unbiased estimator. To simplify, kriging can be based on a linear model for which the residuals are assumed to be spatially dependent.

  First, the trend, μ(.), of the random function Z(.) must be specified among three types:

  • μ(s)=m a known constant all over the studied area; this is simple kriging denoted 𝖲𝖪

  • μ(s)=μ a unknown constant which is considered to fluctuate locally maintaining stationarity within the local neighborhood; this is the ordinary kriging denoted 𝖮𝖪

  • μ(s) smoothly varies within each local neighborhood and is modeled as a linear combination of functions of the spatial coordinates; this is the universal kriging denoted 𝖴𝖪

  Then, a theoretical variogram is fitted on the empirical variogram determined by the sample values to determine the weights, ω _i (.). They are generated when the corresponding system of linear equations, depending on the type of kriging, is solved.

These two methods are exact interpolators, that is to say, $\hat {z}(s_{i})\,=\,z(s_{i})\,\forall i =1..n$.

3.2 Using predictors in interpolation

Contrary to the previous methods (𝖨𝖣𝖶, 𝖲𝖪, 𝖮𝖪, 𝖴𝖪), these methods use auxiliary information to explain the variable we want to map. For example, as temperature commonly depends on the elevation, the goal is then to take into account elevation, called a predictor, to estimate the temperature. Ideally, predictors must be known all over the domain. In this way, four methods which can use auxiliary information as predictors are proposed:

Let p be the number of predictors selected.

• 1. Multiple linear regression (𝖬𝖫𝖱):

  $$ \hat{z}(s)=a_{0}+\sum\limits_{j=1}^{p}{a_{j}.X_{j}(s)} $$

  (3)

  where the coefficients, a _j are determined by the sample values and the least square method. Note that this method imposes n>p. It is recommended to have n>p+40.

• 2. Principal component regression (𝖯𝖢𝖱): The first step is to perform a principal component analysis (PCA) on the p predictors. The q chosen eigenvectors P C _j are then used as predictors in a 𝖬𝖫𝖱:

  $$ \hat{z}(s)=b_{0}+\sum\limits_{j=1}^{q}{b_{j}.PC_{j}(s)} $$

  (4)

  where the coefficients, b _j are determined by the sample values and the least square method. This method is often used instead of 𝖬𝖫𝖱 when n<p.

• 3. Partial least square regression (𝖯𝖫𝖲𝖱):This method bears some relation to principal component regression, since the method consists in maximizing the variance of predictors (X _i ) and the correlation between predictors and the variable of interest.

• 4. External drift kriging (𝖤𝖣𝖪): This method is another type of kriging for which the trend μ(.) is a linear combination of functions of predictors or external drifts. Note that 𝖴𝖪 is a particular case of 𝖤𝖣𝖪 where the external drifts are only the spatial coordinates.

The three types of regression (𝖬𝖫𝖱, 𝖯𝖢𝖱, 𝖯𝖫𝖲) are inexact interpolators, since the values $\hat {z}(s_{i})$ predicted by these models differ from observations z(s _i ). The errors $\hat {z}(s_{i}) - z(s_{i})$, called residuals, follow a gaussian distribution centered at 0. A simple kriging (𝖲𝖪), with μ=0, can be performed on residuals leading to an exact interpolator. In most cases, kriging residuals significantly improves the results of the method (Nalder and Wein 1998; Bessafi et al. 2013) and is usually called regression-kriging (𝖱𝖪). In our case, three types of regression were used and the fact of kriging residuals will be noted 𝖬𝖫𝖱𝖪, 𝖯𝖢𝖱𝖪, and 𝖯𝖫𝖲𝖪.

Remark 1

Although normality is not a prerequisite for kriging, it is a desirable property. Kriging will only generate the best absolute estimate if the random function fits a normal distribution. In this way, applying a mathematical function such as the natural logarithm or power function can be performed on data.

Remark 2

In theory, the predictors for 𝖬𝖫𝖱 or 𝖤𝖣𝖪 must be independent. Nevertheless, in practice, this assumption is not really verified. This is the case in the present study where an exhaustive list of predictors was preferred.

Remark 3

𝖤𝖣𝖪 and 𝖬𝖫𝖱𝖪 seem to be similar but they lead to different results (Hengl et al. 2003). Contrary to 𝖤𝖣𝖪, the parameters of a 𝖬𝖫𝖱 are estimated by the least square method in which spatial dependence is not taken into account. With 𝖤𝖣𝖪, equations are solved at once whereas 𝖬𝖫𝖱𝖪 explicitly separates trend estimation from spatial prediction of residuals. Note that, for 𝖬𝖫𝖱𝖪, there is no danger of instability as is the case with the 𝖤𝖣𝖪 system. Besides, in theory, regression requires independent residuals but kriging relies on dependent residuals. For this reason, generalized linear models can be an alternative but this method was not used here.

3.3 Choosing the spatial prediction method

Several interpolation methods were presented in Sections 3.1 and 3.2 with the pros and the cons related to each option. From the same data, these methods can provide significantly different maps of the variable of interest (see Fig. 3). Choosing the best method is therefore a key point in order to propose a map close to reality.

Fig. 3

Mean annual precipitation distribution according to three different interpolation methods

To achieve this, cross-validation is widely used. The goal is to estimate the expected level of fit of a model to a data set that is independent of the data that were used to train the model. It consists in splitting the dataset into training and validation data. For each split, the model is fitted to the training data, and predictive accuracy is assessed using the validation data. There are different types of cross validation. In our case, only two were used:

• 1. The Leave-One-Out (LOO) procedure involves using only one observation as the validation set and the n−1 remaining observations as the training set. It requires learning and validating only N _split=n times. Then the $n ~\hat {z}(s_{i})$ predicted values are compared to the $n ~\hat {z}(s_{i})$ observed values.

• 2. The repeated random sub-sampling validation involves using randomly p>1 observations among n as the validation and the n−p remaining observations as the training set. In this study, the number of random splits was fixed at N _split=100. Then the $(N_{\text {split}}\times p) \,\hat {z}(s_{i})$ predicted values are compared to the (N _split×p) z(s _i ) observed values.

The best model is the one which minimizes the error between predicted and observed values. To determine this, three criteria were used and are defined below:

Let be $\overline {z}=\frac {1}{n}{\sum }_{i=1}^{n}{z(s_{i})}$, and, $\hat {z^{\prime }}(s_{i}) = \hat {z}(s_{i}) - \overline {z}$, and, $z^{\prime }(s_{i}) = z(s_{i}) - \overline {z}$

• The Root Mean Square Error (RMSE) is expected to be close to 0.

  $$ RMSE=\sqrt{\frac{1}{n}\sum\limits_{i=1}^{n}{(\hat{z}(s_{i})-z(s_{i}))^{2}}} $$

  (5)

• The Nash and Sutcliffe coefficient of efficiency (E F≤1) is expected to be close to 1 (Nash and Sutcliffe 1970).

  $$ EF = 1 - \frac{{\sum}_{i=1}^{n}{(\hat{z}(s_{i})-z(s_{i}))^{2}}}{{\sum}_{i=1}^{n}{(\overline{z}-z(s_{i}))^{2}}} $$

  (6)

• The Willmott index (0≤D≤1) is expected to be close to 1 (Willmott et al. 2012).

  $$ D = 1 -\frac{{\sum}_{i=1}^{n}{(\hat{z}(s_{i})-z(s_{i}))^{2}}}{{\sum}_{i=1}^{n}{\left(\left| \hat{z^{\prime}}(s_{i}) \right|-\left| z^{\prime}(s_{i}) \right|\right)}^{2}} $$

  (7)

3.4 Predictor selection

In Section 3.2, spatial prediction methods which use predictors were presented. In our case, 17 predictors were selected to explain precipitation (see Section 2.2). The fact of taking a predictor into account or not has a significant impact on the prediction. The Pearson correlation coefficient is widely used to show how a predictor is linked with the variable of interest (see Table 2). However, choosing a model with predictors which have the greatest correlation is not suitable because two predictors can be strongly correlated (e.g., z90m and zsmooth1) leading to a redundancy of information which can penalize the mapping. Adding one predictor or another is a critical step in mapping.

Table 2 Pearson correlation coefficient between predictors and the mean annual precipitation (estimated with 35 values)

The Akaike Information Criterion (noted AIC) can be used to select a model.¹ Unlike the criteria presented in Section 3.3, it handles the trade-off between the goodness of fit of the model and the complexity of the model (number of predictors) and is written as follows:

$$ AIC = 2p-2\ln(\mathcal{L}) $$

(8)

where p is the number of predictors and $\mathcal {L}$ the likelihood of the model. Given a set of candidate models for the data, the preferred model is the one with the minimum AIC value. In the case n/p<40 (where n denotes the sample size), it is strongly recommended to use the corrected A I C c:

$$ AICc= AIC+\frac{2p(p+1)}{n-p-1} $$

(9)

The AIC can be linked with the RMSE criterion (Aertsen et al. 2009):

$$ AIC=n\ln(RMSE)+2p $$

(10)

Instead of testing all possible models, stepwise methods are widely used to select the best model. In our case, forward selection was used. This involves starting with no predictor in the model, testing the addition of each predictor using a chosen model comparison criterion, adding the predictor (if any) that improves the model the most, and repeating this process until none improves the model. The comparison criterion differs from spatial prediction methods:

• for 𝖬𝖫𝖱 (2^p different models), the function ”stepAIC” from the R package MASS was used (Venables and Ripley 2002).

• for 𝖯𝖫𝖲 and 𝖯𝖢𝖱 (p different models), the exhaustive method was used: the LOO procedure is applied for each model to estimate the RMSE. Then the model which minimized the A I C c was considered as the best model.

• for 𝖤𝖣𝖪 (2^p different models), forward selection was applied with the A I C c as selection criterion (evaluated by the RMSE) in performing the LOO procedure for each tested model. The initial model is equivalent to 𝖮𝖪.

Remark 4

For the 𝖬𝖫𝖱, 𝖯𝖫𝖲 and 𝖯𝖢𝖱 methods, procedures to select predictors are widely used in the literature. For the 𝖤𝖣𝖪, the proposed procedure is, as far as we know, a novelty.

3.5 Implementing the methods

All the methods were implemented in the software R (R Core Team 2012). For 𝖨𝖣𝖶 and kriging, the package gstat (Pebesma 2004) was used.

The package pls (Mevik et al. 2013) provides functions for regression methods such as 𝖯𝖢𝖱 and 𝖯𝖫𝖲.

After predicting the mean annual and monthly precipitation with these methods, a set of map layers in raster format was generated. These layers were based on grids, where each point represents the center of a 90 m side square (the resolution of the DEM, see Section 2.2 above). Finally, the raster package (Hijmans 2014) was used to illustrate predicted maps (rasters) and to build predictors.

3.6 Theoretical and empirical models in kriging

The Matern model with the Stein representation (Stein 1999) was imposed for the kriging for which the semivariance is

$$ \gamma(h)\,=\,c_{0}\,+\,c_{1} \left(1 \!- \!\frac{1}{2^{\nu-1}\varGamma(\nu)} \left(\frac{2\nu^{1/2}h}{r}\right)^{\nu} K_{\nu}\left(\frac{2\nu^{1/2}h}{r}\right) \right) $$

(11)

where h is the separation distance, K _ν is the Basset function, Γ is the gamma function, r is the range or distance parameter (r>0) which measures how quickly the correlations decay with distance, and ν is the smoothness parameter (ν>0). c ₀ corresponds to the nugget variance and c ₀+c ₁ to the sill variance. The Matern model was chosen since it has great flexibility for modeling the spatial covariance (Minasny and McBratney 2005). Note that the exponential model γ(h) = c ₀+c ₁ exp(−h/r) is a particular case of the Matern model (ν=1/2).

The empirical variogram was calculated by the method of moments:

$$ \hat{\gamma}(h)=\frac{1}{N(h)}~\sum\limits_{i=1}^{N(h)}{\left[ z(s_{i}) - z(s_{i}+h)\right]^{2}} $$

(12)

where N(h) is the number of pairs of observations separated by distance h.

Then, the theoretical model is automatically fitted to the empirical variogram by the weighted least squares by minimizing the objective function:

$$ O(\theta)=\sum\limits_{d}{\frac{N_{d}}{d^{2}} \left[ \hat{\gamma}(d) - \gamma_{\theta}(d)\right]^{2}} $$

(13)

where N _d is the number of pairs for lag d (see Table 3), $\hat {\gamma }$ the empirical variogram, and, γ _𝜃 the Matern model with parameter vector 𝜃.

Table 3 The number of point pairs and the average distance (in meters) of all point pairs considered to estimate variograms (in kriging)

Note that, when a non-stationary (i.e., non-constant) mean is used as in 𝖴𝖪 and 𝖤𝖣𝖪, both for simulation and prediction purposes, the variogram model defined is that of the residual process, not that of the raw observations.

In this study, no nugget effect and no anisotropy² has been considered. For the interpolation neighborhood, global prediction was used, meaning that for each prediction all the data values were used. In fact, kriging was performed with the default options of the gstat R package.

4 Results

All the methods described in Sections 3.1 and 3.2 were performed. Residual kriging improved the performance of the methods 𝖬𝖫𝖱, 𝖯𝖢𝖱, and 𝖯𝖫𝖲 (not shown here). Kriging with only 𝗓90𝗆 as external drift was also performed, noted 𝗓90𝗆𝗄. A log-transformation was also applied on observations in order to obtain more Gaussian data. In order to simplify the tables and figures, the results of only seven methods are mentioned further: 𝖨𝖣𝖶, 𝖴𝖪, 𝖬𝖫𝖱𝖪, 𝖯𝖢𝖱𝖪, 𝖯𝖫𝖲𝖪, 𝗓90𝗆𝗄, and 𝖤𝖣𝖪.

4.1 Predicting performance via the LOO procedure

Table 4 illustrates the performance of the different predicting methods for the annual mean precipitation. First, the gain of the log-transformation depends on the methods and is not really significant. The methods with no predictors (𝗅𝖣𝖶 and 𝖴𝖪) show the worst results and using them on such a territory seems to be inappropriate. Using predictors significantly improves the prediction. Adding only the altitude in kriging (𝗓90𝗆𝗄) provides better results than 𝖴𝖪 but does not appear sufficient to fully explain the precipitation, as adding other predictors greatly improves the predicting values. For example, 𝖬𝖫𝖱𝖪 in which the model is composed of seven predictors shows better results than kriging with altitude. For 𝖯𝖫𝖲𝖪, four eigenvectors suffice to minimize the A I C c. The regression kriging methods (𝖬𝖫𝖱𝖪, 𝖯𝖢𝖱𝖪, and 𝖯𝖫𝖲𝖪) have very similar good performances (RMSE ∼280 and EF ∼0.87). 𝖤𝖣𝖪, which uses only two predictors (see Table 5), seems to be the best method to predict mean annual precipitation (RMSE =223.3, EF =0.91). For information, Fig. 4 illustrates the empirical and the theoretical variograms for 𝖴𝖪, 𝗓90𝗆𝗄, and 𝖤𝖣𝖪.³ Residuals coming from the trend of EDK seem to be more fittable than those of 𝖴𝖪 or 𝗓90𝗆𝖪.

Fig. 4

The empirical (points) and the theoretical (lines) variograms for UK (olive green and triangles pointing upwards), z90mK (in pink and triangles pointing downwards), and EDK (in dark red and crossed squares) for the mean annual precipitation. The empirical variogram was estimated and fitted from the residual process, not from the raw observations

Table 4 Skill scores defined in Section 3.3 of the different interpolation methods estimated by the LOO-procedure for annual mean precipitation

Table 5 External drifts (predictors) chosen to predict the mean monthly mean precipitation with 𝖤𝖣𝖪

The LOO procedure was also carried out for the 12 monthly mean precipitations (with no log-transformation), and the results are shown in Fig. 5 . As for the annual precipitation, 𝖤𝖣𝖪 seems to be the best method to predict mean monthly precipitation, since for any month, the RMSE is the lowest with this method, whereas 𝖨𝖣𝖶 and 𝖴𝖪 are not appropriate. For other two criteria (EF and D), there are only 3 months in which 𝖬𝖫𝖱𝖪 seems to predict monthly precipitation better. Nevertheless, 𝖤𝖣𝖪 generally provides the best results. Note that, with a log-transformation of data, 𝖤𝖣𝖪 is much better and becomes the best method for any criterion and month.

Fig. 5

Skill scores defined in Section 3.3 of the different interpolation methods estimated by the LOO-procedure for the mean monthly precipitation

4.2 Predictors chosen for 𝖤𝖣𝖪

Table 5 lists the predictors used in 𝖤𝖣𝖪 for the different months. The selected predictors differ from 1 month to another. The descriptive variable 𝗓𝗑𝖾1 is the one most often used to predict mean precipitation (9 out of 13 for the Matern variogram), followed by 𝖽𝗂𝗌𝗍_𝖼𝗈𝖺𝗌𝗍 and 𝗓𝗌𝗆𝗈𝗈𝗍𝗁5. Note that 𝗓90𝗆 is never used; in addition, the choice of the function to fit the variogram is introduced only from Section 4.5 below.

The number of predictors varies between one and three leading to a model in which the predictors are not strongly correlated. Using the AICc criterion limits this number (see Fig. 6) while minimizing the RMSE should involve choosing eight predictors for annual precipitation, only two are necessary with the AICc criterion. Note, that for 𝖯𝖢𝖱𝖪 and 𝖯𝖫𝖲𝖪, the optimal number of eigenvectors ranges from 4 to 8 depending on the month.

Fig. 6

Values of RMSE (in blue, scale on the left axis) and AICc (in red, scale on the right axis) during the forward selection procedure for the mean annual precipitation (in Fig. 6a) and the mean precipitation in November (in Fig. 6b). OK (ordinary kriging) indicates no predictors

Note that the complexity of the model (characterized by 2p in Eq. 10) has a different weight for the total AIC depending on the observation range (which heavily impacts the RMSE) of the target variable. Nevertheless, the number of predictors is the highest for February, the month in which the RMSE is the lowest. This comes from using the logarithm of the RMSE which reduces the scale effect.

4.3 Predicting performance according to the size of the training set

Here, we want to test the performance of mapping methods to predict the mean annual precipitation according to the available data. The repeated random sub sampling validation was performed for the seven methods tested with different sizes of training set (n−p).⁴

For 𝖯𝖢𝖱𝖪 (resp. 𝖯𝖫𝖲𝖪), the number of eigenvectors was fixed at five (resp. four) (the optimum number according to the LOO procedure). For 𝖤𝖣𝖪 and 𝖬𝖫𝖱𝖪, their models (predictors) were fixed at the beginning (defined by the LOO procedure). Only the variograms or coefficients were re-estimated for each random split.

Figure 7 illustrates the skill scores of the seven methods according to the size of the training set to predict the mean annual precipitation. For each method, the performance decreases with the size of the training set, as expected. Nevertheless, some methods seem to be more sensitive to the number of available data. For example, the performance of 𝖨𝖣𝖶 degrades only slightly, whereas 𝖬𝖫𝖱𝖪, from a critical value, becomes the worst method. So, applying this method which showed good performances with the LOO procedure seems to be questionable, probably because the number of stations is not much greater than the number of predictors. The behavior of 𝖯𝖢𝖱𝖪 and 𝖯𝖫𝖲𝖪 is very similar while 𝗓90𝗆𝖪 seems to be more robust than 𝖤𝖣𝖪. 𝖤𝖣𝖪 appears to be the best method for a training set greater than 20, then 𝖯𝖫𝖲𝖪 becomes better.

Fig. 7

Skill scores defined in Section 3.3 of the different interpolation methods according to different sizes of training set for the mean annual precipitation

4.4 Regionalization of the mean annual and monthly precipitation

Predictors are known on the whole territory at a 90 m resolution. So, 𝖤𝖣𝖪 can be performed in order to map the mean monthly (or annual) precipitation at the same resolution in Martinique. These maps are illustrated in Fig. 8 (for annual, February and September) and show the highest amounts of precipitation are located in the regions located at the highest altitude. These amounts are questionable because of the gap between maximum DEM and station altitude (see Table 1). Indeed, the predicted precipitations are extrapolated by 𝖤𝖣𝖪 to regions with a higher altitude than the highest altitude station (510 m). A historical station, which was located at an elevation of 1010 m (resp. 965 m) according to metadata (resp. DEM), documented the amount of annual precipitation during 5 complete years (1962–1966). The observed mean annual precipitation at this high altitude station was 4642 versus 5015 mm from the predicted map. This gap of 10 % is relatively small but it cannot validate the extrapolation of precipitation. It only shows that the predicted values at high altitude seem to be of the same order of magnitude as what can expected in reality.

Fig. 8

Mean annual and monthly (February and September) precipitation during 1991–2010 provided by EDK

4.5 Sensitivity of the choice of the function to fit the variogram

Until now, in kriging, only Matern model with the Stein representation was used to fit the variogram because this model is the most appropriate according to observation. In order to study the sensitivity of the method to this choice, the same procedure (selecting predictors by the proposed method, estimating skill scores, mapping) was performed by imposing the exponential model. For most months (9 out of 13), the selected predictors are the same for both models (see Table 5). According to the LOO-procedure, the performances are similar: R M S E=219.5 with an exponential model versus 223.3 with a Matern model for the mean annual precipitation (and log-transformation) or E F=0.88 with exponential model versus 0.89 with the Matern model for the mean precipitation in February (and log-transformation). Even if the selected predictors are not the same between the two models, the performances remain similar (R M S E=23 versus 26 for September). The impact of the model choice on the predicted maps is illustrated in Fig. 9. When the predictors are identical for both models, the gap between the two models does not exceed 10 % (see Fig. 9a, b) whereas this gap rises to 20 % when the predictors differ between the two models (see Fig. 9c).

Fig. 9

Sensitivity of the choice of variogram on the mean annual and monthly (February and September) precipitation: Delta (in percentage) between the maps provided by EDK with a Exponential variogram and with the Matern variogram

5 Discussion

The choice of interpolation method depends on data type, area of interest, and the spatial scale used. Here, we focused on the mean monthly and annual precipitation in a small island with a complex topography and great spatial variation. Several spatial methods which are widely used to interpolate mean climate data were tested via cross-validation.

The principal novelty of the study resides in the predictor selection in 𝖤𝖣𝖪. In the literature, the external drifts are often chosen according to a a priori knowledge. Selecting predictors according to the proposed method improves the predictive performance of 𝖤𝖣𝖪: EF = 0.91 versus EF =0.78 if elevation is the only predictor for the mean annual precipitation (estimated by the LOO-procedure). The gain is similar for all criteria, not only RMSE which is the criterion used to select predictors. The proposed procedure achieves to an accurate prediction of mean precipitation with only one, two, or three covariates. Besides, the chosen predictors are quite stable for each pluviometric regime. For example, the months during the dry season (February to April) are characterized by the similar predictors: zsmooth5 and zxe1 even if the selection procedure for these months was performed independently, whereas in the wet season (June to October), dist_coast is chosen for each month. This indicates that there is a climatological coherence in the choice of predictors. Lastly, 𝖤𝖣𝖪 seems to outperform regression methods such as 𝖬𝖫𝖱𝖪, 𝖯𝖢𝖱𝖪, or 𝖯𝖫𝖲𝖪. Overall, the results for mean annual precipitation are notably good when compared to results reported by other studies (Hong et al. 2005; Sun et al. 2015). Moreover, the proposed method to select predictors, performances, and the resulting maps seems to be little influenced by the choice of the function to fit the variogram. The methods used in this paper have also been tested on Guadeloupe (a very similar island to Martinique) leading to similar results: 𝖤𝖣𝖪 was the most accurate method according to the LOO-procedure and the chosen predictors were coherent and not numerous. Clearly, this method seems to be a great opportunity to improve the accuracy of interpolations in such islands.

Applying this method to a larger territory with a large number of observations may not be straightforward: the computation is more time-consuming than with other methods since a LOO-procedure must be performed for each predictor to select the best one. Nevertheless, it has been used in France to map the parameters of a rainfall generator (Carreau et al. 2013) with about 2000 rain gauge stations. Observations were split into four climatic zones (Cantet et al. 2011) in which the method was performed independently with a reasonable CPU-time. For regions with a (relatively) complex topography such as “Mediterranean” and “Highland”, 𝖤𝖣𝖪 clearly provides the most accurate prediction according to a repeated random sub-sampling validation (as in Section 4.3 above) whereas, in flatter regions, the gain of 𝖤𝖣𝖪 is less pronounced.

6 Conclusion

In this paper, several spatial interpolation techniques were applied to map the annual and monthly mean precipitation in a small complex topography territory. In our case, if physiographical variables are considered in spatial interpolation, the prediction performances are improved. The cross validation shows that methods which incorporate predictors (MLRK, PCRK, PLSK, z90mK, and EDK) clearly outperform methods which consider only coordinates (IDW and UK). This result can be explained by the variable of interest which is a long time scale precipitation estimated over several years. Regression methods (MLRK, PCRK, and PLSK) seem to produce more accurate estimates than kriging with only elevation as drift. However, according to the LOO-procedure, if the predictors selected by the proposed procedure are incorporated in kriging, then EDK gives the best prediction. Note that the choice of the function used to fit the variogram has no significant impact on the selected predictors, performances or resulting maps of EDK. Nevertheless, the fact that the proposed method is influenced by the size of the observed sample (more than PLSK but less than MLRK) means that the precautionary principle must be applied. Further investigation is needed to completely validate this method. An alternative method might be to reinterpret distance in IDW (which is the method that is the least influenced the sampling) as in Ahrens (2006).