1 Introduction

The great interest in climate change during the past 20 years has led to a quasi unanimous conclusion for scientists: the Earth’s climate is changing (IPCC 2007). To prevent hydrological risks, it is important to know if this global change could lead to an increase in extreme events (Groisman et al. 2005). In an hydrological context, it is well known that return period estimations are of fundamental interest. To determine the dimensions of hydraulic works such as dams or dikes, a preliminary study on rainfall, particularly extreme rainfall, should not be missed.

The average temperature has increased 0.6°C (± 0.2°C) since the end of the nineteenth century (IPCC 2007). This change should have consequences on precipitations. Simply stated, in a hotter world, the water evaporation increases which may lead to a global increase in precipitation. On land, a small increase in annual precipitation has been observed during the last century, but this trend is not uniformly distributed across the Earth (IPCC 2007). The increase in annual precipitation seems to be more significant in the middle latitudes than tropical areas. In the United States (Groisman et al. 2001), Canada (Zhang et al. 2000) and northern and western Europe (Schönwiese and Rapp 1997), there was an increasing trend during the last century. In Europe this can be explained by the persistence of the positive phase of the North Atlantic Oscillation in the last two or three decades (Cassou 2004). Unlike these studies, decreases have been detected in China (Zhai et al. 1999) and the Mediterranean area (Xoplaki et al. 2004).

The above studies focused on the evolution of average characteristics of precipitation and not on extreme values. Global Climate Models (GCM) do not efficiently represent extreme events (Moberg and Jones 2004). So GCM outputs are of poor interest for extreme events. Dubuisson and Moisselin (2006) studied the trends of precipitation indices in France and showed that there is no evidence of an increase in heavy precipitation events. Here we are concerned with the frequency of extreme events, looking for a potential variation in time. Classical statistical methods (fitting a probability law) are of limited interest because of a lack of long time series, leading to inaccurate estimation of distribution tails (Renard 2006; Pujol et al. 2007b). As an example, following data quality criteria recommended by Météo-France, only one time series of daily precipitations could be considered to study a climate change in France. This time series comes from 139 rain-gauge stations during the period of 1960–2003. Note that data from 2004 and later are not yet available because of actual homogenization by Météo-France. In the sequel, an original approach is proposed to estimate the impacts of climate change on extreme events, based on the use of an hourly rainfall stochastic generator (Arnaud et al. 2007). It can be coupled with a rainfall-runoff model (Arnaud and Lavabre 2002). Climate evolution is then detected from the values of the generator parameters. Unlike classical statistical approaches, these parameters are estimated from average, not extreme, values of daily climatic characteristics. As a consequence, the estimations are less influenced by the sample than those based on extreme values. The generator parameters we consider are the following: event occurrence, event duration and event intensity. They are particularly well adapted to examine the rainfall signal. From these three characteristics different types of climate that are well known in France can be discriminate. For example the “oceanic” climate can be characterized by events with long duration, the “alpine” climate by a large number of events, and the “Mediterranean” climate by events with a strong intensity. Conditionally to the values of these three parameters, rainfall quantiles for every rainfall duration, from 1 h to 10 days, can be estimated from the generator precipitation outputs. It has been showed in a recent study that the generator correctly estimate rainfall quantiles in such a time range (Neppel et al. 2007).

The first aim of the present work is to study the stability in time of the generator parameters. According to the definition of parameters, we applied the Poisson–Pareto-Peak-Over-Threshold model (POT). This model, commonly used in extreme values theory (Coles 2001), is well adapted to our framework. A linear trend for the generator parameters is tested through a maximum-likelihood ratio test approach. Parey et al. (2007) also applied such an approach on time series of temperatures to detect a trend in extreme temperatures. A procedure which allows us to work on a regional scale is also proposed. Since many climates are present in France, all landscapes might not be subject to the same changes. A hierarchical clustering, based on average rainfall characteristics, led us to divide France into four homogeneous climatic zones. Then generator parameters can be estimated over the period 1960–2003 under the climate change hypothesis. This new estimation allows us to appreciate rainfall distribution changes due to climate change.

The principle of the hourly rainfall generator is explained in Sect. 2. The three generator parameters used in the sequel are presented in details. In Sect. 3, we focus on the test for the stationarity of the rainfall generator parameters in both local and regional scales. Section 4 presents a data application. Data on which the trend test is applied are presented in the Sect. 4.1. Section 4.2 illustrates how the division of France into four homogeneous climatic zones are obtained. Section 4.3 shows the parameters evolution in time and compares the robustness between the local and the regional trend test. Section 4.4 presents the effects of the climate change hypothesis on the rainfall distribution. A general discussion is proposed in Sect. 5. A conclusion and some perspectives are given in Sect. 6.

2 The hourly rainfall generator: SHYPRE

In the literature, the rainfall quantiles can be estimated in two ways. The most well-known method is to fit a probability law on data (Coles 2001). Another method is to use a mathematical structure of rainfall representations (Waymire and Gupta 1981; Wu et al. 2006; Sivakumar and Sharma 2008). In this paper we are concerned with the latter method. Our aim is to propose an original approach for detecting trend in extreme rainfall. In the following, the general principle of the rainfall generator we consider is briefly presented (for details, see Arnaud 2008; Arnaud et al. 2007) and the generator parameters are detailed.

2.1 Generator principle

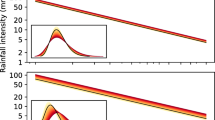
SHYPRE is a model of rainfall hydrograph simulation based on an hourly rainfall generation, which can be coupled with a rainfall-runoff model. It has been developed at Cemagref in Aix-en-Provence (Cernesson 1993; Arnaud 1997). The model is based on descriptive variables from hourly information characterizing the rainfall signal such as the rainfall depth or duration. Each variable was fitted by a probability law (Cernesson et al. 1996). As in Monte-Carlo methods, these variables were simulated, taking into account dependencies. Then time series, statistically equivalent to observations, can be reproduced for any desired time period. Quantiles can be empirically estimated from these simulated times series. The generator’s principle is illustrated in the Fig. 1.

Fig. 1
figure 1

Principle of the hourly rainfall generator. Figure from Arnaud et al. (2007)

Full size image

A regionalized version of the rainfall generator was parameterized according to daily data based on the knowledge of three parameters, leading to relevant results (Arnaud et al. 2006). In fact, unifying the model makes it perfectly applicable to regions with varied rainfall ranges, such as metropolitan France, Reunion island in the Indian Ocean, and Martinique island in the Caribbean (Arnaud et al. 2007). The regionalization of the three model parameters, using 2,812 daily rain gauge stations in the whole of France (Sol and Desouches 2005), allows the estimation of rainfall quantiles for different time durations on a square of 1 km2 everywhere in the French territory (Arnaud et al. 2006). For the Languedoc-Roussillon region, the obtained results have been compared to those of an another regional approach (Neppel et al. 2007). Results are comparable and it appears that the regionalized generator version correctly estimate rainfall quantiles for durations from 1 h to 10 days. As a stochastic model, the rainfall generator do not perfectly represent the rainfall reality but bearing on many studies showing that it represents well extreme rainfall for many types of climate (from temperate to tropical), we assume in the sequel that it correctly reproduce the behavior of extremes rainfall (Arnaud 2004).

2.2 The three generator parameters

The descriptive analysis of rainfall was based on observed rainfall events selected on daily criteria. An event is defined as a succession of daily rainfall depths of more than 4 mm, including one daily rainfall depth of at least 20 mm. Footnote 1 This definition allow us to assume that events are mutually independent. The three following daily variables were considered:

  • NE (event occurence) is the average number of event per year,

  • μPJmax (event intensity) is the average of the maximum rainfall in 1 day of each event,

  • μDTOT (event duration) is the average of event duration.

Moreover we selected two seasons: summer from June to November (when extreme events usually occur), and winter from December to May. From the 3 × 2 daily parameters, say NE W ,  μPJmax W ,  μDTOT W for winter and NE S ,  μPJmax S , μDTOT S for summer, it was possible to run the hourly rainfall generation model for periods as long as needed, leading to a probabilistic study on the extreme rainfall with daily information.

To conclude, from these 3 × 2 daily parameters, we can generate very long time series to estimate rainfall quantiles for different durations and any return periods.

3 Detecting a trend for the generator parameters

We wanted to test the null hypothesis H 0: the parameters are stationary versus the alternative hypothesis H 1: the parameters vary in time. Many studies present an overview of statistical approaches available for detecting and estimating trends in environmental data. However, the trend test power varies according to the nature of the studied data. As in Hess et al. (2001) and Yue and Pilon (2004), a simulation study was done to determine which test appeared as the most powerful when respecting a fixed false rejection rate (type I error). The maximum likelihood ratio test (Coles 2001) appeared as the best approach for our study. Note that Renard (2006) arrived at the same result regarding runoff data.

3.1 Maximum likelihood ratio test: ML test

Let M 0 and M 1 designate two alternative models, of size d 0 and d 1 (the size is the number of parameters) and assume that M 0 is nested into M 1 (i.e., simply stated, M 0 can be obtained from M 1 when assigning particular value for some of his parameters). We test the null hypothesis H 0: M 0 explains well the considered phenomenon versus the alternative H 1: M 1 is a better model. Let \({\mathcal{L}}_i(X;\theta_i)\) be the log-likelihood of a sample X for model M i , i = 0, 1. Let \(\hat{\theta}_i\) be the vector of size d i maximizing \({\mathcal{L}}_i(X;\cdot).\) The deviance statistic is defined as

$$D = -2\left({\mathcal{L}}_0(X;\hat{\theta}_0)-{\mathcal{L}}_1(X; \hat{\theta}_1)\right)$$
(1)

The basic principle is parsimony. The model is chosen according to the value of D. Under H 0 and with a sample size large enough, \(D\;\buildrel{H_0} \over {\sim}\;\chi^2_{d_1-d_0}.\) Therefore hypothesis H 0 is rejected, with a type I error α, if D > u α where \({\mathbb{P}}(\chi^2_{d_1-d_0} > u_{\alpha})\;=\;\alpha.\) The p-value notion is used to decide on rejecting or not H 0: the p-value is the probability of obtaining a result at least as large as the one actually observed, given that the null hypothesis is true. In our case, it corresponds to \({\mathbb{P}}(\chi^2_{d_1-d_0}>D).\) We decide to reject H 0 with a fixed type I error α if the p-value is less than α.

3.2 ML test for the local approach

The hourly rainfall generator is parameterized through the three above mentioned daily variables NE,  μPJmax and μDTOT. Since the parameter μDTOT influences little the extreme behavior of the generator, we restricted our investigations on the non-stationarity of the two following parameters: NE and μPJmax. The approach we used is based on the POT model.

Let n be the number of events between the year A 1 and the year (A 1 + A). Let (X 1, …, X n ) be the depth of the maximum daily rainfall in millimeters for these n events. Let (t 1, …, t n ) be dates (in days) corresponding to (X 1, …, X n ). The time t = 1 corresponds to the first of January, A 1, and t i corresponds to the position, into the series, of the date of the maximum daily rainfall of the event i. For example, if the first event occur the 10th of January, A 1 and the next event occur 10 days after, then, t 1 = 10 and t 2 = 20. Let \(N_[d_1, d_2]\) be the occurrence variable of events between the beginning of the day d 1 and the end of the day d 2. For example N [1,365] counts the number of event occurring during the first year of the sample. When working on values over threshold, it is usual to model the number of events per time unit (frequently per year) by a Poisson’s law (Ramachandra Rao and Hamed 1999; Lang et al. 1999). An event, according to its definition, must have at least a depth of daily rainfall over the threshold 20 mm. Thus we can say \(N_{[t,t]}\buildrel{\rm def} \over {=} N_{[t]}\) follows a non homogeneous Poisson’s law of parameter λ(t). λ(t) corresponds to the average number of excess per day at the time t. Therefore N [1,t] follows a Poisson’s law with rate function tλ(t). The stationarity of a Poisson process can be tested through the stationarity of the process intensity or the inter-arrival times. For a Poisson process with an intensity λ(t), waiting times are exponentially distributed with parameter λ(t) (Lang 1999). According to a study on simulated data, the test on waiting times appears as the best and we decide to use it. The log-likelihood to test the stationarity of the number of events is given by:

$${\mathcal{L}}^{P}_n = \sum_{i=1}^n{\log(\lambda(t_i))} -\sum_{i=1}^n{\lambda(t_i)(t_i-t_{i-1})}\quad\hbox{ with }t_0=1$$
(2)

Concerning the parameter NE, we can test the stationary hypothesis H 0: (M0) λ(t) = λ0 versus the linear trend hypothesis H 1: (M1) λ(t) = λ0 + λ1 t using the ML test with d 1 − d 0 = 2 − 1 = 1.

For the parameter μPJmax, the stationary test is built as follows. The variables (X i )i=1,…, n are distributed according to the same family of probability laws and are independent since events are considered as independent. From the event definition, we have ∀i = 1, …, n, X i  > 20 mm. We used the Generalized Pareto Distribution (GPD) family to model the threshold exceedances (Muller 2006; Coles 2001). The GPD family has three parameters: a location parameter u (here u = 20 mm), a scale parameter σ and a shape parameter ξ. The cumulative distribution function \({\mathbb{P}}(X \langle x|X \rangle u)=F_{(u,\sigma,\xi)}(x)\) is given by:

$$\begin{aligned} F_{(u,\sigma,\xi)}(x) = \left\{ \begin{array}{ll} 1-(1+{\frac{\xi (x-u)}{\sigma}})^{-1/\xi} & \hbox{with ${\frac{x-u}{\sigma}}< -{\frac{1}{\xi}}$ \quad for $\xi<0,$}\\ 1-(1+{\frac{\xi (x-u)}{\sigma}})^{-1/\xi} & \hbox{with ${\frac{x-u} {\sigma}}> -{\frac{1}{\xi}}$ \quad for $\xi>0,$}\\ \exp(-{\frac{(x-u)}{\sigma}}) & \hbox{for $\xi=0.$} \end{array}\right.\end{aligned}$$

Moreover if X ∼F (u,σ,ξ) then \({\mathbb{E}}(X-u|X>u) ={\frac{\sigma}{1-\xi}}.\) Thus we can estimate the generator parameter μPJmax by \({\frac{\hat{\sigma}}{1-\hat{\xi}}}+u.\) Following Renard (2006), we assumed the shape parameter ξ to be constant because of sampling uncertainties. Climate change is then characterized by the non-stationarity of the scale parameter: σ(t) varies in time. Therefore the log-likelihood we considered is given by:

$${\mathcal{L}}^{GPD}_n = -\sum_{i=1}^n{\log(\sigma(t_i))} -\left(1 + {\frac{1}{\xi}}\right)\sum_{i=1}^n{\log\left(1 + {\frac{\xi(x_i-u)}{\sigma(t_i)}}\right)}\quad\hbox{with $u=20$ mm}$$
(3)

The stationary hypothesis \(H_0: (\hbox{M}0) \sigma(t) = {\sigma_0}: \mu{PJmax} = {\frac{\sigma_0}{1-{\xi}}}+u\) versus the linear trend hypothesis \(H_1: (\hbox{M}1) \sigma(t) = {\sigma_0}+ {\sigma_1t}: \mu{PJmax}(t) = {\frac{{\sigma_0}+{\sigma_1}t} {1-{\xi}}}+u\) is tested using the ML test with d 1 − d 0 = 3 − 2 = 1. The parameter λ0 is the only one which can be analytically estimated. For the others parameters, λ1, σ0 and σ1, an optimization algorithm is needed and we use the Broyden–Fletcher–Goldfarb–Shanno (BFGS) method (Broyden 1970; Fletcher 1970; Goldfarb 1970; Shanno 1970) of the “optim()” function implemented in the “stats” package from language R (http://www.r-project.org/).

Remark 1

The two processes being independent (Ramachandra Rao and Hamed 1999), it is possible to analyse them separately.

Remark 2

An exponential law is sometimes used to model threshold exceedances. It corresponds to the case where the shape parameter of the GPD is equal to 0. When ξ ≠ 0, a study on simulated data showed that the ML test based on an exponential likelihood does not respect the theoretical type I error. Since Muller (2006) showed that the hypothesis ξ = 0 is often rejected in France, we prefer to use the ML test with the GPD’s likelihood even if the estimation of ξ is difficult.

Remark 3

The GPD model is often used in trend detection for extreme values (Pujol et al. 2007b; Coles 2001). Here we use it to compute, from estimated parameters, an average in a given time. Extreme quantile estimation from tail distribution model is much more dependent on shape parameter ξ than any average estimation. Then, assuming a constant shape parameter ξ becomes a weaker hypothesis compared to an extreme value framework.

To test locally the stationarity of the rainfall generator parameters, we used the above tests on each station. For a station S, we tested the stationarity of the time series \(X^{S}=(X_{1}^{S}, \ldots, X{_{n_{S}}}^S)\) and \(t^{S}=(t_{1}^{S}, \ldots, t{_{n_{S}}}^S)\) versus a linear trend where X S corresponds to the maximum daily rainfall of the n S observed events occurring at the station S on the dates t S. We also noted \(T^{S}=(t_{1}^{S} - 1, \ldots, t^{S}_{{n_{S}}} - t^{S}_{{n_{S1}}})\) the time series of waiting times of an event occurring at S. Using the above tests, we could conclude regarding to the stationarity of these series according to a fixed type I error α.

3.3 ML test for the regional approach

3.3.1 Building the “regionalized” time series

In the regional approach, we had to build time series we called “regional” by regrouping stations from each homogeneous zone. The GPD model was used for the maximum daily rainfall of an event. In a given zone, the shape parameter was assumed to be constant and only the scale parameter varies between stations (Onibon et al. 2004; Cunnane 1988). The aim of this step is to construct a sample of exceedances identically distributed within each zone.

Let Z be a homogeneous climatic zone. The shape parameter was assumed to be constant in a same Zone and it denotes ξ Z on Z. Let Ω Z be the set of stations which belong to Z and ∀S ∈ Ω Z , let \(\widetilde{X}^S=X^S-u,\) where \(X^S=(X_1^S,\ldots,X_{n_S}^S)\). Then, \(\widetilde{X}^S \sim GPD(0,\sigma_S,\xi_Z).\) It is easy to show that \(\forall S\in\Omega_Z\;{\frac{\widetilde{X}_S} {{\mathbb{E}}(\widetilde{X}_S)}} \sim GPD(0,1-\xi_Z,\xi_Z)\; \hbox{ and } {\frac{T_S}{{\mathbb{E}}(T_S)}} \sim Exp(1),\) where Exp(λ) designates the exponential law with parameter λ. Using the strong law of large numbers, both laws can be used to approximate respectively the laws of \({\frac{\widetilde{X}_S} {\overline{\widetilde{X}_S}}}\) and \({\frac{T_S}{\overline{T_S}}}\) with \(\overline{\widetilde{X}_S} = {\frac{1}{n_S}} \sum_{i=1}^{n_S}{\widetilde{X}_i^S}\) and \(\overline{T_S} = {\frac{1} {n_S}} \sum_{i=1}^{n_S}{T_i^S}.\)

To build “regional” time series for the Z zone, we regrouped stations with the following method (Neppel et al. 2007):

  1. 1.

    ∀S  ∈ Ω Z , we divide \(\widetilde{X}^S\) by its empirical mean \(\overline{\widetilde{X}_S}\); the same for T S.

  2. 2.

    We concatenate the reduced \(\widetilde{X}^S,\) the t S and the reduced T S. We obtain “regional” time series of maximum daily rainfalls noted \((Y^Z_{1:n_Z})\) occurring on dates \((t^Z_{1:n_Z})\) and “regional” time series of waiting times between two events observed on a same station belonging to Z, denoted \((T^Z_{1:n_Z})\) with \(n_Z=\sum_{j \in \Omega_Z}{n_j}.\)

The spatial dependence between stations of the same zone can lead to a bias in the calculus of p-values: a same event can take place on several neighbouring stations. To obtain an independent and identically distributed sample, we had to remove them from the “regional” time series. Assuming that the distance from which two stations are considered as spatially independent is known (below this distance is called the station dependence distance), the “regionalized” time series for the Z zone is built as follows:

  1. 3.

    for each day D ∈ t Z, we search for observed events taking place in Z. We note Ω D Z the set of stations where an event occurred at one of the days D, D − 1 or D + 1.

  2. 4.

    We choose randomly a station i in Ω D Z . Then we remove from T Z and Y Z the events of stations k  ∈ Ω D Z  − {i} if and only if the distance between stations i and k is smaller than the station dependence distance.

  3. 5.

    We repeat the (iii) and (iv) steps K times.

Thus K different “regionalized” time series i.i.d. (but not mutually independents) were built for each homogeneous zone. For a given Z zone, we denote these K time series \((\widetilde{Y}^Z_{1:n_K})^{1:K}\) and \((\widetilde{T}^Z_{1:n_K} )^{1:K}.\) Using the ML test, we tested, for k = 1:K, the stationarity of maximal daily rainfalls with \((\widetilde{Y}^Z_{1:n_K})^{k}\) as well as event occurrence with \((\widetilde{T}^Z_{1:n_K})^{k}.\)

So we had, for each parameter and each zone, K p-values to characterize if the linear trend is significant.

3.3.2 Calculating the p-value for the regional test

For each homogeneous climatic zone and for each parameter, we had K  p-values coming from the ML test on the K “regionalized” time series. How to know, from these K  p-values, if the trend is significant?

Let Z be a fixed zone and consider one of the two sets of K  p-values on this zone. Let α g designates the significance level of the regional test (global type I error). We propose the following method:

  1. 1.

    We use a False Discovery Rate (FDR) approach (see Appendix) to determine, from the K obtained p-values, the number of rejected null hypothesis on Z, that is the number of time series among K for which the stationary hypothesis is rejected at a fixed significance level, say αℓ. Let \(m_{\alpha_{l}}\) be this number.

    Then we want to construct the empirical distribution of the number of rejected null hypothesis among K at risk αℓ under H 0;

  2. 2.

    To remove a possible time dependence under H 0, we permute without replacement the K series using the same permutation in order to keep the dependence between series;

  3. 3.

    We then apply the ML test on each K new series and deduce the number of rejected null hypothesis via the Benjamini and Hochberg procedure at risk αℓ;

  4. 4.

    Repeating (ii) and (iii) many times, an empirical distribution of the random variable \(M_{\alpha_{l}}\) is obtained; \(M_{\alpha_{l}}\) is the number of rejected null hypothesis under H 0 among K at risk αℓ;

  5. 5.

    We use this distribution to estimate the probability \({\mathbb{P}}(M_{\alpha_{\ell}} \geq m_{\alpha_{\ell}}).\) If this probability, which corresponds to the p-value of the regional test, is smaller than α g , then H 0 is rejected on Z and the linear trend of the series is significant on Z at risk α g . Estimations \(\hat{\sigma}_1\) and \(\hat{\sigma}_0\) of the parameters σ0 and σ1 are given by medians values coming from the K series.

Concerning the value of αℓ which is used for calculating the number of rejected null hypothesis among K, it ought to be between 0.2 and 0.3. A study on simulated data showed that the significance level of the regional test was respected for this range of values. The best is to plot \({\mathbb{P}}(M_{\alpha_{\ell}} \geq m_{\alpha_{\ell}})\) according to αℓ in order to see from which αℓ we have \({\mathbb{P}}(M_{\alpha_{\ell}} \geq m_{\alpha_{\ell}})\leq\alpha_g.\) If αℓ is smaller than 0.3, the stationary hypothesis on a whole zone H 0 is rejected at risk α g . We apply this regional trend test to data in Sect. 4.3.2.

4 Hypothesis of climate change

4.1 Studied data

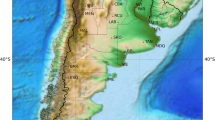
Climate change must be studied only on high quality data otherwise observed changes could come from the data themselves and might represent data artefact, leading to misleading interpretations. The reference daily series has been established by Météo-France for climate study. For example, the IMFREX project (http://medias.cnrs.fr/imfrex/web/) and Dubuisson and Moisselin (2006) worked on such series. This data is associated with quality codes and synthetic criteria to consider the homogeneity-stop in the series. Météo-France’s advice was applied to our data. To establish a compromise between the period length and the number of stations, we restricted our study to the period 1960–2003. 139 rain gauges were chosen, with 10% of missing data at the most. Their location is presented in Fig. 2 (by black points). From these 139 daily rainfall time series, we can extract the date and depth of the maximum rainfall in 1 day and the duration of each event observed between 1960 and 2003, in order to calculate trends of 3 × 2 generator parameters on a local scale. To work regionally, 4 homogeneous climatic zones were created, as explained below.

Fig. 2
figure 2

Four homogeneous climatic zones as regards rainfall generator parameters and location of the 139 rain gauges used in trend test

Full size image

4.2 Climatic zones construction

To use the regional approach for the trend test (see Sect. 3.3), we looked for some homogeneous climatic zones. To achieve this, a hierarchical clustering using Ward’s algorithm was applied. Indeed, the aim of the Ward procedure is to unify groups in such a way that the variation inside these groups does not increase too drastically: the resulting groups are as homogeneous as possible (Saporta 2006). Champeaux and Tamburini (1996) applied it to daily precipitations in France. Here, we chose to cluster according to the coordinates and the 3 × 2 generator parameter values (NE W ,  μPJmax W ,  μDTOT W , NE S ,  μPJmax S and μDTOT S ) of rain gauges. In addition to the above 139 rain-gauges, 2,761 other daily rain-gauges are also available in metropolitan France. This data cannot be used to study climate change because the time-series are not long enough. But these ones allowed us to estimate properly the average parameters of the rainfall generator and to better characterize the climatic zones. The clustering parameters were standardizedFootnote 2 and we just needed to calculate the inter-distance matrix. We chose the Euclidean distance criteria since it favours marked differences and gives more importance to distances between groups. Then four zones were obtained: “highland”, “mainland”, “mediterranean”, and “oceanic”. They are illustrated in Fig. 2.

Table 1 shows the average of the 3 × 2 parameters of the rainfall generator and the number of stations in each zone where climate changes were studied.

Table 1 Number (nb.) of stations to create zones and to detect climate change and the average of generator parameter values in each zone
Full size table

4.3 Results of parameter evolution

This section is concerned with the application of the trend tests (see Sect. 3) on the data presented in Sect. 4.1. First, we illustrate the results of the local trend test and its sensibility about the observation period. Then we apply the regional trend test on the four zones presented in Sect. 4.2.

The significance level for all trend tests is fixed to α = 0.1.

Remark 4

Our test procedure is not limited to time linear trends. For example, an exponential relation σ(t) = exp(σ0 + σ1 t) has also be tested. Tests lead to same results than with a linear trend even for the percentages of evolution parameter. Only the projection in the future will alter the results.

4.3.1 Results of the local trend test

The local trend test presented in Sect. 2 has been applied on the data set in order to conclude regarding to the stationarity of the parameters NE and μPJmax on each of the 139 rain gauge stations between 1960 and 2003. The results are illustrated in Fig. 3. A trend is significant if the test p-value is smaller than α = 0.1. To study the relevance of these results, we also applied the local trend test with different observation periods: we successively removed from the reference observation period (1960–2003) the five 5 years and the last 3 years.

Fig. 3
figure 3

Local trend test results on each of the 139 stations for the variables NE and μPJmax: trend (increase if the triangle points upwards, decrease if the triangle points downwards) and the value of the p-values (according to size). We tested in the summer season (on the top) and the winter season (on the bottom). a Trend of μPJmax in summer. b Trend of NE in summer. c Trend of μPJmax in winter. d Trend of NE in winter

Full size image

Results of the local approach led to some apparent contradictions. First, climatic evolution should be the same for nearby stations, but local results showed that some stations had contradictory significant trends, as for example in northern Brittany for the parameter μPJmax S (see the circle in Fig. 3). Thus it was difficult to establish climatic evolution in a specific region from the local approach. Moreover the period of observations has a (too) big influence on the results. In fact, even if the number of stations where H 0 is rejected is approximately the same for the different observation periods, there are a lot of stations where the test conclusion changes. For example, the parameter μPJmax W has a significant trend for 28 stations between 1960 and 2003. But 13 of them become non-significant between 1965 and 2003. So it is difficult to determine if the observed trends are related to a potential evolution or come from sampling fluctuations. The non-robustness of the local trend test is due to the short length of time series. To enlarge the data set, we use the regional approach presented in Sect. 3.3.

4.3.2 Results of the regional trend test

We now consider the regional trend test presented in Sect. 3.3 with K = 100 in order to test the NE and μPJmax stationarity between 1960 and 2003 on each of the four zones illustrated in Fig. 2. To use the regional test, we have to define a station dependence distance for each zone. Since its estimation varies according to the method used we decided to consider several station dependence distances Dist 0 to Dist 3 (see Table 3). Dist 0 to Dist 2 correspond to the results of three different methodsFootnote 3 leading to three potential different dependence distances, and Dist 3 corresponds to the case where all stations (in a same Zone) are mutually dependents. Moreover, for the station dependence distance Dist 0, we also consider different observation periods as for the local test.

Table 2 The first three rows: numbers of stations (out of 139) where H 0 has been rejected on different observation periods according to the local trend test; the last two rows: .+ (respectively .−) corresponds on numbers of stations where H 0 has (respectively not) been rejected on the observation period while H 0 has not been rejected (resp. has been rejected) on the period 1960–2003
Full size table
Table 3 The different station dependence distances (in km) taken for the “regionalized” time series building for each homogeneous zone
Full size table

First, the regional test results are not affected by the station dependance distance (see Table 4). Significant trends are the same for any distances, even for the estimation of the parameter evolution. This point is important when you know the difficulty to estimate these distances. Unlike the local test, the observation periods have a minor influence on the regional test results (see Table 5). All significant trends detected between 1960 and 2003 are also significant for the two others observation periods. Some differences appear, particularly in Summer and in the “mediterranean” zone where the rainfall variability is the biggest in France. Nevertheless, the regional approach gave us global information, in a given zone, about the climate change.

Table 4 The robustness of the regional test according to the station dependence distance
Full size table
Table 5 The robustness of the regional test according to the considering period
Full size table

The concatenation of several stations enlarges the data set and reduces the sampling variability. In other words, significant regional trends have less chance to come from sampling variability. The regional approach seemed clearly better to establish a real climatic evolution.

Remark 5

The Generalized Pareto Distribution is used to infer on the parameter μPJmax. The threshold u must be large enough to obtain a good approximation of the tail distribution and it is usually determined through the mean-excess-function (Coles 2001). Here the threshold value was u = 20 mm for the four zones because of the event definition. This value seems too small especially for the “mediterranean” zone where the threshold is widely fixed to around 50 mm (Pujol et al. 2007a). The regional trend test has been performed with this threshold and led to the same significant trends.

4.3.3 Observed trends

Some interpretations of the above trend tests results on the period 1960–2003 are proposed in this section. The results presented in Fig. 3 have to be considered as only descriptive ones. They are given to illustrate how perform the local trend test. From these results, no regional interpretation, as for example, “the number of winter events increased significantly around Paris between 1960 and 2003” (see the circle in Fig. 3d) can be deduced. Indeed, for a rigorous statistical analysis, one of the well-known multiple test procedure should be used to provide a regional conclusion from local results (Benjamini and Hochberg 1995). Unfortunately such procedures are known to be not powerful, and we did not use any of them. So we prefer to use the results of the regional trend test.

The main observed changes took place in winter with an increase of event intensity in only “highland” zone. This increase may be caused by the climate warming. Indeed, rain gauge stations underestimate the intensity of solid precipitation. Because of the climate warming, some solid precipitation could be transformed in liquid precipitation which leads to an increase of the intensity. Unlike the “mediterranean” zone, there were more and more winter events in the “highland”, “mainland” and “oceanic” zones. In summer, no trend was detected except for the “mainland” zone where the number of events increased between 1960 and 2003.

The regional trend test was also performed with a nine-zone division. Results show no contradictory trend with those coming from a four-zone division.

4.4 Effects on rainfall distribution

For each of the 139 stations, a significant trend for the rainfall generator parameters was or was not detected. So climate change was integrated in the estimation of generator parameters: if the linear trend of a parameter was significant according to the ML test, an estimation of this parameter was possible for each year between 1960 and 2003.

Let Param 0 be the set of rainfall parameters estimated under the stationary hypothesis by computing the parameters average on the whole observed time series.

Let Param A be the set of rainfall generator parameters under the non-stationary hypothesis estimated in year A. On stations (or zone) where no stationary hypothesis was rejected (for all parameters), we had Param 0 ≡ Param A . In the following, Param Loc A corresponds to the parameter set estimated from the local trend test results, and Param Regio A to the one estimated from the regional trend test results. These parameter sets are estimated from results presented in Sect. 4.3.

With the rainfall generator, rainfall quantiles can be estimated using these parameter sets. So the effects of climate change on extreme rainfall can be evaluated from the comparison between quantiles estimated from Param 0 and quantiles estimated from Param A . We can also assess whether or not an evolution of average parameters leads to a bigger evolution when working with extreme values.

Remark 6

Quantiles from the rainfall generator do not come from a fit of a probability distribution like GPD or exponential. They are estimated empirically from simulated hydrographs. Their estimation is possible for any return period and any duration from 1 h to 10 days. So, generator results can be looked upon as probability distributions.

Considering two sets of parameters for the rainfall generator leads to two different distributions. Let T denote a return period. We can calculate the T-quantiles from these two distributions and compute their ratio. Then we obtain an increase or a decrease (in percentage) of the volume associated with the return period T, and we can assess if an evolution in a small return period is accentuated in a bigger return period.

Let PM24 designate the volume of maximal rainfall in 24 h. Let q 0 T (respectively q A T ) be PM24 associated to the return period T coming from generator results with the parameterization Param 0 (respectively Param A ). We calculated the ratio \(R_T = {\frac{q_{T}^{2003}}{q_{T}^{0}}}\) for T = 2, 5, 10, 100, 1000 years. In Fig. 4, we compared the ratio R 2 with the R T ratios with T > 2 years for each station. The increase of changes between the Param 0 and the Param Loc2003 simulations can be evaluated according to the return period. For most stations, | R T1 − 1 | >  | R T2 − 1| for T1 >  T2. According to the rainfall generator, climate change is likely to have more significant effects on the extreme behavior than on the average one for the maximum daily precipitation. This assumption can be discussed when we compare quantiles (of the maximum daily precipitation) estimated with the parameterizations Param 0 and Param Regio2003 . Table 6 shows the average evolution inside each zone between these 2 parameterizations. Unlike the local approach, the regional one lead to small changes in the quantile estimation. Even for high return period, changes are less than 10% except for the “Highland” zone. It is due to the fact that no significant trend was detected for the μPJmax parameter. In addition, the strongest rainfall events in France occur in summer. The generator takes into account this phenomenon. Its extreme behavior is mainly influenced by the “summer” parameters. Unlike the local approach, no or very few regional trends were detected in “summer”, that is why changes are small. The distinction of two seasons in the trend calculation allowed us to take into account the real impact of climate change. Indeed if we did not distinguish the two seasons, a significant increase in the event occurrences would be found which would lead to bigger changes. These changes would not reflect reality: only winter events have a significant increase.

Fig. 4
figure 4

\(R_T = {\frac{q_{T}^{2003}}{q_{T}^{0}}}\) with T = 5, 10, 100, 1000 years according to R2 with the Param Loc2003 parametrization

Full size image
Table 6 \(R_T ={\frac{q_{T}^{2003}}{q_{T}^{0}}}\) (transformed to percentage) with the Param Regio2003 parametrization
Full size table

Concerning risks, we can look at the evolution of the event occurrence probability. Within the context of a stationary framework, the notion of return period is widely used: “a value with a return period T is expected to be exceeded on average in T years”. Within a non-stationary framework, this definition becomes inadequate. We used the following interpretation, assuming that the climate change is quasi-null within a single year: “the T-quantiles calculated classically, in a certain year A, have a probability 1/T to be exceeded during the considered year A” (Renard 2006). For example, if the volume x is the 100 years-quantile in 1960, whereas in 2003 this same volume x is the 50 years-quantiles, then we say that this event is twice as likely in 2003 than in 1960.

From results established by the parameterizations Param 0 and Param 2003, we evaluated the changes in event frequencies. We use x 0 as the quantiles of reference, that is the T 0-quantiles of the rainfall distribution coming from the parameterization Param 0. Then we calculated T 2003 in such a way that the T 2003-quantile coincides with x 0 of the rainfall distribution coming from the parameterization Param 2003. This procedure was performed with trends established by the local approach and the regional one (see Sect. 4.3). Results are shown in Fig. 5 concerning the maximal rainfall in 24 h (PM24) and for T 0 = 100 years.

Fig. 5
figure 5

Changes in frequency of the maximal rainfall in 24 h between the stationary hypothesis (reference) and non stationary hypothesis (in 2003) for the local approach (a) and the regional one (b)

Full size image

5 Discussion

In this paper, two new approaches are proposed: a regional trend test and an application of a rainfall stochastic generator in the context of a climate change detected from the generator parameters.

Unlike classical regional approach, several regional time series has been built to be independent (but not mutually) and identically distributed. The methodology POT and the ML test have been applied to test the parameters’ stationarity. This trend test can be performed for trend detection in extreme precipitation series. In this case, a threshold (of the GPD distribution) must be better estimated in each considered zone because it is important for the shape parameter estimation. Then the hypothesis of shape parameter stationarity can underestimate changes in the extreme values.

Due to the poor geographical distribution of stations, the results of the regional trend test cannot be generalized to a whole Zone. For example, it may be questionable to deduce from the 20 % increase of the number of events for the sampled stations into the “Oceanic” Zone (see Table 5) that such an increase applies everywhere in this Zone.

The application of the rainfall stochastic generator allowed us to work with average parameters what are less influenced by the shape parameter. However a strong hypothesis was assumed: the rainfall process does not change in time, which means the rainfall signal is always characterized in the same way by the 3 × 2 daily parameters with the passing years. This hypothesis seems to be correct because the current version of the hourly rainfall model is single-structured for all climates, as the relevance of its parameterization allows it to be used without modifying its structure, whatever the climate and over a very broad rainfall range.

Therefore only the parameter values, and not the model structure, allows us to estimate quantiles under different climates, from temperate to tropical (Arnaud et al. 2007). A possible evolution of the climate is taken into account by estimating parameters with the passing years.

6 Conclusion and perspectives

The impacts of climate change on extreme rainfall were studied with a rainfall generator, parameterized by 3 × 2 average parameters. Significant trend research for these parameters allowed us to take into account climatic evolution in order to estimate rainfall quantiles. The fundamental point of this method is that an extremal behavior can be inferred from estimated average values, not extreme ones. Such an approach is more robust to the sampling fluctuations. It is as much important as it is often used afterwards in rainfall-runoff modelling.

The trend was studied, in a local but also in a regional approach, by constructing 4 homogeneous climatic zones linked to the generator parameters. The regional approach seems better to illustrate a real change and to be less subjected to statistical fluctuations. The observed changes occur mainly in winter, from December to May, with an increase of rainfall event occurrence in France. In France, heavy precipitations are likely to be more and more frequent except in the Mediterranean region. Nevertheless, taking into account the climate change lead to small changes in estimating rainfall quantiles.

In this paper, the time evolution of the average parameters was detected from a trend test using data coming from Météo-France. A forthcoming study will enable us to work with global climate models (GCMs), which can generate some climatic variables, such as the daily precipitation, according to scenarios of greenhouse gases and aerosol anthropogenic emissions. So, from these simulations, the parameters of the rainfall generator can easily be estimated over different periods, and then the probable impacts of climate change on extreme rainfall events can be evaluated according to these scenarios.