Hydraulic Diffusivity of a Partially Open Rough Fracture

Abstract

We investigate the impact of closing a fracture with rough surfaces on the fracture hydraulic diffusivity, which controls the spatiotemporal evolution of pore-pressure perturbations in geological formations, particularly those composed of an impermeable matrix and highly permeable natural fractures. We build distributions of synthetic fracture apertures at a reservoir scale ($\sim$ 500 m) from a self-affine model with isotropic Hurst exponents derived from field observations of fault surfaces. To quantify the hydraulic diffusivity of rough fractures, we conduct finite element simulations of transient fluid flow in a single fracture. We use a surface representation of the fracture aperture following the Reynolds lubrication approximation. We verify that our approximation is valid for a steady-state flow and a low Reynolds number (Re $\ll$1) from the comparison with a volume-represented fracture aperture model solved by the Navier–Stokes equations for incompressible fluids (INS). Subsequently, the effective hydraulic diffusivity of the rough fracture is estimated by fitting the computed pressure field with the solution of an equivalent parallel plate model. The results show that the long-range correlation aperture field (up to the fault scale) due to self-affinity significantly affects hydraulic pressure diffusion, which is manifested as a strong variability in the pressure distribution with the orientation of the imposed pressure drop. Based on a rigid-plastic rheology, when closing the fracture stepwise from the initial contact to the flow percolation threshold, a decrease in the hydraulic diffusivity over seven orders of magnitude in one direction along the fracture but over four orders of magnitude in the perpendicular direction is obtained. Our results have strong implications for the interpretation of some measured hydraulic diffusivity data as well as for the use of hydraulic diffusivity in interpreting the spatial distribution of fluid-induced seismic events in faulted reservoirs.

1 Introduction

Fluid injection into deep boreholes is often accompanied by a cluster of microseismic events (Ellsworth 2013; Shapiro 2015; Cornet 2016; Orlecka-Sikora et al. 2020; Cauchie et al. 2020). Pore pressure diffusion through poroelastic rock is thought to be one of the primary mechanisms of fluid injection-induced seismicity since the increase in fluid pressure reduces the effective normal stress on pre-existing interfaces/faults and brings the optimally oriented interfaces/faults close to rupture (Rice 1992; Shapiro et al. 1999; Parotidis et al. 2004; Barth et al. 2013; Blöcher et al. 2018). The temporal and spatial evolution of the induced microseismic events is then controlled by the hydraulic diffusivity of the rock-fracture system in the context of poroelasticity (Shapiro et al. 1997; Jin and Zoback 2017; Segall and Lu 2015). The pore pressure is governed by a diffusion equation that contains the hydraulic diffusivity as the central parameter. Indeed, the linear pressure diffusion relates temporal and spatial derivatives of fluid pressure p with the proportionality factor hydraulic diffusivity D, defined as (Jaeger et al. 2009; Wang 2000; Rozhko 2010):

$$\begin{aligned} \frac{\partial p}{\partial t}=D\nabla ^2p. \end{aligned}$$

(1)

The hydraulic diffusivity delineates how the fluid pressure diffuses in the porous medium (Rice and Cleary 1976) and is an indicator of flow and transport connectivity (Knudby and Carrera 2006). Indeed, it corresponds to the ratio of transport (permeability) and storage (specific storage capacity) properties that in turn depend on rock (geometrical characteristics of conduits, deformation characteristics) and fluid (viscosity, compressibility) properties. Assuming that the Biot coefficient is 1, the hydraulic diffusivity is defined for fractured rock at a macroscopic scale as (Rempe et al. 2020; Renner and Steeb 2015):

$$\begin{aligned} D=\frac{k_m}{\mu (\phi c_f + c_{pp})}, \end{aligned}$$

(2)

where $k_m$ is the effective matrix permeability, $\mu$ is the dynamic viscosity of the fluid, $\phi$ is the porosity, and $c_f$ and $c_{pp}$ are the fluid compressibility and the pore space compressibility, respectively.

Direct measurement of hydraulic diffusivity can be conducted in field tests (Renner and Messar 2006; Talwani and Acree 1985; Doan et al. 2006; Xue et al. 2013) and laboratory experiments, such as via the pressure oscillation method (Song and Renner 2007; Kranz et al. 1990) and the pulse-decay test (Brace et al. 1968; Hsieh et al. 1981; Wang 2000; Nicolas et al. 2020). In hydrogeology, Eq. (2) is commonly used to estimate the effective permeability of a reservoir when the hydraulic diffusivity is determined from hydraulic tests. This may work well when the rock matrix is highly permeable. In the case where fractures dominate the fluid flow, it would be better to consider the contribution of fractures separately (Ortiz R et al. 2013). This is evident by different observed values of hydraulic diffusivity. For example, the hydraulic diffusivity of an intact rock sample is typically smaller than the hydraulic diffusivity derived from field tests where fractures exist, e.g., the values of sandstone range between $10^{-6}$ and $10^{-5}$ m$^2$/s in laboratory measurements Song and Renner (2007), compared with between $10^{-1}$ and $10^{0}$ m$^2$/s in a field test (Renner and Messar 2006).

Our interest here lies in the response of the fracture geometry to the linear fluid pressure diffusion (Eq. 1) when a single fracture acts as the preferential flow pathway. The linear diffusion equation can be derived from the conservation of mass in the fracture, but it requires that the pressure changes inside the fracture be sufficiently small so that the fracture deformation can be ignored, i.e., the fracture aperture remains reasonably constant (Murphy et al. 2004). This assumption is also made in other numerical modeling strategies (Ortiz R et al. 2013; Vinci et al. 2015). Previous studies also show that a small pressure disturbance (< 0.1 MPa) is able to trigger seismicity (Keranen et al. 2014; Dempsey and Riffault 2019; Goebel et al. 2017), particularly for stress-critical faults and during a post-induced seismicity or aftershock stage (Schmittbuhl et al. 2021; Noir et al. 1997; Nur and Booker 1972). It is also relevant for some EGS reservoirs or fractured media where the fluid pressure is close to hydrostatic conditions (drained conditions) and the fluid volume is connected over a long distance to the surface such that the fluid pressure is significantly lower than the solid counterpart (trace of the stress tensor). In the framework of linear pressure diffusion, the fracture hydraulic diffusivity can be approximated as (Murphy et al. 2004)follows:

$$\begin{aligned} D_f=\frac{h^2}{12\mu (c_f+h^{-1}c_j)}, \end{aligned}$$

(3)

where h is the fracture aperture and $c_j$ is the fracture compressibility.

Eq. (3) is suitable for a parallel plate fracture where the permeability is calculated by the cubic law. For real rough fractures/faults, the deviation from the cubic law may be considerable (Zimmerman and Bodvarsson 1996; Almakari et al. 2019; Ji et al. 2020). More specifically, compared to a single parallel plate fracture with an identical mean aperture, roughness can either enhance or inhibit fluid flow (Méheust and Schmittbuhl 2000; Schmittbuhl et al. 2008; Guo et al. 2016). Moreover, the permeability of a self-affine fracture shows a certain degree of anisotropy when the orientation of the imposed pressure drop is changed (Méheust and Schmittbuhl 2003).

To numerically compute the permeability of a rough or partially open fracture, the common approach is to apply Darcy’s law under laminar flow conditions, although it should only be considered as a qualitative measurement (Blöcher et al. 2019). This method leads to replacement of the fracture aperture h by the hydraulic aperture $d_h$ in Eq. (3). The hydraulic aperture of a rough fracture is then classically introduced as an effective measure of the hydraulic performance using the directional total flux and pressure difference (Zimmerman and Bodvarsson 1996; Méheust and Schmittbuhl 2001; Murphy et al. 2004; Neuville et al. 2010) and is, therefore, different from the geometrical fracture aperture, i.e., the mean aperture. Once the permeability is known, it is possible to estimate the diffusivity from Eq. (3). However, this estimation may seem somehow rough for a partially open rough fracture since the permeability calculation may not precisely describe the pressure propagation, i.e., the temporal and spatial pressure evolution.

In this work, we propose a new approach to determine the fracture hydraulic diffusivity. Instead of exploring the relationship between the diffusivity and those intrinsic hydraulic parameters, here, we focus on a direct quantification of the spatiotemporal evolution of the pressure inside the fracture. First, by solving the linear diffusion equation for a rough fracture with given initial and boundary conditions, we obtain the pressure profiles as a function of time and space. The pressure profiles are then compared to those derived from an analytical solution in which hydraulic diffusivity serves as an unknown. Next, we use the least square regression to search for a diffusivity that best matches the two pressure profiles. This diffusivity can then be seen as an effective hydraulic diffusivity of a rough fracture. Finally, we compare our results with the hydraulic diffusivity values obtained from Eq. (3).

Based on the proposed approach, the main objective of this study was to quantify the impact of fracture roughness and fracture closure on hydraulic diffusivity.

We use a rigid deformation to mimic fracture closure by interpenetrating the two fracture halves stepwise into each other. By interpenetrating the two fracture halves, we generate a partial overlap of the two volumes. During laboratory experiments (Kluge et al., under review), brittle deformation in these contact/overlap areas producing fines was observed. This plastic deformation is mimicked by removing the overlapping volume and setting the aperture to zero. Therefore, we call the simulated fracture closure process a ‘rigid-plastic’ deformation.

In the simulation, we close the fracture in a stepwise manner, forming different contact areas, and we compute the effective hydraulic diffusivity at each step. This paper is organized as follows: In Sect. 2, the generation of a self-affine fracture aperture distribution based on field observations is introduced. In Sect. 3, the mathematical formulation for fluid flow through a single fracture is given for the two cases of interest for this study, that is, fluid flow at low Reynolds numbers under either steady state or transient conditions. This is followed by Sect. 4, where the modeling results and the analysis of the influence of roughness and fracture closure on the effective hydraulic diffusivity are presented. In Sect. 5, the anisotropy of the effective hydraulic diffusivity is further discussed, and the results are compared to those available in the literature. The paper ends with a brief conclusion in Sect. 6. In addition, appendices regarding the fluid velocity calculation and the effective hydraulic diffusivity estimation in detail are provided at the end of the paper. A brief workflow of the numerical procedure is given in Fig. 1.

Fig. 1

Sketch of the whole simulation scheme: fracture surface/aperture generation; fracture closure; use of the Navier–Stokes equations for steady-state flow through a volume-represented fracture and the pressure diffusion equation for transient flow along a surface-represented fracture; and determination of the effective hydraulic diffusivity

2 Fracture Aperture Generation

In our modeling, the aperture field of a partially open fracture between two opposite rough surfaces is built in four steps: (1) generate a single fracture surface from a self-affine surface generator; (2) build a self-affine aperture by mirroring the generated surface; (3) stepwise close the fracture based on an imposed normal displacement field and by assuming a perfectly rigid plastic rheology of the asperities; and (4) finite element (FE) mesh the fracture of the generated geometries.

2.1 Step 1: Generation of a Self-affine Fracture Surface

It has been shown that fresh surfaces of lab-scale samples can be well described by self-affinity (Schmittbuhl et al. 1993; Zimmerman et al. 2004; Neuville et al. 2012). Furthermore, scanning measurements of the surface roughness of a set of faults (Fig. 2) also reveal self-affine behavior over nine decades of length scales (i.e., from 50 µm to 50 km) (Renard et al. 2006; Candela et al. 2009, 2012). The data gap in Fig. 2 can be supplemented by the surface roughness measurement of the fault from the Gole Larghe Fault Zone in the range of 0.5 mm–500 m (Bistacchi et al. 2011). The roughness of a two-dimensional (2D) self-affine profile is statistically invariant under the following scaling transformation (Schmittbuhl et al. 1995a):

$$\begin{aligned} \left\{ \begin{array}{lr} \varDelta x \rightarrow \lambda \varDelta x \\ \varDelta z \rightarrow \lambda ^H\varDelta z \end{array}, \right. \end{aligned}$$

(4)

where $\varDelta x$ is the coordinate along the profile, $\varDelta z$ is the vertical direction amplitude, $\lambda$ is a positive dilation factor, and $H\ (0< H < 1)$ is called the self-affine exponent or Hurst exponent, which describes the scaling invariance.

At scales ranging from 50 µm to 10 m, when surfaces in contact experience significant slip, they exhibit anisotropy with the Hurst exponent $H_{\parallel }\sim 0.6$ in the slip direction and $H_{\perp }\sim 0.8$ perpendicular to it (Candela et al. 2009, 2012). For rupture traces on scales of 200 m to 50 km, the self-affinity is isotropic and consistent with the slip-perpendicular behavior of the smaller-scale measurements (i.e., $H\sim 0.8$) (Candela et al. 2012).

To characterize the roughness of the self-affine surface from topographic measurements, the Fourier power spectrum P(k) (i.e., the square of the modulus of the Fourier transform) is introduced as a function of the wavenumber k (Schmittbuhl et al. 1995b; Zimmerman et al. 2004; Candela et al. 2009). The power spectrum and the wavenumber show a linear trend in a log–log plot (Fig. 2) as follows:

$$\begin{aligned} P(k)=Ck^{-1-2H}, \end{aligned}$$

(5)

where C represents the intercept of the power law line, the so-called ‘prefactor’ of the power spectrum (Candela et al. 2012), determining the roughness amplitude $\sigma$ at a given scale, i.e., root mean square (RMS) average. The Hurst exponent H is then directly linked to the power-law slope.

Fig. 2

Log–log graph of Fourier power spectra P(k) as a function of the wavenumber k for our synthetic self-affine surface (large blue dots) and for a group of natural fault surfaces (small dots) from (Candela et al. 2012). The synthetic self-affine surface is generated with $H=0.8$ and $\sigma =0.1$ m at the 512 m scale to match field observations (Color figure online)

To generate a 2D self-affine surface, a Gaussian random field is first created. This random field combined with the roughness exponent is then applied via Fourier transform, introducing spatial correlation. Next, by using inverse Fourier transform, the distribution of the surface can be finally obtained (Candela et al. 2009). The roughness amplitude $\sigma$ is introduced in order to adjust the roughness in the z-direction by normalizing the heights of the discrete points on the 2D grid to obtain a prescribed RMS of the whole height.

As an example, a synthetic self-affine surface is generated with an isotropic roughness exponent $H_{\parallel }=H_{\perp }=0.8$ at the 512 m scale and $\sigma =0.1$ m. The scaling of the power spectral density of our synthetic fault surface (blue dots in Fig. 2) is consistent with that of a collection of major faults from field observations (Candela et al. 2012). The height probability follows a Gaussian distribution with the prescribed $\sigma$ (Fig. 3). The largest height fluctuations are on the order of $3\sigma \approx \pm$0.3 m for a lateral extension of 512 m.

Fig. 3

Histogram of the height distribution of our generated isotropic self-affine surface at the 512 m scale, with Hurst exponent $H=0.8$ and roughness amplitude $\sigma =0.1$ m, consistent with the field observations of (Candela et al. , 2012) (see blue circles in Fig. 1). The largest height fluctuations are on the order of $3\sigma \approx \pm 0.3m$ for a lateral extension of 512 m (Color figure online)

2.2 Step 2: Generation of a Self-affine Aperture Distribution

The fracture aperture is defined by the space between the two facing surfaces, perpendicular to the nominal fracture plane (Zimmerman and Bodvarsson 1996; Méheust and Schmittbuhl 2003; Neuville et al. 2010; Marchand et al. 2020). If the fracture is modeled by two parallel plates, then the aperture is constant. However, for real rock fractures with rough walls, the aperture varies in space, resulting in an aperture distribution h(x, y) (Brown 1987; Méheust and Schmittbuhl 2001). To obtain h(x, y), we first reproduce the generated self-affine surface from the previous section and flip it vertically (along z). We then place the two surfaces such that they face each other with a separation of $d_m$. Because the two facing surfaces are unmated and self-affine, the resulting aperture field h(x, y) is also self-affine and shares the same Hurst exponent (Neuville et al. 2010). Consequently, the aperture distribution h(x, y) can be alternatively generated as a single self-affine object z(x, y) plus the average aperture $d_m$. Accordingly, the upper and lower boundaries of the aperture field can be written as follows:

$$\begin{aligned} s_1(x,y)= & {} +\frac{z(x,y)+d_m}{2}, \end{aligned}$$

(6)

$$\begin{aligned} s_2(x,y)= & {} -\frac{z(x,y)+d_m}{2}, \end{aligned}$$

(7)

where the Fourier power spectra of $s_1(x,y)$ and $s_2(x,y)$ should correspond to Fig. 2. Figure 4a shows a sketch (i.e., vertical exaggeration) of a 2D cross-section of the self-affine aperture model h(x, y) from two unmated symmetrical surfaces $s_1(x,y)$ and $s_2(x,y)$ when $d_m$ is larger than the maximum height. In this case, it is a fully open fracture where the two surfaces are completely separated.

Fig. 4

2D cross-section along the (x, z)-plane and (y, z)-plane (with a vertical magnification 500 times on the z-axis scale with respect to the x, y-axis) of the self-affine fracture aperture h(x, y) at two steps of the fracture closing. a Fully open fracture without contact. $z=z_1$ and $z=z_2$ represent the mean plane of the top surface $s_1(x,y)$ and the bottom surface $s_2(x,y)$, respectively. $d_m=z_1-z_2$ denotes the mean aperture. b Partial open fracture after the contact of some asperities. The shaded area indicates contact regions where the apertures are set to zero; $d_m$ here denotes the mean separation of the open area (light blue zones)

2.3 Step 3: Fracture Closure

When a normal displacement is imposed on the fracture, i.e., to close the fracture along its normal direction, there are regions where the two opposing faces of the fracture wall virtually overlap each other (Fig. 4b). These regions are called contact areas and commonly exist in real rock fractures (Zimmerman and Bodvarsson 1996). In this case, the mean aperture $d_m$ computed over the whole surface assuming a zero aperture at the contact areas will be smaller than the mean aperture of the open areas occupied by the fluid. In this study, since we consider both fractures with and without contact, we hereinafter refer to $d_m$ as the mean aperture of the open area in both cases. For the aperture of overlapping asperities, we set it to zero assuming that the solid part is perfectly plastic. The plastic limit is defined as the strength of the material over which the material will be eroded because of the plastic flow outside of the contact areas with no local conservation of the volume. This is effectively different from an elasto-plastic model. If the stress concentration on asperities is very high, this approximation is relevant. This contact model is based on the interpenetration approach, which is simple but fast and effective (Brown 1987; Méheust and Schmittbuhl 2003; Pei et al. 2005; Watanabe et al. 2008; Liu et al. 2013; Kling et al. 2018).

2.4 Step 4: Finite Element Meshing

The three-dimensional (3D) fracture aperture distribution h(x, y) is a spatial function of the x and y coordinates along the mean plane of the fracture. However, when it is applied to the flow simulation, the requirement of fine isotropic meshes in the 3D volume may lead to difficulties, especially when the scale discrepancy between the aperture (along z) and the fracture size (along x and y) is large. For instance, if we assume that the fracture fluctuations are on the order of $\sigma$ and the length is L, then the aspect ratio of the fracture is $\sigma /L$. If the surface is self-affine, then $\sigma \sim L^H$. Consequently, the aspect ratio can scale as $L^{H-1}$. If $H<1$ and L becomes very large, then the aspect ratio goes to zero (Schmittbuhl et al. 2008). In this case, the 3D isotropic mesh requires very fine elements due to the small scale in the z-direction, leading to a large number of elements for large fractures. However, this fine meshing is unnecessary along the x-axis and y-axis since aperture variations along x and y are on a larger length scale. Accordingly, anisotropic elements for a 3D volume are required. Therefore, we use prism elements with a mean aspect ratio of 1:25 for the volume representation. To reduce the numerical cost for large-scale reservoir simulation, we can approximate the volumetric representation of the 3D fracture by a 2D surface representation, as shown in Fig. 5. A validation of this 3D to 2D approximation is discussed later in the paper. For a 2D surface representation, we make use of quadrilateral mesh elements. In both cases, the meshing stage is done by relying on the open source software Gmsh (Geuzaine and Remacle 2009).

Fig. 5

Schematic diagram of the two representations of a rough fracture with $L=~$64 m. a Volume-represented fracture with 52,128 prism elements (8 layers along z); b surface-represented fracture with 4096 quadrilateral elements. Both representations share the same mesh size of 1 m $\times$ 1 m along x and y

3 Governing Equations for Fluid Flow Through Open Fractures

Fluid flow through a partially open rough fracture is described by the (in)compressible Navier–Stoke equation. Under certain conditions described below, the Navier–Stoke equation can be simplified (Fig. 1) into the Reynolds equation for steady flow through a 3D fracture (Fig. 5a) or into a pressure-diffusion equation for transient flow conditions along a 2D fracture (Fig. 5b). Both forms of equations are implemented in the open source GOLEM/MOOSE simulation environment (Cacace and Jacquey 2017). The use of the two forms of governing equations in this work is shown in Fig. 1.

3.1 From the Navier–Stokes Equation to the Reynolds Equation

The fluid flow of an incompressible Newtonian fluid is governed by the Navier–Stokes equation, which expresses momentum and mass conservation over the fracture void space as follows (Zimmerman and Bodvarsson 1996; Guyon et al. 2001):

$$\begin{aligned}&\frac{\partial {\varvec{u}}}{\partial t}+({\varvec{u}}\cdot \nabla ){\varvec{u}}=-\frac{1}{\rho }\nabla p+\frac{\mu }{\rho }\nabla ^2{\varvec{u}}, \end{aligned}$$

(8)

$$\begin{aligned}&\nabla \cdot {\varvec{u}}=0, \end{aligned}$$

(9)

where ${\varvec{u}}$ is the fluid velocity vector, p denotes the fluid pressure, and $\rho$ and $\mu$ are the fluid density and dynamic viscosity, respectively.

The inertial forces represented by the nonlinear term $({\varvec{u}}\cdot \nabla ){\varvec{u}}$ in Eq. (8) render these equations difficult to solve. This nonlinear inertial term can be neglected if the viscous forces dominate over the inertial forces, that is, for small Reynolds numbers, i.e., Re $\ll 1$ (Méheust and Schmittbuhl 2001). The Reynolds number is defined as the ratio of the inertial terms to the viscous terms as follows:

$$\begin{aligned} \text {Re} = \frac{\rho Ul_z^2}{\mu l_h}, \end{aligned}$$

(10)

where U is the magnitude of the horizontal average velocity and $l_z$ and $l_h$ are the scales of vertical and horizontal velocity variations, respectively.

Considering a steady fluid flow in the low Reynolds number regime, the N-S equation can be linearized as (Zimmerman and Bodvarsson 1996)follows:

$$\begin{aligned} \nabla p-\mu \nabla ^2{\varvec{u}}=0. \end{aligned}$$

(11)

For a rough fracture, assuming that the local aperture h(x, y) variations satisfy the lubrication approximation (i.e., $||\nabla h \ll 1||$), Eq. (11) can be recast in the form of the Reynolds equation as (Zimmerman and Yeo 2000)follows:

$$\begin{aligned} \nabla \cdot \left[ \frac{h(x,y)^3}{12\mu }\nabla p \right] =0. \end{aligned}$$

(12)

The Reynolds equation has been applied to solve fluid flow through rough-walled fractures by many authors (Brown 1987; Renshaw 1995; Brush and Thomson 2003; Marchand et al. 2020), with the local cubic law for computing the flux (Oron and Berkowitz 1998; Klimczak et al. 2010).

3.2 The Pressure Diffusion Equation

Assuming the validity of the lubrication approximation, a surface-represented fracture (Fig. 5b) can be parameterized in terms of an effective aperture. Within the fracture plane, the fluid pressure is governed by the following equation (Cacace and Jacquey 2017):

$$\begin{aligned} \frac{h}{K_f}\frac{\partial p}{\partial t} + \nabla \cdot (h{\varvec{q}}) = 0, \end{aligned}$$

(13)

where $K_f$ is the fluid bulk modulus. The fluid flow is computed by Darcy’s law in the local coordinate system as follows:

$$\begin{aligned} {\varvec{q}} = -\frac{\varvec{k_{frac}}}{\mu }\cdot \nabla {p}, \end{aligned}$$

(14)

where $\varvec{k_{frac}}$ denotes the fracture permeability tensor. Assuming the local cubic law is valid in the laminar flow within the fracture plane, the isotropic permeability in the local coordinate system can be identified as follows:

$$\begin{aligned} \varvec{k_{frac}}=\frac{h^2}{12}{\varvec{I}}, \end{aligned}$$

(15)

where ${\varvec{I}}$ is the unit tensor.

3.3 Finite Element Modeling using the MOOSE/GOLEM Framework

Using the finite element method, the GOLEM simulator is developed based on a flexible, object-oriented framework (MOOSE, Multiphysics Object Oriented Simulation Environment) for modeling-coupled thermal-hydraulic-mechanical (THM) processes in fractured and faulted geothermal reservoirs. In a first step, we test the ability of the numerical approach to numerically approximate transient flow through an open rough fracture by solving the relevant equations describing (1) steady flow through an open rough fracture (Sect. 3.3.1) and (2) transient flow between two parallel plates (Sect. 3.3.2).

3.3.1 Steady Flow Through a Rough Fracture—a Validation of the Volume Representation vs. Surface Representation

The incompressible Navier–Stokes equations are applied to solve for the dynamic pressure and the velocity field inside the fracture opening. These equations correspond exactly to the Navier–Stokes equations in ‘Laplace’ form in the INS Module of MOOSE (Peterson et al. 2018). A stabilized Petrov–Galerkin finite element method is used to solve these equations with appropriate initial and boundary conditions.

For a self-affine fracture aperture model with Hurst exponent H, the Reynolds lubrication approximation is (Méheust and Schmittbuhl 2001):

$$\begin{aligned} l_c\gg \left[ \frac{\varDelta h(L)}{L^H}\right] ^{\frac{1}{1-H}}, \end{aligned}$$

(16)

where $l_c$ denotes the lower bound of self-affine scaling and $\varDelta h(L)$ is the maximum distance between the rough walls at a scale L.

In this study, we consider a uniform mesh size of 1 m. When using $l_c=1$ m and $H=0.8$, for fracture length $L=64$ m, the maximum $\varDelta h(L)$ is $\approx 0.15$ m, and we have $l_c\gg 4.5\times 10^{-12}$ m. For $L=512$ m, $\varDelta h(L)\approx 0.6$ m, and we have $l_c\gg 1.13\times 10^{-12}$ m. Based on Eq. (16), we can conclude that our model satisfies the Reynolds lubrication approximation.

When the fluid flow reaches the steady state, the fluid pressure governing equation of the surface-represented fracture is equivalent to the Reynolds equation (Eq. 12). To test the degree of validity of this approximation, for our transient flow model, we take the following steps: First, a self-affine fracture surface is synthetically generated at an intermediate scale of 64 m with isotropic Hurst exponent $H=0.8$ and roughness amplitude $\sigma =0.025$ m. A set of apertures is then created with the ratio of the mean aperture to the roughness amplitude $d_m/\sigma$ in the range of 1 to 15. Among them, the fracture remains fully open when the ratio is greater than or equal to 3, whereas fracture-wall contact occurs when $d_m/\sigma <3$. The ratio $d_m/\sigma =1$ corresponds to $\sim 20\%$ of the contact area. Next, we build the volume-represented and surface-represented fractures for each aperture distribution, along with one of their finite element meshes, which are shown in Fig. 5a, b, respectively. Finally, fluid flow simulations are conducted for both the surface and volume representations of the fracture. A pressure difference $\varDelta p=10^{-8}$ Pa between the two ends of the model along either the x-axis or the y-axis is set as the boundary conditions (i.e., $10^{-8}$ Pa and 0 Pa pressure for the inlet and outlet boundaries, respectively; see Fig. 6).

Fig. 6

Schematic of the initial conditions and boundary conditions applied in the x- and y-directions for each rough fracture. a Flow along the x-axis; b flow along the y-axis. The inlet and outlet boundaries are marked as red and blue, respectively (Color figure online)

To compare the results of the two types of simulations, we introduce the following definition of the hydraulic aperture $d_h$:

$$\begin{aligned} d_h = \left( \frac{12\dot{V}\mu }{|\varDelta p|}\right) ^{1/3}. \end{aligned}$$

(17)

The total volume flux $\dot{V}$ along the flow of the rough fracture is obtained from the mean of the local flux q(x, y). Considering that the pressure drop is along the x-direction, q(x, y) is then the product of the velocity profile $v_x$ and the local aperture h(x, y).

For the volume-represented fracture case, the velocity has a z component such that $v_x=\overline{v_x}(x,y,z)$. Since the local cubic law is assumed to be valid, the velocity locally follows a parabolic shape along the z-direction, as in the parallel plate model. The estimation of $\overline{v_x}(x,y,z)$ is given in Appendix A. For the surface-represented fracture case, we have $v_x=v_x(x,y)$, which can be directly obtained from the velocity profile.

Figure 7 shows the comparison of the fluid flow between volume-represented fractures and surface-represented fractures for steady-state flow. The results are given in terms of the ratio of the hydraulic aperture $d_h$ to the mean aperture $d_m$ as a function of the $\sigma$-normalized mean aperture. As the roughness increases, a more significant deviation from the parallel plate flow is observed. The same simulations performed in the y-direction indicate anisotropy of the fracture flow. The good consistency between the two kinds of flow illustrates the effectiveness of using 2D surface elements to approximate 3D volumetric elements in fluid flow simulations at low Reynolds numbers (Re $\ll$ 1).

Fig. 7

Comparison of the fluid flow between volume- and surface-represented rough fractures. The aperture evolution is given by the ratio of the hydraulic aperture $d_h$ to the mean aperture $d_m$ as a function of the $\sigma$-normalized mean aperture $d_m/\sigma$. The horizontal dashed line denotes the parallel plate model in which $d_h/d_m=1$, while the solid vertical line indicates the divide where the fracture fully opens (right part) and comes into contact (left part)

3.3.2 Transient Flow in a Parallel Plate Configuration—a Reference Model

In this section, we check the transient flow in a parallel plate model with an analytical solution. Consider an instantaneous increase in the pressure difference along the x-axis from 0 to L. The initial pore pressure $p_0$ is given at $t = 0$. During the whole diffusive process, a fixed pressure $p_1$ is applied at $x = 0$, whereas at the end of the plate $(x = L)$, the pressure is maintained constant as per its initial value ($p_0$):

$$\begin{aligned} \begin{aligned} p&= p_0\quad at\quad t=0\ for\ 0\le x \le L \\ p&= p_1\quad at\quad x=0\ for\ t>0 \\ p&= p_0\quad at\quad x=L\ for\ t>0 \end{aligned}. \end{aligned}$$

(18)

Based on Eq. (18), the 1D solution of the linear diffusion equation Eq. (1) is given by (Turcotte and Schubert 2002; Carlsaw and Jaeger 1959):

$$\begin{aligned} p(x,t)= & {} p_1+(p_0-p_1)\left[ \frac{x}{L}\right. \nonumber \\&\left. +\frac{2}{\pi }\sum _{n=1}^{\infty }\frac{1}{n}exp\left( -\frac{Dn^2\pi ^2t}{L^2} \right) sin\left( \frac{n\pi x}{L}\right) \right] . \end{aligned}$$

(19)

A characteristic time $t^*$ is defined as follows:

$$\begin{aligned} t^*=L^2/D. \end{aligned}$$

(20)

When $t\gg t^*$, the pressure reaches an equilibrium linear profile, and the solution becomes

$$\begin{aligned} p = p_1+(p_0-p_1)\frac{x}{L}. \end{aligned}$$

(21)

A simulation is performed on the parallel plate fracture with dimensions of $L\times L$ (512 m $\times$ 512 m) and an aperture of 0.1 m. The inlet pressure $p_1$ and outlet pressure $p_0$ are set to $10^{-5}$ Pa and 0 Pa along the x-axis, respectively. This small pressure gradient is chosen to separate the effect of fracture deformation on diffusivity. Therefore, a direct relation of the effects of fracture roughness and stepwise fracture closure on diffusivity can be obtained. Regarding the fluid properties, the fluid modulus and the fluid dynamic viscosity are 2.2 GPa and 0.001 Pa$\cdot$s, respectively. In this case, fracture apertures are represented as a surface and modeled by single-node interfacial elements (Jacquey et al. 2017).

On the basis of the settings in the last paragraph, we obtain the fracture hydraulic diffusivity $D_f=1.833\times 10^9$ m$^2$/s (Eq. 13) and the corresponding characteristic time $t^*=1.43\times 10^{-4}$ s (Eq. 20). We then substitute $D_f=1.833\times 10^9$ m$^2$/s and $L=$ 512 m into Eq. (19) to obtain the pressure distribution $p_a(x,t)$. On the other hand, the numerically computed pressure distribution along the parallel plate fracture is $p_{\parallel }(x,y,t)$, which is then averaged along the y-axis as $<p_{\parallel }(x,t)>_y$. We then plot both $p_a(x,t)$ and $<p_{\parallel }(x,t)>_y$ at $t_1= 5\times 10^{-6}$ s, $t_2= 1.5\times 10^{-5}$ s and $t_3= 4.5\times 10^{-5}$ s in Fig. 8. The consistency between $p_a(x,t)$ and $<p_{\parallel }(x,t)>_y$ illustrates that the numerical result $p_a(x,t)$ can be seen as the analytical solution for the parallel plate model averaged along one direction, providing a reference for the rough fracture study.

Fig. 8

Comparison between the simulation results for the parallel plate model (red squares) and analytical solutions (solid lines) of pressure diffusion at $t_1= 5\times 10^{-6}$ s, $t_2= 1.5\times 10^{-5}$ s and $t_3= 4.5\times 10^{-5}$ s (Color figure online)

4 Results

Based on the results described in the previous paragraph, we hereafter consider only a 2D surface representation of the rough fracture to quantify the effective hydraulic diffusivity (and its variations) under transient flow conditions.

4.1 Temporal and Spatial Evolution of the Pressure in a Large-scale Fracture

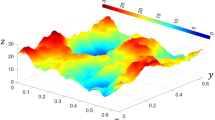
The self-affine aperture distributions are generated with $L=$ 512 m, isotropic $H=0.8$ and $\sigma =0.1$ m. When the mean aperture $d_m$ varies, the fracture remains fully or partially open. As an example, Fig. 9 illustrates the aperture map for $d_m=0.3$ m, i.e., $d_m/\sigma =3$, corresponding to a totally open fracture but close to contact of the asperities on the opposite fracture walls. Given this size and the mean aperture of the fracture, the characteristic time of the equivalent parallel plate model is $t^*=1.5\times 10^{-5}$ s (Eq. 20).

Fig. 9

Map of the aperture distribution with $H=0.8$, $\sigma =0.1$ m and $d_m=0.3$ m at the 512 m scale. The fluid flows from left to right in the x-direction and from bottom to top in the y-direction

For transient fluid flow simulations, all parameters used, initial conditions and boundary conditions are consistent with Sect. 3.3.2. The time step is set small enough to capture the transient pressure diffusion process (e.g., $1\times 10^{-7}$ s in the case of Fig. 9). To investigate the anisotropy, simulations are performed in either the x- or y-direction.

The pressure distributions and the fluid flux distributions of the rough fracture with $d_m=0.3$ m at $t_1=5\times 10^{-7}$ s, $t_2=2\times 10^{-6}$ s and $t_3=5\times 10^{-6}$ s are presented in Figs. 10 and 11, respectively. For comparison, the pressure and flux distribution for a parallel plate model with the same $d_m$ aperture are also shown (Figs. 10 and 11a–c). As expected, the roughness causes deviations of the pressure diffusion from the parallel plate model. Visually, the pressure diffuses faster in the y-direction (Fig. 10g–i) than in the x-direction (Fig. 10d–f), where the pressure front is propagating significantly slower than that in the parallel plate configuration with the same mean aperture (Fig. 10a–c). As fluid flows along the fracture, it follows preferential pathways (i.e., channels) due to the impact of aperture variations (Fig. 11). Moreover, compared to the x-direction (Fig. 11d–f), a stronger channeling effect is observed in the y-direction (Fig. 11g–i).

Fig. 10

Schematic diagram of the pressure diffusion evolution in a rough fracture and the parallel plate model with the same size (512 m) and the same mean aperture (0.3 m) at $t_1=5\times 10^{-7}$ s, $t_2=2\times 10^{-6}$ s and $t_3=5\times 10^{-6}$ s. a–c Fluid flow along the x-axis for the parallel plate model; d–f fluid flow along the x-axis for the rough fracture; and g–i fluid flow along the y-axis for the rough fracture

Fig. 11

Schematic diagram of the local flux evolution in a rough fracture and the parallel plate model with the same size (512 m) and the same mean aperture (0.3 m) at $t_1=5\times 10^{-7}$ s, $t_2=2\times 10^{-6}$ s and $t_3=5\times 10^{-6}$ s. a–c Fluid flow along the x-axis for the parallel plate model; d–f fluid flow along the x-axis for the rough fracture; and g–i fluid flow along the y-axis for the rough fracture

4.2 Effective Hydraulic Diffusivity

To quantify the pressure diffusion along the rough fracture, an effective hydraulic diffusivity $D_e$ is obtained by fitting the pressure solution in time and space for the rough aperture by the parallel plate solution. The approach is similar to the assessment of the hydraulic aperture that is defined by fitting the effective hydraulic flux of a rough fracture by a parallel plate model. The procedure is as follows: The numerical pressure distribution $p_R(x,y,t)$ for the rough aperture is first averaged along the y-axis as $<p_R(x,t)>_y$. We then optimize the hydraulic diffusivity of a parallel plate model with a pressure distribution $<p_{\parallel }(x,t,D_f)>_y$ to match $<p_R(x,t)>_y$ in the least square error sense. Noting the consistency between $<p_{\parallel }(x,t,D_f)>_y$ and the analytical solution $<p_a(x,t,D_f)>$, we have the following:

$$\begin{aligned}<p_R(x, t, D_e)>_y = <p_{\parallel }(x,t,D_f)>_y=p_a(x,t,D_f). \end{aligned}$$

(22)

Details of the procedure are given in Appendix B.

Figures 12 and 13 illustrate how the effective diffusivity $D_e$ is different from the hydraulic diffusivity of the parallel plate model $D_m$, which has the same mean aperture $d_m$ as the rough fracture. The comparison between the parallel plate model and the rough fracture is shown in terms of the pressure distribution at $t_1=5\times 10^{-7}$ s, $t_2=2\times 10^{-6}$ s and $t_3=5\times 10^{-6}$ s and along the x- and y-axes. When they have the same mean aperture (Figs. 12a, 13a), the pressure diffusion of the rough fracture significantly deviates from that in the parallel plate model. In contrast, when they have the same hydraulic diffusivity (Figs. 12b, 13b), the pressure diffusion curves match well with some slight gaps at some positions, which demonstrates that the effective hydraulic diffusivity reflects the rate of the pressure diffusion along the rough fracture as a whole.

Fig. 12

Pressure diffusion along the x-axis (averaged along y) with $d_m/\sigma =3$ at $t_1=5\times 10^{-7}$ s, $t_2=2\times 10^{-6}$ s and $t_3=5\times 10^{-6}$ s. a Comparison between the rough fracture and the parallel plate model with the same $d_m=0.3$ m; b comparison between the rough fracture and the parallel plate model with the best fitting hydraulic diffusivity $D_e=0.423 D_m$

Fig. 13

Pressure diffusion along the y-axis (averaged along x) with $d_m/\sigma =3$ at $t_1=5\times 10^{-7}$ s, $t_2=2\times 10^{-6}$ s and $t_3=5\times 10^{-6}$ s. a Comparison between the rough fracture and the parallel plate model with the same $d_m=0.3$ m; b comparison between the rough fracture and the parallel plate model with the best fitting hydraulic diffusivity $D_e=1.691D_m$

4.3 Effect of Fracture Closure

In this section, we consider normal closure in the direction perpendicular to the mean plane of the fracture, which leads to fracture surfaces contacting each other. Closure is obtained by imposing a normal displacement stepwise along the whole open fracture surface. Under the perfect plastic assumption, owing to the self-affine property of the aperture, an increase in normal displacement leads to a decrease in the mean aperture, which follows a linear trend with the increase in the contact area when the closure becomes significant, as shown in Fig. 14a. The relationship between the hydraulic aperture $d_h$ and the mean aperture $d_m$ during closure is shown in Fig. 14b. When $d_m$ is relatively large (relatively small contact), there is a linear behavior between the two quantities: $d_m=0.863 d_h + 0.053$. Interestingly, the slope is not one, showing that the mean aperture $d_m$ is decreasing slower than the hydraulic aperture $d_h$. Additionally, there exists a residual mean aperture at zero hydraulic aperture, showing that immobile fluid is trapped at the percolation threshold. When approaching the percolation threshold, the decrease rate of $d_h$ is faster than that of $d_m$. This behavior is attributed to the strong increase in tortuosity and channeling of the flow as the contact area increases (Nolte et al. 1989; Unger and Mase 1993; Sahimi 2011).

Fig. 14

(left) Evolution of the contact area as a function of the normal closure and mean aperture $d_m$. (right) Evolution of the hydraulic aperture $d_h$ as a function of the mean aperture $d_m$

For the simulations, we set the pressure drop either along the x-axis or the y-axis. We increase the normal displacement step by step until the fracture aperture reaches the percolation threshold (i.e., loss of the hydraulic connection from the inlet to the outlet and zero fluid velocities) in the two directions. We calculate the hydraulic aperture $d_h$ and the effective hydraulic diffusivity $D_e$ for each stage.

The effective diffusivity $D_e$ is plotted as a function of the mean aperture $d_m$ in log–log space (Fig. 15). As a check, we plot the hydraulic diffusivity calculated by Eq. (3), which is suitable for the parallel plate model (i.e., $D_m$, dashed line in Fig. 15). It shows that the effective hydraulic diffusivity $D_e$ is close to the prediction from Eq. (3) only when the mean aperture is large (i.e., at a relatively low contact area). As $d_m$ decreases, the decrease in effective diffusivity is either faster or slower than that in the diffusivity of the equivalent parallel plate model according to the orientation of the imposed pressure drop.

Fig. 15

Log–log graph of the effective hydraulic diffusivity $D_e$ as a function of the hydraulic aperture $d_h$. The dotted line corresponds to the parallel plate model (Eq. 19)

In the x-direction, the effective diffusivity drops by seven orders of magnitude from $\sim 10^9$ m$^2$/s without contact to $\sim 10^2$ m$^2$/s when it is close to the percolation threshold ($\sim 66\%$). By contrast, we obtain a four orders of magnitude reduction in the y-direction, but with a lower percolation threshold ($\sim 31\%$). Figure 16 shows the pressure distribution as a function of contact area in the x-direction. An increase in contact area causes an increase in tortuosity and channeling of the flow field in the aperture distribution (Fig. 17). Consequently, a longer time is required to reach the steady state, resulting in a decrease in the hydraulic diffusivity. When the contact area exceeds $50\%$, there are still large diffusivities since large channels exist in the aperture distribution. When the contact area approaches the percolation threshold, these channels are drastically reduced, and the diffusivity shows more significant changes (only a small change in contact area can lead to a large decrease in diffusivity).

Fig. 16

Schematic diagram of the pressure diffusion evolution along the x-axis of the rough fracture with different contact areas. a–c $t_1=2\times 10^{-6}$ s, $t_2=4\times 10^{-6}$ s and $t_3=1\times 10^{-5}$ s with $5.43\%$ contact; d–f $t_1=2\times 10^{-4}$ s, $t_2=4\times 10^{-4}$ s and $t_3=0.001$ s with $33.31\%$ contact; and g–i $t_1=0.002$ s, $t_2=0.004$ s and $t_3=0.01$ s with $50.51\%$ contact

Fig. 17

Schematic diagram of the local flux evolution along the x-axis of the rough fracture with different contact areas. a–c $t_1=2\times 10^{-6}$ s, $t_2=4\times 10^{-6}$ s and $t_3=1\times 10^{-5}$ s with $5.43\%$ contact; d–f $t_1=2\times 10^{-4}$ s, $t_2=4\times 10^{-4}$ s and $t_3=0.001$ s with $33.31\%$ contact; and g–i $t_1=0.002$ s, $t_2=0.004$ s and $t_3=0.01$ s with $50.51\%$ contact

5 Discussion

5.1 Anisotropy of Hydraulic Diffusivity

When the mean aperture of our fracture is large enough such that the largest asperities are about to touch each other ($d_m=0.3$ m), the effective hydraulic diffusivity is $D_e=0.423D_m$ and $D_e=1.691D_m$ with the imposed pressure drop in the x-direction (Fig. 12) and in the y-direction (Fig. 13), respectively, which shows anisotropic behavior (Fig. 15). At very large apertures (i.e., $d_m/\sigma > 1$), the diffusivity reaches that of the equivalent parallel plate configuration, $D_e/D_m\rightarrow 1$, and the sensitivity to the direction of the pressure drop disappears (Fig. 18). Interestingly, when closing the fracture, the anisotropy, defined here as the ratio of the effective diffusivities for the pressure drop along the x- or y-direction, is maximum when $d_m/\sigma \approx 3$, which is approximately when the (few) asperity contacts start to develop. Closing the fracture further reduces the diffusivity in both directions. The decrease in diffusivity is more accentuated the closer the system is to the flow percolation threshold (Fig. 15). However, this decrease is different for the two pressure drop directions. At $d_m$ = 0.002 m, the difference between the y- and x-directions reaches two orders of magnitude (Fig. 15). In other words, the anisotropy increases when closing the fracture.

Fig. 18

Ratio of the effective hydraulic diffusivity and the parallel plate fracture diffusivity $D_e/D_m$ as a function of the $\sigma$-normalized mean aperture $d_m/\sigma$. The vertical black line corresponds to the first asperity contacts when closing the fracture at $d_m/\sigma \approx 3$

Anisotropy in the hydraulic behavior depends on the geometrical heterogeneity as well as on the self-affinity of the fracture surfaces/apertures (Méheust and Schmittbuhl 2000). The roughness exponent (self-affinity) introduces spatial correlations to the roughness amplitude and, therefore, to the aperture distribution. Such long-range correlations (up to the fracture scale) of self-affine apertures induce strong channeling of the flow (Neuville et al. 2011). Spatially correlated fractures tend to have only a few dominant flow paths compared to uncorrelated fractures (Pyrak-Nolte and Morris 2000). Although the aperture variation in x and y is statistically isotropic, the resulting aperture distribution is heterogeneous (Fig. 9). This leads to different flow channels along the x- and y-directions and is, therefore, responsible for the anisotropy of the fluid flow. As the fracture closes, the channeling effect becomes more prominent. Accordingly, the anisotropy becomes more noticeable (Fig. 15). The anisotropic flow behavior has been verified by lab experiments (Méheust and Schmittbuhl 2001) and numerical studies (Marchand et al. 2020), both targeting self-affine surfaces with an isotropic Hurst exponent $H=0.8$.

In our study, we observed that the decrease in the hydraulic diffusivity is enhanced along the y-direction and inhibited along the x-direction. This is specific to the chosen surface, i.e., choice of the seed used to generate a random number in the generator of the self-affine surface (Candela et al. 2009). In Fig. 19a, b, the behavior for two other choices of the seed while keeping the Hurst exponent $H=0.8$ and the RMS $\sigma =0.1$ m are shown. This illustrates the variability of the behavior within the same general trend: beginning of departure from the parallel plate model for $d_m/\sigma \approx 3$ and a strong drop in the diffusivity when approaching the percolation threshold. However, the specific sensitivity to the pressure drop orientation is different for the different orthogonal directions.

Fig. 19

Two examples of the evolution of the relative hydraulic diffusivity $D_e/D_m$ for two other aperture fields with the same Hurst exponent $H=0.8$ and the same RMS $\sigma =0.1$ m when changing the seed of the self-affine surface generator. a Diffusivity decreases while it is above the parallel plate model when the fault are fully open; b diffusivity decreases while it is below the parallel plate model when the fault are fully open

The anisotropy of the effective diffusivity has an important influence on the resulting pore pressure diffusion. Some authors found that isotropic diffusivity poorly describes pressure diffusion (seismicity migration) compared to anisotropic diffusivities. For instance, Noir et al. (1997) estimated an isotropic diffusivity of $1.2\times 10^4$ m$^2$/s, whereas the anisotropic hydraulic diffusivities were $D_{xx}\sim 3\times 10^4$ m$^2$/s, $D_{yy}\sim 3\times 10^3$ m$^2$/s and $D_{zz}\sim 3\times 10^3$ m$^2$/s during the 1989 Dobi earthquake sequence, showing that the fastest seismic migration was along the x-direction. Similarly, Antonioli et al. (2005) obtained an $\sim$90 m$^2$/s isotropic diffusivity, while the maximum value of the anisotropic diffusivity was 275 m$^2$/s from the 1997 Umbria–Marche seismic sequence. The maximum diffusivity direction coincides with the strike of the active faults. The author concluded that the large diffusivity is associated with high permeability rough fractures within the damage zone of the active fault system, which essentially supports this study. In turn, if the anisotropic fracture diffusivity can be predicted properly, then it is possible to determine the orientation of the preferential earthquake migration direction.

5.2 Comparison with Hydraulic Measurements and Implications

Our results under large closure (hydraulic diffusivities are on the order of $10^2$ m$^2$/s - $10^4$ m$^2$/s) are consistent with the values derived from the analysis of some earthquake sequences (Noir et al. 1997; Antonioli et al. 2005; Malagnini et al. 2012; Dempsey and Riffault 2019). These earthquakes were assumed to be triggered by the diffusion of pore pressure perturbations in a fractured medium, and the seismicity migration was then evidenced to be compatible with pore pressure relaxation. The hydraulic diffusivity estimated by Noir et al. (1997) for the 1989 Dobi earthquake sequence of Central Afar ranges between $10^3$ and $10^4$ m$^2$/s, which corresponds to a characteristic width (i.e., effective aperture) of 1 mm - 3 cm. The consistency with our results indicates that our model might be used to predict potential earthquake migration, particularly when a single fault path dominates the fluid flow. Compared to diffusivities estimated from direct hydraulic tests, the values obtained from our simulations are somewhat large. The discrepancy could be attributed to several aspects.

First, there is an issue regarding the representative elementary volume (REV) of the measurement. For example, in the laboratory, the tested target is typically an intact rock sample, where fluid flow is restricted by interconnected pores, resulting in small diffusivities generally ranging between $10^{-7}$ m$^2$/s and $10^{-2}$ m$^2$/s (Song and Renner 2006, 2007; Rempe et al. 2020; Kranz et al. 1990; Wibberley 2002). In contrast, hydraulic tests in the field are inherently dominated by discrete fracture conduits. This results in an order of magnitude for the diffusivity that spans from $10^{-1}$ m$^2$/s to $10^{1}$ m$^2$/s (Renner and Messar 2006; Cheng and Renner 2018; Maineult et al. 2008; Talwani et al. 1999; Becker and Guiltinan 2010; Sayler et al. 2018). In some cases, the observed hydraulic diffusivity might be much lower (Doan et al. 2006; Xue et al. 2013) or higher (Becker and Guiltinan 2010; Guiltinan and Becker 2015; Sayler et al. 2018) depending on the site geology. Moreover, different test methods may also provide different diffusivity values, e.g., lower hydraulic diffusivities were observed in constant rate tests than in periodic tests (Guiltinan and Becker 2015). At geothermal sites, the hydraulic diffusivity obtained by fitting seismic events also commonly varies between $10^{-1}$ m$^2$/s and $10^{1}$ m$^2$/s (Shapiro et al. 1997; Shapiro and Dinske 2009). However, it is worth noting that these values represent the averaged hydraulic diffusivity of the whole tested fractured rock system. They are the combination of the matrix diffusivity and the fracture diffusivity (Ortiz R et al. 2013; Sayler et al. 2018). Hence, it is not surprising that our single-fault model renders higher values of diffusivity. These results are also supported by previous studies (e.g., Sayler et al. (2018)), which evidenced that flow between an interval with large diffusivities (up to $10^3$ m$^2$/s) might be dominated by a constrained planar fracture.

For real-world case applications, other factors may also alter the hydraulic diffusivity, such as flow exchange between the fracture and matrix, mineral sealing and the temperature (Wibberley 2002). Furthermore, hydraulic diffusivity has also been correlated with resolved fault movement. For instance, Guglielmi et al. (2015) reported a wide range of diffusivities ($10^{-9}$ m$^2$/s and $10^{3}$ m$^2$/s) during injection-induced fault reactivation experiments. These observations require further studies. In this work, we focused on understanding the impact of the fracture geometry on diffusivity, which is a fundamental topic. As such, one implication of our results is to provide a reference for complex numerical models. As an example, on the basis of the linear diffusion equation, Haagenson and Rajaram (2021) used $2.2\times 10^2$ - $3.3\times 10^{3}$ m$^2$/s for the hydraulic diffusivity of each single fracture (compatible with our results) as an input in their 3D discrete fracture network and matrix (DFNM) numerical model and obtained an effective hydraulic diffusivity of 0.29 m$^2$/s for the whole system (a common value in the field). We infer that the result might be improved if considering roughness and anisotropy (e.g., varied aperture distribution) for the input single fracture diffusivity.

6 Conclusions

We studied the effect of fracture surface roughness and fracture closure on pressure diffusion by numerically simulating transient fluid flow. The effect was evaluated quantitatively in terms of the effective hydraulic diffusivity $D_e$. We considered the self-affinity property for the fracture surfaces as well as the fracture aperture. The implemented fracture geometry was based on synthetically generated surfaces/apertures following field observations. We performed transient pressure diffusion modeling in surface-represented rough fractures for different stages of fracture closure and observed that the roughness could significantly affect the effective hydraulic diffusivity of the fracture. At large openings, the rough fracture exhibits hydraulic behavior similar to the parallel plate model. As the fracture is gradually closed, the effective hydraulic diffusivity increasingly deviates from the parallel plate model and shows anisotropic behavior by enhancing or reducing the diffusivity according to the orientation of the pressure drop. Furthermore, when it approaches the percolation threshold, the increase in the fracture contact area and tortuous flow channels strongly decreases the effective hydraulic diffusivity by seven- and four orders of magnitude in the x- and y-directions, respectively. However, owing to the self-affinity property, a large residual opening (large diffusivity) exists even with a small hydraulic aperture. Although the method is based on a simple linear diffusion equation, our results show good consistency with some previously obtained field observations. Therefore, this study could have important implications for understanding the measurement of hydraulic properties as well as the associated fluid-induced seismicity pattern. The influence of the rock matrix and elastic fracture closure (for the volume representation) will be considered in future studies.

Appendices

Appendix A

For 3D fracture flow, the fluid velocity distribution is the value of the fracture mean plane. To obtain the average velocity, the local velocity profile $v_x(z)$ in the z-direction is first assumed to follow a parabolic equation (similar to the velocity profile of the parallel plate model):

$$\begin{aligned} v_x(x,y,z)=az^2+bz+c. \end{aligned}$$

(23)

The average velocity is defined as the average of the integral of the velocity function along the z-direction:

$$\begin{aligned} \overline{v_x}(x,y,z)=\frac{1}{h}\int _{-\frac{h}{2}}^{\frac{h}{2}}v_x(x,y,z)\,\mathrm {d}z. \end{aligned}$$

(24)

Appendix B

The procedure of searching for the effective hydraulic diffusivity of a rough fracture is as follows:

• 1) First, from the simulation results of a rough fracture flow, we obtain a time-dependent pressure distribution $p_R(x,y,t)$, which is averaged along the y-axis as $<p_R(x,t)>_y$. Figure (20) shows the pressure distribution of the parallel plate model ($d_m=0.3$ m) at $x=L/2$ (averaged along the y-axis) plotted as a function of normalized time $t/t^*$. The pressure is stabilized at $t_s\approx 0.5 t^*$ (i.e., the fluid velocity is zero). Accordingly, we use $t_s$ as the upper bound of time to estimate the effective hydraulic diffusivity (i.e., from $t = 0$ to $t = t_s$). The time resolution matches the spatial resolution, i.e., we have 512$\times$512 points on the fracture plane, so the number of time step is also 512.

• 2) The pressure distribution $p_{\parallel }(x,t,D_f)$ is calculated using different hydraulic diffusivities (hereinafter referred to as the test diffusivities) from the analytical expression Eq. (19). These test diffusivities are given in units of $D_m$, which is the diffusivity for a parallel plate model with the same mean aperture $d_m$ as the rough fracture. For example, when we expect that the pressure diffusion of the rough fracture is reduced compared to the equivalent parallel plate model, we can build the set of test diffusivities in the range $[0.1:0.9]D_m$ with a step $\varDelta D=0.1D_m$. Alternatively, if it is expected to be enhanced, then the test diffusivity set can be $[1:0.1:2]D_m$.

• 3) The differences between $<p_R(x,t)>_y$ and $p_{\parallel }(x,t,D_f)$ in the least square sense is computed and the differences summed, followed by calculating the least square error for each test diffusivity. The diffusivity with the minimum error is assigned as the diffusivity for the rough fracture. The best diffusivity is referred to as $D_{e1}$.

• 4) A set of diffusivities near $D_{e1}$ with a smaller step such as $\varDelta D=0.01D_m$ is rebuilt, and step 3 is repeated to obtain a more accurate diffusivity $D_{e2}$. The step is reduced to $\varDelta D=0.001D_m$ and $D_{e3}$ obtained. In theory, the smaller the step of the test diffusivity used, the higher the accuracy of the diffusivity. In this study, we calculate the test diffusivity up to three decimal places. The final best $D_{e3}$ is regarded as the effective hydraulic diffusivity $D_e$ of the rough fracture. Note that for the obtained best diffusivity at each step, if it is at the boundary of the set of the test diffusivities, we rebuild the set by including this diffusivity inside it and repeat step 3 until an optimal hydraulic diffusivity inside this set is found.

• 5) The effect of different time resolutions is tested. When the resolution is halved to 256 time steps, the results remain almost unaffected. Even when 100 time steps are used, the results only show an error of less than 1%. Therefore, the results obtained at the time resolution we use are considered robust.

Figure (21) shows an example of the least square error when searching for the effective hydraulic diffusivity $D_{e}=0.423 D_m$ for $d_m/\sigma =3$ and an imposed pressure drop along the x-axis. By stepwise selecting the resolution of the test diffusivity as $\varDelta D=0.1 D_m$, $\varDelta D=0.01 D_m$ and $\varDelta D=0.001 D_m$, $D_{e1}=0.4 D_m$, $D_{e2}=0.42 D_m$ and $D_{e3}=0.423 D_m$ are obtained, respectively.

Fig. 20

Pore pressure averaged along the y-axis as a function of $t/t^*$ at $x=L/2$ in the case of the parallel plate model with $d_m=0.3$ m

Fig. 21

Least square error as a function of $D_e/D_m$. a $D_{e1}=0.4 D_m$ with the step of the test diffusivity $\varDelta D=0.1 D_m$; b $D_{e2}=0.42 D_m$ with $\varDelta D=0.01 D_m$; and c $D_{e3}=0.423 D_m$ with $\varDelta D=0.001 D_m$