1 Introduction

Permeability prediction in natural media like fractured rocks is a stepping stone for the development of projects such as disposal sites (Bear et al. 1993) and underground tunnelling (Evans et al. 2013) where low permeability is aimed. However, for reservoir exploitation (Schmittbuhl et al. 2008; Zimmerman and Bodvarsson 1996) such as geothermal sites, high permeability is pursued using hydraulic stimulation to shear the fractured rocks. Through the Darcy’s law for laminar flow, permeability is defined from the proportionality factor linking the flow rate and the fluid viscosity to the pressure gradient. In fractured rocks, fluid flow is affected by the local aperture which is typically linked to the local roughness distribution. Moreover, flow rate depends on mechanical deformations, i.e. shearing or normal opening. It is well known that this can lead to a dependency of flow on orientation, yielding effects of anisotropy and channelling which have been intensively studied by multiple authors (Berkowitz 2002). Auradou et al. (2001) illustrated flow anisotropy with laboratory studies using dyed fluid in a self-affine rough fracture. They observed a dependency of anisotropy on the lateral displacement of the fracture surfaces. Based on natural fracture replica, Gentier et al. (1997) also verified this phenomenon on the permeability field through laboratory experiments. They concluded that hydraulic permeability of a fracture depends clearly on the shear direction at displacements below 0.5 mm with significant changes in flow direction. Méheust and Schmittbuhl (2001) quantified anisotropy by taking into account the direction of the pressure gradient and the geometrical heterogeneities. Auradou et al. (2006) performed an experimental and numerical study demonstrating that shear displacement induces anisotropy with enhanced permeability perpendicular to the shear direction. They extended their model to include flow channels developing perpendicularly to the shear displacement. Channelling is referring to the phenomenon of flow concentration along preferential pathways. Silliman (1989) demonstrated the development of channelling structures by laboratory experiments and underlined the associated presence of flow anisotropy. Channelling was experimentally established when small parts of a fracture plane can concentrate 90% of the fluid flow in single fractures (Rasmuson and Neretnieks 1986). By numerical studies, the importance of channelling for transport phenomena in a strongly heterogeneous medium, such as a fracture, was investigated (Tsang and Tsang 1989) and identified (Moreno and Tsang 1994).

These studies have an important impact on fractured geothermal reservoir systems which tend to be situated in tectonically active areas with an individual history of shearing events. Shearing is noticed through seismic events with a relative movement of fracture surfaces. This can take place under natural or under man-made conditions (“natural vs. induced earthquake”). In a larger context of a fracture network, these studies highlight that anisotropy and channelling are crucial to understand the permeability patterns in reservoirs. Clearly, its quantification depends on the flow law applied and on the geometrical characterization of aperture. Considering a laminar flow and an individual fracture, the widely used equation to evaluate the influence of aperture variability on fluid flow computation is the cubic law (Brown et al. 1995, 1998; Witherspoon et al. 1980). With this approach, the fracture surface is simplified to parallel plates and inertial as well as nonlinear effects are neglected. Under purely tensile conditions when the fracture surfaces are displaced normally to the fracture plane even very rough surfaces could imply a constant aperture (Méheust and Schmittbuhl 2003). However, under normal or strike-slip faulting conditions fracture surfaces will be displaced, and aperture distribution will change locally. Given the crucial importance of mechanical interaction in a fractured geothermal system, its hydraulic impact needs to be investigated as function of the changing local aperture with displacement. In the following, we account for the aperture by defining a local transmissivity derived from the Local Cubic Law (LCL) that is a function of a stochastically generated roughness on the fracture surface. Utilization of the LCL is attractive for a broad range of engineering applications, at least as a first approach, due to its simplicity and computational efficiency. However, one of the critical issues related to LCL is the definition of its geometrical constraint which is the local aperture used in this equation (Konzuk and Kueper 2004; Oron and Berkowitz 1998; Wang Lichun et al. 2015; Zimmerman and Bodvarsson 1996).

The goal of the present work is to establish a recalibration between the LCL simulation results based on the commonly used vertical aperture and the more realistic effective aperture which considers the flow directionality. The limitation of the LCL are not put into question as our aim is to present the first results documenting an alternative to balance computational time and accuracy based on this law. To do so, we need to quantify the accuracy of the generally applied LCL models by accounting on stochastically generated fracture surface geometry. By its small-scale stochastic nature, it concludes on the bandwidth of uncertainty at large-scale numerical model approaches. To provide this quantification, a stochastic approach is presented to generate the roughness distribution of fracture surfaces. This process results in many realizations using the same fractal parameter extracted from a field observation. On these non-identical fractures, different shearing displacements are applied to simulate the individual hydraulic impact assuming viscous Poiseuille flow. The statistical dispersion of the generated datasets is analysed to highlight the uncertainty related to the definition of a LCL aperture. The stochastic investigations are concentrating on anisotropy and channelling, representing two principal hydraulic phenomena in fractured media. In the context of complex fractured systems, this study aims therewith also at improving the reliability of the hydraulically coupled processes, i.e. in geothermal models.

First, we describe the numerical framework and the procedure to generate the stochastic database in Sect. 2. In Sect. 3, the aperture distributions and the statistical dispersion of the hydraulic results are presented to analyse the associated anisotropy variations. Then, in Sect. 4, indicators are defined to quantify channelling and its dependence on shearing under the chosen stochastic approach.

2 Methods

2.1 Generation of Rough Self-Affine Surfaces

The procedure to generate the stochastic database of a sheared single fracture is conducted by constructing 3D surfaces with a software developed by Schmittbuhl and described in (Méheust and Schmittbuhl 2001). Herein, it is assumed that fractal geometries represent a good approximation of the roughness distribution of real fracture surfaces (Bouchaud 1997; Schmittbuhl et al. 1993, 1995). This roughness distribution is defined from self-affine surfaces with isotropic correlation functions. Its associated probability density function \( p_{\text{d}} \) can be stated as follows:

$$ p_{\text{d}} \left( {\Delta h, \Delta \varvec{r}} \right) = \lambda^{H} p_{\text{d}} \left( {\lambda^{H} \Delta h, \lambda \Delta \varvec{r}} \right), $$
(1)

assuming an arbitrary scaling factor \( \lambda \) and the Hurst roughness exponent \( H \). It indicates that \( p_{\text{d}} \) is invariant regarding the transformations on the height difference \( \Delta h \) and the distance \( \Delta \varvec{r} \) defined in Eq. (1) (Méheust and Schmittbuhl 2001; Talon et al. 2010).

A roughness exponent of \( H = 0.8 \) is chosen in this study being widely observed for granite (Amitrano and Schmittbuhl 2002; Schmittbuhl et al. 1993, 1995). Moreover, every surface generated (Fig. 1) is distinct as it is, respectively, based on a distribution extracted from a white noise generator (Press et al. 1992). The generated surfaces have a resolution of \( 2048 \) by \( 2048 \) discretization elements. In addition, we measure that the topothesy of the generated surfaces is \( 4 \times 10^{ - 6} {\text{mm}} \). This value is relatively higher but comparable with the experimental measurements in Schmittbuhl et al. (2008) where the value of \( 2 \times 10^{ - 7} {\text{mm}} \) is found. Moreover, we verify that the Power Spectral Density (\( {\text{PSD}} \)) of the surfaces has a slope of \( - 2.6 \) which is coherent with \( H = 0.8 \) as this slope for self-affine surfaces is of \( - 1 - 2H \) (Méheust and Schmittbuhl 2001). To implement the stochastic approach a total of \( 560 \) fractures were generated. This number of fractures has been chosen to be able to quantify the accuracy of anisotropy and channelling phenomena.

Fig. 1
figure 1

Example of surface generated with a roughness exponent of \( H = 0.8 \) after scaling. Note that \( x,y \)-axis are in m and \( z \)-axis is in mm. The colours refer to the height in the direction of the \( z \)-axis

Full size image

2.2 Sheared Fracture Generation

In a geoscientific context, fractured systems represent discontinuities in the solid rock. Under increasing stress loading, their surfaces are likely to be displaced which is a typical behaviour in deep geothermal reservoirs or in active tectonic systems. To obtain numerically a sheared synthetic fracture from a generated surface, we adopt the methodology of the study realized by Auradou et al. (2006) using sheared fractures made initially of complementary walls. After having duplicated the initial surface, its duplicate is translated horizontally by \( N_{\text{offset}} \) with a periodic boundary due to the small displacements (\( < 1\% \) of the fracture length). Then, a vertical translation results automatically when both surfaces have at least one contact point (Fig. 2). With this last step, we place the study in the limit of a rigid approximation, and thus no plastic deformation and no rigid rotation are considered. The constructed fractures are scaled on the measurements from Schmittbuhl et al. (1993). Also, the scaling of the surfaces considers a total length \( L \) of \( 0.64 \;{\text{m}} \) and a maximum surface amplitude of \( l = 30\; {\text{mm}} \). Based on a self-affine geometry, the fracture-scale studied can be included in larger reservoir models through upscaling procedures. Indeed, this approximation is enabled by the self-affine geometry which is based on the self-similarity property which is featured by scale invariance.

Fig. 2
figure 2

Illustration of the fracture construction from a generated surface. For clarity, the construction steps are shown projected in 2D. Note that the top surface refers to the duplicate of the bottom surface

Full size image

In total, we consider \( 8 \) shear displacements along the \( x \)-axis, noted \( N_{\text{offset}} \), and for each of them \( 70 \) fractures are, respectively, sheared, resulting in a total number of fractures to be generated of \( 560 \). The value of \( N_{\text{offset}} \) controls the shearing displacement and is given in number of elements (i.e. each length has \( 2048 \) elements). The equivalent physical lengths of the different shear displacements are presented in Table 1. The shear displacement is linearly increasing from \( 1 \) to \( 8 \) elements of a surface with the aim to study the early development of anisotropy and channelling processes. Due to the relatively small shearing displacement compared to the overall fracture size, the rigid approximation is applied as stated before. Indeed, a shearing displacement in the millimetre range \( \left[ {0.31;2.50} \right] \) is resulting for a fracture of \( 0.64\; {\text{m}} \). In a mechanically brittle medium, this could be associated with micro-earthquakes of magnitude \( M < 1 \) (Wells and Coppersmith 1994) typically observed during enhanced geothermal exploitations.

Table 1 Shear displacement expressed in number of elements and physical length (mm)
Full size table

2.3 Local Aperture Distributions

The common practice to compute LCL is to measure the aperture normal to the fracture plane, meaning that a constant direction is considered (Brown 1989). Since this practice leads to an overestimation of transmissivity (Berkowitz 2002), a variety of aperture definitions have been proposed for fluid flow simulations. For the definition of an effective aperture herein, we follow the approach from Ge (1997) suggesting to use a “true aperture” calculated from the normal to the local orientation of the centerline between both fracture surfaces. Other authors proposed to define the aperture as the largest sphere fitting into the fracture at a given node (Mourzenko et al. 1995) or defined flow-oriented apertures (Lichun et al. 2015).

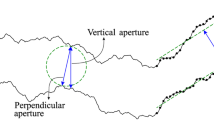
For each of the \( 560 \) generated fractures, two definitions of aperture distributions were used: (1) \( a_{\text{vert}} \) the vertical aperture and (2) \( a_{\text{eff}} \) the effective (“true”) aperture (Fig. 3). This extraction is performed through the framework integrated in Pace3D (Hötzer et al. 2018). First, to obtain \( a_{\text{vert}} \), we consider a constant vertical direction with respect to the horizontal mean plane at each element of a generated fracture. Also, taking the vertical distance between the lower and upper surfaces of the fracture at a fixed position, we obtain the local vertical aperture distribution. Then, a local \( a_{\text{vert}} \) can be formulated as follows:

Fig. 3
figure 3

Schematization of vertical \( a_{\text{vert}} \) and effective aperture \( a_{\text{eff}} \) definitions projected onto the plane \( \left( {x,z} \right) \) in a portion of an open fracture sheared by \( N_{\text{offset}} \). The grey lines represent the fracture surfaces and the red line is the centerline between the fracture surfaces

Full size image
$$ a_{\text{ver}} \left( {x,y,N_{\text{offset}} } \right) = h_{\text{top}}^{{N_{\text{offset}} }} \left( {x,y} \right) - h_{\text{bot}} \left( {x,y} \right) = h_{\text{top}}^{0} \left( {x - N_{\text{offset}} ,y} \right) - h_{\text{bot}} \left( {x,y} \right), $$
(2)

with \( h_{\text{top}}^{{N_{\text{offset}} }} \) and \( h_{\text{bot}} \), respectively, the height of a fracture element on its top and bottom surfaces as labelled on Fig. 3. Note that the shearing is applied on the top surface of the fracture along the \( x \)-axis. Thus, the superscript \( N_{\text{offset}} \) of \( h_{\text{top}}^{{N_{\text{offset}} }} \) indicates the displacement of the top surface relatively to the bottom one. Moreover, the vertical displacement of the top surface is indirectly defined through the common contact point of the sheared surfaces. In addition, \( h_{\text{top}}^{0} \) refers to the initial top surface that has not been sheared.

Second, the effective aperture is defined through the gradient of the median \( m \), noted \( {\mathbf{grad}}\left( \varvec{m} \right) \), between the top and bottom surfaces (Selzer 2014). Considering the shear displacement \( N_{\text{offset}} \), we establish for a given fracture the local height of the median curve at the point \( \left( {x,y} \right) \) as follows:

$$ m\left( {x,y,N_{\text{offset}} } \right) = \frac{{h_{bot} \left( {x,y} \right) + h_{\text{top}}^{{N_{\text{offset}} }} \left( {x,y} \right)}}{2}, $$
(3)

Then, \( a_{\text{eff}} \) is determined as the distance between the intersection points of \( h_{\text{top}}^{{N_{\text{offset}} }} \) and \( h_{\text{bot}} \) surfaces with the line of slope \( {\mathbf{grad}}\left( \varvec{m} \right) \) passing by the point \( \left( {x,y,m} \right) \). Depending on \( {\mathbf{grad}}\left( \varvec{m} \right) \), \( a_{\text{eff}} \) is perpendicular with the flow direction making it more realistic than the \( a_{\text{vert}} \) in the context of LCL application. Using finite differences, we calculate the gradient as follows:

$$ {\mathbf{grad}}\left( \varvec{m} \right) = \left[ {\begin{array}{*{20}c} {\frac{{m\left( {x + 1, y,N_{\text{offset}} } \right) - m\left( {x - 1,y,N_{\text{offset}} } \right)}}{2\Delta x}} \\ {\begin{array}{*{20}c} {\frac{{m\left( {x,y + 1,N_{\text{offset}} } \right) - m\left( {x,y - 1,N_{\text{offset}} } \right)}}{2\Delta y}} \\ 0 \\ \end{array} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {\dot{m}_{x} } \\ {\begin{array}{*{20}c} {\dot{m}_{y} } \\ 0 \\ \end{array} } \\ \end{array} } \right], $$
(4)

Then, we apply a rotation of \( \frac{\pi }{2} \) on it and we obtain \( \varvec{n}\left( \varvec{m} \right) \), the normal vector to the middle plane:

$$ \varvec{n}\left( \varvec{m} \right) = \left[ {\begin{array}{*{20}c} 1 & 0 & 0 \\ 0 & 0 & { - 1} \\ 0 & 1 & 0 \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {\dot{m}_{x} } \\ {\begin{array}{*{20}c} {\dot{m}_{y} } \\ 0 \\ \end{array} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {\dot{m}_{x} } \\ {\begin{array}{*{20}c} 0 \\ {\dot{m}_{y} } \\ \end{array} } \\ \end{array} } \right], $$
(5)

Thus, \( a_{\text{eff}} \) is defined as follows:

$$ a_{\text{eff}} \left( {x,y,N_{\text{offset}} } \right) = \varvec{BT}, $$
(6)

where \( B \) is the intersection point between the line of slope defined at Eq. (5) and passing by the point \( \left( {x,y, m} \right) \) with the bottom surface of the fracture. Similarly, \( T \). is the intersection between this line and the top surface.

To document the difference between the aperture definitions, we compute the aperture ratios \( a_{\text{eff}} /a_{\text{vert}} \) in each fracture and present the distribution associated with one fracture where \( N_{\text{offset}} = 5 \) (Fig. 4). Aperture ratios superior to one confirm that \( a_{\text{eff}} \) is not only a projection of \( a_{\text{vert}} \) onto the direction aligned with \( \varvec{ BT} \). We observed for each fracture of every shear displacement similar histograms. Also, the previous conclusions can be extended to all study.

Fig. 4
figure 4

Histogram of the probability density in terms of aperture ratio \( a_{\text{eff}} /a_{\text{vert}} \) for a given fracture at \( N_{\text{offset}} = 5 \). Values superior to one indicate that \( a_{\text{eff}} \) is not only a projection of \( a_{\text{vert}} \) onto the perpendicular direction given by \( \varvec{BT} \) shown in Fig. 3

Full size image

Furthermore, we compute the \( {\text{PSD}} \) for each of the simulated fractures and we present the results for a given fracture with \( N_{\text{offset}} = 6 \) in Fig. 5. Similar shapes of the \( {\text{PSD}} \) for \( a_{\text{vert}} \) and \( a_{\text{eff}} \) are observed regardless of the shear displacement and the fracture considered. For spatial frequencies lower than \( 10 \;{\text{m}}^{ - 1} \) (i.e. high spatial variations), both aperture definitions lead to the same weighting of these frequencies. From \( 10 \;{\text{m}}^{ - 1} \) to \( 100\; {\text{m}}^{ - 1} \), the \( {\text{PSD}} \) of \( a_{\text{eff}} \) presents the same trend than the one based on \( a_{\text{vert}} \) but with higher values showing that \( a_{\text{eff}} \) weights more this spatial range. Finally, from \( 100 \;{\text{m}}^{ - 1} \) to the largest spatial frequencies, we notice that \( a_{\text{eff}} \) has globally a decreasing weighting of this range compared to \( a_{\text{vert}} \) whose variations are heterogeneous with smaller values than \( a_{\text{eff}} \) of at least one order of magnitude. Thus, we have shown that \( a_{\text{eff}} \) differs from \( a_{\text{vert}} \) notably in the weighting of low spatial variations approximately below \( 10 \;{\text{mm}} \) which include the aperture values. Also, \( a_{\text{vert}} \) distributions present higher averaged apertures as the weight on higher spatial variations is decreasing more rapidly in the range starting from \( 100\; {\text{m}}^{ - 1} \) compared to \( a_{\text{eff}} \) weighting over this range. Note that to investigate the resolution impact on the \( {\text{PSD}} \) curves, we computed it for a resolution smaller by factor 2 and we obtain similar shapes and relative variation according to the aperture definition (Fig. 6). Thus, the relationship between both aperture definitions is transposable to other resolutions.

Fig. 5
figure 5

Power spectral density of \( a_{\text{vert}} \) and \( a_{\text{eff}} \) for a fixed fracture whom \( N_{\text{offset}} = 6 \) with a resolution of \( 2048 \times 2048 \)

Full size image
Fig. 6
figure 6

Power spectral density of \( a_{\text{vert}} \) and \( a_{\text{eff}} \) for a fixed fracture whom \( N_{\text{offset}} = 6 \) with a resolution of \( 1024 \times 1024 \) which is twice smaller compared to the Fig. 5

Full size image

To conclude, both extractions of local aperture distributions are projections where we obtain 2D local aperture distributions from the 3D fractures. Note that the horizontal mean plane resolution is identical to the resolution of the fracture (\( 2048 \) × \( 2048 \)). This numerical resolution is chosen for this study as the finest resolution reachable with an acceptable computational time (less than 10 h of simulation by fracture). Moreover, to analyse the variability of the local aperture distribution for each of the generated fractures, we define \( \bar{a} \) representing the mean aperture defined as follows:

$$ \bar{a} = \frac{1}{N}\mathop \sum \limits_{i = 1}^{N} a_{i} , $$
(7)

where \( a_{i} \) is the aperture value of the ith element taken among the \( N \) elements that constitute the fracture. Note that this definition is identically used for each aperture definition giving \( \bar{a}_{\text{vert}} \) and \( \bar{a}_{\text{eff}} \). Similarly, the distribution of the local aperture is also characterized by its dispersion through \( \sigma^{a} \) which is the standard deviation of the aperture computed for both apertures as follows:

$$ \sigma^{a} = \sqrt {\frac{{\mathop \sum \nolimits_{i = 1}^{N} \left( {a_{i} - \bar{a}} \right)^{2} }}{N - 1}} , $$
(8)

2.4 Fluid Flow Governing Equations

Fluid flow through a single fracture is governed by the Navier–Stokes (\( {\text{NS}} \)) equations. In the case of incompressible and steady Newtonian flow, the \( {\text{NS}} \) equations can be expressed in vector form as follows (Foias et al. 2001):

$$ \left( {\varvec{u} \cdot \nabla } \right)\varvec{u} = - \frac{1}{\rho }\nabla p + \nu \nabla^{2} \cdot {\mathbf{u}} + {\mathbf{f}}, $$
(9)

with \( \varvec{u} \) the flow velocity vector, \( \rho \) the fluid density, \( p \) the hydrodynamic pressure, \( \nu \) the kinematic viscosity of the fluid and \( {\mathbf{f}} \) the body force acting on the fluid, typically \( {\mathbf{f}} = {\mathbf{g}} \) where \( {\mathbf{g}} \) is the acceleration of gravity. Solving the \( {\text{NS}} \) equations requires to solve nonlinear partial differential equations. The source of nonlinearity is in the advective term \( \left( {\varvec{u} \cdot \nabla } \right)\varvec{u} \) which shows the inertial forces acting on the fluid. The Stokes equation can be obtained by neglecting the inertial term in the NS equation if the Reynolds number \( Re \ll 1 \), where \( Re \) is defined as \( \rho Qa/\mu \) with \( \rho = 10^{3} \;{\text{kg}}\;{\text{m}}^{ - 3} \) the density of water, \( Q \) the volumetric flow rate, \( a \) the arithmetic mean aperture and \( \mu = 1.306 \times 10^{ - 3} {\text{Pa}}\,{\text{s}} \) the viscosity of water. The simulations in this work show a maximum local flow rate of approximately \( 10^{ - 8} \; {\text{m}}^{3} \;{\text{s}}^{ - 1} \). Given a maximum local aperture of \( a_{{\max} } = 5 \;\;{\text{mm}} \) and a maximum velocity of \( Q = U \times S \sim 10^{ - 8} \times a_{{\max} } \times L/2048 \), we obtain a maximum local Reynolds number \( Re_{ {\max} }^{\text{local}} \sim 10^{ - 11} \). This allows for reducing the \( {\text{NS}} \) equations to the linear Stokes equation:

$$ 0 = - \frac{1}{\rho }\nabla p + \nu \nabla^{2} \cdot {\mathbf{u}} + {\mathbf{f}}, $$
(10)

The validity of the Stokes equation in rough fracture profiles has been studied in Brown et al. (1995); Brush and Thomson (2003); Mourzenko et al. (1995). Nevertheless, the complexity of the Stokes equation to solve fluid flow in rock fracture requires another level of simplification through geometric and kinematic assumptions allowed in the lubrication approximation context. Then, neglecting the kinematic forces, the following standard simplification is to use the Reynolds equation (Eq. (11)) to compute the pressure distribution with a “cubic law” for the flux (Brown 1987; Mourzenko et al. 1995; Tsang and Tsang 1989; Zimmerman et al. 1991):

$$ \nabla \cdot \left( {\frac{{a_{\text{e}}^{3} \left( {x,y} \right)}}{12\mu }\nabla p} \right) = 0, $$
(11)
$$ Q_{X} = - L_{Y} \frac{{a_{e}^{3} }}{12\mu }\frac{\partial p}{\partial x}, $$
(12)

where \( a_{e} \) is the equivalent fracture aperture in the parallel-plate model, \( \mu \) the dynamic viscosity of the fluid, \( Q_{X} \) is the projected volumetric flow rate on the \( x \)-axis and \( L_{Y} \) is the fracture width. Due to their roughness, rock fractures present aperture variations. Thus, to simply consider this roughness, an approximation is to consider the “Local Cubic Law” with the hypothesis of an isotropic media:

$$ Q_{j}^{x,y} = - L_{j} \frac{{a_{x,y}^{3} }}{12\mu }\frac{{\partial p_{x,y} }}{\partial j}, $$
(13)

with \( Q_{j}^{x,y} \) the total volumetric flow rate for each element of the fracture identified by the coordinates \( \left( {x,y} \right) \) in the direction \( j \) where \( j = \left\{ {X,Y} \right\} \) and \( a_{x,y} \) the local aperture at \( \left( {x,y} \right) \). Then, Eq. (13) is identically used to determined \( Q_{X}^{x,y} \) and \( Q_{Y}^{x,y} \). Widely applied for fluid flow and solute transport (Zimmerman and Bodvarsson 1996; Zimmerman et al. 1991), this simplified model has been investigated theoretically and numerically (Brown 1987; Brown et al. 1995; Brush and Thomson 2003; Mourzenko et al. 1995; Zimmerman and Bodvarsson 1996; Zimmerman et al. 1991). Finally, the flow rate is computed with the software Abaqus using 4-node linear quadrilateral elements to solve the Eq. (13) where the characteristic length is set to \( L_{Y} = L_{X} = L = 0.64 \;{\text{m}} \) (see Sect. 2.1) and the viscosity of water at 10 °C is taken as \( \mu = 1.306 \times 10^{ - 3} \;{\text{Pa}}\;{\text{s}} \). Note that the temperature is considered constant at 10 °C during the simulation. Note that herein \( Q_{j}^{x,y} \) is based on the global length scale \( L \). A discrete volumetric definition of it can be directly obtained by dividing \( Q_{j}^{x,y} \) by the fracture dimensional resolution \( 2048 \).

Using Eq. (13), we want to quantify the evolution of flow anisotropy with shearing by considering the velocity in the outlet layer according to the pressure gradient direction as illustrated in Fig. 7. With the outlet plane as reference, the perpendicular projection of the outgoing flow (\( {\text{OF}} \)) is a measure for the total outgoing flow obtained and the potential fluid recovery associated. For reservoir exploitation, this flow rate is a crucial parameter; mimicking it by \( {\text{OF}} \) enables us to analyse the anisotropy with a field application perspective. Also, we define the \( {\text{OF}} \) for both pressure cases as follows:

$$ {\text{OF}}_{\parallel } = \mathop \sum \limits_{{\begin{array}{*{20}c} {x = N; y = 1} \\ {\overrightarrow {{Q_{X} }} . \vec{x} > 0} \\ \end{array} }}^{x = N; y = N} Q_{X}^{x,y} , $$
(14)
$$ {\text{OF}}_{ \bot } = \mathop \sum \limits_{{\begin{array}{*{20}c} {x = 1; y = N} \\ {\overrightarrow {{Q_{Y} }} . \vec{y} > 0} \\ \end{array} }}^{x = N; y = N} Q_{Y}^{x,y} , $$
(15)
Fig. 7
figure 7

a, b Illustration of the outgoing flow (OF) definitions and boundary conditions for both pressure gradient directions \( \left\{ {\parallel , \bot } \right\} \). The colored lines represent the outlet layer considered for each case of pressure gradient direction. Note that the shear displacement is made along the \( x \)-axis and the pressure gradient is parallel or perpendicular to this shearing direction. c, d Schematization of the boundary conditions applied in each cases of pressure gradient directions \( \left\{ {\parallel , \bot } \right\} \) (color figure online)

Full size image

Based on the quantitative characterization of anisotropy established by Auradou et al. (2005), we quantify the dependence of the \( {\text{OF}} \) with the orientation of the hydraulic pressure gradient through the anisotropy factor (\( {\text{AF}} \)) defined as follows:

$$ {\text{AF}} = \frac{{{\text{OF}}_{ \bot } }}{{{\text{OF}}_{\parallel } }}, $$
(16)

2.5 Boundary Conditions

A fixed hydraulic pressure is imposed at the inlet and outlet of the fracture as shown in Fig. 7. According to the pressure gradient direction considered, the inlet is set to \( 1 \;\; {\text{bar}} \) and the outlet pressure is equal to \( 0\;\; {\text{bar}} \). Then, the two other walls form a closed loop by being virtually connected to obtain an artificial infinite domain. Finally, the rough fracture surfaces are impermeable to flow. Thus, the flow is \( 2D \) in the \( \left( {x,y} \right) \)-plane.

3 Results

3.1 Local Aperture Distribution with Shear Displacement

Both aperture definitions \( \{ a_{\text{vert}} ,a_{\text{eff}} \} \) are successively applied to determine the local aperture distribution as illustrated in Fig. 8. As expected, the local \( a_{\text{eff}} \) distribution reveals lower values compared to the distribution of \( a_{\text{vert}} \). This observation is confirmed by the mean aperture \( \bar{a} \) distribution over the fracture replications. In order to evaluate the variations of \( \bar{a} \), we display the boxplots of its distribution at each shearing offset in Fig. 9. Note, that for all boxplots shown here, the box extends from the lower (\( Q1 \)) to the upper (\( Q3 \)) quartile value with a line at the median. The whiskers show the range of data defined as the following interval: [\( Q1 - 1.5 \times \left( {Q3 - Q1} \right) ; Q3 + 1.5 \times \left( {Q3 - Q1} \right)] \). Finally, the circles at the extremes represent the outliers whom values are outside of the previous range. Using this visualization, we can extend the previous remark by observing that \( \bar{a}_{\text{vert}} \) presents globally higher values than \( \bar{a}_{\text{eff}} \) at each offset. Moreover, the spreading of the distribution is larger for \( \bar{a}_{\text{vert}} \) compared to \( \bar{a}_{\text{eff}} \) and this spreading increases for both cases with higher shear displacements.

Fig. 8
figure 8

Example of local aperture distribution obtained for a generated fracture whom \( N_{\text{offset}} = 5 \) according to the aperture definition \( \left\{ {a_{\text{vert}} , a_{\text{eff}} } \right\} \)

Full size image
Fig. 9
figure 9

Boxplots of the mean aperture \( \bar{a} \) in terms of shear displacement for each simulation configurations based on \( \left\{ {a_{\text{vert}} , a_{\text{eff}} } \right\} \). Note that the box extends from the lower (\( Q1 \)) to the upper (\( Q3 \)) quartile values with a line at the median. The whiskers show the range of data defined at Sect. 3.1. The circles at the extremes represent the outliers

Full size image

Thus, the two definitions of aperture lead to a significant difference of the fracture characterization by \( \bar{a} \), but also by the standard deviation \( \sigma^{a} \) (Fig. 10). In the case of \( \bar{a} \), we observe that \( \sigma^{a} \) distributions show higher values for higher shear displacement, regardless of the aperture definition. It is shown that \( \sigma_{\text{eff}}^{a} \) distribution presents higher spreading with more extreme values than \( \sigma_{\text{vert}}^{a} \). Furthermore, the spreading of \( \sigma_{\text{vert}}^{a} \) increases with shearing values, whereas \( \sigma_{\text{eff}}^{a} \) varies heterogeneously. Finally, the distribution of local vertical apertures reveals higher dispersion of \( \bar{a} \) with shearing than \( \bar{a}_{\text{eff}} \) but concerning their standard deviation, \( \sigma_{\text{vert}}^{a} \) is less dispersed than \( \sigma_{\text{eff}}^{a} \).

Fig. 10
figure 10

Boxplots of the aperture standard deviation \( \sigma^{a} \) in terms of shear displacement for each simulation configurations based on \( \left\{ {a_{\text{vert}} , a_{\text{eff}} } \right\} \). Note that the box extends from the lower (\( Q1 \)) to the upper (\( Q3 \)) quartile values with a line at the median. The whiskers show the range of data defined at Sect. 3.1. The circles at the extremes represent the outliers

Full size image

3.2 Fluid Flow and Total Outgoing Flow

Using \( a_{\text{vert}} \) and \( a_{\text{eff}} \) to spatially characterize the fractures, we study their impact on the fluid flow computed with Eq. (13). For one generated fracture, we analyse four different fluid flow models as presented in Fig. 11 which correspond to the combination of possible simulation configurations parametrized by \( \{ a_{\text{vert}} ,a_{\text{eff}} \} \) and \( \left\{ {\parallel , \bot } \right\} \). As expected, this visualization qualitatively depicts an alignment of the high flow values with the pressure gradient direction. Moreover, the flow rate values calculated with \( a_{\text{vert}} \) are higher than those calculated with \( a_{\text{eff}} \). This observation is consistent with the previous finding showing that \( \bar{a}_{\text{eff}} \) values are lower than \( \bar{a}_{\text{vert}} \) values (Fig. 9).

Fig. 11
figure 11

Example of local flow rate distributions in a given fracture for each simulation configurations based on \( \left\{ {a_{\text{vert}} , a_{\text{eff}} } \right\} \) and \( \left\{ {\parallel , \bot } \right\} \). The flow rate values are given for each simulation element in \( {\text{m}}^{3} \,{\text{s}}^{ - 1} \) which is equivalent to \( 10^{9} {\text{mm}}^{3} \;{\text{s}}^{ - 1} \). Note that the white arrows indicate the direction of the pressure gradient

Full size image

In order to quantify the evolution of fluid flow anisotropy, the variations of \( {\text{OF}}_{\parallel } \) and \( {\text{OF}}_{ \bot } \) (Eqs. 14, 15) are plotted against the shear displacement (Fig. 12). The spreading of the distributions increases with larger whiskers of the boxplots and further outlier values while shearing increases. \( {\text{OF}}_{\parallel } \) and \( {\text{OF}}_{ \bot } \) distributions trends are relatively similar for a given aperture definition, whereas differences are significant of \( {\text{OF}}_{\parallel } \) and \( {\text{OF}}_{ \bot } \) values for \( a_{\text{vert}} \) compared to \( a_{\text{eff}} \) (factor 2 larger).

Fig. 12
figure 12

Boxplots of the outgoing flow OF in terms of shear displacement for each simulation configurations based on \( \left\{ {a_{\text{vert}} , a_{\text{eff}} } \right\} \) and \( \left\{ {\parallel , \bot } \right\} \). Note that the box extends from the lower (\( Q1 \)) to the upper (\( Q3 \)) quartile values with a line at the median. The whiskers show the range of data defined at Sect. 3.1. The circles at the extremes represent the outliers

Full size image

3.3 Flow Anisotropy Results

To highlight and compare the variations of \( {\text{OF}}_{ \bot } \) and \( {\text{OF}}_{\parallel } \) for both aperture definitions, we use their ratio AF (Eq. (16)) which facilitates the quantification of flow anisotropy. Figure 13 shows the evolution of AF over shearing for both aperture definitions. AF is computed for each fracture. It is shown that AF globally increases with increasing shear displacement. Compared to cases based on \( a_{\text{vert}} \), the distributions associated with \( a_{\text{eff}} \) present a larger dispersion independent of the shearing offset. This can be observed through the length of the whiskers as well as the number of outliers. Moreover, \( {\text{AF}}_{\text{vert}} \) distributions reach higher values than \( {\text{AF}}_{\text{eff}} \). For small shearing displacements (up to \( 0.94 \;{\text{mm}} \)) a relative fast increase of anisotropic behaviour with shearing can be observed. Towards higher values of displacement, this increase is saturating. The dispersion of AF values for both cases differ significantly. The spread (interquartile range) for \( a_{\text{eff}} \) is by factor two larger than for \( a_{\text{vert}} \).

Fig. 13
figure 13

Boxplots of AF in terms of shear displacement for each simulation configurations based on \( \left\{ {a_{\text{vert}} , a_{\text{eff}} } \right\} \). Note that the box extends from the lower (\( Q1 \)) to the upper (\( Q3 \)) quartile values with a line at the median. The whiskers show the range of data defined at Sect. 3.1. The circles at the extremes represent the outliers

Full size image

4 Discussions

The previous simulations demonstrate that anisotropy increases relatively fast with increasing shearing for small displacements. For larger displacements, this growth decreases. However, AF variations depend on the aperture definition with higher values observed for \( a_{\text{vert}} \) and more dispersion (\( \sigma_{eff}^{a} \)) related to \( a_{\text{eff}} \). We also note that the range of values obtained for \( \sigma_{\text{eff}}^{a} \) is of the same order of magnitude than the experimental values obtained by Auradou et al. (2005) on a granite replicated fracture sheared until \( 1\,\; {\text{mm}} \). However, replication of such experiment would be needed to confirm that the fractures simulated are geometrically coherent with rock samples.

Concerning the potential fracture scale effects on the previous results, we can consider the experimental study of Kumar Singh et al. (2016). One main result of this previous article is that on real samples increasing the fracture scale leads to a decrease of the flow rate. Also, in the present work, the measured flow rates might decrease if we consider a larger fracture scale. However, the impact on the anisotropy factor is not direct and will be investigated in an additional study. Finally, channelling appears to be fracture scale independent as described in Watanabe et al. 2015.

In order to deepen the investigation of the shearing effects on the hydraulic properties of a fracture, the study is expanded on flow channelling, a phenomenon that can be directly linked to anisotropy (Auradou et al. 2005, 2006).

Channelling is described as a spatial concentration of flow along preferential pathways. Indeed, flow tends to focus on high permeable zones and this creates preferred paths with higher velocity (Knudby and Ramírez 2005; Koltermann and Gorelick 1996). Also, for each simulation, channels are identified as largest connected area of high flow rate values (Fig. 14). In this work, we defined the identification threshold to be the third quartile (\( Q3 \)) of flow rate values. The channel identification method consists in applying this threshold on the fluid flow and detecting the connected zones. Herein, connected areas are defined as areas showing flow rates above the threshold (\( Q3 \)) and being connected, respectively. The maximum number of individual parallel channels developing in a fracture of a side length of \( n \) elements, with \( n \) being an even number, is \( n/2 + 1 \).

Fig. 14
figure 14

Identification of channels (b) and its associated flow rate distribution (a), example based on \( a_{\text{eff}} \) and in the \( \bot \) case. The flow rate values are in \( {\text{m}}^{3} \;{\text{s}}^{ - 1} \) which is equivalent to \( 10^{9} {\text{mm}}^{3} \;{\text{s}}^{ - 1} \). Note that each colour on b labels a different channel and the background colour is set to black corresponding to the flow rates blow the \( Q75 \) quartile

Full size image

For this channel identification, two indicators are applied to follow channelling evolution inspired from Le Goc et al. (2010). The first one (\( I_{1} \)) quantifies the relative proportion of channel area in a fracture and the second one (\( I_{2} \)) quantifies the continuity of the flow path by measuring the maximum channel length in a given fracture. \( I_{1} \) is defined as:

$$ I_{1} = \frac{1}{N}\mathop \sum \limits_{i = 1}^{N} \mathbb{1}_{{\left\{ {\varvec{Q}_{\varvec{i}} > \varvec{Q}75, \varvec{ i} \in {\mathbf{\mathcal{C}}}} \right\}}} , $$
(17)

where \( \varvec{Q}_{\varvec{i}} \) is the flow rate vector at the ith element of the fracture, \( {\mathcal{C}} \) is the set of elements belonging to one of the \( n/2 + 1 \) channels and \( N \) the total number of elements such that \( N = n \times n \). If the flow rate is homogeneous over the fracture area, \( I_{1} \) is equal to zero as no element verifies \( \varvec{Q}_{\varvec{i}} > Q75 \). In the case of a flow rate superior to \( Q3 \) distributed among \( n/2 + 1 \) wide and \( n \) long channel(s), we obtain \( I_{1} \sim (1/N) \times \left( {n^{2} /2} \right) = 1/2 \). More generally, for channel(s) of width \( l_{w} \) and length \( n \), we have \( I_{1} = (1/N) \times n \times l_{w} = l_{w} /n \) for \( l_{w} < n \). Thus, \( I_{1} \) tends toward \( 1 \) for increasing channelling which is defined as a combined increase of the channel(s) size as well as their number.

\( I_{2} \) is defined as the major axis of an ellipse that encapsulates the largest channel normalized by \( n \). \( I_{1} \) and \( I_{2} \) are expressed in percentage where \( I_{2} \) can exceed \( 100\% \) as the orientation of the largest channel is not necessarily parallel to \( \vec{x} \) or \( \vec{y} \) direction. Figure 15 displays the values \( I_{2} \) over \( I_{1} \) for each simulation and for each initial configuration of \( \{ a_{\text{vert}} ,a_{\text{eff}} \} \) and \( \left\{ {\parallel , \bot } \right\} \). Moreover, realizations of the same shearing displacement are shown with identical colour. Thus, the effect of shearing on channelling behaviour, represented by \( I_{1} \) and \( I_{2} \), can be studied for all cases.

Fig. 15
figure 15

Scatter plot of \( I_{2} \) in terms of \( I_{1} \) for each simulation configurations based on \( \left\{ {a_{\text{vert}} , a_{\text{eff}} } \right\} \) and \( \left\{ {\parallel , \bot } \right\} \). The colors refer to the offset displacement and points of same color therefore represent the 70 simulation replications of each offset. The black crosses represent the centroid of each offset cloud and the red line is the linear trend line fitted on them (color figure online)

Full size image

By plotting the centroid for every shearing set of realizations, the general variation of \( I_{1} \) and \( I_{2} \) with shearing can be observed and quantified through the slope \( \alpha \) and the intercept \( \beta \) of the linear trend lines (Table 2). Larger values of \( \alpha \) indicate a faster increase of \( I_{2} \) compared to \( I_{1} \). It is shown that \( I_{2} \) increases faster than \( I_{1} \) for all simulation configurations. Thus, the increasing connectivity of channelling represented by \( I_{2} \) is more fostered by shearing than the proportion of channelled high flow rates indicated by \( I_{1} \). It can also be observed that increasing shearing leads to significantly higher values of \( I_{1} \) and higher or equivalent values of \( I_{2} \) with higher associated uncertainty, defined as the area of the data distribution for a given shearing displacement. Additionally, we notice as well that the data sets are significantly spread along the \( I_{2} \) axis reflecting a higher uncertainty for \( I_{2} \) compared to \( I_{1} \). Higher dispersion is also observed for small shear displacements and in particular for \( N_{\text{offset}} = \left\{ {0.31, 0.62} \right\} \).

Table 2 Coefficients of the linear trend lines for the distribution of centroids (Fig. 15)
Full size table

The analysis of the channelling dependence on the aperture definition exhibits that the evolution of \( \alpha \) for the configurations \( \left\{ {\parallel , \bot } \right\} \) is inverse compared to \( \{ a_{\text{vert}} ,a_{\text{eff}} \} \) With \( a_{\text{vert}} \), we observe that \( \alpha \) is smaller by a factor of \( 2 \) comparing \( \parallel \) to \( \bot \) simulation cases. For \( a_{\text{eff}} \), however, \( \alpha \) more than doubles from \( \parallel \) to \( \bot \). Ultimately, we analysed here an extreme case in terms of the directions of pressure gradient and shearing. Herein, the relative evolution of \( I_{1} \) and \( I_{2} \) defined by \( \alpha \) are inverse according to the aperture considered (Table 2). This reinforces the major impact of aperture definition in channelling process analysis with shearing on dispersion and relative evolution of channelling indicators.

To quantify the dispersion of the channelling indicators, we define the relative standard deviation for both values at a given \( N_{\text{offset}} \) as follows:

$$ \tilde{\sigma }_{{N_{\text{offset}} }}^{I} = \frac{{\sigma_{{N_{\text{offset}} }}^{I} }}{{C_{{N_{\text{offset}} }}^{I} }}, $$
(18)

where \( \sigma_{{N_{\text{offset}} }}^{I} \) is the standard deviation of the indicator \( I \) associated with the shearing \( N_{\text{offset}} \). \( C_{{N_{\text{offset}} }}^{I} \) is the centroid value for all indicators \( I \) of one offset. We observe that \( \tilde{\sigma }_{{N_{\text{offset}} }}^{{I_{1} }} \) and \( \tilde{\sigma }_{{N_{offset} }}^{{I_{2} }} \) differ by more than one order of magnitude (Fig. 16). This quantifies the previous observation that the dispersion of \( I_{2} \) is globally larger than the one of \( I_{1} \) (Fig. 15). Nevertheless, no homogenous tendency of the dispersion with increasing shearing can be observed regardless of the aperture definition for \( I_{1} \). Considering the aperture definitions, only \( I_{1} \) shows variations related to it, whereas \( I_{2} \) varies more significantly with the pressure gradient direction.

Fig. 16
figure 16

Plots of the relative standard deviations in percentage of \( I_{1} \) and \( I_{2} \) in terms of shear displacement for each simulation configurations based on \( \left\{ {a_{\text{vert}} , a_{\text{eff}} } \right\} \) and \( \left\{ {\parallel , \bot } \right\} \). See Eq. (18) for the literal expression of the relative standard deviation

Full size image

After considering the variations of \( I_{1} \) and \( I_{2} \) with shear displacement, we study these variations with the outgoing flow OF values (Fig. 17). Maximum values of OF are obtained for high \( I_{1} \) values corresponding mainly to the largest three shearing displacements spreading widely along the \( I_{2} \) axis. If we analyse these graphs regarding aperture definition, it is shown that two clusters of high OF fractures can be identified (encircled grey in Fig. 17) for \( a_{\text{vert}} \). This clustering may indicate that for \( a_{\text{vert}} \) two types of high OF fractures can be differentiated, showing similar values of \( I_{1} \) and significant differences of \( I_{2} \). However, this typology is not shown in case of \( a_{\text{eff}} \). Also, further experimental investigations should be carried out to determine if channelling clustering is observed. These results then can substantially contribute to identify which aperture definition represents the reality best.

Fig. 17
figure 17

Scatter plot of \( I_{2} \) in terms of \( I_{1} \) for each simulation configurations based on \( \left\{ {a_{\text{vert}} , a_{\text{eff}} } \right\} \) and \( \left\{ {\parallel , \bot } \right\} \). Note that the colors refer to the outgoing flow value OF as defined by the Eq. (14) and (15). Grey circles indicate possible clustering of the fractures according to their channelling behaviour (color figure online)

Full size image

5 Conclusions

Although fluid flow in fractured rock is investigated since many years, the impact of the complex interplay between fracture geometry and hydraulic flow under field scale scenarios remains an important research subject. At larger scales and in the geothermal context, this impact of the geometrical characterization of the fracture may lead to a re-examination of the principles used to predict the fluid circulation in the reservoir and its dynamic with the stress field. The present paper presents an important step towards bridging small-scale to large-scale applications. The current investigation becomes, therefore, most important when the uncertainty range of large reservoir models needs to be quantified. By specifying a stochastic approach, both LCL models, based on \( a_{\text{eff}} \) and on \( a_{\text{vert}} \), yield a large dispersion range of anisotropy (AF) with a doubled dispersion of AF for \( a_{\text{eff}} \) compared to \( a_{\text{vert}} \) models. Moreover, for both aperture definitions, we observe that higher permeability is obtained perpendicular to the shearing direction of the fracture. Being coherent with literature, this statement underlines that both LCL models based on \( a_{\text{eff}} \) and \( a_{\text{vert}} \) capture the anisotropy phenomenon. In addition, \( a_{\text{eff}} \) is considered to be more representative to describe hydraulic phenomena than \( a_{\text{vert}} \) as this first is locally perpendicular to the flow directionality. Also, former prediction LCL models with \( a_{\text{vert}} \) must take into account that results for anisotropy may be overestimated and present higher dispersion range in the case where they will be based on the more representative \( a_{\text{eff}} \) aperture. Finally, regarding the evolution trend of AF, we evaluated that small shear displacements up to \( 0.94 \;{\text{mm}} \) are more reliable to assure an increase of AF regardless of the aperture definition. These observations aim to support the direct calibration of pre-existing LCL anisotropy simulations based on \( a_{\text{vert}} \) toward more representative results using \( a_{\text{eff}} \).

For the channelling indicators (\( I_{1} \), \( I_{2} \)), we observe a higher dispersion of \( I_{1} \) in the case of \( a_{\text{eff}} \) and no specific trend for \( I_{2} \) between the two aperture definitions. The channelling common trends to both apertures are a growing proportion of channels (\( I_{1} \)) with increasing shearing and a significant enhancement of \( I_{1} \) with early shearing compared to later ones. Furthermore, the channel continuity (\( I_{2} \)) is largely dispersed and do not present a trend with shearing. Nevertheless, the variations of \( I_{2} \) with outgoing flow (OF) values indicate a potential typology of the fracture channelling behaviour. Indeed, for a same range of \( I_{1} \), two clusters are observed in the case of \( a_{\text{vert}} \) along \( I_{2} \). Similarly, to the observations made on anisotropy phenomena, the ones related to channelling can adjust existing LCL simulations using \( a_{\text{vert}} \). In addition, the specific clustering of high OF observed with \( a_{\text{vert}} \) is another line of research to deepen the understanding the deviations obtained from LCL models for a crucial parameter for reservoir exploitation.

In future studies, we will weigh our observations with experimental results based on similar synthetic fracture replications using the 3D-printing technology. Moreover, this experimental set up associated with additional numerical simulation will help us to increase the complexity of our model by considering the mechanical effects of shearing on the walls of the fracture and by considering the possible scale effects. This present work can also be a starting point to establish a more accurate prediction of the processes participating into the extension of the flow circulation in reservoir through shearing. In the geothermal context, it could enable us to forecast the dynamic of the heat exchange area with the stress field. Indeed, the shearing displacements studied can be associated with earthquakes of magnitude \( 1 - 2 \) which are representative of a geothermal seismic activity. This paper may also be concluded by remaking that aperture is a determinant factor for fluid flow equations and thus, we estimate that the sensibility of fluid flow interpretation with aperture definition presented here can be found in more refined flow simulations. Finally, the goal to raise attention on the spatial fracture descriptions impacts on averaged and dispersion values of fluid flow phenomena is embodied by this study.