1 Introduction

Fault surface roughness is a principal factor controlling earthquake rupture nucleation, propagation and arrest, and possibly dynamic friction during seismic slip (Scholz, 2002). However, the characterization of fault roughness is limited to a few examples of fault zones exhumed from <5 km depth and generally hosted in sedimentary and volcanic lithologies (e.g., Power et al., 1987; Lee and Bruhn, 1996; Sagy et al., 2007; Candela et al., 2009).

Following Power et al. (1988), roughness is defined as the offset with respect to a mean reference line (1D profiles) or plane (2D surfaces), which statistically represent the mean fault surface. Previous studies of fault roughness were based on direct measurement of exposed fault surfaces, either with some kind of mechanical profilometer (Power et al., 1987; Lee and Bruhn, 1996), or with LIDAR (laser imaging detection and ranging) terrestrial laser-scanning (Renard et al., 2006; Sagy et al., 2007). The first approach yields profiles where topography of the fault surface is expressed as a function of distance along the profile (1D profile), whilst the second methodology provides a point cloud which represents a discrete sampling of the fault surface (2D surface), from which 1D profiles are extracted for analysis along different orientations.

Since the pioneering works by Brown and Scholz (1985) and Power et al. (1987, 1988), who recognized that natural fault and fracture surfaces show a “fractal” (later better defined as self-affine) topography, fault surface roughness has been studied by means of mathematical techniques which allow the assessment and characterization of this behaviour, integrating measurements at different length scales (wavelengths). Different mathematical methodologies are critically reviewed in Power et al. (1988), Schmittbuhl et al. (1995a), Lee and Bruhn (1996) and Candela et al. (2009), whilst Schmittbuhl et al. (1995b) discuss the reliability of such measurements. The general conclusion of these reviews is that Fourier power spectrum methods are amongst the most well-suited and robust to recognize and characterize self-affine fault roughness, and these methods have become a current best practice in this kind of study (e.g., Sagy et al., 2007; Candela et al., 2009).

Here, we investigate the roughness of slip surfaces from the seismogenic dextral-reverse Gole Larghe Fault Zone (GLFZ), exhumed from ca. 10 km depth and hosted in granitoid rocks of the Adamello batholith (Italian Alps, Di Toro and Pennacchioni , 2005). Different sets of joints, related to the cooling of the batholith under a tectonic stress field, were exploited by slip surfaces within the GLFZ (Di Toro  et al.  2009; Pennacchioni et al., 2006). The fault zone dips to the South at about 55°, is 550 m thick, accommodates a total displacement 1–1.5 km, and is composed of numerous sub-parallel major fault strands interconnected by secondary fractures and minor faults. Structural markers (dykes, xenoliths, etc.) are cut by the faults and allow the displacement accommodated by each fault to be determined: main faults accommodate displacements up to 20 m (but usually ranging from 5 to 10 m), while secondary faults accommodate displacements of typically less than 1 m (Di Toro  et al.  2009). The fault rock assemblage consists of green in colour indurated cataclasites (cohesive fault rocks cemented by the precipitation of epidote and K-feldspar from hydrothermal fluids) and black pseudotachylytes (solidified friction melts produced by seismic slip). Pseudotachylytes generally intrude the cataclasites and usually represent the last deformation event recorded by each of the individual fault strands of the GLFZ (for a detailed description of fault rocks and architecture see Di Toro  et al. ( 2009).

In this contribution we show: (1) how data on the morphology of fault traces were collected in the field, using LIDAR and digital photos; (2) how these data were assembled in 3D using Gocad®; (3) how 1D Fourier power spectra were extracted from fault trace profiles (1D Fourier analysis); (4) how some parameters, which efficiently describe the self-affine behaviour of roughness data, were calculated; (5) how fault roughness data can be discussed in terms of fault zone evolution with slip; and finally, (6) how these parameters can be used to generate realistic fault surfaces with 2D Fourier synthesis. The quantitative modelling of the morphology of fault surfaces at seismogenic depths is a basic step of a wide-ranging project aimed at producing highly realistic models of seismic rupture propagation (Di Toro et al., 2009). Realistic modelling should be possible by combining (1) friction constitutive equations obtained in a new generation apparatus that better reproduce seismic deformation conditions at a single point of a fault (SHIVA, Di Toro et al., 2010) with (2) the complex geometry of natural fault surfaces.

2 Data Collection

The Gole Larghe fault zone is approximately 20 km long and has its most spectacular outcrops at 2,300–2,700 m above sea level, at the edge of a hanging valley exposed in the last 10 years at the front of the rapidly retreating Lobbia Glacier in the Adamello Massif (Italian Southern Alps). The undulating topography typical of glacier-polished roches moutonnée (Fig. 1) exposes fault traces (intersections of fault surfaces with the outcrop surface) oriented at a variety of angles relative to the net slip vector, and provides a wealth of other structural information.

Fig. 1
figure 1

Outcrops of the Gole Larghe Fault Zone at the front of the Lobbia Glacier, Adamello Massif, Central Italian Alps. The red lines delimit the Gole Larghe Fault zone (GLFZ, about 550 m in thickness). The network of precursor joints crosscuts all outcrops to the right of the fault zone. The terrestrial laser scanner is located on a high spur at the western end of the study area, offering a good vantage point over the studied outcrops. All other survey locations were situated directly on the outcrops for surveys at much higher spatial resolution

Full size image

Fault surfaces are typically almost perpendicular to surfaces of these outcrops, hence roughness of fault traces represents the real roughness of fault surfaces, sampled along different directions. We determined the geometry of fault traces over five orders of magnitude using 3D mosaics of high-resolution rectified digital photographs (10−3–101 m scale), and terrestrial laser-scanning (LIDAR 100–102 m scale). LIDAR scans and photomosaics were georeferenced in 3D using a Differential Global Positioning System (DGPS; see Table 1 for precision and accuracy) allowing detailed multiscalar reconstruction of fault traces in Gocad®. All other structural data, including kinematic data and fault displacements, were georeferenced to the same precision and accuracy.

Table 1 Data sources and their typical spatial resolutions, precisions and accuracies
Full size table

It must be emphasized that the technique used here is different from the direct measurement of exposed fault surfaces (e.g., Renard et al., 2006) in that: (1) both hanging wall and foot wall are preserved and displacements can be determined using markers separated along the slip surfaces; (2) fault rocks (pseudotachylyte and cataclasite in this case) are well preserved and their occurrence, thickness, and microstructural features can be related to fault roughness and offset; (3) the measured roughness is not affected by weathering, as can occur when directly measuring fault surfaces, particularly in carbonate rocks; (4) data collected with LIDAR and photomosaics can be merged to reconstruct power spectra spanning five orders of magnitude.

2.1 LIDAR Survey

A high resolution terrestrial LIDAR survey was carried out in the first phase of fieldwork (Fig. 1). In addition we obtained lower resolution aerial LIDAR data from the Provincia Autonoma di Trento Geological Survey. All these data were used (1) as the main source of our topography data (which have to be very accurate in this project) and (2) for structural interpretation at the larger scales considered in this study (100–102 m). Aerial LIDAR data were acquired as a pre-processed and resampled Digital Elevation Model (DEM), with 2 m/pixel spatial resolution. This DEM covers the entire study area at the front of the Lobbia Glacier and the valley sides (Fig. 2a).

Fig. 2
figure 2

Airborne and terrestrial LIDAR data. a Downsampled airborne LIDAR point cloud of the whole study area at the front of the Lobbia Glacier. b Downsampled terrestrial LIDAR point cloud of the GLFZ. Some fault traces are represented in red in both images

Full size image

Terrestrial LIDAR data were collected over a period of 5 days in August 2008 using a Riegl LMS Z420i terrestrial laser-scanner (Fig. 1). The scanner has a range of up to 1 km and a quoted accuracy of 5 mm at a distance of 200 m. The scanner collects up to 12,000 individual points per second, and assigns each point a local X Y Z coordinate based on the time of flight of the laser beam. The scanner is also equipped with a calibrated Nikon D70 digital camera that is used to take a series of digital photographs which are merged with the scans to assign each LIDAR point a true RGB colour value, rendering the scan data “photorealistic”. The complete LIDAR dataset is composed of a mosaic of 47 individual scans, collected from 38 different scan positions distributed across the study area. As our strategy, we chose to implement such a large number of different scan positions to ensure maximum coverage (i.e., minimal shadow areas) of the undulating outcrops, at high resolution. Individual scans were merged together using RiSCAN PRO® software by Riegl, based on co-registration of highly reflective survey targets of known size, positioned across the outcrops, each of which was precisely located with DGPS.

The result of the terrestrial LIDAR survey is a photo-realistic point cloud composed of about 40 million points, which represents the topographic surface of the studied outcrops (Fig. 2b). This point cloud was used as the basis for fault analysis in two ways: firstly, larger fault traces (100–102 m) were extracted directly from the point cloud data; secondly, the point cloud provided the topographic base for higher resolution analysis using orthorectified photomosaics. For this purpose, the point cloud was imported into Gocad® and meshed to produce a triangulated surface. Consistent with the observation that the Lobbia outcrops are generally very smooth due to glacial polishing, the resulting triangulated surface was smoothed in Gocad® with the Discrete Smooth Interpolator (DSI; Mallet, 2002) to remove small-scale measurement errors associated with the LIDAR data (10−2 m high frequency noise). This is important when draping high resolution photos, as explained in the following section. We emphasize that this meshing and smoothing technique was only applied to the topographic surface of the outcrops, and not to the fault trace data, so it does not affect the fault roughness analysis.

The spatial resolution of the LIDAR data and the associated photos taken from each tripod position typically allow features on the ground surface larger than around 5–10 cm in size to be resolved, but are inadequate for more detailed analysis of roughness that requires higher resolution data. Moreover, since in this study the tripod positions were located on the topographic surface being scanned, the effective resolution of the LIDAR images was significantly reduced by the low angles of incidence between the LIDAR beam and the outcrop surface. Similarly, photos taken from tripod positions suffer from a strong perspective distortion. To achieve higher resolution images of the topographic surface and fault trace profiles, we applied two different methods (orthorectified photomosaics and close range photogrammetry), which are outlined and discussed below.

2.2 Orthorectified Photomosaics of Fault and Joints Traces

We produced high resolution orthorectified photomosaics to obtain a detailed reconstruction of the fault and joint traces. After a preliminary selection of well exposed fault and joint traces that are oriented at varying angles with respect to the net slip vector, 15 transects were collected along six pseudotachylyte-lined slip surfaces of the GLFZ and four precursor joints outside the fault zone. These transects comprise a total of 154 photos, each covering an area of ca. 60 × 40 cm (Fig. 3a, b), collected with a calibrated Nikon D700 camera with 28 mm lens, resulting in a spatial resolution of ca. 0.15–0.2 mm/pixel (Fig. 3c, d). Photos taken along each transect have been co-registered by recognizing common tie points in adjoining photos (precision estimated at a few pixels, hence better than ca. 0.5–1 mm). Control points in each photo were located with DGPS (accuracy ca. 2–3 cm) and the whole photo set (photomosaic) constituting a transect was georeferenced by means of rigid body translation and rotation using the DGPS control points. Finally, the photomosaics were orthorectified and draped on the LIDAR surface in Gocad® (Fig. 3e, f). This procedure was followed to maintain the best precision from each dataset. The location of each photo with respect to the neighbouring one is well defined at the scale of the spatial resolution of the photos, and draping of photos on the LIDAR surface is consistent with LIDAR and DGPS data accuracy.

Fig. 3
figure 3

Method to acquire the fault and fracture traces and to drape them onto the LIDAR topographic model. a A typical 60 × 40 cm frame captured along a pseudotachylyte fault trace. b The same as a, with a digitized fault trace in red. c, d Enlargement of red box in Fig. 2a, b. Pseudotachylytes are black in colour and cataclasites are green. (e, f) A single orthorectified photo frame, and several frames, draped on the outcrop surface reconstructed in Gocad® from terrestrial LIDAR data. g Final result of the draping and interpretation workflow, with fault traces draped on outcrop surfaces

Full size image

2.3 Close Range Photogrammetry

An alternative approach to high-resolution imaging relies on a complete close-range photogrammetry workflow. A detailed presentation of digital photogrammetry theory and techniques can be found in Kraus (2007). Of relevance to our study, this technique allows one to derive a point cloud, similar to those obtained with LIDAR, from pairs of photos shot from different viewpoints (stereo couples). These data, which were collected for selected outcrops only, can be registered and merged with the lower resolution LIDAR dataset, resulting in a variable-resolution dataset that attains the higher spatial resolution and accuracy only where this is really needed (Fig. 4).

Fig. 4
figure 4

Wavy fault trace 3D image draped on outcrop surface reconstructed by photogrammetry and merged with lower-resolution LIDAR point cloud in Gocad®

Full size image

Once the point cloud is obtained, the same workflow as above, including draping of orthorectified high-resolution photos, can be completed. The same photos used to reconstruct the point cloud or an independent set (e.g., with a higher resolution) can be used. Since these photos can be shot from an arbitrarily close distance (“close-range” photogrammetry), and with an optimal orientation with respect to outcrop surfaces (almost perpendicular), problems arising with photos taken from LIDAR stations (resolution and perspective distortion) are solved. Also, problems related to draping high-resolution photomosaics on LIDAR surfaces that have lower spatial resolution and accuracy may be solved using this methodology. The main limitation with the photogrammetry approach is that it results in huge datasets, which are cumbersome to process and manage during subsequent interpretation, particularly if the very high resolution of the photomosaics is to be maintained (0.2 mm/pixel), thus it has been applied to limited areas only.

2.4 Accuracy, Precision and Spatial Resolution

Data sources and their typical spatial resolutions, precisions and accuracies are shown in Table 1. It is apparent that, although accuracy and precision are separate parameters to spatial resolution, there is a close correlation between them, at least with the different data sources that we have used. The absolute accuracy of topographic data with respect to a global reference frame can be difficult to quantify. However, the main scope of this work is the determination of fault roughness at different length scales. Since roughness is measured as the offset of the fault surface with respect to a local reference line (1D profiles) or plane (2D surfaces), it follows that in this work we are mainly concerned with “internal” precision, since any systematic bias is cancelled by the subtraction operation. Moreover, when assessing the fractal behaviour of a rough surface, the required precision scales with the length scale (or with the inverse of the spatial frequency). Consequently, our multiscale dataset is well suited for the analysis performed here, because for the errors associated with each type of data are much smaller than the minimum scale of objects identified within that data. In particular, the photomosaics provide very high resolution and precision for the more detailed analysis (mm to m scale), whilst the lower resolution and precision of the terrestrial and airborne LIDAR are balanced by their larger area of coverage, which allow high-quality analysis at the larger scales (>1 m in wavelength).

3 Data Analysis and Modelling

In this section, we outline the workflow that leads from 3D high-resolution outcrop imagery to the definition of parameters that characterize fault surface roughness. This workflow can be split into an interpretation phase, carried out in Gocad®, and a Fourier analysis phase, carried out with a custom-made Matlab® toolbox.

3.1 3D Imagery Interpretation

Digitizing fault traces directly in Gocad® or in another 3D tool, either using point or line objects, would result in an incredibly time-consuming procedure if we want to pick points at the same 0.2 mm/pixel resolution of photomosaics. For instance, a typical 15 m long fault trace will result in ca. 75,000 hand-picked points. This problem was solved by digitizing fault traces on photos prior to draping, using a standard digitizing pen (of the kind used by graphic designers) and general-purpose image processing software. This results in a very accurate and quick interpretation (Fig. 3a–d). The fault trace was then imported into Gocad® using the same projection parameters as for the underlying outcrop image (Fig. 3e–g).

At this point in the workflow, we draped the high resolution 3D fault traces on the outcrop surfaces (Fig. 5a), and completed the geological interpretation. Small offsets (<2–3 cm) due to younger cross-cutting fractures were removed and the overall continuity of the pseudotachylyte-bearing fault traces was restored. Using the resulting fault traces we produced a best fit reference plane for each fault surface in Gocad® (Fig. 5b), which is used in Fourier analysis of the roughness (see Sect. 3.2). The undulating topography of the outcrop surface allowed different photomosaic transects to be produced for each slip surface. The different photomosaics have a variety of orientations with respect to the slip vector of the selected fault surface (Fig. 5c). This will be important when analyzing roughness anisotropy (see Sect. 3.2).

Fig. 5
figure 5

Determination of fault surface roughness with respect to a reference average fault plane. a Fault traces draped on outcrops. b Interpolation of best fit plane with Principal Component Analysis (PCA) for each fault strand. c Selection of “almost straight” fault traces, making different angles with respect to slip vector, for Fourier analysis

Full size image

Other structural data (e.g., fault separations) were collected on 3D images and exported as ASCII XYZ tables for the following steps of the analysis.

Additional fault traces were identified and picked directly from the raw airborne and terrestrial laser-scan data (Fig. 2). Due to the lower resolution of these data, this was most effective for faults associated with some topography, such as a small gully or break in slope. Picking of fault traces was carried out manually using RiSCAN PRO® software, and points along the fault traces were exported as ASCII XYZ table for further analysis.

3.2 Fourier Analysis of Fault Traces

The Matlab® script (available upon request from the author) used to analyze fault surface roughness is composed of several data processing and analysis functions, each one with different options: (1) pre-process data (clean and choose monotonic dimension); (2) define best-fit interpolating plane; (3) select “almost straight” segments from a profile; (4) resample data; (5) calculate orthogonal offset from best-fit plane; (6) apply taper function; and (7) conduct power spectrum analysis. In addition, functions for loading and saving data (including ancillary structural data such as slip vector, net slip) and plotting functions are provided, resulting in an integrated analysis toolbox. Here we give details about the most important and critical points in a typical analysis.

In the pre-processing function, raw data imported from Gocad® (or any other source of roughness data) is cleaned to eliminate duplicate points and points that do not follow a strict monotonic succession along a chosen direction, either X, Y or Z. This is necessary for Fourier analysis.

An interpolating best fit reference plane can be defined in different ways. This step of the analysis is non-trivial since roughness is defined as the deviation of points on a non-planar surface measured normal to the reference plane, and in Fourier analysis it is required that the dataset has no trend or large-scale slope discontinuities in general with respect to the reference. Options provided in our Matlab® toolbox include input of the reference plane defined in Gocad® or interpolation of a best fit plane by means of principal component analysis (PCA). PCA seems better suited than traditional least squares to fitting a mean plane to a point cloud, since uncertainty along X, Y and Z is treated in the same way, whilst in least squares the plane is seen as Z = a(X,Y), with uncertainty in Z only, and the result may change if functions X = b(Y,Z) or Y = c(X,Z) are considered.

Then an arbitrary segment or a complete fault trace can be selected for the analysis. We chose transects in the field based on our ability to gather data on fault surface traces at pitches (i.e., rakes) ranging from parallel to nearly perpendicular to slip vectors deduced from fault surface striations. As shown in Fig. 5, this ability was dictated by the intersection of the fault surface with undulating rock outcrop topography (i.e., the fault trace). If roughness anisotropy (i.e., how the roughness in a fault surface varies along profiles oriented at different angles with respect to the slip vector) is to be investigated, it is important that each fault segment selected for Fourier analysis is almost straight so that the fault trace has a constant angle with respect to the rake or pitch.

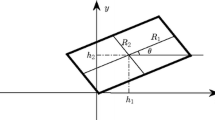
Data from each fault segment are used to calculate the offset function h(x), defined as the distance measured orthogonal from the reference plane (Fig. 6a, b). This kind of profile can be immediately interpreted in terms of root mean square roughness

$$ \sigma_{\text{RMS}} = \sqrt {\frac{1}{L}\int\limits_{L} {h^{2} (x){\text{d}}x} } $$
(1)

where L is the profile length. This is the quadratic mean of the offset with respect to the reference surface, as shown in Fig. 6c.

Fig. 6
figure 6

A typical fault trace profile ready for Fourier analysis, with (b) or without (a) vertical scale exaggeration. Insets highlight the geometrical meaning of h(x) and σ RMS (c), and the moving average filter (d) and taper function (e) applied to profiles prior to Fourier analysis

Full size image

Then the offset function h(x) is re-sampled to a constant spacing (spatial frequency) by means of a moving average filter (Fig. 6d). This, being a low-pass filter, does not introduce biases in power spectra. These data are then multiplied by a taper function (Fig. 6e), to avoid edge effects due to abrupt truncation of data at the extremities of the measured trace, and are ready for Fourier analysis.

Power spectral density functions have been calculated with three different methods, yielding similar results, but with a different noise level. The classical periodogram method (Schuster, 1898), which involves taking the square of the modulus of the Fast Fourier Transform (FFT), gives reliable results, but with a higher noise level. The Thomson Multitaper Method (MTM, Thomson, 1982) and Welch method (Welch, 1967) are characterized by a lower noise level (generally the Welch method is the preferred method), but in general the overall shape of the power spectrum is the same for all three methods. Results of this analysis are shown in Fig. 7, in terms of power spectral density profiles, where f is the spatial frequency in m−1 and P(f) is power spectral density in m3 (these units represent a squared amplitude in m2 divided by a spatial frequency in m−1). Note that spatial frequency can be indicated also as the wavenumber (but sometimes a 2π factor is included in this quantity), and is the reciprocal of the wavelength λ.

Fig. 7
figure 7

Power spectral density analysis of faults and joints. a Power spectral density profiles for joint traces imaged with photomosaics. b Power-law fit for joint profiles. c Power spectral density profiles for fault traces imaged with LIDAR (larger scale) and photos (smaller scale). All data, independently of the orientation and length scale, are included in this plot. d Power-law fit for fault profiles

Full size image

Sensitivity of all methods to different resampling frequencies and taper functions has been tested, and the results are considered quite robust. We have also tested the estimate of power spectral density based on the Lomb-Scargle algorithm (Press et al., 2007), which does not require resampling of the dataset to a constant spacing, as it is not based on the FFT. The Lomb–Scargle algorithm yielded results similar to those of the other methods, but with a higher noise level, particularly at high frequencies, and it is very slow in terms of computation time, so we discarded this method in our analysis.

To better understand the physical meaning of this kind of analysis, we may recall that (Wiener–Khinchin theorem, in James, 2002) the power spectral density P(f) corresponds to the Fourier transform of the autocorrelation function C(Δx) of the offset function h(x)

$$ P(f) \rightleftharpoons C(\Updelta x) $$
(2)

where the autocorrelation function, defined as the cross-correlation of a signal with itself, measures the correlation between a profile and itself, when it is shifted by a certain distance Δx

$$ C(\Updelta x) = \int_{ - \infty }^{ + \infty } {h(x + \Updelta x)h(x)} {\text{d}}x $$
(3)

To clarify its meaning, we recall that the autocorrelation of a periodic signal is periodic with the same period as the signal. On the other hand, the autocorrelation of white noise tends to zero, excluding a sharp maximum at Δx = 0. When applied to spatial data, the meaning of the autocorrelation function is very similar to that of the variogram as defined in geostatistics, and in fact some authors have used this kind of analysis for fault roughness data (e.g., Ecker and Gelfand, 1999).

This being the integral of the power spectral density over a certain interval (in the frequency domain) equals the squared variance of the input signal, hence the root mean square roughness can be also defined as

$$ \sigma_{\text{RMS}} = \sqrt {\int_{{f_{\min } }}^{{f_{\max } }} {P\left( f \right){\text{d}}f} } $$
(4)

This highlights the relationship between the power spectrum and the root mean square roughness, which can be seen as a sort of “averaged” roughness, but still is scale-dependent for a self-affine profile, since it depends on the integration interval [f min , f max], and hence on the length scales over which it is measured.

Up to this point in the discussion, we have assumed, without proving it, that fault or fracture surfaces may show a “fractal”, self-similar or self-affine topography or roughness (Mandelbrot,  1982, 1985). When analyzed by means of power spectral density functions, surfaces are defined “fractal” if they show a linear decay in power spectrum, when represented in a Log–Log diagram, which implies a power-law decay characterized by a certain exponent

$$ P(f) = P_{1} f^{{ - (1 + 2{\text{H}})}} $$
(5)

or

$$ \log (P) = \log (P_{1} ) - (1 + 2H)\log (f) $$
(6)

where H is the Hurst exponent and P 1 is the prefactor of the power spectral density. Both these parameters can be obtained by linear regression in a Log–Log plot. Results are shown in Figs. 7–10. The coefficient of determination R 2 for linear regression was always between 0.92 on 0.96 in this study. Substituting (5) in (4) we obtain

$$ \sigma_{\text{RMS}} = \sqrt {\int_{{f_{\min } }}^{{f_{\max } }} {P\left( f \right){\text{d}}f} } = \sqrt {\int_{{f_{\min } }}^{{f_{\max } }} {P_{1} f^{{ - (1 + 2{\text{H}})}} {\text{d}}f} } = \sqrt {\left[ {{\frac{{P_{1} f^{{ - 2{\text{H}}}} }}{ - 2H}}} \right]_{{f_{\min } }}^{{f_{\max } }} } $$
(7)

where we can easily see that σ RMS scales with f  –H, hence with λ H. This explains why a surface can be defined as self-similar for H = 1 and self-affine for H < 1. In the first case, the geometric pattern of the surface is replicated self-similarly at every length scale, as the amplitude of the deviations from the reference plane increases linearly with wavelength. In the self-affine case, a scaling factor is applied to the replicating pattern (Schmittbuhl et al., 1995a), which introduces a decay of roughness at increasing wavelengths. This implies that the fault trace tends to a straight line (or the fault surface tends to a plane) at large scale. Most natural fault and fracture surfaces, and fracture surfaces produced in experiments, show a self-affine behaviour with 0.8 ≥ H ≥ 0.5 (e.g., Schmittbuhl et al., 1993; Amitrano and Schmittbuhl, 2002).

Roughness anisotropy can be recognized comparing H, σ RMS and P 1 for profiles collected along a single fault, but with different orientation with respect to the slip vector (e.g., Lee and Bruhn, 1996). The same parameters also make it possible to compare roughness of different fault surfaces (e.g., faults with different net slip, or faults developed in different rocks). The root mean square roughness σRMS seems to be a “natural” parameter to compare the average roughness of different profiles, but it should be used with some caution because it is a function of the frequency interval. In this work we have considered σ RMS calculated over a standard interval that covers our entire dataset, with f max = 102 and f min = 10−2. All these results, regarding P(f), H, P 1 and σ RMS for different faults and joints, will be discussed in the following section.

3.3 Generation of Synthetic Self-Affine Fault Surfaces

Synthetic self-affine fault surfaces can be generated using, for example, algorithms by Bierme et al. (2007), and Clausel and Vedel (2009), which have already been applied to natural faults by Candela et al. (2009). Other algorithms are available and are very common in materials science and tribology, as shown for instance in Wu (2002). These algorithms accept as input parameters the Hurst exponent H and the prefactor P 1. The surfaces generated with this method are different at each run (the algorithms produce random surfaces), but they all share the input statistical parameters H, P 1, σ RMS. On mathematical grounds, using parameters determined from 1D power spectrum analysis in 2D Fourier synthesis is justified, since the 2D Fourier transform always has separable variables in the frequency domain, even in cases where variables are not separable in the spatial domain (James, 2002). In other words, the 2D Fourier transform is by definition composed of two separable 1D transforms in the frequency space, hence it is always possible to reconstruct it from its parts as we do here.

In a first instance, we have used this kind of synthetic surface to validate our analysis. After having generated surfaces with given H and P 1, we were able to extract linear profiles oriented in different directions (simulating the sampling operated by outcrops), analyze them as specified in the previous chapter, and obtain correct H and P 1 values (error <10%). This test supports the robustness of our workflow.

Moreover, this kind of algorithm is particularly useful because the output 2D synthetic surfaces can be used in a wide spectrum of applications as a realistic fault surface model.

4 Roughness of Faults at Seismogenic Depths

Traces of slip surfaces of the GLFZ and precursor joints have been analyzed at length scales ranging between ca. 500 m and 0.5 mm with a combination of LIDAR and photomosaic data. In this section we present results of roughness power spectral density analysis for slip surfaces and precursor joints, the latter outcropping a few hundred meters outside the fault zone. We compare these results with the scale of faults, present data on roughness anisotropy, and finally show some modelling results from 2D Fourier synthesis.

Precursor joints (12 m–0.5 mm scale) show a very consistent self-affine roughness, with power spectra that appear as straight lines in a Log–Log diagram (Fig. 7a). Interpolating with a power-law of the form of Eq. 6 (Fig. 7b) yields Hurst exponents H = 0.82 ± 0.02, prefactors P 1 = 3.6 × 10−5 ± 1.5 × 10−5 m2, and root mean square roughness σ RMS = 0.20 ± 0.05 m (integrated over the interval 10−2 ≤ f ≤ 102 m−1) (Fig. 8a). These results are not influenced by the direction of the measured profile, hence roughness of precursor joints is isotropic.

Fig. 8
figure 8

Parameters defined from power-law fit of joint and fault power spectral density profiles. a Hurst exponent versus σ RMS and P 1 for joints. b Hurst exponent versus σ RMS and P 1 for faults. Fields with values of large scale faults and joints are highlighted

Full size image

Considering faults, power spectral density functions are quite consistent over the ca. 500 m to 0.5 mm range, and show a relatively constant slope in a Log–Log diagram, which can be interpreted as evidence for self-affine behaviour (Fig. 7c). Fault traces interpreted directly on the LIDAR data at larger scale show more noise (Fig. 7c), but in any case can be compared with data collected with high-resolution photos, and it must be noted that all profiles lie approximately on the same trend, for frequencies between 4 × 10−2 and 3 × 102 m−1, indicating a general self-affine behaviour. Interpolating with power-laws of the form of Eq. 6 (Fig. 7d) yields Hurst exponents in the range 0.5 ≤ H ≤ 0.9, prefactors in the range 0.03 × 10−5 ≤ P 1 ≤ 15 × 10−5 m2, and root mean square roughnesses in the range 0.04 ≤ σ RMS ≤ 0.55 m (integrated over the interval 10−2 ≤ f ≤ 102 m−1) (Fig. 8b). The root mean square roughness shows a positive relationship with the Hurst exponent, hence smoother profiles are particularly smooth at large wavelengths (small frequencies). On the other hand, prefactors do not show any relationship with H (Fig. 8b). Noteworthy, values measured on precursor joints lie on the same trend, but in a more limited field, as values measured on faults (Fig. 8, compare a, b). Considering faults measured at small scale, with spatial frequencies in the 100 to 3 × 102 m−1 range, the Hurst exponents show a marked variability, between ca. 0.55 and 0.85. Considering larger profiles, picked directly on LIDAR data, which yield power spectra in the 4 × 10−2 to 100 m−1 frequency range, the Hurst exponents do not show this variability and show values of ca. 0.70–0.80 (Fig. 8b).

We have investigated the anisotropy of slip surfaces using data collected along fault traces forming an angle between 0° and 75° to the slip vector. Plotting H and σRMS versus the angle between the measured fault trace and the slip vector, a positive relationship can be detected for both parameters. Considering (as above) the higher spatial frequencies between 100 and 3 × 102 m−1, the Hurst exponent varies between 0.55–0.6 along slip and 0.8–0.85 at a high angle to the slip vector (Fig. 9), whilst the root mean square roughness varies between 0.04 and 0.55 m. This means that faults are smoother along slip, and that this departure from isotropy is more marked at small frequencies (large wavelengths). On the other hand, faults do not show any anisotropy at larger wavelengths (4 × 10−2 to 100 m−1).

Fig. 9
figure 9

Roughness anisotropy of faults. Hurst exponent and σ RMS are plotted versus the angle between the measured fault trace and the slip vector. Parent-values of cooling joints and inferred qualitative trends for small-scale faults (red) are evidenced

Full size image

In Fig. 10 we present four examples of profiles measured on the same fault, but at different angles to the slip vector. In all four examples the slope of the power spectrum is lower (hence H is lower) for profiles collected parallel to the slip vector. This confirms the different distribution of roughness with wavelength depending on direction (faults are relatively smoother at large wavelengths when measured parallel to the slip vector). However, interpreting the absolute elevation of these curves, collected along a single fault trace segment, is more difficult. In fact, the along-slip power spectrum can be locally higher or more depressed than the one measured at high angle to the slip vector. This is due to a fine scale variability in the prefactor P 1, already evidenced by Candela et al. (2009), which, at small scales, strongly depends on where on a single fault it is measured, due to the variability of roughness at large scale (this is another effect of the self-affine nature of fault roughness). Hence, the absolute elevation of roughness profiles is better defined by averaging a large number of measurements carried out on different fault traces.

Fig. 10
figure 10

Roughness anisotropy of individual faults. Each plot represents a fault for which different traces have been measured, with different orientations with respect to the slip vector

Full size image

Finally, in Fig. 11 we show in map view a 40 × 40 m 2D fault surface generated using a 2D synthesis algorithm modified after the one provided by Candela et al. (2009), with mean Hurst exponent and prefactor values of the GLFZ slip surfaces (H = 0.75, P 1 = 0.4 × 10−5). The maximum offset of the synthetic surface with respect to the reference average plane is of ca. 15 cm, and the distribution of roughness at different wavelengths, controlled by the Hurst exponent, is highly realistic. Anisotropy was not considered here because we have seen that it is relevant only at small wavelengths. These synthetic surfaces will be used in next-generation, highly realistic models of seismic rupture propagation which will include constitutive friction equations obtained in the laboratory (Di Toro  et al., 2009).

Fig. 11
figure 11

Map view of a synthetic 2D self-affine surface generated using roughness parameters equivalent to those of the GLFZ. Colour scale indicates deviation with respect to the reference average fault plane

Full size image

5 Discussion

One of the main goals of this study is the development of a methodology which exploits well-exposed fault traces to define the roughness of fault surfaces over several length scales (almost five orders of magnitude in this work). According to the method proposed here, this is possible by combining LIDAR scans of large and polished outcrop surfaces with high-resolution orthorectified photos of fault traces. Compared to the direct measurement of fault surfaces, this methodology has several advantages. One of the major advantages is that it allows reconstruction of fault surface geometry based on numerous exposed fault traces which have variable orientations with respect to the slip vector. This is a common situation in many outcrops (in contrast to the very rare occurrence of exposed fault surfaces), and hence the methodology proposed here may be widely applied. A second advantage is that, since surface roughness is determined from fault traces and not from surfaces exposed to the atmosphere, the measurement of roughness is not influenced by weathering processes. Finally, because both hanging wall and foot wall, and the interposed fault rocks, are preserved, fault displacements, fracture distributions, and fault rock assemblages can be surveyed and quantified, and precisely georeferenced samples can be collected. Then these data can be related to fault surface geometry in order to shed new light on fault zone processes involving roughness development and refinement.

Regarding the GLFZ case study, the analysis of fault surface roughness (sect. 4) yield further insights into the mechanical evolution of this fault zone (Di Toro  et al., 2009).

Precursor cooling joints are relatively smooth, show a Hurst exponent of ca. 0.8, and no anisotropy. This is common for joints in rocks, developed under different conditions (Schmittbuhl et al., 1995a), and has been interpreted as consistent with “Brownian motion” models of fracture growth in heterogeneous materials (e.g., Mandelbrot, 1985). Of interest in this study, these values (Fig. 8a) must be taken as a “starting point” in the evolution of roughness of the GLFZ seismogenic slip surfaces, which exploit the pre-existing joints (Di Toro  et al., 2009).

Roughness of seismogenic slip surfaces can be readily related to that of joints. In fact, the field covered by fault values overlaps that of joints (Fig. 8), but is much larger, extending particularly towards lower H and σ RMS values, with some exceptions showing higher values (Fig. 8). If we consider anisotropy, we see that H and σ RMS values lower than those of joints are represented by measurements of fault traces lying almost parallel to the slip vector, measured at wavelengths in the 1 m to 5 mm range (Fig. 9). On the other hand, the (few) values higher than those of joints result from measurements performed at a high angle to the slip vector. When fault traces are characterized at larger wavelengths, they do not show this evolution and are quite similar to precursor joints (Fig. 8).

This can be interpreted in terms of roughness evolution with slip accumulation, taking place particularly in the along-slip direction, as already evidenced for other faults (e.g., Sagy and Brodsky, 2009; Candela et al., 2009) and also in laboratory experiments (Amitrano and Schmittbuhl, 2002). This evolution should be related to some sort of very generalized “wear” mechanism (e.g., Power et al., 1987), including, for the pseudotachylyte-bearing GLFZ slip surfaces, also frictional melting in “wear” processes. As in experiments (Amitrano and Schmittbuhl, 2002) and other natural faults (Candela et al., 2009), this evolution is associated to a reduction of the Hurst exponent, which means that asperities are smoothed out preferentially at larger wavelengths. However, for the GLFZ we observe this kind of evolution only for the 1 m to 5 mm wavelength range, and not at larger scales, as in previous contributions on natural faults. This deserves a more detailed discussion, but first we must recall that the GLFZ slip surfaces show net slip values in the 1–10 m range, whilst faults considered, e.g., in Candela et al. (2009) show larger displacements of some hundreds of meters.

Importantly, the architecture of these larger-scale fault zones is different from that of the GLFZ, as it usually includes one, or just a few, well-developed, metre-thick fault cores embedded in a well defined damage zone tens to hundreds of metres thick (see Ben-Zion and Sammis, 2003, for an extended discussion). This architecture is consistent with the occurrence of absolutely (in terms of friction coefficient) and relatively (with respect to the wall rocks) weak fault rock assemblages (usually non-cohesive fault gouges). In this case, fault zones show a progressive localization of strain within a few cataclastic horizons (i.e., the fault core). Continued localization of strain within the fault core leads to a significant evolution of fault surface roughness for displacements >ca. 100 m due to refinement (smoothing out) of asperities along slip, resulting in a characteristic large scale “striation” and marked roughness anisotropy (Power et al., 1988; Sagy and Brodsky, 2009). This kind of localization also induced Ben-Zion and Sammis (2003) to conclude that most large-scale fault zones evolve towards a geometrically simple structure, which is satisfactorily modelled as a discrete Euclidean surface embedded in a continuum (see Bistacchi et al., 2010, for a 3D model based on this geometrical framework).

Instead in the GLFZ, exhumed from deeper crustal levels (about 10 km), we witness the competition between a pre-existing weak and anisotropic fabric, represented by the cooling joints, and a syn-kinematic induration process. This (Di Toro et al. 2009) takes place due to cementation (precipitation of epidote and K-feldspar from hydrothermal fluids circulating in the cataclasites) and welding (solidification of friction melts), and contrasts the weakening and localization mechanisms described above. Hence (seismic) slip is initially localized along a “weak link” - a cooling joint, but then, because of the local induration and hardening of fault rocks, it is progressively transferred away from the currently active joint, towards another cooling joint that has not already experienced slip and induration. It follows that induration processes and exploitation and linkage of pre-existing joints results in an array of individual fault strands, which record small individual displacements (<20 m). This de-localization process also results in an unusual thickness of the fault zone (about 550 m) with respect to total accommodated slip (1,100–1,500 m).

The GLFZ-type structure (localized but limited slip on individual fault strands distributed in a wide fault zone) seems common at seismogenic nucleation depths, and appears to be typical of other indurated cataclasite- and pseudotachylyte-bearing fault zones hosted in the crystalline basement (e.g., Grocott, 1981; Swanson, 1988; Allen, 2005; Griffith et al., 2008). In terms of the geometrical frameworks for fault zone characterization discussed by Ben-Zion and Sammis (2003), this structure should be described as a “fractal” fault zone, possibly posing some problems in terms of how to introduce such a complex geometry in numerical models of faults.

Coming back to the roughness evolution, we may interpret our data saying that, on each slip surface, we see an initial roughness evolution with slip, evidenced by an anisotropic decrease in H with respect to the joint’s parent value, but only at wavelengths of the same order of magnitude as the net slip accumulated on that particular slip surface. Then slip migrates to another joint due to induration, and the slip and roughness evolution cycle is repeated.

Concluding, we may say that the mechanical evolution of fault rock assemblages is one of the main factors controlling roughness evolution (including anisotropy) and smoothing of fault surfaces with slip. Particularly, at seismogenic depths, where fault rock induration processes are active, roughness evolution and refinement of the fault surface might be active only at relatively small scales, in contrast to what suggested by studies conducted on fault surfaces exhumed from shallower crustal depths, where localization processes are more effective.

6 Conclusions

We analyzed the surface roughness of faults and joints using an innovative and efficient workflow that can be applied to other well-exposed outcrops of fault zones, potentially improving the database on fault roughness that was previously limited to fault surfaces exposed in quarries or other particular situations. From a methodological point of view, compared to direct measurements of exposed fault surfaces, the technique presented here has the advantages that: (1) it can be applied to a wide range of fault zones and outcrops; (2) hanging wall, foot wall and fault rocks are well preserved and all their structural features can be measured and related to fault roughness; (3) the measured roughness is not affected by weathering processes; (4) data collected with LIDAR and high-resolution photos can be merged to reconstruct power spectra spanning five orders of magnitude.

Regarding the Gole Larghe Fault Zone, our conclusions are that (1) roughness of seismogenic fault surfaces is inherited from precursor cooling joints, and (2) roughness of seismogenic fault surfaces show an evolution with slip only at the same length-scale as the total accumulated slip, which for individual slip surfaces of the GLFZ is in the 1–10 m range. In other words, net slip on these faults was not sufficient to produce significant fault surface refinement and smoothing at large scale. This contrasts with observations from other larger-displacement faults, exhumed from shallower depths, described in the literature. The differences in roughness between shallow (strong smoothing of roughness parallel to slip at all scales) and deep seismogenic faults (roughness evolution limited to the small wavelengths) might result from markedly different mechanical properties of fault rock assemblages. The previously studied shallow faults are weak in a relative and absolute sense; this results in localization and accumulation of slip in a few cataclastic horizons subject to intense surface refinement. The deeper-seated GLFZ is strong both in a relative and absolute sense due to syn-kinematic induration processes; this results in de-localization and reduced fault surface refinement.

Finally, data collected by this methodology are significant for numerical modelling of earthquakes, since they can be used to generate 3D synthetic fault surfaces with a highly realistic geometry.