Abstract
Closed-form solutions for the stresses and deformations induced in the ground and tunnel liner are provided for a deep tunnel in a transversely anisotropic elastic rock, with anisotropic permeability, when subjected to groundwater seepage. Complex variable theory and conformal mapping are used to obtain the solutions; additional complex functions, necessary to prevent multiple solutions of the displacements, are included. The analytical solutions are verified by comparing their results from those of a finite element method. Simplified formulations are presented for tunnels with a perfectly flexible and completely incompressible liner. A spreadsheet is included that can be used to obtain stresses and displacements of the liner due to groundwater flow and far-field geostatic stresses.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
The presence of groundwater affects the response of the ground during construction, as well as the forces acting on the liner. It has been shown that the tunnel advance rate changes the seepage forces ahead of the face of the tunnel, thus impacting face stability (Lee and Nam 2001, 2004) and shield loading (Ramoni and Anagnostou 2011). In addition, the tunnel support has to withstand not only the forces arising from the surrounding ground, but also those from the water (Bobet 2003; Lee et al. 2006). Clearly, ground and liner permeability are two driving factors determining the seepage regime around the tunnel. A perfectly impermeable liner preserves existing groundwater conditions, while a permeable liner induces seepage toward the excavation. The two conditions result in very different stresses in the ground (Bobet 2001; Nam and Bobet 2006, 2007), which are associated with different ground deformations (Bobet 2001, 2007).
The interaction between tunnel construction, ground and tunnel support is complex and may require sophisticated numerical methods that capture the inherent three-dimensional nature of the problem, as well as the ground and support response under complex loading (Bobet and Einstein 2008; Ibrahim et al. 2015; Pachoud and Schleiss 2015). Analytical formulations, however, while limited due to the restrictions imposed by the assumptions needed to reach a solution, have a number of advantages over numerical methods such as (Bobet 2010): (1) they provide insight into the problem, (2) are very useful to identify the most important variables for a given problem, (3) contribute to the understanding of the excavation–rock liner interaction problem, and (4) can be used to verify and calibrate complex numerical models. A number of analytical solutions have been obtained that account for the interplay that exists between ground and support (Einstein and Schwartz 1979; Carranza-Torres and Fairhurst 2000; Bobet 2010) and between ground, water and support (Bobet 2001, 2010; Nam and Bobet 2010). These solutions assume that the ground is isotropic. It is also interesting to explore how the ground and the support stresses and deformations are affected when the tunnel is excavated in a layered material (transversely anisotropic ground), with or without the presence of water (Bobet 2011, 2016). Closed-form solutions were obtained for the ground and the liner when the ground is dry or when there is no drainage at the ground–liner interface.
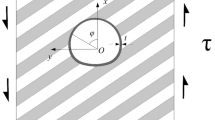
The paper expands the analysis presented by Bobet (2011, 2016) and presents an analytical solution for the stresses and deformations induced in the ground and support due to drainage at the ground–liner interface; that is, when seepage forces exist in the ground; see Fig. 1a for problem definition. The following assumptions are made: (1) The tunnel is deep and so far-field stresses, u ff, can be assumed as uniform and the magnitude of the vertical stress can be taken as the unit weight of the rock times the depth of the center of the tunnel; (2) the cross section of the tunnel is circular; (3) the rock is porous and elastic; (4) the rock has transverse anisotropy; (5) the principal axes of elastic anisotropy, x and y in Fig. 1, coincide with the principal axes of permeability; (6) the liner is elastic and has a small thickness compared to the radius of the tunnel; (7) plane strain conditions apply along the axis of the tunnel.
2 Theoretical Framework
Figure 1a shows the problem to be solved, where the axes of elastic symmetry, x and y, are inclined at and angle β with respect to the horizontal and vertical directions. For convenience, the problem is rotated such that the axes x and y are horizontal and vertical, respectively; see Fig. 1b. This is consistent with the approach taken by Bobet (2011, 2016) for dry ground. Note that the pore pressures remain unchanged with the rotation.
The solution must satisfy the following conditions: equilibrium, constitutive model, strain compatibility, flow through the porous medium and boundary conditions. Equilibrium, in two dimensions, is expressed as:
where σ xx , σ yy , τ xy are the total stresses along the x- and y-axis and the shear stresses, respectively, and x and y are the Cartesian coordinates of the axes of elastic symmetry. The axis z is taken along the axis of the tunnel and is also an axis of elastic symmetry.
The constitutive model is given by the equations of poro-elasticity, which in plane strain are given by (e.g., Detournay and Cheng 1993; Cheng 1998; Wang 2000):
where ε xx , ε yy and γ xy are the strains in the x and y directions, E x and E y are the Young’s modulus in the x and y directions, ν xz and ν yx are the Poisson’s ratios in the xz and yx directions, respectively (ν xy = ν yx E x /E y because of the symmetry of the strain tensor), G xy is the shear modulus, α x and α y are the Biot’s constants in the x and y directions (Biot 1941, 1956), and u is the pore pressure (for incompressible fluid, compressible solid matrix and isotropic properties, α x = α y = 1). Note also that the elastic properties in the z and x directions are the same.
Pore pressures, for steady-state conditions, must obey the following field equation:
where k x and k y are the permeabilities in the x and y axes, respectively.
The equilibrium equations can be satisfied if a stress function F(x, y) is found such that (Lekhnitskii 1963):
The compatibility equation can be written, in terms of the function F(x, y), as:
Lekhnitskii (1963) introduced the complex variable z k = x + μ k y, where μ k is a complex number. Expressing (5) as a function of the complex variable zk, one obtains:
Defining ϕ(z k ) = F′(z k ) = ∂F/∂z k , the stresses are:
where F o is a particular solution of (6) and μ 1 and μ 2 are complex numbers that are the roots of the equation:
Displacements and stresses of the liner, in polar coordinates, are related by (Flügge 1966):
where U sr and U s θ are the radial and tangential displacements of the liner, σ sr and τ s are the radial and shear stresses at the liner–ground contact, r o is the tunnel radius, E s and ν s are the Young’s modulus and Poisson’s ratio of the liner, A s and I s denote the area and moment of inertial of the liner (i.e., A s = t and I s = 1/12 t 3, where t is the thickness of the liner; note that it is assumed that t ≪ r o ), and θ is the tangential coordinate (see Fig. 1b).
The thrust load T s and moment distribution M s in the liner are:
First, the problem of a deep opening subjected only to seepage forces is solved. The solution is then used to find the forces and deformations imposed on the tunnel liner due to the groundwater flow.
3 Unsupported Opening
The problem to be solved is shown in Fig. 2. It depicts a circular opening, at depth, with far-field pore pressure u ff and internal pressures u o . The problem, Fig. 2a, is decomposed into two: the tunnel with internal and far-field pore pressures u ff, Fig. 2b; and the tunnel with internal pressure u o − u ff, Fig. 2c. The solution of the first problem is trivial, with the entire medium subjected to uniform pore pressures u ff. The following provides the solution for the second problem.
The pore pressure distribution in the ground due to the groundwater flow established in the second problem has been provided by Bobet and Yu (2015). For a circular opening, it is given by the following expression:
where R denotes the location where far-field pore pressures are restored and ζ 3 is a complex variable defined as follows:
where \(i = \sqrt { - 1}\). The flow Q into the opening can be obtained from (11):
The solution of the compatibility Eq. (6) can be decomposed into a general solution and a particular solution. The particular solution is discussed first and is given by:
Note that N given (12) is a real number. The stresses associated with the particular solution induce displacements that are not unique because the logarithm function in (14) yields different results when approaching the x-axis from the positive y-axis or from the negative y-axis. Hence, additional expressions are needed to remove the multiple solutions. To accomplish this, the medium is divided into two half spaces (Atkinson and Clements 1977; Clements 1973; Aköz and Tauchert 1972; Bobet and Yu 2015): one for y ≥ 0 and the other for y ≤ 0, and then compatibility of stresses and displacements at the common boundary y = 0 is imposed. We try the following stress functions:
where A 1 and A 2 are complex constants and
and μ k are the complex roots of Eq. (8). Stresses and displacements for the upper half space are:
and for the lower half,
Note that the new stress functions satisfy the far-field boundary condition of no stresses only when R → ∞; that is, when the far-field boundary is very distant from the tunnel. The constants A +1 , A +2 , A −1 and A −2 are found imposing compatibility of displacements and stresses at the common boundary, i.e., at y = 0. Thus,
The constants are obtained from the following system of four equations:
In (20), the following notation is used: Ω i = Ω i1 + iΩ i2, where Ω i1 and Ω i2 are real numbers. Additional stress functions are needed to satisfy the boundary conditions at the perimeter of the tunnel, i.e., to make the radial stresses equal to u o − u ff. They are:
The complete solution is found using (17) and (21). For the upper half space, stresses and displacements are:
where ϕ 1(z 1) and ϕ 2(z 2) are given in (21) and ϕ′1(z 1) and ϕ 2′(z 2) are the derivatives. The last term of the U x displacements satisfies the boundary condition of zero horizontal displacements at x = 0. As mentioned, the solution is correct when the far-field boundary is located far from the tunnel, i.e., when R → ∞. In other words, the solution provides accurate results in the vicinity of the opening, i.e., when r ≪ R. It is interesting to find the displacements at the perimeter of the opening, i.e., at r = r o (note that at r = r o , ζ k = cos θ + isin θ, k = 1, 2, 3). The algebra is tedious, but there are no difficulties in finding the following expressions for the radial and tangential displacements:
Note that Σ1 and Σ2 are real numbers.
The accuracy of the solution is compared with the results from the finite element method program ABAQUS (ABAQUS 2015). The following input properties are used: deep circular tunnel, with radius r o = 2 m, ground properties E x = 7800, E y = 2400 MPa, ν yx = 0.02, ν xz = 0.22, ν zy = 0.07, G xy = 830 MPa (from the bedded sedimentary Waichecheng series, after Tonon and Amadei 2002), and permeability k x /k y = 5. Figure 3 shows a sketch of the discretization used. Eight-node isoparametric elements with pore pressure at the corner nodes are used between the tunnel perimeter and the external boundary, while infinite elements are placed at the external boundary. The use of infinite elements and the shape of the external boundary are adopted to approximate the assumptions made for the derivation of the analytical solution, as the results are sensitive to the location and geometry of the far-field boundary. Figure 4 provides a comparison between the results obtained from the analytical solution and ABAQUS, in terms of the normalized tangential stresses and radial and tangential displacements at the perimeter of the tunnel. As one can see, the differences between the two results are small.
Unsupported tunnel. Normalized tangential stresses and displacements at the tunnel perimeter. Comparison between analytical solution and FEM ABAQUS. r o = 2 m, E x = 7800, E y = 2400 MPa, ν yx = 0.02, ν xz = 0.22, G xy = 830 MPa, k x /k y = 5, a normalized tangential stresses, b normalized displacements
4 Supported Tunnel
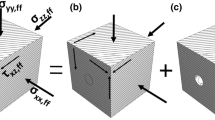
Figure 5a shows a deep tunnel subjected to far-field stresses, including far-field pore pressure u ff and pore pressure u o at the interface between the liner and the ground. Note that for convenience, the horizontal or x-axis is taken along the direction of one of the axes of elastic symmetry. The problem is decomposed into two: Problem I, Fig. 5b, has the far-field stresses and the pore pressures at the ground–liner interface equal to u ff, the far-field pore pressures; and Problem II, with the same geometry as Problem I, but with zero pore pressures in the far-field and u o − u ff pore pressures at the ground–liner interface, Fig. 5c. Clearly, the sum of the solutions of Problems I and II provides the solution of the complete problem. Problem I is that of a deep tunnel with no drainage and has been solved by Bobet (2011, 2016). What follows is the solution of Problem II that provides any additional stresses and displacements that are induced in the liner and ground because of the seepage forces in the medium due to the flow gradient established.
Problem II can be further decomposed into Problem IIa: an unsupported opening with flow, Fig. 5d; Problem IIb that considers the interaction between the ground and the liner, Fig. 5e; and Problem IIc that deals with the stresses and deformations of the liner, Fig. 5f. The unknown stresses of Problem IIb, Δσ r and Δτ, are found by imposing compatibility of stresses and deformations at the contact between the liner and the ground.
For a tied interface (the displacements of the liner are those of the ground in contact),
Problem IIa is analogous to that of the unsupported opening, already discussed, except that there are no stresses at the tunnel perimeter. Equations (22) apply, with the following stress functions:
The displacements at the opening are found from (22), (25) and are:
It is helpful, to understand the effects of groundwater flow, to find the displacements at the perimeter of the opening for the case of anisotropic flow with isotropic ground properties. In this case, μ 1, μ 2 → i, and so (26) reduces to:
The displacements, as one can see, strongly depend on the anisotropic permeability of the medium, given that \(\mu_{32} = \sqrt {k_{x} /k_{y} }\). The groundwater flow, given by (11), is not radial due to the different permeabilities. As a result, the seepage forces in the rock are not radial, and so the ground deformations produced by the groundwater flow are not radial, as in the case of isotropic medium. This is confirmed by the displacement field in (27). With the assumption of k x > k y , i.e., μ 32 > 0, the radial displacements at the springline, i.e., at θ = 0°, are outward when there is inward flow (u o < u ff) and are inward, with the same magnitude, at the crown, θ = 90°. The tangential displacements are clockwise when the flow is toward the opening. This is due to the seepage forces that, as mentioned, are no longer radial and have a tangential component that is clockwise in this case due to the larger horizontal permeability. The tangential seepage forces induce larger compression at the springline than at the crown, which results in the displacement pattern given by (27). Another interesting observation is that the displacements are zero when the flow is isotropic, i.e., when k x = k y which makes μ 32 = 1. In this particular case, the flow established due to different pressures at the tunnel perimeter and the far-field does not induce deformations at the tunnel perimeter, and thus, it does not induce deformations in the liner. This conclusion was already reached by Bobet (2001) who showed that the displacements and stresses in the liner were independent of the drainage conditions at the liner–ground interface. What is worth noting is that groundwater flow does not affect the displacements at the tunnel wall and the stresses of the liner only when the medium has isotropic elastic properties and isotropic permeability, and the tunnel is deep (from Bobet 2001). In all other cases, the flow regime at the liner–ground contact, from no drainage to full or partial drainage, affects the response of the liner.
Problem IIb is concerned with the stress and displacement fields produced in the ground due to the (unknown) radial and shear stresses that are present at the ground–liner interface, Δσ r and Δτ. Due to the symmetry of the problem, the interface stresses must be of the form:
Stresses and displacements can be obtained from the following stress functions:
At the tunnel perimeter, the displacements are:
The displacements and stresses or forces in the liner (Problem IIc) are obtained from (9) and (10), given (28). The solution is:
The values of the unknown stresses due to liner–ground interaction, σ o , σ n and τ n in (28), are obtained from (24) by making the radial and tangential displacements equal term by term, i.e., constant term, sin θ, cos θ, sin 2θ, cos 2θ, etc. The higher the term, the smaller the contribution to the solution, so only a few terms are needed to obtain an accurate result. A comparison between the analytical solution and ABAQUS is presented in Fig. 6. The case analyzed is the same as that shown in Fig. 4, except that the tunnel is supported with a liner with the following properties: E s = 20,000 MPa, ν s = 0.3 and t = 0.2 m. The figure is a plot of the normalized normal and shear stresses, Fig. 6a, and displacements, Fig. 6b, at the interface. As one can see, the comparison is very good, which brings confidence in the approach taken and on the validity of the solution.
Supported tunnel. No slip. Normalized interface stresses and displacements. Comparison between analytical solution and FEM ABAQUS. r o = 2 m, E x = 7800, E y = 2400 MPa, ν yx = 0.02, ν xz = 0.22, G xy = 830 MPa, k x /k y = 5, E s = 20,000 MPa, ν s = 0.3, t = 0.2 m, a normalized interface stresses, b normalized displacements
If one assumes that the liner is flexible and yet fairly incompressible; e.g., shotcrete or segmental liner, a simpler solution is obtained by taking the liner stiffness E s I s → 0 and compressibility E s A s → ∞. The following provides a two-term approximation of the liner response, which can be used as a first estimate.
For a frictionless interface (the shear stresses at the liner–rock contact are zero),
Problem IIa in Fig. 5 remains unchanged, and so Eqs. (26) still apply. The liner–ground interaction stresses, given that the interface is frictionless, are those of Eq. (28), except that the shear stresses, as shown in (33), are zero. The solution for Problem IIb is still given by (29) and (30), but with τ n = 0 for n ≥ 2. The equations for the liner, Problem IIc, are now given by:
Verification of the analytical solution is done by comparing the results from the closed-form solutions with those from ABAQUS. The same problem chosen for the tied interface (Fig. 6) is used for the comparison, except that the contact between the liner and the ground is frictionless. Figure 7 shows the results, in terms of normalized stresses at the liner–ground interface and liner displacements. The differences between the two solutions are small, which provides confidence in the equations obtained. Comparison of the data shown in Figs. 6 and 7 indicates that a frictionless interface is associated with smaller stresses at the interface, and thus with smaller displacements and smaller stresses in the liner (not shown in the figures). If the liner can be considered perfectly flexible and completely incompressible (E s I s → 0 and E s A s → ∞), the liner response is obtained with the following, much simpler equations:
Supported tunnel. Full slip. Normalized interface stresses and displacements. Comparison between analytical solution and FEM ABAQUS. r o = 2 m, E x = 7800, E y = 2400 MPa, ν yx = 0.02, ν xz = 0.22, G xy = 830 MPa, k x /k y = 5, E s = 20,000 MPa, ν s = 0.3, t = 0.2 m, a normalized interface stresses, b normalized displacements
Equations (35) show that the liner is subjected to uniform contact radial stresses and no shear, which results in uniform axial load and no bending moments, and radial deformations that are the same at the springline and at the crown, with opposite sign. This result is in agreement with Peck’s concept of a flexible liner (Peck 1969), where the liner has a pressure distribution and a deflected shape such that the bending moments at all points in the liner are negligible.
5 Discussion
Inspection of Eqs. (26), (30) and (31) or (34) shows that the solution, when α x = α y = 1, can be expressed as a function of the following non-dimensional parameters: t/r o , k x /k y , α 2/α 1, α 3/α 1, 1/(α 1 G xy ), (1 − ν 2s )/(1 − ν 2 xz )E x /E s. Neglecting the effects of the Poisson’s ratios, which are generally small, and also of E x /G xy , the solution is a function of: t/r o , k x /k y , E x /E y , and E x /E s. The effect of these non-dimensional parameters is explored in the following through a (limited) parametric analysis where all variables except one are kept constant, while the other variable is changed within a reasonable range of values. The following is the base case, around which the material properties, loading and geometry are explored: deep tunnel with circular cross section with radius r o = 2 m, rock properties E x = 7800, E y = 2400, G xy = 830 MPa, ν xz = 0.22, ν yx = 0.02, k x /k y = 5.0, liner properties E s = 20,000 MPa, ν s = 0.30 with thickness t = 0.2 m and tied rock–liner interface.
The effects of anisotropic flow are explored by computing the loading and displacements of the liner for isotropic rock, E = 7800 MPa and ν = 0.22, and for a range of permeabilities k x /k y = 1, 2, 5 and 10. Figure 8a is a plot of the normalized axial force, T s/(u o − u ff)/r o , and normalized moment, T s/(u o − u ff)/r 2o , of the liner for the different permeabilities, and Fig. 8b of the normalized radial and tangential displacements U r,θ E s/(1 − ν 2s )/(u o − u ff)/r o . As one can see, the normalized axial force and, to a much smaller extent, the normalized moment acting on the liner increase as the permeability becomes more anisotropic. The normalized axial force is positive at the springline and negative at the crown, which for, e.g., flow toward the tunnel, u o − u ff < 0, induces compression at the springline and tension at the crown. This results in a displacement pattern of negative normalized radial displacements at the springline (outward displacements with flow toward the tunnel) and positive at the crown (inward displacements with flow toward the tunnel) with increasing in magnitude with flow anisotropy. The normalized tangential displacements are always positive (clockwise with flow toward the tunnel) and increase with the anisotropy of the flow. As explained in the preceding section, the groundwater flow creates seepage forces inside the ground that, due to the anisotropy, have a tangential component that increases in magnitude as the k x /k y ratio increases. The tangential seepage forces are those responsible for the differences of loading and displacements between the springline and the crown. Because of the symmetry of the problem along the 45° direction, the solution is also symmetric with respect to this direction.
The loading and displacements of the liner due to the relative stiffness between the rock and the liner, given by the E x /E s ratio, are explored by conducting a number of numerical experiments using the base case and changing the relative stiffness ratio as E x /E s = 0.1, 0.39 (the base case), 0.8, 1.0. This has been accomplished by keeping E x constant and changing E s. Figure 9a shows that as the liner becomes softer, or as the rock gets stiffer, the normalized loading of the liner decreases. This is an expected result as a softer liner attracts less loading and so a larger portion of the load is taken by the rock. The corresponding normalized displacements, Fig. 9b, are larger, again because the rock is taking more load, and thus deforming more.
The effects of the relative anisotropy of the rock, E x /E y, are displayed in Fig. 10. The figure plots the normalized forces and moments, Fig. 10a, and the normalized displacements, Fig. 10b of the liner, for the base case with E x /E y = 1.0, 3.25 (the base case), 5.0 and 10.0. This is done by keeping E x constant and changing E y . As the rock becomes softer in the y direction, the normalized radial displacements at the crown increase while the normalized radial displacements at the springline remain mostly unchanged. The normalized tangential displacements increase as the Ex/Ey ratio increases. This deformation pattern is associated with a reduction in radial stresses at the crown, where the rock is softer, and an increase in radial stresses at the springline (not shown in the figure), as E y decreases with respect to E x . For the liner, this results in smaller normalized axial force at the crown and larger force at the springline. Interestingly, the normalized moment is not much affected, suggesting that changes in relative stiffness of the rock affect mostly the axial force of the liner.
Figure 11 is a plot of the normalized loading, Fig. 11a, and normalized displacements, Fig. 11b, of the liner when t/r o = 0.05, 0.1 (base case), 0.2 and 0.25. The results are as expected, with the liner taking larger load and deforming less when it is thicker (the simulations are run with r o constant).
Finally, the effects of the interface, either no slip or full slip, are explored in Fig. 12. Two scenarios are presented: isotropic ground (same properties as those of Fig. 8) and anisotropic ground (base case), each with a no slip interface (no relative movements between the rock and the liner at the contact; that is, a tied interface) and full slip interface (no shear stresses at the rock–liner contact). The main observations are similar for each scenario. A full slip interface decreases the normalized axial force of the liner compared to the no slip/tied interface and dramatically decreases the moment of the liner, resulting in an almost uniform normalized axial force. This is associated with somewhat of an increase in normalized radial displacements and a decrease in normalized tangential displacements. The reason for this behavior can be found in how the load is transferred from the rock to the liner. As the interface becomes less constrained, i.e., the rock can deform in the tangential direction independently of the liner and cannot transfer shear stresses for the full slip case, the rock is less capable of transferring load to the liner, it carries more load and deforms more. As a consequence, the liner is less loaded and it is less constrained to deform, which results in reduced bending.
A spreadsheet is included with this paper that can be used to compute the rock–liner interface stresses and the liner loading and deformations due to groundwater flow, using the formulation presented, as well as due to geostatic stresses, using the closed-form solutions obtained by Bobet (2011, 2016) for a deep tunnel in transversely anisotropic rock.
6 Summary and Conclusions
The paper addresses the problem of a deep tunnel in a transversely anisotropic medium subjected to seepage forces. It provides closed-form solutions for the case of an unsupported tunnel and for the case of a supported tunnel with a liner. The work complements the analytical formulation that exists for a deep tunnel in transversely anisotropic ground, for dry conditions or for saturated ground with no drainage at the liner–ground interface (Bobet 2011, 2016). It provides the additional deformations and stresses in the ground and liner due to the seepage forces that exist in the ground when there is drainage at the ground–liner interface.
A number of assumptions are made to reach a solution and include: transversely anisotropic elastic ground and isotropic elastic liner; plane strain conditions; deep tunnel; circular cross section; thin liner. For the supported tunnel, two situations are addressed: tied contact and full slip between the liner and ground. The formulation presented has been verified by comparing its predictions with the results obtained with the finite element code ABAQUS, where boundary conditions and type of elements have been chosen such that they match the assumptions made to develop the analytical formulation, e.g., elements with coupled displacements and pore pressures, far-field boundary geometry that matches the analytical formulation for groundwater flow and infinite elements.
An important observation is that seepage forces induce displacements at the tunnel wall, which in turn produce stresses and deformations of the liner when the ground has anisotropic mechanical properties or anisotropic permeability. The analytical solution confirms the previous finding (Bobet 2011, 2016) that the liner experiences no additional deformations or stresses when the groundwater regime changes from no drainage to drainage, or vice versa, at the ground–liner interface, but only when the ground has both isotropic elastic and permeability properties.
In addition to the general formulation for cases with tied (no slip or relative movement between liner and rock) or for frictionless interface (full slip between liner and rock), the paper also presents equations to estimate the liner deformations and load when the liner can be considered flexible and incompressible. For the full slip case, the result agrees with the concept of flexible liner put forward by Peck (Peck 1969), where the liner experiences a uniform radial pressure at the contact with the ground and a displacement distribution such that the bending moments in the liner are zero.
A limited parametric analysis explores the effects of different variables on the load and displacements of the liner. As the anisotropy of the ground increases, either because the permeability ratio, k x /k y , or the stiffness ratio, E x /E y , increases, the loading of the liner increases and its deformations increase. The study also provides findings that are consistent with those obtained for isotropic rock in that, as the relative stiffness of the rock with respect to the liner, E x /E s, increases or the relative thickness of the liner, t/r o , decreases, in other words as the liner becomes softer, the load transferred from the rock to the liner reduces, and thus, the loading that the liner has to carry decreases.
A spreadsheet is included that can be used to obtain the stresses and deformations of the liner of a deep tunnel in anisotropic rock subjected to geostatic (far-field) stresses and groundwater flow, and for a no slip/tied or full slip interface. It is provided as is and free to use. “Appendix” section contains a short summary about how to use the spreadsheet. While an effort has been made to ensure that the results provided in the spreadsheet are correct, the author would welcome any corrections, suggestions and improvements.
Abbreviations
- A s, I s :
-
Cross section and moment of inertia of liner
- E x , E y :
-
Young’s modulus of rock in x- and y-axis
- E s, ν s :
-
Young’s modulus and Poisson’s ratio of the liner
- G xy :
-
Shear modulus of rock
- R :
-
Distance to far-field boundary
- k x , k y :
-
Permeability of rock in x- and y-axis
- r, θ :
-
Polar coordinates
- r o :
-
Radius of the tunnel
- t :
-
Liner thickness
- T s, M s :
-
Axial force and moment of liner
- U r, U θ :
-
Displacement of the rock in polar coordinates
- U sr , U s θ :
-
Displacement of the liner in polar coordinates
- U :
-
Pore pressures
- u ff :
-
Pore pressure at far-field
- u o :
-
Pore pressure at tunnel wall
- x, y :
-
Cartesian coordinates of axes of elastic symmetry
- z :
-
Complex number, z k = x + μ k y, k = 1, 2
- α x , α y :
-
Biot’s constants in x- and y-axis
- ε xx , ε yy , γ xy :
-
Axial and shear strains in x- and y-axis
- ζ k :
-
Complex number that depends on z k through conformal mapping
- ϕ(z k ), ϕ′(z k ):
-
Stress function and its derivative
- μ 1, μ 2 :
-
Roots of compatibility equation
- μ 3 :
-
Root of permeability equation
- ν xy , ν xz , ν yz :
-
Poisson’s ratios of rock
- σ v , σ h , τ vh :
-
Normal and shear stresses at the far-field along axes of elastic symmetry
- σ x , σ y , τ xy :
-
Total normal and shear stresses in Cartesian coordinate system
- σ r, σ θ , τ:
-
Total normal radial, tangential, shear stresses in polar coordinate system
- σ sr , σ s θ , τ s :
-
Stresses of the liner in polar coordinates
References
ABAQUS (2015) User’s manual, version 6.14-4. Dassault Systemes Simulia Corp., Johnston
Aköz AY, Tauchert TR (1972) Thermal stresses in an orthotropic elastic semispace. J Appl Mech 39(March):87–90
Atkinson C, Clements DL (1977) On some crack problems in anisotropic thermoelasticity. Int J Solids Struct 31:855–864
Biot MA (1941) General theory of three dimensional consolidation. J Appl Phys 12:155–164
Biot MA (1956) Theory of deformation of a porous viscoelastic anisotropic solid. J Appl Phys 27(5):459–467
Bobet A (2001) Analytical solutions for shallow tunnels in saturated ground. ASCE J Eng Mech 127(12):1258–1266
Bobet A (2003) Effect of pore water pressure on tunnel support during static and seismic loading. Tunn Undergr Space Technol 18:377–393
Bobet A (2007) Ground and liner stresses due to drainage conditions in deep tunnels. Felsbau 25(4):42–47
Bobet A (2010) Characteristic curves for deep circular tunnels in poroplastic rock. Rock Mech Rock Eng 43:185–200
Bobet A (2011) Lined circular tunnels in transversely anisotropic rock at depth. Rock Mech Rock Eng 44:149–167
Bobet A (2016) Lined circular tunnels in transversely anisotropic rock at depth: complementary solutions. Rock Mech Rock Eng 49(9):3817–3822
Bobet A, Einstein HH (2008) Deep tunnels in clay shales: evaluation of key properties for short and long term support. In: ASCE geocongress 08
Bobet A, Yu H (2015) Stress field near the tip of a crack in a poroelastic transversely anisotropic saturated rock. Eng Fract Mech 141:1–18
Carranza-Torres C, Fairhurst C (2000) Application of the convergence-confinement method design to rock masses that satisfy the Hoek–Brown failure criterion. Tunn Undergr Space Technol 15(2):187–213
Cheng AH-D (1998) On generalized plan strain poroelasticity. Int J Rock Mech Min Sci 35(2):183–193
Clements DL (1973) Thermal stress in an anisotropic elastic half-space. SIAM J Appl Math 24(3):332–337
Detournay E, Cheng AH-D (1993) Fundamentals of poroelasticity. In: Hudson JA (ed) Comprehensive rock engineering: principles, practice and projects, vol 2. Pergamon Press, Oxford, pp 113–171
Einstein HH, Schwartz CW (1979) Simplified analysis for tunnel supports. ASCE J Geotech Eng Div 105(GT4):499–518
Flügge W (1966) Stresses in shells. Springler, New York
Ibrahim E, Soubra A-H, Mollon G, Raphael W, Dias D, Reda A (2015) Three-dimensional face stability analysis of pressurized tunnels driven in a multilayered purely frictional medium. Tunn Undergr Space Technol 49:18–34
Lee IM, Nam SW (2001) The study of seepage forces acting on the tunnel lining and tunnel face in shallow tunnels. Tunn Undergr Space Technol 16:31–40
Lee IM, Nam SW (2004) Effect of tunnel advance rate on seepage forces acting on the underwater tunnel face. Tunn Undergr Space Technol 19:273–281
Lee S-W, Jung J-W, Nam S-W, Lee I-M (2006) The influence of seepage forces on ground reaction curve of circular opening. Tunn Undergr Space Technol 22:28–38
Lekhnitskii SG (1963) Theory of elasticity of an anisotropic elastic body. Holden-Day Inc., San Francisco
Nam S, Bobet A (2006) Liner stresses in deep tunnels below the water table. Tunn Undergr Space Technol 21(6):626–635
Nam S, Bobet A (2007) Radial deformations induced by groundwater flow on deep circular tunnels. Rock Mech Rock Eng 40(1):23–39
Pachoud AJ, Schleiss AJ (2015) Stresses and displacements in steel-lined pressure tunnels and shafts in anisotropic rock under quasi-static internal water pressure. Rock Mech Rock Eng. doi:10.1007/s00603-015-0813-z
Peck RB (1969) Deep excavations and tunneling in soft ground. In: Proceedings 7th international conference on soil mechanics and foundation engineering, state-of-the-art volume. The Sociedad Mexicana de Mecánica de Suelos, Mexico City, pp 225–290
Ramoni M, Anagnostou G (2011) The effect of consolidation on TBM shield loading in water-bearing squeezing ground. Rock Mech Rock Eng 44:63–83
Tonon F, Amadei B (2002) Effect of elastic anisotropy on tunnel wall displacements behind a tunnel face. Rock Mech Rock Eng 35(3):141–160
Wang HF (2000) Theory of linear poroelasticity with applications to geomechanics and hydrogeology. Princeton University Press, Princeton
Author information
Authors and Affiliations
Corresponding author
Electronic supplementary material
Below is the link to the electronic supplementary material.
Appendix
Appendix
This “Appendix” is intended to be a “user manual” for the spreadsheet included with the publication. It also provides a very short summary of the assumptions made to obtain the solution. This information is also included in the spreadsheet, by clicking the “green” button “Read Me First.”
Assumptions
Transversely anisotropic elastic ground and isotropic elastic liner; plane strain conditions; deep tunnel; circular cross section; thin liner; simultaneous tunnel excavation and liner installation. Rock–liner interface: full slip (no shear stresses at the interface) or no slip (tied interface).
Solution
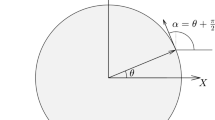
The spreadsheet gives the total radial and shear stresses at the rock–liner interface, σ r and τ; the axial force and moment in the liner, T s, M s; and internal and external tangential stresses in the liner, σ s θ . The solution is given in terms of the angle θ, as defined in Fig. 13. Tension is positive, and compression is negative.
Methodology
The solution is obtained after the following steps:
-
1.
Input problem geometry, rock and liner elastic properties, rock permeability, far-field loading (in total stresses) and pore pressures in the designated cells in Sheet 1.
-
2.
Click the red button labeled “Click to find solution.”
-
3.
Solution it is given as a function of the angle θ in Fig. 13. It is given separately for the contribution of groundwater flow and for far-field stresses. The final result, i.e., the sum of the two contributions, is also provided.
Other information
Sheet 1 includes the input and output. This is the input/output user interface. Sheet 2 contains calculations for groundwater flow, and Sheet 3 contains calculations for far-field stresses. Note that any modifications by the user to cells in Sheets 2 and 3 may result in erroneous results.
Disclaimer
The spreadsheet is provided as is and free to use. The user is requested to acknowledge the source of the work and that any modification and/or improvement made should be shared with the author and with the community.
Rights and permissions
About this article
Cite this article
Bobet, A. Deep Tunnel in Transversely Anisotropic Rock with Groundwater Flow. Rock Mech Rock Eng 49, 4817–4832 (2016). https://doi.org/10.1007/s00603-016-1118-6
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00603-016-1118-6