1 Introduction

Although cases of rapidly converging ground are known in the literature (Ramoni and Anagnostou 2010c), squeezing ground usually exhibits a markedly time-dependent behaviour. Depending on its characteristics, the ground may respond to the excavation with some delay and may continue to deform over a period of days, weeks or even months (Barla 2001; Kovári and Staus 1996). The delay in the ground response is favourable for a tunnel boring machine (TBM) because a TBM can accommodate only relatively small convergences in the machine area and the back-up area without running into problems. However, such favourable time effects can be considered in the planning phase only if there is sufficient advance knowledge of how the ground will behave over time. Failing this, it would be unwise to rely upon the assumption that deformations will develop only slowly and far behind the machine.

As a consequence of the time-dependency of ground behaviour, the overall advance rate not only represents the main outcome of the complex interaction between the ground, the TBM and the tunnel support, but also exercises a decisive influence over this interaction (Ramoni and Anagnostou 2010c). More specifically, as emphasized repeatedly in the literature, a rapid excavation rate (involving high net advance rates and short standstills) reduces the risk of the shield or back-up jamming (e.g., Herrenknecht and Rehm 2007; Kovári 1986a, b; Lombardi 1981; McCusker 1996; Robbins 1982). The frequency and duration of standstills can be reduced through appropriate operational measures and construction site organization. For example, necessary logistical precautions should be taken in order to allow operations within critical zones to proceed as continuously as possible. However, in spite of every effort, it is not always possible to avoid long interruptions (Gehring 1996; Lombardi 1981). Sudden changes in ground conditions, technical problems (e.g., electric power stoppages, mechanical breakdowns of the TBM with consequent repair work, problems in the back-up system), holiday periods, strikes, and, of course, a TBM jamming during regular operation can cause unpredictable stoppages. Major maintenance operations are also an important factor as they may lead to an unfavourably long standstill. At the same time, however, they are important for reducing the risk of mechanical breakdown. The conflict in priorities here can be resolved by carrying out any lengthy maintenance operations before entering a critical zone, provided of course that the location of the critical zone is known and its length is sufficiently short that it can be crossed practically non-stop. In this respect, the timely identification of critical zones by means of reliable advance ground probing is very important (Anagnostou et al. 2010; Peila and Pelizza 2009).

The time-dependency of ground behaviour is mainly (i.e., with the exception of physicochemical processes in certain rock types such as sulfatic rocks) due to the creep and consolidation processes taking place around the tunnel (Anagnostou and Kovári 2005). In the vicinity of the tunnel face, these processes develop simultaneously with the spatial stress redistribution caused by the face advance. Creep is associated with the rheological behaviour of the ground, becoming evident particularly when the ground is highly stressed. The present paper will focus on the consolidation-induced time-dependency of ground response. This mechanism comes into play when tunnelling through water-bearing ground. Consolidation represents a source of time-dependency in the case of a low-permeability ground. It is associated with the transient seepage flow process that is triggered by the tunnel excavation. Understanding the role of consolidation is particularly important for deep alpine tunnels (Vogelhuber 2007) as well as current or planned subsea tunnel projects crossing weak rocks, such as the Lake Mead Intake No. 3 Tunnel in the USA (Anagnostou et al. 2010) or the planned Gibraltar Strait Tunnel between Spain and Morocco (Pliego 2005). In fact, it is well known from experience that pore water under high pressure intensifies squeezing phenomena (Kovári and Staus 1996).

The present paper investigates the interaction between shield and ground by means of hydraulic-mechanical coupled numerical analyses, which account for the highly complex transient process of consolidation around the advancing tunnel heading. The first results of this research have been presented by Ramoni and Anagnostou (2007a, b), while a comprehensive review of the literature on analytical methods used for TBM tunnelling in squeezing ground can be found in Ramoni and Anagnostou (2010a), which investigated the interplay between TBM, ground and tunnel support under the simplifying assumption of time-independent ground behaviour. Other recent publications closely related to the topic of the present paper are those of Ramoni and Anagnostou (2010b), who presented design nomograms for estimating the thrust force requirements, Amberg (2009), Floria et al. (2008) and Lombardi et al. (2009), who analysed the effect of consolidation on squeezing behaviour in the context of the planned Gibraltar Strait Tunnel, as well as the work by Sterpi and Gioda (2007) on the effect of creep on shield loading.

The paper starts with a qualitative discussion of the mechanisms underlying the ground response to tunnelling operations and continues with a quantification of the identified effects. Section 2 sketches out the most important interrelations among the operational parameters (advance rate, standstill duration) and the deformations associated with the development and subsequent dissipation of excess pore pressures around the tunnel. Sections 3 and 4 present the modelling assumptions and outline the numerical solution method, respectively. Section 5 deals with conditions during continuous excavation and analyses the effect of the advance rate on shield loading, while Sect. 6 investigates ground pressure development during a standstill.

2 The Consolidation Mechanism

Squeezing is associated with overstressing and plastic yielding of the ground. Squeezing ground generally experiences an increase in volume (plastic dilatancy). If the ground is saturated, its water content also increases during squeezing. This occurs more or less rapidly depending on the permeability of the ground. In a low-permeability ground, the water content remains constant in the short term. Since the pore water hinders dilatancy, negative excess pore pressures are generated by to the excavation work. As these are higher in the vicinity of the tunnel than further away, a transient seepage flow process starts to develop towards the tunnel. The negative excess pore pressures dissipate over time, thus changing the effective stresses and leading to additional, time-dependent deformations (Anagnostou and Kovári 2005). When a shield or a lining hinders ground deformations, the load acting on it will increase over time.

With respect to the transient process, two important states can be distinguished: the state immediately after excavation (i.e., at time t = 0+) and the long-term state (t = ∞). The first state is characterized by the condition of constant water content (so-called “undrained conditions”). The second state is governed by the steady state pore pressure distribution (so-called “drained conditions”). As in other geotechnical problems involving “unloading” of the ground (e.g., deep excavations), the short-term behaviour is more favourable than the long-term behaviour. In fact, according to theoretical and experimental investigations (e.g., Anagnostou 2007c; Vogelhuber 2007), the negative excess pore pressures developing under undrained conditions strengthen the ground temporarily, as they increase the effective stress and thus the resistance to shearing. This so-called “dilatancy hardening” is temporary because the excess pore pressures dissipate with time.

The reason for the short-term development of excess pore pressures is that pore water imposes a constraint on volumetric strains. In this respect, it has to be noted that the excess pore pressures will be negative (i.e., the pore pressures decrease) only if the volumetric strains are also negative (i.e., if the volume increases). This happens in the present case because (a) the first stress invariant decreases within the plastic zone around the tunnel and (b) the plastic behaviour of the ground is considered to be dilatant. In other situations (e.g., if the initial stress is non-hydrostatic or the ground exhibits contractant plastic behaviour as in the rather rare case of normally consolidated sediments), the ground may experience a volume decrease in the long term and, consequently, the short-term excess pore pressures would be positive.

The time-dependent development of ground deformations is governed by the ratio of advance rate v to ground permeability k (Anagnostou 2007a). If this ratio is high (as in the case of rapid excavation through a low-permeability ground), undrained conditions, which are more favourable, will prevail in the machine area. On the other hand, if the excavation proceeds slowly or the ground permeability is high (low v/k ratio), unfavourable drained conditions will set in almost immediately after excavation. The advance rate v means the gross advance rate resulting from the boring process and including regular short standstills for the installation of the tunnel support or for the execution of inspections and minor maintenance work. The effects of advance rate and permeability will be investigated quantitatively in Sect. 5.

Major maintenance or repair work (planned or not) or other problems may cause longer standstills, which cannot be classified among regular TBM operations and have to be investigated separately. The ground behaviour during such a standstill is governed by the mechanisms described above. If drained conditions have not already been reached during the preceding regular excavation (i.e., if the ratio v/k was high enough), consolidation will continue during the standstill period until the steady state pore pressure distribution is reached. Again, due to the change in the effective stresses, the ground will deform and the ground pressure will increase over time. For a given ground permeability, the higher the advance rate during the preceding excavation, the more the conditions prevailing at the beginning of the standstill will deviate from the drained conditions and, consequently, the more time must elapse before the steady state is reached. Rapid excavation is therefore also advantageous with respect to subsequent standstills. The conditions prevailing during standstills will be investigated quantitatively in Sect. 6.

The risk of the TBM jamming depends on the ratio v/k as this governs the intensity of the deformations in the machine area. In general, the less permeable the ground, the more rapid the excavation and the shorter the standstills, the closer conditions will be to a favourable undrained state. The range of feasible advance rates is relatively narrow (i.e., v = 30 m/day; in difficult ground conditions v = 5–10 m/day), but the ground permeability k may vary over several magnitudes, thus playing a more important role with respect to the risk of the TBM jamming. As reliable estimations are particularly difficult for heterogeneous ground, permeability introduces a prediction uncertainty, which has to be borne in mind in the design phase (Anagnostou and Kovári 2005).

Similar considerations also apply to the creep-induced time-dependency of the ground response. As shown by Sterpi and Gioda (2007), a high advance rate is favourable as it leads to lower deformations in the machine area. In the borderline case of a very high advance rate, only small, elastic deformations develop in the vicinity of the tunnel face. However, as was the case with permeability, a reliable estimation of the ground creep parameters before construction may be very difficult to achieve.

3 Computational Model

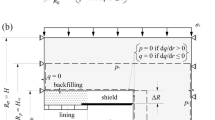
The interaction between the advancing TBM and the consolidating ground will be investigated on the basis of an axially symmetric model (Fig. 1). The underlying simplifying assumptions are: deep, cylindrical tunnel; hydrostatic and uniform initial stress field; uniform initial hydraulic head field; homogeneous and isotropic ground; constant overcut around the circumference of the shield; negligible TBM weight; uniform tunnel support (and uniform annulus grouting along the tunnel periphery in the case of a segmental lining).

Fig. 1
figure 1

Problem layout and boundary conditions

Full size image

The mechanical behaviour of the ground is taken to be linearly elastic and perfectly plastic with the Mohr–Coulomb yield criterion and a non-associated flow rule. As stated in Sect. 1, creep has been disregarded. The mechanical and hydraulic boundary conditions at the far field boundary and also at the tunnel face can be seen from Fig. 1. The tunnel face is considered as being unsupported (the effect of a face support is discussed briefly in Sect. 6).

Pore pressures were taken into account by modelling the ground as a saturated porous medium according to the principle of effective stresses. Seepage flow was modelled by Darcy’s law. Cavitation effects have been disregarded. Incompressible ground constituents have been assumed as the effect of the compressibility of the solid grains or of the pore water is negligible in the case of highly deformable weak rocks.

In order to preserve the condition of axial symmetry, the initial hydraulic head field has been assumed to be uniform. The contribution of the geodetic height to the hydraulic head was therefore disregarded, i.e., the hydraulic head h was taken to be equal to p w/γ w, where p w and γ w denote the pore pressure and the unit weight of the water, respectively. The error introduced by this simplifications is discussed later in this section.

A detailed discussion of the major assumptions can be found in Ramoni and Anagnostou (2010b). The following sections will briefly address the mixed non-uniform boundary conditions used for the simulation of the shield and the lining (Sect. 3.1) as well as the hydraulic boundary condition applied at the tunnel face and wall (Sect. 3.2).

3.1 Ground-Support Interface

The shield and the lining are modelled by the mixed non-uniform boundary condition proposed recently by Ramoni and Anagnostou (2010a, b):

$$ p(y) = \left\{ {\begin{array}{*{20}l} 0 \hfill & {\text{if}}\quad 0 \le y \le L\quad{\text{and}}\quad u(y) - u(0) \le \Updelta R \hfill \\ K_{s} \left( {u(y) - u(0) - \Updelta R} \right) \hfill & {\text{if}}\quad 0 \le y \le L\quad{\text{and}}\quad u(y) - u(0) > \Updelta R \hfill \\ K_{l} \left( {u(y) - u(L)} \right) \hfill & {\text{if}}\quad y > L \hfill \\ \end{array} } \right., $$
(1)

where p is the ground pressure developing upon the shield or the lining, while u denotes the radial displacement of the ground at the excavation boundary, K s and K l the stiffnesses of the shield and of the lining, respectively, L the shield length and ΔR the difference between shield and boring radius. This condition assumes that the backfilling of the segmental lining takes place immediately behind the shield according to Fig. 2a (the effect of a delayed backfilling will be discussed briefly in Sect. 6).

Fig. 2
figure 2

a Single shielded TBM with annulus grouting immediately behind the shield via the shield tail, b single shielded TBM in rock with delayed backfilling of the segmental lining

Full size image

Equation 1 takes due account of the different activation points (at y = 0 and y = L, respectively, cf. Fig. 1), stiffnesses (K s and K l, respectively) and radial gap sizes (ΔR and 0, respectively) of the shield and of the segmental lining, thus allowing a more realistic simulation than the model by Ramoni and Anagnostou (2007a, b), which considered the simplified model of an infinitely long, practically rigid shield having a constant radial gap size ΔR (the same assumption was made by Sterpi and Gioda (2007) in their analysis of the effect of creep).

3.2 Hydraulic Boundary Conditions

Pore pressure at the excavation boundary (tunnel wall and face) can be considered as atmospheric. As a consequence of this boundary condition, a flow towards the ground through the excavation boundary would occur if the pore pressure within the ground were negative (suction). This means that the ground would be watered from the tunnel and presupposes the existence of free water along the tunnel boundary. As this assumption is in most cases unrealistic (Anagnostou 1995), a mixed hydraulic boundary condition was adopted in order to avoid ground watering via the tunnel:

$$ q_{\text{n}} = \left\{ {\begin{array}{*{20}l} - \frac{k}{{\gamma_{\text{w}} }}\frac{{\partial p_{\text{w}} }}{\partial n} \hfill & {\text{if}}\; \frac{{\partial p_{\text{w}} }}{\partial n} \le 0 \hfill \\ 0 \hfill & {\text{if}}\;\frac{{\partial p_{\text{w}} }}{\partial n} > 0 \hfill \\ \end{array} } \right., $$
(2)

where k is the ground permeability, n denotes the boundary surface normal (outwards positive) and q n is the boundary flux. This condition is equivalent to a common Dirichlet condition, if positive pore pressures prevail within the ground, and to a Neumann condition (no flow) in the case of suctions.

As the actual distribution of the hydraulic head and the pore pressures is not axially symmetric, the question arises about the hydraulic head h *0 to be applied as a boundary condition at the far-field boundary of the axially symmetric computational domain (Fig. 1). The computational domain can be seen as a part of the large-scale seepage flow domain (the infinite halfspace defined by the water level; Fig. 3). In order to determine adequate boundary conditions for the axially symmetric model, a seepage flow analysis of the large-scale domain has been carried out using the closed-form solutions recently proposed by Ming et al. (2010). The application of their Equation 24 allows for the determination of the hydraulic head at each point of the large-scale domain and, consequently, also along a circle with radius R m (i.e., at the outer boundary of the axially symmetric computational domain, cf. Fig. 3).

Fig. 3
figure 3

Large-scale seepage flow domain and axially symmetric computational domain

Full size image

Figure 4a is based upon such an analysis and shows the distribution of the hydraulic head h along three lines for the example of a circular tunnel (radius R = 5 m), which is located 100 m below the water table, under the assumption that, due to a sufficiently high groundwater recharge rate, the water table remains constant in spite of the drainage action of the tunnel. Figure 4a makes clear the asymmetry of the hydraulic head distribution. At a given distance (e.g., at R m = 20R = 100 m) from the centre of the tunnel, the hydraulic head is higher above the tunnel (h = 100 m, see point A in Fig. 4a) than lateral to (h = 78 m, point B) or below the tunnel (h = 69 m, point C). It should be noted that the asymmetry of the actual pore pressure field is much bigger than the asymmetry of the hydraulic head field; Fig. 4b shows the distribution of the pore pressure head p w/γ w along the three lines mentioned above and illustrates how big the asymmetry becomes far away from the tunnel. The deviation is, however, relatively small in the vicinity of the tunnel, where the biggest deformations occur and the hydraulic-mechanical coupling is important.

Fig. 4
figure 4

Distribution of the hydraulic head h (a) and of the pore pressure p w (b) above, alongside and below a circular tunnel (radius R = 5 m) located 100 m below a constant remaining water table

Full size image

A reasonable value for the boundary hydraulic head h *0 of the simplified axially symmetric model can be obtained by considering the distribution along the horizontal axis (point B in Fig. 4a), which corresponds to the axially symmetric one, and taking into account the outer radius R m of the computational domain. Figure 5 is based upon the results of a parametric study and shows the normalized hydraulic head h *0 /h 0 to be prescribed at the outer boundary of the axially symmetric computational model as a function of the normalized initial hydraulic head h 0/R for different sizes R m/R of the computational domain. Due to the finite size R m of the computational domain, the hydraulic head at its outer boundary is lower than the initial hydraulic head, as the latter is reached theoretically at an infinite distance lateral to and below the tunnel (cf. Fig. 4a).

Fig. 5
figure 5

Normalized hydraulic head h *0 /h 0 to be prescribed at the far-field boundary of the axially symmetric computational domain as a function of the normalized initial hydraulic head h 0/R and of the normalized outer radius of the computational model R m/R

Full size image

4 Numerical Solution Method

The analysis of an advancing tunnel heading in water-bearing ground, where excess pore pressure dissipation takes place simultaneously with the spatial stress redistribution around the working face, is a time-dependent, three-dimensional problem with a moving boundary. This problem was solved numerically by the so-called “steady state” finite element method, which was proposed by Nguyen Minh and Corbetta (1991) for solving elastoplastic and elasto-viscoplastic tunnelling problems and extended by Anagnostou (1993, 2007a, b) for seepage flow or poro-elastoplastic tunnel analyses. The steady state method solves the advancing tunnel heading problem in just one computational step, thus avoiding the extremely high computational cost and the numerical accuracy and stability problems of step-by-step tunnel advance and support installation simulations.

4.1 Governing Equations

The transient consolidation problem is governed by the equilibrium equation:

$$ {\frac{{\partial \sigma_{\text{ij}}^{*} }}{{\partial x_{\text{j}}^{*} }}} + b_{\text{j}} = 0 $$
(3)

and by the mass balance equation

$$ \dot{\varepsilon }_{\text{kk}}^{*} + n_{\text{g}} c_{\text{w}} \dot{p}_{{_{\text{w}} }}^{*} + {\frac{{\partial q_{{_{\text{k}} }}^{*} }}{{\partial x_{\text{k}}^{*} }}} = 0, $$
(4)

where n g is the porosity of the ground; c w the compressibility of the pore water; and σ *ij (x *k , t), b j, ε *kk (x *k , t), p *w (x *k , t), q k(x k *, t) and x *k denote the stress tensor field, the body force vector, the volumetric strain field, the pore pressure field, the flux vector field and the position vector, respectively, in the spatially fixed co-ordinate system.

The basic idea of the steady state method is to re-formulate and solve these equations in a frame of reference which is fixed to the moving face (co-ordinate y in Fig. 1). The governing equations take account of the fact that, when conditions are steady with respect to the moving face, the objective rate of any arbitrary field function A*(y*, t) in the spatially fixed co-ordinate system (co-ordinate y* in Fig. 1) will be related to its spatial derivative in the face-fixed co-ordinate system:

$$ \left. {{\frac{{\partial A^{*} }}{\partial t}}} \right|_{y*} = v{\frac{\partial A}{\partial y}}, $$
(5)

where v denotes the advance rate (note that for convenience, and in contrast to Anagnostou (2007a, b), the present paper uses asterisks to denote the variables in the spatially fixed co-ordinate system).

Equation 5 is fundamental as it allows the time-coordinate from governing Eqs. 3 and 4 to be eliminated, thereby removing the need for integration in the time-domain. Taking account of Eq. 5, the balance Eqs. 3 and 4 transform into

$$ {\frac{{\partial \sigma_{\text{ij}} }}{{\partial x_{\text{i}} }}} + b_{\text{j}} = 0 $$
(6)

and

$$ v\left( {{\frac{{\partial \varepsilon_{\text{kk}} }}{{\partial x_{ 2} }}} + n_{\text{g}} c_{\text{w}} {\frac{{\partial p_{\text{w}} }}{{\partial x_{ 2} }}}} \right) + {\frac{{\partial q_{\text{k}} }}{{\partial x_{\text{k}} }}} = 0, $$
(7)

respectively, where σ ij(x k), ε kk(x k), p w(x k) and q k(x k) are the fields in the face-fixed co-ordinate system (x 2 = y, cf. Fig. 1). Equations 6 and 7 apply to the steady state for an observer moving with the advancing heading and contain the advance rate v as an additional parameter.

4.2 Matrix Formulation

Since the equilibrium equation remains formally unaffected by the transformation (cf. Eqs. 3 and 6), its spatial discretization under the finite element method leads to the standard matrix equation of nodal equilibrium:

$$ \left[ K \right]\left\{ u \right\} - \gamma_{\text{w}} \left[ L \right]\left\{ h \right\} = \left\{ f \right\},$$
(8)

where γ w, [K], [L], {u}, {h} and {f} denote the unit weight of the water, the stiffness and the coupling matrix and the vectors of nodal displacements, hydraulic heads and external forces, respectively. On the other hand, the discretization of the transformed mass balance equation (Eq. 7) leads to

$$ \left[ {\left[ H \right] - v\left[ V \right]} \right]\left\{ h \right\} - v\left[ W \right]\left\{ u \right\} = \left\{ q \right\}, $$
(9)

where [H] and {q} denote the common permeability matrix and nodal source vector, respectively. Equations 8 and 9 are similar to the common matrix equations of consolidation theory, the only difference being the additional matrices [V] and [W], which include the effect of the advance rate v. For more details the reader is referred to Anagnostou (2007a).

As already mentioned before, Sects. 5 and 6 of the present paper will investigate both continuous excavation and standstills, respectively. The transformed Eqs. 6–9 apply only to ongoing excavation. For the numerical computations dealing with the effect of the duration of a standstill, the usual non-transformed consolidation equations (Eqs. 3, 4) are applied.

4.3 Spatial Discretization

Solving the advancing tunnel heading problem with the steady state method allows very fast, stable and accurate investigations to be performed for coupled problems as well. A major advantage of this method is that only one computational step is required. Another advantage consists in the application of the finite element mesh. In standard step-by-step simulations, the mesh has to be fine everywhere because the location of the face, where the highest deformation and pore pressure gradients occur, moves through the (spatially fixed) computational domain during the numerical simulation. In the steady state method, however, the computational domain moves together with the face and, consequently, the mesh has to be fine only near to the face and the tunnel boundary. This allows for a considerable reduction in the size of the equation system to be solved.

Figure 6 shows the finite element mesh used for the computations in the present paper. The axially symmetric numerical model consists of 1,400 isoparametric, eight-node two-dimensional elements. The shield and the lining are simulated according to Eq. 1, using 45 isoparametric, three-node one-dimensional boundary elements. The same element type is also applied at the tunnel boundary (tunnel wall and face) for the implementation of the hydraulic boundary condition of Eq. 2. All elements of the finite element mesh apply quadratic and linear shape functions for the displacement field and the hydraulic head field, respectively.

Fig. 6
figure 6

Spatial discretization of the computational domain of Fig. 1 and detail of the finite element mesh close to the tunnel face

Full size image

5 Conditions During Regular TBM Operation

The role of excess pore pressure dissipation and the effect of the ratio of advance rate v to ground permeability k (cf. Sect. 2) will be analysed by means of numerical computations concerning the hypothetical case of a 400 m deep tunnel crossing weak ground at a depth of 100 m beneath the water table. The tunnel has a diameter of 10 m and is excavated by a 10 m long single shielded TBM. The segmental lining is 30 cm thick and practically rigid. Table 1 summarizes the material constants and the other model parameters.

Table 1 Assumed parameter values
Full size table

5.1 Distribution of the Pore Water Pressures

As discussed qualitatively in Sect. 2, the distribution of the pore pressures is of paramount importance for the deformations of the ground and, therefore, for its interaction with the shield and for the thrust force that is required for overcoming friction. During regular TBM advance, the ground behaviour will be undrained, drained or somewhere in-between depending on the ratio of advance rate v to ground permeability k.

Figure 7 shows the contour lines of the pore pressure p w for different ratios v/k, thus illustrating the transition from undrained conditions to less favourable drained conditions occurring when the advance rate decreases (or the ground permeability increases). Under practically undrained conditions (i.e., when the v/k ratio is high), negative excess pore pressures develop within an extended region around the tunnel and dissipate far behind the working face. With a decreasing advance rate (or with increasing ground permeability), the dissipation of the excess pressures takes place faster, i.e., closer to the tunnel heading. Of course, the predicted high suctions can occur only in the absence of cavitation (i.e., in extremely fine-grained, clayey ground).

Fig. 7
figure 7

Contour lines of the pore pressure p w for different values of the ratio of advance rate v to ground permeability k (other parameters according to Table 1)

Full size image

5.2 Interaction Between Shield, Ground and Support

The higher the ground permeability k (or the slower the TBM advance rate v), the quicker will be the development of the consolidation process and the larger will be the deformations in the machine area.

Figure 8a shows the radial displacement u of the ground at the tunnel boundary for different ratios v/k and a radial gap size ΔR of 5 cm (left side) or 10 cm (right side). The radial gap size is equal to the difference between the radius of the bored profile and the outer radius of the shield and represents the space which is available for accommodating ground deformations without development of a ground load upon the shield. The radial displacement u according to Fig. 8a includes the “pre-deformation” of the ground, i.e., the deformation u(0) that occurs ahead of the face. The risk of shield jamming depends on the convergence u − u(0) of the bored profile (Fig. 8b). Figure 8b shows that the higher the ground permeability k and the lower the advance rate v, the faster will the convergence develop and the nearer to the tunnel face will be the closure in the radial gap (compare, e.g., point B with point A in Fig. 8b, left side).

Fig. 8
figure 8

Results of numerical computations for a radial gap size of ΔR = 5 or 10 cm (left and right side, respectively) and for different ratios of advance rate v to ground permeability k: a radial displacement u of the ground at the tunnel boundary; b convergence u − u(0) of the bored profile; c ground pressure p acting upon the shield and the lining; other parameters according to Table 1

Full size image

After closing the gap, the ground starts to develop a load upon the shield (Fig. 8c). The ground pressure p increases with the distance y behind the face and drops to zero at the installation point of the lining. Assuming that the annulus grouting is carried out via the shield tail with a very fast hardening mortar (cf., e.g., Pelizza et al. 2010) and simultaneously with the shield advance, a ground pressure starts to develop upon the lining immediately after its installation at the shield tail. It should be noted that the simplified model of Ramoni and Anagnostou (2007a, b) cannot reproduce the stress relief at the installation point of the lining and leads to an underestimation of the shield loading—see Ramoni and Anagnostou (2010a) for a detailed discussion of this point.

According to Fig. 8c, the ratio of advance rate v to ground permeability k is decisive for the shield loading. Consider, for example, the case of a normal overcutting (ΔR = 5 cm, left side). If v/k ≥ 3 × 105, the ground does not close the gap and the shield remains unloaded, while for v/k ≤ 3 × 103 a considerable load develops which may immobilize the shield (due to skin friction) or even endanger its structural safety. Note that for such low v/k values, pore pressure dissipation occurs practically simultaneously with excavation, the system reaches steady state immediately and no time-dependency can be observed.

A larger radial gap ΔR has, as one might expect, a positive effect with respect to the shield loading, as it remains open for a longer interval behind the face (compare, e.g., point C with point B in Fig. 8b, right and left side, respectively) and widens the subcritical range. In order that the shield remains unloaded in this example, the v/k ratio should be higher than about 3 × 105 if ΔR = 5 cm, while a v/k of 2 × 104 would be sufficient if ΔR = 10 cm. For a radial gap of ΔR = 15 cm, the shield would remain unloaded even for v/k → 0 (i.e., standstill or a very rapid, practically time-independent ground response). The feasibility and the reliability of such a large overboring is nevertheless questionable and has to be checked carefully for given project conditions (Ramoni and Anagnostou 2010c).

It should be noted that a high ratio of advance rate v to ground permeability k is favourable with respect to the risk of shield jamming but not with respect to a possible overstressing of the lining. The higher the v/k ratio, the smaller will be the deformations developing prior to lining installation and, consequently, the higher will be the final load developing upon the lining far behind the face. Figure 9 shows a numerical example. As expected, high v/k ratios are favourable with respect to the shield loading (in this example, for v/k = 105–106 the shield remains unloaded). At the same time, the high v/k ratios lead to a higher lining loading far behind the face (e.g., compare points A and C in Fig. 9, which apply for v/k = 105 and v/k = 103, respectively). It is also interesting to note that in this example for v/k = 106 at a distance of y = 90 m behind the face the final value of the ground pressure acting upon the lining has not yet been reached (see point B in Fig. 9). This is due to the fact that the consolidation process has not yet ended.

Fig. 9
figure 9

Ground pressure p acting upon the shield and the lining for different ratios of advance rate v to ground permeability k (other parameters according to Table 1)

Full size image

5.3 Calculation of Thrust Force

The thrust force F f needed to overcome shield skin friction can be calculated by integrating the rock pressure p over the shield length L:

$$ F_{\text{f}} = \mu 2\pi R\int\limits_{0}^{L} {p(y){\text{d}}y}, $$
(10)

where μ is the skin friction coefficient. Two operational stages have to be considered with respect to the thrust force requirements: (a) ongoing excavation, (b) restart after a regular short standstill (e.g., for the installation of the tunnel support or for the execution of routine maintenance work). For stage (a) the thrust force F b needed for boring must also be taken into account (Ramoni and Anagnostou 2010c). Therefore, the required thrust force

$$ F_{\text{r}} = F_{\text{f}} + F_{\text{b}}, $$
(11)

where

$$ F_{{\text{b}}} = \left\{ {\begin{array}{*{20}l} {F_{{\text{c}}} n_{c} } & {\text{for\;ongoing\;excavation}} \\ 0 & {\text{for\;restart\;after\;standstill}} \\ \end{array} } \right. $$
(12)

F c is the maximum cutter force and n c is the number of cutters. For cutters with a diameter of 17 in, F c can be taken as equal to 267 kN (Sänger 2006), while for n c the following empirical expression applies (Vigl et al. 1999):

$$ n_{c} = 6.7D, $$
(13)

where D is the boring diameter. The two operational stages mentioned above are also different with respect to the skin friction coefficient μ. During ongoing excavation, the TBM has to overcome sliding friction, while static friction has to be taken into account when restarting the TBM. Here, the skin friction coefficient μ was taken to be 0.30 and 0.45 for sliding and static friction, respectively (Gehring 1996).

5.4 Effects of Overboring and Lubrication

Figure 10 shows the required thrust force F r as a function of the v/k ratio for a radial gap size of ΔR = 5 cm (normal overcutting) or 10 cm (overboring). The dashed lines apply to ongoing excavation (F b was taken to 18 MN in this example), while the solid lines apply to a restart.

Fig. 10
figure 10

Required thrust force F r during ongoing excavation (including the thrust force F b = 18 MN needed for the boring process) and for restart with lubrication of the shield extrados (skin friction coefficient μ = 0.15 or 0.25) or without lubrication of the shield extrados (skin friction coefficient μ = 0.30 or 0.45) as a function of the ratio of advance rate v to ground permeability k (other parameters according to Table 1)

Full size image

Let us assume that the installed thrust force F i amounts to 150 MN—a high, but feasible value provided that the bearing capacity of the segmental lining is sufficient (cf. Ramoni and Anagnostou 2010b)—and that the radial gap size ΔR is equal to 5 cm. In this case the TBM would be trapped if v/k ≤ 2.5 × 104 (point A in Fig. 10), i.e., if v = 1 m/day and k ≥ 4.6 × 10−10 m/s or v = 10 m/day and k ≥ 4.6 × 10−9 m/s (see axis at the bottom of Fig. 10). Of course, the required thrust force can be reduced considerably by overboring (to less than 100 MN in this example)—this comes, however, at the cost of possible steering difficulties and reduced production rates (Ramoni and Anagnostou 2010c).

Besides overboring, another possible countermeasure for coping with squeezing is the lubrication of the shield extrados (e.g., by bentonite). Lubrication reduces the shield skin friction and thus the required thrust force (compare curves for μ = 0.15 or 0.25 with curves for μ = 0.30 or 0.45 in Fig. 10). The effect of lubrication is smaller than that of overboring in this example. However, as overboring may be not sufficiently reliable, a combination of these two measures would be required in order to mitigate the risk of shield jamming.

5.5 Effects of Permeability

Figure 10 also shows that drained conditions apply during regular TBM operation, i.e., the consolidation process is practically irrelevant, if v/k ≤ 103 or (taking into account an assumed maximum feasible advance rate of v = 10 m/day) if the permeability k is higher than about 10−7 to 10−8 m/s. There is no observable time-dependency in the ground response in such a case. Unfavourable steady state conditions apply continuously during excavation right from the start and may, depending on the countermeasures applied, affect the feasibility of the TBM drive.

On the other hand, if v/k ≥ 106 favourable undrained conditions would prevail and the required thrust force would be considerably lower. In the case of a low-permeability ground (k < 10−10 to 10−11 m/s) the shield would remain unloaded even at moderate advance rates of 1–10 m/day.

A large sensitivity in the results can be observed for permeabilities k between 10−8 and 10−10 m/s (cf. Figure 10). This permeability range is thoroughly relevant in practice. For example, the extensive laboratory testing program carried out for investigating the kakiritic rocks of the Gotthard Base Tunnel (Lot Sedrun) in Switzerland revealed permeabilities between 1.5 × 10−9 and 1.1 × 10−10 m/s (Vogelhuber 2007). This large sensitivity in the numerical results indicates a major source of prediction uncertainty.

5.6 A Counter-Intuitive Aspect of Model Behaviour

According to Fig. 10, the required thrust force F r in the v/k range between 102 and 104 is slightly higher than the force needed for v/k → 0. This behaviour is counter-intuitive because one would expect conditions to become increasingly unfavourable with a decreasing advance rate. As can be seen from the additional computational results of Fig. 11, this effect is more pronounced in the case of a low strength ground, i.e., at higher levels of plastification. This has also been observed by other authors (Boldini et al. 2000; Graziani et al. 2005; Matter et al. 2007) and is associated with the pre-deformations of the ground ahead of the face (the bigger the pre-deformation, the more pronounced the stress relief). The counter-intuitive behaviour occurs at v/k ratios, for which the pore pressures are negative in the core ahead of the face and in the front part of the machine, but positive behind the cutter head (see, e.g., the contour lines for v/k = 2,000 in Fig. 7). The conditions along the shield are therefore close to the steady state, but the strengthening effect of the negative pore pressures ahead of the face is still there and keeps the pre-deformations small (a similar effect might also occur in the case of creep, when the core is still behaving elastically while the rest of the tunnel is already experiencing plastic deformations).

Fig. 11
figure 11

Thrust force F r required for restart as a function of the ratio of advance rate v to ground permeability k (other parameters according to Table 1)

Full size image

5.7 Extrusion Rate of the Core

“Extrusion of the core” means the axial displacement of the working face towards the tunnel. During the boring process, some of the TBM penetration is used up simply to compensate the extrusion, i.e., to excavate the ground that squeezed into the opening from the face. If the extrusion rate e is very high, the penetration effort will be entirely used up in excavating the axially deforming ground at the tunnel face, i.e., the cutter head will penetrate and rotate without moving forward (Ramoni and Anagnostou 2010c). De Biase et al. (2009) recently reported an extreme case where the squeezing ground at the face pushed back the TBM.

In general, the advance rate actually achieved is the advance rate v that would occur in the absence of relevant face deformations minus the extrusion rate of the core e:

$$ v = \max (0,\;\alpha Pr - e), $$
(14)

where α is the utilization degree of the TBM (i.e., the fraction of the total time used for boring), P is the penetration rate (i.e., the TBM advance relative to the ground at the working face per revolution of the cutter head) and r the cutter head rotational speed.

The extrusion rate of the core e can be computed easily from the longitudinal gradient of the axial displacements u e by applying the transformation rule according to Eq. 5:

$$ e = \left. {{\frac{{\partial u_{e} }}{\partial t}}} \right|_{y*} = v{\frac{{\partial u_{e} }}{\partial y}}. $$
(15)

Figure 12 shows the extrusion rate e as a function of the ground permeability k for the numerical example considered throughout the present paper. The extrusion rate is small relative to commonly achievable advance rates. Since this numerical example concerns rather adverse conditions (in terms of ground strength and depth of cover), the results support the hypothesis that the excavation speed is normally high enough to avoid problems with deformations of the working face (Barla 2001; Gehring 1996; Hoek 2001).

Fig. 12
figure 12

Extrusion rate e of the core as a function of ground permeability k (other parameters according to Table 1)

Full size image

5.8 Role of Tunnel Diameter

An issue sometimes arising in the design phase concerns the option of constructing a smaller diameter tunnel (which may be part of the final structure—e.g., the service tunnel of a twin railway tunnel) for exploration or ground improvement in advance of the main, larger diameter tunnel. The underlying idea is that the potential geomechanical problems are less serious in the case of a smaller cross section. It is a fact that there are many statical problems where the size of the opening represents a relevant parameter (e.g., the height and the width of the tunnel face may be decisive for its stability or the stability of the tunnel crown may depend on the round length).

Within the context of the present paper, a question arises as to whether a smaller diameter tunnel offers advantages with respect to the risk of shield jamming. This question cannot be answered on the basis of qualitative considerations because some of the differences between small and large diameter tunnels are in favour of small cross sections and others in favour of large diameter TBMs. More specifically, a smaller diameter TBM will be able, under normal operational conditions, to proceed faster (but the limited space available may present greater difficulties in the case of adverse conditions). Furthermore, a given amount of overboring ΔR (say 5–10 cm) will be more effective in reducing the ground pressure in the case of a small diameter machine (because the load reduction is governed by the ratio of radial gap size ΔR to tunnel radius R). On the other hand, as can be seen from the TBM technical data collected by Ramoni and Anagnostou (2010b), smaller diameter TBMs are relatively longer (the ratio of shield length L to tunnel radius R is higher than for traffic tunnel TBMs—typical values are L/R = 5.0 and 2.0, respectively) and have a lower installed thrust force (reported values, at the upper limit of the proven range, are F i = 50 and 150 MN, respectively). This results in a slightly lower ratio of installed thrust force F i to shield mantle surface 2πRL (i.e., the surface exposed to the ground pressure) for the smaller diameter TBMs than for the larger ones (F i/2πRL = 0.40 and 0.48 MPa, respectively).

Figure 13 compares a “traffic tunnel” TBM (assumed to advance at a rate of v = 10 m/day, solid curves) with a faster advancing “service tunnel” TBM (v = 25 m/day, dashed curves). The diagram shows the utilization degree of the thrust force as a function of the ground permeability k. The utilization degree of the thrust force is defined as the ratio of the thrust force F r, required in order to overcome the frictional resistance of the ground, to the installed thrust force F i. An utilization degree of more than 100% means that the machine will be jammed. A low utilization degree indicates that the machine has a large reserve against jamming. The diagram deals with the thrust force requirements for TBM restart, i.e., for overcoming static friction (and, according to Eqs. 11 and 12, F r = F f). It contains three curves for each TBM in order to show the effect of the overcut (radial gap size ΔR = 5 or 10 cm) and the ground quality (uniaxial compressive strength f c = 1.5 or 3.0 MPa).

Fig. 13
figure 13

Thrust force utilization F r/F i for restarting operation of a “traffic tunnel” TBM and a “service tunnel” TBM (tunnel radius R = 5 and 2 m, respectively) as a function of ground permeability k (other parameters according to Table 1)

Full size image

In a low strength and high permeability ground (f c = 1.5 MPa, k > 10−8 m/s) the thrust force requirements would be critical for both machines in the case of a normal overcut (ΔR = 5 cm). For the reasons mentioned above, the benefit of increasing the overcut (from ΔR = 5 to 10 cm in this example) is greater in the case of the smaller diameter tunnel. Furthermore, it is interesting that in the case of a better quality ground (f c = 3.0 instead of 1.5 MPa) the situation would improve significantly for the smaller diameter TBM but not for the large TBM. The results of Fig. 13 indicate that a smaller diameter TBM would cope slightly better with squeezing than the larger diameter machine under the conditions of this specific example.

6 Conditions During Standstills

6.1 Dissipation of the Excess Pore Water Pressures

The conditions during a standstill will be discussed by means of numerical results relating to the example introduced in Sect. 5. The pore pressure distribution at the beginning of a standstill depends on the ratio of the advance rate v of the preceding excavation to the ground permeability k. As can be seen from Fig. 7, the higher this ratio, the more the pore pressure field prevailing at the start of the standstill will deviate from the steady state. During the standstill, excess pressure dissipation and consolidation of the ground will continue until the steady state is reached.

The transition from favourable undrained conditions to unfavourable drained conditions can be observed in Fig. 14, which shows the contour lines of the pore pressure p w at different times t (since the start of the standstill) assuming that the ground has a permeability of k = 10−9 m/s and that the preceding excavation proceeded at a rate of v = 10 m/day. In this example, the steady state is reached after about 10 days.

Fig. 14
figure 14

Contour lines of the pore pressure p w at different times t during standstill (other parameters according to Table 1)

Full size image

6.2 Longitudinal Arching in the Shield Area

The dissipation of excess pore pressures leads to a time-dependent increase in ground deformations and, as the shield and lining allow only a limited amount of deformation, an increase in the ground pressure as well.

Figure 15a shows the increase of the convergence u − u(0)t=0 over the time t (that has elapsed since the start of the standstill) for two values of radial gap size (ΔR = 5 or 10 cm, on the left and right side, respectively), where u denotes the total radial displacement of the ground at the excavation boundary, while u(0)t=0 is the “pre-deformation” of the ground (i.e., the deformation, which occurred ahead of the face during excavation). Figure 15b shows the time-development and spatial distribution of the ground pressure p acting upon the shield and lining. As in Sect. 5, the simplifying assumption is made that the backfilling of the segmental lining is carried out immediately after installation of the segments (Fig. 2a) and this is why a load starts to develop upon the lining immediately behind the shield. The effect of a delayed annulus backfilling (Fig. 2b) will be discussed in the next section.

Fig. 15
figure 15

Numerical results for a radial gap size of ΔR = 5 or 10 cm (left and right side, respectively): a convergence u − u(0)t=0 of the bored profile as a function of the standstill time t; b ground pressure p acting upon the shield and the lining as a function of the standstill time t; other parameters according to Table 1

Full size image

In the case of normal overcut (ΔR = 5 cm), the ground already closes the gap around the rear part of the shield during TBM advance and, consequently, a load p already acts upon the shield at the start of the standstill (see curve for t = 0, left side of Fig. 15b). During the standstill, the load acting upon the shield and the lining increases and reaches its final value after about 10 days (when the pore pressure distribution reaches the steady state, cf. Fig. 14).

The convergence and pressure distribution are completely different in the case of the bigger overcut (right side of Fig. 15). The 10 cm wide radial gap under consideration remains open during TBM advance. During standstill, the ground takes about 9 days to establish contact with the shield and to start developing a load upon it, and another 10 days to reach the steady state (the longer duration of the consolidation process is due to the lower system stiffness associated with the bigger overcut). During the first phase of the standstill, where the ground remains unsupported over the shield area, a considerable load develops upon the front part of the lining. It is also interesting that the ground first makes contact with the shield in its middle part. The front and the rear parts of the shield remain unloaded due to the support action of the lining and the core, respectively. The observed pressure distribution illustrates a pronounced load transfer via arching in longitudinal direction between the lining and the ground ahead of the face. This effect becomes less pronounced with time due to the plastic yielding of the ground surrounding the middle part of the shield.

On the one hand, the arching effect is favourable with respect to shield loading and to the thrust force that is required in order to overcome the frictional resistance of the ground during TBM restart. On the other hand, arching increases ground pressure behind the shield and may endanger the structural safety of the lining. The practical conclusion is that a reinforcement of the tunnel support close to the shield may be necessary in the case of longer standstills and, as mentioned above, of complete backfilling of the segmental lining immediately behind the shield.

The arching effect discussed above depends on the resistance offered by the lining behind the shield and the stiffness of the core ahead of the shield. The influence of these two factors will be discussed in Sects. 6.3 and 6.4, respectively.

6.3 Effect of Backfilling of the Segments Close to the Shield

A significant load transfer in the longitudinal direction (which is favourable for the shield, but unfavourable for the lining) is possible only if the segments are “perfectly” backfilled directly behind the shield, i.e., if annulus grouting is carried out simultaneously with TBM advance via the shield tail (Fig. 2a). This is normally the case with closed shields, where the counter-pressure offered by the supporting medium prevents the flow of grout around the shield towards the cutter head. In rock TBMs, however, where pea gravel is used for backfilling, it is not possible to achieve a contact between ground and segmental lining right from the start and, as sketched in Fig. 2b, a certain “span” behind the shield remains unsupported (Lavdas 2010). Shield load reduction via longitudinal arching is practically impossible in this case.

For the sake of comparison, let us consider the borderline case of a segmental lining without backfilling. In this case, the ground starts to develop a pressure p upon the lining only after experiencing sufficient deformation and closing the lining annulus gap ΔR l. The latter denotes the difference between the boring radius and the outer radius of the segmental lining and is taken to be ΔR + 7.5 cm, where ΔR is the radial gap size of the shield (cf. Ramoni and Anagnostou 2010b). The lining annulus gap ΔR l is taken into account by prescribing the following boundary condition instead of Eq. 1:

$$ p(y) = \left\{ {\begin{array}{*{20}l} 0 \hfill & {{\text{if}}\quad 0 \le y \le L\quad {\text{and}}\quad u(y) - u(0) \le \Updelta R} \hfill \\ {K_{\text{s}} \left( {u(y) - u(0) - \Updelta R} \right)} \hfill & {{\text{if}}\quad 0 \le y \le L\quad {\text{and}}\quad u(y) - u(0) > \Updelta R} \hfill \\ 0 \hfill & {{\text{if}}\quad y > L\quad {\text{and}}\quad u(y) - u(0) \le \Updelta R_{\text{l}} } \hfill \\ {K_{\text{l}} \left( {u(y) - u(0) - \Updelta R_{l} } \right)} \hfill & {{\text{if}}\quad y > L\quad {\text{and}}\quad u(y) - u(0) > \Updelta R_{\text{l}} } \hfill \\ \end{array} } \right..$$
(16)

Figure 16 presents the numerical results in the same way as Fig. 15 did in the last section, i.e., it shows the spatial distribution and time-development of ground convergence and pressure for two values of the radial gap size ΔR of 5 or 10 cm (on the left and right side, respectively). As expected, the ground starts to develop a pressure p upon the lining later (after closing the lining annulus gap) and the final load is significantly lower than for the case with perfect backfilling of the segments; this, however, at the cost of a much higher shield load (in this computational example, the load developing on the rear part of the shield would endanger its structural safety).

Fig. 16
figure 16

Numerical results for the borderline case of a segmental lining without backfilling for a radial annulus of ΔR l = 12.5 or 17.5 cm (left and right side, respectively): a convergence u − u(0)t=0 of the bored profile as a function of the standstill time t; b ground pressure p acting upon the shield and the lining as a function of the standstill time t; other parameters according to Table 1

Full size image

The comparison of Figs. 15 and 16 shows that conflicting requirements may have to be met. On the one hand, backfilling of the segments immediately behind the shield facilitates longitudinal arching and reduces shield load. On the other hand, ground deformation should be allowed in order to reduce lining load to a manageable level.

For fast excavation through a low permeability ground (i.e., for a high v/k ratio), where undrained conditions prevail in the shield area and the ground pressure p acting upon the shield at the beginning of the standstill is very low (see curves for t = 0 in Fig. 16b), it seems advantageous to delay the backfilling of the segments. It should be noted, however, that improper backfilling of the segments may reduce the bearing capacity of the lining and may therefore limit the effectively available thrust force (it may be impossible to utilize the installed thrust force).

In the other borderline case of a slow excavation or a high permeability ground (i.e., low v/k ratio), where almost drained conditions prevail in the shield area and the shield loading is significant even during continuous excavation, a careful backfilling of the segments close to the shield may help avoid TBM jamming. Nevertheless, it should also be noted that the backfilling work may slow down the TBM advance rate, thus leading, as a rule, to a less favourable situation.

6.4 Load Transfer to the Core Ahead of the Face

Longitudinal arching presupposes, in addition to the development of lining resistance close to the shield tail, a sufficiently stiff core ahead of the face. The radial resistance of the core depends, in general, on the face support pressure (as mentioned in Sect. 3, the computational model applied in this paper regards the tunnel face as being unsupported). The lower the face support pressure, the more the core yields and extrudes in the axial direction, the more the radial stress ahead of the face decreases and the more load is transferred to the shield. This is why the ground pressure in the front part of the shield increases with time during the standstill (see pressure peak at y = 1.5 m behind the face in Fig. 15b, left side).

This effect becomes clearer from Fig. 17a, which shows the ground pressure p at y = 1.5 m behind the face as a function of standstill time t (the inset in Fig. 17a shows the final pressure distribution along the shield). The solid line applies to an unsupported face, while the marked line applies to the case of zero core extrusion (where axial displacement is constrained by the cutter head). In the first case the face experiences an additional axial displacement u e(t) during the standstill (Fig. 17b), while in the second case an axial pressure develops upon the cutter head (Fig. 17c).

Fig. 17
figure 17

a Ground pressure p developing at y = 1.5 m during a standstill as a function of time t (unsupported or fixed face); b core extrusion ue developing during a standstill as a function of time t (unsupported face); c axial loading p developing upon the cutter head as a function of time t (fixed face); other parameters according to Table 1

Full size image

The ground pressure developing upon the shield is lower when the core cannot extrude. Face support therefore has a positive effect on the shield load during standstill. The cutter head provides a certain degree of face support—this however at the cost of higher thrust force and torque requirements (Ramoni and Anagnostou 2010c). Of course, the extrusion of the core u e also plays an important role with respect to face stability, as excessive deformations may lead to collapse. The absence of an asymptotic limit to the axial displacement in Fig. 17b (note that the displacement increases linearly over time) indicates instability.

6.5 Thrust Force Needed for Restarting TBM Operation

Due to the increasing shield load (Figs. 15, 16 and 17), the thrust force F r, which is required in order to overcome skin friction during a TBM restart, increases as well. Figure 18 shows the time-development of the required thrust force F r (as mentioned in Sect. 5.3, the thrust force calculation takes into account static friction, but not the boring thrust force).

Fig. 18
figure 18

Required thrust force F r for different model assumptions (unsupported or fixed face, with and without backfilling of the segmental lining close to the shield) as a function of the standstill time t (other parameters according to Table 1)

Full size image

The solid lines presuppose a complete backfilling of the segments immediately behind the shield and an unsupported face. In the case of an installed thrust force of F i = 150 MN and a normal overcutting of ΔR = 5 cm, the TBM can be restarted if the standstill is shorter than about 2.5 days (see point A in Fig. 18). In the case of a larger radial gap size (ΔR = 10 cm), it would always be possible to restart the TBM in this example. This could be achieved also by lubricating the shield extrados (i.e., reducing the skin friction coefficient μ from 0.45 to 0.25).

The dashed lines in Fig. 18 concern the borderline case without backfilling of the segments (Fig. 2b). The positive effect of backfilling with respect to the risk of shield jamming can be seen clearly by comparing these dashed lines with the solid lines. Without backfilling, the critical standstill duration decreases from 2.5 days to about 1.5 day in the case of a normal overcut of ΔR = 5 cm (see points B and A in Fig. 18). For an overboring of ΔR = 10 cm, the shield becomes loaded earlier (after 5 instead of 9 days, see points D and C in Fig. 18) and the required thrust force increases considerably over time.

The marked lines in Fig. 18 apply to the case of a fixed face, thus illustrating the positive effect of a face support (cf. Sect. 6.4). This effect is, however, of minor relevance in the numerical example under consideration.

As shown in Fig. 18, the required thrust force F r may increase to the level of the installed thrust force F i after a certain period of time t (e.g., 2.5 days for ΔR = 5 cm and complete backfilling of the segmental lining). Figure 19 shows the influence of ground permeability k on the critical standstill duration t crit under the assumption that the advance rate during the preceding excavation was v = 10 m/day and the installed thrust force amounts to F i = 150 MN. The higher the ground permeability k, the faster will be the consolidation and the shorter the critical standstill duration t crit. In this numerical example, for a normal overcutting of ΔR = 5 cm and a uniaxial compressive strength of the ground of f c = 1.5 MPa, regular TBM operation as well as standstills of 1–1.5 day or more (depending on the ground permeability k) will be possible if the ground permeability is lower than 10−9 m/s. On the contrary, for a ground permeability higher than 10−8 m/s the shield would become jammed even during regular TBM operation (cf. Fig. 11). During the standstill, the ground pressure acting upon the shield may increase further, thus making the job of freeing the TBM even more difficult. For ground permeabilities of k = 10−8 to 10−9 m/s the critical standstill duration t crit decreases down to zero. At this permeability range, the required thrust force F r was close to the installed one F i even during the previous regular TBM operation that proceeded with a rate of v = 10 m/day (cf. Fig. 11). From the practical point of view, this means that all possible precautions should be taken in order to make TBM operation as continuous as possible, as each further unexpected standstill will significantly increase the risk of shield jamming.

Fig. 19
figure 19

Critical standstill duration t crit as a function of ground permeability k (other parameters according to Table 1)

Full size image

As shown above (Sects. 2 and 5.1), the ratio of advance rate v to ground permeability k governs the distribution of the pore pressure at the beginning of the standstill. Therefore, for a given ground permeability k, the advance rate v of the preceding regular TBM operation will influence the conditions prevailing at the beginning of the standstill to a considerable extent: the higher the advance rate v, the lower must have been the required thrust force F r during excavation (cf., e.g., Fig. 11) and, therefore, the more time will have to elapse during a standstill before the required thrust force reaches the installed one (Fig. 20). Figure 20 also suggests that a critical advance rate exists for which the critical standstill duration t crit decreases up to zero (e.g., v = 2.6 m/day for ΔR = 5 cm and f c = 1.5 MPa, see point A in Fig. 20). This advance rate corresponds to the borderline case where the required thrust force F r is already equal to the installed one F i during regular TBM operation (cf. Fig. 11). This confirms the practical experience that making the TBM advance as fast as possible may help to avoid shield jamming in squeezing ground.

Fig. 20
figure 20

Critical standstill duration t crit as a function of the advance rate v (other parameters according to Table 1)

Full size image

7 Closing Remarks

Interruptions in the TBM operation may be unfavourable in squeezing ground. Tunnelling experience (Ramoni and Anagnostou 2010c) as well as theoretical considerations (cf. Sects. 5 and 6) suggests that maintaining a high advance rate and reducing the standstill times may have a positive effect. This is, of course, a major goal for any TBM drive. Nevertheless, a fast TBM advance should not be seen as a panacea for coping with squeezing conditions. First, it may be difficult to achieve it in the case of poor quality ground. Second, ground deformations may develop very rapidly and very close to the tunnel face (Ramoni and Anagnostou 2010c). And finally, the possibility of unpredicted long standstills cannot be excluded a priori with sufficient certainty.

Theoretical considerations, together with numerical investigations, improve the understanding of the time-dependency of ground behaviour. With respect to water-bearing squeezing ground, the governing factor is the ratio of advance rate v to ground permeability k. During regular TBM operation (excavation including short standstills), favourable undrained conditions prevail near to the working face if the ratio v/k is high enough (i.e., if the gross advance rate is high or the ground permeability is low). Otherwise, consolidation takes place simultaneously with tunnel excavation and already reaches the steady state in the machine area. As the ratio v/k governs the conditions prevailing at the beginning of a standstill, for a given ground permeability k, a high advance rate v not only reduces the risk of shield jamming when the TBM is advancing regularly but also increases the critical duration of a subsequent standstill.

As with every geomechanical computation, both the underlying simplifying assumptions (e.g., rotational symmetry, absence of cavitation) and the uncertainties associated with the ground parameters must be borne in mind. In this respect, it is particularly important to remember that reliable assessments of ground permeability, which governs the short-term behaviour and thus the shield-ground interaction, can be difficult, particularly for heterogeneous ground (Anagnostou and Kovári 2005). Nevertheless, the results presented in the present paper improve our understanding of the fundamental mechanisms governing the interaction between the shield, the tunnel support and the consolidating ground.