1 Introduction

1.1 Recent Developments of High-Head Hydroelectric Power Plants

The increasing demand for energy and the changes in the electricity market in the last decades impose more drastic operational requirements to hydroelectric power plants. The development of high-strength steels (HSS) together with high-head Pelton turbines result in the design of highly loaded pressure tunnels and shafts (Schleiss and Manso 2012). Therefore in new high-head hydroelectric projects as well as in recently constructed plants the internal water pressure can be higher than 150 bar (Benson 1989; Schleiss and Manso 2012). High-head hydropower plants transient operations result in dynamic pressure surges called water hammer, causing additional loading in the system of about 15 to 25 % of the static head (Brekke and Ripley 1987). In 1998, the Cleuson-Dixence shaft attained world record conditions with a discharge of \(75\,{\rm m}^{3}/{\rm s}\) and a dynamic internal water pressure of more than 200 bar (Ribordy 1998).

Pressure tunnels and shafts of high-head hydropower plants usually have a major influence on the economic feasibility of the project (Vigl 2013; Schleiss 2013). Despite their importance, limited effort has been dedicated to study the design of liners of pressure tunnels in general, compared to other types of tunnels (Bobet and Nam 2007). Larger dimensions, intensified and more frequent dynamic surges impose high mechanical requirements for the steel liners and the use of HSS, which are more difficult to weld than ductile steel grades (Cerjak et al. 2013; Greiner et al. 2013). As a consequence, the need for an appropriate design that guarantees safety arises. When the rock conditions are adequate (depending on the rock overburden and the in situ stress field) the design can consider that a significant part of the internal water pressure can be transfered to the concrete–rock system. Thereby, the thickness of the steel liner can be decreased. This also facilitates welding when using HSS. The standard design methods for steel-lined pressure tunnels and shafts are appropriate and conservative for ductile steel (Brekke and Ripley 1987) but not when using HSS, in which case new design conditions arise and new design methods need to be developed for a wide and safe application in high-head hydropower plants (Cerjak et al. 2013; Hachem and Schleiss 2009).

1.2 Conventional Design for Steel-Lined Pressure Tunnels and Shafts in Isotropic Rock

Pressure tunnels and shafts drilled in rock may be steel-lined where rock confinement is not sufficient or when leakage into the rock mass is not acceptable (Brekke and Ripley 1987). Steel linings address these issues by providing greater stiffness, strength, and impermeability. The basic design criteria for the steel liners are summarized by Schleiss (1988) as follows:

  1. 1.

    The working stress and deformation in the steel liner:

    1. (a)

      Stability of the steel liner under external water pressure (buckling);

    2. (b)

      Limiting working stresses in the steel liner under internal water pressure;

    3. (c)

      Limiting local deformation of the steel liner (crack bridging); and

  2. 2.

    The load-bearing capacity of the rock mass.

The second criterion refers to the verification of the load-sharing assumed for the limiting working stresses in the steel liner and to ensure the required security against the rock mass failure. The portion of the internal water pressure taken by the rock should not exceed the in situ stress or the tensile strength of the rock material (Olsson et al. 1997; Schleiss 1988).

In Europe, the C.E.C.T. (1980) recommendations for the design of steel-lined pressure tunnels and shafts have been developed for both the design and the construction. Load combinations and allowable equivalent stresses in steel liners according to the Hencky–Von Mises theory in triaxial state of stresses are discussed in these recommendations.

For the design it is common practice to consider an isotropic rock behavior, with the most unfavorable elastic modulus measured in situ. This is usually a conservative assumption in the quasi-static case. The axisymmetrical multilayer model used for the design is presented in Sect. 2, with emphasis on the material characteristics and the assumptions for each layer. The associated closed-form solution is discussed in Sect. 3.

1.3 Pressure Tunnels and Shafts in Anisotropic Rocks

Several authors have studied pressure tunnels and shafts subjected to internal water pressure considering the rock mass anisotropy. Experimental studies of linings in anisotropic media and an analytical method of the lining behavior in elastic orthotropic media by partitioning the lining into beam elements were published by Éristov (1967a, b). The latter analytical method is similar to the FEM approach presented in USACE (1997), as noted by Hachem and Schleiss (2009). Baslavskii (1973) derived an analytical solution for the stresses in the lining of a pressure tunnel in a linear elastic rock which is inhomogeneous within a thick ring around the liner. This inhomogeneity was characterized by a slight variation of the shear modulus around the opening. Postol’skaya (1986) performed a series of parametric investigations on the stresses in crack-resistant linings in different anisotropic media using the FEM. Kumar and Singh (1990) studied the effect of jointed rocks on reinforced concrete linings in pressure tunnels by means of the FEM. Their approach is particularly interesting as they introduced a reduction factor in the analytical expression for load-sharing between a lining and an isotropic and homogeneous rock mass to include the effect of joints. They used a continuous constitutive relation according to Singh (1973) to characterize the jointed rock mass. More recent analytical developments were carried out to compute stresses and deformations in unlined and lined tunnels in anisotropic rock subjected to in situ loadings (e.g., Hefny and Lo 1999; Bobet 2011; Tran Manh et al. 2014).

Nevertheless, in these studies, the particular case of steel-lined pressure tunnels and shafts made of four layers with different properties (Sect. 2) and the assumption of cracked layers was not considered. To the authors’ knowledge, there are neither analytical, experimental nor numerical published extensive parametric study characterizing the influence of anisotropic rock behavior on stresses and deformations in steel-lined pressure tunnels and shafts under quasi-static internal water pressure.

In this article, the stresses and displacements in steel liners of pressure tunnels and shafts subjected to quasi-static internal water pressure loading are studied by means of the FEM. The constitutive models considered for anisotropic rocks and for the radially cracked layers are presented in Sects. 4 and 5. The Finite Element (FE) model is presented in Sect. 6 as well as its validation for isotropic rock conditions. A systematic parametric study is performed and presented in Sect. 7, with the main focus on the results in the steel liner, although results in the far-field rock are presented for completion. Correction factors to be included in the closed-form solution in isotropic rock in order to estimate maximum stresses in steel liners in anisotropic rock are derived in Sect. 8. Finally, the results and hypothesis are discussed in Sect. 9 and conclusions are given in Sect. 10.

Fig. 1
figure 1

Definition sketch of the standard multilayer system for pressure tunnels and shafts embedded in: a elastic, isotropic rock mass (axisymmetrical case); b transversely isotropic, elastic rock mass; and c transversely isotropic, elastic rock mass with two sets of discontinuities

Full size image

2 Axisymmetrical Multilayer Model in Isotropic Rock

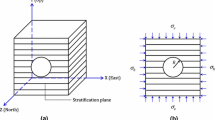
The standard model as well as the nomenclature for the calculation of stresses and displacements in steel-lined pressure tunnels and shafts in isotropic rock are illustrated in Fig. 1. It represents an axisymmetrical multilayer system where five zones are commonly distinguished (see e.g., Brekke and Ripley 1987; Schleiss 1988; USACE 1997; ASCE 2012): (1) the steel liner; (2) an initial gap denoted \(\Delta r_0\) between the steel liner and the backfill concrete; (3) the backfill concrete; (4) the near-field rock; and (5) the far-field rock, of infinite thickness.

2.1 The Steel Liner

The steel liner is regarded as a linear and isotropic material, of elastic modulus \(E_s\) and Poisson’s ratio \(\nu _s\). It is impervious, and its internal surface is in contact with the pressurized water with pressure \(p_i\) (Fig. 1).

2.2 The Initial Gap

The initial gap \(\Delta r_0\) is an annular space at the interface between the steel liner and the backfill concrete (Fig. 1). It results from the thermal shrinking of the steel as a consequence of the contact with cold water and the non-recoverable deformations of the backfill concrete and the rock system (Brekke and Ripley 1987). Hachem and Schleiss (2009) summarize several assumptions made by designers to estimate \(\Delta r_0\).

2.3 The Backfill Concrete

Concrete is a quasi-brittle material with low tensile strength (1–2MPa). Therefore, for the design of steel-lined pressure tunnels and shafts, the backfill concrete is regarded as a radially cracked material (as major principal stresses are tensile stresses in the tangential direction). The result is that the backfill concrete cannot transmit tangential stresses. It is regarded as a linear elastic material and its elastic modulus and Poisson’s ratio are denoted \(E_c\) and \(\nu _c\), respectively.

2.4 The Near-Field Rock

The near-field rock is a loosened (distressed, cracked) zone of the rock mass as a result of the excavation method (e.g., blasting effects), the rock properties, etc. Similarly to the backfill concrete, the near-field rock is regarded as radially cracked, and thus cannot transmit tensile stresses. The depth \(t_{\rm crm}\) of this loosened zone (Fig. 1) is variable and is important to be determined because of its influence on the global deformability of the system. For instance, Benson (1989) states that excavation in hard rock with tunnel boring machines induces a low damage on the rock, resulting in a loosened layer generally restricted to 0.3–0.5 m depending on tunnel diameter. For excavation with the drill and blast method, the loosened layer is generally less than 1 m in good rock, although it can reach 2–3 m in brittle rock. Another important parameter to be determined is the elastic modulus \(E_{\rm crm}\) of the loosened layer. It is in general lower than the sound rock modulus of elasticity, e.g., found to be reduced by 40 % by measurements during the initial filling of a steel-lined pressure tunnel by Bowling (2010). The characteristics of the loosened rock zones for several projects can be found for example in Brekke and Ripley (1987). The Poisson’s ratio for the near-field rock is denoted \(\nu _{\rm crm}\). This near-field zone may be grouted to increase the stress transfer from the lining to the sound rock as well as to decrease irreversible deformations. Then, \(E_{\rm crm}\) may reach or even exceed the modulus of the far-field rock.

2.5 The Far-Field Rock

The far-field rock is a non-disturbed zone of the rock mass, assumed as a homogeneous, isotropic and elastic material. Its elastic modulus and Poisson’s ratio are denoted \(E_{\rm rm}\) and \(\nu _{\rm rm}\), respectively. The far-field rock layer is normally considered as infinite for deep tunnels. The estimation of the mechanical parameters of the rock mass is very important as they have a significant influence on the global deformability of the system and its capability to withstand transmitted load. The deformability of the rock should be measured in the vicinity of the tunnel with in situ testings as for example large plate load tests. Furthermore, in situ stress has to be known in order to verify the capability of the rock to absorb the transmitted internal water pressure (Seeber 1985). Deformations in steel-lined pressure tunnels and shafts can be monitored for a limited time during operation with instruments installed during the construction (Bowling 2010; Chène 2013).

3 Closed-Form Solution in Isotropic Rock

3.1 Compatibility Conditions

The displacements in the axisymmetrical multilayer system (Fig. 1) are derived from the compatibility conditions on the displacements at the interfaces between the layers (Hachem and Schleiss 2011). The radial displacement at \(r_c\) has to be equal in the steel liner and the backfill concrete, as between the backfill concrete and the near-field rock and between the near- and far-field rocks. This is expressed as follows, taking into account a positive initial gap between the steel liner and the backfill concrete:

$$\begin{aligned} u_r^s (r = r_c) - \Delta r_0&= u_r^c (r = r_c) \\&{\text {with}} \;\Delta r_0 \, \ge \, 0; \\ u_r^c (r = r_{\rm crm})&= u_r^{\rm crm} (r = r_{\rm crm}); \\ u_r^{\rm crm} (r = r_{\rm rm})&= u_r^{\rm rm} (r = r_{\rm rm}). \end{aligned}$$
(1)

The superscript s is related to the steel, c to the backfill concrete, crm to the near-field rock mass (cracked) and rm to the far-field rock mass. The subscript r indicates the radial direction.

The steel liner is modeled according to the thick-walled cylinder theory (Timoshenko and Goodier 1970). As already mentioned before it is assumed that tensile stresses cannot be transmitted in the cracked layers (backfill concrete and near-field rock). The far-field rock is modeled as an infinite homogeneous, elastic and isotropic layer. In the case of pressure tunnels and shafts, the longitudinal dimension is very large (out-of-plane in Fig. 1) and the assumption of plane strain condition is made.

Some conventions are used in this article: (1) pressures are always positive; (2) tensile stresses are denoted with positive values and compressive stresses are denoted with negative values; and (3) the sign convention for the displacements are according to the corresponding coordinate axes.

Considering the aforementioned assumptions, the radial displacements at the layers’ interfaces can be expressed analytically (Hachem and Schleiss 2011):

  1. 1.

    In the steel liner:

    $$\begin{aligned} u_r^s (r_c)&=\frac{1 + \nu _s}{E_s}\frac{r_c}{r_c^2 - r_i^2} \\&\cdot \left[ (1 - 2 \nu _s) (p_i r_i^2 - p_c r_c^2) + (p_i - p_c) r_i^2 \right] ; \end{aligned}$$
    (2)
  2. 2.

    In the backfill concrete:

    $$\begin{aligned} u_r^{c} (r_{\rm crm}) = u_r^{c} (r_c) +\frac{(1-\nu _c^2) p_c r_c}{E_c} \ln \left( \frac{r_c}{r_{\rm crm}} \right) \end{aligned}$$
    (3)

    with

    $$\begin{aligned} p_c r_c = p_{\rm crm} r_{\rm crm}; \end{aligned}$$
    (4)
  3. 3.

    In the near-field rock:

    $$\begin{aligned} u_r^{\rm crm}&(r_{\rm rm}) \\&= u_r^{\rm crm} (r_{\rm crm})+\frac{(1 - \nu _{\rm crm}^2) p_{\rm crm} r_{\rm crm}}{E_{\rm crm}} \ln \left( \frac{r_{\rm crm}}{r_{\rm rm}} \right) \end{aligned}$$
    (5)

    with

    $$\begin{aligned} p_{\rm crm}r_{\rm crm} = p_{\rm rm}r_{\rm rm}; \end{aligned}$$
    (6)
  4. 4.

    And in the infinite far-field rock:

    $$\begin{aligned} u_r^{\rm rm} (r_{\rm rm}) =\frac{1 + \nu _{\rm rm}}{E_{\rm rm}} p_{\rm rm} r_{\rm rm}. \end{aligned}$$
    (7)

Combining Eqs. 3–7, and assuming a tied contact between the steel liner and the backfill concrete (\(\Delta r_0 = 0\)), the pressure \(p_c\) taken by the concrete–rock system can be obtained as:

$$\begin{aligned} p_c =\frac{\dfrac{1 + \nu _s}{E_s}\dfrac{r_c}{r_c^2-r_i^2} \left[ (1-2\nu _s) p_i r_i^2 + p_i r_i^2 \right] }{\dfrac{1 + \nu _s}{E_s}\dfrac{r_c}{r_c^2 - r_i^2} \left[ (1-2\nu _s)r_c^2 + r_i^2 \right] + r_c \dfrac{1}{E_{{\rm eq}}}}, \end{aligned}$$
(8)

where

$$\begin{aligned} \frac{1}{E_{{\rm eq}}}& \\&= \dfrac{1-\nu _c^2}{E_c}\ln \left( \dfrac{r_{\rm crm}}{r_c}\right) +\dfrac{1-\nu _{\rm crm}^2}{E_{\rm crm}}\ln \left( \dfrac{r_{\rm rm}}{r_{\rm crm}}\right) +\dfrac{1+\nu _{\rm rm}}{E_{\rm rm}}. \end{aligned}$$
(9)

3.2 Displacements

Given \(p_c\), the radial displacements in the steel liner can be computed by

$$\begin{aligned} u_r^s (r)&=\frac{1 + \nu _s}{E_s}\frac{r}{r_c^2 - r_i^2} \\&\cdot \left[ (1 - 2 \nu _s) (p_i r_i^2 - p_c r_c^2) + (p_i - p_c)\frac{r_i^2 r_c^2}{r^2} \right] . \end{aligned}$$
(10)

In the backfill concrete and the near-field rock, the radial displacements are, respectively

$$\begin{aligned} u_r^{c} (r) = u_r^{s} (r_c) +\frac{(1-\nu _c^2) p_c r_c}{E_c} \ln \left( \frac{r_c}{r} \right) \end{aligned}$$
(11)

and

$$\begin{aligned} u_r^{\rm crm} (r) = u_r^{c} (r_{\rm crm}) +\frac{(1 - \nu _{\rm crm}^2) p_{\rm crm} r_{\rm crm}}{E_{\rm crm}} \ln \left( \frac{r_{\rm crm}}{r} \right) . \end{aligned}$$
(12)

Finally, the radial displacements in the far-field rock are expressed by:

$$\begin{aligned} u_r^{\rm rm} (r) = \frac{1+\nu _{\rm rm}}{E_{\rm rm}}\frac{r_{\rm rm}^2}{r} p_{\rm rm}. \end{aligned}$$
(13)

3.3 Stresses

The tangential, radial and longitudinal stresses in the steel liners are given, respectively, by

$$\begin{aligned} \sigma _{\theta }^s (r) =\frac{1}{r_c^2 - r_i^2} \left[ r_i^2 p_i - r_c^2 p_c -\frac{r_i^2 r_c^2}{r^2} (p_c - p_i) \right] , \end{aligned}$$
(14)
$$\begin{aligned} \sigma _{r}^s (r) =\frac{1}{r_c^2 - r_i^2} \left[ r_i^2 p_i - r_c^2 p_c + \frac{r_i^2 r_c^2}{r^2} (p_c - p_i) \right] , \end{aligned}$$
(15)

and

$$\begin{aligned} \sigma _{z}^s (r) = \nu _s[\sigma _{\theta }^s(r) + \sigma _{r}^s(r)] = \frac{2\nu _s}{r_c^2 - r_i^2}(r_i^2 p_i - r_c^2 p_c). \end{aligned}$$
(16)

For the backfill concrete, \(\sigma _{\theta }^{c} = 0\) and

$$\begin{aligned} \sigma _{r}^c (r) = - \frac{r_c}{r} p_c. \end{aligned}$$
(17)

Similarly, for the near-field rock, \(\sigma _{\theta }^{\rm crm} = 0\) and

$$\begin{aligned} \sigma _{r}^{\rm crm} (r) = - \frac{r_{\rm crm}}{r} p_{\rm crm}. \end{aligned}$$
(18)

Finally, for the far-field rock

$$\begin{aligned} \sigma _{\theta }^{\rm rm} (r) = \left( \frac{r_{\rm rm}}{r} \right) ^2 p_{\rm rm} \end{aligned}$$
(19)

and

$$\begin{aligned} \sigma _{r}^{\rm rm} (r) = -\left( \frac{r_{\rm rm}}{r} \right) ^2 p_{\rm rm}. \end{aligned}$$
(20)

4 Constitutive Modeling of Anisotropic Rock

In engineering problems, when the rock is inhomogeneous or highly discontinuous, the latter is often modeled with a continuum approach (Jing 2003). A jointed rock mass is thus regarded as a continuum with equivalent properties taking into account the effects of the fabric patterns. In the particular cases of excavations in jointed rock masses, the continuum approach is justified when the opening diameter is large compared to the spacing of the discontinuities (Gerrard 1982; Jing 2003).

Amadei et al. (1987) states that the anisotropic behavior of rocks is often related to their fabric pattern in the form of bedding, stratification, layering, schistosity planes, foliation, fissuring or jointing. According to them, this is a general characteristic for rocks such as foliated metamorphic rocks, stratified sedimentary rocks and rocks cut by one or several regular and closely spaced joint sets. To model such discontinuities in rocks, one may consider an elastic transversely isotropic behavior for the constitutive law (Wittke 1990), i.e., with a plane of isotropy which is parallel to the foliation for example.

4.1 Stress–Strain Relations in a Transversely Isotropic Medium

Transverse isotropy is a particular case of orthotropy, i.e., with a plane of isotropy. To characterize a transversely isotropic material, five independent constants denoted E, \(E'\), \(\nu\), \(\nu '\) and \(G'\) (\(G = E/[2+2\nu ]\)) are required. E and \(E'\) are the elastic moduli in the plane of isotropy and perpendicular to it, respectively, \(\nu\) and \(\nu '\) are the Poisson’s coefficients which characterize the reduction in the plane of isotropy for the tension in the same plane and the tension in a direction normal to it, respectively, and G and \(G'\) are the shear moduli for the planes parallel and normal to the plane of isotropy, respectively, (Amadei et al. 1987). \(G'\) is also called the cross-shear modulus. Assuming that the isotropic plane is parallel to the xz-coordinates plane, the stress–strain relation in Cartesian coordinates is expressed as (Lekhnitskii 1963)

$$\begin{aligned} \begin{bmatrix} \epsilon _{x} \\ \epsilon _{y} \\ \epsilon _{z} \\ \gamma _{yz} \\ \gamma _{xz} \\ \gamma _{xy} \end{bmatrix} = \begin{bmatrix} \dfrac{1}{E}&\dfrac{-\nu '}{E'}&\dfrac{-\nu }{E}&0&0&0 \\ \dfrac{-\nu '}{E'}&\dfrac{1}{E'}&\dfrac{-\nu '}{E'}&0&0&0 \\ \dfrac{-\nu }{E}&\dfrac{-\nu '}{E'}&\dfrac{1}{E}&0&0&0 \\ 0&0&0&\dfrac{1}{G'}&0&0 \\ 0&0&0&0&\dfrac{1}{G}&0 \\ 0&0&0&0&0&\dfrac{1}{G'} \\ \end{bmatrix} \begin{bmatrix} \sigma _{x} \\ \sigma _{y} \\ \sigma _{z} \\ \tau _{yz} \\ \tau _{xz} \\ \tau _{xy} \end{bmatrix}. \end{aligned}$$
(21)

4.2 Admissible Values for the Elastic Constants

Thermodynamic considerations require that the strain energy of an elastic material is always positive definite. It implies conditions on the admissible elastic constants (Amadei et al. 1987, 1988):

$$\begin{aligned} E,\;E'&,\;G',\;G > 0; \\& -1<\nu <1; \\ &-\sqrt{\frac{E'}{E}\frac{1-\nu }{2}}\, < \nu ' < \sqrt{\frac{E'}{E}\frac{1-\nu }{2}}. \end{aligned}$$
(22)

4.3 Ranges of Properties of Transversely Isotropic Rocks

The elastic properties of transversely isotropic rocks are usually assessed by in situ and laboratory tests, sometimes associated with numerical modeling (Hakala et al. 2007). However, despite the simplicity of the constitutive relations, the determination of these elastic properties is not simple due to the lack of standardization for the measurement methods (Gonzaga et al. 2008). The cross-shear modulus \(G'\) is the most difficult parameter to assess (Batugin and Nirenburg 1972; Homand et al. 1993).

Amadei et al. (1987) discuss the ranges of properties for transversely isotropic rocks which can be found in nature. For most transversely isotropic rocks, the values of the degree of anisotropy \(E/E'\) and the ratio of the shear moduli \(G/G'\) are between 1 and 3, the Poisson’s ratio \(\nu\) and \(\nu '\) are between 0.15 and 0.35, and the value of \(\nu ' E/E'\) is between 0.1 and 0.7. However, in exceptional cases, \(E/E'\) may reach values between 4 and 6. Gerrard (1977) gathered a large bank of published data of anisotropic rocks, including specific cases of transversely isotropic rocks. He also indicates, as it can be observed in numerous studies providing transversely isotropic rock properties, that the lowest stiffness is usually observed in the direction normal to the bedding, stratification, layering, foliation, schistosity planes, etc.

Gercek (2007) discusses in detail the Poisson’s ratios’ values for rocks. He outlines that for most rocks, the Poisson’s ratios may be between 0.05 and 0.45. However, for most rock engineering applications with poor field data, most probable values between 0.2 and 0.3 are often assumed.

For the estimation of \(G'\), the following empirical relation first introduced by Saint-Venant is widely considered in the literature:

$$\begin{aligned} G'_{S-V} = \frac{E'}{1 + E'/E + 2\nu '}. \end{aligned}$$
(23)

However, although most of the published data support the validity of this empirical equation, there are still major exceptions (Gonzaga et al. 2008) and measured values do not always correspond to \(G'_{S-V}\) (Hakala et al. 2007).

5 Constitutive Modeling of the Cracked Layers

As assumed in Sect. 2, the backfill concrete and the near-field rock layers are radially cracked and thus cannot transfer tensile stresses in the tangential direction. A simple continuum damage-based approach is considered to model this effect of radial cracks in the backfill concrete and in the near-field rock. A scalar damage parameter \(D_i\) that measures the effect of damage is introduced (Cauvin and Testa 1999):

$$\begin{aligned} 1- D_i = R_i, \end{aligned}$$
(24)

where the subscript i denotes a material parameter and \(R_i\) is a scalar factor to be applied to a material property. This approach does not aim at modeling an evolution of damage depending on the internal pressure. Instead it considers an already highly radially damaged material for a pseudo-static analysis. Due to the axisymmetrical nature of the problem, the stress–strain relations are considered in polar coordinates. In accordance with the assumption that the radially cracked materials do not transmit tangential tensile stresses, the elastic modulus in the tangential direction should be decreased by a high scalar factor \(R_{E_{\theta }}\):

$$\begin{aligned} R_{E_{\theta }} = \frac{\tilde{E}_{\theta }}{E_{\theta }}, \end{aligned}$$
(25)

where \(\tilde{E}_{\theta }\) is the elastic modulus of the damaged material in the tangential direction. Accordingly, other elastic parameters are also affected by the drop of stiffness in the tangential direction, and other scalar factors are defined to take into account the effect of damage:

$$\begin{aligned} R_{G_{\theta r}} = R_{G_{\theta z}} = \frac{\tilde{G}_{\theta r}}{G_{\theta r}} = \frac{\tilde{G}_{\theta z}}{G_{\theta r}}, \end{aligned}$$
(26)

and

$$\begin{aligned} R_{\nu _{\theta r}} = R_{\nu _{\theta z}} = \frac{\tilde{\nu }_{\theta r}}{\nu _{\theta r}} = \frac{\tilde{\nu }_{\theta z}}{\nu _{\theta r}}. \end{aligned}$$
(27)

The radially damaged materials are regarded as transversely isotropic materials in polar coordinates, i.e., with the plane of isotropy parallel to the rz-plane. The values of the degrees of damage \(R_i\) are discussed in Sect. 6.

6 Finite Element Model

6.1 Finite Element Method Code

The commercial FEM code ANSYS® Mechanical™ software of the product ANSYS ® Academic Research, Release 14.0 was chosen for this study (ANSYS Inc 2011). This choice was taken in order to use the ANSYS Probabilistic Design System based on the ANSYS Parametric Design Language. Although no probabilistic design is performed in this work, the Probabilistic Design System allows to perform a large number of simulations using User-Defined Sampling for the parameters of the simulations and to build a FE model parametrically.

6.2 Model

The 10 variables used in the FE model are presented in Table 1 and the parameters kept constant are given in Table 2.

Table 1 Variable parameters of the FE model
Full size table
Table 2 Constant parameters of the FE model
Full size table
Fig. 2
figure 2

Example of a mesh of the FE model around the opening for \(r_i = 1.5\,{\rm m}\), \(t_s = 0.050\,{\rm m}\), \(t_c = 0.50\,{\rm m}\) and \(t_{\rm crm} = 0.30\,{\rm m}\)

Full size image

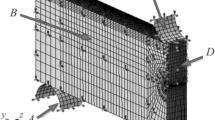
The FE model (see Fig. 2) follows the same assumptions as the analytical solution in isotropic rock (Sect. 3), and some additional hypothesis, namely:

  1. 1.

    The opening has a circular cross-section;

  2. 2.

    All the layers, including the backfill concrete and near-field rock zones have a circular cross-section;

  3. 3.

    2D plane strain conditions;

  4. 4.

    High tunnel overburden, i.e., the dimensions of the far-field rock are large enough to be considered as infinite (equal to \(r_{\rm rm} + 30\times r_i\) in this study) and thus full load transmission occurs through the layers;

  5. 5.

    Tied contact between every layer, without initial gap \(\Delta r_0\); and

  6. 6.

    All materials are linear elastic.

The constitutive laws for the far-field rock and cracked materials are implemented as described in Sect. 4 (Eq. 21) and in Sect. 5, respectively. \(R_{E_{\theta }}\), \(R_{G_{\theta r}}\) and \(R_{G_{\theta z}}\) are set equal to \(10^{-4}\) which is the largest order of magnitude ensuring convergence toward the analytical solution for the isotropic cases. \(R_{\nu _{\theta r}}\) and \(R_{\nu _{\theta z}}\) are set to zero.

The elements used are PLANE183, 8-node squares for the steel liner and the beginning of the far-field rock (for post-processing convenience) and 6-node triangles for all the other zones of the model. The FE model, depending on the geometrical parameters, is meshed with a variable number of elements to ensure convergence toward the corresponding analytical solution in the isotropic case. The steel liner, for instance, is discretized by 400 elements along \(90^\circ\) in the circumferential direction and 12 elements in the radial direction. An example of a coarse mesh around the opening (for presentation purpose) is shown in Fig. 2.

6.3 Nomenclature

The nomenclature used in this article is illustrated in Fig. 3. The plane of isotropy is along the xz-plane in Cartesian coordinates. E denotes the elastic moduli along the x- and z-axis (out-of-plane). \(E'\) denotes the elastic moduli along the y-axis. The angles of location \(\theta = 0\) and \(90^\circ\) in polar coordinates are shown, as well as the locations of the so-called internal and external fibers of the steel liner.

Fig. 3
figure 3

Nomenclature used for the discussion of the results

Full size image

6.4 Validation in Isotropic Rock

Two thousands isotropic cases were generated and solved (see the ranges of variation of the parameters in Sect. 8). The relative error on the maximum major principal stress \(\sigma _{1,{\rm max}}^s\) and the maximum radial displacement \(u_{r,{\rm max}}^s\) in the steel liner (both at the internal fiber for \(r = r_i\)) was computed as

$$\begin{aligned} \text {Error} = \frac{\text {Numerical\, result} - \text {Theoretical\, result}}{\text {Theoretical\, result}} \times 100\,\% \end{aligned}$$
(28)

where the numerical result was obtained with ANSYS and the theoretical result from the analytical solution (Sect. 3, Eqs. 8, 9, 10 and 14). The mean relative error on \(\sigma _{1,{\rm max}}^s\) considering the two thousands simulations is \(-0.38\,\%\), with a minimum of \(-0.17\,\%\) and a maximum of \(-0.81\,\%\). The mean relative error on \(u_{r,{\rm max}}^s\) is \(-0.33\,\%\), with a minimum of \(-0.13\,\%\) and a maximum of \(-0.78\,\%\). These results are in very good agreement with the analytical solution. In addition, results along paths in radial directions were studied for several cases and showed a very good behavior of the FE solution compared to the analytical solution.

Fig. 4
figure 4

Maximum normalized major principal stresses in the steel liner \(\hat{\sigma }_{1,{\rm max}}^s\) as a function of the degree of anisotropy \(E/E'\) for different: a near-field rock thickness to steel liner’s internal radius ratio \(t_{\rm crm}/r_i\); b rock mass elastic modulus to steel elastic modulus ratio \(E/E_s\); and c cross-shear modulus to Saint-Venant empirical relation ratio \(G'/G'_{S-V}\), and by varying the steel liner’s thickness to the internal radius ratio \(t_s/r_i\)

Full size image

7 Systematic Parametric Study

7.1 Preliminary Discussion on the Parameters

Similarly to the methodology described in the following Sect. 7.2, preliminary systematic parametric studies, not detailed herein, were performed in order to assess the influence of the variable parameters of the problem. It was shown that material parameters such as \(E_{\rm crm}\), \(\nu\) and \(\nu '\) cause minor, if any, variations in the results. Concerning the geometrical parameters, it was also shown that the results only depend on the ratio \(t_s/r_i\), i.e., that for different values of \(t_s\) and \(r_i\) which result in a constant ratio, the results do not vary. Finally, because of the assumption of elasticity, the internal pressure \(p_i\) is not investigated.

7.2 Set of Calculation Cases

Considering the aforementioned observations, a systematic parametric study was performed in order to assess the influence of the relevant variable parameters. A so-called reference set of cases was defined with fixed parameters presented in Table 3. With respect to the reference set of cases, three dimensionless parameters were changed, namely:

  1. 1.

    The near-field rock thickness to steel liner’s internal radius ratio \(t_{\rm crm}/r_i\);

  2. 2.

    The rock mass elastic modulus to steel elastic modulus ratio \(E/E_s\); and

  3. 3.

    The cross-shear modulus to Saint-Venant empirical relation ratio \(G'/G'_{S-V}\).

They are shown in Table 3. For each set of cases (reference and others), the liner’s thickness to its internal radius ratio \(t_s/r_i\) and the degree of anisotropy \(E/E'\) were changed as reported in Table 4. For all the simulations, \(r_i = 2\,{\rm m}\), \(\nu = \nu ' = 0.20\) and \(E_{\rm crm}/E' = 0.80\).

Table 3 Variation of the dimensionless parameters with respect to the reference set of cases
Full size table
Table 4 Variation range of the variable dimensionless parameters for each set of cases
Full size table

As a consequence, there were seven sets of simulated cases (including the reference set), each one containing 77 cases, for a total of 1078 simulated cases in anisotropic rock. Every simulated case respected the following thermodynamic constraint and practical range of variation of the \(\nu ' E/E'\) term (see Sect. 4):

$$\begin{aligned} \begin{array}{ll} \nu ' < \sqrt{\frac{E'}{E}\frac{1-\nu }{2}}; \\ 0.1 < \nu ' \frac{E}{E'} < 0.7. \end{array} \end{aligned}$$
(29)

7.3 Normalized Results

All the results are normalized in the following, i.e., presented in a dimensionless form by dividing the numerical solution in transversely isotropic rock by the numerical solution of the most conservative isotropic case, called the reference isotropic case herein. For example, considering an anisotropic rock of parameters E, \(E' < E\), \(\nu\), \(\nu ' < \nu\) and \(G'\), the reference isotropic case will be the case in isotropic rock of parameters \(E'\) and \(\nu\), i.e., \(E_{\rm rm} = E'\) and \(\nu _{\rm rm} = \nu\) correspondingly to Eqs. 8 and 9. Normalized results are denoted with a caret character, as for instance the major principal stress in the steel liner:

$$\begin{aligned} \hat{\sigma }_{1}^s = \frac{\sigma _{1,{\rm aniso}}^s}{\sigma _{1,{\rm iso}}^s} \end{aligned}$$
(30)

where the subscript aniso refers to the results considering anisotropic rock behavior, and iso refers to the results in the corresponding reference isotropic case.

7.4 Stresses and Displacements in the Steel Liner

7.4.1 Maximum Stresses

Maximum normalized major principal stresses in the steel liner \(\hat{\sigma }_{1,{\rm max}}^s\) as a function of the degree of anisotropy \(E/E'\) are shown in Fig. 4. As \(\hat{\sigma }_{1,{\rm max}}^s\) always occurs at the internal fiber of the steel liner in the plane of isotropy (see Sect. 7.4.2), the normalized results are computed as

$$\begin{aligned} \hat{\sigma }_{1,{\rm max}}^s = \frac{\sigma _{1,{\rm aniso}}^s(r=r_i,\theta =0)}{\sigma _{1,{\rm iso}}^s(r=r_i)}. \end{aligned}$$
(31)

Figure 4, in quadrant (a), shows the influence of the relative thickness of the near-field rock compared to the internal radius \(t_{\rm crm}/r_i\) on \(\hat{\sigma }_{1,{\rm max}}^s\). The greater \(t_{\rm crm}/r_i\) and the greater \(t_s/r_i\), the lower the variation \(\hat{\sigma }_{1,{\rm max}}^s\). The influence of \(t_s/r_i\) can be explained by the notion of relative stiffness between the steel liner and the rest of the system. Indeed a stiff liner will limit the deformations induced by the internal pressure \(p_i\), and will withstand large stresses. The influence of anisotropic behavior of the far-field rock compared to the reference isotropic case on \(\hat{\sigma }_{1,{\rm max}}^s\) is thus less significant if the relative stiffness of the liner is large compared to the rest of the system. The role of \(t_{\rm crm}/r_i\) can be explained with similar considerations. An extended near-field rock zone (large \(t_{\rm crm}/r_i\)) decreases the relative stiffness of the concrete–rock system compared to the steel liner and results in the same conclusions. One may also consider an additional effect due to the hypothesis of a cylindrical anisotropy in the cracked near-field zone with a constant elastic modulus in the radial direction. Such an axisymmetrical layer is thus expected to mitigate the effect of far-field anisotropy in terms of variations of \(\hat{\sigma }_{1,{\rm max}}^s\) in the steel liner.

In the quadrant (b) of Fig. 4, the influence of the relative stiffness of the far-field rock compared to the stiffness of the steel \(E/E_s\) is shown. The greater \(E/E_s\), the lower \(\hat{\sigma }_{1,{\rm max}}^s\) compared to the corresponding reference isotropic case. These results depend on the relative stiffness between the steel liner and concrete–rock system. The stiffer the far-field rock (high relative stiffness \(E/E_s\)) the larger the part of \(p_i\) that the latter withstands, and thus considering anisotropic behavior yields a larger change in the estimation of \(\hat{\sigma }_{1,{\rm max}}^s\) in the steel liner. In other words, the lower the relative stiffness of the steel liner, the more conservative the consideration of the reference isotropic case in terms of \(\hat{\sigma }_{1,{\rm max}}^s\).

The third quadrant (c) of Fig. 4 represents the influence of the deviation of the cross-shear modulus \(G'\) from the empirical formula of Saint-Venant \(G'_{S-V}\). The effect of \(G'/G'_{S-V}\) on \(\hat{\sigma }_{1,{\rm max}}^s\) has a different pattern, although the results may also depend on the concept of relative stiffness. For low values of \(E/E'\), a low cross-shear modulus \(G'\) (i.e., lower than the value of G in an isotropic case), \(\hat{\sigma }_{1,{\rm max}}^s\) is larger than in the corresponding reference isotropic case. This is due to the fact that the far-field rock is globally softer than the corresponding reference isotropic case, and thus induces larger stresses in the steel liner to withstand \(p_i\). This effect is canceled and even reversed for higher \(E/E'\), where the influence of the latter becomes more significant. Conversely, a large cross-shear modulus \(G'\) for low degrees of anisotropy will increase the ability of the far-field rock to attract stresses, and therefore \(\hat{\sigma }_{1,{\rm max}}^s\) is lower than in the corresponding reference isotropic case. This effect is moderated for larger \(E/E'\).

Fig. 5
figure 5

Normalized major principal stresses in the steel liner \(\hat{\sigma }_{1}^s\) at the internal and external fibers as a function of the angle \(\theta\) with respect to the plane of isotropy for different: a near-field rock thickness to steel liner’s internal radius ratio \(t_{\rm crm}/r_i\); b rock mass elastic modulus to steel elastic modulus ratio \(E/E_s\); and c cross-shear modulus to Saint-Venant empirical relation ratio \(G'/G'_{S-V}\), and by varying the steel liner’s thickness to the internal radius ratio \(t_s/r_i\) and the degree of anisotropy \(E/E'\)

Full size image
Fig. 6
figure 6

Normalized radial displacements at the internal fiber of the steel liner \(\hat{u}_r^s\) as a function of the angle \(\theta\) with respect to the plane of isotropy for different: a near-field rock thickness to steel liner’s internal radius ratio \(t_{\rm crm}/r_i\); b rock mass elastic modulus to steel elastic modulus ratio \(E/E_s\); and c cross-shear modulus to Saint-Venant empirical relation ratio \(G'/G'_{S-V}\), and by varying the steel liner’s thickness to the internal radius ratio \(t_s/r_i\) and the degree of anisotropy \(E/E'\)

Full size image
Fig. 7
figure 7

Maximum normalized major principal stresses in the far-field rock \(\hat{\sigma }_{1,{\rm max}}^{\rm rm}\) as a function of the degree of anisotropy \(E/E'\) for different: a near-field rock thickness to steel liner’s internal radius ratio \(t_{\rm crm}/r_i\); b rock mass elastic modulus to steel elastic modulus ratio \(E/E_s\); and c cross-shear modulus to Saint-Venant empirical relation ratio \(G'/G'_{S-V}\), and by varying the steel liner’s thickness to the internal radius ratio \(t_s/r_i\)

Full size image

7.4.2 Major Principal Stresses and Radial Displacements

Normalized major principal stresses in the steel liner at the internal fiber \(\hat{\sigma }_{1,{\rm int}}^s\) and at the external fiber \(\hat{\sigma }_{1,{\rm ext}}^s\) as a function of the angle \(\theta\) with respect to the plane of isotropy are shown in Fig. 5. For all the tested cases, \(\hat{\sigma }_{1,{\rm max}}^s\) always occurs in the plane of isotropy (\(\theta = 0\)), at the internal fiber (\(r = r_i\)). The normalized results at internal and external fibers are computed with respect to the maximum major principal stress \(\sigma _{1,{\rm max}}^s\) in the steel liner for the reference isotropic case as:

$$\begin{aligned} \hat{\sigma }_{1,{\rm int}}^s(\theta ) = \frac{\sigma _{1,{\rm aniso}}^s(r=r_i,\theta )}{\sigma _{1,{\rm iso}}^s(r=r_i)} \end{aligned}$$
(32)

and

$$\begin{aligned} \hat{\sigma }_{1,{\rm ext}}^s(\theta ) = \frac{\sigma _{1,{\rm aniso}}^s(r=r_i + t_s,\theta )}{\sigma _{1,{\rm iso}}^s(r=r_i)}. \end{aligned}$$
(33)

To illustrate the deformed shapes of the steel liners, the corresponding normalized radial displacements in the steel liner \(\hat{u}_r^s\) (at the internal fiber) are shown in Fig. 6. The normalized results are computed with respect to the maximum radial displacement of the corresponding reference isotropic case as

$$\begin{aligned} \hat{u}_{r}^s(\theta ) = \frac{u_{r,{\rm aniso}}^s(r=r_i,\theta )}{u_{r,{\rm iso}}^s(r=r_i)}. \end{aligned}$$
(34)

Figure 5a–c shows the influence on \(\hat{\sigma }_{1}^s\) of the relative thickness of the near-field rock compared to the internal radius \(t_{\rm crm}/r_i\), the relative stiffness of the far-field rock compared to the stiffness of the steel \(E/E_s\), and the deviation of the cross-shear modulus \(G'\) from the empirical formula of Saint-Venant \(G'_{S-V}\), respectively. Figure 6a–c shows the influence of the dimensionless parameters on \(\hat{u}_{r}^s\), respectively.

The same observations on the influence of each parameter on \(\hat{\sigma }_{1,{\rm max}}^s\) as in Fig. 4 can me made. However as Fig. 5 shows the normalized major principal stresses on the perimeter of the steel liner both at the internal and external fibers, one can obtain information about the occurrence of bending in the steel liner. Some general observations can be made:

  • The maximum major principal stress \(\hat{\sigma }_{1,{\rm max}}^s\) always occurs at the internal fiber at \(\theta = 0^\circ\), along the springline (i.e., in the plane of isotropy of the far-field rock, see Fig. 5);

  • The minimum major principal stress always occurs at the external fiber at \(\theta = 90^\circ\), along the crown (in the plane perpendicular to the plane of isotropy of the far-field rock, see Fig. 5);

  • The liner is subjected to bending which tends to increase the tension at the internal fiber at \(\theta = 0^\circ\) and to decrease the tension at the internal fiber at \(\theta = 90^\circ\);

  • The larger \(E/E'\), the larger the bending effect.

The aforementioned observations are consistent with the ellipse-like deformed shapes observed in Fig. 6, as the maximum radial displacement \(\hat{u}_{r,{\rm max}}^s\) always occurs at \(\theta = 90^\circ\) along the crown (the direction of the lowest modulus of elasticity \(E'\)), and the minimum radial displacement \(\hat{u}_{r,{\rm min}}^s\) always occurs at \(\theta = 0^\circ\), along the springline (the stiffest direction with the modulus of elasticity E).

Figure 5a shows that an increasing thickness of the near-field rock zone attenuates the effect of the degree of anisotropy: the larger the extent of the near-field rock, the smaller the effect on anisotropy in terms of major principal stresses in the steel liner, and thus the effect of bending. This is in accordance with the radial displacements \(\hat{u}_r^s\) depicted in Fig. 6a and the observations made from the quadrant (a) of Fig. 4. This effect, although observable, is not significant.

One can observe in Fig. 5b that the relative stiffness of the far-field rock \(E/E_s\) have no or minor effect on bending. Only \(\hat{\sigma }_{1,{\rm max}}^s\) is significantly affected, as discussed in Sect. 7.4.1. Indeed, Fig. 6b shows minor variations of \(\hat{u}_r^s\) for different values of \(E/E_s\).

The influence of \(G'/G'_{S-V}\) depicted in Fig. 5c is also minor, if any, on the bending effect. This corresponds to the minor variations in the radial displacements \(\hat{u}_r^s\) in Fig. 6c.

Fig. 8
figure 8

Normalized major principal stresses in the far-field rock \(\hat{\sigma }_{1}^{\rm rm}\) at radius \(r_{\rm rm}\) as a function of the angle \(\theta\) with respect to the plane of isotropy for different: a near-field rock thickness to steel liner’s internal radius ratio \(t_{\rm crm}/r_i\); b rock mass elastic modulus to steel elastic modulus ratio \(E/E_s\); and c cross-shear modulus to Saint-Venant empirical relation ratio \(G'/G'_{S-V}\), and by varying the steel liner’s thickness to the internal radius ratio \(t_s/r_i\) and the degree of anisotropy \(E/E'\)

Full size image
Fig. 9
figure 9

Normalized minor principal stresses in the far-field rock \(\hat{\sigma }_{3}^{\rm rm}\) at radius \(r_{\rm rm}\) as a function of the angle \(\theta\) with respect to the plane of isotropy for different: a near-field rock thickness to steel liner’s internal radius ratio \(t_{\rm crm}/r_i\); b rock mass elastic modulus to steel elastic modulus ratio \(E/E_s\); and c cross-shear modulus to Saint-Venant empirical relation ratio \(G'/G'_{S-V}\), and by varying the steel liner’s thickness to the internal radius ratio \(t_s/r_i\) and the degree of anisotropy \(E/E'\)

Full size image
Fig. 10
figure 10

Normalized major principal stresses in the far-field rock shown up to 2\(r_{\rm rm}\): a \(\hat{\sigma }_1\) in the isotropic case; \(\hat{\sigma }_1\) in the anisotropic case for cross-shear moduli ratios of b \(G'/G'_{S-V} = 0.7\); c \(G'/G'_{S-V} = 1.0\); and d \(G'/G'_{S-V} = 1.3\)

Full size image

7.5 Stresses in the Far-Field Rock

7.5.1 Maximum Stresses

Maximum normalized major principal stresses in the far-field rock \(\hat{\sigma }_{1,{\rm max}}^{\rm rm}\) as a function of the degree of anisotropy \(E/E'\) are shown in Fig. 7, at the interface between the near- and the far-field rock masses (at \(r = r_{\rm rm}\)). Unlike in the steel liner, \(\hat{\sigma }_{1,{\rm max}}^{\rm rm}\) at \(r = r_{\rm rm}\) does not occur at a constant angle of location (see Sect. 7.5.2). The normalized results are thus computed as

$$\begin{aligned} \hat{\sigma }_{1,{\rm max}}^{\rm rm} = \frac{\sigma _{1,{\rm aniso}}^{\rm rm}(r=r_{\rm rm},\theta =\tilde{\theta })}{\sigma _{1,{\rm iso}}^{\rm rm}(r=r_{\rm rm})} \end{aligned}$$
(35)

where \(\tilde{\theta }\) is the angle of location of the maximum stress for each case. From Fig. 7 it can be seen that, contrary to \(\hat{\sigma }_{1,{\rm max}}^s\) in most cases, \(\hat{\sigma }_{1,{\rm max}}^{\rm rm}\) is amplified compared to the reference isotropic case by considering the influence of the anisotropic rock behavior. The following analysis is complementary to the observations made on the variations of \(\hat{\sigma }_{1,{\rm max}}^s\) in Sect. 7.4.1.

The quadrant (a) of Fig. 7 illustrates the influence of \(t_{\rm crm}/r_i\) on \(\hat{\sigma }_{1,{\rm max}}^{\rm rm}\). It is shown that the lower \(t_s/r_i\) and the larger \(t_{\rm crm}/r_i\), the smaller the increase of \(\hat{\sigma }_{1,{\rm max}}^{\rm rm}\). The role of \(t_{\rm crm}/r_i\) can be explained referring to the reference isotropic case. Considering Eqs. 4 and 6 yields \(p_{\rm rm} = (r_c/r_{\rm rm}) p_c\). As a consequence, the larger \(t_{\rm crm}\) (and thus \(r_{\rm rm}\)), the smaller the pressure transmitted to the far-field rock. The variation of \(\hat{\sigma }_{1,{\rm max}}^{\rm rm}\) compared to the corresponding reference isotropic case is therefore smaller with a more extended cracked near-field rock, which mitigates the effect of the far-field anisotropy.

The influence of \(E/E_s\) on \(\hat{\sigma }_{1,{\rm max}}^{\rm rm}\) is shown in the quadrant (b) of Fig. 7. One observes that the larger \(E/E_s\) and the smaller \(t_s/r_i\), the smaller the variation of \(\hat{\sigma }_{1,{\rm max}}^{\rm rm}\). Similarly to the analysis of the stresses in the steel liner, this phenomenon can be explained by the notion of relative stiffness. A relatively stiff far-field rock (high \(E/E_s\) ratio and low \(t_s/r_i\) ratio) attracts a larger part of the internal pressure \(p_i\) and therefore will be less affected by the consideration anisotropic behavior compared to the reference isotropic case. Considering the far-field anisotropy introduces a larger elastic modulus E in the plane of isotropy which makes the rock withstand a larger part of \(p_i\) at the expense of larger \(\hat{\sigma }_{1,{\rm max}}^{\rm rm}\) compared to the reference isotropic case, and a smaller \(\hat{\sigma }_{1,{\rm max}}^{s}\) consistently to the observations in Sect. 7.4.1.

The quadrant (c) of Fig. 7 illustrates the influence of \(G'/G'_{S-V}\) on \(\hat{\sigma }_{1,{\rm max}}^{\rm rm}\). Some general observations can be made:

  • The larger the deviation of the cross-shear modulus \(G'\) from the empirical formula of Saint-Venant \(G'_{S-V}\) (either softer or stiffer), the more \(\hat{\sigma }_{1,{\rm max}}^{\rm rm}\) is underestimated considering the reference isotropic case;

  • The lower \(t_s/r_i\), the lower the change of \(\hat{\sigma }_{1,{\rm max}}^{\rm rm}\) (except for low \(E/E'\) and low \(G'/G'_{S-V}\), although not significant), similarly to the previous observations of quadrants (a) and (b).

The explanation of the magnitude of the variations of \(\hat{\sigma }_{1,{\rm max}}^{\rm rm}\) due to high or low \(G'/G'_{S-V}\) ratios would require further investigations, out of the scope of this article.

7.5.2 Major and Minor Principal Stresses

Normalized major and minor principal stresses in the far-field rock \(\hat{\sigma }_{1}^{\rm rm}\) and \(\hat{\sigma }_{3}^{\rm rm}\) as a function of the angle \(\theta\) with respect to the plane of isotropy are shown in Figs. 8 and 9, respectively, at the interface between the near- and the far-field rock masses (at \(r = r_{\rm rm}\)). Normalized stresses at \(r = r_{\rm rm}\) are computed as

$$\begin{aligned} \hat{\sigma }_{1}^{\rm rm}(\theta ) = \frac{\sigma _{1,{\rm aniso}}^{\rm rm}(r=r_{\rm rm},\theta )}{\sigma _{1,{\rm iso}}^{\rm rm}(r=r_{\rm rm})} \end{aligned}$$
(36)

and

$$\begin{aligned} \hat{\sigma }_{3}^{\rm rm}(\theta ) = \frac{\sigma _{3,{\rm aniso}}^{\rm rm}(r=r_{\rm rm},\theta )}{\sigma _{3,{\rm iso}}^{\rm rm}(r=r_{\rm rm})}. \end{aligned}$$
(37)

The plots of \(\hat{\sigma }_{1}^{\rm rm}\) and \(\hat{\sigma }_{3}^{\rm rm}\) versus \(\theta\) give more information on the stress repartition in the far-field rock. From Fig. 8 it can be seen that for all cases where \(G' = G'_{S-V}\), \(\hat{\sigma }_{1}^{\rm rm}\) is maximum in the plane of isotropy along the springline and in the perpendicular direction of lowest stiffness along the crown, with minor differences. The higher the degree of anisotropy \(E/E'\), the larger the variation along the perimeter at the near- and far-field interface compared to the reference isotropic case. For low values of \(G'\) (see Fig. 8c), \(\hat{\sigma }_{1,{\rm max}}^{\rm rm}\) occurs at \(\theta = 0^\circ\) and there is a large variation of \(\hat{\sigma }_{1}^{\rm rm}\) along the perimeter, with the lowest major principal stress in the shear plane. Indeed, a low cross-shear modulus indicates that the rock attracts less stresses in this direction. Conversely, \(\hat{\sigma }_{1,{\rm max}}^{\rm rm}\) occurs in the shear plane when \(G'\) is larger than \(G'_{S-V}\) (see Fig. 8c). This is illustrated in a xy-plane from \(r = r_{\rm rm}\) to \(2 r_{\rm rm}\) in Fig. 10 for a specific configuration. The isotropic case is shown in Fig. 10a, and the anisotropic cases with different \(G'/G'_{S-V}\) ratios are shown in Fig. 10b–d.

Figure 9 shows the corresponding normalized minor stresses in the far-field rock \(\hat{\sigma }_{3}^{\rm rm}\). One can only observe a minor variation around the perimeter. These results are given herein for completion.

8 Estimation of Maximum Stresses in Steel Liners in Anisotropic Rock by the use of Correction Factors

The maximum stresses in the steel liners of pressure tunnels and shafts have to be assessed according to the design criteria in practice (Sect. 1.2). When the rock mass has an anisotropic behavior, there is no straight forward and efficient method for a fast estimation of the stresses. Therefore, correction factors to be included in the analytical solution of the isotropic case which allow to compute maximum stresses in steel liners embedded in anisotropic rock are derived.

8.1 Database

In order to calibrate and test the validity of the proposed correction factors, a large database of numerical results for anisotropic rock behavior was created by using the FE model described in Sect. 6 and the Probabilistic Design System in ANSYS. A user-defined-sampling of 2000 cases was generated accordingly to the ranges introduced in Table 5 for 9 geometrical and material parameters. The parameters of each case were randomly sampled with a uniform distribution of values under the constraints described by Eq. 29. Every sampled case not included in the aforementioned set of constraints was re-sampled until they were satisfied.

Table 5 Variation range of the parameters for the random user-defined sampling
Full size table

8.2 Correction Factors to be Included in the Analytical Solution in Isotropic Rock

According to Eq. 9, the three terms in the expression for \(E_{{\rm eq}}^{-1}\) refer, respectively, to the participation of the cracked backfill concrete, the cracked near-field rock and the far-field rock to withstand the internal pressure \(p_i\). As a consequence, the expression for \(p_c\) (Eq. 8) physically represents the ratio of the global stiffness of the system divided by the stiffness of the steel liner. Once \(p_c\) is known, the maximum stresses in the liner can be calculated with Eq. 14 for \(r = r_i\).

From a physical insight, correction factors that multiply the term of the far-field rock participation in Eq. 9 were chosen in order to take into account the influence of the anisotropic behavior of the rock mass. The correction factors have to be physically correct, i.e., equal to unity in the isotropic cases, and were defined from dimensionless material parameters of the far-field rock mass. The so-called corrected \(E_{{\rm eq}}^{-1}\) was introduced as

$$\begin{aligned} E_{{\rm eq},{\rm corr}}^{-1} = \dfrac{1-\nu _c^2}{E_c}\ln \left( \dfrac{r_{\rm crm}}{r_c}\right) +\dfrac{1-\nu _{\rm crm}^2}{E_{\rm crm}}&\ln \left( \dfrac{r_{\rm rm}}{r_{\rm crm}}\right) \\&+ \prod _{ i=1 }^{3} X_i^{\alpha _i} \cdot \dfrac{1+\nu }{E'}, \end{aligned}$$
(38)

where the \(X_i^{\alpha _i}\) are the correction factors; the \(X_i\) are the dimensionless parameters \(X_1 = E/E'\), \(X_2 = G/G'\), and \(X_3 = (1+\nu )/(1+\nu ')\); and the \(\alpha _i\) are free coefficients to be optimized. In this aim, the objective function was to minimize the fitness measure as

$$\begin{aligned} \hat{\varvec{\alpha }} = \underset{{\varvec{\alpha }}}{{\rm argmin}} \;{\text MSE}\left[{\hat {\varvec{\sigma }}}^{s}_{1,{\rm num}},{{\hat{\varvec{\sigma }}}}^{s}_{1,{\rm corr}}({\varvec{X}},{\varvec{\alpha} })\right] , \end{aligned}$$
(39)

where \(\text {MSE}\) is the mean squared error; \(\hat{\varvec{\alpha }}= \{\alpha _1,\alpha _2,\alpha _3\}\) is the argument of the minimum; \(\varvec{X} = \{X_1,X_2,X_3\}\); \({{\hat{\varvec{\sigma }}}}^{s}_{1,{\rm num}}\) is computed with the numerical maximum major principal stresses in the steel liner in the isotropic and anisotropic cases; and \({\hat{\varvec{\sigma }}}^{s}_{1,{\rm corr}}\) is computed with the normalized analytical solution including the corrected expression for \(E_{{\rm eq}}^{-1}\) (Eq. 38).

The \(\hat{\varvec{\alpha }}\) leading to the minimum mean squared error was determined using genetic algorithm. From the database, a training group containing 90 % of the results was randomly sampled, and the rest of the samples were contained in a test group. The generation of the training and test groups and the optimization of \(\hat{\varvec{\alpha }}\) was repeated 100 times, and the mean values of the \(\alpha _i\) were computed as

$$\begin{aligned} \hat{\varvec{\alpha }} = \{-0.65,+0.50,-0.56\}, \end{aligned}$$
(40)

with standard deviations equal to 0.03, 0.04 and 0.07, respectively.

The regression between the normalized corrected maximum major principal stresses \(\hat{\sigma }_{1,{\rm corr}}^s\) and the normalized numerical maximum major principal stresses \(\hat{\sigma }_{1,{\rm num}}^s\) is plotted in Fig. 11a for one example of test group. A coefficient of determination \(R^2 = 0.994\) and a root mean squared error RMSE = 0.005 were obtained.

Fig. 11
figure 11

Regression plots of the normalized corrected maximum stresses \(\hat{\sigma }_{{\rm corr}}\) vs. the normalized numerical maximum stresses \(\hat{\sigma }_{{\rm num}}\) with \(\varvec{\alpha }\;=\;\{-0.65,+0.50,-0.56\}\). The maximum a major principal \(\hat{\sigma }_{1,{\rm corr}}^s\) and b equivalent stresses \(\hat{\sigma }_{{\rm eq},{\rm corr}}^s\) in the steel liner are represented for a test group of 10 % of the 2000 cases. The maximum major principal stresses \(\hat{\sigma }_{1,{\rm corr}}^{\rm rm}\) in the far-field rock are represented in c for all the 155 generated cases in which \(G'/G'_{S-V} = 1\) and in d for all the 2000 cases

Full size image
Table 6 Synthesis of the conceptual formulas derived to obtain some maximum stresses in steel-lined of pressure tunnels and shafts in anisotropic rock
Full size table

When designing steel liners of pressure tunnels and shafts, the working stresses criterion usually suggests allowable equivalent stresses in steel liners according to the Hencky–Von Mises theory in triaxial state of stresses, generally expressed as

$$\begin{aligned} \sigma _{{\rm eq}}^s = \sqrt{ \dfrac{1}{2} (\sigma _{1}^s - \sigma _{2}^s)^2 + \dfrac{1}{2} (\sigma _{2}^s - \sigma _{3}^s)^2 + \dfrac{1}{2} (\sigma _{3}^s - \sigma _{1}^s)^2 }. \end{aligned}$$
(41)

A corrected maximum equivalent stress in the steel liner considering anisotropy, denoted \(\sigma _{{\rm eq},{\rm corr}}^s\), would thus be useful for designers. It can be obtained from Eq. 41, by substituting:

  • \(\sigma _{1}^s\) by the corrected value \(\sigma _{1,{\rm corr}}^s\) (Eq. 14, together with Eqs. 8 and 38);

  • \(\sigma _{3}^s\) by its analytical value in the reference isotropic rock (Eq. 15, together with Eqs. 8 and 9); and

  • \(\sigma _{2}^s\) by the corrected value denoted \(\sigma _{2,{\rm corr}}^s\) computed from Eq. 16 with \(\sigma _{1,{\rm corr}}^s\) and \(\sigma _{3}^s\).

The regression between the normalized corrected maximum equivalent stresses \(\hat{\sigma }_{{\rm eq},{\rm corr}}^s\) and the normalized numerical maximum equivalent stresses \(\hat{\sigma }_{{\rm eq,num}}^s\) is plotted in Fig. 11b for the same test group than in Fig. 11a, and shows the same accuracy.

The applicability of these correction factors (Eq. 40) to estimate the normalized maximum major principal stresses in the far-field rock was investigated. The regression between the normalized corrected maximum major principal stresses \(\hat{\sigma }_{1,{\rm corr}}^{\rm rm}\) (computed with Eqs. 19 and 38) and the normalized numerical maximum major principal stresses \(\hat{\sigma }_{1,{\rm num}}^{\rm rm}\) is plotted in Fig. 11d for all the 2000 cases. It can be observed that the correction factors are only applicable to estimate the maximum major principal stresses in the cases where \(G'/G'_{S-V} = 1\), plotted in Fig. 11c which shows a very good accuracy.

8.3 Synthesis

The conceptual formulas for the corrected maximum major principal stresses in the steel liner and in the far-field rock and the corrected maximum equivalent stresses in the steel liner with correction factors are summarized in Table 6. The proposed approach is therefore very efficient as it allows to assess maximum stresses in steel liners in anisotropic rock by introducing only three dimensionless correction factors multiplying the term related to the far-field rock participation in the analytical solution for isotropic rock. It is independent of the variable geometrical parameters and of the relative stiffness between the steel liner and the rest of the system. This approach, however, is not capable of representing the behavior of far-field rocks with a cross-shear modulus \(G'\) deviating from the empirical relation of Saint-Venant in terms of maximum major principal stresses in the far-field rock.

8.4 Examples of Application

In order to illustrate the applicability of the conceptual formulas, two examples are treated below.

8.4.1 Example 1

In this example, a transversely isotropic far-field rock with the elastic properties presented by Tonon and Amadei (2003) is considered, with \(E = 7.80\;{\rm GPa}\), \(E' = 2.40\;{\rm GPa}\), \(G' = 0.83\;{\rm GPa}\), \(\nu = 0.22\), \(\nu ' = 0.07\) and \(G/G' = 3.85\). The degree of anisotropy is \(E/E' = 3.25\). A steel-lined pressure tunnel is considered in this rock with the following characteristics: \(r_i = 1.5\,{\rm m}\), \(t_s = 0.030\,{\rm m}\), \(t_{\rm crm} = 0.5\,{\rm m}\), \(p_i = 100\;\text{bar}\), \(E_{\rm crm} = 2\;{\rm GPa}\). Other steel, backfill concrete and near-field rock characteristics are according to Table 2.

For comparison purposes, two other far-field rocks are considered: (1) the reference isotropic case with \(E = 2.40\;{\rm GPa}\), \(G = 0.98\;{\rm GPa}\) and \(\nu = 0.22\) correspondingly to the conventions of this article; and (2) the rock mass presented by Tonon and Amadei (2003) by substituting \(G'\) by \(G'_{S-V} = 1.66\;{\rm GPa}\).

The numerical results and the results obtained with the conceptual formulas are presented in Table 7. One can observe that the conceptual formulas estimate the maximum major principal stresses in the steel liner \(\sigma _{1,{\rm corr}}^s\) and in the far-field rock \(\sigma _{1,{\rm corr}}^{\rm rm}\) with a high accuracy for the anisotropic rock with \(G' = G'_{S-V}\). In the case where the rock is exactly the one presented by Tonon and Amadei (2003) however, the maximum stress in the far-field rock \(\sigma _{1,{\rm max}}^{\rm rm}\) is underestimated by 27.5 % by the conceptual formula for \(\sigma _{1,{\rm corr}}^{\rm rm}\). In this case \(G'\) deviates from \(G'_ {S-V}\) by 50 %, thus this result is consistent with the analysis presented in Sect. 8.2. The maximum stresses in the steel liner \(\sigma _{1,{\rm max}}^s\) are estimated with accuracy for every case (error \(< 1\,\%\)). Since the cross-shear modulus is relatively low compared to the empirical relation of Saint-Venant in the rock described by Tonon and Amadei (2003), considering anisotropy does not affect significantly the maximum major principal stress in the steel liner \(\sigma _{1,{\rm max}}^s\) (lowered by 3 %). Nevertheless, in the case with \(G' = G'_{S-V}\), \(\sigma _{1,{\rm max}}^s\) is 10 % lower than in the reference isotropic case.

Table 7 Maximum major principal stresses in the steel liner and in the far-field rock for the cases of example 1
Full size table
Table 8 Maximum major principal stresses in the steel liner and in the far-field rock for the cases of example 2
Full size table

8.4.2 Example 2

In this example a transversely isotropic far-field rock with the elastic properties presented by Amadei (1996) is considered, with \(E = 29.30\;{\rm GPa}\), \(E' = 23.90\;{\rm GPa}\), \(G' = 6.20\;{\rm GPa}\), \(\nu = 0.18\), \(\nu ' = 0.13\) and \(G/G' = 2\). The degree of anisotropy is \(E/E' = 1.23\). A steel-lined pressure tunnel is considered in this rock with the following characteristics: \(r_i = 2.5\,{\rm m}\), \(t_s = 0.020\,{\rm m}\), \(t_{\rm crm} = 0.7\,{\rm m}\), \(p_i = 150\;\text{bar}\), \(E_{\rm crm} = 20\;{\rm GPa}\). Other steel, backfill concrete and near-field rock characteristics are according to Table 2.

Similarly to example 1, two other far-field rocks are considered: (1) the reference isotropic case with \(E = 23.90\;{\rm GPa}\), \(G = 10.13\;{\rm GPa}\) and \(\nu = 0.18\); and (2) the rock mass presented by Amadei (1996) by substituting \(G'\) by \(G'_{S-V} = 11.51\;{\rm GPa}\).

The numerical results and the results obtained with the conceptual formulas are presented in Table 8. In the case where \(G' = G'_{S-V}\), the maximum stresses in the steel liner \(\sigma _{1,{\rm max}}^s\) and in the far-field rock \(\sigma _{1,{\rm max}}^{\rm rm}\) are estimated with a high accuracy. In the case where the rock is exactly the one reported by Amadei (1996) with \(G'\) 53 % softer than \(G'_{S-V}\), the maximum major principal stress in the far-field rock \(\sigma _{1,{\rm corr}}^{\rm rm}\) is underestimated by 10.9 %. Since the degree of anisotropy is low (\(E/E' = 1.23\)) and the cross-shear modulus is relatively soft, the maximum major principal stress in the steel liner \(\sigma _{1,{\rm max}}^s\) is underestimated (by 14 %) in the reference isotropic case, which corresponds to the trend presented in Sect. 7.4.1. In the case where \(G' = G'_{S-V}\), and despite the low degree of anisotropy, the maximum major principal stress in the steel liner \(\sigma _{1,{\rm max}}^s\) is significantly lower (by 8 %) than in the isotropic case as the relative stiffness of the rock is high. This is in accordance with the trend observed in Sect. 7.4.1.

9 Discussion

The approach presented in this article includes a series of assumptions (see Sect. 6.2), that are discussed below.

  1. 1.

    The assumptions concerning the extent, shape and the characteristics of the loosened near-field rock zone (as a result of the excavation process) may be questionable in certain cases. In the isotropic case, the near-field rock zone is commonly assumed as circular, radially cracked with no tension transmitted in the tangential direction (see e.g., Schleiss 1988; USACE 1997; Sharma et al. 1997; Hachem and Schleiss 2009, 2011; ASCE 2012), which was also considered herein for transversely isotropic rock. This was done considering a constant radial elastic modulus based on the weakest direction of the transversely isotropic rock. However, the damage may not be axisymmetrical considering the different characteristics of the far-field rock in the two principal directions of anisotropy, as the shape may not be circular. In addition, even if the damage would be radial, one may expect a varying stiffness with orientation, and a less conservative assumption on the tangential stiffness. Some discussions are enumerated below.

    1. (a)

      The latter point was for example treated analytically by Bobet (2009) in isotropic rock. The damaged zone was modeled with cylindrical transverse isotropy, as in this article, but with a tangential modulus of elasticity not equivalent to zero. It seems reasonable to state that considering a constant significant value for the damaged tangential elastic modulus in this work would probably mitigate the effect of anisotropy, as it was discussed in Sect. 7.4.1. The higher the tangential stiffness, the higher this effect would be expected.

    2. (b)

      Should a more complex constitutive law for the damaged near-field rock (e.g., non-radial cracks, varying stiffness) be considered, when the far-field is regarded as transversely isotropic, such a consideration would considerably increase the complexity of its definition. Cylindrical transverse isotropy defined via 5 constants could no longer be used, and 10 constants would be necessary to define such an anisotropic material in 2D (ANSYS Inc 2011), thus introducing new parameters to be varied independently.

    3. (c)

      The qualitative probable influence of these parameters can be discussed a priori. As mentioned previously, a significant damaged tangential modulus of elasticity should diminish the effect of anisotropy in terms of maximum major principal stresses in the steel liner. Conversely, varying radial stiffness in the near-field rock correspondingly to the principal directions of the far-field rock (within the hypothesis of radial cracks) would increase the effect of anisotropy on the steel liner. However, in the case of grouted near-field rock zone, the properties of the rock tend to be homogenized, and the aforementioned effects would be a less significant limitation.

    4. (d)

      It also seems reasonable to state that loosened near-field rock shapes with little variations from the circular shape may not induce significant effect on the results. However, discussing a priori the effects of a highly non circular loosened near-field rock zone due to the formation of plastic deformations during excavation may be controversial, and would require further investigation, e.g., nonlinear numerical analysis. Such considerations would have the serious drawbacks to make the systematic analysis very complicated. Nevertheless, such extensive plastic zone has to be avoided with appropriated primary support measures during excavation.

  2. 2.

    The assumption of linear elasticity of the far-field rock also limits theoretically the applicability of the proposed approach. It requires that there are no plastic deformations further than the loosened near-field rock zone due to the excavation method. This does not have a strong limitation for good-quality rocks, i.e., if adequate primary support measures are implemented during excavation in weaker regions. Also, maximum stresses due to the internal water pressure in the far-field rock shall not exceed the in situ stresses surrounding the tunnel not to put the rock into tension. This requirement refers to the design criteria (2) in Sect. 1.2 regarding a minimum required overburden for steel-lined pressure shafts (Schleiss 1988). In most cases, the tangential stresses around the opening are compressive due to natural in situ stresses in the rock mass. At large depth, this requirement is therefore not a serious limitation.

  3. 3.

    To take into the account the issues enumerated so far, but rarely relevant in practical design cases, it would be required to take into account the stress history due to the tunnel excavation, for instance by means of nonlinear FE analysis.

  4. 4.

    No initial gap between the steel liner and the backfill concrete was considered in this study. However, before such a gap, if any, is closed, the steel liner takes solely a part of the internal pressure. Considering a linear elastic behavior of the materials and that the tangential displacements in the liner are very small, the proposed solution could be superimposed to the initial elastic stresses due to the presence of such a gap as a first approach.

  5. 5.

    The proposed method also relies on an accurate knowledge of the transversely isotropic rock mass properties, i.e., E, \(E'\), \(G'\), \(\nu\), and \(\nu '\). However, as outlined by Jing and Hudson (2002), in rock mechanics and engineering design, having insufficient data is a way of life, rather than a local difficulty. This lack of information may be due to economical factors (costs of measurements campaigns), lack of standard procedures for the estimation of the rock mass parameters, etc. When facing such issues, uncertainties on the rock mass parameters should be assessed and a sensibility analysis should be performed on the proposed conceptual formulas. In practice, large security factors are applied for the working stresses in the liner (see e.g., Schleiss 1988). Despite these uncertainties, in the case of a steel-lined pressure tunnel and shaft embedded in anisotropic rock, it may worth using a model closer to reality than the axisymmetrical assumption, which can in certain case either overestimate the stresses in the steel liner (which is the main element) and underestimate the stresses in the rock mass (whose participation is ensured by enough overburden).

10 Summary and Conclusions

For the design of steel-lined pressure tunnels and shafts, anisotropic rock behavior is rarely taken into account. Designers rather use a conservative model considering an unfavorable isotropic rock behavior in terms of maximum stresses in the steel liner. As a consequence, the mechanical behavior of the steel–concrete–rock system in anisotropic rock is still not fully understood. In this article, the behavior of steel-lined pressure tunnels and shafts in transversely isotropic rock was systematically studied by means of the FEM.

An extensive systematic parametric study was performed over a wide range of geometrical and material parameters, and significant results in terms of normalized stresses and displacements were investigated in the steel liner and the far-field rock mass. It was shown that the results mainly depend on the relative stiffness between the steel liner and the concrete–rock system. In the steel liner, considering the reference isotropic case generally induces an overestimation of the maximum major principal stresses, except for low degrees of anisotropy when the cross-shear modulus is weaker than the empirical relation of Saint-Venant. It was also shown that in anisotropic rock, the steel liner is subjected to bending. In the far-field rock mass, it was observed that the maximum major principal stresses are underestimated compared to the isotropic solution, as a part of the stiffness is not taken into account.

Correction factors to be included in the analytical solution for isotropic rock conditions were derived. This conceptual approach allows a simple and fast estimation of the maximum major principal stresses and the maximum equivalent stresses in the steel liner by a correction of the isotropic analytical solution with a high accuracy if the transversely isotropic rock parameters are known. These correction factors are also applicable to estimate the maximum major principal stresses in the far-field rock when the cross-shear modulus is equivalent to the empirical relation of Saint-Venant.

Although the assumption of linear elasticity and the hypothesis on the extent and the properties of the loosened near-field rock limit the applicability of the results presented in this article for certain conditions in practice, it has the strong advantage to propose a rational framework to carry out a systematic parametric analysis with the relevant parameters.

Further investigation is necessary to study the effects of parameters such as the shape and properties of the loosened near-field rock or nonlinear behaviors.

When using high-strength steels which are subjected to fatigue and brittle failure, the static and dynamic mechanical behavior of steel-lined pressure tunnels and shafts needs to be further understood. This work is a first contribution to this problematic, where new and innovative design guidelines are claimed by engineers in practice.