Analysis of crosstalk noise in coupled MWCNT interconnects using MRTD technique

Abstract

In this paper, the effect of crosstalk noise in a mutually coupled multiwalled carbon nanotube (MWCNT) interconnect were investigated. The multiresolution time-domain method (MRTD) is used to analyze the crosstalk noise model. On the victim line of MWCNT interconnects, the worst-case propagation delay and peak voltage have been measured and compared to those obtained using the conventional finite difference time domain (FDTD) method, and HSPICE simulations for the 22 nm technology node have been validated. The results of the proposed method shows that the crosstalk induced propagation delays in both dynamic in-phase, out-phase, and peak voltage timing and peak voltage in functional crosstalk of the MWCNT interconnects are an average error less than 2% for the proposed model and conventional FDTD model with HSPICE simulations. It has been observed that the simulation results of the proposed model match accurately with HSPICE and dominate the conventional FDTD model. For various cases of input switching, the proposed numerical model is extremely time efficient and effective in evaluating crosstalk mediated propagation delay and peak voltages. The suggested approach could also be used to fix problems including electromagnetic interference and on-chip interconnect reliability.

1 Introduction

Interconnections are becoming more critical with technology scaling, particularly in the nano-scale range for very large integration circuits (VLSI). the latest Copper on-chip interconnects fail to comply with the specifications. The speed and reliability of high-density copper wires on-chip is reduced due to the surface, grain boundary scatterings, and Joule heating (Meindl 2003). Carbon nanotubes (CNTs) and graphene nanotubes are being investigated as alternate material for interconnects solutions, the CNTs properties have made them potential materials, with applications to VLSI circuits (Wong 2011).

Carbon nanotubes (CNTs) are graphene sheets which are rolled up to form hollow cylinder. They can typically be labelled as multi-walled CNTs (MWCNTs) and single-walled CNTs (SWCNTs). Since all of the shells are connected correctly with metal contact, MWCNTs have a higher current carrying capacity. Since MWCNTs are often metallic in design, they are very promising for VLSI on-chip interconnect applications (Li et al. 2009). Multiconductor transmission line circuits are also used to model MWCNTs. When using the complete multiconductor transmission line circuit model to simulate and evaluate a large-scale MWCNT interconnect network, however, it will be difficult and time consuming. In order to prevent the problem, a simple single-driver equivalent model for the MWCNT is proposed in Sarto and Tamburrano (2009), which can be used to rapidly and precisely evaluate multi-wire MWCNT interconnects (D’Amore et al. 2010). MWCNTs were therefore viewed in this work as interconnected material.

In order to evaluate crosstalk noise, previous models interpreted the non-linear CMOS driver to be a Simply linear resistor (Agarwal et al. 2006; Cui et al. 2011) which appears to deviate from the effects. MOSFET operates approximately 50 percent of its operating in the saturation region during the transient period, and later in linear (or) cutoff regions. Several methods with different analytical solution, Finite Difference Time Domains (FDTD) approach and SPICE results have been documented in recent works for the DIL system in Kaushik and Sarkar (2008). In the current state, several researchers have researched the crosstalk results based on the algorithm of the traditional finite-difference time-domain (FDTD) as it is precise (Li et al. 2011) and Kumar et al. (2014a) applied the FDTD approach to a nonlinear driver of CMOS by using the model of alpha-power law and the model of nth-power law, respectively, and studied the effects of crosstalk in Cu interconnects. Process variation has become a major concern in the design of many nanometer circuits, including interconnect pipelines. The purpose of this research work is to provide a comprehensive overview of types and sources of all aspects of interconnect process variations. The impacts of these interconnect process variations on circuit delay and cross-talk noises along with the two major sources of delays, parametric delay variations and global interconnect delays have been discussed (Verma et al. 2009).

For CNT interconnects, the FDTD approach was used in Liang et al. (2011; Kumar et al. (2015b). Liang et al. (2011) used the FDTD approach to model MWCNT interconnects for crosstalk noise analysis compared with Cu interconnects, and the nonlinear CMOS driver is known to be a linear resistive driver. But there was no discussion about the validation of the model using HSPICE. Kumar et al. (2015a) studied the issues of inclusion crosstalk noise of FDTD, two-coupled MWCNT interconnects and also evaluated HSPICE as a linear resistive driver with the nonlinear CMOS driver. In order to study crosstalk noise in coupled MWCNT interconnects, Kumar et al. (2015b) continued the FDTD approach to a nonlinear CMOS driver using the modified alpha-power law model. Agrawal et al. (2016) enhanced MWCNT interconnect accuracy on the basis of the FDTD model over the Cu interconnects.

The FDTD approach is an important computational procedure used to solve problems of electromagnetic and partial differential equations. The FDTD approach is numerically distributive (Tentzeris et al. 1999) and is used for propagation along the discretization. Thus, there is an extreme need for a model with an edge in numerical distribution properties. Tentzeris et al. (1999) have suggested a multi-resolution time domain (MRTD) approach with an additional advantage of the numerical dispersion characteristics (Alighanbari and Sarris 2006; Krumpholz and Katehi 1996). Grivet-Talocia (Grivet-Talocia 2000) suggested the MRTD model in view of the Haar Scaling function as a basic function and gives the same precision with respect to the FDTD model. And MRTD technique used as a basic function based on Daubechies’ scaling function, is proposed by Fujii and Hoefer (2000) as three and four extinguished moments, which are more precise than the FDTD system. Transient analysis for two-conductors transmission lines with admirable numerical dispersion, Tong et al. (2016) proposed an MRTD model. Features and improved precision with SPICE, relative to the FDTD model.

Rebelli, Nistala in Rebelli and Nistala (2018a, 2018b) also suggested the MRTD approach to evaluate the signal integrity of coupled Copper interconnect driven by linear resistive and a nonlinear CMOS dependent on the Daubechies scaling function at four extinct moments. Rebelli and Nistala (2019) applied the MRTD approach driven to non-linear CMOS using the nth-power law model to evaluate crosstalk noises in coupled-MWCNT interconnects, resulting in increased accuracy relative to the FDTD method.

In this paper, the analyses of crosstalk effects of next generations graphene based MWCNTs interconnect were studied using the MTRD technique and considered the nonlinear CMOS driver model using modified Alpha-power law model. The most effective time domain analysis is presented for mutually coupled MRTD based MWCNT interconnect. The obtained results using the MRTD model is compared with the conventional FDTD method and HSPICE as well.

The rest of the paper is arranged as follows. In Sect. 2 involves the electrical modeling of the interconnects of the MWCNT. The transmission line-based MRTD model is discussed in Sect. 3 and the MRTD Model Comparisons and Evaluation is presented Sect. 4. Finally, Sect. 5 conclusions are given.

2 MWCNT interconnects ESC model

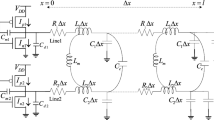
Figure 1 shows the structure of a MWCNT interconnect line for which the model was created (Das and Rahaman 2017). In this diagram the diameters of the outer and innermost CNT shells are represented by Dmax and Dmin. Furthermore, H is the distance above the ground plane, l represents the length of the interconnect, and d represent the van der Waals gaps, with d = 0.34 nm. MWCNT consists of several graphene sheet nesting shells and is represented by equivalent distributed transmissions lines model. In this analysis, the ESC (equivalent single conductor) model was used. Figure 2 shows the ESC model of two-coupled MWCNTs interconnect with driver and load. The parasitic capacitances of CMOS are expressed by $C_{m}$, which stands for gate-to-drain coupled capacitance, and $C_d$, which stands for drain/source diffusion capacitance. $R_{ds}$ is the scatter resistance in per unit length (p.u.l.) and $R_{fixed}$ is the average equivalent resistance value introduced by absolute imperfect contact resistance ($R_{mc}$) and quantum resistances ($R_q$), The MWCNT distributed capacitance p.u.l. $C_q$ is calculated using shell-to-shell and quantum capacitance coupling capabilities. distributed inductance P.u.l. $L_k$ is measured using shell-to-shell and kinetic inductances. Any of these parameters are from reference (Sarto and Tamburrano 2009; Maxwell 2D Student Version 2005). Similarly, the Ansoft Maxwell field solver (Maxwell 2D Student Version 2005) is used to extract the p.u.l. coupling capacitances between coupling interconnects lines ($C_{12}$, $C_{21}$), electrostatic capacitance ($C_e$), mutual inductance between coupling interconnects lines ($L_{12}$,$L_{21}$) and magnetic inductance ($L_h$).

Fig. 1

MWCNT structure on a ground plane

3 MWCNT interconnects in MRTD model

The MRTD model for on-chip mutually two-coupled MWCNT interconnects is built in this section using basis function of Daubechies’ scaling function with four vanishing moments (D4).

Fig. 2

CMOS drivers driven two-coupled MWCNT interconnect lines, which are terminated by capacitive loads

3.1 Model formulations for two-coupled interconnects line

The Telegrapher’s equations can be used to describe the coupled interconnects mathematically. The coupled on-chip interconnects are defined as Paul (1994) using these equations.

$$\begin{aligned}{} & {} \frac{\partial V(z,t)}{\partial z}+L\frac{\partial I(z,t)}{\partial t}=-I(z,t)R \end{aligned}$$

(1)

$$\begin{aligned}{} & {} \frac{\partial I(z,t)}{\partial z}+C\frac{\partial V(z,t)}{\partial t}=0 \end{aligned}$$

(2)

where z and t are the positions and time, respectively. $R_{ds}$, $L_{ds}$, and $C_{ds}$ are two-dimensional interconnect impedances that are measured using Paul (1994). The current and voltage variables for a two-coupled interconnect line are $I=\left[ I_{1},I_{2} \right] ^{T}$ and $V=\left[ V_{1},V_{2} \right] ^{T}$.

$R=diag\left[ R _{ds},R_{ds} \right]$

$$\begin{aligned}L&=\begin{bmatrix} L_{k1}+L_{h1} &{} L_{12}\\ L_{12} &{} L_{k2}+L_{h2}\\ \end{bmatrix}\\ C&=\begin{bmatrix} \left( C_{q1}^{-1} +C_{e1}^{-1}\right) ^{-1} &{} -C_{12}\\ -C_{21} &{} \left( C_{q2}^{-1} +C_{e2}^{-1}\right) ^{-1} \\ \end{bmatrix} \end{aligned}$$

(3)

where subscript 1 corresponded to a line 1 and subscript 2 corresponded to a line 2. The voltage and current evaluations point on interconnect line 1 are shown in Fig. 4.

Alternatively, current and voltage points are considered in time and space to evaluate telegrapher equations. The currents and voltages are separated by $\frac{\varDelta t}{2}$ in time and $\frac{\varDelta z}{2}$ in space for better accuracy, as shown in Fig. 3, where$\varDelta t$ is time and $\varDelta z$ is space represent in discretization intervals.

Fig. 3

Space and time discretizations on MWCNT interconnect line

The interconnects line l of length is resistive driver at $z = 0$ and terminated at $z = l$ is capacitive load. The line is divided consistently to NDZ segments of a length $\varDelta z=\frac{l}{NDZ}$, indicating the discretization voltages(V) and currents(I) nodes, which are coefficients of unknown as seen in Fig. 4, where source current represents $I_0$.

Fig. 4

Spatial discretization for I and V on MWCNT interconnect line

The voltages and currents terms can be extended using a known function ($h_n(t)$ and $\varPhi _{k}(z)$). the coefficients of unknown in order to solve Eqs. (1) and (2) by following the method defined in Krumpholz and Katehi (1996) as:

$$\begin{aligned}{} & {} V(z,t)-\sum _{n,k=-\infty }^{+\infty }V_{k}^{n}\varPhi _{k}^{n}(z)h_{n}(t)=0 \end{aligned}$$

(4a)

$$\begin{aligned}{} & {} I(z,t)-\sum _{n,k=-\infty }^{+\infty }I_{k+\frac{1}{2}}^{n+\frac{1}{2}}\varPhi _{k+\frac{1}{2}}^{n}(z)h_{n}(t)=0 \end{aligned}$$

(4b)

where $I_{k+\frac{1}{2}}^{n+\frac{1}{2}}$ is the coefficient of expansion current and $V_{n}^{k}$ is the coefficients of the voltage expansion in terms of functions scaling, and the indices n and k are discrete time and space indices related to time and space organizes via $t=n\varDelta t$, and $z=k\varDelta z$. Functions $h_n(t)$, and $\varPhi _{k}(z)$ defined as:

$$\begin{aligned} h_{n}(t)-h(\frac{t}{\varDelta t}-n)=0 \end{aligned}$$

(5a)

where pulse function h(t) is defined as

$$\begin{aligned} h(t)= & {} \left\{ \begin{array}{cccc} 1 &{} for |t \langle |&< {}\frac{1}{2} &{} \\ \frac{1}{2} &{} for | t |=\frac{1}{2} &{} &{} \\ 0 &{} for |t | > \frac{1}{2} &{} &{} \ \end{array}\right. \end{aligned}$$

(5b)

$$\begin{aligned} \varPhi _{k}(z)= & {} \varPhi (\frac{z}{\varDelta z}-k) \end{aligned}$$

(5c)

where, $\varPhi (z)$ signifies the scaling function of a

Daubechies, and h(t) represents the Haar scaling function The following integrals (Pan George 2003) are considered in order to derive the MRTD technique for a Eqs. (1) and (2):

$$\begin{aligned}{} & {} \int _{-\infty }^{+\infty }h_{n}(t)h_{n'}(t)dt=\left( \delta _{n,n'}\varDelta t\right) \end{aligned}$$

(6a)

$$\begin{aligned}{} & {} \int _{-\infty }^{+\infty }h_{n}(t)\frac{\partial h_{n'+\frac{1}{2}}(t)}{\partial t}dt=\left( \delta _{n,n'}-\delta _{n,n'+1}\right) \end{aligned}$$

(6b)

$$\begin{aligned}{} & {} \int _{-\infty }^{+\infty }\varPhi _{k}(z)\varPhi _{k'}(z)dt=\left( \delta _{k,k'}\varDelta z\right) \end{aligned}$$

(6c)

$$\begin{aligned}{} & {} \int _{-\infty }^{+\infty }\varPhi _{k}(z)\frac{\partial \varPhi _{k'+\frac{1}{2}}(t)}{\partial z}dt=\sum _{i=-L_{s}}^{L_{s}-1}b(i)\delta _{k+i,k'} \end{aligned}$$

(6d)

where the Kronecker symbol is represented by ’$\delta _{k,k'}$’ and ’$\delta _{n,n'}$’ The effective support sizes of the basis functions is indicated by the Ls. By considering the scaling function of Daubechies as the basis functions with four vanishings moment (D4). The coefficients b(i) are called connections coefficients. Table 1 shows b(i) for $1\le i\le L_{s}$,, whereas b(i) for $i< 1$ it can be accomplished by symmetry condition b(-1-i) =-b(i), and zero for $i> L_{s}$

$$\begin{aligned} b(i)=\frac{1}{\varPi }\int _{0}^{\infty }\left| {\hat{\varPhi }}(\lambda ) \right| ^{2}\lambda sin\lambda (i+\frac{1}{2})d\lambda \end{aligned}$$

(7)

where the scaling function of Fourier transform f (z) is ${\hat{\varPhi }}(\lambda )$.

Table 1 Connections coefficients b(i) for Daubechies’ scaling’s function (D4) (Fujii and Hoefer 2000)

The follow iterative calculations for currents and voltages were carried out to employing the Galerkin technique (Krumpholz and Katehi 1996) in Eqs. (1) and (2) and by using the test functions $\varPhi _{k}h_{n+\frac{1}{2}}(t)$ and $\varPhi _{k+\frac{1}{2}}h_{n}(t)$:

$$\begin{aligned} I_{k+\frac{1}{2}}^{n+\frac{3}{2}}= & {} B_{1}I_{k+\frac{1}{2}}^{n+\frac{1}{2}}-\frac{\varDelta t}{\varDelta z}L^{-1}B_{2}\left( \sum _{i=1}^{L_{s}}b(i) \left( V_{k+i}^{n} -V_{k-i+1}^{n}\right) \right) \end{aligned}$$

(8a)

$$\begin{aligned} V_{k}^{n+1}= & {} V_{k}^{n}-\frac{\varDelta t}{\varDelta z}C^{-1}\sum _{i=1}^{L_{s}}b(i)\left( I_{k+i-\frac{1}{2}}^{n+\frac{1}{2}}-I_{k-i+\frac{1}{2}}^{n+\frac{1}{2}} \right) \end{aligned}$$

(8b)

where,

$B_{1}=\left( 1+\frac{\varDelta t}{2}RL^{-1} \right) ^{-1}\left( 1-\frac{\varDelta t}{2}RL^{-1} \right)$

$B_{2}=\left( 1+\frac{\varDelta t}{2}RL^{-1} \right) ^{-1}$

In the iterative equations (8a) and (8b), the near-end voltage $V_{1}^{n+1}$ and the far-end voltage $V_{NDZ+1}^{n+1}$are obtained and the iterative equation of the currents and voltages near the boundary necessity to be modified. Near the boundary the currents are expressed by $I_{j+\frac{1}{2}}^{n+\frac{1}{2}}$ and $I_{NDZ+1-i+\frac{1}{2}}^{n+\frac{1}{2}}$ for $i=1,2,3,\cdots ,L_{s}-1$ and voltages are $V_{i}^{n+1}$ and $V_{NDZ-i+1}^{n+1}$ for $i=2,3,\cdots ,L_{s}$ Many of these currents and voltages have a number of terms that surpass the index ranges in iterative equations (8a) and (8b)

Equations (8a) and (8b) need to be decomposed using the relationship in Dogaru and Carin (2001) to update the iterative equations of currents and voltages, which satisfies the connection coefficients b(i) provided by the connection coefficients b(i) given by

$$\begin{aligned} \sum _{i=1}^{L_{s}}\left( 2i-1 \right) b(i)=1 \end{aligned}$$

(9)

By Substituting (9) into (8b), to get

$$\begin{aligned}&\sum _{i=1}^{L_{s}}b(i)\left( 2i-1 \right) V_{k}^{n+1} = \sum _{i=1}^{L_{s}}b(i)\left( 2j-1 \right) V_{k}^{n} \nonumber \\&\quad -\sum _{i=1}^{L_{s}}\frac{\varDelta t}{(2i-1)\varDelta z}C^{-1}\left( (2i-1)b(i)\left( I_{k+i-\frac{1}{2}}^{n+\frac{1}{2}}-I_{k-i+\frac{1}{2}}^{n+\frac{1}{2}} \right) \right) \end{aligned}$$

(10)

To decompose (8b) considering a corresponding term with i as:

$$\begin{aligned}&b(i)\left( 2i-1 \right) V_{k}^{n+1}=b(i)\left( 2i-1 \right) V_{k}^{n} -\frac{\varDelta t}{(2i-1)\varDelta z}C^{-1} \nonumber \\&\quad \times \left( (2i-1)b(i)\left( I_{k+i-\frac{1}{2}}^{n+\frac{1}{2}}-I_{k-i+\frac{1}{2}}^{n+\frac{1}{2}} \right) \right) \end{aligned}$$

(11)

for at $i=1,2,3,\cdots ,L_{s}-1$

Equation (11) is further adapted by employ the at boundary conditions as proved in Sects. 3.3 and 3.4.

3.2 Modeling of CMOS driver

Figure 2 shows a two-coupled MWCNT interconnect line equivalent electrical circuit model. The input voltage (Vs) is a two-dimensional vector with the formula $V_{s}=\left[ V_{s1},V_{s2} \right] ^{T}$. The interconnects line is driven by a CMOS driver (International Technology Roadmap for Semiconductors (ITRS) 2012) that follows a modified Alpha power law model. The velocity saturation effects, as well as the finite drain conductance parameters, are included

$$\begin{aligned} I_{n}= & {} \left\{ \begin{matrix} K_{sn}\left( V_{s}-V_{tn} \right) ^{\alpha _{n}} \left( 1+\sigma _{n}V_{1} \right) \\ K_{ln}\left( V_{s}-V_{tn} \right) ^{\frac{\alpha _{n}}{2}}V_{1} \\ 0 \end{matrix}\right. \end{aligned}$$

(12)

$$\begin{aligned} I_{p}= & {} \left\{ \begin{matrix} K_{sp}\left( V_{DD}-V_{s}-\left| V_{tp} \right| \right) ^{\alpha _{p}} \left( 1+\sigma _{p}\left( V_{DD}-V_{1} \right) \right) \\ K_{lp}\left( V_{DD}-V_{tp}-V_{s} \right) ^{\frac{\alpha _{p}}{2}}\left( -V_{1}+V_{DD} \right) \\ 0 \end{matrix}\right. \end{aligned}$$

(13)

The latest equations for PMOS and NMOS are signified by $m\times 1$ vectors, i.e. $I_{p}=\left[ I_{p1},I_{p2} \right] ^{T}$ and $In = \left[ I_{n1},I_{n2} \right] ^{T}$. The linear region transconductance parameters, threshold voltages, saturation region transconductance parameters, drain conductance parameters and velocity saturation index of NMOS(PMOS) are $K_{ln}\left( K_{lp} \right)$, $V_{tn}\left( V_{tp} \right) , and K_{sn}\left( K_{sp} \right)$ respectively. The NMOS/PMOS model parameter values for the 22nm technology node as seen in Table 2 are used for this analysis.

Table 2 Model parameter of 22nm (International Technology Roadmap for Semiconductors (ITRS) 2012)

3.3 Modeling at near-end boundary condition

The DIL system’s modeling is used under boundary conditions. The current and voltage node points are at the near-end terminals defined by $I_0$ and $V_1$, respectively. where the nodal analysis of the terminal equation is given

$$\begin{aligned} I_{0}= & {} \frac{1}{R_{fixed}}\left( V_{0}-V_{1} \right) \end{aligned}$$

(14a)

$$\begin{aligned} I_{0}= & {} C_{m}\frac{d\left( V_{s}-V_{1} \right) }{dt}-C_{d}\frac{dV_{0}}{dt}+I_{p}-I_{n} \end{aligned}$$

(14b)

Applying discretization and Galerkin technique to (14a) and (14b) respectively, then

$$\begin{aligned} I_{0}^{n+1}= & {} \frac{1}{R_{fixed}}\left( V_{0}^{n+1}-V_{1}^{n+1} \right) \end{aligned}$$

(15a)

$$\begin{aligned} I_{0}^{n}= & {} C_{m}\frac{1}{\varDelta t}\left[ \left( V_{s}^{n+1} -V_{s}^{n}\right) -\left( V_{0}^{n+1}-V_{0}^{n} \right) \right] \nonumber \\{} & {} -C_{d}\left( V_{0}^{n+1}-V_{0}^{n} \right) +I_{p}^{n+1}-I_{n}^{n+1} \end{aligned}$$

(15b)

then

$$\begin{aligned} V_{0}^{n+1}= & {} V_{0}^{n}+\left[ C_{m}\frac{1}{\varDelta t}\left( V_{s}^{n+1}-V_{s}^{n} \right) - \left( I_{p}^{n+1}-I_{n}^{n+1}-I_{0}^{n+1} \right) \right] \nonumber \\{} & {} \times \left( \frac{C_{m}+C_{d}}{\varDelta t} \right) ^{-1} \end{aligned}$$

(15c)

the near end terminal a voltage is carry out at k=1 from (8b)

By following the steps from the Eqs. (9) to (11) to decomposed Eqs. (16a) to (16c) as

$$\begin{aligned} b(1)V_{1}^{n+1}= & {} b(1)V_{1}^{n}-b(1)\frac{\varDelta t}{\varDelta z}C^{-1}\left( I_{\frac{3}{2}}^{n+\frac{1}{2}}-I_{\frac{1}{2}}^{n+\frac{1}{2}} \right) \end{aligned}$$

(16a)

$$\begin{aligned} 3b(2)V_{1}^{n+1}= & {} 3b(2)V_{1}^{n}-3b(2)\frac{\varDelta t}{3\varDelta z}C^{-1}\left( I_{\frac{5}{2}}^{n+\frac{1}{2}}-I_{-\frac{1}{2}}^{n+\frac{1}{2}} \right) \end{aligned}$$

(16b)

$\vdots$

$$\begin{aligned}&b(L_{s})(2L_{s}-1)V_{1}^{n+1}=b(L_{s})(2L_{s}-1)V_{1}^{n} \nonumber \\&\quad -(2L_{s}-1)b(L_{s})\frac{\varDelta t}{(2L_{s}-1))\varDelta z}C^{-1}\left( I_{L_{s}+\frac{1}{2}}^{n+\frac{1}{2}}-I_{-L_{s}+\frac{3}{2}}^{n+\frac{1}{2}} \right) \end{aligned}$$

(16c)

Iterative equations (16a)–16c) to be considered as CAD, i.e., central difference equations. in the particular calculations, the subscript to the terms

$I_{-\frac{1}{2}}^{n+\frac{1}{2}},I_{-\frac{3}{2}}^{n+\frac{1}{2}},\cdots , I_{-L_{s}+\frac{3}{2}}^{n+\frac{1}{2}}$ have surpassed the index range. To solve this, substitute the central difference scheme by using the forward difference scheme. By leaving the weight coefficient in each equations unchanged, iterative equations can also be obtained.

$$\begin{aligned} b(1)V_{1}^{n+1}= & {} b(1)V_{1}^{n}-b(1)\frac{\varDelta t}{\varDelta z}C^{-1}\left( I_{\frac{3}{2}}^{n+\frac{1}{2}}-I_{0}^{n+\frac{1}{2}} \right) \end{aligned}$$

(17a)

$$\begin{aligned} 3b(2)V_{1}^{n+1}= & {} 3b(2)V_{1}^{n}-b(2)\frac{\varDelta t}{3\varDelta z}C^{-1}3\left( I_{\frac{5}{2}}^{n+\frac{1}{2}}-I_{0}^{n+\frac{1}{2}} \right) \end{aligned}$$

(17b)

$\vdots$

$$\begin{aligned}&b(L_{s})(2L_{s}-1)V_{1}^{n+1}=b(L_{s})(2L_{s}-1)V_{1}^{n} \nonumber \\&\quad -\frac{\varDelta t}{(2L_{s}-1))\varDelta z}C^{-1}(2L_{s}-1)b(L_{s})\left( I_{L_{s}+\frac{1}{2}}^{n+\frac{1}{2}}-I_{0}^{n+\frac{1}{2}} \right) \end{aligned}$$

(17c)

From the above Eqs. (17a)–(17c), the iterative equation at the near-end boundary node voltage of $V_{1}^{n+1}$ is obtained through the following:

$$\begin{aligned} V_{1}^{n}= & {} V_{1}^{n}-\frac{\varDelta t}{\varDelta z}C^{-1}\sum _{i=1}^{L_{s}}b\left( i \right) \left( I_{i+\frac{1}{2}}^{n+\frac{1}{2}} -I_{-i+\frac{3}{2}}^{n+\frac{1}{2}}\right) \end{aligned}$$

(18a)

$$\begin{aligned} V_{1}^{n}= & {} V_{1}^{n}-\frac{\varDelta t}{\varDelta z}C^{-1}\sum _{i=1}^{L_{s}}2b\left( i \right) \left( I_{i+\frac{1}{2}}^{n+\frac{1}{2}} -I_{0}^{n+\frac{1}{2}}\right) \end{aligned}$$

(18b)

In Eq. (18b), substituting by $I_0^{n+\frac{1}{2}}=\frac{I_0^n+I_0^{n+1}}{2}$ and equation (15a), (15c) we obtained the equation as

$$\begin{aligned} V_{1}^{n+1}&=A_{1}A_{2}V_{1}^{n}+ \nonumber \\&A_{1}A_{3}\left( \sum _{i=1}^{L_{s}} b\left( i \right) \frac{1}{R_{fixed}}\left( V_{0}^{n+1}+V_{0}^{n}\right) -\sum _{i=1}^{L_{s}}2b\left( i \right) I_{i+\frac{1}{2}}^{n+\frac{1}{2}}\right) \end{aligned}$$

(19)

where,

$$A_{1}=\left( 1+\frac{\varDelta t}{\varDelta z} \frac{C^{-1}}{R_{fixed}}\sum _{i=1}^{L_{s}}b\left( i \right) \right) ^{-1}$$

$$A_{2}=\left( 1-\frac{\varDelta t}{\varDelta z} \frac{C^{-1}}{R_{fixed}}\sum _{i=1}^{L_{s}}b\left( i \right) \right)$$

$$A_{3}=\frac{\varDelta t}{\varDelta z}C^{-1}$$

3.4 Modeling at far-end boundary condition

Similarly, the nodal analysis equation at load current $I_{NDZ+1}$ is given by the far-end terminal (k = NDZ+1) is:

$$\begin{aligned} I_{NDZ+1}= & {} \frac{1}{R_{fixed}}\left( V_{NDZ+1}-V_{NDZ+2}\right) \end{aligned}$$

(20a)

$$\begin{aligned} I_{NDZ+1}= & {} C_{L}\frac{\textrm{d} V_{NDZ+1}}{\textrm{d} t} \end{aligned}$$

(20b)

Applying discretization and Galerkin technique to (20a) and (20b) respectively, then

$$\begin{aligned} I_{NDZ+1}^{n+1}= & {} \frac{1}{R_{fixed}}\left( V_{NDZ+1}^{n+1}-V_{NDZ+2}^{n+1}\right) \end{aligned}$$

(20c)

$$\begin{aligned} V_{NDZ+2}^{n+1}= & {} V_{NDZ+1}^{n}+\frac{\varDelta t}{C_{L}}I_{NDZ+1}^{n+1} \end{aligned}$$

(20d)

The final iterative equations given at the far end of the terminal is

$$\begin{aligned}V_{NDZ+1}^{n+1}&=A_{1}A_{2}V_{NDZ+1}^{n}+A_{1}A_{3}\times \nonumber \\&\quad \left( \sum _{i=1}^{L_{s}}b\left( i \right) \frac{1}{R_{fixed}} \left( V_{NDZ+2}^{n+1}+V_{NDZ+2}^{n} \right) \right) \nonumber \\&\quad +A_{1}A_{3}\sum _{i=1}^{L_{s}}2b\left( i \right) I_{NDZ+1-i+\frac{1}{2}}^{n+\frac{1}{2}} \end{aligned}$$

(21)

where Some of the term indices surpass the index ranges for all the nodes between the terminals in the algorithm extension to obtain and update the iterative equations, so a truncation method is applied by taking $V_{k}^{n+1}$as an examples for $k = 2, 3,\ldots , L_{s}$ and by subsequent the steps of Eqs. (10) and (11), it can be decomposed (8b) as an example for $k = 2, 3,\ldots , L_{s}$

$$\begin{aligned} b(1)V_{k}^{n+1}= & {} b(1)V_{k}^{n}-b(1)\frac{\varDelta t}{\varDelta z}C^{-1}\left( I_{k+\frac{1}{2}}^{n+\frac{1}{2}}-I_{k-\frac{1}{2}}^{n+\frac{1}{2}} \right) \end{aligned}$$

(22a)

$$\begin{aligned} 3b(2)V_{k}^{n+1}= & {} 3b(2)V_{k}^{n}-3b(2)\frac{\varDelta t}{3\varDelta z}C^{-1}\left( I_{k+\frac{3}{2}}^{n+\frac{1}{2}}-I_{K-\frac{3}{2}}^{n+\frac{1}{2}} \right) \end{aligned}$$

(22b)

$\vdots$

$$\begin{aligned}&b(k-1)(2k-3)V_{k}^{n+1}=b(k-1)(2k-3)V_{k}^{n} \nonumber \\&\quad -b(k-1)(2k-3)\frac{\varDelta t}{(2k-3))\varDelta z}C^{-1}\left( I_{2k-\frac{3}{2}}^{n+\frac{1}{2}}-I_{1+\frac{1}{2}}^{n+\frac{1}{2}} \right) \end{aligned}$$

(22c)

$$\begin{aligned}&b(k)(2k-1)V_{k}^{n+1}=b(k)(2k-1)V_{k}^{n} \nonumber \\&\quad -b(k)(2k-1)\frac{\varDelta t}{\varDelta z(2k-1))}C^{-1}\left( I_{2k-\frac{1}{2}}^{n+\frac{1}{2}}-I_{\frac{1}{2}}^{n+\frac{1}{2}} \right) \end{aligned}$$

(22d)

$$\begin{aligned}&b(k+1)(2k+1)V_{k}^{n+1}=b(k+1)(2k+1)V_{k}^{n} \nonumber \\&\quad -(2k+1)b(k+1)\frac{\varDelta t}{(2k+1))\varDelta z}C^{-1}\left( I_{2k+\frac{1}{2}}^{n+\frac{1}{2}}-I_{-\frac{1}{2}}^{n+\frac{1}{2}} \right) \end{aligned}$$

(22e)

$\vdots$

$$\begin{aligned}&b(L_{s})(2L_{s}-1)V_{k}^{n+1}=b(L_{s})(2L_{s}-1)V_{k}^{n}-b(L_{s})\times \nonumber \\&\quad (2L_{s}-1)\frac{\varDelta t}{(2L_{s}-1))\varDelta z}C^{-1}\left( I_{k+L_{s}-\frac{1}{2}}^{n+\frac{1}{2}}-I_{k-L_{s}+\frac{1}{2}}^{n+\frac{1}{2}} \right) \end{aligned}$$

(22f)

From the Eqs. (22a) to 22(f) stated above, it is also observed that the indices of the equation do not surpass the index ranges for the first k terms. In addition, all calculations for which the index terms surpass the index spectrum appear in the remaining $L_{s}-k$ term. As $L_{s}-k$terms are out-of-bound these equations are not available for iterative equations in MRTD model. To prevent problem, a truncations is built in calculations where the index range is surpassed. first k terms by summing up the in Eqs. (22a)–22(f), iterative equations can be updated for at $k = 2, 3,\ldots , L_{s}$

$$\begin{aligned}&V_{k}^{n+1}=V_{k}^{n}-\left( \sum _{i=1}^{k}(2i-1) b(i)\right) ^{-1} \nonumber \\&\quad \times B_{2}\left( \sum _{i=1}^{k} b(i)\left( I_{k+i-\frac{1}{2}}^{n+\frac{1}{2}}-I_{k-i+\frac{1}{2}}^{n+\frac{1}{2}} \right) \right) \end{aligned}$$

(23)

Using the same steps illustrated in Eqs. (22a)–(22f), a altered iterative equation of voltages at interiors point as presented in Eq. (23) and voltages near a load as presented in Eq. (24) is.

for at the $k=L_{s}+1, L_{s}+2,NDZ-L_{s}, NDZ-L_{s}+1$

$$\begin{aligned}&V_{k}^{n+1}=V_{k}^{n}-\left( \sum _{i=1}^{k}(2i-1) b(i)\right) ^{-1}\times \nonumber \\&\quad B_{2}\left( \sum _{i=1}^{k} b(i)\left( I_{k+i-\frac{1}{2}}^{n+\frac{1}{2}}-I_{k-i+\frac{1}{2}}^{n+\frac{1}{2}} \right) \right) \end{aligned}$$

(24)

for at the $k=NDZ-L_{s}+2, NDZ-L_{s}+3, \ldots , NDZ$.

$$\begin{aligned}&V_{k}^{n+1}=V_{k}^{n}-\left( \sum _{i=1}^{NDZ-k+1}b(i)(2i-1) \right) ^{-1} \nonumber \\&\quad \times B_{2}\left( \sum _{i=1}^{NDZ-k+1} b(i)\left( I_{k+i-\frac{1}{2}}^{n+\frac{1}{2}}-I_{k-i+\frac{1}{2}}^{n+\frac{1}{2}} \right) \right) \end{aligned}$$

(25)

Iterative current equations can also be modified by subsequent the same voltages iterative equations with minor modifications. As seen in Fig. 5, it is observed that at the half-integer points the current nodes appear. It implies that at the interiors points of the terminals, all the currents are located. Therefore, the current near the terminals need alteration. For iterative current equations near to the terminals, it is necessary to decompose (8a) using the steps of iterative voltage of the equations. The final updated iterative current equations are given as

for at the k =1, near at the source

$$\begin{aligned} I_{1+\frac{1}{2}}^{n+\frac{3}{2}}=B_{1}I_{1+\frac{1}{2}}^{n+\frac{1}{2}}-B_{2}L^{-1}\frac{\varDelta t}{\varDelta z}\left( \sum _{i=1}^{L_{s}}b(i)\left( V_{i+1}^{n+1} -V_{1}^{n+1} \right) \right) \end{aligned}$$

(26)

for k=2, 3,......., $L_s$

$$\begin{aligned}&I_{k+\frac{1}{2}}^{n+\frac{3}{2}}=B_{1}I_{k+\frac{1}{2}}^{n+\frac{1}{2}}-B_{2}L^{-1}\nonumber \\&\quad \times \frac{\varDelta t}{\varDelta z}\left( \sum _{i=1}^{k}\left( V_{k+i}^{n+1} -V_{k-i+1}^{n+1} \right) b(i)\right) \left( \sum _{j=1}^{k}b(i) (2i-1)\right) ^{-1} \end{aligned}$$

(27)

for at the $k=L_{s}+1, L_{s}+2, \cdots , NDZ-L_{s}, NDZ-L_{s}+1.$ at the Interior point iteratives equations

$$\begin{aligned}&I_{k+\frac{1}{2}}^{n+\frac{3}{2}}=B_{1}I_{k+\frac{1}{2}}^{n+\frac{1}{2}}-B_{2}L^{-1}\nonumber \\&\quad \times \frac{\varDelta t}{\varDelta z}\left( \sum _{i=1}^{L_{s}}b(i)\left( V_{i+k}^{n+1} -V_{k-i+1}^{n+1} \right) \right) \end{aligned}$$

(28)

for at the $k=NDZ-L_{s}+2, NDZ-L_{s}+3, \cdots , NDZ$, Near the load, iteratives equations are

$$\begin{aligned}&I_{k+\frac{1}{2}}^{n+\frac{3}{2}}=B_{1}I_{k+\frac{1}{2}}^{n+\frac{1}{2}}-B_{2}L^{-1}\frac{\varDelta t}{\varDelta z}\nonumber \\&\quad \times \left( \sum _{i=1}^{NDZ-k+1}b(i)\left( V_{k+i}^{n+1} -V_{k-i+1}^{n+1}\right) \right) \times \nonumber \\&\quad \left( \sum _{i=1}^{NDZ-k+1} b(i)(2i-1)\right) ^{-1} \end{aligned}$$

(29)

In the context of this bootstrapping method, modified voltage and current iterative equations are tested. Firstly, in terms of historical Voltages and current values, voltages iterative equations are solved at a rigid time using Eqs. (19), (21), (23)–(25). Then, Eqs. (26)–(29) solve the iterative equations of currents in terms of voltages measured initially and past values of current. The courant stability condition (Tong et al. 2016; Dogaru and Carin 2001) is thus known as the stable output for MRTD iteratives equations.

$$\begin{aligned} \varDelta t\le \frac{q\varDelta z}{\vartheta } \end{aligned}$$

(30)

Which states that for each cell, the time of propagation must be higher than the time step. Where q is the current numbers given by $q=1/\sum _{i=1}^{L_{s}}\left| b(i) \right| =\vartheta \varDelta t/\varDelta z$ and $\vartheta$ and v is the phase velocity of the line propagation. However, the boundary conditions will always gratify the stability requirement as these are explicitly derived out of a implicit expression.

4 The MRTD model is compared and validated

Performance analyses of two-lines coupled MWCNT interconnects structure is presented. The proposed model is validated by comparison it to conventional FDTD model and with HSPICE simulation. The interconnects load is driven by CMOS driver, the interconnects dimensions are taken from ITRS (International Technology Roadmap for Semiconductors (ITRS) 2012; Kumar et al. 2017). At 22 nm technology node, the interconnect is placed from a ground plane is 48 nm. the aspect ratio is taken 3. the ratio of diameters inner to outer is 0.35. the interconnect width is 32nm. Imperfect metal contacts resistance is $3.2k\varOmega$. and the distance between shells to shells in MWCNT is 0. 34 nm. The length and load capacitance of the interconnects are 1 mm and 2fF. The voltage $V_{dd}$ is 0.8V. The signal voltage swings from 0 to 0.8 V (Low$\rightarrow$High) or 0.8 to 0V (High$\rightarrow$Low). The input source voltages have a transition time is 20ps. The proposed MRTD model implemented by MATLAB using Intel(R) Xeon(R) CPU E3-1225v6 operating at 3.30GHz and HSPICE tool ( Synopsys for HSPICE tools 2008). The parasitic values of RLC for a two-coupled interconnect line structure are

Fig. 5

Transient response comparison at far-end voltage of victim line (a) for functional (b) for in-phase (c) for out-phase

$R_{ds}=\begin{bmatrix} 2.2&{} 0\\ 0&{} 2.2 \end{bmatrix}_{2\times 2}\frac{M\varOmega }{ m}$, $L_{ds}=\begin{bmatrix} 16.35 &{} 0.66\\ 0.66 &{} 16.35 \end{bmatrix}_{2\times 2}\frac{uH}{m}$

$C_{ds}=\begin{bmatrix} 83.68&{} -68.23\\ -68.23&{} 83.68 \end{bmatrix}_{2\times 2}\frac{pF}{m}$

Fig. 6

Peak voltage timing with varied input transition time for victim line

Fig. 7

Peak voltage with varied input transition time for victim line

Fig. 8

The victim line of dynamic in-phase 50% propagation delay varied input transition time

Fig. 9

The victim line of a dynamic out-phase 50% propagation delay varied input transition time

Fig. 10

Peak voltage timing with varied Load capacitance for victim line

Fig. 11

Peak voltage with varied Load capacitance for victim line

Fig. 12

Dynamic propagation delay varied input transition time

Fig. 13

Computational power delay product with different length of interconnects

Fig. 14

Computational time with different crosstalk switching

4.1 Analysis of transients and crosstalk in two coupled MWCNT interconnects

This section covers the transient and crosstalk studies of a two-line coupled interconnects system. Line 1 is the aggressor in the coupled two MWCNT interconnects system seen in Fig. 2, and line 2 is the victim line. On the other end of the victim spectrum, the effect for functional, dynamic in-phase, and dynamic out-phase switching has been found using the proposed model, HSPICE, and the conventional FDTD model. On the victim line, the transient reaction is investigated. The effect of functional crosstalk is explored by modifying line 1’s aggressor input from 0.8V to 0V while holding line 2’s victim in quiescent mode. When both aggressor and victim stimuli turn at the same time, the impact of in-phase or out-phase is also explored. At the far end of the victim line, the transient graph results based on the above conditions are compared. Figure 5a–c displays the functional, dynamic in-phase, and dynamic out-phase transient responses. Figure 5b, c demonstrate that the victim-line peak solution has higher dispersion errors than the conventional FDTD method. The proposed model, on the other hand, is superior to the conventional FDTD model in terms of precision due to its significant superiority in numerical dispersion properties. Figure 5c illustrates how miller coupled capability allows signal transitions to take longer during out-phase than during in-phase switching. The simulation results of proposed MRTD model match HSPICE correctly in all input switching situations and outperform the conventional FDTD method.

Table 3 Victim line’s computational error for peak voltage timings in functional crosstalk

Table 4 Victim line’s computational error for peak voltage values in functional crosstalk

Table 5 Computational error for dynamic in-phase switching propagation delay for various transition times

Table 6 Computational error for dynamic out-phase switching propagation delay for various transition times

In comparison to HSPICE, Table 3 indicates the computational error associated with estimating functional crosstalk effects over victim line2 for conventional FDTD and then suggested MRTD models. Efficacy at multiple input transition times. The proposed model’s average error in predicting crosstalk peak voltages is found to be 0.57 percent, compared to 1.68 percent for the conventional FDTD method. Table 4 also indicates that the proposed model correctly predicts peak voltage timing, with an average error of 0.77 percent compared to 1.31 percent using the conventional FDTD method.

With respect to HSPICE, Table 5 indicates the computational error associated with estimating dynamic in-phase crosstalk effects over victim line2 for conventional FDTD and proposed MRTD models. sturdiness of input transitions at different times the proposed model is observed to have a 2.18 percent average error in propagation delay estimation, compared to 5.07 percent for the conventional FDTD method.

With respect to HSPICE, Table 6 indicates the computational error associated with estimating dynamic out-phase crosstalk effects over victim line2 for conventional FDTD and proposed MRTD models. sturdiness of input transitions at different times the proposed model has a 0.431 percent average error in propagation delay estimation, compared to 1.48 percent for the conventional FDTD method. The simulation results of proposed MRTD model match HSPICE correctly in all input switching situations and outperform the conventional FDTD method.

The graphs for peak voltage timing and peak voltage value on the victim line as a result in functional crosstalk generated by a varied in input transition time are seen in Figures 6 and 7. At different input transition times, Figures 8 and 9 illustrate dynamic in-phase and out-phase crosstalk propagation delays.The results for both functional and dynamic crosstalk are MRTD model validated with HSPICE and outperform the conventional FDTD model

Figures 10 and 11 demonstrate the peak voltage timing and peak voltage on victim line2 in functional switching with varying values of load capacitance $C_L$. The comparison of the Dynamic propagation delay response of crosstalk switching on victim line for two-coupled interconnect lines between the proposed MRTD method, HSPICE and the conventional FDTD method with reference (Kumar et al. 2014b). It is observed that the proposed MRTD method is in good agreement with the HSPICE simulation results.It is observed from Fig. 12 that the proposed MRTD method dominates the existing conventional FDTD and is in good agreement with HSPICE. The power delay product (PDP) signifies energy dissipation in a system and is an important figure of merit. Thus, a low value of PDP is desirable for any high-performance integrated circuit design (Kumar et al. 2006). The PDP for MWCNT interconnects using MRTD and Conventional FDTD has been analyzed and presented in Fig. 13. Fig. 14 demonstrates the CPU computing time specifications for crosstalk study of coupled-MWCNT interconnect lines in various scenarios. The simulation results of the proposed MRTD model fit HSPICE adequately and outperform the conventional FDTD model, according to the results.

5 Conclusion

The modified alpha power law model is used in this paper to build an analytically dependent MRTD model for functional and dynamic crosstalks study of coupled two transmission lines driven by a CMOS driver. For coupled two MWCNT interconnects, in this work provided a detailed study of functional, dynamic in-phase, and out-phase induced effects on the victim line. The Courant condition is strictly followed by the suggested model’s stability. The influence of input transition time on crosstalk propagation delay under dynamic and peak voltage timing, as well as the peak voltage value for functional crosstalk, is studied. The proposed MRTD model’s effects are in comparison to the results of conventional FDTD and HSPICE simulations. With regard to HSPICE, the proposed MRTD model and the FDTD validate that the proposed MRTD model is in good agreement with HSPICE. The findings show that the average error of crosstalk-induced propagation delays in both dynamic in-phase and out-phase MWCNT interconnects is 2.18 percent and 0.431 percent, respectively, according to the proposed model. Functional crosstalk has a peak voltage timing of 0.57 percent and a peak voltage value of 0.77 percent. Furthermore, the suggested MRTD model and FDTD model are validated with HSPICE for peak voltage timing and peak voltage value on victim line for functional cases for various values of load capacitances with an average error is less than 1%. The proposed model time efficiency over the FDTD model and HSPICE is reported, suggesting that it has the ability to analyses crosstalk in on-chip interconnects quickly and accurately. The analysis was performed on two coupled interconnect, but it can also be generalised to M- mutually coupled MWCNT interconnects and it can be extended to Through Silicon Vias(TSVs).