A Unified Delay, Power and Crosstalk Model for Current Mode Signaling Multiwall Carbon Nanotube Interconnects

Abstract

Multiwall carbon nanotube (MWCNT) has been investigated as a potential interconnect material for future advanced technology nodes. The present paper analyzes performance of MWCNT interconnects using current mode signaling (CMS) scheme. The novelty of the present work can be stated as: Firstly, a unified model is proposed for both copper and MWCNT interconnects using finite-difference time-domain (FDTD) technique. Secondly, this model is applicable for both the conventional voltage mode signaling and more versatile CMS schemes. Furthermore, the presented FDTD-based model is valid for single as well as M-line coupled interconnects in integrated circuits. The model also incorporates CMOS gate as driver for MWCNT interconnect. Thirdly, power model using FDTD technique is investigated for the first time. Accurate formulation and computation of power dissipation in CMS MWCNT interconnects are presented in the paper. Propagation delay, power dissipation and power_delay_product (PDP) are the performance metrics considered for single-line CMS MWCNT interconnect. Crosstalk is analyzed for 2-Line and 5-Line coupled interconnects. It is investigated that CMS scheme leads to about 4 times lesser propagation delay and 2.5 times reduced PDP in MWCNT interconnect than the conventional copper interconnect for interconnect length of 4500 $\upmu$m. The technology node considered is 32 nm. The response of the system is accurately computed using the proposed FDTD-based model. The maximum percentage error between results obtained by the proposed analytical model and SPICE simulation model is <3% for the various test cases.

1 Introduction

The tetravalent and member of group XIV of the periodic table, carbon, forms various allotropes. The most common allotropes of carbon are diamond (in which carbon atoms are sp $^{3}$ bonded with each other and arranged in tetrahedral lattice structure), graphite (where arrangement of sp $^{2}$ bonded carbon atoms are arranged as sheets of hexagonal lattice), graphene (which is a monolayer of graphite and consists of a single hexagonal layer of sp $^{2}$ bonded carbon atoms) and fullerene (where carbon atoms are sp $^{2}$ bonded with each other and are arranged in spherical or ellipsoidal shape) [20, 31]. Graphene-based carbon nanotube (CNT) and graphene nanoribbon (GNR) are other few nanomaterials that have recently gained much attention in microelectronics/nanoelectronics applications [5]. This is due to their high current carrying capability, remarkable physical strength, high mean free path and long ballistic transport length, high thermal conductivity and high mechanical and thermal stability [3, 16, 26, 27, 36, 38].

CNTs comprise of graphene sheets that are rolled-up as hollow cylindrical tube. Depending on the rolled-up direction (chirality) of graphene sheets, CNTs exhibit different structures and properties. The chirality in CNTs is defined by circumferential vector $\mathop {C}\limits ^{\rightarrow }$. $\mathop {C}\limits ^{\rightarrow }$ is expressed as $\mathop {C}\limits ^{\rightarrow } =p\cdot \mathop {a_{1}}\limits ^\wedge +q\cdot \mathop {a_{2}}\limits ^\wedge$, where $\mathop {a_1 }\limits ^\wedge$ and $\mathop {a_{2}}\limits ^\wedge$ are lattice vectors, and p and q are chiral indices [20]. Based on chiral indices (p, q) values, CNTs manifest different structures as chiral or achiral. For chiral CNT structures, the chiral indices are not equal ($p\ne q$). The chiral CNTs are mostly semiconductive in nature. On the other hand, achiral CNTs are categorized as armchair ($p=q$) and zigzag ($p=0$ or $q=0$) [22]. Armchair CNTs are always metallic in nature, whereas zigzag CNTs can be either metallic or semiconductive in nature depending on the chiral indices [38]. For interconnect applications, metallic CNTs are useful. CNTs can be also broadly classified as single-wall carbon nanotube (SWCNT) and multiwall carbon nanotube (MWCNT). SWCNT has only one shell with diameter ranging from 0.4 to 4 nm. MWCNT has several concentric shells, and diameter of the shells varies from several nanometers to tens of nanometers [23]. The large diameter of MWCNTs results in long electron mean free path and large number of conducting channels. As against to SWCNT, MWCNT is always metallic in nature because of large diameter of shells and their contribution in conduction even if these are of semiconductive chirality [36]. MWCNTs and SWCNTs (metallic nature) have similar current carrying capability. However, MWCNTs are easier to fabricate due to better control over growth process [22]. In [11, 22, 23, 25, 31], it is reported that performance of MWCNT at global interconnect levels is better as compared to copper and SWCNT interconnects. MWCNT interconnect is hence one of the promising and potential candidate for future on-chip VLSI interconnections in integrated circuit designs.

Several researches have been performed on MWCNT interconnects [11, 19, 20, 22, 23, 25, 31, 36]. Naeemi et al. [25] have given physics-based circuit models for MWCNT interconnects in. In [11, 22], performance comparison has been shown in between MWCNT, SWCNT and copper interconnects using simulation-based model. However, no mathematical formulation has been presented for the performance analyses of these structures. In [31], performance of CNT interconnect has been evaluated using RC-based model. However, the accuracy of this model has been limited as at high frequencies inductance becomes significant and interconnects need to be modeled as transmission line model. For accurate analysis of driver-interconnect-load (DIL) system, interconnect driver has to be modeled carefully. In [19, 23], crosstalk modeling of MWCNT interconnect has been performed using finite-difference time-domain (FDTD) method. In these methods, nonlinear CMOS gate driver has been approximated by linear resistive and capacitive elements. This approximation, however, leads to less accurate results as CMOS gate operates partially in linear and saturation regions during signal transition periods, and therefore, CMOS gate cannot be approximated by single lumped elements for different regions of operation of MOS transistors in a CMOS gate. Similarly, in [22, 31, 36] resistive driver model has been used. Moreover, analytical formulation for power computation has not been presented in any of these research papers.

Until now, majority of the research work in carbon nanomaterial based interconnects has been implemented and analyzed using voltage mode signaling (VMS) scheme. The voltage swing in VMS scheme is full rail-to-rail. On the contrary, voltage swing over interconnects is smaller in current mode signaling (CMS) [2]. The advantage of CMS scheme is smaller latency and higher bandwidth [7, 37, 40]. Low voltage swing in CMS scheme is achieved by providing small load impedance termination. This is effective realized by incorporating specialized current mode receiver circuits [2, 12, 40]. CMS scheme has been explored for copper interconnects [1, 2, 4, 12, 37, 40]. However, no significant work has been reported in literature for carbon nanomaterial-based interconnects. Hence, analysis of MWCNT interconnects using CMS scheme has become significant and considered in the present research work.

The present work gives a unified model for copper and MWCNT interconnects. This model is applicable for both VMS and CMS schemes as well. The paper comprises of five sections. The current section briefly reviews work related to MWCNT interconnects. In Sect. 2, a unified DIL model for copper and MWCNT interconnects using VMS and CMS schemes is proposed. Analytical model using FDTD technique is formulated in Sect. 3. Performance analyses of copper and MWCNT interconnects for VMS and CMS schemes are presented in Sect. 4. Finally, conclusion is drawn in Sect. 5.

2 Unified DIL Model for Copper and MWCNT Interconnects

A unified DIL model for copper and MWCNT interconnects using VMS and CMS schemes is presented in Fig. 1. The driver is implemented using CMOS gate. In [22], MWCNT interconnect is modeled by multiconductor circuit (MCC). Using this model, MWCNT interconnect with N number of shells leads to computationally expensive 2N system dimensional differential equations solution [19]. This is mitigated by using simplified equivalent single conductor (ESC) model [33] and is considered for the present analysis. In the figure, parameter $\alpha$ determines the interconnect materials. It is ‘0’ for copper and ‘1’ for MWCNT. The load impedance termination in VMS is high and often implemented using CMOS gate. It is equivalently modeled by load capacitance ($C_\mathrm{L}$) [19, 22, 23, 31, 36]. In CMS scheme, impedance termination to interconnect is smaller and current mode receiver is equivalently modeled by load resistance ($R_\mathrm{L}$) and $C_\mathrm{L}$ [1, 4, 37]. Parameter $\beta$ defines the signaling schemes in the proposed DIL model. It is ‘0’ for VMS and ‘1’ for CMS scheme.

Fig. 1

Unified driver-interconnect-load (DIL) model for copper and MWCNT interconnects using VMS and CMS schemes

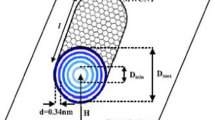
The schematic of MWCNT interconnect with N number of shells is illustrated in Fig. 2. $d_{1}$ and $d_{N}$ are diameters of the innermost and outermost shells of MWCNT interconnect. $\delta$ is the Van der Waal’s gap (0.34 nm) and represents distance between two neighboring concentric shells [20].

The number of shells ($N_\mathrm{shell}$) in MWCNT is given as [19]

$$\begin{aligned} N_\mathrm{shell} =1+\hbox {Integer}\left( {{\frac{d_N -d_1}{2\delta }}} \right) \end{aligned}$$

(1)

The number of conduction channels ($N_\mathrm{ch}$) in MWCNT is obtained as [25]

Fig. 2

Schematic of MWCNT with N shells above ground plane

$$\begin{aligned} N_\mathrm{ch}^i \approx \left( {\begin{array}{ll} k_1 Td_i +k_2 ;&{}\;d_i >{d_\mathrm{T}}/T \\ 2/3; &{}\;d_i <{d_\mathrm{T}}/T \\ \end{array}} \right) \end{aligned}$$

(2)

where i represents the shell number and varies from 1 to N. $d_{i}$ is the diameter of ith shell in MWCNT. $d_{T}$ is the function of gap between sub-bands and thermal energy of electrons and is equal to 1300 nm K at room temperature. T denotes temperature. $k_{1}$ and $k_{2}$ are curve fitted parameters and equal to $3.87 \times 10^{-4}$ nm$^{-1}$ K$^{-1}$ and 0.2, respectively [25].

The MWCNT interconnect represented by ESC model is presented in Fig. 1. It comprises of various interconnect parasitic elements which are formulated in “Appendix 1.” The copper interconnects parasitics are obtained using the formulations presented in “Appendix 2.”

3 Analytical Model Formulation Using FDTD Technique

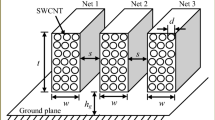
A unified model for M-Line coupled copper and MWCNT interconnects is shown in Fig. 3. N_0, N_1,..., ${N}\_{Nz}+2$ represent node points in Fig. 3. The input voltage [$V_\mathrm{in}$], NMOS [$I_{n}$] and PMOS [$I_{p}$] drain currents are defined as

$$\begin{aligned} \left[ {V_\mathrm{in}} \right] =\left[ {{\begin{array}{l} {V_\mathrm{in} \left( 1 \right) } \\ {V_\mathrm{in} \left( 2 \right) } \\ \vdots \\ {V_\mathrm{in} \left( M \right) } \\ \end{array}}} \right] , \quad \left[ {I_n} \right] =\left[ {{\begin{array}{l} {I_n \left( 1 \right) } \\ {I_n \left( 2 \right) } \\ \vdots \\ {I_n \left( M \right) } \\ \end{array}}} \right] , \quad \left[ {I_p} \right] =\left[ {{\begin{array}{l} {I_p \left( 1 \right) } \\ {I_p \left( 2 \right) } \\ \vdots \\ {I_p \left( M \right) } \\ \end{array}}} \right] \end{aligned}$$

(3)

The drain diffusion capacitance [$C_{d}$], gate-drain coupling capacitance [$C_{m}$], load capacitance [$C_\mathrm{L}$], load resistance [$R_\mathrm{L}$] and lumped resistance [$R_\mathrm{lump}^{\prime }$] are M x M diagonal matrices and expressed as

Fig. 3

Unified model for M-Line coupled CMOS gate-driven copper and MWCNT interconnects

$$\begin{aligned} \begin{array}{l} \left[ {C_m} \right] =\hbox {diag}\left[ {C_m^1, C_m^2,\ldots ,C_m^M} \right] , \\ \left[ {C_\mathrm{d}} \right] =\hbox {diag}\left[ {C_\mathrm{d}^1, C_\mathrm{d}^2,\ldots ,C_\mathrm{d}^M} \right] , \\ \left[ {C_\mathrm{L}} \right] =\hbox {diag}\left[ {C_\mathrm{L}^1, C_\mathrm{L}^2,\ldots ,C_\mathrm{L}^M} \right] , \\ \left[ {R_\mathrm{L}} \right] =\hbox {diag}\left[ {R_\mathrm{L}^1, R_\mathrm{L}^2,\ldots ,R_\mathrm{L}^M} \right] , \\ \left[ {R_\mathrm{lump}^{\prime }} \right] =\hbox {diag}\left[ {R_\mathrm{lump}^{{\prime }1}, R_\mathrm{lump}^{{\prime }2},\ldots ,R_\mathrm{lump}^{{\prime }M}} \right] \\ \end{array} \end{aligned}$$

(4)

The interconnects are driven by CMOS gates. The voltage, current and distributed interconnect elements of the ESC model can be modeled using Telegraph’s equations. This is presented in “Appendix 3.”

3.1 DIL Modeling Using FDTD Technique

The analytical model formulation using FDTD technique is carried out in the following subsections:

3.1.1 Formulation of Recursive Equations for Computation of Currents and Voltages Along the Length of Interconnect

The differential Telegraph’s expressions as represented by (60) and (61) in “Appendix 3” are discretized into difference expressions. The discretization is performed in spatial and temporal domains. This is illustrated in Fig. 4. The discretized voltage and current variables are evaluated alternatively and are separated by $\Delta t/2$ and $\Delta z/2$ in time and position, respectively. $\Delta t$ and $\Delta z$ are infinitesimal small time step and distance in temporal and spatial domains, respectively. These are governed by Courant condition [39] and defined as:

$$\begin{aligned} \Delta t\le {\Delta z}/v \end{aligned}$$

(5)

where v is phase velocity.

Fig. 4

Voltage and current discretization in spatial, nodal and temporal domains

The discretized voltage and current at any instant of time and position in Fig. 4 are defined as

$$\begin{aligned}&\left[ {V_k^n} \right] \equiv \left[ V \right] \quad \left( {k\Delta z,n\Delta t} \right) \end{aligned}$$

(6)

$$\begin{aligned}&\left[ {I_k^{n+1/2}} \right] \equiv \left[ I \right] \quad \left( {\left( {k+1/2} \right) \Delta z,\left( {n+1/2} \right) \Delta t} \right) \end{aligned}$$

(7)

where k and n are positive integer values.

The Telegraph’s first differential equation represented by Eq. (60) in “Appendix 3” is discretized as

$$\begin{aligned}&\left[ {\frac{\left[ {V_{k+1}^{n+1}} \right] -\left[ {V_k^{n+1}} \right] }{\Delta z}+\left[ L \right] \left( {\frac{\left[ {I_k^{n+3/2} } \right] -\left[ {I_k^{n+1/2}} \right] }{\Delta t}} \right) }\right. \nonumber \\&\quad \left. { +\left[ R\right] \left( {\frac{\left[ {I_k^{n+3/2}} \right] +\left[ {I_k^{n+1/2}} \right] }{2}} \right) } \right] =0 \end{aligned}$$

(8)

Simplifying (8) gives:

$$\begin{aligned} \left[ {I_k^{n+3/2}} \right] =\left[ B \right] \left[ D \right] \left[ {I_k^{n+1/2}} \right] +\left[ B \right] \left( {\left[ {V_k^{n+1}} \right] -\left[ {V_{k+1}^{n+1}} \right] } \right) \end{aligned}$$

(9)

where $\left[ B \right] =\left( {\frac{\Delta z}{\Delta t}\left[ L \right] +\frac{\Delta z}{2}\left[ R \right] } \right) ^{-1}$, $\left[ D \right] =\left( {\frac{\Delta z}{\Delta t}\left[ L \right] -\frac{\Delta z}{2}\left[ R \right] } \right)$, $k=1$, 2, 3,..., Nz.

Similarly, discretizing second Telegraph’s equation [Eq. (61) in “Appendix 3”] results in

$$\begin{aligned} \frac{\left[ {I_k^{n+1/2}} \right] -\left[ {I_{k-1}^{n+1/2}} \right] }{\Delta z}+\left[ C \right] \frac{\left[ {V_k^{n+1}} \right] -\left[ {V_k^n} \right] }{\Delta t}=0 \end{aligned}$$

(10)

Equation (10) is further solved as

$$\begin{aligned} \left[ {V_k^{n+1}} \right] =\left[ {V_k^n} \right] +\left[ A \right] \left( {\left[ {I_{k-1}^{n+1/2}} \right] -\left[ {I_k^{n+1/2} } \right] } \right) \end{aligned}$$

(11)

where $\left[ A \right] =\left( {\frac{\Delta t}{\Delta z}\cdot \frac{1}{\left[ C \right] }} \right)$, $k=2, 3, 4,\ldots , Nz$.

Equations (9) and (11) are the recursive expressions to evaluate current and voltage along interconnects. The node voltages and branch currents along interconnect depend on the near-end and far-end boundary conditions. These are formulated in the following subsections.

3.1.2 Formulation of Near-End Boundary Condition

The near-end boundary condition is defined by [$V_{0}$], [$V_{1}$] and [$I_{0}$] at nodesN_0 and N_1. Using KCL, [$I_{0}$] is obtained as

$$\begin{aligned} \left[ {I_0^{n+1}} \right]= & {} \left[ {I_p^{n+1}} \right] -\left[ {I_n^{n+1}} \right] +\left[ {C_m} \right] \left( {\frac{\left[ {V_\mathrm{in}^{n+1}} \right] -\left[ {V_\mathrm{in}^n} \right] }{\Delta t}} \right) \nonumber \\&-\left[ {C_m +C_\mathrm{d}} \right] \left( {\frac{\left[ {V_0^{n+1}} \right] -\left[ {V_0^n} \right] }{\Delta t}} \right) \end{aligned}$$

(12)

$\left[ {I_n^{n+1}} \right]$ and $\left[ {I_p^{n+1}} \right]$ are characterized by nth power law model [32]

The near-end voltage [$V_{0}$] is derived using Ohm’s law as

$$\begin{aligned} \left[ {V_0^{n+1}} \right] =\left[ {V_1^{n+1}} \right] +\alpha \left[ {R_\mathrm{lump}^{\prime }} \right] \cdot \left[ {I_0^{n+1}} \right] \end{aligned}$$

(13)

Using (12) and (13) gives

$$\begin{aligned}&\left[ {I_0^{n+1}} \right] =\left[ H \right] \nonumber \\&\left( {\begin{array}{l} \left[ {I_p^{n+1}} \right] -\left[ {I_n^{n+1}} \right] + \left[ {C_m} \right] \left( {\frac{\left[ {V_\mathrm{in}^{n+1}} \right] -\left[ {V_\mathrm{in}^n} \right] }{\Delta t}} \right) -\left( {\left[ {C_m} \right] +\left[ {C_\mathrm{d}} \right] } \right) \left( {\frac{\left[ {V_1^{n+1}} \right] -\left[ {V_1^n} \right] }{\Delta t}} \right) \\ +\,\alpha \left[ {R_\mathrm{lump}^{\prime }} \right] \left( {\left[ {C_m} \right] +\left[ {C_\mathrm{d}} \right] } \right) \left( {\frac{\left[ {I_0^n} \right] }{\Delta t}} \right) \\ \end{array}} \right) \nonumber \\ \end{aligned}$$

(14)

where

$$\begin{aligned} \left[ H \right] =\left( {U+ \frac{\alpha \left[ {R_\mathrm{lump}^{\prime }} \right] \left( {\left[ {C_m} \right] +\left[ {C_\mathrm{d}} \right] } \right) }{\Delta t}} \right) ^{-1} \end{aligned}$$

(15)

U is a $M \times M$ unity matrix.

The voltage at node N_1 $\left( {\hbox {i.e.,}\;\left[ {V_1^{n+1}} \right] } \right)$ is expressed by substituting $k=1$ in (11) as

$$\begin{aligned} \left[ {V_1^{n+1}} \right] =\left[ {V_1^n} \right] +2\left[ A \right] \left( {\left[ {I_0^{n+1/2}} \right] -\left[ {I_1^{n+1/2}} \right] } \right) \end{aligned}$$

(16)

Here $\Delta z$ is replaced by $\Delta z/2$ in [A] since the current at node N_0 and N_1 are separated by $\Delta z/2$ [1].

$\left[ {I_0^{n+1/2}} \right]$ can be defined as

$$\begin{aligned} \left[ {I_0^{n+1/2}} \right] =\frac{\left[ {I_0^n} \right] +\left[ {I_0^{n+1}} \right] }{2} \end{aligned}$$

(17)

Using (16) and (17), $\left[ {V_1^{n+1}} \right]$ is simplified as

$$\begin{aligned} \left[ {V_1^{n+1}} \right] =\left[ {V_1^n} \right] +2\left[ A \right] \left( {\frac{\left[ {I_0^n} \right] +\left[ {I_0^{n+1}} \right] }{2}-\left[ {I_1^{n+1/2}} \right] } \right) \end{aligned}$$

(18)

Substituting (14) in (18), gives

$$\begin{aligned}&\left[ {V_1^{n+1}} \right] =\nonumber \\&\quad \left( {\begin{array}{l} \left[ {V_1^n} \right] \!-\!2\left[ E \right] \left[ A \right] \left[ {I_1^{n+1/2}} \right] \!+\!\left[ E \right] \left[ A \right] \left[ H \right] \left( {\left[ {I_p ^{n+1}} \right] -\left[ {I_n ^{n+1}} \right] } \right) \\ +\left[ E \right] \left[ A \right] \left[ H \right] \left\{ {\left[ {C_m} \right] \left( {\frac{\left[ {V_\mathrm{in} ^{n+1}} \right] -\left[ {V_\mathrm{in} ^{n}} \right] }{\Delta t}} \right) +\left( {\frac{U}{\left[ H \right] }+\frac{\alpha \left[ {R_\mathrm{lump}^{\prime }} \right] \left( {\left[ {C_m} \right] +\left[ {C_\mathrm{d}} \right] } \right) }{\Delta t}} \right) \left[ {I_0^n} \right] } \right\} \\ \end{array}} \right) \nonumber \\ \end{aligned}$$

(19)

where

$$\begin{aligned} \left[ E \right] =\left( {U+ \frac{\left[ A \right] \left[ H \right] \left( {\left[ {C_m} \right] +\left[ {C_\mathrm{d}} \right] } \right) }{\Delta t}} \right) ^{-1} \end{aligned}$$

(20)

Equations (13), (14) and (19) are used to compute voltage and current variables at near-end boundary condition.

3.1.3 Formulation of Far-End Boundary Condition

The far-end boundary condition is defined by [$V_{Nz+1}$], [$V_{Nz+2}$] and [$I_{Nz+1}$] at nodesN_Nz+1 and N_Nz+2.

$\left[ {I_{Nz+1}^{n+1}} \right]$ can be evaluated by applying KCL at node N_Nz+2 as

$$\begin{aligned} \left[ {I_{Nz+1}^{n+1}} \right] =\left[ {C_\mathrm{L}} \right] \left( {\frac{\left[ {V_{Nz+2}^{n+1}} \right] -\left[ {V_{Nz+2}^n} \right] }{\Delta t}} \right) +\frac{\beta \left[ {V_{Nz+2}^{n+1}} \right] }{\left[ {R_\mathrm{L}} \right] } \end{aligned}$$

(21)

Using Ohm’s law, far-end voltage $\left[ {V_{Nz+2}^{n+1}} \right]$ is computed as

$$\begin{aligned} \left[ {V_{Nz+2}^{n+1}} \right] =\left[ {V_{Nz+1}^{n+1}} \right] -\alpha \left[ {R_\mathrm{lump}^{\prime }} \right] \cdot \left[ {I_{Nz+1}^{n+1}} \right] \end{aligned}$$

(22)

Substituting (22) in (21) gives

$$\begin{aligned}&\left[ {I_{Nz+1}^{n+1}} \right] =\left[ J \right] \nonumber \\&\quad \left( {\left( {\frac{\alpha \left[ {R_\mathrm{lump}^{\prime }} \right] \left[ {C_\mathrm{L}} \right] }{\Delta t}} \right) \left[ {I_{Nz+1}^n} \right] \!+\!\left( {\frac{\left[ {C_\mathrm{L}} \right] }{\Delta t}+\frac{\beta }{\left[ {R_\mathrm{L}} \right] }} \right) \left[ {V_{Nz+1}^{n+1}} \right] \!-\!\left( {\frac{\left[ {C_\mathrm{L}} \right] }{\Delta t}} \right) \left[ {V_{Nz+1}^n} \right] } \right) \nonumber \\ \end{aligned}$$

(23)

where

$$\begin{aligned} \left[ J \right] =\left( {U+ \frac{\alpha \left[ {R_\mathrm{lump}^{\prime }} \right] \left[ {C_\mathrm{L}} \right] }{\Delta t}+\frac{\alpha {}\beta \left[ {R_\mathrm{lump}^{\prime }} \right] }{\left[ {R_\mathrm{L}} \right] }} \right) ^{-1} \end{aligned}$$

(24)

The voltage at node $N\_{Nz}+1\left( {\hbox {i.e.,}\;\left[ {V_{Nz+1}^{n+1}} \right] } \right)$ is computed from recursive voltage expression (11) by substituting $k=Nz+1$. Here also $\Delta z$ is replaced by $\Delta z/2$ in [A].

$$\begin{aligned} \left[ {V_{Nz+1}^{n+1}} \right] =\left[ {V_{Nz+1}^n} \right] +2\left[ A \right] \left( {\left[ {I_{Nz}^{n+1/2}} \right] -\left[ {I_{Nz+1}^{n+1/2}} \right] } \right) \end{aligned}$$

(25)

where

$$\begin{aligned} \left[ {I_{Nz+1}^{n+1/2}} \right] =\frac{\left[ {I_{Nz+1}^n} \right] +\left[ {I_{Nz+1}^{n+1}} \right] }{2} \end{aligned}$$

(26)

Using (23) and (26) in (25) gives

$$\begin{aligned}&\left[ {V_{Nz+1}^{n+1}} \right] =\left( \left[ F \right] \left[ G \right] \left[ {V_{Nz+1}^n} \right] +2\left[ F \right] \left[ A \right] \left[ {I_{Nz}^{n+1/2}} \right] \right. \nonumber \\&\quad \left. -\left[ F \right] \left[ A \right] \left( {U+\frac{\alpha \left[ J \right] \left[ {R_\mathrm{lump}^{\prime }} \right] \left[ {C_\mathrm{L}} \right] }{\Delta t}} \right) \left[ {I_{Nz+1}^n} \right] \right) \end{aligned}$$

(27)

where

$$\begin{aligned} \left[ F \right] =\left( {U+\frac{\left[ A \right] \left[ J \right] \left[ {C_\mathrm{L}} \right] }{\Delta t}+\frac{\beta \left[ A \right] \left[ J \right] }{\left[ {R_\mathrm{L}} \right] }} \right) ^{-1} \end{aligned}$$

(28)

$$\begin{aligned} \left[ G \right] =\left( {U+\frac{\left[ A \right] \left[ J \right] \left[ {C_\mathrm{L}} \right] }{\Delta t}} \right) \end{aligned}$$

(29)

The far-end boundary variables are solved using (22), (23) and (27).

Equations (11), (13), (19), (22) and (27) are used to evaluate voltage at any time instant and position along the interconnect. Similarly, (9), (14) and (23) are used to compute current. The voltage and current are evaluated alternatively in temporal and spatial domains. These variables are used for transient analysis and determination of the system performance.

3.2 Power Modeling for Interconnect System

The power dissipation in DIL model primarily consists of three components, viz. dynamic, static and short-circuit [4]. The DIL system along with these power dissipating components is shown in Fig. 5. The dynamic power dissipation ($P_\mathrm{dyn}$) occurs because of charging and discharging of node capacitors. The generalized expression for $P_\mathrm{dyn}$ at node k is expressed as [9, 18]

$$\begin{aligned} P_\mathrm{dyn} =f C_k V_k^2 \end{aligned}$$

(30)

where f is frequency and defined as ($f=1$/$T_\mathrm{p}$) and $T_\mathrm{p}$ is the time period of the signal. $C_{k}$ and $V_{k}$ represent node capacitance and voltage, respectively. The total average dynamic power dissipation at time instant n is formulated as:

$$\begin{aligned} P_\mathrm{dyn}^n =\left[ {(C_m +C_\mathrm{d})\frac{\left( {V_0^n} \right) ^{2}}{T_\mathrm{p} }+\left( {C_\mathrm{L}} \right) \frac{\left( {V_{Nz+2}^n} \right) ^{2}}{T_\mathrm{p} }+\sum _{k=2}^{Nz+1} {\left( {C_k} \right) \frac{\left( {V_k^n} \right) ^{2}}{T_\mathrm{p}}}} \right] \end{aligned}$$

(31)

The static power dissipation ($P_\mathrm{stat}$) is due to ohmic loss across interconnect parasitic resistance and load resistance $R_\mathrm{L}$. The total $P_\mathrm{stat}$ at time instant n is defined as

$$\begin{aligned} P_\mathrm{stat}^n =\frac{\beta \left( {V_\mathrm{DD}} \right) ^{2}}{2\left[ {R_\mathrm{L} +\beta \cdot Nz\cdot R_\mathrm{dis} \cdot \Delta z+2\beta \cdot \alpha \cdot R_\mathrm{lump}^{\prime } +\beta \left( {\frac{V_\mathrm{DD} -V_0^n}{I_p ^{n}}} \right) } \right] } \end{aligned}$$

(32)

Equation (32) is defined for the case when PMOS transistor of CMOS driver gate is in ON state. As $R_\mathrm{L}$ approaches infinity, static power dissipation becomes zero.

Fig. 5

Power dissipation in DIL system

Also, during transition period, both NMOS and PMOS transistors remain in ON state between the threshold voltages of NMOS and PMOS transistors. As a result, small current flows from $V_\mathrm{DD}$ to ground for fraction of transition period duration which results in short-circuit power dissipation ($P_\mathrm{sc}$) in the circuit. $P_\mathrm{sc}$ can be defined as fraction (x) of total dynamic power dissipation [4, 14]. It is given as

$$\begin{aligned} P_\mathrm{sc}^n =x\cdot P_\mathrm{dyn}^n \end{aligned}$$

(33)

where x ranges from 0.1 to 0.2.

Fig. 6

Propagation delay and power dissipation in copper and MWCNT interconnects using CMS scheme

4 Results and Discussion

In this section, performance of copper and MWCNT interconnects using VMS and CMS schemes is analyzed. The metrics used for performance analyses are propagation delay, energy and crosstalk. The analyses are carried out at 32 nm technology node. The interconnect dimensions are computed as per ITRS and CNIA [6, 15]. $R_\mathrm{dis}$, $C_\mathrm{dis}$, $L_\mathrm{dis}$ and $R_\mathrm{lump}^{\prime }$for MWCNT interconnect are 0.95 M $\Omega$/m, 9.41 pF/m, 9.48 $\upmu$H/m and 79.04 $\Omega$, respectively. The per unit length parameters $R_\mathrm{dis}$, $C_\mathrm{dis}$ and $L_\mathrm{dis}$ for copper interconnect are 3.18 M $\Omega$/m, 21.8 pF/m and 1.48 $\upmu$H/m, respectively. $R_\mathrm{lump}^{\prime }$is zero in case of copper interconnect. The load impedances, $R_\mathrm{L}$ and $C_\mathrm{L}$, are 1K$\Omega$ and 0.5 fF, respectively, for CMS scheme. $C_\mathrm{L}$ is 1 fF for VMS scheme [1]. $R_\mathrm{L}$ in case of VMS scheme is very high and considered as infinity [1, 4, 12, 37]. Gate length of transistors is 32 nm. Widths of NMOS and PMOS transistors considered are 1 and 2.5 $\upmu$m, respectively [1, 18]. For formulation using FDTD, $\Delta z$ for MWCNT and copper are 0.34 and 0.55 mm, respectively. $\Delta t$ is nearly same for both the interconnects and equals to 3.14 ns. The proposed FDTD-based model is validated using Tanner EDA tool, SPICE simulations [35]. The BSIM SPICE level 54 model is considered and taken from predictive technology model (PTM) [30].

4.1 Analysis of Copper and MWCNT Interconnects Using CMS Scheme

A comparative analysis is carried out for copper and MWCNT interconnects using CMS scheme and illustrated in Figs. 6 and 7. Propagation delay and power dissipation variation with interconnect lengths are shown in Fig. 6. It is observed from the figure that CMS MWCNT interconnect results in lower propagation delay in the circuit while CMS copper interconnect possesses lesser power dissipation. Hence, there is a trade-off in the performance parameters for CMS copper and MWCNT interconnects. The efficacy between the two has been inferred by analyzing the power_delay_product (PDP). PDP represents the energy consumption in the circuit and is an important figure-of-merit in e-circuits. PDP should be low for high performance applications. The PDP for CMS copper and MWCNT interconnects using proposed model based on FDTD, and SPICE is presented in Fig. 7. It is seen from the figure that PDP is nearly identical in both the cases for interconnect length of 500 $\upmu$m. However, as the wire length increases, CMS MWCNT interconnect has significantly lesser PDP (nearly 64% lesser) as compared to CMS copper interconnect. Also, from Figs. 6 and 7, it is analyzed that results of the proposed model based on FDTD technique are in close agreement with SPICE results. The maximum error between these is <3%.

Fig. 7

Power_delay_product in copper and MWCNT interconnects using CMS scheme

4.2 Analysis of MWCNT Interconnect Using VMS and CMS Schemes

Propagation delay and power dissipation are analyzed in MWCNT interconnect for both VMS and CMS schemes. Lower latency and thus higher speed are observed in case of CMS scheme [2, 40]. This is evident from Fig. 8. It is observed from the figure that at interconnect length of 4500 $\upmu$m, MWCNT interconnect with CMS scheme has about 72% lesser propagation delay as compared to VMS scheme. Owing to smaller impedance termination, voltage swing over interconnects is reduced in CMS scheme. This causes fast charging and discharging of interconnect node capacitances. It is observed from the figure that power dissipation in case of CMS scheme is higher than VMS scheme. Thus, VMS scheme is better for power centric designs. Also, it is seen that the proposed model and SPICE results match closely with each other. The average percentage error between SPICE and analytical models for VMS and CMS schemes is 2.37 and 2.84%, respectively.

Fig. 8

Propagation delay and power dissipation in MWCNT interconnect using VMS and CMS schemes

Fig. 9

a Driver-interconnect-load model in CMS scheme. Realization of driver using b accurate CMOS gate model c approximate resistive model

4.3 Analysis of CMS MWCNT Interconnect Using Resistive Driver and the Proposed CMOS Gate Driver Models

The driver-interconnect-load model in CMS scheme is shown in Fig. 9a. The driver models using CMOS gate and resistive element are represented in Fig. 9b, c, respectively. In resistive driver model, CMOS gate is approximated as resistive ($R_\mathrm{d}$) and capacitive ($C_\mathrm{d}$) elements [19, 22, 23, 31, 36]. Resistive driver model has limited accuracy as the nonlinear characteristics of MOS transistors cannot be modeled by lumped resistive and capacitive elements in different operating regions of MOS transistor. The output voltage for CMS MWCNT interconnect using resistive and CMOS gate drivers is shown in Fig. 10. The input is a ramp signal with transition period of 5 ps. The input to resistive driver circuit is opposite to that of CMOS driver input since there is no inversion of input signal in the former case. %Error1 in the figure represents percentage error between CMOS gate driver model and SPICE results, while %Error2 gives percentage error between resistive driver model and SPICE results. It is seen from the figure that the resistive driver model leads to significantly less accurate results. This is palpable from the figure, as average error in case of CMOS driver (%Error1) and resistive driver models (%Error2) are 0.94 and 6.49%, respectively. The lower value of %Error1 shows the higher accuracy and efficacy of CMOS gate driver model used in the present work over resistive driver model.

Fig. 10

Output voltage in MWCNT interconnect using CMS scheme

4.4 Crosstalk Analysis of MWCNT Interconnect Using CMS Scheme

Coupling between interconnects causes various non-ideal and signal integrity issues such as spurious noise production and enhanced circuit propagation delay. This is termed as crosstalk [13, 23]. Crosstalk can be broadly categorized as functional and dynamic [11, 19]. In functional crosstalk, input signal to the victim line is quiet. As a result, victim line experiences undershoot or overshoot noise whenever signal on the aggressor line switches, whereas in dynamic crosstalk, input signals to the aggressor and victim lines switch simultaneously either in-phase or out-of-phase with each other. This causes propagation delay and noise in the circuit [1]. Table 1 shows the crosstalk-induced propagation delay in 2-Line coupled MWCNT interconnects using CMS scheme for both in-phase and out-of-phase switching cases. From the table, it is observed that crosstalk-induced delay is lesser for in-phase switching case as compared to out-of-phase switching case. The higher propagation delay in out-of-phase is because of higher Miller capacitance effect [1]. A comparison is also made in between the proposed model using CMOS driver model, resistive driver model and SPICE. It is analyzed that CMOS driver model estimates propagation delay more accurately to SPICE results. The average percentage error between resistive driver model and SPICE for in-phase and out-of-phase cases is 8.54 and 9.52%, respectively. Furthermore, these error values for CMOS driver model and SPICE are 1.25 and 1.78%, respectively.

Table 1 Crosstalk-induced propagation delay in coupled MWCNT interconnects using CMS scheme

The transient responses at the victim line (Line 3) for three different cases in 5-Line coupled MWCNT interconnects using CMS scheme are presented in Fig. 11. Figure 11a, b shows that peak overshoot and peak undershoot obtained by the proposed model are 0.47 and 0.08 V, respectively, at 0.05 ns. Figure 11c shows the crosstalk-induced delay of 22.34 ps. For all the three cases, it is observed that the CMOS driver model using the proposed model based on FDTD technique and SPICE results are in very close agreement with each other.

In the present work, carbon nanotube is considered as uniform wire. However, in practical configurations, it is likely that carbon nanotube may not line up perfectly and may possess bends or non-uniformities. The non-uniform copper interconnects have been modeled and analyzed using perturbation technique, virtual straight lines and modeling interconnect parasitics as line-dependent parameters in [8, 17, 34]. These techniques shall be further explored and implemented for carbon nanotubes as future work of the authors.

Fig. 11

Transient response at the victim line (Line 3) in 5-Line CMS MWCNT interconnect for three different switching cases. a Dynamic crosstalk (out-of-phase switching case). b Functional crosstalk. c Dynamic crosstalk (in-phase switching case)

5 Conclusion

The paper analyzes performance of CMS MWCNT interconnect using FDTD technique. The proposed FDTD-based model can be used for signal integrity analysis of both copper and MWCNT interconnects as well as VMS and CMS schemes. The driver is modeled by CMOS gate and characterized by nth power law model. The interconnects are represented by equivalent ESC model. It is analyzed that using CMS scheme, MWCNT interconnect has an upper edge over the conventional copper interconnects in terms of lower propagation delay and lesser PDP. Also, with reference to traditional VMS scheme, CMS scheme is investigated to be better particularly for high speed applications owing to lesser propagation delay in the circuit. Further, it is validated that CMOS driver model using the proposed model has higher precision than the resistive driver model. The crosstalk is analyzed for 2-Line and 5-Line coupled MWCNT interconnects using CMS scheme. For all the cases considered, FDTD technique-based analytical model and SPICE-based simulation results match closely. The proposed model accurately predicts the system response and can be used for signal integrity analyses of M-Line uniform coupled interconnects. The non-uniform MWCNT interconnects can be modeled by incorporating specialized modeling techniques and can be further explored. Subsequently, from the present research work, it is inferred that MWCNT interconnects using CMS scheme are better solution to achieve high performance and efficiency in integrated circuits at nanoscale regime.

Appendices

Appendix 1

The parasitic elements of MWCNT interconnect can be defined as:

The lumped resistance ($R_\mathrm{lump}$) comprises of quantum resistance ($R_\mathrm{q}$) which is due to quantum confinement of carriers along the interconnect dimensions. The contact resistance ($R_\mathrm{c}$) is due to imperfect contact between the interconnect and substrate. $R_\mathrm{c}$ depends on the fabrication process and varies from 1 to 20 K$\Omega$ [10]. $R_\mathrm{lump}$ is expressed as [19]

$$\begin{aligned} R_\mathrm{lump} =\left[ {\sum _{i=1}^N {\left( {\frac{h}{2e^{2}\cdot N_\mathrm{ch}^i}+R_\mathrm{c}^i} \right) } ^{-1}} \right] ^{-1} \end{aligned}$$

(34)

where h is Planck’s constant and e represents charge on electron.

$R_\mathrm{lump}$ is distributed equally along the two ends of the interconnect as $R_\mathrm{lump}^{\prime }$. It is presented as

$$\begin{aligned} R_\mathrm{lump}^{\prime } =\frac{R_\mathrm{lump}}{2} \end{aligned}$$

(35)

The distributed resistance ($R_\mathrm{dis}$) in the ESC model represents the scattering resistance per unit length (p.u.l.) [22]. It is primarily due to optical and acoustic phonon scattering. $R_\mathrm{dis}$ is predominant when interconnect length is greater than electron mean free path [28]. It is defined as [23]

$$\begin{aligned} R_\mathrm{dis} =\sum _{i=1}^N {\left( {\frac{h}{2e^{2}\cdot N_\mathrm{ch}^i \cdot \lambda _i}} \right) } \end{aligned}$$

(36)

where $\lambda _{i}$ corresponds to effective electron mean free path of ith shell and is obtained as [24]

$$\begin{aligned} \lambda _i =\frac{10^{3}d_i}{\left( {T/{T_0}} \right) -2} \end{aligned}$$

(37)

where $T_{0}$=100 K

The distributed inductance ($L_\mathrm{dis}$) comprises of kinetic inductance p.u.l. ($L_\mathrm{k}$) and magnetic inductance p.u.l. ($L_\mathrm{m}$).

The kinetic inductance p.u.l. per channel ($L_\mathrm{k/channel}$) is given as [19]

$$\begin{aligned} L_\mathrm{k/channel} =\left( {\frac{h}{2e^{2}v_\mathrm{f}}} \right) \left( {\frac{1}{2}} \right) \end{aligned}$$

(38)

where $v_\mathrm{f}$ is Fermi velocity.

Using $L_\mathrm{k/channel}$, kinetic inductance p.u.l. per shell ($L_\mathrm{k/shell}$) is computed.

$$\begin{aligned} L_\mathrm{k/shell}^i =\left( {\frac{L_\mathrm{k/channel}}{N_\mathrm{ch}^i}} \right) ;\quad 1\le i\le N \end{aligned}$$

(39)

The p.u.l. mutual shell to shell inductance ($L_\mathrm{m\_shell\_shell}$) is defined as [23]

$$\begin{aligned} L_\mathrm{m\_shell\_shell}^{i,i+1} =\frac{\mu }{2\pi }\ln \left( {\frac{d_{i+1}}{d_i}} \right) ;\quad 1\le i\le N-1 \end{aligned}$$

(40)

The equivalent kinetic inductance p.u.l. of ith shell ($L_\mathrm{equ}^i$) is obtained using recursive expression as [23]

$$\begin{aligned} L_\mathrm{equ}^i =\left[ {\frac{1}{L_\mathrm{equ}^{i-1} +L_\mathrm{m\_shell\_shell}^{i-1,i}}+\frac{1}{L_\mathrm{k/shell}^i}} \right] ^{-1};\quad 2\le i\le N \end{aligned}$$

(41)

where

$$\begin{aligned} L_\mathrm{equ}^1 =L_\mathrm{k/shell}^1 \end{aligned}$$

(42)

The equivalent kinetic inductance p.u.l. of MWCNT interconnects ($L_\mathrm{k}$) is given by:

$$\begin{aligned} L_\mathrm{k} =L_\mathrm{equ}^N \end{aligned}$$

(43)

The equivalent magnetic inductance p.u.l. of MWCNT interconnect ($L_\mathrm{m}$) is computed as [24].

$$\begin{aligned} L_\mathrm{m} =\frac{\mu }{2\pi }\cosh ^{-1}\left( {\frac{d_N +2h_\mathrm{g}}{d_N}} \right) \end{aligned}$$

(44)

where $d_{N}$ is the outermost shell diameter of MWCNT and $h_\mathrm{g}$ represents the distance between MWCNT and ground plane.

The equivalent inductance in the ESC model ($L_\mathrm{dis}$) is computed as

$$\begin{aligned} L_\mathrm{dis} =L_\mathrm{k} +L_\mathrm{m} \end{aligned}$$

(45)

Similarly, distributed capacitance ($C_\mathrm{dis}$) of MWCNT in the ESC model is obtained. It comprises of p.u.l. quantum capacitance ($C_\mathrm{q}$), and electrostatic capacitance ($C_\mathrm{e}$). $C_\mathrm{dis}$ is expressed as

$$\begin{aligned} C_\mathrm{dis} =\frac{C_\mathrm{q} \cdot C_\mathrm{e}}{C_\mathrm{q} +C_\mathrm{e}} \end{aligned}$$

(46)

$C_\mathrm{e}$ is obtained as [24]

$$\begin{aligned} C_\mathrm{e} =\frac{2\pi \varepsilon }{\cosh ^{-1}\left( {\frac{d_N +h_\mathrm{g}}{d_N}} \right) } \end{aligned}$$

(47)

$C_\mathrm{q}$ is obtained by solving recursive formulae given below [23]

$$\begin{aligned} C_\mathrm{equ}^i= & {} \left[ {\frac{1}{C_\mathrm{equ}^{i-1} }+\frac{1}{C_\mathrm{c\_shell\_shell}^{i-1,i}}} \right] ^{-1}+C_\mathrm{q/shell}^i ;\quad 2\le i\le N \end{aligned}$$

(48)

$$\begin{aligned} C_\mathrm{equ}^1= & {} C_\mathrm{q/shell}^1 \end{aligned}$$

(49)

$$\begin{aligned} C_\mathrm{q}= & {} C_\mathrm{equ}^N \end{aligned}$$

(50)

where $C_\mathrm{equ}^i$is the equivalent capacitance of ith shell. $C_\mathrm{q/shell}$ and $C_\mathrm{c\_shell\_shell}$ are p.u.l. quantum capacitance per shell and coupling capacitance between shells of MWNCT interconnect, respectively [11]. These are defined as [19]

$$\begin{aligned} C_\mathrm{q/shell}^i= & {} 2N_\mathrm{ch}^i \left( {\frac{2e^{2}}{hv_\mathrm{f}}} \right) ;\quad 1\le i\le N \end{aligned}$$

(51)

$$\begin{aligned} C_\mathrm{c\_shell\_shell}^{i,i+1}= & {} \frac{2\pi \varepsilon }{\ln \left( {{d_{i+1}}/{d_i}} \right) };\quad 1\le i\le N-1 \end{aligned}$$

(52)

The p.u.l. mutual inductance ($M_\mathrm{i}$) and coupling capacitance ($C_\mathrm{c}$) between two parallel MWCNT interconnects are given as [11, 21, 24, 31]

$$\begin{aligned} M_\mathrm{i}= & {} \frac{\mu }{2\pi }\left[ {\ln \left( {\frac{l}{h_\mathrm{c} }+\sqrt{1+\left( {\frac{l}{h_\mathrm{c}}} \right) ^{2}}} \right) -\sqrt{1+\left( {\frac{h_\mathrm{c}}{l}} \right) ^{2}}+\frac{h_\mathrm{c}}{l}} \right] \end{aligned}$$

(53)

$$\begin{aligned} C_\mathrm{c}= & {} \frac{\pi \varepsilon }{\ln \left( {\frac{s_p}{d_N}+\sqrt{\left( {\frac{s_p}{d_N}} \right) ^{2}+1}} \right) } \end{aligned}$$

(54)

where l is the length of interconnect and $s_{p}$ is the separation between two interconnects. $h_\mathrm{c}$ is the center-to-center distance between two interconnects and equals to ($s_{p}+d_{N}$).

Appendix 2

The parasitic elements for copper interconnects can be defined as [30, 39]:

$$\begin{aligned} R_\mathrm{dis}= & {} \frac{\rho }{w\cdot t} \end{aligned}$$

(55)

$$\begin{aligned} L_\mathrm{dis}= & {} \frac{\mu }{2\pi }\left[ {\ln \left( {\frac{2l}{w+t}} \right) +\frac{1}{2}+\frac{0.22\left( {w+t} \right) }{l}} \right] \end{aligned}$$

(56)

$$\begin{aligned} C_\mathrm{dis}= & {} \varepsilon \left[ {\begin{array}{l} \frac{w}{h_\mathrm{g}}+2.22\left( {\frac{s_p}{s_p +0.7h_\mathrm{g}}} \right) ^{3.19} \\ +1.17\left( {\frac{s_p}{s_p +1.51h_\mathrm{g}}} \right) ^{0.76}\cdot \left( {\frac{t}{t+4.53h_\mathrm{g}}} \right) ^{0.12} \\ \end{array}} \right] \end{aligned}$$

(57)

$$\begin{aligned} M_\mathrm{i}= & {} \frac{\mu }{2\pi }\left[ {\ln \left( {\frac{2l}{h_\mathrm{c}}} \right) -1+\frac{h_\mathrm{c}}{l}} \right] \end{aligned}$$

(58)

$$\begin{aligned} C_\mathrm{c}= & {} \varepsilon \left[ {\begin{array}{l} 1.14\left( {\frac{t}{s_p}} \right) \left( {\frac{h_\mathrm{g}}{h_\mathrm{g} +2.06s_p}} \right) ^{0.09}+0.74\left( {\frac{w}{w+1.59s_p}} \right) ^{1.14} \\ +1.16\left( {\frac{w}{w+1.87s_p}} \right) ^{0.16}\cdot \left( {\frac{h_\mathrm{g}}{h_\mathrm{g} +0.98s_p}} \right) ^{1.18} \\ \end{array}} \right] \end{aligned}$$

(59)

where $\rho$ is resistivity of copper material. w and t are width and thickness of the copper interconnect. All other parameters for copper interconnects in (55)–(59) have their usual meaning as that for MWCNT interconnect. $R_\mathrm{lump}^{\prime }$in the ESC model for copper interconnect is zero.

Appendix 3

The Telegraph’s equations are given as [29]:

$$\begin{aligned} \frac{\partial \left[ V \right] }{\partial z}+\left[ L \right] \frac{\partial \left[ I \right] }{\partial t}+\left[ R \right] \left[ I \right]= & {} 0 \end{aligned}$$

(60)

$$\begin{aligned} \frac{\partial \left[ I \right] }{\partial z}+\left[ C \right] \frac{\partial \left[ V \right] }{\partial t}= & {} 0 \end{aligned}$$

(61)

where [V] and [I] are $M \times 1$ voltage and current variables along interconnect and are function of position and time. [R], [L] and [C] are $M \times M$ dimensional p.u.l. interconnect parasitics. These are given as

$$\begin{aligned} \left[ R \right]= & {} \hbox {diag}\left( {R_\mathrm{dis}^1,R_\mathrm{dis}^2 ,\cdots ,R_\mathrm{dis}^M} \right) , \\ \left[ L \right]= & {} \left( {{\begin{array}{lllll} {L_\mathrm{dis}^1}&{} {M_\mathrm{i}^{1,2}}&{} {M_\mathrm{i}^{1,3}}&{} \ldots &{} {M_\mathrm{i}^{1,M}} \\ {M_\mathrm{i}^{2,1}}&{} {L_\mathrm{dis}^2}&{} {M_\mathrm{i}^{2,3}}&{} \cdots &{} {M_\mathrm{i}^{2,M}} \\ \vdots &{} \vdots &{} \ddots &{} \vdots &{} \vdots \\ {M_\mathrm{i}^{M,1}}&{} {M_\mathrm{i}^{M,2}}&{} {M_\mathrm{i}^{M,3}}&{} \cdots &{} {L_\mathrm{dis}^M} \\ \end{array}}} \right) \hbox {and} \end{aligned}$$

$$\begin{aligned} \left[ C \right] =\left( {{\begin{array}{lllll} {C_\mathrm{dis}^1 +\sum \limits _{j=2}^M {C_\mathrm{c}^{1,j}}}&{} {-C_\mathrm{c}^{1,2}}&{} {-C_\mathrm{c}^{1,3}}&{} \ldots &{} {-C_\mathrm{c}^{1,M}} \\ {-C_\mathrm{c}^{2,1}}&{} {C_\mathrm{dis}^2 +\sum _{j=1, 3}^M {C_\mathrm{c}^{2,j}}}&{} {-C_\mathrm{c}^{2,3}}&{} \cdots &{} {-C_\mathrm{c}^{2,M}} \\ \vdots &{} \vdots &{} \ddots &{} \vdots &{} \vdots \\ {-C_\mathrm{c}^{M,1}}&{} {-C_\mathrm{c}^{M,2}}&{} {-C_\mathrm{c}^{M,3}}&{} \ldots &{} {C_\mathrm{dis}^M +\sum \limits _{j=1}^{M-1} {C_\mathrm{c}^{M,j}}} \\ \end{array}}} \right) \end{aligned}$$

(62)

where $R_\mathrm{dis}$, $L_\mathrm{dis}$ and $C_\mathrm{dis}$ are distributed resistance, inductance and capacitance, respectively, of MWCNT/copper interconnect in ESC model. $M_\mathrm{i}$ and $C_\mathrm{c}$ represent p.u.l. mutual inductance and coupling capacitance between two parallel MWCNT/copper interconnects.