1 Introduction

Advances in very large-scale integration (VLSI) technology offer gigascale integrated circuits in a system on a chip. The use of interconnects is particularly important in the integration of electronic devices. Because of these requirements, chip complexity and the number of sources of variations have increased, and tightly packed interconnects emit transient crosstalk at high operating frequencies [1, 2]. Accurate peak noise timing and peak crosstalk noise estimation in a driver-interconnect-load (DIL) system has long been a key architectural objective [3]. On the basis of lumped and distributed RC interconnects, various crosstalk and delay models have been proposed [4, 5]. Masoumi et al. [6] computed crosstalk noise effects in a capacitively coupled RC interconnect line using closed-form expressions. Ismail et al. [7] strengthened the model by integrating self-inductance effects and estimated the RLC line propagation delay. With the introduction of low-resistivity interconnect materials and fast operating switching frequencies, parasitic inductance has begun to play an important role in on-chip interconnect efficiency. To accurately estimate the output of on-chip interconnects, they must be viewed as scattered RLC lines or transmission lines [8].

For evaluation of crosstalk noise, previous models have interpreted the nonlinear complementary metal–oxide–semiconductor (CMOS) driver to be a simple linear resistor [9, 10], which appears to deviate from the effects. Approximately 50% of MOSFET operation is in the saturation region during the transient period and later in the linear (or) cutoff regions. Several methods with different analytical solutions have been proposed, including the finite difference time domain (FDTD) approach and SPICE [simulation program with an integrated circuit emphasis], the results of which have been documented in recent works for DIL systems [11]. In the current state of the art, several studies have investigated crosstalk results based on the algorithm of the traditional FDTD, as it offers high precision [12], and Vobulapuram et al. [13] applied the FDTD approach to a nonlinear CMOS driver using the alpha-power law and nth-power law models, respectively, and they studied the effects of crosstalk in Cu interconnects.

The FDTD approach is an important computational procedure used to solve problems of electromagnetic and partial differential equations. The FDTD method is numerically dispersive [14, 15] during the propagation along the discretization. As a result, there is a need for a novel method with advantageous numerical dispersion properties. Krumpholz and Katehi [16] proposed a multiresolution time domain (MRTD) approach with an additional advantage of numerical dispersion characteristics. Grivet-Talocia [17] proposed an MRTD model using the Haar scaling function as the basis function, and achieved the same precision as with the FDTD model. Fujii et al. [18] proposed a model using MRTD as a basis function based on the Daubechies scaling function as three and four vanishing moments, which was more precise than the FDTD system. For effective field computation, Massy and Ney [19] hybridized the Battle–Lemarié-based MRTD model and the FDTD model to take advantage of the characteristics of both models, including the low dispersion characteristics of the MRTD model and the faster computation of the FDTD model. Tong et al. [20, 21] proposed an MRTD model for transient analysis of two-conductor transmission lines which outperformed conventional FDTD in terms of numerical dispersion and accuracy when compared with SPICE. Rebelli et al. [22, 23] proposed an MRTD approach to evaluate the signal integrity of coupled copper interconnects driven by a linear resistive and nonlinear CMOS dependent on the Daubechies scaling function at four vanishing moments. Rebelli et al. [24] applied the MRTD approach to a nonlinear CMOS using the nth-power law model to evaluate crosstalk noise in mutually coupled multiwalled carbon nanotube (MWCNT) interconnects at 32-nm technology. In the current state of the art, the MRTD method has not been used to calculate crosstalk noise, and the delay of the CMOS driver is analyzed using a modified alpha-power law model for coupled on-chip interconnects.

In this paper, the crosstalk effects of on-chip interconnects are analyzed using a Daubechies scaling function-based MRTD technique and considering the nonlinear CMOS driver modeled using a modified alpha-power law model which includes a drain conductance parameter. The most effective time domain model is presented to analyze both functional and dynamic crosstalk issues of two mutually coupled on-chip interconnect lines at 22-nm technology. The results obtained by the present model are compared with those of the conventional FDTD model and validated using HSPICE simulations.

The remainder of the paper is organized as follows. The transmission line-based MRTD model is discussed in Sect. 2, and the MRTD model comparisons and evaluation are presented in Sect. 3. Finally, conclusions are given in Sect. 4.

2 MRTD model of on-chip interconnects

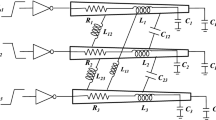
The model of two mutually coupled on-chip interconnects with driver and load is shown in Fig. 1. The parasitic capacitance of the CMOS is expressed by \(C_m\), which represents the gate-to-drain coupled capacitance, and \(C_d\), which represents the drain/source diffusion capacitance. \(R_1\) and \(R_2\) are the line resistance values, \(C_1\) and \(C_2\) are the line capacitance, \(L_1\) and \(L_2\) are the line inductance, and \(C_{L1}\) and \(C_{L2}\) are the load capacitance values of line 1and line 2, respectively. All these values are obtained per unit length (p.u.l.). Both capacitance and inductance are coupled to the interconnect lines. \(C_c\) and \(L_m\) are the p.u.l. coupling capacitance and mutual inductance of coupling interconnect lines, respectively. The position and time of the interconnect lines are denoted by x and t, respectively.

The MRTD model for two mutually coupled on-chip interconnects is built in this section using the basis function of Daubechies’ scaling function with four vanishing moments (\(D_4\)).

Fig. 1
figure 1

CMOS drivers driving two-coupled on-chip interconnect lines, which are terminated by capacitive loads

Full size image

2.1 Model formulations for two mutually coupled on-chip interconnect lines

The telegrapher’s equations can be used to mathematically describe the coupled interconnects. The coupled on-chip interconnects are defined as in [24, 25] using the following equations.

$$\begin{aligned} \frac{\partial V(z,t)}{\partial z}+L\frac{\partial I(z,t)}{\partial t}= & {} -I(z,t)R \end{aligned}$$
(1)
$$\begin{aligned} \frac{\partial I(z,t)}{\partial z}+C\frac{\partial V(z,t)}{\partial t}&= {} 0 \end{aligned}$$
(2)

where x and t are the positions and time, respectively; R, L, and C are two-dimensional interconnect impedance that is measured using [25]. The current and voltage variables for a the coupled interconnect lines are \(I=\left[ I_{1},I_{2} \right] ^{T}\) and \(V=\left[ V_{1},V_{2} \right] ^{T}\).

$$\begin{aligned} R= & {} diag\left[ R _{1},R_{2} \right] \\ L= & {} \begin{bmatrix} L_{1} &{} L_{m}\\ L_{m} &{} L_{2}\\ \end{bmatrix} \\ \end{aligned}$$
$$\begin{aligned} C=\begin{bmatrix} C_{1}+C_{c} &{} -C_{c}\\ -C_{c} &{} C_{2}+C_{c} \\ \end{bmatrix} \end{aligned}$$
(3)

where subscript 1 corresponds to line 1 and subscript 2 corresponds to line 2. The voltage and current evaluation points on interconnect line 1 are shown in Fig. 3.

Alternatively, current and voltage points are considered in time and space to evaluate telegrapher equations. The current and voltage are separated by \(\frac{\varDelta t}{2}\) in time and \(\frac{\varDelta x}{2}\) in space for better accuracy, as shown in Fig. 2, where\(\varDelta t\) is time and \(\varDelta x\) is space represented in discretization intervals.

Fig. 2
figure 2

Space and time discretization on an on-chip interconnect line

Full size image

The interconnect line l of length is the resistive driver at \(x = 0\) and terminated at \(x = l\) is capacitive load. The line is divided consistently into Nx segments of length \(\varDelta x=\frac{l}{Nx}\) indicating the discretization voltage (V) and current (I) nodes, which are unknown coefficients, as seen in Fig. 3, where the source current is represented by \(I_0\).

Fig. 3
figure 3

Spatial discretization for I and V on an on-chip interconnect line

Full size image

The voltage and current terms can be extended using a known function (\(h_n(t)\) and \(\varPhi _{k}(x)\)). In order to solve Eqs. (1) and (2), the unknown coefficients can be found by following the method defined in [16] as:

$$\begin{aligned}&V(x,t)-\sum _{n,k=-\infty }^{+\infty }V_{k}^{n}\varPhi _{k}^{n}(x)h_{n}(t)=0 \end{aligned}$$
(4a)
$$\begin{aligned}&I(x,t)-\sum _{n,k=-\infty }^{+\infty }I_{k+\frac{1}{2}}^{n+\frac{1}{2}}\varPhi _{k+\frac{1}{2}}^{n}(x)h_{n}(t)=0 \end{aligned}$$
(4b)

where \(I_{k+\frac{1}{2}}^{n+\frac{1}{2}}\) is the coefficient of current expansion and \(V_{n}^{k}\) is the coefficient of voltage expansion in terms of function scaling, and the indices n and k are discrete time and space. Indices related to time and space are organized via \(t=n\varDelta t\) and \(x=k\varDelta x\). Functions \(h_n(t)\) and \(\varPhi _{k}(x)\) are defined as:

$$\begin{aligned} h_{n}(t)-h(\frac{t}{\varDelta t}-n)=0 \end{aligned}$$
(5a)

where pulse function h(t) is defined as

$$\begin{aligned} h(t)= & {} \left\{ \begin{matrix} 1 &{} for\left| t \langle \right| < &{}\frac{1}{2} &{} \\ \frac{1}{2} &{} for\left| t \right| =\frac{1}{2} &{} &{} \\ 0 &{} for\left| t \right| > \frac{1}{2} &{} &{} \end{matrix}\right. \end{aligned}$$
(5b)
$$\begin{aligned} \varPhi _{k}(x)= & {} \varPhi (\frac{x}{\varDelta x}-k) \end{aligned}$$
(5c)

where \(\varPhi (x)\) signifies the Daubechies scaling function, and h(t) represents the Haar scaling function.

The following integrals [26] are considered in order to derive the MRTD technique for Eqs. (1) and (2):

$$\begin{aligned}&\int _{-\infty }^{+\infty }h_{n}(t)h_{n'}(t)dt=(\delta _{n,n'}\varDelta t) \end{aligned}$$
(6a)
$$\begin{aligned}&\int _{-\infty }^{+\infty }h_{n}(t)\frac{\partial h_{n'+\frac{1}{2}}(t)}{\partial t}dt=(\delta _{n,n'}-\delta _{n,n'+1}) \end{aligned}$$
(6b)
$$\begin{aligned}&\int _{-\infty }^{+\infty }\varPhi _{k}(x)\varPhi _{k'}(x)dx=(\delta _{k,k'}\varDelta x) \end{aligned}$$
(6c)
$$\begin{aligned}&\int _{-\infty }^{+\infty }\varPhi _{k}(x)\frac{\partial \varPhi _{k'+\frac{1}{2}}(t)}{\partial x}dx=\sum _{i=-L_{s}}^{L_{s}-1}b(i)\delta _{k+i,k'} \end{aligned}$$
(6d)

where the Kronecker delta is represented by \(\delta _{k,k'}\)and \(\delta _{n,n'}\). The effective support sizes of the basis functions are indicated by \(L_s\) by considering the Daubechies scaling function as the basis function with four vanishing moments (D4). The coefficient b(i) is called the connection coefficient. Table 1 shows b(i) for \(1\le i\le L_{s}\), whereas b(i) for \(i< 1\) can be found by symmetry condition b(−1−i) =−b(i) and equals zero for \(i> L_{s}\)

$$\begin{aligned} b(i)=\frac{1}{\varPi }\int _{0}^{\infty }\left| {\hat{\varPhi }}(\lambda ) \right| ^{2}\lambda sin\lambda (i+\frac{1}{2})d\lambda \end{aligned}$$
(7)

where the scaling function of Fourier transform f(x) is \(\hat{\varPhi }(\lambda )\).

Table 1 Connection coefficient b(i) for Daubechies’ scaling function (D4) [18]
Full size table

The following iterative calculations for current and voltage were carried out by employing the Galerkin technique [16] in Eqs. (1) and (2) and by using the test functions \(\varPhi _{k}h_{n+\frac{1}{2}}(t)\) and \(\varPhi _{k+\frac{1}{2}}h_{n}(t)\):

$$\begin{aligned} I_{k+\frac{1}{2}}^{n+\frac{3}{2}}= & {} PI_{k+\frac{1}{2}}^{n+\frac{1}{2}}-\frac{\varDelta t}{\varDelta z}L^{-1}Q\left( \sum _{i=1}^{L_{s}}b(i) \left( V_{k+i}^{n} -V_{k-i+1}^{n}\right) \right) \end{aligned}$$
(8a)
$$\begin{aligned} V_{k}^{n+1}= & {} V_{k}^{n}-\frac{\varDelta t}{\varDelta z}C^{-1}\sum _{i=1}^{L_{s}}b(i)\left( I_{k+i-\frac{1}{2}}^{n+\frac{1}{2}}-I_{k-i+\frac{1}{2}}^{n+\frac{1}{2}} \right) \end{aligned}$$
(8b)

where

$$\begin{aligned} P= & {} \left( 1+\frac{\varDelta t}{2}RL^{-1} \right) ^{-1}\left( 1-\frac{\varDelta t}{2}RL^{-1} \right) \\ Q= & {} \left( 1+\frac{\varDelta t}{2}RL^{-1} \right) ^{-1} \end{aligned}$$

In the iterative Eqs. (8a) and (8b), the near-end voltage \(V_{1}^{n+1}\) and the far-end voltage \(V_{Nx+1}^{n+1}\) are obtained, and the iterative equations of the current and voltage near the boundary need to be modified. Near the boundary, the current is expressed by \(I_{j+\frac{1}{2}}^{n+\frac{1}{2}}\) and \(I_{Nx+1-i+\frac{1}{2}}^{n+\frac{1}{2}}\) for \(i=1,2,3,\cdots ,L_{s}-1\) and the voltage is \(V_{i}^{n+1}\) and \(V_{Nx-i+1}^{n+1}\) for \(i=2,3,\cdots ,L_{s}\) Many of these current and voltage values have a number of terms that surpass the index ranges in iterative Eqs. (8a) and (8b)

Equations (8a) and (8b) need to be decomposed using the relationship in [27] to update the iterative equations of current and voltage, which satisfies the connection coefficient b(i) given by

$$\begin{aligned} \sum _{i=1}^{L_{s}}\left( 2i-1 \right) b(i)=1 \end{aligned}$$
(9)

By substituting (9) into (8b), we get

$$\begin{aligned}&\sum _{i=1}^{L_{s}}b(i)\left( 2i-1 \right) V_{k}^{n+1} = \sum _{i=1}^{L_{s}}b(i)\left( 2j-1 \right) V_{k}^{n}- \nonumber \\&\sum _{i=1}^{L_{s}}\frac{\varDelta t}{(2i-1)\varDelta x}C^{-1}\left( (2i-1)b(i)\left( I_{k+i-\frac{1}{2}}^{n+\frac{1}{2}}-I_{k-i+\frac{1}{2}}^{n+\frac{1}{2}} \right) \right) \end{aligned}$$
(10)

We decompose (8b) considering a corresponding term with i as:

$$\begin{aligned}&b(i)\left( 2i-1 \right) V_{k}^{n+1}=b(i)\left( 2i-1 \right) V_{k}^{n} -\frac{\varDelta t}{(2i-1)\varDelta x}C^{-1} \nonumber \\&\quad \times \left( (2i-1)b(i)\left( I_{k+i-\frac{1}{2}}^{n+\frac{1}{2}}-I_{k-i+\frac{1}{2}}^{n+\frac{1}{2}} \right) \right) \end{aligned}$$
(11)

for at \(i=1,2,3,\cdots ,L_{s}-1\).

Equation (11) is further adapted by employing the boundary conditions as proved in Sects. 2.3 and 2.4.

2.2 Modeling of CMOS driver

The equivalent electrical circuit model for two mutually coupled on-chip interconnect lines is shown in Fig. 2. The input voltage (Vs) is a two-dimensional vector with the formula \(V_{s}=\left[ V_{s1},V_{s2} \right] ^{T}\). The interconnect lines are driven by a CMOS driver [28] that follows a modified alpha-power law model. The velocity saturation effects and the finite drain conductance parameters are included.

$$\begin{aligned} I_{n}= & {} \left\{ \begin{matrix} K_{sn}\left( V_{s}-V_{tn} \right) ^{\alpha _{n}} \left( 1+\sigma _{n}V_{1} \right) \\ K_{ln}\left( V_{s}-V_{tn} \right) ^{\frac{\alpha _{n}}{2}}V_{1} \\ 0 \end{matrix}\right. \end{aligned}$$
(12)
$$\begin{aligned} I_{p}= & {} \left\{ \begin{matrix} K_{sp}\left( V_{DD}-V_{s}-\left| V_{tp} \right| \right) ^{\alpha _{p}} \left( 1+\sigma _{p}\left( V_{DD}-V_{1} \right) \right) \\ K_{lp}\left( V_{DD}-V_{tp}-V_{s} \right) ^{\frac{\alpha _{p}}{2}}\left( -V_{1}+V_{DD} \right) \\ 0 \end{matrix}\right. \end{aligned}$$
(13)

The latest equations for PMOS and NMOS are signified by \(m\times 1\) vectors, i.e. \(I_{p}=\left[ I_{p1},I_{p2} \right] ^{T}\) and \(In = \left[ I_{n1},I_{n2} \right] ^{T}\). The linear region transconductance parameter, threshold voltage, saturation region transconductance parameter, drain conductance parameter and velocity saturation index of NMOS (PMOS) are \(K_{ln}\left( K_{lp} \right)\), \(V_{tn}\left( V_{tp} \right) , K_{sn}\left( K_{sp} \right),\sigma _{n}(\sigma _{p}), {\text{ and }} {\alpha_{n}(\alpha _{p}}), \) respectively. The NMOS/PMOS model parameter values for the 22-nm technology node as shown in Table 2 are used for this analysis.

Table 2 Model parameters of 22 nm [28]
Full size table

2.3 Modeling at the near-end boundary condition

The DIL system is modeled under boundary conditions. The current and voltage node points are at the near-end terminals defined by \(I_0\) and \(V_1\) , respectively, where the nodal analysis of the terminal equation is given by

$$\begin{aligned} I_{0}=C_{m}\frac{\mathrm {d} (V_{s}-V_{1})}{\mathrm {d} x}-C_{d}\frac{\mathrm {d} V_{1}}{\mathrm {d} x}+I_{p}-I_{n} \end{aligned}$$
(14)

Applying discretization and the Galerkin technique to (14), then

$$\begin{aligned} \varDelta xI_{0}&=\varDelta xC_{m}\frac{1}{\varDelta t}\left[ \left( V_{s}^{n+1} -V_{s}^{n}\right) -\left( V_{1}^{n+1} -V_{1}^{n}\right) \right] \nonumber \\&\quad -\varDelta xC_{d}\left( V_{1}^{n+1}-V_{1}^{n} \right) +\varDelta xI_{p}^{n+1}-\varDelta xI_{n}^{n+1} \end{aligned}$$
(15a)

and

$$\begin{aligned} V_{1}^{n+1}&=V_{1}^{n}+\left( \frac{C_{m}+C_{d}}{\varDelta t} \right) ^{-1}\times \nonumber \\&\quad \left[ C_{m}\frac{1}{\varDelta t}\left( V_{s}^{n+1}-V_{s}^{n} \right) +\left( I_{p}^{n+1}-I_{n}^{n+1}-I_{0}^{n+1} \right) \right] \end{aligned}$$
(15b)

The near-end terminal voltage is carried out at k=1 from (8b)

$$\begin{aligned} V_{1}^{n+1}=V_{1}^{n}-\frac{\varDelta t}{\varDelta x}C^{-1}\sum _{i=1}^{L_{s}}b(i)(I_{i+\frac{1}{2}}^{n+\frac{1}{2}}-I_{-i+\frac{3}{2}}^{n+\frac{1}{2}}) \end{aligned}$$
(16)

By following the steps from Eqs. (9)–(11), Eq. (16) is decomposed as

$$\begin{aligned} b(1)V_{1}^{n+1}= & {} b(1)V_{1}^{n}-b(1)\frac{\varDelta t}{\varDelta x}C^{-1}\left( I_{\frac{3}{2}}^{n+\frac{1}{2}}-I_{\frac{1}{2}}^{n+\frac{1}{2}} \right) \end{aligned}$$
(17a)
$$\begin{aligned} 3b(2)V_{1}^{n+1}= & {} 3b(2)V_{1}^{n}-3b(2)\frac{\varDelta t}{3\varDelta x}C^{-1}\left( I_{\frac{5}{2}}^{n+\frac{1}{2}}-I_{-\frac{1}{2}}^{n+\frac{1}{2}} \right) \end{aligned}$$
(17b)

\(\vdots\)

$$\begin{aligned}b(L_{s})(2L_{s}-1)V_{1}^{n+1}&=b(L_{s})(2L_{s}-1)V_{1}^{n} \nonumber \\&\quad -(2L_{s}-1)b(L_{s})\frac{\varDelta t}{(2L_{s}-1))\varDelta x}C^{-1}\left( I_{L_{s}+\frac{1}{2}}^{n+\frac{1}{2}}-I_{-L_{s}+\frac{3}{2}}^{n+\frac{1}{2}} \right) \end{aligned}$$
(17c)

Iterative Eqs. (17a)–(17c) are considered computer-aided design (CAD), i.e., central difference equations. In the particular calculations, the subscript to the terms \(I_{-\frac{1}{2}}^{n+\frac{1}{2}},I_{-\frac{3}{2}}^{n+\frac{1}{2}},\cdots , I_{-L_{s}+\frac{3}{2}}^{n+\frac{1}{2}}\) has surpassed the index range. To solve this, we substitute the central difference scheme by using the forward difference scheme. By leaving the weight coefficient in each equation unchanged, iterative equations can also be obtained.

$$\begin{aligned} b(1)V_{1}^{n+1}= & {} b(1)V_{1}^{n}-b(1)\frac{\varDelta t}{\varDelta x}C^{-1}\left( I_{\frac{3}{2}}^{n+\frac{1}{2}}-I_{0}^{n+\frac{1}{2}} \right) \end{aligned}$$
(18a)
$$\begin{aligned} 3b(2)V_{1}^{n+1}= & {} 3b(2)V_{1}^{n}-b(2)\frac{\varDelta t}{3\varDelta x}C^{-1}3\left( I_{\frac{5}{2}}^{n+\frac{1}{2}}-I_{0}^{n+\frac{1}{2}} \right) \end{aligned}$$
(18b)

\(\vdots\)

$$\begin{aligned}b(L_{s})(2L_{s}-1)V_{1}^{n+1}&=b(L_{s})(2L_{s}-1)V_{1}^{n} \nonumber \\&\quad -\frac{\varDelta t}{(2L_{s}-1))\varDelta x}C^{-1}(2L_{s}-1)b(L_{s})\left( I_{L_{s}+\frac{1}{2}}^{n+\frac{1}{2}}-I_{0}^{n+\frac{1}{2}} \right) \end{aligned}$$
(18c)

From the above iterative Eqs. (18a)−(87c), at the near-end boundary node a voltage of \(V_{1}^{n+1}\) is obtained through the following:

$$\begin{aligned} V_{1}^{n+1}=V_{1}^{n}-\frac{\varDelta t}{\varDelta x}C^{-1}\sum _{i=1}^{L_{s}}2b\left( i \right) \left( I_{i+\frac{1}{2}}^{n+\frac{1}{2}} -I_{0}^{n+\frac{1}{2}}\right) \end{aligned}$$
(19)

In Eq. (19), substituting by \(I_0^{n+\frac{1}{2}}=\frac{I_0^n+I_0^{n+1}}{2}\) and Eq. (15a) we obtain the equation

$$\begin{aligned} V_{1}^{n+1}&=V_{1}^{n}-AB \sum _{i=1}^{L_{s}}2b(i)I_{i+\frac{1}{2}}^{n+\frac{1}{2}} \nonumber \\&\quad -AB\sum _{i=1}^{L_{s}}b(i)\left( I_{0}^{n+1}+I_{p}^{n+1}-I_{n}^{n+1}+C_{m}\left( \frac{V_{s}^{n+1}-V_{s}^{n}}{\varDelta t} \right) \right) \end{aligned},$$
(20)

where

$$\begin{aligned} A=\left( 1+(C_{m}+C_{d})\frac{C^{-1}}{\varDelta x}\sum _{i=1}^{L_{s}}b(i) \right) ^{-1}, ~ B=\frac{\varDelta t}{\varDelta x}C^{-1} \end{aligned}$$

2.4 Modeling at the far-end boundary condition

Similarly, the nodal analysis equation at load current \(I_{Nx+1}\) given by the far-end terminal \((k = N_x+1)\)is:

$$\begin{aligned} I_{Nx+1}=C_{L}\frac{\mathrm {d}V_{Nx+1} }{\mathrm {d} t} \end{aligned}$$
(21)

Then the final iterative equation given at the far end of the terminal is

$$\begin{aligned}&V_{Nx+1}^{n+1}=V_{Nx+1}^{n}-EF \nonumber \\&\quad \left( \sum _{i=1}^{L_{s}}b(i)I_{Nx+1}^{n+\frac{1}{2}}-\sum _{i=1}^{L_{s}}2b(i)I_{Nx+1-i+\frac{1}{2}}^{n+\frac{1}{2}} \right) \end{aligned}$$
(22)

where \(E=\left( 1+\frac{C_{L}}{\varDelta t}C^{-1}\sum _{i=1}^{L_{s}}a(i) \right)\)

$$\begin{aligned} F=\frac{\varDelta t}{\varDelta x}C^{-1} \end{aligned}$$

where some of the term indices surpass the index ranges for all the nodes between the terminals in the algorithm extension to obtain and update the iterative equations, so a truncation method is applied by taking \(V_{k}^{n+1}\) as an example for \(k = 2, 3,\cdots , L_{s}\), and by subsequent steps of Eqs. (10) and (11) it can be decomposed (8b) as an example for \(k = 2, 3,\cdots , L_{s}\)

$$\begin{aligned} b(1)V_{k}^{n+1}= & {} b(1)V_{k}^{n}-b(1)\frac{\varDelta t}{\varDelta x}C^{-1}\left( I_{k+\frac{1}{2}}^{n+\frac{1}{2}}-I_{k-\frac{1}{2}}^{n+\frac{1}{2}} \right) \end{aligned}$$
(23a)
$$\begin{aligned} 3b(2)V_{k}^{n+1}= & {} 3b(2)V_{k}^{n}-3b(2)\frac{\varDelta t}{3\varDelta x}C^{-1}\left( I_{k+\frac{3}{2}}^{n+\frac{1}{2}}-I_{K-\frac{3}{2}}^{n+\frac{1}{2}} \right) \end{aligned}$$
(23b)

\(\vdots\)

$$\begin{aligned}b(k-1)(2k-3)V_{k}^{n+1}&=b(k-1)(2k-3)V_{k}^{n} \nonumber \\&\quad -b(k-1)(2k-3)\frac{\varDelta t}{(2k-3))\varDelta x}C^{-1}\left( I_{2k-\frac{3}{2}}^{n+\frac{1}{2}}-I_{1+\frac{1}{2}}^{n+\frac{1}{2}} \right) \end{aligned}$$
(23c)
$$\begin{aligned}b(k)(2k-1)V_{k}^{n+1}&=b(k)(2k-1)V_{k}^{n} \nonumber \\&\quad -b(k)(2k-1)\frac{\varDelta t}{\varDelta x(2k-1))}C^{-1}\left( I_{2k-\frac{1}{2}}^{n+\frac{1}{2}}-I_{\frac{1}{2}}^{n+\frac{1}{2}} \right) \end{aligned}$$
(23d)
$$\begin{aligned}b(k+1)(2k+1)V_{k}^{n+1}&=b(k+1)(2k+1)V_{k}^{n} \nonumber \\&\quad -(2k+1)b(k+1)\frac{\varDelta t}{(2k+1))\varDelta x}C^{-1}\left( I_{2k+\frac{1}{2}}^{n+\frac{1}{2}}-I_{-\frac{1}{2}}^{n+\frac{1}{2}} \right) \end{aligned}$$
(23e)

\(\vdots\)

$$\begin{aligned}&b(L_{s})(2L_{s}-1)V_{k}^{n+1}=b(L_{s})(2L_{s}-1)V_{k}^{n}-b(L_{s})\times \nonumber \\&\quad (2L_{s}-1)\frac{\varDelta t}{(2L_{s}-1))\varDelta x}C^{-1}\left( I_{k+L_{s}-\frac{1}{2}}^{n+\frac{1}{2}}-I_{k-L_{s}+\frac{1}{2}}^{n+\frac{1}{2}} \right) \end{aligned}$$
(23f)

From Eqs. (23a)–(23f) stated above, it is also observed that the indices of the equation do not surpass the index ranges for the first k terms. In addition, all calculations for which the index terms surpass the index spectrum appear in the remaining \(L_{s}-k\) term. As \(L_{s}-k\) terms are out of bound, these equations are not available for iterative equations in the MRTD model. To prevent this problem, a truncation is built into the calculations where the index range is surpassed.

The first k terms can be found by summing Eqs. (23a)–(23f), and the iterative equations can be updated at \(k = 2, 3,\cdots , L_{s}\)

$$\begin{aligned}&V_{k}^{n+1}=V_{k}^{n}-Q\left( \sum _{i=1}^{k}(2i-1)b(i) \right) ^{-1} \nonumber \\&\quad \left( \sum _{i=1}^{k} b(i)\left( I_{k+i-\frac{1}{2}}^{n+\frac{1}{2}}-I_{k-i+\frac{1}{2}}^{n+\frac{1}{2}} \right) \right) \end{aligned}$$
(24)

Using the same steps illustrated in Eqs. (23a)–(23f), an altered iterative equation of voltage at interior points, as presented in Eq. (25), and voltage near the load, as presented in Eq. (26), become \(k=L_{s}+1, L_{s}+2, \cdots ,Nx-L_{s}, Nx-L_{s}+1\)

$$\begin{aligned} V_{k}^{n+1}=V_{k}^{n}-Q\left( \sum _{i=1}^{L_{s}} b(i)\left( I_{k+i-\frac{1}{2}}^{n+\frac{1}{2}}-I_{k-i+\frac{1}{2}}^{n+\frac{1}{2}} \right) \right) \end{aligned}$$
(25)

for \(k=Nx-L_{s}+2, Nx-L_{s}+3, \cdots , N_{x}\).

$$\begin{aligned}V_{k}^{n+1}&=V_{k}^{n}-Q\left( \sum _{i=1}^{Nx-k+1}b(i)(2i-1) \right) ^{-1}\times \nonumber \\&\quad \left( \sum _{i=1}^{Nx-k+1} b(i)\left( I_{k+i-\frac{1}{2}}^{n+\frac{1}{2}}-I_{k-i+\frac{1}{2}}^{n+\frac{1}{2}} \right) \right) \end{aligned}$$
(26)

Current iterative equations can also be modified by the same voltage iterative equations with minor modifications. As seen in Fig. 3, at the half-integer points, the current nodes appear, implying that all the current is located at the interior points of the terminals. Therefore, the current near the terminals needs alteration. For iterative current equations near the terminals, it is necessary to decompose (8a) using the steps of iterative voltage of the equations. The final updated iterative current equations are given as

for k =1, near at the source

$$\begin{aligned} I_{1+\frac{1}{2}}^{n+\frac{3}{2}}=PI_{1+\frac{1}{2}}^{n+\frac{1}{2}}-\frac{\varDelta t}{\varDelta x}L^{-1}Q\left( \sum _{i=1}^{L_{s}}b(i)\left( V_{i+1}^{n+1} -V_{1}^{n+1} \right) \right) \end{aligned}$$
(27)

for k=2, 3, ....\(\ldots\), \(L_s\)

$$\begin{aligned}I_{k+\frac{1}{2}}^{n+\frac{3}{2}}&=PI_{k+\frac{1}{2}}^{n+\frac{1}{2}}-Q\left( \sum _{i=1}^{k}b(i) (2i-1)\right) ^{-1}\times \nonumber \\&\quad \frac{\varDelta t}{\varDelta x}L^{-1}\left( \sum _{i=1}^{k}b(i)\left( V_{k+i}^{n+1} -V_{k-i+1}^{n+1} \right) \right) \end{aligned}$$
(28)

for \(k=L_{s}+1, L_{s}+2, \cdots , Nx-L_{s}, Nx-L_{s}+1.\) at the interior point iterative equations

$$\begin{aligned}I_{k+\frac{1}{2}}^{n+\frac{3}{2}}&=PI_{k+\frac{1}{2}}^{n+\frac{1}{2}}-QL^{-1}\times \nonumber \\&\quad \frac{\varDelta t}{\varDelta x}\left( \sum _{i=1}^{L_{s}}b(i)\left( V_{i+k}^{n+1} -V_{k-i+1}^{n+1} \right) \right) \end{aligned}$$
(29)

for \(k=Nx-L_{s}+2, Nx-L_{s}+3, \cdots , Nx\) Near the load, iterative equations are

$$\begin{aligned}I_{k+\frac{1}{2}}^{n+\frac{3}{2}}&=PI_{k+\frac{1}{2}}^{n+\frac{1}{2}}-Q\frac{\varDelta t}{\varDelta x}L^{-1}\times \nonumber \\&\quad \left( \sum _{i=1}^{Nx-k+1} b(i)(2i-1)\right) ^{-1}\times \nonumber \\&\quad \left( \sum _{i=1}^{Nx-k+1}b(i)\left( V_{k+i}^{n+1} -V_{k-i+1}^{n+1}\right) \right) \end{aligned}$$
(30)

In the context of this bootstrapping method, modified voltage and current iterative equations are tested. Firstly, in terms of historical voltage and current values, voltage iterative equations are solved at a rigid time using Eqs. (20), (22), (24)–(26). Then, Eqs. (27)–(30) solve the iterative equations of current in terms of voltage measured initially and past values of current. The Courant stability condition [20, 27] is thus known as the stable output for MRTD iterative equations.

$$\begin{aligned} \varDelta t\le \frac{q\varDelta x}{\vartheta } \end{aligned}$$
(31)

which states that for each cell, the time of propagation must be higher than the time step, where q is the current number given by \(q=1/\sum _{i=1}^{L_{s}}\left| b(i) \right| =\vartheta \varDelta t/\varDelta x\) and \(\vartheta\), and v is the phase velocity of the line propagation. However, the boundary conditions will always satisfy the stability requirement, as these are explicitly derived from an implicit expression.

3 MRTD model validation and benchmark

The performance analyses of the structure of the two mutually coupled on-chip interconnect lines are presented in this section. The proposed model is validated in comparison to the conventional FDTD model and HSPICE simulations. The numerical computations are carried out using MATLAB. The interconnect load is driven by a CMOS driver; the interconnect dimensions are taken from the International Technology Roadmap for Semiconductors (ITRS) [29, 30]. At the 22-nm technology node, the interconnect is placed 99 nm from a ground plane. The thickness of the line is 66 nm. The width and space between the lines are equal, at 33 nm. The inter-level dielectric medium permittivity is 2.3. The length and load capacitance of the interconnects are 1 mm and 2 fF. The Vdd voltage is 0.8 V. The signal voltage swings from 0 to 0.8 V (low\(\rightarrow\)high) or 0.8 to 0 V (high\(\rightarrow\)low). The input source voltages have a transition time of 20 ps. The parasitic values of RLC for the coupled interconnect line structure are

$$\begin{aligned} R= & {} \begin{bmatrix} 10.10&{} 0\\ 0&{} 10.10 \end{bmatrix}_{2\times 2}\frac{M\varOmega }{ m} ,~ L=\begin{bmatrix} 2.082 &{} 1.86\\ 1.86 &{} 2.082 \end{bmatrix}_{2\times 2}\frac{uH}{m} \\ C= & {} \begin{bmatrix} 90.75&{} -75.16\\ -75.16&{} 90.75 \end{bmatrix}_{2\times 2}\frac{pF}{m} \end{aligned}$$
Fig. 4
figure 4

Transient response comparison at the far-end voltage on victim line for (a) functional, (b) in-phase, and (c) out-of-phase switching

Full size image

3.1 Transient and crosstalk analysis in two mutually coupled on-chip interconnects

This section covers the transient and crosstalk analysis of the -coupled on-chip interconnect system. Line 1 is the aggressor and line 2 is the victim line, as shown in Fig. 1. On the other side of the victim line, the crosstalk effects for functional, dynamic in-phase, and dynamic out-of-phase switching are found using the proposed model, the conventional FDTD model and HSPICE simulations [31]. The transient response is investigated on the victim line. The effect of functional crosstalk is explored by modifying line 1 (aggressor) input from 0.8 V to 0 V while holding line 2 (victim) in quiescent mode. When both aggressor and victim line stimuli turn at the same time, the impact of in-phase or out-of-phase is also explored. At the far end of the victim line, the transient graph results based on the above conditions are compared. The functional, dynamic in-phase, and dynamic out-of-phase transient responses on the victim line are shown in Fig. 4a–c, respectively. Figure 4b and c demonstrate that the victim line peak solution has higher dispersion errors in the conventional FDTD method. The proposed model is superior to the conventional FDTD model in terms of precision due to its significant superiority in numerical dispersion properties. Figure 4c illustrates how the Miller effect increases the capacity, which allows signal transitions to take longer during out-of-phase than in-phase switching. The results of the proposed MRTD model correctly matched with HSPICE in all input switching situations and outperform the conventional FDTD method.

Table 3 Victim line’s computational error for peak voltage timings in functional crosstalk
Full size table
Table 4 Victim line’s computational error for peak voltage values in functional crosstalk
Full size table
Table 5 Computational error for dynamic in-phase switching propagation delay for various transition times
Full size table
Table 6 Computational error for dynamic out-of-phase switching propagation delay for various transition times
Full size table
Fig. 5
figure 5

Peak voltage timing with varied input transition time for the victim line

Full size image
Fig. 6
figure 6

Peak voltage with varied input transition time for the victim line

Full size image
Fig. 7
figure 7

Dynamic in-phase 50% propagation delay with varied input transition time for the victim line

Full size image
Fig. 8
figure 8

Dynamic out-of-phase 50% propagation delay with varied input transition time for the victim line

Full size image

Table 3 shows the computational error associated with the estimation of functional crosstalk effects over the victim line for conventional FDTD and the proposed MRTD model in comparison to HSPICE. The efficiency of the proposed model at multiple input transition times shows an average error for crosstalk peak voltage timing of 0.42% versus 0.92% for the conventional FDTD method when compared with HSPICE. Table 4 also indicates that the proposed model correctly predicts the peak voltage, with an average error of 0.27% versus 1.05% using the conventional FDTD method when compared with HSPICE.

The computational error associated with estimating dynamic in-phase crosstalk effects over the victim line for the conventional FDTD and proposed MRTD models is shown in Table 5. The sturdiness of input transitions of the proposed model at different times has an average error of 0.53% versus 1.4% average error in the conventional FDTD method for propagation delay estimation when compared to HSPICE.

Table 6 shows the computational error associated with the estimation of dynamic out-of-phase crosstalk effects over the victim line for the conventional FDTD and proposed MRTD models. The sturdiness of input transitions at different times for the proposed model has an average error of 0.18% versus 0.38% average error in the conventional FDTD method for propagation delay estimation when compared with HSPICE. The simulation results for the proposed MRTD model match HSPICE correctly in all input switching situations and outperform the conventional FDTD model.

The graphs for peak voltage timing and peak voltage value on the victim line results in functional crosstalk generated by varying input transition time, which is shown in Figs. 5 and 6, respectively. Figures 7 and 8 illustrate the dynamic in-phase and out-of-phase crosstalk propagation delays at different input transition times. The results for both functional and dynamic crosstalk of the MRTD model are validated with HSPICE, and the proposed model outperforms the conventional FDTD model.

Fig. 9
figure 9

Peak voltage timing with varying load capacitance for the victim line

Full size image
Fig. 10
figure 10

Peak voltage with varying load capacitance for the victim line

Full size image
Fig. 11
figure 11

Computational time with different crosstalk switching

Full size image

Figures 9 and 10 demonstrate the peak voltage timing and peak voltage on the victim line for functional switching with varying values of load capacitance \(C_L\). For instance, using an interconnect length of 1 mm with 20 space segments and 3500 time segments, the elapsed CPU time for the proposed MRTD model, the conventional FDTD model, and the HSPICE is measured using a PC Intel® Xeon® CPU operating at 3.30 GHz. The elapsed CPU times are shown in Fig. 11. The figure demonstrates the elapsed CPU times for crosstalk analysis of the coupled on-chip interconnect lines in various functional, dynamic in-phase, and dynamic out-of-phase switching. In terms of simulation time, HSPICE has a higher CPU runtime than both the MRTD and conventional FDTD models. However, the MRTD is slightly slower than the conventional FDTD due to the higher number of iterations required for better accuracy. As a result, there exists a trade-off between simulation time and accuracy.

4 Conclusion

The modified alpha-power law model is used in this paper to build an analytically dependent MRTD model for functional and dynamic crosstalk study of two mutually coupled transmission lines driven by a CMOS driver. This work provides a detailed study of a two-line coupled on-chip interconnects for functional, dynamic in-phase, and dynamic out-of-phase switching which induced crosstalk effects on the victim line. The Courant condition is strictly followed by the proposed model’s stability. The influence of input transition time on crosstalk propagation delay under dynamic and peak voltage timing is investigated, as well as the peak voltage value for functional crosstalk. With regard to HSPICE, the proposed MRTD model and the FDTD confirm that the proposed MRTD model is in good agreement with HSPICE. According to the proposed model, the results show average errors of crosstalk-induced propagation delays in dynamic in-phase and out-of-phase on-chip interconnects of 0.53% and 0.18%, respectively, and functional crosstalk has peak voltage timing of 0.42% and a peak voltage value of 0.27%. Furthermore, the proposed MRTD model and FDTD model are validated with HSPICE for peak voltage timing and peak voltage value on the victim line for functional cases of various values of load capacitance, with average error of less than 1%. When compared to HSPICE, the elapsed CPU runtime for the MRTD model is significantly less. The analysis was performed on two mutually coupled interconnect lines but it can also be extended to M mutually coupled on-chip interconnect lines.