1 Introduction

Order abatement of the system both in the field of science and engineering plays a pivotal role in transforming high order systems (HOS) to reduced order model (ROM) while keeping the inherent properties of high order system which is under investigation The large-scale practical control systems analysis and design are very complicated and time-consuming hence order abatement of the system is very necessary (Zhe et al. 2011; Kumar and Parmar 2020; Narwal and Prasad 2015). A system can be called a large scale, in which dimensions are very large so that conventional methods of analysis, design, modelling, calculation are unable to yield better results. Eliminating these types of problems to low dimensional systems are necessary and these are equivalent to the large-scale systems (Prajapati and Prasad 2020).

The model order reduction (MOR) or order abatement methods are needed to obtain an appropriate ROM which can reflect the dominant properties of the original system which is under investigation. ROM is used to understand the original system in a better way, reduces the computational difficulties and also simplify the control design (Ganji et al. 2017). It is always useful to convert HOS to its equivalent low order state variable or transfer function (TF) models (Parmar et al. 2007a).

The researchers are getting more attention towards order abatement because of its simplicity and cost reduction capability (Alsmadi et al. 2011; Fridman 2006). Numerious order abatement methods have been floated in the literature but each and every method has its own merits and demerits while trying on a particular system (Singh et al. 2014; Desai and Prasad 2013a; Parmar et al. 2007b; Rana et al. 2016; Gupta and Manocha 2021; Sikander and Prasad 2017). On the other hand, there are many optimization techniques available in the literature but more emphasis is being given to the advancement of global optimization techniques and hence researchers are striving very hard to get a universal optimization technique that can be implemented to all multifaceted problems with the same efficiency (Desai and Prasad 2013a). Furthermore, various other hybrid techniques are available in the literature like stability equation method (SEM) and genetic algorithm (GA) (Parmar et al. 2007b). Pole clustering (PC) and factor division algorithm (FDA) (Rana et al. 2016). Pole clustering (PC) and genetic algorithm (GA) (Gupta and Manocha 2021). Cuckoo search (CS) and Eigen spectrum analysis (ESA) (Sikander and Prasad 2017). The reduced order model must be achieved by preserving the characteristics of the original model in a realistic manner. In reference (Reis and Stykel 2008) another technique was presented for order abatement which shows preservance of essential qualities of HOS in the reduced model provides a meaningful physical interpretation. Recently, few techniques for order abatement of LTI system have suggested based on pole clustering but still response matching error is very high as compared to other methods available in the literature (Prajapati and Prasad 2022a, b; Prajapati et al. 2020). The drawback of almost all methods is that none of the method exhibit zero error between the response of HOS and ROM. Therefore, motivated by optimization based order abatement approach, a newly developed Bonobo optimizer based order abatement of LTI systems is contributed in this study.

2 Problem formulation

Let the TF of the original HOS having the order 'n' is mentioned in Eq. 1.

$$G_{n} \left( s \right) = \frac{{a_{0} + a_{1} s + a_{2} s^{2} + \cdots \cdots + a_{n - 1} s^{n - 1} }}{{b_{0} + b_{1} s + b_{2} s^{2} + \cdots \cdots + b_{n} s^{n} }}$$
(1)

where ai (i = 0, 1, 2…, n-1) and bi (i = 0, 1, 2…, n) are known as scalar constants.

Let the TF of the ROM having the order ‘k’ is mentioned in Eq. 2.

$$R_{k} \left( s \right) = \frac{{c_{0} + c_{1} s + c_{2} s^{2} + \cdots \cdots + c_{k - 1} s^{k - 1} }}{{d_{0} + d_{1} s + d_{2} s^{2} + \cdots \cdots \cdots + d_{k} s^{k} }}$$
(2)

where ci (i = 0, 1, 2…, k -1) and di (i 0, 1, 2…, k) are unknown scalar constants.

The main aim is to get all the unknown parameters of the ROM mentioned in equation No. 2 using Bonobo Optimizer from the original HOS mentioned in equation No. 1 by minimizing the objective while retaining the important features of HOS.

3 Proposed BO algorithm

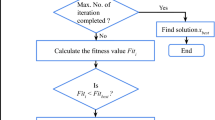
The proposed Bonobo Optimizer (BO) algorithm is a metaheuristic technique based on both the social behaviour and reproductive strategies of bonobos that have been artificially modelled for solving the optimization problem (Das and Pratihar 2019, 2021). The reproductive technique of Bonobos is based on the fission–fusion strategy. Fission–fusion behaviour defines the Bonobo community search for food and other necessary things (Waal 1995, Sultan et al. (2020)). The BO algorithm is a population-based technique having fixed population size as well as initial population takes place randomly. Each solution in the population is called a bonobo and the fitness values of all the bonobos are calculated. In the bonobo community, alpha bonobo (αbonobo) has the highest rank, it is selected as the best fitness getter among all the bonobos in the population and it is the current best solution. BO non-user defined parameters can be initialised with their respective starting values whereas random numbers are in the use of the BO algorithm are created between 0.0 and 1.0 range. The flowchart has been depicted in Fig. 1 which describes the process of the proposed BO technique. In the literature (Das and Pratihar 2019, 2021) more information is available about the BO algorithm. The following performance indices have been considered in this paper for analyzing the proposed BO for finding the ROM of the LTI systems.

$${\text{ISE}} = \int_{0}^{\infty } {\left[ {C\left( t \right) - C_{r} (t)} \right]}^{2} dt$$
(3)
$${\text{ITSE}} = \int_{0}^{\infty } {t\left[ {C\left( t \right) - C_{r} (t)} \right]^{2} dt}$$
(4)
$${\text{IAE}} = \int_{o}^{\infty } {\left| {C\left( t \right) - C_{r} \left( t \right)} \right|} \;dt$$
(5)
$${\text{ITAE}} = \int_{0}^{\infty } {t\left| {C\left( t \right) - C_{r} \left( t \right)} \right|} \;dt$$
(6)

where ISE, ITSE, IAE, ITAE are integral square error, integral time multiplied by square error, integral absolute error and integral time multiplied by absolute error respectively. C(t) and Cr(t) are the step responses of the original system which has been taken into consideration and the ROM found by the proposed BO algorithm respectively. The difference between C(t) and Cr(t) is the error for evaluating the performance indices as well as determining the efficacy of the proposed methodology on BO.

Fig. 1
figure 1

Flow chart of proposed BO algorithm

Full size image

4 Results and discussion

Five examples of the different systems have been considered to illustrate the competency of the proposed algorithm BO algorithm for solving the optimization problem. The result has been presented in tabular form of each example.

Example-1: Consider a system having fourth-order (Sikander and Thakur 2018; Desai and Prasad 2013b; Tiwari and Kaur 2020) is mentioned in Eq. 7.

$$G_{4} \left( S \right) = \frac{{s^{3 } + 7s^{2 } + 24s + 24}}{{s^{4 } + 10s^{3 } + 35s^{2 } + 50s + 24}}$$
(7)

The ROM is found from the proposed BO algorithm is mentioned in Eq. 8.

$$R_{2} \left( S \right) = \frac{0.7645s + 1.6889}{{s^{2 } + 2.5909s + 1.6889}}$$
(8)

The ROM using the MCS technique (Sikander and Thakur 2018) is

$$R_{2} \left( S \right) = \frac{0.77s + 1.649}{{s^{2} + 2.548s + 1.649}}$$
(9)

The ROM using RA and BB-BC technique (Desai and Prasad 2013b) is

$$R_{2} \left( S \right) = \frac{0.8058s + 0.7944}{{s^{2} + 1.65s + 0.7944}}$$
(10)

The ROM using C and DPR technique (Tiwari and Kaur 2020) is

$$R_{2} \left( S \right) = \frac{0.7523s + 2.384}{{s^{2} + 3.384s + 2.384}}$$
(11)

In Example-1 a comparison of the fourth-order system (HOS) and proposed ROM with three other existing techniques of recent literature (Sikander and Thakur 2018; Desai and Prasad 2013b; Tiwari and Kaur 2020) have been made. It can be seen that the reduced system found by the proposed BO offers a better close approximation to the system which has been taken into consideration in example-1. Step response and Bode plot of respective HOS and proposed ROM with other three different existing techniques of Example-1 have been depicted in Figs. 2 and 3. The convergence of the objective function is depicted in Fig. 4. After 100 iterations of the BO algorithm the ISE = 7.4367 \(\times {10}^{-5}\) which is less than all three existing techniques mentioned in the Table 1. Performance indices: ISE, ITSE, IAE and IATE, have been calculated and compared for HOS as well as proposed ROM with other existing techniques mentioned in Table 1. The proposed BO algorithm offers the better value of ISE, ITSE, IAE and IATE than all other techniques mentioned in the recent literature (Sikander and Thakur 2018; Desai and Prasad 2013b; Tiwari and Kaur 2020) this exhibits the efficacy of the BO algorithm and hence the proposed BO algorithm provides a better result.

Fig. 2
figure 2

Comparison of step response for Example-1

Full size image
Fig. 3
figure 3

Comparison of bode plot for Example-1

Full size image
Fig. 4
figure 4

Iteration graph for Example-1

Full size image
Table 1 Performance analysis of HOS and LOS for Example-1
Full size table

Example-2 Consider a system having eighth order (Singh et al. 2014; Sikander and Thakur 2018; Bhatt et al. 2019) mentioned in Eq. 12.

$$G_{8} \left( S \right) = \frac{{18s^{7} + 514s^{6} + 5982s^{5} + 36380s^{4 } + 122664s^{3 } + 222088s^{2 } + 185760s + 40320}}{{s^{8 } + 36s^{7 } + 546s^{6 } + 4536s^{5 } + 22449s^{4 } + 67284s^{3 } + 118124s^{2} + 109584s + 40320}}$$
(12)

The ROM is found from the proposed BO algorithm is mentioned in Eq. 13.

$$R_{2} \left( S \right) = \frac{16.9181s + 5.2600}{{s^{2} + 6.8701s + 5.2600}}$$
(13)

The ROM using the MCS technique (Sikander and Thakur 2018) is

$$R_{2} \left( S \right) = \frac{16.39s + 4.865}{{s^{2} + 6.627s + 4.865}}$$
(14)

The ROM using the EP and IPA technique (Singh et al. 2014) is

$$R_{2} \left( S \right) = \frac{14.0097s + 4.5}{{s^{2 } + 5.5s + 4.5}}$$
(15)

The ROM using the SFS technique (Bhatt et al. 2019) is

$$R_{2} \left( S \right) = \frac{16.14315s + 5.03619}{{0.95698s^{2} + 6.55351s + 5.03619}}$$
(16)

In Example-2 a comparison of the eighth order system (HOS) and proposed ROM with three other existing techniques of recent literature (Singh et al. 2014; Sikander and Thakur 2018; Bhatt et al. 2019) have been made. The step response and Bode Plot of high order and reduced systems with three different techniques of example-2 have been depicted in Figs. 5 and 6 respectively. After 100 iterations of the BO algorithm the value of ISE = 0.00069182 which is less than all three existing techniques mentioned in the Table 2. Performance indices ISE, ITSE, IAE, IATE has been calculated and compared for HOS and proposed ROM with other existing techniques mentioned in Table 2.

Fig. 5
figure 5

Comparison of STEP response for Example-2

Full size image
Fig. 6
figure 6

Comparison of Bode plot for Example-2

Full size image
Table 2 Performance analysis of HOS and LOS for Example-2
Full size table

Example-3. A sixth-order system is given by Singh et al. (2014); Tiwari and Kaur 2020; Bhatt et al. 2019) is mentioned in equation No.17.

$$G_{6} \left( s \right) = \frac{{2s^{5} + 3s^{4} + 16s^{3 } + 20s^{2 } + 8s + 1}}{{2s^{6} + 33.6s^{5 } + 155.9s^{4 } + 209.5s^{3 } + 102.4s^{2} + 18.3s + 1}}$$
(17)

The ROM is found from the proposed BO algorithm is mentioned in equation No. 18.

$$R_{2} \left( S \right) = \frac{0.0517s + 0.4789}{{0.0517s^{2 } + 4.9996s + 0.4789}}$$
(18)

The ROM using the C and DPR technique (Tiwari and Kaur 2020) is.

$$R_{2} \left( S \right) = \frac{ - 0.48088s + 0.6396}{{s^{2 } + 6.107s + 0.6396}}$$
(19)

The ROM using EP & IPA technique (Singh et al. 2014) is

$$R_{2} \left( S \right) = \frac{0.0496s + 0.168}{{s^{2} + 1.78s + 0.168}}$$
(20)

The ROM using the SFS technique (Bhatt et al. 2019) is

$$R_{2} \left( S \right) = \frac{0.4753s + 0.4110}{{4.4617s^{2 } + 4.7307s + 0.4110}}$$
(21)

In Example-3 a comparison of a sixth-order system (HOS) and proposed ROM with three other exiting techniques of recent literature (Singh et al. 2014; Tiwari and Kaur 2020; Bhatt et al. 2019) have been made. It can be noticed that the reduced system found by the proposed BO offers an excellent close approximation to the system which has been considered in Example-3. The step response and bode plot of HOS and proposed ROM with three different techniques of example-3 have been depicted in Fig. 7 and Fig. 8 respectively. After 100 iterations of the BO algorithm, the value of is ISE = 0.00048407 and the convergence of the objective function is shown in Fig. 9. Performance indices: -ISE, ITSE, IAE and IATE have been calculated and compared for HOS as well as proposed ROM with other existing techniques in recent literature (Singh et al. 2014; Sikander and Thakur 2018; Bhatt et al. 2019) of Example-3 and it is also found that the proposed BO algorithm is providing better results than other existing techniques in the literature mentioned in Table-3. The proposed BO algorithm provides a low value of ISE, ITSE, IAE and IATE than all three techniques of recent literature (Singh et al. 2014; Tiwari and Kaur 2020; Bhatt et al. 2019) in Example-3.

Fig. 7
figure 7

Comparison of step response for Example-3

Full size image
Fig. 8
figure 8

Comparison of Bode plot for Example-3

Full size image
Fig. 9
figure 9

Iteration graph for Example-3

Full size image

Example-4. A ninth-order system with complex roots is given by Desai and Prasad 2013a; Desai and Prasad 2013b; Tiwari and Kaur 2020) is mentioned in Eq. 22.

$$G_{9} \left( s \right) = \frac{{s^{4 } + 35s^{3 } + 291s^{2 } + 1093s + 1700}}{{s^{9} + 9s^{8 } + 66s^{7} + 294s^{6} + 1029s^{5 } + 2541s^{4} + 4684s^{3 } + 5856s^{2} + 4620s + 1700}}$$
(22)

The ROM is found from the proposed BO algorithm is mentioned in Eq. 23.

$$R_{3} \left( S \right) = \frac{1.0614}{{s^{3 } + 1.6465s^{2 } + 2.1733s + 1.0614}}$$
(23)

The ROM using the MCS technique (Sikander and Thakur 2018) is

$$R_{3} \left( S \right) = \frac{{0.001935s^{2 } + 0.005725s + 1.073}}{{s^{3} + 1.681s^{2 } + 2.183s + 1.073}}$$
(24)

The ROM using SE and BBBC technique (Desai and Prasad 2013a) is

$$R_{3} \left( S \right) = \frac{{0.0789s^{2} + 0.3142s + 0.493}}{{s^{3} + 1.3s^{2 } + 1.34s + 0.493}}$$
(25)

The ROM using C and DPR technique (Tiwari and Kaur 2020) is

$$R_{3} \left( S \right) = \frac{{ - 0.2388s^{2} - 0.4458s + 2.192}}{{s^{3} + 3s^{2 } + 4.192s + 2.192}}$$
(26)

In Example-4 a comparison of the ninth order system (HOS) and proposed ROM with three other existing techniques of recent literature (Desai and Prasad 2013a; Sikander and Thakur 2018; Tiwari and Kaur 2020) have been made. It can be seen that the reduced system found by the proposed BO offers a very good close approximation to the system under investigation in Example-4. The step response and bode plot of respective HOS and proposed ROM with three different existing techniques of Example-4 have been depicted in Figs. 10 and 11. The convergence of the objective function is shown in Fig. 12. After 100 iterations of the BO algorithm the value of ISE = 0.0162 which is less than all three existing techniques mentioned in Table 3. Performance indices: -ISE, ITSE, IAE and IATE have been calculated and compared for HOS and proposed ROM with other existing techniques in recent literature (Desai and Prasad 2013a; Sikander and Thakur 2018; Tiwari and Kaur 2020) of example-4 mentioned in Table 4.

Fig. 10
figure 10

Comparison of step response for Example-4

Full size image
Fig. 11
figure 11

Comparison of Bode plot for Example-4

Full size image
Fig. 12
figure 12

Iteration graph for Example-4

Full size image
Table 3 Performance analysis of HOS and LOS for Example-3
Full size table
Table 4 Performance analysis of HOS and LOS for Example-4
Full size table

Example-5. Consider a TF of a fourth-order system having repeated poles is given in Sikander and Thakur (2018) is mentioned in Eq. 27.

$$G_{4} \left( s \right) = \frac{1}{{\left( {s + 1} \right)^{4} }}$$
(27)

The ROM (Third-order) and ROM (Second-order) are found from the proposed BO algorithm are mentioned in equation No. 28 and equation No. 29 respectively.

$$R_{3} \left( S \right) = \frac{0.2496}{{s^{3 } + 1.4365s^{2} + 0.9987s + 0.2496}}$$
(28)
$$R_{2} \left( S \right) = \frac{0.1674}{{s^{2 } + 0.6336s + 0.1674}}$$
(29)

he reduced third and second-order systems using the MCS technique (Sikander and Thakur 2018) are mentioned in Eqs. 30 and 31 respectively.

$$R_{3} \left( S \right) = \frac{{0.0001064s^{2} + 0.2325}}{{s^{3} + 1.238s^{2 } + 0.9371s + 0.2325}}$$
(30)
$$R_{2} \left( S \right) = \frac{0.1s + 0.1158}{{s^{3} + 0.5202s + 0.1158}}$$
(31)

In Example-5 a comparison of the fourth-order system (HOS) and proposed reduced-order models (Third-order and second-order) with reduced-order models (Third-order and second-order) of an existing technique of recent literature (Sikander and Thakur 2018) have been made. After 100 iterations of the BO algorithm the value of ISE = 0.00046737 for the third-order system and 0.0149 for the second-order system which is less than the existing technique mentioned in Table 5. The proposed third-order model offers a better close approximation than the proposed second-order model. The step response and Bode plot of HOS and proposed reduced-order models (third order and second-order) with a recent existing technique (Third-order and second-order) of example-5 have been depicted in Figs. 13 and 14 respectively. The convergence of the objective function is depicted in Fig. 15. Performance indices: -ISE, ITSE, IAE and IATE have been calculated and compared for HOS and proposed reduced-order models with an existing technique in recent literature (Sikander and Thakur 2018) mentioned in Table 5. The proposed BO algorithm provides a low value of ISE, ITSE, IAE and IATE than the existing techniques of recent literature (Sikander and Thakur 2018).

Table 5 Performance analysis of HOS and LOS of Example-5
Full size table
Fig. 13
figure 13

Comparison of step response for Example-5

Full size image
Fig. 14
figure 14

Comparison of Bode plot for Example-5

Full size image
Fig. 15
figure 15

Iteration graph for Example-5

Full size image

5 Conclusion

This study contributes a novel strategy for order abatement/reduction of large scale LTI systems based on parameter estimation. The BO algorithm has been utilised to obtain unknown parameters of the abated/reduced system by minimizing the ISE between the large scale and reduced order systesm. Five different test systems have been taken into consideration to illustrate the efficacy of the proposed BO algorithm. The obtained results have been compared with the recent existing methods such as MCS, RA and BB-BC, SFS, EP and IPA, C and DPR, SE and BB-BC algorithms. It can be observed that the reduced system achieved by the BO algorithm offers a better close approximation to the large scale system in all five examples. The time response speficiations such as settling time, peak overshoot and various performance indices have been calculated and compared with the proposed model and recent existing reduced-order models. The BO algorithm provides a lower ISE value in all five examples as compared to other existing techniques.