1 Introduction

Most of the actual system designs are complicated from a research perspective, which increases the computational requirements for analysis. It is preferable to reduce the complex model with their equivalent approximate model that lowers the cost, uses less computing power, and simplifies the analysis, which maintains the significant characteristics of the original system, like time response parameters, stability margin, and so forth.

All the developed order reduction techniques have been categorized in three ways: conventional order reduction techniques, optimization-based model order reduction, and a combination of the above two. In a single conventional or optimization technique, the numerator and denominator of the reduced model are obtained by any conventional technique. In a mixed-order reduction method, the numerator and denominator coefficients are obtained by two different methods, and then, a stable reduced-order model is obtained. Commonly used conventional methods of order reduction in the frequency domain are Pade approximation [1], Routh approximation [2], Routh stability [3], stability equation [4], Mihailov stability criterion [5], differentiation method [6], pole clustering method [7], continued fraction [8], dominate pole [9], moment matching [10]. Ghosh [11] developed a balanced truncation method for model order reduction. Desai and Prasad [12] has developed a new reduced-order method for LTI structures based on Routh approximation (RA). Sikander et al. [13] suggested a basic model order reduction technique based on improved Hermite normal form. Prajapati and Prasad [14] devised an order reduction methodology for a linear dynamic system using a generalized version of the pole clustering method. The conventional pole clustering method is a generalized form of this approach. The researchers suggest four common approaches for simplifying higher-order systems in the time domain: Hankel norm approximation [15], Singular perturbation [16], balanced truncation method, and Krylov subspaces. In [17], various time domain order reductions for the large-scale dynamical system are thoroughly examined.

The optimization approach is not recent in the new era of machine engineering. Different researchers working in the field of model order reduction have taken different cost functions, such as minimizing the integral square of impulse response error [18], minimizing integral error, minimizing weighted time integral error [19], or minimizing \(L_1\) and \(L_2\) norm [20] for finding the reduced model using optimization techniques. Recently, Ahamad et al. [21] proposed an order reduction technique based on ant lion optimization. Sikander and Thakur [22] proposed a modified cuckoo search algorithm (MCS) to find the reduced model of the complex system. Nature-inspired optimization methods have been commonly employed to create the reduced-order model of complex systems. Goldberg et al. [23] proposed a genetic algorithm (GA), which is the most common algorithm inspired by the concept of biology, and Kennedy et al. [24] proposed particle swarm optimization (PSO).

In addition, researchers in the different literature have proposed various mixed approaches for reduced-order modeling. Erol and Eksin [25] proposed a mixed approach based on Routh Approximation and Big Bang-Big Crunch (BB-BC) optimization for model order reduction. In this reduction approach, the coefficients of denominator polynomials are calculated using Routh Approximation to maintain stability, and the numerator polynomial is evaluated with the BB-BC algorithm. In these mixed processes, the idea is to retain the reduced system’s stability. The stability-preserving model order reduction method always leads to a stable reduced model polynomial [26,27,28]. Sikander and Prasad [27] suggested a combination of stability equation and optimization approach to find the reduced model. The stability equation approach was used to derive the denominator coefficients, and then, PSO was used to calculate the numerator polynomial of the simplified model. Prajapati and Prasad [29] developed a mixed method that combines two conventional techniques to obtain the reduced-order models. Jain and Hote [30] proposed a mixed method of order reduction based on the Big Bang Big Crunch Algorithm and Pade Approximation. Other literature that discussed the model order reduction concepts could be found in [27, 31,32,33].

Each time and frequency domain method have unique benefits and drawbacks and can be applied in a particular circumstance. The mismatch of DC gain and time/frequency responses are the main concerns in the reduced model. This technique fails to maintain the stability of numerous types of complex original models into their corresponding reduced models. Additionally, they take more time and cost more to compute. As a result, since they lessen hardware complexity, machine cost, and compilation time, innovative techniques for lower-order modeling are much sought after nowadays. This encourages the researchers to investigate new, more potent, all-encompassing, and computationally quicker system approximation strategies. So, motivated by various optimization techniques and reduction problems in system engineering, a new search algorithm based on molecular dynamics is proposed for order abatement of continuous-time SISO systems [34]. The proposed method tides over all the drawbacks of the previously mentioned techniques, namely the instability issue for large-scale systems with orders equal to and greater than four, because it ensures the stability of the reduced order model. The suggested technique is simple and builds a stable lower-order system. The competency of the proposed algorithm is shown by finding a reduced model for standard systems, including a system of order 10, and the results thus obtained are better than the other techniques existing in the literature. Also, the performance of the proposed approximated system is analyzed not only in the time domain but also in the frequency domain. Therefore, this article contributes a more effective, computationally less expensive, and general technique of system approximation.

2 Problem description

Let us define a system transfer function for the \(n^{th}\) order as given in Eq. (1):

$$\begin{aligned} G_{n}(s): u \rightarrow y_{n} \end{aligned}$$
(1)

Transfer function \(G_r(s)\) given in Eq. (2) of order r is to be obtained using the order reduction techniques

$$\begin{aligned} G_{r}(s): u \rightarrow y_{r} \quad \text{ with } r<n \end{aligned}$$
(2)

For the two systems mentioned above, input and output characteristics must be the same. If input u(t) given to both the system is the same, then output \(y_{n}(t) \approx y_{r}(t)\). SISO LTI systems are considered in this work for the explanation.

Continuous-time SISO LTI system of the higher-order is also modeled as Eq. (3):

$$\begin{aligned} G_{n}(s)=\frac{N_{n-1}(s)}{D_{n}(s)}=\frac{\sum _{i=0}^{n-1} p_{i} s^{i}}{\sum _{i=0}^{n} q_{i} s^{i}} \end{aligned}$$
(3)

where \(p_{i}\) and \(q_{i}\) are the coefficients of numerator and denominator polynomials of the original complex system, respectively. The steady-state value is unity for \(p_{0}=q_{0}\). The goal of model order reduction is to produce the lower-order system of order ’r’ \((r<n)\) that retains all of the original large-scale system’s significant properties. In the transfer function form, the reduced-order model can be represented as Eq. (4):

$$\begin{aligned} G_{r}(s)=\frac{N_{r-1}(s)}{D_{r}(s)}=\frac{\sum _{i=0}^{r-1} c_{i} s^{i}}{\sum _{i=0}^{r} d_{i} s^{i}} \end{aligned}$$
(4)

where \(c_{i}\) and \(d_{i}\) are the coefficients of the lower-order model’s numerator and denominator, respectively.

By minimizing the ISE value as an objective function given in Eq. (5), optimization helps in determining the reduced-order model \(G_r(s)\) from the \( n^{th} \) order complex plant \(G_n(s)\):

$$\begin{aligned} \text {ISE}=\int _{0}^{t}\left[ y_{n}(t)-y_{r}(t)\right] ^{2} \textrm{dt} \end{aligned}$$
(5)

Other performance indices such as integral time multiplied by squared error (ITSE), integral of absolute error (IAE), and integral of time multiplied by absolute error (ITAE) given in Eqs. (6)–(8) are also computed to compare the closeness of the obtained reduced-order model.

$$\begin{aligned} ITSE= & {} \int _{0}^{t} t\left[ y_{n}(t)-y_{r}(t)\right] ^{2} \textrm{dt} \end{aligned}$$
(6)
$$\begin{aligned} IAE= & {} \int _{0}^{t} \mid y_{n}(t) - y_{r}(t) \mid \textrm{dt} \end{aligned}$$
(7)
$$\begin{aligned} ITAE= & {} \int _{0}^{t} t\mid y_{n}(t)-y_{r}(t) \mid \textrm{dt} \end{aligned}$$
(8)

where \(y_{n}(t)\) and \(y_{r}(t)\) are the step response of original and reduced-order model and t is the simulation time.

3 Proposed methodology based on Atom search optimization

Atom search optimization (ASO) [34] is a revolutionary optimization algorithm inspired by molecular dynamics. Each atom’s position is considered a mass-based solution. The atom’s mass is heavier if the solution found in the search space is better and vice versa. According to molecular dynamics, every atom in the search space attracts or repels each other due to this; the lower mass atoms migrate towards the heavier mass atoms. Because atoms with more mass have a lower acceleration, they are more aggressive in seeking better solutions in local search space. Also, atoms with low mass accelerate more quickly, exploring a larger area to find new approximate positions in the search space.

Mathematically, unconstrained optimization problems can be stated as Eq. (9):

$$\begin{aligned}{} & {} Minimize \, f(\varvec{x}), \quad \varvec{x}=\left( x^{1}, \ldots , x^{D}\right) \end{aligned}$$
(9)
$$\begin{aligned}{} & {} Lb \le x \le Ub,\quad Lb=\left[ lb^{1}, \ldots , lb^{D}\right] ,\nonumber \\{} & {} \qquad Ub=\left[ ub^{1}, \ldots , ub^{D}\right] \end{aligned}$$
(10)

where \(x^{d}(d=1, \ldots , D)\) represents \(d_{th}\), element of the search space, \(lb^{D}\) and \(ub^{D}\) represent \(d_{th}\) elements of the lower and upper bounds, respectively, and D indicates the dimension of variables.

To solve the problem discussed in Eq. (9), the population of an atom is assumed as N. The location of \(i_{th}\) atom is given by \(x_i\)

$$\begin{aligned} x_{i}=\left[ x_{i}^{1}, \ldots , x_{i}^{D}\right] , \quad i=1, \ldots , N \end{aligned}$$
(11)

where \(d_{th}\) position component of the \(i_{th}\) atom in a D multidimensional space is \(x_{i}^{d}(d=1, \ldots , D)\). Every atom interacts with another atom in the early phases of ASO through attraction or repulsion. The repulsion can reduce the atom’s over-concentration and premature algorithm convergence, allowing for a more thorough exploration of the solution space. The repulsion reduces as iterations pass, while the attraction grows, indicating that exploration decreases and exploitation increases. Each atom connects with others simply by attraction in the final rounds, ensuring that the algorithm has a strong exploitation potential.

The following steps are to be followed to find the optimal value of numerator and denominator coefficients of the reduced system

  1. Step 1:

    A set of atoms X and their velocity v are created and initialized

  2. Step 2:

    Calculate the interaction force \(F_{i}\) and the constraint force \(G_{i}\) using Eqs. (12) and (13).

    $$\begin{aligned}{} & {} F_{i}^{d}(t)=\sum _{j \in K_{best}} {\text {rand}}_{j} F_{ij}^{d}(t) \end{aligned}$$
    (12)
    $$\begin{aligned}{} & {} G_{i}^{d}(t)=-\lambda (t) \nabla \theta _{i}^{d}(t)\nonumber \\{} & {} \quad \qquad =-2 \lambda (t)\left( x_{i}^{d}(t)-x_{\text{ best } }^{d}(t)\right) \end{aligned}$$
    (13)

    where \(F_{ij}^{d}(t)\) is the interaction force acting on the \(i_{th}\) atom from \(j_{th}\) atom in the \(d_{th}\) dimension at \(t_{th}\) iteration and where \({rand}_j\) is a random number in the range of [0,1], \(\lambda (t)\) is the Lagrangian multiplier, and \(\theta _i\) is the constraint of the \(i_{th}\) atom.

  3. Step 3:

    Calculate the acceleration using Eq. (14)

    $$\begin{aligned} \begin{aligned} a_{i}^{d}(t)=&\frac{F_{i}^{d}(t)}{m_{i}^{d}(t)}+\frac{G_{i}^{d}(t)}{m_{i}^{d}(t)} \\ =&-\alpha \left( 1-\frac{t-1}{T}\right) ^{3} e^{-\frac{20 t}{T}} \\&\sum _{j \in K b e s t} \frac{{\text {rand}}_{j}\left[ 2 \times \left( h_{ij}(t)\right) ^{13}-\left( h_{ij}(t)\right) ^{7}\right] }{m_{i}(t)} \\&\frac{\left( x_{j}^{d}(t)-x_{i}^{d}(t)\right) }{\left\| x_{i}(t), \varvec{x}_{j}(t)\right\| _{2}} + \beta e^{-\frac{20 t}{T}} \frac{x_{best}^{d}(t)-x_{i}^{d}(t)}{m_{i}(t)} \end{aligned} \end{aligned}$$
    (14)

    where \(m_i(t)\) is the mass of the \(i_{th}\) atom at the \(t_{th}\) iteration, \(m_i^d(t)\) is the mass of the \(i_{th}\) atom in the \(d_{th}\) dimension at the \(t_{th}\) iteration and \(h_{ij}(t)\) is the limit of attraction and repulsion between \(i_{th}\) and \(j_{th}\) atom.

  4. Step 4:

    Calculate the mass using equations Eq. (15)

    $$\begin{aligned} \begin{aligned} M_{i}(t)=&e^{-\frac{{Fit}_{i}(t) - {Fit}_{best}(t)}{{Fit}_{worst}(t) - {Fit}_{best}(t)}}\\ m_i(t)=&\frac{M_i(t)}{\sum _{j=1}^N M_j(t)} \end{aligned} \end{aligned}$$
    (15)

    where \(M_{i}(t)\) is the mass of the \(i_{th}\) atom, \(Fit_{best}(t)\), \(Fit_{worst}(t)\) are the fitness values of best and worst atom at the \(t_{th}\) iteration and \(Fit_{i}(t)\) is the functional fitness value of the \(i_{th}\) atom at the \(t_{th}\) iteration. \(Fit_{best}(t)\), \(Fit_{worst}(t)\) are expressed as:

    $$\begin{aligned} \begin{aligned}&{Fit}_{best}(\textrm{t})=\min _{i \in \{1,2, \ldots , N\}} {Fit}_i(t) \\&{Fit}_{worst}(\textrm{t})=\max _{i \in \{1,2, \ldots , N\}}{Fit}_i(t) \end{aligned} \end{aligned}$$
    (16)
  5. Step 5:

    Using Eq. (17), the velocity and position of the atoms are continuously updated

    $$\begin{aligned} \begin{aligned}&v_{i}^{d}(t+1)={\text {rand}}_{i}^{d} v_{i}^{d}(t)+a_{i}^{d}(t) \\&x_{i}^{d}(t+1)=x_{i}^{d}(t)+v_{i}^{d}(t+1) \end{aligned} \end{aligned}$$
    (17)

ISE is considered the objective function to select the optimal values of the numerator and denominator coefficients. The standard form of a reduced-order model of second order is studied in this work and expressed in Eq. (18). This strategy, however, can be used to produce a reduced model of any order system.

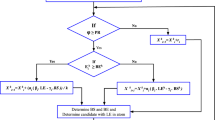
$$\begin{aligned} R_{2}(s)=\frac{c_{0}+c_{1} s}{d_{0}+d_{1} s+d_{2} s^{2}} \end{aligned}$$
(18)

where \(c_{0}, c_{1}\) and \(d_{0}, d_{1}\), \(d_{2}\) are undetermined numerator and denominator variables, respectively. Using the flowchart of ASO given in Fig. 1 and the parameters of atom search optimization given in Table 1, the coefficients of the reduced-order model given in Eq. (18) are obtained.

Parameters for the calculation of ROM using the proposed algorithm are given in Table 1.

Fig. 1
figure 1

Flowchart of ASO

Full size image
Table 1 Parameters of ASO algorithm
Full size table
Fig. 2
figure 2

Response plots for Example 1

Full size image
Table 2 Comparative analysis of the original and reduced system for Example 1
Full size table

3.1 Advantages of Atom search optimization

  • In ASO, the attractive force is easy to cause the atoms to gather in the early stage, which will cause faster convergence.

  • The inertial weight is a nonlinear function that decreases from 1 to 0, and this trend fits the process of atomic optimization and better balance exploration and exploitation.

  • The neighborhood learning effectively helps the exchange of population information, and the increase in population diversity leads to faster convergence.

4 Simulation results

This section presents step response and frequency response (bode plot) analysis for different test systems. MATLAB R2021a has been used for simulation purposes. A total of eight different examples of different orders taken from the recently published article are considered for obtaining the reduced-order model. To approve the suggested scheme’s precision, adequacy, and prevalence with some other standard MOR algorithms, ISE, ITSE, IAE, and ITAE are determined and characterized as Eqs. (6)–(8). The suggested algorithm is applied to simplify a standard real-time system for illustrating the accuracy and verifying the conservation of essential characteristics of the higher-order system in the reduced model.

Example 1

A fourth-order stable system given below is considered from [22].

$$\begin{aligned} G_{4}(s)=\frac{s^{3}+7 s^{2}+24 s+24}{s^{4}+10 s^{3}+35 s^{2}+50s+24} \end{aligned}$$

The original system has poles: \(-1, -2, -3, and -4\). The second-order reduced model achieved by the recommended algorithm is given as:

$$\begin{aligned} R_{2}(s)=\frac{4.1267s + 9.9602}{5.4616s^2 + 14.9110s + 9.9602} \end{aligned}$$

The reduced-order model obtained by MCS [22] is

$$\begin{aligned} R_{2}(s)=\frac{0.77 s+1.649}{s^{2}+2.548 s+1.649} \end{aligned}$$

The reduced-order model obtained using RA and BB-BC [12] is

Fig. 3
figure 3

Response plots for Example 2

Full size image
Table 3 Performance comparison for Example 2
Full size table
$$\begin{aligned} R_{2}(s)=\frac{0.8058 s+0.7944}{s^{2}+1.65 s+0.7944} \end{aligned}$$

The reduced-order model obtained by GA [35] is

$$\begin{aligned} R_{2}(s)=\frac{0.4 s+1}{0.5 s^{2}+1.5 s+1} \end{aligned}$$

The step response of the original and reduced-order models obtained using the suggested method is compared with other previously published research and shown in Fig. 2a. The bode plot of the original system and the reduced-order model generated by the suggested approach are presented in Fig. 2b. The suggested technique’s step response and bode plot of the reduced system are also compared with [12, 22, 35]. These responses direct that the behavior of the reduced model accomplished by the suggested algorithm is wholly matching with the behavior of the original higher-order system. The convergence graph of Example 1 is shown in Fig. 2c. Table 2 presents a quantitative evaluation of time response parameters and different error indices. Using the suggested method, the ISE value obtained is \(7.596 \times 10^{-5}\), which is smaller than the recently developed reduced-order system using the MCS algorithm [22]. Several time response parameters, such as settling time, peak value, and performance indices, such as ITAE, IAE, and ITSE, are also determined to illustrate the efficacy of the proposed method. By using this reduction process, the design of the controller for the original higher-order system can be done quickly with less effort and less mathematical computation.

Example 2

In this example, an eighth-order system given below is taken from [22] for obtaining the second-order reduced-order model.

$$\begin{aligned} G_{8}(s)=\frac{18 s^{7}+514 s^{6}+5982 s^{5}+36380 s^{4}+ 122664 s^{3}+222088 s^{2}+185760 s+40320}{{s^{8}+36 s^{7}+546 s^{6}+4536 s^{5}+22449 s^{4}+ 67284 s^{3}+118124 s^{2}+109584 s+40320}} \end{aligned}$$

Poles of the original system are -1, -2, -3, -4, -5, -6, -7, and -8. By applying the proposed method, a reduced-order model is obtained as:

$$\begin{aligned} R_{2}(s)=\frac{16.7526s + 5.2150}{s^{2} + 6.7997s + 5.2150} \end{aligned}$$

The reduced-order model obtained by MCS [22] is

$$\begin{aligned} R_{2}(s)=\frac{17.6109 s + 5.4316}{s^{2}+ 7.1752 s + 5.4316} \end{aligned}$$

The reduced-order model obtained by genetic algorithm (GA) [35] is

$$\begin{aligned} R_{2}(s)=\frac{16.9686 s+15.2295}{s^{2}+6.8996 s+15.2295} \end{aligned}$$

The reduced-order model obtained using RA and BB-BC [12] is

$$\begin{aligned} R_{2}(s)=\frac{24.11429 s+8}{s^{2}+9 s+8} \end{aligned}$$
Fig. 4
figure 4

Response plots for Example 3

Full size image
Table 4 Performance comparison for Example 3
Full size table

The contrast of behavior of the higher-order system and the ROMs attained from the endorsed process and other available algorithms in step responses are displayed in Fig. 3a. The displayed graph clearly shows that the reduced and original higher-order models’ responses match perfectly. The Bode plot of the original system and the reduced-order model generated by the recommended approach are presented in Fig. 3b. The suggested technique’s step response and bode plot of the reduced system are also compared with [12, 22, 35, 37]. The convergence graph of Example 2 is shown in Fig. 3c. Table 3 presents a numerical data comparison of time response parameters and different error indices. Using the suggested method, the ISE value calculated is \(7.10 \times 10^{-4}\), which is smaller than the recently developed reduced-order system using the MCS algorithm [22]. This evaluation is completed using various performance indices such as ISE, ITSE, IAE, and ITAE. It can be summarized that the suggested diminution algorithm gives the smallest values of the performance indices compared to the traditional procedures and the latest methods available in the literature.

Example 3

An approximate model of the thermal diffusion system is considered in this example, which is of 10th order and represented as follows:

$$\begin{aligned} G_{10}(s)=\frac{540.70748 \times 10^{17}}{\prod _{i=1}^{10}\left( s+\lambda _{i}\right) } \end{aligned}$$

where \(\lambda _{1}=2.04, \quad \quad \lambda _{2}=18.3, \quad \quad \lambda _{3}=50.13, \quad \lambda _{4}=95.15\), \(\lambda _{5}=148.85, \quad \lambda _{6}=205.16, \quad \lambda _{7}=252.21\) \(\lambda _{8}=298.03, \quad \lambda _{9}=320.97, \quad \lambda _{10}=404.16\)

Fig. 5
figure 5

Response plots for Example 4

Full size image
Table 5 Performance comparison for Example 4
Full size table

The reduced-order model obtained by proposed technique is

$$\begin{aligned} R_{2}(s)=\frac{-0.9332s + 26.4520}{s^{2} + 14.9093s + 26.4520} \end{aligned}$$

The reduced-order model obtained by MCS [22] is

$$\begin{aligned} R_{2}(s)=\frac{0.007842 s+16.06}{s^{2}+9.868 s+16.06} \end{aligned}$$

The reduced-order model obtained by ESA and PA [26] is

$$\begin{aligned} R_{2}(s)=\frac{-28.367 s+647.60193}{s^{2}+359.999 s+647.60193} \end{aligned}$$

The reduced-order model obtained using FDA and ESA [36] is

$$\begin{aligned} R_{2}(s)=\frac{-28.3902 s+647.6004}{s^{2}+359.999 s+647.6004} \end{aligned}$$

Figure 4a and b shows the time, and frequency domain comparison of the original higher-order system and reduced model obtained by the proposed method and the recently developed methods [22, 35, 37]. The cost versus iteration graph is shown in Fig. 4c. Table 4 presents a numerical evaluation in terms of time response parameters and different integral error parameters. Using the suggested method, the ISE value obtained is \(9.75 \times 10^{-6}\), which is less than the recently developed reduced-order system using the MCS algorithm [22]. Several time response parameters, like settling time, peak value, and integral error, such as ITAE, IAE, and ITSE, are also determined to illustrate the efficacy of the proposed method. These values are better than the other method of order reduction.

Example 4

In this example, a ninth-order complex roots system is considered to obtain a third-order reduced-order model.

$$\begin{aligned} G_{9}(s)=\frac{s^{4}+35 s^{3}+291 s^{2}+1093 s+1700}{{s^{9}+9 s^{8}+66 s^{7}+294 s^{6}+1029 s^{5}+2541 s^{4}+4684 s^{3}+5856 s^{2}+4620 s+1700}} \end{aligned}$$

The reduced-order model obtained by the proposed technique is

$$\begin{aligned} R_{3}(s)=\frac{0.0743s^2 - 0.4261s + 0.8679}{0.3355s^3 + 0.8405s^2 + 1.3914s + 0.8679} \end{aligned}$$

The reduced-order model obtained by MCS [22] is

$$\begin{aligned} R_{3}(s)=\frac{0.001935 s^{2}+0.005725 s+1.073}{s^{3}+1.681 s^{2}+2.183 s+1.073} \end{aligned}$$

The reduced-order model obtained by [12] is

$$\begin{aligned} R_{3}(s)=\frac{0.0789 s^{2}+0.3142 s+0.493}{s^{3}+1.3 s^{2}+1.34 s+0.493} \end{aligned}$$
Fig. 6
figure 6

Response plots for Example 5

Full size image
Table 6 Performance comparison for Example 5
Full size table

Time domain response and frequency domain response of the original higher-order system and the reduced-order model generated by the recommended approach are presented in Fig. 5a and b. The proposed method has a step response, and bode plot close to the original system and comparable with other recently developed methods [18, 22, 28, 35, 37]. The convergence graph is shown in Fig. 5c. The convergence graph seems constant between 10 and 50 iterations but decreases quickly after 50. The quantitative evaluation of the recommended scheme and other traditional and recently proposed methods is done in Table 5. Using the suggested method, the ISE value calculated is \(1.7 \times 10^{-3}\), which is smaller than the recently developed reduced-order system using the MCS algorithm [22]. The table shows that the settling time and peak value of the proposed reduced model are approximately the same as the original system’s values, showing the proposed method’s efficacy in retaining essential features. Also, different performance indices such as ITAE, IAE, ISE, and ITSE are calculated, which are the least compared to the recently developed method.

Example 5

In this example, a fourth-order simple pole system of repeating poles is considered.

$$\begin{aligned} G_{4}(s)=\frac{1}{(s+1)^{4}} \end{aligned}$$

The third-order reduced-order model by proposed technique given in Sect. 3 is

$$\begin{aligned} R_{3}(s)=\frac{0.0006s^2 + 0.0210s + 0.2075}{s^{3} + 1.2615s^2 + 0.8541s + 0.2075} \end{aligned}$$

The second-order reduced-order model by proposed technique given in Sect. 3 is

$$\begin{aligned} R_{2}(s)=\frac{1.0101}{3.9414s^{2} + 4.019s + 1.0101} \end{aligned}$$

The third-order reduced-order model obtained by MCS [22] is

$$\begin{aligned} R_{3}(s)=\frac{0.0001064 s^{2}+0.2325}{s^{3}+1.238 s^{2}+0.9371 s+0.2325} \end{aligned}$$

The second-order reduced-order model obtained by MCS [22] is

$$\begin{aligned} R_{2}(s)=\frac{0.1 \mathrm {~s}+0.1158}{s^{2}+0.5202 s+0.1158} \end{aligned}$$
Fig. 7
figure 7

Response plots for Example 6

Full size image
Table 7 Performance comparison for Example 6
Full size table

Figure 6a and b exhibit the step response and bode plot of the original and reduced-order models obtained by the suggested approach and the other recently developed techniques [22]. It can be noted from the bode plot that the reduced model obtained is reliable for higher and lower frequencies. The proposed third-order model utilizing the approach better approximates the original model than the second-order system when comparing simulation results. The convergence rate of the proposed method is shown in Fig. 6c. The convergence graph shows that ISE values decreased very fast, and they became almost constant after 50 iterations. Comparative analysis of the original and reduced system is depicted in Table 6. As shown in Table 6, the ISE value is significantly lower than the ISE value of a recently developed MCS algorithm [22]. As a result, it is discovered that the proposed third-order model performs better than the recently developed techniques.

Example 6

In this example, a third-order system of actual power system model is considered from [41,42,43], whose transfer function is given below:

$$\begin{aligned} G_{3}(s)=\frac{250}{s^3 + 15.88s^2 + 42.46s + 106.2} \end{aligned}$$

The reduced-order model by the proposed technique is

$$\begin{aligned} R_{2}(s)=\frac{-0.8855s + 17.5598}{s^{2} + 2.5436s + 7.4594} \end{aligned}$$

The reduced-order model obtained using Balance Truncation, and Routh Approximation [29] is

$$\begin{aligned} R_{2}(s)=\frac{-1.268s + 17.25}{s^2 + 2.391s + 7.327} \end{aligned}$$

The reduced-order model obtained using the Routh–Hurwitz method [3] is

$$\begin{aligned} R_{2}(s)=\frac{250}{15.88s^2 + 35.772s + 106.2} \end{aligned}$$
Fig. 8
figure 8

Response plots for Example 7

Full size image
Table 8 Performance comparison for Example 7
Full size table

Step response of the original and reduced-order model obtained using the suggested method is compared with other previously published research and shown in Fig. 7a. The Bode plot of the original system and the reduced-order model generated by the recommended approach are presented in Fig. 7b. The Bode plot demonstrates that all techniques operate effectively for a small range of frequencies but are unreliable for greater frequencies. The suggested technique’s step response and bode plot of the reduced system are also compared with [3, 27, 29]. The convergence graph shown in Fig. 7c decreases fast, showing the proposed method’s effectiveness. A quantitative evaluation of the step response parameters and different error indices are drawn in Table 7. Time response parameters like settling time and peak value of the reduced system are approximately the same as the original higher-order system. Also, the ISE value obtained for the reduced model is \(7.8 \times 10^{-4}\), which is significantly less compared to the recently developed reduced-order system using the MCS algorithm [29].

Example 7

In this example, a fifth-order system is considered from [29, 44], whose transfer function is given below:

$$\begin{aligned} G_{5}(s)=\frac{s^4 + 7s^3 + 42s^2 + 142s + 156}{s^5 + 25s^4 + 258s^3 + 930s^2 + 1441s + 745} \end{aligned}$$

The reduced-order model obtained by proposed technique given in Sect. 3 is

$$\begin{aligned} R_{2}(s)=\frac{0.1972s + 0.0022}{s^2 + 0.9508s + 0.0104} \end{aligned}$$

The reduced-order model obtained by Balance Truncation and Routh Approximation [29] is

$$\begin{aligned} R_{2}(s)=\frac{0.1922s + 0.002387}{s^2 + 0.9295s + 0.0114} \end{aligned}$$

The reduced-order model obtained by Stability equation and Pade Approximation [45] is

$$\begin{aligned} R_{2}(s)=\frac{142.0174s + 156}{909.5238s^2 + 1441s + 745} \end{aligned}$$

Step response and bode plot of the original and reduced-order model obtained using the suggested method are shown in Fig. 8a and b. It is evident that the response in time and frequency domains is very well approximated by the proposed method. This approach approximates lower and higher frequencies, as shown in the bode plot. This system is also considered by [4, 29, 45, 46]. The convergence graph is shown in Fig. 8c, which shows that all the ISE values of the reduced model decreased fast before ten iterations which becomes inferior later on, but the final obtained value of ISE is the least. Table 8 presents a numerical data comparison of time response parameters and different error indices. Using the suggested method, the ISE value calculated is \(1.35 \times 10^{-4}\), which is smaller than the recently developed reduced-order model by the mixed method of Balance truncation and Routh approximation [29].

Example 8

The next system which we consider is an eighth-order system. It has been taken from [29]. The transfer function of the system is given as:

$$\begin{aligned} G_{8}(s)=\frac{{35s^7 + 10086s^6 + 13285s^5 + 82402s^4+ 278376s^3 + 511812s^2+ 482964s + 194480}}{{s^8 + 33s^7 + 437s^6 + 3017s^5 + 11870s^4 + 27470s^3 + 37492s^2 + 28880s + 9600}} \end{aligned}$$

On applying the proposed technique, the second-order reduced model is given by

$$\begin{aligned} R_{2}(s)=\frac{31s + 27.7819}{s^{2} + 2.2043s + 1.3714} \end{aligned}$$

whereas the reduced-order model obtained by a mixed method of Balance truncation and Routh approximation [29] is given by

$$\begin{aligned} R_{2}(s)=\frac{30.85 s + 30.65}{s^{2} + 2.317 s+ 1.513} \end{aligned}$$

The same example was reduced using a mixed method of Routh and Pade Approximation [47]. The reduced-order model hence obtained is

$$\begin{aligned} R_{2}(s)=\frac{17.022968s + 6.8574}{s^{2}+1.018 s+0.3385} \end{aligned}$$

The step responses and Bode plots of the original system, reduced-order model obtained by the proposed technique, Balance Truncation and RA [29], Routh and PA [47], and Routh Approximation [2] are depicted in Fig. 9a and b, respectively. It is seen that the response of the reduced model obtained by the proposed method iscloser to the response of the original model, thus demonstrating the successful applicability of the proposed order reduction scheme. Figure 9c depicts the change in fitness function value ISE with the increase in the number of iterations. In addition to the plots, the values of different error-based performance indices and the time response specifications are tabulated in Table 9 for quantitative evaluation. The ISE, ITSE, IAE, and ITAE values for the proposed scheme are the least compared to recently developed reduction methods. Thus, we can conclude that the proposed method exhibits better performance for the given system than the other methods.

Fig. 9
figure 9

Response plots for Example 8

Full size image
Table 9 Performance comparison for Example 8
Full size table

5 Conclusion

This study proposed a novel order abatement method for the SISO LTI systems. In this method, atom search optimization algorithm is used for finding the reduced model of the higher-order systems. The proposed method assesses a stable and approximate reduced-order model, considering the ISE as an error between the original and reduced-order model. A variety of examples are considered to show the superiority of the suggested reduction approach. The step response and bode plot of the reduced-order model developed utilizing suggested method and the recently published articles are compared graphically. The truthfulness and usefulness of the suggested algorithm are authenticated by evaluating the performance error indices like ISE, ITSE, IAE, and ITAE values and found to be least compare to the other techniques. The proposed reduction strategy is the most effective for both SISO LTI systems and a real-time LFC of the power system. In future work, the proposed method can be used to obtain the reduced-order model for interval systems, non-minimum phase systems, and MIMO systems. This method can also solve real-time practical challenges such as controller design in load frequency control, microgrids, and robots.