1 Introduction

Often, high-order differential equations or difference equations are used to represent the mathematical model of a system. By using these differential/difference equations it is difficult to analyse the system. Hence, for simplification of such systems, the order of these equations must be reduced such that the simplified/lower order system retains all necessary properties of the higher order system. Therefore, for better understanding of the system, this lower order system is used to analyse behaviour of higher order system by which simulation time reduces and design work become easier. Hence, modal order reduction is the most widely used concept in different fields of engineering due to its simplicity in control designing, low cost, computational speed, satisfactory performance and because it is easy to understand in many applications. These interesting features have made the modal order reduction as an attractive research topic in the past several decades. A detailed survey on this topic is given by Sinha and Lastman [1].

Recently, Ghosh and Senroy [2] proposed a technique for system simplification that is based on balanced truncation technique. The advantage of factor division algorithm and stability equation method is being utilized for reduced order modelling by Sikander and Prasad [3]. Also, Desai and Prasad [4] proposed a new technique for linear time-invariant (LTI) systems, which is based on Routh Approximation (RA) [5] and Big Bang–Big Crunch (BB–BC) algorithm [6] to obtain the lower order system. RA is used to evaluate the denominator polynomial of the lower order system to preserve the stability, whereas the numerator polynomial is evaluated using the BB–BC algorithm. Another composite technique was suggested by Parmar et al [7], by which they demonstrated the advantages of combining Eigen spectrum analysis (ESA) and factor division algorithm. This approach is applied on the system having real poles only and extended for MIMO systems also. ESA along with Padé approximation (ESA & PA) [8] and Cauer second from (ESA & CAUER-II) [9] is proposed by the authors for system simplification. The major drawback of these techniques is that in some cases, the lower order model becomes a non-minimum phase model.

Also, Parmar et al [10] suggested a new technique to obtain a stable lower order model, in which the coefficients of denominator polynomial are evaluated by stability equation technique and the numerator polynomial is evaluated by a genetic algorithm. They emphasized on preserving the stability. One more composite technique was suggested by Vishwakarma and Prasad [11], where denominator of the lower order system is evaluated by clustering technique and its numerator is obtained by Padé approximation technique. This technique also produces a non-minimum phase lower order system. Recently, stability equation technique along with particle swarm optimization was suggested by Sikander and Prasad [12]. They used the concept of integral square error (ISE) minimization. Despite having so many order reduction techniques, no technique provides satisfactory results so far for all systems. Hence, there is a scope for finding efficient new algorithms for system simplification.

Therefore, this paper contributes a new technique based on ESA and Cuckoo search (ESA & CS) for simplification of linear dynamical systems. The coefficients of the denominator polynomial of the lower order system are calculated by ESA whereas the coefficients of the numerator polynomial are obtained by minimizing the ISE using a new meta-heuristic search algorithm called Cuckoo search. In this technique, stability of the system is retained and it is computationally very simple. Comparative analysis of the results obtained using the proposed technique is presented. To analyse the performance of the lower order systems, three performance indices, ISE, integral absolute error (IAE) and integral of time multiplied by absolute error (ITAE), are used in this study.

2 Problem statement

Let us consider an nth order single input single output system represented as follows:

$$\begin{aligned} {G_n}(s) = \frac{{{N_{n - 1}}(s)}}{{{D_n}(s)}} = \frac{{\sum \limits _{i = 0}^{n - 1} {{f_i}{s^i}} }}{{\sum \limits _{i = 0}^n {{h_i}{s^i}} }} \end{aligned}$$
(1)

where \({f_i}\) and \({h_i}\) are constants and let us assume \({f_0} = {h_0}\) for unity steady-state output response when the system is subjected to unit step input. The objective is to evaluate the unknown scalar constants of lower order system (kth) \((k < n)\) described by the following equation:

$$\begin{aligned} {R_k}(s) = \frac{{{N_{k - 1}}(s)}}{{{D_k}(s)}} = \frac{{\sum \limits _{i = 0}^{k - 1} {{c_i}{s^i}} }}{{\sum \limits _{i = 0}^k {{d_i}{s^i}} }}\quad \end{aligned}$$
(2)

where \({c_i}\) and \({d_i}\) are unknown constants.

3 Proposed methodology

The proposed algorithm for system simplification or to obtain reduced order model is divided into the following two steps.

Step 1: Calculation of denominator polynomial of lower order system using ESA [7].

Step 1.1: Considering denominator polynomial of the original system and rearranging in the following form:

$$\begin{aligned} {D_n}(s) = (s + {p_1})(s + {p_2})...(s + {p_n}) \end{aligned}$$
(3)

such that \( - {p_1}< - {p_2}< \cdots < - {p_n}\) are the poles of the higher order original system \({G_n}(s)\).

Step 1.2: Represent the poles (Eigen Spectrum Points (ESP)) of \({G_n}(s)\) in Eq. (3) on the negative real axis of the s plane as shown in figure 1.

Figure 1
figure 1

Representation of ESP of the original system.

Full size image

Step 1.3: Calculate the pole centroid given by

$$\begin{aligned} {\sigma _p} & = {} \frac{\sum {absolute\, value \,of\, real \,part \,of\, poles}}{number \,of\, poles}\nonumber \\ {\sigma _p}= & {} \frac{{\sum \limits _{j = 1}^n {\left| \mathrm{Re}{p_j} \right| } }}{n} \end{aligned}$$
(4)

Step 1.4: Determine the system stiffness K using the following formula:

$$\begin{aligned} K = \frac{{\left| {\mathrm{Re}{p_1}} \right| }}{{\left| {\mathrm{Re}{p_n}} \right| }}\quad \;\left| {\mathrm{Re}{p_1}} \right|< \left| {\mathrm{Re}{p_2}} \right|< \cdots < \left| {\mathrm{Re}{p_n}} \right| . \end{aligned}$$
(5)

Step 1.5: Computation of \({\mathrm{Re}{p_k}^{'},\;M}\).

Let \({{\sigma _p}^{'},\;{K^{'}}}\) be the pole centroid and system stiffness of \({R_k}(s),\) respectively. If \({\sigma _p^{'} = {\sigma _p}}\) and \({{K^{'}} = K}\) then

\(K = \frac{{\left| {\mathrm{Re} p_1^{'}} \right| }}{{\left| {\mathrm{Re} p_k^{'}} \right| }} = {K^{'}}\) and \({\sigma _p} = \frac{{\sum \limits _{j = 1}^k {\left| {\mathrm{Re} p_j^{'}} \right| } }}{k} = \sigma _p^{'}\)

\(\mathrm{Re} p_j^{'}\) are the real parts of poles of \({R_k}(s);{\sigma _p}\) can be rewritten as follows:

$$\begin{aligned} {\sigma _p} & = {} \frac{{\mathrm{Re} p_1^{'} + \mathrm{Re} p_2^{'} + \mathrm{Re} p_3^{'} + \cdots + \mathrm{Re} p_{k - 1}^{'} + \mathrm{Re} p_k^{'}}}{k}\\= & {} \frac{{\mathrm{Re} p_1^{'} + (\mathrm{Re} p_1^{'} + M) + (\mathrm{Re} p_1^{'} + 2M) + \cdots + (\mathrm{Re} p_1^{'} + (k - 2)M) + \mathrm{Re} p_k^{'}}}{k}\\= & {} \mathrm{Re} p_1^{'} + \mathrm{Re} p_1^{'}(k - 2) + (M + 2M + \cdots + (k - 2)M + \mathrm{Re} p_k^{'})\\ M= & {} \frac{{\mathrm{Re} p_k^{'} - \mathrm{Re} p_1^{'}}}{{(k - 1)}} \end{aligned}$$

Replacing \(\mathrm{Re} p_1^{'} = K\mathrm{Re} p_k^{'}\)

$$\begin{aligned} M(k - 1) = \mathrm{Re} p_k^{'} - K\mathrm{Re} p_k^{'}. \end{aligned}$$
(6)

We have

$$\begin{aligned} \begin{array}{l} N = {\sigma _p}k\\ QM = (M + 2M + \cdots + (k - 2)M). \end{array} \end{aligned}$$
(7)

Substituting the values of \({\sigma _p}\), and QM, Eq. (7) gives

$$\begin{aligned} N = K\mathrm{Re} p_k^{'}(k - 1) + \mathrm{Re} p_k^{'} + QM. \end{aligned}$$
(8)

Equations (6) and (8) can be rearranged in the following matrix form:

$$\begin{aligned} \left[ \begin{array}{l} K(k - 1) + 1\quad \quad \;Q\\ (1 - K)\quad \quad \quad (1 - k) \end{array} \right] \left[ \begin{array}{l} \mathrm{Re} p_k^{'}\\ \;M \end{array} \right] = \left[ \begin{array}{l} N\\ \,0 \end{array} \right] . \end{aligned}$$
(9)

The value of \(\mathrm{Re} p_k^{'},\;M\) is obtained by solving Eq. (9).

Step 1.6: Calculate ESP from \(\mathrm{Re} p_k^{'},\) and M, and form denominator polynomial \({D_k}(s)\) of lower order system.

Step 2: Calculation of numerator polynomial of lower order system using Cuckoo search algorithm [13].

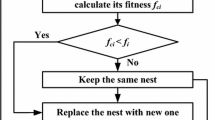
Step 2.1: Specify the fitness function as given in Eq. (12) and the number of chosen variables (say q) as per Eq. (2) along with their range. Set the probability of the worst nests and step size also. After initialization of a population of p host nests the problem is summarized as follows:

minimize fitness function, i.e., ISE \({Z_\alpha }\), subject to \({c_{iL}}< {c_i} < {c_{iU}}\) and \({d_{iL}}< {d_i} < {d_{iU}}\) where \({c_{iL}},{d_{iL}}\) and \({c_{iU}},{d_{iU}}\) are the lowest and highest values of the chosen variables, respectively, and \(i = 0,1, \ldots ,q.\)

Step 2.2: Obtain the value of \({Z_\alpha }\) for a randomly selected cuckoo \((\alpha )\) and select a nest \((\beta )\) randomly among p.

Step 2.3: If \(({Z_\alpha } > {Z_\beta })\) then interchange \(\beta \) by the current obtained solution, else go to the next step.

Step 2.4: Check whether the predefined stopping criterion has been reached or the maximum generation has occurred or not. If yes, then the solution obtained in the current generation would be the best solution; otherwise, go to the next step.

Step 2.5: Abandon a fraction of worst nests with optimal value of probability \({p_a}\) and step size a.

Step 2.6: Using Eq. (10), the obtained solution must be updated by calculating \(Y_i^{(t + 1)}\) and repeating this algorithm, until the predefined condition or the maximum generation is obtained.

For simplicity, the fraction of \({p_a}\) of n nests, which are interchanged new nests, is considered as an approximation of the previous assumption.

The Lévy flight can be represented by the following relation for the generation of new solution \(Y(t + 1)\) of cuckoo i [14]:

$$\begin{aligned} {Y_i}^{(t + 1)} = {Y_i}^{(t)} + a \otimes \text {L}{\acute{\hbox{e}}}\text {vy}(\lambda ) \end{aligned}$$
(10)

where \(a\,(a > 0)\) is a step size that is related to the level of the problem optimized by the technique. The random step size of the Lévy flights is calculated as follows:

$$\begin{aligned} \text {L}{\acute{\hbox {e}}}\text {vy } \tilde{u} = {t}^{-\lambda }\quad \quad \;(1 < \lambda \le 3). \end{aligned}$$
(11)

Furthermore, the efficacy of the lower order system obtained by the proposed technique is evaluated using the following performance indices:

$$\begin{aligned} ISE & = {} \int _0^\infty {{{[{g_n}(t) - {r_{k}}(t)]}^2}} dt \end{aligned}$$
(12)
$$\begin{aligned} IAE & = {} \int _0^\infty {\left| {{g_n}(t) - {r_{k}}(t)} \right| \;} dt \end{aligned}$$
(13)
$$\begin{aligned} ITAE & = {} \int _0^\infty {t.\left| {{g_n}(t) - {r_{k}}(t)} \right| \;} dt \end{aligned}$$
(14)

where ISE, IAE and ITAE are integral square error, integral of absolute error and integral of time multiplied by absolute error, respectively; \({g_n}(t)\) and \({r_{k}}(t)\) are step responses of higher and lower order system, respectively.

4 Numerical examples and results

Example 1

Let us consider a 10th order model [8] for reduction that is as follows:

$$\begin{aligned} {G_{10}}(s) = \frac{{540.70748 \times {{10}^{17}}}}{{\prod \nolimits _{i = 1}^{10} {(s + {p_i})} }} \end{aligned}$$

where

\(\begin{array}{l} {p_1} = 2.04,{p_2} = 18.3,{p_3} = 50.13,{p_4} = 95.15,\\ {p_5} = 148.85,{p_6} = 205.16,{p_7} = 257.21,{p_8} = 298.03,\\ {p_9} = 320.97,{p_{10}} = 404.16. \end{array}\)

On applying the proposed technique, the following lower second order model is obtained with \(ISE = 5.10 \times {10^{ - 4}}\):

$$\begin{aligned} {R_2}(s) = \frac{{0.1729s + 646.7}}{{{s^2} + 360s + 647.6}} \end{aligned}$$

whereas the lower second order system obtained by (ESA & PA) [8] with \(ISE =1.3646\) is represented as follows:

$$\begin{aligned} {R_2}(s) = \frac{{ - 28.367s + 647.60193}}{{{s^2} + 359.999s + 647.60193}} \end{aligned}$$
Figure 2
figure 2

Comparison of time response of higher and lower order systems with different reduction techniques for Example 1.

Full size image

The step responses of higher order system and lower order system obtained by proposed technique (ESA & CS), (ESA & PA) [8] and (ESA & CAUER-II) [9] are shown in figure 2. It is clearly observed that the lower order system obtained by the proposed technique provides good approximation to the higher order system. Also, a comparison of lower order system obtained by the proposed technique and by alternative techniques in terms of rise time (\(t_r\)), settling time (\(t_s\)), maximum peak overshoot (\(M_p\)) and performance indices is presented in table 1 for Example 1. It is noticed that the proposed technique provides lesser ISE value, i.e., \(5.10 \times {10^{ - 4}}\), as compared with the values obtained using other techniques and in recently published work available in the literature, i.e., 1.3646 by (ESA & PA) [8] and \(1.5 \times \mathrm{{1}}{0^{ - 3}}\) by (ESA & CAUER-II) [8]. Therefore, it is clearly noticed that the proposed technique is much better as compared with other techniques available in the literature.

Table 1 Comparison of different reduction techniques for Example 1.
Full size table

Example 2

The second model [8], which is to be reduced by the proposed technique, is given as follows:

$$\begin{aligned} {G_4}(s) = \frac{{s + 4}}{{{s^4} + 19{s^3} + 113{s^2} + 245s + 150}} \end{aligned}$$

On applying the proposed technique, the lower second order system with \(ISE =8.176 \times {10^{-7}}\) is obtained as follows:

$$\begin{aligned} {R_2}(s) = \frac{{ - 0.03s + 0.2007}}{{{s^2} + 9.5s + 7.459}} \end{aligned}$$

whereas the lower second order system with \(ISE = 2.7663\times {10^{-5}}\) obtained by (ESA & PA) [8] is represented as follows:

$$\begin{aligned} {R_2}(s) = \frac{{ - 0.02187s + 0.19915}}{{{s^2} + 9.5s + 7.45868}} \end{aligned}$$
Figure 3
figure 3

Comparison of time response of higher and lower order systems with different reduction techniques for Example 2.

Full size image

To demonstrate the efficacy of the proposed technique, the step responses of higher order system and lower order system obtained using the proposed technique (ESA & CS), (ESA & PA) [8] and (ESA & CAUER-II) [9] are plotted in figure 3. It is perceived that the response of lower order system evaluated by the proposed technique is much closer than the responses of reduced models obtained by alternative techniques. In addition, the values of performance indices, such as ISE, IAE and ITAE values, along with rise time (\(t_r\)), settling time (\(t_s\)) and maximum peak overshoot (\(M_p\)) of reduced models are also tabulated in table 2 for Example 2. Using the proposed technique, the ISE value for Example 2 is found to be \(8.176 \times {10^{-7}}\) whereas the lowest value of ISE, using the other well-known techniques, is only \(2.7663\times {10^{-5}}\) (ESA & PA) [8] and \(1.6\times {10^{-6}}\) (ESA & CAUER-II) [9]. The values of IAE and ITAE for the proposed technique are also found to be much lesser as compared with other techniques. Hence, the proposed technique exhibits better performance comparatively.

Table 2 Comparison of different reduction techniques for Example 2.
Full size table

Example 3

Let us reduce an 8th order model [8], which is given as follows:

$$\begin{aligned} {G_8}(s) = \frac{{18{s^7} + 514{s^6} + 5982{s^5} + 36380{s^4} + 122664{s^3} + 222088{s^2} + 185760s + 40320}}{{{s^8} + 36{s^7} + 546{s^6} + 4536{s^5} + 22449{s^4} + 67284{s^3} + 118124{s^2} + 109584s + 40320}}. \end{aligned}$$

On applying the proposed technique, the lower second order system obtained is

$$\begin{aligned} {R_2}(s) = \frac{{22.51s + 8.151}}{{{s^2} + 9s + 8}}. \end{aligned}$$

The same example is reduced by (ESA & PA) [8] to obtain

$$\begin{aligned} {R_2}(s) = \frac{{24.1144s + 8}}{{{s^2} + 9s + 8}} \end{aligned}$$
Figure 4
figure 4

Comparison of time response of higher and lower order systems with different reduction techniques for Example 3.

Full size image

The time responses of higher and lower order system when subjected to unit step input are depicted in figure 4 for Example 3. The enlarged view of the responses depicts the closeness of higher and lower order systems more clearly. To exhibit the excellence and effectiveness of the proposed technique, ISE, IAE and ITAE values along with rise time (\(t_r\)), settling time (\(t_s\)) and maximum peak overshoot (\(M_p\)) of different lower order systems are also compared as depicted in table 3. It is found that the proposed technique performs well comparatively.

Table 3 Comparison of different reduction techniques for Example 3.
Full size table

5 Conclusion

In this study, a new simplification technique for LTI systems is presented, which is based on ESA and recently developed Cuckoo search algorithm. The coefficients of denominator polynomial of lower order system are calculated by ESA and the coefficients of numerator polynomial of lower order system are obtained by minimizing the ISE between higher and lower order systems using Cuckoo search algorithm. The comparison of step response shows that the response of lower order system obtained by proposed technique is much closer to the response of higher order system as compared with other techniques. The efficacy and effectiveness of the proposed technique are also observed by comparing ISE, IAE and ITAE values of different lower order systems. Therefore, it is concluded that the proposed technique performs well as compared with other popular techniques available in the literature.