1 Introduction

Energy harvester refers to a system which enables generating energy from nature sources like fluid flows, vibration or light. Consequently an independent energy source would be available for radio transmitters or wireless sensors. Here in this research, energy harvesting from converting the mechanical energy of the vibration of a cantilever beam into the electric energy via piezoelectricity effect is studied. An optimal piezoelectric cantilever is designed in order to harvest maximum energy form vibratory mining equipment. Multi-objective artificial immune system (AIS) is utilized as the optimization tool for designing shape parameters.

Since, the common available electrical power supply in mining plants is 3-phase 400 V power supply, it is not applicable to be used for structural health monitoring (SHM) sensors. Therefore, usually batteries or energy harvesters are suggested as power supplies. Limited operation time, harmful chemical effects on the environment, significant time and money cost for replacing are the main disadvantages for battery usage for such systems.

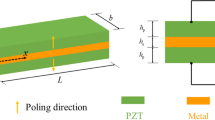
It is desired to derive maximum electrical power from minimum piezoelectric volume, and to obtain uniform stress distribution along piezoceramic layer. In order to achieve these objectives, the generalized equations for the energy harvester cantilever with variable width, length and thickness are derived. Multi-objective AIS tool is utilized for optimal calculation of the design parameters. Figure 1 demonstrates the generalized shape of the harvester cantilever beam.

Fig. 1
figure 1

Piezoelectric cantilever scheme

Full size image

There is considerable literature on energy harvester modeling and design. Hagood et al. (1990) proposed the theories for Rayleigh–Ritz modeling of piezoelectric materials under mechanical loading. However, no design or optimization was studied in that research. In the field of modeling of piezoelectric systems, Sodano et al. (2004) used a generalized Hamiltonian of the coupled electromechanical system. They suggested finite number of shape functions to derive coupled differential equations of the system.

Anderson and Sexton (2006) derived the equations for the cantilever energy harvester with base vibration. They used lumped element form method to find the peak power. Several simple optimization studies were performed on a simple bimorph harvester configuration.

Erturk and Inman utilized Hamiltonian energy equations and then applied constitutive laws of piezoelectric to the Euler–Bernoulli beam deformation formulations for unimorph (Erturk and Inman 2008) and bimorph (Erturk and Inman 2009) configurations. They derived generalized equation and investigated a simple cantilever harvester case study with uniform width and equivalent layers length.

Goldschmidtboeing and Woias (2008) proposed rectangular and triangular shapes for piezoelectric energy harvesters, modeled via Rayleigh–Ritz method. They also showed that triangular-shaped cantilever is more effective in terms of curvature homogeneity. No test verification on final curved beam was presented. Sunithamani et al. (2014) only optimized the length of piezoelectric energy harvester with a non-traditional cross section by simulating in Finite Element (FE) software.

Dietl and Garcia (2010) proposed an optimized shape with the aim to concentrate the strain in a section of the cantilever beam, which generates the most part of the total power. They studied the tip mass effect and used a heuristic code for optimization. They validated their simple model, but no experiment on final optimized model was implemented.

Hadas et al. (2012) implemented shape optimization on electro-magnetic energy harvester via artificial intelligence methods. They also considered multi-objective fitness functions to have maximum output power.

Benasciutti et al. (2010) optimized trapezoidal shape for cantilever configuration with the aim of increasing generated power per volume. Except simple linear equation for boundaries other shape parameters are considered constant. FE simulation and experiments are reviewed in this work.

Lai et al. (2010) used genetic algorithms for shape optimization of unimorph MEMS piezoelectric cantilever energy harvesters in order to obtain maximum output power. Optimization was performed on basic linear boundaries of trapezoid and reverses trapezoid shapes, and then compared with reference rectangular shape. No experiment was performed in this research.

Alrashdan et al. (2014) optimized a piezoelectric micro-power generator in frequency range 1–1.7 Hz. Various control parameters were considered to be tuned by ANOVA and Taguchi methods. Results were also simulated in FE software. No experiment and analytical study were performed in this research.

AIS is an evolutionary soft computing method inspired by the biological immune systems. Originally, AIS method was developed in computer science field. In engineering, AIS has found applications in pattern recognition, scheduling, control, and machine-learning. AIS has also been applied successfully to a variety of optimization problems. Studies have shown that AIS possesses several attractive properties that allow evolutionary algorithms to avoid premature convergence (Dasgupta 1999) and improve local search (Bersini 1991). Ecologically inspired optimization methods are also reviewed for optimal control design (Ghosh et al. 2011).

No specific research has been found in the application of AIS on piezoelectric energy harvester optimization. However, there is literature on application of immunity inspired method on multi-objective optimization problems (Carlos and Narelli 2005; Olivetti et al. 2005; Tan et al. 2008).

To compare GA and AIS in solving engineering problems, Freschi and Repetto (2006) have shown that GA solved optimization problems faster, while AIS succeeded more in detecting a larger number of optimal points. Proposed intelligent AIS tool results in faster optimization process and deriving more feasible solutions.

The main research contributions in the current paper are as follow;

  • Energy harvester equations for a generalized shape cantilever (i.e., non-uniform width and variable length and thickness of the layers), applicable to both unimorph and bimorph configurations are presented by means of the well-established Rayleigh–Ritz method.

  • Innovative intelligent AIS for multi-objective optimization of energy harvester is proposed.

  • The highest generality in the optimization parameters, such as the shape of the cantilever boundaries, piezoceramic and substructure thicknesses, piezoceramic and substructure lengths, tip mass weight, number of active layers (unimorph or bimorph) is considered, while just some of them have been overlooked in prior work. Experiments and finite element analysis verification for both original and optimized shapes are presented.

  • System based and multi-objective optimization is performed considering important objectives such as maximum power output, uniform stress along piezoceramic, and minimum piezoceramic volume. Mechanical failure check in piezoceramic and passive materials, and setting the natural frequency of energy harvester equal to desired working frequency are also considered as constraints.

The paper is organized as follows. After the introduction, the theory and analytical modeling of cantilever piezoelectric beam is described. In the next section, flowchart of the intelligent multi-objective optimization by means of AIS is discussed. In subsequent sections, a case study is described and optimized. Then, FE modeling and experiments verifications are presented. Finally, the main results are summarized and related conclusions are given.

2 Energy harvesting configuration

A piezoelectric unimorph cantilever beam includes one active (piezoelectric) and one inactive (substructure) layer, whereas a bimorph has two active and one inactive layers as shown in Fig. 2. A tip mass (M t ) is also considered at the end of the cantilever. g(t) is transverse base displacement.

Fig. 2
figure 2

Piezoelectric cantilever. a Unimorph. b Series connection bimorph

Full size image

Following assumptions are considered true in deriving the dynamic equations of the system:

  • Cantilever is excited by transverse vibration of the base. The axial excitation is negligible.

  • Poling direction of each piezo layer is in 3-direction and opposite to each other (refer to Fig. 2).

  • Cantilever is symmetric with respect to the xz plane (refer to Fig. 2), while the width may varies along the x direction.

  • Piezoelectric and substructure may have different lengths.

  • Transverse faces of piezoelectric layers are completely covered by thin electrode with negligible thickness.

  • Electrical circuit impedance is modeled with a simple resistive load (R L ).

  • Euler–Bernoulli beam deformation equation is used considering the length to thickness ratio greater than 10.

  • Excitation is considered in the range which linear vibration can supposedly impose.

  • In bimorph case, piezoelectric layers are electrically connected in series.

Assumed-mode method based on Hamilton energy principle for distributed electromechanical system is used for modeling. This method is discussed by Meirovitch as closely related to Rayleigh–Ritz method (Ertruk and Inman 2011). Equations of Hamilton energy principle without damping effect are as the following. It has to be noted that the damping effect is taken into account later.

$$\int\limits_{{t_{1} }}^{{t_{2} }} {\left( {\delta K - \delta U + \delta W_{ie} + \delta W_{nc} } \right)dt = 0}$$
(1)

Here, K represents the total kinetic energy, U represents the total potential energy of the structure, W ie is the internal electrical energy in piezoelectric layer and W nc is the virtual work of the non-conservative mechanical force and the electrical charge. K is calculated via;

$$K = \frac{1}{2}\left( {\int\limits_{{V_{s} }} {\rho_{s} \frac{{\partial r_{m}^{t} }}{\partial t}\frac{{\partial r_{m} }}{\partial t}dV_{s} } + \int\limits_{{V_{P} }} {\rho_{P} \frac{{\partial r_{m}^{t} }}{\partial t}\frac{{\partial r_{m} }}{\partial t}dV_{P} } } \right)$$
(2)

where, t is the time and ρ is the density. From now on, “P” and “S” subscript represents piezoelectric and substructure layers respectively. r m is the absolute of the displacement vector which is the summation of the beam’s relative displacement and the base displacement. The superscript t denotes the transpose of the vector. The integrations are performed over the volume (V) of the respective material. Vector form of cantilever’s relative displacement field is:

$$r\left( {x,z,t} \right) = \left[ {\begin{array}{*{20}c} {u\left( {x,t} \right) - z\frac{{\partial w\left( {x,t} \right)}}{\partial x}} & 0 & {w\left( {x,t} \right)} \\ \end{array} } \right]^{t}$$
(3)

Here, u(x,t) and w(x,t) are the axial and transverse displacements of the neutral axis at point x and time t respectively. z is the transverse distance from the neutral axis. The transverse base displacement is assumed to be:

$$w_{b} \left( {x,t} \right) = g\left( t \right)$$
(4)

For harmonic excitation, it is assumed that g(t) = Ae jωt. Total potential energy of the structure can be calculated from:

$$U = \frac{1}{2}\left( {\int\limits_{{V_{s} }} {S^{t} TdV_{s} } + \int\limits_{{V_{P} }} {S^{t} TdV_{P} } } \right)$$
(5)

while, S and T are the vector of strain and stress components. The only non-zero strain component is:

$$S_{xx} = \frac{{\partial r\left( {x,z,t} \right)}}{\partial x} = \frac{{\partial u\left( {x,t} \right)}}{\partial x} - z\frac{{\partial^{2} w\left( {x,t} \right)}}{{\partial x^{2} }}$$
(6)

According to Hook’s law, tension in the substructure is as below:

$$T_{xx} \left( {x,z,t} \right) = Y_{s} S_{xx} \left( {x,z,t} \right)$$
(7)

Y s is elasticity module. The constitutive equation for the stress component in the piezoelectric layer is:

$$T_{xx} \left( {x,z,t} \right) = c_{11}^{E} S_{1} - e_{31} E_{3}$$
(8)

In which, \(c_{ 1 1}^{E}\) is the elasticity module of the piezoelectric material in the short circuit condition, e 31 is piezoelectric stress constant and can be found via \(e_{31} = d_{31} c_{ 1 1}^{E}\). E 3 is considered as uniform electric field and for each configuration can be calculated as following:

$${\text{Unimorph}}{:}\;E_{3} \left( t \right) = \frac{ - v\left( t \right)}{{h_{p} }}$$
(9)
$${\text{Series bimorph top layer}}{:}\;E_{3} \left( t \right) = \frac{ - v\left( t \right)}{{h_{p} }}$$
(10)
$${\text{Bottom layer}}{:}\;E_{3} \left( t \right) = \frac{v\left( t \right)}{{h_{p} }}$$
(11)

where, h p is piezoelectric thickness. The equation for the internal electrical energy in piezoelectric layer(s) is:

$$W_{ie} = \frac{1}{2}\int\limits_{{V_{P} }} {E^{t} DdV_{P} }$$
(12)

where, E is the electric field vector and D represents the electric displacement. The virtual work of the non-conservative mechanical force and the electrical charge in Eq. (1) is derived from:

$$\delta W_{nc} = Q\left( t \right)\delta v\left( t \right)$$
(13)

Next step is discretizing the distributed parameters and implementing them in the equations of Hamilton energy principle. Distributed parameters of the system are transverse and axial displacement. Assuming “N” number of mode shapes for vibration system, transverse and axial displacement can be discretized through the following finite series.

$$w\left( {x,t} \right) = \sum\limits_{r = 1}^{N} {a_{r} (t)\phi_{r} \left( t \right)} \;u\left( {x,t} \right) = \sum\limits_{r = 1}^{N} {b_{r} \left( t \right)\alpha_{t} \left( t \right)}$$
(14)

where, Φ r (t) and α r (t) are the shape functions of rth modes for transverse and axial displacements respectively. a r (t) and b r (t) represent unknown generalized coordinates. Shape function formulation for transverse displacement is:

$$\phi_{r} (x) = \cos \frac{{\lambda_{r} }}{L}x - \cosh \frac{{\lambda_{r} }}{L}x + \varsigma_{r} (\sin \frac{{\lambda_{r} }}{L}x - \sinh \frac{{\lambda_{r} }}{L}x)$$
(15)

where, ϛ r for each mode is:

$$\varsigma_{r} = \frac{{\sin \lambda_{r} - \sinh \lambda_{r} + \lambda_{r} \frac{{M_{t} }}{mL}(\cos \lambda_{r} - \cosh \lambda_{r} )}}{{\cos \lambda_{r} + \cosh \lambda_{r} - \lambda_{r} \frac{{M_{t} }}{mL}(\sin \lambda_{r} - \sinh \lambda_{r} )}}$$
(16)

Here, λ r is eigenvalue of rth mode and is the rth root in the below equation:

$$\begin{aligned} 1 + \cos \lambda \cosh \lambda + \lambda \frac{{M_{t} }}{mL}(\cos \lambda \sinh \lambda - \sin \lambda \cosh \lambda ) - \frac{{\lambda^{3} I_{t} }}{{mL^{3} }}(\cosh \lambda \sin \lambda + \sinh \lambda \cos \lambda ) \hfill \\ + \frac{{\lambda^{4} M_{t} I_{t} }}{{m^{2} L^{4} }}(1 - \cos \lambda \cosh \lambda ) = 0 \hfill \\ \end{aligned}$$
(17)

where, L is the cantilever length, m is the mass of the unit length and I t is the moment of inertia of the tip mass. After finding λ r , related natural frequency can be calculated via:

$$\omega_{r} = \lambda_{r}^{2} \sqrt {\frac{YI}{{mL^{4} }}}$$
(18)

where, YI represents flexural rigidity. Shape function of the rth mode of the axial vibrations of the cantilever is calculated from:

$$\alpha_{r} \left( x \right) = \sin \frac{{\eta_{r} }}{L}x$$
(19)

where η r is the rth root in the below transcendental equation:

$$\frac{{M_{t} }}{mL}\eta_{r} \sin \eta_{r} - \cos \eta_{r} = 0$$
(20)

In order to find the system behavior, electromechanical Lagrange equations is utilized. Discretized distributed parameters are used for calculating the potential and kinetic energy formulations that should be put in the following formulations:

$$\frac{d}{dt}\left( {\frac{\partial T}{{\partial \dot{a}_{i} }}} \right) - \frac{\partial T}{{\partial a_{i} }} + \frac{\partial U}{{\partial a_{i} }} - \frac{{\partial W_{ie} }}{{\partial a_{i} }} = 0$$
(21)
$$\frac{d}{dt}\left( {\frac{\partial T}{{\partial \dot{b}_{i} }}} \right) - \frac{\partial T}{{\partial b_{i} }} + \frac{\partial U}{{\partial b_{i} }} - \frac{{\partial W_{ie} }}{{\partial b_{i} }} = 0$$
(22)
$$\frac{d}{dt}\left( {\frac{\partial T}{{\partial \dot{v}}}} \right) - \frac{\partial T}{\partial v} + \frac{\partial U}{\partial v} - \frac{{\partial W_{ie} }}{\partial v} = 0$$
(23)

System equations derived from simplifying electromechanical Lagrange equations by considering damping effect are modified as following:

$$\left[ {\begin{array}{*{20}c} {m^{aa} } & { - m^{ab} } \\ { - m^{ab} } & {m^{bb} } \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {\textit{\"{a}}} \\ {\textit{\"{b}}} \\ \end{array} } \right] + \left[ {\begin{array}{*{20}c} {d^{aa} } & { - d^{ab} } \\ { - d^{ab} } & {d^{bb} } \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {\dot{a}} \\ {\dot{b}} \\ \end{array} } \right] + \left[ {\begin{array}{*{20}c} {k^{aa} } & { - k^{ab} } \\ { - k^{ab} } & {k^{bb} } \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} a \\ b \\ \end{array} } \right] + \left[ {\begin{array}{*{20}c} { - \theta^{a} } \\ {\theta^{b} } \\ \end{array} } \right]v = \left[ {\begin{array}{*{20}c} f \\ 0 \\ \end{array} } \right]$$
(24)
$$C_{P} \dot{v} + \frac{v}{{R_{l} }} + \left( {\theta^{a} } \right)^{t} \dot{a} - \left( {\theta^{b} } \right)^{t} \dot{b} = 0$$
(25)

where, dot over any parameter is to represents the time derivative; m aa , m bb and m ab are submatrices of mass matrix; k aa , k bb and k ab are submatrices of stiffness matrix and d aa , d bb and d ab are submatrices of damping matrix. Each of these submatrices is an N × N matrix. it should be noted that aa and bb superscripts stand for submatrices related to transverse vibrations and axial vibrations respectively; while ab superscript stands for transverse and axial coupling submatrices. These can be calculated as below:

$$m_{rl}^{aa} = \int\limits_{0}^{L} {\left( {\rho_{s} A_{s} + \rho_{p} A_{p} } \right)\phi_{r} \left( x \right)\phi_{l} \left( x \right)dx}$$
(26)
$$m_{rl}^{bb} = \int\limits_{0}^{L} {\left( {\rho_{s} A_{s} + \rho_{p} A_{p} } \right)\alpha_{r} \left( x \right)\alpha_{l} \left( x \right)dx}$$
(27)
$$m_{rl}^{ab} = \int\limits_{0}^{L} {\left( {\rho_{s} H_{s} + \rho_{p} H_{p} } \right)\phi^{\prime}_{r} \left( x \right)\alpha_{l} \left( x \right)dx}$$
(28)
$$k_{rl}^{aa} = \int\limits_{0}^{L} {\left( {Y_{s} I_{s} + c_{11}^{E} I_{p} } \right)\phi^{\prime\prime}_{r} \left( x \right)} \phi^{\prime\prime}_{l} \left( x \right)dx$$
(29)
$$k_{rl}^{bb} = \int\limits_{0}^{L} {\left( {Y_{s} I_{s} + c_{11}^{E} I_{p} } \right)\alpha^{\prime}_{r} \left( x \right)} \alpha^{\prime}_{l} \left( x \right)dx$$
(30)
$$k_{rl}^{ab} = \int\limits_{0}^{L} {\left( {Y_{s} H_{s} + c_{11}^{E} H_{p} } \right)\phi^{\prime\prime}_{r} \left( x \right)} \alpha^{\prime}_{l} \left( x \right)dx$$
(31)

where prime over the parameters is to represent the x derivative. It should be noticed that if piezoelectric and substructure lengths are different, consequently the integral should be separately calculated for each layer substituting layer length as L. In above equation A stands for cross section area:

$$A = hb\left( x \right)$$
(32)

where h is the thickness and b(x) is the width of the cantilever at point x; here, b(x) is considered as 3rd order polynomial equation. H and I are the first and second moment of area respectively and are calculated as follow:

$$\begin{aligned} H = \iint\limits_{s} {zdydz} \hfill \\ I = \iint\limits_{s} {z^{2} dydz} \hfill \\ \end{aligned}$$
(33)

Integrals are calculated over the cross section of cantilever for each layer.

θ a and θ b in Eqs. (24) and (25) are N × 1 vectors of electromechanical coupling for transverse and axial vibrations respectively and are calculated from:

$$\begin{aligned} \theta^{a} = \int\limits_{0}^{L} {N_{p} \phi^{\prime\prime}_{r} \left( x \right)} dx \hfill \\ \theta^{b} = \int\limits_{0}^{L} {M_{p} \alpha^{\prime}_{r} \left( x \right)} dx \hfill \\ \end{aligned}$$
(34)

where:

$$N_{p} = \iint\limits_{{s_{p} }} {\frac{{e_{31} }}{{h_{p} }}}dydz$$
(35)
$$M_{p} = \iint\limits_{{s_{p} }} {\frac{{e_{31} }}{{h_{p} }}}zdydz$$
(36)

These integrals are calculated over the cross section of piezoelectric layer(s).

It is important to note that for a structure which is symmetric with respect to the neutral plane (e.g. a bimorph cantilever), the first moment of area equals to zero. As a result, there is no coupling between u(x,t) and w(x,t) and therefore no axial displacement is caused by the base displacement w b (x,t). In other words, all submatrices and vectors containing superscript bb or ab become zero and the number of calculations is reduced significantly. More Details are referred to (Ertruk and Inman D 2011).

Cp in Eq. (25) is internal capacitance of piezoelectric material and for series connection of piezoelectric layers, is calculated from:

$$C_{p} = \frac{{\varepsilon_{33}^{S} A_{p} }}{{2h_{p} }}$$
(37)

where, \(\varepsilon_{33}^{S}\) is the permittivity coefficient at constant strain and A p is the area of piezoelectric in xy plane. Proportional damping matrix is calculated by:

$$\left[ {\begin{array}{*{20}c} {d^{aa} } & { - d^{ab} } \\ { - d^{ab} } & {d^{bb} } \\ \end{array} } \right] = \mu \left[ {\begin{array}{*{20}c} {m^{aa} } & { - m^{ab} } \\ { - m^{ab} } & {m^{bb} } \\ \end{array} } \right] + \gamma \left[ {\begin{array}{*{20}c} {k^{aa} } & { - k^{ab} } \\ { - k^{ab} } & {k^{bb} } \\ \end{array} } \right]$$
(38)

in which μ and γ are mass and stiffness coefficients calculated by:

$$\frac{\mu }{{2\omega_{i} }} + \frac{{\gamma \omega_{i} }}{2} = \zeta_{i}$$
(39)

in which ζ i is modal damping coefficient and ω i is the ith natural frequency. f in Eq. (24) is the N × 1 forcing vector. Each element of this vector is calculated by:

$$f_{i} = - \int\limits_{0}^{L} {\left( {\rho_{s} A_{s} + \rho_{p} A_{p} } \right)\phi_{i} \left( x \right)\frac{{\partial^{2} w_{b} (x,t)}}{{\partial t^{2} }}dx}$$
(40)

3 Optimal shape design methodology

To present the utilized AIS terminology and methodology, at first, the biological immune system is discussed. Generally, the duty of the biological immune system is to keep the body safe from pathogenic organisms. Lymphocyte, which is a subset of white blood, is the most intelligent and dynamic part of the whole biological immune system that specifically determines immunity process. The external micro-organisms, who attack the body, are called antigens and the lymphocyte tool against them is known as antibody.

The process for generating antibodies that has greater binding affinity to antigens is called clonal selection. Enveloping the antigens prevents them to be fed and consequently results in killing them. In other words, biological immune system evolutionary optimizes the type and the sizes of generated antibodies in order to find the proper antibodies for surrounding and removing antigens. AIS uses similar strategy for finding the best solution for an optimization problem.

Each fitness objective for optimization problem is considered as an antigen, while design parameters as antibodies are the tools to conquer antigens.

Figure 3 schematically shows how each antigen (fitness) can be surrounded by its proper antibody. Some antigens may require more than one antibody to be removed completely.

Fig. 3
figure 3

Antigen and related antibody colony

Full size image

The relation between fitness (antigens) and parameters (antibodies) are defined in a library by means of domain engineering knowledge. Proposed intelligent AIS flowchart defined in this research is enhanced with the following specifications:

  • Library of antibodies: A knowledge-based library of relationship between different design goals (removing antigens) and design parameters (antibodies) is prepared, based on the engineering knowledge.

  • Feasible search: In order to guide the evolutionary algorithm to feasible solutions, exploring regions of these algorithms can be limited through incorporating expert knowledge of the system.

  • Multi-objective weakness analysis: The proposed method analyzes the amount of difference in defined fitness values for each solution. Considering the weakness of each fitness, proper design modification is suggested from the library of antibodies.

  • Supervisory loop: A supervisory control loop is going to be implemented in the design flowchart, which is responsible for dynamically modifying design and optimization algorithm. After a specific number of design evolutions of the main loop, a supervisory loop evaluates the performance of the design process, and dynamically and intelligently tunes optimization procedure by changing the conduction rate of AIS different techniques.

In order to develop new system configuration, different strategies are defined for cooperation and proliferation of antibodies in AIS. The main technique is clonal selection (Brownlee 2011). Generally, clonal selection algorithm (CLONALG) is used for minimizing a fitness function. The proposed intelligent CLONALG algorithm in this research works as following:

  1. 1.

    Generating a set of N candidate solutions (colony of antibodies).

  2. 2.

    Selecting n 1 highest affinity colonies relative to the antigen set and the function being optimized. Affinity refers to the degree of binding antibodies colonies with the antigens.

  3. 3.

    Generating identical copies of these n 1 selected colonies. This technique is called selection.

  4. 4.

    Selecting n 2 highest affinity colonies and analyzing the weakness points by evaluating fitness values. Referring to proper antibody library to decide for proper mutation.

Mutating with high rates (hypermutation) these selected n 2 colonies with a rate inversely proportional to their objective affinities. This technique is called hypermutation.

  1. 5.

    Replacing some low affinity colonies by randomly generated new ones makes n 3 remaining colonies. This technique is called metadynamic.

  2. 6.

    Analyzing the performance of optimization by investigating the best solution modification. Tuning the optimization parameters, such as n 1 , n 2 , n 3 .

  3. 7.

    Repeat steps 2 through 5, until a defined terminating condition is reached.

4 Case study

4.1 Problem definition

The objective of the present work is to harvest energy from an industrial magnetic vibratory feeder, utilized for conveying and distributing iron ore. The feeder is vibrated in 50 Hz frequency and 0.6 mm displacement amplitude, imposed by an AVITEQ “MV D 50-4” motor.

The designed energy harvester is going to provide the required power for an accelerometer sensor. In order to harvest the generated power continuously, the power is stored in a super capacitor via an electric circuit. Obtained voltage from the open circuit known as reasonable benchmark for optimization. Detail of electric circuit is not the research objective of the current paper and is not discussed.

Figure 4 demonstrates a magnetic vibratory feeder manufactured by FMS Company, on which the energy harvester is going to be installed.

Fig. 4
figure 4

Magnetic vibratory feeder, vibrating at 50 Hz

Full size image

4.2 Analytical optimization

It has been proved that when energy harvester vibrates at its fundamental frequency, induced strain would be maximized and eventually the output power becomes maximum (Ertruk and Inman 2011).

Optimization assumptions for tuning the design parameters are discussed here. Piezoceramic length, substructure length, substructure thickness, and tip mass weight are optimized continuously in feasible range. Piezoceramic thickness is tuned in the range which is available in market. Number of the layers can be varied between one and two (unimorph and bimorph cases). The cantilever width shape is considered symmetric and each boundary is defined by a 3rd order polynomial equation.

Fitness objectives and constrains, according which the process is designed, are listed below:

  • Generating maximum power.

  • Minimizing piezoelectric volume.

  • Stress ratio which is defined as the ratio of Max. to Min. stresses along the beam is supposed to be under 1.2.

  • The fundamental frequency of the energy harvester should be in 2 % tolerance of the feeder’s working frequency (i.e. 50 ± 1 Hz).

  • Tension in piezoceramic and substructure materials should be lower than their correspondent fatigue strength.

Mechanical properties of the utilized PZT-5A piezoceramic and substructure are presented in Table 1.

Table 1 Material properties
Full size table

Modal damping coefficients for the first and second vibration modes are considered 0.05 and 0.055 respectively, identified by half-power points method in the frequency domain. Proposed AIS tool, enhanced with domain knowledge library, is utilized as the optimization tool for designing the desired energy harvester. Here, the constraints and fitness functions are assumed as antigens, while design parameters are the antibodies.

The domain knowledge library determines the binding affinity between antibodies and antigens. In other words, it defines the design parameters’ behavior in order to overcome the constraints and the criteria of the fitness functions. For instance, in order to acquire uniform stress along the cantilever, the boundary equation should be modified only, and the substructure thickness is not affected. As another example, when the stress in piezo layer exceeds the fatigue strength, the boundary equation and piezo thickness should be adjusted. Two examples are schematically illustrated in Fig. 5.

Fig. 5
figure 5

AIS strategy for multi-objective optimization

Full size image

Considering the colony size (number of antibody population in each generation) as 200, and the maximum number of generation as 500 in AIS optimization process, final dimension data acquired from cantilever optimization are presented in Table 2.

Table 2 Optimized cantilever dimension data. All dimensions are in millimeters
Full size table

Figure 6 shows the initial purchased bimorph piezoceramic cantilever from GUOLIN Company.

Fig. 6
figure 6

Original shape of the bimorph cantilever beam

Full size image

The dimensions of the original bimorph are as the following; the total beam length: 73 mm, substructure thickness: 0.412 mm, substructure length: 62 mm, piezo thickness: 0.15 mm and piezo length: 52 mm.

Figure 7a demonstrates the shape of the optimal solution. The original bimorph was then cut by the engraving laser machine in order to obtain the exact optimal shape, shown in Fig. 7b. Kim et al. proved that the laser cutting does not have major effect on the electrical properties of the piezoelectric cantilevers (Hyunuk 2008).

Fig. 7
figure 7

Optimal designed and manufactured cantilever beam

Full size image

The optimized cantilever successfully satisfies the defined design objectives. Analytical study shows that the 1st natural frequency of the piezo’s original rectangular shape has been shifted from 107.2 to 49.81 Hz. The peak frequency in frequency response function (FRF) diagram of the normalized output voltage, determines the 1st natural frequency shown in Fig. 8. The base displacement amplitude is assumed to be constant and equal to 0.6 mm.

Fig. 8
figure 8

FRF diagram of the normalized output voltage

Full size image

According to Fig. 8, a lower maximum voltage value for optimized shape is observed, comparing to the original shape. The reason is considering constant amplitude for transvers base vibration through analysis. This is a fact that the acceleration amplitude and consequently the exerted force are related to the square of the excitation frequency and linearly related to the base vibration amplitude. Therefore, due to the lower peak frequency of the optimized shape, the generated voltage at the fundamental frequency is decreased. It should be noted that the original shape generates almost negligible voltage at 50 Hz working frequency.

In order to investigate uniformity of stress distribution a ratio of the maximum to the minimum stress along the piezoceramic layer is defined; which is 5.58, while for optimized shape it is successfully decreased to 1.19 which is in defined range.

As illustrated in Fig. 9 stress along piezo layer in original shape is decreasing significantly from base to the end of the cantilever, so that, the ending part is not efficiently being used for the voltage generation.

Fig. 9
figure 9

Normalized stress in piezo layer at fundamental frequency

Full size image

Encouraging result for uniform stress distribution in the optimized shape in comparison with the original shape is presented in Fig. 9.

4.3 Test experiments

In this section, test equipment, test process and the results are discussed. A function generator for generating harmonic signal and an oscilloscope for displaying output voltage of energy harvester, both made by HAMEG Instruments, are used. Internal resistance of the oscilloscope is 10 MΩ, which is big enough to assume open circuit condition.

The voltage generated by CUSSONS vibrator derive unit is used to stimulate the DERRITRON TV2MM type shaker. Base displacement is measured by a RION VM82 manual vibration meter. The experiment setup is demonstrated in Fig. 10.

Fig. 10
figure 10

Experiment set

Full size image

The cantilever energy harvester is clamped to the vibrating shaker. Desired amplitude and frequency of the voltage wave function are tuned in the function generator and are amplified via vibrator derive unit. To control the cantilever base displacement, the vibration meter is installed exactly on the center of the base. The output voltage can be observed on the oscilloscope.

The output voltage of the energy harvester for constant 0.6 mm base displacement and different frequencies are tested, and shown in Fig. 11. The results show a peak in the voltage at 107 Hz for original shape, and 51 Hz for the optimized shape with tip mass, which shows good agreement with the analytical optimization.

Fig. 11
figure 11

FRF diagram of the output voltage

Full size image

4.4 FEM analysis

Exact models of both original and optimized cantilever energy harvester have been modeled in FE software, as shown in Fig. 12. Material properties are defined according to Table 1.

Fig. 12
figure 12

Modeling of optimal energy harvester in FE software

Full size image

In the first step, an Eigen frequency FE analysis (open-circuit condition) is performed, in order to calculate the fundamental frequency, which resulted 107.145 and 50.275 Hz for original and optimized shapes respectively. The response of the system in frequency domain is studied, considering electrical circuit with total impedance equal to oscilloscope impedance. The results are demonstrated in Fig. 13.

Fig. 13
figure 13

FRF diagram of output voltage

Full size image

Stress behavior, along the piezo length, is also derived via FE method. Stress concentration effect of cantilever at base joint is the reason of stress increase in that region, comparing to theoretical simulation. The comparison diagram is presented in Fig. 14. It should be noted that the sudden stress increase in the beginning of optimized cantilever is happened due to the stress concentration consideration in FE analysis.

Fig. 14
figure 14

Normalized Von-Misses stress along the piezo length in fundamental frequency

Full size image

Figure 15 clearly shows uniformity of Von-Misses stress distribution on the piezoelectric layer after optimization, while in the original shape, not all the piezo layers have been used efficiently for power generation.

Fig. 15
figure 15

Von-Mises stress distribution on piezo layer. a Original shape without tip mass b and optimized shape with tip mass

Full size image

5 Conclusion

The authors derived the equations of Euler–Bernoulli/Rayleigh–Ritz cantilever for both unimorph and bimorph configurations, considering variable layers width, length and thickness.

Test verification of equations around peak frequency indicated the close agreement between simulation equations and test results which reasonably ensured accuracy of further optimization process. The equations were used for multi-objective shape optimization of cantilever. For the first time, AIS optimization tool enhanced with the domain engineering library have been proposed in piezoelectric energy harvesting field to effectively explore different feasible configurations of energy harvesters.

Optimization objectives included maximum power output, uniform stress along piezoceramic, and minimum piezoceramic volume. Constraints such as setting the natural frequency of energy harvester equal to desired working frequency and failure check of piezoceramic material were taken into account.

We manufactured the optimized shape with variable width by use of laser engraving machine. In addition, theoretical simulation results were successfully verified by FE analysis.

The resulted values for natural frequencies out of theoretical analysis, experiments and FE analysis, have been reported as 49.81, 51 and 50.275 Hz respectively. In addition, Von-Misses stress distribution also demonstrated good agreement with diagram drawn by derived theoretical equations, except the stress concentration on the edges.

Moreover, it was observed that the laser machining does not change the piezoelectric behavior significantly.