Simplified robust and multiobjective optimization of piezoelectric energy harvesters with uncertain parameters

Abstract

Harvesting energy from mechanical vibrations using piezoelectric materials presents itself as an interesting alternative energy source, particularly for embedded and integrated designs considering the high electric charge density that can be stored in these materials. To amplify the amount of energy available at narrow predefined frequency ranges, resonant cantilever devices are usually considered. Nevertheless, energy output is still small and highly sensitive to device parameters, mounting and operating conditions. Thus, these devices must be designed using optimization techniques, to ensure maximum extraction of energy available, and accounting for uncertainties in parameters, mounting and operating conditions. This work presents two methodologies to design cantilever piezoelectric energy harvesters using deterministic and robust optimization and accounting for the presence of uncertain parameters. The proposed methodology employs an electromechanical coupled finite element model to estimate mean and variance of harvestable power for given base excitation and parametric uncertainties. The electromechanical model is then used in two design methodologies, a robust design based on Taguchi’s method and a multiobjective deterministic Compromise Programming method. Both methods are shown to be capable of providing design solutions that allow maximization of nominal or mean harvesting performance and minimization of variability (increased robustness). As general design guidelines, it is shown that devices with larger mass lead to better mean performance but also to higher variability, thus a compromise solution is advisable. Also, a reduction of the effective harvesting circuit resistance, from nominally optimal value, may improve robustness without substantial decrease in mean performance.

1 Introduction

Energy consumption has been increasing considerably in last decades, encouraging researchers to study alternative energy sources. Also, powered devices located in isolated places or with difficult access, such as wireless sensor networks, sensors in road bridges, devices for animal tracking, devices placed inside living bodies such as pacemakers, and global positioning systems (GPS), still rely strongly on batteries with limited capacity, life span, durability and sustainability. Furthermore, the technological breakthrough that some computer components have experienced in recent years is well above the increase in energy density of batteries (Rafique 2018). Thus, the design of self-powered systems and devices presents a great technological advantage in the sense that batteries may last longer or even be unnecessary, leading to more useful computers, wearable and portable electronic devices. This development requires the search for new and alternative energy sources that could also be standalone and/or portable. One potentially interesting idea would be to harvest energy from different environmental sources, such as mechanical, thermal, chemical, electromagnetic and wind power sources (Lesieutre et al. 2004). In this context, the term energy harvesting is directly related to the process of conversion of energy into electricity from environmental sources for different uses. Particularly, in this work, the focus relies on harvesting usable and frequently wasted electrical energy from mechanical vibration signals.

There are some alternatives to harvest energy from moving objects by installing a device to it that would somehow capture and transform its motion into usable energy. The main difference between them is the transduction method needed to convert ambient motion into electric energy, the most known being the electromagnetic (dynamo), but electrostatic and piezoelectric converters are increasingly used, particularly for small-scale generators where electromagnetic transduction poses an operational challenge (Mitcheson et al. 2008; Narita and Fox 2018). Whenever ambient motion can induce structural vibrations leading to oscillatory strains in harvesting device elements, piezoelectric materials can be considered as the conversion transducers. Piezoelectric materials are composed of electric dipoles that move within the material when an external strain or electrical field is applied to generate electricity (direct effect) or strain (inverse effect), respectively (Leo 2007). They present as advantages high energy densities and absence of moving parts such that small-scale devices can be achieved (Erturk and Inman 2011). The most common piezoelectric harvesting device construction exploits resonant cantilever beams in which the piezoelectric material is installed, aiming at transforming small base motions into larger strains in the piezoelectric converter (Sodano et al. 2004; Dutoit et al. 2005; Erturk and Inman 2011; Godoy et al. 2014).

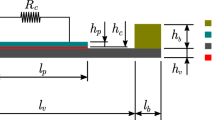
Figure 1 presents a schematic representation of a typical cantilever piezoelectric harvester composed of a tip mass, a cantilever beam (substrate), a piezoelectric patch adhesively bonded to the substrate, a harvesting circuit represented by a simple resistive load, and a clamp that is attached to the moving object (vibration source). The general idea is to design the cantilever beam stiffness and tip mass inertia parameters such the fundamental resonance frequency of the device matches the base excitation frequency, such that the vibration amplitude is maximized. The deformation of the cantilever beam induces strains in the piezoelectric patch which, in turn, induces electric charges in its electroded surfaces that are harvested by the electrical circuit. Besides the frequency tuning, the amount of harvestable energy can be maximized by properly optimizing geometrical and material properties of the device components, such as substrate elastic modulus, length and thickness, tip mass density and geometry, piezoelectric patch material, length, position, shape and thickness, circuit effective resistance and dynamic behavior, among others (Godoy et al. 2014; Salas et al. 2018).

Fig. 1

Schematic representation of a typical cantilever piezoelectric energy harvester

Various standard deterministic optimization algorithms may be used to perform such harvesting devices design. Depending on the solution space and the convexity of the global cost function, one may consider either mathematical programming techniques, such as Sequential Quadratic Programming (SQP), among others, or metaheuristic techniques, such as Genetic Algorithms (GA), Particle Swarm Optimization (PSO), among others (Rao 2009).

Deterministic optimization techniques have been used extensively for improving the performance of structures with piezoelectric elements, including not only energy harvesting applications, but also for passive and active control and structural health monitoring. The optimization of location, shape and distribution of the piezoelectric elements received much attention is the last two decades (Frecker 2003; Trindade 2007; Rupp et al. 2009; Benasciutti et al. 2010; Ducarne et al. 2012; Godoy et al. 2014; Tikani et al. 2018; Nabavi and Zhang 2019). Even in deterministic problems, multiobjective optimization techniques are often required for the design of such piezoelectric structures (Chattopadhyay and Seeley 1994; Kim et al. 2015; Datta et al. 2016; Franco Correia et al. 2017; Salas et al. 2018; Liseli et al. 2019; Lopes et al. 2021). Nevertheless, although nominal harvested energy can be maximized using deterministic optimization methods, uncertainties generally are inherently present in the device parameters themselves and/or mounting between the device and moving object and/or operating conditions of the moving object and device. Thus, these uncertainties must be accounted for in the design and/or optimization process in order to achieve more robust and/or reliable designs.

The effect of uncertainties on the performance of piezoelectric energy harvesters has been studied in a few previous works (Ali et al. 2010; Godoy and Trindade 2012; Franco and Varoto 2017; Aloui et al. 2019), which mostly dedicated efforts in assessing the effects of uncertainties arising from geometric, material properties, and electric parameters on the overall performance of the energy harvesting system. As previously mentioned, the majority of base driven energy harvesting models employ the cantilever beam model with a rigid tip mass at the beam’s free end, shown in Fig. 1. In practical engineering applications, the cantilever boundary condition is nearly impossible to be achieved. Reproduction of the theoretical zero deflection/slope requires infinite values of the equivalent linear and angular stiffness at the boundary. In practice, a reasonable attempt to achieve this condition comprises of sandwiching an extra portion of the beam’s length through a clamping device. Hence, independently of its geometry and material used to build the clamping device, it will present some level of compliance, being subjected to elastic deformations under the base driven input signal. Moreover, if the clamping device contains bolts and nuts, which is often the case, these can be subjected to variations in the tightening torque due to the surrounding vibration, which in turn can affect the overall performance of the harvesting system. Hence, it is desirable to have a theoretical energy harvesting model that can account for possible variations on the boundary conditions due to the practical imperfections just mentioned.

As it will be discussed in details later, the present work employs a dynamic model of the energy harvesting system that can account for uncertainties on the boundary condition parameters. The model replaces the ideal zero deflection/slope condition by equivalent linear and torsional spring constants. These parameters can then be varied according to a given uncertainty framework in order to predict variations on the boundary conditions of the energy harvesting system under investigation. Uncertainties in boundary conditions has been previously studied in beam systems (Ritto et al. 2008), but not in the context of piezoelectric energy harvesting. Additional investigations were performed proposing methods to identify the unknown boundary parameters (Pabst and Hagedorn 1995; Ahmadian et al. 2001; Ritto et al. 2016; Joo et al. 2017; Hermansen and Thomsen 2018). Despite being also valuable source of information, the aforementioned contributions do not convey an appropriate sensitivity or uncertainty analysis of the parameters involved. Therefore, among other specific goals, the present study proposes to investigate the energy harvesting performance under uncertain boundary characteristics, which represents an incremental contribution to the general area of design and optimization of piezoelectric energy harvesting systems, since no similar study has been reported so far.

To account for uncertainties in the design and optimization process, specialized techniques must be considered rather than deterministic or nominal optimization. Well-known robust design and optimization approaches may be used, such as robust design optimization (RDO), reliability-based optimization (RBO) and fuzzy optimization (Schuëller and Jensen 2008). In the first case, the sensitivity concept is addressed such that design solutions that are less sensitive to variations in the environment are defined as robust designs. Alternatively, in RBO, failure probabilities are established in terms of input variability and the idea is to search for design solutions that minimize these failure probabilities. In fuzzy optimization, uncertainties are based on possibility theory and modeled as fuzzy numbers considering the subjectivity of the analyst (Beck et al. 2012; Lü et al. 2021). In all cases, one important step is to estimate the mean and variance of the objective function, such as the harvested energy (Mann et al. 2002), that can then be considered as target functions in weighted or multi-objective optimization (Kim et al. 2017) and/or to build worst-case scenarios (Hosseinloo and Turitsyn 2016) or failure probabilities (Seong et al. 2017).

The estimation for mean and variance is an important task in robust optimization, in which, for instance, after a sensitivity analysis designs less sensitive to sources of variability may be chosen (Zang et al. 2005). Thus, a substantial effort must be dedicated in precise and cost-effective methodologies for this estimation (Park et al. 2006; Schuëller and Jensen 2008; Carneiro and António 2019). Provided a stochastic model is available for the uncertain parameters, which can be used to produce as many samples or realizations required, Monte Carlo Simulation (MCS) method may be used to calculate, with good enough precision, the mean and variance of the objective function. Nevertheless, the total computational cost increases rapidly with the cost of objective function evaluation and the number of samples required for satisfactory convergence. Alternative methods to provide less expensive estimations of mean and variance of the objective function, such as First-order Taylor Approximations (FTA), Polynomial Chaos Expansions (PCE), Karhunen-Loève Expansions (KLE), Artificial Neural Networks (ANN), among others, are the object of several recent research efforts (Sudret et al. 2017; Beyer and Sendhoff 2007; Park et al. 2006; Paiva et al. 2017).

Typically, variability decreases in RDO problems whereas the mean value increases such that the analyst must establish the criteria to achieve the best-compromise between mean and variance. In this case, multi-objective optimization can be employed to achieve design variables or parameters that minimize/maximize different functions one at a time (Lobato and Steffen 2017). Additionally, the concept of Pareto-front is assumed for decision making since a set of ideal points is found in multi-objective optimization. In other words, the Pareto-front is an efficient frontier in which points are found in convergence criterion and each point cannot be changed without compromising other goals (Marler and Arora 2004). Hence, the analyst can choose subjectively a point in the frontier according to another specific criteria. Thus, a formulation for Bi-Objective Robust Design (BORD) is presented in this work to assure satisfactory trade-offs between mean and variance harvested energy to design cantilever piezoelectric energy harvesters with uncertainties in selected parameters. The BORD method defines weighting factors for the mean and variance functions aiming at finding a compromise solution based on the concept of maximum or $L_\infty$. This technique is derived from the Compromise Programming (CP) method (Chen et al. 1999).

A simpler methodology with no need for specific methods to estimate mean and variance put forward by Taguchi (Tsui 1992), that is based on the concepts of robustness and sensitivity, may be used to choose between a set of nominally optimal design parameters that yield lower sensitivity or higher robustness. The method involves the construction of so-called orthogonal arrays that contain a number of combinations of design and uncertain parameters to evaluate the sensitivity, mean and variance. Due to the limited number of columns and rows in these arrays, the number of analyzed solutions is restricted, but it is a quite simple and computationally inexpensive way to obtain relevant information on the optimality and robustness of a set of solutions and may be also used for comparison purposes.

In this work, robust design of cantilever piezoelectric energy harvesters when subjected to uncertainties in certain device, mounting and environmental parameters, namely the effective circuit resistance, the imperfect clamping stiffness and the effective damping factor, is studied. Two methodologies are considered, Taguchi’s method and CP method. For the latter, First-order Taylor Approximations are used to estimate the mean and variance. The harvestable energy for given base excitation and parametric uncertainties is predicted using an electromechanical coupled finite element model. The results and conclusions obtained with the two methods are analyzed. The main novel contributions of the manuscript are: (i) the study of the effect of imperfect clamping on energy harvesting devices performance and robustness, proposing a model able to account for uncertainties on the clamping conditions and (ii) the application of simple yet conclusive methodologies to identify important parameters and design adaptations to improve robustness of energy harvesting devices.

2 Finite element model of a cantilever piezoelectric energy harvester considering imperfect clamp

The general setup for the energy harvesting device considered in this work, schematically represented in Fig. 2, is composed of a cantilever beam (substrate) with uniform rectangular cross-section, length $l_v$ and thickness $h_v$, a piezoelectric patch with length $l_p$ and thickness $h_p$ adhesively bonded to the beam’s upper surface at a distance $d_p$ from the clamp, a cubic tip mass with length $l_b$ and height $h_b$ rigidly fixed to the free end portion of the cantilever beam, and an electric resistor $R_c$ connected to the piezoelectric patch upper and lower electrodes. The imperfect clamping of the harvesting device is simulated using linear and torsional springs, with constants $k_w$ and $k_\theta$, respectively. The width of cantilever beam, piezoelectric patch, adhesive layer and tip mass are the same.

Fig. 2

Schematic representation of the cantilever piezoelectric energy harvester considering imperfect clamp

A finite element model, based on (Santos and Trindade 2011), is proposed to evaluate the motion transmissibility frequency response function (FRF) of electric power output P for given base excitation input $w_0$. The model assumes three perfectly-bonded independent layers, where the core (intermediate) layer is allowed to present transverse shear strains and is modeled using Timoshenko theory, whereas the face (external) layers are not and are modeled using Bernoulli-Euler theory. The model also fully accounts for direct and inverse electromechanical coupling leading to mechanical (displacements) and electrical (charges) degrees of freedom.

After assembling for all finite elements, the linear and torsional springs, $k_w$ and $k_\theta$, and the tip mass translational and rotational inertias, $M_t$ and $I_t$, are added to the proper mechanical degrees of freedom (transverse displacements and cross-section rotations). In fact, since the tip mass is placed on a portion of the substrate, their composition is modeled as a single rigid body which centroid is offset from the rightmost finite element node (at the lower-left edge of the tip mass in Fig. 2) and, thus, the rotational inertia $I_t$ is evaluated relative to this point and a inertia coupling term $\bar{x}M_t$ between transverse displacement and cross-section rotation is also added to the mass matrix. $\bar{x}$ is the longitudinal component of the distance between the rightmost node and the composed tip mass centroid.

Equations of motion are written in terms of the relative motion between the cantilever beam and base excitation, defined as $\mathbf {u}_r = \mathbf {u} - \mathbf {L} w_0(t)$, where $\mathbf {u}$ is the absolute generalized displacements of the cantilever beam and $\mathbf {L}$ is a boolean column vector in which only elements relative to the nodal transverse displacements are unitary. Then,

$$\begin{aligned} \mathbf {M}_{rr} \ddot{\mathbf {u}}_r + \mathbf {K}_{rr} \mathbf {u}_r -\bar{\mathbf {K}}_{me} q_c&= -\mathbf {M}_{rw}\ddot{w}_0(t), \end{aligned}$$

(1)

$$\begin{aligned} R_c \dot{q}_c - \bar{\mathbf {K}}^\mathrm {t\,}_{me} \mathbf {u}_r + \bar{K}_e q_c&= 0, \end{aligned}$$

(2)

where $\mathbf {M}_{rr}$ and $\mathbf {K}_{rr}$ are the mass and mechanical stiffness matrices. $\bar{\mathbf {K}}_{me}$ and $\bar{K}_e$ correspond to the piezoelectric and dielectric stiffnesses. Constant $R_c$ is an electrical resistance representing the equivalent load of the energy harvesting circuit connected to the piezoelectric patch. Variable $q_c$ stands for the electric charges that flow between the piezoelectric patch electrodes and harvesting circuit. Vector $\mathbf {M}_{rw}=\mathbf {M}_{rr} \mathbf {L}$ is formed by summation of mass matrix terms and leads to the distribution of the acceleration input as an equivalent transversal inertia force applied to the relative transversal displacements.

To reduce the computational cost, a model reduction based on projection onto a truncated mass-normalized undamped modal basis $\varvec{\phi }$ is considered. The mechanical degrees of freedom are then approximated by $\mathbf {u}_r\approx \varvec{\phi }\varvec{\alpha }_r$ and considering a harmonic base excitation, such that $\ddot{w}_0(t)=\tilde{a}_0\, e^{j\omega t}$, the reduced equations of motions are written as

$$\begin{aligned} (-\mathbf {I}\omega ^2 +j2\omega \varvec{\varLambda }\varvec{\varOmega } + \varvec{\varOmega }^2)\tilde{\varvec{\alpha }}_r - \mathbf {K}_p\tilde{q}_c&=\varvec{\phi }^\mathrm {t\,}\mathbf {M}_{rw}\tilde{a}_0, \end{aligned}$$

(3)

$$\begin{aligned} ( j\omega R_c +\bar{K}_e)\tilde{q}_c - \mathbf {K}_p^\mathrm {t\,}\tilde{\varvec{\alpha }}_r&=0, \end{aligned}$$

(4)

where $\mathbf {I} =\varvec{\phi }^\mathrm {t\,}\mathbf {M}_{rr} \varvec{\phi }$, $\varvec{\varOmega }^2 = \varvec{\phi }^\mathrm {t\,}\mathbf {K}_{rr} \varvec{\phi }$, $\mathbf {K}_p = \varvec{\phi }^\mathrm {t\,}\mathbf {K}_{me}$. Also, an ad-hoc diagonal modal damping matrix $\varvec{\varLambda }$ is assumed. $\tilde{\varvec{\alpha }}_r$ and $\tilde{q}_c$ are the corresponding modal displacements and electric charge amplitudes.

By solving (3) and (4), it is possible to evaluate the electromechanical coupled system response, in terms of transverse displacements along the cantilever beam and/or electric charge induced in the electric circuit, for a known base acceleration input. To allow comparison with experimental results that are given in terms of point acceleration measurements at the tip mass, the acceleration at the rightmost FE node is defined as $a_t=\mathbf {c}_t\ddot{\mathbf {u}}$, where $\mathbf {c}_t$ is a boolean row vector in which only the element corresponding to the transverse displacement at the rightmost FE node is unitary. For harmonic base excitation input, the tip acceleration output is also harmonic with amplitude $\tilde{a}_t$, that can be written in terms of the modal displacements as $\tilde{a}_t = \tilde{a}_0 - \omega ^2\mathbf {c}_t\varvec{\phi }\tilde{\varvec{\alpha }}_r$. Then, the FRF of tip acceleration output per unit base acceleration input $G_{a_t a_0}(\omega ) = \tilde{a_t}/\tilde{a}_0$ resulting in

$$\begin{aligned} G_{a_t a_0}(\omega ) =1-\omega ^2(j\omega R_c +\bar{K}_e)\mathbf {c}_t\varvec{\phi }\mathbf {D}^{-1}\varvec{\phi }^\mathrm {t\,}\mathbf {M}_{rw}, \end{aligned}$$

(5)

where $\mathbf {D} = (j\omega R_c +\bar{K}_e)(-\mathbf {I}\omega ^2 +j2\omega \varvec{\varLambda } \varvec{\varOmega } + \varvec{\varOmega }^2) - \mathbf {K}_p \mathbf {K}_p^\mathrm {t\,}$.

Besides the electric charge itself, other electric quantities may be considered as outputs. The electric current in the circuit can be defined as $i_c=\dot{q}_c$. It is also possible to evaluate the voltage across the resistance as $V_c = R_c i_c$, such that its amplitude for a harmonic input can be written as $\tilde{V}_c = j\omega R_c \tilde{q}_c$. Thus, the FRF of output voltage per unit base acceleration input $G_{V_c a_0}(\omega ) = \tilde{V}_c/\tilde{a}_0$ is

$$\begin{aligned} G_{V_c a_0}(\omega ) = j\omega R_c\mathbf {K}_p^\mathrm {t\,}\mathbf {D}^{-1} \varvec{\phi }^\mathrm {t\,}\mathbf {M}_{rw}. \end{aligned}$$

(6)

Finally, the potentially harvestable power is approximated by the power dissipated in the purely resistive load, such that $P_c = V_c^2/R_c$. Then, the FRF of peak power output per unit squared base acceleration is written as

$$\begin{aligned} G_{P_c a_0}(\omega ) = \left[ G_{V_c a_0}(\omega )\right] ^2/R_c. \end{aligned}$$

(7)

In the present work, (7) is used to evaluate and compare the potentially harvestable power by using devices depicted in Fig. 2 and also to estimate its variability due to uncertainties in certain parameters.

3 Experimental validation

This section is devoted to describing an experimental analysis that was performed on an unimorph piezoelectric energy harvester in order to validate the theoretical electromechanical model shown in Fig. 2 and described in the previous section. The goal is to measure the electromechanical frequency response functions of the prototype and compare them to the corresponding results from numerical simulations. A diagram of the experimental setup for the tests is shown in Fig. 3 and photos of the actual experimental apparatus used during the tests is shown in Fig. 4. The unimorph piezoelectric energy harvester prototype is made of aluminum (substrate) and fully covered on the upper surface with a PZT-5A monolithic piezoelectric ceramic patch, bonded on the beam’s surface using a high shear strength epoxy adhesive. An aluminum lumped mass is attached to the free end of the cantilever harvester in order to enhance the kinetic behavior and consequently the mechanical to electrical energy conversion process.

The geometrical properties of the harvester prototype are: beam length $l_v=74.7$ mm and height $h_v=1$ mm, adhesive layer height $h_c=0.08$ mm, piezoelectric patch length $l_p=73.6$ mm, height $h_p=0.13$ mm and distance to clamp $d_p=1.1$ mm. All layers are assumed to have equal widths of 12.8 mm. Aluminum was chosen for the beam and PZT-5A for the piezoelectric patch, whose properties are available from manufacturers (Mide Technology 1989). Aluminum material properties are: Young’s modulus 69 GPa and mass density 2700 kg/m$^3$. For the adhesive layer, they are: Young’s modulus 2 GPa and mass density 1126 kg/m$^3$. The piezoelectric material is assumed to be orthotropic and subjected only to transversal electric fields and plane stress, which results in modified properties, according to the literature (Trindade and Benjeddou 2008): $\bar{c}^E_{11}=73.7$ GPa, $\bar{e}_{31}=-18.4$ C/m$^2$, $\bar{\epsilon }^{\varepsilon }_{33}=9.8$ nF/m, mass density 7950 kg/m$^3$.

The tip mass essentially consists of a rigid aluminum square block, of side length 12.8 mm, that is attached to the beam’s end through small stainless steel screws. Thus, the block mass is thus approximately 5.1 g but the total tip lumped mass to be considered in the FE model should also account for additional contributions from the portion of beam underneath the block, the screws, the accelerometer positioned at the top of the aluminum block and a portion of the accelerometer cable. The moment of inertia of the lumped mass is also accounted for in the FRF calculations and was evaluated based on an estimation of the position of center of gravity of composed lumped mass. A first estimation of the lumped mass translational and rotational inertias was $M_t=7.7$ g and $I_t=0.7$ kg mm$^2$.

Signals flows and connection between the instruments used can be seen in Fig. 3. Initially the beam is rigidly mounted on the vibration exciter (Bruel and Kjaer 4809) table through a clamping device, that is used to experimentally approach the elastic boundary conditions of the model, as seen from Fig. 4. Miniature ICP (PCB 352A24 with sensitivity 100 mV/g and mass 0.8 g) uni-axial piezoelectric accelerometers are mounted on the top surface of the clamping device (not shown in the photo) and on the lumped mass at the beam’s free end. The sensor positioned on the clamping device is used to measure the input base acceleration to the harvester and it will be the reference signal to the measured mechanical and electromechanical transmissibility frequency response functions. The accelerometer positioned on the beam’s free end is used to acquire the tip mass acceleration that will further be used to get the mechanical FRF related to the input base motion. A fixed point laser vibrometer (Polytec CLV 700) with the associated control unit (Polytec CLV 1000) is used in order to measure the tip velocity, needed in obtaining the tip mass mobility transmissibility FRF. The voltage generated by the unimorph piezoelectric is acquired in order to obtain the electromechanical voltage per input acceleration electromechanical FRF.

Fig. 3

Diagram of the experimental setup used in tests

Fig. 4

Photo of the actual experimental setup used in tests: a global view and b view zoomed at the energy harvesting device

Based on the experimental setup diagram shown in Fig. 3, signals flow as follows: (1) A 500 mV rms white noise broadband driving signal is generated by the spectrum analyzer (Data Physics QUATTRO) in the 0-100 Hz frequency range and sent to the power amplifier (Bruel and Kjaer Type 2712); (2) The amplifier gain is adjusted and the resulting signal is fed into the vibration exciter; (3) The base drive signal is measured and acquired at the reference channel of the spectrum analyzer; (4)/(5) The piezoelectric layer is connected in parallel to a variable magnitude load resistance adjusted on the resistor box and then fed into the analyzer, where this resulting voltage normalized by the input base acceleration corresponds to the electromechanical FRF from the harvester; (6) Tip mass acceleration is measured by the sensor positioned at the beam’s free end tip mass and the corresponding signal is used to obtain the mechanical accelerance FRF; (7)/(8) The tip mass velocity is measured by the laser sensor head and fed into the analyzer through the vibrometer control unit, and the velocity signal, normalized by the input base acceleration signal is used to get the tip mass mobility FRF.

As previously mentioned, signals were gathered in the 0-100 Hz frequency range. Each frequency domain sampled signal contains 3200 spectral lines thus giving a frequency resolution $\varDelta f = 31.25$ mHz. Since a random type signal was used to drive the vibration exciter, Hanning windows were used in all measured channels in order to reduce possible FRF amplitude distortions due to digital filter leakage (McConnell and Varoto 2008).

The modal damping factor was estimated from the purely mechanical accelerance FRF measured at the tip mass for an electrical load resistance of $R_c = 100\ \varOmega$. This electrical resistance value has been selected to simulate the short circuit (SC) condition. Through the half power method and using the first resonance, a resulting value of 1.1% was predicted for the damping ratio. Later, the electrical resistance $R_c = 1 \ \mathrm {M}\varOmega$ was used to simulate the open-circuit (OC) condition, enabling the determination of the effective modal electromechanical coupling coefficient (EMCC). The effective EMCC is needed in order to quantify the mechanical energy converted into electricity by the piezoelectric patch and may be evaluated according to different methods found in the literature (Trindade and Benjeddou 2009). An alternative for estimating the effective modal EMCC using the i-th natural frequencies $f_{i,oc}$ in OC and $f_{i,sc}$ in SC leads to the following equation

$$\begin{aligned} k_i^2 = \frac{f_{i,oc}^2 - f_{i,sc}^2}{f_{i,oc}^2}, \end{aligned}$$

(8)

where $k_i^2$ is the EMCC for i-th frequency, emphasizing the fact that in this work only the first vibration mode is analyzed. Thus, the material parameters of PZT-5A, the aluminum beam Young Modulus and the tip mass inertia were adjusted aiming at bringing the short- and open-circuit resonance frequencies and the EMCC closer in the experimental and numerical cases.

The total tip lumped mass translational and rotational inertias to be used in the FE model were then adjusted to 9.2 g and 0.8 kg mm$^2$, respectively. This adjustment is potentially due to the contributions of the portion of accelerometer cable and errors in the estimation of individual masses and geometry. The material properties of the PZT-5A and the Young’s modulus of the aluminum beam were also adjusted to: $\bar{c}^E_{11} = 66.3$ GPa, $\bar{e}_{31} = -13.3$ C/m$^2$, $\bar{\epsilon }^{\varepsilon }_{33} = 12.3$ nF/m and 68 GPa for the beam Young’s modulus. Table 1 presents the short- and open-circuit fundamental resonance frequencies, $f_{oc}$ and $f_{sc}$, respectively, obtained from numerical and experimental FRFs after parameter adjustments. The EMCC and the relative error with respect to the experimental results are also presented. Fig. 5 shows the numerical and experimental FRFs of acceleration output measured at the tip mass for OC and SC conditions, indicating that the amplitudes and frequencies are satisfactorily well fitted considering the updated parameters.

Table 1 Experimental and numerical results for the fundamental natural frequencies in short- and open-circuit and corresponding effective modal EMCC

Fig. 5

FRFs of acceleration output for $R_c=100 \ \varOmega$ and $R_c=1 \ \mathrm {M}\varOmega$

Fig. 6

Numerical and experimental FRFs of voltage output for different values of circuit’s resistance $R_c$

The updated model was verified by comparing numerical and experimental results for the FRFs of voltage output considering electrical resistances of 100 $\varOmega$, 1000 $\varOmega$, 10 k$\varOmega$, 100 k$\varOmega$, 500 k$\varOmega$ and 1 M$\varOmega$. These are presented in Fig 6. As expected, the voltage output increases for increasing resistance up to a saturation point when the OC condition is approached. It can be noticed that, in all cases, the numerical results match satisfactorily well the corresponding experimental results. Thus, it is expected that the model would also be able to well estimate the potentially harvestable power output.

4 Robust optimization of piezoelectric energy harvesters

The main known levers for optimizing the energy harvested by resonant piezoelectric energy harvesting devices are: (1) maximization of the effective piezoelectric coupling; (2) proper tuning between base excitation (operating) frequency and device’s fundamental resonance frequency; (3) proper tuning of harvesting circuit impedance; and (4) minimization of mechanical (damping) and dielectric losses. These are all related and sometimes conflicting. For instance, higher effective piezoelectric couplings also lead to a performance that is more sensitive to the circuit’s resistance. The latter affects the effective device’s resonance frequency when coupled with the harvesting circuit. Moreover, by reducing at most all sources of mechanical and electrical losses, the resonance peak becomes sharper and, thus, increasing the performance sensitiveness to mistuning between operating and resonance frequencies.

Also, there are several sources of environmental variabilities and parametric uncertainties that may affect the effective performance of the devices and, thus, lead to a harvested energy that is much smaller than predicted. Thus, it is important to design devices aiming at both performance and robustness. For that, two strategies are proposed in the present work. They were chosen because they do not require too much function evaluations, which seems more practical and less computationally expensive. The first is based on the methodology of orthogonal arrays introduced by Taguchi, and the second estimates the performance mean and variance and searches for a compromise between them.

Assuming that the device’s material properties are constant and that its geometrical properties can be defined in terms of the target resonance frequency and either tip mass or beam length, two design variables are defined: (1) device’s tip mass and (2) circuit’s effective resistance. Also, four uncertain parameters were considered: (1) clamping equivalent transversal stiffness; (2) clamping equivalent rotational stiffness; (3) effective system damping; and (4) circuit’s effective resistance. The first two uncertain parameters were selected since precise estimates of these parameters are often difficult to obtain during the design phase. In fact, most models consider ideal clamping while realistic clampings have some flexibility and, even when well predicted, these may loosen up during device’s operation. The effective system damping is also difficult to be precisely estimated during design phase and, usually, can only be measured for each device after assembling, and may also be subjected to variations over time. The circuit’s effective resistance was considered uncertain mainly due to the fact that a resistance gives only an approximation of the dynamic behavior of a real harvesting circuit.

4.1 Optimization using orthogonal arrays

The first strategy to design devices maximizing the harvested energy and minimizing its variance considers a methodology proposed by Taguchi (Tsui 1992), in which orthogonal arrays are composed of many experiments to evaluate mean, variance and a so-called signal-to-noise sensitivity (S/N) that are used to obtain effect plots (Zang et al. 2005). The orthogonal arrays are built considering so-called inner arrays for control factors and outer arrays for noise factors, and their form depend on the number of levels considered for each factor. Manufacturing imperfections, environmental changes or tolerances can be viewed as noise factors (uncertain parameters). Due to the difficulty of changing process tolerances, control factors (design variables) are chosen appropriately to modify the response and decrease the variance.

The signal-to-noise ratio S/N may be defined differently depending on the design objective but, usually, larger values of S/N mean an increase in robustness. Table 2 presents the most common types of problems considered in terms of range and ideal value of the objective function y, namely: smaller-the-better (SB), larger-the-better (LB), nominal-the-best (NB), and signed-target (ST). The larger-the-better and smaller-the-better relations are used to determine proper control factors that, respectively, maximize and minimize the cost function. When the target values are known, the nominal-the-best and signed-target relations are appropriate, where the latter is considered for null targets (Phadke 1995). For a specific experiment i, the $\text {S/N}_i$ ratio may be evaluated from the objective function realizations $y_{ij}$, where j is the trial number for the observations, their mean $\mu _{Yi}$ or standard deviation $\sigma _{Yi}$. In Table 2, $n_t$ represents the number of trials for each experiment.

For NB and ST problems, it is necessary to adjust or scale the factors to find the target values. An alternative is to deterministically optimize the problem to obtain a target value and, then, to apply the Taguchi method (Park et al. 2006). The analysis is divided into two steps: first, the S/N ratio is maximized to decrease variance and, then, by finding a control factor that does not influence much the S/N ratio, the mean is changed to the target. In some cases, it is not easy to find this control factor, also named adjustment or scale factor. Thus, by first optimizing the problem deterministically, it is possible to choose control factors near the optimum value (Lee and Park 2001).

Table 2 Problem types of optimization using orthogonal arrays in terms of function responses $y_{ij}$ and mean and variance of i-th experiment for $n_t$ trials, $\mu _{Yi} = \frac{1}{n_t}\sum _{j=1}^{n_t}y_{ij}$, $\sigma ^2_{Yi} = \frac{1}{n_t-1}\sum _{j=1}^{n_t}(y_{ij}-\mu _{Yi})^2$ (adapted from (Phadke 1995))

For the energy harvesting problem studied here, the objective function is defined as the harvested power FRF (7) evaluated at a target excitation frequency $\omega _e$, such that $g=G_{P_c a_0}(\omega _e)$. Two design variables (control factors) are considered, the length of the cantilever beam $l_v$ and the circuit’s effective resistance $R_c$, and are stored in a design vector $\mathbf {x}_d = [l_v, R_c]$. The tip mass height $h_b$ is internally optimized for a given solution $\mathbf {x}_d$ to ensure a precise tuning between excitation and resonance frequencies. The distance from clamp and tip mass of the piezoelectric patch is kept at $d_p=1.1\,$mm and, thus, the length of the piezoelectric patch follows the length of the beam such that $l_p=l_v-2d_p$. All other geometrical and material properties are kept constant using the values presented in the previous section. Also, four parameters are considered as uncertain (noise factors), the clamping effective stiffnesses, $k_w$ and $k_{\theta }$, the system effective damping factor $\xi$, and the circuit’s effective resistance $R_c$. They are stored in a vector of uncertain parameters $\mathbf {x}_u = [k_w,\ k_\theta ,\ \xi ,\ R_c]$.

Then, a deterministic optimization is performed to obtain a number of optimal nominal design solutions for reasonable ranges of beam length (or tip mass), such that

$$\begin{aligned} \begin{aligned}&\text {find}&\mathbf {x}_d, \\&\text {maximizing}&g(\mathbf {x}_d), \\&\text {subject to}&\mathbf {x}_d \in \mathbf {X}_d,\\ \end{aligned} \end{aligned}$$

(9)

where $\mathbf {X}_d$ is defined by the lower and upper bounds of the design variables.

Further, the signed-target (ST) problem is used to verify the sensitivity by considering the noise factors $\mathbf {x}_u$ while the function responses are evaluated from the power output at target frequency, such that $y_{ij}=g(\mathbf {x}_d^{(i)},\mathbf {x}_u^{(j)})$. The robustness analysis with the S/N ratio aims to reduce the variability of the problem and at the same time keep the mean power as close as possible to the maximum power value found using (9). In the Taguchi methodology, it is necessary to choose inner and outer arrays for control and noise factors, respectively, to calculate the S/N ratio. Some standard orthogonal arrays with different levels and ways of changing rows and columns can be found in (Phadke 1995). The number of levels corresponds to the quantity of values that each control or noise factor may assume. Because of the finite number of matrix levels in this methodology, the number of devices that can be considered is limited.

Table 3 Definition of experiments (inner array) as i-th combinations of control factor levels, trials (outer array) as j-th combinations of noise factor levels and corresponding ij-th combinations of experiments (rows) and trials (columns) for the evaluation of function responses $y_{ij}$

Here, it was chosen to first design five nominal devices, represented by design variables $l_v$ and $R_c$, using the deterministic optimization problem (9). Then, alternative resistance values are considered for each optimal design. For that, an auxiliary control factor is defined as the circuit’s effective resistance relative to the nominal optimum, $\bar{R}_c = R_c/R_{opt}$. Here, ten levels for the relative resistance $\bar{R}_c$ are considered so that values smaller or greater than the nominal optimum can be tested. This leads to 50 potential solutions (five nominal devices with ten resistance variations for each). Following Taguchi’s methodology, these solutions are represented in a so-called inner array with all combinations (also called experiments), as shown in the left part of Table 3. Next, to account for the uncertain parameters or noise factors, two levels are defined for each noise factor, corresponding to their lower and upper bounds, $\mu _X \mp \sigma _X$. The noise factors levels are combined in a so-called outer array. Here, for four noise factors, $k_w$, $k_\theta$, $\xi$ and $\bar{R}_c$, with two levels each, 8 combinations (also called trials) are defined, as shown in the upper part of Table 3.

With the inner and outer arrays defined, it is then possible to evaluate the function responses $y_{ij}$ for each combination of i-th experiment (row in Table 3) and j-th trials (column in Table 3). Using the present choice of inner and outer arrays, with 50 experiments and 8 trials, this leads to 400 function evaluations. For each one of the 50 experiments (i-th row in Table 3), the function responses corresponding to its 8 trials (columns) are used to evaluate the mean $\mu _{Yi}$, the variance $\sigma _{Yi}^2$ and the signal-to-noise ratio $\text {S/N}_i=-10 \log _{10}\left( \sigma ^2_{Yi}\right)$ (see Table 2). The methodology also returns the effect of each control factor on the mean and variance and, thus, indicates the more robust solutions among those predefined. To evaluate the effect of each control factor, the averages of the means $\mu _{Yi}$ and sensitivity ratios $\text {S/N}_i$ from each row in Table 3 corresponding to a given control factor level are computed. For instance, the mean $\mu _Y$ and $\text {S/N}$ ratio corresponding to level 1 of control factor $l_v$ are obtained from the arithmetic mean of the values of $\mu _{Yi}$ and $\text {S/N}_i$ computed for the experiments with $l_v$ in level 1 ($i=1,6,11,\ldots ,46$). Then, the mean $\mu _Y$ and sensitivity ratio $\text {S/N}$ can be plotted for each control factor level. This allows an approximate analysis of the overall effect of each control factor on mean, variance and sensitivity of the response. This was done for the cases studied in this work and will be presented in Sect. 5.1

4.2 Optimization using compromise programming

The second strategy for designing harvesting devices with satisfactory mean performance and robustness follows the CP methodology (Chen et al. 1999; Marler and Arora 2004). The general idea is to allow the designer to predefine levels of priority between mean performance and robustness and obtain the design solutions that correspond to these criteria. For that, it is necessary to estimate the mean and variance of the objective function for any given potential solution and for known statistical information regarding the uncertain parameters. Thus, this is potentially computationally expensive since the mean and variance estimation are internal to the bi-objective optimization procedure. Here, it is proposed to use First-order Taylor Approximations for this estimation aiming at reducing the total optimization computational cost.

4.2.1 Mean and variance estimation using Taylor series expansion

Uncertainties in device’s parameters induce or propagate to uncertainties or variability in the device’s performance. Based on available statistical information on the parametric uncertainties, it is possible to estimate the mean and standard deviation of the performance output using a Taylor Series expansion (Sudret et al. 2017; Beyer and Sendhoff 2007; Park et al. 2006).

Considering a continuous random vector $\varvec{X} = \{X_1, X_2, \ldots X_n\}$ with n variables and joint distribution $f_\mathbf {X}$, the mathematical expectation for a function $Y = g(X_1, X_2, \ldots X_n)$ can be obtained as follows

$$\begin{aligned} \begin{aligned} E(Y)&= E[g(X_1,\ldots ,X_n)]\\&=\int _{-\infty }^{\infty }\ldots \int _{-\infty }^{\infty }g(x_1,\ldots ,x_n) \, f_{X_1,\ldots ,X_n} \,\mathrm {d}x_1\ldots \mathrm {d}x_n. \end{aligned} \end{aligned}$$

(10)

The function $Y = g(X_1,\ldots ,X_n)$ is analyzed using the Taylor-series expansion about the mean values $\mu _{X_1},\ldots ,\mu _{X_n}$ such that

$$\begin{aligned}&Y = g(\mu _{X_1},\ldots ,\mu _{X_n}) + \sum _{i=1}^{n}(X_i-\mu _{X_i})\frac{\partial g}{\partial X_i} \nonumber \\&\quad +\frac{1}{2}\sum _{i=1}^{n}\sum _{j=1}^{n}(X_i-\mu _{X_i})(X_j-\mu _{X_j})\frac{\partial ^2g}{\partial X_i \partial X_j} + \ldots , \end{aligned}$$

(11)

in which the derivatives are computed in relation to the mean values. Truncation of this expansion using only linear terms leads to

$$\begin{aligned} Y \simeq g(\mu _{X_1},\ldots ,\mu _{X_n}) + \sum _{i=1}^{n}(X_i-\mu _{X_i})\frac{\partial g}{\partial X_i}. \end{aligned}$$

(12)

The mean and variance of (12) can be represented by (Ang and Tang 1975)

$$\begin{aligned}&\mu _Y = E(Y) \simeq g(\mu _{X_1},\mu _{X_2}, \ldots \mu _{X_n}), \end{aligned}$$

(13)

$$\begin{aligned}&\sigma ^2_Y \simeq \sum _{i=1}^{n}\sigma ^2_{X_i}\left( \frac{\partial g}{\partial X_i}\right) ^2 + \sum _{i=1}^{n}\sum _{j=1, j\ne i}^{n} \rho _{ij}\sigma _{X_i}\sigma _{X_j}\frac{\partial g}{\partial X_{i}}\frac{\partial g}{\partial X_{j}}, \end{aligned}$$

(14)

where $\rho _{ij}$ is the correlation coefficient between variables ${X_i}$ and ${X_j}$ whereas $\sigma _{X_i}$ and $\sigma _{X_j}$ are their standard deviations. For independent or uncorrelated variables, the variance (14) is approximated as

$$\begin{aligned} \sigma ^2_Y \simeq \sum _{i=1}^{n}\sigma ^2_{X_i}\left( \frac{\partial g}{\partial X_i}\right) ^2. \end{aligned}$$

(15)

The approximations shown in (13) and (15) are reasonable for functions with weak nonlinearity and negligible correlation coefficients (Benjamin and Cornell 2014). These equations are fundamental for multi-objective and non-deterministic problems allowing to include both the mean and standard deviation in the design criteria.

Considering the harvested power FRF (7) at target excitation frequency as objective function, as done previously, such that $g=G_{P_c a_0}(\omega _e)$ and the set of uncertain parameters $\mathbf {x}_u = [k_w,\ k_\theta ,\ \xi ,\ R_c]$, for which the nominal values are used as mean values and the standard variations are assumed to be known, the Taylor approximations for mean and variance of the objective function can be written as

$$\begin{aligned}&\mu _Y \simeq g({\bar{k}}_w, {\bar{k}}_{\theta },{\bar{\xi }}, {\bar{R}}_c), \end{aligned}$$

(16)

$$\begin{aligned}&\sigma ^2_Y = \left[ \frac{\partial g}{\partial k_w}\right] ^2\sigma ^2_{k_w} + \left[ \frac{\partial g}{\partial k_\theta }\right] ^2\sigma ^2_{k_\theta } + \left[ \frac{\partial g}{\partial \xi }\right] ^2\sigma ^2_{\xi }+ \left[ \frac{\partial g}{\partial R_c}\right] ^2\sigma ^2_{R_c}, \end{aligned}$$

(17)

where the pairs $[{\bar{k}}_w,\ \sigma _{k_w}]$, $[{\bar{k}}_\theta ,\ \sigma _{k_\theta }]$, $[{\bar{\xi }},\ \sigma _{\xi }]$ and $[{\bar{R}}_c,\ \sigma _{R_c}]$ are the predefined nominal values and standard deviations of the uncertain parameters, clamping transversal stiffness, clamping rotational stiffness, effective harvesting circuit’s resistance and effective damping factor, respectively. The first derivative of the objective function with respect to each uncertain parameter can be evaluated using finite differences numerical approximation applied to finite element model.

4.2.2 Definition of the optimization problem

The Compromise Programming (CP) optimization strategy is based on the concept that multiple objective functions are to be extremized (minimized/maximized) at the same time and, since these may be conflicting, an optimal design solution can only attain a compromise between the extremization of the objective functions (Chen et al. 1999). The compromise solution may be found by defining an equivalent global mono-objective function, in which it is required that all individual objective functions $g_i(\mathbf {x}_d)$ tend towards their individual extremes, also called as utopia values ${\bar{g}}_i$. Hence, the multiobjective optimization problem can be stated as

$$\begin{aligned} \begin{aligned}&\text {find}&\mathbf {x}_d\\&\text {minimizing}&\left( \sum _{i=1}^{m}w_i\left| g_i(\mathbf {x}_d) - {\bar{g}}_i\right| ^p\right) ^{1/p}\\&\text {subject to}&\mathbf {x}_d \in \mathbf {X}_d, \\ \end{aligned} \end{aligned}$$

(18)

where $w_i$ are positive weighting factors that define the priority of each individual objective function such that $\sum _{i=1}^{m}w_i =1$. The optimization problem, and thus its solution, also depends on parameter p. The $L_\infty$ or Tchebycheff norm is obtained with $p=\infty$ and is useful to optimize convex and non-convex problems and provide Pareto fronts for compromise solutions according to the chosen weighting factor (Moreira 2015; Lobato and Steffen 2017). The CP method is also known as Weighted Tchebycheff method and may be stated as a min-max problem in the form

$$\begin{aligned} \min _{\mathbf {x}_d\in \mathbf {X}_d} \max _{i} \left\{ w_i \left| g_i (\mathbf {x}_p) - {\bar{g}}_i \right| \right\} . \end{aligned}$$

(19)

Here, the latter problem was considered using the mean and standard deviation of the harvested power output as individual objective functions leading to a bi-objective robust optimization problem posed as

$$\begin{aligned} \min _{\mathbf {x}_d\in \mathbf {X}_d} \max \left\{ w_1 \left| \frac{\mu _Y}{\mu ^\star _Y} - 1\right| , (1-w_1) \left| \frac{\sigma _Y}{\sigma ^\star _Y} -1 \right| \right\} , \end{aligned}$$

(20)

where $\mu ^\star _Y$ is the utopia (maximum) value for the mean harvested power and $\sigma ^\star _Y$ is the utopia (minimum) for its standard deviation. These are obtained by maximizing $\mu _Y$ (16) and minimizing $\sigma _Y$ (17), one at a time, respectively. The normalization of the individual objective functions considerably simplifies the problem of finding weighting factors to obtain the Pareto-front. It is necessary, though, to find the extremes of the individual objective functions through prior optimization. This was performed using genetic algorithm optimization in which, for each candidate design solution $\mathbf {x}_d$, a finite element model is built and used to estimate the nominal (mean) harvested power (16), its numerical derivatives with respect to the uncertain parameters and, then, its standard deviation using the Taylor series expansion (17).

For the implementation of the optimization problem represented by (20), genetic algorithm was used for a set of predefined equally spaced weighting factor $w_1 \in \{0,\ldots ,1\}$ to provide a set of potentially interesting design solutions that may plotted in a Pareto-front. Additionally, a statistical analysis using a box plot chart can be performed to compare the design solutions in terms of confidence intervals.

5 Results for robust optimization

The two robust design methodologies presented in the previous section are then considered to design energy harvesters based on the one that was built for experimental results and model verification. For that and according to Fig. 2, the base material and geometrical parameters of the harvesting device are those already presented. To search for and analyze potential robust design solutions that are similar to the tested harvester, the bounds for the two design variables, namely the cantilever beam length $l_v$ and the effective circuit’s resistance ${R}_c$, are set to $65 \ \mathrm {mm} \le {l}_v \le 85 \ \mathrm {mm}$ and $20 \ \mathrm {k}\varOmega \le {R}_c \le 200 \ \mathrm {k}\varOmega$. Recall that the piezoelectric patch length $l_p$ internally follows the beam length so that a distance of $d_p=1.1\,$mm from clamp and tip mass is always maintained. Similarly, the tip mass height $h_b$ also follows the beam length so that the fundamental resonance frequency of the device is approximately equal to the target excitation frequency of 40 Hz.

For the four parameters considered as uncertain, namely the clamping effective transversal and rotational stiffnesses, $k_w$ and $k_{\theta }$, the system effective damping factor $\xi$, and the circuit’s effective resistance $R_c$, assumptions were made to predefine their nominal (or mean) values and standard deviations. For the effective damping factor, the value identified from experimental measurements of 1.1% was assumed as its nominal and mean value and a ±10% 6$\sigma$-tolerance was used based on additional sets of experiments available. This leads to a relative dispersion (or coefficient of variation) of 3.33%. Nevertheless, an analysis is also performed latter on using a higher relative dispersion of 10%. This is justified by the fact that effective damping comes from several different sources, may vary due to environmental conditions and greatly affects the harvesting performance since it reduces the vibration amplitude. Also, the damping model is a simplification of reality and, thus, its uncertainties also account in some sense for epistemic uncertainties. In the case of the circuit’s resistance, since it is also a design variable, it was considered that its nominal value is the design variable and a relative dispersion of 10% was assumed. A relatively large dispersion for the resistance is justified by the fact that it greatly affects the harvesting performance and also since an effective resistance gives only an approximation of the dynamic behavior of a real harvesting circuit.

Fig. 7

Peak tip acceleration output per unit base acceleration input for varying clamping effective transversal stiffness and different circuit’s resistances

Fig. 8

Peak tip acceleration output per unit base acceleration input for varying clamping effective rotational stiffness and different circuit’s resistances

For the clamping effective transversal and rotational stiffnesses, since no information is yet available, a parametric analysis was performed to identify critical clamping stiffness values that minimally affect the frequency response of the device. This was done using the parameters presented in the experimental validation and three resistance values (10, 100 and 1000 k$\varOmega$). The FRF for base acceleration input and tip acceleration output, $G_{a_t a_0}(\omega )$, evaluated at the target excitation frequency (40 Hz) was numerically evaluated by varying the clamping transversal and rotational stiffnesses, one at a time, and are shown in Figs. 7 and 8. As expected, the response tends to saturate for high enough clamping stiffness and, thus, it may be concluded that higher values of clamping stiffness, representing less imperfect clamping conditions, also lead to smaller dispersion. Then, in order to account for imperfect clamping, it is necessary to consider clamping stiffness values that are smaller than those leading to a saturation in the response. For that, in all cases, the stiffness values that induce a 5% amplitude reduction, as compared to the convergence values, that is for very stiff or perfect clamps, were identified. Then, rounding the average between the extreme critical values leads to $k_w = 50$ kN/m and $k_{\theta }=0.3$ kNm/rad. These are considered as the nominal values and a ±50% 6$\sigma$-tolerance, or 16.67% relative dispersion, is assumed for both stiffnesses. A relatively large dispersion for the clamping stiffnesses is justified by the fact that these parameters are certainly the most difficult to identify, since they greatly depend on the type or construction of the clamping device and its interaction with the clamped portion of the beam.

5.1 Results for robust optimization using orthogonal arrays

To apply Taguchi’s method to the robust design of energy harvesters similar to the one experimentally tested and considering the orthogonal arrays presented in Table 3, first, five potentially optimal devices were determined in five different ranges of beam length. For that, a deterministic optimization was performed considering the bounds presented in Table 4 aiming at finding the devices that maximize the harvested power output in each range. The optimization was performed using a genetic algorithm implementation with 50 individuals, 90% crossover, 30% mutation and 50 iterations. Notice that Taguchi’s method does not allow a continuous design variable, as will be done later on using CP method, since only a few solutions (sets of design variables) can be used and compared in terms of mean performance and robustness.

Table 4 Design variables bounds for the search of optimal devices in each length range and optimal parameters found

As shown in Table 4, the optimal lengths all tend to the minimum of each range. The optimal resistances decrease for increasing beam length. Table 4 also shows the resulting tip mass height and effective mass which also decrease for increasing beam length to assure a proper tuning between excitation and resonance frequencies. The FRFs of voltage and power outputs near the resonance frequency by considering the base acceleration input for the five optimum devices are shown in Figs. 9 and 10. These indicate that, from the five devices considered, the nominal harvested power output is larger for devices with shorter cantilever beams and larger tip masses. This is true for the whole frequency range considered, but especially near the target (resonance or peak) frequency. Previous analyses suggest that this conclusion also applies to cantilever devices with different target frequencies and geometries.

Fig. 9

FRF of voltage output per unit base acceleration input for the five optimal devices

Fig. 10

FRF of power output per unit squared base acceleration input for the five optimal devices

The interest in a robust analysis, optimization and design would be to verify whether these conclusions still hold when there are parametric uncertainties in the devices. The Taguchi’s method is then applied considering known uncertainties in the clamp stiffnesses, damping factor and circuit’s resistance. Thus, $k_w$, $k_\theta$, $\xi$ and $R_c$ are considered as noise factors to build the orthogonal (outer) array. The cantilever beam length $l_v$ and circuit’s resistance relative to the nominal optimum for each nominal device $R_c/R_{opt}$ are considered as design variables or control factors. In practice, when a length $l_v$ is chosen, other parameters are internally defined such as the tip mass height, piezoelectric patch length, nominal optimal circuit’s resistance. Thus, each value of $l_v$ actually represents a specific device design, and there are five of them as shown in Table 4. The relative circuit’s resistance $R_c/R_{opt}$ then allows to vary the resistance from the corresponding nominal optimal value. Ten values were considered for this control factor in the range $0.5\le R_c/R_{opt} \le 1.4$ with a 0.1 step, so that it is possible to verify the sensitivity and potential more robust solutions around the nominal optimal resistance $R_c/R_{opt} = 1$.

As mentioned in Section 4.1, the overall effect of each control factor on mean, variance and sensitivity of the response is analyzed here. For each combination of $l_v$, which represents each device in Table 4, and $R_c/R_{opt}$, the corresponding values of mean, variance and S/N sensitivity are evaluated. First, the effects of each control factor were estimated for a damping factor with 10% of tolerance as displayed in Fig. 11. The two charts in this figure present the effect of each control factor in the mean harvested power and S/N sensitivity. The effect of length $l_v$ on the mean power confirms the results observed in Fig. 10, that is mean power decreases with increasing length (decreasing tip mass). The effect plot also shows, however, that this decrease is accompanied with an increase in robustness as measured by the S/N ratio. Thus, one may conclude that devices with higher beam lengths (smaller tip masses) are less well performing nominally but are also more robust. In terms of circuit’s resistance, both nominal performance and robustness are maximized by the nominal optimal value ($R_c/R_{opt}=1$), which corresponds the level 6 of relative resistance. Additionally, the reduction in the mean power and robustness is more pronounced for lower relative resistance values.

Fig. 11

Effect of control factors on the mean performance and robustness for damping with tolerance of 10%

Fig. 12

Effect of control factors on the mean performance and robustness for damping with tolerance of 30%

A second analysis was performed considering a higher tolerance of 30% for the damping factor. The tolerance for the other noise factors was kept unchanged. Figure 12 shows the effects of the control factors on the mean power and robustness, in which it is noticeable that the effect of beam length is very similar to the previous case. Nevertheless, for the present case, smaller relative resistance values lead to more robust performances. This results suggests that for larger damping, the choice of devices with resistance smaller than the nominal optimal value may be interesting since it may lead to improved robustness with little decrease in mean performance. This is certainly the case of resistance levels 5 (90% of nominal optimal resistance) and 4 (80% of nominal optimal resistance) for which the mean performance is nearly unchanged while the robustness is improved, as compared to level 6 (nominal optimal resistance).

5.2 Robust analysis using Taylor series approximations

Robust analysis using orthogonal arrays is based on the use of discrete controls and noise factors in correlation with the limited numbers of levels in arrays. This methodology is used to calculate the mean, variance and the sensitivity factor corresponding to each row of inner array and to evaluate the effects of each control factor. Thus, this estimation depends on a limited number of levels for each control factor and arrays chosen.

An alternative solution is to use Taylor series approximations as put forward in (16) and (17). This was done here for the energy harvesting problem so that the mean and variance of the peak power output can be estimated for each nominal optimal beam length, and corresponding harvesting device, for various nominal values of circuit’s resistance. The main aim would be to obtain a better assessment of the effect of relative resistance on power output mean and dispersion and also of the cross-effect between relative resistance and damping factor.

For this analysis, various values were considered for the circuit’s resistance, relative to the nominal optimal, such that $R_c/R_{opt} \le 1.5$. The effect analysis was performed for two values of tolerance for the damping factor, $t_{d}=10\%$ and $t_{d}=30\%$. Nominal values and tolerances for all other uncertain parameters were kept unchanged from those discussed in the preceding subsection. Figure 13 presents the mean $\mu _Y$, standard deviation $\sigma _Y$ and coefficient of variation (or relative dispersion) $\delta _Y=\sigma _Y/\mu _Y$ for the device with length of 75 mm, which is closer to the experimentally tested device and for which the properties were presented in Table 4.

Fig. 13

Mean, standard deviation and coefficient of variation of power output of the device with 75 mm length for various relative circuit’s resistance and two damping factor tolerances

The first row in Fig. 13 shows the mean power at different ratios of electrical resistances up to 1.5. As per the Taylor series approximation, the mean power output is equal to the power output evaluated for the mean values of the random variables. Notice, however, that all other parameters are kept unchanged with variation of the resistance. Thus, this may also lead to a mistuning between resonance and operation/target frequency. That is why, the resistance value yielding maximum mean power is slightly smaller than the nominal optimal value, at $R_c = 0.96\, R_{opt}$. Also, the mean power decreases more rapidly when decreasing than when increasing the resistance from the optimal value. This result is independent of the dispersion of the damping factor. On the other hand, the standard deviation of power output behaves differently depending on the damping factor dispersion. For $t_d = 10$% and $0.5 \le R_c/R_{opt} \le 1.5$, the standard deviation is minimal for resistance values slightly smaller than the nominal optimal, at $R_c = 0.94\, R_{opt}$. This resistance value also provides minimum relative dispersion $\delta _Y$. Contrarily, for higher damping dispersion with $t_d = 30$% and $0.5 \le R_c/R_{opt} \le 1.5$, the standard deviation increases almost linearly with the resistance, suggesting that indeed, as also indicated in the Taguchi’s method results, resistance values somewhat smaller than the nominal values may be more interesting for a more robust design. In fact, in this case, the relative dispersion is minimal for a resistance value substantially smaller than the nominal optimal, at $R_c = 0.77\, R_{opt}$. This analysis then indicates that in the presence of higher dispersion in the damping factor, resistance values that are smaller than the nominal optimal should be considered for a better balance between mean performance and robustness.

5.3 Results for robust optimization using CP method

The robust optimization using CP method seeks to directly determine devices with satisfactory compromise between mean performance and robustness without the need to divide the procedure into preliminary optimization to define a small number of good nominal solutions and then to evaluate their robustness as in Taguchi’s method. The CP method also allows the designer to define from the start the relative priority between mean performance and robustness.

Since the objective here is also to obtain a Pareto-front, a number of weighting factors were considered to obtain solutions that are intermediate from the solutions with best nominal performance to the one with best robustness. The CP design solutions are constrained by the bounds for the two design variables previously defined and recalled here, $65 \ \mathrm {mm} \le {l}_v \le 85 \ \mathrm {mm}$ and $20 \ \mathrm {k}\varOmega \le {R}_c \le 200 \ \mathrm {k}\varOmega$.

The first step is to determine the utopia values, namely the maximum mean power $\mu ^\star _Y$ and minimum standard deviation $\sigma ^{\star }_Y$. For each candidate solution, the mean and standard deviation are estimated using Taylor series approximations (16) and (17). The relative dispersions considered for the uncertain parameters are: 16.67% for the clamping stiffnesses, 10% for the circuit’s resistance and 3.33% for the damping factor.

The device leading to the maximum mean power output was found with $l_v = 65$ mm, $h_b=18.58$ mm and $R_c=71\ \mathrm {k}\varOmega$ such that $\mu ^\star _Y = 60.84\ \mathrm {mW g}^{-2}$. For minimum variance, another device was obtained with $l_v = 85$ mm, $h_b = 8.26$ mm and $R_c = 36.4\ \mathrm {k}\varOmega$ leading to $\sigma ^{\star }_Y = 1.20\ \mathrm {mW g}^{-2}$. These solutions were obtained using a genetic algorithm optimization implementation with parameters tuned for satisfactory convergence: 90% crossover, 30% mutation, 30 individuals and 150 iterations.

Then, other compromise solutions were designed in accordance with (20) and using the utopia values $\mu ^\star _Y$ and $\sigma ^{\star }_Y$. For that, 11 weighting factors between $w_1=0$ and $w_1=1$ with uniform steps of 0.1 were considered. Table 5 presents the optimal values of design variables, $l_v$ and $R_c$, resulting tip mass height $h_b$, and mean and standard deviation, relative to the utopia values, $\mu _Y/ \mu ^{\star }_Y$ and $\sigma _Y / \sigma ^{\star }_Y$, for the 11 weighting factors. The first and last solutions, corresponding to the maximum mean and minimum standard deviation, respectively, are repeated in Table 5, but were already determined in the search for the utopia values.

Table 5 Design variables and power output mean and standard deviation for different values of $w_1$

It is clear from Table 5 that mean performance and robustness are competing targets, that is, an increase in robustness can only be obtained by reducing the mean performance. Therefore, the compromise solutions presented in Table 5 may also be used to obtain a discrete Pareto-front, as shown in Fig. 14, which indicates the amount of the minimum of standard deviation that unavoidably accompanies a given desired mean performance. An increase in the weighting factor $w_1$ implies devices with shorter beams and heavier tip masses that lead to higher mean power output, but this comes with a larger output variance. The device, through the weighting factor, must be chosen according to the decision-maker’s preferences.

Fig. 14

Pareto-front considering power output mean and standard deviation for selected energy harvesting devices

Fig. 15

FRF of harvestable power output per unit squared acceleration input for selected energy harvesting devices

It is also worthwhile to analyze the power output FRF near the resonance for these selected devices, shown in Fig. 15, in which one can observe that all devices are equally well tuned to the target frequency and, although the peak amplitude reduces for increasing length (increasing device number) the differences in amplitude are reduced for frequencies farther from the resonance or target one.

Fig. 16

Error bars plot of harvestable power output for each device considering a $\pm 3 \sigma$ confidence interval

Using the mean and standard deviation estimations shown in Table 5, it is also possible to extrapolate a statistical analysis for these devices, presented in the form of error bars plot in Fig. 16 considering a $\pm 3 \sigma$ confidence interval. This allows to compare the harvestable power output of a particular device with the other design choices in terms of probability of being higher or lower. For instance, in nominal (or mean) terms, device 1 performs better than device 2, as already noted in Table 5 and noticeable by comparing the red squares in Fig. 16. Nevertheless, one may also affirm that, given the uncertainties considered, there is a good chance that device 2 performs better than device 1. This is also due to the fact that device 2 is more robust than device 1. While the mean performance is reduced by 4% from device 1 to device 2, the corresponding standard deviation is reduced by 7%. On the other hand, it is sure enough to state that the device 1 is always better than devices 5 to 11, although its variability is higher, since even the worst-case performance of device 1 is higher than the best-case performance of devices 5 to 11.

6 Conclusions

This work presented recent results for the robust design of energy harvesting resonant devices using two different techniques considering uncertainties in effective clamping stiffness, damping factor and circuit’s resistance. For that, a finite element model was used to evaluate the frequency response function for power output. The numerical model was verified by comparison with experimental results. The first technique based on Taguchi’s method allowed to compared nominally optimal devices in terms of robustness. This technique was shown to be quite effective in the sense that important global design information and conclusions can be drawn with a small computational cost. Nevertheless, the number of devices that can be analyzed and compared is quite limited. The second technique based on Compromise Programming method and combined to Taylor series approximations to estimate mean and variance of the power output, on the other hand, allows to obtain any number of compromise solutions for a given set of weighting factors for mean and variance. However, the number of required function evaluations, and consequently the computational cost, increase substantially. Similar conclusions can be drawn from the analyses with both techniques. In particular, that devices with shorter cantilever beams, and thus larger tip masses, lead to better mean performance but also to higher standard deviation. Results also suggest that the use of circuit’s resistance values a little smaller than the nominal optimal may improve robustness without much decrease in nominal or mean performance.