1 Introduction

The concept of adding a single type of nanoparticle into the base fluid was initiated by Choi and Eastman [1] in 1995. This mixture is called ‘nanofluid’ which is believed that it can improve the thermal conductivity of the base fluid. The advantages of nanofluids in a rectangular enclosure have been reported by Khanafer et al. [2], Tiwari and Das [3], and Oztop and Abu-Nada [4]. Several researchers have published papers on nanofluids with various physical aspects, for example, magnetic field [5, 6], viscous dissipation and chemical reaction [7], mixed convection [8], activation energy [9], Dufour and Soret [10], magnetic dipole [11], and velocity slip [12]. Apart from that, the discussion on the fabrication of various nanomaterials using bubble electrospinning is elaborated by He and Liu [13]. Meanwhile, the rheological model of nanoparticles using the two-scale fractal theory is reported by several researchers, see Refs. [14,15,16,17].

Besides, this concept has been improved by considering two or more nanoparticles that dispersed simultaneously into the base fluid and called ‘hybrid nanofluid’. Hybrid nanofluid is utilized to signal a promising increase in the thermal performance of working fluids since this technology has resulted in a significant change in the design of thermal and cooling systems. As a result of the addition of more types of nanostructures, a fluid with better thermal conductivity has been created. Furthermore, hybrid nanofluids are used in several applications, for example, in the vehicle brake fluid, domestic refrigerator, solar water heating, transformer, and heat exchanger [18]. The earlier experimental works utilizing the hybrid nanoparticles were reported by Turcu et al. [19] and Jana et al. [20]. Besides, Suresh et al. [21] conducted experimental works using Al2O3-Cu hybrid nanoparticles to study the enhancement of the fluid thermal conductivity. Besides, the significance of the combination of Al2O3 and other nanoparticles was reported by Singh and Sarkar [22] and Farhana et al. [23]. In recent years, hybrid nanofluid is attracting the researcher's attention to study the flow and thermal behaviour, numerically. For instance, the flow in the mini-channel heat sink is done by Kumar and Sarkar [24]. Meanwhile, the flow between two parallel plates with the squeezing effect is reported by Salehi et al. [25]. Moreover, Khashi’ie et al. [26] and Muhammad et al. [27] examined the squeezing flow in a horizontal channel. Apart from that, Waini et al. [28], Khan et al. [29], Zainal et al. [30], and Jamaludin et al. [31] considered the flow towards a shrinking surface.

Most of the processes in manufacturing compromise with the non-Newtonian fluids such as lubricants, paints, biological fluids, polymeric suspensions, and colloidal solutions. In this respect, Eringen [32, 33] has introduced the micropolar theory to describe the microscopic characteristics of these fluids. Since then, many authors have considered micropolar fluid with the effects of various physical parameters like radiation, MHD, viscous dissipation, Joule heating, and chemical reaction as reported in Refs. [34,35,36,37,38,39,40]. Moreover, the micropolar nanofluid flow by using Buongiorno [41] nanofluid model has been examined by several researchers, see Refs. [42,43,44,45,46,47,48]. Furthermore, the effect of nanoparticles on the micropolar fluid by using the Tiwari and Das [3] nanofluid model with different physical parameters was reported by several researchers. For example, Gangadhar et al. [49] considered the effects of MHD and Newtonian heating, Zaib et al. [50] examined the entropy generation effects, and Souayeh and Alfannakh [51] studied the thermal radiation effects. Moreover, Ghadikolaei et al. [52], Subhani and Nadeem [53, 54], Al-Hanaya et al. [55], Hosseinzadeh et al. [56], Nabwey and Mahdy [57], and Roy et al. [58] reported on the effects of hybrid nanoparticles.

Thus, this paper considers the radiative and MHD micropolar fluid flow over a stretching/shrinking sheet containing Al2O3 and Cu nanoparticles. The effects of the Joule heating and the viscous dissipation on the flow behaviour are examined. The dual solutions and their stabilities are also reported in this study.

2 Mathematical formulation

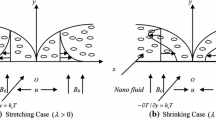
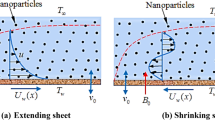
Consider the steady laminar two-dimensional flow of a micropolar fluid over a stretching/shrinking sheet with the hybrid nanoparticles as shown in Fig. 1. The surface velocity is represented by \(u_{w} \left( x \right) = ax\) where \(a\) is constant. The flow is subjected to the effect of a transverse magnetic field of strength \(B_{0}\) which is assumed to be applied normally to the surface in the positive \(y\)-direction. Also, the radiation, the viscous dissipation, and the Joule heating effects are taken into consideration. Accordingly, the micropolar hybrid nanofluid equations are [34, 36, 37]:

$$\frac{\partial u }{{\partial x}} + \frac{\partial v }{{\partial y}} = 0$$
(1)
$$u\frac{\partial u}{{\partial x}} + v\frac{\partial u}{{\partial y}} = \left( {\frac{{\mu_{{{\text{hnf}}}} + \kappa }}{{\rho_{{{\text{hnf}}}} }}} \right)\frac{{\partial^{2} u}}{{\partial y^{2} }} + \frac{\kappa }{{\rho_{{{\text{hnf}}}} }}\frac{\partial N}{{\partial y}} - \frac{{\sigma_{{{\text{hnf}}}} }}{{\rho_{{{\text{hnf}}}} }}B_{0}^{2} u$$
(2)
$$u\frac{\partial N}{{\partial x}} + v\frac{\partial N}{{\partial y}} = \frac{\omega }{{\rho_{{{\text{hnf}} }} j}}\frac{{\partial^{2} N}}{{\partial y^{2} }} - \frac{\kappa }{{\rho_{{{\text{hnf}} }} j}} \left( {2N + \frac{\partial u}{{\partial y}}} \right)$$
(3)
$$u\frac{\partial T}{{\partial x}} + v\frac{\partial T}{{\partial y}} = \frac{1}{{\left( {\rho C_{p} } \right)_{{{\text{hnf}}}} }}\left( {k_{{{\text{hnf}}}} + \frac{{16\sigma^{*} T_{\infty }^{3} }}{{3k^{*} }}} \right)\frac{{\partial^{2} T}}{{\partial y^{2} }} + \frac{1}{{\left( {\rho C_{p} } \right)_{{{\text{hnf}}}} }}\left[ {\begin{array}{*{20}c} {\left( {\mu_{{{\text{hnf}}}} + \kappa } \right)\left( {\frac{\partial u}{{\partial y}}} \right)^{2} + \sigma_{{{\text{hnf}}}} B_{0}^{2} u^{2} } \\ \end{array} } \right]$$
(4)
Fig. 1
figure 1

The flow configuration of a stretching and b shrinking sheets

Full size image

subject to:

$$u = \lambda u_{w} , v = v_{0} , N = - n\frac{\partial u}{{\partial y }},\, T = T_{w},\, {\text{at}} y = 0$$
$$u \to 0, N \to 0, T \to T_{\infty }\, {\text{ as}} y \to \infty$$
(5)

where \(\left( {u,v} \right)\) are the corresponding velocity components, \(N\) is the microrotation velocity, \(T\) is the temperature, \(\kappa\) is the vortex viscosity, \(n\) is the micro-gyration parameter, \(k^{*}\) is the mean absorption coefficient, and \(\sigma^{*}\) is the Stefan–Boltzmann constant. Here, the temperature distribution at the sheet is given by \(T_{w} \left( x \right) = T_{\infty } + T_{0} \left( {x/L} \right)^{2}\) with the temperature characteristic \(T_{0}\), the characteristic length \(L\), and the ambient temperature \(T_{\infty }\). Besides, \(\omega\) and \(j\) are the spin gradient viscosity and the microinertia coefficient, respectively, which are defined as:

$$\omega = \left( {\mu_{{{\text{hnf}}}} + \frac{\kappa }{2}} \right)j,\quad j = \frac{{\nu_{f} }}{a}$$
(6)

Further, the thermophysical properties are obtained from Refs. [59,60,61] and are given in Tables 1 and 2. Note that the nanoparticles volume fraction is symbolized by \(\varphi_{1}\) (Al2O3) and \(\varphi_{2}\) (Cu). Besides, the subscripts \(n1\) and \(n2\) are for Al2O3 and Cu solid components, whereas \(f\) and \({\text{hnf}}\) are for base fluid and the hybrid nanofluid.

Table 1 Thermophysical properties of nanoparticles and water [59,60,61]
Full size table
Table 2 Thermophysical properties of hybrid nanofluid [59,60,61]
Full size table

Now, following the dimensionless variables [34, 36, 37]:

$$\psi = \sqrt {a\nu_{f} } xf\left( \eta \right), N = ax\sqrt {\frac{a}{{\nu_{f} }}} g\left( \eta \right), \theta \left( \eta \right) = \frac{{T - T_{\infty } }}{{T_{w} - T_{\infty } }}, \eta = y\sqrt {\frac{a}{{\nu_{f} }}}$$
(7)

with the stream function \(\psi\). Here, \(u = \partial \psi /\partial y\) and \(v = - \partial \psi /\partial x\), then:

$$u = {ax}f^{\prime}\left( \eta \right), v = - \sqrt {a\nu_{f} } f\left( \eta \right)$$
(8)

On using Eqs. (7) and (8), the continuity equation, i.e., Equation (1) is satisfied. Thus, Eqs. (2)–(4) are transformed to:

$$\frac{1}{{\rho_{{{\text{hnf}}}} /\rho_{f} }}\left( {\frac{{\mu_{{{\text{hnf}}}} }}{{\mu_{f} }} + K} \right)f^{\prime\prime\prime} + ff^{\prime\prime} - f^{{\prime}{2}} + \frac{K}{{\rho_{{{\text{hnf}}}} /\rho_{f} }}g^{\prime} - \frac{{\sigma_{{{\text{hnf}}}} /\sigma_{f} }}{{\rho_{{{\text{hnf}}}} /\rho_{f} }}{Mf}^{\prime} = 0$$
(9)
$$\frac{1}{{\rho_{{{\text{hnf}}}} /\rho_{f} }}\left( {\frac{{\mu_{{{\text{hnf}}}} }}{{\mu_{f} }} + \frac{K}{2}} \right)g^{\prime\prime} + fg^{\prime} - f^{\prime}g - \frac{K}{{\rho_{{{\text{hnf}}}} /\rho_{f} }}\left( {2g + f^{\prime\prime}} \right) = 0$$
(10)
$$\frac{1}{{{\text{Pr}}}}\frac{1}{{\left( {\rho C_{p} } \right)_{{{\text{hnf}}}} /\left( {\rho C_{p} } \right)_{f} }}\left( {\frac{{k_{{{\text{hnf}}}} }}{{k_{f} }} + \frac{4}{3}R} \right)\theta^{\prime\prime} + f\theta^{\prime} - 2f^{\prime}\theta + \frac{{{\text{Ec}}}}{{\left( {\rho C_{p} } \right)_{{{\text{hnf}}}} /\left( {\rho C_{p} } \right)_{f} }} \left[ {\begin{array}{*{20}c} {\left( {\frac{{\mu_{{{\text{hnf}}}} }}{{\mu_{f} }} + K} \right)f^{{\prime\prime}{2}} + \frac{{\sigma_{{{\text{hnf}}}} }}{{\sigma_{f} }}{Mf}^{{\prime}{2}} } \\ \end{array} } \right] = 0$$
(11)

subject to:

$$f\left( 0 \right) = S, f^{\prime}\left( 0 \right) = \lambda , g\left( 0 \right) = - {nf}^{\prime\prime}\left( 0 \right), \theta \left( 0 \right) = 1,$$
$$f^{\prime}\left( \eta \right) \to 0, g\left( \eta \right) \to 0, \theta \left( \eta \right) \to 0 \ {\text{as}} \ \eta \to \infty$$
(12)

The physical parameters in Eqs. (9)–(12) are the material or micropolar parameter \(K\) which provides the ratio of the vortex and the dynamic viscosities, the magnetic parameter \(M\), the Prandtl number \({\text{Pr}}\), Eckert number \(Ec\) \(c\), the radiation parameter \(R\), and the mass flux velocity parameter \(S\), defined as:

$$K = \frac{\kappa }{{\mu_{f} }},{ }M = \frac{{\sigma_{f} B_{0}^{2} }}{{a \rho_{f} }},{\text{ Pr}} = \frac{{\left( {\mu C_{p} } \right)_{f} }}{{k_{f} }}, {Ec} = \frac{{a^{2} L^{2} }}{{(C_{p} )_{f} T_{0} }}, R = \frac{{4\sigma^{*} T_{\infty }^{3} }}{{k^{*} k_{f} }}, S = - \frac{{v_{0} }}{{\sqrt {a\nu_{f} } }}$$
(13)

Note that, \(S > 0\) for suction and \(S < 0\) for injection. Besides, \(\lambda\) is the stretching/shrinking parameter with \(\lambda = 0\) is for the static sheet, whereas \(\lambda > 0\) and \(\lambda < 0\) are for the stretching and shrinking sheets.

The skin friction coefficient \(C_{f}\), local couple stress \(M_{w}\), and local Nusselt number \({\text{Nu}}_{x}\) are expressed as [46, 62]:

$$C_{f} = \frac{1}{{\rho_{f} u_{w}^{2} }} \left( {\left( {\mu_{{{\text{hnf}}}} + \kappa } \right)\frac{\partial u}{{\partial y}} + \kappa N} \right)_{y = 0} , M_{w} = \frac{1}{{\rho_{f} xu_{w}^{2} }}\left( {\mu_{{{\text{hnf}}}} + \frac{\kappa }{2}} \right)j\left( {\frac{\partial N}{{\partial y}}} \right)_{y = 0} ,$$
$${\text{Nu}}_{x} = - \frac{x}{{k_{f} \left( {T_{w} - T_{\infty } } \right)}}\left( { k_{{{\text{hnf}}}} + \frac{{16\sigma^{*} T_{\infty }^{3} }}{{3k^{*} }} } \right)\left( {\frac{\partial T}{{\partial y}}} \right)_{y = 0}$$
(14)

Using Eqs. (7) and (14), one gets:

$${\text{Re}}_{x}^{1/2} C_{f} = \left( {\frac{{\mu_{{{\text{hnf}}}} }}{{\mu_{f} }} + \left( {1 - n} \right)K} \right)f^{\prime\prime}\left( 0 \right), {\text{Re}}_{x} M_{w} = \left( {\frac{{\mu_{{{\text{hnf}}}} }}{{\mu_{f} }} + \frac{K}{2}} \right)g^{\prime}\left( 0 \right)$$
$${\text{Re}}_{x}^{ - 1/2} {\text{Nu}}_{x} = - \left( {\frac{{k_{{{\text{hnf}}}} }}{{k_{f} }} + \frac{4}{3}R} \right)\theta ^{\prime}\left( 0 \right)$$
(15)

with the local Reynolds number, \({\text{Re}}_{x} = u_{w} x/\nu_{f}\).

Moreover, by taking \(\varphi_{1} = \varphi_{2} = M = 0\), and \(n = 0.5\), Eq. (9) has the exact solution, see [35, 36]:

$$f\left( \eta \right) = S - \frac{2 + K}{{S \pm \sqrt {S^{2} - 2K - 4} }}\left[ {1 - {\text{exp}}\left( { - \frac{{S \pm \sqrt {S^{2} - 2K - 4} }}{2 + K } \eta } \right)} \right]$$
(16)

Then,

$$f^{\prime\prime}\left( 0 \right) = \frac{{S \pm \sqrt {S^{2} - 2K - 4} }}{2 + K }$$
(17)

Therefore, the comparison values of \(f^{\prime\prime}\left( 0 \right)\) between the present numerical solution and the exact solution (17) can be done for validation purposes.

3 Stability analysis

Here, the temporal stability is conducted by referring to Merkin [63] and Weidman et al. [64]. In this regard, the unsteady form of Eqs. (2)–(4) and the similarity variables as given in Eq. (18) are considered. Therefore,

$$\psi = \sqrt {a\nu_{f} } {xf}\left( {\eta ,\tau } \right), N = {ax}\sqrt {\frac{a}{{\nu_{f} }}} g\left( {\eta ,\tau } \right), \theta \left( {\eta ,\tau } \right) = \frac{{T - T_{\infty } }}{{T_{w} - T_{\infty } }}, \eta = y\sqrt {\frac{a}{{\nu_{f} }}} , \tau = {at}$$
(18)

where \(\tau\) is the dimensionless time variable. Then

$$u = {ax}\frac{\partial f}{{\partial \eta }}\left( {\eta ,\tau } \right), v = - \sqrt {a\nu_{f} } f\left( {\eta ,\tau } \right)$$
(19)

On using Eqs. (18) and (19), one obtains

$$\frac{1}{{\rho_{{{\text{hnf}}}} /\rho_{f} }}\left( {\frac{{\mu_{{{\text{hnf}}}} }}{{\mu_{f} }} + K} \right)\frac{{\partial^{3} f}}{{\partial \eta^{3} }} + f\frac{{\partial^{2} f}}{{\partial \eta^{2} }} - \left( {\frac{\partial f}{{\partial \eta }}} \right)^{2} + \frac{K}{{\rho_{{{\text{hnf}}}} /\rho_{f} }}\frac{\partial g}{{\partial \eta }} - \frac{{\sigma_{{{\text{hnf}}}} /\sigma_{f} }}{{\rho_{{{\text{hnf}}}} /\rho_{f} }}M\frac{\partial f}{{\partial \eta }} - \frac{{\partial^{2} f}}{\partial \eta \partial \tau } = 0$$
(20)
$$\frac{1}{{\rho_{{{\text{hnf}}}} /\rho_{f} }}\left( {\frac{{\mu_{{{\text{hnf}}}} }}{{\mu_{f} }} + \frac{K}{2}} \right)\frac{{\partial^{2} g}}{{\partial \eta^{2} }} + f\frac{\partial g}{{\partial \eta }} - \frac{\partial f}{{\partial \eta }}g - \frac{K}{{\rho_{{{\text{hnf}}}} /\rho_{f} }}\left( {2g + \frac{{\partial^{2} f}}{{\partial \eta^{2} }}} \right) - \frac{\partial g}{{\partial \tau }} = 0$$
(21)
$$\frac{1}{{{\text{Pr}}}}\frac{1}{{\left( {\rho C_{p} } \right)_{{{\text{hnf}}}} /\left( {\rho C_{p} } \right)_{f} }}\left( {\frac{{k_{{{\text{hnf}}}} }}{{k_{f} }} + \frac{4}{3}R} \right)\frac{{\partial^{2} \theta }}{{\partial \eta^{2} }} + f\frac{\partial \theta }{{\partial \eta }} - 2\frac{\partial f}{{\partial \eta }}\theta + \frac{Ec}{{\left( {\rho C_{p} } \right)_{{{\text{hnf}}}} /\left( {\rho C_{p} } \right)_{f} }} \left[ {\begin{array}{*{20}c} {\left( {\frac{{\mu_{{{\text{hnf}}}} }}{{\mu_{f} }} + K} \right)\left( {\frac{{\partial^{2} f}}{{\partial \eta^{2} }}} \right)^{2} + \frac{{\sigma_{{{\text{hnf}}}} }}{{\sigma_{f} }}M\left( {\frac{\partial f}{{\partial \eta }}} \right)^{2} } \\ \end{array} } \right] - \frac{\partial \theta }{{\partial \tau }} = 0$$
(22)

subject to:

$$f\left( {0,\tau } \right) = S, \frac{\partial f}{{\partial \eta }}\left( {0,\tau } \right) = \lambda , g\left( {0,\tau } \right) = - n\frac{{\partial^{2} f}}{{\partial \eta^{2} }}\left( {0,\tau } \right), \theta \left( {0,\tau } \right) = 1,$$
$$\frac{\partial f}{{\partial \eta }}\left( {\eta ,\tau } \right) \to 0, g\left( {\eta ,\tau } \right) \to 0, \theta \left( {\eta ,\tau } \right) \to 0 {\text{ as}} \eta \to \infty$$
(23)

Then, the disturbance is applied to the steady solution \(f = f_{0} \left( \eta \right)\), \(g = g_{0} \left( \eta \right)\), and \(\theta = \theta_{0} \left( \eta \right)\), of Eqs. (9–12) by employing the following relations [64]:

$$f\left( {\eta ,\tau } \right) = f_{0} \left( \eta \right) + e^{ - \gamma \tau } F\left( {\eta ,\tau } \right), g\left( {\eta ,\tau } \right) = g_{0} \left( \eta \right) + e^{ - \gamma \tau } G\left( {\eta ,\tau } \right),$$
$$\theta \left( {\eta ,\tau } \right) = \theta_{0} \left( \eta \right) + e^{ - \gamma \tau } H\left( {\eta ,\tau } \right)$$
(24)

Here Eq. (24) is employed to obtain the eigenvalue problems of Eqs. (20)-(23) where \(F\left( {\eta ,\tau } \right)\),\(G\left( {\eta ,\tau } \right)\), and \(H\left( {\eta ,\tau } \right)\) are relatively small compared to \(f_{0} \left( \eta \right)\), \(g_{0} \left( \eta \right)\), and \(\theta_{0} \left( \eta \right)\). After linearization and by setting \(\tau = 0\), then \(F\left( {\eta ,\tau } \right) = F_{0} \left( \eta \right)\), \(G\left( {\eta ,\tau } \right) = G_{0} \left( \eta \right)\), and \(H\left( {\eta ,\tau } \right) = H_{0} \left( \eta \right)\). Therefore, the final form of the linearized eigenvalue problems is:

$$\frac{1}{{\rho_{hnf} /\rho_{f} }}\left( {\frac{{\mu_{hnf} }}{{\mu_{f} }} + K} \right)F^{\prime\prime\prime}_{0} + f_{0} F^{\prime\prime}_{0} + f^{\prime\prime}_{0} F_{0} - 2f^{\prime}_{0} F^{\prime}_{0} + \frac{K}{{\rho_{hnf} /\rho_{f} }}G^{\prime}_{0} - \frac{{\sigma_{hnf} /\sigma_{f} }}{{\rho_{hnf} /\rho_{f} }}MF^{\prime}_{0} + \gamma F^{\prime}_{0} = 0$$
(25)
$$\frac{1}{{\rho_{{{\text{hnf}}}} /\rho_{f} }}\left( {\frac{{\mu_{{{\text{hnf}}}} }}{{\mu_{f} }} + \frac{K}{2}} \right)G_{0}^{{^{\prime\prime}}} + f_{0} G_{0}^{^{\prime}} + g_{0}^{^{\prime}} F_{0} - f_{0}^{^{\prime}} G_{0} - g_{0} F_{0}^{^{\prime}} - \frac{K}{{\rho_{{{\text{hnf}}}} /\rho_{f} }}\left( {2G_{0} + F_{0}^{^{\prime\prime}} } \right) + \gamma G_{0} = 0$$
(26)
$$\frac{1}{{{\text{Pr}}}}\frac{1}{{\left( {\rho C_{p} } \right)_{{{\text{hnf}}}} /\left( {\rho C_{p} } \right)_{f} }}\left( {\frac{{k_{{{\text{hnf}}}} }}{{k_{f} }} + \frac{4}{3}R} \right)H_{0}^{{^{\prime\prime}}} + f_{0} H_{0}^{^{\prime}} + \theta_{0}^{^{\prime}} F_{0} - 2\left( {\theta_{0} F_{0}^{^{\prime}} + f_{0}^{^{\prime}} H_{0} } \right) + \frac{{{\text{Ec}}}}{{\left( {\rho C_{p} } \right)_{{{\text{hnf}}}} /\left( {\rho C_{p} } \right)_{f} }} \left[ {\begin{array}{*{20}c} {2\left( {\frac{{\mu_{{{\text{hnf}}}} }}{{\mu_{f} }} + K} \right)f_{0}^{^{\prime\prime}} F_{0}^{{^{\prime\prime}}} + 2\frac{{\sigma_{{{\text{hnf}}}} }}{{\sigma_{f} }}{\text{Mf}}_{0}^{^{\prime}} F_{0}^{^{\prime}} } \\ \end{array} } \right] + \gamma H_{0} = 0$$
(27)

subject to:

$$F_{0} \left( 0 \right) = 0, F_{0}^{^{\prime}} \left( 0 \right) = 0, G_{0} \left( 0 \right) = - nF_{0}^{^{\prime\prime}} \left( 0 \right), H_{0} \left( 0 \right) = 0,$$
$$F_{0}^{^{\prime}} \left( \eta \right) \to 0, G_{0} \left( \eta \right) \to 0, H_{0} \left( \eta \right) \to 0\,{\text{ as}} \eta \to \infty$$
(28)

Here the values of \(\gamma\) from Eqs. (25)–(27) are generated by setting the new boundary condition \(F_{0}^{^{\prime\prime}} \left( 0 \right) = 1\) in Eq. (28) to replace \(F_{0}^{^{\prime}} \left( \eta \right) \to 0 \,{\text{as}}\, \eta \to \infty\) [65]. For additional reference, He et al. [66] investigated the interface stability of a system confined between two horizontal rigid planes and saturated porous media. They concluded that further physical parameters in the stability configuration are shown in the numerical calculations. The involvement of the linear/nonlinear curves shows stability is only judged by the linear curve.

4 Results and discussion

This section provides a discussion of the results obtained from the numerical computations. Here, Eqs. (9)–(12) are solved numerically by utilizing the package bvp4c in MATLAB software [67]. Further, the effect of several physical parameters is examined and then presented in tabular and graphical forms. Here, the hybrid nanofluid \(\left( {\varphi_{hnf} = \varphi_{1} + \varphi_{2} } \right)\) consists of Al2O3 (\(\varphi_{1}\)) and Cu (\(\varphi_{2}\)) nanoparticles with one-to-one ratio.

The value of \(f{^{\prime\prime}}\left( 0 \right)\) and \(g^{\prime}\left( 0 \right)\) when \(\varphi_{{{\text{hnf}}}} = S = n = 0\) and \(\lambda = 1\) (stretching case) for several values of \(K\) and \(M\) is given in Table 3. These values are compared to those obtained by Hsiao [42] and Atif et al. [37] and found in good agreement. The exact solution for the case \(K = 0\) and \(\lambda = 1\) (stretching case) is given by

$$f\left( \eta \right) = s + \frac{2}{{S + \sqrt {S^{2} + 4\left( {M + 1} \right)} }} - \frac{2}{{S + \sqrt {S^{2} + 4\left( {M + 1} \right)} }}{\text{exp}}\left( { - \frac{{S + \sqrt {S^{2} + 4\left( {M + 1} \right)} }}{2 } \eta } \right)$$
(29)
Table 3 Values of \(f{^{\prime\prime}}\left( 0 \right)\) and \(g^{\prime}\left( 0 \right)\) when \(\varphi_{{{\text{hnf}}}} = S = n = 0\) and \(\lambda = 1\) (stretching case)
Full size table

which yields \(f^{\prime\prime}\left( 0 \right) = - \frac{{S + \sqrt {S^{2} + 4\left( {M + 1} \right)} }}{2 }\). By substituting \(s = 0\) and \(M = 1\) for example, one obtains \(f^{\prime\prime}\left( 0 \right) = - \sqrt 2 \approx - 1.414214,\) as shown in Table 3. Moreover, when \(s = 0\) and \(M = 0\), Eq. (29) reduces to \(f\left( \eta \right) = 1 - {\text{exp}}\left( { - \eta } \right)\), which was first reported by Crane [68].

Table 4 provides the values of \(f{^{\prime\prime}}\left( 0 \right)\) when \(\varphi_{{{\text{hnf}}}} = M = 0\), \(n = 0.5,\) and \(\lambda = - 1\) (shrinking case) for various values of \(K\) and \(S\). The present results are validated with the exact solution given in Eq. (17) and also with Lund et al. [36]. Here, the numerical values of the exact solution are approximately taken in six decimal places. The comparisons show an excellent agreement and consequently give us confidence in the validity and accuracy of the present numerical results.

Table 4 Values of \(f{^{\prime\prime}}\left( 0 \right)\) when \(\varphi_{hnf} = M = 0\), \(n = 0.5\) and \(\lambda = - 1\) (shrinking case)
Full size table

Besides, Table 5 shows the effect of various parameters on \({\text{Re}}_{x}^{1/2} C_{f}\), \({\text{Re}}_{x} M_{w}\), and \({\text{Re}}_{x}^{ - 1/2} {\text{Nu}}_{x}\) when \(\lambda = - 1\), \(S = 2\), \(n = 0.5\), and \({\text{Pr}} = 6.2\). Some of the physical parameters such as \(\varphi_{{{\text{hnf}}}}\), \(M\), and \(K\) have a direct impact on these physical quantities. The values of \({\text{Re}}_{x}^{1/2} C_{f}\), \({\text{Re}}_{x} M_{w}\), and \({\text{Re}}_{x}^{ - 1/2} {\text{Nu}}_{x}\) are enhanced with the rise of \(\varphi_{{{\text{hnf}}}}\) and \(M\), but their values are decreased as \(K\) increases. However, no changes are observed in the values of \({\text{Re}}_{x}^{1/2} C_{f}\) and \({\text{Re}}_{x} M_{w}\) for \(Ec\) and \(R\), whereas the values of \({\text{Re}}_{x}^{ - 1/2} {\text{Nu}}_{x}\) are decreased with these parameters.

Table 5 Values of \({\text{Re}}_{x}^{1/2} C_{f}\), \({\text{Re}}_{x} M_{w}\), and \({\text{Re}}_{x}^{ - 1/2} {\text{Nu}}_{x}\) when \(\lambda = - 1\), \(S = 2\), \(n = 0.5\), and \({\text{Pr}} = 6.2\)
Full size table

Further, Fig. 2 is provided to have a better insight into the effect of \(Ec\), \(R\), and \(\varphi_{hnf}\) on \({\text{Re}}_{x}^{ - 1/2} {\text{Nu}}_{x}\) when \(\lambda = - 1,S = 2,K = M = 0.1,n = 0.5,\) and \(\Pr = 6.2\). A reduction in the values of \({\text{Re}}_{x}^{ - 1/2} {\text{Nu}}_{x}\) on the first solution is observed with the rise of \(Ec\) and \(R\). Meanwhile, it is noticed that an increase in \(\varphi_{{{\text{hnf}}}}\) led to a decrease in the values of \({\text{Re}}_{x}^{ - 1/2} {\text{Nu}}_{x}\) for smaller values of \(R\). However, the values of \({\text{Re}}_{x}^{ - 1/2} Nu_{x}\) start to boost up as \(\varphi_{{{\text{hnf}}}}\) increases when \(R\) becomes large. From these observations, \(R\) and \(\varphi_{hnf}\) can be the control parameters to enhance or reduce the heat transfer rate.

Fig. 2
figure 2

Variations of \({\text{Re}}_{x}^{ - 1/2} {\text{Nu}}_{x}\) for various values of \(R, Ec \,{\text{and}}\, \varphi_{{{\text{hnf}}}}\)

Full size image

Next, the variations of \({\text{Re}}_{x}^{1/2} C_{f}\), \({\text{Re}}_{x} M_{w}\), and \({\text{Re}}_{x}^{ - 1/2} {\text{Nu}}_{x}\) against \(S\) for \(\varphi_{{{\text{hnf}}}} = 0\% ,1\% ,\) and \(2\%\) when \(\lambda = - 1,n = 0.5,\,K = M = Ec = 0.1,R = 1,\) and \(\Pr = 6.2\) are presented in Figs. 3–5, respectively. It can be concluded from these figures that the values of \({\text{Re}}_{x}^{1/2} C_{f}\), \({\text{Re}}_{x} M_{w}\), and \({\text{Re}}_{x}^{ - 1/2} {\text{Nu}}_{x}\) on the first solution are higher for hybrid nanofluid with a volume fraction of \(2\%\) (\(\varphi_{{{\text{hnf}}}} = 2\%\)) compared to water (\(\varphi_{hnf} = 0\%\)). Besides, two solutions are observed for the limited range of \(S\) and these solutions are terminated at \(S = S_{c}\) (critical value). Here, the critical values are \(S_{c1} = {1}{\text{.9409, }}S_{c2} = {1}{\text{.9152,}}\) and \(S_{c3} = {1}{\text{.8924}}\) for \(\varphi_{{{\text{hnf}}}} = 0\% ,1\% ,\) and \(2\%\), respectively.

Fig. 3
figure 3

Variations of \({\text{Re}}_{x}^{1/2} C_{f}\) for various values of \(S\, {\text{and}}\, \varphi_{{{\text{hnf}}}}\)

Full size image
Fig. 4
figure 4

Variations of \({\text{Re}}_{x} M_{w}\) for various values of \(S\, {\text{and}}\, \varphi_{{{\text{hnf}}}}\)

Full size image
Fig. 5
figure 5

Variations of \({\text{Re}}_{x}^{ - 1/2} Nu_{x}\) for various values of \(S\, {\text{and}}\, \varphi_{{{\text{hnf}}}}\)

Full size image

The effects of \(M\) and \(K\) on \({\text{Re}}_{x}^{1/2} C_{f}\), \({\text{Re}}_{x} M_{w}\), and \({\text{Re}}_{x}^{ - 1/2} {\text{Nu}}_{x}\) when \(\lambda = - 1,S = 2, n = 0.5, Ec = 0.1,R = 1,\Pr = 6.2,\) and \(\varphi_{{{\text{hnf}}}} = 2\%\) are given in Figs. 6–8, respectively. It is noticed that the values of \({\text{Re}}_{x}^{1/2} C_{f}\), \({\text{Re}}_{x} M_{w}\), and \({\text{Re}}_{x}^{ - 1/2} {\text{Nu}}_{x}\) are lower in the absence of the magnetic field (\(M = 0\)). Moreover, the values of these physical quantities are boosted when a stronger magnetic field is applied to the flow. Besides, an increase in \(K\) declines the values of \({\text{Re}}_{x}^{1/2} C_{f}\), \({\text{Re}}_{x} M_{w}\), and \({\text{Re}}_{x}^{ - 1/2} {\text{Nu}}_{x}\). Interestingly, it is noticed that the solutions only exist up to certain values of \(K\) with \(K_{c1} = {0}{\text{.1152, }}K_{c2} = {0}{\text{.2327}},\) and \(K_{c3} = {0}{\text{.3649}}\) for \(M = 0, 0.05,\) and 0.1.

Fig. 6
figure 6

Variations of \({\text{Re}}_{x}^{1/2} C_{f}\) for various values of \(K\, {\text{and}}\, M\)

Full size image

Furthermore, the influence of \(K\) on the velocity \(f^{\prime}\left( \eta \right)\), the microrotation \(g\left( \eta \right)\), and the temperature \(\theta \left( \eta \right)\) profiles when \(\lambda = - 1,S = 2, n = 0.5, M = 0.05, Ec = 0.1,R = 1,\) \(\Pr = 6.2\), and \(\varphi_{{{\text{hnf}}}} = 2\%\) is presented in Figs. 9, 10, and 11. There exist dual solutions on these profiles that satisfy the infinity boundary conditions (12) asymptotically. These solutions are merging up to certain values of \(K\) and terminated at \(K = K_{c}\), as evidently shown in Figs. 6, 7, and 8. Besides, it can be seen in Figs. 9 and 10 that the values of \(f^{\prime}\left( \eta \right)\) and \(g\left( \eta \right)\) on the first solution are declined for larger \(K\). Physically, the micropolarity is neglected when \(K = 0\). The effect of the vortex and the dynamic viscosities takes place as \(K\) increases and consequently raises the momentum boundary layer thickness. Similar observations are reported by several researchers such as Ishak et al. [69], Yacob and Ishak [70], and Soid et al. [71]. Contrarily, the observations are reversed for \(\theta \left( \eta \right)\) as shown in Fig. 11.

Fig. 7
figure 7

Variations of \({\text{Re}}_{x} M_{w}\) for various values of \(K\, {\text{and}}\, M\)

Full size image
Fig. 8
figure 8

Variations of \({\text{Re}}_{x}^{ - 1/2} {\text{Nu}}_{x}\) for various values of \(K\, {\text{and}}\, M\)

Full size image
Fig. 9
figure 9

Velocity profiles \(f^{\prime}\left( \eta \right)\) for various values of \(K\)

Full size image
Fig. 10
figure 10

Microrotation profiles \(g\left( \eta \right)\) for various values of \(K\)

Full size image
Fig. 11
figure 11

Temperature profiles \(\theta \left( \eta \right)\) for various values of \(K\)

Full size image

The flow patterns can be determined by plotting the dimensionless stream functions given in Eq. (7) where \(\overline{\psi } = \psi /\sqrt {a\nu_{f} }\). In this respect, the streamlines of the first and the second solutions for the shrinking sheet \(\left( {\lambda = - 1} \right)\) when \(S = 2\) (suction), \(n = 0.5, K = M = 0.1,\) and \(\varphi_{{{\text{hnf}}}} = 2\%\) are shown in Figs. 12 and 13, respectively. It is noticed that the fluid is shrunk towards the slot (\(x = 0\)) on both solution branches and consequently sucked through the surface. Meanwhile, the effect of different \(S\) on the flow patterns for the stretching sheet \(\left( {\lambda = 1} \right)\) when \(n = 0.5, K = M = 0.1,\) and \(\varphi_{{{\text{hnf}}}} = 2\%\) are shown in Figs. 14, 15, and 16. For \(S = 0.5\) (suction case), the fluid stretches away from the slot (\(x = 0\)) and being sucked into the surface. Meanwhile, the flow is moving away from the slot for \(S = 0\) (impermeable case) and \(S = - 0.5\) (injection case). Also, it is noted that the flow acts as the normal stagnation point flow for \(S = 0\) (impermeable case) and the flow is split into two regions for \(S = - 0.5\) (injection case).

Fig. 12
figure 12

Streamlines when \(\lambda = - 1\) (shrinking sheet) for the first solution

Full size image
Fig. 13
figure 13

Streamlines when \(\lambda = - 1\) (shrinking sheet) for the second solution

Full size image
Fig. 14
figure 14

Streamlines when \(\lambda = 1\) (stretching sheet) and \(S = 0.5\) (suction)

Full size image
Fig. 15
figure 15

Streamlines when \(\lambda = 1\) (stretching sheet) and \(S = 0\) (impermeable)

Full size image
Fig. 16
figure 16

Streamlines when \(\lambda = 1\) (stretching sheet) and \(S = - 0.5\) (injection)

Full size image

The variation of \(\gamma\) against \(S\) when \(\lambda = - 1,n = 0.5, K = M = 0.1,\) and \(\varphi_{{{\text{hnf}}}} = 2\%\) is designated in Fig. 17. For the positive value of \(\gamma\), it is noted that \(e^{ - \gamma \tau } \to 0\) as time evolves \(\left( {\tau \to \infty } \right)\). For the negative value of \(\gamma\), \(e^{ - \gamma \tau } \to \infty\). As shown in Fig. 17, it is noted that the first solution is stable and vice versa.

Fig. 17
figure 17

Eigenvalues \(\gamma\) against \(S\)

Full size image

5 Conclusion

The radiative and magnetohydrodynamic micropolar fluid flow over a stretching/shrinking sheet consists of Al2O3 and Cu nanoparticles with viscous dissipation, and the Joule heating effect is examined in this paper. The problem is solved numerically with the aid of the bvp4c function. The numerical results are validated with those previously published data to confirm the accuracy of the current formulation and method. Findings reveal that two solutions are possible when a sufficient suction strength is imposed on the shrinking sheet. It is interesting to note that the solutions only exist for a certain range of \(K\). Also, the similarity solutions terminate at \(S = S_{c}\) and \(K = K_{c}\). The values of \({\text{Re}}_{x}^{ - 1/2} {\text{Nu}}_{x}\) reduce with the rise of \(Ec\) and \(R\). Besides, an increase in \(\varphi_{{{\text{hnf}}}}\) leads to a decrease in the values of \({\text{Re}}_{x}^{ - 1/2} {\text{Nu}}_{x}\) for smaller values of \(R\). However, the values of \({\text{Re}}_{x}^{ - 1/2} {\text{Nu}}_{x}\) increase with the increase in \(\varphi_{{{\text{hnf}}}}\) for larger values of \(R\). The values of \({\text{Re}}_{x}^{1/2} C_{f}\), \({\text{Re}}_{x} M_{w}\), and \({\text{Re}}_{x}^{ - 1/2} {\text{Nu}}_{x}\) intensify with the rise of \(M\). Contrarily, the effect of \(K\) lowers the values of these physical quantities. The plots of the streamlines show that the fluid is shrunk towards the slot (\(x = 0\)) on both solution branches for the shrinking sheet and consequently sucked into the surface. Lastly, it is discovered that the first solution is physically reliable and in a stable mode.