Magnetohydrodynamic Micropolar Nanofluid Flow in a Shrinking Channel with Second-Order Velocity Slip and Thermal Radiation

Abstract

Magnetohydrodynamic (MHD) micropolar nanofluid flow in a shrinking channel is important due to its use in metallurgical processes, manufacturing industries and industrial applications. In this study, the flow and heat transfer of an electrically conducting micropolar nanofluid passing through a shrinking channel is investigated with the effects of second-order velocity slip conditions and thermal radiation. Using the similarity transformations, the governing dimensional equations were transformed into ordinary differential equations, which have been solved by the finite difference method. The results for skin friction coefficient (Re_x^1/2C_fx), couple stress (m_x), and local Nusselt number (Re_x^−1/2Nu_fx), as well as flow profiles were presented graphically with variations of material constant (K), volume fraction of alumina nanoparticles (φ), micro-rotation parameter (n), second-order slip parameter (B), first-order slip parameter (A), magnetic parameter (M), suction parameter (S), and radiation parameter (R). The influences of φ, K, n, A, M, and S were significant. With higher K, A, n, and M, Re_x^1/2C_fx and Re_x^−1/2Nu_fx increased. On the other hand, an increase in S caused a decrease in Re_x^1/2C_fx and an increase in Re_x^−1/2Nu_fx. In the case of higher A and M, velocity increased, but angular velocity decreased. However, the converse was observed for the increase in φ and S. It is worth noting that the boundary layer separation was delayed for increasing values of K, n, A, and M, but accelerated for higher φ, B, and S.

1 Introduction

Micropolar nanofluid flow has been the topic of research because of its various applications in manufacturing industries, aerospace engineering, and metallurgical processes. For industrial purposes, nanofluid flow in a channel is important. Several authors considered micropolar nanofluid flow in different aspects. Saraswathy et al. [1] investigated micropolar fluid flow in a channel with variable surface temperature and variable viscosity. The results were discussed in terms of flow properties considering the variable boundary conditions. Between two parallel plates, Pasha et al. [2] studied the impact of the Peclet number on micropolar fluid flow. They nicely derived the governing equations and compared the consequences with two different numerical methods. Fluid concentration and heat transfer increased with a higher Peclet number. Rehman et al. [3] studied micropolar nanofluid flow in a rectangular geometry. Mahmood et al. [4] explored the peristaltic flow of micropolar fluid in a two-dimensional asymmetric medium taking into account slip conditions. Velocity decreased near the upper wall while increased near the lower wall. Over the surface of a parabola, MHD micropolar fluid flow was examined by Reddy and Reddy [5]. They conducted the study for a three-dimensional case with the effects of thermal radiation. It was reported that the results may be applied to exotic lubricants, polymer fluids, electronic chips, the drawing of copper wire, and artificial fibers.

The combined effects of micro-rotation, Lorentz force, and thermo-migration associated with thermal radiation were analyzed by Xiu et al. [6]. Results showed that the micro-rotation field was strongly dominated by the spins of a tiny number of particles. The spins of the particles were caused by the collision with the boundary. Patel et al. [7] considered the impact of a magnetic field on an unsteady micropolar fluid over a nonlinear stretching sheet. The velocity and temperature profiles were augmented with a larger Eckert number. Sharma and Mishra [8] numerically investigated the time-independent micropolar fluid flow with the thermal radiation effect. The micropolar fluid flow over a stretching sheet with chemical reactions and melting heat transfer was numerically examined by Singh et al. [9]. On the other hand, MHD micropolar fluid flow over a sheet subject to thermal radiation was numerically conducted by Rehman et al. [10].

Due to the lack of heat transfer in the base fluid, nanoparticles are used in the base fluid to enhance thermal conductivity. Fluids with suspended nanomaterials are known as nanofluids. Recent studies [11,12,13] have experimentally investigated how the nanoparticles affect the thermal conductivity of the nanofluid. Ali et al. [14] examined the enhancement of heat transport by water-based micropolar fluids suspending TiO₂ nanoparticles. The finite element scheme was imposed to solve the leading equations. Several studies [15,16,17,18,19,20,21] investigated the heat transfer characteristics of nanofluids in different shapes of geometry and boundary conditions.

The stagnation-point micropolar fluid flow along a circular heated object was analyzed by Salahuddin et al. [22]. On the other hand, Abbas et al. [23] illustrated the thermal and velocity slip boundary conditions on MHD micropolar nanofluid flow toward a circular cylinder. They have taken three different types of nanoparticles (Titania, Alumina, and Copper,) and by mixing them with water (the base fluid), they have made three types of nanofluids. From the numerical tables and graphs of the study, it can be observed that copper–water nanofluid showed a strong heat transport rate compared to others. The micropolar fluid flow based on suction or injection, thermal radiation, and gravity modulation was explored by Ali et al. [24]. Outcomes showed that the fluctuation of Nusselt number and temperature increased with higher radiation parameters. Wang et al. [25] reviewed a number of literature on the improvement of heat transfer of nanofluids by applying a magnetic or electric field. They also proposed different effective mechanisms for the improvement of nanofluids. Goud and Nandeppanavar [26] investigated the combined impacts of Ohmic heat and chemical reactions on MHD micropolar fluid along a stretching surface.

Yadav and Kumar [27] studied the entropy production of non-Newtonian micropolar fluid and immiscible Newtonian fluid over a rectangular channel with an inclined magnetic field. They imposed no-slip boundary conditions on the static wall. A satisfactory derivation of the governing equations was found in the literature. Results were arranged in graphs with variations of physical parameters. Results showed that the friction of the fluid caused by the surface is for the increasing nature of the entropy generation number. It was mentioned that the results could be used in the petroleum industry. Contrary to this, Yusuf et al. [28] examined the entropy generation of micropolar fluid flow with slip effects on a porous medium. Increasing values of micro-rotation parameters increased the entropy generation profiles but declined the velocity profiles. Usafzai and Aly [29] mathematically described the single and multiple exact solutions of a micropolar fluid, considering the constant velocity slip. Kumar et al. [30] explored the effects of velocity slips (first and second order) on micropolar fluid flow in the presence of Lorentz force over a convective surface. It was found that velocity boosted up for second-order slip parameters while temperature was an increasing function of first-order slip parameters.

Su [31] theoretically established a weak solution of compressible micropolar fluid in a bounded domain. On the other hand, Slayi et al. [32] derived the Gauge Uzawa method for incompressible micropolar fluid. Results confirmed the unconditional stability of the method. Some numerical simulations were performed for the validation of theoretical results. The creeping movement of spherical particles in a micropolar fluid orthogonal to the plane interface of a viscous fluid was investigated by Sherief et al. [33]. To examine the comparative outcomes of heat and mass transport of several fluids, Habib et al. [34] analyzed the existence of activation energy, Cattaneo-Christov heat flux, and micro-organism bioconvection over a stretching surface. To compare the results, they have taken four types of fluids: Newtonian fluid, Williamson nanofluid, Maxwell nanofluid, and micropolar nanofluid. The results showed that velocity was higher for micropolar fluid compared to the other fluids.

The above review exposed not only the necessity of in-depth knowledge of MHD micropolar nanofluid flow in a shrinking channel with second-order velocity slip but also its technological importance. However, this topic still remains untouched by the researchers. So, the objective of this study is to investigate electrically conducting micropolar nanofluid flow in a shrinking channel with the effects of second-order velocity slip conditions and thermal radiation. The governing dimensional equations are transformed into a non-dimensional form using a set of similarity variables. These are then solved by the finite difference method. The parametric investigation is carried out in terms of skin friction coefficient, couple stress, local Nusselt numbers, and flow properties. The flowchart of the present work is presented below:

2 Formulation of the Problem

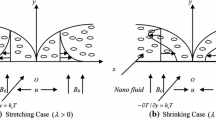
A two-dimensional, steady, micropolar nanofluid flow is considered in a channel with a shrinking wall as presented in Fig. 1, where the Cartesian coordinates are $\left( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{x} ,\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{y} } \right)$, such that the $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{x}$-axis goes along the center of the channel and the $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{y}$-axis is in the orthogonal direction to the channel. A magnetic field of strength B₀ is applied to the fluid along the perpendicular direction of the channel walls. The upper wall’s velocity is $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{u} = u_{w} \left( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{x} } \right) = \lambda a\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{x}$, where a is a positive constant, λ < 0 for the shrinking wall and λ = 0 for a static wall, respectively. Also, T_h, and T_c are the bottom and top wall temperatures, respectively. The walls are located in two horizontal positions $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{y} = \pm h$. As the upper wall is assumed to be shrinking, velocity slip may happen. However, it is kept at cold temperature and so temperature jump is not considered here. Further assumption between the nanoparticles and the carrier fluid is thermal equilibrium. The fluid is a water (H₂O) based nanofluid containing uniform sized and shaped nanoparticles.

Fig. 1

Schematic of nanofluid flow in a channel

Then, under the usual Boussinesq’s approximation, the governing equations for a nanofluid flow in a channel are given as Rees and Pop [35]:

$$\frac{{\partial \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{u} }}{{\partial \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{x} }} + \frac{{\partial \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{v} }}{{\partial \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{y} }} = 0,$$

(1)

$$\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{u} \frac{{\partial \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{u} }}{{\partial \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{x} }} + \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{v} \frac{{\partial \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{v} }}{{\partial \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{y} }} = u_{{\text{e}}} \frac{{\partial u_{{\text{e}}} }}{\partial x} + \frac{{\mu_{{{\text{nf}}}} + \kappa }}{{\rho_{{{\text{nf}}}} }}\frac{{\partial^{2} \tilde{u}}}{{\partial \tilde{y}^{2} }} + \frac{\kappa }{{\rho_{{{\text{nf}}}} }}\frac{{\partial \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{N} }}{{\partial \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{y} }} - \frac{{\sigma_{{{\text{nf}}}} B_{0}^{2} }}{{\rho_{{{\text{nf}}}} }}\left( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{u} - u_{{\text{e}}} } \right),$$

(2)

$$\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{u} \frac{{\partial \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{N} }}{{\partial \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{x} }} + \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{v} \frac{{\partial \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{N} }}{{\partial \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{y} }} = \frac{1}{{\rho_{{{\text{nf}}}} }}\left( {\mu_{{{\text{nf}}}} + \frac{\kappa }{2}} \right)\frac{{\partial^{2} \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{N} }}{{\partial \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{y}^{2} }} - \frac{\kappa }{{\rho_{{{\text{nf}}}} j}}\left( {2\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{N} + \frac{{\partial \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{u} }}{{\partial \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{y} }}} \right),$$

(3)

$$\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{u} \frac{{\partial \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{T} }}{{\partial \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{x} }} + \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{v} \frac{{\partial \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{T} }}{{\partial \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{y} }} = \alpha_{{{\text{nf}}}} \frac{{\partial^{2} \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{T} }}{{\partial \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{y}^{2} }} - \frac{1}{{\left( {\rho c} \right)_{{{\text{nf}}}} }}\frac{{\partial q_{{{\text{rd}}}} }}{{\partial \tilde{y}}},$$

(4)

with the boundary conditions

$$\begin{gathered} \,\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{u} = \lambda u_{w} \left( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{x} } \right) + u_{{w,{\text{slip}}}} \left( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{x} } \right) = \lambda a\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{x} + A_{1} \frac{{\partial \tilde{u}}}{{\partial \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{y} }} + A_{2} \frac{{\partial^{2} \tilde{u}}}{{\partial \tilde{y}^{2} }},\,\hfill \\ N = - n\frac{{\partial \tilde{u}}}{{\partial \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{y} }},\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{T} = T_{c} \;{\text{at}}\;\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{y} = h, \hfill \\ \,\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{u} = u_{w} \left( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{x} } \right),v = v_{{\text{w}}} = v_{0} ,\,N = 0,\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{T} = T_{h} \;{\text{at}}\;\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{y} = - h, \hfill \\ \end{gathered}$$

(5)

where $\left( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{u} ,\,\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{v} } \right)$ are the components of velocity along $\left( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{x} ,\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{y} } \right)$ axes, $u_{e} \left( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{x} } \right) = a\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{x}$ is the local edge velocity, $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{T}$ refers the temperature of the nanofluid, $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{N}$ indicates the micro-rotation component orthogonal to the xy-plane, v₀ indicates the constant mass flux velocity, where v₀ > 0 for suction and v₀ < 0 for injection, respectively, κ is the vortex viscosity, j is the microinertia density, (A₁, A₂) are the velocity slip factors, and n refers a constant such that 0 ≤ n ≤ 1. In case of n = 0, the fluid has a strong concentration, so that the particles near the surface are unable to rotate. For n = 1/2, the fluid has a weak concentration, and the particles’ spin for fine-particle suspension is same as the fluid vorticity at the surface. However, n = 1 corresponds to turbulent boundary layers. Therefore, an increase in n from 0 to 1 relates to the increasing velocity of microelements.

Here the thermophysical properties of the nanofluid are expressed according to Refs. [36, 37]:

$$\begin{gathered} \rho_{{{\text{nf}}}} = \left( {1 - \varphi } \right)\rho_{f} + \varphi \rho_{s} ,\;{{\mu_{{{\text{nf}}}} } \mathord{\left/ {\vphantom {{\mu_{{{\text{nf}}}} } {\mu_{{\text{f}}} }}} \right. \kern-0pt} {\mu_{{\text{f}}} }} = 1 + 4.93\varphi + 222.4\varphi^{2} ,\;\hfill\\ {{\kappa_{{{\text{nf}}}} } \mathord{\left/ {\vphantom {{\kappa_{{{\text{nf}}}} } {\kappa_{{\text{f}}} }}} \right. \kern-0pt} {\kappa_{{\text{f}}} }} = 1 + 2.944\varphi + 19.67\varphi^{2} , \hfill \\ {{\left( {\rho c} \right)_{{{\text{nf}}}} } \mathord{\left/ {\vphantom {{\left( {\rho c} \right)_{{{\text{nf}}}} } {\left( {\rho c} \right)_{f} }}} \right. \kern-0pt} {\left( {\rho c} \right)_{f} }} = 1 - \varphi + \varphi {{\left( {\rho c} \right)_{s} } \mathord{\left/ {\vphantom {{\left( {\rho c} \right)_{s} } {\left( {\rho c} \right)_{{\text{f}}} }}} \right. \kern-0pt} {\left( {\rho c} \right)_{{\text{f}}} }},\;\hfill\\{{\left( {\rho c} \right)_{{{\text{nf}}}} } \mathord{\left/ {\vphantom {{\left( {\rho c} \right)_{{{\text{nf}}}} } {\left( {\rho c} \right)_{{\text{f}}} }}} \right. \kern-0pt} {\left( {\rho c} \right)_{{\text{f}}} }} = 1 - \varphi + \varphi {{\left( {\rho c} \right)_{s} } \mathord{\left/ {\vphantom {{\left( {\rho c} \right)_{s} } {\left( {\rho c} \right)_{{\text{f}}} }}} \right. \kern-0pt} {\left( {\rho c} \right)_{{\text{f}}} }}, \hfill \\ {{\sigma_{{{\text{nf}}}} } \mathord{\left/ {\vphantom {{\sigma_{{{\text{nf}}}} } {\sigma_{{\text{f}}} }}} \right. \kern-0pt} {\sigma_{{\text{f}}} }} = \frac{{\left( {{{\sigma_{s} } \mathord{\left/ {\vphantom {{\sigma_{s} } {\sigma_{{\text{f}}} }}} \right. \kern-0pt} {\sigma_{{\text{f}}} }} + 2} \right) + 2\left( {{{\sigma_{s} } \mathord{\left/ {\vphantom {{\sigma_{s} } {\sigma_{{\text{f}}} }}} \right. \kern-0pt} {\sigma_{{\text{f}}} }} - 1} \right)\varphi }}{{\left( {{{\sigma_{s} } \mathord{\left/ {\vphantom {{\sigma_{s} } {\sigma_{{\text{f}}} }}} \right. \kern-0pt} {\sigma_{{\text{f}}} }} + 2} \right) - \left( {{{\sigma_{s} } \mathord{\left/ {\vphantom {{\sigma_{s} } {\sigma_{{\text{f}}} }}} \right. \kern-0pt} {\sigma_{{\text{f}}} }} - 1} \right)\varphi }}. \hfill \\ \end{gathered}$$

(6)

In Eq. (6), (ρ_f, ρ_s) are densities, (μ_nf, μ_f) are dynamic viscosities, ((ρc)_f, (ρc)_s) are heat capacities, and, (σ_f, σ_s) are electrical conductivities of the conventional fluid and nanoparticles, respectively, α_f is the thermal diffusivity of the fluid, and φ is the nanoparticles volume fraction. The subscript nf represents the quantities of the nanofluid. It is mentioned that φ = 0 indicates a regular fluid. In Table 1, the characteristics of the base fluid and nanoparticles are tabulated.

Table 1 Thermo-physical characteristics of H₂O and Al₂O₃ nanoparticles [38]

In this study, the radiative heat flux q_rd is defined below based on Rosseland approximation [39,40,41]:

$$q_{{{\text{rd}}}} = - \frac{{4\sigma_{{\text{c}}} }}{{3k_{{\text{c}}} }}\frac{{\partial \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{T}^{4} }}{{\partial \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{y} }},$$

(7)

where k_c denotes the mean absorption coefficient, and σ_c stands for the Stefan-Boltzmann constant.

Guided by the boundary condition (5), the similarity variables are defined as,

$$\begin{gathered} \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{u} {=} a\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{x} f^{\prime } \left( \eta \right),\,\,\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{v} {=} - \left( {a\nu_{f} } \right)^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0pt} 2}}} f\left( \eta \right),N {=} a\left( {{a \mathord{\left/ {\vphantom {a {\nu_{{\text{f}}} }}} \right. \kern-0pt} {\nu_{{\text{f}}} }}} \right)^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0pt} 2}}} \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{x} g\left( \eta \right),\,\, \hfill \\ \theta \left( \eta \right) = \frac{{T - T_{c} }}{{T_{h} - T_{c} }},\,\,\,\eta = \left( {{a \mathord{\left/ {\vphantom {a {\nu_{{\text{f}}} }}} \right. \kern-0pt} {\nu_{{\text{f}}} }}} \right)^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0pt} 2}}} \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{y} . \hfill \\ \end{gathered}$$

(8)

so that

$$v_{{\text{w}}} = v_{0} = - \left( {a\nu_{{\text{f}}} } \right)^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0pt} 2}}} S,$$

(9)

where primes denotes differentiation with respect to η and S indicate the constant mass flux velocity, where S > 0 indicates suction and S < 0 indicates injection, respectively.

$$\left( {\frac{{\mu_{r} + K}}{{\rho_{r} }}} \right)f^{\prime \prime \prime } + ff^{\prime \prime } + 1 - f^{\prime 2} + \frac{K}{{\rho_{r} }}g^{\prime } - M\frac{{\sigma_{r} }}{{\rho_{r} }}\left( {f^{\prime } - 1} \right) = 0,$$

(10)

$$\left( {\frac{{\mu_{r} + K}}{{2\rho_{r} }}} \right)g^{\prime \prime } + fg^{\prime } - f^{\prime } g - \frac{K}{{\rho_{r} }}\Gamma \left( {2g + f^{\prime \prime } } \right)\, = 0,$$

(11)

$$\frac{1}{\Pr }\left\{ {\alpha_{r} + \frac{4R}{{3\left( {\rho c} \right)_{r} }}\left( {1 + \Delta \theta } \right)^{3} } \right\}\theta^{\prime \prime } + \frac{4\Delta }{{\Pr \left( {\rho c} \right)_{r} }}\left( {1 + \Delta \theta } \right)^{2} \theta^{\prime 2} + f\theta^{\prime } = 0.$$

(12)

where ρ_r = ρ_nf/ρ_f, μ_r = μ_nf/μ_f, α_r = α_nf/α_f, (ρC)_r = (ρC)_nf/(ρC)_f, α_f is known as thermal diffusivity of the fluid, Pr = ν_f/α_f is the Prandtl number, R = 4σ_cT_c³/(k_cκ_f) stands for the radiation parameter, K = κ/μ_f indicates the material parameter, M = σ_fB₀²/(ρ_fa) refers the magnetic parameter, Γ = ν_f/(ja) is the microinertia parameter, and Δ = T_h/T_c − 1 is the surface temperature parameter.

The boundary conditions are

$$\begin{gathered} f = 0,\,\,f^{\prime } = \lambda + Af^{\prime \prime } + Bf^{\prime \prime \prime } ,\,\,\hfill\\ g = - nf^{\prime \prime } ,\,\,\theta = 0\,\,\,{\text{at}}\,\,\eta = 1, \hfill \\ f = S,f^{\prime } = 1,\,\,g = 0,\,\,\theta = 1\,\,{\text{at}}\,\,\eta = - 1. \hfill \\ \end{gathered}$$

(13)

here A and B are the first- and second-order velocity slip parameters with $0 < A < \left( {{a \mathord{\left/ {\vphantom {a {\nu_{f} }}} \right. \kern-0pt} {\nu_{f} }}} \right)^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0pt} 2}}}$ and $- {a \mathord{\left/ {\vphantom {a {\nu_{f} }}} \right. \kern-0pt} {\nu_{f} }} < B < 0$.

Now the results are analyzed in terms of local skin friction coefficient, C_fx, couple stress coefficient, m_x, and local Nusselt number, Nu_x, as defined below:

$$\begin{gathered} C_{fx} = \frac{1}{{\rho_{{{\text{nf}}}} u_{w}^{2} }}\left[ {\left( {\mu_{{{\text{nf}}}} + \kappa } \right)\left( {\frac{{\partial \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{u} }}{{\partial \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{y} }}} \right)_{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{y} = - h}} + \kappa \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{N} } \right], \hfill \\ m_{x} = \frac{x}{{\rho_{{{\text{nf}}}} u_{w}^{2} }}\left( {\mu_{{{\text{nf}}}} + \frac{\kappa }{2}} \right)\left( {\frac{{\partial \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{N} }}{{\partial \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{y} }}} \right)_{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{y} = - h}} , \hfill \\ {\text{Nu}}_{x} = - \frac{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{x} }}{{\kappa_{{\text{f}}} \left( {T_{h} - T_{c} } \right)}}\left[ {\kappa_{{{\text{nf}}}} \left( { - \frac{{\partial \tilde{T}}}{{\partial \tilde{y}}}} \right)_{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{y} = - h}} + \left( {q_{{{\text{rd}}}} } \right)_{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{y} = - h}} } \right] \hfill \\ \end{gathered}$$

(14)

Using the definitions of (5) into (23), we find

$$\begin{gathered} {\text{Re}}_{x}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0pt} 2}}} C_{fx} = \frac{{\rho_{{\text{f}}} }}{{\rho_{{{\text{nf}}}} }}\left\{ {\frac{{\mu_{{{\text{nf}}}} }}{{\mu_{{\text{f}}} }} + \left( {1 - n} \right)K} \right\}f^{\prime \prime } \left( { - 1} \right), \hfill \\ m_{x} = \frac{{\rho_{{\text{f}}} }}{{\rho_{{{\text{nf}}}} }}\left( {\frac{{\mu_{{{\text{nf}}}} }}{{\mu_{{\text{f}}} }} + \frac{K}{2}} \right)g^{\prime } \left( { - 1} \right), \hfill \\ {\text{and}}\;{\text{Re}}_{x}^{{ - {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0pt} 2}}} {\text{Nu}}_{x} = - \left( {\frac{{\kappa_{{{\text{nf}}}} }}{{\kappa_{{\text{f}}} }} + \frac{4}{3}R \left( {1 + \Delta \theta } \right)^{3} } \right)\theta^{\prime } \left( { - 1} \right), \hfill \\ \end{gathered}$$

(15)

where ${\text{Re}}_{x} = {{u_{w} \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{x} } \mathord{\left/ {\vphantom {{u_{w} \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{x} } {\nu_{{\text{f}}} }}} \right. \kern-0pt} {\nu_{{\text{f}}} }}$ stands for local Reynolds number.

3 Results and discussion

In this study, Eqs. (10–12) with boundary conditions (13) are solved using the finite difference method. To implement this method, Eq. (10) is first reduced to a second-order differential equation taking V = f and U = f′:

$$\left( {\frac{{\mu_{r} + K}}{{\rho_{r} }}} \right)U^{\prime \prime } + VU^{\prime } + 1 - U^{2} + \frac{K}{{\rho_{r} }}g^{\prime } - M\frac{{\sigma_{r} }}{{\rho_{r} }}\left( {U - 1} \right) = 0.$$

(16)

Now the Eqs. (11), (12) and (16) are discretized employing the central difference formula. The resulting equations are tridiagonal algebraic equations of the form:

$$B_{n} \Gamma_{i - 1} + A_{n} \Gamma_{i} + C_{n} \Gamma_{i + 1} = R_{n,i} .$$

(17)

In the above equation, the subscript i (= 1, 2,…, M_η) is the grid point in η direction, M_η = 2001 is the total number of grids, n = 1, 2, 3 corresponds to U, g and θ, respectively. For a fixed n, the tridiagonal system (17) is solved utilizing Thomas algorithm [42]. The convergence criterion for the numerical solutions is less than 10⁻⁵. Once U is found, f can easily be determined from the relation U = f′.

Before discussing the results, a comparison is presented to validate the present numerical solutions. When n = 0.0, λ = 0.0, M = 0.0, A = 0.0, B = 0.0, R = 0.0, Δ = 0.0, φ = 0.0, third and fourth terms of Eq. (10) are zero, second and third terms of Eq. (11) are zero, the coefficient of f‴ is unity, coefficient of g″ is G, domain of solutions [− 1, 1] is [0, η_max], and the boundary condition fʹ(0) = 0, the present problem becomes similar to Takhar and Soundalgekar [43]. Table 2 shows the comparisons between the present results and corresponding values of Takhar and Soundalgekar [43] which give a good agreement. Moreover, the present model can be considered as in Jena and Mathur [44] by adding and deleting some terms in Eqs. (10–12). A comparison is shown in Table 3 which provides an excellent agreement.

Table 2 Values of − fʺ(0) and − θʹ(0)

Table 3 Values of fʺ(0) and gʹ(0)

The influences of micro-rotation parameter, n, on Re_x^1/2C_fx, m_x, and Re_x^–1/2Nu_fx are elucidated in Fig. 2a–c. For a fixed n, when λ is slowly decreased, then Re_x^1/2C_fx and Re_x^–1/2Nu_fx monotonically decrease and m_x increases. With further decrease in λ, these quantities tend to their asymptotic values at a certain value of λ which is known as critical point of λ and denoted by λ_c. For n = 0.0, 0.25, 0.50, 0.75, and 1.0 the critical points of (λ_c, Re_x^1/2C_fx, m_x, Re_x^–1/2Nu_fx) are (− 2.49000, − 5.13309, 10.60400, 1.33849), (− 2.59750, − 4.54428, 10.61009, 2.36997), (− 2.68750, − 3.86584, 10.63340, 3.23197), (− 2.77000, − 3.34062, 10.64091, 4.11338), and (− 2.84000, − 2.78209, 10.66011, 4.81145). It suggests that higher n augments |λ_c| and delays the boundary layer separation. Results show the noticeable enhancement in Re_x^1/2C_fx and m_x with higher n. The curves also show that the highest values of Re_x^1/2C_fx, m_x, and Re_x^–1/2Nu_fx are found at n = 1.0. For n = 1.0, the concentration of the fluid is lower, which leads to the increase in fluid velocity. Also, Re_x^–1/2Nu_fx increases with higher n, but the increasing rate is slower than Re_x^1/2C_fx, and m_x.

Fig. 2

Variations in a Re_x^1/2C_fx, b m_x, and c Re_x^−1/2Nu_fx for different n, when φ = 0.05, S = 2.5, K = 1.0, B = 2.0, A = 2.0, M = 1.0, and R = 1.0

In Fig. 3a–c, the effects of φ on Re_x^1/2C_fx, m_x, and Re_x^−1/2Nu_fx are depicted. Due to the increase in φ, the value of Re_x^1/2C_fx is noticeably decreased and m_x is increased. However, when φ is increased, the value of Re_x^−1/2Nu_fx is higher for λ ≥  − 2.2 and lower for λ <  − 2.2. It can be understood from the fact that the inclusion of heavier nanoparticles reduce the fluid velocity. Moreover, the stronger shrinking velocity diminishes the heat transfer from the surface to the fluid. For φ = 0.0, 0.025, 0.05, the critical points of (λ_c, Re_x^1/2C_fx, m_x, Re_x^−1/2Nu_fx) are (− 4.08000, − 3.47943, 10.47069, 4.33102), (− 3.74250, − 3.90046, 10.46082, 4.38944), (− 3.56250, − 5.02539, 10.43017, 4.81063). Therefore, the higher φ reduces |λ_c| and so it accelerates the boundary layer separation.

Fig. 3

Variations in a Re_x^1/2C_fx, b m_x, and c Re_x^−1/2Nu_fx for different φ, when n = 0.5, S = 2.5, K = 1.0, B = 2.0, A = 2.0, M = 1.0, and R = 1.0

Figure 4a–c describe the effects of material constant, K, on Re_x^1/2C_fx, m_x, and Re_x^−1/2Nu_fx. For higher values of K, Re_x^1/2C_fx and Re_x^−1/2Nu_fx are higher. However, m_x shows a distinct behavior depending on the value of λ. When K increases, a significant increase in Re_x^–1/2Nu_fx is found. For K = 1.0, 1.5, 2.0, 2.5, and 3.0, the values of (λ_c, Re_x^1/2C_fx, m_x, Re_x^−1/2Nu_fx) are (− 1.56250, − 5.16558, 13.33656, 4.67991), (− 1.77000, − 5.62940, 13.33346, 4.99653), (− 1.77000, –5.62940, 13.33346, 4.99653), (− 2.21250, − 6.77470, 13.32125, 6.15376), and (− 2.43250, − 7.43634, 13.31315, 6.90201). In this regard, increasing K augments the domain (λ_c, 0) of boundary layer approximation.

Fig. 4

Variations in a Re_x^1/2C_fx, b m_x, and c Re_x^−1/2Nu_fx for higher K, when φ = 0.05, S = 3.0, n = 0.5, A = 1.0, B = 1.0, M = 0.5, and R = 0.5

Figures 5a–c exhibit the impacts of second-order slip parameter, B, on Re_x^1/2C_fx, m_x, and Re_x− ^1/2Nu_fx. Due to the increasing values of B, Re_x^1/2C_fx and Re_x^−1/2Nu_fx are higher near λ = 0.0 then become lower for decreasing λ. The converse is found for variations in m_x. This is because the second-order velocity slip parameter slows down the fluid velocity. For B = 0.0, 0.5, 1.0, 2.0, and 4.0 the values of (λ_c, Re_x^1/2C_fx, m_x, Re_x^−1/2Nu_fx) are (− 3.04500, − 7.60761, 12.13064, 8.13728), (− 2.42500, − 6.24009, 12.32572, 6.16187), (− 2.05000, − 5.30791, 12.43843, 4.99621), (− 1.63000, − 4.23681, 12.55424, 3.79354), and (− 1.29750, − 3.22834, 12.65335, 2.76880). It indicates that higher B reduces |λ_c| and hence accelerates the boundary layer separation.

Fig. 5

Variations in a Re_x^1/2C_fx, b m_x, and c Re_x^−1/2Nu_fx for higher B, when φ = 0.05, S = 3.0, K = 1.0, A = 1.0, n = 0.5, M = 1.0, and R = 1.0

In Fig. 6a–c the effects of first-order slip parameter, A, on Re_x^1/2C_fx, m_x, and Re_x^−1/2Nu_fx are illustrated. Results reveal that Re_x^1/2C_fx and Re_x^−1/2Nu_fx are higher and m_x is lower with the increase in A. For A = 0.0, 1.0, 2.0, 3.0, and 4.0, the critical values of (λ_c, Re_x^1/2C_fx, m_x, Re_x^−1/2Nu_fx) are (− 1.01000, − 3.14097, 8.79938, 2.41515), (− 2.03750, − 3.36592, 8.75435, 2.61731), (− 3.08000, − 3.54222, 8.71767, 2.77925), (− 4.12750, − 3.61950, 8.70118, 2.85124), and (− 5.17750, − 3.64656, 8.69534, 2.87660). These results imply that |λ_c| increases with A and so the boundary layer separation becomes delay for increasing A.

Fig. 6

Variations in a Re_x^1/2C_fx, b m_x, and c Re_x^−1/2Nu_fx for higher A, when φ = 0.05, S = 2.0, n = 0.5, K = 1.0, B = 2.0, M = 1.0, and R = 1.0

The influences of magnetic parameter, M, on Re_x^1/2C_fx, m_x, and Re_x^−1/2Nu_fx are exhibited in Fig. 7a–c. One can easily observe that an increase in M reduces m_x but augments Re_x^1/2C_fx and Re_x^−1/2Nu_fx. It is because the magnetic field impedes the flow velocity. For M = 0.0, 0.5, 1.0, 1.5, and 2.0, the critical points of (λ_c, Re_x^1/2C_fx, m_x, Re_x^−1/2Nu_fx) are (− 1.22000, − 4.40988, 10.56570, 3.55113), (− 1.69000, − 4.59059, 10.53128, 3.84671), (− 2.23250, − 4.74686, 10.49830, 4.14691), (− 2.85500, − 4.90565, 10.46225, 4.48337), and (− 3.56250, − 5.02539, 10.43017, 4.81063). Since the value of |λ_c| increases with the increase in M, hence the boundary layer approximation is valid for larger shrinking velocity.

Fig. 7

Variations in a Re_x^1/2C_fx, b m_x, and c Re_x^−1/2Nu_fx for higher M, when φ = 0.05, S = 2.5, n = 0.5, K = 1.0, B = 1.0, A = 1.0, and R = 1.0

Figure 8a–c depicts the impacts of suction parameter, S, on Re_x^1/2C_fx, m_x, and Re_x^−1/2Nu_fx. For S = 4.0, Re_x^1/2C_fx obtains the lowest value but, m_x and Re_x^−1/2Nu_fx reach their highest values. In this sense, Re_x^1/2C_fx declines due to an elevation in S. Contrary to this, the variations in m_x and Re_x^−1/2Nu_fx are decreased for higher S. For S = 2.0, 2.5, 3.0, 3.5, and 4.0, the expected corresponding turning points of (λ_c, Re_x^1/2C_fx, m_x, Re_x^−1/2Nu_fx) are (− 1.68250, − 3.75639, 9.20359, 2.93195), (− 1.51250, − 4.32839, 11.25685, 3.80439), (− 1.39750, − 4.94207, 13.32961, 4.87724), (− 1.32500, − 5.68142, 15.41376, 6.29996), and (− 1.28500, − 6.60304, 17.50606, 8.24196). So, the boundary layer separation expedites owing to the increase in S.

Fig. 8

Variations in a Re_x^1/2C_fx, b m_x, and c Re_x^−1/2Nu_fx for higher S, when φ = 0.05, n = 0.5, M = 0.5, K = 0.5, B = 1.0, A = 1.0, and R = 0.5

Figure 9 elucidates the influences of radiation parameter, R, on Re_x^−1/2Nu_fx. The higher radiation leads to radiate more heat. With higher values of R, that is, for R = 2.0, 2.5, and 3.0, Re_x^−1/2Nu_fx is an increasing function of R. However, Fig. 8 exhibits two different pattern curves relating to R > or < 1.5. When R is increased from 0 to 1.5, the value of Re_x^−1/2Nu_fx decreases. On the other hand, for increasing R in the domain R > 1.5, the value of Re_x^−1/2Nu_fx increases. For R = 1.0, 1.5, 2.0, 2.5, and 3.0, the values of (λ_c, Re_x^−1/2Nu_fx) are (− 2.29750, 4.30461), (− 2.29750, 4.30461), (− 2.29750, 4.30461), (− 2.29750, 4.30461), and (− 2.29750, 4.30461). These indicate that the boundary layer approximation remains unchanged against λ.

Fig. 9

Variations in Re_x^−1/2Nu_fx for higher R, when φ = 0.05, M = 0.5, n = 0.5, K = 2.0, B = 1.0, A = 1.0, and S = 2.0

The effect of alumina nanoparticles, φ, on f′, g, and θ is shown in Fig. 10a–c. An increase in φ causes to decrease in f′ and increase in g and θ. It is also evident from Fig. 10a, b that the strong influence of φ is on f′ and g. As the fluid becomes heavier with the inclusion of nanoparticles, the fluid velocity is lower for increasing φ. On the contrary, the nanoparticles’ thermal conductivity is higher than the pure fluid, resulting in an increase in temperature.

Fig. 10

Variations in a f′, b g, and c θ for changing φ, when K = 1.0, S = 3.0, n = 0.5, A = 1.0, B = 1.0, M = 0.5, R = 0.5, and λ = − 1.0

Figure 11a–b illustrates the influences of material constant, K, on f′ and g. With larger K, f′ grows slowly, but, the converse is found in g. However, the rate of change of f′ and g becomes slow for increasing K. The cause is that the material constant K is strongly related to the angular velocity of the fluid, which decreases with higher K. When fluid particles move with lower spin, the fluid velocity is thus accelerated.

Fig. 11

Variations in a f′ and b g for changing K, when φ = 0.05, S = 3.0, n = 0.5, A = 1.0, B = 1.0, M = 0.5, R = 0.5, and λ = − 1.0

The effects of micro-rotation parameter, n, on f′ and g are discussed in Fig. 12a–b. Figure 12a shows the slow increase in f′, but a rapid increase in g for varying n from lower to higher values. From the definition of n, when n = 0 it corresponds to strong concentration, and n = 1 relates to turbulent layer. For this reason, both f′ and g increase with the increase in n.

Fig. 12

Variations in a f′ and b g for higher n, when φ = 0.05, S = 2.5, K = 1.0, A = 2.0, M = 1.0, B = 2.0, R = 1.0, and λ = –1.0

The influences of second-order slip parameter, B, on f′ and g are depicted in Figs. 13a–b. With the increase in B, f′ increases and g decreases. However, the changes are very small. Indeed, Fig. 13a, b shows the negligible effects for B = 0.0, 0.5, and 1.0. But, for B = 2.0, f′ and g show a considerable increment or decrement effect, respectively.

Fig. 13

Variations in a f′ and b g for higher B, when φ = 0.05, S = 3.0, K = 1.0, A = 1.0, n = 0.5, M = 1.0, R = 1.0, and λ = − 1.0

The impacts of first-order slip parameter, A, on f′, g, and θ are described in Fig. 14a–c. It is seen that A has strong influence on f′ and g. For larger A, f′ increases but g decreases. A big change in f′ and g is observed for changing A from 0.0 to 1.0. So, there is a big impact of the first-order slip parameter on f′ and g.

Fig. 14

Variations in a f′, b g, and c θ for higher A, when φ = 0.05, S = 2.0, n = 0.5, K = 1.0, B = 2.0, M = 1.0, R = 1.0, and λ = − 1.0

Figure 15a–c shows the effects of magnetic field parameter, M, on f′, g, and θ. Generally, the magnetic field controls the fluid flow. Here, the flow is considered through a channel. Figure 15a clears the increment of f′ for higher M. Contrary to this, g shows a decreasing nature with higher M. However, θ exhibits negligible effect for larger M. With higher M, thermal does not show any significant effect on boundary increases.

Fig. 15

Variations in a f′, b g, and c θ for higher M, when φ = 0.05, S = 2.5, n = 0.5, K = 1.0, B = 1.0, A = 1.0, R = 1.0, and λ = − 1.0

The impacts of suction parameter, S, on f′, g, and θ are elucidated in Fig. 16a–c. Results indicate that f′ and θ decrease, but g significantly increases with larger S. The nonlinear decreasing pattern is recognized in f′ due to the improvement in S. On the other hand, g attains its largest value for S = 4.0. For S = 2.0, 2.5, and 3.0, the decreasing rate is higher in θ compared to S = 3.5 and 4.0. The thermal boundary layer gradually decreases for larger S.

Fig. 16

Variations in a f′, b g and c θ for higher S, when φ = 0.05, M = 0.5, n = 0.5, K = 0.5, B = 1.0, A = 1.0, R = 0.5, and λ = − 1.0

Figure 17 exhibits the influences of radiation parameter, R, only on θ. It is found that θ increases for larger R. The curve also shows that thermal boundary layer accelerates due to the augmenting in R. The reason for such behaviors is that the higher radiation parameter leads to more heat owing to the collision of fluid particles.

Fig. 17

Variations θ for higher R, when φ = 0.05, M = 0.5, n = 0.5, K = 2.0, B = 1.0, A = 1.0, and S = 2.0, and λ = − 1.0

4 Conclusion

In this study, the micropolar nanofluid flow in a shrinking channel has been investigated with the influence of second-order velocity slip, magnetic field and thermal radiation. Using the similarity variables, the governing equations are transformed into a system of ordinary differential equations. These are solved by the finite difference method. From the results, the following conclusions are drawn:

• (i) Boundary layer separation is accelerated for higher suction parameter, second-order slip parameter and volume fraction of alumina nanoparticles, however, it is slowed down for increasing material constant, micro-rotation parameter, first-order slip parameter, and magnetic parameter.

• (ii) Higher suction parameter leads to a decrease in skin friction coefficient and an increase in local Nusselt number.

• (iii) Both skin friction coefficient and local Nusselt number are found to increase with the increase in micro-rotation parameter, material constant, first-order slip parameter, and magnetic parameter.

• (iv) With the increase in material constant, first and second-order slip parameters, and magnetic parameter, the fluid velocity is increased, but the microrotation field is decreased.

• (v) For increasing suction parameter, the temperature and the velocity of the fluid are decreased, whereas the microrotation field is increased.

The limitations of the current study are that the model is suitable for thermal equilibrium between the base fluid and nanoparticles and constant thermo-physical properties of the nanofluid. In this regard, the present model can be extended for non-equilibrium and temperature dependent thermo-physical cases.