Magnetohydrodynamic micropolar nanofluid past a permeable stretching/shrinking sheet with Newtonian heating

Abstract

In this present study, a numerical investigation has been carried out to discuss the steady, two dimensional flow and heat transfer on micropolar nanofluid over a stretching/shrinking sheet with variable suction or injection in the presence of magnetic field and Newtonian heating. Copper (${\text{Cu}}$), alumina (${\text{Al}}_{ 2} {\text{O}}_{ 3}$) and titanium (${\text{TiO}}_{ 2}$) in water-based micropolar nanofluid has been considered for the present investigation. The solutions of the transformed nonlinear equations have been obtained using Runge–Kutta–Gill procedure together with the shooting method. The results are presented graphically and discussed for various resulting parameters. Dual solutions are found to exist in a certain range of the governing parameters. The thickness of thermal boundary layer for Cu nanofluid is more than that of other nanofluids in the cases of shrinking and stretching sheets. Newtonian heating effect significantly increases the thermal boundary layer thickness for both sheets under investigation.

1 Introduction

Nanofluids are suspensions of nano-sized particles in common fluids that show significant enhancement of their properties at modest nanoparticle concentrations. Most generally used nanoparticles are aluminum, copper, iron and titanium or their oxides. Consideration of nanofluids in a variety of processes results in noteworthy applications in engineering and sciences since materials with sizes of nanometers possesses unique physical and chemical properties. Several investigations in literature reveals the fact that nanofluids have been found to have enhanced thermo-physical properties such as thermal conductivity, thermal diffusivity, viscosity and convective heat transfer coefficients compared to those of base fluids like oil or water. Choi [8] is the first who introduced the term nanofluids to refer to the fluid with suspended nanoparticles. Choi et al. [9] reported that the addition of a small amount of nanoparticles to conventional heat transfer liquids notably increases the thermal conductivity of the fluid up to approximately two times. Buongiorno [6] concluded that only Brownian diffusion and thermophoresis are essential slip mechanisms in nanofluids. Makinde and Aziz [24] examined the flow of a nanofluid past a stretching sheet with a convective boundary condition and found that as the Prandtl number increases, the thickness of the thermal boundary layer decreases as the curves become increasingly steeper. Makinde and Mishra [25] studied the stagnation point flow of variable viscosity nanofluids past a stretching surface with radiative heat.

The study of fluids with micro-structures has acquired a great attention due to its significant role playing in industrial and engineering applications. Micropolar fluids are fluids with micro-structure. They belong to a class of fluids with non-symmetric stress tensor that shall call polar fluids and include as a special case, the well-constructed Nevier–Stokes model of classical fluids that we shall call ordinary fluids. Physically, micropolar fluids may represent fluids consisting of rigid, randomly oriented (or spherical) particles suspended in a viscous medium, where the deformation of fluid particles is ignored. The theory of micropolar fluids were introduced by Erignen [13, 14]. Arafa and Gorla [2] carried out a work on the buoyancy and curvature on convection of micropolar fluid along vertical cylinders and needles. It is concluded that non-homogeneous boundary conditions for microrotation significantly enhance the microrotation. Nadeem et al. [29] investigated the stagnation point flow of a micropolar nanofluid in a moving cylinder with finite radius. It is confirmed that the velocity, angular velocity and temperature at the surface increased by increasing micropolar parameter value. Bourantas and Loukopoulos [4] presented an analysis of natural convection of a micropolar nanofluid (Al₂O₃/water) along inclined rectangular enclosure. Noor et al. [32] discussed the mixed convection flow of a micropolar nanofluid near a stagnation point past a vertical stretching sheet. It is found that the flow becomes cooler and the nanoparticle volume fraction is reduced with an increase in Prandtl number. Rehman and Nadeem [39] reported the applicability of boundary layer theory for the mixed convection flow of micropolar nanofluid on a vertical slender cylinder. It was illustrated that the velocity and temperature of the fluid at the boundary is decreased as the micropolar parameter increased. Ram Reddy et al. [37] examined the similarity solution for the steady free convection flow of a micropolar fluid past a vertical plate with convective boundary condition. They proved that microrotation, temperature, and concentration distributions and skin friction coefficients are more in the case of a micropolar fluid with strong concentration when compared to the case of a micropolar fluid with weak concentration.

Magnetohydrodynamic (MHD) boundary layers with heat and mass transfer over flat surfaces are found in many engineering and geophysical applications such as geothermal reservoirs, thermal insulation, enhanced oil recovery, packed-bed catalytic reactors, and cooling of nuclear reactors. Many chemical engineering processes like metallurgical and polymer extrusion processes involve cooling of a molten liquid being stretched into a cooling system. The fluid mechanical properties of the penultimate product depend mainly on the cooling liquid used and the rate of stretching. Some polymer liquids like polyethylene oxide and polyisobutylene solution in cetane, having better electromagnetic properties are normally used as cooling liquid as their flow can be regulated by external magnetic fields to improve the quality of the final product. Jat and Jhankal [19] concluded that the skin friction coefficient increases with increasing the values of Reynolds number and magnetic parameter up to a certain value of Reynolds number and afterwards it decreases with the increasing values of these parameters and also the heat transfer rate increases with increasing the values of these parameters. Hayat and Nawaz [18] studied the effects of MHD on three dimensional flow of a second grade fluid with heat transfer and they concluded that dimensionless tangential velocity is a decreasing function of magnetic field, whereas dimensionless lateral velocity increases by increasing magnetic parameter. Turkyilmazoglu [42] analyzed the three dimensional MHD laminar stagnation point flow of an electrically conducting fluid in the presence of a uniform vertical magnetic field. It is observed that the stagnation velocities and shear stresses are strongly dependent upon the magnetic field parameter. Hayat et al. [17] reported that the three dimensional flow of MHD Eyring–Power fluid with radiation effect and then concluded that magnetic field causes a decrease in the magnitude of velocity components. Kar et al. [21] investigated the effects of MHD, heat source and chemical reaction in a vertical channel through a porous medium and reported that the presence of heavier species contributes to surface mass transfer significantly. Rajagopal et al. [35] examined MHD flow due to impulsive motion with heat and mass transfer past a stretching sheet in a saturated porous medium. It is reported that the magnetic parameter affects significantly the surface shear stress and surface mass transfer. El-Dabe et al. [12] proved that the velocity distribution decreases with increasing the values of magnetic parameter while it increases the values of Casson fluid parameter. Ramzan [38] discussed the influence of Newtonian heating, viscous dissipation and joule heating on the magnetohydrodynamic (MHD) three dimensional couple stress nanofluid past a stretching surface. It is found that velocity components decrease with an increase in couple stress parameter. Gireesha et al. [16] investigated the MHD boundary layer three dimensional flow and heat transfer towards a linearly stretching sheet in the presence of nanoparticle. Das and Jana [11] considered the natural convective magneto-nanofluid flow and radiative heat transfer past a moving vertical plate. It is concluded that the rate of heat transfer at the plate is found to be higher for ${\text{Cu}}$–water nanofluid. Baag and Mishra [3] investigated the impact of heat and mass transfer analysis on MHD water-based nanofluid and they found that boundary layer thickness reduces in the presence of magnetic field.

The study of stretched flows with heat transfer is given much importance. The heat transfer is through constant wall temperature or constant wall heat flux. Also there are another class of flow problems in which the rate of heat transfer is proportional to the local surface temperature from the boundary surface with finite heat capacity known as Newtonian heating or conjugate convective flow. The boundary layer natural convective flow with Newtonian heating is reported by Merkin [27]. Chaudhary and Jain [7] obtained the similarity solution for unsteady free convection flow past on impulsive vertical surface in the presence of Newtonian heating. It is reported that the increase in the Grashof number, the contribution from the buoyancy near the plate becomes significant. Mohamed et al. [28] concluded that when the value of the conjugate parameter γ decreases it is found that the temperature also decreases. Khan et al. [22] explicated the effects of Newtonian heating and mass diffusion on MHD free convection flow over vertical plate with shear stress at the wall.

The above cited articles in the literature explicates the flow and the heat transfer characteristics of different working fluids in permeable stretching/shrinking sheet with or without variable suction or injection in detail. Obviously, presence or absence of magnetic field and Newtonian heating becomes significant in many research works as explained above. It can be noticed that consideration of copper (${\text{Cu}}$), alumina (Al₂O₃) and titania (TiO₂) in water-based micropolar nanofluid as working fluid in the place of base fluids is of greater interest in practical applications in science and engineering. It is found that the solutions of the transformed ordinary differential equations have dual solutions in a certain range of the governing parameters. As a trial attempt, the authors intend to provide the knowledge of the effects of the steady, two dimensional flow of heat transfer on micropolar nanofluid with variable suction or injection in the presence of magnetic field and Newtonian heating.

2 Mathematical formulation

Consider the steady two-dimensional boundary layer flow over a permeable stretching/shrinking sheet in an electrically conducting water-based micropolar nanofluid containing different types of nanoparticles: copper (${\text{Cu}}$), alumina (${\text{Al}}_{ 2} {\text{O}}_{ 3}$) and titanium dioxide (${\text{TiO}}_{ 2}$). The micropolar nanofluid is assumed as incompressible laminar flow. It is also presumed that the base fluid (i.e., water) and the nanoparticles are in thermal equilibrium and no slip occurs between them in quiescent micropolar nanofluid. The thermo-physical properties of the nanofluid are specified in Table 1.

Table 1 Thermo-physical properties of water and nanoparticles [33]

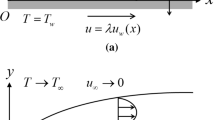
The sheet stretching velocity is $u_{w} (x) = \lambda x$, where $\lambda$ is a constant with $\lambda > 0$ corresponds to a stretching sheet. The wall mass transfer velocity is $v_{w} (x) = v_{0}$, with $v_{0} < 0$ for suction. The $x$-axis is measured along the stretching surface in the direction of the motion and the $y$-axis is perpendicular to it. A uniform transverse magnetic field of strength $B_{0}$ is applied parallel to the $y$-axis. It is assumed that induced magnetic field produced by the fluid motion is negligible in comparison with the applied one so that we consider the magnetic field as $\vec{B} = (0,0,B_{0} )$. This assumption is justified, since the magnetic Reynolds number is very small for metallic liquids and partially ionized fluids [10]. Also, no external electric field is applied such that the effect of polarization of fluid is negligible [10], so we assume $\vec{E} = (0,0,0)$. Schematic diagram of the physical model is shown in Fig. 1.

Under the above assumptions, the governing equations of continuity, momentum, angular momentum, and energy are written as follows:

$$ \frac{\partial u}{\partial x} + \frac{\partial v}{\partial y} = 0, $$

(2.1)

$$ u\frac{\partial u}{\partial x} + v\frac{\partial u}{\partial y} = \frac{{\mu_{\text{nf}} + \kappa }}{{\rho_{\text{nf}} }}\frac{{\partial^{2} u}}{{\partial y^{2} }} + \frac{\kappa }{{\rho_{\text{nf}} }}\frac{\partial N}{\partial y} - \frac{{\sigma_{\text{nf}} B_{0}^{2} }}{{\rho_{\text{nf}} }}u, $$

(2.2)

$$ \rho_{\text{nf}} j\left( {u\frac{\partial N}{\partial x} + v\frac{\partial N}{\partial y}} \right) = \delta_{\text{nf}} \frac{{\partial^{2} N}}{{\partial y^{2} }} - \kappa \left( {2N + \frac{\partial u}{\partial y}} \right), $$

(2.3)

$$ u\frac{\partial T}{\partial x} + v\frac{\partial T}{\partial y} = \alpha_{\text{nf}} \frac{{\partial^{2} T}}{{\partial y^{2} }}. $$

(2.4)

Fig. 1

Schematic diagram of the physical model

The suitable boundary conditions are

$$ \begin{aligned} y = 0:u = u_{w} (x) = \lambda cx,\quad v = v_{0} ,\quad N = - n\frac{\partial u}{\partial x},\quad - \frac{\partial T}{\partial y} = h_{\text{s}} T \hfill \\ y \to \infty :u \to 0,\quad N \to 0,\quad T \to T_{\infty } , \hfill \\ \end{aligned} $$

(2.5)

where $u$ and $v$ are the velocity components along the $x$ and $y$ axes, respectively, $N$ is the microrotation component normal to the $xy$-plane, $\kappa$ is the vortex viscosity, $j$ is the microinertia density, $v_{{w}}$ is the mass transfer velocity, $h$ is the convective heat transfer coefficient, $T$ is the temperature of the nanofluid, $h_{\text{s}}$ is the heat transfer coefficient, $T_{\infty }$ is the ambient temperature and $n$ is a constant which varies in the range $0 \le n \le 1$. The strong concentration case ($n = 0$) represents the concentrated particle flows in which the microelements close to the wall surface are unable to rotate [20]. The weak concentration case ($n = 1/2$) indicates the vanishing of the anti-symmetrical part of the stress tensor and denotes weak concentration [1]. The case $n = 1$, as suggested by Peddieson [34], is used for the modeling of turbulent boundary layer flows. $\mu_{\text{nf}}$ is the viscosity of the nanofluid, $\alpha_{\text{nf}}$ is the thermal diffusivity of the nanofluid and $\rho_{\text{nf}}$ is the density of the nanofluid, which are given by Oztop and Abu-Nada [33].

$$ \begin{aligned} \alpha_{\text{nf}} & = \frac{{k_{\text{nf}} }}{{(\rho C_{\text{p}} )_{\text{nf}} }},\quad \rho_{\text{nf}} = (1 - \phi )\rho_{f} + \phi \rho_{\text{s}} , \quad \mu_{\text{nf}} = \frac{{\mu_{{f}} }}{{(1 - \phi )^{2.5} }},\quad \gamma_{\text{nf}} = (\mu_{\text{nf}} + \kappa /2)j = \mu_{f} (\mu_{\text{nf}} /\mu_{f} + K/2)j \\ (\rho c_{\text{p}} )_{\text{nf}} & = (1 - \phi )(\rho c_{\text{p}} )_{f} + \phi (\rho c_{\text{p}} )_{\text{s}} ,\quad \frac{{k_{\text{nf}} }}{{k_{{f}} }} = \frac{{(k_{\text{s}} + 2k_{f} ) - 2\phi (k_{f} - k_{\text{s}} )}}{{(k_{\text{s}} + 2k_{f} ) + \phi (k_{f} - k_{\text{s}} )}} \\ \sigma_{\text{nf}} & = \sigma_{f} \left[ {1 + \frac{3(\sigma - 1)\phi }{(\sigma + 2) - (\sigma - 1)\phi }} \right],\quad \sigma = \frac{{\sigma_{\rm{s}} }}{{\sigma_{f} }}. \\ \end{aligned} $$

(2.6)

Here $\phi$ is the nanoparticle volume fraction, $(\rho c_{\text{p}} )_{\text{nf}}$ is the heat capacity of the nanofluid, $\delta_{\text{nf}}$ is the spin-gradient nanofluid viscosity, $K = \frac{\kappa }{{\mu_{f} }}$ is the micropolar or material parameter, $\sigma_{{f}}$ is the electrical conductivity of the base fluid, $\sigma_{\text{s}}$ is the electrical conductivity of the nanoparticle, $k_{\text{nf}}$ is the thermal conductivity of the nanofluid, $k_{f}$ and $k_{\text{s}}$ are the thermal conductivities of the fluid and of the solid fractions, respectively, and $\rho_{f}$ and $\rho_{\text{s}}$ are the densities of the fluid and of the solid fractions, respectively. It should be mentioned that the use of the above expression for $k_{\text{nf}}$ is restricted to spherical nanoparticles where it does not account for other shapes of nanoparticles [33]. Also, the viscosity of the nanofluid $\mu_{\text{nf}}$ has been approximated as viscosity of a base fluid $\mu_{f}$ containing dilute suspension of fine spherical particles [5].

The continuity Eq. (2.1) is satisfied by the Cauchy–Riemann equations

$$ v = - \psi_{x} \;{\text{and}}\;u = \psi_{y} , $$

(2.7)

where $\psi (x,y)$ is the stream function.

To transform the Eqs. (2.2)–(2.5) into a set of ordinary differential equations, the following similarity transformations and dimensionless variables are introduced.

$$ \begin{aligned} \eta & = \left( {\frac{c}{{\upsilon_{f} }}} \right)^{1/2} y,\quad X = (c/\upsilon_{f} )^{1/2} x,\quad \psi (x,y) = \upsilon_{f} X\,f(\eta ) \\ N(x,y) & = c\sqrt {c/\upsilon_{f} } xg(\eta ),\quad \theta (\eta ) = \frac{{T - T_{\infty } }}{{T_{w} }}, \\ \end{aligned} $$

(2.8)

where $\eta$ is the similarity variable, $\upsilon_{{f}}$ is the kinematic viscosity of the fluid fraction and $c$ is a constant.

After the substitution of these transformations (2.8) along with the Eq. (2.7) into the Eqs. (2.2)–(2.6), the resulting non-linear ordinary differential equations are written as

$$ \frac{{1 + K(1 - \phi )^{2.5} }}{{(1 - \phi )^{2.5} 1 - \phi + \phi \left( {\frac{{\rho_{\text{s}} }}{{\rho_{{f}} }}} \right)}}f^{\prime\prime\prime}(\eta ) + f(\eta )f^{\prime\prime}(\eta ) - f^{\prime}(\eta )^{2} + \frac{K}{{1 - \phi + \phi \left( {\frac{{\rho_{\text{s}} }}{{\rho_{{f}} }}} \right)}}g^{\prime}(\eta ) - M\frac{{1 + \frac{3(\sigma - 1)}{(\sigma + 2) - (\sigma - 1)\phi }}}{{1 - \phi + \phi \left( {\frac{{\rho_{\text{s}} }}{{\rho_{f} }}} \right)}}f^{\prime}(\eta ) = 0, $$

(2.9)

$$ \frac{{1 + \frac{K}{2}(1 - \phi )^{2.5} }}{{(1 - \phi )^{2.5} 1 - \phi + \phi \left( {\frac{{\rho_{\text{s}} }}{{\rho_{f} }}} \right)}}g^{\prime\prime}(\eta ) + g^{\prime}(\eta )f(\eta ) - f^{\prime}(\eta )g(\eta ) - \frac{K}{{1 - \phi + \phi \left( {\frac{{\rho_{\text{s}} }}{{\rho_{f} }}} \right)}}(2g(\eta ) - f^{\prime\prime}(\eta )) = 0, $$

(2.10)

$$ \frac{1}{\Pr }\frac{{k_{\text{nf}} /k_{f} }}{{\left[ {1 - \phi + \phi (\rho C_{\text{p}} )_{\text{s}} /(\rho c_{\text{p}} )_{f} } \right]}}\theta^{\prime\prime}(\eta ) + f(\eta )\theta^{\prime}(\eta ) - f^{\prime}(\eta )\theta (\eta ) = 0. $$

(2.11)

Together with the boundary conditions

$$ f(0) = f_{{w}} ,\quad f^{\prime}(0) = \lambda ,\quad g(0) = - n\,f^{\prime\prime}(0),\quad \theta^{\prime}\left( 0 \right) = - \gamma (1 + \theta (0)), $$

$$ f^{\prime}(\eta ) \to 0,\quad g(\eta ) \to 0,\quad \theta (\eta ) \to 0\;\;{\text{as}}\;\;\eta \to \infty . $$

(2.12)

Here primes denote differentiation with respect to $\eta$.

$f_{w} > 0$ is the suction parameter and $f_{w} < 0$ corresponds to injection, $Pr$ is the Prandtl number, $M$ is the magnetic parameter and $\gamma$ is the conjugate parameter for Newtonian heating and which are given by

$$ \begin{aligned} f_{w} & = - \frac{{v_{0} }}{{\sqrt {c\upsilon_{f} } }},\quad Pr = \frac{{\mu_{f} (c_{\text{p}} )_{f} }}{{k_{{f}} }} \\ M & = \frac{{\sigma_{f} B_{0}^{2} }}{{\rho_{f} c}},\quad \gamma = h_{\text{s}} \left( {\frac{{\upsilon_{f} }}{c}} \right)^{1/2} , \\ \end{aligned} $$

(2.13)

with $\lambda > 0$ for stretching and $\lambda < 0$ for shrinking.

The physical quantities of interest are the skin friction coefficient $C_{f}$, the couple stress $C_{{n}}$ and the local Nusselt number $Nu_{x}$, which are defined as

$$ \begin{aligned} C_{f} & = \frac{{\tau_{w} }}{{\rho u_{w}^{2} }} \\ C_{{n}} & = \frac{x}{a}\left( {\frac{\partial N}{\partial y}} \right)_{y = 0} \\ Nu_{x} & = \frac{{xq_{w} }}{{k\left( {T_{\infty } } \right)}}, \\ \end{aligned} $$

(2.14)

where the surface shear stress $\tau_{w}$ and the surface heat flux $q_{w}$ are given by

$$ \begin{aligned} \tau_{w} & = (\mu + \kappa )\left( {\frac{\partial u}{\partial y}} \right)_{y = 0} + \kappa (N)_{y = 0} \\ q_{w} & = - k\left( {\frac{\partial T}{\partial y}} \right)_{y = 0} , \\ \end{aligned} $$

(2.15)

with $\mu_{\text{nf}}$ and $k_{\text{nf}}$ being the dynamic viscosity and thermal conductivity of the nanofluids, respectively.

Using the similarity variables (2.8), we obtain

$$ \begin{aligned} C_{{f}} Re_{x}^{1/2} & = (1 + (1 - n)K)f^{\prime\prime}(0) \\ Re_{x}^{ - 1} C_{{n}} & = g^{\prime}(0) \\ \frac{{Nu_{x} }}{{Re_{x}^{1/2} }} & = - \theta^{\prime}(0), \\ \end{aligned} $$

(2.16)

where $Re_{x} = \frac{{u_{w} x}}{\upsilon }$ is the local Reynolds number.

3 Solution of the problem

The governing equations for the present problem are transformed into a set of coupled nonlinear differential equations by applying similarity transformation. The Eqs. (2.9)–(2.11) together with the boundary conditions (2.12) are integrated numerically using Runge–Kutta–Gill method along with the shooting technique. Runge–Kutta–Gill method has the advantage of compensation for accumulated round-off error and less storage requirements than the other Runge–Kutta formulae (Kumar and Unny [23]). This method is concisely outlined as below:

$$ \begin{aligned} y_{1} = f,\quad y_{2} = f^{\prime},\quad y_{3} = f^{\prime\prime},\quad y_{4} = g,\quad y_{5} = g^{\prime},\quad y_{6} = \theta ,\quad y_{7} = \theta^{\prime} \hfill \\ y^{\prime}_{3} = \left[ {\frac{{a_{1} a_{2} }}{{1 + Ka_{1} }}} \right]\left( {y_{2}^{2} - y_{1} y_{3} - \frac{K}{{a_{2} }}y_{5} + M\frac{{a_{3} }}{{a_{2} }}y_{2} } \right) \hfill \\ y^{\prime}_{5} = \left[ {\frac{{a_{1} a_{2} }}{{1 + \frac{K}{2}a_{1} }}} \right]\left( {y_{2} y_{4} - y_{1} y_{5} + \frac{K}{{a_{2} }}(2y_{4} - y_{3} )} \right) \hfill \\ y^{\prime}_{7} = Pr\left[ {\frac{{a_{5} }}{{a_{4} }}} \right](y_{1} y_{7} - y_{2} y_{6} ). \hfill \\ \end{aligned} $$

(3.1)

The boundary conditions are transformed as follows:

$$ \begin{aligned} y_{1} (0) = f_{{w}} ,\quad y_{2} (0) = \lambda ,\quad y_{4} (0) = - ny_{3} (0),\quad y_{7} (0) = - \gamma (1 + y_{6} (0)) \hfill \\ y_{2} (\infty ) \to 0,\quad y_{4} (\infty ) \to 0,\quad y_{6} (\infty ) \to 0. \hfill \\ \end{aligned} $$

(3.2)

To carry out the step by step integration for the Eqs. (2.9)–(2.12), Gill’s procedures have been used (Ralston and Wilf [36]). To start the integration it is necessary to provide all the values of $y_{1} ,\;y_{2} ,\,y_{3} ,\,y_{4} ,\,y_{5} ,\,y_{6}$ at $\eta = 0$ from which point, the forward integration has been carried out but from the boundary conditions it is seen that the values of $y_{3} ,\,y_{4} ,\,y_{7}$ are not known. So, we are to provide such values of $y_{3} ,\,y_{4} ,\,y_{7}$ along with the known values of the other function at $\eta = 0$ as would satisfy the boundary conditions as $\eta \to \infty$ to a prescribed accuracy after step by step integrations are performed. Since the values of $y_{3} ,\,y_{4} ,\,y_{7}$ which are supplied merely as rough values, some corrections have to be made in these values in order that the boundary conditions to $\eta \to \infty$ are satisfied. These corrections in the values of $y_{3} ,y_{4} ,y_{7}$ are taken care of by a self-iterative procedure which can for convenience be called corrective procedure.

4 Results and discussion

A numerical approach has been made out to investigate the effects of micropolar nanoparticles (${\text{Cu}}$, ${\text{Al}}_{ 2} {\text{O}}_{ 3}$, ${\text{TiO}}_{ 2}$) in water-based fluid over a permeable stretching/shrinking sheet with variable suction or injection in the presence of magnetic field and Newtonian heating. To gain the physics of the problem, the velocity, angular velocity and temperature distribution profiles have been illustrated by varying controlling parameters, namely, nanoparticle volume fraction parameter ($\phi$), magnetic field parameter ($M$), material parameter ($K$), stretching/shrinking parameter ($\lambda$), suction or injection parameter ($f_{{w}}$), Newtonian heating parameter ($\gamma$), Prandtl number ($Pr$), and concentration variation parameter ($n$). The numerical results are tabulated and exhibited with the graphical illustrations. The dual solutions (upper and lower branch solutions) are obtained for the present problem. The graphical illustrations of velocity, angular velocity and temperature distributions corresponding to dual solutions for some fixed values of governing parameters are presented in detail. From Figs. 3, 4, 5, 6, 7, 8, 9, 10, 11 and 12, it is noted that for a particular value of some parameter, there exists two different profiles with various boundary layer thicknesses, which shows the existence of dual solutions. The Prandtl number is fixed at 6.2 and the parameter $n$ is set as 0.5.

To get a clear view of the flow field, the stream line patterns are plotted in Figs. 2 and 3 for stretching and shrinking cases. Figures 4, 5 and 6 demonstrate the influence of nanoparticles (${\text{Cu}}$, ${\text{Al}}_{ 2} {\text{O}}_{ 3}$, ${\text{TiO}}_{ 2}$) on dimensionless velocity, angular velocity and temperature profiles, respectively. The other controlling parameters are set as $\phi$ = 0.1, $M$ = 2, $K$ = 0.3, $f_{w}$ = 2.5 and $\gamma$ = 0.1. The velocity of ${\text{Cu}}$ nanofluid accelerates more than that of other nanofluids for both solutions. In the case of the second solution, it is noted that the angular velocity profile exhibits an overshoot near the shrinking sheet. ${\text{Al}}_{ 2} {\text{O}}_{ 3}$ nanofluid shows more angular velocity distribution than the other nanofluids under consideration. It is observed that the thickness of thermal boundary layer for ${\text{Cu}}$ nanofluid is more predominant than that of other two nanofluids in the case of shrinking and stretching sheets. The physical reason behind this behavior is that ${\text{Cu}}$ has the highest thermal conductivity compared to ${\text{TiO}}_{ 2}$ and ${\text{Al}}_{ 2} {\text{O}}_{ 3}$.

Fig. 2

Stream lines for stretching sheet when $\phi$ = 0.1, $Pr$ = 6.2, $M$ = 2, $K$ = 0.3, $f_{{w}}$ = 0.5, $\gamma$ = 0.1 and $n$ = 0.5

Fig. 3

Stream lines for shrinking case when $\phi$ = 0.1, $Pr$ = 6.2, $M$ = 2, $K$ = 0.3, $f_{{w}}$ = 0.5, $\gamma$ = 0.1 and $n$ = 0.5

Fig. 4

Velocity profiles for different nanofluids when $\phi$ = 0.1, $Pr$ = 6.2, $M$ = 2, $K$ = 0.3, $f_{{w}}$ = 2.5, $\gamma$ = 0.1, $n$ = 0.2 for λ = −1.5 (shrinking surface) and λ = 1.5 (stretching surface)

Fig. 5

Angular velocity profiles for different nanofluids when $\phi$ = 0.1, $Pr$ = 6.2, $M$ = 2, $K$ = 0.3, $f_{{w}}$ = 2.5, $\gamma$ = 0.1, $n$ = 0.5 for λ = −1.5 (shrinking surface) and λ = 1.5 (stretching surface)

Fig. 6

Temperature profiles for different nanofluids when $\phi$ = 0.1, $Pr$ = 6.2, $M$ = 2, $K$ = 0.3, $f_{{w}}$ = 2.5, $\gamma$ = 0.1, $n$ = 0.5 for λ = −0.5 (shrinking surface) and λ = 0.5 (stretching surface)

From Figs. 7, 8, 9, 10, 11, 12 and 13, the working fluid is considered as ${\text{Cu}}$–water nanofluid. The influence of suction ($f_{{w}} > 0$) parameter on velocity, angular velocity, and temperature profiles are shown in Figs. 7, 8 and 9, respectively. The other controlling parameters are fixed as $\phi$ = 0.1, $M$ = 2, $K$ = 0.3 and $\gamma$ = 0.1. For the first solution, when the suction increases, the velocity and angular velocity of the fluid increases for shrinking and decrease for stretching sheets, respectively. But, the reverse results are found in the case of second solution. The thermal boundary layer thicknesses notably reduces in both solutions by increasing suction for shrinking and stretching sheets, these variations can be viewed in Fig. 9. It can be noticed that suction leads to fast cooling of the sheet and this process results in notable applications in engineering and industries.

Fig. 7

Velocity profiles for f _w with ${\text{Cu}}$–water nanofluid when $\phi$ = 0.1, $Pr$ = 6.2, $K$ = 0.3, $M$ = 2, $\gamma$ = 0.1, $n$ = 0.5 for λ = −1.5 (shrinking surface) and λ = 1.5 (stretching surface)

Fig. 8

Angular velocity profiles for f _w with ${\text{Cu}}$–water nanofluid when $\phi$ = 0.1, $Pr$ = 6.2, $K$ = 0.3, $M$ = 2, $\gamma$ = 0.1, $n$ = 0.5 for λ = −1.5 (shrinking surface) and λ = 1.5 (stretching surface)

Fig. 9

Temperature profiles for f _w with ${\text{Cu}}$–water nanofluid when $\phi$ = 0.1, $Pr$ = 6.2, $K$ = 0.3, $\gamma$ = 0.1, $M$ = 2, $n$ = 0.5 for λ = −1.5 (shrinking surface) and λ = 2.0 (stretching surface)

Fig. 10

Velocity profiles for $M$ with ${\text{Cu}}$–water nanofluid when $\phi$ = 0.1, $Pr$ = 6.2, $K$ = 0.3, $f_{w}$ = 2.5, $\gamma$ = 0.1, $n$ = 0.5 for λ = −1.5 (shrinking surface) and λ = 2.0 (stretching surface)

Fig. 11

Angular velocity profiles for $K$ with ${\text{Cu}}$–water nanofluid when $\phi$ = 0.1, $Pr$ = 6.2, $M$ = 2, $f_{w}$ = 2.5, $\gamma$ = 0.1, $n$ = 0.5 for λ = −1.5 (shrinking surface) and λ = 1.5 (stretching surface)

Fig. 12

Temperature profiles for ϕ with ${\text{Cu}}$–water nanofluid when $Pr$ = 6.2, $M$ = 2, $f_{{w}}$ = 2.5, n = 0.5, $\gamma$ = 0.1, K = 0.3 for λ = −1.5 (shrinking surface) and λ = 2.0 (stretching surface)

Fig. 13

Temperature profiles for $\gamma$ with ${\text{Cu}}$–water nanofluid when $\phi$ = 0.1, $\Pr$ = 6.2, $M$ = 2, $K$ = 0.3, $f_{{w}}$ = 2.5, $n$ = 0.5 for λ = −1.5 (shrinking surface) and λ = 2.0 (stretching surface)

The effect for the variation of the magnetic parameter ($M$) on the dimensionless velocity profile is exemplified in Fig. 10. The other parameters are assumed as $\phi$ = 0.1, $K$ = 0.3, $f_{w}$ = 2.5 and $\gamma$ = 0.1. It is confirmed that for the first solution, the velocity distribution is significantly increased near the shrinking sheet while the value of magnetic parameter is increased. An increase in the magnetic parameter leads to a stronger Lorentz force. Stronger Lorentz force creates resistance in the fluid flows that appears in the reduction of velocities. As far as the second solution is considered magnetic field remarkable affects the velocity profile for both sheets.

The influence of material parameter ($K$) on dimensionless velocity, angular velocity and temperature profiles is presented in Fig. 11. The discussion is carried out for the constant values of the other parameters such as $\phi$ = 0.1, $M$ = 2, $f_{{w}}$ = 2.5 and $\gamma$ = 0.1. As a result, it can be observed that the angular velocity strictly increases considerably when material parameter increases for shrinking sheet. Furthermore, opposite results are observed for stretching sheet.

The effects of solid volume fraction of nanoparticles ($\phi$) on the dimensionless temperature profile are exemplified in Fig. 12a, b. The effects of solid volume fraction ($\phi$) are described by assuming the values of other parameters as $M$ = 2, $K$ = 0.3, $f_{{w}}$ = 2.5 and $\gamma$ = 0.1. It is noticed that for both solutions, as solid volume fraction parameter increases, the thermal boundary layer thickness increases for shrinking and stretching sheets.

The effects of Newtonian heating ($\gamma$) parameter on the dimensionless temperature profile are depicted in Fig. 13. The other controlling parameters are set as $\phi$ = 0.1, $M$ = 2, $K$ = 0.3 and $f_{{w}}$ = 2.5. When conjugate parameter for Newtonian heating ($\gamma$) increases, thicknesses of the thermal boundary layer considerably increase for both surfaces. In fact, the conjugate parameter for Newtonian heating effect not only has the tendency to increase the fluid temperature but also increases the thermal boundary layer thickness of sheets sizeably.

Dual solutions are classified as first solution and second solution. Weidman et al. [43], Rosca and Pop [40], Nazar et al. [31], Merkin [26], and Sharma et al. [41] are examined stability analysis to determine which solution is stable and physically applicable. They are proved that the first solution is the stable solution and second one is unstable. Moreover, it is worth mentioning that both solutions satisfied the far field boundary conditions asymptotically, which are supporting the validity of the obtained numerical results. To verify the accuracy of our present results, comparisons have been made with the available results of Fauzi et al. [15] and Nazar et al. [30] in the literature, which are shown in Tables 2, 3, 4, 5, 6, 7 and 8. In Table 2, comparison of the local skin friction ($Re_{x}^{1/2} C_{f}$) for stretching case and viscous fluid in the absence of suction or injection is presented. Tables 3, 4 and 5 illustrate the comparison results of skin friction coefficient for ${\text{Cu}}$, ${\text{Al}}_{ 2} {\text{O}}_{ 3}$ and ${\text{TiO}}_{ 2}$ in water-based micropolar nanofluids, respectively. Tables 6, 7 and 8 shows the comparison results of couple stress ($Re_{x}^{ - 1} C_{{n}}$) for various nanofluids under investigation. It is established that the results obtained in the present work demonstrate a good agreement with the previously published results.

Table 2 Comparison of $Re_{x}^{1/2} C_{{f}}$ for $K$ and $n$ when $\lambda$ = 1, $\phi$ = 0 and $f_{{w}}$ = 0

Table 3 Comparison of ${\textit{Re}}_{x}^{1/2} C_{f}$ for $f_{w}$ when $\lambda$ = 1, $K$ = 2, $n$ = 0.5, $Pr$ = $M$ = $\gamma$ = 0 for $\rm{Cu}$

Table 4 Comparison of $Re_{x}^{1/2} C_{f}$ for $f_{w}$ when $\lambda$ = 1, $K$ = 2, $n$ = 0.5, $Pr$ = $M$ = $\gamma$ = 0 for ${\text{Al}}_{ 2} {\text{O}}_{ 3}$

Table 5 Comparison of $Re_{x}^{1/2} C_{f}$ for $f_{w}$ when $\lambda$ = 1, $K$ = 2, $n$ = 0.5, $Pr$ = $M$ = $\gamma$ = 0 for ${\text{TiO}}_{ 2}$

Table 6 Comparison of $Re_{x}^{ - 1} C_{{n}}$ for $f_{{w}}$ when $\lambda$ = 1, $K$ = 2, $n$ = 0.5, $Pr$ = $M$ = $\gamma$ = 0 for ${\text{Cu}}$

Table 7 Comparison of $Re_{x}^{ - 1} C_{{n}}$ of $f_{{w}}$ when $\lambda$ = 1, $K$ = 2, $n$ = 0.5, $Pr$ = $M$ = $\gamma$ = 0 for ${\text{Al}}_{ 2} {\text{O}}_{ 3}$

Table 8 Comparison of $Re_{x}^{ - 1} C_{n}$ for $f_{{w}}$ when $\lambda$ = 1, $K$ = 2, $n$ = 0.5, $Pr$ = $M$ = $\gamma$ = 0 for ${\text{TiO}}_{ 2}$

5 Conclusions

In the present paper, the steady, two dimensional flow of micropolar nanofluids with heat transfer over permeable stretching/shrinking sheet with variable suction/injection in the presence of magnetic field and Newtonian heating is investigated. The governing equations are approximated to a system of non-linear ordinary differential equations by similarity transformation. Numerical calculations are carried out for various values of the dimensionless parameters of the problem. The results also show the existence of dual solutions for both stretching and shrinking cases. The drawn conclusions for the present work after a thorough observation are summarized as follows:

• 1. Dual solutions are found for some values of the governing parameters for both stretching and shrinking sheets.

• 2. The thermal boundary layer thicknesses notably reduce by increasing suction parameter for shrinking sheet.

• 3. On increasing material parameter, the angular velocity of the fluid significantly increases near the shrinking sheet.

• 4. For both solutions, when the solid volume fraction parameter is increased, an increase in the thermal boundary layer thickness is found for the sheets under consideration.