1 Introduction

In recent years, the numbers of natural disasters have increased significantly, and these have consistently caused serious damages to the socio-economic viabilities of the infrastructure and that of the cities at large. Some recent notable examples of these significant damages are the natural disasters of the Japanese earthquake and tsunami of 2011, Pakistani heat wave of 2015, North Korean floods of 2018, just to mention a few. Natural disaster could be described as an occurrence in the ecosystem that leads to the instability in the socio-economic systems, imbalance between demand and supply [1], among others. Geological, meteorological, biological, and environmental pollution, fire, and marine disasters are six categories of natural disasters [2]. In the past decades, relevant researches on natural disasters have been extensively carried out by many scholars in different domains. Some have employed high likelihood, serious severity and wide coverage, as well as rising cost of catastrophes [3].

Floods can destroy infrastructures, damage rivers and surrounding floodplains [4,5,6]; its inceassant occurrence worldwide has led to and still leading to climate change [7]. Therefore, timely and efficient mitigating plans are required for sustainable development. In fact, the control of floods is germane for long-term risk reduction worldwide [8]. Iran is a country with frequent natural disasters especially floods [8,9,10,11]. Flooding has become inceassant and has resulted in the enormous economic loss to Iran every single year. Therefore, pragmatic approaches are needed by the decision-makers to ameliorate the effects of these disruptive events within a short period of time [12, 13]. However, due to uncertainty (the lack of information for decision-makers [14]), it is difficult to arrive at reliable decisions in emergency situations through the conventional techniques [15]. Therefore, multi-criteria decision-making (MCDM) tools that can help decision-makers to choose the best opinion among a set of alternatives amidst some conflicting criteria [16, 17]. MCDM techniques are considered efficient as practical tools that are deployed for finding the optimal solution in the typical emergency decision-making problems. These MCDM approaches have received much scholarly studies in finding solutions to the emergency decision-making problems [12, 18]. It should be added that MCDM methods are one of the solution models in operations research that evaluates multiple contradictory criteria in decision-making process through the selection of an optimum alternative among a set of possible alternatives. According to reports, emergency decision-making is defined as an effective way of dealing with emergency situations [19,20,21,22,23].

In dealing with the natural disasters, due to the level of the uncertainty, decision-makers are challenged with the inability to properly qualitative opinions using accurate informations [24]. Therefore, the mathematical models of decision-making problems can be geared towards obtaining the optimal solution employing any of the categories of Bayesian network [12, 25], Game theory [12, 26], Markov decisions [27] and Fuzzy set theory [28,29,30]. In this studies, as mentioned above, scholars have widely applied the combination of decision-making tools with different inherent features and have developed many hybrid models. Considering the complexity of each method with their inherent merits and demerits highlighting the differences and priorities would be a difficult task. The way to solving these difficulties would require an evaluation to determine an adequate and well-fitted model for the decision-making problem under consideration. In this paper, a hybrid decision-making tool for the specific-type decision-making problem is proposed. For more clarifications on the proposed subject matter, please refer to [2].

1.1 Bibliometric analysis

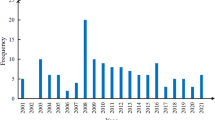
A bibliometric analysis is performed on the number of articles published per year till December 2020. The idea behind this analysis is to make clear presentation of the articles published by different groups and the research trends in the emergency decision-making field. Figure 1 demonstrates the emergency decision-making methods that are commonly utilized in different dimensions.

Fig. 1
figure 1

(Source: Web of Science, keywords search: (Title: “emergency decision-making or emergency decision making” OR “emergency decision-making or emergency decision making”))

Percentage of published works per application area by the end of year December 2020 in the field of emergency decision-making

Full size image

Figure 2 illustrates that the numbers of publications on emergency decision-making application domains have increased since 2008. This trend depicts the highest increase in 2018; it is can be vividly projected that emergency decision-making models used in different studies will continue to evolve in the coming years.

Fig. 2
figure 2

(Source: Web of Science, keywords search: (source: Web of Science, keywords search: (Title: “emergency decision-making” OR “emergency decision making”))

Distribution of published works per year till the end of the December 2020 in the field of emergency decision-making

Full size image

In Table 1, the relevance of the highly cited published works is presented by analysing the “Average Citations per Year” of each published work as they are related to the emergency decision-making concept. By thoroughly reviewing the emergency decision-making concepts and its relevant applications, it is clear that emergency decision-making requires and demands further development and improvement from different viewpoints, particularly the various gaps that have been identified. In view of these identified gaps that have been pointed out earlier, the authors are motivated to scope of the existing model into a development emergency decision-making model to cope with the identified drawbacks.

Table 1 The highly cited papers according to the citation measures by the end of April 2020
Full size table

In current paper, three different methods are combined to deal with an emergency decision-making problem, particularly natural disasters like floods. These methods are best–worst method (BWM) [31], Z numbers [32] and zero-sum game [33]. Initially, the BWM is applied to find the important weight of the criteria in emergency decision-problem according to the strategies of nature. BWM is a comparison-based method and statistical analysis method that have been found to possess better performance than the analytical hierarchy method (AHP) in terms of the consistent ratio, conformity, total deviation and minimum violation [31, 34].

In the second step, decision-makers express their opinions, as well as their confidence level according to the idea of Z numbers. Z numbers, proposed by Zadeh, depicts uncertain decision information that can handle circumstances where the reliability of opinions is questionable. The concept of the Z numbers is more powerful compared to the quantification of other types of linguistic terms especially in the emergency decision-making problems [35,36,37]. Furthermore, aside the ability of the Z numbers to accurately reveal the uncertainty in the decision-makers’ opinions, they can also retain the decision-makers’ opinions or original data’s integrity [38].

Lastly, the zero-sum game based on a confrontational game is utilized to determine the optimal emergency decision-making solution. In a zero-sum game, there is no possibility of collaboration between the two players in the game. By starting the competition, the gain or loss of the profits for one player is precisely stabilized and balanced with the gains or losses of the other player. According to this point, the complete gains and losses of the players are thereby close to zero. The zero-sum game has been used in decision-making problems [39,40,41] and compares the other methods, it takes the features and non-cooperative behaviour between players (decision-makers) and nature. This renders the main goal of both sides of players as the maximization of their profits in the decision-making procedure which is within the purview of the ideals of the emergency decision-making process.

The first contribution to this study is the proposition of a hybrid model with the utilization of BWM and Game theory to the recently proposed fuzzy concepts. Therefore, it provides much more reliable results. The second contribution is in the applicability of the proposed hybrid methodology in a real case study of absolute natural disaster. This case study has not been studied or reported under emergency decision-making purposes. This proposed model is therefore the first of its kinds to assess this natural disaster using emergency decision-making criteria.

The rest of the paper is organized as follows; In Sect. 2, a new framework is considered to deal with an emergency decision-making problem. In Sect. 3, a natural disaster as a flood in the northern part of Iran is studied to illustrate the feasibility and effectiveness of the proposed emergency decision-making approach. The implications of the proposed model for researchers and practitioners/policy-makers are explained in Sect. 4. In Sect. 5, the conclusion highlighting the advantages and disadvantages of the proposed approach, as well as directions for future studies, are provided.

2 Methodology

In this section, a new framework for making a reliable decision in an emergency decision-making circumstance is proposed (see Fig. 3). The introduced decision-making procedure has three key stages: (1) Computing the weight of the criteria, (2) Constructing the group of the payoff matrix and (3) Determining the best solution. First, the importance weight of all criteria needs to be evaluated. In this current study, the best–worst method [31] is utilized to obtain the importance weight of criteria. Thereafter, the payoff evaluation matrix based on the opinions obtained from decision-makers is derived. The concept of Z numbers includes the individual decision-makers’ opinion, as well as the reliability of the opinions. Lastly, the best response of the interventions and an emergency disruptive event is recognized according to the zero-sum game theory [15]. In this study, a collaborative and hybrid method is proposed with many advantages compared to a angle MCDM tool. Zavadskas and colleagues [42] highlighted that.

Because individual MCDM methods can yield different rankings, selecting an appropriate method is a great challenge. It is therefore recommended to use a hybrid approach based on many methods and to integrate those results in the final decision-making step. Another advantage of the hybrid approach over individual methods is based on an opportunity of integrating subjective and objective criteria importance into the value of the utility function. Simultaneously, applying fuzzy logic can help to overcome uncertainties arising from human qualitative judgements, incomplete preference relationships and to bring a model closer to real-life representation. Hybrid MCDM involves four groups of decision-making methods or their combinations with other methods such as fuzzy sets or grey numbers.

Fig. 3
figure 3

The proposed framework of emergency decision-making method

Full size image

This can deal with the shortages of a single decision-making tools such as (i) different decision-making tools most of the times leads to different alternatives’ rankings. Accordingly, it is recommended to use more than one decision-making tools and to integrate the results in the final decision-making step, (ii) ranking of the alternatives significantly depends on the importance weights of each criterion in the analysed problem although hybrid and collaborative approaches recommended resolving two jobs instantaneously [43, 44], (iii) fuzzy set theory can assist to cope with the uncertainties due to human qualitative judgements and incomplete preference relationships [45, 46] and (iv) there are more tools which can also be employed to obtain robust formulation of the problem [47, 48].

Let \(A = \left\{ {A_{{1~}} ,A_{{2~}} ,~A_{{3~}} , \ldots ,A_{{m~}} } \right\}\) be set of alternatives, which is known as a strategy of decision-makers for \(l\) number of the decision-makers, \(DM = \left\{ {DM_{{1~}} ,DM_{{2~}} ,DM_{{3~}} , \ldots ,DM_{{l~}} } \right\}\) be set of criteria \(C = \left\{ {C_{{1~}} ,C_{{2~}} ,~C_{{3~}} , \ldots ,C_{{n~}} } \right\}\) as a strategy of nature, and \(\omega _{{j~}} = \left\{ {\omega _{{1~}} ,\omega _{{2~}} ,\omega _{{3~}} ,~ \ldots ,\omega _{{n~}} } \right\}\) is the decision-makers’ importance weight according to the quality of experts’ profile. It falls into the condition \(0 \le \omega _{{j~}} \le 1\) and \(\mathop \sum \nolimits_{{j = 1~}}^{{n~}} \omega _{{{\text{j}}~}} = 1\). In this regard, each participating decision-maker expresses individual payoff opinions of \(A_{{\text{i}}}\) concerning the criterion \(C_{{\text{j}}}\) underlying the concept of Z numbers. Besides, the \(~l\) payoff matrices \(P_{{\text{k}}} = \left[ {p_{{{\text{ij}}~}}^{{{\text{k}}~}} } \right]_{{{\text{m}}~ \times ~{\text{n}}}}\) \(\left( {k = 1,2, \ldots ,l} \right)\) can be derived, where \(~p_{{{\text{ij}}~}}^{{{\text{k}}~}} = [\mu _{{A_{{{\text{ij}}}}^{{\text{k}}} ~}} ,\mu _{{R_{{{\text{ij}}}}^{{{\text{k}}~}} ~}} ]\) \(\mu _{{R_{{ij~}}^{{k~~}} ~}} ]\), where \(\mu _{{A_{{ij~}}^{{k~}} ~}}\) is the decision-makers’ opinion over \(~A_{i}\), concerning the criterion \(C_{{\text{j}}}\) collected from decision-maker, \(\mu _{{R_{{ij~}}^{{k~~}} ~}}\) is the reliability of the decision-makers’ opinion over \(~A_{{\text{i}}}\) related to the criterion \(C_{{\text{j}}}\) collected from decision-maker \(l\). Accordingly, based on the results, a zero-sum game between the decision-makers and nature can be illustrated as \(B = \left\{ {{\text{decisionmakers'~nature}},{\text{A}},{\text{C}},{\text{P}}} \right\}\).

Therefore, the detailed procedures of the introduced emergency decision-making problems can be derived as explained in the following sections. It should be noted that the decision-makers are collaborators through the sharing of opinions, and using the methodology provided would be used to integrate into decision-maker’s as a task.

2.1 Computing the weight of criteria utilizing BWM

The best–worst method (BWM) is a proper alternative to the analytical hierarchical process (AHP) for computing the importance weight of criteria [31, 49]. BWM need less data compared to the AHP, and it has the tendency for obtaining viable results consistently based on its unique pairwise comparison procedure. BWM method has been broadly utilized in different application domains based on the different kinds of decision-making problems [50,51,52,53,54]. Hence, BWM is employed to determine the importance weight of the identified criteria in emergency decision-making procedure.

The procedure of BWM is briefly provided in the following steps.

  1. (i)

    Identifying the most importance criterion or the best and least importance criterion or the worst.

    The most important criterion \(~C_{B}\) and the least important criterion \(~C_{W}\) have to be obtained using decision-makers’ evaluation of the proposed \(n\) criterion.

  2. (ii)

    Calculating the preference of the significant criterion over the others,

    in current stage, DMs use the nine-scale structure presented in Table 2 to find the most important criterion and its evaluation over other criteria. Then, the best to other vector (BO) defined as \(C_{{BO~}}^{{k~}} ,~k = 1,~2,~3, \ldots ,l\) is computed using the following equation:

    $$C_{{{\text{BO}}}}^{{\text{k}}} = \left( {C_{{{\text{B}}1~}}^{{{\text{k}}~}} ,C_{{{\text{B}}2~}}^{{{\text{k}}~}} , \ldots ,C_{{{\text{Bn}}~}}^{{{\text{k}}~}} } \right)$$
    (1)

    where \(~C_{{{\text{Bj}}~}}^{{\text{k}}}\) is the opinion of the \(C_{{B~}}\) over the \(C_{{j~}}\), and \(~C_{{BB~}} = 1\). Therefore, \(l\) best to others’ vectors can be combined into a single best to others’ vector \(C_{{BO~}} = \left( {C_{{B1~}} ,C_{{B2~}} , \ldots ,C_{{Bn~}} } \right)\) using following the equation:

    $$C_{{{\text{Bj~}}}} = \frac{{C_{{{\text{Bj}}~}}^{{{\text{k}}~}} }}{l}~,\quad ~j = 1,~2,..,n$$
    (2)
    Table 2 The nine-scale of comparison
    Full size table

    The preference of other criteria over the most important one must be calculated. Similarly, others to worst vectors \(C_{{{\text{OW}}}} ,~k = 1,~2,~3, \ldots ,l\) is computed using the following equation:

    $$C_{{{\text{OW}}~}}^{{{\text{k}}~}} = \left( {C_{{1{\text{W}}~}}^{{{\text{k}}~}} ,C_{{2{\text{W}}~}}^{{{\text{k}}~}} , \ldots ,C_{{{\text{nW}}~}}^{{{\text{k}}~}} } \right)$$
    (3)

    where \(~C_{{{\text{jW~}}}}^{{{\text{k}}~}}\) is the opinion of the \(C_{{\text{j}}}\) over the \(~C_{{\text{W}}}\), and \(~C_{{{\text{WW~}}}} = 1\). Therefore, others to worsts’ vectors can be further aggregated into a single worst to others’ vector \(C_{{{\text{OW}}~}} = \left( {C_{{1{\text{W}}~}} ,C_{{2{\text{W}}~}} , \ldots ,C_{{{\text{nW}}~}} } \right)\) using the following equation:

    $$C_{{{\text{jW}}~}} = \frac{{C_{{{\text{jW}}~}}^{{{\text{k}}~}} }}{l}, \quad {{j}} = 1,~2,..,n$$
    (4)
  3. (iii)

    The criteria’s optimal weight is calculated.

    In BWM, the ratio of \(~\frac{{W_{{\text{B}}} }}{{W_{{\text{j}}} }}\) and \(\frac{{W_{{j~}} }}{{W_{W} }}\) is followed by \(\frac{{W_{{{\text{B~}}}} }}{{W_{{\text{j}}} }} = C_{{{\text{Bj}}}}\) and \(~\frac{{W_{{\text{j}}} }}{{W_{{\text{W}}} }} = C_{{{\text{jW}}~}}\). In order to satisfy the aforementioned conditions, a solution by maximizing the value of \(\left| {\frac{{W_{{{\text{B}}~}} }}{{W_{{\text{j}}} }}~ - C_{{{\text{Bj}}~}} } \right|\) and minimizing the value of \(\left| {C_{{{\text{jW}}~}} - ~\frac{{W_{{\text{j}}} }}{{W_{{\text{W}}} }}} \right|\) should be derived. According to this point, the following optimization model can be determined by the optimal weight of criteria:

    Model 1:

    \({\text{Min~}}\max ~\left\{ {\left| {\frac{{W_{{\text{B}}} }}{{W_{{{\text{j~}}}} }} - C_{{{\text{Bj}}~}} } \right|{\text{~}},\left| {C_{{{\text{jW}}~}} - \frac{{W_{{{\text{j}}~}} }}{{W_{{\text{W}}} }}} \right|{\text{~}}} \right\}\),

    Subject to.

    \(\mathop \sum \limits_{{j = 1~}}^{{n~}} w_{{{\text{j}}~}} = 1\),

    $$w_{{\text{j}}} \ge 0, \,{{j}} = 1,~2, \ldots n.$$

    Re-establishment of Model 1 to Model 2:

    $$\min ~\xi$$

    Subject to.

    \(\left| {\frac{{W_{{\text{B}}} }}{{W_{{\text{j}}} }} - C_{{{\text{Bj}}~}} } \right|~ \le ~\xi\),

    \(\left| {C_{{{\text{jW}}}} - \frac{{W_{{\text{j}}} }}{{W_{{\text{W}}} }}} \right|~ \le ~\xi\),

    \(\mathop \sum \limits_{{j = 1~}}^{n} w_{{j~}} = 1\),

    $$w_{{{\text{j~}}}} \ge 0 , \,{{j}} = 1,~2, \ldots n.$$

    The optimal importance weights are denoted as \(w^{{*~}} = \left( {w_{{1~}}^{{*~}} ,w_{{2~}}^{{*~}} , \ldots ,w_{{n~}}^{{*~}} } \right)\).

  4. (iv)

    The consistency of the results must be computed.

    The consistency ratio is shown in Eq. (5):

    $$CR = \frac{{\xi ^{{*~}} }}{{CI}}$$
    (5)

    where \(CR\) is known as a consistency index based on the maximum value of \(\xi\) according to Table 3. Better consistency is shown by smaller CR value. In this paper, the acceptance condition is \(CR \le 0.2\).

    Table 3 Consistency index
    Full size table

2.2 Constructing the group of payoff evaluation matrix utilizing Z numbers

Zadeh [24, 32] proposed Z numbers to capture the vagueness ambiguous, and uncertainty during the elicitation of decision-makers’ opinions. To understand how Z numbers performs, an example has been highlighted by Yazdi et al. [69] in the safety and reliability engineering application domain. In the mentioned example, one way of finding the probability of occurrence of an event is using expert judgement, in which each expert expresses their personal opinions to show how an event may occur. The profile quality of experts has a direct effect on the final aggregated results. This simply means that the results are close to the opinion of an expert which has a high importance weight. Yazdi et al. [69] argued that this typical elicitation procedure cannot be reliable. The main reason falls into the lack of confidence in the collection of experts’ opinions. For example, let us assume that the highly qualified expert (more importance weight) expresses some opinions with low confidence, and the lesser qualified expert (less important weight) expresses some opinions with high confidence. The question that arises from the final results is that whether is it the same or not it can be truly said that the final results would be different.

Returning to Z numbers proposed by Zadeh, it is \(Z = \left( {A,R} \right)\) as an ordered pairwise fuzzy number. The first parameter in Z numbers \(\left( A \right)\) shows the restriction on the real-valued uncertain variable, and the second component highlights the reliability of the first component. Both \(A~{\text{and~}}R\) are perception-based and could be presented in natural and normal ways (for example, it takes two hours). A set of Z numbers is denoted by Z information, meaning that most of our everyday decision-making and reasoning is based on Z information. Therefore, to represent the Z information mathematically, \(A~{\text{and~}}R\) are denoted in natural languages which means that they should fall into the relation of membership functions, \(\mu _{A}\) and \(\mu _{{R~}}\). The representation of membership functions can be in a different form (i.e. triangular, intuitionistic, Pythagorean, etc.) [55,56,57]. The membership function of \(A,~~\mu _{{{\text{A}}~}}\) shows the possibility of success in such following question “To what extent does the number, \(a \in A\) appropriately fit with your perception of \(\mu _{{A~}}\)”. For an instant, to what extent does two hours appropriately fit with decision-makers’ opinions about driving home from the school. Similarly, the aforementioned explanations can be extended to \(R\) as well.

As Zadeh [24] showed, the Z numbers can be applied in different engineering application domains. In current study, the first linguistic term shows the opinion of decision-makers related to a subject, and the second term illustrates how much decision-makers are confident to express specific opinions. It can be added that the second component in Z numbers is highlighting the reliability of the first component, which has been underlined by the same concept mentioned earlier. To consider the effects of the second component on the first component, the following four key steps are involved: (i) the procedure of elicitation of the experts’ opinion, (ii) conversion of the confidence level, (iii) addition of weight of confidence level to the decision-makers’ opinions and (iv) conversion of the asymmetrical fuzzy number to the “symmetricalized” fuzzy number. A brief explanation of each step is presented; however, interested readers could refer to the study of Yazdi et al. (2019) for detailed explanation.

  1. (i)

    Experts’ opinion elicitation procedure.

    Let us consider that \(Z = \left( {\tilde{A},\tilde{R}} \right)~is~\) a Z number, where the left component is called restriction (decision-makers’ opinions), and the right component is denoted the reliability (confidence level). \(\tilde{A} = \left\{ {x,~\mu _{{\widetilde{{A~}}}} \left( x \right)|~x \in \left[ {0,1} \right]} \right\}\) and \(\tilde{R} = \left\{ {x,~\mu _{{\tilde{R}~}} \left( x \right)|~x \in \left[ {0,1} \right]} \right\}\). \(\mu _{{\widetilde{{A~}}}}\) and \(\mu _{{\tilde{R}~}}\) can be defined in any form (e.g. triangular, intuitionistic, Pythagorean, etc.).

    In this step, it is critical to collect a proper group of decision-makers. Many studies have been performed to show the features of a group of decision-makers including democratic and autocratic decision-making styles. As an example, it can be asked from a heterogeneous group of decision-makers to share their individual opinions about a specific subject. Afterward, they are asked to express their opinion on how confident they were on opinions concerning the specific subjects. Therefore, the Z numbers garnered from each decision-making fall into a fuzzy set theory. For instance, in triangular form, it can be denoted \(Z = \left( {a_{{1~}} ,a_{{2~}} ,a_{{3~}} ,r_{{1~}} ,r_{{2~}} ,r_{{3~}} } \right).\)

  2. (ii)

    Converting the confidence level

    in this step, it is needed to transfer the confidence level into crisp values according to the fuzzy numbers. The details of defuzzification procedure for any type of fuzzy numbers have been reported [58,59,60].

    Adding the weight of confidence level to the decision-makers’ opinions

    , the weight of reliability in Z number is indicated as \(\tilde{Z}^{{\alpha ~}} = \left\{ {x,~~\mu _{{\tilde{A}^{{\alpha ~}} }} \left( x \right)|~\mu _{{\tilde{A}^{{\alpha ~}} }} \left( x \right) = \alpha \mu _{{\widetilde{{A~}}}} \left( x \right),x \in \left[ {0,1} \right]} \right\}\). Let us assume that \(E_{{A~}} \left( x \right) = \mathop \int \nolimits_{{X~}}^{{}} x\mu _{{A~}} \left( x \right)dx\) is the fuzzy expectation of a fuzzy set with its clear divergence compared to the probability space expectation. According to this point, \(E_{{\tilde{A}^{{\alpha ~}} }} \left( x \right)\) is defined as the following equation:

    $$E_{{\tilde{A}^{{\alpha ~}} }} \left( x \right) = ~\alpha E_{{\tilde{A}^{{\alpha ~}} }} \left( x \right)~,~~~x \in X$$
    (6)

    Subject to.

    $$\mu _{{\tilde{A}^{{\alpha ~}} }} \left( x \right) = \alpha \mu _{{\widetilde{{A~}}~}} \left( x \right)~,~~~x \in X$$
    (7)

    where \(E_{{\tilde{A}^{{\alpha ~}} }} \left( x \right) = \mathop \int \nolimits_{{X~}}^{~} x\mu _{{\tilde{A}^{{\alpha ~}} }} \left( x \right)dx = \mathop \int \nolimits_{{X~}}^{~} \alpha x\mu _{{\widetilde{{A~}}}} \left( x \right)dx = \alpha \mathop \int \nolimits_{{X~}}^{~} x\mu _{{\widetilde{{A~}}}} \left( x \right)dx = \alpha E_{{\tilde{A}^{{\alpha ~}} }} \left( x \right)\).

  3. (iii)

    Converting the asymmetrical fuzzy number to the symmetrical fuzzy number,

    the symmetrical fuzzy set is signified as \(\tilde{Z}^{{'~}} = \left\{ {x,\mu _{{\tilde{Z}^{{'~}} }} \left( x \right)|~\mu _{{\tilde{Z}^{{'~}} }} \left( x \right) = \mu _{{\tilde{A}}} \left( {\frac{{~x~}}{{\sqrt {~\alpha ~} }}} \right)~,~x \in \left[ {0,1} \right]} \right\}\). Subsequently, \(E_{{\tilde{Z}^{{'~}} }} \left( x \right)\) is defined as the following:

    $$E_{{\tilde{Z}^{{'~}} }} \left( x \right) = \alpha E_{{\tilde{Z}^{{'~}} }} \left( x \right)~,~~~x \in \sqrt {~\alpha ~} X$$
    (8)

    Subject to.

    $$\mu _{{\tilde{Z}^{{'~}} }} \left( x \right) = \mu _{{\widetilde{{A~}}}} \left( {\frac{{~x~}}{{\sqrt {~\alpha ~} }}} \right),~~~x \in \sqrt {~\alpha } X$$
    (9)

    where

    $$E_{{\tilde{Z}^{{'~}} }} \left( x \right) = \mathop \int \limits_{{\sqrt {~\alpha ~} X}}^{~} x\mu _{{\tilde{Z}^{{'~}} }} \left( x \right)dx = \mathop \int \limits_{{\sqrt {~\alpha ~} X}}^{~} x\mu _{{\widetilde{{A~}}}} \left( {\frac{{~x~}}{{\sqrt {~\alpha ~} }}} \right)dx\mathop \to \limits^{{x~ = ~\sqrt \alpha t}} = \mathop \int \limits_{{X~}}^{~} \left( {\sqrt {~\alpha } t} \right)\mu _{{\widetilde{{A~}}}} \left( t \right)d\left( {\sqrt {~\alpha ~} t} \right) = \alpha \mathop \int \limits_{X}^{~} t\mu _{{\tilde{A}}} \left( t \right)dt = \alpha E_{{\tilde{A}}} \left( x \right)$$

    According to Eq. (4), it can be further concluded that \(E_{{\tilde{Z}^{{'~}} }} \left( x \right) = E_{{\tilde{A}^{{\alpha ~}} }} \left( x \right)\), where \(E_{{\tilde{A}^{{\alpha ~}} }} \left( x \right) = \alpha E_{{\tilde{A}^{{\alpha ~}} }} \left( x \right)\) and \(E_{{\tilde{Z}^{{'~}} }} \left( x \right) = \alpha E_{{\widetilde{{A~}}}} \left( x \right)\), then \(E_{{\tilde{A}^{{\alpha ~}} }} \left( x \right) = E_{{\tilde{Z}^{{'~}} }} \left( x \right)\).

2.3 Determining the best solution utilizing the zero-sum game

A zero-sum game is a theoretical game, which has a maximum of two players or decision-makers in an existing game under specific competition rules. In a typical zero-sum game, the income of one decision-maker (also known as a player) is considered an offset by the loss of the second decision-maker. Besides, the summation of the two decision-makers’ payoff must be equal to zero, and there is no collaboration or connection between the two [12, 33, 61].

Let us consider two decision-makers (DMs) in a zero-sum game as the DM.1 and DM.2, respectively. In the zero-sum game, the DM.1 consistently selects the strategy of maximizing his or her returns. On the other side, DM.2 wants to select the strategy of minimizing his or her returns. According to this point, the payoff summation of DM.1 and DM.2 is equal to zero. Note that, DM.1 and DM.2 represented the players in a zero-sum game and should not be considered as decision-makers.

Definition 1

A zero-sum game involving two DMs (players) is defined as a five-tuple in the following:

$$A = \left\{ {DM.1,DM.2,~{\mathcal{C}}_{{D~}} ,{\mathcal{C}}_{{N~}} ,P} \right\}$$
(10)

where \({\mathcal{C}}_{{\text{D}}} = \left\{ {c_{{\text{i}}} |~c_{{\text{i}}} \in {\mathcal{C}}_{{1~}} \ge 0,~\mathop \sum \nolimits_{{i = 1~}}^{{m~}} c_{{\text{i}}} = 1,~\;i = 1,~2,~3, \ldots ,m} \right\}\) shows the mixed-based strategy set of DM.1, \({\mathcal{C}}_{{\text{N}}} = \left\{ {\tilde{c}_{{{\text{j}}~}} |~\tilde{c}_{{{\text{j}}~}} \in {\mathcal{C}}_{{1~}} \ge 0,~\;\mathop \sum \nolimits_{{j = 1~}}^{{n~}} \tilde{c}_{{{\text{j}}~}} = 1,~\;i = 1,~2,~3, \ldots ,n} \right\}\) shows the mixed-based strategy set of DM.2 (player 2), and \(P\) denotes the payoff matrix of \(~DM.1\) (player 1).

Note that, the \(DM.1~\) (player 1) and \(DM.2\) (player 2) can be denoted as the decision-maker and nature, respectively.

Definition 2

The payoff matrix can be defined according to the study of Ma et al. [62]. Let us assume that \(\left( {c_{{\text{i}}} ,\tilde{c}_{{\text{j}}} } \right) \in {\mathcal{C}}_{{1~}} \times {\mathcal{C}}_{2}\), for \(i = 1,~2,~3, \ldots ,m\), is a strategy pair where \({c}_{i}\) is the strategy that DM.1 selects and \(~\tilde{c}_{{j~}}\) is the strategy that DM.2 selects. Accordingly, for any strategy \(\left( {c_{{\text{i}}} ,\tilde{c}_{{\text{j}}} } \right)\), consider that \(P = \left( {p_{{{\text{ij}}}} } \right)_{{m \times n~}}\) signifies the payoff matrix based on \(DM.1\). Therefore, the payoff matrix of DM.2 is equal to the \(- P\).

Zero-sum games are frequently solved using the Minimax theorem which is based on the linear programming duality or Nash equilibrium [63]. To solve the zero-sum game, Neumann [64] developed the min–max theorem. The main idea of the Minimax theorem is that DM.1 takes the best reaction that can make his or her payoff the minimum and selects the optimal strategy which has the greatest advantage for his or her. Besides, DM.2 also follows similar ideas for the Nash equilibrium to be optimized.

For a zero-sum game, where \(\nu\) shows the expected value of DM.1; a strategy pair \(\left( {c_{{\text{i}}}^{{*~}} ,\tilde{c}_{{\text{j}}}^{{*~}} } \right)\) will be the Nash equilibrium point of \(A = \left\{ {DM.1,DM.2,~{\mathcal{C}}_{{D~}} ,{\mathcal{C}}_{{N~}} ,P} \right\}\). In this accordance, for DM.1, the following condition in model 3 is satisfied:

Model 3:

\(min~\frac{{~1~}}{{~\nu ~}} = \mathop \sum \limits_{{i = 1~}}^{{m~}} c_{{\text{i}}}\),

subject to.

\(\mathop \sum \limits_{{i = 1~}}^{{~m~}} p_{{{\text{ij}}}} c_{{{\text{i}}~}} \ge 1\), \(j = 1,~2,~3, \ldots ,n\),

\(c_{{i~}} \ge 0~,\) \(i = 1,~2,~3, \ldots ,m\).

According to the aforementioned models, the Nash equilibrium strategies of DM.1 and DM.2 are derived by \(c_{{\text{i}}}^{{*~}} = \left( {\nu c_{1} , \ldots ,\nu c_{{\text{i}}} , \ldots ,\nu c_{{\text{m}}} } \right)\) and \(\tilde{c}_{{\text{j}}}^{{*~}} = \left( {\nu \tilde{c}_{{1~}} , \ldots ,\nu \tilde{c}_{{\text{i}}} , \ldots ,\nu \tilde{c}_{{\text{n}}} } \right)\), respectively.

Finally, the expected values of strategies \(c_{i} ~\left( {i = 1,~2,~3,~ \ldots ,~m} \right)\) for the group of decision-makers are derived by using the following equation:

$${\mathcal{G}}_{{\text{i}}} = c_{{\text{i}}}^{{*~}} \cdot \mathop \sum \limits_{{j = 1~}}^{{n~}} \left( {p_{{{\text{ij}}}} \tilde{c}_{{\text{j}}}^{{*~}} } \right) \cdot w_{{{\text{j}}~}}^{*} \;\forall ~~i = 1,~2,~3,~ \ldots ,~m$$
(11)

Regarding the \({\mathcal{G}}_{{i~}}\) values in which \({\mathcal{G}}_{{i~}} \ne 0\), the best solution to strategy \(~c_{i} ~\) according to the maximum \({\mathcal{G}}_{i}\) value can be therefore derived for an emergency decision-making problem. If there \({\mathcal{G}}_{{i~}} = 0\), the row vectors related to \({\mathcal{G}}_{{i~}} \ne 0\) are detached from the assessment matrix, and afterwards, return to apply model 1 and model 2. The rest of the strategies are handled similarly to the priority of all alternatives is obtained.

3 Application of study

In this section, a natural disaster case study is presented. Often, investigation into any accident always reveals blame games that are usually passed on who is responsible for one thing or the other and why the accident occurred. However, the most expedient question to ask is “are the correct things being done timely and efficiently in the right way?”. From this case study,valuable lessons could be learnt that would be useful for preventing similar disruptive occurrences in the future [65, 66]. In March 2019, a catastrophic flood engulfed Gorgan and the surrounding cities in the Golestan province of Iran having 4,042,746.86–4,220,286.86 m latitude and 219,426.41–439,746.41 m longitude UTM (Universal Transverse Mercator) zone 40 and extended for 20,178.12 km2 (see Figs. 4 and 5).

Fig. 4
figure 4

The location map of the Golestan province (Iran), as well as a hillshade map of the province [11]

Full size image
Fig. 5
figure 5

Flooding in Golestan Province, Iran March 21, 2019, (in order to find more photographs, please refer to the website like IRNA (Islamic Republic News Agency), and ISNA (Iranian Students News Agency))

Full size image

The flash floods struck 70 villages leaving 360 villages in total darkness after the electricity supply was lost [67]. Golestan’s population is nearly 1.8 million and has a population density of 88 people per km2 [4]. In addition, Golestan has experienced similar disasters in last decade with more than 60 floods causing 112 million dollars damage to assets and 468 fatalities [68]. The population density of Gorgan considered to be at a high level compared to the country per capital, with considerable number of people mostly farmers living below a low- or medium-income brackets. The high mountains and the thick jungles around also constituted secondary disasters based on the domino effect thereby making it difficult for emergency rescue crews to access those in need. The three days after a natural disaster called the “golden 72 h” is a vital time to respond. The rescuers must invest time and resources during this golden period to improve the facilities and utilities. Meanwhile, Gorgan City is accessible by air, land and sea so relief materials can be transported throughout the province. Thus, in considering the literature [12], the interview conducted among local experts revealed that there are four alternative routes available out which the decision-makers would have to select the optimum route to transport relief materials. This optimum route would improve the effectiveness and feasibility of the delivery system much more significantly.

Therefore, four alternative routes and five criteria are considered by the decision-makers (see Table 4).

Table 4 Alternative routes and corresponding criteria with description for a post-flood management situation plans (note: the criteria \(C_{1}\) and \(C_{2}\) are benefit-based and \(C_{3}\), \(C_{4}\), and \(C_{5}\) are cost-based)
Full size table

A group of decision-makers including four with relevant expertise and background related to emergency decision-making on post-flood cases are invited to complete the evaluation survey using Z numbers. Let us take \(DM = \{ DM_{{1~}} ,DM_{{2~}} ,DM_{{3~}} ,DM_{{4~}} \}\) express their individual opinions and confidence level in the qualitative term set \(Q = \left\{ {q_{{0~}} = {\text{very~low~}}\left( {{\text{VL}}} \right),{\text{~}}q_{{1~}} = {\text{low~}}\left( {\text{L}} \right),~q_{{2~}} = {\text{fairly~low~}}\left( {{\text{FL}}} \right),{\text{~}}~q_{{3~}} = {\text{medium~}}\left( {\text{M}} \right),~q_{{4~}} = {\text{fairly~high~}}\left( {{\text{FH}}} \right),~q_{{5~}} = {\text{high~}}\left( {\text{H}} \right),~q_{{6~}} = {\text{very~high~}}\left( {{\text{VH}}} \right)} \right\}\). More details can be obtained from [69].

First of all, all the decision-makers select the most important and least important criteria as \(C_{{2{\text{~}}}}\) and \(C_{{1{\text{~}}}}\), respectively. Afterward, decision-makers express their preferred opinions from best-to-other and from other to worst criterion. Utilizing Eqs. 2 and 4, the five best to others and other to worst criterion are aggregated into a single group of best-to-other and other-to-worst vectors. The obtained results are provided in Table 5.

Table 5 The importance weights of criteria using BWM
Full size table

Next, the optimal criteria weight is computed using model 1 or model 2, and the results fall into the vector set as \(w^{*} = \left( {0.0432,{\text{~}}0.4216,{\text{~}}0.0973,{\text{~}}0.1459,{\text{~}}0.2919} \right)\). Subsequently, the consistency ratio is computed using Eq. (5). The CR value is derived as 0.16, implying an acceptable consistency. Thus, the importance weight of the five criteria falls into the set as \(w = \left\{ {0.0432,{\text{~}}0.4216,{\text{~}}0.0973,{\text{~}}0.1459,{\text{~}}0.2919} \right\}\).

The payoff matrices \(P_{{k~}} = \left( {p_{{ij~}}^{{k~}} } \right)_{{4 \times 5~}} ~\left( {k = 1,~2,~3,..5} \right)\) are in qualitative terms and by the numbers obtained by the decision-makers are provided in Tables 5, 6, 7, 8 and 9, respectively. Next, the aim is to find the best strategy for the emergency event using the proposed emergency decision-making approach.

Table 6 The corresponding fuzzy numbers of payoff matrices based on qualitative terms (Table 5)
Full size table
Table 7 The weighted payoff matrix
Full size table
Table 8 The crisp group of payoff matrix
Full size table
Table 9 The computation of \({A}_{1}\) in terms of \({C}_{1}\)
Full size table

Next, the optimal criteria weight was computed using model 1 or model 2, and the results fall into the vector set as \(w^{{*~}} = \left( {0.0432,{\text{~}}0.4216,{\text{~}}0.0973,{\text{~}}0.1459,{\text{~}}0.2919} \right)\). Subsequently, the consistency ratio is computed using Eq. (5). The value of CR is derived as 0.16, which implies an acceptable consistency. Thus, the importance weight of the five criteria is \(w = \left( {0.0432,{\text{~}}0.4216,{\text{~}}0.0973,{\text{~}}0.1459,{\text{~}}0.2919} \right)\).

Model 3 is used to solve the Nash equilibrium strategy. Then, model 4 and 5 are used to obtain the vector weight of \(A_{{i~}}^{{~*}}\) and \(C_{{j~}}^{{~*}}\), respectively.

Model 4:

\({\text{min}}~~A_{{1~}} + A_{{2~}} + A_{{3~}} + A_{{4~}} ~\),

Subject to.

$$0.5317 \times ~A_{{1~}} + ~0.4919 \times ~A_{{1~}} + ~0.6170 \times ~A_{{1~}} + ~0.3348 \times ~A_{{1~}} + ~0.5881 \times ~A_{{1~}} + 0.3950 \times ~A_{{2~}} + ~0.4441 \times ~A_{{2~}} + ~0.5232 \times ~A_{{2~}} + ~0.2215 \times ~A_{{2~}} + ~0.4431 \times ~A_{{2~}} + 0.3416 \times ~A_{{3~}} + ~0.3415 \times ~A_{{3~}} + ~0.4884 \times ~A_{{3~}} + ~0.4053 \times ~A_{{~3~}} + ~0.4889 \times ~A_{{3~}} + 0.3323 \times ~A_{{4~}} + ~0.3391 \times ~A_{{4~}} + ~0.3651 \times ~A_{{4~}} + ~0.5166 \times ~A_{{~4~}} + ~0.5057 \times ~A_{{4~}} \ge 1$$

\(A_{{1{\text{~}}}} \ge 0\),

\(A_{{2{\text{~}}}} \ge 0\),

\(A_{{3{\text{~}}}} \ge 0.\)

Model 5:

\({\text{Max~}} = {\text{~}}C_{{1~}} + C_{{2~}} + C_{{3~}} + C_{{4~}} + C_{{5~}} {\text{~}}\),

subject to.

$$0.5317 \times ~C_{{1~}} + {\text{~}}0.3950 \times ~C_{{1~}} + 0.3416 \times ~C_{{1~}} + {\text{~}}0.3323 \times C_{{1~}} + {\text{~}} 0.4919 \times ~C_{{2~}} + {\text{~}}0.4441 \times ~C_{{2~}} + 0.3415 \times ~C_{{2~}} + {\text{~}}0.3391 \times C_{{2~}} + {\text{~}} 0.6170 \times ~C_{{3~}} + {\text{~}}0.5232 \times ~C_{{3~}} + 0.4884 \times ~C_{{3~}} + {\text{~}}0.3651 \times C_{{3~}} + {\text{~}} 0.5166 \times ~C_{{4~}} + {\text{~}}0.4053 \times ~C_{{4~}} + 0.2215 \times ~C_{{4~}} + {\text{~}}0.3348 \times C_{{4~}} + 0.5881 \times {\text{~}}C_{{5{\text{~}}}} + {\text{~}}0.4431 \times {\text{~}}C_{{5{\text{~}}}} + 0.4889 \times {\text{~}}C_{{5{\text{~}}}} + {\text{~}}0.5057 \times C_{{5{\text{~}}}} \le 1$$

\(C_{{1{\text{~}}}} \ge 0\),

\(C_{{2{\text{~}}}} \ge 0\),

\(C_{{3{\text{~}}}} \ge 0\),

\(C_{{4{\text{~}}}} \ge 0\),

\(C_{{5{\text{~}}}} \ge 0\).

By solving model 4 and 5 using linear programming software (www.lindo.com), the Nash equilibrium strategy falls into the \(A_{{\text{i}}}^{~} = \left( {0.390,~0.000,~0.000,~0.000} \right)\) and \(C_{{\text{j}}}^{~} = \left( {0.000,~0.000,~0.000,~0.676,~0.000} \right)\). In model 5 and 6, the value of \(v\) is obtained as 2.56 and 1.479. Therefore, the vector weights are \(A_{i}^{{*~}} = \left( {1.000,~0.000,~0.000,~0.000} \right)\) and \(C_{{\text{j}}}^{*} = \left( {0.000,~0.000,~0.000,~1.000,~0.000} \right)\). The expected values of alternatives from decision-makers are determined using Eq. (10) as \({\mathcal{G}}_{{1~}} = 0.295\), \({\mathcal{G}}_{{2~}} = 0\),\(~{\mathcal{G}}_{{3~}} = 0\), and \({\mathcal{G}}_{{4~}} = 0\). Therefore, the strategy 1 (alternative \(A_{{1~}}\), “aircraft emergency delivery of relief supplies”) is the best solution for decision-makers to be selected. Subsequently, by eliminating \({\mathcal{G}}_{{i~}} \ne 0\), the procedure is continued, and the final rank of alternatives falls into the order of \(A_{{1~}} \succ A_{{3~}} \succ A_{{4~}} \succ A_{{2~}}\). This ranking showed that considering the actual situation in the crises, priority should be placed on the aircraft emergency alternative for the delivery of the relief supplies. However, in the emergency response to the Gorgan City flooding, the decision-makers gave priority to the alternative route “Transport based on the cooperation of large group of people”. According to ISNA and IRNA reports a couple of days later, choosing this alternative found that as much more ineffective way for emergency decision-making response. Therefore, these intuitive rankings can be justified with actually obtained decision-making acts.

4 Sensitivity analysis

According to Saltelli (2002) [70], sensitivity analysis (SA) can be defined as a study of how the uncertainty in the output can be assigned to several sources of uncertainty. SA can show how much the prediction of results is accurate. It helps decision-makers to assess the level of the risk that is associated with the outcome of the decision-making process by evaluating how much the output is dependent on a specific input parameter. In this study, SA is performed by taking into account the original form of the decision-makers’ opinions without considering their confidence level and also with different confidence levels.

Figure 6 illustrates the emergency decision-making solutions in different approaches including the proposed methodology without confidence level, and with different confidence level. From Fig. 6, it can be seen that changing and ignoring the confidence levels have significant impact on setting the priority for the emergency decision-making solutions. However, the ranking of the solutions based on “without confidence level” and “with different confidence level” is the same. This further gives credence to the fact that the priority for finding solutions to the emergency decision-making problems is sensitive to the decision-makers’ confidence level. Therefore, from SA carried out in this studies, the consideration of the confidence level is vital in any decision-making elicitation procedure. This same result corroborates the findings [32, 36, 37, 54, 71].

Fig. 6
figure 6

The ranking results based on the sensitivity analysis

Full size image

4.1 Comparison analysis using TOPSIS and simple average method

This subsection aims to find out the feasibility and practicality of the proposed methodology via comparison analysis with TOPSIS and the Simple Average Method. Both methods have been widely accepted as applied tools in the MCDM field [43, 72, 74,75,76,77,78]. These three methods (TOPSIS, simple average method and the proposed methodology) used to determine the ranking of emergency decision-making solutions are presented in Fig. 7. The figure reflects that the priority of all solutions is completely consistent with the first highest of the solutions. It simply means that the first solution in all methods is the same. This simply implies that the decision-makers based on some realistic restrictions such as time and complexity can rely on other types of methods as well. However, as reflected by the results of the selected three models, this deduction is not true for the selection of the optimal solution.

Fig. 7
figure 7

The ranking results based on different approaches

Full size image

By computing the Spearman correlation coefficient between each pair of the methods, the conformity priority of methods is precisely reflected. The Spearman rank correlation coefficient between “proposed methodology” and “TOPSIS” is 0.2, between “Proposed methodology” and “Simple Average Method” is 0.8, and finally, between “TOPSIS” and “Simple Average Method” is 0.4. By obtaining a summation of the importance weight of each method based on Spearman rank correlation coefficient, the weight of each method falls into 1, 0.6, 1.2 for “Proposed methodology”, “TOPSIS” and “Simple Average Method”, respectively. It can be deduced that Simple Average Method has the highest correlation, and this can be significantly used for different purposes. Moreover, the “Proposed methodology” has the highest correlation close to the “Simple Average Method”, which shows its feasibility and practicality and “TOPSIS” method has the lowest correlation.

As a comparison with the existing approaches in terms of simplicity of computation, it could be said that the proposed approach in this study is complex and time consuming.

5 Implications

This study provides a couple of grounds as implications to the Country Crisis Management Organization (CCMO). CCMO is the only organization in Iran that can use these implications and grounds to improve the decision-making policies in case of future with natural disasters such as earthquake and floods. The natural crisis is stochastic in nature, which means that there is a significant path to be followed. Therefore, the system should be improved by focusing on the policies and emergency responses.

First of all, a group of decision-makers should be employed with different backgrounds in psychology, sociology, different engineering fields, politics, educational, environmental, cultural, etc. The group can identify all potential alternatives and criteria. In addition, this group could evaluate the applicability and effectiveness of the system.

Second, all hazards caused by human or nature should be identified, and the level of the risks should be evaluated. Once the risk is evaluated, the two tasks needed to be performed are (i) reduction in the probability of occurrence if hazards are human-based and (ii) reduction in the consequences of the event. Third, emergency response should be provided for all possible hazards including the sequence of the response team, resources, the accessibility of the path to the located event, estimating the loss, etc. These procedures would help in the reduction in the uncertainties that are inherent in the decision-making process. This study shows how much performing risk-based decision-making models is vital to improving output of the emergency-decision-making process. Therefore, it is required to conduct such a study to provide different emergency plans prior to the occurrence of the disaster.

6 Conclusion

In this paper, a new approach is introduced by combining three different methods including BWM, Z numbers and zero-sum game to deal with emergency decision-making problems in uncertain environments. The BWM is utilized to compute the importance weights of criteria, which could assist decision-makers to obtain more reliable results. Afterwards, the payoff matrix examination of decision-makers is constructed with the underlying idea of Z numbers to help decision-makers express their individual opinions in realistic ways. Finally, the zero-sum game theory is used to obtain the optimal solution in an emergency decision-making problem.

The flood in the northern part of Iran (referred to as the Golestan flood) is selected as a case study to demonstrate the feasibility and practicality of the introduced hybrid approach. Besides, the results compared with existing emergency decision-making approaches further illustrated how this study has enough propensity to be used in such similar cases.

The main challenge of the current study and most other decision-making problems is the effect of time on decision-making outputs is usually ignored. As a direction for future research, decision-making methods can be further developed using a probabilistic approach like the Bayesian updating mechanism. Besides, Z-numbers can be combined with other types of fuzzy numbers (e.g. Pythagorean, intuitionistic, etc.) to reflect the decision-makers’ opinion as accurately as possible. Moreover, in an emergency decision-making problem, the cooperative and psychosocial behaviour of decision-makers may influence the decision-making output. This needs to be studied further. The proposed method can be compared with different types of models of quality techniques in MCDM such as VIKOR, MABAC and MARCOS.