1 Introduction

Due to such hazards associated with flooding as disruption of services, health impacts, famine and disease, flood protection must be taken into account in almost all development projects (Elmoustafa 2012). The projections showed that flood potential, intensity and occurrence may become more pronounced (Kundzewicz 2005). Owing to mentioned hazards plus alarming projections, the new approaches in flood risk management are needed. In this regard, multiple criteria analysis of flood risk management alternatives based upon sustainable development criteria would promote facing this thorny issue. Thus, flood protection and management options must consider sustainable features such as social, economical and environmental criteria (Kundzewicz 1999; Kundzewicz and Takeuchi 1999). Prior to recent changes, conventional flood management approaches had focused on economic aspects while social and environmental factors had not been taken in to account (Hansson et al. 2013). Due to the fact that decision making based upon multiple criteria is a challenging issue, the application of Multi Criteria Decision Making Models (MCDM) were suggested (Yacov and Haimes 2011). Decision-making processes are often complicated according to multiple conflicting criteria, yet the MCDM methods have been successfully employed to identify desired policy alternatives (Kim and Chung 2013). The application of MCDM methods to various fields of water management has been demonstrated in a number of international literatures (e.g. Azarnivand et al. 2014; Geng and Wardlaw 2013; Duckstein and Opricovic 1980; Tecle and Duckstein 1994; Simonovic 1989; Duckstein et al. 1991; Srdjevic 2007). Evaluation of different alternatives and making a decision on the best alternative may depend on the MCDM method (Yilmaz and Harmancioglu 2010; Yacov and Haimes 2011). In this paper, some MCDMs, namely, Simple Additive Weighing (SAW), Compromise Programming (CP), VlseKriterijumska optimizacija I Kompromisno Resenje (VIKOR), Technique for Order Preference by Similarity to Ideal Solution (TOPSIS), Modified TOPSIS (M-TOPSIS), Analytical Hierarchy Process (AHP), and Elimination Et Choice Translating Reality (ELECTRE I and ELECTRE III) were employed. These models benefit various computational mechanisms such as ideal and negative-ideal solution, pair-wise comparisons, non-compensatory decision making and etc. The details regarding mathematical structures of each model could be referred to in section 3.

One of the criticisms over MCDM states that different techniques may yield different results when applied to the same problem. An analyst looks for a solution that is closest to the ideal, in which alternatives are evaluated according to all established criteria (pourjavad and Shirouyehzad 2011). Therefore, it is necessary to compare the MCDMs plus assessment of subjectivity with sensitivity analysis of input data. There are few researches in comparison of different methods for assessing flood management options. Spearman Correlation Coefficient Test (SCCT) and Kendall Tau Correlation Coefficient Test (KTCCT) as two stochastic tests can be used to determine the correlation between ranks obtained by different MCDM models (Gibbons 1971; Athawale and Chakraborty 2011). Five MCDM methods, namely, Preference Ranking Organization Method for Enrichment Evaluations (PROMETHEE2), Extended PROMETHEE2 (EXPROM2), ELECTRE III, ELECTRE IV and CP were used to priorities water resources planning options by Raju et al. (2000). He used SCCT to assess the correlation coefficient between the ranking patterns obtained by the mentioned MCDM methods. Ten most popular MCDM methods were compared in industrial robots selection by Athawale and Chakraborty (2011). SCCT and KTCCT were used to determine the applicability and suitability of the MCDM methods. Three MCDM methods such as COmplex PRoportional ASsessment (COPRAS), TOPSIS and VIKOR were used to evaluate building redevelopment decisions as revitalization of derelict and mismanaged buildings in rural areas of Lithuania by Antucheviciene et al. (2011). They conclude that Spearman Correlation Coefficients (SCC) between COPRAS and TOPSIS was appropriate within the probability of P ≥ 0.95. As well, Borda and Copland are some aggregation methods that can be used to incorporate different ranking results to find out the best result (Favardin et al. 2002). In this regard, the model with less sensitivity to the criteria weights would be the best.

This paper is categorized in the following sections: after this introduction, section 2 is a description of the study area and introduction of the seven flood management alternatives plus 11 criteria. In addition, the criteria weighing methods are also described in this section. Section 3 deals with explanation of the proposed MCDM models. Section 4 would reveal brief description of non-parametric stochastic tests and aggregation methods for comparing MCDM models. The result and discussion along with the technical highlights and methodological innovations of the paper are presented in section 5. Finally, conclusions are presented in section 6.

2 Material and Methods

2.1 Case Study

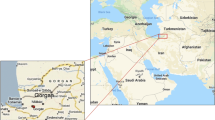
Located in Golestan Province, north-east of Iran and eastern part of the Caspian Sea coastline, Gorganrood basin was considered as the study area of the present research. Covering an area of about 20,380 km2, it is geographically bounded by 37°00′–37°30′ north latitude and 54°00′–54°30′ east longitude. The boundaries of downstream and upstream of the case study limits to Golestan dam (1) and Gonbad city, respectively (Fig. 1).

Fig. 1
figure 1

The case study of research (Ardalan et al. 2009)

Full size image

The province includes 11 cities and five main water basins, namely, Atrak, Gorganrood, Gharasoo, Neka and Gulf (MPO 2004). The population of the province is approximately 1.8 million; hence, the population density in this province is around 88 individuals per square kilometer. Although Iran is categorized in arid and semi-arid climate, the case study receives high to moderate precipitation. The absolute minimum and maximum daily temperature varies between −1.4 and 46.5 ° C, while the annual precipitation varies from 450 to 250 mm in the west to east direction (hashemi et al. 2014; Saghafian et al. 2008). According to the statistics, during the former decade, the province experienced more than 60 flood events that had resulted in approximately 115 million U.S. dollars along with more than 300 deaths (Ardalan et al. 2009).

2.2 Flood Management Alternatives

Flood risk management alternatives were divided in two groups of structurally and non-structurally-based measures by water resources engineering experts (Kundzewicz and Takeuchi 1999). Yazdandoost and Bozorgy (2008) suggested flood risk management alternatives according to physical and socio-economic conditions. Thus, throughout these researches, with respect to the operational and geographical circumstance of Gorganrood River, the suggested alternatives were applied (Table 1).

Table 1 Structural and non-structural flood management alternatives
Full size table

The first alternative is the current natural condition of the case study. In natural condition, neither structural nor non-structural flood mitigation measurements would be considered. Although as a consequence of Golestan dam’s construction the region’s natural condition would be changed, floodplain area is assumed without any modification such as flood routing by Golestan reservoir. As a result, this alternative, would consider socio-economic and environmental consequences of flood in the current condition of the study area.

The second alternative emphasizes on utilization of flood control capacity of Golestan dam (1). During flood occurrence, water level of reservoir stays in normal level while the reservoir storage rising above normal level. Hence, this reservoir storage could be used for flood routing and as a result, construction, operation and maintenance costs of Golestan dam (1) plus its social, economic and environmental outflow consequences should be considered.

The third alternative, uses levees to protect the reach of study area against 50-years flood while stronger floods can break them besides increasing the damages risks in the floodplain. This stark fact is considered in the process of the evaluation of criteria through the prioritization context. Based upon one-dimensional simulation of flood flow in the river, height of the levees is determined between 1 to 3.5 m. The length of the required levees in two sides of the river, their crest width, and their sides’ slopes are equaled to 41,150 m, 5 m, and 1 vertical to 2 horizontal, respectively (Yazdandoost and Bozorgy 2008).

The fourth alternative uses flood diversion channel along the river in the north (upstream) of the river-reaches of the study area with the depth of 3 m and width of 100 m. As discharge of this river exceeds 355 m3/s, this flood division structure starts to carry the surplus flow and discharge of 204 m3/s. Thus, the designed reach is protected against the floods with maximum peak discharge of 559 m3/s (Yazdandoost and Bozorgy 2008). The fifth alternative uses flood forecasting and warning systems. Similar to the first alternative, no physical changes would be occurred in the natural condition. The sixth alternative is flood insurance, which can compensate flood damages by insurance paid for damaged and casualties. Similar to the first and fifth alternatives, no physical changes would be occurred in the natural condition. Finally, the seventh alternative is a combination of fifth and sixth alternatives.

As it was stated earlier, prioritization of the alternatives is in demand of evaluation criteria. Thus, it is necessary to identify social, economic, and environmental criteria. Finally, each alternative would be prioritized based upon proposed MCDMs to investigate the most conclusive alternative.

2.3 Evaluation Criteria

The popular criteria in the international literatures related to water esources engineering are given in Table 2. As can be seen, Expected Average Number of Casualties per year (EANC), Expected Annual Damage (EAD), Protection of wild life habitat, and Technical feasibility and construction speed have more repetitions in comparison with other criteria. As a result, the criteria have been classified in four main groups as social, economic, environmental and technical features. In the present study, the sustainable development criteria and their classifications were selected on the basis of repetitions in the international literatures. Moreover, the evaluation criteria have been divided into two quantitative and qualitative groups. The qualitative criteria scored by expert’s votes, while others calculated by their relevant mathematical formulas.

Table 2 Selected criteria based on existed evaluation criteria in international references
Full size table

2.4 Evaluation of Quantitative Criteria

The (EANC), the (EAD) and gradually Rate belongs to quantitative group. These criteria are evaluated by following formulas (De Bruijn 2005).

$$ EAD={\displaystyle \underset{1/10000}{\overset{P\left(D=0\right)}{\int }}}PD(P)dP\sqrt{a^2+{b}^2} $$
(1)
$$ EANC={\displaystyle \underset{1/10000}{\overset{P\left(D=0\right)}{\int }}PC(P)dP} $$
(2)

where EAD is measured in € million/year, EANC in number of persons/year, P is flood probability, D(P) is the expected damage as a function of probability (€ million) and C(P) is the number of casualties as function of probability (De Bruijn 2005).

$$ \mathrm{Recovery}\ \mathrm{Rate}=1-{\displaystyle \sum_{n=1}^{n=N}}\frac{\left|\varDelta {Q}_n^{\prime }-\varDelta {D}_n^{\prime}\right|}{200} $$
(3)
$$ \varDelta {Q}_n^{\prime } = \left[\frac{100\left({Q}_n-{Q}_{min}\right)}{{\mathrm{Q}}_{\max }-{\mathrm{Q}}_{\min }}\right]-\left[\frac{100\left({Q}_{n-1}-{Q}_{min}\right)}{{\mathrm{Q}}_{\max }-{\mathrm{Q}}_{\min }}\right] $$
(4)
$$ \varDelta {D}_n^{\prime }=\left[\frac{100\left({D}_n-{D}_{min}\right)}{{\mathrm{D}}_{\max }-{\mathrm{D}}_{\min }}\right]-\left[\frac{100\left({D}_{n-1}-{D}_{min}\right)}{{\mathrm{D}}_{\max }-{\mathrm{D}}_{\min }}\right] $$
(5)

where Q′ is relative discharge (%), Q is discharge (m 3/s), \( {Q}_{\max }=Q\left(P=\frac{1}{10000}\right) \), Q min is the highest Q for which D = 0, D′ is relative damage (%), D is damage (€ million) as a function of Q, D max = D(Q max), D min = 0 and n is the ranking number of the discharge level.

2.5 Assigning Criteria Weights

The various methods assigning the criteria weights, may cause different ranking results for MCDM models. In this paper, Eigen-vector and average of experts’ votes were used to evaluate criteria weights. Averaging method applies simple mean of relative weights, while Eigen-vector is computed based on pair-wise comparison matrix. In the present research, the data set for both techniques is driven from experts’ votes. Throughout Eigen-vector method, the Saaty’s linguistic scales of pair-wise comparisons (Table 3) should be converted to quantitative values (Saaty 1980). Later, the criteria weights in this methodology were evaluated by two following formulas:

$$ A.W=\lambda .W $$
(6)
$$ \left(A-{\lambda}_{max}.I\right)\times W=0 $$
(7)

where λ and W are Eigen-value and Eigen-vector in pair-wise comparison matrix respectively.

Table 3 Number and linguistic values of criteria in Eigen-vector method (Saaty 1980)
Full size table

3 MCDM Models

3.1 SAW

Simple additive weighted is known as weighted linear combination method. In this model, alternative score are determined by following formula:

$$ {A}^{*}=\left\{{A}_i\left| \max {}_i{\displaystyle \sum_{j=1}^m}{W}_j{r}_{ij}\right.\right\} $$
(8)

where \( {r}_{ij}=\frac{x_{ij}}{ma{x}_i\left\{{x}_{ij}\right\}} \) is a normalized decision matrix element, x ij shows performance of alternative as in criteria j, and W j is the weight of criteria j. (Ustinovichius et al. 2007; Chou et al. 2008; Afshari et al. 2010; Manokaran et al. 2011)

3.2 CP

In CP, the ranking is determined based upon the distance to ideal solution, and the best alternative will be as ‘close’ as possible to ideal point. The ideal solution for the maximizing criteria is given as f j * = max f ij and for the minimizing criteria is given as f j * = min f ij . Apparently, \( {f_j}^{{}^{-}} \) is a negative-ideal solution that is equal to min f ij for maximizing and max f ij for minimizing criteria respectively.

Ideal solution distance are given as follows:

$$ {L}_P\left({A}_i\right)={\left[{\displaystyle \sum_{j=1}^n}{\left({\mu}_j.\frac{f_j^{*}-{f}_{ij}}{f_j^{*}-{f}_j^{-}}\right)}^p\right]}^{\frac{1}{p}} $$
(9)

where: Lp(a) = ideal solution distance for alternative A, μ j  = weight of each criterion j, p = parameter showing the attitude of the decision maker with respect to compensation between deviations and it is changes from 1 to ∞ (Raju et al. 2000; Zeleny and Cochrane 1973).

3.3 VIKOR Model

In this model, compromise ranking could be performed by comparing the measure of closeness to the ideal solution, like L p used in CP model. The VIKOR procedure consists of the following steps:

  1. 1)

    Calculating the normalized decision matrix as Eq. (10):

    $$ {f}_{ij}=\frac{x_{ij}}{\sqrt{{\displaystyle {\sum}_{i=1}^m}{x}_{ij}^2}} $$
    (10)

    where f ij is a normalized decision matrix element and x ij is the A th alternative performance in j th criteria.

  2. 2)

    Computing the values S (utility) and R (regret) as Eqs. (11) and (12), respectively as follows:

    $$ {S}_i={\displaystyle \sum_{j=1}^n}{w}_j.\frac{f_j^{*}-{f}_{ij}}{f_j^{*}-{f}_j^{-}} $$
    (11)
    $$ {R}_i= \max \left\{{w}_j.\frac{f_j^{*}-{f}_{ij}}{f_j^{*}-{f}_j^{-}}\right\} $$
    (12)

    where f * j  = maxf ij and \( {f}_j^{{}^{-}}= min{f}_{ij} \) for maximizing criteria, f j * = minf ij and \( {f}_j^{{}^{-}}= max{f}_{ij} \) for minimizing criteria and W j is the weight of the criterion j. f j * is the ideal solution and \( {f}_j^{{}^{-}} \) is the negative-ideal solution.

  3. 3)

    Computing the values Q by Eq. (13):

    $$ {Q}_i=v\left[\frac{S_i-{S}^{-}}{S^{*}-{S}^{-}}\right]+\left(1-v\right)\left[\frac{R_i-{R}^{-}}{R^{*}-{R}^{-}}\right] $$
    (13)

    where S − = min S i , S* = max S i , R − = min R i , R* = max R i and ν is introduced as a weight of the strategy of “the maximum group utility” or “the majority of criteria”. This parameter could be valued as 0–1 and when the ν > 0.5, the index of Q will tend to majority rule.

  4. 4)

    Ranks of the alternatives were sorted by considering the value of S, R and Q. The best alternative has the least value of these three parameters.

  5. 5)

    The highest ranked alternative in Q parameter would be the best alternative if the two following conditions were satisfied:

    1. C1:
      $$ Q\left({A}_2\right)-Q\left({A}_1\right)\ge \frac{1}{n-1} $$
      (14)

      where A 1 and A 2 are the alternatives with first and second position in ranking list and n is the number of the criteria.

    2. C2:

      Alternative that has the first rank in Q, must also has the first rank in S and R, or both of them.

      If condition C2 is not satisfied, set of alternatives ranking would be A 1, A 2, …, A m . Which A m is determined by the following formula:

      $$ \left({A}_m\right)-Q\left({A}_1\right)<\frac{1}{n-1} $$
      (15)

      If condition C1 was not satisfied, A 1 and A 2 would be selected as the best solution (Opricovic and Tzeng 2004, 2007; Mohaghar et al. 2012; Pourjavad and Shirouyehzad 2011).

3.4 TOPSIS

The central principle in TOPSIS model, is that the best alternative should have the shortest distance from the ideal solution while the farthest distance from the negative-ideal solution. Normalized decision matrix is similar to VIKOR model, while the rest of the procedure consists of the following steps:

  1. 1)

    To calculate the weighted normalized decision matrix as Eq. (16):

    $$ {V}_{ij}={W}_{ij}{r}_{ij} $$
    (16)

    where V ij is weighted normalized matrix element, r ij is normalized matrix elements and W j is weight of criteria j.

  2. 2)

    Determining the ideal and negative-ideal solution by following formulas:

    $$ {A}^{*}=\left\{{V}_1^{*}, \dots,\ {V}_n^{*}\right\}=\left\{\left( jmax{V}_{ij}\left|i\in \epsilon {I}^{\prime}\right.\right),\ \left( jmin{V}_{ij}\left|i\in {I}^{{\prime\prime}}\right.\right.\right\} $$
    (17)
    $$ {A}^{-}=\left\{{V}_1^{-}, \dots,\ {V}_n^{-}\right\}=\left\{\left( jmin{V}_{ij}\left|i\in {I}^{\prime}\right.\right),\ \left( jmax{V}_{ij}\left|i\in {I}^{{\prime\prime}}\right.\right.\right\} $$
    (18)

    where I′ and I″ are related to increasing and decreasing criteria, respectively.

  3. 3)

    Measuring the ideal and negative-ideal solution distance as follows:

    $$ {S}_i^{*}=\sqrt{{\displaystyle \sum_{j=1}^n}{\left({V}_{ij}-{V}_j^{*}\right)}^2} $$
    (19)
    $$ {S}_i^{-}=\sqrt{{\displaystyle \sum_{j=1}^n}{\left({V}_{ij}-{V}_j^{-}\right)}^2} $$
    (20)
  4. 4)

    The last stage involved the calculation of the similarity index to prioritize the alternatives. Therefore, the alternatives with higher similarity index are the superiors (Manokaran et al. 2011; Pourjavad and Shirouyehzad 2011; Ustinovichius et al. 2007; Opricovic and Tzeng 2004).

    $$ {C}_i^{*}=\frac{S_i^{-}}{S_i^{*}+{S}_i^{-}} $$
    (21)

3.5 M-TOPSIS

Ranking system in the modified TOPSIS is based on combination ideal and negative-ideal solution distance as presented by Eq. (22). The alternative with more similarity to ideal solution is the best one. M-TOPSIS model has results that are more reasonable and compensate some restriction in TOPSIS model (Ren et al. 2007).

$$ {C}_{iM}^{*}=\sqrt{{\left[{S}_i^{*}- \min \left({S}_i^{*}\right)\right]}^2+{\left[{S}_i^{-}- \max \left({S}_i^{-}\right)\right]}^2} $$
(22)

3.6 ELECTRE I

ELECTRE I is a version of ELECTRE method. The difference between this model and previously mentioned models rooted in its concept of non-compensatory decision making. This means, in particular, a “very bad” score on a criterion cannot be compensated by “very good” scores on the other criteria (Pourjavad and Shirouyehzad 2011; Rogers et al. 2000; Roy 1968, 1991). Normalizing the decision matrix and also weighing the normalized decision matrix is similar to TOPSIS model and remain process are as follows:

  1. 1)

    Calculating the concordance matrix by Eq. (23):

    $$ {C}_{ke}={\displaystyle \sum_{j\in {S}_{ke}}}Wj $$
    (23)

    where C ke is sum of the weights of those criteria where alternative k outranks alternative e and W j is weight of criteria j.

  2. 2)

    Calculating the discordance matrix by Eq. (24):

    $$ {d}_{ke}=\frac{\underset{j\in {I}_{ke}}{ \max}\left|{V}_{kj}-{V}_{ej}\right|}{\underset{j\in j}{ \max}\left|{V}_{kj}-{V}_{ej}\right|} $$
    (24)

    where I ke  = J − S ke , and V ij is the weighted normalized matrix element.

  3. 3)

    Calculating the domain concordance matrix by Eq. (25)-(26):

    $$ {f}_{ke}=\left\{\begin{array}{c}\hfill 1\kern2.5em {C}_{ke}\ge \overline{C}\kern3em \hfill \\ {}\hfill 0\kern2.75em {C}_{ke}<\overline{C}\kern3.25em \hfill \end{array}\right. $$
    (25)
    $$ where\kern0.5em \overline{C}={\displaystyle \sum_{\begin{array}{c}\hfill k=1\hfill \\ {}\hfill k\ne e\hfill \end{array}}^m}{\displaystyle \sum_{\begin{array}{c}\hfill e=1\hfill \\ {}\hfill e\ne k\hfill \end{array}}^m}\frac{C_{ke}}{m\left(m-1\right)} $$
    (26)
  4. 4)

    Calculating the domain discordance matrix by Eq. (27)-(28):

    $$ {g}_{ke}=\left\{\begin{array}{c}\hfill 0\kern2.5em {d}_{ke}>\overline{d}\kern3em \hfill \\ {}\hfill 1\kern2.75em {d}_{ke}\le \overline{d}\kern3.25em \hfill \end{array}\right. $$
    (27)
    $$ where\kern0.5em \overline{d}={\displaystyle \sum_{\begin{array}{c}\hfill k=1\hfill \\ {}\hfill k\ne e\hfill \end{array}}^m}{\displaystyle \sum_{\begin{array}{c}\hfill e=1\hfill \\ {}\hfill e\ne k\hfill \end{array}}^m}\frac{d_{ke}}{m\left(m-1\right)} $$
    (28)
  5. 5)

    Calculating the final domain matrix by Eq. (29):

    $$ {h}_{ke}={f}_{ke}.{g}_{ke} $$
    (29)
  6. 6)

    Choosing the best alternative based on the most domain and the least beaten. In this regard, throughout the final domain matrix, number one shows dominant of alternatives in each row and beaten in each column.

3.7 AHP

AHP is based on pair-wise comparisons. In this model, pair-wise comparison matrix of criteria and alternatives in each criterion are needed (Mohaghar et al. 2012; Frei and Harker 1999; Ramanathan and Ganesh 1995; Saaty 1977).

The process consisted of the following steps:

  1. 1)

    Determination of the local priority for each criteria and alternatives:

    Throughout the paper, arithmetic mean method is used to determine local priority.

  2. 2)

    Determination of the overall priority by Eq. (30):

    $$ {A}_{AH{P}_{score}}={\displaystyle \sum_{j=1}^n}{a}_{ij}.{W}_j $$
    (30)

    where a ij is local priority for i th alternatives in j th criteria and W j is local priority for j th criteria.

  3. 3)

    Calculation of the inconsistency index by Eq. (31):

    $$ I.I.=\frac{\uplambda_{max}-n}{n-1} $$
    (31)

    where λ max is maximal Eigen-value and n is number of alternatives.

  4. 4)

    Calculation of the inconsistency ratio by Eq. (32):

    $$ I.R=\frac{I.I}{R.I.I} $$
    (32)

    where R. I. I = 1.98(n − 2/n) and is called random index.

    If I.R is less than 10 %, then the matrix can be considered consistent.

3.8 ELECTRE III

ELECTRE III is a version of ELECTRE method. It uses various mathematical functions to indicate the degree of dominance of an alternative or a group of alternatives over the remaining ones (Roy 1968, 1978; Roy et al. 1986; Miettinen and Salminen 1999; Raju et al. 2000). This method includes three different thresholds: a preference threshold p, an indifference threshold q and a veto threshold v. Where g(x i ) v g(x j ) means x j is rejected by x i , g(x i ) p g(x j ) means x i is preferred to x j and g(x i ) q g(x j ) means x i is indifferent to x j .

This method involves the following steps:

  1. 1)

    Calculation the concordance matrix for each criterion by Eq. (33):

    $$ {C}_L\left({x}_i,{x}_j\right)=\left\{\begin{array}{l}1\kern2em if\kern2.25em {g}_l\left({x}_i\right)+{q}_l\left({g}_l\left({x}_i\right)\right)\ge {g}_l\left({x}_j\right)\\ {}0\kern1.5em if\kern2.25em {g}_l\left({x}_i\right) + {p}_l\left({g}_l\left({x}_i\right)\right)\le {g}_l\left({x}_j\right)\\ {}\frac{p_l\left({g}_l\left({x}_i\right)\right)+{g}_l\left({x}_i\right)-{g}_l\left({x}_j\right)}{p_l\left({g}_l\left({x}_i\right)\right)-{q}_l\left({g}_l\left({x}_i\right)\right)}\kern6.75em otherwise\end{array}\right. $$
    (33)
  2. 2)

    Calculation the final concordance matrix by Eq. (34):

    $$ c\left({x}_i,\ {x}_j\right)=\frac{1}{w}{\displaystyle \sum_{l=1}^m}{w}_l{c}_l\left({x}_i,\ {x}_j\right) $$
    (34)

    where \( W={\displaystyle \sum_{l=1}^m}Wl \)

  3. 3)

    Calculating the discordance matrix for each criterion by Eq. (35):

    $$ {C}_L\left({x}_i,{x}_j\right)=\left\{\begin{array}{l}1\kern2em if\kern2.25em {g}_l\left({x}_i\right)+{\nu}_l\left({g}_l\left({x}_i\right)\right)\le {g}_l\left({x}_j\right)\\ {}0\kern1.5em if\kern2.25em {g}_l\left({x}_i\right) + {p}_l\left({g}_l\left({x}_i\right)\right)\ge {g}_l\left({x}_j\right)\\ {}\frac{g_l\left({x}_j\right)-{g}_l\left({x}_i\right)-{p}_l\left({g}_l\left({x}_i\right)\right)}{\nu_l\left({g}_l\left({x}_i\right)\right)-{p}_l\left({g}_l\left({x}_i\right)\right)}\kern6.75em otherwise\end{array}\right. $$
    (35)
  4. 4)

    Calculating the final discordance matrix by Eq. (36):

    $$ d\left({x}_i,\ {x}_j\right)=\frac{1}{w}{\displaystyle \sum_{l=1}^m}{w}_l{d}_l\left({x}_i,\ {x}_j\right) $$
    (36)
  5. 5)

    Calculating the credibility matrix by Eq. (37):

    $$ S\left({x}_i,{x}_j\right)=\left\{\begin{array}{l}C\left({x}_i,{x}_j\right)\kern10em if\kern0.75em {d}_l\left({x}_i,{x}_j\right)\le C\left({x}_i,{x}_j\right)\kern1.25em \forall l\\ {}C\left({x}_i,{x}_j\right).{\displaystyle \prod_{l\epsilon J\left({x}_i,{x}_j\right)}}\frac{1-{d}_l\left({x}_i,{x}_j\right)}{1-C\left({x}_i,{x}_j\right)}\kern1.25em if\kern0.75em {d}_l\left({x}_i,{x}_j\right) > C\left({x}_i,{x}_j\right)\end{array}\right. $$
    (37)
  6. 6)

    Calculating the final matrix by Eq. (38):

    $$ T\left({x}_i,{x}_j\right)=\left\{\begin{array}{c}\hfill 1\kern4.75em if\kern1.5em S\left({x}_i,{x}_j\right) > \lambda -s\left(\lambda \right)\kern3em \hfill \\ {}\hfill 0\kern9.75em otherwise\kern4.75em \hfill \end{array}\right. $$
    (38)

    where \( \lambda = \max {}_{X_i,{X}_j\int X}S\left( Xi,Xj\right) \) and S(λ) = − 0.15(λ) + 0.3

    Finally, an alternative with high difference in summation of rows and columns was chosen as the first priority. Then, the alternative with first place omitted and ranking continues for the remain alternatives. For ascend ranking, set of alternatives with the lowest qualification is in the first place. Final ranking is based on the sharing descend and ascend ranking.

4 Non-Parametric Correlation Tests and Aggregation Methods to Comparing Models Ranking

Since MCDMs have different ranking results, Aggregation methods and correlation tests are used to determine the best MCDM as the final result. Non-parametric correlation tests like SCCT and KTCCT determine the model with more correlation to other MCDMs. Aggregation methods like Borda and Copland visualized and structure to find out the final ranks of alternatives (Shih et al. 2004; Saari 1995; Pomerol and Barba-Romero 2000; Hwang and Lin 1987; Jahan et al. 2011).

SCCT and KTCCT are depended on the ranks of the data instead of their values (Athawale and Chakraborty 2011; Szmidt and Kacprzyk 2011). In these methods, a mutual comparison between each two random variable is possible. The number of comparisons is equal to \( \frac{n\left(n-1\right)}{2} \) where n is the number of alternatives. KTCC will be obtained by formula (39), provided that each of the two compared model has no same ranks. Whereas, formula (40) will be employed if one of the compared model has the same ranks.

$$ \tau =\frac{C-D}{\frac{n\left(n-1\right)}{2}} $$
(39)

Where C = |{(i, j)|x i  < x j  and y i  < y j }| and D = |{(i, j)|x i  < x j  and y i  < y j }| are the numbers of concordant pair and the number of discordant pair, respectively. where x and y are compared multi criteria methods ranks, i and j are alternatives.

$$ \tau =\frac{C-D}{\sqrt[2]{\left(\frac{n\left(n-1\right)}{2}-T\right)\times \left(\frac{n\left(n-1\right)}{2}-U\right)}} $$
(40)

where T and U are the numbers of pairs of the same ranks in each compared models. (For example T = number of pairs for which x i  = x j and U = number of pairs for which y i  = y j )

SCCT presenting by formula (41) will be applied if each of two compared model has no same ranks. Whereas, formula (42) utilized if one of the compared model has same ranks (Szmidt and Kacprzyk 2011; Raju et al. 2000; Raju and Pillai 1999).

$$ {r}_s=1-\frac{6{\displaystyle {\sum}_{i=1}^n}{d}_i^2}{n\left({n}^2-1\right)} $$
(41)

where d i is the difference between the ranks of models for each alternatives (d i  = x i  − y i ).

$$ {r}_s=\frac{{\displaystyle {\sum}_{i=1}^n}\left({x}_i-\overline{x}\right)\times \left({y}_i-\overline{y}\right)}{\sqrt[2]{{\displaystyle {\sum}_{i=1}^n}{\left({x}_i-\overline{x}\right)}^2\times {\displaystyle {\sum}_{i=1}^n}{\left({y}_i-\overline{y}\right)}^2}\ } $$
(42)

where \( \overline{x} \) and \( \overline{y} \) are the mean of x and y model, respectively.

Borda aggregation method uses pair-wise comparison matrix of alternatives to investigate the final ranking. In this method, number one means, the number of victories are more than the number of defeats while number zero operates vise versa. The alternative with more victories is the best. Copland aggregation method is the improved Borda method. In this method, difference between pair-wise victories and pair-wise defeats obtains the ranks of alternatives score.

5 Results and Discussion

5.1 Choosing the Appropriate Model for Determination of the Criteria Weights

Table 4 illustrates the decision matrix along with three required thresholds in ELECTRE III method and criteria weights which obtained by experts’ votes. According to Table 4, Eigen-vector and averaging generated different criteria weights. A clear solution to find the better one would be using KTCCT. To do so, the ranks of each alternative on the basis of both driven weights for each MCDM model should be evaluated. As can be seen in Table 5, except in SAW technique, Eigen-vector and averaging method generated various ranks. To compare Eigen-vector and averaging method the KTCC were computed (Table 6). The null hypothesis is the lack of correlation. For n = 7, the critical value, which is in Kendall tau table, was equal to 0.619. So for τ > 0.619, null hypothesis was rejected. As can be seen in Table 6, the lowest correlation in Eigen-vector method was 0.428 while the highest was equaled to one. Moreover, in this technique 52 out of 55 data had the acceptable correlation values (>0.619). However, the lowest correlation in averaging method was 0.3 and just 37 out of 55 data had the acceptable correlations. As a result, the criteria weights for overall assessment should be chosen among Eigen-vector’s weights. The superiority of Eigen-vector to averaging method might be contributed to the facts that, in averaging method besides some difficulties in normalizing different units, some probability mistakes are made by experts in the valuation process, while in Eigen-vector method, both experts’ votes and mathematical methods are used simultaneously. Thus, the probability mistakes could be decreased which is resulted in more accurate outcomes.

Table 4 Alternative’s score, criteria weights, and the three required thresholds
Full size table
Table 5 Ranks of models based on Eigen-vector and averaging methods
Full size table
Table 6 Comparing Eigen-vector and averaging methods with respect to KTCC
Full size table

5.2 Determination of the Selected MCDM Model Based on the Correlation Coefficient Tests

The two stochastic tests, namely, KTCCT and SCCT were applied to obtain the most conclusive MCDM model with respect to Eigen-vector’s weights. According to Table 6, the highest KTCC was between CP (p = ∞) and VIKOR methods, yet these two methods had a low correlation with others. The next highest correlation was between CP (p = 2) and ELECTRE III method which equal to 0.975. Furthermore, these two methods also had a high correlation with others. As a result, CP (p = 2) and ELECTRE III had the highest correlation in comparison to other MCDM methods. Consequently, in the lights of KTCC, CP (p = 2) and ELECTRE III were chosen as the most suitable methods for the case study, whereas TOPSIS and M-TOPSIS could not appropriately fitted the case study (Fig. 2).

Fig. 2
figure 2

The KCC of CP (p = 2) and ELECTRE III methods with other MCDM methods

Full size image

According to SCCT, with the null hypothesis of the lack of correlation; for n = 7, the critical value, in Spearman table, was equaled to 0.786. So for S r   > 0.786 the null hypothesis was rejected. According to Table 7, similar to KTCCT, ELECTRE III and CP (p = 2) had the highest correlation with others. TOPSIS again had the lowest correlation with the others. The mean of SCC with 25 % confidence interval for the MCDMs (Fig. 3) proved the outcomes of Table 7.

Table 7 SCC in Eigen-vector method
Full size table
Fig. 3
figure 3

The mean of SCC with 25 % of confidence interval

Full size image

5.3 Determination of the Selected MCDM Model Based on the Aggregation Methods

In addition to the stochastic tests, the aggregation methods (Borda and Copland) were used. The aggregation results are shown in Table 8. Both of aggregation methods represented similar ranking for the alternatives. The ranks in aggregation methods showed the most similarity to the ranks of ELECTRE III method. Hence, it can be concluded that among the proposed MCDMs, ELECTRE III was chosen as the most suitable case specific model.

Table 8 Results of aggregation methods
Full size table

5.4 Sensitivity Analysis to Changes in Criteria Weights

Sensitivity analysis was performed to examine the response of alternatives when the criteria weights changed to its minimum and maximum values (Table 9). Table 10 represents the changes in the ranking for the modified weights of the criteria. The least sensitivity belonged to ELECTRE III, CP (p= ∞) and VIKOR, respectively. This outcome proved the robustness of ELECTRE III in multiple criteria analysis among MCDM models.

Table 9 Maximal and minimal weights of each criterion based on decision makers’ attitude
Full size table
Table 10 New ranking list with respect to changes in criteria weights
Full size table

5.5 Technical and Methodological Remarks

As stated earlier, Eigen-vector and ELECTRE III were chosen as the most appropriate weighing and ranking methods, respectively. From the technical (operational) points of view, due to the Eigen-vector driven weights of ELECTRE III (Table 5), the integration of flood insurance and flood warning system (A7) was chosen as the most conclusive procedure for flood hazard mitigation. This alternative is a combination of a pre and post disaster action.

According to the Eigen-vector results (Table 4), EANC as a social criteria stood superior to the others. It is interesting that through the research by Yazdandoost and Bozorgy (2008) the highest priority belonged to the socio-economy criteria in flood risk management. Hence, our research proved the significance of social consideration in flood hazard management; of course with application of a hybrid weighing approach.

From the methodological point of view, the novelties of the paper were as follows:

  1. 1.

    Throughout the ongoing research, two different weighing methods were used for obtaining the criteria significances. Although many researchers (Athawale and Chakraborty 2011; Hajkowicz and Higgins 2008; Raju et al. 2000) used average weighing, the comparison between these two methods illustrated that Eigen-vector was by far the best weighing procedure for complex decision making.

  2. 2.

    The paper employed various MCDMs with such different computational mechanisms as pair-wise comparison, similarity to ideal solution, non-compensatory technique and etc., simultaneously. This package of MCDMs provides an opportunity for comparison of their robustness.

  3. 3.

    Owing to different computational mechanism of the proposed MCDMs, selection of the best one is a challenging issue. The present study creatively used non-parametric stochastic tests, aggregation methods and finally sensitivity analysis. The MCDM model that performed better through these three tools could be chosen as the most robust model.

6 Conclusion

Due to the high flood potential of Gorganrood River, the feasibility of proposed structural and non-structural measures should be checked. MCDMs can provide a mechanism for simultaneous consideration of social, economic, environmental, and technical criteria associated with flood risk management. Overall assessment indicated that the conjunction of a pre and post disaster in flood risk management was the best solution, within the dominance of Gorganrood basin. The three-stage process of choosing most proper model constituting stochastic tests, aggregation methods and sensitivity analysis represented that ELECTRE III, a non-compensatory model, made a valid contribution to the study area. Most of the former researches ignored using either the potentials of stochastic tests or aggregation methods for their multi methodological research works. This study highlighted the significant role of stochastic tests in multi methodological studies, particularly in the cases with different computational methodologies. Former researches used aggregation methods to find out the final ranking, whilst throughout this research, these methods were employed as the tools for analyzing the robustness of the proposed models. Due to the fact that capability of proposed framework was proved in three different stages, this methodology is recommended for decision making on complex water and environmental management issues.