1 Introduction

Streamflow forecasting at various temporal scales and time steps ahead is important for engineering purposes (e.g. hydro-power generation, dam regulation and other water resources engineering purposes), as well as environmental and societal purposes (e.g. flood protection and long-term water resources planning). Here, we are interested in one-step-ahead daily streamflow forecasting.

In streamflow forecasting, the predictive ability of the implemented model is of high importance; therefore, more flexible albeit less interpretable models (e.g. machine learning algorithms) are acceptable, given that they are more accurate. While accuracy is important in engineering, the current trend in the field of hydrology favours model interpretability (see, for example, [11]). The reader is referred to [18, 45, pp 24–26)] and [73], for a general discussion on the issue of interpretability versus flexibility or, equivalently, understanding versus prediction in algorithmic modelling. Here, focus is on accuracy.

The dominant approach in daily streamflow forecasting is the implementation of machine learning regression algorithms, while linear models (mostly time series models) have been found to be more competitive at larger time scales (e.g. monthly and annual; [62, 63]). Regression algorithms model the dependent variable (streamflow at some time) as function of a set of selected predictor variables (e.g. past streamflow values, past precipitation values and past temperature values, with the latter two types of information being collectively referred to as “exogenous predictor variables” for this particular forecasting problem). In the case of machine learning regression, this function is learnt directly from data through an algorithmic approach. Popular algorithms include neural networks (see, for example, [1, 25, 54, 78]), support vector machines [69], decision trees, random forests and their variants [85], with numerous algorithmic variants (see, for example, [28] for the most representative ones) having been more or less applied to hydrologic case studies. Note, however, that existing approaches to daily streamflow forecasting are mostly based on the implementation of a single machine learning algorithm.

Combining forecasts from different methods has been proved to increase the forecasting accuracy. This point was initially raised by [7], while the argumentation in favour of forecast combinations, referred to as “ensemble learning” in the literature, was further strengthened in the early 90s (see, for example, [37, 93]). The “no free lunch theorem” [103] implies that no universally best machine learning algorithm exists. Thus, ensemble learning, i.e. combining multiple machine learning algorithms (hereinafter termed as base-learners) instead of using a single one, may increase the predictive accuracy of the forecasts. Overviews of model combinations in general and ensemble learning in particular can be found in [29] and [72], respectively. Here, we are interested in stacked generalization (also referred to as stacking), a particular type of ensemble learning where base-learners are properly weighted, so certain performance metrics are minimized (see, for example, [66, 87] for specific applications in probabilistic hydrological post-processing), which was initially suggested by [102] and later investigated by [16] for regression.

The simplest combination of models is equal weight averaging. The latter combination approach has been proved “hard to beat in practice” by more complex combination methods, a finding that has been termed “forecast combination puzzle” by [79]. While research on the causes of the “forecast combination puzzle” is currently inconclusive (see, for example, [23, 76, 83]), one can intuitively attribute its sources to the fact that as the level of uncertainty (or equivalently the number of base-learners) increases, weight optimization may not lead to significant improvements relative to simple averaging, i.e. a uniform weighting scheme that assigns equal weights to all base-learners (see [87]).

Most published studies focusing on daily streamflow forecasting use small datasets (e.g. data collected from a couple of rivers) to present some type of new method, usually referred to as hybrid when combining, for example, neural networks with an optimization algorithm. While such studies may be useful from a hydrological standpoint, the obtained results cannot be conclusive regarding the accuracy of the proposed method, due to the high degree of randomness induced by sample variability. While small-scale applications were acceptable in the early era of neural network hydrology, the current status of data availability allows for large-scale applications. Actually, recent studies based on big datasets have revealed ground breaking results in the field of hydrological forecasting (see, for example, [62, 65]), as large-scale applications allow for less biased simulation designs to assess the relative performance of new and existing methods (see, for example, the commentary in [12]).

The aim of our study is to propose a new practical system for streamflow forecasting based on a stacking algorithm, specifically super ensemble learning [90]. We conduct a large-scale investigation and find that the proposed practical system outperforms a diverse and wide variety of methods that are commonly used in hydrology for daily streamflow forecasting. Along with the introduction of the new practical system, our study aims at advancing the existing knowledge and current state of the art in the field of machine learning by:

  1. a.

    Introducing a super ensemble learning framework to combine 10 machine learning algorithms, together with a predictor variable selection scheme based on random forests importance metrics, and comparing super ensemble learning with the “hard to beat in practice” equal weight combiner.

  2. b.

    Assessing the relative performance of two time series models and 10 individual machine learning algorithms in daily streamflow forecasting, and comparing them with the super ensemble learning framework.

  3. c.

    Using more than 500 streamflow time series to support the quantitative conclusions reached.

Beyond presentation of the new practical system, we consider remarks (b) and (c) above equally important, since most studies in the field use small datasets (i.e. formed by a single-digit number of time series) to compare a limited number of machine learning algorithms. Use of big datasets can provide insights and facilitate understanding and contrasting of the properties of various algorithms in predicting daily streamflow, consisting an important asset for engineering applications.

2 Methods

In this section, we present short descriptions of the individual machine learning algorithms (base-learners) used (please note that an exhaustive presentation of the algorithms is out of the scope of the present study), the three combiner learners (i.e. super ensemble learner, equal weight combiner and best learner), the variable selection methodology, the statistical time series forecasting methods, the metrics used to assess the relative performance of the algorithms and the testing procedure.

2.1 Statistical time series forecasting methods

Here, we present the statistical time series forecasting methods that are compared to the proposed practical system. These methods are well established in the literature, while their implementation is fully automated in the forecast R package [43, 44]; therefore, in what follows, short descriptions are provided. A typical property of such models is that they are fitted to the time series of interest (i.e. the streamflow time series in our case), thereby not exploiting available information from other predictor variables (i.e. temperature and precipitation variables in our case). Furthermore, such models can exploit temporal dependencies in the observations [14], while most machine learning algorithms cannot. Details regarding the training periods of the time series models can be found in Sect. 2.6.

2.1.1 Exponential smoothing method

Simple exponential smoothing methods compute weighted moving averages of past time series values. They were introduced by [19, 41, 101]. Variants of exponential smoothing models that can account for drifts and seasonality also exist. Here, we used the automated method of the forecast R package, which employs a procedure for automatic estimation of trend parameters. We did not let the algorithm estimate the seasonality of the data, because this would result in unstable forecasts, given that 365 seasons should be estimated. An alternative option is to fit different models to each month, but we did not choose this option, due to the secondary benchmarking role of the model. It should be noted that the first application of exponential smoothing models in geophysical time series forecasting can be found in [27], and that a large-scale comparison with other models can be found in [65]. While use of exponential smoothing models has been limited to geophysical time series forecasting, these algorithms are popular in other fields (econometrics, etc.).

2.1.2 ARIMA models

Autoregressive Integrated Moving Average (ARIMA) stochastic processes model time series by combining autoregressive (where dependent variables depend linearly on their previous values) and moving average (where dependent variables depend linearly on previous white noise terms) stochastic schemes, and simultaneously model trends. They have been popularized by [14], while a more recent treatment can be found in [15]. A first application in hydrology can be found in [20]. Here, we use the automated forecasting procedure implemented in the forecast R package.

2.2 Base-learners

A detailed description of the majority of the base-learners exploited herein is out of the scope of the manuscript and can be found in [39, 45]. All algorithms have been implemented and documented in the R programming language. Details on their software implementation can be found in “Appendix”. To ensure reproducibility of the results, “Appendix” also includes the versions of the software packages used herein.

2.2.1 Linear regression

Linear regression is the simplest model used herein. It is described in detail by [39 pp 43–55]. The dependent variable is modelled as a linear combination of the predictor variables, while the weights are estimated by minimizing the residual sum of squares (least squares method).

2.2.2 Lasso

The least absolute shrinkage and selection operator (lasso) algorithm [82] performs variable selection and regularization by imposing the lasso penalty (L1 shrinkage) in the least squares method, aiming to shrink its coefficients, while allowing for elimination of non-influential predictor variables by nullifying their coefficients.

2.2.3 Loess

Locally estimated scatterplot smoothing (loess, [24]) fits a polynomial surface (determined by the predictor variables) to the data by using local fitting. Here, we used a second-degree polynomial.

2.2.4 Multivariate adaptive regression splines

Multivariate adaptive regression splines (MARS, [30, 31]) is a weighted sum of basis functions, with total number and associated parameters (i.e. product degree and knot locations, respectively) being automatically determined from data. Here, we build an additive model (i.e. a model without interactions), where the predictor variables enter the regression through a linear sum of hinge basis functions.

2.2.5 Multivariate adaptive polynomial spline regression

Multivariate adaptive polynomial spline regression (polyMARS, [49, 80]) is an adaptive regression procedure that uses piecewise linear splines to model the dependent variable. It is similar to MARS, with main differences being that “(a) it requires linear terms of a predictor to be in the model before nonlinear terms using the same predictor can be added and (b) it requires a univariate basis function to be in the model before a tensor-product basis function involving the univariate basis function can be in the model” [48].

2.2.6 Random forests

Random forests [17] are bagging (abbreviation for bootstrap aggregation) of regression trees with an additional degree of randomization, i.e. they randomly select a fixed number of predictor variables as candidates when determining the nodes of the decision tree.

2.2.7 XGBoost

Extreme Gradient Boosting (XGBoost, [21]) is an implementation of gradient boosted decision trees (see, for example, [32, 56, 58], albeit considerably faster and better performing. Gradient boosting is an approach that creates new models (in this case decision trees) to predict the errors of prior models. The final model adds all fitted models. A gradient descent algorithm is used to minimize the loss function when adding new decision trees. XGBoost uses a model formalization that is more regularized to control overfitting. This procedure renders XGBoost more accurate than gradient boosting.

2.2.8 Extremely randomized trees

Extremely randomized trees [36] are similar to random forests. These two models mostly differ in the splitting procedure. Contrary to random forests, in extremely randomized trees the cut-point is fully random.

2.2.9 Support vector machines

The principal concept of support vector regression is to estimate a linear regression model in a high-dimensional feature space. In this space, the input data are mapped using a (nonlinear) kernel function [77, 91]. Here, we used a radial basis kernel.

2.2.10 Neural networks

The principal concept of neural networks is to extract linear combinations of the predictor variables as derived features and then model the dependent variable as a nonlinear function of these features [39, p 389]. Here, we used feed-forward neural networks [70, pp 143–180].

2.3 Super ensemble learning

Super ensemble learner is a convex weighted combination of multiple machine learning algorithms, with weights that sum to unity and are equal or higher than zero (see [88,89,90]). The weights are estimated through a k-fold cross-validation procedure (here, we choose k = 5) in the training set (see Sect. 2.6), so that a properly selected loss function is minimized. Here, we minimize the quadratic loss function, which is equivalent to minimizing the root-mean-squared error (RMSE). Then, the base-learners are retrained in the full training dataset, and the super ensemble learner predictions are obtained as the weighted sum (using the estimated weights of the cross-validation procedure) of the retrained base-learners. The design of the algorithm is presented in Fig. 1. Super ensemble learning (as every stacking algorithm) can combine ensemble learners (e.g. bagging algorithms, boosting algorithms and more) and different types of base-learners, while, for example, bagging or boosting algorithms use a single type of base-learners.

Fig. 1
figure 1

Design of the super ensemble learner corresponding to Algorithm 1. Red blocks in the training dataset are used for training, and blue blocks are used for validation

Full size image

Algorithm 1 presents the formal procedure of super ensemble learning for a training set of N observations. Some theoretical results and recommendations for the implementation of super learning algorithms can be found in [90]. In particular:

  1. a.

    It is recommended to use as many as possible sensible base-learners.

  2. b.

    Due to the cross-validation procedure, overfitting is avoided.

  3. c.

    Different loss functions can be applied. For instance, by construction random forests are not a minimization procedure. However, if one wants to minimize the L1 loss, one can still include random forests in the mix of base-learners, as the optimization procedure of super ensemble learning will assign appropriate weights to them.

  4. d.

    The super ensemble learner will perform asymptotically as well as the best base-learner.

figure a

2.4 Other ensemble learners

In addition to super ensemble learning, we applied the equal weight combiner by assigning a uniform weighting scheme (i.e. weights equal to 1/10) to all base-learners. Furthermore, we used an ensemble learner (referred to as best learner), which selects the best base-learner based on its performance in the k-fold cross-validation procedure in the training set.

2.5 Variable selection

Variable selection constitutes a complex problem that has been extensively investigated with no exact solution (see, for example, [40]) as selection of variables is strictly linked to the problem at hand. In daily streamflow forecasting, daily streamflow qi may depend on past streamflow, precipitation and temperature values (qj, pj, tj, j = 1, …, i – 1, respectively). Past precipitation and temperature values are exogenous predictor variables in our problem. If non-informative predictor variables are included in the model, the performance of some algorithms (e.g. linear regression) may decrease considerably, while if too many predictor variables are included, the computational burden may become prohibitive. Missing some informative predictor variables may also harm the performance of the model.

Several strategies can be employed to select predictor variables, e.g. an exhaustive search [84], use of correlation measures, partial mutual information [55] and the like. An overview of variable selection procedures in water resources engineering can be found in [13].

Here, we selected to use the permutation variable importance metric (VIM) used by random forests algorithms for variable selection. The permutation VIM measures the mean decrease in accuracy in the out-of-bag (OOB) sample by randomly permuting the predictor variable of interest. OOB samples are the samples remaining after bootstrapping the training set (see also Sect. 2.2.6). VIM permits ranking of the relative significance of predictor variables [85] and is a commonly used variable selection procedure. We computed VIM of daily values of streamflow, precipitation and temperature of the last month, i.e. 90 predictor variables in total. We selected the resulting five most important predictor variables for each process type (i.e. streamflow, precipitation and temperature). The fitting problem is formulated as:

$$q_{i} = f(\{ q_{j} ,p_{k} ,t_{l} ,\} ),j,k,l \in \{ {\text{five}}\;{\text{values}}\;{\text{in }}(i{-} \, 30, \ldots ,i{-} \, 1)\}$$
(1)

If some of the best ranked possible predictor variables display negative VIM values, they are excluded from the set of predictor variables, since they are non-informative (see, for example, [86] and references therein). In this case, the set of predictor variables includes less than 15 variables.

2.6 Training and testing

Machine learning algorithms in regression settings approximate the function f in Eq. (1) through training on data. During training, some hyperparameter optimization can be performed to enhance the performance of the model. However, default hyperparameter values used in software implementations usually display favourable properties, as, for example, proved in large-scale empirical studies in hydrology [64], while hyperparameter optimization may be computationally costly with little improvement in performance. That said, in the present study, we decided to use default hyperparameter values, as suggested in the corresponding software implementations (see “Appendix”).

Time series models are fitted in the training period using the automated procedure of the forecast R package. One-step-ahead forecasts are delivered in the testing period by using the estimated parameters during the training phase.

To estimate the generalization error of the implemented algorithms, one should compare to an independent set, i.e. a set not used for training, termed as test set. Following recent theoretical studies [4], we use training and test sets of equal size (i.e. each one corresponding to 50% of the full time series) to assess the performance of the algorithms.

2.7 Metrics

Although the super ensemble learner is optimized with respect to RMSE, we use multiple metrics to understand the effect of this optimization and quantitatively assess the relative performance of the algorithms. An overview of metrics that can be used to assess the performance of forecasting methods can be found in [42]. Here, we use RMSE, the mean of absolute errors (MAE), the median of absolute errors (MEDAE) and the squared correlation r2 between the forecasts fn and the observations on. All metrics, defined by the following equations, are computed in the testing period.

$$E_{n} : = f_{n} - o_{n}$$
(2)
$${\text{MAE}}: = \, \left( {1/|N|} \right) \, \sum\nolimits_{n} \left| {E_{n} } \right|$$
(3)
$${\text{RMSE : = ((1/|N|) }}\sum\nolimits_n {\text{E}}^{2} n )^{1/2}$$
(4)
$${\text{MEDAE}}: = {\text{ median}}_{n} \left\{ {|E_{n} |} \right\}$$
(5)
$$r^{2} : = \, \left( {{\text{corr}}\left( \varvec{{f,o}} \right)} \right)^{2}$$
(6)

In Eq. (6), f and o denote the vectors of the forecasts and observations, respectively, in the testing period. MAE, RMSE and MEDAE take values in the range [0, ∞), with 0 values indicating perfect forecasts. r2 takes values in the range [0, 1], with values equal to 1 denoting perfect forecasts.

Following relevant suggestions by [6], we do not use hypothesis tests to report the significance of the differences between forecasting performances of pairs of methods, as their use in the field of forecasting may lead to misinterpretations. Instead, we prefer to use “effect sizes”, as, for example, done in forecasting competitions [6], which in our case are “percent error reductions” in terms of a specified metric. Our choice also overcomes the problems of (a) computing significance of the forecasting performance differences between every pair of the implemented algorithms and (b) using some type of scaled metrics (e.g. the widely used in hydrology Nash–Suttcliffe efficiency) which is usually accompanied by other disadvantages.

3 Data and application

3.1 Data

We used CAMELS (Catchment Attributes and MEteorology for Large-sample Studies) dataset, which is used for benchmarking purposes in hydrology [61] and can be found online in [2, 59]. A detailed documentation of the dataset can be found in [3, 60]. The dataset includes daily minimum temperatures, maximum temperatures, precipitation and streamflow data from 671 small- to medium-sized basins in the contiguous US (CONUS). Temperature and precipitation time series for the needs of the analysis have been obtained by processing the daily dataset by [81]. The mean daily temperature was estimated by averaging the minimum and maximum daily temperatures. Changes in the basins due to human influences are minimal. Here, we focus on the 10-year period 2004–2013, while basins with missing data or other inconsistencies have been excluded. The final sample consists of 511 basins representing diverse climate types over CONUS; see Fig. 2.

Fig. 2
figure 2

The 511 basins over CONUS used in the study

Full size image

3.2 Implementation of methods

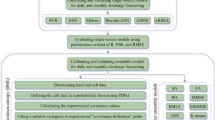
In what follows, we detail the implementation of the algorithms and their testing, while the workflow is presented in Fig. 3.

Fig. 3
figure 3

Workflow of the proposed practical system. Time periods in which the models are applied. T1 is the training period, while T2 is the testing period

Full size image
  1. a.

    The training and testing periods (hereafter denoted by T1 and T2, respectively) are set to T1 = {2004-01-01, …, 2008-12-31} and T2 = {2009-01-01, …, 2013-12-31}.

  2. b.

    For an arbitrary basin, random forests VIM approach (see Sect. 2.5) is applied in period T1 by using qj, pk, tl, j, k, l∈ {i−30, …, i−1) as predictor variables (90 predictor variables in total) and qi as dependent variable. The training sample includes 1827 instances, i.e. as many as the number of days in period T1. The five most important predictor variables for each process type (i.e. q, p, t) are selected based on their VIM values (see Sect. 2.5) and used for training of the algorithms. In the case, when less than five predictor variables have positive VIM values for a certain process type, the predictor variables with negative (or zero) VIM values are excluded and the number of the selected predictor variables reduces to less than 15. The selected predictor variables are used in the next steps.

  3. c.

    All algorithms of Sects. 2.2.1–2.2.10 are trained in period T1 in a fivefold cross-validation setting.

  4. d.

    The time series models of Sect. 2.1 are trained in period T1 using the procedure of the forecast R package.

  5. e.

    The super ensemble learner (composed by the ten base-learners of step (c); see Sect. 2.3) is also trained in period T1 using fivefold cross-validation. This is done by estimating the fivefold cross-validated risk for each base-learner in step (c) and computing its weight.

  6. f.

    The ten trained base-learners of step (c) are retrained in the full T1 period and predict streamflow in period T2. The testing sample includes 1826 instances, i.e. as many as the number of days in period T2.

  7. g.

    The super ensemble learner (which uses the estimated weights of step (e) and weights the retrained base-learners), the equal weight combiner (which averages the 10 retrained base-learners; see Sect. 2.4) and the best learner (i.e. the retrained base-learner with the least fivefold cross-validated risk in period T1; see Sect. 2.4 and step (c)) predict daily streamflow in period T2.

  8. h.

    The metrics of Sect. 2.7 are computed for each of the 15 algorithms (see steps (e) and (f)) in period T2.

  9. i.

    Finally, the metric values are summarized for all basins in period T2.

4 Results

Here, we summarize the predictive performance of the 15 algorithms in period T2 for the 511 basins. We present the rankings of the algorithms (Sect. 4.1) and their relative improvements with respect to the linear regression benchmark (Sect. 4.2). An investigation on the estimated weights of the super ensemble learner is also presented (Sect. 4.3).

4.1 Ranking of methods

Figure 4 presents the mean rankings of the 15 algorithms according to their performance in terms of the examined metrics. Rankings range from 1 to 15, with lower values indicating better performance. For instance, when examining an arbitrary basin, the 15 algorithms are ranked according to their performance in terms of each metric separately. Then, these rankings are averaged over all basins, conditional on the metric.

Fig. 4
figure 4

Mean rankings of the 15 algorithms according to their performance in the 511 basins

Full size image

Super ensemble learner is the best performing algorithm in terms of RMSE and MAE, and the second best algorithm in terms of MEDAE and r2; nonetheless, its difference from the best performing algorithm in terms of r2 (i.e. the equal weight combiner) is minimal. In terms of RMSE, the equal weight combiner is the second best performing algorithm, followed by the best learner. From the base-learners, neural networks, extremely randomized trees and loess are the best performing algorithms (ranked from best to worst) in terms of RMSE, while support vector machines are worse compared to the linear regression benchmark. It is remarkable that time series models seem to outperform some base-learners in terms of RMSE, although they do not exploit information from exogenous predictor variables. Two possible explanations are that: (a) temporal dependencies include rich information, which is exploited by time series models but not by regression algorithms, and (b) additional information introduced by exogenous variables is relatively limited.

When focusing on metrics other than RMSE, one sees that the rankings of the algorithms remain similar, albeit not identical. For instance, while MARS is not well performing in terms of RMSE, it is the best performing learner in terms of MEDAE, contrary to the equal weight combiner, which does not perform well.

Figure 5 presents the rankings of the 15 algorithms according to their performance in terms of RMSE for the 511 basins considered. While, in general, one sees similar rankings of an algorithm at all basins (i.e. similar colours dominate a given row), there are cases where the rankings of an algorithm vary with respect to its mean performance. Take, for instance, the super ensemble learner. While it is on average the best performing algorithm, there are cases where other algorithms perform better.

Fig. 5
figure 5

Rankings of the 15 algorithms according to their performance in terms of RMSE for the 511 basins considered

Full size image

4.2 Relative improvements

The median relative improvement introduced by each algorithm with respect to the linear regression benchmark is important for understanding whether a more flexible (yet less interpretable) algorithm is indeed worth implementing. In this context, Fig. 6 presents the percentage of decrease in the RMSE, MAE, MEDAE and r2 introduced by each of the 15 examined learners relative to that of the linear regression benchmark.

Fig. 6
figure 6

Median relative improvements of the 15 algorithms with respect to the linear regression benchmark in the 511 basins considered

Full size image

Focusing on RMSE, super ensemble learner improves over the performance of the linear regression algorithm by 20.06%. The improvement introduced by the equal weight combiner is equal to 19.21% (not negligible as well), followed by the best learner with relative improvement equal to 16.64%. The best base-learner is neural networks, which improves over the performance of the linear regression algorithm by 16.73%, followed by extremely randomized trees (16.4%), XGBoost (15.92%) and loess (15.36%).

An important note to be made here is that the specific ranking of an algorithm in terms of the improvement it introduces relative to the linear regression benchmark depends significantly on the metric used, i.e. RMSE, MAE, MEDAE and r2. For instance, while the equal weight combiner is the second best performing learner in terms of RMSE, MAE and r2, it is the fourth worst performing in terms of MEDAE. In addition, please note that the magnitudes of the relative improvements differ considerably for the various metrics. For instance, relative improvements in terms of MAE mostly range between 25 and 35%, while the respective relative improvements in terms of RMSE are mostly between 10 and 20%.

To facilitate understanding of the range of forecast errors, Fig. 7 presents boxplots of the RMSE values for all 15 algorithms considered. While in most cases the forecast errors lie below 5 mm/day, one sees that MARS and PolyMARS forecasts may fail considerably (see the exceptionally high outliers), and this is the case for neural networks as well. This form of instability could also explain why MARS is amongst the best performing methods in terms of MEDAE (a metric based on medians), while it appears to be less performing when assessed using metrics based on mean errors (i.e. RMSE, MAE and r2).

Fig. 7
figure 7

Boxplots of the RMSE values computed for the 15 algorithms in the 511 basins considered

Full size image

Values of r2 are also of interest. Close inspection of Fig. 8 reveals that the super ensemble learner and the equal weight combiner display values that lie mostly in the range 0.60–0.65, while the best learner exhibits somewhat lower values. The remainder base-learners display, in general, lower r2 values, while the mean r2 of linear regression is somewhat higher than 0.5.

Fig. 8
figure 8

Boxplot of the r2 values computed for the 15 algorithms in the 511 basins considered

Full size image

Figure 9 presents a comparison of the two best performing methods in terms of RMSE (left panel) and ranking (right panel) for each of the 511 considered basins. In terms of RMSE, the performances of the two methods seem similar, with the equal weight combiner being slightly more stable (see the few points lying above the 45° line). This behaviour should be attributed to the fact that, in some basins, the super ensemble learner may assign higher weights to inferior base-learners. Note, however, that based on Figs. 4 and 6, the median behaviour of the super ensemble learner is better than that of the equal weight combiner, and this is also observable in Fig. 9b, where the number of red points lying below the 45° line (a total of 313) is larger than those lying above (a total of 198). In other words, the super ensemble learner is ranked higher relative to the equal weight combiner in 313 out of the 511 basins considered.

Fig. 9
figure 9

Visual comparison between the equal weight combiner and the super ensemble learner, based on their performances in the testing set for each of the 511 basins considered (red points): a scatterplot of RMSEs. b Scatterplot with jitter of the ranking of the two methods (i.e. multiple co-located points are randomly displaced to appear as clusters (red points) around their exact location (black dots)) (color figure online)

Full size image

4.3 Weights

The weights of the base-learners (used to compose the super ensemble learner) are strongly linked to the performance of the 10 base-learners in the test set. This becomes apparent from Fig. 10, which presents the weights assigned to the 10 base-learners per basin. More precisely, close inspection of Fig. 10 alongside with Fig. 6 reveals that less performing algorithms in the test set are assigned smaller weights.

Fig. 10
figure 10

Weights assigned to the 10 base-learners in the 511 basins considered

Full size image

The boxplots in Fig. 11 also confirm the aforementioned observation/finding, i.e. that the best performing methods in the cross-validation set (i.e. methods that are assigned higher weights) are those displaying the highest performance in the test set (see also Fig. 6). The highest weights are assigned to XGBoost, which is one of the best performing algorithms.

Fig. 11
figure 11

Boxplot of the weights assigned to the 10 base-learners in the 511 basins considered

Full size image

The boxplots in Fig. 12 summarize results from all basins considered and present how the weights assigned to the base-learners composing the super ensemble learner are related to their individual rankings within the testing period. Clearly, the higher the weight, the better the performance of the algorithm in the testing period.

Fig. 12
figure 12

Boxplots of the weights assigned to the 10 base-learners conditional on their ranking in terms of RMSE

Full size image

5 Discussion

An advantage of super ensemble learning is that it can be optimized with respect to any loss function; in our case, this loss function was RMSE. Albeit base-learners may be designed to optimize other loss functions, a combination approach (such as the super ensemble learner proposed herein) may be useful to extract their advantages with respect to a specific loss function. In general, other loss functions could also be used for optimizing the super ensemble learner.

Regarding the usefulness of the proposed method, one should consider that it is fully automated and does not need any assumptions, since it exploits a k-fold cross-validation procedure (in contrast, for example, to Bayesian model averaging, which is widely used in hydrology).

In this paper, it is empirically shown that predictive performance improvements can be obtained by combining algorithms. We would like to emphasize that the simplest combination methods (best learner and simple averaging) resulted in significant improvements with respect to the exploited base-learners. Therefore, it is worth applying as many algorithms as possible, with the aim to further combine them. Moreover, it is empirically shown that the exploitation of exogenous predictor variables can lead to considerable improvements in forecasting performance (especially when forecasts are made by ensemble learning algorithms), relative to forecast schemes (e.g. ARIMA and exponential smoothing methods) that exclusively use past information.

Due to its automation, the super ensemble learner can be considered a practical system for hydrological time series forecasting based on available data. Furthermore, it can be integrated with weather forecasts of the exogenous variables of interest, which can be provided a day earlier and can be incorporated into the practical system. Perhaps, weather forecasts for the day of interest can provide significant information, in addition to observed data from previous days. Another extension of the practical system would be to use the full available information of precipitation and temperature from weather stations, instead of averaging this information over the basin area.

The results of the present study can improve understanding of the relative performance of the implemented base-learners and time series models when used for daily streamflow forecasting, while allowing for interpretations beyond the area of hydrological applications. Considering that many large datasets are available in hydrology and atmospheric sciences, information from these fields could benefit machine learning applications by facilitating better understanding of algorithmic properties.

6 Conclusions

We presented a new method for daily streamflow forecasting. This method is based on super ensemble learning. The introduced algorithm combines 10 base-learners and was compared to an equal weight combiner and a best learner (identified in the cross-validation procedure). We applied the algorithms to a dataset consisting of 511 river basins with 10 years of daily streamflow, precipitation and temperature. The machine learning algorithms modelled the relationship between next-day streamflow and daily streamflow, precipitation and temperature up to the present day.

The super ensemble learner improved over the performance of the linear regression benchmark by 20.06% in terms of the RMSE, while the respective improvements provided by the other ensemble learners were 19.21% (equal weight combiner) and 16.64% (best learner). The best base-learner was neural networks (16.73%), followed by extremely randomized trees (16.40%), XGBoost (15.92%), loess (15.36%), random forests (12.75%), polyMARS (12.36%), MARS (4.74%), lasso (0.11%) and support vector machines (− 0.45%). Exponential smoothing and ARIMA time series models improved over the linear regression benchmark by 13.89% and 8.77%, respectively.

All ensemble learners improved over the performance of the single base-learners. The performance of the super ensemble learner was somewhat higher than that of the equal weight combiner, which according to the “forecast combination puzzle” is a “hard to beat in practice” combination method. Consequently, we consider that the equal weight combiner can be effectively used as a benchmark for new combination methods, while super ensemble learning can result in better performances. One could claim that based on statistical tests, this difference may be insignificant; however, as mentioned by [6], these tests should be avoided when comparing forecasting methods, as they can be misleading.

We emphasize that our results are based on a big dataset comprising of 511 basins with 10 years of daily data each. Therefore, the reported relative improvements against the linear regression benchmark (i.e. in the range 0–20% in terms of RMSE, 0–35.5% in terms of MAE, 0–70% in terms of MEDAE and 0–21% in terms of r2) can be considered realistic and can provide insightful guidance in understanding whether results reported in the literature (e.g. single case studies indicating improvements more than 50% in terms of RMSE) could be attributed to chance related to the use of small datasets. Assessments based on big datasets can emulate neutral comparison studies, i.e. studies focusing on comparison rather than aiming to promote a single method [12].

Future research could focus on improving the variable selection procedure and comparing the ensemble learner with optimized base-learners, while testing on different datasets could be also useful. Furthermore, pre-processing approaches based on clustering techniques, as well as frameworks formulated in a reinforcement learning context (e.g. [50, 51, 53]), including spatial information (e.g. [52]), may improve the performance of the proposed practical system. Besides machine learning, other techniques (e.g. graphs [38]) can also be tested in such problems. An additional topic of potential interest is to compare super ensemble learning with other combination methods, e.g. Bayesian model averaging or stacking using more flexible combiners.