Univariate Time Series Forecasting of Temperature and Precipitation with a Focus on Machine Learning Algorithms: a Multiple-Case Study from Greece

Abstract

We provide contingent empirical evidence on the solutions to three problems associated with univariate time series forecasting using machine learning (ML) algorithms by conducting an extensive multiple-case study. These problems are: (a) lagged variable selection, (b) hyperparameter handling, and (c) comparison between ML and classical algorithms. The multiple-case study is composed by 50 single-case studies, which use time series of mean monthly temperature and total monthly precipitation observed in Greece. We focus on two ML algorithms, i.e. neural networks and support vector machines, while we also include four classical algorithms and a naïve benchmark in the comparisons. We apply a fixed methodology to each individual case and, subsequently, we perform a cross-case synthesis to facilitate the detection of systematic patterns. We fit the models to the deseasonalized time series. We compare the one- and multi-step ahead forecasting performance of the algorithms. Regarding the one-step ahead forecasting performance, the assessment is based on the absolute error of the forecast of the last monthly observation. For the quantification of the multi-step ahead forecasting performance we compute five metrics on the test set (last year’s monthly observations), i.e. the root mean square error, the Nash-Sutcliffe efficiency, the ratio of standard deviations, the coefficient of correlation and the index of agreement. The evidence derived by the experiments can be summarized as follows: (a) the results mostly favour using less recent lagged variables, (b) hyperparameter optimization does not necessarily lead to better forecasts, (c) the ML and classical algorithms seem to be equally competitive.

1 Introduction

1.1 Background Information

Machine learning (ML) algorithms are widely used for the forecasting of univariate geophysical time series as an alternative to classical algorithms. Popular ML algorithms are the rather well-established Neural Networks (NN) and the new-entrant in most scientific fields Support Vector Machines (SVM). The latter algorithm has been presented in its current form by Cortes and Vapnik (Cortes and Vapnik 1995; see also Vapnik 1995, Vapnik 1999). The large number and wide range of the relevant applications is apparent in the review papers of Maier and Dandy (2000), and Raghavendra and Deka (2014) respectively. The competence of ML algorithms in univariate time series forecasting has been empirically proven in Papacharalampous et al. (2017a), and Tyralis and Papacharalampous (2017) through extensive simulation experiments.

Nevertheless, univariate time series forecasting using ML algorithms also implies the handling of specific factors that may improve or deteriorate the performance of the algorithms, i.e. the lagged variables and the hyperparameters. In contrast to the typical regression problem, in a forecasting problem the set of predictor variables is a set of lagged variables, formed using observed past values of the process to be forecasted and, consequently, holding information about the temporal dependence. Although the amount of the available historical information taken into account increases when using a large number of lagged variables, the length of the fitting set concomitantly decreases; for more details, see Tyralis and Papacharalampous (2017). While there is a wide literature on applications of ML algorithms in hydrological univariate time series forecasting, mainly comprising single- or few-case studies that particularly focus on details about the model structure (e.g. Atiya et al. 1999; Guo et al. 2011; Hong 2008; Kumar et al. 2004; Moustris et al. 2011; Ouyang and Lu 2017; Sivapragasam et al. 2001; Wang et al. 2006), studies explicitly stating information concerning the variable selection issue, such as Belayneh et al. (2014), Nayak et al. (2004), Hung et al. (2009) and Yaseen et al. (2016), are less. Tyralis and Papacharalampous (2017) have investigated the effect of a sufficient number of lagged variable selection choices on the performance of the Breiman’ s random forests algorithm (Breiman 2001) in one-step ahead univariate time series forecasting.

On the other hand, information on the hyperparameter selection is usually emphasized in the hydrological literature (e.g. Belayneh et al. 2014; Hung et al. 2009; Koutsoyiannis et al. 2008; El-Shafie et al. 2007; Tongal and Berndtsson 2017; Valipour et al. 2013; Yu et al. 2004). An example of a hyperparameter is the number of hidden nodes within a neural networks structure. Hyperparameters are distinguished from the basic parameters, because they are usually optimized or tuned with the aim to improve the performance of a ML algorithm. Hyperparameter optimization can be performed using a single validation set extracted from the fitting set or k-fold cross-validation, which involves multiple set divisions and tests. The optimal hyperparameter values are most frequently searched heuristically, either using grid search or random search, while ML or Bayesian methods can be adopted for this task as well (Witten et al. 2017). However, non-tuned ML models are also used in hydrology (e.g. Yaseen et al. 2016). Finally, a popular problem arising when using ML forecasting algorithms is the comparison between ML and classical algorithms. This problem is mostly examined within single-case studies (e.g. Ballini et al. 2001; Koutsoyiannis et al. 2008; Tongal and Berndtsson 2017; Valipour et al. 2013; Yu et al. 2004), as applying to lagged variable and hyperparameter selection as well.

1.2 Main Contribution of this Study

The main contribution of this study is the exploration in geoscience concepts of the problems presented in detail in Section 1.1 and summarized here below, together with their related research questions of focus:

• Problem 1: Lagged variable selection in time series forecasting using ML algorithms

• Research question 1: Should we select less recent lagged variables or a large number of lagged variables in time series forecasting using ML algorithms?

• Problem 2: Hyperparameter selection in time series forecasting using ML algorithms

• Research question 2: Does hyperparameter optimization necessarily lead to a better performance in time series forecasting using ML algorithms?

• Problem 3: Comparison between ML and classical algorithms

• Research question 3: Do the ML algorithms exhibit better (or worse) performance than the classical ones?

In fact, exploration is indispensable for understanding the phenomena involved in a specific problem and, therefore, it constitutes an essential part within every theory-development process.

1.3 Research Method and Implementation

We adopt the multiple-case study research method (presented in detail in Yin (2003)), which embraces the examination of more than one individual cases, facilitating the observation of specific phenomena from multiple perspectives or within different contexts (Dooley 2002). For the detection of systematic patterns across the individual cases a cross-case synthesis can be performed (Larsson 1993). Given the fact that the boundaries between the phenomena and the context are not clear (thus, it is meaningful to consider a case study design, as explained in Baxter and Jack (2008)), it is important that each individual case keeps its identity within the multiple-case study, so that one can specifically focus on it. This exploration within and across the individual cases can provide interesting insights into the phenomena under investigation, as well as a form of generalization named “contingent empirical generalization”, while retaining the immediacy of the single-case study method (Achen and Snidal 1989).

We explore the three problems summarized in Section 1.2 by conducting an extensive multiple-case study composed by 50 single-case studies, which use temperature and precipitation time series observed in Greece. We examine these two geophysical processes, because they exhibit different properties, which may affect differently the results within the explorations. We focus on two ML algorithms, i.e. NN and SVM, for an analogous reason. Moreover, the explorations are conducted for the one- and a multi-step ahead horizons, as their corresponding forecasting attempts are not of the same difficulty. We apply a fixed methodology to each individual case. This fixed methodology provides the common basis to further perform a cross-case synthesis for the detection of systematic patterns across the individual cases. The latter is the novelty of our study.

2 Data and Methods

2.1 Methodology Outline

We conduct 50 single-case studies by applying a fixed methodology to each of the 50 time series presented in Section 2.2, as explained subsequently. First, we split the time series into a fitting and a test set. The latter is the last monthly observation for the one-step ahead forecasting experiments and the last year’s monthly observations for the multi-step ahead forecasting experiments. Second, we fit the models to the seasonally decomposed fitting set, within the context described in Section 2.3, and make predictions corresponding to the test set. Third, we recover the seasonality in the predicted values and compare them to their corresponding observed using the metrics of Section 2.4. Finally, we perform a cross-case synthesis to demonstrate similarities and differences between the single-case studies conducted. We present the results per category of tests, which is determined by the set {set of methods, process, forecast horizon}, and further summarize them, as discussed in Section 2.4. The sets of methods are defined in Section 2.3, while the total number of categories is 20. We place emphasis on the exploration of the three problems summarized in Section 1.2, but we also present quantitative information about the produced forecasts and search for evidence regarding the existence of a possible relationship between the forecast quality, and the standard deviation (σ), coefficient of variation (cv) and Hurst parameter (H) estimates for the deseasonalized time series (available in Section 2.2). Statistical software information is summarized in the Appendix section.

2.2 Time Series

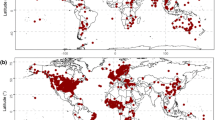
We use 50 time series of mean monthly temperature and total monthly precipitation observed in Greece. These time series are sourced from Lawrimore et al. (2011), and Peterson and Vose (1997) respectively. We select only those with few missing values (blocks with length equal or less than one). Subsequently, we use the Kalman filter algorithm of the zoo R package (Zeileis and Grothendieck 2005) for filling in the missing values. The basic information about the time series is provided in Table 1, while Fig. 1 presents the locations of the stations at which the data has been recorded. We use the deseasonalized fitting sets for fitting the forecasting models, as suggested in Taieb et al. (2012) for the improvement of the forecast quality. The time series decomposition is performed exclusively on the fitting sets using the multiplicative model for the temperature time series and the additive model for the precipitation ones. The reason for this differentiation is that the use of the multiplicative model on the precipitation time series results in zero forecasts for some methods, as a result of zero precipitation observations in the summer months.

Table 1 Time series of the present study

Fig. 1

Maps of the locations of the (a) temperature and (b) precipitation stations; their sources are Lawrimore et al. (2011), and Peterson and Vose (1997) respectively

We also apply the time series decomposition models to the entire time series to deseasonalize them. We then estimate the mean (μ), σ and H parameters of the Hurst-Kolmogorov process for each of the seasonally decomposed entire time series using the maximum likelihood estimator (Tyralis and Koutsoyiannis 2011) implemented via the HKprocess R package (Tyralis 2016). We further estimate cv, which is defined by Eq. 1. The μ, σ, cv and H estimates are presented in Tables 2 and 3. The Hurst parameter is assumed to be informative about the magnitude of long-range dependence observed in geophysical time series.

$$ \mathrm{cv}:= \sigma /\mu $$

(1)

Table 2 Mean (μ), standard deviation (σ), coefficient of variation (cv) and Hurst parameter (H) estimates for the deseasonalized temperature time series

Table 3 Mean (μ), standard deviation (σ), coefficient of variation (cv) and Hurst parameter (H) estimates for the deseasonalized precipitation time series

2.3 Forecasting Algorithms and Methods

We focus on two ML forecasting algorithms, i.e. NN and SVM. The NN algorithm is the mlp algorithm of the nnet R package (Venables and Ripley 2002), while the SVM algorithm is the ksvm algorithm of the kernlab R package (Karatzoglou et al. 2004). These algorithms implement a single-hidden layer Multilayer Perceptron (MLP), and the Radial Basis kernel “Gaussian” function with C = 1 and epsilon = 0.1 respectively. Their application is made using the CasesSeries, fit and lforecast functions of the rminer R package (Cortez 2010, 2016). We also include four classical algorithms, i.e. the Autoregressive order one model (AR(1)), an algorithm from the family of Autoregressive Fractionally Integrated Moving Average models (auto_ARFIMA), the exponential smoothing state space algorithm with Box-Cox transformation, ARMA errors, Trend and Seasonal Components (BATS) and the Theta algorithm, and a naïve benchmark in the comparisons. The latter sets each monthly forecast equal to its corresponding last year’s monthly value. We apply the classical algorithms using the forecast R package (Hyndman and Khandakar 2008; Hyndman et al. 2017) and, specifically, five functions included in the latter, namely the Arima, arfima, bats, forecast and thetaf functions. The auto_ARFIMA algorithm applies the Akaike Information Criterion with a correction for finite sample sizes (AICc) for the estimation of the p, d, q values of the ARFIMA(p,d,q) model, while both the AR(1) and auto_ARFIMA algorithms implement the maximum likelihood method for the estimation of the ARMA parameters. The auto_ARFIMA algorithm considers the long-range dependence observed in the time series through the d parameter. The AR(1), auto_ARFIMA and BATS algorithms apply Box-Cox transformation to the input data before fitting a model to them. All the algorithms used herein are well-grounded in the literature; thus, in their presentation we place emphasis on implementation information.

While the classical methods are simply defined by the classical algorithm, the ML methods are defined by the set {ML algorithm, hyperparameter selection procedure, lags}. We compare 21 regression matrices, each using the first n time lags, n = 1, 2, …, 21, and two procedures for hyperparameter selection, i.e. predefined hyperparameters (default values of the algorithms) or defined after optimization. The symbol * in the name of a ML method is hereafter used to denote that the model’s hyperparameters have been optimized. The hyperparameter optimization is performed with the grid search method using a single validation set (last 1/3 of the deseasonalized fitting set). The hyperparameters optimized are the number of hidden nodes and the number of variables randomly sampled as candidates at each split of the NN and SVM models respectively. For the NN* method the hyperparameter optimization procedure is described subsequently. First, we fit 16 different NN models (defined by the grid values 0, …, 15) to the fist 2/3 of the deseasonalized fitting set. Second, we use these models to produce forecasts corresponding to the validation set. Third, we select the one exhibiting the smallest root mean square error (RMSE) on the validation set. To produce the forecast corresponding to the test set we further fit the selected model to the whole deseasonalized fitting set. For the SVM* method the procedure is the same, except that the candidate models are five (defined by the grid values 1, … 5). Hereafter, we consider that the ML models are used with predefined hyperparameters and that the regression matrix is built using only the first lag, unless mentioned differently. We use the sets of methods defined in Table 4. Each of them has a specific utility within our experiments, which is also reported in Table 4. A secondary utility of set of methods no 5 is the investigation of the existence of a possible relationship between the forecast quality and the parameter estimates for the deseasonalized time series.

Table 4 Sets of methods and their main utility within this study

2.4 Metrics and Summary Statistics

The one-step ahead forecasting performance is assessed by computing the absolute error (AE) of the forecast, while the multi-step ahead forecasting performance by computing the RMSE, the Nash-Sutcliffe efficiency (NSE), the ratio of standard deviations (rSD), the index of agreement (d) and the coefficient of correlation (Pr). Subsequently, we provide the definitions of the five latter metrics. For these definitions we consider a time series of N values. Let us also consider a model fitted to the first N−n values of this specific time series and subsequently used to make predictions corresponding to the last n values. Let x₁, x₂, …, x_n represent the last n values and f₁, f₂, …, f_n represent the forecasts.

The RMSE metric is defined by

$$ \mathrm{RMSE}:= {\left(\left({\sum}_{i=1}^n{\left({f}_i-{x}_i\right)}^2\right)/n\right)}^{1/2} $$

(2)

It can take values between 0 and +∞. The closer to 0 it is, the better the forecast.

Let $\overline{x}$ be the mean of the observations, which is defined by

$$ \overline{x}:= \left(1/n\right){\sum}_{i=1}^n{x}_i $$

(3)

The NSE metric is defined by (Nash and Sutcliffe 1970)

$$ \mathrm{NSE}:= 1-\left({\sum}_{i=1}^n{\left({f}_i-{x}_i\right)}^2/{\sum}_{i=1}^n{\left({x}_1-\overline{x}\right)}^2\right) $$

(4)

It can take values between −∞ and 1. The closer to 1 it is, the better the forecast, while NSE values above 0 indicate acceptable forecasts.

Let s_x be the standard deviation of the observations, which is defined by

$$ {s}_x:= {\left(\left(1/\left(n-1\right)\right){\sum}_{i=1}^n{\left({x}_i-\overline{x}\right)}^2\right)}^{1/2} $$

(5)

Let $\overline{f}$ be the mean of the forecasts and s_f be the standard deviation of the forecasts, which are defined by Eqs. (6) and (7) respectively.

$$ \overline{f}:= \left(1/n\right){\sum}_{i=1}^n{f}_i $$

(6)

$$ {s}_f:= {\left(\left(1/\left(n-1\right)\right){\sum}_{i=1}^n{\left({f}_i-\overline{f}\right)}^2\right)}^{1/2} $$

(7)

The rSD metric is defined by Zambrano-Bigiarini (2017a)

$$ \mathrm{rSD}:= {s}_f/{s}_x $$

(8)

It can take values between 0 and +∞. The closer to 1 it is, the better the forecast.

The Pr metric is defined by (Krause et al. 2005)

$$ \Pr := \left({\sum}_{i=1}^n\left({x}_i-\overline{x}\right)\left({f}_i-\overline{f}\right)\right)/{\left({\sum}_{i=1}^n{\left({x}_i-\overline{x}\right)}^2{\sum}_{i=1}^n{\left({f}_i-\overline{f}\right)}^2\right)}^{1/2} $$

(9)

It can take values between −1 and 1. The closer to 1 it is, the better the forecast.

The d metric is defined by (Krause et al. 2005)

$$ d:= 1-\left({\sum}_{i=1}^n{\left({f}_i-{x}_i\right)}^2/{\sum}_{i=1}^n{\left(|{f}_i-\overline{x}|+|{x}_i-\overline{x}|\right)}^2\right) $$

(10)

It can take values between 0 and 1. The closer to 1 it is, the better the forecast.

To summarize the results of the multiple-case study we compute some summary statistics for the values of each metric, i.e. the minimum, median and maximum, separately for each algorithm. For the ML ones, these summary statistics are computed by aggregating the total of the values of each metric computed for methods that are based on each specific ML algorithm (tested for the exploration of Problems 1, 2 or 3). We also compute the linear regression coefficient (LRC) for each method per category of tests. This summary statistic can be used to measure the dependence of the forecasts f_j on their corresponding target values x_j, when this dependence is expressed by the following linear regression model:

$$ {f}_j=\left(\mathrm{LRC}\right)\ {x}_j+b $$

(11)

It can take values between −∞ and +∞. The closer to 1 it is, the better the forecasts. The subscript j in the above notations indicates the serial number of each of the pairs {forecast, target value} formed for a specific category of tests.

3 Results and Discussion

In Section 3 we present and discuss the results of our multiple-case study. We place emphasis on the qualitative presentation of the results, because of its importance in the exploration of the research questions of Section 1.2. Especially the heatmap visualization adopted herein allows the examination of each single-case study alone and in comparison to the rest simultaneously. Quantitative information, derived by our multiple-case study and particularly significant for the case of Greece, is also presented. Regarding this type of information, the present study could be viewed as an expansion of Moustris et al. (2011). The latter study has focused on four long precipitation time series observed in Alexandroupoli, Athens, Patra and Thessaloniki (a subset of the time series examined within our multiple-case study), with the aim to present forecasts for the monthly maximum, minimum, mean and cumulative precipitation totals using NN methods.

3.1 Exploration of Problem 1

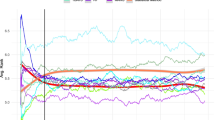
Section 3.1 is devoted to the exploration of Problem 1. In Figs. 2 and 3 we visualize the one and twelve-step ahead temperature forecasts respectively, produced for this exploration for the NN and SVM algorithms, in comparison to their corresponding target values. We observe that, for a specific target value, the forecasts are more scattered (in the vertical direction) for the NN algorithm than they are for the SVM algorithm. This fact indicates that the performance of the SVM algorithm is affected less than the performance of the NN algorithm by changes in the lagged regression matrix used in the fitting process. The effect under discussion may result in more or less accurate NN forecasts (laying closer or farther from the 1:1 line included in the scatterplots of Figs. 2 and 3) than the ones produced by the SVM algorithm. Evidence that the NN algorithm is more prone to changes in the regression matrix than the SVM one is provided by the tests conducted using the precipitation time series as well. In Fig. 4 we present the twelve-step ahead precipitation forecasts in comparison to their corresponding target values.

Fig. 2

One-step ahead temperature forecasts, produced for the exploration of Problem 1 for the (a) NN and (b) SVM algorithms, in comparison to their corresponding target values

Fig. 3

Twelve-step ahead temperature forecasts, produced for the exploration of Problem 1 for the (a) NN and (b) SVM algorithms, in comparison to their corresponding target values

Fig. 4

Twelve-step ahead precipitation forecasts, produced for the exploration of Problem 1 for the (a) NN and (b) SVM algorithms, in comparison to their corresponding target values

More importantly, in Figs. 5 and 6 we comparatevely present the AE, RMSE, NSE and d values computed for the temperature forecasts, produced for the exploration of Problem 1 for the NN and SVM algorithms, for each individual case examined. By the examination of these two figures we observe the following:

• (a) There are variations in the results across the individual cases, to an extent that it is impossible to decide on a best or worst method. Therefore, no evidence is provided by the respective categories of tests that any of the compared lagged regression matrices systematically leads to better forecasts than the rest, either for the NN or the SVM algorithms.

• (b) The heatmaps formed for the SVM algorithm are smoother in the row direcion than those formed for the NN algorithm, a fact rather expected from Figs. 2 and 3. In other words, the variations within each single-case study are of small magnitude for the case of the SVM algorithm, while they are significant for the NN algorithm.

• (c) For the SVM algorithm there are no systematic patterns and the small variations seem to be rather random.

• (d) For the NN algorithm and especially for the twelve-step ahead forecasts the left parts of the heatmaps are smoother with no white cells. Alternatively worded, it seems that is is more likely that the forecasts are better when using less recent lagged variables in conjuction with this algorithm.

Fig. 5

Cross-case synthesis for the exploration of Problem 1 for the NN and SVM algorithms using the temperature time series (part 1)

Fig. 6

Cross-case synthesis for the exploration of Problem 1 for the NN and SVM algorithms using the temperature time series (part 2)

Observation (a) is particularly important, because it reveals that the forecast quality is subject to limitations. Each forecasting method has some specific theoretical properties and, due to the latter, it performs better or worse than other forecasting methods, depending on the case examined. Even forecasting methods based on the same algorithm can produce forecasts with very different quality, as indicated by the results obtained for the NN algorithm. Observation (d), on the other hand, provides some interesting evidence, which however is contigent and, therefore, should be further investigated within larger forecast-comparing studies, such as Tyralis and Papacharalampous (2017). Furthermore, in Fig. 7 we present the AE and RMSE values computed for the precipitation forecasts, produced for the exploration of Problem 1 for the NN and SVM algorithms, within each single-case study. Observations (a) and (b) apply here as well. Moreover, both the ML algorithms, seem to perform rather better, to a small extent though, when given a lagged regression matrix using less recent lags.

Fig. 7

Cross-case synthesis for the exploration of Problem 1 for the NN and SVM algorithms using the precipitation time series

3.2 Exploration of Problem 2

Section 3.2 is devoted to the exploration of Problem 2. In Fig. 8 we present the twelve-step ahead precipitation forecasts, produced for this exploration for the NN and SVM algorithms, in comparison to their corresponding target values. Figure 8 could be studied alongside with Fig. 4, providing contingent evidence that hyperparameter optimization affects less the performance of these two ML algorithms than lagged variable selection does. The latter observation applies more to the NN algorithm. Furthermore, in Fig. 9 we comparatively present the AE, RMSE, rSD and d values computed for the one- and twelve-step ahead temperature forecasts, produced for the exploration of Problem 2, within each single-case study. By the examination of Fig. 9 we observe the following:

• (a) Here as well, none of the compared methods seems to be systematically better across the individual cases examined. In other words, the results do not systematically favour any of the two tested hyperparameter selection procedures and, therefore, we can state that hyperparameter optimization does not necessarily lead to better forecasts than the use of the default values of the algorithms.

• (b) For both the ML algorithms the observed variations within each of the single-case studies are of smaller magnitude for the one-step ahead forecasts than they are for the twelve-step ahead ones.

• (c) For the case of the NN algorithm the twelve-step ahead forecasts seem to be rather better when hyperparameter optimization precedes the fitting process, while the opposite applies to the case of the SVM algorithm.

Fig. 8

Twelve-step ahead precipitation forecasts, produced for the exploration of Problem 2 for the NN and SVM algorithms, in comparison to their corresponding target values

Fig. 9

Cross-case synthesis for the exploration of Problem 2 for the NN and SVM algorithms using the temperature time series

Finally, in Fig. 10 we present the AE, NSE, rSD and d values computed for the one- and twelve-step ahead precipitation forecasts, produced for the exploration of Problem 2, within each single-case study. Observation (a) also applies to the precipitation forecasts, while the variations can be significant for both the one- and twelve-step ahead forecasts. For the latter it seems that hyperparameter optimization mostly leads to less accurate forecasts. This may be explained by the fact that the default values of the algorithms are usually set based on tests performed by their developers or in the scientific literature, so that the performance of the algorithms is mostly maximized for a variety of problems.

Fig. 10

Cross-case synthesis for the exploration of Problem 2 for the NN and SVM algorithms using the precipitation time series

3.3 Exploration of Problem 3

Section 3.3 is devoted to the exploration of Problem 3. In Fig. 11 we present the one- and twelve-step ahead temperature forecasts, produced for this exploration, in comparison to their corresponding target values, while in Fig. 12 we present an analogous visualization for the precipitation forecasts serving the same purpose. Moreover, in Figs. 13 and 14 we comparatively present all the metric values computed for the temperature forecasts and the AE, RMSE and d values computed for the precipitation forecasts respectively within each single-case study. By the examination of these four figures we observe the following:

• (a) Here as well, the results of the single-case studies vary significantly.

• (b) The best method within a specific single-case study depends on the criterion of interest. In fact, even within a specific single-case study, we cannot decide on one best (or worst) method regarding all the criteria set simultaneously.

• (c) Observations (a) and (b) apply equally to the ML and the classical methods. In fact, it seems that both categories can rarther perform equally well, under the same limitations.

• (d) We observe that the Naïve benchmark, competent as well, frequently produces far different forecasts than those produced by the ML or classical algorithms.

Fig. 11

(a) One- and (b) twelve-step ahead temperature forecasts, produced for the exploration of Problem 3, in comparison to their corresponding target values

Fig. 12

(a) One- and (b) twelve-step ahead precipitation forecasts, produced for the exploration of Problem 3, in comparison to their corresponding target values

Fig. 13

Cross-case synthesis for the exploration of Problem 3 using the temperature time series

Fig. 14

Cross-case synthesis for the exploration of Problem 3 using the precipitation time series

If we further compare Figs. 11a, b and 12 with Figs. 2, 3 and 4 respectively, we observe that the performance of the NN algorithm (when given the 21 regression matrices examined in the present study) can vary more than the performance of the here compared ML and classical methods. This observation does not apply to the case of the SVM algorithm. Finally, we note that the exploration presented in Section 3.3 and Papacharalampous et al. (2017a) effectively complement each other. In fact, the former illustrates and provides evidence on important points by presenting real-world results, while the latter confirms the evidence derived by the former by conducting simulation experiments of large scale. Both illustration and confirmation are integral parts of every theory-building process.

3.4 Additional Information

Section 3.4 is devoted to some additional worth-discussed information derived by our multiple-case study. In fact, the results produced mainly for the exploration of Problems 1, 2 and 3 can also be examined from different points of view, which are considered of secondary importance within this study. In Tables 5 and 6 we present the summary statistics of the metric values, separately for each algorithm, and in Table 7 the LRC values for each category of tests. This information stands as a summary of the quantitative information provided by our multiple-case study and, together with Figs. 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, and 14, can facilitate the below discussion in a satisfactory manner. Regarding an overall assessment of the algorithms, they are all found to mostly have a better average-case forecasting performance than the Naïve benchmark, with the NN algorithm being the worst. This is due to the reported high effect of the lagged regression matrix on the performance of this algorithm. On the contrary, the SVM algorithm has a better average-case performance, (almost) as good as the one of the best-performing classical algorithms, i.e. BATS, Theta and auto_ARFIMA.

Table 5 Summary statistics of the metric values computed for the temperature forecasts. The values reported for the NN and SVM algorithms are computed for the total of the NN and SVM methods implemented in this study respectively

Table 6 Summary statistics of the metric values computed for the precipitation forecasts. The values reported for the NN and SVM algorithms are computed for the total of the NN and SVM methods implemented in this study respectively

Table 7 LRC values computed for each category of tests

The reported values of the summary statistics, as well as Figs. 2, 3, 4, 8, 11 and 12, reveal that the temperature forecasts are remarkably better than the precipitation ones. This may be explained by the cv estimates presented in Tables 2 and 3. Finally, in Fig. 15 we visualize the AE values computed for the one-step ahead temperature forecasts, produced using the set of methods no 5 of Table 4, in comparison to their corresponding σ, cv and H estimates for the deseasonalized time series (presented in Table 2), while in Figs. 16 and 17 we present an analogous visualization for the AE values computed for the one-step ahead precipitation forecasts and the RMSE values computed for the twelve-step ahead precipitation forecasts respectively, produced for the exploration of Problem 3. The estimated parameters for the deseasonalized precipitation time series are presented in Table 3. These figures are representative of the conducted investigation of the existence of a possible relationship between the forecast quality and the estimated parameters for the deseasonalized time series and provide no evidence of such existence either for temperature or precipitation. This fact may be related to our methodological framework and, in particular, to the way that we handle seasonality to produce better forecasts.

Fig. 15

AE values of the one-step ahead temperature forecasts, produced by set of methods no 5 (see Table 4), in comparison to the σ, cv and H estimates

Fig. 16

AE values of the one-step ahead precipitation forecasts, produced by set of methods no 5 (see Table 4), in comparison to the σ, cv and H estimates

Fig. 17

RMSE values of the twelve-step ahead precipitation forecasts, produced by set of methods no 5 (see Table 4), in comparison to the σ, cv and H estimates

4 Summary and Conclusions

We have examined 50 mean monthly temperature and total monthly precipitation time series observed in Greece by applying a fixed methodology to each of them and, subsequently, by performing a cross-case synthesis. The main aim of this multiple-case study is the exploration of three problems associated with univariate time series forecasting using machine learning algorithms, i.e. the (a) lagged variable selection, (b) hyperparameter selection, and (c) comparison between machine learning and classical algorithms. We also present quantitative information about the quality of the forecasts (particularly important for the case of Greece) and search for evidence regarding the existence of a possible relationship between the forecast quality, and the standard deviation, coefficient of variation and Hurst parameter estimates for the deseasonalized time series (used for model-fitting). We have focused on two machine learning algorithms, i.e. neural networks and support vector machines, while we have also included four classical algorithms and a naïve benchmark in the comparisons. We have assessed the one- and twelve-step ahead forecasting performance of the algorithms.

The findings suggest that forecasting methods based on the same machine learning algorithm may exhibit very different performance, to an extent mainly depending on the algorithm and the individual case. In fact, the neural networks algorithm can produce forecasts of many different qualities for a specific individual case, in contrast to the support vector machines one. The performance of the former algorithm seems to be more affected by the selected lagged variables than by the adopted hyperparameter selection procedure (use of predefined hyperparameters or defined after optimization). While no evidence is provided that any of the compared lagged regression matrices systematically leads to better forecasts than the rest, either for the neural networks or the support vector machines algorithms, the results mostly favour using less recent lagged variables. Furthermore, for the algorithms used in the present study hyperparameter optimization does not necessarily lead to better forecasts than the use of the default hyperparameter values of the algorithms. Regarding the comparisons performed between machine learning and classical algorithms, the results indicate that methods from both categories can perform equally well, under the same limitations. The best method depends on the case examined and the criterion of interest, while it can be either machine learning or classical. Some information of secondary importance derived by our experiments is subsequently reported. The average-case performance of the algorithms used to produce one- and twelve-step ahead monthly temperature forecasts ranges between 0.66 °C and 1.00 °C, and 1.14 °C and 1.70 °C, in terms of absolute error and root mean square error respectively. For the monthly precipitation forecasts the respective values are 39 mm and 72 mm, and 41 mm and 52 mm. Finally, no evidence is provided by our multiple-case study that there is any relationship between the forecast quality and the estimated parameters for the deseasonalized time series.

Appendix Statistical software

The analyses and visualizations have been performed in R Programming Language (R Core Team 2017) by using the contributed R packages devtools (Wickham and Chang 2017), forecast (Hyndman and Khandakar 2008; Hyndman et al. 2017), fracdiff (Fraley et al. 2012), gdata (Warnes et al. 2017), ggplot2 (Wickham 2016), HKprocess (Tyralis 2016), hydroTSM (Zambrano-Bigiarini 2017b), kernlab (Karatzoglou et al. 2004), knitr (Xie 2014, 2015, 2017), maps (Brownrigg et al. 2017), nnet (Venables and Ripley 2002), readr (Wickham et al. 2017), rminer (Cortez 2010, 2016), tidyr (Wickham and Henry 2017) and zoo (Zeileis and Grothendieck 2005).