1 Introduction

Constructing a neural network model to mimic the human brain is an important potential applications in the future. In the past decades, there were many researchers paying attention to the investigations of neural networks [1–5]. For example, the authors studied the properties of cellular neural networks in [1]. In [2, 3], the authors investigated the second-order dynamic consensus of multi-agent network systems. The authors discussed the linear programming problem of a recurrent neural networks in [4]. Hu and Wang [5] constructed a memristor-based neural network model with time delays by exploring a piecewise-linear mathematical model of the memristor to characterize its feature of pinched hysteresis. In these studies, the dynamical behaviors of neural networks are very important research fields. For instance, the authors investigated the attractivity of memristor-based delayed cellular neural networks in [6]. In [7], the authors studied the exponential stability of memristive neural networks. The consensus of multi-agent network systems has been investigated in [8–10].

Since the delayed neural networks may undergo abrupt changes arising from unexpected internal or external effects, it is necessary to study the dynamical behaviors of impulsive control neural networks. In [11–13], the synchronization problems of complex dynamical networks with delays were studied via impulsive distributed control. Recently, the stability of impulsive differential equations has been widely investigated [14–18]. For instance, in [14, 15], the stability of impulsive delayed neural networks was investigated by means of differential inequality. The authors in [16] studied the robust exponential stability of delayed neural networks with parameter uncertainties, stochastic perturbation, and impulses. Chen and Zhang [17] investigated the global exponential stability of impulsive neural networks with variable delay by means of an LMI approach. In [18], the authors studied the stability of high-order BAM neural networks with time delays and impulse effects. All these results are about the case of time-triggered impulse control. Event-triggered impulse control strategy [9, 19] may be considered in the future research.

Since the first physical memristor device was invented by Hewlett-Packard (HP) Laboratory [20, 21], memristor has attracted much attention [22–25] because it has the similar features just as the neurons in the human brain. Moreover, it may promote the development of the next-generation computer and powerful brain-like neural computers [24]. As a new neural network model, memristor-based neural network (MNN) systems have attracted much attention in recent years. Investigating the dynamic properties of MNNs is very important because it could play the key role in the designation of MNNs. Wu et al. [26] formulated the memristor-based neural networks and investigated their dynamical properties. In [27, 28], the authors studied the stability of memristor-based delayed recurrent neural networks. Zhang et al. researched the synchronization stability of chaotic memristive neural networks in [29]. As the literature indicates, the majority of these works focused on the stability analysis and synchronization of delayed MNNs without considering abrupt internal or external changes. However, the states of delayed MNNs (DMNNs) are not usually stable, and they could also undergo abrupt internal or external changes. Therefore, it is necessary to consider the impulsive effect on the stability of DMNNs. Recently, the stability problem of the memristive delayed neural networks with impulses was studied in [30]. In [31], the passivity and passification of stochastic impulsive memristive systems was investigated . Although there have been several dynamic study results of impulsive DMNNs, the stability analysis of these systems has not been fully investigated, which motivates the research of this paper.

In this paper, we formulate a generalized impulsive delayed memristor-based recurrent neural network (DMRNN) model and analyze the exponential stability of this model. The global exponential stability of DMRNNs with impulse effects is investigated by utilizing impulsive differential inequality and Lyapunov function. Several stability criteria are obtained, which implies that frequency and strength of impulses can maintain the stability of the original stable continuous delayed DMRNNs. Furthermore, it is worth noting that several uniformly stable criteria of the impulsive DMRNNs could also be derived. Two examples and their simulations are given to illustrate the effectiveness of the results.

The remaining part of this paper consists of four sections. In Sect. 2, models and preliminaries are introduced. And the main results are derived in Sect. 3. In Sect. 4, two illustrative examples are given to demonstrate the effectiveness of the proposed results. Finally, concluding remarks are included in Sect. 5.

2 Preliminaries

2.1 DMRNN model and notations

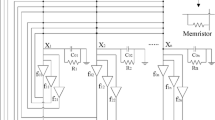
In recent years, some initial study results of the DMRNNs have been obtained [5, 26–28], where the DMRNN model can be described by the following differential equation:

$$\begin{aligned} \dot{u}_{i}(t)= & {} -d_{i}(u_{i}(t))u_{i}(t)+\sum _{j=1}^{n}a_{ij}(u_{i}(t))f_{j}(u_{j}(t))\nonumber \\&+\sum _{j=1}^{n}b_{ij}(u_{i}(t)) g_{j}(u_{j}(t-\tau _{ij}(t)))+I_{i},t\ge 0,\quad i=1,2,\ldots ,n, \end{aligned}$$
(1)

where n denotes the number of units, \(u_{i}(t)\) corresponds to the state of the ith unit at time t, the time-varying delays \(\tau _{ij}(t)\) are nonnegative continuous functions satisfying \(0\le \tau _{ij}(t)\le \tau\) (\(\tau >0\) is a constant) for \(i,j=1,2,\ldots ,n,\) \(f_{j}(\cdot )\) and \(g_{j}(\cdot )\) are the bounded feedback functions satisfying \(f_{j}(0)=g_{j}(0)=0,\) \(I_{i}\) denotes external constant input, \(d_{i}(u_{i}(t)),\) \(a_{ij}(u_{i}(t))\) and \(b_{ij}(u_{i}(t))\) represent memristor-based weights, and

$$\begin{aligned}&d_{i}(u_{i}(t))=\left\{ \begin{array}{ll} \hat{d}_{i} &{} |u_{i}(t)|<T_{i}\\ \check{d}_{i} &{} |u_{i}(t)|>T_{i} \end{array} \right. ,a_{ij}(u_{i}(t))=\left\{ \begin{array}{ll} \hat{a}_{ij} &{} |u_{i}(t)|<T_{i}\\ \check{a}_{ij} &{} |u_{i}(t)|>T_{i} \end{array} \right. ,\\&b_{ij}(u_{i}(t))=\left\{ \begin{array}{ll} \hat{b}_{ij} &{} |u_{i}(t)|<T_{i}\\ \check{b}_{ij} &{} |u_{i}(t)|>T_{i} \end{array} \right. , \end{aligned}$$

in which the switching jumps \(T_{i}>0,\) \(\hat{d}_{i}>0,\) \(\check{d}_{i}>0,\) \(\hat{a}_{ij},\) \(\check{a}_{ij},\) \(\hat{b}_{ij}\) and \(\check{b}_{ij}\) are constants for \(i,j=1,2,\ldots ,n.\) When \(|u_{i}(t)| = T_{i},\) \(d_{i}(u_{i}(t))\) is \(\check{d}_{i}\) or \(\hat{d}_{i},\) \(a_{ij}(u_{i}(t))\) is \(\check{a}_{ij}\) or \(\hat{a}_{ij},\) \(b_{ij}(u_{i}(t))\) is \(\check{b}_{ij}\) or \(\hat{b}_{ij}.\)

In this paper, solutions of all the considered systems are intended in the Filippov’s [32] sense. \({\varvec{R}}^{\varvec{n}}\) denotes the n-dimensional space with the Euclidean vector norm \(|\cdot |,\) and \([\cdot ,\cdot ]\) represents the interval. Let \(\overline{d}_{i}=\max \{\hat{d}_{i},\check{d}_{i}\},\) \(\underline{d}_{i}=\min \{\hat{d}_{i},\check{d}_{i}\},\) \(\overline{a}_{ij}=\max \{\hat{a}_{ij},\check{a}_{ij}\},\) \(\underline{a}_{ij}=\min \{\hat{a}_{ij},\check{a}_{ij}\},\) \(\overline{b}_{ij}=\max \{\hat{b}_{ij},\check{b}_{ij}\},\) \(\underline{b}_{ij}=\min \{\hat{b}_{ij},\check{b}_{ij}\},\) \(\tilde{d}_{i}=\min \{|\hat{d}_{i}|,|\check{d}_{i}|\},\) \(\tilde{a}_{ij}=\max \{|\hat{a}_{ij}|,|\check{a}_{ij}|\},\) \(\tilde{b}_{ij}=\max \{|\hat{b}_{ij}|,|\check{b}_{ij}|\},\) for \(i,j=1,2,\ldots ,n.\) \(co[\underline{a},\overline{a}]\) denotes closure of the convex hull generated by real numbers \(\underline{a}\) and \(\overline{a}\) or real matrices \(\underline{a}\) and \(\overline{a}.\)

2.2 Impulsive DMRNN model

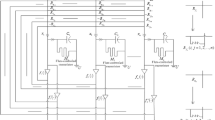
In this subsection, basing on the references [5, 26–28], the impulsive DMRNN model can be described as the following differential inclusion by applying the theories of set-valued maps and differential inclusions [32]:

$$\begin{aligned} \left\{ \begin{array}{ll} \dot{u}_{i}(t)\in -co[\underline{d}_{i},\overline{d}_{i}]u_{i}(t)+\sum _{j=1}^{n}co[\underline{a}_{ij},\overline{a}_{ij}]f_{j}(u_{j}(t))+\sum _{j=1}^{n} \\ \qquad \quad \qquad \quad \qquad \quad co[\underline{b}_{ij},\overline{b}_{ij}]g_{j}(u_{j}(t-\tau _{ij}(t)))+I_{i}, \qquad t\ne t_{k},t\ge 0, \\ u_{i}(t_{k}^{+})=J_{ik}(u_{i}(t_{k}^{-})), \qquad \quad \qquad \quad \qquad \quad \qquad \quad \qquad \quad \qquad k\in Z^{+}, \\ u_{i}(t)=\phi _{i}(t), \qquad \qquad \quad \qquad \quad \qquad \quad \qquad \quad t\in [-\tau ,0],\quad i=1,2,\ldots ,n, \end{array} \right. \end{aligned}$$
(2)

or equivalently, for \(i,j=1,2,\ldots ,n,\) there exist \(\breve{d}_{i}(t)\in co[\underline{d}_{i},\overline{d}_{i}],\) \(\breve{a}_{ij}(t)\in co[\underline{a}_{ij},\overline{a}_{ij}],\) \(\breve{b}_{ij}(t)\in co[\underline{b}_{ij},\overline{b}_{ij}],\) such that

$$\begin{aligned} \left\{ \begin{array}{ll} \dot{u}_{i}(t)=-\breve{d}_{i}(t)u_{i}(t)+\sum _{j=1}^{n}\breve{a}_{ij}(t)f_{j}(u_{j}(t))+ \sum _{j=1}^{n}\breve{b}_{ij}(t) g_{j}(u_{j}(t-\tau _{ij}(t)))\\ \qquad \quad \qquad \quad \qquad \quad \qquad \quad \qquad \quad \qquad \quad \qquad \quad +I_{i},\qquad t\ne t_{k},t\ge 0, \\ u_{i}(t_{k}^{+})=J_{ik}(u_{i}(t_{k}^{-})), \qquad \quad \qquad \qquad \quad \qquad \quad \qquad \quad \qquad \quad k\in Z^{+},\\ u_{i}(t)=\phi _{i}(t), \qquad \qquad \quad \qquad \quad \qquad \quad \qquad \quad t\in [-\tau ,0],\quad i=1,2,\ldots ,n, \end{array} \right. \end{aligned}$$
(3)

where \(J_{ik}(u)\in {\mathcal {C}}[{\varvec{R}}^{\varvec{n}},{\varvec{R}}^{\varvec{n}}]\) is the jump operator at time \(t_{k},\) \(u(t_{k})=u(t_{k}^{+})=\lim _{h\rightarrow 0+}u(t_{k}+h),\) \(u(t_{k}^{-})=\lim _{h\rightarrow 0-}u(t_{k}+h),\) \(k=1,2,\ldots ,\) and \(0<t_{1}<t_{2}<\ldots <t_{k}<\cdots (t_{k}\rightarrow \infty\) as \(k\rightarrow \infty ),\) \(\phi (t)=(\phi _{1}(t),\phi _{2}(t), \dots ,\phi _{n}(t))^{T}\) and \(\phi (t)\in {\mathcal {PC}}([-\tau ,0],{\varvec{R}}^{\varvec{n}}),\) here \({\mathcal {PC}}([-\tau ,0],{\varvec{R}}^{\varvec{n}})\) denotes the set of piecewise right continuous function \(\phi (t):[-\tau ,0]\rightarrow {\varvec{R}}^{\varvec{n}}\) with the norm defined by \(||\phi (t)||_{\tau }=\sup _{-\tau \le s\le 0}|\phi (t+s)|.\) If \(J_{ik}(u_{i}(t_{k}^{-}))=u_{i}(t_{k}^{-}),\) then model (3) becomes model (1), which have been widely investigated in [26–29].

Suppose \(u^{*}=(u_{1}^{*},u_{2}^{*},\cdots ,u_{n}^{*})\) is an equilibrium point of the impulsive DMRNN (2) or (3), let \(x_{i}(t)=u_{i}(t)-u_{i}^{*}\) for \(i=1,2,\ldots ,n;\) then, we have

$$\begin{aligned} \left\{ \begin{array}{ll} \dot{x}_{i}(t)\in -co[\underline{d}_{i},\overline{d}_{i}]x_{i}(t)+\sum _{j=1}^{n}co[\underline{a}_{ij},\overline{a}_{ij}]\tilde{f}_{j}(x_{j}(t)) +\sum _{j=1}^{n}\\ \qquad \quad \qquad \quad \qquad \quad \qquad \quad co[\underline{b}_{ij},\overline{b}_{ij}]\tilde{g}_{j}(x_{j}(t-\tau _{ij}(t))), \quad t\ne t_{k},t\ge 0 ,\\ x_{i}(t_{k}^{+})=\mu _{ik}(x_{i}(t_{k}^{-})), \qquad \quad \qquad \quad \qquad \quad \qquad \quad \qquad \quad \qquad k\in Z^{+},\\ x_{i}(t)=\varphi _{i}(t), \qquad \quad \qquad \quad \qquad \quad \qquad \quad \qquad t\in [-\tau ,0],\quad i=1,2,\ldots ,n, \end{array} \right. \end{aligned}$$
(4)

or equivalently,

$$\begin{aligned} \left\{ \begin{array}{ll} \dot{x}_{i}(t)=-\breve{d}_{i}(t)x_{i}(t)+\sum _{j=1}^{n}\breve{a}_{ij}(t)\tilde{f}_{j}(x_{j}(t))+ \sum _{j=1}^{n}\breve{b}_{ij}(t) \tilde{g}_{j}(x_{j}(t-\tau _{ij}(t))),\\ \quad \qquad \quad \qquad \quad \qquad \quad \qquad \quad \qquad \quad \qquad \quad \qquad \quad \qquad t\ne t_{k},t\ge 0,\\ x_{i}(t_{k}^{+})=\mu _{ik}(x_{i}(t_{k}^{-})), \quad \qquad \qquad \qquad \quad \qquad \quad \qquad \quad \qquad \quad k\in Z^{+},\\ x_{i}(t)=\varphi _{i}(t), \qquad \qquad \qquad \quad \qquad \quad \qquad \quad t\in [-\tau ,0],\quad i=1,2,\ldots ,n, \end{array} \right. \end{aligned}$$
(5)

where \(\varphi _{i}(t)=\phi _{i}(t)-u_{i}^{*},\) \(\tilde{f}_{j}(x_{j}(t))=f_{j}(x_{j}(t)+u_{j}^{*})-f_{j}(u_{j}^{*}),\) \(\tilde{g}_{j}(x_{j}(t))=g_{j}(x_{j}(t)+u_{j}^{*})-g_{j}(u_{j}^{*}),\) \(\mu _{ik}(x_{i}(t))=J_{ik}(x_{i}(t)+u_{i}^{*})-J_{ik}(u_{i}^{*}).\)

In order to derive the exponential stability criteria, the following definitions, assumptions, and lemmas are needed to be introduced.

Definition 1

([16]) The Dini’s upper right-hand derivative of a continuous function \(V(t):{\varvec{R}}\rightarrow {\varvec{R}}\) is defined by

$$\begin{aligned} D^{+}V(t)=\lim _{h \rightarrow 0^{+}}sup\frac{1}{h}\{V(t+h)-V(t)\}. \end{aligned}$$

Definition 2

([26, 28]) Let \(u^{*}=(u_{1}^{*},u_{2}^{*},\cdots ,u_{n}^{*})\) be an equilibrium point of system (2.3). If there exist constants \(\lambda >0\) and \(\beta \ge 1\) such that for every solution \(u(t)=(u_{1}(t),u_{2}(t),\cdots ,u_{n}(t))\) of system (2.3) with any initial value \(\phi (t)=(\phi _{1}(t),\phi _{2}(t),\dots ,\phi _{n}(t))^{T}\),

$$\begin{aligned} |u(t)-u^{*}|\le \beta ||\phi (0)-u^{*}||_{\tau } e^{-\lambda t},\qquad t\ge 0, \end{aligned}$$

where \(||\phi (0)-u^{*}||_{\tau }=\sup _{-\tau \le s\le 0}|\phi (s)-u^{*}|,\) then the equilibrium point \(x^{*}\) is said to be globally exponentially stable.

Lemma 1

([14]) Let a, b be an constants with \(0<b<a\) and u(t) satisfy the following scalar impulsive differential inequality

$$\begin{aligned} \left\{ \begin{array}{ll} D^{+}u(t)\le -au(t)+b{\bar{u}(t)},&{} t\ne t_{k},t\ge t_{0},\\ u(t_{k}^{+})\le \mu _{k}u(t_{k}^{-}), &{} k\in Z^{+} ,\\ u(t)=\phi (t), &{} t\in [t_{0}-\tau ,t_{0}], \end{array} \right. \end{aligned}$$

where u(t) is continuous at \(t\ne t_{k},\) \(t\ge t_{0},\) \({\bar{u}(t)}\triangleq \sup _{t-\tau \le s\le t}\{u(s)\},\) \(u(t_{k}^{+})=u(t_{k})\) and \(u(t_{k}^{-})\) exists, \(\phi (t)\in {\mathcal {PC}}\) with \(n=1.\) Then,

$$\begin{aligned} u(t)\le \left( \prod _{t_{0}<t_{k}\le t}\delta _{k}\right) ||\phi (t_{0})||_{\tau }e^{-\lambda (t-t_{0})},\quad t\ge t_{0}, \end{aligned}$$

where \(\delta _{k}=\max \{1,|\mu _{k}|\}\) and \(\lambda >0\) is a solution of the inequality \(\lambda -a+be^{\lambda \tau }\le 0.\)

Assumption 1

For \(j=1,2,\ldots ,n,\) the neuron activation functions \(f_{j}(u_{j})\) and \(g_{j}(u_{j})\) in (2) are bounded, and there exist nonnegative scalars \(\rho _{j}\) and \(\sigma _{j}\) such that, for \(\forall x_{1},x_{2}\in \varvec{R},\) \(x_{1}\ne x_{2},\)

$$\begin{aligned} 0\le \frac{f_{j}(x_{1})-f_{j}(x_{2})}{x_{1}- x_{2}}\le \rho _{j},\quad 0\le \frac{g_{j}(x_{1})-g_{j}(x_{2})}{x_{1}- x_{2}}\le \sigma _{j}. \end{aligned}$$

Lemma 2

Under Assumption 1, we have

$$\begin{aligned} 0\le \sup _{x_{j}\ne 0}\frac{\tilde{f}_{j}(x_{j})}{x_{j}}\le \rho _{j}, \quad 0\le \sup _{x_{j}\ne 0}\frac{\tilde{g}_{j}(x_{j})}{x_{j}}\le \rho _{j}. \end{aligned}$$

Assumption 2

For \(i=1,2,\ldots, n,\) the jump operator \(J_{ik}(u)\) satisfies the Lipschitz condition with \(J_{ik}(0)=0,\) i.e., there exists nonnegative scalar \(\mu _{ik}\) such that for \(\forall x_{1},x_{2}\in \varvec{R},\) \(x_{1}\ne x_{2},\)

$$\begin{aligned} |J_{ik}(x_{1})-J_{ik}(x_{2})|\le \mu _{ik} |x_{1}- x_{2}|. \end{aligned}$$

3 Main results

In this section, the global exponential stability of the impulsive DMRNNs (2) or (3) will be investigated, and the stability criteria will be presented by the following theorems.

Theorem 1

Let \(u^{*}\) be the equilibrium point of impulsive DMRNN (2) or (3) and suppose Assumption 1 and Assumption 2 hold. Then, the equilibrium point \(u^{*}\) of impulsive DMRNN (2) or (3) is globally exponentially stable if for \(k\in Z^{+},\) the following conditions are satisfied.

  • (i) \(a>b,\) where \(a=\min _{1\le j\le n}\bigg (\tilde{d}_{j}-\max \bigg \{0,\tilde{a}_{jj}+\sum _{j\ne i,i=1}^{n}|\tilde{a}_{ij}|\bigg \}\rho _{j}\bigg )>0,\) \(b=\max _{1\le j\le n}(\sum _{i=1}^{n}|\tilde{b}_{ij}|\sigma _{j})\);

  • (ii) \(\lambda >\delta,\) where \(\lambda >0\) is a solution of \(\lambda -a+be^{\lambda \tau }\le 0,\) \(\delta =\sup _{k\in Z^{+}}\{\frac{\ln \delta _{k}}{t_{k}-t_{k-1}}\}\) with \(\delta _{k}=\max \{1,|\mu _{k}|\}\) and \(\mu _{k}=\max _{1\le i \le n}\{\mu _{ik}\}.\)

Proof

We only consider the exponential stability of the equilibrium point of impulsive DMRNN (4) or (5), which can guarantee the exponential stability of impulsive DMRNN (2) or (3).

Construct a Lyapunov function \(V(t)=\sum _{i=1}^{n}|x_{i}|,\) when \(t\ne t_{k},\) the Dini right derivative of V(t) can be calculated as follows:

$$\begin{aligned} D^{+}V(t)= & {} \sum _{i=1}^{n}sgn(x_{i}(t))\left[ -\breve{d}_{i}(t)x_{i}(t)+\sum _{j=1}^{n}\breve{a}_{ij}(t)\tilde{f}_{j}(x_{j}(t)) \right. \nonumber \\&\left. +\sum _{j=1}^{n}\breve{b}_{ij}(t) \tilde{g}_{j}(x_{j}(t-\tau _{ij}(t)))\right] \nonumber \\\le & {} -\sum _{i=1}^{n}\tilde{d}_{i}|x_{i}(t)|+\sum _{i=1}^{n}\bigg (\tilde{a}_{ii}+\sum _{i\ne j,j=1}^{n}|\tilde{a}_{ij}|\bigg )|\tilde{f}_{j}(x_{j}(t))|\nonumber \\&+ \sum _{i=1}^{n}\sum _{j=1}^{n}|\tilde{b}_{ij}||\tilde{g}_{j}(x_{j}(t-\tau _{ij}(t)))|\nonumber \\\le & {} -\sum _{i=1}^{n}\tilde{d}_{i}|x_{i}(t)|+\sum _{i=1}^{n}\bigg (\tilde{a}_{ii}+\sum _{i\ne j,j=1}^{n}|\tilde{a}_{ij}|\bigg )\rho _{j}|x_{j}(t)|\nonumber \\&+ \sum _{i=1}^{n}\sum _{j=1}^{n}|\tilde{b}_{ij}|\sigma _{j} |x_{j}(t-\tau _{ij}(t))|\nonumber \\= & {} \sum _{j=1}^{n}\bigg [-\tilde{d}_{j}+\bigg (\tilde{a}_{jj}+\sum _{j\ne i,i=1}^{n}|\tilde{a}_{ij}|\bigg )\rho _{j}\bigg ]|x_{j}(t)|\nonumber \\&+ \sum _{j=1}^{n}\sum _{i=1}^{n}|\tilde{b}_{ij}|\sigma _{j} |x_{j}(t-\tau _{ij}(t))|\nonumber \\\le & {} -a V(t)+b{\bar{V}(t)}, \end{aligned}$$
(6)

where \(\bar{V}(t)=\sup _{t-\tau \le s\le t}\{V(s)\}.\)

When \(t= t_{k},\)

$$\begin{aligned} V(t_{k}^{+})=\sum _{i=1}^{n}|x_{i}(t_{k}^{+})|\le \sum _{i=1}^{n}|\mu _{ik}x_{i}(t_{k}^{-})|\le \sum _{i=1}^{n}|\mu _{k}||x_{i}(t_{k}^{-})|=|\mu _{k}|V(t_{k}^{-}). \end{aligned}$$
(7)

Employing Lemma 1, from (6), (7) and conditions (i) and (ii), we can get

$$\begin{aligned} V(t)\le & {} \delta _{1}\delta _{2}\cdots \delta _{k-1}||V(0)||_{\tau }e^{-\lambda t},\quad t\in [t_{k-1},t_{k}),k\in Z^{+}\nonumber \\\le & {} e^{\delta t_{1}}e^{\delta (t_{2}-t_{1})}\cdots e^{\delta (t_{k-1}-t_{k-2})}||V(0)||_{\tau }e^{-\lambda t}\nonumber \\\le & {} e^{\delta t}||V(0)||_{\tau }e^{-\lambda t}\nonumber \\= & {} ||V(0)||_{\tau }e^{-(\lambda -\delta )t}. \end{aligned}$$

Hence, we have

$$\begin{aligned} V(t)\le ||V(0)||_{\tau }e^{-(\lambda -\delta )t},\quad t\ge 0. \end{aligned}$$

That is,

$$\begin{aligned} \sum _{i=1}^{n}|x_{i}|\le \sup _{-\tau \le s\le 0}|\varphi (s)|e^{-(\lambda -\delta )t},\quad t\ge 0. \end{aligned}$$

Since \(x_{i}(t)= u_{i}(t)-u^{\star },\) we have

$$\begin{aligned} \sum _{i=1}^{n}|u(t)-u^{\star }|\le \sup _{-\tau \le s\le 0}|\phi (s)-u^{\star }|e^{-(\lambda -\delta )t} \end{aligned}$$
(8)

for any \(t\ge 0.\) Therefore, the equilibrium point \(u^{*}\) of impulsive DMRNN (2) or (3) is globally exponentially stable. This completes the proof. \(\square\)

Remark 1

Let \(\lambda =\delta,\) the inequality (8) can be rewritten by \(\sum _{i=1}^{n}|u(t)-u^{\star }|\le \sup _{-\tau \le s\le 0}|\phi (s)-u^{\star }|.\) Then, we can conclude that the equilibrium point \(u^{*}\) of impulsive DMRNN (2) or (3) is uniformly stable. Therefore, under the conditions of Theorem 1, the equilibrium point of system (2) or (3) is uniformly stable if \(\lambda \ge \delta .\) In this theorem, impulsive differential inequality was used to obtain the stability criteria, which is different with the techniques used in [10, 11]. Impulsive differential equations were used to study the consensus multi-agent networks in [10], and impulsive distributed control scheme was designed to achieve the network synchronization based on the concept of control topology in [11].

Theorem 2

Let \(u^{*}\) be the equilibrium point of impulsive DMRNN (2) or (3) and suppose Assumption 1 and Assumption 2 hold. Then, the equilibrium point \(u^{*}\) of impulsive DMRNN (2) or (3) is globally exponentially stable if for any \(k\in Z^{+},\) there exist \(\gamma _{j}>0, j=1,2,\dots ,n,\) such that the following conditions are satisfied.

  • (i) \(c>d,\) where \(c=\min _{1\le j\le n}(\tilde{d}_{j}-2 \sum _{i=1}^{n}\sum _{k=1}^{n}\frac{\gamma _{i}(\tilde{a}_{ik}\rho _{k})^{2}}{\tilde{d}_{i}\gamma _{j}})>0,\) \(d=\max _{1\le j\le n} \sum _{i=1}^{n} \sum _{k=1}^{n}\frac{2\gamma _{i}(\tilde{b}_{ik}\rho _{k})^{2}}{\tilde{d}_{i}\gamma _{j}}\) ;

  • (ii) \(\lambda >\delta,\) where \(\lambda >0\) is a solution of \(\lambda -c+de^{\lambda \tau }\le 0,\) \(\delta =\sup _{k\in Z^{+}}\{\frac{\ln \delta _{k}}{t_{k}-t_{k-1}}\}\) with \(\delta _{k}=\max \{1,|\mu _{k}|\}\) and \(\mu _{k}=\max _{1\le i \le n}\{\mu _{ik}\}.\)

Proof

In this theorem, we still consider the exponential stability of the equilibrium point of impulsive DMRNN (4) or (5), which can also guarantee the exponential stability of impulsive DMRNN (2) or (3).

Construct a Lyapunov function \(V(t)=\sum _{i=1}^{n}\frac{1}{2}\gamma _{i}x_{i}^{2}(t),\) when \(t\ne t_{k},\) the Dini right derivative of V(t) can be calculated as follows:

$$\begin{aligned} D^{+}V(t)= & {} \sum _{i=1}^{n}\gamma _{i}x_{i}(t)\bigg [-\breve{d}_{i}(t)x_{i}(t)+\sum _{j=1}^{n}\breve{a}_{ij}(t)\tilde{f}_{j}(x_{j}(t))\nonumber \\&+ \sum _{j=1}^{n}\breve{b}_{ij}(t) \tilde{g}_{j}(x_{j}(t-\tau _{ij}(t)))\bigg ]\\\le & {} \sum _{i=1}^{n}\bigg \{-\tilde{d}_{i}\gamma _{i}x_{i}^{2}(t)+|x_{i}(t)|\sum _{j=1}^{n}\gamma _{i}|\tilde{a}_{ij}||\tilde{f}_{j}(x_{j}(t))|\nonumber \\&+ |x_{i}(t)|\sum _{j=1}^{n}\gamma _{i}|\tilde{b}_{ij}||\tilde{g}_{j}(x_{j}(t-\tau _{ij}(t)))|\bigg \}\\\le & {} \sum _{i=1}^{n}\bigg \{-\frac{1}{2}\tilde{d}_{i}\gamma _{i}x_{i}^{2}(t)+|x_{i}(t)|\sum _{j=1}^{n}\gamma _{i}|\tilde{a}_{ij}||\tilde{f}_{j}(x_{j}(t))|-\frac{1}{2}\tilde{d}_{i}\gamma _{i}x_{i}^{2}(t)\nonumber \\&+|x_{i}(t)|\sum _{j=1}^{n}\gamma _{i}|\tilde{b}_{ij}||\tilde{g}_{j}(x_{j}(t-\tau _{ij}(t)))|\bigg \}. \end{aligned}$$

According to Lemma 2 and mean-value inequality, we have

$$\begin{aligned} D^{+}V(t)\le & {} \sum _{i=1}^{n}\bigg \{-\frac{1}{2}\tilde{d}_{i}\gamma _{i}x_{i}^{2}(t)+|x_{i}(t)|\sum _{j=1}^{n}\gamma _{i}|\tilde{a}_{ij}|\rho _{j}|x_{j}(t)|\nonumber \\&-\frac{1}{2}\tilde{d}_{i}\gamma _{i}x_{i}^{2}(t)+|x_{i}(t)|\sum _{j=1}^{n}\gamma _{i}|\tilde{b}_{ij}|\sigma _{j}|x_{j}(t-\tau _{ij}(t))|\bigg \}\\\le & {} \sum _{i=1}^{n}\bigg \{-\frac{1}{2}\tilde{d}_{i}\gamma _{i}x_{i}^{2}(t)+\frac{1}{4}\tilde{d}_{i}\gamma _{i}x_{i}^{2}(t)+ \frac{1}{\tilde{d}_{i}\gamma _{i}}\left( \sum _{j=1}^{n}\gamma _{i}|\tilde{a}_{ij}|\rho _{j}|x_{j}(t)|\right) ^{2}\\&-\frac{1}{2}\tilde{d}_{i}\gamma _{i}x_{i}^{2}(t)+\frac{1}{4}\tilde{d}_{i}\gamma _{i}x_{i}^{2}(t)+\frac{1}{\tilde{d}_{i}\gamma _{i}}\left( \sum _{j=1}^{n}\gamma _{i}|\tilde{b}_{ij}|\sigma _{j}|x_{j}(t-\tau _{ij}(t))|\right) ^{2}\bigg \}\\= & {} \sum _{i=1}^{n}\bigg \{-\frac{1}{2}\tilde{d}_{i}\gamma _{i}x_{i}^{2}(t)+ \frac{1}{\tilde{d}_{i}\gamma _{i}}\left( \sum _{j=1}^{n}\gamma _{i}|\tilde{a}_{ij}|\rho _{j}|x_{j}(t)|\right) ^{2}\\&+\frac{1}{\tilde{d}_{i}\gamma _{i}} \left( \sum _{j=1}^{n}\gamma _{i}|\tilde{b}_{ij}|\sigma _{j}|x_{j}(t-\tau _{ij}(t))|\right) ^{2}\bigg \}, \end{aligned}$$

Then, by Cauchy-Schwarz inequality, we obtain

$$\begin{aligned} \left( \sum _{j=1}^{n}\gamma _{i}|\tilde{a}_{ij}|\rho _{j}|x_{j}(t)|\right) ^{2}\le & {} \sum _{j=1}^{n}(\gamma _{i}\tilde{a}_{ij}\rho _{j})^{2}\sum _{j=1}^{n}x_{j}^{2}(t) = \sum _{k=1}^{n}(\gamma _{i}\tilde{a}_{ik}\rho _{k})^{2}\sum _{j=1}^{n}x_{j}^{2}(t),\\ \left( \sum _{j=1}^{n}\gamma _{i}|\tilde{b}_{ij}|\sigma _{j}|x_{j}(t-\tau _{ij}(t))|\right) ^{2}\le & {} \sum _{j=1}^{n}(\gamma _{i}\tilde{b}_{ij}\sigma _{j})^{2}\sum _{j=1}^{n}x_{j}^{2}(t-\tau _{ij})\\= & {} \sum _{k=1}^{n}(\gamma _{i}\tilde{b}_{ik}\sigma _{k})^{2}\sum _{j=1}^{n}x_{j}^{2}(t-\tau _{ij}), \end{aligned}$$

As a result,

$$\begin{aligned} D^{+}V(t)\le & {} \sum _{i=1}^{n}\bigg \{-\frac{1}{2}\tilde{d}_{i}\gamma _{i}x_{i}^{2}(t)+ \frac{1}{\tilde{d}_{i}\gamma _{i}}\sum _{k=1}^{n}(\gamma _{i}\tilde{a}_{ik}\rho _{k})^{2}\sum _{j=1}^{n}x_{j}^{2}(t)\nonumber \\&+ \frac{1}{\tilde{d}_{i}\gamma _{i}}\sum _{k=1}^{n}(\gamma _{i}\tilde{b}_{ik}\sigma _{k})^{2}\sum _{j=1}^{n}x_{j}^{2}(t-\tau _{ij})\bigg \}\nonumber \\= & {} \sum _{j=1}^{n}\bigg \{-\tilde{d}_{j}+ 2\sum _{i=1}^{n}\sum _{k=1}^{n}\frac{\gamma _{i}(\tilde{a}_{ik}\rho _{k})^{2}}{\tilde{d}_{i}\gamma _{j}}\bigg \}\frac{1}{2}\gamma _{j}x_{j}^{2}(t)\nonumber \\&+ \sum _{j=1}^{n} \sum _{i=1}^{n}\sum _{k=1}^{n}\frac{2\gamma _{i}(\tilde{b}_{ik}\rho _{k})^{2}}{\tilde{d}_{i}\gamma _{j}}\frac{1}{2}\gamma _{j}x_{j}^{2}(t-\tau _{ij})\nonumber \\\le & {} -c V(t)+d{\bar{V}(t)}, \end{aligned}$$
(9)

where \(\bar{V}(t)=\sup _{t-\tau \le s\le t}\{V(s)\}.\)

When \(t= t_{k},\)

$$\begin{aligned} V(t_{k}^{+})= & {} \sum _{i=1}^{n}\frac{1}{2}\gamma _{i}x_{i}^{2}(t_{k}^{+}) \le \sum _{i=1}^{n}\frac{1}{2}\gamma _{i} (\mu _{ik}x_{i}(t_{k}^{-}))^{2}\nonumber \\\le & {} \sum _{i=1}^{n}\frac{1}{2}\gamma _{i} \mu _{k}^{2} x_{i}^{2}(t_{k}^{-}) = \mu _{k}^{2} V(t_{k}^{-}). \end{aligned}$$
(10)

Employing Lemma 1, from (9), (10) and conditions (i) and (ii), we can get

$$\begin{aligned} V(t)\le & {} \delta _{1}\delta _{2}\cdots \delta _{k-1}||V(0)||_{\tau }e^{-\lambda t},\quad t\in [t_{k-1},t_{k}),k\in Z^{+}\nonumber \\\le & {} e^{\delta t_{1}}e^{\delta (t_{2}-t_{1})}\cdots e^{\delta (t_{k-1}-t_{k-2})}||V(0)||_{\tau }e^{-\lambda t}\nonumber \\\le & {} e^{\delta t}||V(0)||_{\tau }e^{-\lambda t}\nonumber \\= & {} ||V(0)||_{\tau }e^{-(\lambda -\delta )t}. \end{aligned}$$

Hence, we have

$$\begin{aligned} V(t)\le ||V(0)||_{\tau }e^{-(\lambda -\delta )t},\quad t\ge 0. \end{aligned}$$

Simultaneously,

$$\begin{aligned} \frac{1}{2}\min _{1\le i\le n}\{\gamma _{i}\}\sum _{i=1}^{n}x_{i}^{2}(t)\le V(t)=\sum _{i=1}^{n}\frac{1}{2}\gamma _{i}x_{i}^{2}(t)\le \frac{1}{2}\max _{1\le i\le n}\{\gamma _{i}\}\sum _{i=1}^{n}x_{i}^{2}(t). \end{aligned}$$

Therefore,

$$\begin{aligned} \sum _{i=1}^{n}x_{i}^{2}(t)\le M\sup _{-\tau \le s\le 0}|\varphi (s)|e^{-(\lambda -\delta )t},\quad t\ge 0, \end{aligned}$$

where \(M=\frac{1}{\min _{1\le i\le n}\{\gamma _{i}\}}.\) Since \(x_{i}(t)= u_{i}(t)-u^{\star},\) we have

$$\begin{aligned} \sum _{i=1}^{n}(u(t)-u^{\star })^{2}\le M\sup _{-\tau \le s\le 0}|\phi (s)-u^{\star }|e^{-(\lambda -\delta )t} \end{aligned}$$
(11)

for any \(t\ge 0.\) Thus, the equilibrium point \(u^{*}\) of impulsive DMRNN (2) or (3) is globally exponentially stable. This completes the proof. \(\square\)

Remark 2

Let \(\lambda =\delta,\) the inequality (11) can be rewritten by \(\sum _{i=1}^{n}(u(t)-u^{\star })^{2}\le M\sup _{-\tau \le s\le 0}|\phi (s)-u^{\star }|.\) Then, we can conclude that the equilibrium point \(u^{*}\) of impulsive DMRNN (2) or (3) is uniformly stable. Therefore, under the conditions of Theorem 2, the equilibrium point of system (2) or (3) is also uniformly stable if \(\lambda \ge \delta.\) Moreover, if \(\mu _{ik}(u)=u\) for any \(i,k\in Z^{+}\) in the system (2) or (35), then we can obtain new stable criteria of delayed memristor-based recurrent neural networks (DMRNNs) without impulsive effects from Theorem 1 and 2.

Remark 3

The two theories are about the stability criteria of impulsive delayed memristor-based recurrent neural networks. By means of impulsive differential inequality and some assumptions, several important stability conditions have been obtained, which is different with some published results. In [26–29], the authors mainly studied the dynamic behaviors of DMRNNs without impulsive effects. The authors only discussed the dynamic behaviors of classical impulsive complex networks and neural networks instead of memristor-based neural networks in [10–18]. In this paper, both memristor-based recurrent neural networks and impulsive effects are combined to be investigated, which enriches the research results of neural networks.

In Theorem 2, if different numerical numbers of \(\gamma _{i}\) are chosen, we can obtain several important results. For example, let \(\gamma _{i}=1\) for any \(i=1,2,\ldots, n;\) then, we can get the following corollary.

Corollary 1

Let \(u^{*}\) be the equilibrium point of impulsive DMRNN (2) or (3) and suppose Assumption 1 and Assumption 2 hold. Then, the equilibrium point \(u^{*}\) of impulsive DMRNN (2) or (3) is globally exponentially stable if for any \(k\in Z^{+},\) the following conditions are satisfied.

  • (i) \(\min _{1\le j\le n}(\tilde{d}_{j}-2 \sum _{i=1}^{n}\sum _{k=1}^{n}\frac{(\tilde{a}_{ik}\rho _{k})^{2}}{\tilde{d}_{i}})-\max _{1\le j\le n} \sum _{i=1}^{n}\sum _{k=1}^{n}\frac{2(\tilde{b}_{ik}\rho _{k})^{2}}{\tilde{d}_{i}}>0\);

  • (ii) \(\lambda >\delta,\) where \(\lambda >0\) is a solution of \(\lambda -c+de^{\lambda \tau }\le 0,\) \(\delta =\sup _{k\in Z^{+}}\{\frac{\ln \delta _{k}}{t_{k}-t_{k-1}}\}\) with \(\delta _{k}=\max \{1,|\mu _{k}|\}\) and \(\mu _{k}=\max _{1\le i \le n}\{\mu _{ik}\}.\)

If let \(\sum _{j=1}^{n}\gamma _{i}|\tilde{a}_{ij}|=1,\) the following corollary can be obtained.

Corollary 2

Let \(u^{*}\) be the equilibrium point of impulsive DMRNN (2) or (3) and suppose Assumption 1 and Assumption 2 hold. Then, the equilibrium point \(u^{*}\) of impulsive DMRNN (2) or (3) is globally exponentially stable if for any \(k\in Z^{+},\) the following conditions are satisfied.

  • (i) \(\min _{1\le i\le n}(\tilde{d}_{i}-2 \sum _{j=1}^{n}\frac{|\tilde{a}_{ij}|\rho _{k}^{2}}{\tilde{d}_{j}\gamma _{i}})-\max _{1\le i\le n}\sum _{j=1}^{n} \sum _{k=1}^{n}\frac{2(\tilde{b}_{jk}\rho _{k})^{2}\gamma _{j}}{\tilde{d}_{j}\gamma _{i}}>0\);

  • (ii) \(\lambda >\delta ,\) where \(\lambda >0\) is a solution of \(\lambda -c+de^{\lambda \tau }\le 0,\) \(\delta =\sup _{k\in Z^{+}}\{\frac{\ln \delta _{k}}{t_{k}-t_{k-1}}\}\) with \(\delta _{k}=\max \{1,|\mu _{k}|\}\) and \(\mu _{k}=\max _{1\le i \le n}\{\mu _{ik}\}.\)

Remark 4

In this two corollaries, if let \(\mu _{ik}(u)=u\) for any \(i,k\in Z^{+},\) we can obtain the Theorems 1 and 2 of [28], which only considered the exponential stability of DMRNNs without impulse effects. In this sense, we push on the research of the DMRNNs. Furthermore, in these theories and corollaries, we could choose \(|\mu _{ik}|>1\) or \(|\mu _{ik}|\le 1\) for any \(i,k\in Z^{+}.\) As we know, when \(|\mu _{ik}|>1,\) Lyapunov function may jump out of the state trajectories of DMRNNs (2) or (3) at impulsive points \(t_{k}(k\in Z^{+}).\) Thus, the impulse effects may potentially destroy the stability of the original continuous DMRNNs (1). However, from these theories and corollaries, we can obtain that sufficient conditions concerned with the proper frequency and strength of impulses can maintain the stability of the original continuous stable DMRNNs.

4 Illustrative examples

Two numerical examples will be presented to illustrate the effectiveness of the above results in this section.

Example 1

Consider the following two-dimensional impulsive memristor-based recurrent neural networks with time-varying delays

$$\begin{aligned} \left\{ \begin{array}{ll} \dot{u}_{1}(t)=-4u_{1}(t)+a_{11}(u_{1}(t))f_{1}(u_{1}(t))+a_{12}(u_{1}(t))f_{2}(u_{2}(t))\\ \qquad \quad +b_{11}(u_{1}(t))g_{1}(u_{1}(t-\tau _{11}(t)))+b_{12}(u_{1}(t))g_{2}(u_{2}(t-\tau _{12}(t))) , t\ne t_{k},\\ \dot{u}_{2}(t)=-3u_{2}(t)+a_{21}(u_{2}(t))f_{1}(u_{1}(t))+a_{22}(u_{2}(t))f_{2}(u_{2}(t))\\ \qquad \quad +b_{21}(u_{2}(t))g_{1}(u_{1}(t-\tau _{21}(t)))+b_{22}(u_{2}(t))g_{2}(u_{2}(t-\tau _{22}(t))) , t\ne t_{k},\\ u_{i}(t_{k}^{+})=P_{ik}u_{i}(t_{k}^{-}), \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \quad k\in Z^{+}, \end{array} \right. \end{aligned}$$
(12)

where \(i=1,2,\) \(f_{i}(x)=g_{i}(x)=1/2(|x+1|-|x-1|),\) \(\tau _{11}(t)=\tau _{12}(t)=\tau _{21}(t)=\tau _{22}(t)=1-0.6\sin (t),\) \(\tau =1\) and

$$\begin{aligned} a_{11}=\left\{ \begin{array}{ll} -2, &{} |u_{1}(t)|<6 \\ 2, &{} |u_{1}(t)|>6 \end{array} \right. , a_{12}=\left\{ \begin{array}{ll} 2, &{} |u_{1}(t)|<6 \\ -2, &{} |u_{1}(t)|>6 \end{array} \right. ,\\ a_{21}=\left\{ \begin{array}{ll} 3, &{} |u_{2}(t)|<6 \\ -3, &{} |u_{2}(t)|>6 \end{array} \right. , a_{22}=\left\{ \begin{array}{ll} -2, &{} |u_{2}(t)|<6 \\ 2, &{} |u_{2}(t)|>6 \end{array} \right. ,\\ b_{11}=\left\{ \begin{array}{ll} 1, &{} |u_{1}(t)|<6 \\ -1, &{} |u_{1}(t)|>6 \end{array} \right. , b_{12}=\left\{ \begin{array}{ll} 1, &{} |u_{1}(t)|<6\\ -1, &{} |u_{1}(t)|>6 \end{array} \right. ,\\ b_{21}=\left\{ \begin{array}{ll} 1, &{} |u_{2}(t)|<6 \\ -1, &{} |u_{2}(t)|>6 \end{array} \right. , b_{22}=\left\{ \begin{array}{ll} 1, &{} |u_{2}(t)|<6 \\ -1, &{} |u_{2}(t)|>6 \end{array} \right. . \end{aligned}$$
Fig. 1
figure 1

Time–response curves without impulsive effects

Full size image
Fig. 2
figure 2

Time–response curves with impulsive effects \(P_{ik}>1\)

Full size image
Fig. 3
figure 3

Time–response curves with different impulsive effects \(P_{ik}>1\)

Full size image

In terms of the parameters defined in Theorem 1, we can obtain \(a=3>b=2,\) and the solution of \(\lambda -a+be^{\lambda \tau }=0\) is \(\lambda \approx 0.3001.\) Let \(t_{k}-t_{k-1}=0.35,\) \(P_{ik}=\delta _{k}=1.1\) for any \(i=1,2,\ldots ,n\) and \(k=1,2,\ldots,\) we can get \(\delta =\frac{\ln \delta _{k}}{t_{k}-t_{k-1}}\le 0.2725\le \lambda \approx 0.3001.\) Therefore, the equilibrium point \((0,0)^{T}\) of impulsive DMRNN (12) is globally exponentially stable, which is shown by Fig. 2. If let \(t_{k}-t_{k-1}=0.7,\) \(P_{ik}=-1.23\) for any \(i=1,2,\ldots ,n\) and \(k=1,2,\ldots ,\) we can get \(\delta =\frac{\ln \delta _{k}}{t_{k}-t_{k-1}}\le 0.2960\le \lambda \approx 0.3001\) according to the conditions (ii) and (iii) of Theorem 1. Then, the equilibrium point \((0,0)^{T}\) of impulsive DMRNN (12) is also globally exponentially stable. The simulations are shown in Fig. 3.

Remark 5

From Fig. 1, it can be seen that the equilibrium point \((0,0)^{T}\) of DMRNN (12) without impulse effects is globally exponentially stable. As we all know, if let \(\delta _{k}>1,\) impulsive disturbances may potentially destroy the neural network stability. However, from Figs. 2 and  3, it can be seen that sufficient conditions concerned with the magnitude and frequency of impulses can maintain the exponential stability of DMRNN (12).

Example 2

In impulsive DMRNNs (12), let \(f_{i}(x)=g_{i}(x)=\tanh (x),\) \(\tau _{11}(t)=\tau _{21}(t)=1-0.6\cos (t), \tau _{12}(t)=\tau _{22}(t)=1+0.6\sin (t)\) and

$$\begin{aligned} d_{1}= & {} \left\{ \begin{array}{ll} 1.5, &{} |u_{1}(t)|<1 \\ 1, &{} |u_{1}(t)|>1 \end{array} \right. , d_{2}=\left\{ \begin{array}{ll} 1, &{} |u_{2}(t)|<1\\ 1.5, &{} |u_{2}(t)|>1 \end{array} \right. ,\\ a_{11}= & {} \left\{ \begin{array}{ll} \frac{1}{5}, &{} |u_{1}(t)|<1 \\ -\frac{1}{5}, &{} |u_{1}(t)|>1 \end{array} \right. , a_{12}=\left\{ \begin{array}{ll} \frac{1}{4}, &{} |u_{1}(t)|<1 \\ -\frac{1}{4}, &{} |u_{1}(t)|>1 \end{array} \right. ,\\ a_{21}= & {} \left\{ \begin{array}{ll} \frac{1}{6}, &{} |u_{2}(t)|<1 \\ -\frac{1}{6}, &{} |u_{2}(t)|>1 \end{array} \right. , a_{22}=\left\{ \begin{array}{ll} \frac{1}{8}, &{} |u_{2}(t)|<1 \\ -\frac{1}{8}, &{} |u_{2}(t)|>1 \end{array} \right. ,\\ b_{11}= & {} \left\{ \begin{array}{ll} \frac{1}{5}, &{} |u_{1}(t)|<1\\ -\frac{1}{5}, &{} |u_{1}(t)|>1 \end{array} \right. , b_{12}=\left\{ \begin{array}{ll} \frac{1}{4}, &{} |u_{1}(t)|<1 \\ -\frac{1}{4}, &{} |u_{1}(t)|>1 \end{array} \right. ,\\ b_{21}= & {} \left\{ \begin{array}{ll} \frac{1}{6}, &{} |u_{2}(t)|<1\\ -\frac{1}{6}, &{} |u_{2}(t)|>1 \end{array} \right. , b_{22}=\left\{ \begin{array}{ll} \frac{1}{4}, &{} |u_{2}(t)|<1\\ -\frac{1}{4}, &{} |u_{2}(t)|>1 \end{array} \right. . \end{aligned}$$

In terms of the parameters defined in Theorem 2, we can obtain \(c=0.7082>d=0.3856,\) and the solution of \(\lambda -c+de^{\lambda \tau }=0\) is \(\lambda \approx 0.1683.\) Let \(t_{k}-t_{k-1}=0.35,\) \(P_{ik}=\delta _{k}=1.05\) for any \(i=1,2,\ldots ,n\) and \(k=1,2,\ldots,\) we can get \(\delta =\frac{\ln \delta _{k}}{t_{k}-t_{k-1}}\le 0.1395\le \lambda \approx 0.1683.\) Therefore, the equilibrium point \((0,0)^{T}\) of impulsive DMRNN (12) is globally exponentially stable, which is shown by Fig. 5. If let \(t_{k}-t_{k-1}=0.7,\) \(P_{ik}=1.12\) for any \(i=1,2,\ldots ,n\) and \(k=1,2,\ldots,\) we can get \(\delta =\frac{\ln \delta _{k}}{t_{k}-t_{k-1}}\le 0.1620\le \lambda \approx 0.1683\) according to the conditions (ii) and (iii) of Theorem 2. Then, the equilibrium point \((0,0)^{T}\) of impulsive DMRNN (12) is also globally exponentially stable. The simulations are shown in Fig. 6. On the other hand, if let \(t_{k}-t_{k-1}=0.7,\) \(P_{ik}=2.12\) for any \(i=1,2,\ldots ,n\) and \(k=1,2,\ldots,\) we can get \(\delta =\frac{\ln \delta _{k}}{t_{k}-t_{k-1}}\approx 1.0735>\lambda \approx 0.1683,\) which shows that the conditions of Theorem 2 are not satisfied. The simulation results are shown in Fig. 7.

Fig. 4
figure 4

Time–response curves without impulsive effects

Full size image
Fig. 5
figure 5

Time–response curves with impulsive effects \(P_{ik}>1\)

Full size image
Fig. 6
figure 6

Time–response curves with different impulsive effects \(P_{ik}>1\)

Full size image
Fig. 7
figure 7

Time–response curves with improper impulses \(P_{ik}>1\)

Full size image

Remark 6

We can see that the equilibrium point \((0,0)^{T}\) of DMRNN (12) without impulse effects is globally exponentially stable in Fig. 4. From Figs. 5 and 6, it can be seen that the exponential stability of DMRNN (12) depends on the values of \(t_{k}-t_{k-1}\) and \(P_{ik}.\) And the values of \(t_{k}-t_{k-1}\) are directly proportional to that of \(P_{ik},\) which shows that the proper magnitude and frequency of impulses can maintain the exponential stability of DMRNN (12).

Remark 7

When the impulsive jump operators \(\delta _{k}>1,\) the stable neural network could be potentially destroyed by impulsive disturbances, which is shown in from Fig. 7. In this case, some conditions are needed to give to maintain the stability. From Figs. 2, 3, 5, and 6, it can be seen that sufficient conditions concerned with the magnitude and frequency of impulses can maintain the stability of DMRNN, which illustrates that the conditions of this paper are effective.

5 Conclusions

In this paper, impulse effects have been exerted on the delayed memristor-based recurrent neural networks (DMRNNs), and a generalized impulsive DMRNN model has been introduced. Based on the published works of impulsive system and DMRNNs, the global exponential stability of the impulsive DMRNNs has been investigated. By means of impulsive differential inequality and Lyapunov function, several novel exponential stabilization criteria of this system have been obtained. Furthermore, it can be found that the uniformly stable criteria have also been derived by weakening the condition of Theorem 1 and 2. Finally, two numerical examples have been given to illustrate the effectiveness of the presented results, which shows that frequency and strength of impulses could stabilize the original DMRNNs. In the future, the concept of control topology and event-triggered impulse control strategy could be used to design impulsive control scheme to study the stability and synchronization of DMRNNs.