The stabilization of BAM neural networks with time-varying delays in the leakage terms via sampled-data control

Abstract

This paper is concerned with the stabilization of bidirectional associative memory neural networks with time-varying delays in the leakage terms using sampled-data control. We apply an input delay approach to change the sampling system into a continuous time-delay system. Based on the Lyapunov theory, some stability criteria are obtained. These conditions are expressed in terms of linear matrix inequalities and can be solved via standard numerical software. Finally, one numerical example is given to demonstrate the effectiveness of the proposed results .

1 Introduction

As we all know, time delays are unavoidable in many practical systems such as biology systems, automatic control systems and artificial neural networks [1–4]. The existence of time delays may lead to oscillation, divergence or instability of dynamical systems [2, 3]. Various types of time-delay systems have been investigated, and many significant results have been reported [4–10].

Recently, the stability of systems with leakage delays becomes one of the hot topics. The research about the leakage delay (or forgetting delay), which has been found in the negative feedback of system, can be traced back to 1992. In [11], it was observed that the leakage delay had great impact on the dynamical behavior of the system. Since then, many researchers have paid much attention to the systems with leakage delay and some interesting results have been derived. For example, Gopalsamy [12] considered a population model with leakage delay and found that the leakage delay can destabilization system. In [13], the bidirectional associative memory (BAM) neural networks with constant leakage delays were investigated based on Lyapunov–Krasovskii functions and properties of M-matrices. Inspired by [13], in [14], a class of BAM fuzzy cellular neural networks (FCNNs) with leakage delays was considered, in which the global asymptotic stability was studied by using the free-weighting matrices method. Furthermore, Liu [15] discussed the global exponential stability for BAM neural networks with time-varying leakage delays, which extended and improved the main results in [13, 14]. In addition, Lakshmanan et al. considered the stability of BAM neural networks with leakage delays and probabilistic time-varying delays via the Lyapunov–Krasovskii functional and stochastic analysis approach [16]. Li et al. [17] investigated the existence, uniqueness and stability of recurrent neural networks with leakage delay under impulsive perturbations and showed that the impact of leakage delay cannot be ignored. In particular, Li et al. gave the following example to describe this phenomenon [17].

Remark 1

Consider the following system with leakage delays.

$$\left\{ \begin{array}{ll} &\dot{x}(t)=-A x(t-\rho _1)+W {f}(y(t-\tau _1{(t)})),\\ &\dot{y}(t)=-Cy(t-\rho _2)+D x(t-\tau _2{(t)}), \end{array} \right.$$

(1)

where

$$\begin{aligned} A&= \left[ \begin{array}{ccc} 9&{} 0 \\ 0 &{} 8 \end{array} \right] ,\quad W= \left[ \begin{array}{ccc} -1.5&{} 0 \\ 1 &{} 2 \end{array} \right] ,\\ C&= \left[ \begin{array}{ccc} 8&{} 0 \\ 0 &{} 9 \end{array} \right] ,\quad D= \left[ \begin{array}{ccc} -0.9&{} 0 \\ 0&{} 1 \end{array} \right] , \end{aligned}$$

and $f=[f_1,\,f_2]^{T},\,{f_{i}}(y)=\frac{y^2}{1+y^2},\ \ \tau _1(t)=0.01{\sin ^2}t,\,\tau _2(t)=0.01{\cos ^2}t$.

If there is no leakage delay, system is stable. However, if leakage delays $\rho _1=\rho _2 =0.2$, system becomes unstable (see Figs. 1, 2).

The phenomena mentioned above show that a larger leakage delay can cause fluctuant. As we all know, stability is an important index of the system in application [18, 19]. So it is very important to take some control strategies to stabilize the instable system. Up to now, various control approaches have been adopted to stabilize those instable systems. Controls such as feedback control [20, 21], intermittent control [22, 23], impulsive control [24–27], fuzzy logical control [28] and sampled-data control [29] are adopted by many authors. The sampled-data control deals with continuous system by sampled data at discrete time. It drastically reduces the amount of transmitted information and increases the efficiency of bandwidth usage [30]. Compared with continuous control, the sampled-data control is more efficient, secure and useful [31], so it has a lot of applications. For example, Wu et al. [32] investigated the stability of neural network by using a sampled-data control with an optimal guaranteed cost. The synchronization problem of some networks was studied via sampled-data control [33, 34]. In addition, the performance of some nonlinear sampled-data controllers was analyzed in terms of the quantitative trade between robustness and sampling bandwidth in [35].

Fig. 1

The trajectories of state variables ($\rho _1=\rho _2=0$)

Fig. 2

The trajectories of state variables ($\rho _1=\rho _2=0.2$)

Motivated by the above discussion, the main purpose of this paper is to investigate the stabilization of BAM neural networks with time-varying leakage delays via sampled-data control. To the best of our knowledge, so far, there were no results on the stabilization analysis of BAM neural networks with time-varying leakage delays. By using the input delay approach, the BAM with leakage delay under the sampled-data control is transformed into a continuous system. Then, by using the Lyapunov stability theory, a stability criterion was expressed in terms of LMI toolbox. The paper is organized as follows. In the next section, the problem is formulated and some basic preliminaries and assumptions are given. In Sect. 3, an appropriate sampled-data controller is designed to stabilize BAM neural networks with time-varying leakage delays. In Sect. 4, one illustrative example is given to show the effectiveness of our results. Some conclusions are made in Sect. 5.

2 Preliminaries

Consider the following BAM neural network with time-varying leakage delays:

$$\begin{aligned} \left\{ \begin{array}{lll} \dot{\mu _{i}}(t)=-a_{i}\mu _{i}(t-\sigma (t))+\sum \nolimits _{j=1}^{n} b_{ij}^{(1)} \tilde{g}_j(\nu _j(t)) +\sum \nolimits _{j=1}^{n} b_{ij}^{(2)} \tilde{g}_j(\nu _j(t-\tau _1(t))) +I_{i},\\ \dot{\nu _j}(t)=-c_j\nu _j(t-\rho (t))+\sum \nolimits _{i=1}^{n} d_{ji}^{(1)} \tilde{f}_{i}(\mu _{i}(t)) +\sum \nolimits _{i=1}^{n} d_{ji}^{(2)} \tilde{f}_{i}(\mu _{i}(t-\tau _2(t)))+J_j, \end{array} \right. \end{aligned}$$

(2)

where $\mu _{i}(t)$ and $\nu _j(t)$ are the state variables of the neuron at time $t$, respectively. The positive constants $a_{i}$ and $c_j$ denote the time scales of the respective layers of the networks. $b_{ij}^{(1)}, b_{ij}^{(2)}, d_{ji}^{(1)}, d_{ji}^{(2)}$ are connection weights of the network. $I_{i}$ and $\ J_j$ denote the external inputs. $\sigma (t)$ and $\rho (t)$ are leakage delays; $\tau _1(t)$ and $\tau _2(t)$ are time-varying delays; $\tilde{g}_j(\cdot ),\ \tilde{f}_{i}(\cdot )$ are neuron activation functions.

Let $(\mu ^{*},\nu ^{*})^{T}$ be an equilibrium point of Eq. (2). Then, $(\mu ^{*},\nu ^{*})^{T}$ satisfies the following equations:

$$\begin{aligned} \left\{ \begin{array}{lll} 0=-a_{i}\mu _{i}^{*}+\sum \nolimits _{j=1}^{n} b_{ij}^{(1)} \tilde{g}_j(\nu _j^{*}) +\sum \nolimits _{j=1}^{n} b_{ij}^{(2)} \tilde{g}_j(\nu _j^{*}) +I_{i},\\ 0=-c_j\nu _j^{*}+\sum \nolimits _{i=1}^{n} d_{ji}^{(1)} \tilde{f}_{i}(\mu _{i}^{*}) +\sum \nolimits _{i=1}^{n} d_{ji}^{(2)} \tilde{f}_{i}(\mu _{i}^{*})+J_j. \end{array} \right. \end{aligned}$$

(3)

Shift the equilibrium point $(\mu ^{*},\nu ^{*})^{T}$ to the origin by $x_{i}(t)=\mu _{i}(t)-\mu _{i}^{*},\ \ y_{i}(t)=\nu _{i}(t)-\nu _{i}^{*}$. System (2) can be rewritten into the following compact matrix form:

$$\begin{aligned} \left\{ \begin{array}{lll} \dot{x}(t)=-A x(t-\sigma (t))+B_1 g(y(t))+ B_2 g(y(t-\tau _1(t))) \\ \dot{y}(t)=-C y(t-\rho (t))+D_1 f(x(t))+D_2 f(x(t-\tau _2(t))), \end{array} \right. \end{aligned}$$

(4)

where $A=\hbox {diag}[a_1,a_2\ldots a_n]>0,\ \ C=\hbox {diag}[c_1,c_2\ldots c_n]>0$, $B_k=(b_{ij}^{(k)})_{n\times n}$, $D_k=(d_{ij}^{(k)})_{n\times n},\,k=1,2$, $g(y(t))=\tilde{g}(y(t)+\nu ^{*})-\tilde{g}(\nu ^{*})$, and $f(x(t))=\tilde{f}(x(t)+\mu ^{*})-\tilde{f}(\mu ^{*})$.

Remark 2

In [17], the impact of leakage delay on stability of systems was discussed. That is, larger leakage delay can lead to the instability of system. However, how to control the harmful effect is not investigated. Next, we will study the stabilization of (4) via sampled-data control.

Let $\mu (t)=K x(t_k),\ \ \nu (t)=M y(t_k),$ where $K,M \in R^{n\times n}$ are the sampled-data feedback controller gain matrices to be designed. $t_k$ denotes the sample time point and satisfies $0=t_0<t_1\cdots <t_k<\cdots$, and $\lim \nolimits _{k\rightarrow +\infty }t_k=+\infty$. Moreover, there exists a positive constant $\tau _3$ such that $t_{k+1}-t_k\le \tau _3,\ \forall k\in {\mathbb {N}}$.

Under the sampled-data control, system (4) can be modeled as:

$$\begin{aligned} \left\{ \begin{array}{lll} \dot{x}(t)=-A x(t-\sigma (t))+B_1 g(y(t))+ B_2 g(y(t-\tau _1(t)))+\mu (t) \\ \dot{y}(t)=-C y(t-\rho (t))+D_1 f(x(t))+D_2 f(x(t-\tau _2(t)))+\nu (t), \end{array} \right. \end{aligned}$$

(5)

Let $\tau _3(t)=t-t_k$, for $t\in [t_k,\ t_{k+1}).$ Using the input delay method, we have

$$\begin{aligned} \left\{ \begin{array}{lll} \dot{x}(t)=-A x(t-\sigma (t))+B_1 g(y(t))+ B_2 g(y(t-\tau _1(t)))+K x(t-\tau _3(t)) \\ \dot{y}(t)=-C y(t-\rho (t))+D_1 f(x(t))+D_2 f(x(t-\tau _2(t)))+M y(t-\tau _3(t)), \end{array} \right. \end{aligned}$$

(6)

The initial conditions of model (6) are given as:

$$\begin{aligned} \begin{array}{lll} x(t)=\phi (t),\quad t\in [-s_1, 0]\\ y(t)=\psi (t),\quad t\in [-s_2, 0]\\ \end{array} \end{aligned}$$

where $s_1=\max \{\sigma _2, \tau _2, \tau _3 \},\ \ s_2=\max \{\rho _2, \tau _1, \tau _3 \}$

Remark 3

As is well known, it is difficult to analyze the stabilization of system (5) because of discrete term $\mu (t)=K x(t_k),$ and $\nu (t)=M y(t_k)$. Based on the input delay approach, which was put forward by Fridman in [36], the system (5) is changed as a continuous-time system (6). So we can discuss the stabilization of system (6).

In order to investigate stabilization of system (6) and calculate the sampled-data feedback controller gain matrices $K, M$, we need the following assumptions and lemmas.

Assumption 1

The leakage delays $\sigma (t),\ \rho (t)$ and the time-varying delays $\tau _1(t),\ \tau _2(t)$ are continuous differential functions and satisfy $0\le \sigma _1\le \sigma (t)<\sigma _2,\ \ 0\le \rho _1\le \rho (t)<\rho _2,\ \dot{\sigma }(t)<\sigma ,\ \dot{\rho }(t)<\rho ,\ 0<\tau _1(t)<\tau _1,\ \dot{\tau }_1(t)<\tau _{11}<1,\ 0<\tau _2(t)<\tau _2,\ \dot{\tau }_2(t)<\tau _{22}<1,$ where $\sigma _1,\sigma _2,\rho _1,\rho _2,\sigma ,\rho ,\tau _1,\tau _2,\tau _{11}$ and $\tau _{22}$ are constants.

Remark 4

It is worth pointing out that only upper bounds of leakage delays were considered in [37–39]. In this paper, we considered not only the upper bounds of leakage delays but also the lower bounds. Therefore, our results are more general than that in [37–39].

Assumption 2

There exist positive constants $\mu _{i}, \nu _{i}$, such that

$$\begin{aligned} 0 <\frac{g_{i}(x_{i})-g_{i}(\tilde{x}_{i})}{x_{i}-\tilde{x}_{i}}\le u_{i},\quad 0<\frac{f_{i}(x_{i})-f_{i}(\tilde{x}_{i})}{x_{i}-\tilde{x}_{i}}\le v_{i} \end{aligned}$$

for all $x_{i},\,\tilde{x}_{i} \in {\mathbb {R}}$, $x_{i}\ne \tilde{x}_{i},\,i=1,2\ldots n$

Lemma 1

[40] Given any real positive define symmetric matrix $M$ and a vector function $\omega (\cdot ): [a,b]\rightarrow {\mathbb {R}}^{n}$; then,

$$\begin{aligned} \left[ \int _a^b \omega (s)\mathrm{d}s\right] ^{T} M\left[ \int _a^b \omega (s)\mathrm{d}s\right] \le (b-a)\int _a^b \omega ^{T}(s)M\omega (s)\mathrm{d}s. \end{aligned}$$

Lemma 2

(Barbalat’s lemma) [41] If $w(t)$ is uniformly continuous, and $\int _{t_{0}}^{t}w(s)\mathrm{d}s$ has a finite limit as $t\rightarrow +\infty$, then $\lim \nolimits _{t\rightarrow +\infty }w(t)=0$

3 Main results

In this section, the stability of system (6) is investigated and the sufficient conditions for ensuring the stability of system are derived. By solving the LMIs, a suitable sampled-data controller is obtained to stabilize the BAM neural networks with time-varying leakage delays.

Theorem 1

Let Assumption 1 and 2 hold; then, the trivial solution of system (6) is globally asymptotically stable if there exist positive-definite symmetric matrices $P,\ Q,$ $P_{i}(i=1,2, 3),\ Q_{i}(i=1,2, 3),\ R_{i}(i=1,\ldots , 6),\ T_{i}(i=1,\ldots , 8),\ S_{i}(i=1,\ldots , 6)$, positive-definite diagonal matrices $X_{i}(i=1,\ldots , 4)$ and any matrices $X,Y$ such that the following LMIs hold:

$$\begin{aligned} \Pi _1&= \left[ \begin{array}{cccccccccccccccccccccccc} \pi ^1_{1,1}&{} \pi ^1_{1,2}&{} \pi ^1_{1,3}&{} \pi ^1_{1,4}&{}\pi ^1_{1,5}&{} 0&{}\pi ^1_{1,7}&{}\pi ^1_{1,8}&{} \pi ^1_{1,9}&{}0&{}\pi ^1_{1,11}\\ *&{}\pi ^1_{2,2} &{} 0&{} 0&{}\pi ^1_{2,5}&{}0&{}0&{}\pi ^1_{2,8}&{}\pi ^1_{2,9}&{}0&{}\pi ^1_{2,11}\\ *&{} *&{}\pi ^1_{3,3}&{}0&{}\pi ^1_{3,5}&{}0&{}0&{}0&{}0&{}0&{}0\\ *&{} *&{}*&{}\pi ^1_{4,4}&{}\pi ^1_{4,5}&{}0&{}0&{}0&{}0&{}0&{}0\\ *&{} *&{}*&{} *&{}\pi ^1_{5,5}&{}0&{}0&{}0&{}0&{}0&{}0\\ *&{} *&{}*&{} *&{}*&{}\pi ^1_{6,6}&{}0&{}0&{}0&{}0&{}0\\ *&{} *&{}*&{} *&{}*&{} *&{}\pi ^1_{7,7}&{}0&{}0&{}0&{}0\\ *&{} *&{}*&{} *&{}*&{}*&{} *&{}\pi ^1_{8,8}&{}0&{}0&{}0\\ *&{} *&{}*&{} *&{}*&{} *&{}*&{} *&{}\pi ^1_{9,9}&{}0&{}0\\ *&{} *&{}*&{} *&{}*&{} *&{}*&{}*&{} *&{}\pi ^1_{10,10}&{}\pi ^1_{10,11}\\ *&{} *&{}*&{} *&{}*&{} *&{}*&{} *&{}*&{} *&{}\pi ^1_{11,11}\\ \end{array} \right] <0. \end{aligned}$$

(7)

$$\begin{aligned} \Pi _2&= \left[ \begin{array}{cccccccccccccccccccccccc} \pi ^2_{1,1}&{} \pi ^2_{1,2}&{} \pi ^2_{1,3}&{} \pi ^2_{1,4}&{}\pi ^1_{1,5}&{} 0&{}\pi ^2_{1,7}&{}\pi ^2_{1,8}&{} \pi ^2_{1,9}&{}0&{}\pi ^2_{1,11}\\ *&{}\pi ^2_{2,2} &{} 0&{} 0&{}\pi ^2_{2,5}&{}0&{}0&{}\pi ^2_{2,8}&{}\pi ^2_{2,9}&{}0&{}\pi ^2_{2,11}\\ *&{} *&{}\pi ^2_{3,3}&{}0&{}\pi ^2_{3,5}&{}0&{}0&{}0&{}0&{}0&{}0\\ *&{} *&{}*&{}\pi ^2_{4,4}&{}\pi ^2_{4,5}&{}0&{}0&{}0&{}0&{}0&{}0\\ *&{} *&{}*&{} *&{}\pi ^2_{5,5}&{}0&{}0&{}0&{}0&{}0&{}0\\ *&{} *&{}*&{} *&{}*&{}\pi ^2_{6,6}&{}0&{}0&{}0&{}0&{}0\\ *&{} *&{}*&{} *&{}*&{} *&{}\pi ^2_{7,7}&{}0&{}0&{}0&{}0\\ *&{} *&{}*&{} *&{}*&{}*&{} *&{}\pi ^2_{8,8}&{}0&{}0&{}0\\ *&{} *&{}*&{} *&{}*&{} *&{}*&{} *&{}\pi ^2_{9,9}&{}0&{}0\\ *&{} *&{}*&{} *&{}*&{} *&{}*&{}*&{} *&{}\pi ^2_{10,10}&{}\pi ^2_{10,11}\\ *&{} *&{}*&{} *&{}*&{} *&{}*&{} *&{}*&{} *&{}\pi ^2_{11,11}\\ \end{array} \right] <0. \end{aligned}$$

(8)

where

$$\begin{aligned} \pi ^1_{1,1}&= P_1+P_2+P_3+R_3+R_4-S_2-S_3-T_1+T_3-T_4+(\tau _{22}-1)T_8+U^{T} X_1 U,\\ \pi ^1_{1,2}&= P-R_5, \ \pi ^1_{1,3}=S_2,\ \pi ^1_{1,4}=S_3,\ \pi ^1_{1,5}=-R_5 A,\\ \pi ^1_{1,7}&= T_1+(1-\tau _{22})T_8,\ \pi ^1_{1,8}=R_5 B_1,\ \pi ^1_{1,9}=R_5 B_2,\ \pi ^1_{1,11}=T_4+X,\\ \pi ^1_{2,2}&= \sigma _{12}^2 S_1+\sigma _1^2 S_2+\sigma _2^2 S_3+\tau _2^2 T_1+\tau _3^2 T_4+\tau _2^2 T_8 -R_5-R_5^{T},\\ \pi ^1_{2,5}&= -R_5 A,\ \ \pi ^1_{2,8}=R_5 B_1,\ \pi ^1_{2,9}=R_5 B_2,\ \pi ^1_{2,11}=X,\\ \pi ^1_{3,3}&= -P_2-S_1-S_2,\ \pi ^1_{3,5}=S_1,\\ \pi ^1_{4,4}&= -P_3-S_1-S_3,\ \pi ^1_{4,5}=S_1,\\ \pi ^1_{5,5}&= (\sigma -1)P_1-S_1-S_1^{T},\\ \pi ^1_{6,6}&= -R_4-T_1,\ \pi ^1_{6,7}=T_1,\\ \pi ^1_{7,7}&= (\tau _{22}-1)R_3-T_1-T_1^{T}+(\tau _{22}-1)T_8+U^{T} X_3 U,\\ \pi ^1_{8,8}&= -X_2,\\ \pi ^1_{9,9}&= -X_4,\\ \pi ^1_{10,10}&= -T_3-T_4,\ \pi ^2_{10,11}=T_4,\\ \pi ^1_{11,11}&= -T_4-T_4^{T},\\ \pi ^2_{1,1}&= Q_1+Q_2+Q_3+R_1+R_2-S_5-S_6-T_2+T_5-T_6+(\tau _{11}-1)T_7+V^{T} X_2 V,\\ \pi ^2_{1,2}&= Q-R_6, \ \pi ^1_{1,3}=S_5,\ \pi ^2_{1,4}=S_6,\ \pi ^2_{1,5}=-R_6 C,\\ \pi ^2_{1,7}&= T_2+(1-\tau _{11})T_7,\ \pi ^2_{1,8}=R_6 D_1,\ \pi ^2_{1,9}=R_6 D_2,\ \pi ^2_{1,11}=T_6+Y,\\ \pi ^2_{2,2}&= \rho _{12}^2 S_4+\rho _1^2 S_5+\rho _2^2 S_6+\tau _1^2 T_2+\tau _3^2 T_6+\tau _1^2 T_7 -R_6-R_6^{T},\\ \pi ^2_{2,5}&= -R_6 C,\ \ \pi ^2_{2,8}=R_6 D_1,\ \pi ^1_{2,9}=R_6 D_2,\ \pi ^2_{2,11}=Y,\\ \pi ^2_{3,3}&= -Q_2-S_4-S_5,\ \pi ^2_{3,5}=S_4,\\ \pi ^2_{4,4}&= -Q_3-S_4-S_6,\ \pi ^2_{4,5}=S_4,\\ \pi ^2_{5,5}&= (\rho -1)Q_1-S_4-S_4^{T},\\ \pi ^2_{6,6}&= -R_2-T_2,\ \pi ^2_{6,7}=T_2,\\ \pi ^2_{7,7}&= (\tau _{11}-1)R_1-T_2-T_2^{T}+(\tau _{11}-1)T_7+V^{T} X_4 V,\\ \pi ^2_{8,8}&= -X_1,\\ \pi ^2_{9,9}&= -X_3,\\ \pi ^2_{10,10}&= -T_5-T_6,\ \pi ^2_{10,11}=T_6,\\ \pi ^2_{11,11}&= -T_6-T_6^{T}, \ \sigma _{12}=\sigma _2-\sigma _1, \ \rho _{12}=\rho _2-\rho _1. \end{aligned}$$

Moreover, desired controller gain matrices are given as $K=R_5^{-1}X,\ \ M=R_6^{-1}Y$.

Proof

Consider the following general Lyapunov–Krasovskii functional:

$$\begin{aligned} V(t)=\sum \limits _{i=1}^8 V_{i}(t) \end{aligned}$$

where

$$\begin{aligned} V_1(t)&= x^{T}(t)P x(t)+y^{T}(t)Q y(t)\\ V_2(t)&= \int _{t-\sigma (t)}^t x^{T}(s)P_1x(s)\mathrm{d}s+\int _{t-\sigma _1}^t x^{T}(s)P_2 x(s)\mathrm{d}s+\int _{t-\sigma _2}^t x^{T}(s)P_3 x(s)\mathrm{d}s\\ V_3(t)&= \int _{t-\rho (t)}^t y^{T}(s)Q_1y(s)\mathrm{d}s+\int _{t-\rho _1}^t y^{T}(s)Q_2 y(s)\mathrm{d}s+\int _{t-\rho _2}^t y^{T}(s)Q_3 y(s)\mathrm{d}s\\ V_4(t)&= \int _{t-\tau _1(t)}^t y^{T}(s)R_1 y(s)\mathrm{d}s+\int _{t-\tau _1}^t y^{T}(s)R_2 y(s)\mathrm{d}s\\&\quad +\int _{t-\tau _2(t)}^t x^{T}(s)R_3 x(s)\mathrm{d}s+\int _{t-\tau _2}^t x^{T}(s)R_4 x(s)\mathrm{d}s\\ V_5(t)&= \sigma _{12}\int _{-\sigma _2}^{-\sigma _1} \int _{t+\theta }^t \dot{x}^{T}(s)S_1\dot{x}(s) \mathrm{d}s\mathrm{d}\theta +\sigma _1\int _{-\sigma _1}^0 \int _{t+\theta }^t \dot{x}^{T}(s) S_2\dot{x}(s) \mathrm{d}s\mathrm{d}\theta \\&\quad +\sigma _2\int _{-\sigma _2}^0 \int _{t+\theta }^t \dot{x}^{T}(s) S_3\dot{x}(s) \mathrm{d}s\mathrm{d}\theta + \tau _2\int _{-\tau _2}^0 \int _{t+\theta }^t \dot{x}^{T}(s)T_1\dot{x}(s) \mathrm{d}s\mathrm{d}\theta \\ V_6(t)&= \rho _{12}\int _{-\rho _2}^{-\rho _1} \int _{t+\theta }^t \dot{y}^{T}(s)S_4\dot{y}(s) \mathrm{d}s\mathrm{d}\theta +\rho _1\int _{-\rho _1}^0 \int _{t+\theta }^t \dot{y}^{T}(s) S_5\dot{y}(s) \mathrm{d}s\mathrm{d}\theta \\&\quad +\rho _2\int _{-\rho _2}^0 \int _{t+\theta }^t \dot{y}^{T}(s) S_6\dot{y}(s) \mathrm{d}s\mathrm{d}\theta + \tau _1\int _{-\tau _1}^0 \int _{t+\theta }^t \dot{y}^{T}(s)T_2\dot{y}(s) \mathrm{d}s\mathrm{d}\theta \\ V_7(t)&= \int _{t-\tau _3}^t x^{T}(s)T_3 x(s)\mathrm{d}s+\tau _3\int _{-\tau _3}^0 \int _{t+\theta }^t \dot{x}^{T}(s)T_4\dot{x}(s) \mathrm{d}s\mathrm{d}\theta \\&\quad +\int _{t-\tau _3}^t y^{T}(s)T_5 y(s)\mathrm{d}s+\tau _3\int _{-\tau _3}^0 \int _{t+\theta }^t \dot{y}^{T}(s)T_6\dot{y}(s) \mathrm{d}s\mathrm{d}\theta \\ V_8(t)&= \tau _1\int _{-\tau _1(t)}^0 \int _{t+\theta }^t \dot{y}^{T}(s)T_7\dot{y}(s) \mathrm{d}s\mathrm{d}\theta +\tau _2\int _{-\tau _2(t)}^0 \int _{t+\theta }^t \dot{x}^{T}(s)T_8\dot{x}(s) \mathrm{d}s\mathrm{d}\theta \end{aligned}$$

Calculate the derivative of $V(t)$ along the solution of the system (6),

$$\begin{aligned} \dot{V_1}(t)&= 2x^{T}(t)P \dot{x}(t)+2y^{T}(t)Q\dot{y}(t)\end{aligned}$$

(9)

$$\begin{aligned} \dot{V_2}(t)&= x^{T}(t)P_1x(t)-x^{T}(t-\sigma (t))P_1x(t-\sigma (t))(1-\sigma ) \nonumber \\&\quad +x^{T}(t)P_2x(t)-x^{T}(t-\sigma _1)P_2x(t-\sigma _1)\nonumber \\&\quad +x^{T}(t)P_3x(t)-x^{T}(t-\sigma _2)P_3x(t-\sigma _2) \end{aligned}$$

(10)

$$\begin{aligned} \dot{V_3}(t)&= y^{T}(t)Q_1 y(t)-y^{T}(t-\rho (t))Q_1 y(t-\rho (t))(1-\rho )\nonumber \\&\quad +y^{T}(t)Q_2 y(t)-y^{T}(t-\rho _1)Q_2 y(t-\rho _1)\nonumber \\&\quad +y^{T}(t)Q_3 y(t)-y^{T}(t-\rho _2)Q_3 y(t-\rho _2) \end{aligned}$$

(11)

$$\begin{aligned} \dot{V_4}(t)&= y^{T}(t)R_1y(t)-y^{T}(t-\tau _1(t))R_1y(t-\tau _1(t))(1-\tau _{11})\nonumber \\&\quad +y^{T}(t)R_2y(t)-y^{T}(t-\tau _1)R_2y(t-\tau _1)\nonumber \\&\quad +x^{T}(t)R_3x(t)-x^{T}(t-\tau _2(t))R_3x(t-\tau _2(t))(1-\tau _{22})\nonumber \\&\quad +x^{T}(t)R_4x(t)-x^{T}(t-\tau _2)R_4x(t-\tau _2) \end{aligned}$$

(12)

$$\begin{aligned} \dot{V_5}(t)&=\,\sigma _{12}\int _{-\sigma _2}^{-\sigma _1} \dot{x}^{T}(t)S_1\dot{x}(t)\mathrm{d}\theta -\sigma _{12}\int _{-\sigma _2}^{-\sigma _1} \dot{x}^{T}(t+\theta )S_1\dot{x}(t+\theta )\mathrm{d}\theta \nonumber \\&\quad +\sigma _1\int _{-\sigma _1}^0 \dot{x}^{T}(t)S_2\dot{x}(t)\mathrm{d}\theta -\sigma _1\int _{-\sigma _1}^0 \dot{x}^{T}(t+\theta )S_2\dot{x}(t+\theta )\mathrm{d}\theta \nonumber \\&\quad +\sigma _2\int _{-\sigma _2}^0 \dot{x}^{T}(t)S_3\dot{x}(t)\mathrm{d}\theta -\sigma _2\int _{-\sigma _2}^0 \dot{x}^{T}(t+\theta )S_3\dot{x}(t+\theta )\mathrm{d}\theta \nonumber \\&\quad +\tau _2\int _{-\tau _2}^0 \dot{x}^{T}(t)T_1\dot{x}(t)\mathrm{d}\theta -\tau _2\int _{-\tau _2}^0 \dot{x}^{T}(t+\theta )T_1\dot{x}(t+\theta )\mathrm{d}\theta \nonumber \\&= \sigma _{12}^2\dot{x}^{T}(t)S_1\dot{x}(t) -\sigma _{12}\int _{t-\sigma _2}^{t-\sigma _1}\dot{x}^{T}(\mu )S_1\dot{x}(\mu )\mathrm{d}\mu \nonumber \\&\quad +\sigma _1^2\dot{x}^{T}(t)S_2\dot{x}(t) -\sigma _1\int _{t-\sigma _1}^t\dot{x}^{T}(\mu )S_2\dot{x}(\mu )\mathrm{d}\mu \nonumber \\&\quad +\sigma _2^2\dot{x}^{T}(t)S_3\dot{x}(t) -\sigma _2\int _{t-\sigma _2}^t\dot{x}^{T}(\mu )S_3\dot{x}(\mu )\mathrm{d}\mu \nonumber \\&\quad +\tau _2^2\dot{x}^{T}(t)T_1\dot{x}(t) -\tau _2\int _{t-\tau _2}^t\dot{x}^{T}(\mu )T_1\dot{x}(\mu )\mathrm{d}\mu \nonumber \\&\le \sigma _{12}^2\dot{x}^{T}(t)S_1\dot{x}(t)-[x(t-\sigma _1)-x(t-\sigma (t))]^{T} S_1[x(t-\sigma _1)-x(t-\sigma (t))]\nonumber \\&-[x(t-\sigma (t))-x(t-\sigma _2)]^{T} S_1 [x(t-\sigma (t))-x(t-\sigma _2)]+\sigma _1^2 \dot{x}^{T}(t)S_2\dot{x}(t)\nonumber \\&- [x(t)-x(t-\sigma _1)]^{T} S_2 [x(t)-x(t-\sigma _1)]+\sigma _2^2 \dot{x}^{T}(t)S_3\dot{x}(t)\nonumber \\&- [x(t)-x(t-\sigma _2)]^{T} S_3[x(t)-x(t-\sigma _2)]+\tau _2^2\dot{x}^{T}(t)T_1\dot{x}(t)\nonumber \\&- [x(t-\tau _2(t))-x(t-\tau _2)]^{T} T_1[x(t-\tau _2(t))-x(t-\tau _2)]\nonumber \\&-[x(t)-x(t-\tau _2(t))]^{T} T_1 [x(t)-x(t-\tau _2(t))] \end{aligned}$$

(13)

$$\begin{aligned} \dot{V_6}(t)&= \rho _{12}^2\dot{y}^{T}(t)S_4\dot{y}(t) -\rho _{12}\int _{t-\rho _2}^{t-\rho _1}\dot{y}^{T}(\mu )S_4\dot{y}(\mu )\mathrm{d}\mu \nonumber \\&\quad +\rho _1^2\dot{y}^{T}(t)S_5\dot{y}(t) -\rho _1\int _{t-\rho _1}^t\dot{y}^{T}(\mu )S_5\dot{y}(\mu )\mathrm{d}\mu \nonumber \\&\quad +\rho _2^2\dot{y}^{T}(t)S_6\dot{y}(t) -\rho _2\int _{t-\rho _2}^t\dot{y}^{T}(\mu )S_6\dot{y}(\mu )\mathrm{d}\mu \nonumber \\&\quad +\tau _1^2\dot{y}^{T}(t)T_2\dot{y}(t) -\tau _1\int _{t-\tau _1}^t\dot{y}^{T}(\mu )T_2\dot{y}(\mu )\mathrm{d}\mu \nonumber \\&\le \rho _{12}^2\dot{y}^{T}(t)S_4\dot{y}(t)-[y(t-\rho _1)-y(t-\rho (t))]^{T} S_4[y(t-\rho _1)-y(t-\rho (t))]\nonumber \\&-[y(t-\rho (t))-y(t-\rho _2)]^{T} S_4 [y(t-\rho (t))-y(t-\rho _2)]+\rho _1^2 \dot{y}^{T}(t)S_5\dot{y}(t)\nonumber \\&- [y(t)-y(t-\rho _1)]^{T} S_5 [y(t)-y(t-\rho _1)]+\rho _2^2 \dot{y}^{T}(t)S_6\dot{y}(t)\nonumber \\&- [y(t)-y(t-\rho _2)]^{T} S_6[y(t)-y(t-\rho _2)]+\tau _1^2\dot{y}^{T}(t)T_2\dot{y}(t)\nonumber \\&- [y(t-\tau _1(t))-y(t-\tau _1)]^{T} T_2[y(t-\tau _1(t))-y(t-\tau _1)]\nonumber \\&-[y(t)-y(t-\tau _1(t))]^{T} T_2 [y(t)-y(t-\tau _1(t))] \end{aligned}$$

(14)

$$\begin{aligned} \dot{V_7}(t)&\le x^{T}(t) T_3 x(t)-x^{T}(t-\tau _3) T_3 x(t-\tau _3)+\tau _3^2 \dot{x}^{T}(t)T_4\dot{x}(t)\nonumber \\&-[x(t-\tau _3(t))-x(t-\tau _3)]^{T} T_4 [x(t-\tau _3(t))-x(t-\tau _3)]\nonumber \\&-[x(t)-x(t-\tau _3(t)]^{T} T_4 [x(t)-x(t-\tau _3(t)]\nonumber \\&\quad +y^{T}(t) T_5 y(t)-y^{T}(t-\tau _3) T_5 y(t-\tau _3)+\tau _3^2 \dot{y}^{T}(t)T_6\dot{y}(t)\nonumber \\&-[y(t-\tau _3(t))-y(t-\tau _3)]^{T} T_6 [y(t-\tau _3(t))-y(t-\tau _3)]\nonumber \\&-[y(t)-y(t-\tau _3(t)]^{T} T_6[y(t)-y(t-\tau _3(t)] \end{aligned}$$

$$\begin{aligned} \dot{V_8}(t)&\le \tau _1^2\dot{y}^{T}(t)T_7\dot{y}(t)-\tau _1(1-\tau _{11})\int _{t-\tau _1(t)}^t \dot{y}^{T}(s)T_7\dot{y}(s)\mathrm{d}s\nonumber \\&\quad +\tau _2^2\dot{x}^{T}(t)T_8\dot{x}(t)-\tau _2(1-\tau _{22})\int _{t-\tau _2(t)}^t \dot{x}^{T}(s)T_8\dot{x}(s)\mathrm{d}s\nonumber \\&\le \tau _1^2\dot{y}^{T}(t)T_7\dot{y}(t)-(1-\tau _{11})[y(t)-y(t-\tau _1(t))]^{T} T_7[y(t)-y(t-\tau _1(t))]\nonumber \\&\quad +\tau _2^2\dot{x}^{T}(t)T_8\dot{x}(t)-(1-\tau _{22})[x(t)-x(t-\tau _2(t))]^{T} T_8[x(t)-x(t-\tau _2(t))] \end{aligned}$$

(15)

In addition,

$$\begin{aligned} 0&= 2[x^{T}(t)+\dot{x}^{T}(t)]R_5[-\dot{x}(t)+\dot{x}(t)]\nonumber \\&= 2[x^{T}(t)+\dot{x}^{T}(t)]R_5[-\dot{x}(t)-A x(t-\sigma (t))+B_1 g(y(t))+ B_2 g(y(t-\tau _1(t)))+K x(t-\tau _3(t))]\nonumber \\&= -2x^{T}(t)R_5\dot{x}(t)-2x^{T}(t)R_5 Ax(t-\sigma (t))+2x^{T}(t)R_5 B_1 g(y(t))+2x^{T}(t)R_5 B_2 g(y(t-\tau _1(t)))\nonumber \\&\quad +2x^{T}(t)R_5 K x(t-\tau _3(t)) -2\dot{x}^{T}(t)R_5\dot{x}(t)-2\dot{x}^{T}(t)R_5 Ax(t-\sigma (t))+2\dot{x}^{T}(t)R_5 B_1 g(y(t)\nonumber \\&\quad +2\dot{x}^{T}(t)R_5 B_2 g(y(t-\tau _1(t)))+2\dot{x}^{T}(t)R_5 K x(t-\tau _3(t)) \end{aligned}$$

(16)

$$\begin{aligned} 0&= 2[y^{T}(t)+\dot{y}^{T}(t)]R_6[-\dot{y}(t)+\dot{y}(t)]\nonumber \\&= 2[y^{T}(t)+\dot{y}^{T}(t)]R_6[-\dot{y}(t)-C y(t-\rho (t))+D_1 f(x(t))+D_2 f(x(t-\tau _2(t)))+M y(t-\tau _3(t))]\nonumber \\&= -2y^{T}(t)R_6 \dot{y}(t)-2y^{T}(t)R_6 Cy(t-\rho (t))+2y^{T}(t)R_6 D_1 f(x(t))+2y^{T}(t)R_6 D_2 f(x(t-\tau _2(t)))\nonumber \\&\quad +2y^{T}(t)R_6 My(t-\tau _3(t))-2\dot{y}^{T}(t)R_6 \dot{y}(t)-2\dot{y}^{T}(t)R_6 C y(t-\rho (t))+2\dot{y}^{T}(t)R_6 D_1 f(x(t))\nonumber \\&\quad +2\dot{y}^{T}(t)R_6 D_2 f(x(t-\tau _2(t)))+2\dot{y}^{T}(t)R_6 My(t-\tau _3(t)) \end{aligned}$$

(17)

From Assumption 2, we have

$$\begin{aligned}&f^{T}(x(t))X_1 f(x(t))\le x^{T}(t)U^{T} X_1 U x(t)\\&g^{T}(y(t))X_2 g(y(t))\le y^{T}(t)V^{T} X_1 V y(t)\\&f^{T}(x(t-\tau _2(t)))X_3 f(x(t-\tau _2(t)))\le x^{T}(t-\tau _2(t))U^{T} X_3 U x(t-\tau _2(t))\\&g^{T}(y(t-\tau _1(t)))X_2 g(y(t-\tau _1(t)))\le y^{T}(t-\tau _1(t))V^{T} X_1 V y(t-\tau _1(t)) \end{aligned}$$

So,

$$\begin{aligned} \dot{V}(t)\le -\xi _1^{T}(t)\Pi _1^\star \xi _1(t)-\xi _2^{T}(t)\Pi _2^\star \xi _2(t) \end{aligned}$$

(18)

where $\Pi _1^\star =-\Pi _1>0,\ \Pi _2^\star =-\Pi _2>0$ are defined in (7) and (8) and

$$\begin{aligned} \xi _1^{T}(t)&= \left[ x^{T}(t),\dot{x}^{T}(t),x^{T}(t-\sigma _1), x^{T}(t-\sigma _2),x^{T}(t-\sigma (t)),x^{T}(t-\tau _2), x^{T}(t-\tau _2(t)),\right. \\&\left. g^{T}(y(t)),g^{T}(y(t-\tau _1(t)), x^{T}(t-\tau _3), x^{T}(t-\tau _3(t))\right] ,\\ \xi _2^{T}(t)&= \left[ y^{T}(t),\dot{y}^{T}(t),y^{T}(t-\rho _1), y^{T}(t-\rho _2),y^{T}(t-\rho (t)),y^{T}(t-\tau _1), y^{T}(t-\tau _1(t)),\right. \\&\left. f^{T}(x(t)),f^{T}(x(t-\tau _2(t)), y^{T}(t-\tau _3), y^{T}(t-\tau _3(t))\right] \end{aligned}$$

From (19), one has

$$\begin{aligned} V(t)+\int _0^t \xi _1^{T}(s)\Pi _1^\star \xi _1(s)\mathrm{d}s+\int _0^t \xi _2^{T}(s)\Pi _2^\star \xi _2(s)\mathrm{d}s\le V(0),\ \ t\ge 0. \end{aligned}$$

(19)

Moreover,

$$\begin{aligned} V(0)&\le \left[ \lambda _{\mathrm{max}}(P)+\sigma _2 \lambda _{\mathrm{max}}(P_1)+\sigma _1 \lambda _{\mathrm{max}}(P_2)+\sigma _2 \lambda _{\mathrm{max}}(P_3)+\tau _2 \lambda _{\mathrm{max}}(R_3)\right. \nonumber \\&\quad + \tau _2 \lambda _{\mathrm{max}}(R_4)+\frac{\sigma _2^2-\sigma _1^2}{2} \sigma _{12}\lambda _{\mathrm{max}}(S_1)+\frac{1}{2}\sigma _1^3 \lambda _{\mathrm{max}}(S_2)+\frac{1}{2}\sigma _2^3 \lambda _{\mathrm{max}}(S_3)\nonumber \\&\left. + \frac{1}{2}\tau _2^3 \lambda _{\mathrm{max}}(T_1)+\tau _3 \lambda _{\mathrm{max}}(T_3)+\frac{1}{2}\tau _3^3 \lambda _{\mathrm{max}}(T_4) +\frac{1}{2}\tau _2^3 \lambda _{\mathrm{max}}(T_8)\right] \Phi ^2\nonumber \\&\quad +\left[\lambda _{\mathrm{max}}(Q)+\rho _2 \lambda _{\mathrm{max}}(Q_1)+\rho _1 \lambda _{\mathrm{max}}(Q_2)+\rho _2 \lambda _{\mathrm{max}}(Q_3)+\tau _1 \lambda _{\mathrm{max}}(R_1)\right. \nonumber \\&+ \tau _1 \lambda _{\mathrm{max}}(R_2)+\frac{\rho _2^2-\rho _1^2}{2} \rho _{12}\lambda _{\mathrm{max}}(S_4)+\frac{1}{2}\rho _1^3 \lambda _{\mathrm{max}}(S_5)+\frac{1}{2}\rho _2^3 \lambda _{\mathrm{max}}(S_6)\nonumber \\&\left. + \frac{1}{2}\tau _1^3 \lambda _{\mathrm{max}}(T_2)+\tau _3 \lambda _{\mathrm{max}}(T_5)+\frac{1}{2}\tau _3^3 \lambda _{\mathrm{max}}(T_6) +\frac{1}{2}\tau _1^3 \lambda _{\mathrm{max}}(T_7)\right] \Psi ^2\nonumber \\&= \Delta _1 \Phi ^2 +\Delta _2 \Psi ^2<\infty \end{aligned}$$

(20)

where $\Phi =\max \{\sup \limits _{\theta \in [-s_1,0]}\parallel \phi (\theta )\parallel ,\sup \limits _{\theta \in [-s_1,0]} \parallel \dot{\phi }(\theta )\parallel \},$ $\Psi =\max \{\sup \limits _{\theta \in [-s_2,0]}(\parallel \psi (\theta )\parallel ,\sup \limits _{\theta \in [-s_2,0]} \parallel \dot{\psi }(\theta )\parallel )\}.$

On the other hand, by the definition of $V(t)$, we get

$$\begin{aligned} V(t)&\ge x^{T}(t)P x(t)+y^{T}(t)Q y(t)\nonumber \\&\ge \lambda _{\mathrm{min}}(P)x^{T}(t) x(t)+\lambda _{\mathrm{min}}(Q)y^{T}(t)y(t)\nonumber \\&= \lambda _{\mathrm{min}}(P)\parallel x(t)\parallel ^2+\lambda _{\mathrm{min}}(Q)\parallel y(t)\parallel ^2\nonumber \\&= \min \{\lambda _{\mathrm{min}}(P),\lambda _{\mathrm{min}}(Q)\} [\parallel x(t)\parallel ^2+\parallel y(t)\parallel ^2]. \end{aligned}$$

(21)

Then, combining (21) and (22), we obtain

$$\begin{aligned} \parallel x(t)\parallel ^2+\parallel y(t)\parallel ^2\le \frac{V(0)}{\min \{\lambda _{\mathrm{min}}(P),\lambda _{\mathrm{min}}(Q)\}}<\infty , \end{aligned}$$

(22)

which demonstrates that the solution of (6) is uniformly bound on $[0,\infty )$. Next, we shall prove that $(\parallel x(t)\parallel ,\parallel y(t)\parallel )\rightarrow (0,0)$ as $t\rightarrow \infty$. On the one hand, the boundedness of $\parallel \dot{x}(t)\parallel$ and $\parallel \dot{y}(t)\parallel$ can be deduced from (6) and (23). On the other hand, from (19), we have $\dot{V}(t)\le -\xi _1^{T}(t)\Pi _1^\star \xi _1(t)-\xi _2^{T}(t)\Pi _2^\star \xi _2(t)\le -\lambda _{\mathrm{min}}(\Pi _1^\star )x^{T}(t) x(t)-\lambda _{\mathrm{min}}(\Pi _2^\star )y^{T}(t) y(t).$ So, $\int _0^t x^{T}(s)x(s)\mathrm{d}s< \infty$ and $\int _0^t y^{T}(s)y(s)\mathrm{d}s< \infty$. By the lemma 2, we have $(\parallel x(t)\parallel ,\parallel y(t)\parallel )\rightarrow (0,0)$. That is, the equilibrium point of system (6) is globally asymptotically stable, which implies that the designed sampled-data control can stabilize the instable BAM neural networks with leakage delays. $\square$

In particular, if the leakage delays are constant, that is, $\sigma (t)=\sigma ,\ \ \rho (t)=\rho$. Then, the (6) becomes

$$\begin{aligned} \left\{ \begin{array}{lll} \dot{x}(t)=-A x(t-\sigma )+B_1 g(y(t))+ B_2 g(y(t-\tau _1(t)))+K x(t-\tau _3(t)) \\ \dot{y}(t)=-C y(t-\rho )+D_1 f(x(t))+D_2 f(x(t-\tau _2(t)))+M y(t-\tau _3(t)), \end{array} \right. \end{aligned}$$

(23)

Similar to the proof of Theorem 1, we have the following corollary.

Corollary 1

Let Assumptions 1 and 2 hold; then, the trivial solution of system (24) is globally asymptotically stable if there exist positive-definite symmetric matrices $P,\ Q,$ $P_1,\ Q_1,\ R_{i}(i=1,\ldots , 6),\ T_{i}(i=1,\ldots , 8),\ S_{i}(i=1,2)$, positive-definite diagonal matrices $X_{i}(i=1,\ldots , 4)$ and any matrices $X,Y$ such that the following LMIs hold:

$$\begin{aligned} \Pi _1=(\pi _{i,j}^1)_{9\times 9} <0,\ \ \Pi _2=(\pi _{i,j}^2)_{9\times 9} <0 \end{aligned}$$

(24)

where

$$\begin{aligned} \pi ^1_{1,1}&= P_1+R_3+R_4-S_1-T_1+T_3-T_4+(\tau _{22}-1)T_8+U^{T} X_1 U,\\ \pi ^1_{1,2}&= P-R_5, \ \pi ^1_{1,3}=S_1-R_5 A,\ \\ \pi ^1_{1,5}&= T_1+(1-\tau _{22})T_8,\ \pi ^1_{1,6}=R_5 B_1,\ \pi ^1_{1,7}=R_5 B_2,\ \pi ^1_{1,9}=T_4+X,\\ \pi ^1_{2,2}&= \sigma ^2 S_1 +\tau _2^2 T_1+\tau _3^2 T_4+\tau _2^2 T_8 -R_5-R_5^{T},\\ \pi ^1_{2,3}&= -R_5 A,\ \ \pi ^1_{2,6}=R_5 B_1,\ \pi ^1_{2,7}=R_5 B_2,\ \pi ^1_{2,9}=X,\\ \pi ^1_{3,3}&= -P_2-S_1,\ \\ \pi ^1_{4,4}&= -R_4-T_1,\ \pi ^1_{4,5}=T_1,\\ \pi ^1_{5,5}&= (\tau _{22}-1)R_3-T_1-T_1^{T}+(\tau _{22}-1)T_8+U^{T} X_3 U,\\ \pi ^1_{6,6}&= -X_2,\\ \pi ^1_{7,7}&= -X_4,\\ \pi ^1_{8,8}&= -T_3-T_4,\ \pi ^2_{8,9}=T_4,\\ \pi ^1_{9,9}&= -T_4-T_4^{T},\\ \pi ^2_{1,1}&= Q_1+R_1+R_2-S_2-T_2+T_5-T_6+(\tau _{11}-1)T_7+V^{T} X_2 V,\\ \pi ^2_{1,2}&= Q-R_6, \ \pi ^1_{1,3}=S_2-R_6 C,\ \\ \pi ^2_{1,5}&= T_2+(1-\tau _{11})T_7,\ \pi ^2_{1,6}=R_6 D_1,\ \pi ^2_{1,7}=R_6 D_2,\ \pi ^2_{1,9}=T_6+Y,\\ \pi ^2_{2,2}&= \rho ^2 S_5 +\tau _1^2 T_2+\tau _3^2 T_6+\tau _1^2 T_7 -R_6-R_6^{T},\\ \pi ^2_{2,5}&= -R_6 C,\ \ \pi ^2_{2,8}=R_6 D_1,\ \pi ^1_{2,9}=R_6 D_2,\ \pi ^2_{2,11}=Y,\\ \pi ^2_{3,3}&= -Q_1-S_2,\ \\ \pi ^2_{4,4}&= -R_2-T_2,\ \pi ^2_{4,5}=T_2,\\ \pi ^2_{5,5}&= (\tau _{11}-1)R_1-T_2-T_2^{T}+(\tau _{11}-1)T_7+V^{T} X_3 V,\\ \pi ^2_{6,6}&= -X_1,\\ \pi ^2_{7,7}&= -X_3,\\ \pi ^2_{8,8}&= -T_5-T_6,\ \pi ^2_{8,9}=T_6,\\ \pi ^2_{9,9}&= -T_6-T_6^{T}. \end{aligned}$$

Moreover, desired controller gain matrices are given as $K=R_5^{-1}X,\ \ M=R_6^{-1}Y$.

Remark 5

From Fig. 2, we can see that system (1) is unstable if $\rho _1=\rho _2=[0.2,0.2]^{T}$. Taking the sampling time points $t_k=0.01k,\ \ k=1,2,\ldots \ldots$ and solving LMIs (25), the gain matrices of the designed sampled-data controller can be obtained as follows:

$$\begin{aligned}K=R_5^{-1} X=\left[ \begin{array}{ccc} -48.5668 &{} 0.7458\\ 0.6336 &{} -48.9883 \end{array} \right] ,\,M=R_6^{-1} Y= \left[ \begin{array}{ccc} -46.4711 &{} -0.8717\\ -0.8318 &{} -49.8324 \end{array} \right] , \end{aligned}$$

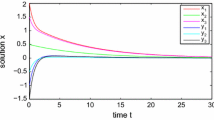
By Corollary 1, system (1) is asymptotically stable under the given sampled-data control. Figure 3 shows the trajectories of state variables.

Fig. 3

The trajectories of state variables ($\rho _{i}=0.2$) under the sampled-data control

Remark 6

In fact, the leakage delay has very important effect on the dynamic behavior of systems. The larger leakage delay can cause instability of system. This phenomenon can be seen in [17]. In pervious papers [13–17], the author only considered the stability of BAM with leakage delays based on Lyapunov–Krasovskii functionals, free-weighting matrices and so on. Different from those articles, our paper mainly investigates the stabilization of BAM neural networks with leakage delays. The sampled-data controllers are designed by solving LMIs. When the leakage delays lead to the instability of system, we can stabilize the system by sampled-data control.

4 Numerical examples

In this section, a simulation example is given to show the feasibility and efficiency of the theoretic results.

Example 1

Consider the following BAM neural networks with leakage delays

$$\begin{aligned} \left\{ \begin{array}{lll} \dot{x}(t)=-A x(t-\sigma (t))+B_1 g(y(t))+ B_2 g(y(t-\tau _1(t)))+K x(t-\tau _3(t)) \\ \dot{y}(t)=-C y(t-\rho (t))+D_1 f(x(t))+D_2 f(x(t-\tau _2(t)))+M y(t-\tau _3(t)), \end{array} \right. \end{aligned}$$

(25)

where

$$\begin{aligned} A&= \left[ \begin{array}{ccc} 0.6&{} 0&{} 0 \\ 0 &{} 0.6&{} 0\\ 0&{} 0 &{}0.5 \end{array} \right] ,\quad B1= \left[ \begin{array}{ccc} 0.9&{} 0&{} -1.2 \\ -0.7 &{} 0&{} 1\\ 0&{}0.2 &{}1.3 \end{array} \right] ,\\ B2&= \left[ \begin{array}{ccc} 1&{} 0&{} 0.2 \\ -1.2 &{} 0&{} 0.4\\ 0.5&{}-0.2 &{}0 \end{array} \right] ,\quad C= \left[ \begin{array}{ccc} 0.9&{} 0&{} 0 \\ 0 &{} 0.8&{} 0\\ 0&{}0 &{}0.9 \end{array} \right] ,\\ D1&= \left[ \begin{array}{ccc} 0.4&{} -0.8&{} 0 \\ -0.5 &{} 0.4&{} 0.8\\ 1&{}0 &{}0.4 \end{array} \right] ,\quad D2= \left[ \begin{array}{ccc} 0.3&{} 0&{} 0 \\ 0 &{} 0.3&{} 0\\ 0&{}0 &{}0.3 \end{array} \right] . \end{aligned}$$

The neuron activation functions $g_{i}(y)={\tan }h(y_{i}),\ \ f_j(x)={\tan }h(x_j)$. The time-varying leakage delays $\sigma (t)=0.5+0.01 {\sin }t,\ \ \rho (t)=0.4+0.01 {\cos }t$. Time-varying delays are chosen as $\tau _1(t)=0.1 \sin ^2 t,\ \ \tau _2(t)=0.1 \cos ^2 t.$

It is easy to see that $\sigma _1=0.51,\ \sigma _2=0.49,\ \ \rho _1=0.41,\ \ \rho _2=0.39,\ \ \sigma = \rho =0.01,\ \ \tau _{11}=\tau _{12}=0.2<1.$ $\mu _{i}^+=1,\ \ \nu _{i}^+=1,\ \ U=\hbox {diag}[1,1,1], \ \ V=\hbox {diag}[1,1,1].$ By the simulation results, it can be observed that the system (26) is unstable (Fig. 4).

Fig. 4

The state trajectories of system (26)

In addition, the stabilization of the system (26) by designing suitable sampled-data controller is investigated. Taking sampling time points $t_k=0.02k, \,k=1,2,\ldots \ldots ,$ and the sampling period is $\tau =0.02$. Solving LMIs (7) and (8), we have:

$$\begin{aligned} P&= \left[ \begin{array}{ccc} 0.0393 &{} 0.0140 &{} 0.0035\\ 0.0140 &{} 0.0383 &{} 0.0018\\ 0.0035 &{} 0.0018 &{} 0.0299\\ \end{array} \right] ,\quad Q= \left[ \begin{array}{ccc} 0.0415 &{} 0.0042 &{} -0.0028\\ 0.0042 &{} 0.0387 &{} 0.0001\\ -0.0028 &{} 0.0001 &{} 0.0372\\ \end{array} \right] ,\\ P_1&= \left[ \begin{array}{ccc} 0.0082 &{} 0.0048 &{} 0.0013\\ 0.0048 &{} 0.0081 &{} 0.0003\\ 0.0013 &{} 0.0003 &{} 0.0060\\ \end{array} \right] ,\quad P_2= \left[ \begin{array}{ccc} 0.0046 &{} 0.0029 &{} 0.0008\\ 0.0029 &{} 0.0044 &{} 0.0003\\ 0.0008 &{} 0.0003 &{} 0.0030\\ \end{array} \right] ,\\ P_3&= \left[ \begin{array}{ccc} 0.0046 &{} 0.0031 &{}0.0008\\ 0.0031 &{} 0.0044 &{} 0.0003\\ 0.0008 &{} 0.0003 &{} 0.0030\\ \end{array} \right] ,\quad Q_1= \left[ \begin{array}{ccc} 0.0082 &{} 0.0016 &{} -0.0011\\ 0.0016 &{} 0.0071 &{} 0.0001\\ -0.0011 &{} 0.0001 &{} 0.0067\\ \end{array} \right] ,\\ Q_2&= \left[ \begin{array}{ccc} 0.0078 &{} 0.0019 &{} -0.0013\\ 0.0019 &{} 0.0066 &{} 0.0001\\ -0.0013 &{} 0.0001 &{} 0.0059\\ \end{array} \right] ,\quad Q_3= \left[ \begin{array}{ccc} 0.0078 &{} 0.0019 &{}-0.0013\\ 0.0019 &{} 0.0066 &{} 0.0001\\ -0.0013 &{} 0.0001 &{} 0.0060\\ \end{array} \right] ,\\ R_1&= \left[ \begin{array}{ccc} 0.0204 &{} 0.0008 &{} -0.0005\\ 0.0008 &{} 0.0198 &{} -0.0001\\ -0.0005 &{} -0.0001 &{} 0.0195\\ \end{array} \right] ,\quad R_2= \left[ \begin{array}{ccc} 0.0118 &{} 0.0016 &{} -0.0011\\ 0.0016 &{} 0.0108 &{} 0.0001\\ -0.0011 &{}0.0001 &{} 0.0103\\ \end{array} \right] ,\\ R_3&= \left[ \begin{array}{ccc} 0.0135 &{} 0.0048 &{} 0.0012\\ 0.0048 &{} 0.0132 &{} 0.0004\\ 0.0012 &{} 0.0004 &{} 0.0110\\ \end{array} \right] ,\quad R_4=\left[ \begin{array}{ccc} 0.0110 &{}0.0048 &{} 0.0013\\ 0.0048 &{} 0.0107 &{} 0.0004\\ 0.0013 &{} 0.0004 &{} 0.0085\\ \end{array} \right] ,\\ R_5&= \left[ \begin{array}{ccc} 0.0223 &{} 0.0181 &{} 0.0045\\ 0.0181 &{} 0.0212 &{} 0.0021\\ 0.0045 &{} 0.0021&{} 0.0113\\ \end{array} \right] ,\quad R_6= \left[ \begin{array}{ccc} 0.0204&{} 0.0063 &{} -0.0042\\ 0.0063 &{} 0.0164 &{} 0.0003\\ -0.0042 &{} 0.0003 &{} 0.0142\\ \end{array} \right] ,\\ X&= \left[ \begin{array}{ccc} -0.0401 &{} -0.0126 &{} -0.0035\\ -0.0128 &{} -0.0389 &{} -0.0013\\ -0.0034 &{} -0.0011 &{} -0.0339\\ \end{array} \right] ,\quad Y= \left[ \begin{array}{ccc} -0.0412 &{} -0.0033 &{} 0.0021\\ -0.0032 &{} -0.0396 &{} -0.0001\\ 0.0021 &{}-0.0001&{} -0.0380\\ \end{array} \right] , \end{aligned}$$

The gain matrices of the designed controller can be obtained as follows:

$$\begin{aligned} K=R_5^{-1} X= \left[ \begin{array}{ccc} -4.6177 &{} 3.2262 &{} 0.9644\\ 3.2443 &{} -4.5385 &{} -0.5644\\ 0.9622 &{} -0.5668 &{} -3.2755\\ \end{array} \right] ,\quad M=R_6^{-1} Y= \left[ \begin{array}{ccc} -2.3625 &{} 0.7271 &{} -0.5697\\ 0.7230 &{} -2.7043 &{} 0.2700\\ -0.5696 &{} 0.2709 &{}-2.8503\\ \end{array} \right] , \end{aligned}$$

Due to the limitation of space, the other solution matrices $\left( T_{i}(i=1,\ldots , 8),\ \ S_{i}(i=1,\ldots , 6),\ \ X_{i}(i=1,\ldots , 4)\right)$ are not given. This indicates that all conditions in Theorem 1 are satisfied. By Theorem 1, system (26) is globally asymptotically stable under the given sampled-data control. Figure 5 shows the trajectories of the state variables.

Fig. 5

The state trajectories of system (26) with sampled-data control

5 Conclusion

In this paper, a new sampled-data control strategy and its stability analysis are developed to stabilize BAM neural networks with leakage delays. We firstly analyzed instability phenomena caused by the leakage delays. Afterward, we employed sampled-data control strategy to stabilize the instable systems. Some LMIs were derived to calculate the gain matrix of the designed sampled-data controller. Finally, a numerical example was given to show the effectiveness of our theoretic results. The complexity of some control strategies will be considered in future. Some biological networks with leakage delay are also important research direction in our future work.