1 Introduction

Statistical process control methodology is used to assess the performance of processes. Control charts are applied to attain this objective. These charts help in decision making either to declare process is in control or out of control. Process stability and improved capability by decreasing variability can be achieved using a set of tools called statistical process control (SPC). These tools include conventional control charts and exponentiated weighted moving average (EWMA) charts. Conventional control charts are called Shewhart charts like average \(\left(\overline{x }\right)\) and range (R) for variable data. Anyhow these charts are less sensitive to small shifts. EWMA charts are considered better than traditional charts for detecting small shifts. Another major difference between Shewhart control charts and EWMA charts is their structure and measurement procedure. In the Shewhart chart, conclusion about a shift in the process is made on the basis of the distribution arrangement of data on the Shewhart chart. In EWMA charts, statistic is a directly estimated parameter, see DeVor et al. (2007). Conventionally data in any process is considered exact numbers but in real life, the nature of data is fuzzy due to ambiguity in measurement and ecological conditions. In the presence of uncertainty fuzzy EWMA (FEWMA) charts are used to achieve better results. In this situation, fuzzy set theory is applied using fuzzy numbers and verbal variables to seize uncertainty. According to Gülbay and Kahraman (2007), fuzzy set theory plays a vital role in presenting and modeling vague data where human subjectivity is involved in the definition of characteristics. The fuzzy set theory provides a base to deal with ambiguous data. In this situation application of fuzzy control charts is unavoidable.

The concept of fuzzy control charts was introduced by Raz and Wang (1990) and Wang and Raz (1990). They gave the concept of dealing with linguistic variables mathematically and suggested a probabilistic approach and membership approach. The concept of fuzzy data was introduced by Kanagawa et al. (1993). The rules of statistical process control were modified using fuzzy logic to overcome the frequency of false alarms and enhance the ability of true alarms [(El-Shal and Morris (2000)]. The fuzzy SPC approach for control and assessment was proposed as a combination of process control and intelligence system [Rowlands and Wang (2000)]. The idea of an α-cut control chart was suggested using triangular fuzzy numbers to deal with attributes for checkups [Gülbay et al. (2004)]. The technique to develop fuzzy control charts dealing with fuzzy outcomes was suggested by Cheng (2005). Furthermore, two fuzzy control charts based on fuzzy numbers were proposed. A direct fuzzy approach to deal with fuzzy data for attribute charts was proposed and implemented to calculate probabilities of fuzzy events, see Gülbay and Kahrama (2006, 2007). Faraz and Moghadam (2007) suggested a fuzzy control chart as an alternative to the average control chart.

Fuzzy individual and moving control charts with α-cuts were introduced by Erginel (2008). They applied the median transformation technique to get the final results. Senturk and Erginel (2009) gave the idea of \(\stackrel{\sim }{\overline{X} }-\tilde{R }\) and \(\stackrel{\sim }{\overline{X} }-\tilde{S }\) fuzzy charts using \(\alpha -cuts\) with median transformation technique. Furthermore, they develop these charts using a triangular fuzzy number. Similarly, a regression control chart in a fuzzy environment was suggested by Sentürk (2010). Senturk et al. (2011) suggested a fuzzy attribute control chart \(\tilde{u }\). Kaya and Kahraman (2011) proposed fuzzy control charts to measure quality characteristics and also used them to check the capability of processes. The average-run length (ARL) approach which is the most popular and successful way, determines the performance of the EWMA control chart (Montgomery 2009). Khan et al. (2018) proposed a fuzzy EWMA chart that detects small shifts in the mean of a process in a fuzzy environment. The chart is more appropriate, more flexible, and more useful in real-life quality control problems.

The researchers developed a fuzzy EWMA scheme based on an np chart and tested the fuzzy EWMA chart on real-life data from the food industry. The performance of the chart was evaluated using the out of control (ARL1) values. The fuzzy EWMA chart outperforms the conventional EWMA chart in terms of small ARL1s. It was concluded that conventional ARLs may be misleading in fuzzy environments; thus, fuzzy ARLs were the most accurate way to evaluate EWMA control charts in fuzzy environments.

Moghadam et al. (2016) indicated fuzzy EWMA control charts for phase II fuzzy profile monitoring. These charts were extensions of conventional EWMA control charts for phase II profile monitoring. They used the ranking method to detect small shifts in the process. Using fuzzy data, Senturk et al. (2014) transformed the conventional EWMA control chart into a fuzzy form to detect changes in the process and determined that the proposed chart is effective for detecting small changes and improving process performance.

Senturk et al. (2014) proposed a control chart using fuzzy logic and did not study the performance of the proposed chart using the average run length (ARL). The novelty of this study is that the performance of both conventional and fuzzy exponentiated weighted moving average (FEWMA) charts are presented in terms of ARLs and compared to the conventional chart. The fuzzy EWMA chart is a better alternative to the conventional chart in the fuzzy environment in the presence of small shifts and is more sensitive to small shifts comparatively.

2 Methodology

In this section, the control limits of the fuzzy EWMA chart and algorithm are presented to perform the simulation study.

2.1 Control limits of fuzzy EWMA control chart: structure and calculation

The control limits of the chart Senturk et al. (2014) using the food color measurements data of Zabihinpour et al. (2014) are given as

$${{U\tilde{C }L}^{\alpha }}_{\mathrm{med}-\mathrm{EWMA}}={\tilde{C }L}_{\mathrm{med}-\mathrm{EWMA}}+{\frac{1}{3}A}_{2}\left({{\overline{R} }^{\alpha }}_{a},{\overline{R} }_{b},{{\overline{R} }^{\alpha }}_{c}\right)\sqrt{\left(\frac{\lambda }{2-\lambda }\right)}$$
(1)
$$ \tilde{C}L_{{{\text{med}} - {\text{EWMA}}}} = \frac{1}{3}\left( {\bar{\bar{X}}_{a} ^{\alpha } + \bar{\bar{X}}_{b} + \bar{\bar{X}}_{c} ^{\alpha } } \right) $$
(2)
$${{L\tilde{C }L}^{\alpha }}_{\mathrm{med}-\mathrm{EWMA}}={\tilde{C }L}_{\mathrm{med}-\mathrm{EWMA}}+{\frac{1}{3}A}_{2}\left({{\overline{R} }^{\alpha }}_{a},{\overline{R} }_{b},{{\overline{R} }^{\alpha }}_{c}\right)\sqrt{\left(\frac{\lambda }{2-\lambda }\right)}$$
(3)

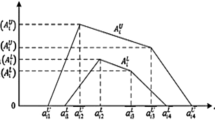
where \( \left( {\bar{\bar{X}}_{a} ^{\alpha } + \bar{\bar{X}}_{b} + \bar{\bar{X}}_{c} ^{\alpha } } \right) \) is \(\alpha \)-cut of \( {\bar{\bar{X}}} \) of triangular fuzzy number, \(\left({{\overline{R} }^{\alpha }}_{a},{\overline{R} }_{b},{{\overline{R} }^{\alpha }}_{c}\right)\) is \(\alpha -\) cut of \(\overline{R }\) of triangular fuzzy number, \({A}_{2}\) is constant of control chart, and \(\lambda \) is parameter.

The calculations of the control limits when \(\lambda =0.9\) are given as follows

$$ \overline{\overline{X}}_{a}^{\alpha } = 8..8312 + 0.65\left( {7.995 - 8.8312} \right),\;\overline{\overline{X}}_{a}^{\alpha } = 8.93,\;\overline{\overline{X}}_{c}^{\alpha } = \overline{\overline{X}}_{c} - \alpha \left( {\overline{\overline{X}}_{c} - \overline{\overline{X}}_{b} } \right) $$
$$ \overline{\overline{X}}_{c}^{\alpha } = 8.1525 - \left( {8.1525 - 8.995} \right),\;\overline{\overline{X}}_{c}^{\alpha } = 8.25,\;\overline{\overline{X}}_{b}^{\alpha } = 8.59 $$
$$ \overline{R}_{a}^{\alpha } = 0.6808 + 0.65\left( {1.0164 - 06808} \right),\;\overline{R}_{a}^{\alpha } = 0.8989,\;\overline{R}_{b} = 1.0164 $$
$$ {\overline{\text{R}}}_{{\text{c}}}^{{\upalpha }} = 1.2984 - 0.65\left( {1.2984 - 1.0164} \right),\;{\overline{\text{R}}}_{{\text{c}}}^{{\upalpha }} = 1.4817 $$
$${{U\tilde{C }L}^{\alpha }}_{\mathrm{med}-\mathrm{EWMA}}=8.36+\frac{1}{3}\left(0.8989+1.0164+1.4817\right)(0.57)\sqrt{\frac{0.9}{2-0.9}}$$
$${{U\tilde{C }L}^{\alpha }}_{\mathrm{med}-\mathrm{EWMA}}=8.70$$
$${\tilde{C }L}_{\mathrm{med}-\mathrm{EWMA}}=8.36$$
$${{L\tilde{C }L}^{\alpha }}_{\mathrm{med}-\mathrm{EWMA}}=8.36-\frac{1}{3}\left(0.8989+1.0164+1.4817\right)(0.57)\sqrt{\frac{0.9}{2-0.9}}$$
$${{L\tilde{C }L}^{\alpha }}_{\mathrm{med}-\mathrm{EWMA}}=7.91$$

The average run length (ARL) is indicated on average when the process can go out of control. The ARL is an important performance measurement to compare and validate the fuzzy EWMA control chart. The ARL is defined by

$${\mathrm{ARL}}_{0}=\frac{1}{{P}_{in0}}$$
(4)

where \({P}_{in0}\) denotes the probability of the in-control process.

The ARL for the shifted process is defined by

$$AR{L}_{1}=\frac{1}{{P}_{in1}}$$
(5)

where \({P}_{in1}\) denotes the probability of in-control for the shifted process.

The performance of the control chart proposed by Senturk et al. (2014) is discussed using the simulated data. The values of ARL1 are calculated for various specified values of ARL0 and shown in Tables 1, 2, 3.

Table 1 Average run length when the process is in control limits (ARL0)
Full size table
Table 2 Average run length when the process is not in control (ARL1) for EWMA chart
Full size table
Table 3 Fuzzy average-run length when the process is not in control (ARL1) for fuzzy chart
Full size table

In Tables 2, 3, \({{\varvec{\mu}}}_{0}\) denotes the average for the in-control process, \(k\) is a constant and \({{\varvec{\mu}}}_{1}\) is average at the shifted process. From Tables 1, 2, 3, the following trends can be noted in ARL1.

  1. 1.

    For a fixed value of, the values of ARL0 decrease as \(\lambda \) decreases.

  2. 2.

    For a fixed value of µ1, the values of ARL1 increase as \(\lambda \) decreases.

2.2 Simulation

In this section, the detail of the simulation study is given. A total of 25 samples, each of size 5, are simulated for this purpose. The first 15 subgroups of size 5 are simulated when the process is in the in-control state using the standard normal distribution and the next 10 subgroups are generated at a shift in mean that is 1. Furthermore, use simulated data with 25 samples each of size 5 and construct control limits of conventional and fuzzy EWMA charts. The simulated data is shown in Tables 4, 5.

Table 4 Simulated data normal random variable (sample size \(n\)=5)
Full size table
Table 5 Simulated data from fuzzy normal random variable when n = 5
Full size table

The algorithm used to compute the control chart coefficients and the ARLs is given as follows.

  1. 1.

    Generate a standard normal random variable with 25 samples, each with sample size n = 5 using MATLAB.

  2. 2.

    Determine the in-control limits using \({\mu }_{0}\)=0, \(\sigma \)=1, \(\lambda \)=0.5 so that the in-control ARL, ARL0, as a function of \({\mu }_{0}\), σ, and λ, becomes 371 using 10,000 simulations, with 25 samples.

  3. 3.

    Similarly, to estimate the ARL1, the process is simulated 100,000 times for an out-of-control process with \(k\)= (1, 1.5, 2, 2.5) and, \(\lambda \)= (0.02, 0.03, 0.04, 0.05, 0.07). In this case, the ARL1, which is a function of \(\sigma \) and \(\lambda \).

  4. 4.

    The same simulation process is repeated in a fuzzy environment, the difference being the use of a fuzzy normal random variable with 25 samples, each sample size \(n\)=5, and each observation as a triangular fuzzy number.

  5. 5.

    Furthermore, conventional and fuzzy EWMA control charts are constructed based on simulated data.

  6. 6.

    Shift in the process is presented for the conventional and fuzzy control chart graphically.

3 Results and discussion

The fuzzy EWMA chart proposed by Senturk et al. (2014) is applied to the data. In Table 1, the values of ARL0 are shown when the process is in control. The values of ARL0 decrease with an increase in \(\lambda \). Similarly, in Table 2 the ARL1 for conventional EWMA control is presented. Finally, in Table 3 ARL1 for fuzzy EWMA control is calculated. Results clearly show that ARL1 of fuzzy EWMA control chart is less than that of conventional EWMA control chart. Furthermore, conventional EWMA control chart Fig. 1a detects shift at the 25th sample at \(\lambda \)=0.02 and mean shift of 0.5, while fuzzy EWMA chart Fig. 1b detects shift at the 20th sample. It indicates better performance of the fuzzy EWMA control chart as compared to the conventional EWMA control chart. Figure 2a shows the fuzzy EWMA control chart, while Fig. 2b displays the conventional EWMA control chart. The fuzzy EWMA control chart shows less variation than a conventional EWMA control chart. Additionally, the ARL1 of the fuzzy EWMA chart is lower than the ARL1 of conventional EWMA charts. It is concluded that a fuzzy EWMA control chart performs better in a fuzzy environment. In this situation, the traditional EWMA chart is less effective.

Fig. 1
figure 1

a Conventional control chart identifies shift at 25th sample. b The fuzzy control chart shows a shift at the 20th sample

Full size image
Fig. 2
figure 2

(a) Fuzzy EWMA chart (b) Conventional EWMA control chart

Full size image

4 Conclusions

A simulation study was carried out on the basis of the average run length (ARL) in order to compare the performance of the conventional EWMA control chart with that of the fuzzy EWMA control chart. The efficiency of the fuzzy EWMA control chart was shown over the traditional EWMA control chart in terms of ARL. The results showed a significant difference between the two charts. The in-control ARL values for fuzzy EWMA were larger than those for conventional EWMA charts. The fuzzy EWMA chart identified shifts in the process mean more rapidly than conventional EWMA control charts. Likewise, the out-of-control ARL values s for fuzzy EWMA were better (smaller) than those for the non-fuzzy EWMA control chart. The fuzzy EWMA control chart outperformed the standard EWMA control chart in this case. In addition, sample data showed that the fuzzy EWMA chart was more sensitive than the traditional EWMA chart in capturing out-of-control signals, which were graphically displayed. It has been shown that in a fuzzy environment this technique is very effective in detecting small shifts and faster than conventional EWMA charts. It was observed that the fuzzy EWMA control chart performed better than the conventional chart in a fuzzy environment. In future, the same analysis can be extended to other properties of control charts, such as standard deviation of the run length (SDRL), the median of run length (MDRL), standard error of the average run length (SEARL), and percentiles of run length, for traditional and fuzzy EWMA control charts. The proposed control chart using repetitive sampling can be extended for future research.