1 Introduction

It is acknowledged that quality is an integral part of virtually all products and services. Over the last decades, quality has become one of the essential services in the selection of competing manufactured goods and commodities [1]. There are three major areas in statistical methods for quality control and improvement which are statistical process control, design of experiments and acceptance sampling. Statistical Process Control (SPC) has absorbed a significant amount of attention as an effective tool in reducing the variability of processes and improving quality. It is used to measure, record, analyse and make a decision in solving the problem of the company. Control chart was first projected in the 1920s by Walter Andrew Shewhart. It is employed to monitor processes and to perform different tests using a wide variety of information about causes of variability in the data. The process gives information about the product’s situation and the necessary precautions that should be taken by noticing abnormal and normal situations of the process of the product. Normally in the production process, Shewhart control charts are used to detect shifts in a process. Nonetheless, Shewhart control charts or known as conventional charts are relatively insensitive for detecting changes in the analysis, particularly when the shift is relatively small. Therefore, the Exponentially Weighted Moving Average (EWMA) chart is the most excellent choice for detecting small shifts in the process variation. Besides, the conventional charts depict independent sample data points, of which each of these points is interpreted according to the probability law of the sampling distribution of the statistic in question and inferences about possible shifts in the process parameters are made indirectly through the distribution patterns of the data on conventional chart [2]. Nevertheless, EWMA can estimate the corresponding process parameter and the EWMA data on the chart tends to move slowly to the new level following a shift in the process, or will vary about the centerline with small fluctuations when the process is in control [3].

Historically, the EWMA chart was introduced by Roberts in 1959 and has been used by several organizations in the industries as the basis of new control or performance charts. EWMA also known as geometric moving average (GMA) plots the exponentially weighted moving average of individual measurements or subgroup means. Besides, it is used in time series modeling and forecasting as the calculated weights decline geometrically when connected by a smooth curve. This indicates that it is very insensitive to the normality assumption, so it is the superlative chart to replaces the conventional chart when normality cannot be assumed. In fact, Borror et al. [4] proves that the EWMA chart is robust to the normality assumption by comparing the performance of average run length (ARL) between the conventional chart and the EWMA chart for the non-normal distribution data. As a result, they conclude that when the assumption of normality is violated, the ARL of the conventional chart is adversely affected but the EWMA chart can be designed in which the “in-control” ARL is reasonably close to the normal theory value for both skewed and heavily tailed symmetric non-normal distributions. Yet, it is not always feasible to analyse the non-normal distribution data. The data comes in many forms that include “uncertainty” or “vagueness” due to some difficulties while obtaining the handled data from operators or process records. Thus, fuzzy control charts are proposed to evaluate the process with fuzzy data as the concepts and techniques of fuzzy control charts contribute towards dealing with uncertainty or impression while monitoring the process. The fuzzy set theory was first introduced in 1965 by Zadeh. It is a mathematical tool that deals with the uncertainty that comes from a shortage of information, incompleteness, vagueness and inaccurate measurements [5]. Fuzzy control charts are inevitable to be used when the data are uncertain or vague [6].

In recent years, many studies have used type-1 fuzzy numbers which is also referred as fuzzy numbers in control charts. Özdemir et al. [7] investigated the application of fuzzy \(\overline{X }\) and R control charts as well as fuzzy Cumulative Sum (CUSUM) control charts, employing α-cut methods based on trapezoidal fuzzy numbers. Conversely, Kaya et al. [8] developed a fuzzy attribute control chart and implemented it in a real-world scenario within a manufacturing facility. Furthermore, Ahmad et al. [9] devised fuzzy \(\overline{X }\) and s charts specifically tailored for unbalanced data sets, a contribution made in 2022. Additionally, investigations into process capability have been undertaken to validate the performance of these methodologies. In 2016, Darestani and Nasiri [10] studied the fuzzy \(\overline{X }\) and s control chart, and so did process capability indices in normal data environments. A research by Shu et al. [11] studied the fuzzy s control charts in 2017. They integrated fuzzy number theories to establish the fuzzy control charts under a general variable sample size condition. Sabahno et al. [12] utilised the fuzzy mode defuzzification technique using fuzzy \(\overline{X }\) and R control chart to design the decision procedure in the proposed fuzzy adaptive control chart. Other than that, Truong et al. [13] analysed the attribute control chart construction based on fuzzy score numbers in China for sustainable manufacturing in the Vietnam textile dyeing industry to monitor the fuzzy average number of nonconformities per unit. Nevertheless, much of the data used in daily life cannot be designated as type-1 fuzzy numbers and some of it is more suitable for type-2 fuzzy numbers [14]. With the recent development in fuzzy theory, the interval type-2 fuzzy (IT2F) control chart is one of the potential methods to overcome the limitation of a type-1 fuzzy control chart. Furthermore, IT2F charts are more capable in detecting the meaning of process shifts. For example, Erginel et al. [15] monitoring a special case of type-2 fuzzy number was more suitable to use due to the human imprecise judgment on quality characteristics in monitoring the process with statistical control charts which is IT2F number. Almeida et al. [16] concluded that type-2 fuzzy numbers demonstrated enhanced efficacy in analyzing \(\overline{X }\) and R control charts, suggesting their superior robustness. Subsequently, Kaya et al. [17] introduced attribute type-2 fuzzy sets and implemented them within the automotive sector. Their findings suggest that the IT2F chart exhibits greater sensitivity when compared to conventional charting methods. Mohd Razali et al. [18] similarly affirmed the superiority of the IT2F chart over traditional approaches, noting its heightened capability in capturing and interpreting ambiguous and vague data. Therefore, this paper attempts to combine the knowledge of IT2F numbers and the EWMA chart. So far, to the best of the authors' knowledge, there has been no research paper on the interval type-2 fuzzy EWMA (IT2F-EWMA) control charts. It is an effort to depart from conventional control charts. Previously, researchers used the conventional control chart as an alternative to \(\overline{X }\) and R in analysing of an unruly process into statistical control [1]. It is noticed that, the conventional chart is relatively cannot handle the small process shifts because the conventional control chart ignores the information given by the entire sequence of points [1]. Alternatively, the EWMA control chart can be used in identifying the small shifts in the process that are less than 1.5σ.

In light of the advantages of EWMA and the ability of IT2F numbers to deal with uncertain data, the main contribution of this study is the development of IT2F-EWMA charts as a new method in the industrial area. Among the highlights in the new method are the substitution of crisp numbers into EWMA with interval type-2 fuzzy numbers and the insertion of defuzzification step in the algorithm where this step can improve the control limits. Moreover, the method introduces the utilization of Sigma XL software, employing the Markov Chain rule to assess performance, as evidenced by the average run length values. In addition, Razali et al. [19] provided a review and learned that there is no research has been studied on type-2 fuzzy EWMA since only type-2 fuzzy attribute charts have been explored until now. Aside from that, this study also provides a comparison between conventional EWMA, type-1 fuzzy EWMA, and type-2 fuzzy EWMA control charts. This comparative analysis is made to find out the most vulnerable chart in detecting non-conformance thereby supporting manufacturers in eliminating nonconformists and ultimately reducing the manufacturing costs. Ultimately, the average run length (ARL) for each chart has been calculated to obtain the best charts in EWMA.

The new method of the IT2F-EWMA chart is the main contribution to this study, and it is implemented in the agricultural sector which is focusing on fertilizer production. The study is structured into 6 sections. Section 2 delivers a comprehensive review of previous studies on EWMA charts and their applications. The theoretical framework of the proposed method is developed and discussed in Sect. 3. In Sect. 4, computational procedures of the proposed method to the data of fertilizers’ production are implemented. A comparative analysis is made in Sect. 5. Lastly, the conclusions of this study are reserved in Sect. 6.

2 Literature Review

EWMA is a moving mean chart where an “exponentially weighted mean” is calculated, and a new result or conformant data is obtained. Very recently, de Vasconcellos et al. [20] studying the EWMA control chart using flow history and assured energy levels to small hydroelectric power plants in Brazil. The researcher analysed the flow history of 24 plants using EWMA control charts to verify whether climate change, land use or occupation could have changed the average annual flow available in the basin over time because the electricity generation at the plants has been below the Assured Energy Levels (AELs). As a result, EWMA control charts prove that the sensitivity of assured energy to hydrological variations evaluates the use of daily average flow rates for calculating and analysing the energy generated by small power plants. Also very recently, Perry [21] analysed some issues related to manufacturing processes regarding social networks by using an open-source Enron e-mail corpus. The researcher develops a network monitoring strategy using an EWMA control chart to detect shifts in the hierarchical tendency of directed graphs over time. The strategies are important to the organization’s stakeholders when interest lies in monitoring shifts in the general health of the organization.

In another research, Saghir et al. [22] examined the EWMA control chart on an auxiliary variable and repetitive sampling for efficient detection of small to moderate shifts in process location. The researcher compares the proposed EWMA chart with the competitive existing control charts. Accordingly, they conclude that the proposed EWMA chart is the best chart to identify the small changes in the analysis. Still, to provide past evidence on the edges of EWMA control chats, Lal and Kane [23] developed the EWMA charts by analysing the acceleration-time domain signals for the condition monitoring of the gearbox to recognize the fault at an initial stage. Nowadays, the gearbox is used in many manufacturing and engineering areas. However, the common fault in the gearbox is gear tooth failure due to scoring, wear, pitting, and tooth fracture. Therefore, in their research, the EWMA chart has been plotted based on the severity of faults. In a nutshell, the chart is observed as an effective tool in identifying the deviation from the normal condition.

At this juncture, EWMA control charts have been dealing with crisp data where the data is assumed to be precise and correct. However, one of the most important and critical considerations in the manufacturing area is the failure of data due to manufacturing processes and also expert opinions. This situation is more prevalent particularly when dealing with qualitative data [14]. Therefore, fuzzy set theories are capable in representing vague data. Fuzzy theory is one of the most applicable tools that academia has employed to deal with uncertainty [10]. On top of that, the use of a fuzzy approach in the design of control charts has allowed for improving the performance of conventional control charts, as well as enabled a simple approach for the design of control charts for linguistic variables with multinomial distributions for both, the univariate case and the multivariate case [24]. The development of a chart is not only to examine the process of central tendency, but it will also to indicate the degree of fuzziness of the data itself [25].

In the very recent work of fuzzy sets theory combined with quality control, Khan et al. [26] developed a fuzzy EWMA control chart for monitoring a production system. The comparison between the fuzzy EWMA charts and conventional EWMA was made and the average run length was computed for the fuzzy environments. Goztok et al. [27] studied the use of triangular fuzzy numbers with an α-level cut technique and process performance with the process capability index to monitor a pumice block plant. The α-level cut technique is sensitive to analyze the process requirement. As a result, the researcher concludes that the proposed fuzzy EWMA charts are sensitive in detecting small shifts. Another triangular fuzzy EWMA research, Hesamian et al. [28] employs a common notion of a normal fuzzy random variable with fuzzy mean and non-fuzzy variance in industry. The existing methods which rely on induced imprecise observations of a normal distribution with fuzzy mean and variance are not helpful since it does not investigate the statistical properties relevant to a fuzzy EWMA chart. Hence, in the study, the concept of triangular fuzzy EWMA was implemented in the detection of shifts in small persistent processes and it shows that the fuzzy EWMA is more vulnerable in identifying the small process displacements. The use of triangular fuzzy numbers again appeared in the works of. They demonstrated that triangular fuzzy EWMA charts in monitoring process mean of cooking oil filling process in a food industry in Pakistan. Ten samples of fuzzy observations are being computed by using the α-cut median approach. From the results, the newly developed EWMA charts point out that it is effective in identifying small process shifts.

Evidence of using triangular fuzzy numbers in EWMA was further provided by Senturk et al. [2]. They developed EWMA control charts for univariate data in the clothing industry in Turkey. Plastic buttons that were produced by small-scale enterprises had been produced by using molds. The shifts and deviations were small due to the production of molds. Consequently, fuzzy data on the external diameter of circular plastic buttons that were collected from the production process shows that triangular fuzzy EWMA control charts not only detect small shifts in processes under a fuzzy environment but also increase the flexibility of control limits to prevent false alarms. Further, Alipour and Noorossana [30] investigated vectors of variable quality characteristics by using a fuzzy EWMA control chart. The proposed fuzzy EWMA chart is being compared with fuzzy Hotelling’s T2 control chart based on the process mean of the data. Accordingly, the researcher indicates that uniformly superior performance of the triangular fuzzy EWMA control chart over the fuzzy Hotelling’s T2 control chart.

It is good to note that all triangular fuzzy numbers mentioned here are a kind of type-1 fuzzy numbers of which there is one single membership with no concept of interval. One of the limitations of type-1 fuzzy numbers in quality control is the possibility of degrading the performance of inputs and outputs. This limitation was shared by [31] those who asserted that type-1 fuzzy chart cannot handle the uncertainties associated with inputs and outputs membership functions As a result, it may degrade the performance of type-1 fuzzy numbers especially when the plant is subjected to the disturbances. To overcome this limitation, type-2 fuzzy charts were introduced to model such uncertainties because their membership functions are given in two layers. Type 2 fuzzy set theory captures ambiguity that associates the uncertainty of membership functions by incorporating footprints and models high-level uncertainty [15]. Once the process monitoring tools have detected an assignable cause, this cause is removed to bring the process back into control [32]. The development of fuzzy EWMA control charts and their applications are presented in this section is summarised in Table 1.

Table 1 Summary of literature on EWMA control chart
Full size table

It can be seen that most of the previous research is focused on conventional EWMA charts and type-1 fuzzy EWMA (T1F-EWMA) charts. This review also provides evidence of the scarcity of type-2 EWMA in quality control studies. Indeed, Razali et al. [19] conducted a comprehensive examination of recent research pertaining to fuzzy control charts over the preceding five years. The prevailing emphasis within prior investigations has predominantly centered on type-1 fuzzy control charts. Conversely, limited attention has been devoted to attributes specific to type-2 fuzzy charts by previous scholars. Consequently, this highlights the lack of exploration concerning numerous other control chart variants utilizing type-2 fuzzy numbers. To bridge this research gap, this study aims to propose an IT2F EWMA control chart and its application to fertilizer production. Furthermore, the feasibility and validity of the proposed method are checked with a comparative analysis and Average Run Length (ARL).

3 Proposed IT2F-EWMA Control Charts

This section provides the definitions of IT2F sets and their arithmetic operations. These definitions are the prerequisite concepts prior to developing IT2F-EWMA.

3.1 Definitions and Arithmetic Operations

Zadeh [34] was first introduced to the type-2 fuzzy set in 1965. He suggested that type-1 fuzzy numbers is different from type-2 fuzzy numbers despite similarity in the concept of membership functions.

Definition 3.1.1: The type-2 fuzzy numbers, \(\widetilde{A}\), are demonstrated as follows:

$$ \tilde{A} = \left\{ {\left( {\left( {x,u} \right),\mu _{{\tilde{A}}} \left( {x,u} \right)} \right)|\forall x \in X,\forall u \in J_{x} \subseteq \left[ {0,1} \right],0 \le \mu _{{\tilde{A}}} (x,u) \le 1} \right\} $$
(1)

while Jx is designated as an interval [0, 1]. However, \(\tilde{A}\) is described as IT2F numbers when all \(\mu_{{\tilde{A}}} \approx (x,u) = 1\)[35]. In this definition, Jx is another fuzzy sets in interval [0,1] and it is indeed a subset of \(\tilde{A}\).

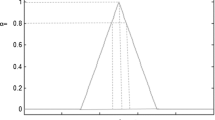
Definition 3.1.2: A trapezoidal fuzzy number in type-2 fuzzy sets is three-dimensional as provided in Fig. 1 [36].

Fig. 1
figure 1

The upper trapezoidal membership functions and the lower trapezoidal membership function of the IT2F set \(\tilde{A}\)

Full size image

In this figure, the intervals of fuzzy numbers and their corresponding memberships are readily apparent. For example, the number \(a_{12}\) has an interval of \(a_{12}^{u}\) and \(a_{12}^{L}\).

In this study, the upper trapezoidal membership function, and the lower trapezoidal membership function of the IT2F set are illustrated as:

$$ \tilde{A}_{i} = (\tilde{A}_{i}^{U} ,\tilde{A}_{i}^{L} )\; = \;\left( {\begin{array}{*{20}c} {(a_{i1}^{U} ,\;\;a_{i2}^{U} ,\;a_{i3}^{U} ,\;a_{i4}^{U} \;;\;\;H_{1} (A_{i}^{U} ),\;H_{2} (A_{i}^{U} ))} \\ {(a_{i1}^{L} ,\;\;a_{i2}^{L} ,\;a_{i3}^{L} ,\;a_{i4}^{L} \;;\;\;H_{1} (A_{i}^{L} ),\;H_{2} (A_{i}^{L} ))} \\ \end{array} } \right) $$
(2)

where \({A}_{i}^{U}\) and \({A}_{i}^{L}\) are type-2 fuzzy sets, \(a_{i1}^{U} ,\;a_{i2}^{U} ,\;a_{i3}^{U} ,\;a_{i4}^{U} ,a_{i1}^{L} ,\;a_{i2}^{L} ,\;a_{i3}^{L}\) and \(a_{i4}^{L}\) are the reference points of \({\widetilde{A}}_{i} .\) \({H}_{j}\left({A}_{i}^{U}\right)\) is the membership value of \({a}_{i\left(j+1\right)}^{U}\) in the \({A}_{i}^{U},\) 1 ≤ j ≤ 2, whereas \({H}_{j}\left({A}_{i}^{L}\right)\) is the membership value of \({a}_{i\left(j+1\right)}^{L}\) in the\({A}_{i}^{L}\), \(1 \le j \le 2,H_{1} \left( {A_{i}^{U} } \right),H_{2} \left( {A_{i}^{U} } \right),H_{1} \left( {A_{i}^{L} } \right),H_{2} \left( {A_{i}^{L} } \right) \subseteq \left[ {0,1} \right],\;1 \le i \le n.\)

Let \({\widetilde{A}}_{1}\) and \({\widetilde{A}}_{2}\) are the trapezoidal in the fuzzy sets:

$$ \tilde{A}_{1} = (A_{1}^{U} ,\;A_{1}^{L} )\; = \left( {\begin{array}{*{20}c} {(a_{11}^{U} ,\;\;a_{12}^{U} ,\;a_{13}^{U} ,\;a_{14}^{U} \;;\;\;H_{1} (A_{1}^{U} ),\;H_{2} (A_{1}^{U} )),} \\ {(a_{11}^{L} ,\;\;a_{12}^{L} ,\;a_{13}^{L} ,\;a_{14}^{L} \;;\;\;H_{1} (A_{1}^{L} ),\;H_{2} (A_{1}^{L} ))} \\ \end{array} } \right) $$
(3)
$$\tilde{A}_{2} = (A_{2}^{U} ,\;A_{2}^{L} )\; = \;\left( {\begin{array}{*{20}c} {(a_{21}^{U} ,\;\;a_{22}^{U} ,\;a_{23}^{U} ,\;a_{24}^{U} \;;\;\;H_{1} (A_{2}^{U} ),\;H_{2} (A_{2}^{U} )),\;\;} \\ {(a_{21}^{L} ,\;\;a_{22}^{L} ,\;a_{23}^{L} ,\;a_{24}^{L} \;;\;\;H_{1} (A_{2}^{L} ),\;H_{2} (A_{2}^{L} ))} \\ \end{array} } \right).$$
(4)

The arithmetic operations of the trapezoidal interval type-2 are described as follows [36]:

i. Addition operation:

$$ \tilde{A}_{1} \oplus \tilde{A}_{2} = \;(A_{1}^{U} ,\;A_{1}^{L} ) \oplus (A_{2}^{U} ,\;A_{2}^{L} ) = \left( {\;\begin{array}{*{20}c} {(a_{11}^{U} + \;a_{21}^{U} ,\;\;a_{12}^{U} + \;a_{22}^{U} ,\;\;a_{13}^{U} + \;a_{23}^{U} ,\;a_{14}^{U} + \;a_{24}^{U} )\;;\;} \\ {\begin{array}{*{20}c} {min\;(H_{1} (A_{1}^{U} );H_{1} (A_{2}^{U} )\;),\;min\;(H_{2} (A_{1}^{U} );H_{2} (A_{2}^{U} )\;),} \\ {\begin{array}{*{20}c} {(a_{11}^{L} + \;a_{21}^{L} ,\;\;a_{12}^{L} + \;a_{22}^{L} ,\;\;a_{13}^{L} + \;a_{23}^{L} ,\;a_{14}^{L} + \;a_{24}^{L} )\;;} \\ {min\;(H_{1} (A_{1}^{L} );H_{1} (A_{2}^{L} )\;),\;min\;(H_{2} (A_{1}^{L} );H_{2} (A_{2}^{L} )\;)\;} \\ \end{array} } \\ \end{array} } \\ \end{array} } \right) $$
(5)

ii. Subtraction operation:

$$\tilde{A}_{1} { \ominus }\;\tilde{A}_{2} = \;(A_{1}^{U} ,\;A_{1}^{L} ) { \ominus }(A_{2}^{U} ,\;A_{2}^{L} ) = \left( {\;\begin{array}{*{20}l} {(a_{11}^{U} - \;a_{24}^{U} ,\;\;a_{12}^{U} - \;a_{23}^{U} ,\;\;a_{13}^{U} - \;a_{22}^{U} ,\;a_{14}^{U} - \;a_{21}^{U} )\;;\;} \\ {\begin{array}{*{20}c} {min\;(H_{1} (A_{1}^{U} );H_{1} (A_{2}^{U} )\;),\;min\;(H_{2} (A_{1}^{U} );H_{2} (A_{2}^{U} )\;),} \\ {\begin{array}{*{20}c} {(a_{11}^{L} - \;a_{24}^{L} ,\;\;a_{12}^{L} - \;a_{23}^{L} ,\;\;a_{13}^{L} - \;a_{22}^{L} ,\;a_{14}^{L} - \;a_{21}^{L} )\;;} \\ {min\;(H_{1} (A_{1}^{L} );H_{1} (A_{2}^{L} )\;),\;min\;(H_{2} (A_{1}^{L} );H_{2} (A_{2}^{L} )\;)\;} \\ \end{array} } \\ \end{array} } \\ \end{array} } \right) $$
(6)

iii. Multiplication operation:

$$ \tilde{A}_{1} \otimes \;\tilde{A}_{2} = \;(A_{1}^{U} ,\;A_{1}^{L} ) \otimes (A_{2}^{U} ,\;A_{2}^{L} ) = \left( {\;\;\begin{array}{*{20}l} {(a_{11}^{U} x\;a_{21}^{U} ,\;\;a_{12}^{U} x\;a_{22}^{U} ,\;\;a_{13}^{U} x\;a_{23}^{U} ,\;a_{14}^{U} x\;a_{24}^{U} )\;;\;} \\ {\begin{array}{*{20}c} {min\;(H_{1} (A_{1}^{U} );H_{1} (A_{2}^{U} )\;),\;min\;(H_{2} (A_{1}^{U} );H_{2} (A_{2}^{U} )\;),} \\ {\begin{array}{*{20}c} {(a_{11}^{L} x\;a_{21}^{L} ,\;\;a_{12}^{L} x\;a_{22}^{L} ,\;\;a_{13}^{L} x\;a_{23}^{L} ,\;a_{14}^{L} x\;a_{24}^{L} )\;;} \\ {min\;(H_{1} (A_{1}^{L} );H_{1} (A_{2}^{L} )\;),\;min\;(H_{2} (A_{1}^{L} );H_{2} (A_{2}^{L} )\;)\;} \\ \end{array} } \\ \end{array} } \\ \end{array} } \right) $$
(7)

iv. Arithmetic operations and the crisp value k:

$$ kx\;\tilde{A}_{1} = \left( {\;\begin{array}{*{20}c} {(k\; \times \;a_{11}^{U} ,\;\;k\; \times \;a_{12}^{U} ,\;\;k\; \times \;a_{13}^{U} ,\;\;k\; \times \;a_{14}^{U} )\;;\;\;;\;\;H_{1} (A_{1}^{U} ),\;H_{2} (A_{1}^{U} )\;),} \\ {\begin{array}{*{20}c} {} \\ {(k\; \times \;a_{11}^{L} ,\;\;k\; \times \;a_{12}^{L} ,\;\;k\; \times \;a_{13}^{L} ,\;\;k\; \times \;a_{14}^{L} )\;;\;\;;\;\;H_{1} (A_{1}^{L} ),\;H_{2} (A_{1}^{L} )\;)} \\ \end{array} } \\ \end{array} } \right) $$
(8)
$$ \frac{{\tilde{A}_{1} }}{k} = \left( {\;\;\begin{array}{*{20}c} {(\frac{1}{k}\; \times \;a_{11}^{U} ,\;\;\frac{1}{k}\; \times \;a_{12}^{U} ,\;\;\frac{1}{k}\; \times \;a_{13}^{U} ,\;\;\frac{1}{k}\; \times \;a_{14}^{U} )\;;\;\;;\;\;H_{1} (A_{1}^{U} ),\;H_{2} (A_{1}^{U} )\;),} \\ {\begin{array}{*{20}c} , \\ {(\frac{1}{k}\; \times \;a_{11}^{L} ,\;\;\frac{1}{k}\; \times \;a_{12}^{L} ,\;\;\frac{1}{k}\; \times \;a_{13}^{L} ,\;\;\frac{1}{k}\; \times \;a_{14}^{L} )\;;\;\;;\;\;H_{1} (A_{1}^{L} ),\;H_{2} (A_{1}^{L} )\;)} \\ \end{array} } \\ \end{array} } \right) $$
(9)

where k > 0.

The above definitions and arithmetic operations are prevalently used in the proposed method and also in implementing computational procedures. The next subsection proposes IT2F-EWMA control charts specifically for the case of process control in the production of fertilizers where the data is translated into interval type-2 trapezoidal fuzzy numbers.

3.2 Conventional EWMA Control Chart

Previously, the fuzzy EWMA control chart was first introduced by Alipour and Noorossana [30]. They developed T1F-EWMA control chart and make a comparison with fuzzy Hotelling’s T2 chart. In a nutshell, the results show uniformly superior performance of T1F-EWMA than Hotelling’s T2 chart. In this subsection, differently from the previous work, an IT2F-EWMA control chart is proposed where the interval type-2 trapezoidal fuzzy numbers are used instead of type-1 fuzzy numbers.

The method begins with the equation of the EWMA control chart.

The EWMA control chart is formed by plotting one of the following quantities [1].

$$ z_{t} = \lambda \overline{X}_{t} + (1 - \lambda )z_{t - 1} $$
(10)

\(z_{t}\) is the t-th exponentially weighted moving average, \(\overline{X}_{t}\) denotes the t-th sample average, 0 < λ ≤ 1 is a constant. t = 1,2,…,n and n is the sample size of the study.

\(z_{0}\) is defined as follows,

$$ z_{0} = \overline{{\overline{X} }} $$
(11)

whereas \(\overline{{\overline{X} }}\) is the overall mean. If \(\overline{X}_{i}\) are independent random variables with variance \(\frac{{\sigma^{2} }}{n}\) (σ is the population standard deviation and known), then the variance \(\sigma_{zt}^{2}\) is defined as

$$ \sigma_{zt}^{2} = \frac{{\sigma^{2} }}{n}\left( {\frac{\lambda }{2 - \lambda }} \right)[1 - (1 - \lambda )^{2t} ] $$
(12)

As t increases, \(\sigma_{zt}^{2}\) will increase to a limiting value as

$$ \sigma^{2}_{zt} = \frac{{\sigma^{2} }}{n}\left( {\frac{\lambda }{2 - \lambda }} \right) $$
(13)

When the subgroup number is large, indicating that the sample size is more than 30, the conventional EWMA control chart is obtained. When the sample is small, the upper control limit (UCL) centerline (CL) and lower control limit (LCL) are defined as Eq. (14), Eq. (15) and Eq. (16) respectively.

$$ \text{UCL}= \;\overline{\overline{X}} \; + \;3\frac{\sigma }{\sqrt n }\sqrt {\frac{\lambda }{(2 - \lambda )}} $$
(14)
$$ \text{CL}= \overline{\overline{X}} $$
(15)
$$ \text{LCL}= \;\overline{\overline{X}} \; - \;3\frac{\sigma }{\sqrt n }\sqrt {\frac{\lambda }{(2 - \lambda )}} $$
(16)

However, when the subgroup number is small, meaning the sample size is less than 30 (t < 30), the upper control limit (UCL) and lower control limit (LCL) of the conventional EWMA control chart is written as follows:

$$ \text{UCL}= \;\overline{\overline{X}} \; + \;3\frac{\sigma }{\sqrt n }\sqrt {\frac{\lambda }{(2 - \lambda )}[1 - (1 - \lambda )^{2t} ]} $$
(17)
$$ \text{LCL}= \;\overline{\overline{X}} \; - \;3\frac{\sigma }{\sqrt n }\sqrt {\frac{\lambda }{(2 - \lambda )}[1 - (1 - \lambda )^{2t} ]} $$
(18)

Unlike Eq. (14) and Eq. (16), Eq. (17) and Eq. (18) do take into account the number of samples 't' in the computation of UCL and LCL. The centerline for this case is the same as Eq. (15).

If σ is estimated from the sample, \(\overline{R}\) is used for constructing a conventional EWMA control chart. The limits can be written as,

$$ \text{UCL}= \;\overline{\overline{X}} \; + \;A_{{_{2} }} \overline{R} \sqrt {\frac{\lambda }{(2 - \lambda )}} $$
(19)
$$ \text{LCL}= \;\overline{\overline{X}} \; - \;A_{{_{2} }} \overline{R} \sqrt {\frac{\lambda }{(2 - \lambda )}} $$
(20)

where \(\overline{R}\) is the average of the \(R_{i} ^{\prime}s\) and \(R_{i}\) is the range for each sample of the study. The centerline is also the same as Eq. (15). The constant \(A_{{_{2} }}\) is the factor for control limits which is tabulated from the quality control variables control chart’s table.

The performance of the EWMA chart is evaluated under the assumption of known or unknown parameters of the standard deviation [37]. If the population standard deviation (σ) is unknown, the formula for σ unknown is used, and vice versa when σ is known, the formula for σ known is used to analyse the control chart. This section provides these two scenarios in proposing IT2F-EWMA.

3.3 IT2F-EWMA Control Chart When \((\sigma_{1} ,\sigma_{2} ,\sigma_{3} ,\sigma_{4} )\) Are Known

When the standard deviations are known, and sample number t is large (t ≥ 30), fuzzy average and λ are used to construct the IT2F-EWMA based on the following limits:

UCL = 

$$ \left[ {\begin{array}{*{20}c} {\;\overline{\overline{X}}_{{a_{i}^{U} }} \;;\;min\;(H_{1} (A_{1}^{U} ),\;H_{2} (A_{1}^{U} ))} \\ {\;\overline{\overline{X}}_{{a_{i}^{L} }} ;\;min\;(H_{1} (A_{1}^{L} ),\;H_{2} (A_{1}^{L} ))\;\;} \\ \end{array} } \right] + \frac{3}{\sqrt n }\left[ {\begin{array}{*{20}c} {\;\sigma_{{a_{i}^{U} }} \;} \\ {\;\sigma_{{a_{i}^{L} }} \;} \\ \end{array} } \right]\sqrt {\frac{\;\lambda }{{(2 - \lambda )}}} $$
(21)

where i = 1,2,3,4

CL = 

$$ \;\left[ {\begin{array}{*{20}c} {\;\overline{\overline{X}}_{{a_{1}^{U} }} ,\;\;\overline{\overline{X}}_{{a_{2}^{U} }} ,\;\;\overline{\overline{X}}_{{a_{3}^{U} }} ,\;\;\overline{\overline{X}}_{{a_{4}^{U} }} \;;\;min\;(H_{1} (A_{1}^{U} ),\;H_{2} (A_{1}^{U} ))} \\ {\;\overline{\overline{X}}_{{a_{1}^{L} }} ,\;\;\overline{\overline{X}}_{{a_{2}^{L} }} ,\;\;\overline{\overline{X}}_{{a_{3}^{L} }} ,\;\;\overline{\overline{X}}_{{a_{4}^{L} }} ;\;min\;(H_{1} (A_{1}^{L} ),\;H_{2} (A_{1}^{L} ))\;\;} \\ \end{array} } \right] $$
(22)

LCL = 

$$ \left[ {\begin{array}{*{20}c} {\;\overline{\overline{X}}_{{a_{i}^{U} }} \;;\;min\;(H_{1} (A_{1}^{U} ),\;H_{2} (A_{1}^{U} ))} \\ {\;\overline{\overline{X}}_{{a_{i}^{L} }} ;\;min\;(H_{1} (A_{1}^{L} ),\;H_{2} (A_{1}^{L} ))\;\;} \\ \end{array} } \right] - \frac{3}{\sqrt n }\left[ {\begin{array}{*{20}c} {\;\sigma_{{a_{i}^{U} }} \;} \\ {\;\sigma_{{a_{i}^{L} }} } \\ \end{array} } \right]\sqrt {\frac{\;\lambda }{{(2 - \lambda )}}} $$
(23)

where i = 1,2,3,4

Nevertheless, when the sample number t is small, the limits are given as follows:

UCL = 

$$ \left[ {\begin{array}{*{20}c} {\;\overline{\overline{X}}_{{a_{i}^{U} }} ;\;min\;(H_{1} (A_{1}^{U} ),\;H_{2} (A_{1}^{U} ))} \\ {\;\overline{\overline{X}}_{{a_{i}^{L} }} ;\;min\;(H_{1} (A_{1}^{L} ),\;H_{2} (A_{1}^{L} ))\;\;} \\ \end{array} } \right] + \frac{3}{\sqrt n }\left[ {\begin{array}{*{20}c} {\;\sigma_{{a_{i}^{U} }} \;} \\ {\;\sigma_{{a_{i}^{L} }} } \\ \end{array} } \right]\sqrt {\frac{\;\lambda }{{(2 - \lambda )}}[1 - (1 - \lambda )^{2t} ]} $$
(24)

where i = 1,2,3,4

LCL = 

$$ \left[ {\begin{array}{*{20}c} {\;\overline{\overline{X}}_{{a_{i}^{U} }} ;\;min\;(H_{1} (A_{1}^{U} ),\;H_{2} (A_{1}^{U} ))} \\ {\;\overline{\overline{X}}_{{a_{i}^{L} }} ;\;min\;(H_{1} (A_{1}^{L} ),\;H_{2} (A_{1}^{L} ))\;\;} \\ \end{array} } \right] - \frac{3}{\sqrt n }\left[ {\begin{array}{*{20}c} {\;\sigma_{{a_{i}^{U} }} } \\ {\;\sigma_{{a_{i}^{L} }} } \\ \end{array} } \right]\sqrt {\frac{\;\lambda }{{(2 - \lambda )}}[1 - (1 - \lambda )^{2t} ]} $$
(25)

where i = 1,2,3,4

The centerline is the same as Eq. (22).

Note that the terms \([1 - (1 - \lambda )^{2t} ]\) in Eq. (24) and Eq. (25) will approach to the value of 1 as the number of samples (t) gets larger. This means, that after the control limits have been running for several periods, the control limits will approach steady-state values. Hence, the new control limits can.

be obtained using Eqs. (21) - (23). It should be noted that all equations from Eq. (14) to Eq. (25) are adopted from [2].

3.4 IT2F-EWMA Control Chart When \((\sigma_{1} ,\sigma_{2} ,\sigma_{3} ,\sigma_{4} )\) Are Unknown

The IT2F-EWMA control chart can also be developed when the fuzzy standard deviations are unknown. Like the limits shown above, the limits also depend on sample size t. In the case where t is large, the control limits are defined as,

UCL = 

$$ \left[ {\begin{array}{*{20}c} {\;\overline{\overline{X}}_{{a_{i}^{U} }} \;;\;min\;(H_{1} (A_{1}^{U} ),\;H_{2} (A_{1}^{U} ))} \\ {\;\overline{\overline{X}}_{{a_{i}^{L} }} ;\;min\;(H_{1} (A_{1}^{L} ),\;H_{2} (A_{1}^{L} ))\;\;} \\ \end{array} } \right] + A_{2} \left[ {\begin{array}{*{20}c} {\overline{R}_{{a_{i}^{U} }} } \\ {\;\overline{R}_{{a_{i}^{L} }} } \\ \end{array} } \right]\sqrt {\frac{\;\lambda }{{(2 - \lambda )}}} $$
(26)

where i = 1,2,3,4

LCL = 

$$ \left[ {\begin{array}{*{20}c} {\;\overline{\overline{X}}_{{a_{i}^{U} }} \;;\;min\;(H_{1} (A_{1}^{U} ),\;H_{2} (A_{1}^{U} ))} \\ {\;\overline{\overline{X}}_{{a_{i}^{L} }} ;\;min\;(H_{1} (A_{1}^{L} ),\;H_{2} (A_{1}^{L} ))\;\;} \\ \end{array} } \right] - A_{2} \left[ {\begin{array}{*{20}c} {\overline{R}_{{a_{i}^{U} }} } \\ {\;\overline{R}_{{a_{i}^{L} }} } \\ \end{array} } \right]\sqrt {\frac{\;\lambda }{{(2 - \lambda )}}} $$
(27)

where i = 1,2,3,4

Note that the centerline is the same as Eq. (22).

When the sample size t is small, the control limits are given as,

UCL = 

$$ \left[ {\begin{array}{*{20}c} {\;\overline{\overline{X}}_{{a_{i}^{U} }} \;;\;min\;(H_{1} (A_{1}^{U} ),\;H_{2} (A_{1}^{U} ))} \\ {\;\overline{\overline{X}}_{{a_{i}^{L} }} ;\;min\;(H_{1} (A_{1}^{L} ),\;H_{2} (A_{1}^{L} ))\;\;} \\ \end{array} } \right] + A_{2} \left[ {\begin{array}{*{20}c} {\;\overline{R}_{{a_{i}^{U} }} \;} \\ {\;\overline{R}_{{a_{i}^{L} }} } \\ \end{array} } \right]\sqrt {\frac{\;\lambda }{{(2 - \lambda )}}[1 - (1 - \lambda )^{2t} ]} $$
(28)

where i = 1,2,3,4

LCL = 

$$ \left[ {\begin{array}{*{20}c} {\;\overline{\overline{X}}_{{a_{i}^{U} }} \;;\;min\;(H_{1} (A_{1}^{U} ),\;H_{2} (A_{1}^{U} ))} \\ {\;\overline{\overline{X}}_{{a_{i}^{L} }} ;\;min\;(H_{1} (A_{1}^{L} ),\;H_{2} (A_{1}^{L} ))\;\;} \\ \end{array} } \right] - A_{2} \left[ {\begin{array}{*{20}c} {\;\overline{R}_{{a_{i}^{U} }} \;} \\ {\;\overline{R}_{{a_{i}^{L} }} } \\ \end{array} } \right]\sqrt {\frac{\;\lambda }{{(2 - \lambda )}}[1 - (1 - \lambda )^{2t} ]} $$
(29)

where i = 1,2,3,4

Again, the centerline used the same equation (see Eq. 22). Note that in the Eqs. (26)-(29), \((\overline{R}_{{a_{1}^{{}} }} ,\overline{R}_{{a_{2}^{{}} }} ,\overline{R}_{{a_{3}^{{}} }} ,\overline{R}_{{a_{4}^{{}} }} )\) is the ranges of the sample. The values \((\overline{R}_{{a_{1}^{{}} }} ,\overline{R}_{{a_{2}^{{}} }} ,\overline{R}_{{a_{3}^{{}} }} ,\overline{R}_{{a_{4}^{{}} }} )\) represented for upper and lower are the arithmetic means of the least possible values and the largest possible values for the sample, respectively. Therefore, \((R_{a1} ,R_{a2} ,R_{a3} ,R_{a4} )\) and \((\overline{R}_{{a_{1}^{{}} }} ,\overline{R}_{{a_{2}^{{}} }} ,\overline{R}_{{a_{3}^{{}} }} ,\overline{R}_{{a_{4}^{{}} }} )\) for upper and lower are obtained as follows:

Firstly, \((R_{a1} ,R_{a2} ,R_{a3} ,R_{a4} )\) values are calculated based on:

$$ R_{aj} = \max \{ X_{aj} \} - \min \{ X_{dj} \} ,\begin{array}{*{20}c} {} & {} \\ \end{array} R_{bj} = \max \{ X_{bj} \} - \min \{ X_{bj} \} , $$
$$ R_{cj} = \max \{ X_{cj} \} - \min \{ X_{cj} \} ,\begin{array}{*{20}c} {} & {} \\ \end{array} R_{dj} = \max \{ X_{dj} \} - \min \{ X_{dj} \} , $$

where \(\max \{ X_{ij} \}\) is the maximum of fuzzy numbers in the sample and \(\min \{ X_{ij} \}\) is the minimum of fuzzy numbers in the sample. Then, \((\overline{R}_{{a_{1}^{{}} }} ,\overline{R}_{{a_{2}^{{}} }} ,\overline{R}_{{a_{3}^{{}} }} ,\overline{R}_{{a_{4}^{{}} }} )\) is calculated based on the average for each range of the sample.

Similar to the standard deviations known, the term \([1 - (1 - \lambda )^{2t} ]\) approaches to 1 as t gets larger. Henceforth, the same concept of the control limits will move toward steady-state values as in Eqs. (26)–(27).

3.5 Defuzzification Method for IT2F-EWMA Control Chart

In type-2 fuzzy numbers, various defuzzification techniques can be used in the reduction process of the data. However, Ercan and Anagun [38] proves that all the methods can be used by the researchers based on their preferences since the results are similar in the context of “in control” and “out of control” situations. The approaches that have been suggested are the centroid method (Mendel, et al. [39]), indices method (Niewiadomski [40]), likelihood method (Chen [41]), Best Nonfuzzy Performance (BNP) method (Tsaur, et al. [42]), and defuzzification method (Kahraman, et al. [43]). Therefore, in this research, we would like to apply Kahraman et. al’s defuzzification method because of the flexibility in the calculation as well as easier to be implemented in analysing manufacturing data. Kahraman et al. [43] improved the method of control limits as follows:

$$ CDIT2_{Trap(i)}^{U} = \frac{{(a_{i4}^{U} - \;a_{i1}^{U} )\; + (H_{2} (A_{1}^{U} )a_{i2}^{U} - \;a_{i1}^{U} )\; + \;(H_{1} (A_{1}^{U} )\;\;a_{i3}^{U} - \;a_{i1}^{U} )\;}}{4}\; + \;\;a_{i1}^{U} $$
(30)
$$ CDIT2_{Trap(i)}^{L} = \frac{{(a_{i4}^{L} - \;a_{i1}^{L} )\; + (H_{2} (A_{1}^{L} )a_{i2}^{L} - \;a_{i1}^{L} )\; + \;(H_{1} (A_{1}^{L} )\;\;a_{i3}^{L} - \;a_{i1}^{L} )\;}}{4}\; + \;\;a_{i1}^{L} $$
(31)
$$ CDIT2_{Trap(i)}^{{}} = \frac{{CDIT2_{Trap(i)}^{U} + \;\;CDIT2_{Trap(i)}^{L} }}{2};\;\;i = 1,\;2,...n $$
(32)

where \(CDIT2_{Trap(i)}^{U}\) is the upper defuzzification limit, \(CDIT2_{Trap(i)}^{L}\) is the lower defuzzification limit and \(CDIT2_{Trap(i)}^{{}}\) is the mean of the lower and upper defuzzification limit. Whereas \(H_{1} (A_{1}^{U} )\;\) and \(H_{2} (A_{1}^{U} )\;\) are the maximum membership degree of the upper membership functions. The highest and the lowest values of upper and lower membership functions are\({a}_{i4}^{U}\), \({a}_{i1}^{U}\) and \({a}_{i4}^{L}\) \({a}_{i1}^{L}\) respectively. While\({a}_{i2}^{U}\), \({a}_{i3}^{U}\) and \({a}_{i2}^{L}\), \({a}_{i3}^{L}\) are the second and third parameters of the upper and lower membership functions respectively. In this study, we compare the defuzzified control limit (\(CDIT2_{Trap(i)}^{{}}\)) with the defuzzified samples to identify whether the samples are “in control” or “out of control”.

Defuzzification of sample can be obtained using Eqs. (33)–(35).

$$ DIT2_{Trap(i)}^{U} = \frac{{(Z_{d}^{U} - Z_{a}^{U} )\; + (H_{2} (A_{1}^{U} )Z_{b}^{U} - Z_{a}^{U} )\; + \;(H_{1} (A_{1}^{U} )\;\;Z_{c}^{U} \overline{u} - Z_{a}^{U} )\;}}{4}\; + Z_{a}^{U} $$
(33)
$$ DIT2_{Trap(i)}^{L} = \frac{{(Z_{d}^{L} - \;Z_{a}^{L} )\; + (H_{2} (A_{1}^{L} )Z_{b}^{L} - \;Z_{a}^{L} )\; + \;(H_{1} (A_{1}^{L} )\;\;Z_{c}^{L} - \;Z_{a}^{L} )\;}}{4}\; + \;\;Z_{a}^{L} $$
(34)
$$ DIT2_{Trap(i)}^{{}} = \frac{{DIT2_{Trap(i)}^{U} + \;\;DIT2_{Trap(i)}^{L} }}{2} $$
(35)

where \(DIT2_{Trap(i)}^{U}\) is the upper defuzzification, \(DIT2_{Trap(i)}^{L}\) is the lower defuzzification and \(DIT2_{Trap(i)}^{{}}\) is the mean of the defuzzification value of the IT2F numbers.

3.6 Performance of Control Chart

This section introduces the performance of the control chart based on the calculation of the average run length (ARL). ARL is the mean number of subgroups before an “out of control” situation is identified on the control chart. Two conditions can be identified in ARLs which are the “in control” state, ARL0, and the “out of control” condition, ARL1. The most effective chart is identified based on the lowest value of the ARL in the analysis. The lowest value of the ARLs is the best chart in detecting the small shift in the process [5, 26, 44].

Formerly, Roberts [45] and Robinson and Ho [46] calculated the ARL traditionally using monographs and numeric procedures. Nevertheless, Crowder [47], Chananet et al. [48], Molnau et al. [49] and Lucas and Saccucci [50] use computer programs such as FORTRAN to evaluate the ARLs by using the Markov Chain. Recently, You et al. [51], Qiao et al. [52] also used the Markov Chain method in calculating the ARL of the EWMA chart and they concluded that the Markov Chain is the most excellent method that can be used to assess the run length of the EWMA chart since it is easier and more accurate to be implemented. Thus, Sigma XL software based on the Markov Chain rule will be used in this study. Markov Chain procedures involve by dividing the interval between the UCL and LCL into t = 2m-1 subintervals, each of width 2d. The EWMA statistics, Zi, is said to be in transient state j at time i if \(S_{j} - d < Z_{i} < S_{j} + d\), for j = -m,-m + 1,…,0,…,m-1,m where Sj represents the midpoint of the jth subinterval. Hence, the formula for ARL is computed based on:

$$ ARL = 1 - \lambda e^{{\frac{(1 - \lambda )u}{\lambda }}} \frac{{e^{{\frac{ - b}{\lambda }}} - e^{{\frac{ - a}{\lambda }}} }}{{\lambda + e^{ - b} - e^{ - a} }} $$
(36)

where u represents the \(z_{0}\) or initial value, a is the LCL and b is the UCL of the study.

This section presents the detailed development of IT2F-EWMA and also Markov Chain-based ARL as the performance measures. Figure 2 shows the flowchart of the proposed IT2F-EWMA control chart.

Fig. 2
figure 2

Flow diagram of the IT2F-EWMA control chart

Full size image

To design this scheme, the following computational steps can explain on how to build the IT2F-EWMA chart.

Begin

Step 1: Fuzzification of data.

Step 2: Decide the control limit’s formula.

  1. i)

    choose either σ is known or σ is unknown.

  2. ii)

    indicate the sample's number either large (t ≥ 30 samples) or small (t < 30 samples).

Step 3: Determine the values of λ and z0. Then, calculate the fuzzification input needed in the formula.

such as fuzzy ranges and fuzzy means.

Step 4: Defuzzification process.

  1. i)

    Defuzzify the control limits for every first sample to the sixth sample. Then, the control limits for samples 7 and onwards are used in the formula as the control limits have approached steady-state values since it has been running for several periods.

  2. ii)

    Defuzzify each sample of the study.

Step 5: Compare the limits from Step 4 (i) with all the samples from Step 4 (ii).

End

The proposed IT2F-EWMA is implemented in the data of fertilizer production. The following section presents the detailed computations of the production data.

4 Application to Fertilizer Production

The proposed method has been applied to an agricultural system that focuses on fertilizer production in one of the well-known agriculture and rural development companies in Malaysia. In planting the plant, fertilizers act as a source of food for the plant for the plant to grow efficiently. It supplies macro and micronutrients to the plant. Two kinds of fertilizer can be found in the market nowadays such as organic and chemical fertilizers. Organic fertilizers are naturally produced, for instance, mineral sources and all animal wastes including manure, slurry, and guano. Chemical fertilizers on the other hand are any number of synthetic compound substances that have been created to increase the yield of the plant.

Twenty samples of chemical fertilizers have been used in the analysis of this study. The weights of the fertilizers have been collected for an hour in every ten minutes with a sample size of six. High toxicity in the defect’s fertilizer might affect the soil pH of the plants and hence make the plants grow unsuccessfully. In processing the fertilizers, the company used two machines to package the product and grind the soil in the mixers. Thus, the IT2F-EWMA chart is the most inventible tool to deal with the uncertainties of the data.

4.1 Control Chart Based on IT2F Number

Samples are transformed into type-2 fuzzy numbers as follows: (Note that the original data are attached in Appendix 1 as Table 2).

Table 2 Data of 20 fertilizers production in grams
Full size table

The values for upper type-2 fuzzy numbers \((a_{i1}^{U} ,\;a_{i2}^{U} ,\;a_{i3}^{U} ,\;a_{i4}^{U} )\) is calculated as (a-Δ, a, a + Δ, a + 2Δ) with Δ = 0.1. For sample no 1:\(a_{1a}^{U} = 15.8 - 0.1 = 15.7\), \(a_{1b}^{U} = 15.8\), \(a_{1c}^{U} = 15.8 + 0.1 = 15.9\), \(a_{1d}^{U} = 15.8 + 0.2 = 16\).

Then, values of lower type-2 fuzzy numbers \((a_{i1}^{L} ,\;a_{i2}^{L} ,\;a_{i3}^{L} ,\;a_{i4}^{L} )\) with Δ + 0.2 are used to find the differences between AU and AL. For sample no 1: \(a_{1a}^{L} = 15.7 + 0.1 = 15.8\), \(a_{1b}^{L} = 15.8 + 0.1 = 15.9\), \(a_{1c}^{L} = 15.9 + 0.1 = 16\), \(a_{1d}^{L} = 16 + 0.1 = 16.1\)

All the fuzzified data of upper and lower IT2F numbers are shown in Tables 3 and 4 respectively.

Table 3 Upper IT2F number for 20 subgroups (in minutes)
Full size table
Table 4 Lower IT2F number for 20 subgroups (in minutes)
Full size table

Since the standard deviation of the production of fertilizers is unknown, the standard deviation is estimated from the samples. Hence, we use the Eqs. (22), (28) - (29) for \((\sigma_{1} ,\sigma_{2} ,\sigma_{3} ,\sigma_{4} )\) are unknown and t is small since our sample is less than 30, which is considered as small. This means, there is no case for \((\sigma_{1} ,\sigma_{2} ,\sigma_{3} ,\sigma_{4} )\) are known is used in this study.

Firstly, fuzzy ranges for the first sample of the upper is given as follows:

\(R_{a1}^{u} = \max \{ X_{aj} \} - \min \{ X_{dj} \} = 16.5 - 16 = 0.5\),

\(R_{b1}^{u} = \max \{ X_{bj} \} - \min \{ X_{bj} \} = 16.6 - 15.8 = 0.8\),

\(R_{c1}^{u} = \max \{ X_{cj} \} - \min \{ X_{cj} \} = 16.7 - 15.9 = 0.8\),

$$ R_{d1}^{u} = \max \{ X_{dj} \} - \min \{ X_{aj} \} = 16.8 - 15.7 = 1.1 $$

Then, \((\overline{R}_{{a_{1}^{{}} }} ,\overline{R}_{{a_{2}^{{}} }} ,\overline{R}_{{a_{3}^{{}} }} ,\overline{R}_{{a_{4}^{{}} }} )\) is calculated based on the average for each range and the result for upper trapezoidal is as follows:

\(\overline{R}_{{a_{1}^{U} }}\) = 0.2762 \(\overline{R}_{{a_{2}^{U} }}\) = 0.5169 \(\overline{R}_{{a_{3}^{U} }}\) = 0.5169 \(\overline{R}_{{a_{4}^{U} }}\) = 0.7576.

It is noted that the above computations are made using the arithmetic operations of subtraction and multiplication of fuzzy numbers (see Eq. (6) and Eq. (7)).

Next, data from Tables 3 and 4 are calculated using the arithmetic operations of addition and multiplication with scalar k (see Eq. (5) and Eq. (8)), and the results are presented in Table 5 and 6. The calculation for sample 1 of Xa from Table 5 is the average of the first row of the Xa in Table 3 as follows:

$$ {\text{X}}_{a} \, = \, \frac{{\left( {15.7 + 16.2 + 16.1 + 16 + 16.5 + 16.3} \right)}}{6} = 16.1333 $$
Table 5 Upper IT2F number for \(\overline{X}\) 20 Subgroups
Full size table

For the second sample of Xb from Table 5, the calculation is:

$$ {\text{X}}_{b} \, = \, \frac{{\left( {15.8 + 16.3 + 16.2 + 16.1 + 16.6 + 16.4} \right)}}{6} = 16.2333 $$

For the sample number 3 of Xc:

$$ {\text{X}}_{c} \, = \, \frac{{\left( {15.9 + 16.4 + 16.3 + 16.2 + 16.7 + 16.5} \right)}}{6} = 16.3333 $$

Next, for the sample number 4 of Xd, the calculation is:

$$ {\text{X}}_{d} \, = \, \frac{{\left( {16 + 16.5 + 16.4 + 16.3 + 16.8 + 16.6} \right)}}{6} = 16.4333 $$

Table 5 shows the upper IT2F number for \(\overline{X}\) control chart and Table 6 is the lower IT2F for \(\overline{X}\) control chart.

Table 6 Lower IT2F for \(\overline{X}\) of 20 Subgroups
Full size table

Then, the exponentially weighted moving average (IT2-EWMA) control chart is calculated using Eq. (10) and the results is presented at Tables 7 and 8. Following Senturk et al. [2], λ = 0.2 is used due to general approach in production process, meanwhile value of \(z_{0}\) is set at 16. The computation for the first sample of the upper average Za, Zb, Zc and Zd from Table 7 is as follows:

$$ z_{a} = (0.2)(16.1333) + (1 - 0.2)(16) = 16.0267 $$
$$ z_{b} = (0.2)(16.2333) + (1 - 0.2)(16) = 16.0467 $$
$$ z_{c} = (0.2)(16.3333) + (1 - 0.2)(16) = 16.0667 $$
$$ z_{d} = (0.2)(16.4333) + (1 - 0.2)(16) = 16.0867 $$
Table 7 Upper IT2F-EWMA
Full size table

Afterwards, the calculation for the second sample of Za is as follows:

$$ z_{a} = (0.2)(16.0500) + (1 - 0.2)(16.0267) = 16.0313 $$

Tables 7 and 8 is the upper and lower averaged IT2F-EWMA control chart respectively.

Table 8 Lower IT2F-EWMA
Full size table

The centerline of IT2F control charts for EWMA are calculated by using Eq. (22) as follows:

$$ \overline{X}_{{a_{1}^{U} }} = \, \frac{{\left( {16.0267 + 16.0313 + 16.0584 + ... + 16.0115} \right)}}{20} = 15.9960 $$
$$ \overline{X}_{{a_{2}^{U} }} = \, \frac{{\left( {16.0467 + 16.0673 + 16.1072 + ... + 16.1103} \right)}}{20} = 16.0763 $$

\(\overline{X}_{{a_{3}^{U} }}\) = 16.1565 \(\overline{X}_{{a_{4}^{U} }}\) = 16.2367.

\(\overline{X}_{{a_{1}^{L} }}\) = 16.1565 \(\overline{X}_{{a_{2}^{L} }}\) = 16.2367 \(\overline{X}_{{a_{3}^{L} }}\) = 16.3170 \(\overline{X}_{{a_{4}^{L} }}\) = 16.3972.

Next, the IT2F-EWMA upper and lower control limits are calculated by using Eq. (28)–(29) for first sample until sample number 6. However, after the EWMA control chart has been running for several time periods, the control limits will approach steady-state values. Therefore, the control limits for the 7th sample until 20th sample, are calculated based on Eq. (26) – (27). The results of all the control limits are presented at Table 9 and the calculation for the first control limits is shown as follows:

Table 9 Control Limits of IT2F-EWMA Control Chart
Full size table

\(\text{LCL}=\left[ {\begin{array}{*{20}c} {\;15.9960,\;\;16.0763,\;\;16.1565,\;\;16.2367\;;\;1,\;1} \\ {\;16.1565,16.2367,16.3170,16.3972;\;0.7,0.7\;\;} \\ \end{array} } \right] - 0.483\left[ {\begin{array}{*{20}c} {\;0.2762,0.5169,0.5169,0.7576\;} \\ {\;0.2762,0.5169,0.5169,0.7576} \\ \end{array} } \right]\sqrt {\frac{\;0.2}{{(2 - 0.2)}}[1 - (1 - 0.2)^{2(1)} ]}\) = 

$$ \left[ {\begin{array}{*{20}c} {15.9415,16.0391,16.1193,16.2168\;;\;1,\;1} \\ {\;16.1020,16.1995,16.2797,16.3773\;;\;0.7,0.7\;\;} \\ \end{array} } \right] $$
$$ \text{UCL}=\left[ {\begin{array}{*{20}c} {\;15.9960,\;\;16.0763,\;\;16.1565,\;\;16.2367\;;\;1,\;1} \\ {\;16.1565,16.2367,16.3170,16.3972;\;0.7,0.7\;\;} \\ \end{array} } \right] + 0.483\left[ {\begin{array}{*{20}c} {\;0.2762,0.5169,0.5169,0.7576\;} \\ {\;0.2762,0.5169,0.5169,0.7576} \\ \end{array} } \right]\sqrt {\frac{\;0.2}{{(2 - 0.2)}}[1 - (1 - 0.2)^{2(1)} ]} $$

 = \(\left[ {\begin{array}{*{20}c} {\;16.0159,16.1135,16.1937,16.2913\;;\;1,\;1} \\ {\;16.1764,16.2740,16.3542,16.4517;\;0.7,0.7\;\;} \\ \end{array} } \right]\).

Then, the control limits are defuzzied based on the limits of the IT2F-EWMA control chart using Eq. (30)–(32). The calculations of defuzzification for interval type-2 control limits and the centerline are shown as below. For example, n = 1, the calculation is given as follows:

\(CDIT2_{Trap}^{U} \;= \;\frac{(16.2168 - 15.9415) + (1 \times 16.0391 - 15.9415) + (1 \times 16.1193 - 15.9415)}{4} + 15.9415\) = 16.0792

$$ CDIT2_{Trap}^{L}=\;\frac{{(16.3773 - 16.1020) + (0.7 \times 16.1995 - 16.1020) + (0.7 \times 16.2797 - 16.1020)}}{4} + 16.1020 =13.8037$$
$$ LCL\_CDIT2_{TRAP} = \frac{16.0792 + \;13.8037}{2} = 14.9414 $$

\(CDIT2_{TRAP}^{U}= \frac{{\left( {16.2367 - 15.9960} \right) + \left( {1 \times 16.0763 - 15.9960} \right) + \left( {1 \times 16.1565 - 15.9960} \right)}}{4} + 15.9960\) = 16.1164

\(CDIT2_{TRAP}^{L}= \frac{(16.3972 - 16.1565) + (0.7 \times 16.2367 - 16.1565) + (0.7 \times 16.3170 - 16.1565)}{4} + 16.1565\) = 13.8353

$$CL\_CDIT2_{TRAP} =\frac{16.1164 + 13.8353}{2} = 14.9759 $$

\(CDIT2_{Trap}^{U} = = \frac{{\left( {16.2913 - 16.0159} \right) + \left( {1 \times 16.1135 - 16.0159} \right) + \left( {1 \times 16.1937 - 16.0159} \right)}}{4} + 16.0159\) = 16.1536.

\(CDIT2_{Trap}^{L} = \frac{(16.4517 - 16.1764) + (0.7 \times 16.2740 - 16.1764) + (0.7 \times 16.3542 - 16.1764)}{4} + 16.1764\) = 13.8670

$$ UCL\_DIT2_{Trap}^{ = } \frac{16.1536 + 13.8670}{2} = 15.0103 $$

The results of all the defuzzifed control limits are presented in Table 10.

Table 10 Defuzzified Control Limits of IT2F-EWMA Chart
Full size table

The table above shows the defuzzified upper control limit, lower control limit and centerline. In this context, defuzzification relies on the utilization of fuzzified trapezoidal fuzzy numbers derived from IT2-EWMA of subgroup data. In the following, we will calculate the defuzzified IT2-EWMA chart for each sample using Eq. (33)–(35).

The calculations of sample number 1 of DIT2Upper, DIT2Lower and DIT2 are shown below.

$$ DIT2_{Trap(1)}^{U} = \frac{(16.0867 - 16.0267) + (1 \times 16.0467 - 16.0267) + (1 \times 16.0667 - 16.0267)}{4}\; + \;16.0267\; $$

 = 16.05667

$$ DIT2_{Trap(1)}^{L} = \frac{(16.1267 - 16.0667) + (0.7 \times 16.0867 - 16.0667) + (0.6 \times 16.1067 - 16.0667)}{4}\; + \;16.0667 $$

 = 13.2795

$$ DIT2_{Trap(1)}^{ = } \frac{16.0567 + 13.2795}{2} = 14.6681 $$

Then, the defuzzification of each of the sample of the data are compared with the defuzzification of control limits for the evaluation of the process control. If the values of the defuzzification of data is in the limits, then the process is “in control”. However, if the defuzzification of the data is out of limits, then the data is defined as “out of control”. Table 11 presents the \(DIT2_{Trap(1)}^{ = }\), LCL, UCL and the results of control.

Table 11 Defuzzied Values of The Sample
Full size table

As depicted in Table 11, 18 samples are identified as "out of control," while 2 samples are categorized as "in control." This suggests that the proposed IT2F-EWMA method effectively detects shifts in defective products. This observation aligns with previous research findings indicating that a higher number of defective products analyzed reflects greater sensitivity of the method in assessing product quality [16, 26].

Nevertheless, this result is incomplete without having a comparative study. Henceforward, the next section provides a comparative study between the proposed method against the conventional EWMA chart and T1F-EWMA control chart.

5 Comparative Study

This section gives a comparative study between the three types of EWMA charts to find out the stability between them. The results of the IT2F-EWMA control chart are compared with the conventional EWMA chart and T1F-EWMA control chart. This comparative study is meant to identify the method that is more sensitive in analysing the defects. The conventional chart of EWMA was calculated using the conventional equation (see Eq. (19–20)) and T1F-EWMA was calculated by using the fuzzy midrange method. Table 11 shows the result of the comparison in terms of “in control” and “out of control” among the IT2F-EWMA, T1F-EWMA and conventional EWMA control charts.

Table 12 Comparison of IT2F-EWMA, T1F EWMA and Conventional EWMA Control Charts
Full size table

It can be seen from Table 12 that the conventional EWMA has 12 samples that are “in control”, and 8 samples that are “out of control”. In contrast, the TIF-EWMA detects 16 samples are “out control”. Our proposed IT2F-EWMA detects 18 samples are “out of control”. Consequently, this proves that IT2F-EWMA control chart is more precise and vulnerable than conventional EWMA chart and T1F-EWMA control chart as it takes the smallest number of samples compared to others chart.

These results are further visualised in a figure which can show the distribution of fertilizers production versus control lines. Figure 3 (i), (ii) and (iii) depict the distribution of the production and control lines for the IT2F-EWMA, T1F-EWMA and conventional EWMA respectively.

Fig. 3
figure 3

Control charts of IT2F-EWMA, T1F-EWMA and Conventional EWMA Charts

Full size image

Next, the ARL is calculated to measure the performance of a control chart. Hence, in this study, the ARL with different value of shift was computed using Sigma XL based on Eq. (36) and the output are presented as in Table 13.

Table 13 Average Run Length (ARL) for IT2F-EWMA, T1F-EWMA and Conventional EWMA Control Charts
Full size table
Fig. 4
figure 4

Graph of Average Run Length (ARL) for IT2F-EWMA, T1F-EWMA and Conventional EWMA Control Charts

Full size image

Referring to Table 13 and Fig. 4, it is evident that the IT2F-EWMA chart exhibits the lowest ARL value. This finding suggests that the combination of EWMA charts with IT2F numbers yields the most effective performance in analyzing fertilizer data. This outcome corroborates previous research [5, 26, 44], which asserts that charts with the lowest ARL values are optimal for detecting minor shifts in the process.

Figure 4 (i), (ii), and (iii) illustrate the graph of ARL’s in EWMA control charts which comprise of IT2F-EWMA, T1F-EWMA and conventional EWMA

6 Conclusion

Generally, a conventional chart is used widely in many fields of manufacturing, servicing and engineering. Nevertheless, a conventional control chart can identify the causes in time but does not consider the severity of the incidence. When the real data is composed of interval-valued fuzzy, it is not feasible to use such an approach of conventional statistical process control to monitor the fuzzy chart. Furthermore, the conventional control chart is not suitable to be used in the monitoring process, if the data collected is in terms of type-1 or type-2 fuzzy numbers. The conventional chart could monitor the substantial changes in adverse events’ occurrence rates but sometimes the vagueness of the data makes fuzzy linguistics more vulnerable to monitoring the changes in the fertilizers’ characteristics. So, that is the reason why a fuzzy control chart is important in increasing the flexibility and sensitivity of the data to make the right decision for the industry. For example, it will not only increase customer satisfaction levels and reduce complaints but also reduce or eliminate the need for inspection in the supply chain. Existing research showed that the type-1 fuzzy number was widely used. However, from our readings, there is no study has been done in comparison to conventional EWMA charts, T1F-EWMA and IT2F-EWMA control charts until now. To fill this gap, this paper develops IT2F- EWMA control charts as a new method and makes a comparison between conventional charts and type-1 fuzzy in EWMA charts.

There are three contributions of this paper which are: (1) We intended to use IT2F numbers as it able to develop higher levels of vagueness than type-1 fuzzy numbers. Regarding the EWMA charts, although there is much existing research on conventional fuzzy charts, still there is no research on type-2 fuzzy control charts that have been used so far. (2) Afterwards, we made a comparative study between the proposed method towards the conventional EWMA chart and the T1F-EWMA control chart. The comparative study is not only to gain information on the performance of all three charts but also gives an overview to the researcher on the inspection of the products. (3) Finally, we calculated the ARL of all the three charts. The calculations enriched the measurement technique in the performance of the charts, so it is useful in finding the most excellent charts between them. From the results of the case study, we can summarize that the IT2F-EWMA control chart is more precise and vulnerable in monitoring the variations of the product’s characteristics than the T1F-EWMA chart and conventional EWMA chart since the IT2F-EWMA control chart found 18 defects out of 20 samples, but T1F-EWMA control chart found 16 defects and conventional EWMA chart only found 12 defects. If the company includes the defective product in the production cost, it might increase the percentage of nonconformists and will increase the manufacturing cost. Moreover, it will not satisfy the customer’s satisfaction towards the quality of the fertilizer if they buy the defective products. Further research can be conducted to investigate the IT2F-EWMA control chart for monitoring defects using another type of data which is variable sample size. Besides, fuzzy sets control charts from other families also can be used for instance hesitant fuzzy sets, intuitionistic fuzzy sets or neutrosophic fuzzy sets.