Binary imbalanced big data classification based on fuzzy data reduction and classifier fusion

Abstract

The era of big data has arrived, making it impossible for traditional machine learning algorithms to perform training in a stand-alone computing environment. In this paper, we propose a method for imbalanced binary classification of large-scale datasets based on undersampling and ensemble. More specifically, our method first adaptively partitions the majority class big data into k clusters, followed by undersampling to create k balanced datasets. Subsequently, k base classifiers are trained on each balanced dataset and are combined to perform the final prediction. Existing undersampling methods randomly select a subset of the majority class; thus, important instances may be lost during the process. In contrast, our proposed fuzzy data reduction scheme selects informative instances from each cluster, preventing information loss. Traditional ensemble methods have negative correlations between the base classifiers, whereas our proposed classifier fusion scheme fuses the base classifiers using fuzzy integral to facilitate modeling the relations between the base classifiers. The proposed algorithm is evaluated on six imbalanced large data sets and compared with state-of-the-art undersampling and ensemble methods, including the synthetic minority oversampling technique bagging (SMOTE-Bagging), SMOTE-Boost, and Binary Ensemble Classification for Imbalanced big data based on MapReduce and Upper sampling (BECIMU). Quantitative evaluations and theoretical analysis demonstrate that the proposed method outperforms the three state-of-the-art methods by 1.47%, 2.00% and 2.03%, and by 3.15%, 2.15% and 2.52%, in terms of the average G-mean and AUC-area, respectively.

1 Introduction

Many real-life binary imbalanced big data classification problems exist, for example, extreme weather prediction (Wang and Ding 2015), software defect prediction (Zhong et al. 2016), machinery fault diagnosis (Ding et al. 2017), spam filtering (Murtaza et al. 2020), and medical image classification (Murtaza et al. 2020). Since the class imbalance problem was originally proposed by Japkowicz (2000), different researchers have developed many methods. However, most of them focus only on small-scale datasets. With the emergence of big data, it is impossible for conventional machine learning algorithms to perform training in a stand-alone computing environment.

In this paper, we propose an imbalanced binary classification method based on undersampling and ensemble method for large-scale datasets. Specifically, we propose to (1) adaptively partition the majority class of the big data into k clusters using the open-source big data platforms, (2) use undersampling to create k balanced datasets and (3) train k base classifiers on the balanced datasets which are combined to perform the final prediction.

Undersampling (Japkowicz 2000; Liu et al. 2009; Ofek et al. 2017; Lin et al. 2017) is a popular method for imbalanced binary classification. Let S be an imbalanced data set, $S=S^{+}\cup S^{-}$, where $S^{+}$ and $S^{-}$ denote the positive class (minority class) and the negative class (majority class). First, a subset $S'$ from $S^{-}$ is randomly selected to ensure that $|S'| = |S^{+}|$. Then, a balanced training set $S_{tr}$ is obtained by combining $S'$ and $S^{+}$. Finally, a classifier is trained on $S_{tr}$ to classify the imbalanced test set $S_{te}$. Although the undersampling method is straightforward, it has the drawback that some essential negative class instances may be lost due to random sampling. The ensemble method fuses the base classifiers (which are often weaker) to create a stronger classifier. It should be noted that the base classifiers are not independent because the k balanced training subsets contain the same positive class subset. Existing studies (Wang et al. 2009; Chawla et al. 2003b; Zhai et al. 2018a) failed to consider this, resulting in negative correlations between base classifiers.

To address these problems, we propose fuzzy data reduction and classifier fusion schemes. After the negative big data set $S^{-}$ has been clustered into k clusters $S_{1}^{-}, S_{2}^{-}, \ldots , S_{k}^{-}$ using an adaptive clustering method¹, fuzzy data reduction is adopted to select the informative instances from $S_{i}^{-}$ for each obtained cluster $S_{i}^{-}(1\le i\le k)$. As a result, k undersampled negative class subsets $R_{i}^{-}(1\le i\le k)$ are obtained. Selecting informative instances instead of random instances guarantees that less information is lost during the undersampling process. Given the k balanced training sets $S_{i}=R_{i}^{-}\cup S^{+}(1\le i\le k)$, the base classifiers are trained and fused using fuzzy integral, which can accurately model the relations between the k base classifiers. The fusion via fuzzy integral can reduce the negative correlations between the base classifiers and enhance the classification accuracy of binary imbalanced data.

To summarize, we propose a binary imbalanced big data classification approach based on fuzzy data reduction and classifier fusion. The main contributions of this paper are threefold. First, we propose an undersampling method for negative big data based on fuzzy data reduction to minimize information loss. Second, we present a binary imbalanced big data classification approach based on classifier fusion to prevent negative correlations between base classifiers. Third, extensive experiments are conducted on two big data open-source platforms (MapReduce and Spark) to compare the G-mean and AUC-area of the proposed methods and three state-of-the-art methods on six binary imbalanced big data sets. In addition, we present a theoretical analysis on the running time, the number of task synchronizations, and the number of files of the proposed methods implemented on the MapReduce and Spark.

2 Related works

Existing binary imbalanced data classification methods can be classified into three categories: data-level, algorithm-level, and ensemble methods. Since this paper focuses on undersampling and ensemble methods, we only review these two methods.

2.1 Undersampling methods

Undersampling is a popular method that uses a subset of the majority class to deal with class imbalance (Liu et al. 2009). Japkowicz and Stephen (2002) provided a theoretically proof that classifiers trained on the sample data set provided equivalent generalization performance to classifiers trained on the original data set. Ofek et al. (2017) proposed a clustering-based undersampling technique that clusters the minority class instances and selects a similar number of majority class instances from each cluster. The algorithm exhibited high predictive performance with linear complexity bound by the size of $S^{+}$. Bach et al. (2019) proposed a clustering-based undersampling method that clusters the majority class instances and removes the instances from the high-density domains in contrast to the approach in Ofek et al. (2017), which clusters the minority class instances. Lin et al. (2017) introduced two clustering-based undersampling strategies, in which set the number of clusters in the majority class is equal to the number of data points in the minority class. The Tomek-link (T-Link) was proposed as a data compression and cleaning technique in Tomek (1976). Given two instances $\varvec{x}_{i}$ and $\varvec{x}_{j}$ belonging to different classes, $d(\varvec{x}_{i}, \varvec{x}_{j})$ be the distance between $\varvec{x}_{i}$ and $\varvec{x}_{j}$. A pair $(\varvec{x}_{i}, \varvec{x}_{j})$ is called a T-Link, if there is no instance $\varvec{x}_{l}$, such that $d(\varvec{x}_{i}, \varvec{x}_{l})<d(\varvec{x}_{i}, \varvec{x}_{j})$ or $d(\varvec{x}_{j}, \varvec{x}_{l})<d(\varvec{x}_{i}, \varvec{x}_{j})$. If a T-Link exists between 2 instances, one of the instances is noise, or both are borderline instances. Batista et al. (2004) used the T-Link as an undersampling method; only majority instances were removed. Kang et al. (2017) proposed an undersampling scheme that incorporates a noise filter for minority samples before the undersampling step. In undersampling, the deleted samples are never used to train the classifier, which may result in information loss. Therefore, Fan et al. (2016) presented a one-sided dynamic undersampling (ODU) method that utilizes all samples for training and dynamically determines whether a majority sample should be used for classifier learning. The novelty of ODU is the dynamic undersampling of the majority class to balance the dataset. Vuttipittayamongkol and Elyan (2020) proposed an undersampling framework designed to identify and eliminate majority class instances from the overlapping region. Accurate identification and elimination of these instances maximizes the visibility of the minority class instances and prevents excess data reduction, minimizing information loss. Koziarski (2020) developed an undersampling method based on radial basis function for imbalanced data classification. García and Herrera (2009) were among the first researchers to investigate evolutionary undersampling (EUS). The objective of EUS is to increase the accuracy of the classifier by reducing instances mainly belonging to the majority class. A good trade-off is achieved between data reduction, data balancing, and classification accuracy by designing a suitable fitness function. The authors (García and Herrera 2009) proposed eight EUS methods and categorized them depending on the objective, selection scheme, and performance metrics. Triguero et al. (2015, 2016, 2017) extended the EUS approach to big data scenarios and proposed three EUS approaches for imbalanced big data classification. The first method (Triguero et al. 2015) is a divide-and-conquer approach based on the MapReduce paradigm. The drawback of this approach is the low density of the minority class in the subsets in extremely imbalanced cases. Reference Triguero et al. (2016) proposed the second approach to overcome this drawback; it was implemented on the Spark platform. The methods in Triguero et al. (2015) and Triguero et al. (2016) utilized divide-and-conquer strategy to split big data set into several subsets that are addressed individually. However, the global view of the data may be lost, reducing the model accuracy. The third method, a global EUS approach for imbalanced big data, addresses this problem (Triguero et al. 2017). Liang et al. (2021) proposed fast and efficient undersampling method for imbalanced learning. It combines the classification boundary adjustment and sample selection to improve the efficiency and effect of imbalanced learning. Zheng et al. (2021) proposed a three-stage undersampling method, in which noise removal, clustering and representative sample selection were carried out in the three stages, respectively. The method can overcome the shortcomings of undersampling methods based on clustering.

2.2 Ensemble methods

Ensemble methods used for the classification of imbalanced data can be divided into methods combined with undersampling and methods combined with oversampling approaches.

Regarding the first category, Liu et al. (2009) proposed two undersampling-based ensemble methods called EasyEnsemble and BalanceCascade for class imbalance learning. EasyEnsemble randomly samples l subsets from the majority class as training sets to train l base classifiers, l is a predefined parameter, and combines the outputs of the l classifiers. BalanceCascade trains the classifiers sequentially; the majority class instances that are correctly classified by the trained learners are removed in each step. Seiffert et al. (2010) proposed a simpler and faster ensemble method (RUSBoost) that combines random undersampling and a boosting algorithm. Galar et al. (2013) proposed EUSBoost, an improvement of the RUSBoost algorithm, which combines random undersampling with a boosting algorithm. EUSBoost has higher performance of the base classifiers than RUSBoost due to EUS approach. Besides, EUSBoost is more versatile because it uses different subsets of majority class instances to train each base classifier. Similarly, Sun et al. (2018) combined EUS with the bagging algorithm and proposed an EUS-based ensemble method called EUS-Bag. The advantage of EUS-Bag is a new fitness function that considers performance, balance, and diversity. Lu et al. (2017) proposed a hybrid ensemble method that combines ensemble learning, undersampling techniques, and an adaptive boundary decision strategy. Sun et al. (2015) proposed a split balancing ensemble (SBE) approach for solving the class-imbalance problem. The SBE randomly partitions the set of majority class into several subsets with same sizes as the set of minority class. Each subset is combined with the minority class instances to obtain balanced subsets. The basic classifiers of the ensemble approach are trained on these balanced subsets, and the outputs of the base classifiers are integrated using a combination rule. However, underfitting may occur if a training set with a high imbalance ratio is used in the SBE method. Chen et al. (2019) proposed a distance-based balanced ensemble (DBE) method for classifying data with a high imbalance ratio to handle this issue. The DBE divides the highly imbalanced data set into multiple imbalanced subsets with a much lower imbalance ratio and uses a modified adaptive semi-unsupervised weighted oversampling method for each subset to obtain balanced subsets to train base classifiers used in the ensemble approach. Guo et al. (2020) proposed a two-step ensemble learning method for classifying imbalanced data. In the first step, a projection matrix is used to enhance the separability between the diverse class examples to improve the performance of the base classifier. In the second step, undersampling is applied to improve the performance of the base classifiers in the minority class and further increase the diversity between the individual base classifiers. Wang et al. (2020c) proposed an entropy and confidence-based undersampling boosting framework called ECUBoost for imbalanced data sets. The entropy and confidence levels are used in ECUBoost to avoid losing informative samples, and ensure the validity and adequate structural distribution of the majority samples during undersampling. Yang et al. (2020) presented a hybrid classifier ensemble method for classifying imbalanced data. This approach combines density-based undersampling and cost-effective methods using state-of-the-art solutions and a multi-objective optimization algorithm. Raghuwanshi and Shukla (2019) proposed an undersampling-based ensemble method that creates several balanced training subsets by random undersampling of the majority class samples. The number of training subsets is determined by the degree of the class imbalance. The generated balanced training subsets are used for training the base classifiers, and bagging is used as the ensemble method. The drawback of this method is that the number of training subsets is very large if the original data set has a high imbalance ratio.

Regarding the second category, Chen et al. (2018) proposed an ensemble method for classifying imbalanced data. The method consists of two steps. First, it generates synthetic samples in a local domain of the training samples and trains the base classifiers using the original training samples and synthetic neighborhood samples. Finally, the classifiers are fused for classifying imbalanced data. The proposed method addresses the class imbalance problem and promotes diversity. Chawla et al. (2003a) combined base the SMOTE algorithm and a boosting and proposed SMOTEBoost to improve prediction the accuracy of the minority class instances during boosting. Lim et al. (2017) developed an evolutionary cluster-based oversampling ensemble method (ECO-Ensemble) that combines a cluster-based synthetic data generation method with an evolutionary algorithm. Zhai et al. (2018b) presented an imbalanced big data classification algorithm that combines an oversampling method and an ensemble approach. Oversampling is carried out in an enemy nearest neighbor hypersphere of a positive instance, and the ensemble technique is implemented using fuzzy integral. The enemy nearest neighbor of each positive instance is obtained by Ren et al. (2017) proposed an ensemble-based adaptive over-sampling method for imbalanced data classification and used it for computer-aided detection of microaneurysm. Li et al. (2017) utilized the Wiener process oversampling (WPO) technique for classifying imbalanced data and combined it with ensemble learning to create the WPOBoost algorithm. Abdi and Hashemi (2015) integrated the Mahalanobis distance-based over-sampling (MDO) technique with a boosting algorithm and proposed the MDOBoost algorithm for multi-class imbalanced data. Galar et al. (2012) conducted a comprehensive review of ensemble methods for classifying imbalanced data, focusing on bagging and boosting. Huang et al. (2020) proposed an ensemble method based on conditional image generation (Zhai et al. 2021, 2019; Zhang et al. 2020) for imbalanced image classification, which uses the generative adversarial network for oversampling and uses data cleaning for downsampling. Yan et al. (2019) proposed an ensemble method based on the three-way decision model for imbalanced data classification. The key point of this method lie in considering the difference in the cost of selecting key samples selected by the three-way decision model.

The literature indicates a lack of studies on imbalanced big data classification, a topic that was only researched by Triguero et al. (2015, 2016, 2017). In this paper, we present a classification algorithm for binary imbalanced big data that combines fuzzy data reduction and classifier fusion. In the following section, we present the details of the proposed algorithm.

3 The proposed algorithm

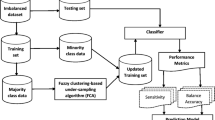
In this section, we present the proposed algorithm in detail. Let $S=S^{-}\cup S^{+}$ be an imbalanced big data set, where $S^{-}$ is an imbalanced big data set, and $S^{+}$ is a small or medium-size data set. The proposed algorithm is illustrated in Fig. 1. It consists of four stages: (1) Adaptively clustering negative big data; (2) calculating the reduction in each cluster; (3) constructing balanced training sets and training base classifiers; (4) integrating the trained base classifiers using fuzzy integral. We present the details of each stage below.

Fig. 1

The idea of the proposed algorithm

3.1 Adaptively clustering negative big data

The K-means algorithm is a very popular clustering algorithm; however, its major drawback is that the parameter K must be determined by the user. The X-means algorithm (Pelleg and Moore 2000) proposed by Pelleg and Moore overcomes this drawback. It is a hierarchical clustering approach that can efficiently estimate the parameter K by optimizing the Bayes information criterion (BIC). The X-means algorithm assumes a minimum number of clusters and dynamically increases them. It uses the BIC to guide splitting of clusters. If a single cluster (parent) is split into two clusters (children), and the BIC increases, two clusters are preferred to one cluster. Let $C_i(i=1,2)$ be the two child clusters; it is assumed that the data $\varvec{x}$ contained in $C_i$ follow a d-dimensional normal distribution:

$$\begin{aligned} f(\varvec{\theta }_{i}; \varvec{x})\!=\!(2\pi )^{-\frac{p}{2}}|\varvec{\Sigma }_i|^{-\frac{1}{2}}{\text {exp}}\left[ \!-\!\frac{1}{2}(\varvec{x}\!-\!\varvec{\mu }_i)^{\text {T}}\varvec{\Sigma }_{i}^{-1}(\varvec{x}-\varvec{\mu }_i)\right] \end{aligned}$$

(1)

The calculation of BIC is given by equation (2).

$$\begin{aligned} \text {BIC}=-2\log L(\hat{\varvec{\theta }}_{i}; \varvec{x})+q\log n_i \end{aligned}$$

(2)

where $\hat{\varvec{\theta }}_{i}=(\hat{\varvec{\mu }}_i, \hat{\varvec{\Sigma }}_i)$ is the maximum likelihood estimate of the d-dimensional normal distribution; $\varvec{\mu }_i$ is the d-dimensional means vector, and $\varvec{\Sigma }_i$ is the $d\times d$ dimensional variance-covariance matrix; q is the number of the parameters. $\varvec{x}$ is the d-dimensional data point in $C_i$; $n_i$ is the number of elements in $C_i$. L is the likelihood function.

In this paper, we extend the X-means algorithm to the big data scenario and use it to cluster negative big data adaptively. The pseudocode of the extended X-means algorithm for big data is given in Algorithm 1.

The main operation of the X-means algorithm is the big data K-means clustering, and the main computation is the calculation of the BIC. It is straightforward to compute a cluster’s BIC due to the simplicity of estimating its mean vector $\hat{\varvec{\mu }_{i}}$ and the covariance matrix $\hat{\varvec{\Sigma }_{i}}$. Accordingly, the bottleneck of Algorithm 1 is the clustering of big data, which is performed using the big data computing framework MapReduce, as illustrated in Fig. 2.

Fig. 2

The technical route of big data K-means clustering based on MapReduce

Specifically, the process of big data K-means clustering based on MapReduce includes the following three stages:

• (1) map: at each map node $i(1\le i\le m)$, the distance between each sample $\varvec{x}_{ij}\in S_{i}^{-}(1\le i\le m; 1\le j\le |S_{i}^{-}|)$ and each local cluster center $\varvec{c}_{ik}\in C_{ik}(1\le i\le m; 1\le j\le K)$ is calculated in parallel, and $\varvec{x}_{ij}$ is assigned to the nearest cluster.

• (2) combiner: the local cluster center $\varvec{c}_{ik}\in C_{ik}$ is updated in parallel by the formula (3),

  $$\begin{aligned} \varvec{c}_{ik}=\frac{1}{|C_{ik}|}\sum \limits _{\varvec{x}_{ij}\in C_{ik}}\varvec{x}_{ik} \end{aligned}$$

  (3)

• (3) At a reduce node, the global cluster center $\varvec{c}_{k}\in C(1\le k\le K)$ is updated by formula (4).

  $$\begin{aligned} \varvec{c}_{k}=\frac{1}{m}\sum \limits _{i=1}^{m}\varvec{c}_{ik} \end{aligned}$$

  (4)

3.2 Calculating the reduction in each cluster

After performing adaptively clustering, the negative big data set $S^{-}$ is clustered into k subsets: $S_{1}^{-}, S_{2}^{-}, \ldots , S_{k}^{-}$. The negative class big data set is regarded as a k-class data set. We can use a data reduction approach (Wang et al. 2020a, 2019; Sun et al. 2019a; Ni et al. 2020, 2019) to eliminate unimportant data points from each cluster or use the instance selection method (Zhai et al. 2016; Wang et al. 2020b; Sun et al. 2019b) to select informative data points from each cluster. Since the cluster (or class) of a sample $\varvec{x}$ in the local data subset $S_{i}^{-}$ is known, data reduction or instance selection can be performed on a local data subset in parallel at each computing node.

In this paper, we use the fuzzy set method to calculate the reduction in $S_{i}^{-}(1\le i\le k)$. Specifically, we calculate the reduction $R_{i}^{-}$ of each $S_{i}^{-}$ using the condensed fuzzy k-nearest neighbor (CFKNN) method. Why use this data reduction method because the k clusters are subsets of the negative big data set $S^{-}$, and they might overlap. CFKNN is an instance reduction or instance selection approach for fuzzy k-nearest neighbors (FKNN) (Keller et al. 2009) that overcomes the following three drawbacks of the k-nearest neighbor (KNN) method (Cover and Hart 1967).

• (1) Given a test instance $\varvec{x}$, the KNN method does not consider the difference in the contribution between the k nearest neighbors of $\varvec{x}$ to classify $\varvec{x}$.

• (2) The KNN method does not consider the probability of $\varvec{x}$ belonging to different classes.

• (3) The KNN method is sensitive to noise.

The FKNN method uses the fuzzy membership degree to describe the probability of $\varvec{x}$ belonging to a class. The fuzzy membership degree of $\varvec{x}$ is determined by its k nearest neighbors using Eq. (5).

$$\begin{aligned} \mu _{j}(\varvec{x})=\frac{\sum _{i=1}^{k}\mu _{ij}\left( \frac{1}{\parallel \varvec{x}-\varvec{x}_{i}\parallel ^{\frac{2}{m-1}}}\right) }{\sum _{i=1}^{k}\left( \frac{1}{\parallel \varvec{x}-\varvec{x}_{i}\parallel ^{\frac{2}{m-1}}}\right) } \end{aligned}$$

(5)

where j is the index of classes, $\mu _{ij}$ is given by equation (6).

$$\begin{aligned} \mu _{ij}=\mu _{j}(\varvec{x}_i)=\frac{\frac{1}{\parallel \varvec{x}_i-\varvec{c}_{j}\parallel ^{\frac{2}{m-1}}}}{\sum _{j=1}^{k}\left( \frac{1}{\parallel \varvec{x}_i-\varvec{c}_{j}\parallel ^{\frac{2}{m-1}}}\right) } \end{aligned}$$

(6)

where $\varvec{x}_i$ is the ith nearest neighbor of $\varvec{x}$, $\varvec{c}_j$ is the center of the jth class. In Eq. (5) and (6), m is a parameter that determines how the weight of the distance when calculating the neighbors’ contributions to the membership value (Keller et al. 2009). In our experiments, we set $m=2$, as suggested by Keller et al. (2009), i.e., the contribution of each neighboring point is weighted by the reciprocal of its distance from the point being classified.

In the CFKNN method, given an instance $\varvec{x}$ in a subset $S_{i}^{-}(1\le i\le k)$, we use the fuzzy membership degree $\mu _{j}(\varvec{x})$ to calculate the information entropy $E(\varvec{x})$ using Eq. (7).

$$\begin{aligned} E(\varvec{x})=-\sum _{i=1}^{k}\mu _{j}(\varvec{x})\log _{2}\mu _{j}(\varvec{x}) \end{aligned}$$

(7)

The entropy is a measure of class uncertainty of the instances; the larger the entropy of an instance, the more difficult it is to determine its class. Accordingly, instances with larger information entropy are more informative. In the CKKNN method, we use entropy as a criterion to select informative instances. The pseudo-code of the CFKNN algorithm is given in Algorithm 2, where we omit the subscript of subset $S_{i}^{-}$ for convenience; thus, S denotes the negative subset $S_{i}^{-}$.

3.3 Constructing balanced training sets and training classifiers

In previous section, we obtained k reduction subsets, $R_{1}, R_{2}, \ldots , R_{k}$. Next, we construct k balanced training sets, $S_{1}, S_{2}, \ldots , S_{k}$, by unionizing each reduction subset $S_{i}$ and the positive class subset $S^{+}$, i.e., $S_{i}=R_{i}^{-}\cup S^{+}(1\le i \le k)$. Next, we train k extreme learning machine (ELM) (Huang et al. 2006) classifiers $L_{1}, L_{2}, \ldots , L_{k}$, and their outputs are transformed into posterior probability by softmax function.

An ELM classifier is a Single hidden Layer Feed-forward neural Network (SLFN). A SLFN with m hidden nodes can be modeled with the following equation:

$$\begin{aligned} f(\varvec{x})=\sum _{i=1}^mG(\varvec{x}, \varvec{w}_i, b_i)\varvec{\beta }_i \end{aligned}$$

(8)

where G denotes the hidden node activation function, $\varvec{w}_i$ is the input weight vector connecting the $i^\text {th}$ hidden node with the input nodes. $b_i$ is the bias of the $i^\text {th}$ hidden node. $\varvec{\beta }_i$ is the output weight vector connecting the $i^\text {th}$ hidden node with the output nodes. In ELM, $\varvec{w}_i$ and $b_i$ are randomly assigned, while $\varvec{\beta }_i$ are analytically determined.

Given a training set, $S=\{(\varvec{x}_i,y_i)|x_i\in R^{d},y_i\in Y\}_{i=1}^{n}$, where $\varvec{x}_i$ is an input vector and $y_i$ is a class label in Y, $Y=\{\omega _{1},\omega _{2},\ldots ,\omega _{l}\}$ be a set of class labels. Substitute $\varvec{x}_i$ and $y_i$ for x and f(x) in (8), respectively, we obtain Eq. (9).

$$\begin{aligned} y_i=\sum _{j=1}^mG(\varvec{x}_i, \varvec{w}_j, b_j)\varvec{\beta }_{j} \end{aligned}$$

(9)

Eq. (9) can be written in a more compact format as

$$\begin{aligned} \varvec{H}\varvec{\beta }=\varvec{Y} \end{aligned}$$

(10)

where

$$\begin{aligned}&\varvec{H}=\begin{bmatrix} G(\varvec{x}_1, \varvec{w}_1, b_1)&{}\ldots &{} G(\varvec{x}_1, \varvec{w}_m, b_m)\\ \vdots &{}\cdots &{}\vdots \\ G(\varvec{x}_n, \varvec{w}_1, b_1)&{}\cdots &{} G(\varvec{x}_n, \varvec{w}_m, b_m) \end{bmatrix} \end{aligned}$$

(11)

$$\begin{aligned}&\varvec{\beta }=(\varvec{\beta }^T_1,\ldots ,\varvec{\beta }^T_m)^T \end{aligned}$$

(12)

and

$$\begin{aligned} \varvec{Y}=(\varvec{y}^T_1,\ldots ,\varvec{y}^T_n)^T \end{aligned}$$

(13)

Because usually the number of hidden nodes is much less than the number of training samples, $\varvec{H}$ is a non-square matrix and one cannot expect an exact solution of the system (10). Yet, we can find its smallest norm least square solution by solving the optimization problem (14).

$$\begin{aligned} \min _{\varvec{\beta }}\Arrowvert \varvec{H}\varvec{\beta }-\varvec{Y} \Arrowvert \end{aligned}$$

(14)

The smallest norm least-squares solution of (14) can be easily obtained using Eq. (15).

$$\begin{aligned} \hat{\varvec{\beta }}=\varvec{H}^{\dagger }\varvec{Y} \end{aligned}$$

(15)

where $\varvec{H}^{\dagger }=\left( \varvec{HH}^T\right) ^{-1}\varvec{H}$ is the Moore–Penrose generalized inverse of matrix $\varvec{H}$.

Given a test instance $\varvec{x}$, the predicted posterior probability by softmax transformation is given using Eq. (16).

$$\begin{aligned} p(\omega _{i}|\varvec{x})=\frac{e^{y_{i}}}{\sum _{j=1}^{l}{e^{y_{j}}}} \end{aligned}$$

(16)

3.4 Integrating the trained classifiers by fuzzy integral

Let $L=\{L_{1}, L_{2}, \ldots , L_{k}\}$ be the set of k ELM classifiers trained on the k constructed balanced training sets, $Y=\{\omega _{1},\omega _{2},\ldots ,\omega _{l}\}$ be the set of class labels of the training instances. For test instance $\varvec{x}$, the output of classifier $L_i$ is a l-dimensional vector denoted by

$$\begin{aligned} L_{i}(\varvec{x})=(p_{i1}(\varvec{x}), p_{i2}(\varvec{x}), \ldots , p_{il}(\varvec{x})) \end{aligned}$$

(17)

where $p_{ij}(\varvec{x}) \in [0,1](1\le i \le k; 1\le j \le l)$ denotes the support degree given by classifier $L_{i}$ to the hypothesis that $\varvec{x}$ comes from class $\omega _{j}$, $\sum _{j=1}^{l}p_{ij}(\varvec{x})=1$, $p_{ij}(\varvec{x})$ is estimated by Eq. (16).

The following matrix is called decision matrix Abdallah et al. (2012) with respect to $\varvec{x}$.

$$\begin{aligned} DM(\varvec{x})= \begin{bmatrix} p_{11}(\varvec{x}) &{}\cdots &{}p_{1j}(\varvec{x}) &{}\cdots &{}p_{1l}(\varvec{x})\\ \vdots &{} &{}\vdots &{} &{}\vdots \\ p_{i1}(\varvec{x}) &{}\cdots &{}p_{ij}(\varvec{x}) &{}\cdots &{}p_{il}(\varvec{x})\\ \vdots &{} &{}\vdots &{} &{}\vdots \\ p_{k1}(\varvec{x}) &{}\cdots &{}p_{kj}(\varvec{x}) &{}\cdots &{}p_{kl}(\varvec{x}) \end{bmatrix} \end{aligned}$$

(18)

where the ith row of the matrix are the support degrees that classifier $L_{i}$ classify $\varvec{x}$ into classes $\omega _{1}, \omega _{2}, \ldots , \omega _{l}$, the jth column of the matrix are the support degrees from classifiers $L_{1}, L_{2}, \ldots , L_{k}$ for class $\omega _{j}$.

Let P(L) be the power set of L, the fuzzy measure on L is a set function $g: P(L) \rightarrow [0, 1]$, which satisfies the following two conditions:

• (1) $g(\varnothing )=1$, $g(L)=1$;

• (2) For $\forall A, B \subseteq L$, if $A \subset B$, then $g(A)\le g(B)$.

For $\forall A, B \subseteq L$ and $A \cap B = \varnothing$, g is called $\lambda$-fuzzy measure, if it satisfies the following condition:

$$\begin{aligned} g(A \cup B)=g(A)+g(B)+\lambda g(A)g(B) \end{aligned}$$

(19)

where $\lambda > -1$ and $\lambda \ne 0$.

The value of $\lambda$ can be obtained by solving the equation (20).

$$\begin{aligned} \lambda +1=\prod _{i=1}^{k}(1+\lambda g_{i}) \end{aligned}$$

(20)

where $g_{i}=g(\{L_{i}\})$, which is called fuzzy density of classifier $L_{i}$. It is noted that the equation (20) has only one solution which meets the conditions $\lambda > -1$ and $\lambda \ne 0$. Usually, $g_i$ can be determined using Eq. (21).

$$\begin{aligned} g_i=\frac{p_i}{\sum _{j=1}^{k}p_{j}}\delta . \end{aligned}$$

(21)

where $\delta \in [0,\, 1]$ and $p_i$ is testing accuracy or verification accuracy of classifier $L_i(1\le i\le l)$.

Let $h:L \rightarrow [0, 1]$ be a function defined on L. The Choquet fuzzy integral (Abdallah et al. 2012) of function h with respect to g is defined using Eq. (22).

$$\begin{aligned} (C)\int h d\mu =\sum \limits _{i=2}^{l+1}\left[ h(L_{i-1})-h(L_{i})\right] g(A_{i-1}) \end{aligned}$$

(22)

where $h(L_{1})\ge h(L_{2})\ge \cdots \ge h(L_{k})$, $h(L_{l+1})=0$, $A_{i-1}=\{L_1, L_2, \ldots , L_{i-1}\}$.

Given a test instance $\varvec{x}$, when we use fuzzy integral to integrate the k trained classifiers $L_{1}, L_{2},\ldots , L_{k}$ for classifying $\varvec{x}$, we first compute decision matrix $DM(\varvec{x})$, and then sort $j{\text {th}}(1\le j\le k)$ column of $DM(\varvec{x})$ in descending order and obtain $(p_{i_{1}j}, p_{i_{2}j}, \ldots , p_{i_{k}j})$. The support degree $p_{j}(\varvec{x})$ is calculated using Eq. (23).

$$\begin{aligned} p_{j}(\varvec{x})=\sum _{t=2}^{k+1}\left[ p_{i_{t-1}j}(\varvec{x})-p_{i_{t}j}(\varvec{x})\right] g(A_{t-1}) \end{aligned}$$

(23)

The pseudo-code of integrating the trained classifiers by fuzzy integral is given in Algorithm 3.

4 Experimental results and analysis

We compared the proposed method with three state-of-the-art approaches on a big data platform with 8 computing nodes. The three approaches are SMOTE-Bagging (Wang et al. 2009), SMOTE-Boost (Chawla et al. 2003b), and BECIMU (Zhai et al. 2018a). The assessment metrics are G-mean and AUC-area which are commonly used for evaluating the performance of imbalanced data classification algorithms (Bach et al. 2019). The G-mean is defined in Eq. (24); it is obtained from the confusion matrix (contingency table) (Table 1). The AUC refers to the Area Under the Curve of receiver operating characteristics (ROC) (Liu et al. 2009).

Table 1 Confusion matrix of binary imbalanced classification problem

$$\begin{aligned} \text {G-mean}=\sqrt{\frac{\text {TP}}{\text {TP+FN}}\times \frac{\text {TN}}{\text {TN+FP}}} \end{aligned}$$

(24)

The data sets used in the experiments include 2 artificial data sets and 4 UCI data sets (Dua and Graff 2019). The first artificial data set (Gaussian 1) is a two-dimensional data set with two classes followed two Gaussian distributions whose mean vectors and covariance matrices are listed in Table 2. The second artificial data set (Gaussian 2) is a three-dimensional data set with four classes followed four Gaussian distributions whose the mean vectors and covariance matrices are listed in Table 3. The basic information of the 6 data sets is provided in Table 4, where #Negative and #Positive denote the number of negative and positive samples, respectively, and #Attribute denotes the number of attributes.

Table 2 The mean vectors and covariance matrices of Gaussian 1

Table 3 The mean vectors and covariance matrices of Gaussian 2

Table 4 The basic information of the 6 data sets

All experiments were conducted on a big data platform with 8 computing nodes; the configuration of the computing nodes is given in Table 5. It should be noted that the configuration of the master node and the slave node are the same in this platform.

Table 5 The configuration of the nodes in the cloud computing platform

Table 6 The experimental results of G-mean compared with the three state-of-the-art methods with Hadoop

Table 7 The experimental results of G-mean compared with the three state-of-the-art methods with Spark

Table 8 The experimental results of AUC-area compared with the three state-of-the-art methods with Hadoop

Table 9 The experimental results of AUC-area compared with the three state-of-the-art methods with Spark

Fig. 3

The relationship between testing accuracy and number of iteration on Hadoop and Spark

We implemented the proposed algorithm using Hadoop and Spark on the big data platform. The G-means and AUC-area of the proposed algorithm and the three state-of-the-art methods are listed in Tables 6 and 7, and Tables 8 and 9, respectively.

Table 10 The comparison of file number, synchronous number and running time on Hadoop and Spark

The results indicate that the proposed method achieved 5 maximum of G-mean (bold values in column 5 of Tables 6 and 7), SMOTE-Boost achieved another maximum of G-mean (bold values in column 3 of Tables 6 and 7). The experiment results of AUC-area are similar to those of G-mean (bold values in Tables 8 and 9). Overall, the proposed method outperformed the 3 state-of-the-art methods. We believe that the proposed method is superior to the 3 state-of-the-art methods for the following three reasons:

• (1) Adaptive clustering of the negative class big data partitions the data into several groups and maintains the intrinsic distribution.

• (2) As a heuristic undersampling method, the instance selection prevents the loss of useful samples by random undersampling and selects informative samples from each cluster.

• (3) Since the training sets used for training the base classifiers are not independent, they include the same positive subset. In other words, there are correlations between the base classifiers. The correlations can be positive, the base classifiers enhance each other in this case. The correlations can also be negative, the base classifiers restrain each other in this situation. The fuzzy integral can accurately model the two types of correlations between the base classifiers, increasing the classification performance of the ensemble learning system.

If an algorithm is implemented on different big data platforms, there should be no statistical difference in the testing accuracy. Figure 3 shows the experimental results on the Gaussian 1 data set on Hadoop and Spark. However, the number of files, number of task synchronizations, and running times may be significantly different for the two big data platforms. Therefore, we conducted a theoretical analysis regarding these three aspects.

The number of files refers to the number of intermediate files produced when the algorithm runs on the two big data platforms Hadoop and Spark. The number of intermediate files not only affect occupy the memory space but also affects the input/output (I/O) performance, potentially increasing the running time of the algorithm. On the Hadoop platform, the shuffle operation of MapReduce sorts and merges the intermediate results produced by the map task. MapReduce reduces the amount of data transferred between the computing nodes by merging and sorting the intermediate results. As a result, each map task produces only one intermediate data file. In contrast, the Spark platform does not have a merge and sort operation for intermediate data files, and data from different partitions are saved in a single file, i.e., the number of partitions is the number of intermediate files.

Regarding the number of task task synchronization, the reduce operation cannot be performed until all map operations are completed because MapReduce is a synchronous model. Spark is an asynchronous model, the number of synchronizations is larger on Hadoop than on Spark. The fewer synchronizations, the faster the algorithm is executed.

The running time T of the algorithm is determined by the sorting time $T_{\text {sort}}$ and the transfer time $T_{\text {trans}}$ of the intermediate data. When MapReduce sorts and merges the intermediate results, we assume that each map task requires m splits of the data, and each reduce task requires r splits of the data; thus, the sorting time of the intermediate data is $T_{\text {MR-sort}}=m\log m+r$. Since $r\le m$ in most cases, $T_{\text {MR-sort}}=O(m\log m)$. In contrast, Spark has no shuffling process; therefore, $T_{\text {Sport-sort}}=0$. $T_{\text {trans}}$ is determined by the size of the intermediate data |D| and the speed of network transmission $C_r$. If we ignore the difference between network transmission speeds, $T_{\text {trans}}\propto |D|$. The difference in transmission time between Hadoop and Spark depends largely on the number of synchronizations. Spark uses pipeline technique to reduce the number of synchronizations, as the number of iterations increases, Spark has more advantages over MapReduce on $T_{\text {trans}}$. We summarize the results of the number of files, number of task synchronizations, and running time of the proposed method in Table 10. The results are consistent with the results of the above analysis.

5 Conclusion

A binary imbalanced classification method for big data based on fuzzy data reduction and classifier fusion via a fuzzy integral was proposed in this paper. The proposed method has three advantages: (1) It uses MapReduce to cluster negative big data adaptively into subsets to maintain the intrinsic distribution of the data. (2) Heuristic undersampling (i.e., the instance selection) prevents the loss of useful samples, especially for imbalanced big data sets. Furthermore, the heuristic undersampling method can select informative samples from negative subset. (3) The ensemble method that uses a fuzzy integral improves the classification accuracy. Future studies will investigate (1) extending the proposed method to classifying multi-class imbalanced big data classification set and (2) conducting experimental comparisons with additional methods using more imbalanced big data sets and various evaluation indices.