1 Introduction

Binary imbalanced data refer to a type of data, where one class (positive class) is highly under-represented compared to another class (negative class). In the scenario of binary imbalanced classification (He and Garcia 2009; Krawczyk 2016), to which both traditional classification approaches (such as support vector machines, decision trees, neural networks) and assessment metrics (such as classification accuracy) can’t be directly applied. Because there are large requirements for dealing with binary imbalanced data in practice, and many methods have been proposed in the last two decades. These methods can be roughly classified into three categories: data-level methods, algorithm-level methods and hybrid methods (He and Garcia 2009; Krawczyk 2016). For convenience of description, we introduce some notations. Let S be original set with n instances, i.e., \(|S|=n\), \(S^{+}\) and \(S^{-}\) denote the set of minority class (positive class) instances and majority class (negative class) instances in S, respectively. Obviously, \(S=S^{+}\cup S^{-}\) and \(|S^{+}|<<|S^{-}|\).

In the data-level methods, an imbalanced data distribution is modified to a balanced data distribution by random sampling, the random sampling can be categorized into two classes: random undersampling and random oversampling. The random undersampling randomly selects a subset \(S'\) from \(S^{-}\) and removes \(S'\) from original data set S. The random undersampling is straightforward, it is usually combined with other approaches for binary imbalanced classification. For example, Liu et al. (2009) combined random undersampling and ensemble method and proposed two ensemble algorithms for class imbalanced learning, the methods in Liu et al. (2009) achieved good classification results. Ofek et al. (2017) combined random undersampling and clustering method and proposed a clustering-based undersampling technique for addressing binary-class imbalance problems, the method in Ofek et al. (2017) demonstrates high predictive performance, while its time complexity is bound by the size of the minority class instances. Bao et al. (2016) combined random undersampling and ensemble of support vector machine and proposed a learning approach for concept detection in large-scale imbalanced data sets. The training data set for each base support vector machine is constructed by a boosted near-miss undersampling technique. The random oversampling increases the size of \(S^{+}\) by generating new positive instances. The most striking generation-based random oversampling method is the so-called Synthetic Minority Oversampling TEchnique (SMOTE) (Chawla et al. 2002), which generates artificial instances based on k-nearest neighbors of positive instances. Inspired by the idea of SMOTE, many promising synthetic sampling approaches have been proposed in recent years. For instance, Das et al. (2015) proposed two probabilistic oversampling methods named RACOG and wRACOG, which considered the probability distribution of the minority class in the process of synthetically generating new samples. Rivera (2017) proposed a noise reduction synthetic oversampling algorithm which results in improvement for prediction of minority class. Based on Mahalanobis distance, in the framework of multi-class imbalanced data classification, Abdi and Hashemi (2016) proposed a new oversampling technique which generates synthetic instances which have the same Mahalanobis distance from the considered class mean as other minority class instances. In order to increase classification sensitivity in imbalanced data sets, Rivera and Xanthopoulos (2016) proposed a priori synthetic oversampling methods.

In the algorithm-level methods, which directly modify existing classification algorithms to adapt to imbalanced classification scenarios. This kind of method mainly includes cost-sensitive methods and instance weight methods. Cost-sensitive methods take into account the variable costs of misclassifications of instances belonging to different classes, in the scenario of binary imbalanced classification, the costs can be modeled by a cost matrix whose element c(i, j) is the cost of predicting an instance belonging to class i when in fact it belongs to class j. The pioneering works of cost-sensitive methods are presented by Sun and her co-researchers (2007). They proposed three cost-sensitive boosting algorithms in Sun et al. (2007), i.e., the well-known AdaC1, AdaC2 and AdaC3, which are developed by introducing cost items into the learning framework of AdaBoost. Based on cost matrix, Krawczyka et al. (2014) proposed an approach of ensemble of cost-sensitive decision tree for imbalanced classification, the cost-sensitive decision trees are constructed according to a given cost matrix, and are trained on random feature subspaces to ensure sufficient diversity of the base classifiers. In order to overcome the difficulty of determining the precise misclassification costs in cost-sensitive methods, Cao et al. (2013) proposed an optimized cost-sensitive support vector machine (SVM) for imbalanced classification. The proposed method in Cao et al. (2013) incorporates the evaluation measure (AUC and G-mean) into the objective function of cost-sensitive SVM to improve the performance of binary imbalanced classification. In order to deal with problem of imbalanced big data classification, based on the MapReduce, López et al. (2015) proposed a cost-sensitive fuzzy classification method, which uses the MapReduce framework to distribute the computational operations of the cost-sensitive learning fuzzy model into different cloud computing nodes. Castro and Braga (2013) proposed a novel cost-sensitive approach to improve the performance of MLPs by optimizing a joint cost function which corresponds to the sum of squared errors for positive class and negative class. In the instance weight methods, based on fuzzy rough set theory (Zhao et al. 2015, 2013; Zhai et al. 2017; El-Monsef et al. 2017; Tsang et al. 2017), Ramentol et al. (2015) proposed a classification algorithm for imbalanced data, the proposed algorithm uses fuzzy rough set and aggregation approach to build a weight vector for weighting samples. Inspired by a simple notion that a trained support vector machine provides information regarding bounded and unbounded support vectors, Lee et al. (2017) proposed a method for imbalanced data classification, which introduces a new weight adjustment factor to the proposed algorithm. Zong et al. (2013) proposed an instance weight approach named weighted extreme learning machine (W-ELM). The W-ELM has two merits: (1) the weighted ELM is able to deal with data with imbalanced class distribution while maintain the good performance on well balanced data as unweighted ELM; (2) by assigning different weights for each example according to users’ needs, the weighted ELM can be generalized to cost-sensitive learning.

In the hybrid methods, which generally combine the advantages of the two kinds of methods mentioned above by ensemble learning, including cost-sensitive ensemble methods and data preprocessing ensemble methods. The cost-sensitive ensembles keep the general learning framework of AdaBoost, but at the same time introduce cost items into the weight update formula, the predominant cost-sensitive ensembles include AdaCost (Fan et al. 1999), RareBoost (Joshi et al. 2001), and AdaCx \((x=1, 2, 3)\) (Sun et al. 2007). In the data preprocessing ensemble methods, each base classifier is trained with a pre-processed data set, and the data preprocessing techniques are embedded into boosting algorithms. The representative works include SMOTEBoost (Chawla et al. 2003), RUSBoost (Seiffert et al. 2010), and EUSBoost (Galar et al. 2013) etc. Galar et al. (2012) present an excellent review on the ensembles for the class imbalance problem.

Although many works have addressed the problem of imbalanced data classification, limited studies have been devoted to classifying imbalanced big data, the pioneering works investigated the problem of imbalanced big data classification are reported in literature Ghanavati et al. (2014) and Río et al. (2014). By combining metric learning and balancing techniques, Ghanavati et al. (2014) proposed a integrated method to learn from imbalanced big data. Río et al. (2014) discussed the extensions of oversampling, undersampling and cost-sensitive learning in imbalanced big data scenario, and gave their implementation frameworks with MapReduce. Aiming at classifying extremely imbalanced big data, Triguero et al. (2016) proposed an approach of evolutionary undersampling and implement the proposed algorithm with Apache Spark. Under the sparsity assumption, Maurya et al. (2016) discussed the problem of online sparse class imbalance learning on big data, and presented an effective solution for the problem. Recently, Fernández et al. (2017) provided an insight into the problem of imbalanced big data classification with researchers including some outcomes and challenges.

Regarding the training approaches for basic classifiers of neural networks in ensemble learning, compared with iterative approaches, such as gradient-based learning approaches, non-iterative approaches are much more efficient and effective, because that non-iterative approaches have fast learning speed and good generalization performance. In the past decade, non-iterative approaches have attracted wide attention of the researchers. Non-iterative approaches can be classified into two categories: deterministic non-iterative approaches and random non-iterative approaches. In the first category, the first deterministic non-iterative method was proposed by Schmidt et al. (1991) for training feed-forward networks, which was motivated by the computation of concave piecewise linear discriminant functions. Based on the memory desaturation technique, Reznik (1999) proposed a non-iterative method for training Hopfield neural networks. Recently, Oscar et al. (2017) proposed an incremental non-iterative method for training one-layer feed-forward neural networks without hidden layers. As pointed out by Oscar et al. (2017), the deterministic non-iterative approaches are quite scarce, actually only a few salient methods mentioned above are proposed. On the contrary, the random non-iterative approaches are very plentiful, many researchers (Schmidt et al. 1992; Pao et al. 1992, 1994; Igelnik and Pao 1995) have contributed their efforts to this field. Recently, Wang et al. (2017) introduced non-iterative approach into deep learning, and proposed a new training algorithm for training deep neural networks, Cao et al. (2018) presented a comprehensive survey on neural networks with random weights. Extreme learning machines (ELMs) (Huang et al. 2006, 2011, 2015) were initially proposed by Huang and his co-researchers for training SLFNs. Huang (2015) presented the relationships and the differences between the ELMs and some earlier similar works by clarifying the essential elements of ELMs. The key superiority of ELM is that it has fast learning speed and good generalization capacity (Huang et al. 2006). With respect to generalization capacity of classifiers, Wang et al. (2017, 2015) and Wang and Dong (2009) studied the relationship between generalization capacity and uncertainties of classifiers, and proposed corresponding technique to enhance the generalization capacity of classifiers. Recently, on the study of the relationship between generalization and complexity of classification problem, Wang et al. (2018) obtained an important conclusion that the generalization ability of a classifier is statistically becoming better with the increase in uncertainty when the complexity of the classification problem is relatively high, and the generalization ability is statistically becoming worse with the increase in uncertainty when the complexity is relatively low. Furthermore, they applied this conclusion to multiple-instance active learning to enhance the generalization ability of the learning system (Wang et al. 2017). ELM not only can be used to solve many classical problems, such as function approximation (Huang et al. 2012), decision making (Ren and Wei 2017; Ye 2017; Mao et al. 2017), data reduction (Meng et al. 2017; Cai et al. 2017; Li et al. 2017; Ding et al. 2017) and so on, but also can be used to solve some new problems, for example, Zhang and Zhang (2016); Zhang et al. (2016) and Zhang and Zhang (2015) addressed the problem of visual knowledge adaptation by ELM, and proposed ELM-based cross-domain network learning framework called ELM-based domain adaptation (EDA), extensive experiments on benchmark visual data sets demonstrate that the EDA outperforms the existing cross-domain learning methods. The latest advances in extreme learning machine can be found in Huang et al. (2011).

In general framework of classifier ensemble or classifier fusion, there is an acquiescent assumption that the basic classifiers used for fusion are independent or noninteractive (Ralescu and Adams 1980; Abdallah et al. 2012; Kuncheva 2001; Zhan et al. 2012). However, this assumption is not realistic in many applications. Actually, there are some inherent interactions among different basic classifiers, the interactions may be positive synergy, and in this case the basic classifiers cooperate and enhance each other. The ensemble system can take advantages of the strengths of the individual classifiers, and can overcome their weaknesses, finally achieve a higher accuracy than any individuals. The interaction also may be negative synergy, i.e., the corresponding basic classifiers restrain each other. Fuzzy integral (Ralescu and Adams 1980) is distinguished from other ensemble methods by this desirable property. Furthermore, fuzzy integral can also characterize the significance of basic classifiers by fuzzy measure. Motivated by these merits of fuzzy integral, in this paper we proposed an algorithm for imbalanced big data classification, which combines sampling technique, non-iterative learning and fuzzy integral-based ensemble learning, and we implement the proposed algorithm with MapReduce. The paper is structured as follows: the preliminaries used in this paper are briefly reviewed in Sect. 2. The proposed algorithm is given in Sect. 3. The experimental results and analysis are presented in Sect. 4 and Sect. 5 concludes this paper.

2 Preliminaries

In the proposed approach, the base classifiers used in ensemble for imbalanced big data classification are SLFNs which are trained with an efficient non-iterative learning approach ELM. The reason why we select ELM is that it is effective and efficient, in other words, it has fast learning speed with very good generalization capacity. The selected ensemble method is fuzzy integral, we employ fuzzy integral as ensemble tool because that it can well model the interactions among the base classifiers. In the following, we will briefly review the ELM and fuzzy integral.

2.1 Extreme learning machine (ELM)

ELM is an efficient random non-iterative algorithm for training SLFNs, it randomly assigns the weights between input layer and hidden layer, and analytically determined the weights between hidden layer and output layer. Given a training set, \(D=\{(x_i,y_i)|x_i\in R^{d},y_i\in R^{k},i=1,2,\ldots ,n\)}, where \(x_i\) is a \(d\times 1\) input vector and \(y_i\) is a \(k\times 1\) target vector, the SLFNs with m hidden nodes can be modeled by

$$\begin{aligned} f(x_i)=\sum _{j=1}^m\beta _jg(w_j\cdot x_i+b_j),\, i=1,2,\ldots ,n \end{aligned}$$
(1)

where \(w_j=(w_{j1},w_{j2},\ldots ,w_{jd})^\mathrm{T}\) is the weight vector connecting the jth hidden node with the input nodes, \(b_j\) is the bias of the jth hidden node. The \(w_j\) and \(b_j\) are randomly assigned. \(\beta _j=(\beta _{j1},\beta _{j2},\ldots ,\beta _{jm})^\mathrm{T}\) is the weight vector connecting the jth hidden node with the output nodes. The parameters \(\beta _j (j=1,2,\ldots ,m)\) may be estimated by least square fitting with the given training set D, i.e., we have

$$\begin{aligned} f(x_i)=\sum _{j=1}^m\beta _jg(w_j\cdot x_i+b_j)=y_i \end{aligned}$$
(2)

Equation (2) can be written in a more compact format as

$$\begin{aligned} H\beta =Y \end{aligned}$$
(3)

where

$$\begin{aligned}&H=\begin{bmatrix} g(w_1 \cdot x_1+b_1)&\quad \ldots&\quad g(w_m \cdot x_1+b_m)\\ \vdots&\quad \ldots&\quad \vdots \\ g(w_1 \cdot x_n+b_1)&\quad \ldots&\quad g(w_m \cdot x_n+b_m) \end{bmatrix} \end{aligned}$$
(4)
$$\begin{aligned}&\beta =(\beta ^\mathrm{T}_1,\ldots ,\beta ^\mathrm{T}_m)^\mathrm{T} \end{aligned}$$
(5)

and

$$\begin{aligned} Y=(y^\mathrm{T}_1,\ldots ,y^\mathrm{T}_n)^\mathrm{T} \end{aligned}$$
(6)

H is the hidden layer output matrix of SLFN, where the jth column of H is the jth hidden nodes output vector with respect to inputs \(x_1,x_2,\ldots ,x_n\), and the ith row of H is the output vector of the hidden layer with respect to input \(x_i\). If the number of hidden nodes is equal to the number of distinct training samples, the matrix H is square and invertible, and SLFN can approximate these training samples with zero error. But generally, the number of hidden nodes is much less than the number of training samples. Therefore, H is a non-square matrix and one can’t expect to find an exact solution of the system (3). Fortunately, we can find its smallest norm least square solution by solving the following optimization problem (Cao et al. 2018; Huang et al. 2012).

$$\begin{aligned} \min _{\beta }\Arrowvert H\beta -Y \Arrowvert \end{aligned}$$
(7)

The smallest norm least-squares solution of (7) can be easily obtained by

$$\begin{aligned} {\hat{\beta }}=H^{\dagger }Y \end{aligned}$$
(8)

where \(H^{\dagger }=\left( HH^\mathrm{T}\right) ^{-1}H\) is the Moore–Penrose generalized inverse of matrix H. The ELM can be described by the Algorithm 1 (Cao et al. 2018).

figure a

In order to make the outputs of the trained SLFN by ELM to be a approximated posterior probability distribution, we can transform the outputs of SLFN by the following softmax function.

$$\begin{aligned} p(w_{j}|x)=\frac{e^{y_{j}}}{\sum _{i=1}^{k}{e^{y_{i}}}} \end{aligned}$$
(9)

where x is a testing instance, \(p(w_{j}|x)\) is the approximation of the posterior probability that instance x belongs to class j.

2.2 Fuzzy integral

In this section, we present the notations related to fuzzy integral (Ralescu and Adams 1980). Let \(D=\{(x_i,y_i)|x_i\in R^{d},y_i\in R^{k},i=1,2,\ldots ,n\}\) be a training set, \(Y=\{\omega _{1},\omega _{2},\ldots ,\omega _{k}\}\) be a set of class labels, \(L=\{L_{1}, L_{2},\ldots , L_{l}\}\) be a set of classifiers trained on D or on subsets of D. In the context of ensemble learning, \(L_{i}(1\le i\le l)\) are called base classifiers or component classifiers. For \(\forall x \in R^{d}\), \(L_{i}\) assigns a class label to x from Y. As given by Kuncheva Kuncheva (2001), we may define the output of classifier \(L_i\) to be a k-dimensional vector:

$$\begin{aligned} L_{i}(x)=(p_{i1}(x),p_{i2}(x),\ldots ,p_{ik}(x)) \end{aligned}$$
(10)

where \(p_{ij}(x) \in [0,1](1\le i \le l; 1\le j \le k)\) denotes the support degree given by classifier \(L_{i}\) to the hypothesis that x comes from class \(\omega _{j}\), \(\sum _{j=1}^{k}p_{ij}(x)=1\). In this paper, \(p_{ij}(x)\) is an estimation of the posterior probability \(p(\omega _{j}|x)\) by classifier \(L_{i}\).

Given \(L=\{L_{1}, L_{2},\ldots , L_{l}\}\), \(Y=\{\omega _{1},\omega _{2},\ldots ,\omega _{k}\}\), and arbitrary testing sample x. The following matrix is called decision matrix with respect to x.

$$\begin{aligned} DM(x)= \begin{bmatrix} p_{11}(x)&\ldots&p_{1j}(x)&\ldots&p_{1k}(x)\\ \vdots&\vdots&\vdots \\ p_{i1}(x)&\ldots&p_{ij}(x)&\ldots&p_{ik}(x)\\ \vdots&\vdots&\vdots \\ p_{l1}(x)&\ldots&p_{lj}(x)&\ldots&p_{lk}(x) \end{bmatrix} \end{aligned}$$
(11)

where the ith row of the matrix is the output of classifier \(L_{i}\), the jth column of the matrix is the support degree from classifiers \(L_{1}, L_{2},\ldots ,L_{l}\) for class \(\omega _{j}\).

Let P(L) be the power set of L, the fuzzy measure on L is a set function: \(g: P(L) \rightarrow [0, 1]\), which satisfies the following two conditions:

  1. (1)

    \(g(\varnothing )=1\), \(g(L)=1\);

  2. (2)

    For \(\forall A, B \subseteq L\), if \(A \subset B\), then \(g(A)\le g(B)\).

For \(\forall A, B \subseteq L\) and \(A \cap B = \varnothing \), g is called \(\lambda \)-fuzzy measure, if it satisfies the following condition:

$$\begin{aligned} g(A \cup B)=g(A)+g(B)+\lambda g(A)g(B) \end{aligned}$$
(12)

where \(\lambda > -1\) and \(\lambda \ne 0\).

The value of \(\lambda \) can be determined by solving the following Eq. (12).

$$\begin{aligned} \lambda +1=\prod _{i=1}^{l}(1+\lambda g_{i}) \end{aligned}$$
(13)

where \(g_{i}=g(\{L_{i}\})\), which is called fuzzy density of classifier \(L_{i}\). It is noted that Eq. (13) has only one solution which meets the conditions \(\lambda > -1\) and \(\lambda \ne 0\). Usually, \(g_i\) can be determined by the following formula (Zhan et al. 2012):

$$\begin{aligned} g_i=\frac{p_i}{\sum _{j=1}^{l}p_{j}}\delta . \end{aligned}$$
(14)

where \(\delta \in [0,\, 1]\) and \(p_i\) is testing accuracy or verification accuracy of classifier \(L_i(1\le i\le l)\).

Let \(h:L \rightarrow [0, 1]\) be a function defined on L. The Choquet fuzzy integral and the Sugeno fuzzy integral of function h with respect to g are defined by (15a) and (15b), respectively.

$$\begin{aligned} (C)\int h d\mu&=\sum \limits _{i=2}^{l+1}\left( h(L_{i-1})-h(L_{i})\right) g(A_{i-1}), \end{aligned}$$
(15a)
$$\begin{aligned} (S)\int h d\mu&=\bigvee _{i=1}^{l}\left( h(L_{i})\bigwedge g(A_{i})\right) . \end{aligned}$$
(15b)

where \(h(L_{1})\ge h(L_{2})\ge \cdots \ge h(L_{l})\), \(h(L_{l+1})=0\), \(A_{i-1}=\{L_1, L_2, \cdots , L_{i-1}\}\).

Given a testing instance x, when we use fuzzy integral to integrate the l trained base classifiers \(L_{1}, L_{2},\ldots , L_{l}\) for classifying x, we first compute decision matrix DM(x), and then sort jth \((1\le j\le k)\) column of DM(x) in descending order and obtain \((p_{i_{1}j}, p_{i_{2}j}, \cdots , p_{i_{l}j})\).

If the trained base classifiers \(L_{1}, L_{2},\ldots , L_{l}\) are integrated by the Choquet fuzzy integral with formula (15a) for classifying x, then the support degree \(p_{j}(x)\) is calculated by the following formula (16).

$$\begin{aligned} p_{j}(x)=\sum _{t=2}^{l+1}\left( p_{i_{t-1}j}(x)-p_{i_{t}j}(x)\right) g(A_{t-1}) \end{aligned}$$
(16)

If the trained base classifiers \(L_{1}, L_{2},\ldots , L_{l}\) are integrated by the Sugeno fuzzy integral with formula (15b) for classifying x, then the support degree \(p_{j}(x)\) is calculated by the following formula (17).

$$\begin{aligned} p_{j}(x)=\mathop {max}\limits _{1\le t\le l}\{min\{p_{i_{t}j}, g(A_{t})\}\} \end{aligned}$$
(17)

In this paper, we use the Choquet fuzzy integral to integrate the trained base classifiers.

Fig. 1
figure 1

The idea of randomly oversampling approach with \(p=9\)

Full size image
Fig. 2
figure 2

Data manipulation processes of MapReduce

Full size image

3 The proposed algorithm

In this section, we introduce the proposed algorithm which includes three stages: (1) randomly oversampling referred to enemy nearest neighbor which is found by a parallel framework with MarReduce. (2) Construction of balanced training sets and training base classifiers SLFNs with ELM. (3) Ensemble the trained SLFNs with fuzzy integral.

Let \(S=S^{+}\cup S^{-}\) be imbalanced big data, \(|S^{+}|=n^+\), \(|S^{-}|=n^{-}\), \(n^{+}<<n^{-}\). The \(S^{+}\) and \(S^{-}\) denote the set of positive class instances and negative class instances in S, respectively. The idea of our proposed randomly oversampling approach can be depicted by Fig. 1, where the symbol “\(\square \)” denotes a negative instance, “\(\vartriangle \)” denotes a positive instance, while “\(\blacktriangle \)” denotes a positive instance randomly generated with uniform distribution within the nearest circle of \(x^+\) which is a positive instance, \(x^-\) is its enemy nearest neighbor. For each \(x^+\in S^{+}\), we randomly generate p instances in its corresponding nearest neighbor circle (or hypersphere in high dimensional space) with uniform distribution, p is a parameter defined by user.

Fig. 3
figure 3

The process of constructing l balanced training sets and training l base classifiers SLFNs (the part in the dashed rectangle)

Full size image

Because that \(n^{+}<<n^{-}\), S is a big data set indicates that \(S^{-}\) is a big data set. For \(\forall x^{+}\in S^{+}\), in order to efficiently find its enemy nearest neighbor from big data set \(S^{-}\), MapReduce (Dean and Ghemawat 2008; Zhai et al. 2016, 2017; Ludwig 2015) is employed in the proposed algorithm. MapReduce is a parallel programming framework which uses the strategy of divide and conquer to deal with big data (Emani et al. 2015; Wang 2015). It automatically partitions big data into some small pieces and deploys them into different parallel computing nodes (see Fig. 2). Based on the idea of functional programming language LISP (Berkeley and Bobrow 1964), MapReduce provides a simple and feasible method of parallel programming, two functions Map and Reduce are used to fulfill the basic parallel computing tasks. Map and Reduce are two abstract interfaces of parallel programming. For a given specific big data problem, one only needs to implement the two functions, many programming details in system bottom level have been abstracted away for users. In the proposed algorithm, the designed Map and Reduce functions are presented in Algorithms 2 and 3, respectively.

figure b
figure c

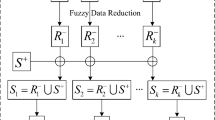
After randomly oversampling, we obtain a new positive instance subset \(S_{up}^{+}\) whose size is \(q=(1+p)n^{+}\). Next we construct l balanced training sets and train l base classifiers SLFNs on the l balanced training sets with ELM, this process can be depicted by Fig. 3 (the part in the dashed rectangle), where \(S^{-}=S_{1}^{-}\cup S_{2}^{-}\cup \cdots \cup S_{l}^{-}\) and l is determined by the following formula (18).

$$\begin{aligned} l=\frac{n^{-}}{q}=\frac{n^{-}}{(1+p)n^{+}} \end{aligned}$$
(18)

The l is the number of balanced training sets, it is also the number of base classifiers of an ensemble. Given an imbalanced big data set, because that \(n^{-}\) is a constant, we can find from formula (18) that l is actually determined by q, while q is determined by p which is the number of randomly generated positive instances with uniform distribution in a nearest neighbor hypersphere.

The final stage of the proposed algorithm is to integrate the trained base classifiers SLFNs with fuzzy integral. In the proposed algorithm, we use the Choquet fuzzy integral to integrate the trained SLFNs whose results are transformed into the interval [0, 1] by softmax function (9). The pseudo code of the proposed algorithm is given in Algorithm 4.

figure d

4 Experimental results and analysis

For convenience, the proposed algorithm is denoted by MR-FI-ELM. If the ELM algorithm is replaced with BP algorithm to train the basic classifiers in the proposed algorithm MR-FI-ELM, then the corresponding algorithm is denoted by MR-FI-BP. In order to verify the effectiveness of MR-FI-ELM, we conduct two experiments on 6 data sets and present a statistical analysis on the experimental results. The first experiment is to compare the MR-FI-ELM with three related algorithms: SMOTE (Chawla et al. 2002), SMOTE-RF-BigData (Río et al. 2014) and MR-V-ELM (Zhai et al. 2017) on two measures: F-measure and G-mean. The second experiment is to compare MR-FI-ELM with MR-FI-BP on running time. All experiments are carried out on 6 data sets which include 2 artificial imbalanced big data sets, 3 UCI imbalanced big data sets (Lichman 2013) and 1 real world data set (Liu and Liu 2016). The basic information of the 6 data sets is listed in Table 1. In Table 1, the imbalanced ratio is the ratio between the number of positive class instances and the number of negative class instances.

Table 1 The basic information of the 6 data sets
Full size table

The first artificial imbalanced big data set denoted by Artificial-1 which is generated with the following formula (19). If \(f(x_1,x_2,\ldots ,x_{10})>1\), then the corresponding instances are belonged to negative class, otherwise the corresponding instances are belonged to positive class. The artificial-1 includes 24,134 positive instances and 217,201 negative instances.

$$\begin{aligned} f(x_1,x_2,\ldots ,x_{10})=\frac{x_{1}^{2}}{a_{1}^{2}}+\frac{x_{2}^{2}}{a_{2}^{2}} +\cdots +\frac{x_{10}^{2}}{a_{10}^{2}} \end{aligned}$$
(19)

The second artificial imbalanced big data set denoted by Artificial-2 which is generated with two two-dimensional Gaussian distribution \(p(x|\omega _{i})\sim N(\mu _{i}, \varSigma _{i})\) \((i=1, 2)\), which are corresponding to two classes, their mean vectors and covariance matrices are given in Table 2. The artificial-2 includes 32,156 positive instances and 318,348 negative instances.

Table 2 The mean vectors and covariance matrices of two Gaussian distributions
Full size table

The first UCI data set is transformed from data set Skin_segment (Lichman 2013), it includes 21,870 positive class instances and 196,834 negative class instances. The second UCI data set is transformed from data set PokerHand (Lichman 2013), it includes 47,012 positive class instances and 423,108 negative class instances. The third UCI data set is transformed from UCI data set CoverType (Lichman 2013), it includes 20,911 positive class instances and 211,439 negative class instances. For convenience, the three transformed UCI data sets are also denoted by Skin_segment, PokerHand and CoverType.

The real-world data set is a liver data set (Liu and Liu 2016) with two imbalanced classes, which includes 12,500 negative class instances and 500 positive class instances. All instances were collected from a hospital located in Baoding of Hebei Province, we omitted the name of the hospital and removed three attributes name, sex and data from the original liver data set due to protection of privacy of the patients. Among the 6 data sets, Liver has the highest imbalanced ratio 0.04, but it is not a large data set rather than a medium-size data set. Liver data set has 5 attributes, which are alanine aminotransferase (ALT), aspertate aminotransferase (AST), total protein (TP), albumin (ALB) and globulin (GLB). We have three purposes to carry out the experiment on this medium-size data set. The first one is to verify whether the proposed algorithm is feasible on medium-size data set? the second one is to verify whether the proposed algorithm is feasible on extremely imbalanced data sets? the third one is to verify the applicability of the proposed algorithm, i.e., to verify whether the proposed algorithm can deal with practical problems?

4.1 Experiment 1: compare MR-FI-ELM with SMOTE, SMOTE-RF-BigData and MR-V-ELM on F-measure and G-mean

The experiments are conducted on a cloud computing platform with 5 nodes. The configuration of the cloud computing platform is given in Table 3, the configuration of nodes of the cloud computing platform is given in Table 4.

Table 3 The configuration of the cloud computing platform
Full size table
Table 4 The configuration of the nodes of the cloud computing platform
Full size table

In the scenario of binary imbalanced classification, let p and n are the true positive class label and true negative class label, respectively, Y and N are the predicted positive class label and predicted negative class labels, respectively. Then, a representation of classification performance can be formulated by a confusion matrix (see Fig. 4).

Fig. 4
figure 4

The confusion matrix

Full size image

The commonly used assessment metrics for imbalanced data classification algorithms include Precision, Recall, F-measure and G-mean, their definition are given as follows (He and Garcia 2009).

$$\begin{aligned}&{} { Precision}=\frac{\hbox {TP}}{\hbox {TP}+\hbox {FP}} \end{aligned}$$
(20)
$$\begin{aligned}&{} { Recall}=\frac{\hbox {TP}}{\hbox {TP}+\hbox {FN}} \end{aligned}$$
(21)
$$\begin{aligned}&\hbox {F-measure}=\frac{(1+\beta )^{2}\times { Recall}\times { Precision}}{\beta ^{2} \times { Recall}+{ Precision}} \end{aligned}$$
(22)

where \(\beta \) is a coefficient to adjust the relative importance of precision versus recall (usually, \(\beta =1\)).

$$\begin{aligned} \hbox {G-mean}=\sqrt{\frac{\hbox {TP}}{\hbox {TP}+\hbox {FN}}\times \frac{\hbox {TN}}{\hbox {TN}+\hbox {FP}}} \end{aligned}$$
(23)
Fig. 5
figure 5

The relationship between the parameter l and F-measure

Full size image
Fig. 6
figure 6

The relationship between the parameter l and G-mean

Full size image
Table 5 The experimental results of F-measure
Full size table
Table 6 The experimental results of G-mean
Full size table

In this paper, we use F-measure and G-mean as the measures to evaluate the performance of the proposed algorithms. From formula (18), we can find that the parameter p, i.e., the number of oversampling instances, determines the parameter l, i.e., the number of basic classifiers, while l has a significant influence on the performance of the integrated classification system. In other words, the parameter p has a significant influence on the performance of the integrated classification system. We experimentally analyze the relationships between the parameter l and F-measure and G-mean, the results are given in Figs. 5 and 6. From Figs. 5 and 6, we can find that the suitable value of l should be 5 or 6. In our experiments, we set the parameter \(l=5\) for the six selected data sets. The experimental results of F-measure and G-mean compared with SMOTE, SMOTE+RF-BigData and MR-V-ELM are listed in Tables 5 and 6, respectively. The experimental results listed in Tables 5 and 6 demonstrate that the performance of the proposed algorithm outperforms the three related algorithms. We realize that the reasons why the MR-FI-ELM outperforms the three related algorithms on the performance include the following two points: (1) as a tool for classifier fusion, fuzzy integral can well model the interactions among the basic classifiers which have complementary information. (2) The proposed oversampling method extends the domain of positive instances, which enhances the classification ability of the integrated classification system. In addition, from the experimental results on the data set liver, we can find that (1) the proposed algorithm is not only feasible on imbalanced big data sets, but also feasible on medium-size data sets, (2) the proposed algorithm is also effective on extremely imbalanced data sets. It imply for the experimental results on the data set liver that the proposed algorithm can effectively deal with medium-size real life tasks.

4.2 Experiment 2: compare MR-FI-ELM with MR-FI-BP on running time

The MR-FI-ELM and the MR-FI-BP are similar, the only difference is that the former uses non-iterative algorithm ELM to train basic classifiers, whereas the later uses iterative algorithm BP to train basic classifiers. The purpose of this experiment is to verify that the MR-FI-ELM is more efficient than the MR-FI-BP due to the non-iterative learning. In this experiment, we mainly focus on comparing the running time that the two algorithms used on the six data sets under the circumstance that the accuracy (F-measure and G-mean) at the same level as given in the second columns of Tables 5 and 6, the experimental results of the running time of the two algorithms are given in Table 7. From Table 7, we can find that for every data set the running time of MR-FI-ELM is much lower than the time of MR-FI-BP. In other words, from the view point of experiments, the conclusion that the MR-FI-ELM is more efficient than the MR-FI-BP is true.

Table 7 The comparison of MR-FI-ELM and MR-FI-BP on running time (second)
Full size table
Table 8 The results of statistical analysis on F-measure and G-mean
Full size table

4.3 The statistical analysis on the experimental results of F-measure and G-mean

In order to further verify the effectiveness of the proposed algorithm, we statistically analyzed the experimental results of F-measure and G-mean with paired T test in confidence level 0.05 (Janez 2006; Zhai 2011; Zhai et al. 2012). For the limitation of pages, we only provide here the statistical analysis on F-measure and G-mean, and omit the statistical analysis on running time. Firstly, for each data set and for each algorithm, we run the 10-fold cross-validation 10 times and obtain 4 statistics denoted by \(X_1, X_2\), \(X_3\) and \(X_4\) (where \(X_i(i=1, 2, 3, 4)\) are 100-dimensional vector) corresponding to SMOTE, SMOTE+RF-BigData, MR-V-ELM and MR-FI-ELM, respectively. Next the paired T test is applied to the experimental results by computing the values of MATLAB function \(ttest2(X_1, X_4)\), \(ttest2(X_2, X_4)\) and \(ttest2(X_3, X_4)\). The results of the statistical analysis on the F-measure and the G-mean are listed in Table 8. From the p values listed in Table 8, we can confirm that MR-FI-ELM statistically outperforms SMOTE, SMOTE+RF-BigData and MR-V-ELM.

5 Conclusion

Based on MapReduce, non-iterative learning, ensemble learning and oversampling, this paper proposed an efficient classification algorithm for imbalanced big data. The proposed algorithm MR-FI-ELM has three advantages: (1) its idea is simple and it is easy to implement. (2) It not only can effectively classify imbalanced big data, but also can deal with practical problems with medium-size. (3) It is feasible and effective for extremely imbalanced data. The experimental results show that (1) the MR-FI-ELM is much more feasible and outperforms the three related algorithms: SMOTE, SMOTE+RF-BigData and MR-V-ELM, (2) the MR-FI-ELM is more efficient than MR-FI-BP. In the future work, we will investigate that the parameter p is dynamically changed and that the influence of the dynamic p on the performance of the proposed algorithm. In addition, we will extend the proposed algorithm to the scenario of multiple classification of imbalanced big data.