Energy-efficient green ant colony optimization for path planning in dynamic 3D environments

Abstract

With the proliferation in demand for navigation systems for reconnaissance, surveillance, and other day-to-day activities, the development of efficient and robust path planning algorithm is an open challenge. The uncertain and dynamic nature of the real-time scenario imposes a challenge for the autonomous systems to navigate in the environment, avoiding collision with the moving obstacles without compromising on the energy-time trade-off. Motivated by this challenge, an efficient gain-based dynamic green ant colony optimization (GDGACO) metaheuristic has been proposed in this paper. The energy consumption while path planning in a dynamic scenario will be humongous owing to its nature. The proposed algorithm reduces the total energy consumed during path planning through an efficient gain function-based pheromone enhancement mechanism. The memory efficiency of Octrees is incorporated for workspace representation because of its ability to map large 3D environments to limited memory. Comprehensive simulation experiments are conducted to demonstrate the efficacy of GDGACO. Results are analysed through comparison with other methods in terms of path length, computation time, and energy consumed. Also, the results are verified for statistical significance.

1 Introduction

Strategic path planning is one of the most important functionalities of logistic systems and supply chain management in urban environments (Li et al. 2020; Zhao and Pan 2020; Savuran and Karakaya 2016). An intelligent logistics distribution planning system will not only increase the efficiency of distribution but also reduce the overall cost of delivery (Zhao and Pan 2020). But with the boom due to rapid development in present-day technology, enterprises are seeking for intelligent systems for efficient route planning. Logistic distribution optimization is a classic NP-hard problem that can be easily related to the classical travelling salesman problem (Li et al. 2020). Rational and reasonable route planning systems that can work on an autonomous system is the need of the hour. The present-day technology enables us to acquire precise geographic data on any location. Using this accurate location information, route planning can be done for logistics distribution. But the volume of such location information is high and the variety is heterogeneous. So, the traditional algorithms may fail to produce an efficient solution. Conventionally, path planning problem is categorized into static and dynamic based on the nature of their environment. A static path planning problem will have a prior knowledge of its environment and the obstacle position. But on the other hand, dynamic path planning problem will not have a prior knowledge of the environment with respect to the obstacle and their position. Real-world scenarios are dynamic without a prior knowledge of the obstacles in it. The position of obstacles tends to change over time. In the real world, route planning tends to be dynamic in a 3D environment where the obstacles may be moving and there would not be a prior knowledge of the environment, thereby adding additional complexity to the process. In the past decade, a noticeable change in trend towards metaheuristics (Savuran and Karakaya 2016) has been observed in the areas of path planning for logistics distribution. Their ability to produce quasi-optimal promising solutions irrespective of the environment has made them a strong contender in the field of optimization (BoussaïD et al. 2013). Many works could be found in the literature regarding dynamic path planning. Table 1 investigates some of the findings from recent researches. A biogeography-based optimization with a harmony-based embedded search was proposed for fault diagnosis and detection by Yu et al. (2018). The search ability of the algorithm was enhanced at the mutation stage with a pitch adjustment in the harmony search. Elhoseny et al. (2018) proposed a modified genetic algorithm for the robot path planning for behaviour analysis in dynamic environments. Miao and Tian (2013) proposed an enhanced simulated annealing approach for dynamic robot path planning. Experiments were performed with both static and dynamic obstacles under different simulated environments. Willms and Yang (2008) proposed a real-time robot path planning system. The system was able to integrate safety margins around obstacles using local penalty function and implemented on various real-time simulations. A probabilistic road map-based ant colony optimization approach was developed by Adolf et al. (2007) for UAV 3D space planning. The experiments proved that a path planner could be integrated with a task planner for real-time uses. Yin et al. (2017) proposed a multi-objective path planning system for dynamic urban environments. Safety index maps were designed for both static and dynamic obstacles, using which the position of obstacle was predicted. Extensive simulations on both synthetic and real-time datasets have been performed for verifying the efficiency of the system. A stochastic dynamic environment-based path planning system was proposed by Subramani and Lermusiaux (2019) by considering the risks in uncertain and dynamic scenarios. Initially, the probability distribution of environmental flows and risks were predicted. The path with minimum risk is chosen as the optimum path.

Table 1 Investigation of the recent literature

The system experimented with coastal and urban environments. An improved gravitational search-based multi-robot path planning algorithm in a dynamic environment was proposed by Das et al. (2016). The positions were updated using particle swarm optimization and greedy strategy. The simulations were done in C and Khepera II environment. Luo et al. (2019) proposed an improved ant colony-based method for path planning of mobile robots. An improvement was made on pheromone initialization, pheromone update, deadlock avoidance, and simulations that were made in MATLAB. Navigation planning in dynamic environments using a Genetic algorithm was proposed by Uçan and Altilar (2012). Simulations were done using USA waypoints of southern states. The algorithm achieved better results in terms of speedup, flexibility, and quality in dynamic scenarios. An effective routing protocol for vehicular ad hoc networks based on fuzzy logic, namely F-Ant was proposed by Fatemidokht and Rafsanjani (2018), taking into consideration challenges like self-organization, dynamicity of vehicles. The simulations were done in NS-2 simulator. The proposed method was able to achieve high packet delivery ratio and low end-to-end delay. Zhang and Zhang (2018) proposed an improved ant colony optimization method with strengthened pheromone updating mechanism for solving constraint satisfaction problems. A set of benchmark CSP test cases were used for simulation and was able to achieve better results based on convergence speed and quality of the solution. A literature review on UAV 3D path planning was done by Yang et al. (2014). A different perspective in the application of heuristic method in the process of routing and planning was experimented by Yu and Wang (2013). A model-based fault diagnosis system through the vehicle steering of CyCab electric vehicle was instrumented to identify different faults abrupt fault, incipient fault, and intermittent fault. The methods were classified into five categories based on its nature, and a comprehensive analysis of its complexity was also stated. From the literature, then it can be observed that though many algorithms were proposed for dynamic path planning in the presence of moving obstacles without a prior knowledge of environment, a consolidates method for intelligent path optimization with obstacle avoidance consuming least energy has not been proposed.

1.1 Challenges from the literature analysis

From the literature analysis made above, the following challenges can be observed:

• 1. In the case of real-time dynamic environments, there would be no prior information regarding obstacles and their position. Additionally, 3D real time is generally large in size and heterogeneous. This increases the storage complexity of the algorithm. The challenge regarding handling the huge volume of real-time data is not effectively addressed in the literature.

• 2. Though there are algorithms that enable minimum length and collision-free path in the literature, they suffer from high energy consumption. Energy efficiency of the path is not elaborated in the literature.

• 3. When dealing with dynamic environment without a prior knowledge, the metaheuristic methods in the literature tend to consume more time and also result in lengthy paths (Elhoseny et al. 2018; Bhasin et al. 2016). This is because these methods concentrate on the non-dominated points during their search.

• 4. When dealing with real-time dynamic environments, the stability and convergence of the algorithm are important performance metrics. From the literature, it is evident that there is an urge for the faster convergence of the algorithm with greater stability.

1.2 Contributions of this paper

Motivated by the challenges mentioned above, and to alleviate the same, in this work, an energy-efficient gain-based dynamic green ant colony optimization is proposed for planning safe and energy-efficient path. The main contributions of the work are:

• 1. A gain-based pheromone enhancing mechanism for cost and energy-efficient dynamic path planning has been proposed. The enhanced pheromone update phase of the ant system will eliminate the unwanted traversals during the current best solution search and thus reduce energy consumption.

• 2. Due to the volume and variety of the 3D data, memory-efficient storage becomes substantial, which is addressed by using Octrees data structure.

• 3. In addition to the distance-based obstacle avoidance during the next node to be visited, an obstacle avoidance strategy is added during the gain-based pheromone enhancement phase. Thus, the current best solution will be collision-free.

• 4. Faster convergence has been observed because of the pheromone enhancement mechanism (Fig. 11a–f).

• 5. The proposed method is found to be stable with a lower standard deviation (Table 5) and efficient in terms of satisfying the objectives.

1.3 Organization of the paper

The remainder of the paper is constructed as follows. Section 2 focuses on the basic ideas that are essential for the design of the proposed idea. Section 3 is the core section, which deals with the proposed idea for energy-efficient path planning in 3D dynamic environments. To realize the applicability of the proposed algorithm, simulation experiments with real-time data are conducted. Further, comparative investigation is carried out with state-of-the-art methods to understand the strengths and weaknesses of the proposed algorithm. Finally, Sect. 5 provides the conclusion and future direction of research in 3D path planning.

2 Preliminaries

2.1 Environment modelling

The first step for path planning is environment modelling. The path of an unmanned vehicle (UV) is continuous, while computers can process discrete data. The environment for path planning is represented using a digital elevation model (DEM). With the advancements in modern-day GIS, DEM is easily available for many locations of the earth. A DEM is a representation of the ground surface using the elevation information. The ground elevation is represented using a surface model that contains regularly spaces numerical array of elevation values. A DEM is usually expressed as $\left( {X_{i} ,Y,Z_{i} } \right)$ where $X_{i}$ and $X_{i}$ are the planar coordinates, $Z_{i}$ is the elevation for $\left( {X,Y_{i} } \right)$. DEM data can be represented either as a raster format (in terms of the grid as called as elevation map) or as a vector-based triangular irregular network. Raster-based height maps are used in this work for DEM representation and processing. Figure 1a shows a DEM data realized as a surface model, and Fig. 1b shows the corresponding height map.

Fig. 1

a A DEM data realized as surface model and b height map

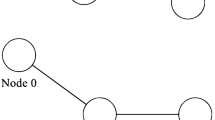
The DEM is processed using MATLAB functions and stored in a two-dimensional array where each array index contains the elevation value of the corresponding coordinates. To facilitate path planning, the DEM is modelled as a grid map $G$ with $V$ as nodes and $H$ as edges, where each node has eight connected neighbours, as shown in Fig. 2. The environment is modelled into a three-coordinate system ($XYZ$), where each point can be represented in terms of $\left( {X,Y,Z} \right)$. Let $V_{i}$ be the current node denoted as $X_{i} ,Y_{i} ,Z_{i}$ and $V_{j}$ be the neighbour node that is to be visited next denoted as $X_{j} ,Y_{j} ,Z_{j}$.

Fig. 2

Eight-neighbour representation of DEM data

The Euclidean distance (planimetric distance) between current node $V_{i}$ and neighbouring node $V_{j}$ in the X–Y plane is given by Eq. (1),

$$ pd(V_{i} ,V_{j} ) = \sqrt {(X_{i} - X_{j} )^{2} + (Y_{i} - Y_{j} )^{2} } $$

(1)

The difference in elevation between $V_{i}$ and $V_{j}$ along the $Z$ plane is given by Eq. (2),

$$ h(V_{i} ,V_{j } ) = Z_{i} - Z_{j} $$

(2)

The Euclidean surface distance between $V_{i}$ and $V_{j}$ on a three-dimensional space ($XYZ$) is thus given by Eq. (3),

$$ d(V_{i} ,V_{j} ) = \sqrt {(X_{i} - X_{j} )^{2} + (Y_{i} - Y_{j} )^{2} + h(V_{i} ,V_{j } )^{2} } $$

(3)

The slope between $V_{i}$ and $V_{j}$ is given by Eq. (3),

$$ \theta (V_{i} ,V_{j } ) = \frac{{h(V_{i} ,V_{j } )}}{{pd(V_{i} ,V_{j} )}} $$

(4)

On DEM, plain euclidean distance (plainmetric length) is different from surface length (Jenness 2004). The rationale behind calculation true distance using Eqs. (3) and (4) is adapted from Ganganath et al. (2015).

The main objective of dynamic path planning is minimizing the total path length during the target seeking behaviour without colliding with the obstacles, but through the least energy consumption. With regard to the first objective, path length can be determined using Eq. (3). Obstacle avoidance behaviour and energy cost model for path planning will be discussed in the forthcoming sections.

2.2 Linear regression-based energy cost model

Energy reduction is one of the main challenges when using a UV for path planning. Researchers have identified many factors like road grade, velocity, on-board system configuration, vehicle mass, driving style as some of the factors that play a major role in determining the energy consumption of UV. From the methods in Sadrpour et al. (2012, 2013) and Jabbarpour et al. (2017), the energy consumption of UV during path planning can be determined. Parameters like vehicle mass and velocity, road grade, and rolling resistance are considered from Sadrpour et al. (2012). Power at (t) can be calculated by Eq. (5) as

$$ \begin{aligned} P(t)& = F(t)v(t) + b \\ &= (W\sin (\gamma (t)) + fW\cos (\gamma (t)) + ma(t) + C) * v(t) + b + \varepsilon (t) \\ \end{aligned} $$

(5)

where $P(t)$ = power at t; $F(t)$ = traction force; $v(t)$ = velocity at t; $m$ = mass of vehicle; $a(t)$ = acceleration at t; $W$ = weight of vehicle; $\gamma$(t) = road grade; $f$ = rolling resistance coefficient; $C$ = internal resistance coefficient; $b$ = energy consumed by on-board equipment, ε(t) = model error.

By Sadrpour et al. (2012), the value of γ does not increase more than 15°. Therefore Eq. (5) can be linearized into Eq. (6).

$$ \begin{aligned} P(t)& = F(t)v(t) + b \\ &= (W\left( {\gamma (t) + fW + ma(t) + C} \right)* v(t) + b + \varepsilon (t) \\ \end{aligned} $$

(6)

Rewriting Eq. (6) as a linear regression model, we get Eq. (7).

$$ P(t) - ma(t)v(t) = v(t)W(\gamma (t) + f + C^{*} ) + b + \varepsilon (t) $$

(7)

where $C^{*} = C /W$.

Rewriting Eqs. (7) to (8), the regression model for energy reduction calculation can be got.

$$ A\left( t \right) = b + C.B\left( t \right) + \varepsilon \left( t \right) $$

(8)

where the response is $A\left( t \right) = \left[ { P\left( t \right) - ma\left( t \right)v\left( t \right)} \right]$; predictor is $v\left( t \right)W = B\left( t \right)$; and the regression model is $C = \left[ {\left( {\gamma \left( t \right) + f + C^{*} } \right)} \right]$ containing information regarding road grade, resistance, and fractional losses.

Recursive least squares prediction method is used to determine the values of C and b. From Sadrpour et al. (2012, 2013) and Jabbarpour et al. (2017), more details on the method can be found. The time taken to reach the destination $T_{D}$ can be found using the known start and destination positions. The energy consumed during path planning can be got by integrating power over the mission duration as given by Eq. (9)

$$ E_{c} = \mathop \int \limits_{0}^{{T_{D} }} P(t){\text{d}}t \approx \mathop \sum \limits_{i = 1}^{v} P(j)\Delta t $$

(9)

2.3 Obstacle avoidance and target seeking behaviour

The main aim of path planning towards the target seeking behaviour of UV is to minimize the distance towards the destination and maximize the distance towards obstacles. Path planning in a dynamic environment is a challenging task because of the changing position of the obstacles. Figure 3 shows the navigation of UV in the presence of dynamic obstacles. A safe path planning requires effective obstacle avoidance mechanism. From Fig. 3, let UV be the position of unmanned vehicle. As the UV moves forward, it is confronted by static and moving obstacles. The UV senses obstacles in its sensing range. Upon sensing the obstacles, a collision cone is formed by the UV (Luh and Liu 2007). From Fig. 3, PP and QQ are the tangents from the UV to obstacle forming the collision cone. Let V_UV-Ob be the relative velocity between the UV and obstacle. Let V_Ob be the velocity of obstacle and V_UV be the velocity of UV. For the UV to avoid collision, the relative velocity between UV and obstacle, V_UV-Ob should lie outside the collision cone. Also, from Luh and Liu (2007) V_UV-Ob is the result of velocity between UV and obstacles. Though V_Ob can be measured using sensors, it cannot be adjusted. Thus, for safe path planning of UV, during the neighbour search, the next position is chosen based on the maximum distance from the obstacle.

Fig. 3

Scenario representing obstacle avoidance behaviour

Let o be the number of obstacles in the environment represented as $(Ob_{1} ,Ob_{1} ,Ob_{2} ,Ob_{3} , \ldots ,Ob_{o} )$ with the coordinates as $((X_{{Ob_{1} }} ,Y_{{Ob_{1} }} ),(X_{{Ob_{2} }} ,Y_{{Ob_{2} }} ) \cdots (X_{{Ob_{o} }} ,Y_{{Ob_{o} }} ))$. Let s be the number of obstacles in the environment represented as $(Ob_{1} ,Ob_{1} ,Ob_{2} ,Ob_{3} , \ldots ,Ob_{s} )$. The Euclidean surface distance between the current position and the nearest obstacle is given by Eq. (10),

$$ d\left( {V_{i} ,Ob_{i} } \right) = \sqrt {\left( {X_{{Ob_{i} }} - X_{i} } \right)^{2} + \left( {Y_{{Ob_{i} }} - Y_{i} } \right)^{2} + \left( {Z_{{Ob_{i} }} - Z_{i} } \right)^{2} } $$

(10)

where $X_{{Ob_{i} }}$ and $Y_{{Ob_{i} }}$ are X and Y coordinates of the nearest obstacle $Ob_{i}$ such that $Ob_{i} \in Ob_{s}$, $Z_{{Ob_{i} }}$ is the elevation of $(X_{{Ob_{i} }} ,Y_{{Ob_{1} }} )$.

During the pursuit of destination, it is mandatory to choose the shortest path with the minimum distance to the goal for effective planning. The UV must move towards the next best position without colliding with the obstacle to reach the destination safely. The Euclidean distance between the current position and the destination node $V_{dest}$ is given by Eq. (11),

$$ d\left( {V_{i} ,V_{dest} } \right) = \sqrt {\left( {X_{dest} - X_{i} } \right)^{2} + \left( {Y_{dest} - Y_{i} } \right)^{2} + \left( {Z_{dest} - Z_{i} } \right)^{2} } $$

(11)

where $X_{dest}$ and $Y_{dest}$ are the X and Y coordinates of the destination and $Z_{dest}$ is the elevation at ($X_{dest} ,Y_{dest}$).

In the presence of multiple moving obstacles, the chances of collision with each obstacles must be calculated so that an obstacle which has more chances of collision can be avoided. The collision distance index (Luh and Liu 2007) is calculated using Eq. (12) as

$$ C\_Id = \frac{{d\left( {V_{i} ,Ob_{i} } \right)}}{{V_{Ob} *\Delta t}} $$

(12)

From Eq. (12), an obstacle with high collision index has least chances of collision.

2.4 Ant colony optimization

Ant colony optimization proposed by Italian Scholars Marco Dorigo et al.(1996) is a swarm-based stochastic algorithm that was inspired by the foraging behaviour of ants to obtain their food. It is a population-based metaheuristic that is carried out by a colony of ants resulting in an optimal path between their nest and food source. Ants communicate among themselves through Stigmergy. As the ants move, they deposit a chemical liquid named pheromone on their way. The remaining ants follow the pheromone trail. The amount of pheromone on a trail increases when more ants take the path and decrease vice versa. A typical food searching behaviour of ants is shown in Fig. 4. The process of adding up pheromone on a trail is called pheromone reinforcement/accrual leading to positive feedback. Artificial ants are the counterparts of real-world ants. They are most similar to natural ants, but they possess their memory and internal state. Like any other metaheuristics, a proper balance between exploration and exploitation will help in the optimal convergence of the ant colony optimization. Pheromone evaporation on least-used trails helps in the exploration process, thus avoiding convergence to local optima. In the case of no evaporation, all ants will tend to follow the path by the first ant without exploring the solution space. There are many variants of ACO like ant colony system, elitist ants, ant density model, and so on (Padhy 2005). In this work, the ant system is used because of its simplicity and robustness towards applications of any interest.

Performing a local search on the current neighbour window of the ants will lead to exploitation. In this work, a pheromone enhancement mechanism adopted from Sangeetha et al. (2019) is used to determine the current best path among moving obstacles.

Fig. 4

Foraging behaviour of ants in finding the shortest path between food and source

The notations and parameters used in ant colony optimization are as given in Table 2.

Table 2 Parameters of the ant colony algorithm

3 Materials and methods

3.1 Problem formulation and dataset description

Given S and D as start and destination positions, $V_{f}$ as the set of traversable nodes such that $V_{f} \subset V$, the problem of path planning, can be formulated as a minimization problem.

The main objective is to minimize target distance with collision avoidance from Eqs. (10) and (11). The objective function for obstacle avoidance and target seeking can be framed as given by Eq. (13). The final solution obtained should be of least distance without any collision with the obstacles thus satisfying both the objectives. An energy-efficient safe path is obtained by minimizing Eq. (13)

$$ {\text{Min}}\;g(x) = \mathop \sum \limits_{i = 1}^{r} \mathop \sum \limits_{j = 1}^{r - 1} x_{ij} \left( {G_{1} \left( {\frac{1}{{{\text{minimum}}_{{Ob_{o} \in Ob_{s} }} \left( {d\left( {V_{i} ,Ob_{i} } \right)} \right)}}} \right) + G_{2} \left( {d\left( {V_{i} ,V_{dest} } \right)} \right)} \right) $$

(13)

Subject to

$$ \mathop \sum \limits_{i = 1,i \ne j}^{r - 1} x_{ij} = 1 ,\;\;j = 1, \ldots ,r - 1,\quad \forall j \in \varLambda \backslash {\text{\{ }}S{\text{\} }} $$

(14)

$$ \mathop \sum \limits_{j = 1,j \ne i}^{r - 1} x_{ij} = 1,\;\;i = 1, \ldots ,r - 1,\quad \forall i \in \varLambda \backslash \{ D\} $$

(15)

$$ d_{ij} = \sqrt {\left( {X_{i} - X_{j} } \right)^{2} + \left( {Y_{i} - Y_{j} } \right)^{2} + \left( {Z_{i} - Z_{j} } \right)^{2} } $$

(16)

$$ x_{ij} = \left\{ {\begin{array}{*{20}l} 1 \hfill & {{\text{for}}\;{\text{path}}\;{\text{between}}\;i\;{\text{and}}\;j} \hfill \\ 0 \hfill & {\text{otherwise}} \hfill \\ \end{array} } \right. $$

(17)

where r is the size of input.

Equations (14) and (15) indicate that there can be only one arrival (except start S) and one departure (except Destination D) at a time. Equation (16) represents the distance function to calculate distance that can be calculated using. Equation (17) indicates that either the node is included or discarded from the list.

In Eq. (13), let $Ob_{s}$ be the obstacles sensed by UV during its course of navigation. $G_{1}$, $G_{2}$, are weightage parameters given to the objective function. From Eq. (13), it can be inferred that the value of $\left( {d\left( {V_{i} , V_{dest} } \right)} \right)$ decreases as the UV gets nearer to the destination. Also, the value of ${\text{minimum}}_{{Ob_{o} \in Ob_{s} }} \left( {d\left( {V_{i} , Ob_{i} } \right)} \right)$ increases as the UV is away from an obstacle. Equation (13) can be divided into two parts viz., obstacle avoidance and target seeking. The first part of Eq. (13) can be related to obstacle avoidance, where the focus is to maintain a maximum distance from the obstacle. The farther the UV is from obstacle, the higher is the value of this part of (13). The second part of Eq. (13) can be related to target seeking, where the focus is to minimize the total distance to the target. Since the problem of path planning can be formulated as a minimization problem, obstacle avoidance is given in the denominator of the first part of Eq. (13), target seeking, and intermediate path optimization is giving in the numerator of the second and third part. If the primary focus of navigation of UV is towards safe path planning, then $G_{1}$ can be given maximum weightage. If $G_{2}$ is given maximum weightage, then the focus of navigation is towards shortest path planning. If $G_{2}$ is given maximum weightage, then the focus of navigation is towards optimizing the intermediate path segments. Proper selection of weightage parameter will decide the success of the objective function towards path planning. In this work, equal importance is given to both the weightage parameters and its value is considered as 0.5, thus realizing energy-efficient and safe path for traversal.

Satellite images with their corresponding ground truth and digital surface model (DSM) have been taken from International Society for Photogrammetry and Remote Sensing (ISPRS) (http://www2.isprs.org/commissions/comm3). Elevation data of 100 points of 30–90 m resolution can also be freely acquired from Shuttle Radar Topography Mission (SRTM) (Farr 2007). SRTM elevation data are obtained from http://earthexplorer.usgs.gov/.

3.2 Gain-based green obstacle avoidance and intermediate path optimization

Two important aspects namely ant colony optimization: pheromone trail $\tau_{ij}$ and the heuristic $\eta_{ij}$ guide ACO. These two aspects are related to the exploration and exploitation of ant colony optimization. An extensive search on the solution space is made possible by the heuristic, whereas pheromone update determines the speed of convergence of the algorithm. As the ant traverses around the solution space, it constructs complete solutions. Once solutions are built, pheromone evaporation and pheromone reinforcement are performed using the pheromone update rules. The pheromone update rule generally increases the pheromone on the most used trail and decreases the amount of pheromone on the least used trail, thereby reducing the possibility of trapping in local optima.

The traditional pheromone update mechanism updates trails based on the intensity of pheromone on them. In this work, the pheromone enhancement is carried out based on the gain quantity. The gain is determined by a local heuristic based on the relative distance to the destination with respect to the neighbour and the maximum distance from the obstacle. This gain quantity enhances the pheromone on the current best path based on the local heuristic. It enables all the ants to move towards the current best solution without colliding with the obstacles. The proposed gain function will help in avoiding unnecessary traversals and obstacle collision, thus leading to minimum energy consumption.

3.2.1 Calculating gain

Pheromone gain is an additional amount of pheromone added to the best path found so far to make the process of pathfinding quicker. Thus, the new quantity added will enable quicker pathfinding by eliminating the unwanted traversals during the local search. Pheromone gain is given by (19).

$$ progress_{jDest} = \frac{{\delta_{jDest} + d\left( {V_{i} ,Ob_{i} } \right)}}{{d_{iDest} }} $$

(18)

$$ Gain_{ij} = \frac{1}{{\left( {1 + e^{{ - \lambda *dprogress_{jDest} }} } \right)}} $$

(19)

where $V_{dest}$ = destination vertex; $V_{j}$ = neighbour vertex; $V_{i} = {\text{current node}}$. λ decides the degree of smoothness, which ranges from 0 to 1; δ_jDest = dj_Dest, where $d_{jDest } = \sqrt {\left( {V_{j} - V_{Dest} } \right)^{2} + h_{jDest}^{2} }$ for j = 1, 2, 3,…, 8,$d\left( {V_{i} ,Ob_{s} } \right)$ is the maximum distance between the UV and the nearest sensed obstacle as computed by Eq. (10) and $h_{ij}$ is the elevation difference calculated using Eq. (2) and $d_{iDest}^{k} = \sqrt {\left( {V_{i}^{k} - V_{Dest}^{k} } \right)^{2} + h_{jDest}^{2} }$. For all values of λ and progress, the value of the gain always lies between 0 and 1. Values obtained from the Sigmoidal function will help in the smooth traversal of UV to the destination.

Consider a configuration space of 20 × 20, as shown in Fig. 5.

Fig. 5

Pictorial representation of pheromone gain process

The algorithm starts from the known start position. Upon reaching $V_{i}$ (current position), the next node to be visited is searched from the neighbours ($V_{j1} \;{\text{to}}\; V_{j8}$). The node with relative minimum distance to destination $(progress_{jDest} )$ is marked as the next node to be visited, and the corresponding pheromone trail is updated. During pheromone update, $Gain_{ij}$ is added to $\tau_{ij}^{new}$ of node with minimum $progress_{jDest}$, and subtracted from the $\tau_{ij}^{new}$ of other neighbours. If all the neighbours of current nodes have the same distance, then gain is added to all nodes. Mathematically the procedure can be written as,

δ_jDest = dj_Dest, where $d_{jDest } = \sqrt {(V_{j} - V_{Dest} )^{2} + h_{jDest}^{2} }$ for j = 1, 2, 3,…,0.8. $h_{ij}$ is the elevation difference calculated using Eq. (2). If the path provides minimum δ_jDest and $\max_{1,2, \ldots s} \left( {d\left( {V_{i} ,Ob_{s} } \right)} \right)$, then the gain will be added along with the current pheromone quantity, otherwise subtracted.

$$ \tau_{ij}^{new} = \left\{ {\begin{array}{*{20}l} {\left( {1 - \rho } \right)\tau_{ij}^{old} + \mathop \sum \limits_{k = 1}^{N} \Delta \tau_{ij}^{k} + Gain_{ij}^{k} } \hfill & {{\text{for}}\;\hbox{min} (\delta_{ij} ) \;{\text{and}}\;\max_{1,2, \ldots s} d\left( {V_{i} ,Ob_{s} } \right)} \hfill \\ {\left( {1 - \rho } \right)\tau_{ij}^{old} + \mathop \sum \limits_{k = 1}^{N} \Delta \tau_{ij}^{k} - Gain_{ij}^{k} } \hfill & {\text{otherwise}} \hfill \\ \end{array} } \right. $$

(20)

Using Eq. (20), $\tau_{ij}^{new}$ is calculated and used in Eq. (22).

Adding the $Gain_{ij}^{k}$ of kth ant to the trail from a node with min δ_jDest, $\max_{1,2, \ldots s} \left( {d\left( {V_{i} ,Ob_{s} } \right)} \right)$ and subtracting from other trails by Eq. (20) will result in the accumulation of pheromone on the current best path and evaporation from other paths. This enhancement will induce the ants to settle down towards the current best solution and thereby leading to faster convergence.

3.3 Methodology for GDGACO

Path planning using GDGACO on uneven terrain consists of two stages, and its detailed explanation is given below:

• 1. Terrain data preparation.

• 2. Gain-based green ant colony optimization.

3.3.1 Terrain data preparation

The acquired satellite images from ISPRS and its corresponding elevation data are processed using MATLAB 2018b.

From the terrain matrix, slope ($\theta$) is calculated for all points. With the help of slope values, the traversable map is prepared. In addition, the obstacles that are already present in the environment, certain areas in the environment may not be traversable by the UV because of the geographic elevation of the location. To handle such situation, two mechanisms, surpassing and searching, is considered.

Surpassing: For $\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{z} < \theta < \bar{z},$ the corresponding points of $\theta$ will be considered traversable. Ants will be able to surpass those points and continue their traversal.

Searching: For $\theta \notin \left[ { \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{z} ,\bar{z} } \right]$, the corresponding points of $\theta$ will be considered non-traversable. Ants will treat them as obstacles.

The parameters $\bar{z},\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{z}$ are tunable depending upon the unmanned system. $\bar{z},\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{z}$ is the upper and lower limits of the tunable parameters. They determine the maximum and minimum value of $\theta$ that can be surpassed by the unmanned system.

3.3.2 Gain-based dynamic green ant colony optimization

3.3.2.1 Environment understanding

The environment for path planning must be transformed into a form to carry out the path planning process. The traversable map created from the elevation data is modelled into a 3D occupancy map using the Octree data structure. The grid resolution for occupancy grid is one cell per metre, i.e. each cell is of 1 m in size. An Octree data structure recursively subdivides the environment into cubic volumes called voxels. For a given map area, space is divided into eight voxels called octants that stores the probability values for each location. The entire recursive division is mapped into a tree. The traversable area in the environment are marked as white nodes, obstacles are marked as black nodes, and current nodes under consideration are marked as grey nodes.

3.3.2.2 ACO parameter initialization

The parameters of the ant colony system are initialized in this phase. Initially $\tau_{o}$ is set to 0.$\alpha ,\beta ,\rho$, start node and destination node are initialized subsequently. The values used for simulation are given in Table 4. The ants during the ACO process either move in a forward direction or backward direction. Using the Node Transition Probability function, the ants move forward and reach the destination. The ants use their memory to travel back to the starting point using the pheromone update rules. The flow diagram for GDGACO working is given in Fig. 6.

Fig. 6

Flow diagram of proposed GDGACO

3.3.2.3 Cost and energy calculation

Upon reaching a vertex, ants check in the $visit_{k}$ for the next node to be visited, resulting in the forward phase of map exploration. Using the node transition probability, the next node to be visited is chosen. By Eq. (21), the pheromone values of all links are updated. Using Eq. (21), gain is calculated for pheromone enhancement on the current best trail.

$$ Gain_{ij}^{k} = \frac{1}{{\left( {1 + e^{{ - \lambda *progress_{jdest}^{k} }} } \right)}} $$

(21)

where $progress_{jdest}^{k} = \frac{{\delta_{jDest}^{k} + (d\left( {V_{i} ,Ob_{i} } \right)}}{{d_{iDest}^{k} }}$.

Here $\delta_{jDest}^{k} = d_{jDest}^{k}$; $d_{jDest}^{k} = \sqrt {\left( {V_{j}^{k} - V_{Dest}^{k} } \right)^{2} + h_{jDest}^{2} }$$d_{iDest}^{k} = \sqrt {\left( {V_{i}^{k} - V_{Dest}^{k} } \right)^{2} + h_{jDest}^{2} }$. The pheromone gain on the current best trail is calculated using a sigmoid function. Sigmoid function has a characteristic ‘S’-shaped curve with an interval from 0 to 1. It could be found from the meticulous observation that the curve is very similar to a path with smooth turns, which is the desired path in most of the UV path planning problems (Ravankar et al. 2018). The natural inclination towards smoothness and bounded intervals of the sigmoid function is used to determine the current best path. Also, during the calculation of $progress_{jdest}^{k}$, the maximum distance of all the sensed obstacles is added to $\delta_{jDest}^{k}$ to enable obstacle avoidance. Therefore, the pheromone is enhanced on the current trail that has the maximum distance from the obstacle.

Using the node transition probability, the next node to be visited is chosen. Equation (22) is used for the forward move.

$$ NTP_{ij}^{k} (t) = \left\{ {\begin{array}{*{20}l} {\frac{{\left( {\tau_{ij}^{k} } \right)^{\alpha } \left( {\eta_{ij}^{k} } \right)^{\beta } }}{{\sum_{{h \in visit_{k } }} \left( {\tau_{ih}^{k} } \right)^{\alpha } \left( {\eta_{ih}^{k} } \right)^{\beta } }}* \frac{{n_{j} }}{{n_{j} + 1}}} \hfill & {{\text{if}}\;j \in visit_{k } } \hfill \\ 0 \hfill & {\text{otherwise}} \hfill \\ \end{array} } \right. $$

(22)

In Eq. (22), $\eta_{ij}$ is the cost of edge (i, j). $\tau_{ij}$ is the pheromone intensity in (i, j) and is calculated by (20) through the backward move. h are those nodes that are allowed to be visited ant the ants. $v_{j}$ is used to compute the connected components of the next vertex j. $\eta_{ij}$ is calculated using (23).

$$ \eta_{ij} = \frac{1}{{d_{ij} }} $$

(23)

where

$$ d_{ij } = \sqrt {\left( {V_{i}^{k} - V_{j}^{k} } \right)^{2} + h_{ij}^{2} } $$

(24)

$v_{ij}$ denotes the speed of vehicle, $\varphi$ indicates the maximum speed and is set to 2 m/s (Jabbarpour et al. 2017) to normalize the value, and $h_{ij}$ is the elevation difference between i and j that could be calculated using Eq. (2).

The cost of traversal between i and j is calculated using (23). By Eq. (23), the choice of the next node has an inverse relationship with distance.

3.3.2.4 Path planning

The final phase is the path planning phase. Once the forward move is completed, the ants start their backward move by tracing the path using their memory. During this move, the pheromone update rule is used to find the current pheromone quantity. The intensity of pheromone is updated using (25). The usability of the path is either increased by pheromone reinforcement or decreased through pheromone evaporation.

The quantity of $\Delta \tau_{ij}^{k}$ is given by (25),

$$ \Delta \tau_{ij}^{k} = \left\{ {\begin{array}{*{20}l} {\frac{1}{{d_{ij}^{k} }} + \frac{1}{{E_{ij}^{k} }} + \left( {d\left( {V_{i} ,Ob_{i} } \right)} \right)} \hfill & {{\text{if }}\;k{\text{th}}\;{\text{ant}}\;{\text{passes}}\; i\; {\text{and}}\;j} \hfill \\ 0 \hfill & {\text{otherwise}} \hfill \\ \end{array} } \right. $$

(25)

where $d_{ij}^{k}$ and $E_{ij}^{k}$ are the distance and energy consumed over the edge i and j by kth ant.

According to Eq. (25), pheromone is updated on the trail that has the least distance to the target and maximum distance from the obstacle with least energy consumption.

The pseudo-code for GDGACO is given below:

The algorithm continues until either of the following conditions is achieved: the shortest path is obtained, or a predetermined number of iterations have been completed.

4 Results and discussion

4.1 Experimental setup

The proposed algorithm was implemented in MATLAB R2018b (The MathWorks, Natick, 2018). Simulations were performed in three different scenarios. Elevation values of 100 × 100 points of 18°N 76°E and 19°N 78°E were obtained from USGS for scenarios 1 and 2. Real-time city landscape (1189 × 1002) of the Vaihingen dataset from ISPRS have been considered for scenario 3. Figure 7a–c shows the three different scenarios used for simulations. Table 3 shows the details regarding the obstacles in all three scenarios. The following assumptions were made for the simulations:

• 1. Start and destination are known and remain the same during the process of path planning. However, they differ in each scenario.

• 2. All dynamic obstacles were considered to move at a uniform speed of 0.5 m/s in the case of uniform obstacle speed. In the case of varying speed of obstacle, the speed is taken randomly between 0.5 and 1.2 m/s.

Fig. 7

a–c Scenarios considered for simulation (all units in metres (m))

Table 3 Scenarios used for simulation

4.2 Performance measures

The proposed method is compared with existing methods with the following performance measures. Each algorithm was run for 20 runs, and performance has been analysed.

• Mean, and Standard Deviation of 20 runs is estimated and compared to determine the stability of the method.

• Average and Median of the Computation time consumed in 20 runs are compared for computational run-time analysis of the algorithm.

• Energy consumed during path planning is computed and compared with other algorithms to determine the reduced energy consumption.

4.3 Parameter setting

Simulations were conducted on the different scenarios for varying values of ρ. The values used for simulations are taken from Jabbarpour et al. (2017) and are given in Table 4. The algorithm executed for 20 runs on each scenario and average for each scenario is considered. Variations of ρ on scenario 1 are given in Fig. 8. Varying the values of ρ from 0.1 to 0.9, the length is computed as given in Fig. 8a, and time is calculated as given in Fig. 8b. From both the box plots, it can be inferred that for ρ = 0.5, the algorithm shows minimum deviation with no outliers for both length and fitness. Also, obstacle avoidance behaviour was observed for ρ = 0.5.

Table 4 Parameters and values of GDGACO (proposed), MGA, FA, MACO, GWO used in simulation

Fig. 8

a Variation of ρ with regard to length and b variation of ρ with regard to time

4.4 Performance evaluation

The proposed GDGACO was compared with most frequently used metaheuristic algorithms like Modified Genetic Algorithm (MGA) (Elhoseny et al. 2018), Firefly Algorithm (FA) (Patle et al. 2018), Modified Ant Colony Optimization (MACO) (Sangeetha et al. 2019), Grey Wolf Optimization (GWO) (Rao et al. 2018) and results are given in Table 5. Although existing algorithms exhibit obstacle avoidance behaviour, reduction in energy consumption during path planning is not considered effective. The proposed GDGACO exhibits obstacle avoidance behaviour with reduced energy consumption.

Table 5 Performance analysis of GDGACO against MGA, FA, MACO, and GWO

It can be inferred from the literature that as the number of turns in a path increases, the energy consumed to traverse on it also increases. Figure 9a–c shows the path planned on three different scenarios. The scenarios are simulated with both static and dynamic obstacles. The motion of dynamic obstacles as represented with a directed arrow. From Fig. 9a–c, it can be seen that the number of turns in the path obtained through GDGACO has less number of turns than the path obtained through other algorithms with the help of enhanced pheromone update mechanism. In scenario 1 and 2 (Fig. 9a, b), GDGACO was able to swiftly reach the destination despite the moving obstacles with less number of turns and least path length. Though FA was able to reach the destination promptly, the path obtained by FA has more number of turns than GDGACO. In scenario 3 (Fig. 9c), the path obtained by GDGACO has less number of turns and traverses through low elevation areas, thereby reducing energy consumption. In all the three scenarios (Fig. 9a–c), the path obtained by MGA and MACO has more number of turns. Also in order to avoid moving obstacles, the obtained paths are longer than GDGACO and FA. Also From Fig. 9a, b, though the path obtained from GWO is as good as that obtained from GDGACO, the path from GWO has more number of turns. In the case of Fig. 9c, the path obtained from GWO is longer than that of GDGACO. From Fig. 9, it can also be inferred that proposed GDGACO exhibits robustness and effectiveness irrespective of the size of environment. Scenario 1 and 2 differs from 3 in terms of size and nature of landscape. Scenario 3 is a real-time urban data. In all the three scenarios, it can be seen that proposed GDGACO outperforms other methods in terms of length and path safety. Furthermore, from the effectiveness of GDGACO in scenario 3 (real-time data from Vaihingen city), it can be inferred that GDGACO can also be applied for real-time day-to-day life-based path planning.

Fig. 9

Path obtained through GDGACO (proposed), MGA, FA, GWO, and MACO in a scenario 1, b scenario 2, and c scenario 3 (all units in metres (m))

4.4.1 Obstacle avoidance behaviour in the case of obstacles with uniform speed

Of the three objectives of path planning, the main objective with regard to dynamic path planning is obstacle avoidance. GDGACO was able to compute a smooth and safe path among moving obstacles. Figure 10a–c shows the working of GDGACO in the presence of moving obstacles. As the algorithms begin, the UV starts from the known start position towards the known destination position. During path planning, UV senses both the static and dynamic obstacles as shown in Fig. 10a and calculates the collision distance index of each obstacle. The spherical obstacle is found to be the most imminent obstacle since it was found to be closer to current position of UV. The algorithm steers the UV out of the collision cone of UV thus avoiding collision. Since obstacle avoidance is incorporated in pheromone-enhancing mechanism, GDGACO increases the pheromone value on the path that is at the maximum distance from the obstacle. From Fig. 10b, upon confronting the next obstacle, the procedure is again repeated and UV is steered out of the collision zone. Table 5 shows the performance analysis of GDGACO against MGA, FA, MACO, GWO verified through Wilcoxon signed-rank at a 95% confidence level. It can be seen that the path length obtained through GDGACO is the least in all three scenarios. With regard to time, GDGACO computes path in the least time. Standard deviation is used to measure the stability of the algorithm over a certain number of runs. From Table 5, it can be inferred that GDGACO is more stable than MGA, FA, MACO, GWO in terms of time, length, and energy.

Fig. 10

a–c Working of GDGACO in the presence of moving obstacles (all units in metres (m))

Though MACO performs closely on par with GDACO in terms of length, GDGACO outperforms MACO in terms of time and energy consumed. From Table 5, it can be concluded that for the optimal value of ρ, GDGACO will be able to find an optimal path in the presence of moving obstacles.

Figure 11a–f shows the convergence analysis of GDGACO against MGA, FA, MACO, GWO in terms of length and time. Figure 11a–c shows the convergence graphs of scenario 1, 2, 3 with regard to the number of iterations and time. Figure 11d–f shows the convergence graphs of scenario 1, 2, 3 with regard to the number of iterations and length. GDGACO is found to converge faster than the other methods because of the enhanced pheromone update mechanism. Also, it can be inferred that GDGACO does not meet with local optima, unlike FA and MACO.

Fig. 11

a–c Convergence analysis of time w.r.t no. of iterations and d–f convergence analysis of length w.r.t no. of iterations in scenarios 1, 2, and 3

4.4.2 Obstacle avoidance in the case of obstacles with varying speed

Simulations were performed on the above-mentioned three scenarios with obstacles under varying speed and the results are tabulated in Table 6. From Table 6, it can be inferred that the varying speed of obstacles does not affect the collision avoidance behaviour of the algorithm. It was found that the path length was 0.4%, 0.3%, 0.7% shorter than that computed from GDGACO in the case of obstacle with uniform speed in scenario 1, 2, 3, respectively. In terms of time and energy GDGACO consumed 0.4%, 0.4%, 0.3% and 0.5%, 0.3%, 0.07% more time and energy than that computed from GDGACO in the case of obstacle with uniform speed in scenario 1, 2, 3, respectively.

Table 6 Performance of GDGACO in the case of obstacle with varying speed. Median from 20 runs

Similar to the case of obstacle with uniform speed, the proposed algorithm GDGACO identifies the imminent and non-imminent obstacles and calculates the collision index of each obstacle. Based on the collision index, the UV is steered out of the collision cone of the imminent obstacle.

4.5 Discussions

From the above performance analysis, the following inferences are made:

• 1. In scenario 1, proposed GDGACO outperforms MGA, FA, MACO, and GWO in terms of length by 9.7%, 5%, 3.4%, 5.3%.

• 2. In scenario 2, proposed GDGACO outperforms MGA, FA, MACO, and GWO in terms of length by 7%, 7.9%, 6.3%, 3.3%.

• 3. In scenario 2, proposed GDGACO outperforms MGA, FA, MACO, and GWO in terms of length by 9.4%, 7.9%, 4.2%, 6.1%.

• 4. GDGACO exhibits higher stability when compared with existing algorithms in all the three scenarios with low standard deviation among its independent runs.

It can also be inferred clearly from the results in scenario 3 that GDGACO produces promising results on real-time data with dynamic obstacles.

5 Conclusion

A novel extension to ACO, GDGACO, has been proposed in this paper for safe, cost, and energy effective dynamic path planning. The modified pheromone enhancement mechanism will enable the ants to settle down in the current safe path by reducing unwanted traversals. The proposed GDGACO determines a collision-free path with minimum time and reduced energy consumption. Thus, the overall energy consumption is reduced. Applicability of the proposed algorithm is demonstrated by using real-time data collected from ISPRS repository and performing simulation experiments with dynamic obstacles. Furthermore, from the convergence analysis (Fig. 11a–f), it is evident that the proposed GDGACO algorithm converges faster than the state-of-the-art methods and also avoids local optima. From the investigation made on the performance of GDGACO against other algorithms (Table 5), it is clear that GDGACO certainly provides safe, cost, and energy effective path in minimum time. The stability of the GDGACO was also analysed in three different scenarios and is found to be stable with less standard deviation among the 20 runs of execution. GDGACO algorithm is also statistically significant at 95% confidence, which is inferred from the Wilcoxon test. The time complexity of GDGACO is found to be ${\text{O}}\left( {N*\left| {V_{f} } \right|* N_{r} } \right)$, where $N$ is the number of ants, $N_{r}$ is the number of iterations, and $\left| {V_{f} } \right|$ is the cardinality of traversable vertex set. GDGACO requires ${\text{O}}\left( {ph^{2} } \right)$ number of operations to update the pheromone at all traversals. Constructing a complete solution requires ${\text{O}}\left( {N*\left| {V_{f} } \right|} \right)$ space. Thus, the space complexity of GDGACO will be ${\text{O}}\left( {N*\left| {V_{f} } \right|} \right) + {\text{O}}\left( {ph^{2} } \right)$. Some of the limitations of the proposed work are: Method Perspective- (i) from simulation results it can be seen that GDGACO produces slightly less efficient results in the case of higher uneven terrain. Though scenario 1 and 2 are of same size, the scenario 2 is more uneven when compared with scenario 1 in terms of altitude variations of the landscape; (ii) also, GDGACO was found to be less stable in scenario 2 when compared with its stability in scenario 1. As, nature of terrain gets more uneven in terms of altitude variations, GDGACO tends to exhibit slightly less stability. Application Perspective- (i) modelling of UV with varying speed introduces additional overhead to the research problem, which is planned to be addressed in the future; and (iii) finally, the tuned parameters are feasible for path planning in ground (uneven/even terrains), but additional investigation and optimization is needed to manage path planning in aerial and underwater contexts. Limitations mentioned above are planned to be addressed. With regard to the future scope, GDGACO can be extended to be hybridized with reinforcement learning and new algorithms can be developed along with evolutionary programming concepts for efficient path planning in dynamic 3D environments.