1 Introduction

Over the past decades, Traveling Salesman Problem (TSP) and the Vehicle Routing Problem with capacity constraints (CVRP) were studied as the classic combinatorial optimization and the NP-hard problems. These days, the mentioned problems are still hot research topics. Expanding the scale of the problems causes, the traditional methods cannot effectively address them well. Swarm intelligence optimization algorithms were increasingly proposed to be applied to various complex optimization problems, such as the logistics transportation, the traffic management, and the storage allocation. Therefore, addressing the TSP and the CVRP problem using swarm intelligence optimization algorithms would be feasible effective.

Study of the Traveling Salesman Problem have been developed rapidly since it was first mathematically described by Merrill (Schrijver 2005). Hassler Whitney from the Princeton University raised the name of the traveling salesman shortly afterwards. Given the list of cities and the distance between the two cities, what is the shortest path to visit each city and return to the city of origin? The solution method was employed to calculate its precise value. Later, it was found that with the expansion of city scale, the time complexity of accurate solution is exponentially increased. Therefore, this complex TSP problem can not be solved properly at all, where the approximation algorithms and the heuristic algorithms were emerging. Among heuristic algorithms, the ant colony optimization algorithm can optimize the combinatorial optimization problems better than other algorithms (Jiang et al. 2020a; Zou and Qian 2019). Marco Dorigo described a method that heuristically generates well defined solutions to the TSP problems by simulating ant colonies named ant colony systems (ACS) (Colorni et al. 1991; Dorigo and Stützle 2019).

The Vehicle Routing Problem (VRP) was first introduced by George Dantzig and John Ramser in 1959. What is the best route setting to dispatch a fleet to meet a given set of customers? Which is a classical integer programming problem (Dantzig and Ramser 1959). Generally, in the VRP, goods in the warehouse should be delivered to the corresponding customers, and its goal is to minimize the total cost of the transportation route. The solution is feasible if the total number allocated to each path does not exceed the capacity of vehicles. Meanwhile, the CVRP is similar to the VRP, with the additional constraint that each vehicle must have a uniform capacity for a single path. For such large-scale path optimization problems, heuristic algorithms do not require many related parameters and are more adaptive to various constraints (He et al. 2016). These heuristic algorithms which are represented by the ant colony optimization algorithm show excellent performance in terms of accuracy, computational speed, and robustness within the optimization of various objective functions (Li and Meng 2020).

The Ant Colony Optimization algorithm (ACO) was originally proposed by Dorigo and Maniezzo in 1990, which generated from foraging behavior of ant colonies (Colorni et al. 1991; Dorigo and Stützle 2019). The activities of ants are always carried out in groups but in separated paths. Within each different path, ant has its own self information named pheromone which is generated by the activities of ants path (Bonabeau et al. 2000; Che et al. 2020; Deng et al. 2019; Jovanovic et al. 2019). The higher the concentration of pheromone on a certain path at the same time, the higher the probability of ants choosing to move forward , which will form a virtuous circle, prompting the ants to gradually move in the right direction to find food during the entire forced feeding process (Kumar et al. 2018; Manfrin et al. 2006; Randall and Lewis 2002). The ACO algorithm is a stochastic search method within the process of biological evolution inside the nature (Wang et al. 2020b; Li et al. 2019; Mirjalili and Dong 2020).

As a meta-heuristic algorithm, the basic ant colony algorithm has the advantages of strong robustness and high search efficiency. Ant colony algorithm is a population-based evolutionary algorithm, which is essentially parallel and easy to implement in parallel. Ant colony algorithm is easy to integrate with various heuristics and improves the performance of the algorithm. However, due to these features of ant colony algorithms, there are often many shortcomings, such as: Firstly, if parameters are not selected properly, the rate of solution may be slow and the quality of the solution could be particularly poor. Secondly, the basic ant colony algorithm has a large amount of calculations which will take a long time to be solved. Finally, the basic ant colony algorithm theoretically requires all ants to choose the same route, which is the optimal route sought. But in actual calculations, it is difficult to achieve this under the condition of a given number of cycles.

In view of the basic characteristics of the above-mentioned ant colony optimization algorithms, a lot of work has been done to overcome the shortcomings of the ant colony.

Enhanced local optimization is a very good strategy, it can make the ant colony avoid local optimization as much as possible in the search process, and enhance the local ability of the ant colony to make the algorithm more efficient. A lot of work have been done in this area. Liang et al. (2019) designed an efficient ant colony system (EACS) based on pre-selection strategy and local pruning strategy. Lim et al. (2008) proposed a hybrid ant colony algorithm (HACA) to describe the path planning problem in sparse graphs. To solve the problem of too long convergence time and falling into local optimal solution, Hlaing and Khine (2011) proposed an improved ant colony optimization algorithm to solve the TSP problem. Firstly, candidate set strategy is adopted to speed up convergence. Secondly, a heuristic parameter dynamic update rule based on entropy is proposed to improve the performance of solving TSP.

The traditional ant colony algorithm converges to an optimal path quickly due to its continuous search process. Therefore, the diversity of the population in the offspring will become smaller and smaller. At this time, the range that the ant colony can explore will become narrower and narrower, so it is easy to fall into a local optimal solution. This problem can be well solved by multi-group strategy. The ant colony will be divided into multiple populations at a certain moment. These populations will evolve together to explore different paths and share with other groups. This strategy can greatly increase the diversity of the group, expand the search range of the ant colony, and improve the performance of the algorithm. Roshanzamir et al. (2019) proposed a new method to prevent ant colony algorithm from iteratively decomposing individual structure. This approach enhances individual performance from generation to generation through a constructive process. Unlike the generation process, the individual is produced by the combination of other individuals. In the construction process, the individual is produced according to the experience of the previous generation. Under this mechanism, uncertainty can be managed in a random environment. Mavrovouniotis (2020) studied existing ant colony optimization algorithms specifically designed for combinatorial optimization problems in dynamic environments. The research algorithm is divided into two frameworks: evaporation-based algorithm and population-based algorithm. Describes a case study of using these algorithms to solve the dynamic traveling salesman problem. The proposed dynamic benchmark framework can be used to systematically conduct experiments, then analyze the impact of important ant colony optimization functions on numerous test cases.

With the continuous improvement in the optimization solution of the evolutionary algorithm (Wang et al. 2020a; Jiang et al. 2020b), abundant feature information around fitness can be presented by the ACO algorithm, which is mainly shown in the fitness, self-organizing, self-adaptive, self-learning, and high robustness. These ACO algorithm have some special search features reflect the population diversity, convergence speed, and optimal solution distribution. This paper focuses to describe the basic principles of the TSP and CVRP problem, establish appropriate models, and propose an adaptive ant colony optimization algorithm based on greedy strategy. In the GSACO algorithm, the control parameters are continuously adjusted based on greedy search strategy, and this novel algorithm speeding up the convergence and obtaining a higher accuracy.

The remainder of this paper is organized as follows: The first section analyzes the development status of ant colony algorithm and introduces the algorithm proposed by some outstanding scholars. Section 2 introduces the fundamental models of the TSP and CVRP problems respectively. GSACO algorithm is described in detail in Sect. 3. Numerical test and experiments to solve the TSP and CVRP problems using the GSACO algorithm are reported in Sect. 4. At the end, conclusions and future research are summarized.

2 The models of TSP and CVRP problems

2.1 The model of TSP problem

TSP problem is one of the commonly applied problems in transportation systems (Wang et al. 2021). Organizations that handle the delivery and transfer of objects have special difficulties while designing transportation networks. For instance, a businessman starts to navigate from a city, intends to sell products pass through n cities which have been already identified, and finally returns to the city of origin. Assuming that the distance between any two cities is known, the goal of this scenario is to find a path that only takes one trip to each city to minimize the total path.

For the modeling of TSP problem, some knowledge of graph theory are quoted. Let G= (V,E) be a function represents the path, where V is the vertex set, representing a set of locations inside the cities, and E is a set of edges, which is used to denote the distance of the path between different cities. N={1,2, ,N} denotes the number of visited cities.

Fig. 1
figure 1

A graphical representation of the TSP problem

Full size image

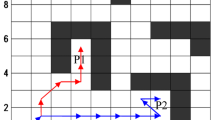
Figure 1 shows a graphical representation of the TSP problem, which should be tracked between identified cities. The objects denoted by a circle are the boundaries of initial path through each city.

The scenario parameters are as follows:

  • \(d_{ij}\): Distance between city i and j.

  • S: All the city nodes.

  • \({x_{ij}^{k}}= \left\{ \begin{array}{rcl} 1: &{}\text{ If } \text{ object } \text{ travels } \text{ from }\textit{ i }\text{ to }\textit{ j}\\ 0: &{} \text{ Otherwise } \end{array}\right.\)

The TSP model should minimize the travel path from an initial city 0 to the cities \(\{{i_{1}}, {i_{2}}, \dots , {i_{n}}\}\) which is formulated as \(\sum _{k=1}^{n}{d}({i_{k}, {i_{k+1}}})\), where \({d}({i_{k}, {i_{k+1}}})\) is the distance from the city \(i_{k}\) to \(i_{k+1}\). The objective function and constraints are as follows:

$$\begin{aligned}&{\text{min}}\sum _{i\ne {j}}{d_{ij}}{x_{ij}} \nonumber \\&\quad \textit{s.t.} \left\{ \begin{array}{ll} \sum _{i=0}^{n}{x_{ij}}=1\\ \sum _{j=0}^{n}{x_{ij}}=1\\ \sum _{(i,j\in {S})}{x_{ij}}<|\textit{S}|-1 &{} (\textit{i,j}\in {S},|S|>2)\\ {x_{ij}}=0 \textit{ or } 1 \end{array}\right. \ \end{aligned}$$
(1)

Where Eq. 1 denotes the shortest path to all cities. The first row of constraint 2 denotes that the city j can only be entered once. The second row denotes the departure city i can only be left. The third row denotes that the shortest path between all cities after traveling, is less than or equal to the sum of all undirected edges, and the fourth row denotes whether the object is passed from city i to city j.

2.2 The model of CVRP problem

CVRP shows that each vehicle has a fixed on-board capacity. It is a variant of the VRP problem which also is a typical NP-hard problem. The CVRP problem is described as the following to be modeled:

Objective: The objective is to reduce the number of vehicles and transportation time as much as possible on the promising that the total customer demand is less than the vehicle load.

Feasibility: The scheme is feasible if the total vehicle load assigned to each path is greater than the total demand of all the paths, and the number of vehicles on all paths are less than the total number of vehicles.

To model the CVRP problem, we also quote knowledge of graph theory as in the previous section. The requirement of CVRP problem involved the node and the communication path between the edge of the graph, which is different from the TSP problem. Therefore, N is a set of vertices, and each vertex denotes a customer with specific demands.

Fig. 2
figure 2

A graphical representation of the CVRP problem

Full size image

Figure 2 shows an overview of the CVRP problem, and represents the relationship between the customer node and the warehouse. In this sample, vehicles are dispatched from the warehouse to each customer node. The customer node is denoted by a circle. There is a directed edge from the warehouse to each customer node. The arrows in the figure denote the direction of the vehicle to the next node.

The CVRP problem mainly includes finding the K shortest vehicle paths to minimize the transportation cost of the vehicle (Toth and Vigo 2002).

The parameters of this scenario are identified as follows:

  • \(c_{ij}\): The cost between the point \(v_{i}\) and \(v_{j}\).

  • \(V_{c}\): A collection of all customer nodes.

  • V: A collection of all customer nodes and depot.

  • K: Maximum number of vehicles available.

  • S: All the customer nodes.

  • cap: The capacity of each car.

  • Cap: The capacity of all cars.

Decision variables:

  • \({x_{ij}^{k}}= \left\{ \begin{array}{rcl} 1: &{}\text{ If } \text{ edge( }\textit{i,j}\text{) } \text{ is } \text{ serviced } \text{ by } \text{ vehicle } \textit{k}\\ 0: &{} \text{ Otherwise } \end{array}\right.\)

  • \({y_{i}^{k}}= \left\{ \begin{array}{rcl} 1: &{}\text{ customer } \text{ points } {v_{i}} \text{ by } \text{ vehicle } \textit{k }\text{ service }\\ 0: &{} \text{ Otherwise } \end{array}\right.\)

In this paper, the goal of the CVRP problem is to minimize the total consumption of the current line. It is necessary to specify an initial starting point and meet the capacity conditions. The objective function and constraint conditions are as follows:

$$\begin{aligned}&{\text{min}}\sum _{(i,j)\in A}{c_{ij}} \sum _{k=1}^{K}{c_{ij}^{k}} \nonumber \\&\quad {s.t.} \left\{ \begin{array}{ll} \sum _{j\in V}\sum _{k=1}^{K}{x_{ij}^{k}}=1 &{} ({\forall }{} \textit{i}\in {V_{c}}) \\ \sum _{i\in V}{x_{ij}^{k}}={y_{j}^{k}} &{} ({\forall }{} \textit{j}\in {V_{c}},k=1,...,K)\\ \sum _{j\in V}{x_{ij}^{k}}={y_{i}^{k}} &{} ({\forall }{} \textit{j}\in {V_{c}},k=1,...,K)\\ \sum _{k=1}^{K}{y_{i}^{k}}=1 &{} ({\forall }{} \textit{i}\in {V_{c}}) \\ \sum _{k=1}^{K}\sum _{j\in {V_{c}}}{x_{0i}^{k}}=K \\ \sum _{(i,j)\in S}{x_{ij}^{k}}<|S|-1 &{} (\textit{i,j}\in S,|S|>2) \\ \sum _{i\in {V_{c}}}{cap_{i}}{y_{i}^{k}}\le Cap &{} ({\forall }{} \textit{k}=1\textit{,...,K}) \\ {x_{ij}^{k}}\in \{0,1\} &{} ({\forall }\{\textit{i,j}\}\in A,k=1,...,K) \\ {y_{i}^{k}}\in \{0,1\} &{} ({\forall }{} \textit{i}\in {V_{c}},k=1,...,K) \end{array}\right. \ \end{aligned}$$
(2)

Where Eq. 2 denotes the total cost of all accessible customers. In constraint, the first line denotes that customer point \(v_{i}\) is served by a certain vehicle. The second and third rows denote that customer point (\(v_{i},v_{j}\)) is on the service line of vehicle k, then the demand of these two customers points is served by vehicle k. The fourth line denotes that each customer point \(v_{i}\) can be served only once. The fifth line denotes that there are K lines serving customers from depot \(v_{0}\). The sixth line denotes that the sum of the shortest paths of all customer nodes are less than or equal to the sum of the directed edges of all customer nodes. The seventh line denotes that the sum of the onboard capacity of each line is not greater than the total capacity of the available vehicles. The eighth line denotes whether the client node \(v_{i}\) is being served. The ninth line denotes whether the k-th car has been visited, and each car corresponds to a route.

3 The proposed GSACO algorithm

Ant colony optimization algorithm is a meta-heuristic algorithm that integrates the advantages of random algorithm and local search. It provides a low cost feasible solution to optimize problems (referring to computing time and space). The ACO algorithm has good positive feedback and robustness, so performs well in addressing NP-hard problems, including the TSP and CVRP problems. In Sect. 2, the TSP and CVRP problems are described and specific models are proposed. The operation rules of the ACO algorithm which are based on greedy strategy. The two models mentioned above are as follows:

$$ p_{{ij}}^{k} (t) = \left\{ \begin{gathered} \frac{{\tau _{{ij}}^{\alpha } (t)\eta _{{ij}}^{\beta } (t)}}{{\sum _{{\mu \in N_{i}^{k} (t)}} \tau _{{ij}}^{\alpha } (t)\eta _{{ij}}^{\beta } (t)}}\,\,\,\,\,\,\,\,ifj \in N_{i}^{k} (t) \hfill \\ 0\qquad \qquad \qquad\qquad{ifj \in N_{i}^{k} (t)} \hfill \\ \end{gathered} \right. $$
(3)

where \(p_{ij}^{k}\)(t) is the transition probability, \(\eta _{ij}^{\beta }\)(t) is the pheromone value on edge(i,j) which denotes the memory of the high-quality path from node i to node j, \(\eta _{ij}^{\beta }\)(t) is heuristic information calculated by heuristic function, which denotes the exploration path of node i moving to node j. \(\alpha\) is the relative importance of residual information, which determines the level of pheromone concentration and the ants memories of better paths, and \(\beta\) is the relative importance of the predictive value, which determines both the size of heuristic information and the path of ant exploration.

In the path exploration process of traditional ant colony optimization algorithm, the concentration of pheromone will continuously increase during each generation of ants exploring the path. The descendant ants will concentrate on exploring the places with high pheromone concentration. In this case, as the number of iterations increases, the diversity of the population will gradually decrease, and the ants will not explore other paths. The algorithm is easy to fall into the local optimal solution. Based on this situation, the greedy strategy is applied in this paper. As the number of iterations increases, the concentration of pheromone and the relative importance of heuristic information are constantly adjusted, and the diversity of the population is dynamically changed, so that the algorithm is not easy to fall into a local optimal solution, and it improves the search ability of the algorithm.

$$\begin{aligned} \alpha =({x_{\text{max}}}-{x_{\text{min}}})\times \frac{n}{\text{Max}} \end{aligned}$$
(4)
$$\begin{aligned} \beta ={y_{\text{max}}}-({y_{\text{max}}}-{y_{\text{min}}})\times \frac{n}{\text{Max}} \end{aligned}$$
(5)

Within the continuous exploration process, ants would continuously converge to a high pheromone concentration place until finding an optimal solution. Within the Eqs. 4 and 5, \(x_{\text{max}}\) and \(x_{\text{min}}\) denotes the maximum and minimum relative importance of residual information respectively. \(y_{\text{max}}\) and \(y_{\text{min}}\) denotes the maximum and minimum value of the relative importance of the predicted value respectively. n denotes the current number of iteration, and Max denotes the maximum number of iteration.

Initially, a limited range of pheromone concentration and heuristic information will be set. In this article, the pheromone concentration and heuristic information are defined, and will be changed in the form of non-linear changes as the number of iterations increases. As the pheromone concentration increases in the process of ant colony exploration, we set the expression of the relationship between pheromone concentration to show the overall upward trend. On the contrary, the heuristic information is constantly decreasing, and we set the overall heuristic information relation expression to show a downward trend. Due to this change relationship, the downward trend of heuristic information will gradually accelerate during each iteration, thus ensuring that the ant colony is fully explored in the search process and enhancing the diversity of the population. It also ensures that the algorithm is not easy to fall into a local optimal solution.

The pheromone concentration of the first generation of ants would be increased continuously within the process of path exploration. The offspring ants will explore towards the place where the initial concentration of ant pheromone is high, however the offspring ants would also continue to explore the other paths.

As the number of iteration increases, the ant colony will gradually approach to the optimal solution, so the pheromone concentration would not be increased, while the heuristic information will continue to decrease, the above is expressed by Eqs. 4 and  5. Due to the above reasons, the pheromone is gradually enhanced, and the heuristic information is gradually reduced.

In the process of continuous iteration, \(\alpha\) and the concentration of pheromone would be increased while the number of iteration is increasing, that shows the ants would follow to search high pheromone concentrated locations. \(\beta\) and the heuristic information would be decreased while the number of iteration is decreasing.

The path exploration of ACO algorithm is a balance between \(\tau _{ij}\) and \(\eta _{ij}\), the function of heuristic information (\(\eta _{ij}\)) is usually a distinct function related to the problem. In this problem, the heuristic equation is:

$$\begin{aligned} \eta _{ij}=\frac{1}{{d_{ij}}} \end{aligned}$$
(6)

Where \(d_{ij}\) denotes the distance from position i to position j.

In the process of exploring the path, the concentration of pheromone also volatilizes naturally. The equation of pheromone volatilization are as follows:

$$\begin{aligned} \tau _{ij}(t+1)= & {} \tau _{ij}(t)+\frac{Q}{\text{length}} \end{aligned}$$
(7)
$$\begin{aligned} \tau _{ij}(t)= & {} (1-\rho )\times \tau _{ij}(t) \end{aligned}$$
(8)

Where length is the sum of the paths traveled by ants, and \(\rho\) is the degree of forgetting the previous path by ants.

3.1 An adaptive greedy search strategy of the TSP problem

In TSP problem, the proposed strategy is to greedy search, path construction, and roulette selection are proposed as the strategies to achieve next goals. The GSACO algorithm as a parallel search implementation method would reduce the searching time. Adjusting the constant value in an actual situation can improve algorithm efficiency.

GSACO algorithm process to solve the TSP problem is constructed as the following:

  • Step1: Initialize the strategy of each object according to the target of the TSP problem.

  • Step2: Construct a feasible solution to the TSP problem.

  • Step3: Update local pheromone.

  • Step4: Calculate and update the non-dominant solution.

  • Step5: Update global pheromone.

  • Step6: Determine whether the termination criterion is satisfied. If it is satisfied, the algorithm stops. Otherwise, go to Step 2.

The pseudocode of the GSACO algorithm for solving the TSP problem are shown below.

figure a

In the above process, Max is the maximum number of iteration, \(\rho\) represents the volatility coefficient, Q represents the pheromone intensity, NA is the number of ants, \(\alpha _{\text{max}}\) and \(\alpha _{\text{min}}\) represent the relative importance of the maximum and minimum residual information, and \(\beta _{\text{max}}\) and \(\beta _{\text{min}}\) represent the maximum and minimum values of the relative importance of the foreseen value respectively.

3.2 An adaptive greedy search strategy of the CVRP problem

Determine the next customer node from the probability selection is proposed as the model strategy within the CVRP problem. Then it minimizes the cost to meet the limited capacity of the vehicle. The efficiency of the algorithm can be improved by adjusting the constant value to be adaptive according to the actual situation. The GSACO algorithm proposed to solve the CVRP problem are as follows:

  • Step1: The requirements and costs of initializing the customer node, as well as the initialization of algorithm parameters.

  • Step2: The selection probability is calculated to select the feasible solution satisfying the vehicle capacity.

  • Step3: Record the current path and update the local pheromone.

  • Step4: Update the global pheromone.

  • Step5: Calculate the cost of all customer nodes and update the global optimal path.

  • Step6: Determine whether the termination criterion is satisfied. If it is satisfied, the algorithm stops. Otherwise, go to Step 2.

The pseudocode of using GSACO algorithm for solving the CVRP are shown below.

figure b

In Algorithm 2, c denotes the cost of the customer node, K denotes the maximum number of vehicles available, cap denotes the capacity each vehicle, and Cap denotes the capacity of all vehicles. To optimize the TSP and CVRP problems by this GSACO algorithm, the control parameters are continuously adjusted based on greedy search strategy.

4 Experimental results

4.1 The GSACO algorithm parameter settings

In order to verify the advantages of GSACO algorithm to solve the TSP and CVRP problems, 12 TSP standard instances and 10 CVRP standard instances were selected from the TSPLIB standard library and CVRP standard library respectively. Matlab2018a, core CPU i5, 8.0gb memory on Windows10 were employed as the experimental setup.

The main parameters of ant colony optimization algorithm in solving combinatorial optimization problems are \(\alpha\), \(\beta\), \(\rho\). \(\alpha\) and \(\beta\), representing the relative importance of residual information and the relative importance of heuristic information respectively. The GSACO algorithm would dynamically be changed through an adaptive form. \(\rho\) is the evaporation coefficient of pheromone, which is usually controlled within the range of [0.01,0.05], because the value of fitness evaluation function is relatively ideal within this range. The x and y coordinate in Fig. 3 represents the value of the parameter \(\rho\) and the fitness value respectively. Fig. 3 show the experimental results that reveal a higher stability performance of the GSACO algorithm when it is \(\rho =0.02\). In this experiment, small-scale test cases kroA100 and d198, and the larger scale test cases att532 and rat783 are employed. Initialization of other parameters is shown in Table 1. The performance of different parameter values within test cases kroA100, d198, att532, and rat783 are shown in Fig. 3. The optimal performance of the algorithm are obtained when \(\rho =0.02\).

MMAS (MAX–MIN ant system) algorithm was proposed by Stutzle T in 2000 (Stützle and Hoos 2000). This algorithm sets a maximum minimum value for the pheromone concentration on each path. The minimum pheromone increases the possibility of exploring a better solution where maximum pheromone concentration guarantees the heuristic of experience to the ant colony. The method of pheromone updating makes the algorithm to reach to the optimum value step by step. ACS (Ant Colony System) algorithm was proposed by Dorigo in 1997 (Dorigo and Gambardella 1997). The algorithm can be optimized step by step to the optimal ant path by applying the local and global pheromone update rules. IACO (Improved Ant Colony Algorithm) algorithm is an improved algorithm to solve the distribution problem of automobile chain maintenance parts which was proposed by Gao et al. (Gao et al. 2016).. It uses a new method to improve the update of local pheromone, and then modifies the global pheromone update rules to solve various combinatorial optimization problems. In the experiment of TSP and CVRP, the MMAS, ACS and IACO are compared as the three proposed algorithms.

Table 1 Parameter settings of the GSACO algorithm
Full size table

In the Table 1, Max denotes the maximum number of iteration, Q denotes the pheromone intensity, NA denotes the number of ants, \(\alpha _{\text{max}}\) and \(\alpha _{\text{min}}\) denotes the maximum and minimum values of the relative importance of the residual information, and \(\beta _{\text{max}}\) and \(\beta _{\text{min}}\) denotes the maximum and minimum values of the relative importance of the foreseen value respectively.

4.2 The GSACO algorithm for solving TSP problem

The MMAS, ACS, IACO and GSACO algorithms are simulated 10 times within each TSP standard instance. The maximum, minimum, mean and variance of the results are used to compare the performance of each algorithm which are shown in Table 2.

Dantzig42, Eil51, KroA100, Pr107, Ch130, D198, KroA200, Lin318, Pcb442, Att532, Rat783 and Pcb1173 as the banchmark cities in Table 2 are borrowed from web pages which are employed in the experiments (Codenotti et al. 1996). Figure 4 shows the convergence diagram of each TSP instance solved by MMAS, ACS, IACO and GSACO algorithms.

The first column of Table 2 is 12 examples of TSP problems. The second column is the maximum, minimum, average and standard deviation. The horizontal row is the fitness value or standard deviation corresponding to the four algorithms. The horizontal and vertical coordinates of Fig. 4 are the number of iteration and fitness values respectively. From Table 2 and Fig. 4, the performance of solving the TSP problems with GSACO algorithm is significantly better than the MMAS, ACS and IACO algorithms. The GSACO algorithm can effectively address the TSP problem and break through the local loop in a certain time and a certain number of iteration. However, there are still drawbacks: when the population becomes larger, the progress will slow down due to the large amount of calculation. Although the enhanced pheromones cause a decrease in searching time process, but the algorithm sometimes falls into the local optimal solution.

Fig. 3
figure 3

The GSACO algorithm parameters \(\rho\) different values to solve the test function

Full size image
Table 2 Instances comparison for solving the TSP problems
Full size table
Fig. 4
figure 4figure 4

Iterative convergence graph of four algorithms for solving TSP problems

Full size image

4.3 Comparison based on convergence analysis

The convergence of four classical ant colony optimization algorithms will be analyzed in this section. The performance of the algorithm is evaluated by observing the convergence curve and convergence period of the algorithm. In the convergence curve of the two-dimensional coordinate system, the abscissa represents the quantity and indicates the fitness evaluation time. The ordinate is the fitness evaluation index under the fitness function value of the algorithm, and is also the shortest path for travelers to visit all cities.

As shown in Fig. 4, GSACO algorithm converges faster when solving small-scale TSP test cases. For example, in the test cases of Dantzig42, Eil51, kroA100, Pr107 and d198, GSACO algorithm converges faster on these issues than ACS, MMAS and IACO algorithms. Among them, in the test cases of Dantzig42, kroA100 and d198, the convergence speed of GSACO algorithm is about 10 times, 40 times and 10 times of the fitness evaluation respectively, which is much faster than other algorithms. When solving medium-sized test cases, there is not much difference between the convergence speed of GSACO algorithm and ACS, MMAS and IACO algorithm. For instance, in the test cases of Ch130, kroA200 and lin318, the convergence speed of GSACO algorithm is not significantly different from ACS, MMAS and IACO algorithms. However, GSACO algorithm converges slower than ACS, MMAS and IACO algorithms when solving large test cases. For example, in test cases such as att532, Rat783 and pcb1173, GSACO algorithm converges slower than ACS, MMAS and IACO algorithms in these problems. What’s more, when GSACO algorithm converges, it is better than ACS, MMAS and IACO algorithm in the adaptability evaluation index. In this process, the adaptive parameter strategy based on greedy strategy makes the algorithm stable and convergent.

As described in the convergence curve analysis, a search mechanism based on greedy strategy and an adaptive parameter strategy are included in the GSACO algorithm, which is very effective for solving TSP test cases. In this way, the convergence speed of the algorithm is accelerated, the efficiency of the algorithm is improved, and the excitation quality is improved.

4.4 The GSACO algorithm for solving CVRP problem

Each standard CVRP instance is executed 10 times by the proposed GSACO, MMAS, ACS and IACO algorithms. The comparisons of experimental results are shown in Table 3 and Fig. 5. The first column of Table 3 is ten examples of the CVRP problem. The second column is the maximum, minimum, average and standard deviation. The horizontal row is the fitness value or standard deviation corresponding to the four algorithms. Figure 5 is a box diagram, which consists of 5 equivalents and 2 line segments, which can directly reflect the distribution of experimental data, and can also be used to analyze and compare various algorithms. The five characteristic values are the maximum value, upper quartile, median, lower quartile, and minimum value from top to bottom, and display possible outliers. The abscissa is four different algorithms, the ordinate is the cost in solving the path problem. The CVRP examples used in this article are respectively from Rochat and Taillard (1995) and Uchoa et al. (2017), which include the instances of Tai75a, X-n101-k25, X-n148-k46, X-n181-k23, X-n200-k36, X-n237-k14, X-n251-k28, X-n303-k21, X-n351-k40 and X-n401-k29.

When solving the NP-hard problems, only approximate solutions can be obtained, not exact solutions, through the swarm intelligence optimization algorithm. This algorithm tends to converge to a specific value while increasing the iteration times, however this value is often not an exact one. Table 3 and Fig. 5 show that the efficiency of the GSACO algorithm for solving the CVRP problem is significantly higher than the other MMAS, ACS and IACO algorithms, although in some CVRP instances, the standard deviations of IACO, MMAS and ACS algorithms are better than GSACO algorithm. However, from Table 3, we can see that when the scale of the example gradually increases, the optimal value of the GSACO algorithm proposed in this paper is better than the IACO, MMAS and ACS algorithms, and the difference in standard deviation also gradually decreases. The proposed GSACO algorithm can break through local loop within a certain time and a certain number of iteration. However, there are still some drawbacks. GSACO algorithm will often seek multiple paths, and then compare the length and the cost of the path. When the number of customers and the demand of customers is large. This results in a long searching time where the optimal solution is not very ideal. It may lead to the local optimal solution due to a robust randomness of the algorithm.

Table 3 Instances comparison for solving the CVRP problems
Full size table
Fig. 5
figure 5

Four algorithms are used to solve the box diagram of CVRP problems

Full size image

4.5 Comparison of algorithms based on descriptive statistics

To evaluate the algorithm from a statistical point of view, the box plot and the table of mean standard deviation will be described in this section. Box diagram is composed of 5 equal values and 2 line segments, which can not only directly reflect the distribution of experimental data, but also be used to analyze and compare various algorithms. The five characteristic values are the maximum value, the upper quartile, the median, the lower quartile and the minimum value from top to bottom respectively, and the possible abnormal values are displayed. Figure 5 shows the specific experimental data of four experimental ant colony optimization algorithms for solving 10 TSP test cases.

According to the eigenvalue data distribution of the box chart, the GSACO algorithm is compared with the MMAS algorithm, the ACS algorithm and the IACO algorithm. It is concluded that the fitness evaluation value of the GSACO algorithm is better than the other three algorithms when solving small and medium-scale CVRP test cases. Such as in tai75a, in the test cases of X-n101-k25, X-n148-k46, X-n181-k23, X-n200-k36, X-n251-k28 and X-n303-k21, the GSACO algorithm is superior to the MMAS, ACS and IACO algorithms in the maximum, upper quartile, median, lower quartile and minimum values. When the improved GSACO algorithm solves large-scale CVRP test cases, there is no much difference between the stability of GSACO algorithm and other algorithms. However, GSACO algorithm has better fitness evaluation indexes than MMAS, ACS and IACO algorithm in average, upper quartile and median, lower quartile and minimum. Therefore, the search mechanism based on greedy strategy and the adaptive parameter strategy play an important role in solving CVRP problems.

For each test case (Tai75a, X-n101-k25) and four algorithms (MMAS, ACS, IACO and GSACO), X-n148-k46, X-n181-k23, X-n200-k36, X-n237-k14, X-n251-k28, X-n303-k21, X-n351-k29, X-n351-k29 are independently executed 200 times to generate fitness function values. This paper mainly describes the experimental results from four statistical angles: maximum, minimum, average and standard deviation. Specific experimental statistics are shown in Table 3.

By analyzing the data in Table 3, it can be seen that GSACO algorithm is superior to MMAS, ACS and IACO algorithm in solving the mean and standard deviation of small and medium CVRP algorithm test cases. This result is consistent with the conclusion of the block diagram. When GSACO algorithm is used to solve large-scale CVRP test cases, there is not much different between the standard deviation of GSACO algorithm and other algorithms. However, the average value of GSACO algorithm is better than MMAS, ACS and IACO algorithms. When solving X-n351-k40 and X-n401-k29 test cases, the standard deviation of GSACO algorithm is not significantly different from the other three test algorithms. The results show that the algorithm has good stability for solving CVRP problems. However, for some individual test cases, such as X-n351-k40, although the standard deviation of GSACO algorithm is not optimal, it is still very stable, which is mainly due to the search mechanism of greedy strategy in the later stage of the algorithm.

5 Conclusion

An ant colony optimization algorithm based on a greedy strategy search mechanism and adaptive parameters is proposed to solve TSP and CVRP problems in this paper. The proposed GSACO algorithm has a lower time cost, a faster convergence speed, and a higher operational efficiency while comparing with other algorithms. However, the algorithm still has some drawback, although enhanced pheromones can speed up the search progress, the algorithm becomes easily fall into a local optimal. If the population become relatively large, due to the large amount of calculation, the algorithm progress will become slowly. Therefore, our future work will focus on designing a more ideal search operator that can prevent the algorithm from falling into a local optimal and better solving the large-scale and multi-constrained path optimization problems.