The uncertain two-stage network DEA models

Abstract

The two-stage network DEA models based on the framework that the efficiency of the whole stage is equal to the product of the efficiencies of two sub-stages can not only turn the ‘black box’ into the ‘glass box’ to identify the root causes of the inefficiency of the network system, but also consider the relationship between the two sub-stages within the whole stage. Nowadays, the two-stage network DEA models have been widely applied in the field of economy and management, such as green supply chain and reverse supply chain. Due to the novelty of evaluation indexes, these emerging research objects with network structure, such as green supply chain, involve not only traditional evaluation indexes such as cost and time, but also some novel evaluation indexes such as customer satisfaction and flexibility. However, these new evaluation indexes are difficult to quantify accurately, which will lead to the failure of the traditional two-stage network DEA models. Therefore, this paper attempts to extend the traditional two-stage network DEA models to the uncertain two-stage network DEA models with the application of uncertainty theory. In the new models, inputs, intermediates and outputs are considered to be uncertain variables to deal with the problem of inaccurate data. Finally, a numerical example of the uncertain two-stage network DEA models will be presented for illustration.

1 Introduction

With the globalization of economy and the popularity of supply chain, the traditional ‘black-box’ DEA models such as CCR or BCC models Charnes et al. (1978) which can only recognize DMU as a whole rather than break down the whole system into sub-stages are no longer perfectly suitable for evaluating a system with complex network structure Cook and Zhu (2010). This is because the ‘black-box’ models ignore the internal structure of the network system and hence cannot provide enough information on identifying the root causes of the inefficiency of the network system Esmaeilzadeh and Matin (2019). For decision makers, it is not enough to evaluate whether the network system is efficient or not from a holistic perspective. In order to improve the performance of the network system comprehensively, decision makers need to investigate the running states of sub-stages to make the optimal decisions Chen (2009). Therefore, many researchers have put forward that the traditional ‘black-box’ models should be converted into ‘glass-box’ models in which the internal structure of the network system should be taken into account in the efficiency evaluation Kao (2014).

In order to transform ‘black-box’ models into ‘glass-box’ models, many scholars have devoted great efforts to the study of network DEA models. For example, Fa̋re and Grosskopf (2000) proved the usefulness of network DEA by analyzing several network models with different structures. Seiford and Zhu (1999) established the two-stage network DEA models to assess sub-stages of 55 top banks in US. Cook et al. (2014) summarized the latest researches of network DEA models.

Among all the network structures, the two-stage network structure has been considered as the most fundamental and straightforward structure because it can be expanded to some more intricate structures and has been widely used in numerous practical studies Kao and Hwang (2008). For example, Seiford and Zhu (1999) decomposed the entire operation process of a commercial bank into two sub-stages: profitability and marketability, and the efficiencies of two sub-stages and the whole stage were calculated by CCR models respectively. Some other examples contain the performance of bank branch affected by information technology (Chen and Zhu 2004) and the performance of two-stage Major League Baseball (Sexton and Lewis 2003).

Some of the above studies are based on the two-stage network DEA models in which two sub-stages are regarded as independent individuals with their own inputs and outputs respectively. However, this research method does not consider the influence of the relationship between the two sub-stages within the whole stage on efficiency evaluation of the two-stage network system. From the perspective of supply chain, due to the close cooperation between upstream and downstream enterprises, each individual does not exist independently, whose inputs and outputs are affected by neighboring enterprises. For instance, for the purpose of reaching an efficient status, the downstream enterprise may choose to cut down its inputs (intermediates). But this action means that the outputs of the upstream enterprise will be reduced, which may lead to the decrease of the efficiency of the upstream enterprise. Thus, there will be potential conflict among the two sub-stages, which is caused by their relationship.

In order to solve this potential conflict caused by the relationship between two sub-stages, a framework that the efficiency of the whole stage is equal to the product of the efficiencies of two sub-stages was proposed by Kao and Hwang (2008). This reasonable relationship reflects the close connection between the two sub-stages within the whole stage, which can effectively cope with this potential conflict. Moreover, the two-stage network DEA models considering their relationship are more reliable in identifying the efficiencies of the network system and consequently are capable of more accurately finding out the root causes of the inefficiency of the network system (Kao and Hwang 2008). Therefore, it is essential to establish the two-stage network DEA models that conform to their relationship Kao (2016).

Recently, some burgeoning issues such as green supply chain and reverse supply chain have received increasing attention in many researches Dyckhoff and Allen (2001). Due to the novelty of evaluation indexes, these emerging research objects with network structure, such as green supply chain, involve not only traditional evaluation indexes such as cost and time, but also some new evaluation indexes such as customer satisfaction, social benefits and flexibility. However, these new evaluation indexes are difficult to quantify accurately and hence considered as inaccurate data, which will lead to the failure of the traditional two-stage network DEA models (Sadjadi and Omrani 2008). Therefore, in order to accurately evaluate these emerging issues, it is urgent to handle the problem of inaccurate data.

In order to solve the imprecise data, many stochastic DEA models have been built up based on the probability theory by Sengupta (1982), Banker (1993), Sueyoshi (2000) and Olesen and Petersen (2016). Furthermore, fuzzy methods have been used to deal with the inaccurate data in DEA. Kao (2011) developed the fuzzy forms of the two-stage network DEA models. Some other researchers also have been devoted to the application of fuzzy method in two-stage network DEA, including Tavana (2018), Hatami-Marbini and Saati (2018) and Wanke et al. (2018).

Nowadays, there is a tendency to use uncertainty theory established by Liu (2007) to cope with the problem of inaccurate data. The core advantage of uncertainty theory lies in the reasonable construction of belief degree to solve the problem of inaccurate data on the basis of overcoming the limitations of human beings Liu (2012). Moreover, uncertainty theory has constantly been applied in many fields of science and engineering. Liu (2009) put forward uncertain programming in 2009. Many other scholars have also been devoted to the application in the field of programming from uncertain machine scheduling (Liu 2010) and uncertain multi-objective programming (Liu and Chen 2015) to uncertain multilevel programming model (Liu and Yao 2015).

In recent years, uncertainty theory has been also studied and proved by many experts in the field of DEA. Wen et al. (2014) proposed the first uncertain DEA model. Then, Lio and Liu (2018) introduced an uncertain DEA model containing imprecise inputs and outputs. Jiang et al. (2019) further established an uncertain DEA model to recognize the scale efficiency in uncertain situation. In addition, Jiang et al. (2020) developed two new uncertain DEA models capable of further identifying specific scale efficiency. However, up to now, there is no research on the uncertainty theory in the two-stage network DEA models.

Thus, the purpose of this paper is to apply and extend the uncertainty theory to the two-stage network DEA models. In general, the contributions of this paper are as follows. Firstly, this article expands the application of uncertainty theory in the field of DEA. Secondly, this paper expands the evaluation method of unobservable variables and the scope of application of DEA models by establishing the uncertain two-stage network DEA models. At last, for the contribution of practice, the new models can provide more constructive opinions for decision makers to identify the root causes of the inefficiency of the network system in complex and uncertain environment and to further enhance the performance of the network system.

The rest of this article is organized as follows. Section 2 will provide some basic theoretical knowledge of uncertainty theory. The uncertain two-stage network DEA models and their equivalent forms will be presented and proved in Sect. 3. In Sect. 4, a numerical example will be given for illustration. The final section is the conclusion remarks.

2 Preliminaries

In order to better expand the application of uncertainty theory in two-stage network DEA models, we will introduce the basic knowledge and concepts of uncertainty theory. The fundamental and essential definition of uncertainty theory is uncertain measure. The uncertain measure ${\mathcal {M}}$ is defined as a set function on a $\sigma$-algebra ${\mathcal {L}}$ over a nonempty set $\varGamma$ by the following three axioms Liu (2007):

Axiom 1. (Normality Axiom) ${\mathcal {M}}\{\varGamma \}=1$ for the universal set $\varGamma$.

Axiom 2. (Duality Axiom) ${\mathcal {M}}\{\varLambda \}+{\mathcal {M}}\{\varLambda ^{c}\}=1$ for any event $\varLambda$.

Axiom 3. (Subadditivity Axiom) For every countable sequence of events $\varLambda _1, \varLambda _2, \!\ldots ,$ we have

$$\begin{aligned} \displaystyle {\mathcal {M}}\left\{ \bigcup _{i=1}^{\infty }\varLambda _i\right\} \le \sum _{i=1}^{\infty }{\mathcal {M}}\{\varLambda _i\}. \end{aligned}$$

Besides, Liu (2009) proposed the product axiom for the product uncertain measure in 2009 as follows:

Axiom 4. (Product Axiom) Let $(\varGamma _{k}, {\mathcal {L}}_{k}, {\mathcal {M}}_{k})$ be uncertainty spaces for $k=1, 2, \ldots .$ The product uncertain measure ${\mathcal {M}}$ is an uncertain measure satisfying

$$\begin{aligned} \displaystyle {\mathcal {M}}\left\{ \prod \limits _{k=1}^{\infty }\varLambda _k\right\} =\bigwedge _{k=1}^{\infty }{\mathcal {M}}_{k}\{\varLambda _k\} \end{aligned}$$

where $\varLambda _{k}$ are arbitrarily chosen events from ${\mathcal {L}}_{k}$ for $k = 1, 2, \ldots ,$ respectively.

Definition 1

(Liu 2007) Uncertain variable is a measurable function $\tau$ from an uncertainty space ($\varGamma$, ${\mathcal {L}}$, ${\mathcal {M}}$) to the set of real numbers such that

$$\begin{aligned} \{ \tau \in B \} = \{ \gamma \in \varGamma \ | \ \tau (\gamma ) \in B \} \end{aligned}$$

is an event for any Borel set B of real numbers.

Definition 2

(Liu 2007) The uncertainty distribution $\varPsi$ of an uncertain variable $\tau$ is defined by

$$\begin{aligned} \varPsi (x) = {\mathcal {M}}\{ \tau \le x \} \end{aligned}$$

for any real number x.

We will introduce some common uncertainty distributions based on the definitions above. Firstly, we will introduce the most common one called linear uncertainty distribution, which is

$$\begin{aligned} \varPsi (x) = \left\{ \begin{array}{ll} \displaystyle 0, &{} \qquad \text{ if } x \le a \\ \displaystyle (x - a)/(b - a), &{} \qquad \text{ if } a < x \le b \\ \displaystyle 1, &{} \qquad \text{ if } x > b; \end{array} \right. \end{aligned}$$

and the second common uncertainty distribution is called zigzag uncertainty distribution, which is

$$\begin{aligned} \varPsi (x) = \left\{ \begin{array}{ll} \displaystyle 0, &{} \qquad \text{ if } x \le a \\ \displaystyle (x - a)/[2(b - a)], &{} \qquad \text{ if } a< x \le b \\ \displaystyle (x + c - 2b)/[2(c - b)], &{} \qquad \text{ if } b < x \le c \\ \displaystyle 1, &{} \qquad \text{ if } x > c. \end{array} \right. \end{aligned}$$

An uncertainty distribution $\varPsi (x)$ is deemed to be regular (Liu 2010) if it is a continuous function and strictly increasing with respect to x at which $0<\varPsi (x)<1$, and

$$\begin{aligned} \displaystyle \lim _{x \rightarrow -\infty } \varPsi (x) = 0, \qquad \lim _{x \rightarrow \infty } \varPsi (x) = 1. \end{aligned}$$

If $\tau$ is an uncertain variable with regular uncertainty distribution $\varPhi (x)$, the inverse function $\varPsi ^{-1}(\alpha )$ is called the inverse uncertainty distribution of $\tau$ (Liu 2010).

Definition 3

(Liu 2009) Uncertain variables $\tau _1$, $\tau _2$, $\ldots$, $\tau _k$ are said to be independent provided that

$$\begin{aligned} \displaystyle {\mathcal {M}}\left\{ \bigcap _{i=1}^{k} (\tau _{i} \in B_{i}) \right\} = \bigwedge _{i=1}^{k} {\mathcal {M}}\left\{ \tau _{i} \in B_{i} \right\} \end{aligned}$$

for any Borel sets $B_{1}$, $B_{2}$, $\ldots$, $B_{k}$ of real numbers.

The following theorem proposed by Liu (2010) can calculate the inverse uncertainty distribution of a strictly monotonous function of independent uncertain variables with regular uncertainty distributions as below:

Theorem 1

(Liu 2010) Let $\tau _{1}, \tau _{2}, \ldots , \tau _{k}$ be independent uncertain variables with regular uncertainty distributions $\varPsi _{1}, \varPsi _{2}, \ldots , \varPsi _{k}$, respectively. If f is strictly increasing with respect to $\tau _{1}, \tau _{2}, \ldots , \tau _{q}$ (q $\le$ k) and strictly decreasing with respect to $\tau _{q+1}, \tau _{q+2}, \ldots , \tau _{k}$, then $\tau = f(\tau _{1}, \tau _{2}, \ldots , \tau _{k})$ is an uncertain variable with an inverse uncertainty distribution

$$\begin{aligned} \begin{aligned}&\displaystyle \varPhi ^{-1}(\alpha ) = f(\varPsi ^{-1}_{1}(\alpha ), \ldots , \varPsi ^{-1}_{q}(\alpha ), \varPsi ^{-1}_{q+1}(1-\alpha ), \ldots ,\\ {}&\varPsi ^{-1}_{k}(1-\alpha )).\end{aligned}\end{aligned}$$

Expected value can be used to represent the size of $\tau$, which is the average value of uncertain variable in the sense of uncertain measure. The formal definition is shown below.

Definition 4

(Liu 2007) The expected value of uncertain variable $\tau$ is defined by

$$\begin{aligned} \displaystyle E[\tau ] = \int _{0}^{+\infty } {\mathcal {M}}\{\tau \ge x \}\mathrm {d} x - \int _{-\infty }^{0} {\mathcal {M}}\{\tau \le x \}\mathrm {d} x \end{aligned}$$

provided that at least one of the two integrals is finite.

Suppose that $\tau$ is defined as an uncertain variable with uncertainty distribution $\varPsi$. Afterwards, Liu (2007) Liu (2010) represented the formulas about the expected values of $\tau$ as below:

$$\begin{aligned} \displaystyle E[\tau ]= & {} \int _{0}^{+\infty } (1 - \varPsi (x))\mathrm {d} x - \int _{-\infty }^{0} \varPsi (x) \mathrm {d} x, \\ \displaystyle E[\tau ]= & {} \int _{0}^{1} \varPsi ^{-1}(\alpha ) \mathrm {d} \alpha . \end{aligned}$$

Theorem 2

(Liu and Ha 2010) Assume $\tau _{1}, \tau _{2}, \ldots , \tau _{k}$ are independent uncertain variables with regular uncertainty distributions $\varPsi _{1}, \varPsi _{2}, \ldots , \varPsi _{k}$, respectively. If f($\tau _{1}, \tau _{2}, \ldots , \tau _{k}$) is strictly increasing with respect to $\tau _{1}, \tau _{2}, \ldots , \tau _{q}$ (q $\le$ k) and strictly decreasing with respect to $\tau _{q+1}, \tau _{q+2}, \ldots , \tau _{k}$, then the expected value of $\tau$ = f($\tau _{1}, \tau _{2}, \ldots , \tau _{k}$) is

$$\begin{aligned} \begin{aligned}&\displaystyle E[\tau ] = \int _{0}^{1} f(\varPsi _{1}^{-1}(\alpha ), \ldots , \varPsi _{q}^{-1}(\alpha ), \varPsi _{q+1}^{-1}(1-\alpha ),\\ {}&\quad \ldots , \varPsi _{k}^{-1}(1-\alpha )) \mathrm {d} \alpha . \end{aligned} \end{aligned}$$

3 The uncertain two-stage network DEA models

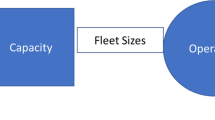
In this part, we will introduce the uncertain two-stage network DEA models considering the relationship between the two sub-stages within the whole stage. Similar to the traditional two-stage network DEA models, the structure of the uncertain two-stage network DEA models is also composed of two sub-stages, which is shown in Fig. 1. The inputs are transformed into intermediates through the first stage, and then the intermediates are totally put into the second stage. In the new models, inputs, intermediates and outputs are considered to be uncertain variables.

Fig. 1

Two-stage network system

In order to build the whole stage model, the first stage model and the second stage model of the uncertain two-stage network DEA models, some basic symbols need to be defined as below:

$\hbox {DMU}_{k}$: the kth DMU, $k = 1,2, \ldots , j$

$\hbox {DMU}_{o}$: the target DMU

$\tilde{{{x}}}$$_{k}$ = (${\tilde{x}}_{k1}$, ${\tilde{x}}_{k2}$, ..., ${\tilde{x}}_{kn}$): the uncertain inputs vector of $\hbox {DMU}_{k}$, $k = 1,2, \ldots , j$

$\tilde{{{x}}}$$_{o}$ = (${\tilde{x}}_{o1}$, ${\tilde{x}}_{o2}$, ..., ${\tilde{x}}_{on}$): the uncertain inputs vector of $\hbox {DMU}_{o}$

$\tilde{{{y}}}$$_{k}$ = (${\tilde{y}}_{k1}$, ${\tilde{y}}_{k2}$, ..., ${\tilde{y}}_{kh}$): the uncertain outputs vector of $\hbox {DMU}_{k}$, $k = 1,2, \ldots , j$

$\tilde{{{y}}}$$_{o}$ = (${\tilde{y}}_{o1}$, ${\tilde{y}}_{o2}$, ..., ${\tilde{y}}_{oh}$): the uncertain outputs vector of $\hbox {DMU}_{o}$

$\tilde{{{z}}}$$_{k}$ =(${\tilde{z}}_{k1}$, ${\tilde{z}}_{k2}$, ..., ${\tilde{z}}_{kp}$): the uncertain intermediates vector of $\hbox {DMU}_{k}$, $k = 1,2, \ldots , j$

$\tilde{{{z}}}$$_{o}$ =(${\tilde{z}}_{o1}$, ${\tilde{z}}_{o2}$, ..., ${\tilde{z}}_{op}$): the uncertain intermediates vector of $\hbox {DMU}_{o}$

u $\in \mathfrak {R}^{n}$: the vector of input weights

v $\in \mathfrak {R}^{h}$: the vector of output weights

w $\in \mathfrak {R}^{p}$: the vector of intermediate weights

3.1 The whole stage model

In order to establish the whole stage model more reasonably, we will take into account the proportional constraint of each sub-stage based on the relationship between the two sub-stages within the whole stage. Moreover, the multiplier of the intermediate ${\tilde{z}}$ we take in this model is always the same regardless of whether it plays the role of input or output throughout the process. Based on the above statement and uncertainty theory, this model is formulated as below:

$$\begin{aligned} \left\{ \begin{array}{ll} \max \limits _{{ u}, { v}, { w}} &{} c_{w}= E \left[ \frac{ { u} ^{T} { {\tilde{y}}} _{o} }{{ v} ^{T} { {\tilde{x}}} _{o}} \right] \\ {s.t.} &{} E \left[ \frac{ { u} ^{T} { {\tilde{y}}} _{k} }{{ v} ^{T} { {\tilde{x}}} _{k}} \right] \le 1,\quad k = 1,2, \ldots , j\\ &{} E \left[ \frac{ { w} ^{T} { {\tilde{z}}} _{k} }{{ v} ^{T} { {\tilde{x}}} _{k}} \right] \le 1,\quad k = 1,2, \ldots , j\\ &{} E \left[ \frac{ { u} ^{T} { {\tilde{y}}} _{k} }{{ w} ^{T} { {\tilde{z}}} _{k}} \right] \le 1, \quad k = 1,2, \ldots , j \\ {} &{} { u} \ge 0 \\ {} &{} { v} \ge 0 \\ {} &{} { w} \ge 0. \end{array} \right. \end{aligned}$$

(1)

Definition 5

(Uncertain DEA Efficiency) If and only if the optimal solution $\overline{c_{w}}$ of the model (1) can reach 1, $\hbox {DMU}_{o}$ can be considered as efficient.

The efficiency of $\hbox {DMU}_{0}$ can be calculated by evaluating the optimal value of the whole stage model. The equivalent form of model (1) is proved as below:

Theorem 3

For each k, let inputs ${\tilde{x}}_{k1}, {\tilde{x}}_{k2}, \ldots , {\tilde{x}}_{kn}$, outputs ${\tilde{y}}_{k1}, {\tilde{y}}_{k2},\ldots , {\tilde{y}}_{kh}$ and intermediates ${\tilde{z}}_{k1}, {\tilde{z}}_{k2},\ldots , {\tilde{z}}_{kp}$ be independent uncertain variables with regular uncertainty distributions $\varPsi _{k1}, \varPsi _{k2},\ldots , \varPsi _{kn}$, $\varPhi _{k1}, \varPhi _{k2}, \ldots , \varPhi _{kh}$ and $\varOmega _{k1}, \varOmega _{k2},\ldots , \varOmega _{kp}$, respectively. Then the whole stage model (1) is equal to the following form:

$$\begin{aligned} \left\{ \begin{array}{ll} \max \limits _{{ u}, { v}, w} &{} c_{w} = \int _{0}^{1} \frac{ \sum \nolimits _{t=1}^{h} u_{t} \varPhi _{ot}^{-1}(\alpha ) }{\sum \nolimits _{i=1}^{n} v_{i} \varPsi _{oi}^{-1}(1-\alpha )} \mathrm {d} \alpha \\ {s.t.} &{} \int _{0}^{1} \frac{ \sum \nolimits _{t=1}^{h} u_{t} \varPhi _{kt}^{-1}(\alpha ) }{\sum \nolimits _{i=1}^{n} v_{i} \varPsi _{ki}^{-1}(1-\alpha )} \mathrm {d} \alpha \le 1, \quad k = 1,2, \ldots , j\\ &{} \int _{0}^{1} \frac{ \sum \nolimits _{q=1}^{p} w_{q} \varOmega _{kq}^{-1}(\alpha ) }{\sum \nolimits _{i=1}^{n} v_{i} \varPsi _{ki}^{-1}(1-\alpha )} \mathrm {d} \alpha \le 1,\quad k = 1,2, \ldots , j\\ &{} \int _{0}^{1} \frac{ \sum \nolimits _{t=1}^{h} u_{t} \varPhi _{kt}^{-1}(\alpha ) }{\sum \nolimits _{q=1}^{p} w_{q} \varOmega _{kq}^{-1}(1-\alpha )} \mathrm {d} \alpha \le 1,\quad k = 1,2, \ldots , j\\ &{} { u} = (u_{1}, u_{2}, \ldots , u_{h}) \ge 0\\ &{} { v} = (v_{1}, v_{2}, \ldots , v_{n}) \ge 0\\ &{} { w} = (w_{1}, w_{2}, \ldots , w_{p}) \ge 0 \end{array} \right. \end{aligned}$$

(2)

where $\varPsi _{o1}, \varPsi _{o2}, \ldots , \varPsi _{on}$, $\varPhi _{o1}, \varPhi _{o2}, \ldots , \varPhi _{oh}$ and $\varOmega _{o1}, \varOmega _{o2}, \ldots , \varOmega _{op}$ are the regular uncertainty distributions of ${\tilde{x}}_{o1}, {\tilde{x}}_{o2}, \ldots , {\tilde{x}}_{on}$, ${\tilde{y}}_{o1}, {\tilde{y}}_{o2}, \ldots ,{\tilde{y}}_{oh}$ and ${\tilde{z}}_{o1}, {\tilde{z}}_{o2}, \ldots , {\tilde{z}}_{op}$, respectively.

Proof

Since the function ${u} ^{T} { {\tilde{y}}}_{k} / {v} ^{T} { {\tilde{x}}} _{k}$ is strictly increasing with respect to ${{\tilde{y}}}_{k}$ and strictly decreasing with respect to ${{\tilde{x}}}_{k}$ for each k. According to Theorem 1, we can conclude that the inverse uncertainty distribution of ${u} ^{T} {{\tilde{y}}}_{k} / {v} ^{T} {{\tilde{x}}} _{k}$ is

$$\begin{aligned} \displaystyle G_{k}^{-1}(\alpha ) = \frac{\sum \nolimits _{t=1}^{h} u_{t} \varPhi _{kt}^{-1}(\alpha ) }{\sum \nolimits _{i=1}^{n} v_{i} \varPsi _{ki}^{-1}(1-\alpha )}. \end{aligned}$$

From Theorem 2, we obtain

$$\begin{aligned} E \left[ \frac{ {u} ^{T} {{\tilde{y}}} _{k} }{{v} ^{T} {{\tilde{x}}} _{k}} \right] = \int _{0}^{1} \frac{ \sum \nolimits _{t=1}^{h} u_{t} \varPhi _{kt}^{-1}(\alpha ) }{ \sum \nolimits _{i=1}^{n} v_{i} \varPsi _{ki}^{-1}(1-\alpha )} \mathrm {d} \alpha , \quad k=1,2, \ldots , j. \end{aligned}$$

Similarly, for each k, according to the above proof, it can be drawn at once that the function

$$\begin{aligned} E \left[ \frac{ {w} ^{T} {{\tilde{z}}} _{k} }{{v} ^{T} { {\tilde{x}}} _{k}} \right] = \int _{0}^{1} \frac{ \sum \nolimits _{q=1}^{p} w_{q} \varOmega _{kq}^{-1}(\alpha ) }{ \sum \nolimits _{i=1}^{n} v_{i} \varPsi _{ki}^{-1}(1-\alpha )} \mathrm {d} \alpha \end{aligned}$$

is strictly increasing with respect to ${\tilde{z}}_{k}$ and strictly decreasing with respect to ${ {\tilde{x}}}_{k}$. Identically, for each k, it can be inferred very quickly that the function

$$\begin{aligned} E \left[ \frac{ {u} ^{T} { {\tilde{y}}} _{k} }{{w} ^{T} { {\tilde{z}}} _{k}} \right] = \int _{0}^{1} \frac{ \sum \nolimits _{t=1}^{h} u_{t} \varPhi _{kt}^{-1}(\alpha ) }{ \sum \nolimits _{q=1}^{p} w_{q} \varOmega _{kq}^{-1}(1-\alpha )} \mathrm {d} \alpha \end{aligned}$$

is strictly increasing with respect to ${ {\tilde{y}}}_{k}$ and strictly decreasing with respect to ${{\tilde{z}}}_{k}$.

The theorem has been proved. $\square$

3.2 The first stage model

The first stage model is established based on the whole stage model. Therefore, the first stage model is trying to find the maximum efficiency of the first stage while maintaining the efficiency of the whole stage. Then the first stage model is formulated as follows:

$$\begin{aligned} \left\{ \begin{array}{ll} \max \nolimits _{{ u}, { v}, { w}} &{} c _{1}= E \left[ \frac{ { w} ^{T} { {\tilde{z}}} _{o} }{{ v} ^{T} { {\tilde{x}}} _{o}} \right] \\ {s.t.} &{} E \left[ \frac{ { u} ^{T} { {\tilde{y}}} _{0} }{{ v} ^{T} { {\tilde{x}}} _{0}} \right] = c_{w}\\ &{} E \left[ \frac{ { u} ^{T} { {\tilde{y}}} _{k} }{{ v} ^{T} { {\tilde{x}}} _{k}} \right] \le 1,\quad k = 1,2, \ldots , j\\ &{} E \left[ \frac{ { w} ^{T} { {\tilde{z}}} _{k} }{{ v} ^{T} { {\tilde{x}}} _{k}} \right] \le 1,\quad k = 1,2, \ldots , j\\ &{} E \left[ \frac{ { u} ^{T} { {\tilde{y}}} _{k} }{{ w} ^{T} { {\tilde{z}}} _{k}} \right] \le 1, \quad k = 1,2, \ldots , j \\ {} &{} { u} \ge 0 \\ {} &{} { v} \ge 0 \\ {} &{} { w} \ge 0. \end{array} \right. \end{aligned}$$

(3)

Definition 6

(Uncertain DEA Efficiency) If and only if the optimal solution $\overline{c_{1}}$ of the model (3) can reach 1, $\hbox {DMU}_{o}$ can be considered as efficient.

The efficiency of $\hbox {DMU}_{0}$ can be calculated by evaluating the optimal value of the first stage model. The equivalent form of model (3) is proved as below:

Theorem 4

For each k, let inputs ${\tilde{x}}_{k1}, {\tilde{x}}_{k2}, \ldots , {\tilde{x}}_{kn}$, outputs ${\tilde{y}}_{k1}, {\tilde{y}}_{k2},\ldots , {\tilde{y}}_{kh}$ and intermediates ${\tilde{z}}_{k1}, {\tilde{z}}_{k2},\ldots , {\tilde{z}}_{kp}$ be independent uncertain variables with regular uncertainty distributions $\varPsi _{k1}, \varPsi _{k2},\ldots , \varPsi _{kn}$, $\varPhi _{k1}, \varPhi _{k2}, \ldots , \varPhi _{kh}$ and $\varOmega _{k1}, \varOmega _{k2},\ldots , \varOmega _{kp}$, respectively. Then the first stage model (3) is equal to the following form:

$$\begin{aligned} \left\{ \begin{array}{ll} \max \nolimits _{{ u}, { v}, w} &{} c_{1} = \int _{0}^{1} \frac{ \sum \nolimits _{q=1}^{p} w_{q} \varOmega _{oq}^{-1}(\alpha ) }{\sum \nolimits _{i=1}^{n} v_{i} \varPsi _{oi}^{-1}(1-\alpha )} \mathrm {d} \alpha \\ {s.t.} &{}\int _{0}^{1} \frac{ \sum \nolimits _{t=1}^{h} u_{t} \varPhi _{ot}^{-1}(\alpha ) }{\sum \nolimits _{i=1}^{n} v_{i} \varPsi _{oi}^{-1}(1-\alpha )} \mathrm {d} \alpha = c_{w}\\ &{} \int _{0}^{1} \frac{ \sum \nolimits _{t=1}^{h} u_{t} \varPhi _{kt}^{-1}(\alpha ) }{\sum \nolimits _{i=1}^{n} v_{i} \varPsi _{ki}^{-1}(1-\alpha )} \mathrm {d} \alpha \le 1, \quad k = 1,2, \ldots , j\\ &{} \int _{0}^{1} \frac{ \sum \nolimits _{q=1}^{p} w_{q} \varOmega _{kq}^{-1}(\alpha ) }{\sum \nolimits _{i=1}^{n} v_{i} \varPsi _{ki}^{-1}(1-\alpha )} \mathrm {d} \alpha \le 1,\quad k = 1,2, \ldots , j\\ &{} \int _{0}^{1} \frac{ \sum \nolimits _{t=1}^{h} u_{t} \varPhi _{kt}^{-1}(\alpha ) }{\sum \nolimits _{q=1}^{p} w_{q} \varOmega _{kq}^{-1}(1-\alpha )} \mathrm {d} \alpha \le 1,\quad k = 1,2, \ldots , j\\ &{} { u} = (u_{1}, u_{2}, \ldots , u_{h}) \ge 0\\ &{} { v} = (v_{1}, v_{2}, \ldots , v_{n}) \ge 0\\ &{} { w} = (w_{1}, w_{2}, \ldots , w_{p}) \ge 0 \end{array} \right. \end{aligned}$$

(4)

where $\varPsi _{o1}, \varPsi _{o2}, \ldots , \varPsi _{on}$, $\varPhi _{o1}, \varPhi _{o2}, \ldots , \varPhi _{oh}$ and $\varOmega _{o1}, \varOmega _{o2}, \ldots , \varOmega _{op}$ are the regular uncertainty distributions of ${\tilde{x}}_{o1}, {\tilde{x}}_{o2}, \ldots , {\tilde{x}}_{on}$, ${\tilde{y}}_{o1}, {\tilde{y}}_{o2}, \ldots ,{\tilde{y}}_{oh}$ and ${\tilde{z}}_{o1}, {\tilde{z}}_{o2}, \ldots , {\tilde{z}}_{op}$, respectively.

Proof

Since the function ${u} ^{T} { {\tilde{y}}}_{k} / {v} ^{T} { {\tilde{x}}} _{k}$ is strictly increasing with respect to ${{\tilde{y}}}_{k}$ and strictly decreasing with respect to ${{\tilde{x}}}_{k}$ for each k. According to Theorem 1, we can conclude that the inverse uncertainty distribution of ${u} ^{T} {{\tilde{y}}}_{k} / {v} ^{T} {{\tilde{x}}} _{k}$ is

$$\begin{aligned} \displaystyle J_{k}^{-1}(\alpha ) = \frac{\sum \nolimits _{t=1}^{h} u_{t} \varPhi _{kt}^{-1}(\alpha ) }{\sum \nolimits _{i=1}^{n} v_{i} \varPsi _{ki}^{-1}(1-\alpha )}. \end{aligned}$$

From Theorem 2, we obtain

$$\begin{aligned} E \left[ \frac{ { u} ^{T} { {\tilde{y}}} _{k} }{{ v} ^{T} { {\tilde{x}}} _{k}} \right] = \int _{0}^{1} \frac{ \sum \nolimits _{t=1}^{h} u_{t} \varPhi _{kt}^{-1}(\alpha ) }{ \sum \nolimits _{i=1}^{n} v_{i} \varPsi _{ki}^{-1}(1-\alpha )} \mathrm {d} \alpha , \quad k=1,2, \ldots , j. \end{aligned}$$

Similarly, for each k, according to the above proof, it can be drawn at once that the function

$$\begin{aligned} E \left[ \frac{ { w} ^{T} { {\tilde{z}}} _{k} }{{ v} ^{T} { {\tilde{x}}} _{k}} \right] = \int _{0}^{1} \frac{ \sum \nolimits _{q=1}^{p} w_{q} \varOmega _{kq}^{-1}(\alpha ) }{ \sum \nolimits _{i=1}^{n} v_{i} \varPsi _{ki}^{-1}(1-\alpha )} \mathrm {d} \alpha \end{aligned}$$

is strictly increasing with respect to ${ {\tilde{z}}}_{k}$ and strictly decreasing with respect to ${{\tilde{x}}}_{k}$. Identically, for each k, it can be inferred very quickly that the function

$$\begin{aligned} E \left[ \frac{ { u} ^{T} { {\tilde{y}}} _{k} }{{ w} ^{T} { {\tilde{z}}} _{k}} \right] = \int _{0}^{1} \frac{ \sum \nolimits _{t=1}^{h} u_{t} \varPhi _{kt}^{-1}(\alpha ) }{ \sum \nolimits _{q=1}^{p} w_{q} \varOmega _{kq}^{-1}(1-\alpha )} \mathrm {d} \alpha \end{aligned}$$

is strictly increasing with respect to ${ {\tilde{y}}}_{k}$ and strictly decreasing with respect to ${{\tilde{z}}}_{k}$.

The theorem has been proved. $\square$

3.3 The second stage model

Similarly, the efficiency of the second stage model is based on the efficiencies of the first stage and the whole stage. While maintaining the efficiencies of the whole stage and the first stage, the efficiency of the second stage reaches the maximum. The second stage model is presented as follows:

$$\begin{aligned} \left\{ \begin{array}{ll} \max \limits _{{ u}, { v}, { w}} &{} c _{2}= E \left[ \frac{ { u} ^{T} { {\tilde{y}}} _{o} }{{ w} ^{T} { {\tilde{z}}} _{o}} \right] \\ {s.t.} &{} E \left[ \frac{ { u} ^{T} { {\tilde{y}}} _{0} }{{ v} ^{T} { {\tilde{x}}} _{0}} \right] = c_{w}\\ &{} E \left[ \frac{ { w} ^{T} { {\tilde{z}}} _{0} }{{ v} ^{T} { {\tilde{x}}} _{0}} \right] = c _{1}\\ &{} E \left[ \frac{ { u} ^{T} { {\tilde{y}}} _{k} }{{ v} ^{T} { {\tilde{x}}} _{k}} \right] \le 1,\quad k = 1,2, \ldots , j\\ &{} E \left[ \frac{ { w} ^{T} { {\tilde{z}}} _{k} }{{ v} ^{T} { {\tilde{x}}} _{k}} \right] \le 1,\quad k = 1,2, \ldots , j\\ &{} E \left[ \frac{ { u} ^{T} { {\tilde{y}}} _{k} }{{ w} ^{T} { {\tilde{z}}} _{k}} \right] \le 1, \quad k = 1,2, \ldots , j \\ {} &{} { u} \ge 0 \\ {} &{} { v} \ge 0 \\ {} &{} { w} \ge 0. \end{array} \right. \end{aligned}$$

(5)

Definition 7

(Uncertain DEA Efficiency) If and only if the optimal solution $\overline{c_{2}}$ of the model (5) can reach 1, $\hbox {DMU}_{o}$ is considered as efficient.

The efficiency of $\hbox {DMU}_{0}$ can be calculated by evaluating the optimal value of the second stage model. The equivalent form of model (5) is proved as below:

Theorem 5

For each k, let inputs ${\tilde{x}}_{k1}, {\tilde{x}}_{k2}, \ldots , {\tilde{x}}_{kn}$, outputs ${\tilde{y}}_{k1}, {\tilde{y}}_{k2},\ldots , {\tilde{y}}_{kh}$ and intermediates ${\tilde{z}}_{k1}, {\tilde{z}}_{k2},\ldots , {\tilde{z}}_{kp}$ be independent uncertain variables with regular uncertainty distributions $\varPsi _{k1}, \varPsi _{k2},\ldots , \varPsi _{kn}$, $\varPhi _{k1}, \varPhi _{k2}, \ldots , \varPhi _{kh}$ and $\varOmega _{k1}, \varOmega _{k2},\ldots , \varOmega _{kp}$, respectively. Then the second stage model (5) is equal to the following form:

$$\begin{aligned} \left\{ \begin{array}{ll} \max \limits _{{ u}, { v}, w} &{} c_{2} = \int _{0}^{1} \frac{ \sum \nolimits _{t=1}^{h} u_{t} \varPhi _{ot}^{-1}(\alpha ) }{\sum \nolimits _{q=1}^{p} w_{q} \varOmega _{oq}^{-1}(1-\alpha )} \mathrm {d} \alpha \\ {s.t.} &{}\int _{0}^{1} \frac{ \sum \nolimits _{t=1}^{h} u_{t} \varPhi _{ot}^{-1}(\alpha ) }{\sum \nolimits _{i=1}^{n} v_{i} \varPsi _{oi}^{-1}(1-\alpha )} \mathrm {d} \alpha = c_{w} \\ &{}\int _{0}^{1} \frac{ \sum \nolimits _{q=1}^{p} w_{q} \varOmega _{oq}^{-1}(\alpha ) }{\sum \nolimits _{i=1}^{n} v_{i} \varPsi _{oi}^{-1}(1-\alpha )} \mathrm {d} \alpha = c_{1} \\ &{} \int _{0}^{1} \frac{ \sum \nolimits _{t=1}^{h} u_{t} \varPhi _{kt}^{-1}(\alpha ) }{\sum \nolimits _{i=1}^{n} v_{i} \varPsi _{ki}^{-1}(1-\alpha )} \mathrm {d} \alpha \le 1, \quad k = 1,2, \ldots , j\\ &{} \int _{0}^{1} \frac{ \sum \nolimits _{q=1}^{p} w_{q} \varOmega _{kq}^{-1}(\alpha ) }{\sum \nolimits _{i=1}^{n} v_{i} \varPsi _{ki}^{-1}(1-\alpha )} \mathrm {d} \alpha \le 1,\quad k = 1,2, \ldots , j\\ &{} \int _{0}^{1} \frac{ \sum \nolimits _{t=1}^{h} u_{t} \varPhi _{kt}^{-1}(\alpha ) }{\sum \nolimits _{q=1}^{p} w_{q} \varOmega _{kq}^{-1}(1-\alpha )} \mathrm {d} \alpha \le 1,\quad k = 1,2, \ldots , j \\ {} &{} { u} = (u_{1}, u_{2}, \ldots , u_{h}) \ge 0 \\ {} &{} { v} = (v_{1}, v_{2}, \ldots , v_{n}) \ge 0 \\ {} &{} { w} = (w_{1}, w_{2}, \ldots , w_{p}) \ge 0 \end{array} \right. \end{aligned}$$

(6)

where $\varPsi _{o1}, \varPsi _{o2}, \ldots , \varPsi _{on}$, $\varPhi _{o1}, \varPhi _{o2}, \ldots , \varPhi _{oh}$ and $\varOmega _{o1}, \varOmega _{o2}, \ldots , \varOmega _{op}$ are the regular uncertainty distributions of ${\tilde{x}}_{o1}, {\tilde{x}}_{o2}, \ldots , {\tilde{x}}_{on}$, ${\tilde{y}}_{o1}, {\tilde{y}}_{o2}, \ldots ,{\tilde{y}}_{oh}$ and ${\tilde{z}}_{o1}, {\tilde{z}}_{o2}, \ldots , {\tilde{z}}_{op}$, respectively.

Proof

Since the function ${u} ^{T} { {\tilde{y}}}_{k} / {v} ^{T} { {\tilde{x}}} _{k}$ is strictly increasing with respect to ${{\tilde{y}}}_{k}$ and strictly decreasing with respect to ${{\tilde{x}}}_{k}$ for each k. According to Theorem 1, we can conclude that the inverse uncertainty distribution of ${u} ^{T} {{\tilde{y}}}_{k} / {v} ^{T} {{\tilde{x}}} _{k}$ is

$$\begin{aligned} \displaystyle Q_{k}^{-1}(\alpha ) = \frac{\sum \nolimits _{t=1}^{h} u_{t} \varPhi _{kt}^{-1}(\alpha ) }{\sum \nolimits _{i=1}^{n} v_{i} \varPsi _{ki}^{-1}(1-\alpha )}. \end{aligned}$$

From Theorem 2, we obtain

$$\begin{aligned} E \left[ \frac{ { u} ^{T} { {\tilde{y}}} _{k} }{{ v} ^{T} { {\tilde{x}}} _{k}} \right] = \int _{0}^{1} \frac{ \sum \nolimits _{t=1}^{h} u_{t} \varPhi _{kt}^{-1}(\alpha ) }{ \sum \nolimits _{i=1}^{n} v_{i} \varPsi _{ki}^{-1}(1-\alpha )} \mathrm {d} \alpha , \quad k=1,2, \ldots , j. \end{aligned}$$

Similarly, for each k, according to the above proof, it can be drawn at once that the function

$$\begin{aligned} E \left[ \frac{ { w} ^{T} { {\tilde{z}}} _{k} }{{ v} ^{T} { {\tilde{x}}} _{k}} \right] = \int _{0}^{1} \frac{ \sum \nolimits _{q=1}^{p} w_{q} \varOmega _{kq}^{-1}(\alpha ) }{ \sum \nolimits _{i=1}^{n} v_{i} \varPsi _{ki}^{-1}(1-\alpha )} \mathrm {d} \alpha \end{aligned}$$

is strictly increasing with respect to ${ {\tilde{z}}}_{k}$ and strictly decreasing with respect to ${{\tilde{x}}}_{k}$. Identically, for each k, it can be inferred very quickly that the function

$$\begin{aligned} E \left[ \frac{ { u} ^{T} { {\tilde{y}}} _{k} }{{ w} ^{T} { {\tilde{z}}} _{k}} \right] = \int _{0}^{1} \frac{ \sum \nolimits _{t=1}^{h} u_{t} \varPhi _{kt}^{-1}(\alpha ) }{ \sum \nolimits _{q=1}^{p} w_{q} \varOmega _{kq}^{-1}(1-\alpha )} \mathrm {d} \alpha \end{aligned}$$

is strictly increasing with respect to ${ {\tilde{y}}}_{k}$ and strictly decreasing with respect to ${{\tilde{z}}}_{k}$.

The theorem has been verified. $\square$

4 A numerical example

In this section, the expected results of the uncertain two-stage network DEA models we have established are shown as follows. We will use a set of data to test the uncertain two-stage network DEA models. The original data which is shown in Table 1 is composed of three uncertain inputs, three uncertain intermediates and three uncertain outputs of five DMUs. The results of the efficiency evaluation are shown in Table 2, including the efficiency values for the whole stage, the first stage and the second stage.

Table 1 Five DMUs with three inputs, three intermediates and three outputs, in which ${\mathcal {L}}(a,b)$ represents linear uncertain variable and ${\mathcal {Z}}(a,b,c)$ represents zigzag uncertain variable

Table 2 The results of evaluating the efficiencies by the uncertain two-stage network DEA models

The efficiency of the whole stage is the chief observation object for decision makers, which enables them to understand the network system from a holistic perspective. As is shown in Table 2, we can observe the efficiencies ($c_{w}^{*}$) of the whole stage of five DMUs by the uncertain two-stage network DEA models. It can be clearly seen that the optimal value ($c_{w}^{*}$) of $\hbox {DMU}_{1}$ reaches 1.0000 which means that $\hbox {DMU}_{1}$ is efficient at the whole stage. By comparison, the efficiency ($c_{w}^{*}$) of the whole stage of the $\hbox {DMU}_{2}$ is 0.2549 which is lower than 1.0000 and considered to be inefficient at the whole stage. The analyses of the $\hbox {DMU}_{3}$, $\hbox {DMU}_{4}$ and $\hbox {DMU}_{5}$ can be shown in the same way.

After identifying the efficiency of the whole stage, the efficiencies of the internal sub-stages also need to be analyzed in order to find out the root causes of the inefficiency of the network system. As shown in Table 2, the efficiencies ($c_{1}^{*}$, $c_{2}^{*}$) of two sub-stages of $\hbox {DMU}_{1}$ are both 1.0000, which is the real reason why $\hbox {DMU}_{1}$ is efficient at the whole stage. That is because only when the efficiency of each sub-stage reaches 1.0000, the whole stage can be efficient as a whole. In other words, the efficiencies of the two sub-stages of $\hbox {DMU}_{1}$ can correspond to the relationship between the two sub-stages that the efficiency of the whole stage is equal to the product of the efficiencies of the two sub-stages. For decision makers, efficient $\hbox {DMU}_{1}$ can be viewed as a benchmark to further improve other inefficient DMUs.

Different from $\hbox {DMU}_{1}$, the efficiency ($c_{1}^{*}$) of the first stage of $\hbox {DMU}_{2}$ is 1.0000 while the efficiency ($c_{2}^{*}$) of the second stage is 0.2545. It is easy to draw the conclusion that the inefficiency of the whole stage of $\hbox {DMU}_{2}$ is due to the inefficiency of the second stage. Similarly, the efficiency ($c_{2}^{*}$) of the second stage of $\hbox {DMU}_{3}$ is 1.0000, whereas the efficiency ($c_{1}^{*}$) of the first stage is 0.1779, which can be regarded as the root cause of the inefficiency of $\hbox {DMU}_{3}$. Through the comparison of the above two DMUs, we can easily find out that $\hbox {DMU}_{2}$ and $\hbox {DMU}_{3}$ are similarly inefficient at the whole stage. But the reasons for the inefficiency are quite different, which are due to the different internal inefficient stages. Since the reasons for each DMU being inefficient are different, it is very important to be able to identify the inefficient sub-stages, which can prevent decision makers from allocating finite resources to efficient stages and neglecting inefficient stages.

By further observation, we can find out more things worthy of our attention from $\hbox {DMU}_{4}$ and $\hbox {DMU}_{5}$. The efficiency ($c_{1}^{*}$) of the first stage of $\hbox {DMU}_{4}$ is 0.1331 while the efficiency ($c_{2}^{*}$) of the second stage is 0.2545. The result for $\hbox {DMU}_{5}$ can be interpreted in a similar way. Different from $\hbox {DMU}_{2}$ and $\hbox {DMU}_{3}$, the $\hbox {DMU}_{4}$ and $\hbox {DMU}_{5}$ are not only inefficient at the whole stage, but also at all the sub-stages. It is a common situation faced by most policy makers. However, due to the limited resources, it is impossible for policy makers to invest resources in all the inefficient sub-stages to improve performance. Therefore, decision makers can firstly choose to improve the inefficient sub-stages with lower efficiency. This is because the inefficient sub-stage with lower efficiency is more likely to be improved when the same resources are invested. Moreover, a slight improvement in the relatively low efficiency of the sub-stage will result in a higher improvement of the overall performance. This fully demonstrates the importance of identifying efficiencies of sub-stages for decision makers.

5 Conclusions

In the research of the economics, the key element to improve the performance of network system is to identify the internal root causes of the inefficiency. Moreover, due to the novelty of evaluation indexes, the traditional DEA models cannot deal with the emerging indexes such as social welfare, which cannot be quantified accurately. Thus, based on uncertainty theory, this paper establishes the uncertain two-stage network DEA models, which have the most basic structure that can be extended to other more complex network models. The new models can accurately identify the root causes of the inefficiency of the network system and deal with the problem of inaccurate data in uncertain environments.

In addition to theoretical expansion, the models can also be used in empirical application. In reality, there are many systems with complex network structure, such as maritime supply chain. Generally speaking, the maritime supply chain consists of two sub-stages: ports and shipping companies. For decision makers, in addition to identifying the overall efficiency of the maritime supply chain, it is also important to explore its internal structure and hence identify the internal root causes of the inefficiency. By the uncertain two-stage network DEA models, decision makers can identify the inefficient supply chain members and make the right resource allocation decisions in uncertain environment.

In general, the contributions of this paper are as follows. Firstly, this article expands the application of uncertainty theory in the field of DEA. Secondly, this paper expands the evaluation method of unobservable variables and the scope of application of DEA models by establishing the uncertain two-stage network DEA models. Despite some theoretical and practical contributions, this research concentrates on only a simple two-stage network structure. In practice, the parallel structure is also common, especially for enterprises with multiple homogenous sub factories. Therefore, in the future, our research will focus on the efficiency evaluation of parallel structure systems with inaccurate data.