1 Introduction

The fractional-order chaotic systems are the special cases of nonlinear systems. The dynamical behavior of these systems is more complicated than regular nonlinear systems. These systems are highly sensitive to the initial conditions and also to the derivative orders. The chaotic systems exhibit a broadband, noise-like, and unpredictable dynamic behavior. Over the past decades, synchronization of the fractional-order chaotic systems has been one of the most interesting topics in science and engineering communities and many chaotic synchronization schemes have been introduced. For instance, in Li and Deng (2006) by using Laplace transform theory, two identical fractional chaotic systems are synchronized. The pole placement technique is proposed in Wu et al. (2009), to synchronize a class of fractional-order chaotic systems. An adaptive feedback control method is proposed in Odibat (2010) for the synchronization of two chaotic systems with different fractional orders. Projective synchronization of fractional-order chaotic systems is investigated in Liu et al. (2012). The fractional PID control scheme is proposed in Odibat (2012), and a nonlinear feedback control method is used in Jie et al. (2011).

Sliding mode control technique, because of its easy designing and robustness property, has been frequently employed for robust synchronization. For instance, the sliding mode control method is used in Ke et al. (2015). Additionally, the adaptive sliding mode control method Zhang and Yang 2013, the terminal sliding mode technique Dong-Feng et al. 2013, and the modified sliding mode scheme (Liu et al. 2014) are presented by different researchers. In all of the mentioned works it is assumed that no delay exists in the dynamics of the system. Also, the dynamics of the system are assumed to be known and only some parametric uncertainties and external disturbances are considered.

Time-delay systems are infinite dimensional in nature, and delay in model enriches its dynamics (Bhalekar and Daftardar-Gejji 2010). Time-delay differential equations are useful to describe many real-life phenomena such as metal cutting, traffic models, chemical kinetics, neuroscience, population dynamics, etc (Davis 2003). The effect of delay on the chaotic behavior of fractional-order Liu system and logistic time-delay system is studied in Bhalekar and Daftardar-Gejji (2010) and Wang and Yu (2008), respectively. Chaos behavior in fractional-order neural networks with varying time delays has been studied in Zhou et al. (2009), by using the Laplace transformation theorem and bifurcation graphs. In Lin and Lee (2011), an adaptive fuzzy sliding mode control is presented for synchronization of the fractional-order time-delay systems. In Tang et al. (2012), synchronization of the fractional- order time-delay Chen system is investigated based on the Laplace transformation theory. The stability of linear fractional differential equation with time delays is studied in Deng et al. (2007) by using the Laplace transform.

To deal with unknown functions in the dynamics of the system, some fuzzy controllers have been presented (Chen et al. 2016; Zhang et al. 2009). For instance, an adaptive fuzzy sliding mode control method is used in Lin et al. (2011), Li-Ming et al. (2014) and Luo and Liu (2014). Also, a fuzzy fractional integral sliding mode control is presented in Balasubramaniam et al. (2014). In Huang et al. (2014), a fractional-order chaotic system is described by T–S fuzzy model, and then, a fuzzy state feedback controller is designed. In Boulkroune et al. (2014), an adaptive fuzzy logic system is used for the estimation of unknown functions, and then, the projective synchronization problem for integer-order chaotic systems is solved.

In this paper, a robust nonlinear model-based predictive control (NMPC) is presented for synchronization of the fractional-order chaotic systems. It is based on a recurrent non-singleton type-2 fuzzy neural network (RNT2FNN). In the non-singleton fuzzification, the input uncertainties are considered.

Model-based predictive control (MPC) is an optimal control technique, which has been successfully applied to the control of many industrial processes. All aspects of MPC such as robustness, stability and its computational cost for linear systems have been extensively investigated in the literature (Li et al. 2015, 2016). Since many processes and industrial systems are nonlinear and could not be adequately described by linear models, NMPC methods need to be developed. Some NMPC techniques have been presented in Pan and Wang (2012), Schlipf et al. (2013) and Heidarinejad et al. (2012). A key issue in NMPC problem is that the effectiveness of NMPC depends on the model accuracy.

The main advantages of this present study are summarized as follows:

  • The dynamics of the system are assumed to be unknown; then, the proposed controller can be used in many applications. To show this property, in addition to the synchronization problem, the proposed controller is applied to the high-performance position control of a hydraulic actuator with unknown dynamics.

  • In addition to uncertain dynamics, time delays are also considered in some states of the system. It is shown that the time delays do not affect the performance of the controller.

  • A robust NMPC control method is presented. The performance of NMPC strongly depends on the model accuracy. In many real-world applications, the models are not known very well, or the accuracy of the available model is decreased as time proceeds, by some factors such as imperfections of physical devices, external disturbances, time-varying parameters. In this paper, the dynamics of the system are online estimated by the proposed RNT2FNN.

  • The robustness of the synchronization is investigated in terms of the effect of the approximation errors and the external disturbances.

To deal with the mentioned problems, in this study, it is assumed that the dynamics of the system are unknown and are perturbed by the external disturbances and also there is the unknown time-delay in the states of the system. In the proposed control scheme, the tracking error is modeled in an online fashion by the proposed RNT2FNN, and then, based on this model, a nonlinear model-based predictive controller is designed. Furthermore, a compensator eliminates the effect of approximation error and the asymptotic stability is derived based on Lyapunov stability analysis theorem.

The remainder of this paper is organized as follows: Problem formulation and preliminaries are given in Sect. 2. The proposed recurrent non-singleton type-2 fuzzy neural network is presented in Sect. 3. Nonlinear model-based predictive controller is designed in Sect. 4. Stability analysis is given in Sect. 5. Simulation results are given in Sect. 6, and the main results obtained are summarized and concluded in Sect. 7.

Fig. 1
figure 1

The proposed control block diagram

Full size image

2 Problem formulation and preliminaries

\(\mathbf {Definition \ 1}\): Let f be a continuous function on \(\mathbb {R^{+}}\) and \(q > 0\), then the fractional-order integral and derivative in the sense of Caputo are defined as follows, respectively:

$$\begin{aligned} I^q f(t)= & {} \frac{1}{{\Gamma (q)}}{\int _0^t {\left( {t - \tau } \right) } ^{q - 1}}f(\tau )\mathrm{d}\tau \end{aligned}$$
(1)
$$\begin{aligned} D_t^q f(t)= & {} \frac{1}{{\Gamma (m - q)}}\int _0^t {\frac{{{f^m} (\tau )}}{{{{(t - \tau )}^{q - m + 1}}}}\mathrm{d}\tau } \end{aligned}$$
(2)

where \(\Gamma ( \cdot )\) is Gamma function, m is an integer so that \(m - 1< q < m\).

The following class of fractional-order time-delay chaotic system is considered as the master system:

(3)

where \(0< \mathrm{{ }}q\mathrm{{ }} < 1\) is the fractional derivative order, is unknown, but bounded function, \({y_i} \in R,\,\,\,i = 1,2,\ldots ,n\) are the states of master system and are the previous states of the master system.

The slave system is considered as:

(4)

where is unknown, but bounded function, d(t) is the bounded external disturbance, u(t) is control signal, \({x_i} \in R,\,\,\,i = 1,2,\ldots ,n\) are the outputs of the slave system.

The control objective is to design nonlinear controller u(t), such that the slave system tracks the master system.

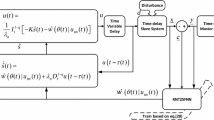
The proposed control block diagram is shown in Fig. 1. As it can be seen, in (4) is estimated by RNT2FNN.

Tracking error vector is defined as:

(5)

where \(e = {x_1} - {y_1}\), and .

Fig. 2
figure 2

Proposed NST2FNN structure

Full size image

The proposed control signal is as:

(6)

where is determined such that the stability condition \(\left| {\arg (eig(A))} \right| > q\pi /2,\,\,\,\,0< q < 1\) is satisfied, eig(A) is the eigenvalues of matrix A, which is given in (8), \({\hat{f}}\) is the output of RNT2FNN which estimates in (4), \({u_p}\) is a nonlinear predictive control signal, and \({u_c}\) is an adaptive compensator which is used to attenuate the approximation error. By substituting (6) into (4), the tracking error dynamic is obtained as follows:

(7)

where

$$\begin{aligned} A = \left[ {\begin{array}{ccccccc} 0&{}1&{}0&{}0&{} \cdots &{}0&{}0\\ 0&{}0&{}1&{}0&{} \cdots &{}0&{}0\\ \cdots &{} \cdots &{} \cdots &{} \cdots &{} \cdots &{} \cdots &{} \cdots \\ 0&{}0&{}0&{}0&{} \cdots &{}0&{}1\\ { - {k_1}}&{}{ - {k_2}}&{}{ - {k_3}}&{}{ - {k_4}}&{} \cdots &{}{ - {k_{n - 1}}}&{}{ - {k_n}} \end{array}} \right] ,\,\,\,b = \left[ {\begin{array}{c} 0\\ 0\\ \vdots \\ 0\\ 1 \end{array}} \right] \end{aligned}$$
(8)

We assume that the tracking error can be modeled by an RNT2FNN as follows:

$$\begin{aligned} {\hat{e(t)}} = \psi \left[ {e(t - {\tau _1}),\ldots ,e(t - {\tau _r}),{u_c}(t - 1 ),{u_p}(t - 1)} \right] \end{aligned}$$
(9)

where \({\hat{e(t)}}\) is the estimation of tracking error e(t), \(\psi \) is an RNT2FNN, \({u_c}(t - 1 )\) and \({u_p}(t - 1 )\) are the compensator and predictive control signal in previous sample times. \(e(t - {\tau _i}),i = 1,\ldots ,r\), are tracking errors in previous times \(t - {\tau _i},i = 1,\ldots ,r\). Based on this model, a nonlinear model-based predictive controller (NMPC) is designed.

Fig. 3
figure 3

Non-singleton fuzzification by using product inference

Full size image

3 Proposed recurrent non-singleton type-2 fuzzy neural network

In this section, a recurrent non-singleton type-2 fuzzy neural network is presented. The proposed structure is shown in Fig. 2.

As we know, the non-singleton fuzzifier works better in contrast to its singleton counterpart in the presence of noise and disturbance. Since the inputs of RNT2FNN are assumed to be corrupted by external disturbances, a non-singleton fuzzifier is used to handle the uncertainty. The layers of the proposed RNT2FNN are explained as follows:

\(Input \, Layer\): The inputs of RNT2FNN are the states of the slave system, which are corrupted by external disturbance.

\(Fuzzification \, Layer\): In this layer, the uncertainty of inputs is modeled by the type-2 membership functions (MFs). Let \({{{\tilde{B}}}_{{x_i}}}\) be the type-2 MF for ith input (\({x_i}\)). \({{{\tilde{B}}}_{{x_i}}}\) is considered as Gaussian membership function with mean \({x_i}\) and standard deviation , the upper and lower memberships of this MF are, respectively, computed as follows:

(10)

Larger values of \({{\bar{\sigma }} _{{x_i}}}\,\) and represent the more uncertainties in the ith input.

Consider ith input \(x_i\), to compute the upper and lower membership of jth MF for this input (\({\tilde{A}}_i^j\) see Fig. 3), \(x_i\) is transformed to \({\bar{x}}_i^j\) and , by the non-singleton fuzzifier, respectively.

Then by using product inference, for \({\bar{x}}_i^j\) and , we have (Castro et al. 2008):

(11)

where \(m_i^j\) is the center of jth MF for ith input (\({\tilde{A}}_i^j\)), \({\bar{\sigma }} \,_i^{\,j}\) and are the upper and lower widths of jth MF for ith input, respectively. \({\bar{\sigma }} _{x_i}\) and are the upper and lower widths of type-2 MF for input \({x_i}\) in the fuzzification layer (\({{\tilde{B}}}_{{x_i}}\)) (see Fig. 3).

\(Membership \ Layer\): In this layer, the upper and lower memberships of MFs are obtained as below:

(12)

where \({\tilde{A}}_i^j\) is the j-th type-2 MF for the i-th input in the membership layer, \({{{\bar{\mu }} }_{{\tilde{A}}_i^j}}\left( {{x_i}(t)} \right) \) and are the upper and lower memberships of jth MF for ith input at time t, \({\bar{\lambda }} _{\,i}^j\) and are the recurrent weights. \({\bar{x}}_i^j\) and are generated in fuzzification layer.

\(Rule \, Layer\): Each node in this layer represents a fuzzy rule which computes the upper and lower firing degrees. Each rule has the following form:

$$\begin{aligned} {R^l}:\,\,If\,{x_1}\,\,is\,\,{\tilde{A}}_1^{{p_1}}\,\,\,\text {and}\,\, \cdots \,\,\text {and}\,\,{x_n}\,\,is\,\,{\tilde{A}}_n^{{p_n}}\,\,\,\text {Then}\,\,\,{\hat{f}}\,\,is\,\,\,{w^l} \end{aligned}$$
(13)

where \({\tilde{A}}_i^{{p_i}}\) is the \({p_i} - th\) type-2 MF, for ith input, and \({w^l}\) is the consequent parameter in \(l-th\) rule. The upper and lower firing degrees of \(l-th\) rule are computed as follows:

(14)

in which \({\bar{Z}}_{}^l\) and are the upper and lower firing degrees of \(l-th\) rule, respectively. \({{{{\bar{\mu }} }_{{\tilde{A}}_k^{{p_k}}}}}\) and are the upper and lower memberships of \({p_k} - th\) MF for \(k-th\) input, respectively. n is the number of inputs.

\(Type-reduction \,Layer\): To decrease the number of free parameters, a simple type-reduction is applied as follows (Nie and Tan 2008):

(15)

in which \(w^l\) is the consequent parameter for \(l-th\) rule. \({\bar{Z}}^l\) and are the upper and lower firing degrees of \(l-th\) rule, respectively. M is the number of total rules. If the number of MFs for each input is N, then M is \(M=N^n\).

\(Output \, Layer\): In this layer, the defuzzified crisp output \(\left( {\hat{f}} \right) \) is computed as follows:

(16)

Equation (16) can be written as follows:

(17)

4 The proposed nonlinear model-based predictive control method

In this section, an improved nonlinear type-2 fuzzy model-based predictive control method is presented. The problem is as follows:

$$\begin{aligned} \begin{array}{l} \mathop {\min }\limits _{{u_p}(k),\ldots ,{u_p}(k + Nc)} \,\,J = \sum \limits _{k = t}^{t + Np} {\,\,\,{\hat{e}}{{(k)}^T} Q{\hat{e}}(k) + \delta {u_p}{{(k)}^T}R\,\,\delta {u_p}(k)} \\ subject\,\,\,to\\ {\hat{e(t)}} = \psi \left[ {e(t - {\tau _1}),\ldots ,e(t - {\tau _r}),{u_c}(t - 1),{u_p}(t - 1)} \right] \end{array} \end{aligned}$$
(18)

where \(e(t - {\tau _i}),\,i = 1,\ldots ,r\) are the tracking errors at times \((t - {\tau _i})\), \({u_p}\) is predictive control signal, \({u_c}\) is a compensator which is designed in the next section, \(\delta u_p(t) = u_p(t) - u_p(t - 1)\), Q and R are positive definite matrices, \({N_p}\) and \({N_c}\), are prediction and control horizon and \(\psi \) is a RNT2FNN which estimates the tracking error e(t).

The consequent parameters of \( \psi \bigl [e(t - {\tau _1}),\ldots ,e(t - {\tau _r}), {u_c}(t - 1),{u_p}(t - 1)\bigr ] \) are tuned based on the recursive least square algorithm as follows:

(19)

where is the consequent parameters of \(\psi \) (see (18)) at time t (it must be noted that, similar to (17), \(\psi \) can be written as vector form ), \({e_{est}}(t)\) is the estimation error \({e_{est}}(t) = e(t) -{\hat{e(t)}}\), and p(t) and \(\varphi (t)\) are as follows:

(20)

The future k-step output of the estimated tracking error can be predicted by:

$$\begin{aligned} {\hat{e}}(t + k|t) = {{\hat{e}}_\mathrm{forced}}(t + k|t) + {{\hat{e}}_\mathrm{free}}(t + k|t) \end{aligned}$$
(21)

where \({{\hat{e}}_\mathrm{free}}(t + k|t)\) depends on the past inputs and outputs, and \({{\hat{e}}_\mathrm{forced}}(t + k|t)\) depends on the future inputs. \({{\hat{e}}_\mathrm{free}}(t + k|t)\) is computed as:

$$\begin{aligned} {{\hat{e}}_\mathrm{free}}(t + k|t)= & {} \psi \left[ e(t + k - {\tau _1}),\ldots ,e(t + k - {\tau _r}), \right. \nonumber \\&\left. {u_c}(t - 1 + k),{u_p}(t - 1 + k) \right] \end{aligned}$$
(22)

The values of the controllers \({u_p}\) and \({u_c}\) at future times are considered to be constant and equal to the last input \({u_p}(t - 1)\) and \({u_c}(t - 1)\). The force response term \({{\hat{e}}_\mathrm{forced}}(t + k|t)\) can be calculated by:

$$\begin{aligned} {{\hat{e}}_\mathrm{forced}}(t + k|t) = \sum \limits _{i = 0}^{k - 1} {{\vartheta _i}\,\delta {u_p}(t + k - i + 1|t)} \end{aligned}$$
(23)

where \(\vartheta _i, i=0,\ldots ,k-1\) are the step response coefficients which are computed by applying unit step on RNT2FNN model (\(\psi \)). Step response can be estimated as follows (Oviedo et al. 2006):

$$\begin{aligned} g(t - 1) = \frac{{{{\hat{e}}_\mathrm{step}}(t + k|t) - {{\hat{e}}_\mathrm{free}}(t + k|t)}}{{d{u_p}(t)}} \end{aligned}$$
(24)

where \(d{u_p}(t)\) is the step size and \({{\hat{e}}_\mathrm{step}}(t + k|t)\) is:

$$\begin{aligned} \begin{aligned} {{\hat{e}}_\mathrm{step}}(t + k|t)&= \psi \left[ e(t + k - {\tau _1}),\ldots ,e(t + k - {\tau _r}),\right. \\&\quad \left. {u_c}(t - 1 + k),{u_p}(t - 1 + k) \right] \\ {u_p}(t)&= \left\{ \begin{array}{l} {u_p}(t - 1) + d{u_p}(t) \,\, \forall \,\, k > t - 1 \\ {u_p}(t) \qquad \text {otherwise} \end{array}\right. \end{aligned} \end{aligned}$$
(25)

In the matrix form, the optimization problem can be written as:

$$\begin{aligned} E = G\Delta {U_p} + {E_\mathrm{free}} \end{aligned}$$
(26)

in which

$$\begin{aligned}&E = \left[ {\begin{array}{c} {{\hat{e}}(t + 1|t)}\\ {{\hat{e}}(t + 2|t)}\\ \vdots \\ {{\hat{e}}(t + Np|t)} \end{array}} \right] \,,\,\,G = \left[ {\begin{array}{cccc} {{g_0}}&{}0&{} \cdots &{}0\\ {{g_1}}&{}{{g_0}}&{} \cdots &{}0\\ \vdots &{} \vdots &{} \ddots &{} \vdots \\ {{g_{Np}} - 1}&{}{{g_{Np}} - 1}&{} \cdots &{}{{g_0}} \end{array}} \right] \end{aligned}$$
(27)
$$\begin{aligned}&\Delta {U_p} = \left[ {\begin{array}{c} {\delta u(t|t)}\\ {\delta u(t + 1|t)}\\ \vdots \\ {\delta u(t + Np - 1|t)} \end{array}} \right] ,\,\,{E_\mathrm{free}} = \left[ {\begin{array}{c} {{{\hat{e}}_\mathrm{free}}(t + 1|t)}\\ {{{\hat{e}}_\mathrm{free}}(t + 2|t)}\\ \vdots \\ {{{\hat{e}}_\mathrm{free}}(t + Np|t)} \end{array}} \right] \end{aligned}$$
(28)
$$\begin{aligned}&\begin{array}{l} \begin{array}{c} {{\hat{e}}_\mathrm{free}}(t + k|t) = \\ \psi \left[ {e(t + k - {\tau _1}),\ldots ,e(t + k - {\tau _r}),{u_c}(t - 1 + k),{u_p}(t - 1 + k)} \right] \end{array}\\ {{u_p}(t) = \left\{ {\begin{array}{c} {{u_p}(t - 1) \,\, \forall \,\, k > t - 1}\\ {{u_p}(t) \quad \text {otherwise}} \end{array}} \right. } \end{array}\nonumber \\ \end{aligned}$$
(29)

The cost function defined in (18) can be written as follows:

$$\begin{aligned} \begin{array}{l} J = {E^T}QE + \Delta U_p^TR\Delta {U_p}\\ = {\left( {G\Delta {U_p} + {E_\mathrm{free}}} \right) ^T}Q\left( {G\Delta {U_p} + {E_\mathrm{free}}} \right) + \Delta U_p^TR\Delta {U_p} \end{array} \end{aligned}$$
(30)

By making the gradient of J in (30) equal to zero, we have:

$$\begin{aligned} \frac{{\partial J}}{{\partial \Delta {U_p}}} = 2{G^T}Q{E_\mathrm{free}} + 2\left( {{G^T}QG + R} \right) \Delta {U_p} = 0 \end{aligned}$$
(31)

Then, \(\Delta {U_p}\) is obtained as:

$$\begin{aligned} \Delta {U_p} = {\left( {{G^T}QG + R} \right) ^{ - 1}}{G^T}Q{E_\mathrm{free}} \end{aligned}$$
(32)

The control signal which is applied to plant is

$$\begin{aligned} {u_p}(t) = {u_p}(t - 1) + \delta {u_p}(t) \end{aligned}$$
(33)

where \(\delta {u_p}(t)\) is the first element of \(\Delta {U_p}\) in (32).

Remark 1

\(d{u_p}(t)\) in (24) can be considered as the second element of \(\Delta {U_p}(t - 1)\). When the system reached to steady state, \(\Delta {U_p}(t - 1) \rightarrow 0\) then (24) is badly conditioned; to cope with this problem \(d{u_p}(t)\) is determined as follows:

$$\begin{aligned} \begin{array}{l} if\,\,\Delta {U_p}(t - 1)\, \le d{u_{\min }}\\ \,\,d{u_p}(t) = d{u_{\min }}\\ else\\ d{u_p}(t) = \Delta {U_p}(t - 1)\, \end{array} \end{aligned}$$
(34)

Remark 2

An upper bound is considered for the predictive control signal \({u_p}\) as follows:

$$\begin{aligned} \begin{array}{*{20}{l}} {if {u_p} \ge Ma{x_{{u_p}}}}\\ { {u_p} = Ma{x_{{u_p}}}} \end{array} \end{aligned}$$
(35)

where \(Ma{x_{{u_p}}}\) is the maximum value of \({u_p}\).

5 Stability analysis

In this section, an adaptive compensator is designed to eliminate the effect of the approximation error on the stability of the closed-loop system. Let us consider the following Lyapunov function candidate:

(36)

where and is the vector of consequent parameters of \({\hat{f}}\) (see (17)). is the optimal value of . \(\gamma \) is the adaptation rate. is the vector of tracking error (see (5)). P is a symmetric positive matrix which satisfies the following Lyapunov equation:

$$\begin{aligned} {A^T}P + PA = - \,H \end{aligned}$$
(37)

where A has been defined in (8) and H is an arbitrary positive definite matrix.

The following theorem gives the necessary condition to derive the asymptotic stability.

Theorem 1

(Chen et al. 2014): Consider the system . If there exists a positive definite Lyapunov function V(x) such that \({D^q}V < 0\), then the trivial solution of system is asymptotically stable.

Based on Theorem 1, and by using (7), the fractional time derivative of V is:

(38)

By using (37), and adding and subtracting \({{\hat{f}}^ * }\) (an RNT2FNN with optimal parameters ) into (38), and some simplification we have:

(39)

From (39), the adaptation law for is obtained as follows:

(40)

We define the approximation error as follows:

$$\begin{aligned} \varepsilon = \left[ {f + d - {{{\hat{f}}}^ * }} \right] \end{aligned}$$
(41)

By considering relations (37), (40) and (41), \({D^q}V\) becomes:

(42)

From (35) and (42), we have:

(43)

By considering (43), \({u_c}\) is proposed as follows:

(44)

where \(Ma{x_{\left| \varepsilon \right| }}\) is the maximum value of approximation error \(\left| \varepsilon \right| \). By considering and substituting (44) into (43), we attain:

(45)

Then asymptotic stability is derived.

6 Simulation

In this section, several examples are presented that verify the effectiveness of the proposed method for the synchronization of fractional-order time-delay chaotic systems.

Example 1

In this example, the proposed controller is applied to synchronize two different uncertain fractional-order Duffing–Holmes time-delay chaotic systems. The master system is given as follows (Lin and Lee 2011):

$$\begin{aligned} \left\{ \begin{array}{l} {D^q}{y_1} = {y_2}\\ {D^q}{y_2} = - \frac{1}{{{{2.5}^2}}}y_1^3 - {y_1} - 0.1{y_2} + 0.025{y_1}\left( {t - \tau } \right) \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, + 0.025y_1^2\left( {t - \tau } \right) + 0.01{y_2}\left( {t - \tau } \right) + 62.5\cos (1.29t) \end{array} \right. \end{aligned}$$
(46)

The slave system is given as follows:

$$\begin{aligned} \left\{ \begin{array}{l} {D^q}{x_1} = {x_2}\\ {D^q}{x_2} = - \frac{{2.2}}{{{{2.5}^2}}}x_1^3 - \frac{{2.2}}{{1.8}}{x_1} - 0.1{x_2} + 0.022{x_1}\left( {t - \tau } \right) \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, + 0.022x_1^2\left( {t - \tau } \right) + 0.01{x_2}\left( {t - \tau } \right) \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, + 55\cos (1.29t) + d(t) + u(t) \end{array} \right. \end{aligned}$$
(47)

where \(\tau = 0.001\), \(d(t) = 0.7\sin (t)\) is the external disturbance and u(t) is the control input. The initial conditions are \({y_1}(0) = 0\), \({y_2}(0) = 0\), \({x_1}(0) = 1\) and \({x_2}(0) = - 1\). The fractional derivative order is \(q = 0.98\). The simulation sample time is 0.001. To apply the proposed controller, the dynamic of the slave system in (47) is rewritten as follows:

$$\begin{aligned} \left\{ \begin{array}{l} {D^q}{x_1} = {x_2}\\ {D^q}{x_2} = f + u \end{array} \right. \end{aligned}$$
(48)

We assume that f in (48) is unknown and is estimated by the proposed RNT2FNN \(\left( {{\hat{f}}} \right) \). We consider three MFs for each input of RNT2FNN with centers \(m = \left[ {10,0,\,10} \right] \) and width \( \sigma \in \left[ {5,\,10} \right] \). In the non-singleton fuzzification for each input \({x_i}\), a type-2 MF with center \(m = {x_i}\) and width \({\sigma _x} \in \left[ {0.01,\,0.1} \right] \) is considered. The controller is designed as follows:

(49)

where . By considering \(Ma{x_{{u_p}}} = 10\) and \(Ma{x_{\left| \varepsilon \right| }} = 1\), \({u_c}\) designed as follows:

(50)

where \(b = {\left[ {0\,\,\,1} \right] ^T}\) and P are obtained from solving (37). To design the predictive control signal \({u_p}\), the following cost function is considered (see (18))

$$\begin{aligned} \begin{array}{l} \mathop {\min }\limits _{{u_p}(k),\ldots ,{u_p}(k + 10)} \,\,J = \sum \limits _{t = k}^{k + 10} {\,\,\,{\hat{e}}{{(t)}^2} + \delta {u_p}{{(t)}^2}} \\ subject\,\,\,to\\ {\hat{e(t)}} = \psi \left[ {e(t - 1),e(t - 2),{u_c}(t - 1),{u_p}(t - 1)} \right] \end{array} \end{aligned}$$
(51)

The consequent parameters of \(\psi \) in (51) are tuned based on the recursive least square algorithm. The initial value of p(t) in (19) is considered as \(p = 100eye(16)\), where eye(16) is a unit matrix with dimension \(16 \times 16\). We considered two MFs for each input of \(\psi \) in (51). Then the number of consequent parameters in \(\psi \) is 16.

The synchronization performance and the tracking error are shown in Figs. 4 and 5, respectively. The control signal is given in Fig. 6. As it can be seen, the proposed controller gives high performance in the synchronization of two uncertain time-delay fractional-order chaotic systems. To show the effectiveness of the proposed controller, another reference signal as a square pulse is considered for slave system. The tracking performance with tracking error is shown in Fig. 7. As it can be seen, the output of the slave system tracks the square pulse, well.

The results of our method are compared with the results of Lin and Lee (2011) in Fig. 8. In Lin and Lee (2011), the fractional sliding mode technique has been applied for the synchronization of master and slave systems in Example 1. The mean square errors (MSEs) of \(e_1=y_1-x_1\) and \(e_2=y_2-x_2\) for different methods are compared in Table 1. As it can be seen from Fig. 8 and Table 1, the proposed method in this paper gives better results in contrast to proposed sliding mode technique in Lin and Lee (2011). Also it can be seen that using of RNT2FNN is more effective than using of recurrent non-singleton type-1 fuzzy neural network (RNT1FNN). It must be noted that, because of using the simple Nie–Tan type-reduction (Nie and Tan 2008), the complexity of the proposed type-2 fuzzy system is not much more than type-1 fuzzy system.

Fig. 4
figure 4

Synchronization performance in Example 1

Full size image
Fig. 5
figure 5

Tracking error, Example 1

Full size image
Fig. 6
figure 6

Control signal in Example 1, the synchronization case

Full size image
Fig. 7
figure 7

Tracking performance of square pulse, Example 1

Full size image
Fig. 8
figure 8

Comparison of synchronization performance in Example 1, a the result of fractional sliding mode technique (Lin and Lee 2011) b the result of proposed method in this paper

Full size image

Example 2

In this example, the proposed controller is used for synchronization of two nonidentical fractional-order time-delay chaotic systems. The master system is given as follows (Wang et al. 2014):

$$\begin{aligned} \left\{ {\begin{array}{*{20}{l}} {{D^q}{y_1}(t) = {y_3}(t) - 3{y_1}(t) + {y_1}(t){y_2}(t - \tau ) + d_1^m(t)}\\ {{D^q}{y_2}(t) = 1 - 0.1{y_2}(t) - y_1^2(t - \tau ) + d_2^m(t)}\\ {{D^q}{y_3}(t) = - {y_1}(t - \tau ) - {y_3}(t) + d_3^m(t)} \end{array}} \right. \end{aligned}$$
(52)

where \(q = 0.92\), \(\tau = 0.01\), \(d_i^m(t),i = 1,2,3\) are the external disturbances which are taken to be as \(d_1^m(t) = 0.1\cos (10t)\), \(d_2^m(t) = 0.2\cos (20t)\) and \(d_3^m(t) = 0.1\sin (10t)\); the initial conditions are \({y_1}(0) = 0.1\) , \({y_2}(0) = 4\) and \({y_3}(0) = 0.5\). The slave system is Liu fractional-order time-delay chaotic system, the dynamics of which are as follows (Wang et al. 2014):

$$\begin{aligned} \left\{ {\begin{array}{*{20}{l}} {{D^q}{x_1}(t) = 10\left( {{x_2}(t) - {x_1}(t)} \right) + d_1^s(t) + {u_1}(t)}\\ {{D^q}{x_2}(t) = 40{x_1}(t - \tau ) - {x_1}(t){x_3}(t) + d_2^s(t) + {u_2}(t)}\\ {{D^q}{x_3}(t) = - 2.5{x_3}(t - \tau ) + 4x_1^2(t) + d_3^s(t) + {u_3}(t)} \end{array}} \right. \end{aligned}$$
(53)

where \(q = 0.92\), \(\tau = 0.01\), \(d_i^s(t),i = 1,2,3\) are external disturbances which are taken to be as \(d_1^s(t) = 0.1\sin (20t)\), \(d_2^s(t) = - 0.3\sin (10t)\) and \(d_3^s(t) = - 0.5\cos (10t)\); the initial conditions are \({x_1}(0) = 1.2\) , \({x_2}(0) = 2.4\) and \({x_3}(0) = 11\). The controller design procedure is the same as Example 1.

The synchronization performance and the control signals are shown in Figs. 9 and 10, respectively. As can be seen, the proposed controller is able to synchronize the two nonidentical fractional-order time-delay chaotic systems effectively.

Simulation studies are carried out on the same example using the hybrid projective synchronization method described in Wang et al. (2014), and the synchronization errors of Wang et al. (2014) and the approach described in this paper are given in Figs. 11 and 12, respectively. It can be seen that proposed controller results in a good performance in the presence of the external disturbances and the unknown functions in the dynamics of the system.

Table 1 Comparison the values of MSE for different methods, Example 1
Full size table
Fig. 9
figure 9

Synchronization performance in Example 2

Full size image
Fig. 10
figure 10

Control signals in Example 2, the synchronization case

Full size image
Fig. 11
figure 11

Results of hybrid projective synchronization method (Wang et al. 2014), Example 2

Full size image
Fig. 12
figure 12

Tracking error, Example 2

Full size image

Example 3

As has been stated earlier, the nonlinear model of the system is estimated by the proposed RNT2FNN online. This enables the application of the proposed control scenario to a wide class of nonlinear systems. To shows this property, we employ the proposed method for the position control of a high-performance hydrostatic actuation system as shown in Fig. 13.

Fig. 13
figure 13

Hydrostatic actuation system, Example 3

Full size image
Fig. 14
figure 14

Mechanical nonlinear model of the hydrostatic actuation system, Example 3

Full size image
Fig. 15
figure 15

Tracking performance of hydrostatic actuation system, Example 3

Full size image
Fig. 16
figure 16

Tracking performance of hydrostatic actuation system with varying amplitudes in reference input signal, Example 3

Full size image
Table 2 Comparison of delay effect on the synchronization performance (see Remark 3)
Full size table

The proposed controller is applied to the mechanical nonlinear model of the system which is shown in Fig. 14.

We assume that the position output of the system is as follows:

$$\begin{aligned} {D^q}{x_\mathrm{Actuator\,position}}= & {} f\left( {{x_\mathrm{Actuator\,position}},{x_\mathrm{Actuator\,speed}}} \right) \nonumber \\&+ K{u_\mathrm{Motor\,voltage}} \end{aligned}$$
(54)

where \({x_\mathrm{Actuator\,position}}\), \({x_\mathrm{Actuator\,speed}}\) and \({u_\mathrm{Motor\,\,voltage}}\) are the actuator position, actuator speed and motor voltage, respectively. f is an unknown function, K is a constant and q is considered to be 0.98.

The controller design procedure is the same as Example 1. We have

$$\begin{aligned} u = - {\hat{f}} - 1000e + {D^q}r + {u_c} + {u_p} \end{aligned}$$
(55)

where \({\hat{f}}\) is the output of RNT2FNN, r is the reference signal, \({u_c} = - 100\tanh \left( {e/10} \right) \) and \({u_p}\) is designed as in Example 1 (see (51)). The tracking performances of the two reference signals are shown in Figs. 15 and 16. It can be seen that the proposed control strategy shows high performance and it can easily be used in practical problems.

Remark 3

To show the effect of the time delay on the synchronization performance, the simulation studies of Examples 1 and 2 are repeated for different delays. The results are given in Table 2, in which \(t_s=0.001\) is sampling time and \(\tau = \kappa {t_s}\). As it can be seen, the effect of the time delay on the synchronization performance is significantly eliminated by the proposed control scheme.

7 Conclusion

In this paper, synchronization of the fractional-order time-delay chaotic systems is considered. A recurrent non-singleton type-2 fuzzy neural network (RNST2FNN) is used for the estimation of the unknown functions in the dynamics of the slave system. A nonlinear model-based predictive controller is designed to minimize the tracking error. The asymptotic stability analysis is done by the use of the Lyapunov stability theorem. Two examples are presented for the synchronization of the fractional-order time-delay chaotic systems, and a further example is given that involves the position control of a high-performance hydraulic actuator. Simulation results presented indicate that the proposed control method gives good performance in the presence of external disturbances, time-delay, and unknown functions in the dynamic of the system. As application prospects of this research, the proposed control strategy can be applied to a wide class of nonlinear systems. Also, it must be noted that the robust synchronization of the chaotic systems has potential applications in many branches of science and engineering such as secure communications, information processing, biological systems.